An Electro-Thermal Actuation Method for Resonance Vibration of a Miniaturized Optical-Fiber Scanner for Future Scanning Fiber Endoscope Design
Abstract
1. Introduction
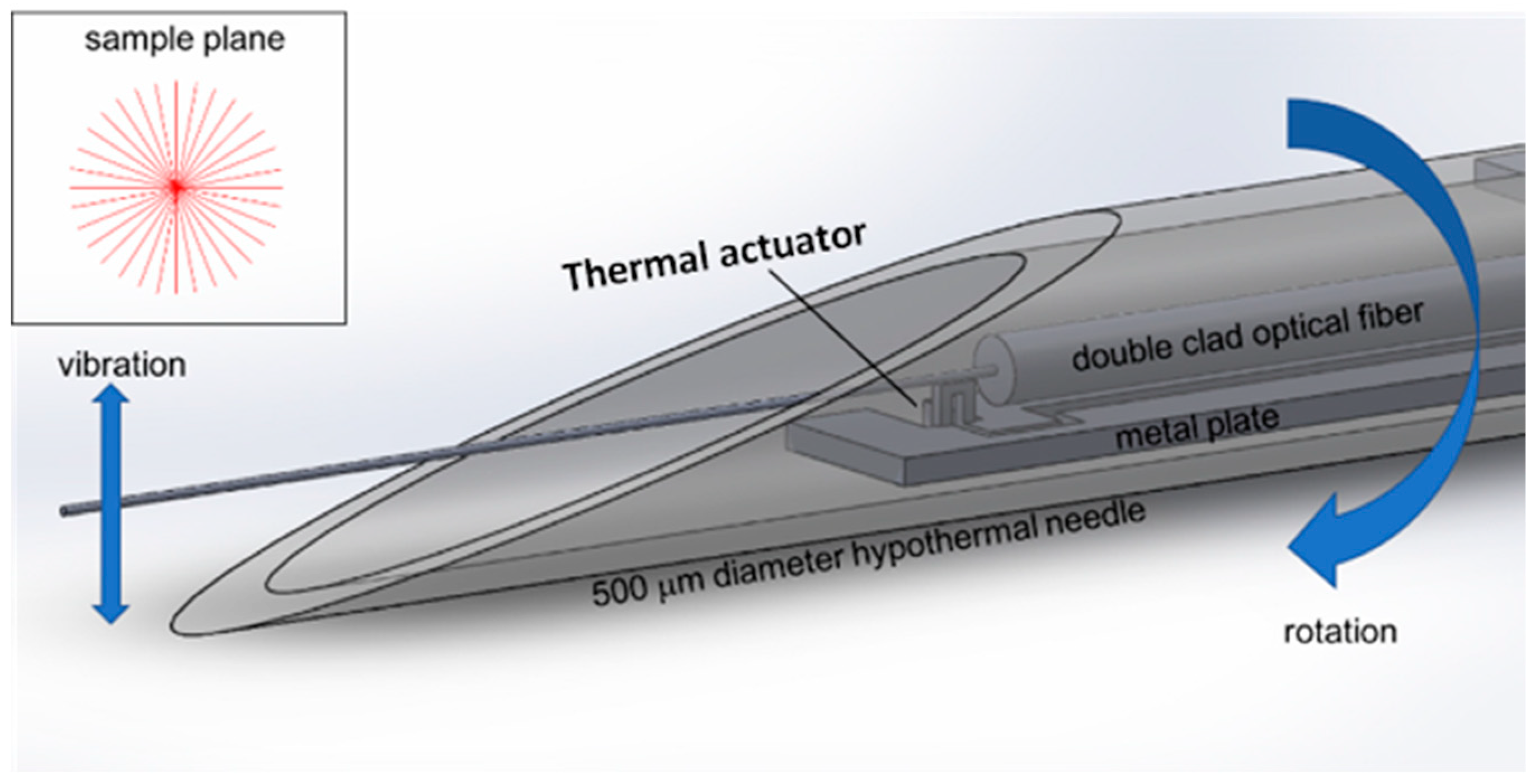
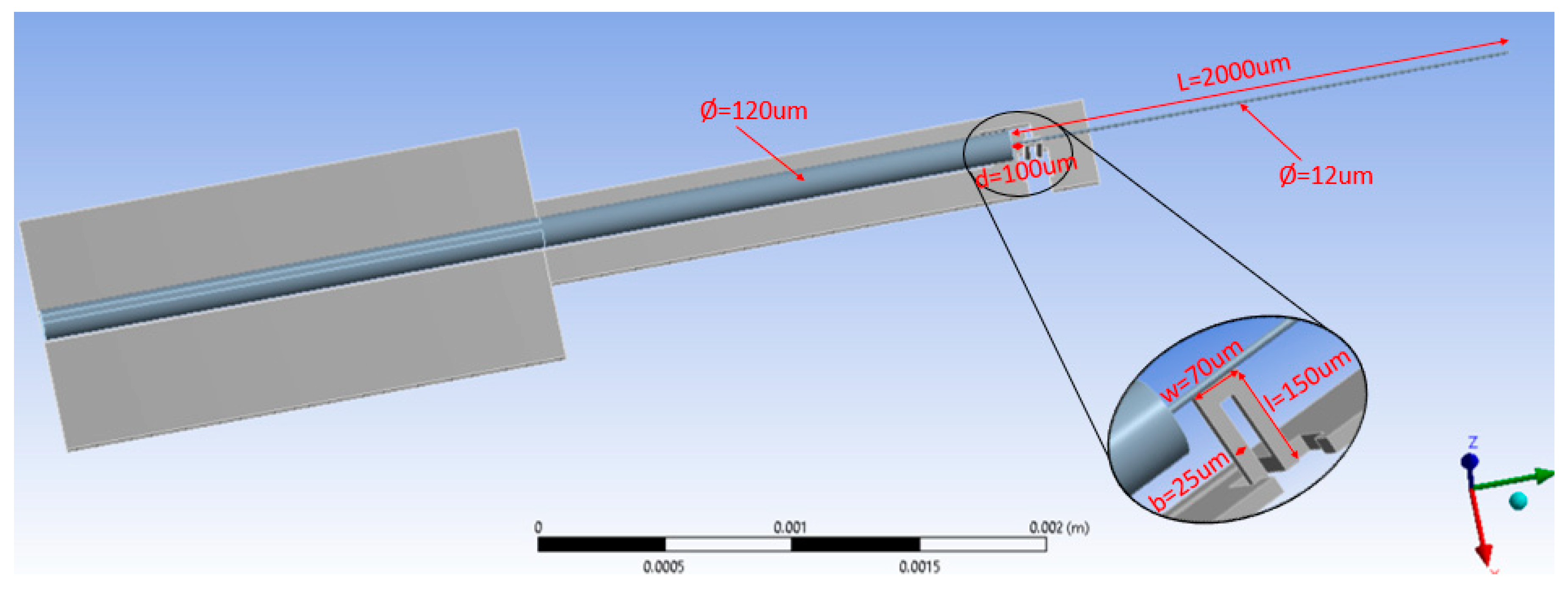
2. Actuator Design and Fabrication Process
2.1. Material Selection
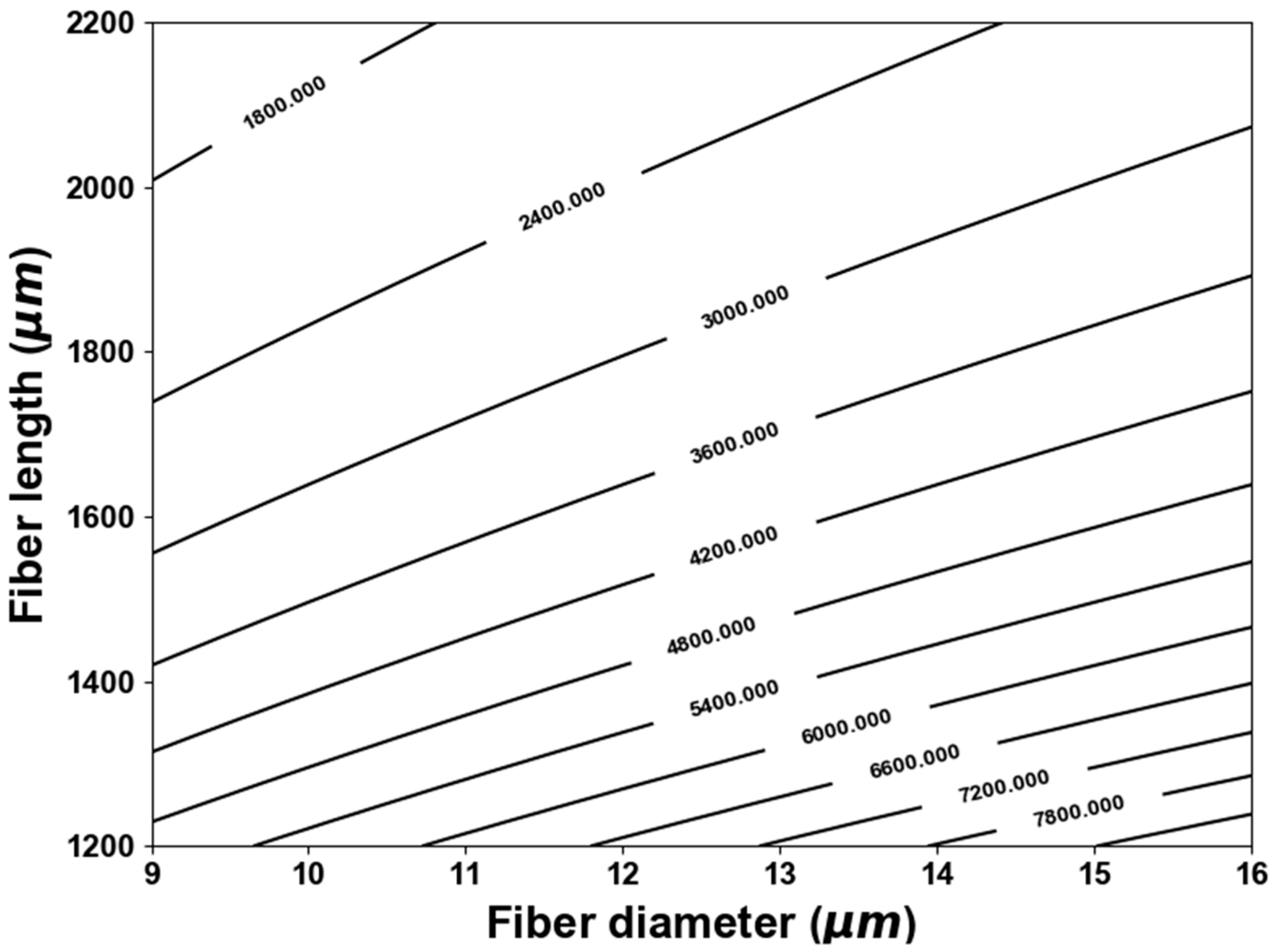
2.2. Resonance Frequency
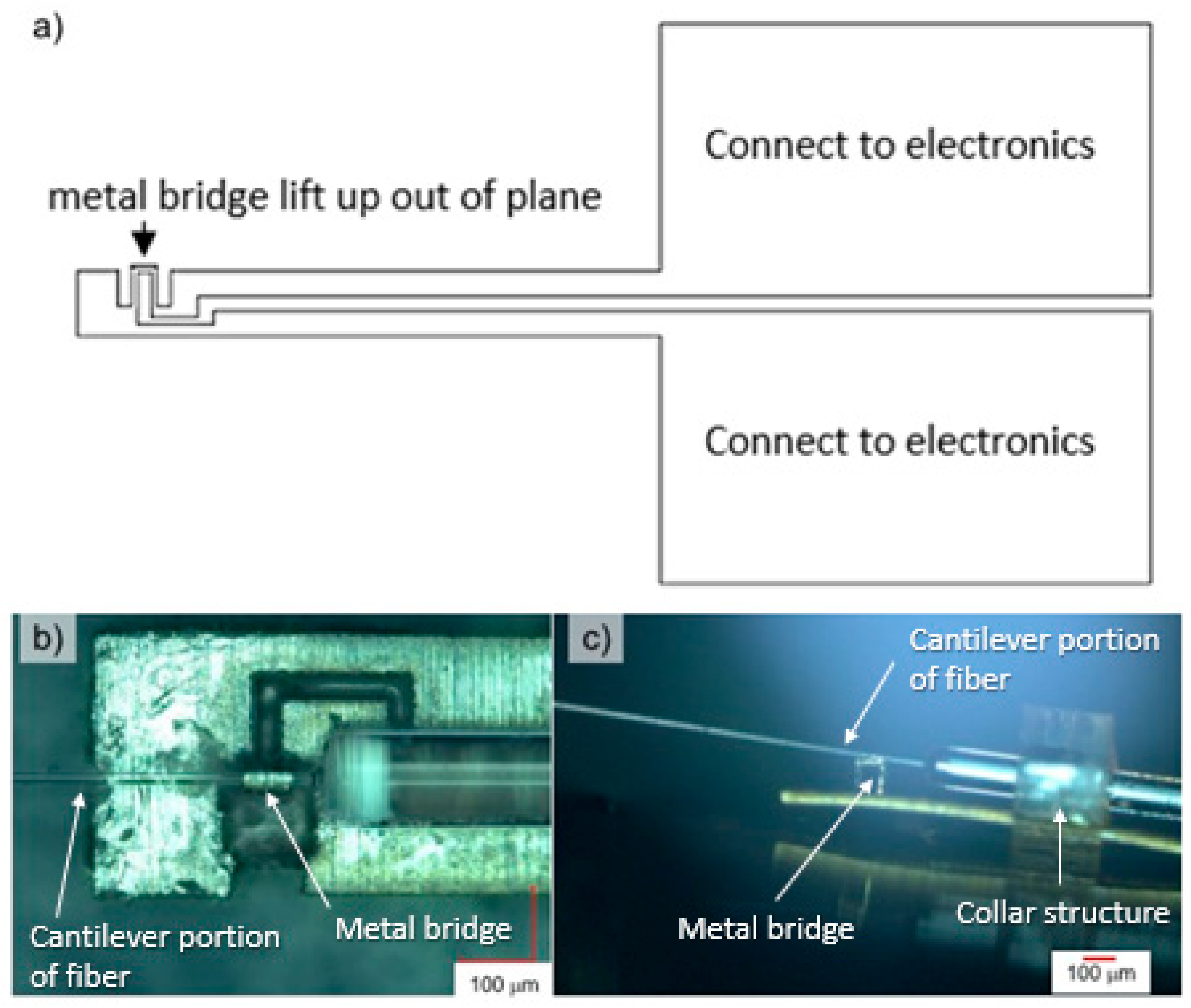
2.3. Thermal Actuator
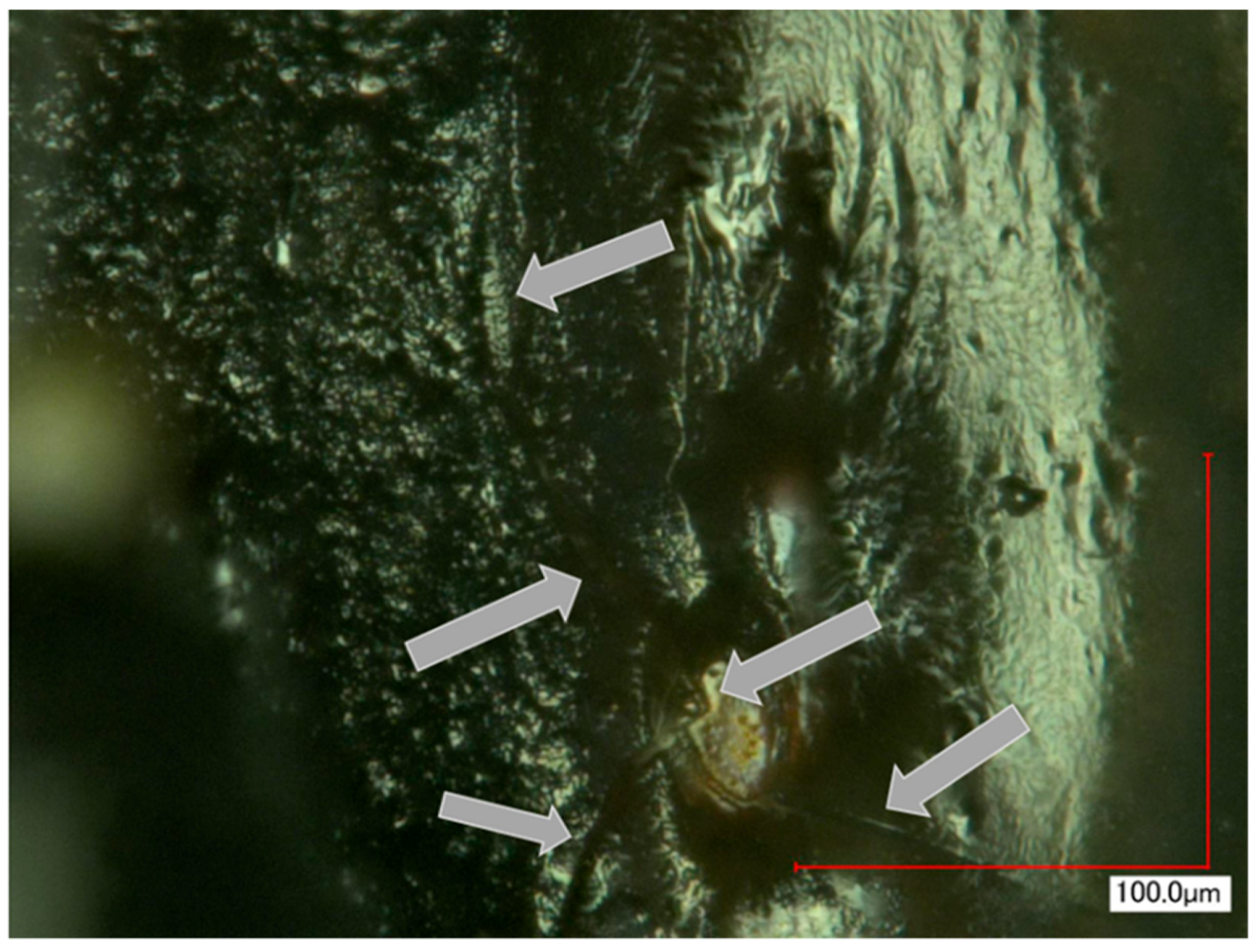
2.4. Housing, Packaging, and Adhesives
3. Simulation for Optimization
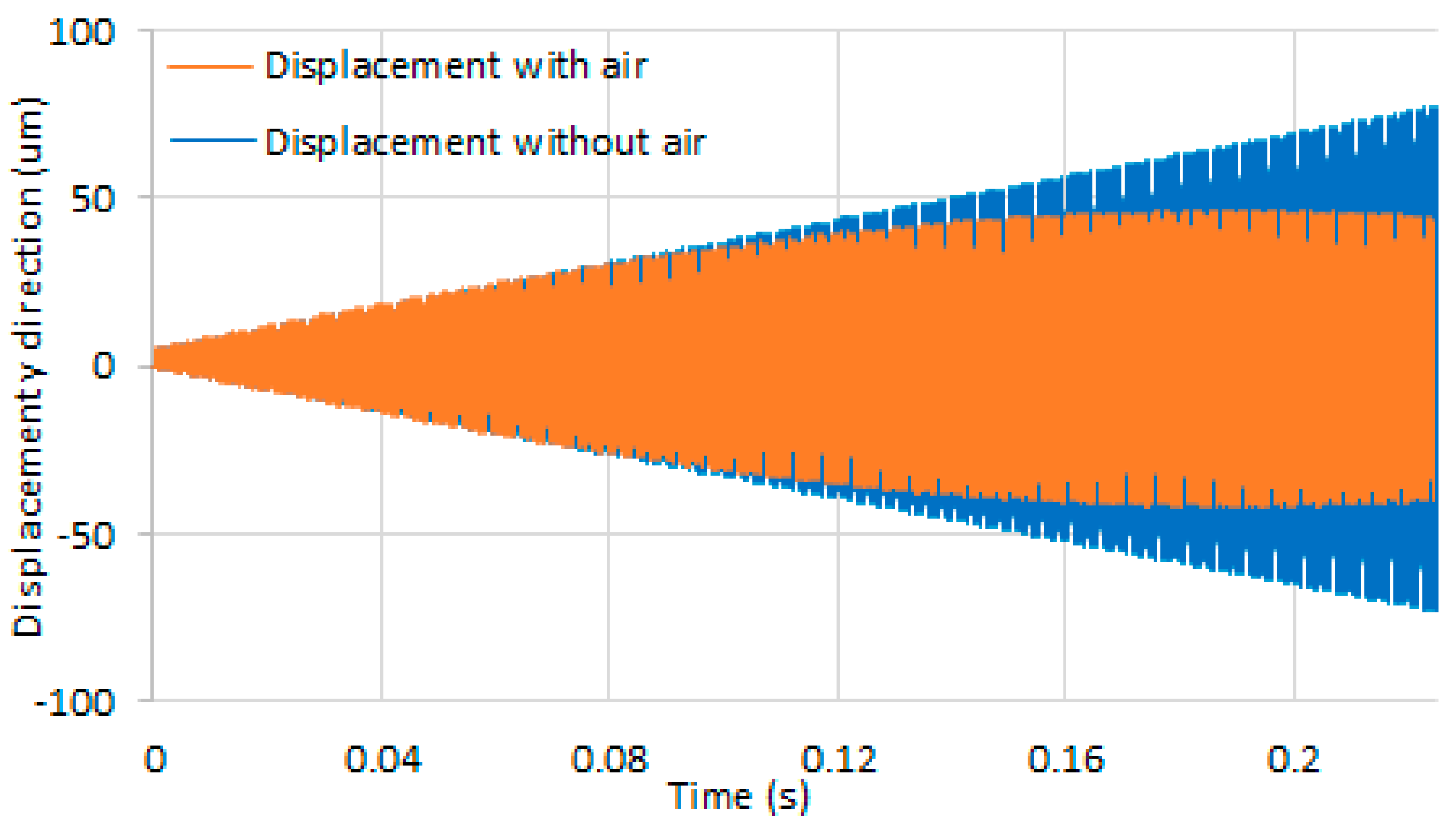
3.1. Fiber-Tip Displacement vs. Time
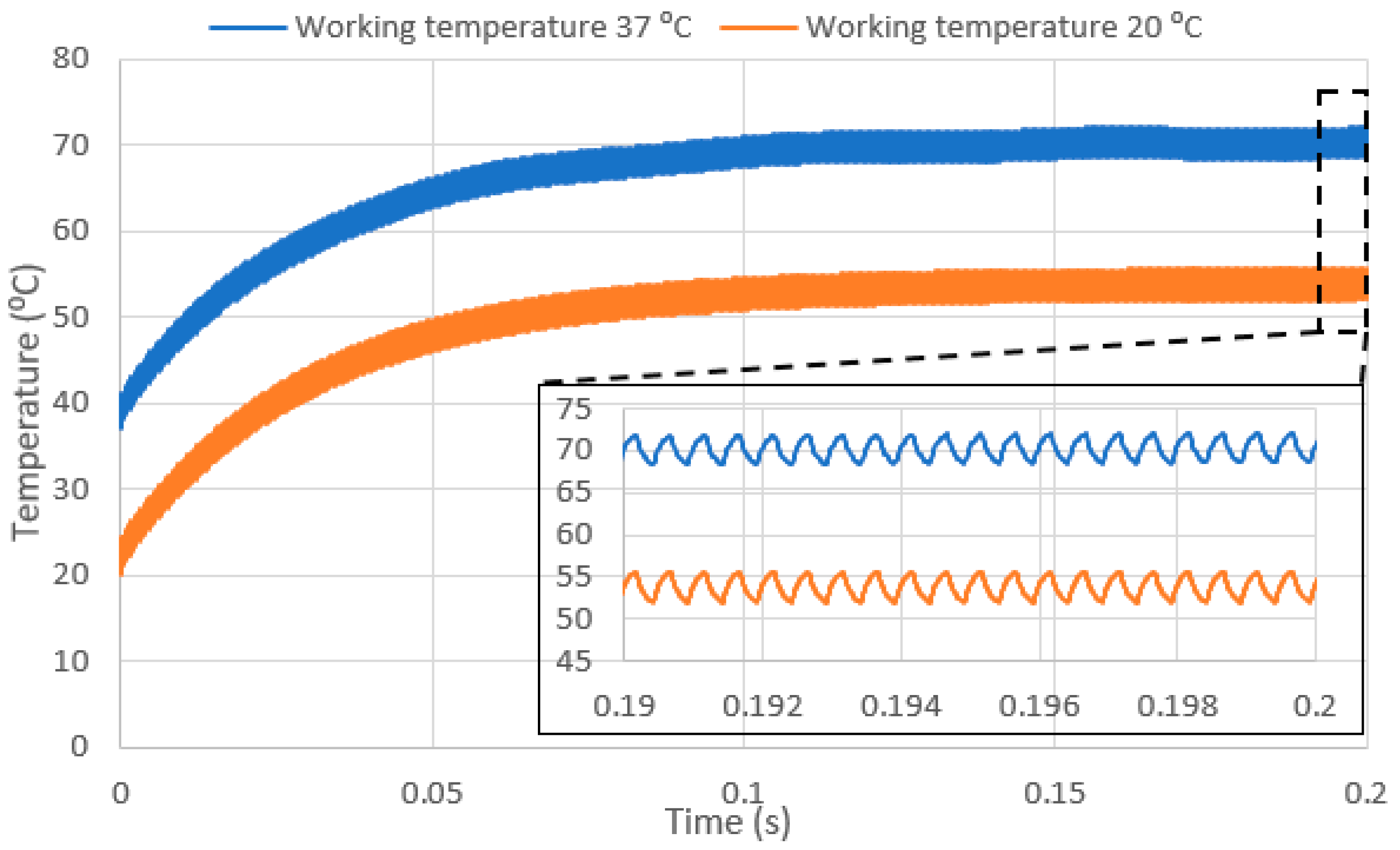
3.2. Bridge Temperature vs. Time
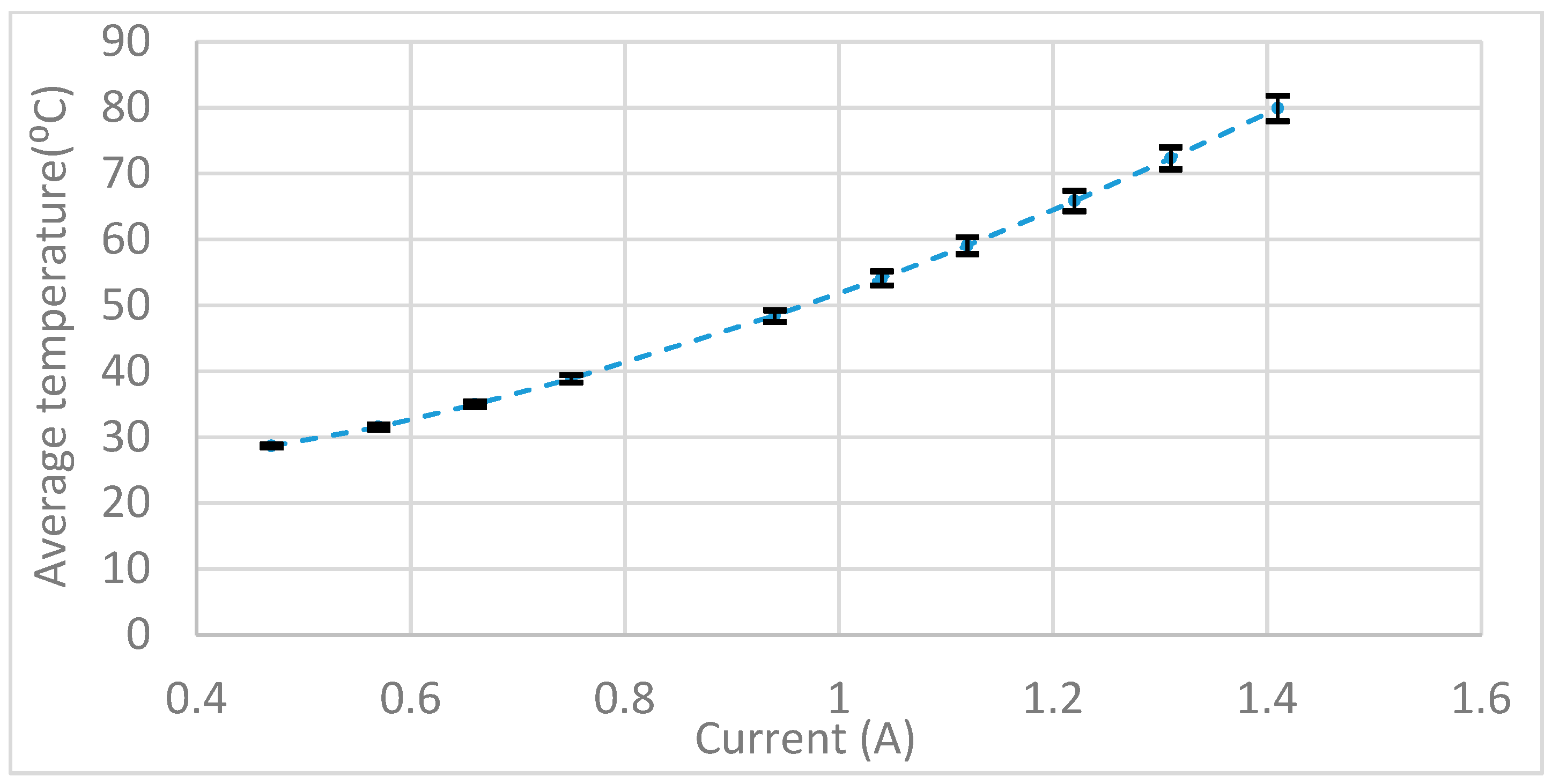
3.3. Bridge Temperature vs. Input Current
4. Experimental Validation and Discussion
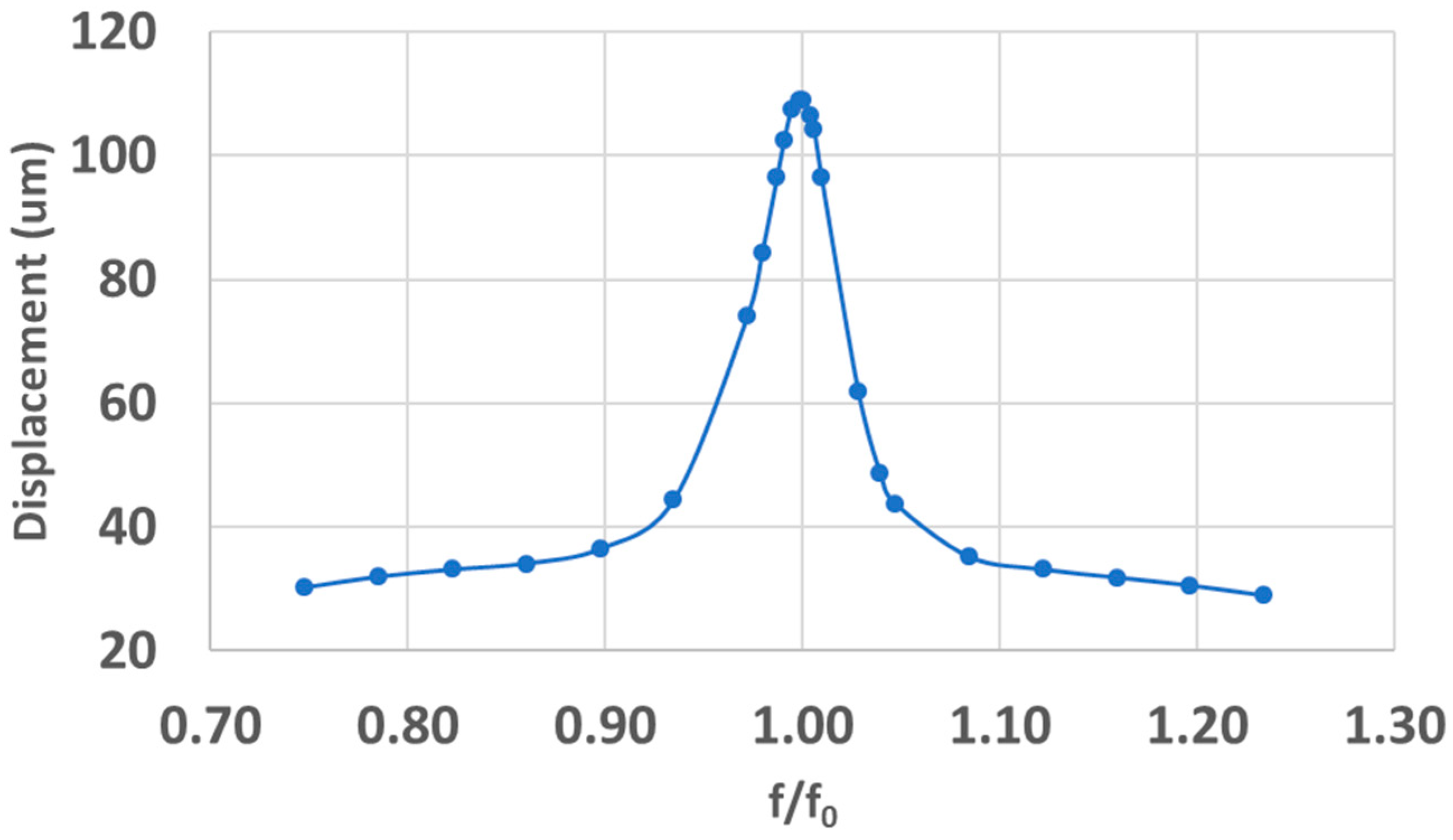
4.1. Harmonic Response
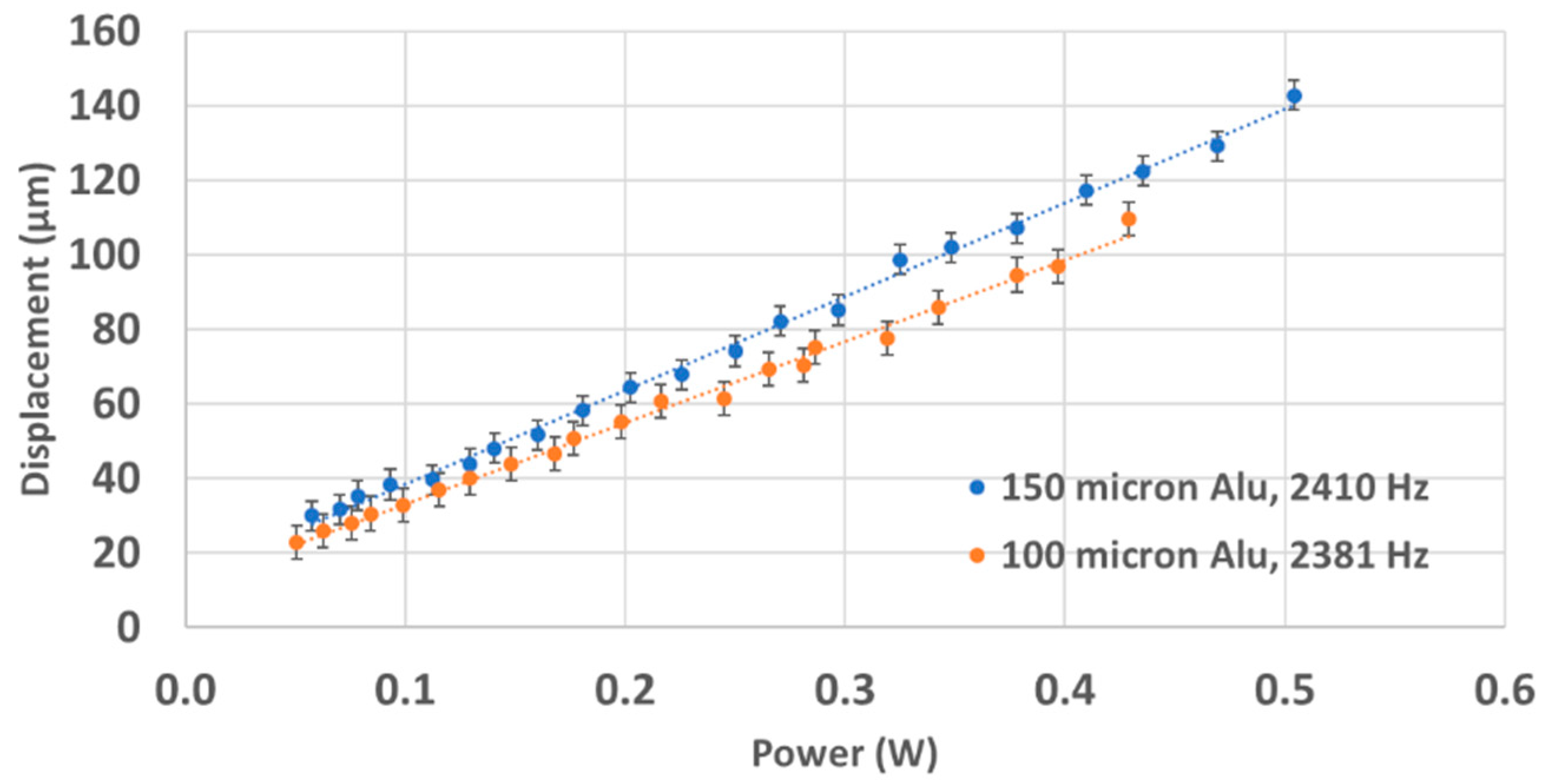
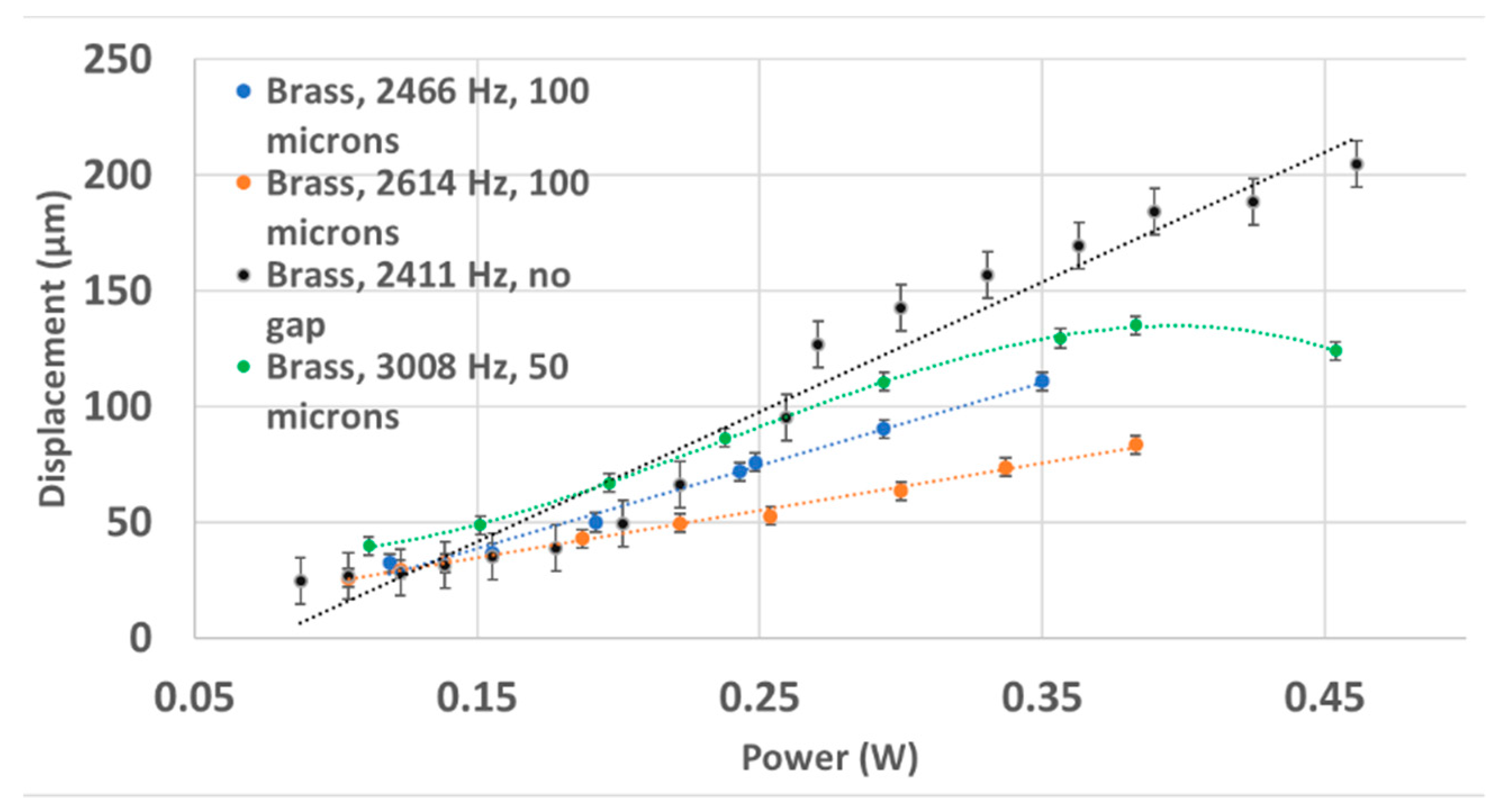
4.2. Tip Displacement at Natural Frequency
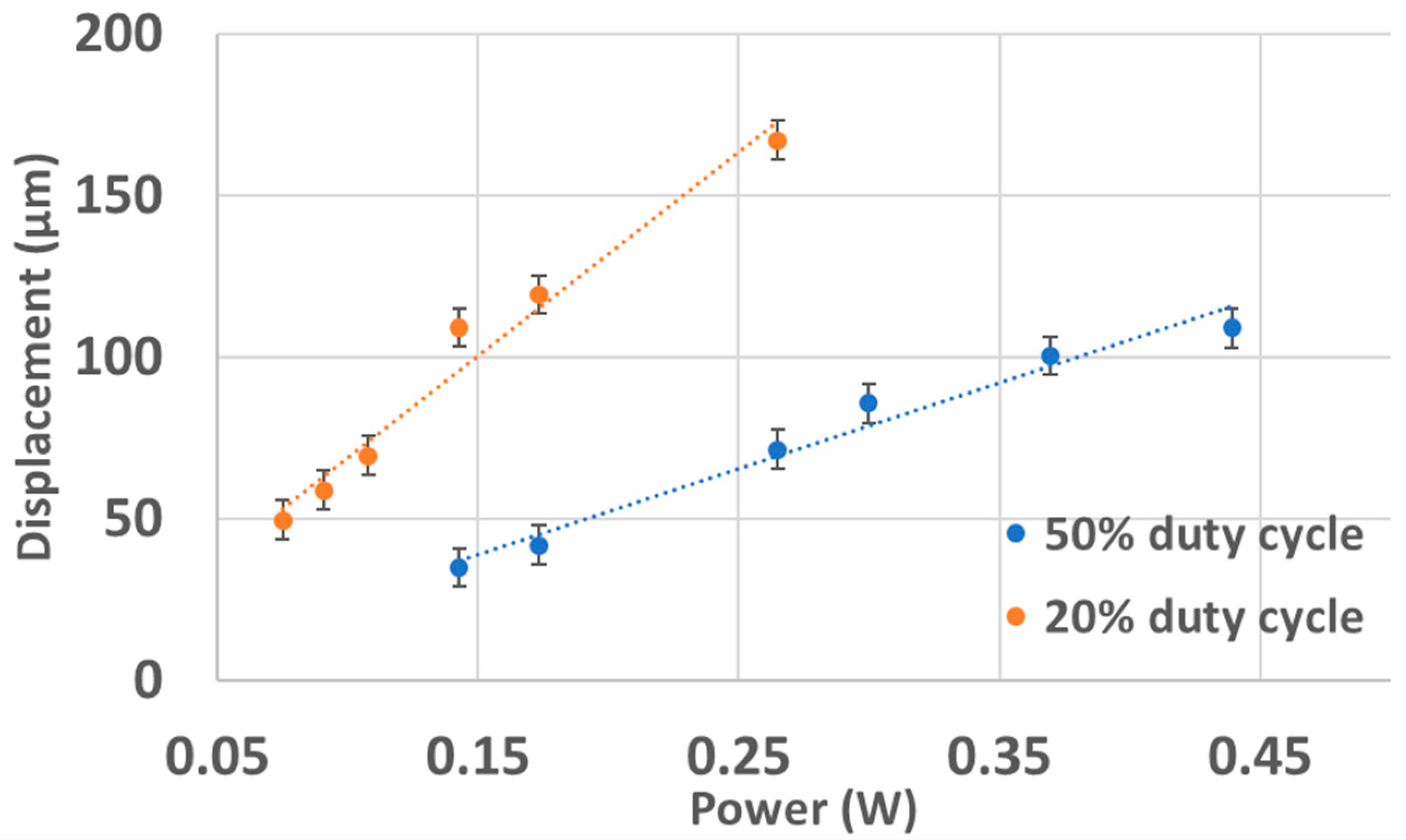
4.3. Tip Displacement at Different Duty Cycles
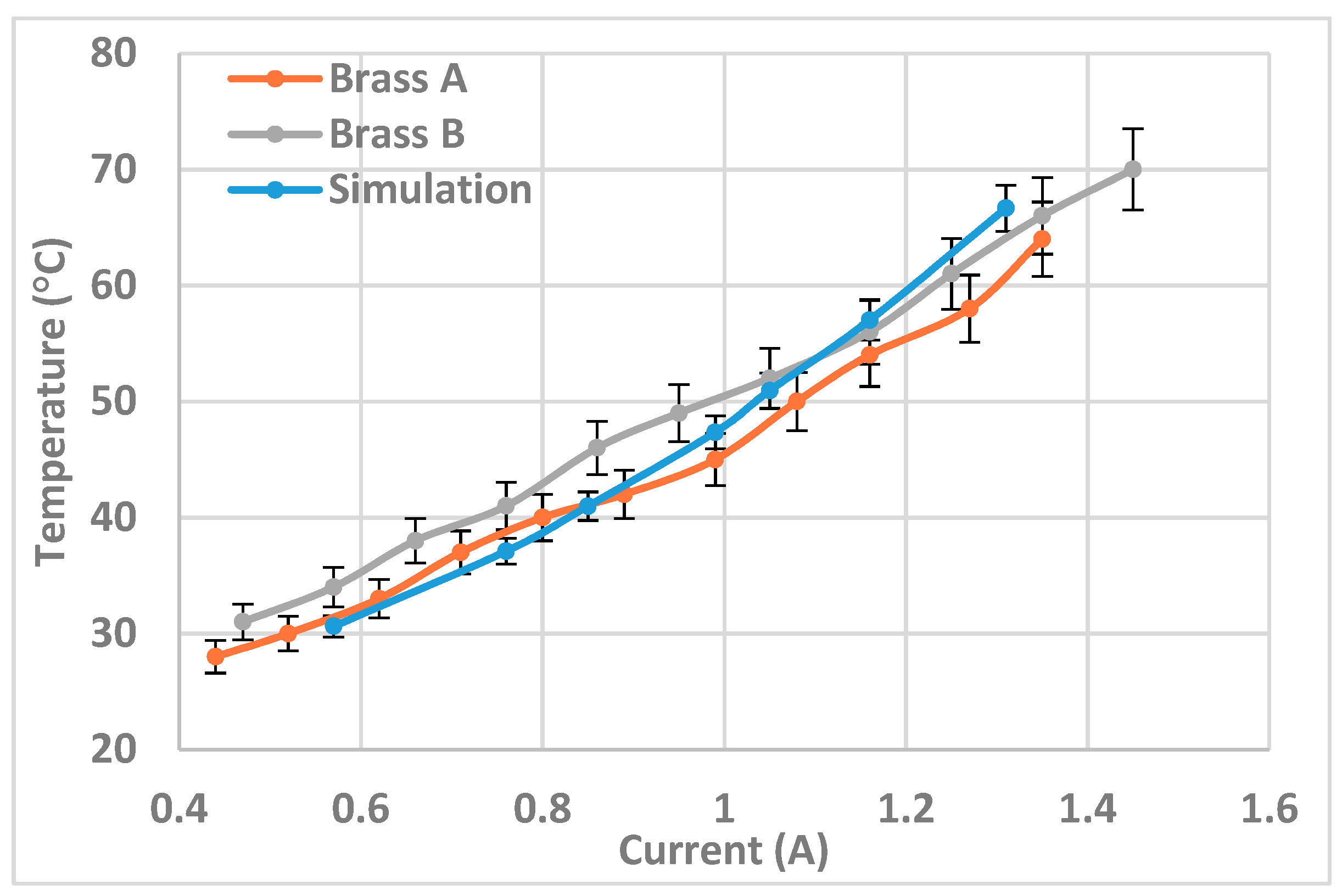
4.4. Bridge Temperature Measurements
4.5. Discussion
5. Conclusion
Author Contributions
Funding
Conflicts of Interest
References
- Farncombe, T.; Iniewski, K. Medical Imaging: Technology and Applications; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2014. [Google Scholar]
- Chun, H.J.; Yang, S.-K.; Choi, M.-G. Clinical Gastrointestinal Endoscopy: A Comprehensive Atlas; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Ducourthial, G.; Leclerc, P.; Mansuryan, T.; Fabert, M.; Brevier, J.; Habert, R.; Braud, F.; Batrin, R.; Vever-Bizet, C.; Bourg-Heckly, G.; et al. Development of a real-time flexible multiphoton microendoscope for label-free imaging in a live animal. Sci. Rep. 2007, 5, 18303. [Google Scholar] [CrossRef] [PubMed]
- Baillie, J. The endoscope. Gastrointest. Endosc. 2007, 65, 886–893. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.M.; Engelbrecht, C.J.; Soper, T.D.; Helmchen, F.; Seibel, E.J. Scanning fiber endoscopy with highly flexible, 1 mm catheterscopes for wide-field, full-color imaging. J. Biophotonics 2010, 3, 385–407. [Google Scholar] [CrossRef] [PubMed]
- Seibel, E.J.; Smithwick QY, J.; Brown, C.M.; Reinhall, P.G. Single-fiber flexible endoscope: General design for small size, high resolution, and wide field of view. Biomonit. Endosc. Technol. 2001, 4158, 29–39. [Google Scholar]
- Seibel, E.J.; Johnston, R.S.; Melville, C.D. A full-color scanning fiber endoscope. Proc. SPIE 2006, 6083, 608303. [Google Scholar] [CrossRef]
- Seibel, E.J.; Brown, C.M.; Dominitz, J.A.; Kimmey, M.B. Scanning single fiber endoscopy: A new platform technology for integrated laser imaging, diagnosis, and future therapies. Gastrointest. Endosc. Clin. N. Am. 2008, 18, 467–478. [Google Scholar] [CrossRef] [PubMed]
- Savastano, L.E.; Zhou, Q.; Smith, A.; Vega, K.; Murga-Zamalloa, C.; Gordon, D.; McHugh, J.; Zhao, L.; Wang, M.M.; Pandey, A.; et al. Multimodal laser-based angioscopy for structural, chemical and biological imaging of atherosclerosis. Nat. Biomed. Eng. 2017, 1, 0023. [Google Scholar] [CrossRef] [PubMed]
- Seibel, E.J. 1-mm catheterscope. Proc. SPIE 2008, 6852, 685207. [Google Scholar] [CrossRef]
- Wu, Y.C.; Xi, J.F.; Cobb, M.J.; Li, X.D. Scanning fiber-optic nonlinear endomicroscopy with miniature aspherical compound lens and multimode fiber collector. Opt. Lett. 2009, 34, 953–955. [Google Scholar] [CrossRef] [PubMed]
- Myaing, M.T.; MacDonald, D.J.; Li, X. Fiber-optic scanning two-photon fluorescence endoscope. Opt. Lett. 2006, 31, 1076–1078. [Google Scholar] [CrossRef] [PubMed]
- Fu, L.; Gan, X.S.; Gu, M. Nonlinear optical microscopy based on double-clad photonic crystal fibers. Opt. Express 2005, 13, 5528–5534. [Google Scholar] [CrossRef] [PubMed]
- Barhoum, E.; Johnston, R.; Seibel, E. Optical modeling of an ultrathin scanning fiber endoscope, a preliminary study of confocal versus non-confocal detection. Opt. Express 2015, 13, 7548–7562. [Google Scholar] [CrossRef]
- Yang, C.; Hou, V.W.; Girard, E.J.; Nelson, L.Y.; Seibel, E.J. Target-to-background enhancement in multispectral endoscopy with background autofluorescence mitigation for quantitative molecular imaging. J. Biomed. Opt. 2014, 19, 076014. [Google Scholar] [CrossRef] [PubMed]
- Sökmen, Ü.; Stranz, A.; Waag, A.; Ababneh, A.; Seidel, H.; Schmid, U.; Peiner, E. Evaluation of resonating Si canilevers sputter-deposited with AlN piezoelectric thin films for mass sensing applications. J. Micromech. Microeng. 2010, 20, 064007. [Google Scholar] [CrossRef]
- Tran, A.T.; Pandraud, G.; Schellevis, H.; Alan, T.; Aravindh, V.; Wunnicke, O.; Sarro, P.M. Fabrication of AlN slender piezoelectric cantilevers for high-speed MEMS actuations. Procedia Eng. 2011, 25, 673–676. [Google Scholar] [CrossRef]
- Seo, Y.H.; Hwang, K.; Park, H.C.; Jeong, K.H. Electrothermal MEMS fiber scanner for optical endomicroscopy. Opt. Express 2016, 24, 3903–3909. [Google Scholar] [CrossRef] [PubMed]
- Hwang, K.; Seo, Y.H.; Ahn, J.; Kim, P.; Jeong, K.H. Frequency selection rule for high definition and high frame rate Lissajous scanning. Sci. Rep. 2017, 7, 14075. [Google Scholar] [CrossRef] [PubMed]
- Komeili, M.; Menon, C. Robust design and analysis of thermally actuated micro-cantilever using 3D finite element method. Int. J. Simul. Model. 2016, 15, 409–422. [Google Scholar] [CrossRef]
- Komeili, M.; Menon, C. Analysis and design of thermally actuated micro-cantilevers for high frequency vibrations using finite element method. World J. Mech. 2016, 6, 94. [Google Scholar] [CrossRef]
- Komeili, M.; Menon, C. Modelling a micro-cantilever vibrating in vacuum, gas or liquid under thermal base excitation. Mech. Res. Commun. 2016, 73, 39–46. [Google Scholar] [CrossRef]
- Komeili, M.; Menon, C. Resonance vibration of a thermally-actuated optical fiber with arbitrary periodic excitation: Analysis and optimization. Int. J. Mech. Sci. 2017, 123, 287–296. [Google Scholar] [CrossRef]
- Komeili, M.; Ahrabi, A.; Menon, C. Resonance vibration of an optical fiber micro-cantilever using electro-thermal actuation. J. Math. Models Eng. 2017, 3, 1–17. [Google Scholar]
- Dissemination of IT for the Promotion of Materials Science. Phase Diagram for Al-Cu. 2018. Available online: https://www.doitpoms.ac.uk/miclib/phase_diagrams.php?id=2 (accessed on 1 September 2018).
- Chung, S.; Park, S. Effects of temperature on mechanical properties of SU-8 photoresist material. J. Mech. Sci. Technol. 2013, 27, 2701–2707. [Google Scholar] [CrossRef]
- Preece, W.H. On the heating effects of electric currents. Proc. R. Soc. Lond. 1883, 36, 464–471. [Google Scholar]
- Preece, W.H. On the heating effects of electric currents. No. II. Proc. R. Soc. Lond. 1887, 43, 280–295. [Google Scholar]
- Preece, W.H. On the heating effects of electric currents. No. III. Proc. R. Soc. Lond. 1888, 44, 109–111. [Google Scholar]


| Aluminum 1199 (Pure) | Aluminum 6061 | Brass 7030 | High-Tensile Manganese Brass | |
|---|---|---|---|---|
| Linear thermal expansion (µstrain/°C) | 22.4 | 24.6 | 19 | 21 |
| Thermal conductivity (W/m·K) | 220 | 170 | 126 | 121 |
| Young’s modulus (GPa) | 75 | 71 | 110 | 91 |
| Electrical resistivity (µΩ∙cm) | 2.5 | 4.4 | 6.5 | 23 |
| Current SFE | Proposed SFE | |
|---|---|---|
| Diameter (mm) | ~1.2 | ~0.5 |
| Length of distal rigid part (mm) | ~10 | 3–5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aghajanzadeh Ahrabi, A.; Kaur, M.; Li, Y.; Lane, P.; Menon, C. An Electro-Thermal Actuation Method for Resonance Vibration of a Miniaturized Optical-Fiber Scanner for Future Scanning Fiber Endoscope Design. Actuators 2019, 8, 21. https://doi.org/10.3390/act8010021
Aghajanzadeh Ahrabi A, Kaur M, Li Y, Lane P, Menon C. An Electro-Thermal Actuation Method for Resonance Vibration of a Miniaturized Optical-Fiber Scanner for Future Scanning Fiber Endoscope Design. Actuators. 2019; 8(1):21. https://doi.org/10.3390/act8010021
Chicago/Turabian StyleAghajanzadeh Ahrabi, Aydin, Mandeep Kaur, Yasong Li, Pierre Lane, and Carlo Menon. 2019. "An Electro-Thermal Actuation Method for Resonance Vibration of a Miniaturized Optical-Fiber Scanner for Future Scanning Fiber Endoscope Design" Actuators 8, no. 1: 21. https://doi.org/10.3390/act8010021
APA StyleAghajanzadeh Ahrabi, A., Kaur, M., Li, Y., Lane, P., & Menon, C. (2019). An Electro-Thermal Actuation Method for Resonance Vibration of a Miniaturized Optical-Fiber Scanner for Future Scanning Fiber Endoscope Design. Actuators, 8(1), 21. https://doi.org/10.3390/act8010021







