Abstract
Piezoelectric vibration-based energy harvesting systems have been used as an interesting alternative power source for actuators and portable devices. These systems have an inherent disadvantage when operating in linear conditions, presenting a maximum power output by matching their resonance frequencies with the ambient source frequencies. Based on that, there is a significant reduction of the output power due to small frequency deviations, resulting in a narrowband harvester system. Nonlinearities have been shown to play an important role in enhancing the harvesting capacity. This work deals with the use of nonsmooth nonlinearities to obtain a broadband harvesting system. A numerical investigation is undertaken considering a single-degree-of-freedom model with a mechanical end-stop. The results show that impacts can strongly modify the system dynamics, resulting in an increased broadband output power harvesting performance and introducing nonlinear effects as dynamical jumps. Nonsmoothness can increase the bandwidth of the harvesting system but, on the other hand, limits the energy capacity due to displacement constraints. A parametric analysis is carried out monitoring the energy capacity, and two main end-stop characteristics are explored: end-stop stiffness and gap. Dynamical analysis using proper nonlinear tools such as Poincaré maps, bifurcation diagrams, and phase spaces is performed together with the analysis of the device output power and efficiency. This offers a deep comprehension of the energy harvesting system, evaluating different possibilities related to complex behaviors such as dynamical jumps, bifurcations, and chaos.
1. Introduction
Vibration-based energy harvesting is becoming a remarkable technology since it allows the use of alternative sources of vibration to supply small devices, eliminating the need for frequent battery replacements or power cables. This is especially interesting for applications that include oil drilling or production and for aerospace structures [1,2,3].
An archetypal energy harvesting system model is a mechanical oscillator connected to an electronic circuit by a piezoelectric element. A typical experimental device is built of a cantilever beam with a tip mass and piezoelectric patches excited in the transverse direction by its base harmonic or random movement that is representative of ambient vibration.
In general, ambient vibration provides the energy harvesting system excitation and, once the excitation frequency is close to the natural system frequency, a maximum output power is captured. This linear analysis defines a narrowband harvester system since the ambient vibrations are usually varying in frequency or totally random with energy distributed over a wide frequency range [4].
Several researchers are investigating alternatives that can enhance energy harvesting capacity by introducing nonlinearities into the system [5,6]. A usual approach is to explore bistable structures with double-well potential and, depending on vibration conditions, it is possible to achieve high-orbit motion visiting the two potentials. This is essentially a Duffing-type oscillator that can be experimentally built using magnetic forces to modify the effective stiffness of the harvester [7,8,9,10,11,12,13,14,15,16,17,18].
Besides this kind of nonlinearity, constitutive nonlinear effects have also been exploited with the same objective. The majority of the literature addresses linear electro-mechanical conversion approaches [19,20,21,22,23]. Crawley and Anderson [24] explored nonlinear aspects related to piezoelectric coupling, showing that there is a significant dependence of strains. Triplett and Quinn [25] investigated nonlinear piezoelectric coupling behavior and some aspects related to the mechanical nonlinearities. Stanton et al. [17] proposed a quadratic dependence of the piezoelectric coupling coefficient on the induced strain. Experimental tests showed a good agreement with the numerical results. Silva et al. [26] investigated the hysteretic behavior of piezoelectric coupling, comparing the results with linear models. The results suggested that there is an optimum hysteretic behavior that can increase the harvested power output of energy harvesting systems. Silva et al. [27] showed a comparison among experimental data and numerical simulations performed with distinct nonlinear piezoelectric coupling models. The conclusions showed that the inclusion of nonlinear terms reduces the discrepancies predicted by linear models. Moreover, nonlinear aspects such as dynamical jumps are associated with dramatic changes in system responses.
Another interesting nonlinear approach to enhance energy harvesting system capacity is the synergistic use of smart materials. The inclusion of shape memory alloy (SMA) elements can enhance system performance by using the SMA’s unique properties related to solid-phase transformations that allow us to exploit either stiffness change or energy dissipation. Avirovik et al. [28] developed a hybrid device coupling piezoelectric elements with SMAs for dual functionality, both as an actuator and an energy harvester. Silva et al. [29] employed a numerical analysis of an SMA–piezoelectric energy harvesting system and indicated that the inclusion of the SMA element can be used to extend the operational range of the system.
The tunability of an energy harvesting system is a special procedure to be employed, and different alternatives can be implemented to alter the vibration behavior of the harvester: the use of mechanical preload [30]; the inclusion of asymmetric tip mass [31]; or the alteration of the structural energy harvester geometry [32,33]
Lesieutre and Davis [34] showed that compressive axial preloads can increase the effective coupling coefficient of an electrically driven piezoelectric bimorph element. Leland and Wright [35] developed an energy harvester by applying an axial compressive load to tune the resonance by changing its effective stiffness. Betts et al. [36] presented a nonlinear device through an arrangement of bistable composites combined with piezoelectric elements for broadband energy harvesting of ambient vibrations. The results showed that it is possible to improve the power harvest over that by conventional devices. Bai et al. [31] showed that an asymmetric tip mass can induce nonlinear and hysteretic behavior to a piezoelectric energy harvester with a free-standing thick-film bimorph structure. Friswell et al. [33] presented a nonlinear piezoelectric energy harvester using an inverted elastic beam–mass system with nonlinear electro-mechanical coupling. The results showed that the system nonlinearity has two potential wells for large tip masses that are responsible for rich system behavior including chaos. The authors showed that the bandwidth of harvested power can be increased compared with that for a linear harvester.
The use of nonsmooth nonlinearity is another approach to increase the bandwidth of energy harvesting systems. The basic idea is to confine energy harvester displacements using end-stops. Nevertheless, this approach has the disadvantage that the output power saturation at high excitation levels reduces the amount of generated power for high displacements. Despite this disadvantage, transforming an energy harvester into a broadband system can be achieved by using appropriate parameters to enhance the power generated at different frequencies [30,37,38,39,40,41,42].
Nonsmooth dynamical systems present rich behavior with unusual, complex mathematical descriptions. Savi et al. [43] and Divenyi et al. [44,45] presented numerical and experimental efforts to investigate discontinuous oscillators. Soliman et al. [37] investigated a harvester with a stopper where the results showed that the performance is highly influenced by the stiffness ratio of the rigid support, the energy harvester element, and the velocity of the cantilevered beam at the impact point. Rysak et al. [42] developed an energy harvesting system through an aluminum beam with a piezoceramic patch subjected to harmonic excitation and impacts. Hardening effect characteristics and a broader frequency range increasing the efficiency of the energy harvesting process were observed. Jacquelin et al. [46] developed a model for a piezoelectric impact energy harvester system consisting of two piezoelectric beams and a seismic mass. They analyzed the influence of different parameters (gap, seismic mass, and beam length, among others) on the system performance. Vijayan et al. [40,47] considered a vibro-impact system with the capacity to convert low-frequency responses to high frequencies using nonlinear impacts. Kaur and Halvorsen [48] developed an experimental setup and a lumped model of an electrostatic energy harvester with end-stop impacts. The results showed that the harvester device response is highly sensitive to the end-stop position at fixed bias and small acceleration amplitudes. Much of these research efforts have been devoted to exploring the effect of the main parameters of nonsmooth energy harvester systems using experimental or/and numerical approaches but, in general, the power output improvement analyses are not coupled with dynamics system analysis, which is herein performed in order to allow us to better comprehend nonsmooth energy harvesting devices.
This work develops a numerical investigation exploiting nonsmoothness in piezoelectric vibration-based energy harvesting systems. A piezoelectric energy harvesting single-degree-of-freedom model with a one-side mechanical end-stop is investigated. Numerical simulations are carried out presenting a parametric analysis that shows the main parameter’s influence on the system dynamical behavior. Dynamical analysis using proper nonlinear tools such as Poincaré maps, bifurcation diagrams, and phase spaces is performed together with analysis of the device output power and efficiency. This offers deep comprehension of the energy harvesting system and the evaluation of different possibilities related to complex behaviors such as dynamical jumps, bifurcations, and chaos. The results show that impacts can strongly modify the system dynamics, resulting in broadband output power harvesting performance. This shows that deep nonlinear dynamical analysis needs to be performed for design purposes.
2. The Vibration-Based Energy Harvesting System
A nonsmooth vibration-based energy harvesting system is analyzed by considering a single-degree-of-freedom system with discontinuous support, shown in Figure 1. The system is composed of a mechanical oscillator with mass m connected to a linear spring with stiffness k and linear damping with coefficient c. The oscillator movement is restricted by a massless support, separated by a gap . The support is represented by a linear spring with stiffness and linear damping with coefficient . This oscillator is subjected to a base excitation , and the mass displacement is represented by y; z is the mass displacement relative to the base. The mechanical system is connected to an electric circuit by a piezoelectric element that converts mechanical energy into electrical energy. The electrical circuit is represented by an electrical resistance, R; V denotes the voltage across the piezoelectric element, is the capacitance term, and the electro-mechanical coupling is provided by the piezoelectric element represented by . The system dynamics has two modes, with contact and without contact, which are described by the following equations:
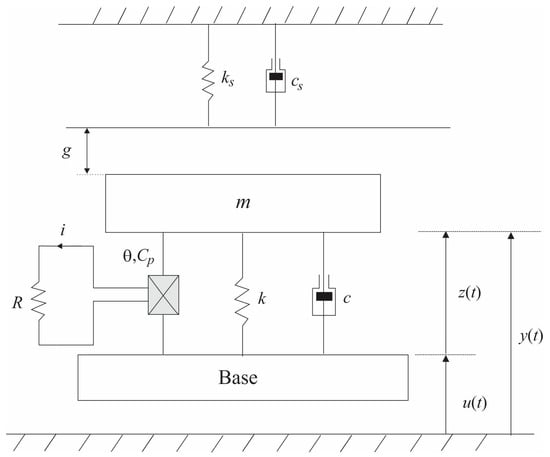
Figure 1.
Archetypal model of a vibration-based energy harvesting system with discontinuous support.
The electrical differential equation for both situations is given by
The instantaneous energy harvesting electrical power is defined by , and the output and input average powers are given by
where the harmonic acceleration is given by . The system performance can be evaluated by considering the conversion efficiency, , which establishes a relation between the electrical (output) and mechanical (input) powers, .
3. Numerical Simulations
Numerical simulations were carried out using the system parameters presented in Table 1, based on the work of Kim et al. [23]. In general, the parametric analysis considers different values of support stiffness, , and gap, .

Table 1.
System parameters [23].
The equations of motion were integrated using the fourth-order Runge–Kutta method. Time steps less than 10−4 s were assumed after a convergence analysis. Numerical simulations were carried out to provide a parametric analysis evaluating the energy harvesting capacity. Displacement, power, and efficiency were monitored as a function of forcing frequency and different values of support stiffness () and gap (). In this regard, it is interesting to define the nondimensional parameter that establishes a ratio between support and oscillator stiffness:
Figure 2 presents the system frequency response resulting from numerical simulations showing the maximum displacement under a slow quasi-static variation of forcing frequency. Different values were considered to show the influence of the end-stop on system dynamics. For = 70 m, the vibrating mass does not touch the support at maximum displacement, named WI (without impact), resulting in a non-contact behavior and a narrowband harvester system. As decreases to 50 m, the impacts lead to a typical nonsmooth characteristic with dynamical jumps. This behavior is more evident as the support stiffness increases, when the resonance peaks become less sharp and broader. Impact causes the excitation of higher frequencies, increasing the bandwidth. Nevertheless, the increase in the support stiffness also restricts the displacement. It is noticeable that the displacement response increases monotonically until the vibrating mass reaches the support and the slope of the frequency–response curve drops abruptly. This behavior is displayed over a large range of frequencies, especially when the support stiffness increases. After a dynamical jump, the response becomes identical to that associated with the linear system.
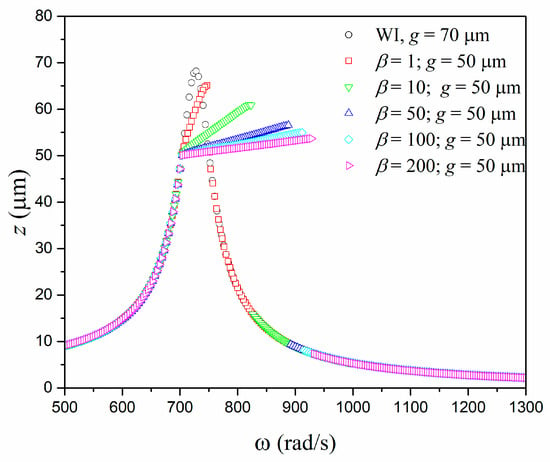
Figure 2.
Maximum displacement versus forcing frequency: comparison between linear model without impacts ( = 70 m) and a system incorporating impacts using = 50 m at different values of .
Based on this conclusion, the support stiffness and gap can be used to establish a proper system design. Figure 3 shows situations for the same ratio between support and oscillator stiffness using different gaps: and . Note that the gap reduction causes a decrease in the maximum displacement due to the contact constraint, which implies that the effectiveness of the harvester system is reduced but, on the other hand, there is an extension of the higher-frequency range. In order to clarify this behavior, Figure 4 shows the maximum displacement response for different values of considering a fixed value of . A significant reduction of the maximum displacement associated with an amplification of the bandwidth is noticeable.
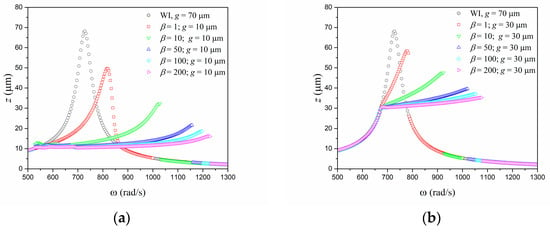
Figure 3.
Maximum displacement versus forcing frequency: comparison between linear model without impacts ( = 70 m) and a system incorporating impacts with different values of : (a) = 30 m; (b)
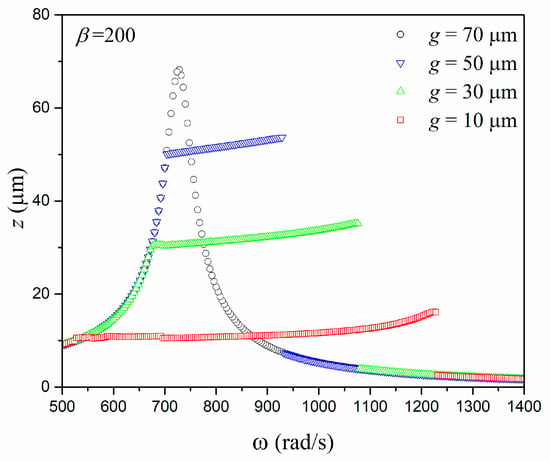
Figure 4.
Maximum displacement versus forcing frequency with different gap values, .
The previous results are now presented in the form of phase spaces and Poincaré sections (Figure 5). It is noticeable that the phase space is split into two regions associated with contact and non-contact behaviors. The system without contact has a symmetric orbit since the contact mode response is not reached. In this regard, the decrease of gap g tends to present more considerable changes in the phase spaces since it increases the contact region. All presented responses are related to period-1 behavior, characterized by a Poincaré section with a single point. As expected, the effect is more pronounced when the support stiffness increases.
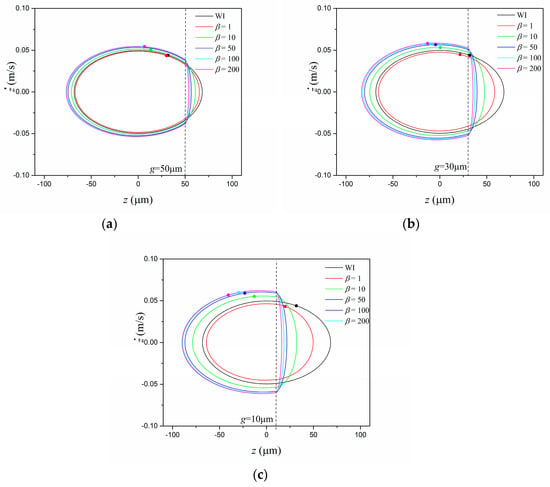
Figure 5.
Phase spaces and Poincaré sections at resonance frequencies. A comparison between a linear model without impacts (WI, using = 70 m) and a system incorporating impacts with different values of : (a) = 10 m, (b) = 30 m, and (c) = 50 m.
The influence of impacts is now analyzed from the energy harvesting perspective. Figure 6 shows the average power curves for all cases discussed. These curves show that the same conclusions related to displacement and broadband apply to harvested energy.
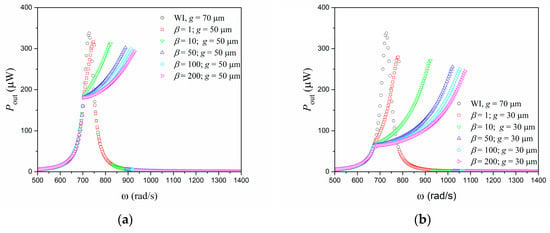
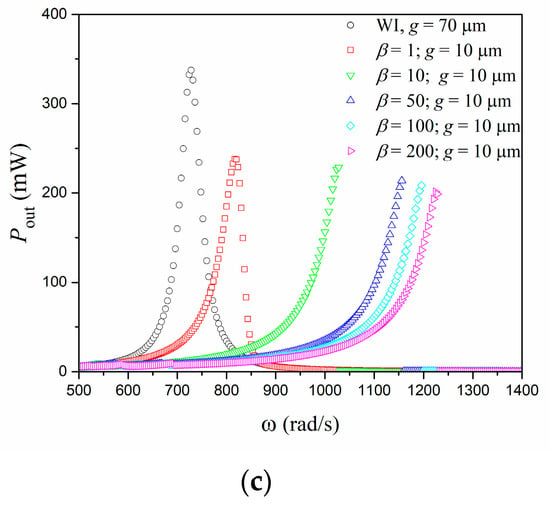
Figure 6.
Average power versus forcing frequency using = 70 m (without impact) and incorporating impacts with different values of : (a) = 50 m, (b) = 30 m, and (c) = 10 m.
Dynamical jumps are associated with dramatic changes in system response that can reduce the system amplitude and the harvested energy. Figure 7 shows the average power in the steady state for the up-sweep and down-sweep frequency cases. The gap increase tends to increase the frequency where the jump occurs and also the jump magnitude.
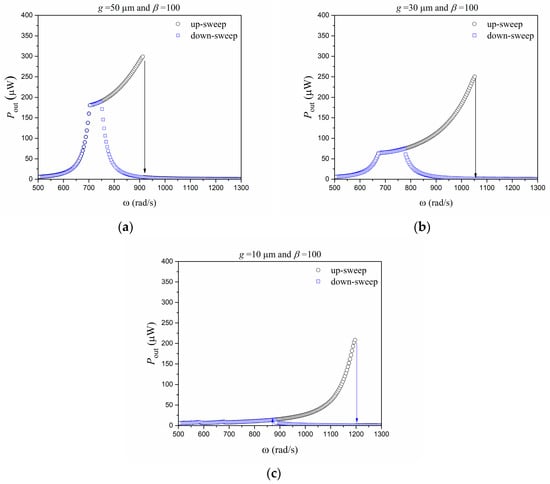
Figure 7.
Dynamical jumps of average power for frequency up-sweep and down-sweep assuming : (a) = 50 m, (b) = 30 m, and (c) = 10 m.
Another way to evaluate energy harvesting capacity is in terms of system efficiency (), which establishes a power output/input ratio. Figure 8 shows the system efficiency under slow quasi-static variation of the forcing frequency for different values. Once again, a system without impact is compared with systems incorporating impacts: = 50 m, = 30 m, and = 10 m. The results show more or less the same trend, but it is possible to identify a variation in the impact region.
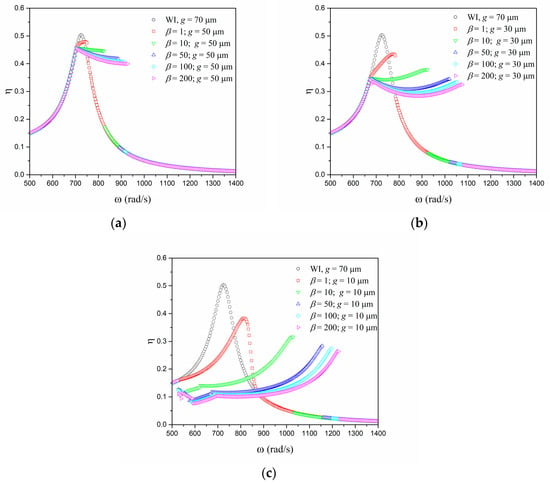
Figure 8.
Efficiency versus forcing frequency: comparison between a linear model without impacts ( = 70 m) and systems incorporating impacts with different values of support stiffness, : (a) = 50 m, (b) = 30 m, and (c) = 10 m.
Numerical simulations show that the use of nonsmoothness can be useful to spread the frequency band of an energy harvesting system, generating a broadband system. On the other hand, displacement limits can restrict the amount of generated power. Hence, there is a competition between amplitude and distribution along the frequency. Basically, the gap reduction decreases the maximum value but enlarges the frequency band. This conclusion illustrates the necessity to investigate the most interesting conditions for a specific application.
In this regard, variations of support stiffness and gap are the essential points to be investigated. The forthcoming analysis considers average values for simulations for different frequencies within the range of 500 to 1400 rad/s. Therefore, average values of output power , , and efficiency , are evaluated. We note that this approach allows one to evaluate the average energy harvesting capacity through a frequency range. Figure 9 shows the average harvested power output () for different values of stiffness ratio represented by parameter β. Different gaps are investigated: = 70 m (without contact), = 50 m, = m, and = m. Impacts tend to maximize the power output, and an increase in β causes a monotonic increase of power up to an asymptotic value. Nevertheless, the energy harvesting capacity tends to decrease for small values of gap due to excessive displacement restrictions. Note that the case with = 10 m is associated with power output smaller than that for the linear, non-impact case. Therefore, there is a limit case where the use of impact is interesting for energy harvesting purposes.
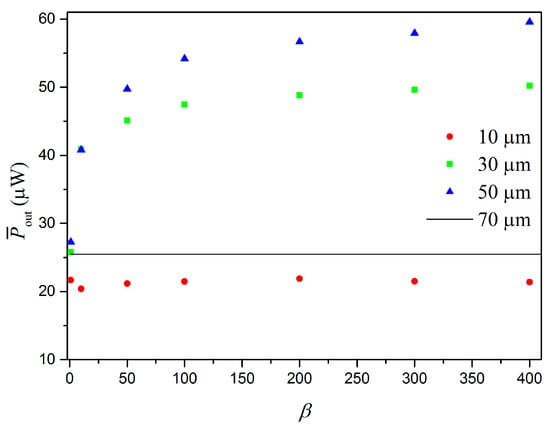
Figure 9.
Average harvested power output for different frequencies (interval of 500 to 1400. rad/s), for different values of gap, as a function of .
Figure 10 considers the average efficiency () values for the same situations. Efficiency follows the same trend observed for the power output. Nevertheless, this analysis allows one to define the transition where the nonsmoothness is interesting. The case for = 50 m is more efficient than all the cases, including the non-impact system ( = 70 m) and the cases with = 30 m and = 10 m for all β values. It should be pointed out that the case with = 30 m is the transition case, presenting a greater efficiency compared with the non-impact system case only for β = 10. In order to establish a comparison, we consider the case with , and all cases are compared with a reference value defined for the non-impact system ( = 70 m): when = 50 m, the system with impacts is 23.1% more efficient, generating 56.7 W; when = 30 m, the system is 4.2% less efficient, generating 48.8 W; when = 10 m, the system is 47.4% less efficient, generating 21.9 W. Therefore, power output and efficiency can be analyzed together in order to define energy harvesting capacity.
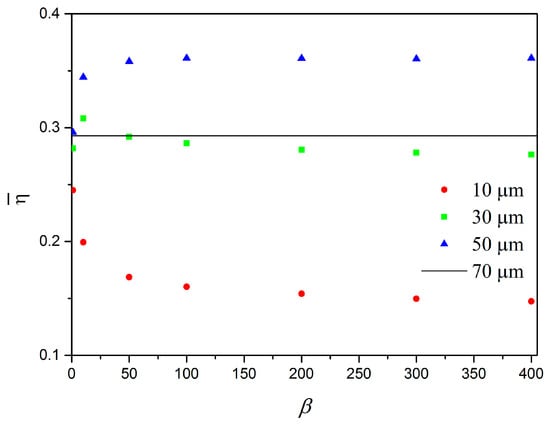
Figure 10.
Average efficiency for different frequencies (interval of 500 to 1400 rad/s), for different values of gap, as a function of .
In order to have a global comprehension of energy harvesting system dynamics, bifurcation diagrams were built considering slow quasi-static variation of the forcing frequency parameter and plotting a Poincaré section of the response. This is of special interest since different kinds of response can alter the energy harvesting capacity. Figure 11a shows the bifurcation diagram for g = 50 μm considering β = 200. The results show period-1 motion for all frequencies and a discontinuity close to the dynamical jump. The details of the system dynamics are depicted in Figure 11b,c through phase spaces and Poincaré sections for two different frequencies, 708 and 936 rad/s, respectively. It is noticeable that, although the system dynamics is always related to period-1 motion, it is associated with different solutions with distinct amplitudes and, therefore, different energy harvesting capacities. The average power value for 708 rad/s is 180 , and that for 936 rad/s is 3.91 , showing a large difference between them.
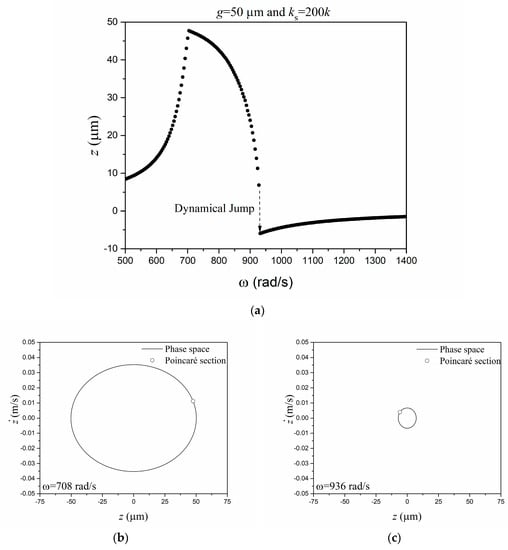
Figure 11.
(a) Bifurcation diagram for g = 50μm and β = 200. Phase space and Poincaré sections for (b) ω = 708 rad/s and (c) ω = 936 rad/s.
When considering a gap g = 10 μm (Figure 12a), the system dynamics presents several bifurcations at low frequencies (500–700 rad/s) and in the region close to the dynamical jump. The phase spaces and Poincaré sections for three different frequencies offer another view confirming the dynamical system complexity: see Figure 12b for ω = 536 rad/s, Figure 12c for ω = 684 rad/s, and Figure 12d for ω = 1228 rad/s. Different kinds of response can be noticed in the detailed pictures: chaotic (536 rad/s), period-2 (684 rad/s), and period-1 (1228 rad/s). It should be highlighted that nonsmooth characteristics cause dramatic, sudden changes in the system dynamics. The efficiency values are more or less the same between 500 and 1000 rad/s (see Figure 8c), and after that, the efficiency increases with the frequency. The efficiency values for the identified simulations are 0.1057 (536 rad/s), 0.09799 (684 rad/s), and 0.2627 (1228 rad/s). Note that period-1 response has greater amplitudes and, therefore, generates more energy with an efficiency that is of interest. Hence, although the case with a small gap has lower efficiency than do the other investigated cases, its richer nonlinear dynamics can be useful to enhance its energy harvesting capacity.
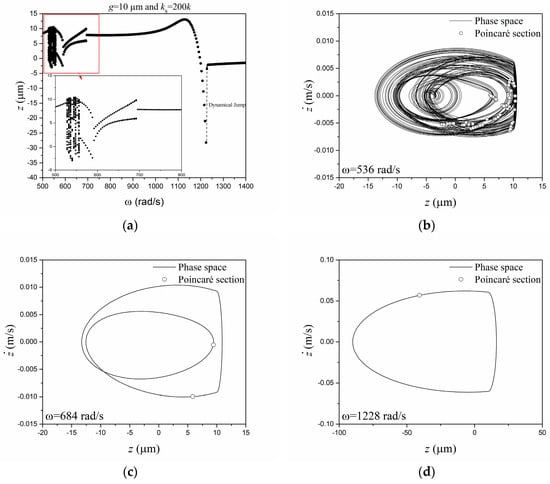
Figure 12.
(a) Bifurcation diagram for g = 10μm and β = 200. Phase spaces and Poincaré sections for (b) ω = 536 rad/s, (c) ω = 684 rad/s, and (d) ω = 1228 rad/s.
4. Conclusions
This paper exploits nonsmoothness for piezoelectric vibration-based energy harvesting. A single-degree-of-freedom oscillator with discontinuous support connected to an electric circuit by a piezoelectric element was investigated. A parametric analysis was carried out for varying values of support stiffness and gap. Numerical simulations were carried out comparing nonsmooth systems with a linear system without impact. A frequency response analysis showed the sensitivity of the power generated to the support stiffness and gap, which compete to define the energy harvesting capacity. Larger gaps reduce the possibility of impacts, leading the system to the linear regime without impacts. On the other hand, small gaps are related to small amplitudes that considerably decrease the device efficiency but increase the frequency bandwidth. Concerning support stiffness, the results indicate that increased support stiffness makes it possible for a system to produce more power than a linear system using a gap with an appropriate value. Besides this, nonsmooth characteristics cause complex responses with dramatic and sudden changes to the system dynamics. Nonsmoothness can strongly modify the system dynamics, tending to increase the broadband output power harvesting performance. On the other hand, its constraints limit the energy harvesting capacity due to displacement restrictions. Dynamical investigation suggests that there are optimum values of support stiffness and gap that increase the power output of energy harvesters operating in broadband source vibration conditions. Besides this, richer nonlinear dynamics related to a high nonsmoothness level can be useful to increase energy harvesting capacity. In conclusion, the results indicate that the use of nonsmoothness is an interesting option to improve the operational bandwidth of energy harvesting systems. A proper dynamical analysis with a parametric study is an interesting methodology for the design of a nonsmooth energy harvesting system and points out situations where the energy harvesting capacity is enhanced.
Author Contributions
Investigation, R.A., L.L.S.M., P.C.C.M.J., P.M.C.L.P. and M.A.S.; Software, R.A, L.L.S.M. and P.C.C.M.J.; Supervision, L.L.S.M., P.C.C.M.J., P.M.C.L.P. and M.A.S.; Writing—original draft, L.L.S.M. and M.A.S..; Writing—review & editing, L.L.S.M. and M.A.S.
Funding
The authors would like to acknowledge the support of the Brazilian Research Agencies CNPq, CAPES, and FAPERJ. The Air Force Office of Scientific Research (AFOSR) is also acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hadas, Z.; Vetiska, V.; Huzlik, R.; Singule, V. Model-based design and test of vibration energy harvester for aircraft application. Microsyst. Technol. 2014, 20, 831–843. [Google Scholar] [CrossRef]
- Silva, T.M.P.; De Marqui, C. Self-powered active control of elastic and aeroelastic oscillations using piezoelectric material. J. Intell. Mater. Syst. Struct. 2017, 28, 2023–2035. [Google Scholar] [CrossRef]
- Arsalan, M.J.; Ahmad, T.; Saeed, S.A. Energy Harvesting for Downhole Applications in Open-hole Multilaterals. Soc. Pet. Eng. 2018. [Google Scholar] [CrossRef]
- Tang, L.; Yang, Y.; Soh, C.K. Toward Broadband Vibration-based Energy Harvesting. J. Intell. Mater. Syst. Struct. 2010, 21, 1867–1897. [Google Scholar] [CrossRef]
- Daqaq, M.F.; Masana, R.; Erturk, A.; Dane Quinn, D.D. On the Role of Nonlinearities in Vibratory Energy Harvesting: A Critical Review and Discussion. ASME. Appl. Mech. Rev. 2014, 66, 040801–040824. [Google Scholar] [CrossRef]
- Zhang, H.; Corr, L.R.; Ma, T. Issues in vibration energy Harvesting. J. Sound Vib. 2018, 421, 79–90. [Google Scholar] [CrossRef]
- Mann, B.P.; Sims, N.D. Energy harvesting from the nonlinear oscillations of magnetic levitation. J. Sound Vib. 2009, 319, 515–530. [Google Scholar] [CrossRef]
- Sebald, G.; Kuwano, H.; Guyomar, D.; Ducharne, B. Experimental Duffing oscillator for broadband piezoelectric energy harvesting. Smart Mater. Struct. 2011, 20, 102001. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Broadband piezoelectric power generation on high-energy orbits of the bistable Duffing oscillator with electromechanical coupling. J. Sound Vib. 2011, 330, 2339–2353. [Google Scholar] [CrossRef]
- Leadenham, S.; Erturk, A. Unified nonlinear electroelastic dynamics of a bimorph piezoelectric cantilever for energy harvesting, sensing, and actuation. Nonlinear Dyn. 2015, 79, 1727–1743. [Google Scholar] [CrossRef]
- De Paula, A.S.; Inman, D.J.; Savi, M.A. Energy harvesting in a nonlinear piezomagnetoelastic beam subjected to random excitation. Mech. Syst. Signal Process. 2015, 54, 405–416. [Google Scholar] [CrossRef]
- Challa, V.R.; Prasad, M.G.; Shi, Y.; Fisher, F.T. A Vibration Energy Harvesting Device with Bidirectional Resonance Frequency Tunability. Smart Mater. Struct. 2008, 17, 015035. [Google Scholar] [CrossRef]
- Reissman, T.; Wolff, E.M.; Garcia, E. Piezoelectric Resonance Shifting Using Tunable Nonlinear Stiffness. In Proceedings of the SPIE Active and Passive Smart Structures and Integrated Systems, San Diego, CA, USA, 9–12 March 2009; Volume 7288, p. 72880G. [Google Scholar]
- Erturk, A.; Hoffmann, J.; Inman, D.J. A piezomagnetoelastic structure for broadband vibration energy harvesting. Appl. Phys. Lett. 2009, 94, 254102. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Piezoelectric Energy Harvesting; John Wiley & Sons Ltd.: Chichester, UK, 2011. [Google Scholar]
- Ferrari, M.; Ferrari, V.; Guizzetti, M.; Andò, B.; Baglio, S.; Trigona, C. Improved Energy Harvesting from Wideband Vibrations by Nonlinear Piezoelectric Converters. Sens. Actuators A Phys. 2010, 162, 425–431. [Google Scholar] [CrossRef]
- Stanton, S.C.; Erturk, A.; Mann, B.P.; Inman, D.J. Nonlinear piezoelectricity in electroelastic energy harvesters: Modeling and experimental identification. J. Appl. Phys. 2010, 108, 074903. [Google Scholar] [CrossRef]
- Cammarano, A.; Neild, S.A.; Burrow, S.G.; Inman, D.J. The bandwidth of optimized nonlinear vibration-based energy harvesters. Smart Mater. Struct. 2014, 23, 055019–055028. [Google Scholar] [CrossRef]
- Roundy, S.; Zhang, Y. Toward self-tuning adaptive vibration based micro-generators. In Proceedings of the SPIE Smart Structures, Devices, and Systems II, Singapore, 24–26 October 2005; Volume 5649, pp. 373–384. [Google Scholar]
- Dutoit, N.E.; Wardle, B.L. Performance of microfabricated piezoelectric vibration energy harvesters. Integr. Ferroelectr. 2006, 83, 13–32. [Google Scholar] [CrossRef]
- Anton, S.R.; Sodano, H.A. A review of power harvesting using piezoelectric materials (2003–2006). Smart Mater. Struct. 2007, 16, R1. [Google Scholar] [CrossRef]
- Erturk, A.; Vieira, W.G.R.; De Marqui, C., Jr.; Inman, D.J. On the energy harvesting potential of piezoaeroelastic systems. Appl. Phys. Lett. 2010, 96, 184103. [Google Scholar] [CrossRef]
- Kim, M.; Hoegen, M.; Dugundji, J.; Wardle, B.L. Modeling and experimental verification of proof mass effects on vibration energy harvester performance. Smart Mater. Struct. 2010, 19, 045023. [Google Scholar] [CrossRef]
- Crawley, E.F.; Anderson, E.H. Detailed models of piezoceramic actuation of beams. J. Intell. Mater. Syst. Struct. 1990, 1, 4–25. [Google Scholar] [CrossRef]
- Triplett, A.; Quinn, D.D. The Effect of Non-linear Piezoelectric Coupling on Vibration-based Energy Harvesting. J. Intell. Mater. Syst. Struct. 2009, 20, 1959–1967. [Google Scholar] [CrossRef]
- Silva, L.L.; Monteiro, P.C.; Savi, M.A.; Netto, T.A. Effect of the piezoelectric hysteretic behavior on the vibration-based energy harvesting. J. Intell. Mater. Syst. Struct. 2013, 24, 1285. [Google Scholar] [CrossRef]
- Silva, L.L.; Monteiro, P.C.; Savi, M.A.; Netto, T.A. On the Nonlinear Behavior of the Piezoelectric Coupling on Vibration-Based Energy Harvesters. Shock Vib. 2015, 2015, 739381. [Google Scholar] [CrossRef]
- Avirovik, D.; Kumar, A.; Bodnar, R.J.; Priya, S. Remote light energy harvesting and actuation using shape memory alloy-piezoelectric hybrid transducer. Smart Mater. Struct. 2013, 22, 052001–052007. [Google Scholar] [CrossRef]
- Silva, L.L.; Oliveira, S.A.; Pacheco, P.M.C.L.; Savi, M.A. Synergistic Use of Smart Materials for Vibration-Based Energy Harvesting. Eur. Phys. J. Spec. Top. 2015, 224, 3005–3012. [Google Scholar] [CrossRef]
- Le, C.P.; Halvorsen, E.; Sørasen, O.; Yeatman, E.M. Wideband excitation of an electrostatic vibration energy harvester with power-extracting end-stops. Smart Mater. Struct. 2013, 22, 075020–075029. [Google Scholar] [CrossRef]
- Bai, Y.; Carl, M.; Button, T.W. Investigation of using free-standing thick-film piezoelectric energy harvesters to develop wideband devices. Int. J. Struct. Stab. Dyn. 2014, 14, 1440016. [Google Scholar] [CrossRef]
- Hu, H.P.; Cui, Z.J.; Cao, J.G. Performance of a piezoelectric bimorph harvester with variable width. J. Mech. 2007, 23, 197–202. [Google Scholar] [CrossRef]
- Friswell, M.I.; Ali, S.F.; Adhikari, S.; Lees, A.W.; Bilgen, O.; Litak, G. Nonlinear piezoelectric vibration energy harvesting from a vertical cantilever beam with tip mass. J. Intell. Mater. Syst. Struct. 2012, 23, 1505–1521. [Google Scholar] [CrossRef]
- Lesieutre, G.A.; Davis, C.L. Can a coupling coefficient of a piezoelectric actuator be higher than those of its active material? J. Intell. Mater. Syst. Struct. 1997, 8, 859–867. [Google Scholar] [CrossRef]
- Leland, E.S.; Wright, P.K. Resonance Tuning of Piezoelectric Vibration Energy Scavenging Generators Using Compressive Axial Preload. Smart Mater. Struct. 2006, 15, 14131420. [Google Scholar] [CrossRef]
- Betts, D.N.; Kim, H.A.; Bowen, C.R.; Inman, D.J. Optimal configurations of bistable piezo-composites for energy harvesting. Appl. Phys. Lett. 2012, 100, 114104. [Google Scholar] [CrossRef]
- Soliman, M.S.M.; Abdel-Rahman, E.M.; El-Saadany, E.F.; Mansour, R.R. A wideband vibration-based energy harvester. J. Micromech. Microeng. 2008, 18, 115021. [Google Scholar] [CrossRef]
- Kaur, S.; Halvorsen, E. Parameter sensitivity of an in-plane gap closing electrostatic energy harvester with end-stop impacts. J. Intell. Mater. Syst. Struct. 2016, 1, 11. [Google Scholar] [CrossRef]
- Blystad, L.C.J.; Halvorsen, E. A piezoelectric energy harvester with a mechanical end stop on one side. Microsyst. Technol. 2011, 17, 505–551. [Google Scholar] [CrossRef]
- Vijayan, K.; Friswell, M.I.; Khodaparast, H.H.; Adhikari, S. Energy harvesting in a coupled system using nonlinear impact. Struct. Health Monit. 2014, 5, 255–261. [Google Scholar]
- Basset, P.; Galayko, D.; Cottone, F.; Guillemet, R.; Blokhina, E.; Marty, F.; Bourouina, T. Electrostatic vibration energy harvester with combined effect of electrical nonlinearities and Mechanical impact. J. Micromech. Microeng. 2014, 24, 035001. [Google Scholar] [CrossRef]
- Rysak, A.; Müller, M.; Borowiec, M.; Zubrzycki, J.; Litak, G.; Godlewska-Lach, A.; Wittstock, V. Broadband Concept of Energy Harvesting in Beam Vibrating Systems for Powering Sensors. Adv. Sci. Technol. Res. J. 2014, 8, 62–67. [Google Scholar]
- Savi, M.A.; Divenyi, S.; Franca, L.F.P.; Weber, H.I. Numerical and experimental investigations of the on linear dynamics and chaos in non-smooth systems. J. Sound Vib. 2007, 30, 59–73. [Google Scholar] [CrossRef]
- Divenyi, S.; Savi, M.A.; Franca, L.F.P.; Weber, H.I. Nonlinear dynamics and chaos in systems with discontinuous support. Shock Vib. 2006, 13, 315–326. [Google Scholar] [CrossRef]
- Divenyi, S.; Savi, M.A.; Weber, H.I.; Franca, L.F.P. Experimental investigation of an oscillator with discontinuous support considering different system aspects. Chaos Solitons Fractals 2008, 38, 685–695. [Google Scholar] [CrossRef]
- Jacquelin, E.; Adhikari, S.; Friswell, M.I. A piezoelectric device for impact energy harvesting. Smart Mater. Struct. 2011, 20, 105008–105020. [Google Scholar] [CrossRef]
- Vijayan, K.; Friswell, M.I.; Khodaparast, H.H.; Adhikari, S. Non-linear energy harvesting from coupled impacting beams. Int. J. Mech. Sci. 2015, 96, 101–109. [Google Scholar] [CrossRef]
- Kaur, S.; Halvorsen, E.; Søråsen, O.; Yeatman, E.M. Numerical Analysis of Nonlinearities due to Rigid End-Stops in Energy Harvesters. In Proceedings of the Conference: Power MEMS Technical Digest Poster Sessions, Leuven, Belgium, 1–3 December 2010. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).