Seismic Fragility Analysis of CFST Frame-Shear Wall Structures Based on the IDA Method

Abstract

To improve the seismic performance of buildings and reduce earthquake-related disaster risks, this study employs the MIDAS finite element analysis platform to establish a numerical model of a 15-story concrete-filled steel tube frame-shear wall structure. Recorded natural ground motion data are used as the primary input, and a main shock-aftershock sequence is constructed using an attenuation-based method. On this basis, a seismic fragility analysis framework is adopted to derive structural fragility curves, which are subsequently assembled into a comprehensive seismic fragility matrix. The results indicate that, under identical main shock-aftershock sequences, aftershock effects increase the collapse probability of the unretrofitted structure by approximately 17–37%. Furthermore, when buckling-restrained braces are introduced, the structural strength at the same damage state increases by about 8% under the action of the main shock alone and by nearly 24% when both the main shock and aftershocks are considered.

1. Introduction

Historical seismic records indicate that strong aftershocks with considerable destructive potential often occur successively following a main shock [1]. Owing to the extremely short time interval between the main shock and subsequent aftershocks, it is generally impractical to implement timely and effective repair or strengthening measures for damaged buildings [2]. For instance, during the Ms 8.0 Wenchuan Earthquake in 2008 [3], many building structures were initially damaged by the main shock, and the subsequent aftershocks further aggravated the destruction, rendering numerous residential buildings unsafe or even leading to collapse. Moreover, the cumulative effects resulting from progressive structural damage were particularly pronounced. Under such seismic conditions, the interaction and combined influence of main shocks and aftershocks deserve special attention [4].

In current seismic design practice, building structures are typically designed considering only a single seismic event. However, to ensure structural safety and resilience, more comprehensive quantitative evaluations of seismic performance under aftershock sequences are required. Giovanni Rinaldin et al. [5] selected seismic records with peak ground acceleration (PGA) values not lower than those of the main shock as aftershock inputs for time-history analyses, demonstrating that structures subjected to multiple seismic excitations demand significantly higher ductility capacity. Raghunandan et al. [6] performed analytical studies on multi-degree-of-freedom reinforced concrete (RC) frame systems under main shock-aftershock sequences and reported that the maximum interstory drift ratio exhibited limited sensitivity to aftershock effects. Chorafa et al. and Panagiota et al. [7,8] emphasized that multiple seismic scenarios, structure-specific characteristics, and soil-structure interaction (SSI) effects should be comprehensively considered in the seismic design of concrete-filled steel tube (CFST) frame structures and steel structures equipped with buckling-restrained braces (BRBs). Katsimpini et al. [9] proposed an empirical formulation for evaluating the bearing capacity of CFST members based on finite-element numerical simulations. Hua Huang et al. [10,11] further pointed out that the residual strength and stiffness of structures after seismic damage may differ substantially from estimations based solely on drift ratios, suggesting that damage states induced by main shocks can be more accurately characterized by explicitly incorporating residual bearing capacity. Overall, traditional time-history analysis methods based on specific ground motion parameters are insufficient to capture the inherent randomness and uncertainty of structural seismic responses. Consequently, probabilistic approaches for assessing seismic performance and damage have emerged as an important and promising direction for future research.

Incremental dynamic analysis (IDA) is currently one of the most widely adopted methods for evaluating the seismic performance of structures [12,13]. Cornell et al. [14] established a rigorous probabilistic framework for seismic design and performance-based assessment, which was subsequently applied to steel moment-resisting frame systems. Building on this foundation, Wen et al. and Zhou et al. [15,16] proposed fragility assessment frameworks that explicitly account for main shock-aftershock sequences, thereby offering valuable references for seismic design that incorporates aftershock effects. Kinali et al. [17] examined steel frame structures with three different heights, quantified the probabilities associated with four performance limit states, and discussed their implications for seismic risk evaluation. Nazari et al. [18] demonstrated that structural damage assessment based solely on main-shock intensity may lack sufficient accuracy, and suggested that damage states can be more reliably identified through pushover analysis, IDA, or by modifying constitutive relationships.

Shear walls exhibit high lateral stiffness and favorable ductility, making them effective seismic-resistant components. Dowden et al. [19] incorporated thin steel plate shear walls into self-centering steel frames as both lateral load-resisting and energy-dissipating elements, and derived analytical expressions for the internal forces of individual components. Clayton et al. [20,21] proposed corresponding design approaches for self-centering flat steel plate shear walls with either four-edge or two-edge connections. Li Zhuoyu [22] conducted seismic fragility analyses of core tube systems composed of CFST frames combined with steel plate shear walls. Silva et al. [23] investigated the mechanical behavior of CFST columns manufactured with rubberized concrete (RuC) and further evaluated the seismic performance of moment-resisting frames incorporating such members. Dou et al. [24], recognizing the superior seismic behavior of shear walls using CFSTs as boundary confinement elements, proposed a novel prefabricated composite RC shear wall integrated with a CFST frame (CCRCSW-CFST). Nevertheless, studies focusing on the seismic fragility of CFST frame-shear wall structures subjected to main shock-aftershock sequences remain limited. Consequently, it is essential to conduct systematic fragility analyses of CFST frame-shear wall systems under combined main shock and aftershock excitations.

This study focuses on CFST frame-shear wall structures as the primary research object. Through numerical simulations, the seismic performance and corresponding fragility curves of the structural system under main shock and aftershock excitations are evaluated for two structural configurations: with and without BRBs. On this basis, a comparative investigation is carried out to quantify the influence of main shock-aftershock sequences on the overall seismic performance of the structure.

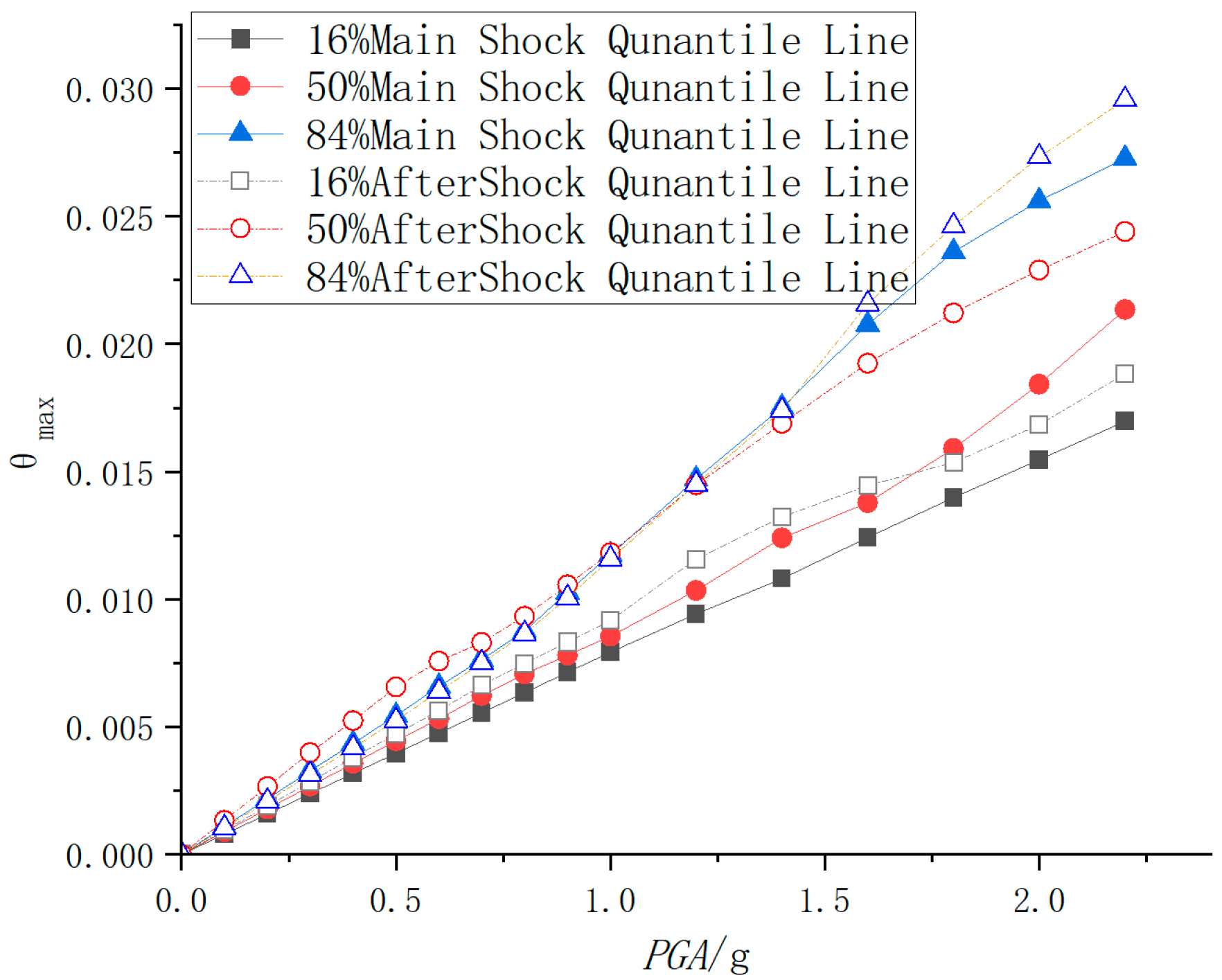
Considering the characteristics of sequential ground motions, this research further examines the correlation among different intensity measures (IMs) associated with main shock-aftershock sequences and clarifies their interdependence. The effects of various aftershock types on the probabilistic seismic demand of CFST frame-shear wall systems are systematically analyzed. Moreover, a multivariate probabilistic seismic demand model incorporating aftershock-related parameters is developed to characterize structural fragility under both single main shock excitation and combined main shock-aftershock loading conditions.

2. Establishment of Finite Element Model and Construction of Seismic Waves

A 15-story CFST frame-shear wall structure is modeled using MIDAS finite element software. The building consists of six spans in the longitudinal direction, with an overall length of 43.2 m, and three spans in the transverse direction, with a total width of 15.0 m. The first story has a height of 4.2 m, while all remaining stories have a uniform height of 3.3 m, resulting in a total structural height of 50.4 m. The shear walls are designed with a thickness of 200 mm. The vertical reinforcement is arranged as 12@200, and the horizontal reinforcement is configured as 10@200. The seismic design parameters adopted in the numerical model are specified in Ref. [25], and the detailed component properties are summarized in

Table 1. Component Parameters.

Component Name	Material Grade	Section Dimension (mm)
Column	C30 Q345	D600 × 10
Longitudinal Beam	Q345	HM550 × 300 × 11 × 18
Cross Member	Q345	HM594 × 302 × 15 × 23
Shear Wall	C30	200

. The standard live load is taken as 2.0 kN/m² for all typical floors and 0.5 kN/m² for the roof, whereas the standard dead load is 3.5 kN/m² for each floor and 5.0 kN/m² for the roof. A three-dimensional perspective view of the structural model is illustrated in Figure 1.

Shell elements were adopted to simulate concrete floor slabs and shear walls, while nonlinear beam elements were employed to model beams and columns. Connection elements were utilized for the modeling of BRBs. For concrete materials, the confined concrete constitutive model was selected, whereas the kinematic hardening model with bilinear characteristics was adopted for steel materials [26]. BRBs were connected to the frame structure exclusively through their core materials, ensuring that the core materials bear all axial forces, while the external steel tubes only serve to constrain the core materials. No bonding treatment was applied between the core materials and external steel tubes to minimize interfacial friction. The Bouc-Wen model was selected for relevant simulations [26,27]. During the dynamic analysis procedure, the P-Δ effect was taken into consideration, and structural control over convergence was implemented based on the displacement criterion. The Newmark integration method was used for solution, with the structural damping ratio set to 0.05. The parameters of BRBs are presented in

Table 2. BRBs Parameters.

Story Number	Yield Bearing Capacity/kN	Elastic Rigidity (kN/mm)	Effective Cross-Sectional Area (mm2)
1–4	1692.81	238.22	4906.7
5–15	1151.16	162.13	3336.7

, and a schematic diagram of the BRBs-CFST frame-shear wall structure is illustrated in Figure 2.

Modal analyses were conducted on the CFST frame-shear wall structures with and without BRBs using two finite element analysis platforms, MIDAS and PKPM. The resulting natural vibration frequencies for both structural configurations are summarized in

Table 3. Comparison Table of Natural Vibration Periods for CFST Frame-Shear Wall Structure.

Modal Shape	Period (s)		Relative Deviation (%)
	MIDAS	PKPM
MODE1	1.806	1.800	0.3
MODE2	1.081	1.082	0.1
MODE3	0.743	0.775	4.3
MODE4	0.594	0.583	1.9

and

Table 4. Comparison Table of Natural Vibration Periods for CFST Frame-Shear Wall Structure with BRBs.

Modal Shape	Period (s)		Relative Deviation (%)
	MIDAS	PKPM
MODE1	1.581	1.575	0.3
MODE2	1.072	1.083	1.0
MODE3	0.762	0.767	0.7
MODE4	0.499	0.513	2.8

, respectively.

As indicated in Table 3 and Table 4, the maximum discrepancy in the calculated natural vibration periods of the CFST frame-shear wall structure without BRBs is within 4.3%, while the corresponding error for the structure equipped with BRBs does not exceed 2.8%. These results demonstrate that the dynamic responses of the structural systems can be predicted with satisfactory accuracy using the MIDAS finite element analysis platform. Moreover, MIDAS enables efficient post-processing and interpretation of dynamic response data. Accordingly, MIDAS is adopted in this study as the primary tool for conducting subsequent numerical analyses.

In accordance with the Chinese Standard for the Seismic Resilience Assessment of Buildings [28], a dual-control criterion based on PGA and peak ground velocity was adopted to ensure that the selected ground motions satisfied the minimum requirements for both acceleration and velocity. A total of ten seismic records were employed in the subsequent analyses, comprising six recorded natural ground motions and four synthetic motions. All ground motion data were obtained from the Pacific Earthquake Engineering Research center (PEER), and the corresponding parameters are summarized in

Table 5. Seismic Wave Information.

Serial Number	Seismic Wave Name	Station Information	Time	Magnitude	PGA/g		Time/s
					Main Shock	Aftershock
1	TRB1	“Lab. Gran Sasso”	2009	6.3	0.021	0.029	100
2	TRB2	“Jiashi”	1997	6.1	0.300	0.274	100
3	TRB3	“TCU138”	1999	7.2	0.212	0.152	100
4	TRB4	“LA—Wonderland Ave”	1994	6.69	0.103	0.055	100
5	TRB5	LA—Obregon Park	1989	6.93	0.428	0.344	100
6	TRB6	“Imperial Valley Wildlife Liquefaction Array”	1987	6.54	0.179	0.131	100
7	RGB1	“Benton”	1986	6.19	0.209	0.11	100
8	RGB2	“Pleasant Valley P.P.—yard”	1983	6.36	0.602	0.575	100
9	RGB3	Alhambra—Fremont School	1987	5.99	0.290	0.181	100
10	RGB4	“Managua_ ESSO”	1972	6.24	0.372	0.263	100

. In addition, the normalized response spectra of the selected ground motions are presented in Figure 3.

Main shock-aftershock sequences were generated using the attenuation method [29,30], and amplitude modulation was performed through the Hunt-Fill unequal-step modulation technique. Considering the realistic dynamic response characteristics of structures subjected to seismic loading, a time interval of 30 s was introduced between the main shock and aftershock inputs. This interval was selected to allow the structural response induced by the main shock to fully develop while preserving the plastic damage accumulated during the initial excitation. The detailed procedure for constructing the main shock-aftershock sequences is illustrated in Figure 4. A bidirectional seismic input scheme was adopted, in which the longitudinal and transverse axes of the structure were designated as the principal and secondary input directions, respectively. For the primary direction, the ground motion was applied without scaling, whereas the input in the secondary direction was scaled by a factor of 0.8.

3. Fragility Analysis Based on IDA

3.1. Classification of Structural Limit States

Based on the recommendations for deformation limits of hybrid frame structures under seismic action in the Reference Technical Specification for Concrete Structures of Tall Buildings [26] and in line with the seismic performance requirements for structural members at different damage stages, the deformation capacity limit of this structural system is determined. This study defines four performance levels for the structure [31]: Normal Operation (N O), Immediate Occupancy (I O), Life Safety (L S), and Collapse Prevention (C P). The limit values for inter story displacement angles are shown in

Table 6. Different Performance Levels of the Structure.

Limit States	N O	I O	L S	C P
$[\theta ]$	1/550	1/250	1/120	1/50

.

3.2. Seismic Incremental Dynamic Analysis (IDA)

3.2.1. Incremental Dynamic Analysis (IDA) Curve

The IDA method [32] was employed to perform elastoplastic dynamic analyses of the steel-concrete frame-shear wall structure, resulting in the generation of IDA curves. These results are presented in Figure 5 and Figure 6. In the plots, the horizontal axis represents the maximum PGA, while the vertical axis corresponds to the structure’s maximum interstory drift ratio.

Figure 5 and Figure 6 indicate that the IDA curve clusters for both structural configurations exhibit good overall convergence, suggesting a relatively stable structural response under seismic excitation. As the PGA increases, the maximum interstory drift angle (θ_max) correspondingly rises. For PGA values below 0.5 g, the interstory displacement responses of both structures are highly consistent. When PGA exceeds 0.8 g, the IDA curves begin to diverge noticeably, with the distribution of responses remaining relatively uniform.

This behavior reflects that the selected ground motions adequately account for seismic uncertainty in the design. Under stronger seismic excitations, differences in response between the two structural types become apparent. For PGA values below the ultimate working condition of the members, BRBs effectively absorb seismic energy and support the structure, maintaining stability. When PGA surpasses the ultimate capacity of the members, structural resistance to seismic action is further reduced. In contrast, the CFST frame-shear wall system equipped with BRBs exhibits significantly lower responses. Overall, the initial main shock induces substantial damage and generates large residual deformations in the structure. Subsequent aftershocks amplify this damage, further compromising seismic resistance. However, the inclusion of BRBs mitigates structural deformation, enhances lateral stiffness, and improves overall stability and performance under seismic loading.

3.2.2. IDA Quantile Curves

When seismic records of varying intensities are applied to the CFST structure, some dispersion is observed in the resulting IDA curves. To characterize the structural response under different seismic intensities, the 16th, 50th, and 84th percentile lines are adopted. These quantile curves serve to reduce the variability inherent in the IDA results [33]. The corresponding quantile curve plots are presented in Figure 7 and Figure 8, while the quantile line intensity matrices are summarized in

Table 7. Quantile Line Intensity Matrix of Limit States for CFST Frame-Shear Wall Structure.

Percentile	Main Shock				Main-Aftershock
	N O	I O	L S	C P	N O	I O	L S	C P
16%	0.277	0.506	1.141	>2.000	0.202	0.406	0.868	1.955
50%	0.181	0.369	0.772	1.780	0.173	0.347	0.790	1.506
84%	0.120	0.278	0.615	1.311	0.107	0.214	0.356	1.228

and

Table 8. Quantile Line Intensity Matrix of Limit States for CFST Frame-Shear Wall Structure with BRBs.

Percentile	Main Shock				Main-Aftershock
	N O	I O	L S	C P	N O	I O	L S	C P
16%	0.329	0.564	1.127	>2.2	0.211	0.422	0.902	>2.2
50%	0.264	0.449	0.970	2.108	0.191	0.401	0.803	1.677
84%	0.167	0.368	0.762	1.553	0.174	0.383	0.772	1.525

.

Analysis of Figure 7 and Figure 8 indicates that the structural IDA curves exhibit reasonable dispersion, demonstrating that they effectively capture the dynamic response of the structure under seismic loading. As shown in Table 7 and Table 8, for the same damage states, the ultimate intensity under aftershock excitation is lower than that under the main shock, with reductions ranging from approximately 17% to 37%. This decrease arises because the structure sustains significant damage and retains residual deformation after the initial seismic event, and the aftershocks further amplify the deterioration, thereby reducing seismic resistance. The incorporation of BRBs mitigates this effect, increasing the ultimate intensity for the same damage states by roughly 8% to 24%. BRBs not only limit seismic-induced deformations but also enhance lateral stiffness, thereby improving the structure’s overall stability and resilience under combined main shock-aftershock loading.

3.3. Seismic Fragility Analysis

Yu Xiaohui [33] highlighted that a relationship exists between the structural deformation measure (DM) and the seismic ground motion intensity measure (IM) in seismic response analysis:

$$\mathrm{DM}=\mathrm{a}{\left(\mathrm{IM}\right)}^{\mathrm{b}}$$

(1)

Applying a logarithmic transformation to Equation (1) results in a linear relationship between the structural DM and the seismic IM in the logarithmic domain.

$$\ln (\mathrm{DM})=\ln (\mathrm{a})+\mathrm{b}\ln (\mathrm{IM})$$

(2)

Data fitting and regression analyses were conducted using Origin software, and the resulting regression plots are presented in Figure 9 and Figure 10.

Through the fitting analysis, the probabilistic seismic demand functions for the main shock, expressed in Equations (3)–(6) based on interstory drift angles, were obtained.

Uncontrolled structure (Main shock):

$$\ln ({\mathsf{\theta }}_{\max })=0.9905\ln (\mathrm{PGA})-4.5126$$

(3)

BRBs (Main shock):

$$\ln ({\mathsf{\theta }}_{\max })=1.0037\ln (\mathrm{PGA})-4.6222$$

(4)

Uncontrolled structure (Aftershock):

$$\ln ({\mathsf{\theta }}_{\max })=0.9767\ln (\mathrm{PGA})-4.3995$$

(5)

BRBs (Aftershock):

$$\ln ({\mathsf{\theta }}_{\max })=1.0009\ln (\mathrm{PGA})-4.5300$$

(6)

The probability that a structure exceeds a specified damage state under seismic loading can be expressed mathematically using the standard normal distribution function, as follows:

$${\mathrm{P}}_{\mathrm{f}}=\mathsf{\Phi }\left({\displaystyle \frac{\ln [\mathsf{\alpha }{(\mathrm{PGA})}^{\mathsf{\beta }}]/[\mathsf{\theta }]\hspace{1em}}{0.5}}\right)$$

(7)

Using Equations (3)–(7), the exceedance probabilities of the structure corresponding to different PGA levels were determined. The resulting seismic fragility curves are presented in Figure 11.

As shown in Figure 11, the exceedance probabilities for the four defined performance levels increase progressively with rising PGA, consistent with the specified interstory drift limits. At low PGA values, structural displacements are small, easily satisfying the NO criteria, resulting in a relatively high exceedance probability for NO. Conversely, at high PGA values, large structural displacements make it difficult to satisfy the CP criteria, leading to a marked increase in the exceedance probability of CP. These observations indicate a nonlinear relationship between structural performance levels and PGA, with performance gradually degrading from superior to inferior states as seismic intensity increases. Comparative analysis of the exceedance probability curves for structures with and without BRBs across different PGA levels and seismic sequences highlights the influence of BRBs on structural fragility. Structures equipped with BRBs exhibit a significant reduction in collapse risk under identical PGA conditions, demonstrating enhanced seismic resilience and improved structural reliability. The main shock-aftershock fragility curves of BRB-equipped structures display broader intervals, reflecting their superior capacity for seismic energy absorption and dissipation. Under main shock-aftershock sequences, BRBs effectively reduce plastic deformation in structural members, maintaining the structure’s load-bearing capacity and lowering the likelihood of overall structural failure.

A detailed analysis of the fragility curves presented in Figure 11 allows for the determination of the exceedance probabilities of the structure at each performance limit state under three representative seismic intensities: frequent earthquake (0.07 g), design-basis earthquake (0.2 g), and rare earthquake (0.4 g). Based on these results, the corresponding seismic fragility matrices of the structure can be constructed. The complete data for these matrices are provided in

Table 9. Seismic Fragility Matrix of CFST Frame-Shear Wall Structure (%).

Earthquake Magnitude	Main Shock				Main-Aftershock
	N O	I O	L S	C P	N O	I O	L S	C P
Many Encounters	3.12	0.06	0.00	0.00	5.89	0.16	0.00	0.00
Fortify	58.54	12.09	0.43	0.00	68.66	18.41	0.91	0.00
Rare Encounter	94.40	58.03	10.43	0.13	96.71	67.51	15.72	0.29

and

Table 10. Seismic Fragility Matrix of CFST Frame-Shear Wall Structure with BRBs (%).

Earthquake Magnitude	Main Shock				Main-Aftershock
	N O	I O	L S	C P	N O	I O	L S	C P
Many Encounters	1.56	0.02	0.00	0.00	2.54	0.04	0.00	0.00
Fortify	48.17	7.60	0.19	0.00	55.86	10.77	0.35	0.00
Rare En-counter	91.08	48.37	6.67	0.00	93.76	55.91	9.49	0.00

.

Analysis of the data in Table 9 and Table 10 indicates that aftershocks exacerbate the cumulative structural damage caused by the main shock. Furthermore, the changes in exceedance probabilities differ between structures without and with BRBs across various performance limit states and seismic intensities. For a frequent earthquake intensity (0.07 g), the exceedance probabilities of the NO limit state during the main shock are 3.12% for the uncontrolled structure and 1.56% for the BRB-equipped structure. When aftershocks are superimposed, these probabilities increase by 2.77% and 0.98%, respectively. Under a design-basis earthquake intensity (0.2 g), the exceedance probabilities for the IO limit state during the main shock are 12.09% for the structure without BRBs and 7.60% for the structure with BRBs. After aftershocks, the probabilities rise by 6.32% and 3.17%, respectively, while neither structure reaches the LS limit state at this intensity. For a rare earthquake intensity (0.4 g), the exceedance probabilities for the LS limit state during the main shock are 10.43% for the uncontrolled structure and 6.67% for the BRB-equipped structure, increasing by 5.29% and 2.82%, respectively, when aftershocks are considered.

The inclusion of BRBs as seismic energy-dissipating components enhances structural ductility and lateral stiffness, improves overall stability and safety margins, and substantially reduces the likelihood of the structure entering a damage state under seismic excitation.

4. Conclusions

This study investigates the seismic fragility of a 15-story CFST frame-shear wall structure. Using IDA, the exceedance probabilities of the structure at various performance limit states under three representative seismic intensities were determined. Based on these results, fragility curves were constructed and fragility matrices formulated, providing a foundation for structural seismic risk assessment.

(1)

When the main shock induces only minor damage, the subsequent effect of aftershocks on structural fragility is limited. In contrast, if the main shock causes significant initial damage, the seismic resistance of the structure gradually declines. Notably, when the structure reaches the LS limit state due to the main shock, its fragility under subsequent aftershocks becomes more pronounced.

(2)

Under the same damage conditions, the ultimate intensity under aftershock excitation is approximately 17–37% lower than that under the main shock, indicating that main shock-aftershock sequences exacerbate structural damage. The inclusion of BRBs increases the ultimate intensity by roughly 8–24% for the same damage states, substantially improving the structure’s seismic capacity and overall stability.

(3)

The installation of BRBs effectively reduces structural damage under seismic loading, including aftershocks, while enhancing overall stability and safety. For instance, under rare earthquake conditions, the exceedance probabilities of the LS limit state during the main shock are 10.43% for the structure without BRBs and 6.67% for the structure with BRBs. When aftershocks are considered, these probabilities increase by 5.29% and 2.82%, respectively, demonstrating the significant protective effect of BRBs in mitigating seismic damage.