Seismic Performance of the Full-Scale Prefabricated Concrete Column Connected in Half-Height: Experimental Study and Numerical Analysis

Abstract

To improve the seismic performance of prefabricated structures, this study suggested putting grouted sleeves at the half-height of the column (at the point of contraflexure). A quasi-static test under constant axial load was conducted on the full-scale cast-in-place column and the full-scale prefabricated column connected in half-height. The hysteresis loops, skeleton curves, ductility, stiffness degradation, and energy dissipation capacity were compared. The test results indicate that the prefabricated column connected in half-height exhibited reliable seismic performance. Compared with the cast-in-place specimen, the bearing capacity of the prefabricated column decreased by only 1.45%, the energy dissipation decreased by 5.61%, and the initial secant stiffness and ductility coefficient increased by 8.88% and 9.09%, respectively. ABAQUS finite element software was used to establish finite-element models based on the experimental results. The damage pattern and seismic performance indicators of the two types of columns were verified by resolving issues related to the bonding interface model of sleeve-connected columns and the convergence of the multidimensional constitutive model. The formula for calculating the shear bearing capacity was put forward to evaluate the failure pattern. The study provides a basis for further investigation of the seismic performance of sleeve-connected columns with different connection positions under extreme conditions.

1. Introduction

Green, ultra-low energy, high-quality, and digitally integrated buildings are predominantly realized through prefabricated construction [1]. Numerous earthquake disasters demonstrate that they are characterized by sudden onset, high destructive potential, wide impact range, difficulty in rescue operations, concentrated casualties, and significant economic losses [2]. The primary factor restricting the development of prefabricated structures is the relatively lower structural integrity and seismic performance of assembled concrete frames compared with traditional cast-in-place concrete frames [3,4]. These prefabricated structures depend heavily on various connection technologies, which are critical for ensuring structural integrity [5]. Structural failure of buildings during earthquakes is primarily caused by inadequate mechanical properties of the connections [6].

The mechanical properties of concrete columns, as the primary load-bearing elements of prefabricated buildings, become increasingly critical for structural safety as building height increases. Among them, prefabricated concrete columns with grouted sleeve connections have been widely used in assembly construction [7]. The seismic performance of prefabricated columns with grouted sleeve connections has been extensively evaluated through numerous experimental studies [8,9,10,11,12]. Sleeve-connected columns were affected by grouting defects [13], axial compression ratio [14], shear span ratio [15], concrete strength [16], and reinforcement detailing [17]. Bompa et al. [18] reported that the deformation capacity of the columns decreased when grouted sleeves were placed in the plastic hinge region. Zeng et al. [19] conducted an experimental study on the seismic performance of prefabricated concrete columns with circular cross-sections connected by grouted sleeves. They found that, although a few steel bars were pulled out at the sleeves of prefabricated columns, the failure mode of sleeve-connected columns was similar to that of cast-in-place concrete columns. Haber et al. [20] used the location of the grouted sleeve within the plastic hinge zone as a test variable and found that it could significantly affect the plastic hinge mechanism. Most studies on sleeve-connected prefabricated columns focus on column-to-foundation connections (plastic hinge zone), while information on the seismic performance of prefabricated columns with column-to-column connections (away from the plastic hinge zone) remains limited. The quasi-static tests were primarily conducted on half-columns. Few studies have investigated the seismic performance of full-scale prefabricated columns with column-to-column connections under realistic operating conditions.

Sleeve-connected specimens possess multiple bonding interfaces, including the concrete–sleeve interface, sleeve–grouting material interface, grouting material–steel bar interface, and steel bar–concrete interface. Achieving convergence in numerical simulations is challenging due to the multidimensional constitutive relationships and the advanced modeling of bonding interactions. Since the length of the grouted sleeve connection is much smaller than the height of prefabricated components, Ameli et al. [21] developed an efficient stress–strain model for the grouted sleeve connection by modifying the constitutive relationship of the steel bars. Su et al. [22] simplified the sleeve connection as a beam element with equivalent properties, including cross-sectional area, elastic modulus, and yield strength. Based on tensile tests of sixty half-grouted sleeve connections under uniaxial and cyclic loads, Zhang et al. [23] developed a bilinear stress–strain model corresponding to the load–displacement curve. The bond-slip effect between concrete and sleeve is completely ignored in the simplified constitutive model of sleeve connection, which is very different from the modeling used in real-world engineering applications. Therefore, it remains unclear how the stress–strain model of the sleeve connection can be applied in finite-element analyses to evaluate the seismic performance of full-scale prefabricated columns with column-to-column connections more accurately.

To enhance the connection strength and ductility, the connection in this study is placed at the mid-height of the column, corresponding to the point of minimum bending moment. It is important to note that shear stress damage in prefabricated concrete columns with mid-height connections cannot be neglected, particularly at the connection, which represents the structural weak point of the column. The full-scale cast-in-place column and the full-scale prefabricated column connected in half-height were fabricated in this study. The two types of full-scale columns subjected to horizontal cyclic loading were evaluated using multiple seismic performance criteria, including failure modes, hysteretic behavior, skeleton curves, ductility, energy dissipation capacity, and stiffness degradation. Abaqus 2021 software was employed for numerical simulations, implementing the full constitutive model of the half-grouted sleeve connection to investigate the seismic performance of the sleeve-connected column. The study also addressed convergence challenges and verified the feasibility of finite-element simulations. This approach provides a theoretical foundation for the design of precast column connections in subsequent stages and for assessing their seismic response under extreme conditions.

2. Experimental Program

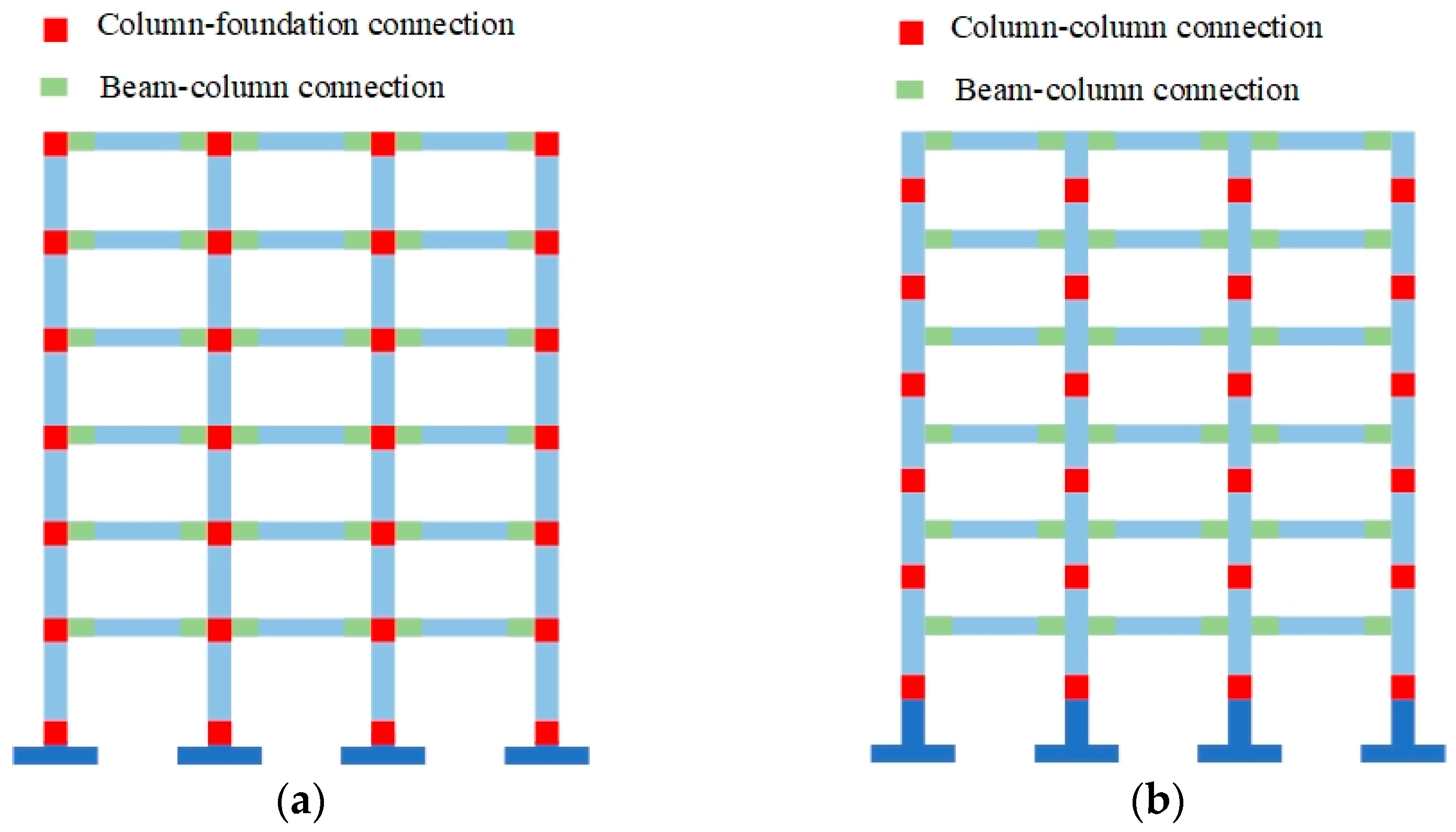
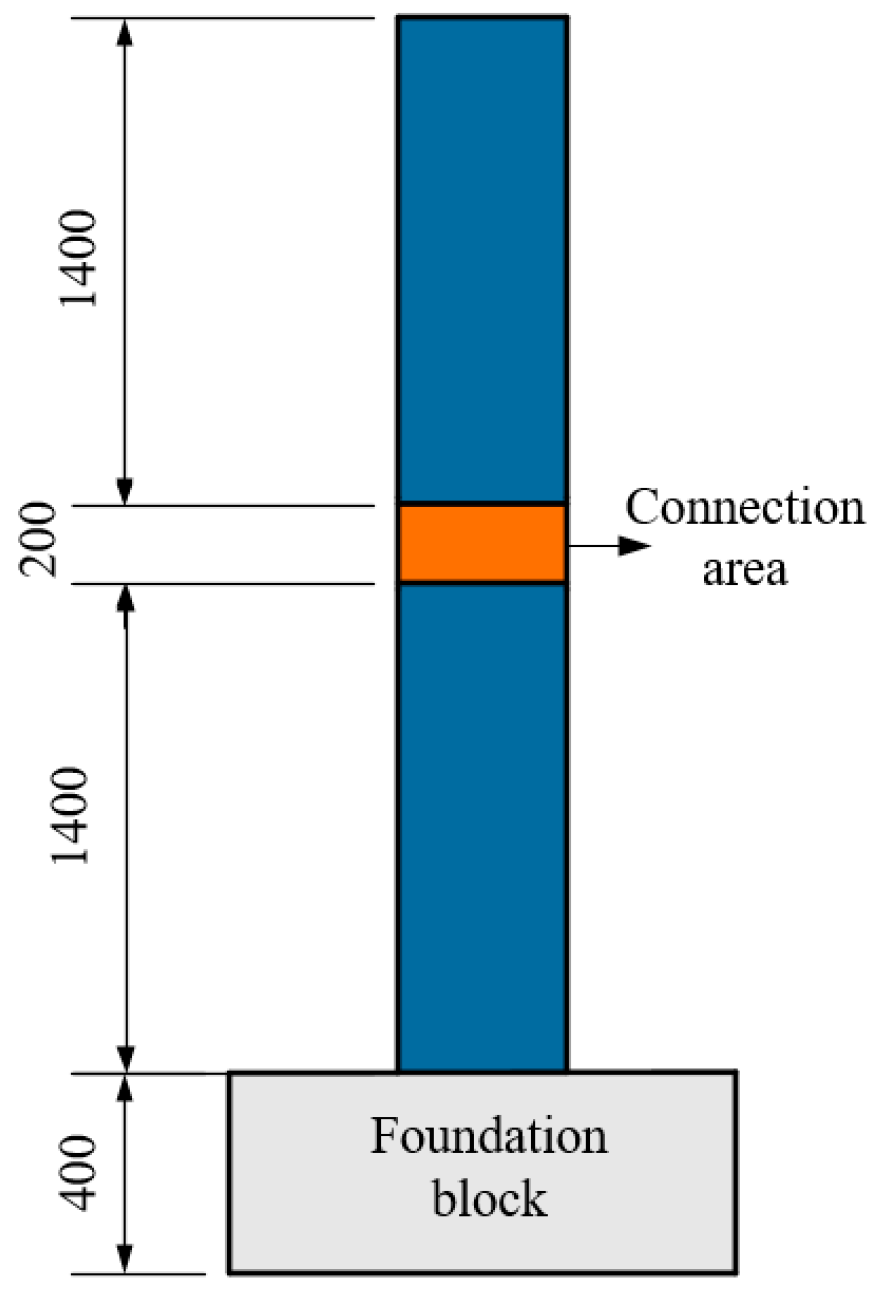
2.1. Connection Design

The reliability of connections between prefabricated components critically influences the seismic performance of the overall structure. Interfacial connections—notably beam–column joints and column–foundation joints—constitute the principal means of assembling prefabricated frame systems. These connections are characterized by stress concentration, complex construction requirements, and challenges in quality inspection. As shown in Figure 1a, such joints often constitute the weak zones in prefabricated members. The mechanical behavior of the test specimen is presented in Figure 2, where the grouted sleeve connection is placed at the column’s half-height, coinciding with the point of minimum bending moment. The proposed connection (Figure 1b) effectively mitigates the issues described above and endows the column with enhanced structural integrity, ductility, and strength. The design requirement—namely, that the connection be located at the column’s half-height—is fulfilled by setting the 25 mm grouting layer placing the connection 1400 mm from the top (or bottom) of the column, as illustrated in Figure 3. Although the bending moment peaks at the column ends, the shear stress remains relatively uniform along its height. The shear force is still large even though the connecting position avoids the area with an elevated level of bending moment. The primary objective of this study is to prevent severe shear failure in prefabricated columns that are connected in half-height.

2.2. Test Specimen

Two full-scale columns, having identical geometry and reinforcement details, were tested (Figure 4) to compare their seismic performance. The test variable in this study was the column type (cast-in-place vs. precast), as summarized in

Table 1. Details of specimens.

Specimen Type	Sectional Size (mm)	Height (mm)	n	Concrete Strength	Longitudinal Reinforcement	Stirrups (Stirrups Near Mid-Connection)
CIPC	300 × 300	3000	0.2	C35	8C16	B8@100 (B8@50)
PCCH	300 × 300	3000	0.2	C35	8C16	B8@100 (B8@50)

Notes: CIPC represents cast-in-place reinforced concrete columns; PCCH represents prefabricated column connected in half-height.

. The objective of this study was to assess the seismic performance of the half-height connection under earthquake loading. The columns were 3000 mm tall with a square cross-section of 300 × 300 mm. The columns were cast in C35 concrete, with a nominal compressive strength of 35 MPa. According to GB 50010-2010 [24], the distance from the outer edge of the reinforcing bars to the surface of the structural member is defined as the concrete cover. A concrete cover (protective layer) thickness of 30 mm was adopted. The longitudinal bars in the specimens were HRB400 grade (hot-rolled ribbed bars with a nominal yield strength of 400 MPa) with a nominal diameter of 16 mm. The stirrups were HRB335 grade (hot-rolled ribbed bars with a nominal yield strength of 335 MPa) with a nominal diameter of 8 mm. The columns contained eight 16 mm-diameter longitudinal bars, corresponding to a reinforcement ratio of 1.79%. The stirrups, with a diameter of 8 mm, were spaced at 50 mm pitch near the connection region and at 100 mm pitch away from the connection region. In fact, columns in single-story buildings or peripheral columns in multi-story buildings may experience very low axial compression [12]. The axial compression ratio is determined based on the Chinese design code for seismic design of buildings [25]. n is the axial compression ratio when n is 0.2 take 350 kN. The calculation formula of the axial compression ratio is n = N_u/(f_cA_c + f_yA_s), where N_u is the axial compression load. Figure 5 illustrates the fabrication process of the specimens.

2.3. Material Properties

The material tests for reinforcement, concrete, and grout are summarized in Figure 5e. The average compressive strength of the concrete specimens was 35.7 MPa, determined according to the GB/T 50081-2019 standard [26]. A tensile test was performed on batches of reserved reinforcement following the ISO 6892-1 standard [27]. The results of the tensile tests are presented in

Table 2. Mechanical properties of steel reinforcement.

Material	Diameter (mm)	Yield Strength (MPa)	Ultimate Strength (MPa)
HRB400	16	400.37	551.85
HRB335	8	346.13	433.36

. The grout used in the grouting layer and sleeves was tested on 40 × 40 × 160 mm rectangular prisms, in accordance with ISO 679 [28] and JG/T 408 [29]. The grout exhibited a flexural strength of 13.77 MPa and a compressive strength of 95.30 MPa.

Table 3. Geometric parameters of half-grouted sleeve.

Type	Total Length (mm)	Anchor Length (mm)	Thread Length (mm)	Outer Diameter (mm)	Inner Diameter (mm)
GTB4Z-16/16 *	175	144	29	38	28

* GTB4Z-16/16, G represents direct rolling forming; T represents grouted sleeve.; B represents the standard type; 4 represents 400 MPa which is the yield strength of the connecting reinforcement; Z represents the straight-thread design of the thread end; 16/16 represents that the diameter of the protruded bar and the embedded bar is 16 mm.

presents the detailed geometric specifications of the half-grouted sleeve (model GTB4Z-16/16) used in the connection. The sleeves were supplied by Qingdao Zhongke Kuntai Assembly Construction Technology Co., Ltd., Qingdao, China. Uniaxial tensile tests showed that the sleeve’s ultimate tensile strength reached 404.56 MPa [30].

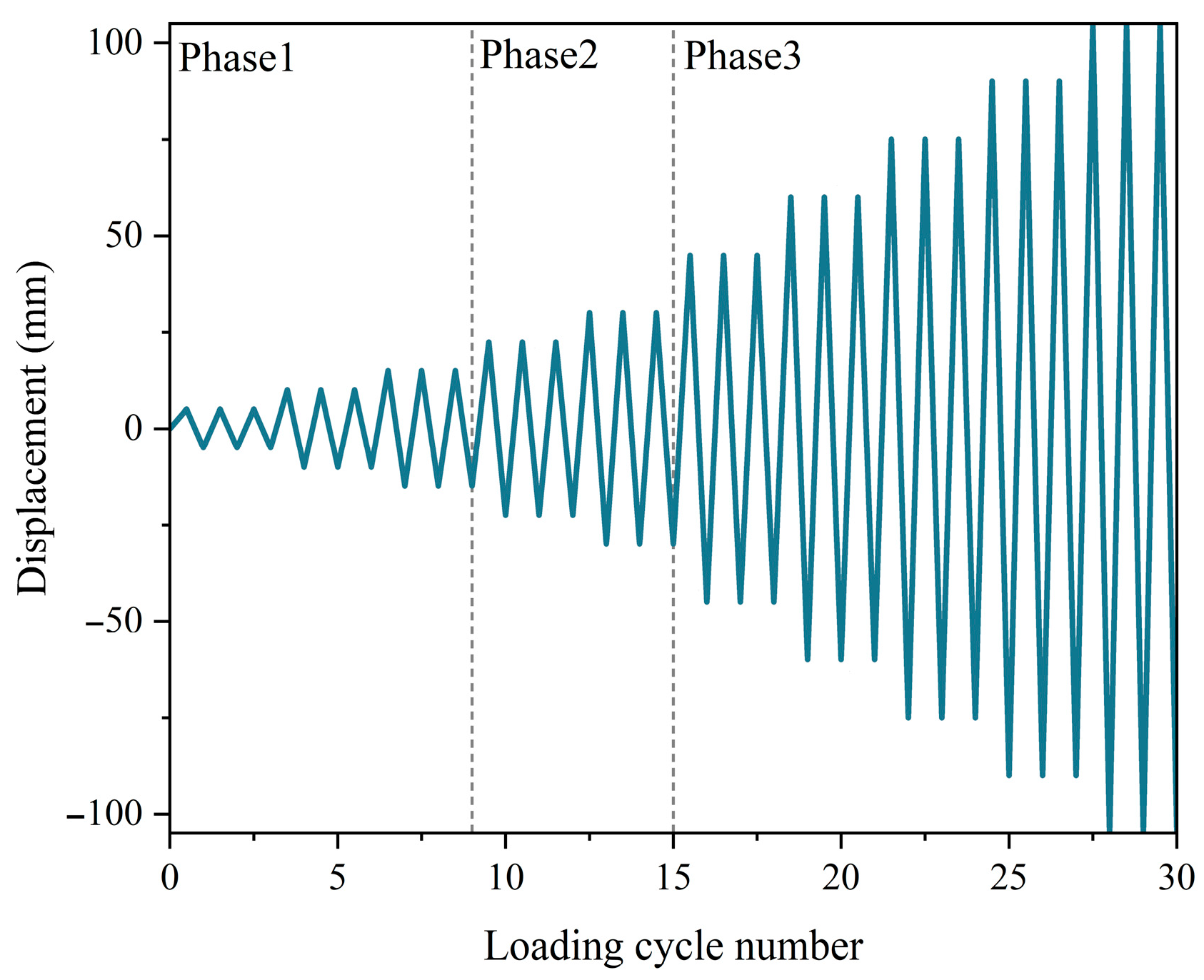
2.4. Test Setup and Instrumentation

The specimens were tested under pseudo-static loading using a servo-controlled MTS hydraulic actuator, as illustrated in Figure 6. First, an axial load was applied, followed by a lateral load. The design axial compression ratio was set to 0.20. The boundary condition was implemented as a “fixed–fixed” (both ends fixed) connection, in accordance with the actual project configuration. The column’s top was fastened to the loading beam using bolts, L-shaped steel plates, and embedded steel plates, while its base was anchored to the foundation by anchor bolts. The loading protocol was displacement-controlled and consisted of three phases comprising a total of ten displacement stages. The loading protocol is displacement-controlled and divided into three phases. The first phase comprised displacement levels of 5 mm, 10 mm, and 15 mm; the second phase included 22.5 mm and 30 mm; and the third phase comprised 45 mm, 60 mm, 75 mm, 90 mm, and 105 mm. At each level, three loading cycles were performed. The test was terminated when the column’s load-bearing capacity dropped to 85% of its peak value. Figure 7 illustrates the loading setup. Moreover, following each cycle, a one-minute hold was introduced to document damage to the column, as shown in Figure 5d.

3. Experimental Results and Discussions

3.1. Damage Progression

CIPC specimen: Drift (Δ/H) represents the ratio of lateral displacement at the top of the column to the column height. At the fifth loading step (1.0% drift level), cracks initiated on the loaded side, with a measured width of approximately 0.21 mm. When loaded to a displacement of 45 mm (1.5% drift level), an inclined crack appeared at the top of the column, measuring approximately 0.28 mm in width, along with minor concrete spalling. As the displacement increased to 60 mm (2.0% drift level), cracks became more numerous, and the spalling region at the top expanded. At 75 mm displacement (2.5% drift level), inclined cracks at the bottom of the column further propagated and widened, reaching a maximum width of roughly 0.30 mm. Under 90 mm displacement (3.0% drift level), significant concrete spalling occurred at the base of the column. As shown in Figure 8a, at a displacement of 105 mm (3.5% drift level) the specimen failed: the reinforcing bars were exposed, and severe concrete spalling occurred at both the top and the base of the column.

PCCH specimen: At a loading displacement of 30 mm (1.0% drift level), cracks appeared on the loading side, with widths of approximately 0.20 mm. When the displacement reached 45 mm (1.5% drift level), cracks at the base of the column measured around 0.25 mm. As loading increased to 60 mm (2.0% drift level), slight concrete spalling occurred at the bottom, and the maximum crack width widened to about 0.28 mm. At 75 mm displacement (2.5% drift level), inclined cracks developed at the top and bottom: the top crack reached a maximum width of approximately 0.30 mm, while the bottom crack measured around 0.26 mm. Upon further loading to 90 mm (3.0% drift level), substantial concrete spalling took place at the base of the column. Finally, at 105 mm displacement (3.5% drift level), large fragments of concrete detached from both the top and bottom, the reinforcing steel was exposed, and the specimen failed completely (Figure 8b).

In conclusion, both specimen types exhibited flexural failure, and their failure mechanisms were nearly identical. Cracks initially developed at both the top and bottom of the column during the early loading phase. As loading progressed into the intermediate stage, these cracks deepened and widened, gradually propagating from the column ends toward the half-height region. In the later loading stages, extensive concrete spalling occurred at both the top and base of the column; the plastic hinge expanded, the reinforcing steel became exposed, and ultimately the specimen failed. Compared with the cast-in-place columns, the half-height grouted-sleeve connection enhanced the stiffness and, together with increased stirrup density in the connection region, resulted in smaller crack widths and less localized damage under the same displacement. The sleeve connection also demonstrated excellent tensile performance and no observable bond–slip failure, as illustrated in Figure 9.

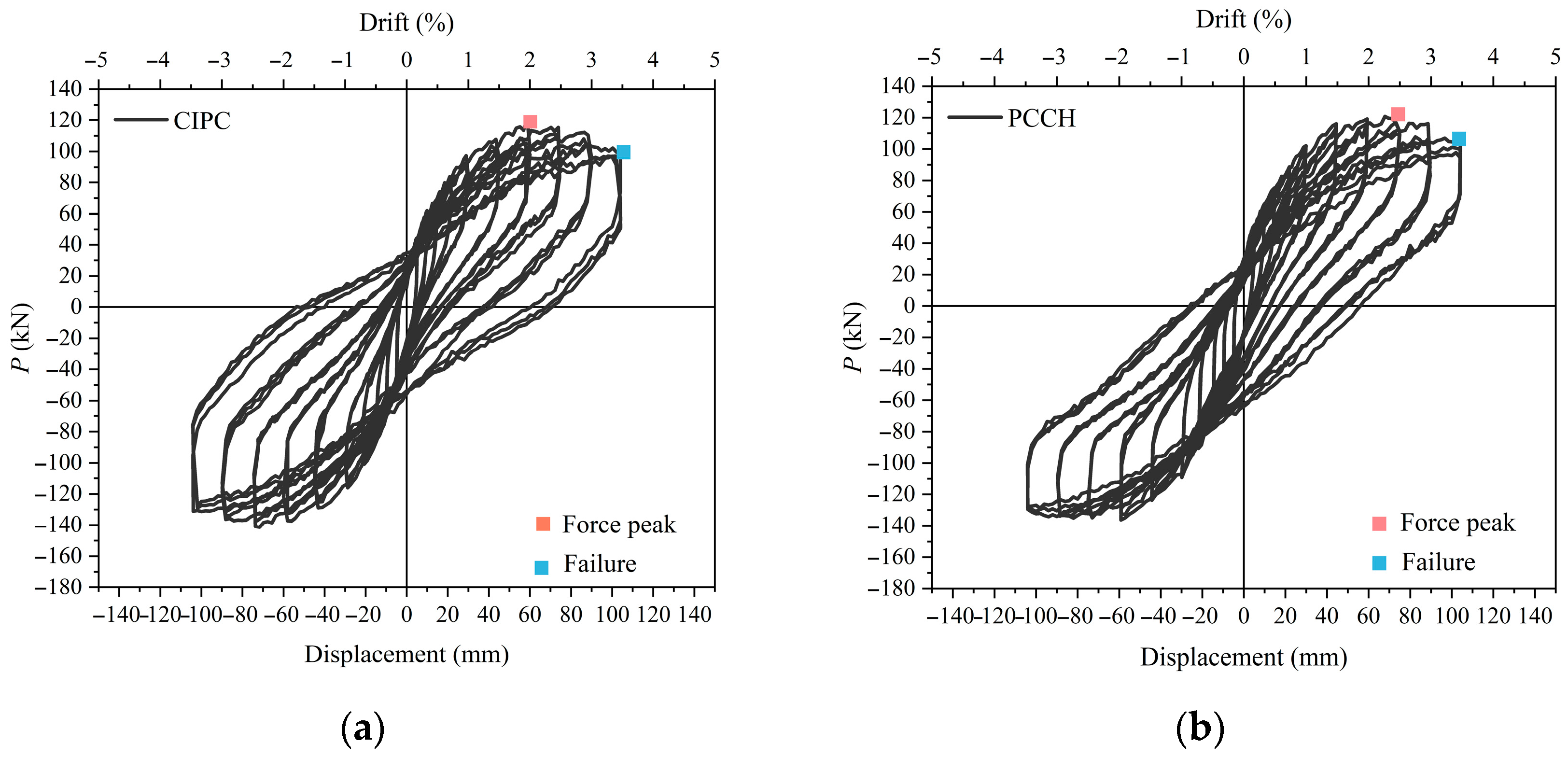
3.2. Hysteretic Response

The hysteresis curves—depicting the load–displacement relationship under cyclic loading—are fundamental for evaluating seismic performance, including bearing capacity, deformation capacity, stiffness degradation, energy dissipation, and ductility. Figure 10 shows the hysteretic loops for the two specimen types. Initially, both the loading and unloading branches were nearly linear and overlapped closely, indicating minimal residual deformation prior to yielding. As displacement increased, the slope of the loops gradually decreased, demonstrating stiffness degradation. Simultaneously, residual deformations accumulated over cycles, and the pinching effect became more pronounced, reflecting reduced energy dissipation efficiency.

Compared with the cast-in-place columns, the half-height grouted-sleeve prefabricated columns exhibited essentially the same peak load and failure load. Under identical displacement cycles, the pinching effect in the hysteresis loops of the precast columns was more pronounced, and this divergence between the two column types became increasingly evident with larger loading amplitudes. This behavior can be attributed to deeper cracks forming at the grouted-sleeve interface, where repeated crack opening and closing intensified bond-slip between the concrete and reinforcing bars. As the specimens approached their ultimate load, precast columns exhibited more severe performance degradation and significantly increased slip. The ultimate displacement under positive loading was correspondingly larger, while slip in the negative direction delayed the attainment of ultimate strength. Consequently, the precast columns showed more pronounced asymmetry, stronger pinching, and a more deteriorated hysteretic response, as illustrated in Figure 11. These factors explain why the drift ratio at ultimate strength in the precast specimens was smaller than that observed in the cast-in-place column. The prefabricated concrete column connected in half-height still demonstrated excellent seismic performance, although its hysteretic behavior was slightly inferior to that of the cast-in-place columns.

3.3. Skeleton Curve

The skeleton curve—an envelope connecting the peak points of the hysteresis loops under cyclic loading—encapsulates the component’s load-deformation trend across multiple loading stages. Figure 12 compares the skeleton curves of the two specimen types. They exhibited similar overall seismic resistance behavior, indicating that the half-height grouted-sleeve connection offered reliable seismic performance.

Damage from positive loading was more significant, suggesting that positive loading primarily governs the ultimate strength. Based on previous research [17,31], the ultimate bearing capacity in the positive direction was chosen for analysis. The prefabricated columns reached a slightly lower peak load (119.15 kN) and ultimate displacement (100.32 mm) than the cast-in-place columns (120.90 kN, 104.01 mm). However, their load-drop trend was more gradual, suggesting better post-peak stability. Under negative loading stages, the cast-in-place column consistently exhibited higher bearing capacity than the precast column at each displacement level. This suggests that the precast column suffered more pronounced damage and degradation under repeated tensile and compressive stresses. Cracks initially developed primarily on the loading side during cyclic displacement loading, inducing an asymmetric degradation of mechanical behavior between the loading and unloading directions. As loading progressed, the loading side exhibited an increasing number and width of cracks, leading to a markedly greater stiffness reduction on the loading side compared to the unloading side. The more pronounced hysteretic asymmetry in the prefabricated concrete column connected in half-height—relative to the cast-in-place columns—can be attributed to two main mechanisms: (a) Under positive loading, relative slip at the interface between the grouting and concrete reduced effective displacement; (b) Under negative loading, interface slip delayed the attainment of the ultimate load in that direction. The skeleton curves of the two specimens nearly perfectly overlapped despite the observable discrepancies. Overall, the skeleton curve confirmed that the seismic capacity of the half-height prefabricated column was comparable to that of the cast-in-place counterpart.

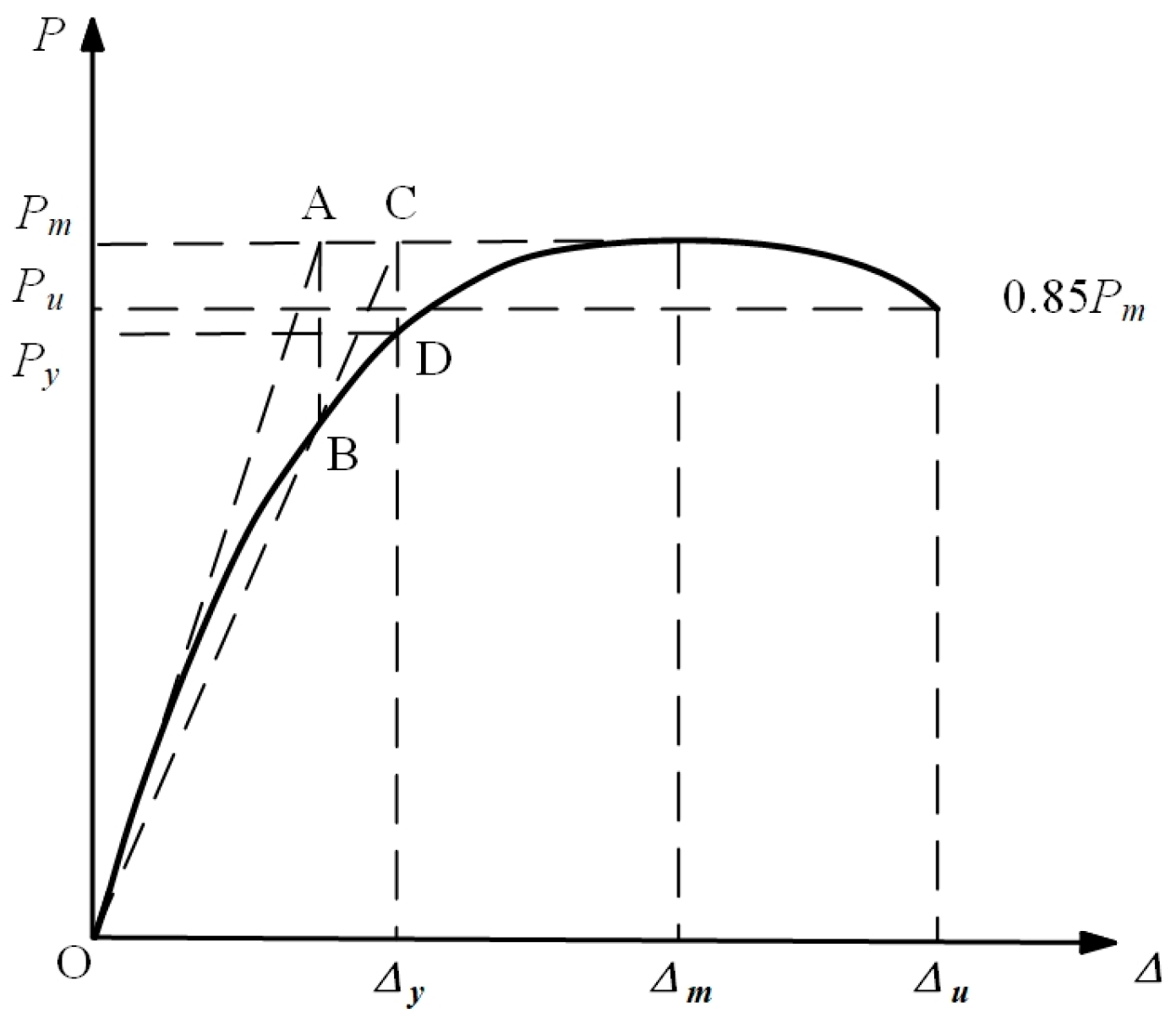
3.4. Ductility

Ductility is quantified using the ductility coefficient (μ), defined as the ratio of ultimate deformation (Δ_u) to yield deformation (Δ_y) while retaining the component’s basic load-bearing capacity, seen as Equation (1). In this study, the geometric method was employed to determine the yield point [32], as the load–displacement response of the specimens may not exhibit a distinct yield plateau (Figure 13). The ultimate deformation is defined as the displacement corresponding to 85% of the peak load (P = 0.85 P_m) on the skeleton curve. Envelope curves, shown in Figure 12, were used to evaluate the ductility coefficients for both specimen types (

Table 4. Ductility factor of specimens.

Specimen	Δy (mm)	Δu (mm)	μ
CIPC	27.8	104.0	3.74
PCCH	24.6	100.3	4.08

). The cast-in-place column had a yield displacement of 27.8 mm and an ultimate displacement of 104.0 mm, while the prefabricated column had a yield displacement of 24.6 mm and an ultimate displacement of 100.3 mm. Consequently, the ductility coefficient of the prefabricated column was approximately 9.09% higher than that of the cast-in-place column. This increase was attributed to a slip at the grouting–concrete interface, which enhanced the column’s overall deformation capacity. These results indicate that the half-height grouted-sleeve connection provides sufficient ductility and deformation capacity for seismic applications.

$$\mu ={\displaystyle \frac{{\mathsf{\Delta }}_u}{{\mathsf{\Delta }}_y}}$$

(1)

3.5. Secant Stiffness Deterioration

Stiffness, commonly defined as the ratio of load to displacement, represents a specimen’s ability to resist overall deformation under cyclic loading. In this study, stiffness degradation is quantified by the slope of the line connecting the positive and negative peak loads of the first hysteresis loop in each cycle, as defined in Equation (2). As cyclic loading progresses, concrete cracking and the formation of plastic hinges lead to a continuous decrease in stiffness. During the initial loading phase, stiffness declines rapidly (Figure 14). After the displacement reached approximately 45 mm (1.5% drift), the rate of stiffness degradation slowed noticeably, indicating a reduced pace of damage accumulation.

$$K_i={\displaystyle \frac{\left|+F_i\right|+\left|-F_i\right|}{\left|+X_i\right|+\left|-X_i\right|}}$$

(2)

where K_i represents the cyclic secant stiffness for each cycle. +F_i and −F_i denote the peak loads in the positive and negative loading directions, respectively, while +X_i and −X_i are the corresponding displacements for these peak loads.

Notably, due to the added stiffness of the grouted sleeve, the prefabricated column exhibited significantly higher rigidity in the initial loading phase, exceeding that of the cast-in-place column by approximately 8.88%. The increased stiffness provided by the sleeve connection delays concrete damage and the yielding of longitudinal reinforcement under cyclic loading. In comparison to the cast-in-place concrete column, the lateral displacement of precast concrete columns at 1250 mm, 1500 mm, and 1750 mm from the bottom of the column was 11.93%, 14.45%, and 10.54% less, respectively. This also indicates that precast concrete columns have high lateral stiffness. Throughout most of the same displacement range, the prefabricated column maintained slightly higher stiffness compared to the cast-in-place column. Beyond a displacement of about 45 mm (1.5% drift), the difference in stiffness degradation between the two column types became negligible. Even at a large displacement of 105 mm (3.5% drift), the stiffness of the prefabricated column only exceeded that of the cast-in-place column by around 0.01 kN/mm. Overall, the half-height grouted-sleeve connection contributed to more stable stiffness deterioration under cyclic loading, indicating superior seismic performance in terms of stiffness degradation.

3.6. Energy Dissipation

Energy dissipation capacity refers to a structure’s ability to absorb and release externally applied energy through mechanisms such as plastic deformation, material degradation, and friction under cyclic loading. This capacity is commonly quantified by the area enclosed by the hysteresis loops. Figure 15 illustrates the relationship between the cumulative energy dissipated and the displacement for each specimen.

The cast-in-place concrete column dissipated more energy than the prefabricated column, and this energy gap widened progressively as displacement increased. The cast-in-place specimens demonstrated excellent energy dissipation capacity, maintaining good structural integrity and exhibiting gradual material degradation. Even near failure, their hysteresis loops remained wide and relatively stable. In contrast, the prefabricated columns—with cracks developing at the grouting–concrete interface—suffered from strain concentration that compromised their integrity. The interface slip reduced their ability to dissipate energy and caused more pronounced pinching in the hysteresis loops, seen in Figure 10b. Overall, the cumulative energy dissipation of the cast-in-place specimen was approximately 5.95% higher than that of the prefabricated column.

3.7. Comprehensive Seismic Response

Based on the above analysis of seismic response indices (seen as

Table 5. Experimental results of specimens.

Experimental Results	CIPC	PCCH
Ultimate load (kN)	120.90	119.15
Ultimate displacement (mm)	104.01	100.32
Energy dissipation (kN·mm)	60,462.09	57,069.17
Ductility coefficient	3.74	4.08
Initial stiffness (kN/mm)	9.23	10.05

), compared with cast-in-place columns, the precast columns exhibit minor reductions in ultimate bearing capacity, ultimate displacement, and energy dissipation—decreasing by approximately 1.45%, 3.55%, and 5.61%, respectively. In contrast, the ductility coefficient of the precast columns increases by 9.09%, and their initial stiffness improved by 8.88%. These results suggested that, although precast columns sacrificed a small amount of strength and energy capacity, they gained enhanced deformability and stiffness, which could be beneficial for seismic performance. In this paper, it is thus justifiable to position the grouted-sleeve connection away from the expected plastic-hinge region, so as to confine inelastic deformation there and better preserve the seismic performance and reparability of the main column.

4. Numerical Analysis

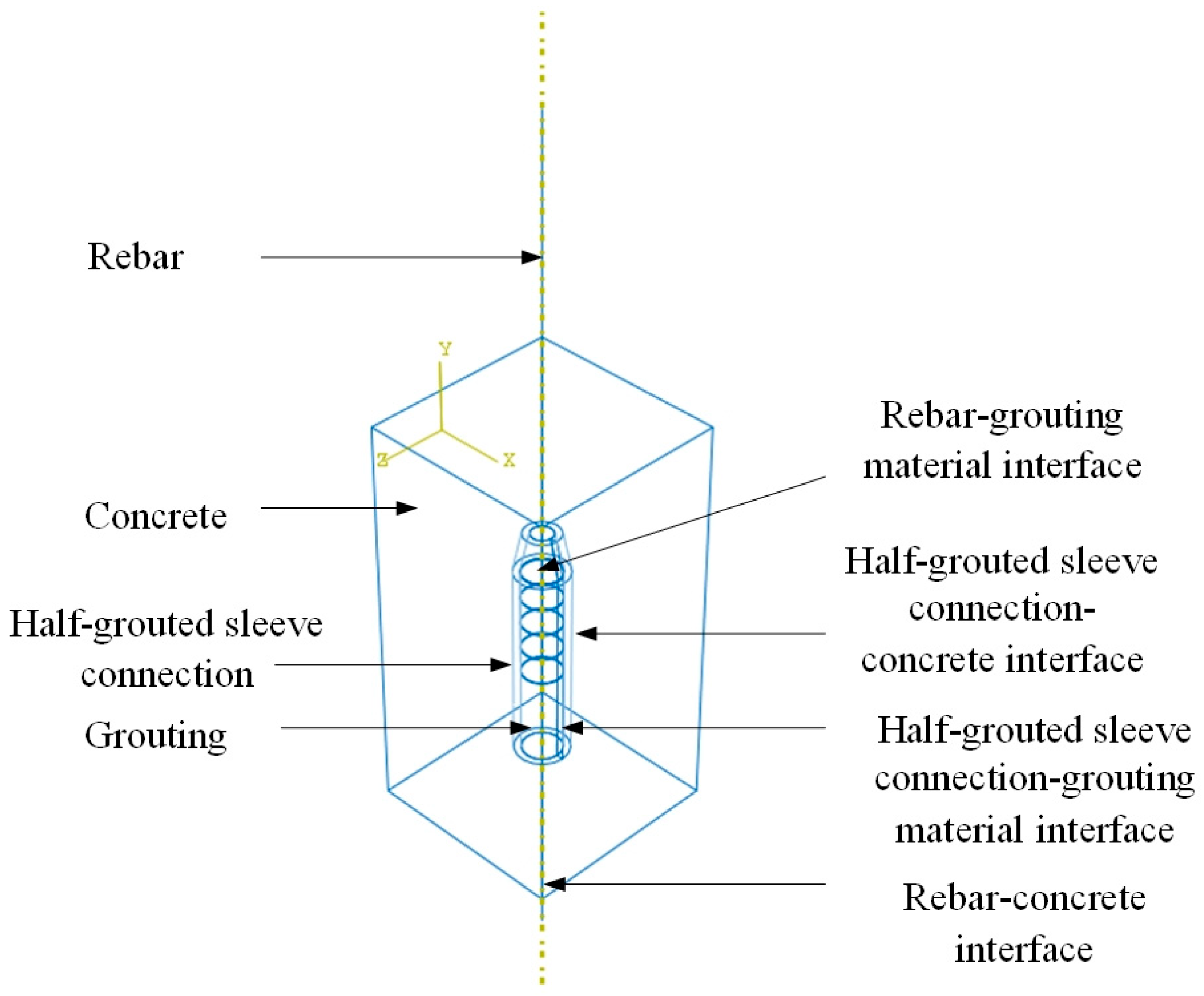
4.1. Model Description

Although experimental research accurately captures the mechanical properties, the high cost of testing and the lack of objective settings make it challenging to develop an international standard. In structural engineering, numerical simulation is becoming more and more common. Finite-element modeling of the specimens was carried out in Abaqus using their actual geometric dimensions. Concrete was represented by three-dimensional, eight-node, reduced-integration solid elements (C3D8R), while the reinforcement and half-sleeve connections were modeled using three-dimensional, two-node truss elements (T3D2). The use of reduced-integration elements helps mitigate shear locking under bending, and large-deformation effects were included in the analysis to improve displacement predictions. The finite—element model for the reinforcing cage and the column is illustrated in Figure 16.

4.2. Material Constitutive Selection

4.2.1. Concrete

Considering the complex failure behavior of specimens under low-cycle cyclic loading, this study aims to accurately simulate the degradation of concrete stiffness resulting from damage accumulation. Concrete behavior was modeled using the Concrete Damaged Plasticity (CDP) model. The CDP model, which considers three key factors—plasticity, compressive behavior, and tensile behavior—is essential for defining the material damage parameters. The following equations are used to compute the stress–strain relationship of concrete under uniaxial compression.

$${\sigma }_c=(1-d_c)E_c{\epsilon }_c$$

(3)

$$d_c=\left\{\begin{array}{l}1-{\displaystyle \frac{{\rho }_{c}n}{n-1+x_c^n}}\cdots \cdots \cdots \cdots x_c\le 1\hfill \\ 1-{\displaystyle \frac{{\rho }_c}{{\alpha }_c{\left(x_c-1\right)}^2+x_c}}\cdots \cdots \cdots x_c>1\hfill \end{array}\right.$$

(4)

$${\rho }_c={\displaystyle \frac{f_{c,r}}{E_c{\epsilon }_{c,r}}}$$

(5)

$$n={\displaystyle \frac{E_c{\epsilon }_{c,r}}{E_c{\epsilon }_{c,r}-f_{c,r}}}$$

(6)

$$x_c={\displaystyle \frac{{\epsilon }_c}{{\epsilon }_{c,r}}}$$

(7)

Equations (8)–(11) present the constitutive stress–strain relationship of concrete under tension.

$${\sigma }_t=(1-d_t)E_c{\epsilon }_t$$

(8)

$$d_t=\left\{\begin{array}{c}1-{\rho }_t\left(1.2-0.2x_t^5\right)\cdots \cdots x_t\le 1\\ 1-{\displaystyle \frac{{\rho }_t}{{\alpha }_t{\left(x_t-1\right)}^{1.7}+x_t}}\cdots \cdots \cdots \cdots x_t>1\end{array}.\right.$$

(9)

$${\rho }_t={\displaystyle \frac{f_{t,r}}{E_c{\epsilon }_{t,r}}}$$

(10)

$$x_t={\displaystyle \frac{{\epsilon }_t}{{\epsilon }_{t,r}}}$$

(11)

where σ_c, σ_t denotes compressive stress and tensile stress, respectively. ε_c, ε_t denotes compressive strain and tensile strain, respectively. ε_c,r, ε_t,r denotes peak compressive strain and peak tensile strain, respectively. E_c, E_d denotes the initial and unloading elastic moduli, respectively. d_c, d_t represents the damage evolution parameters under compression and tension, respectively. f_c,r, f_t,r denotes the representative values of uniaxial compressive and tensile strength, respectively. ρ_c, ρ_t, n are computational parameters. x_c, x_t represents the ratios of compressive and tensile strain to their respective peak strain values.

The damage evolution parameters (d_c and d_t) for concrete in compression and tension at any point on the normalized stress–strain curve are calculated using Equations (4) and (9). These parameters were subsequently substituted into Equations (3) and (8), and combined with the strain and elastic modulus of concrete to compute the corresponding compressive and tensile stresses, σ_c and σ_t. The damage variables are determined using an inelastic-strain-based approach, as defined in Equation (12). It is also important to note that the initial values of cracking strain (in tension) and inelastic strain (in compression) must be set to zero when input into Abaqus.

$$d=1-{\displaystyle \frac{\sigma /E}{{\epsilon }_{ni}\left(\frac{1}{r}-1\right)+\sigma /E}}$$

(12)

where ε_ni denotes the tensile cracking strain or compressive inelastic strain of concrete; r represents the reduction factor, taken as 0.7 for tension and 0.1 for compression; the meanings of other parameters remain unchanged from the previous definition.

4.2.2. Reinforcement and Half-Grouted Sleeve Connection

The tangential modulus of elasticity E_s during the reinforcement strengthening stage is 0.01 E_r. Based on previous experimental studies and analyses of the tensile behavior of externally confined concrete sleeve connections, the integral sleeve-connected specimen is modeled using the simplified “equivalent reinforcement” method, assuming a Poisson’s ratio of 0.2 [33]. The load–displacement relationship of half-grouted sleeve connections with concrete cover is described by Equations (13) and (14), incorporating parameters such as concrete cover and concrete strength, seen as Figure 17. A corresponding bilinear stress–strain model was subsequently developed based on this load–displacement relationship. This modeling strategy avoids using solid elements to represent the half-grouted sleeve and the grout material, and simultaneously eliminates the need for springs or connector elements to imitate bond-slip behavior at multiple interfaces (concrete–sleeve, sleeve–grouting, and grouting–reinforcement). As a result, the computational efficiency was improved, and convergence issues often encountered in detailed sleeve-connected models were mitigated. In this simplified scheme, by assuming perfect bond between the concrete and reinforcement (neglecting slip between the bars and the concrete), both the actual reinforcing bars and sleeve connections (equivalent reinforcement) can be embedded directly in the concrete solid.

$$P=A_2+{\displaystyle \frac{A_1-A_2}{1+{\left(\frac{s}{s_0}\right)}^p}}$$

(13)

where P is tensile force, kN; A₁, A₂ represents coefficients, kN; s represents displacement obtained by experiment, mm; s₀ represents coefficients, kN.

$$z=z_0+a{f}_{cu}+bT$$

(14)

where z is coefficients in Equation (13), which can be A₁, A₂, and p. f_cu is the standard compressive strength of the grout, 95.3 MPa. T represents temperature, 20 °C. z₀ is 7.62, 84.28, and 3.44 for A₁, A₂ and p, individually. a is 0.027, 0.19, and 0.01, individually. b is −0.003, −0.003, and −0.001, individually.

4.3. Boundary Condition Settings

An axial compressive load of 350 kN the first step for was applied to the top of the column. The second step was to apply horizontal load. For the boundary conditions, the top of the specimen was rigidly fastened to the cross-beam via bolts and embedded steel plates, and all two rotational degrees of freedom at that node were restricted. At the base, ground anchors constrained the column so that all translational (U1, U2, U3) and rotational (UR1, UR2, UR3) degrees of freedom were fixed (U1 = U2 = U3 = UR1 = UR2 = UR3 = 0), simulating a fully fixed support. In the Abaqus model, a reference point (RP1) was defined at the top, through which displacement-controlled cyclic horizontal loading and axial compressive load were applied. Because the cyclic loading path is applied along the global X-axis, the rotational constraints around the Y-axis at the top ensure that the model reproduces the experimental tension–compression path (U2 = UR1 = UR3 = 0).

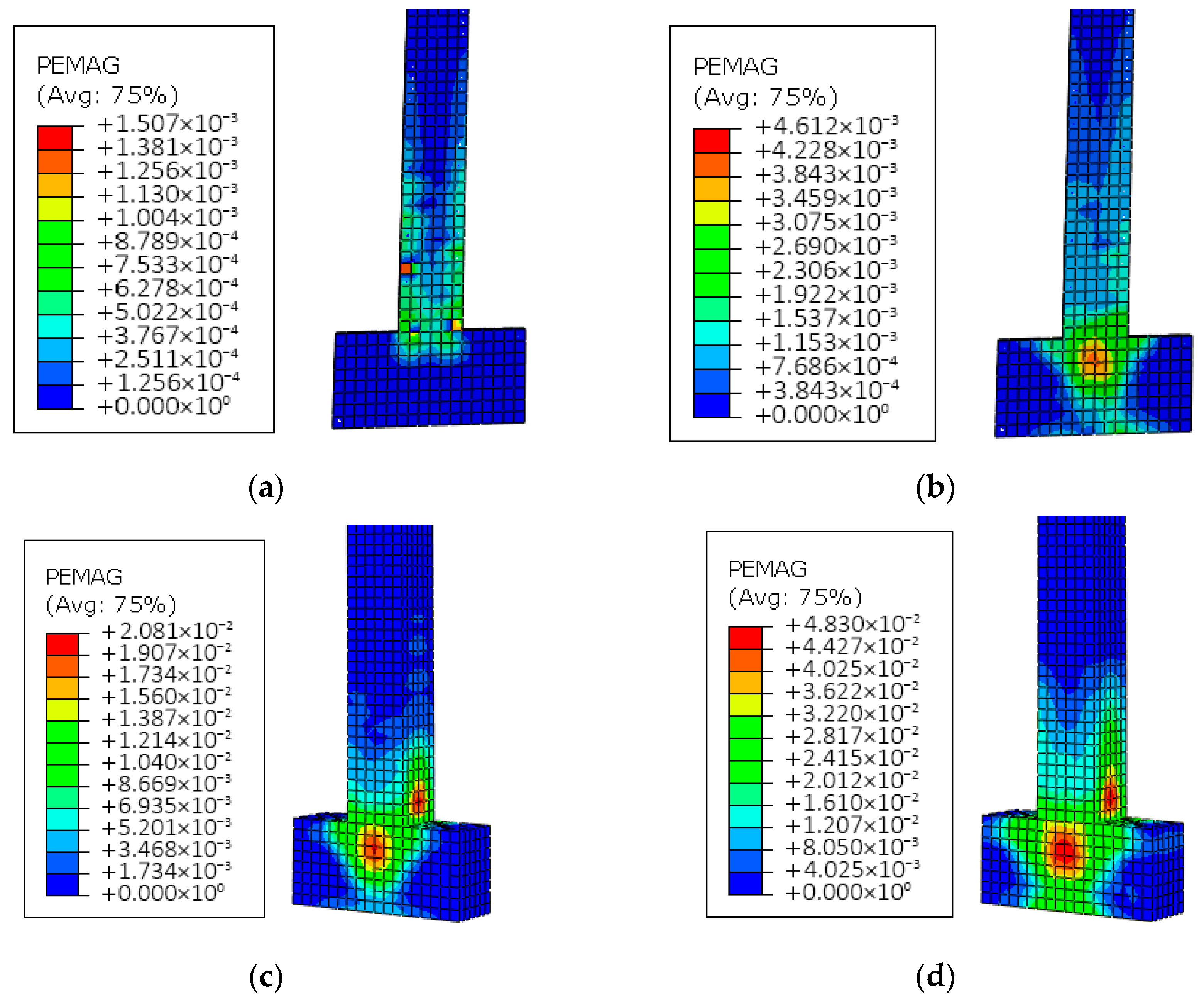
4.4. Model Validation

Figure 18 compares the experimental hysteresis and skeleton curves with those obtained from the finite-element simulation of the CIPC specimen. The numerical results predicted key characteristics—such as the ultimate load and ultimate displacement—quite accurately, and generally aligned well with the experimental data. Specifically, the simulation estimated an ultimate load of 118.61 kN, compared to the measured 120.90 kN in the test. The discrepancy between the simulation and experimental results in the ultimate load was only 1.89%, indicating a very close match and high accuracy of the numerical model. While the skeleton curves of both the experimental and simulated specimens showed very similar overall trends, the initial stiffness of the simulated model was noticeably higher than that of the experimental specimen. The skeleton curve and hysteretic curve simulation results were more symmetrical than experimental results.

An equivalent plastic strain contour plot (PEEQ diagram) was generated from the Abaqus simulation results to investigate the specimen’s failure mode and crack propagation pattern [34]. As the loading process progressed, the PEEQT values increased and the contours showed a progressive spread of plastic strain from the base of the column upward (Figure 19). The most intense plastic strain concentrated at the column base, where a plastic hinge rapidly developed due to accumulating damage—a trend that mirrored the concrete spalling observed in the experiment. Compared with the test specimens, the Abaqus simulation predicts earlier onset and more rapid development of concrete damage. Although the simulation could not quantitatively reproduce the exact crack widths or the detailed crack paths under every loading-displacement scenario, it effectively captured the qualitative trends in fracture growth and distribution. This demonstrated that, despite some limitations, the numerical model had strong predictive power for damage localization and failure mechanisms.

Figure 20 presents a comparison between the hysteresis and skeleton curves obtained from finite-element simulation of the PCCH specimen and the corresponding experimental data. The simulation predicted an ultimate load of 119.53 kN, closely matching the experimental value of 119.15 kN. The ratio of the simulated result to the experimental data in the ultimate load was 1.00, indicating an almost perfect match between the simulation and the test. According to the test results (see Figure 21), the PEEQT value for the PCCH specimen was larger than that of the cast-in-place column under different loading process. In the last loading stages, the PEEQT value of the precast columns was approximately 12.01% higher than that of the cast-in-place columns, which aligned well with the experimental observations. This increase in PEEQT suggested greater accumulation of plastic strain in the precast specimens under high cyclic deformation. Numerical simulation provides a robust basis for evaluating and comparing the damage levels of the specimens.

While the experimental hysteresis loops displayed marked asymmetry, the numerical loops from the simulation were notably more symmetric. This discrepancy likely arose from uncontrollable experimental factors and the fact that the test used full displacement control. Moreover, the load–displacement behavior under both positive and negative loading directions showed considerable differences in bearing capacity for the precast column. The absence of a clearly defined descending branch and pronounced pinching in the simulated load–displacement hysteresis loops highlighted another source of discrepancy between experiment and analysis. This mismatch likely occurred from three key modeling assumptions: (a) Neglecting reinforcement stiffness degradation under low-cycle cyclic loading; (b) Ignoring bond–slip behavior between the reinforcement and concrete, and (c) Omitting shear deformation in the elements. Despite the simplifications made in the modeling approach, the simulation methodology developed in this study demonstrates strong reliability, as it captured the behavioral trends exhibited by the test specimens.

In this study, Abaqus software is employed for numerical simulations, implementing the full constitutive model of the half-grouted sleeve connection with concrete cover to investigate the seismic performance of prefabricated concrete columns connected in half-height. The study also addresses convergence challenges associated with sleeve-connected columns and verifies the feasibility of finite-element simulations for prefabricated columns. This approach provides a theoretical foundation for the design of precast column connections in subsequent stages and for assessing their seismic response under extreme conditions.

4.5. Simplified Calculation of Shear Bearing Capacity

The ratio of test value to simulation value was nearly 1.0 due to the great simulation accuracy on ultimate load. The ultimate load of the specimen was not significantly affected by its type. The calculated value of shear bearing capacity (205.7 kN) was significantly higher than the experimental and simulation data when using the shear bearing capacity calculation formula, as indicated in Equation (15). It can be used to determine the specimen’s mode of failure. The two types of specimens experienced bending failure, which was consistent with the behavior seen in the experiment. It serves as a foundation for the examination of the failure mechanism of prefabricated concrete columns connected in half-height using an extreme state simulation.

$$V_1={\displaystyle \frac{1.75}{\lambda +1.0}}{f}_{\mathrm{t}}{\mathrm{bh}}_0+0.9f_{\mathrm{yv}}{\displaystyle \frac{{\mathrm{A}}_{\mathrm{sv}}}{\mathrm{s}}}{\mathrm{h}}_0$$

(15)

where V_c is the formula for calculating the shear bearing capacity of two types of columns; f_t is the tensile strength of concrete; A_sv is the total cross-sectional area of stirrups in the same section; s is stirrup spacing; f_yv is the design value of stirrup tensile strength; b is the section width; h₀ is the effective height of the section.

5. Conclusions

According to this study, the connection should be positioned at the column’s half-height to improve the integrity and seismic performance of sleeve-connected columns. The connection area’s susceptibility to earthquake loads should be given particular consideration. Based on the experimental and numerical findings, the following key conclusions can be drawn:

(1)

The cash-in-place column and the half-height prefabricated column exhibited flexural failure characteristics. Smaller crack widths and less localized damage under the same displacement were the results of the grouted-sleeve connection’s increased stiffness. No observable bond–slip failure occurred in the sleeve connection.

(2)

The repeated opening and closing of these cracks observed at the grouting-concrete interface aggravated bond-slip, intensifying the pinching effect in hysteretic response. The cumulative energy dissipation of the prefabricated column was approximately 5.61% lower than that of the cast-in-place specimen.

(3)

The precast column showed slight decreases in ultimate bearing (1.45%), capacity, and energy dissipation (5.61%) when compared to cast-in-place columns; nevertheless, their initial stiffness and ductility coefficient rose by 8.88% and 9.09%, respectively. This indicates that the prefabricated concrete column connected in half-height is reliable.

(4)

Using the full constitutive model of the half-grouted sleeve connection with concrete cover to address convergence challenges associated with sleeve-connected columns. The numerical results generally aligned well with the experimental data and had strong predictive power for damage localization and failure mechanisms.

(5)

The formula for calculating shear bearing capacity can be used to determine the failure mode. It serves as a guide for simulating whether, in extreme situations, the specimen connected in various positions experiences brittle shear failure.