Fuzzy AHP Approach for Enhancing Excavation Support System Selection in Building Projects: Balancing Safety and Cost-Effectiveness
Abstract
1. Introduction
1.1. Background and Key Challenges
1.2. Overview of Excavation Support Systems and Decision-Making Methods
1.3. Study Context, Research Gap, and Objectives
- To develop a context-specific, MCDM framework for ESS selection that incorporates the unique geotechnical and operational challenges of building construction in Egypt.
- To demonstrate the effectiveness of the fuzzy AHP approach in capturing expert judgment uncertainty and improving the prioritization of selection criteria and alternatives.
- To validate the proposed framework through a real-world case study, thereby illustrating its practical applicability and value for construction practitioners.
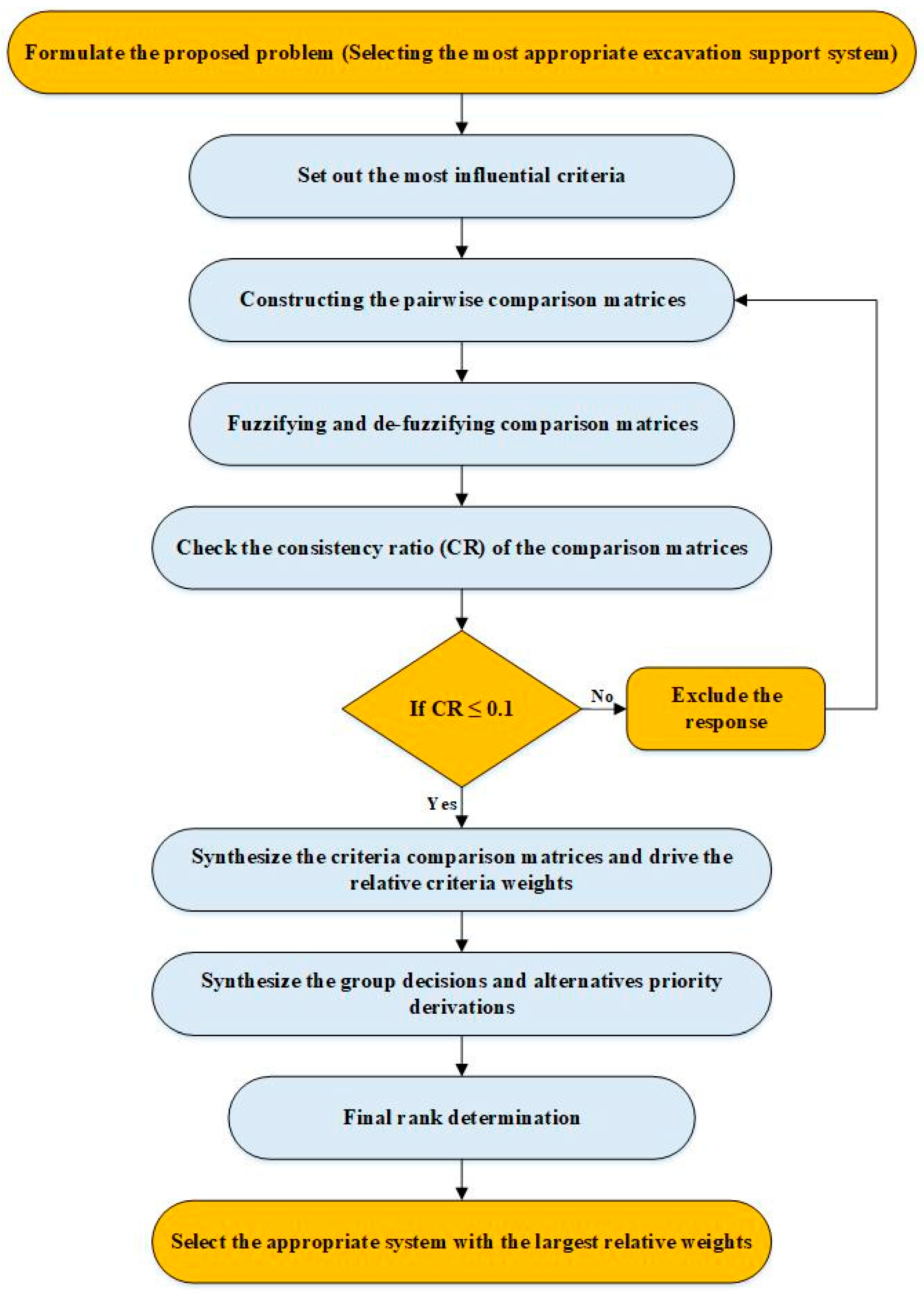
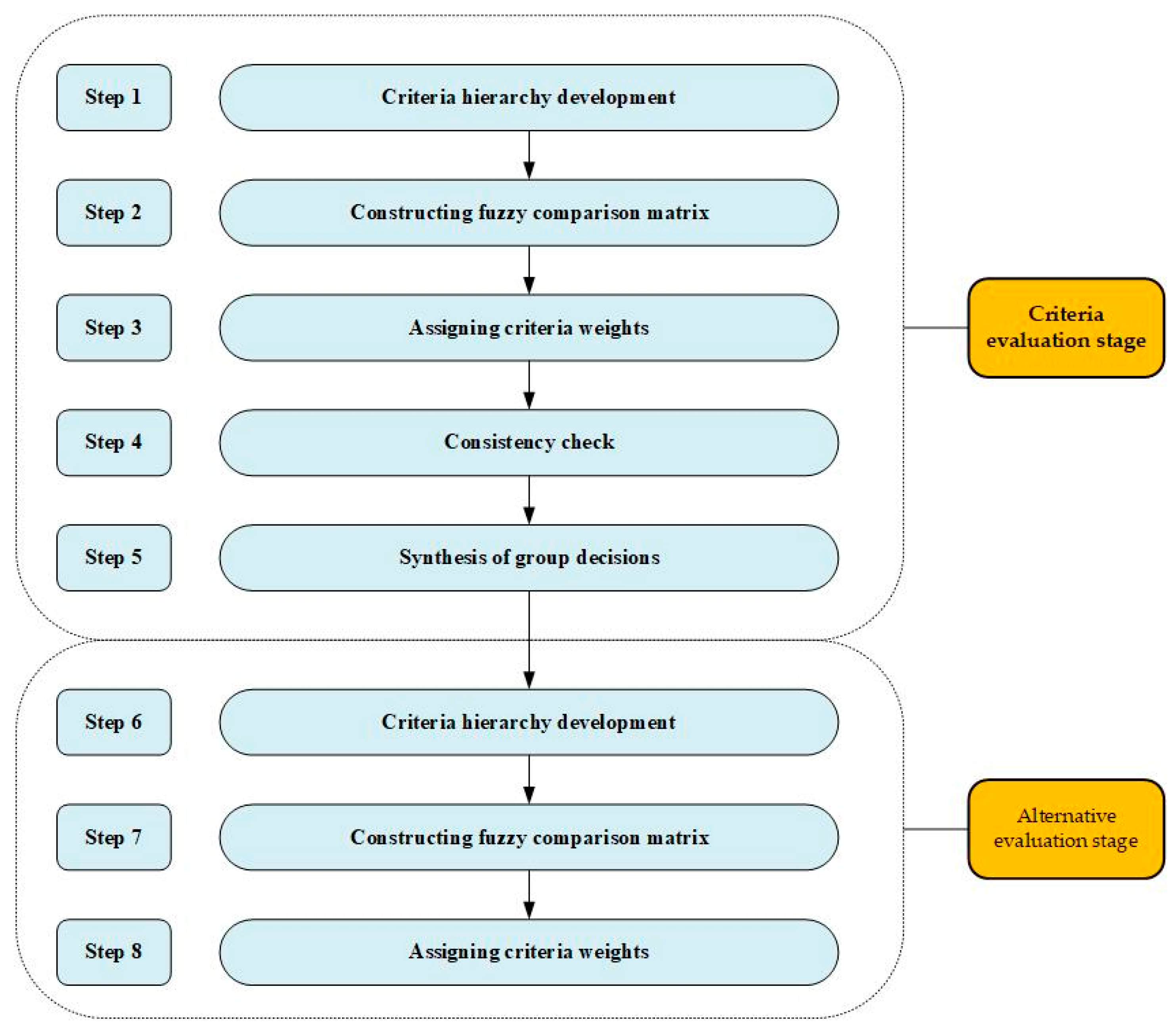
2. Research Methodology and Model Development
2.1. Development of the Decision Hierarchy
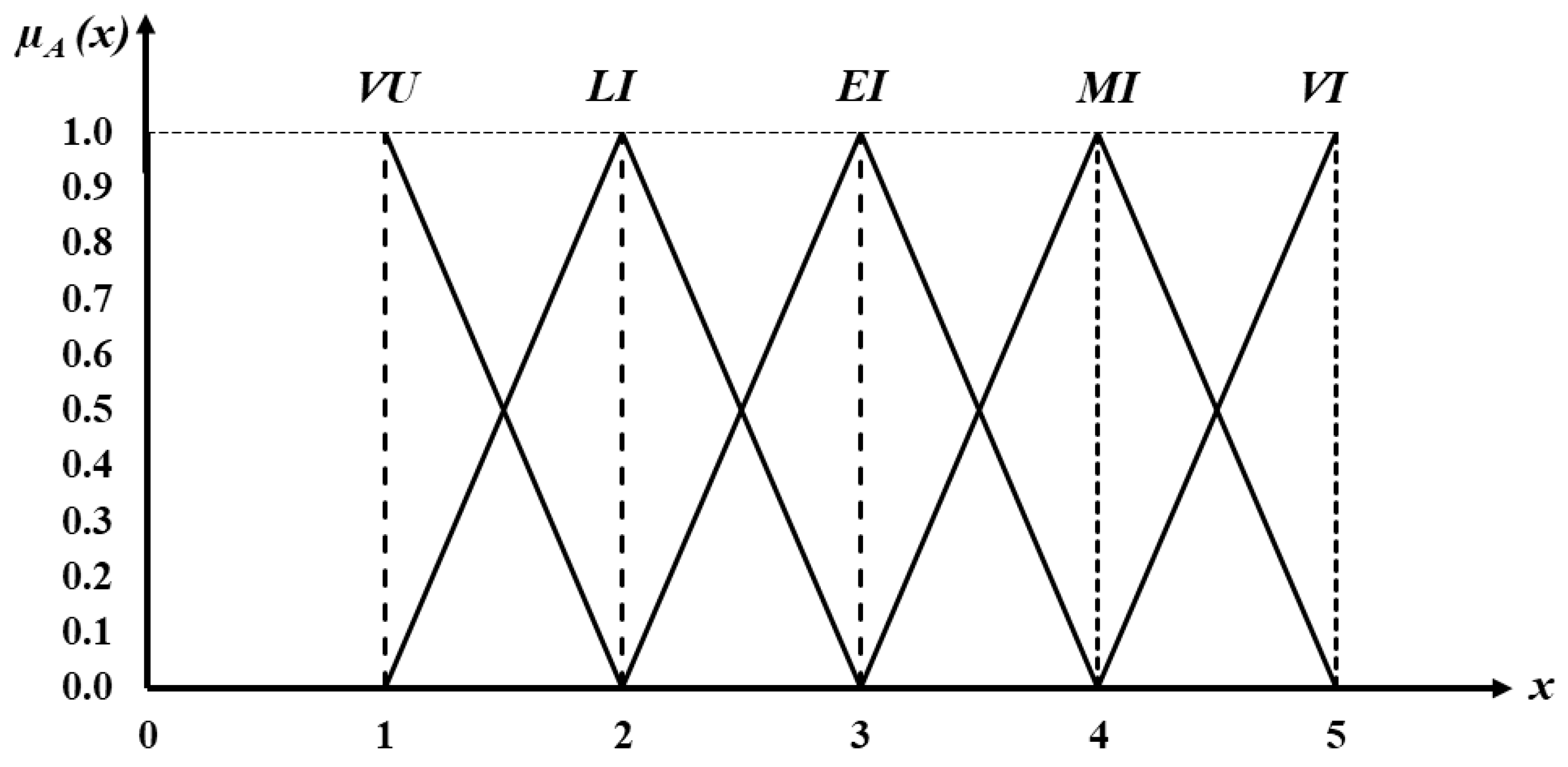
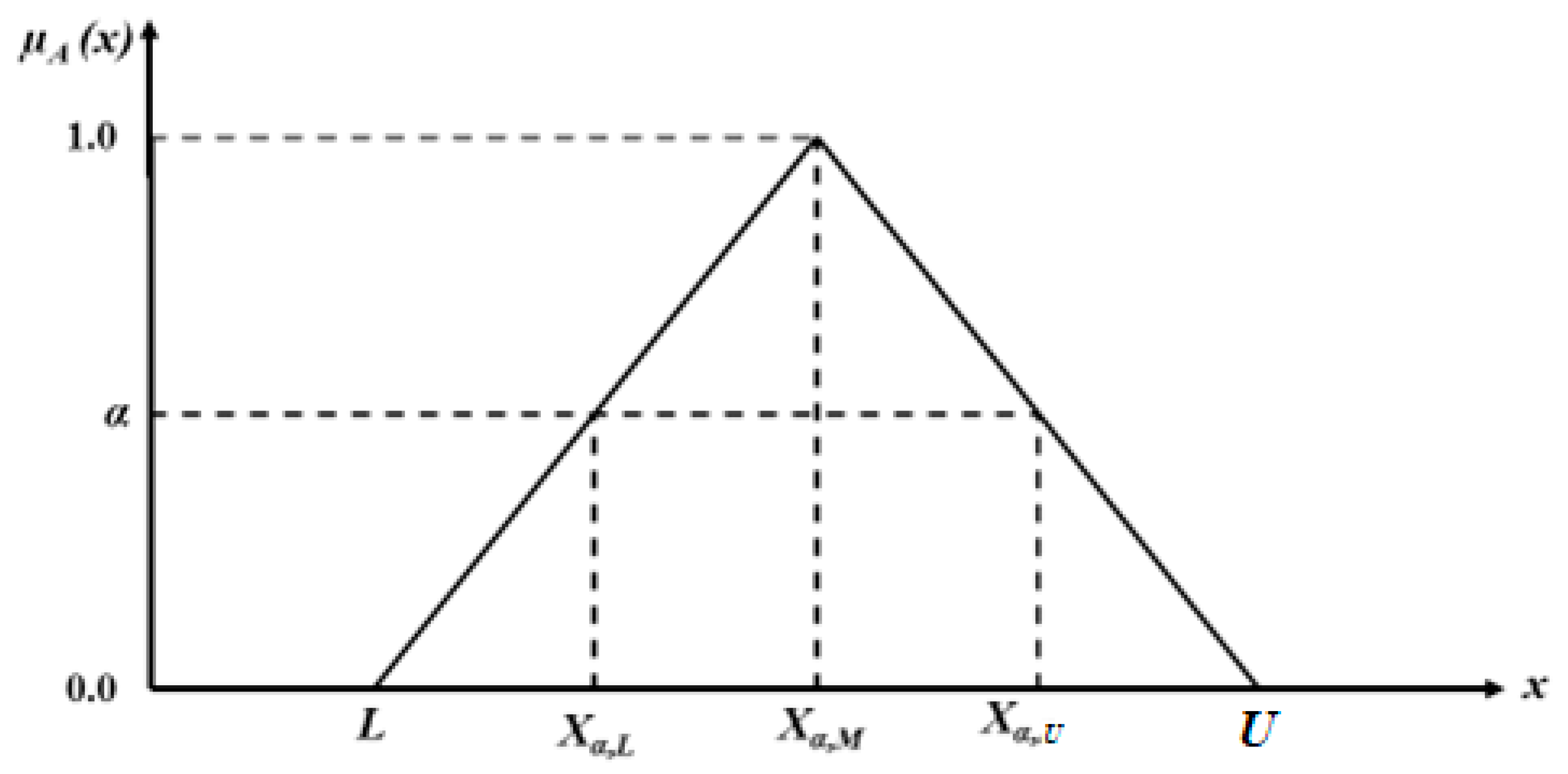
2.2. Fuzzy Pairwise Comparisons
2.3. Relative Weight Calculations
2.4. Consistency Checks
2.5. Synthesis of Group Decisions
3. Case Study and Model Implementation
3.1. Criteria Hierarchy Development
3.2. Constructing Fuzzy Comparison Matrix
3.3. Assigning Criteria Weights
| B11 | B12 | B13 | B14 | ||
| B11 | 1 | (2.5, 3, 4.5) | (2.5, 3, 4.5) | (3.5, 4, 4.5) | |
| B12 | (2.5, 3, 4.5) | 1 | (2.5, 3, 4.5) | (2.5, 3, 4.5) | |
| B13 | (2.5, 3, 4.5) | (2.5, 3, 4.5) | 1 | (2.5, 3, 4.5) | |
| B14 | (1.5, 2, 3.5) | (2.5, 3, 4.5) | (2.5, 3, 4.5) | 1 |
3.4. Consistency Checks
3.5. Synthesis of Group Decisions
3.6. Alternatives Evaluation
3.7. Determine the Final Ranking
3.8. Selecting the Appropriate System
4. Discussion
5. Practical Implications
5.1. Relevance to Construction Practice
5.2. Benefits of the Fuzzy AHP Approach
5.3. Potential Broader Applications
6. Limitations and Future Research
6.1. Study Limitations
6.2. Opportunities for Future Research
6.3. Recommendations for Practice
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, G.B.; Huang, P.; Shi, J.W.; Ng, C.W.W. Performance of a Deep Excavation and Its Effect on Adjacent Tunnels in Shanghai Soft Clay. J. Perform. Constr. Facil. 2016, 30, 04016041. [Google Scholar] [CrossRef]
- Ghorbani, M.; Sharifzadeh, M.; Yasrobi, S.; Daiyan, M. Geotechnical, structural and geodetic measurements for conventional tunnelling hazards in urban areas—The case of Niayesh road tunnel project. Tunn. Undergr. Space Technol. 2012, 31, 1–8. [Google Scholar] [CrossRef]
- Corral, G.; Whittle, A.J. Re-analysis of deep excavation collapse using a generalized effective stress soil model. In Proceedings of the 2010 Earth Retention Conference, Bellevue, WA, USA, 1–4 August 2010. [Google Scholar]
- Alaghbandrad, A.; Hammad, A. Framework for multi-purpose utility tunnel lifecycle cost assessment and cost-sharing. Tunn. Undergr. Space Technol. 2020, 104, 103528. [Google Scholar] [CrossRef]
- Askarian, S.; Fakher, A. Design of deep urban excavations using life cycle cost in comparison with acceptable risk and conventional method. Tunn. Undergr. Space Technol. 2021, 112, 103868. [Google Scholar] [CrossRef]
- Ying, H.W.; Cheng, K.; Zhang, L.S.; Ou, C.Y.; Yang, Y.W. Evaluation of excavation-induced movements through case histories in Hangzhou. Eng. Comput. 2020, 37, 1993–2016. [Google Scholar] [CrossRef]
- Kim, D.I.; Yoo, W.S.; Cho, H.; Kang, K.I. A fuzzy AHP-based decision support model for quantifying failure risk of excavation work. KSCE J. Civ. Eng. 2014, 18, 1966–1976. [Google Scholar] [CrossRef]
- Tan, Y.; Wang, D.L.; Lu, Y.; Fang, T. Excavation of Middle Huai-Hai Road Station of Shanghai Metro Line 13: Challenges, Risks, Countermeasures, and Performance Assessment. Pract. Period. Struct. Des. Constr. 2017, 22, 05017003. [Google Scholar] [CrossRef]
- Bryson, L.S.; Romana Giraldo, J. Erratum for “Excavation Support System Design Method to Limit Damage in Adjacent Infrastructure” by Jorge Romana Giraldo and L. Sebastian Bryson. J. Geotech. Geoenviron. Eng. 2022, 148, 08221003. [Google Scholar] [CrossRef]
- Cheng, X.S.; Zheng, G.; Diao, Y.; Huang, T.M.; Deng, C.H.; Nie, D.Q.; Lei, Y.W. Experimental study of the progressive collapse mechanism of excavations retained by cantilever piles. Can. Geotech. J. 2017, 54, 574–587. [Google Scholar] [CrossRef]
- Tan, Y.; Huang, R.; Kang, Z.; Bin, W. Covered Semi-Top-Down Excavation of Subway Station Surrounded by Closely Spaced Buildings in Downtown Shanghai: Building Response. J. Perform. Constr. Facil. 2016, 30, 04016040. [Google Scholar] [CrossRef]
- Richards, T.L.; Suarez, S.; Restrepo, J.I.; Morrison, M.L.; Jaradat, O. Steel Pipe Pile Strain Limits for Performance-Based Seismic Design of Marine Structures. In Ports 2022: Port Engineering, Proceedings of the 16th Triennial International Conference, Honolulu, HI, USA, 18–21 September 2022; ASCE Press: Reston, VA, USA, 2022; Volume 1, pp. 767–776. [Google Scholar] [CrossRef]
- Goh, A.T.C. Basal heave stability of supported circular excavations in clay. Tunn. Undergr. Space Technol. 2017, 61, 145–149. [Google Scholar] [CrossRef]
- Temiz, I.; Calis, G. Selection of Construction Equipment by using Multi-criteria Decision Making Methods. Procedia Eng. 2017, 196, 286–293. [Google Scholar] [CrossRef]
- Tan, Y.C.; Koo, K.S.; Chow, C.M. Underground stations excavation of up to 45m deep for mass rapid transit in limestone formation Malaysia. Jpn. Geotech. Soc. Spec. Publ. 2015, 2, 170–175. [Google Scholar] [CrossRef]
- Richards, D.J.; Wiggan, C.A.; Powrie, W. Seepage and pore pressures around contiguous pile retaining walls. Geotechnique 2016, 66, 523–532. [Google Scholar] [CrossRef]
- Lee, L.M. Design and construction of soil nail reinforced soldier pile wall as a temporary shoring system for deep excavation—A case study. Int. J. Geotech. Eng. 2022, 16, 850–864. [Google Scholar] [CrossRef]
- Meng, F.; Xu, J.; Xia, C.; Chen, W.; Zhu, M.; Fu, C.; Chen, X. Optimization of deep excavation construction using an improved multi-objective particle swarm algorithm. Autom. Constr. 2024, 166, 105613. [Google Scholar] [CrossRef]
- Lin, S.S.; Zhou, A.; Shen, S.L. Safety assessment of excavation system via TOPSIS-based MCDM modelling in fuzzy environment. Appl. Soft Comput. 2023, 138, 110206. [Google Scholar] [CrossRef]
- Issa, U.; Saeed, F.; Miky, Y.; Alqurashi, M.; Osman, E. Hybrid AHP-Fuzzy TOPSIS Approach for Selecting Deep Excavation Support System. Buildings 2022, 12, 295. [Google Scholar] [CrossRef]
- Shahpari, M.; Saradj, F.M.; Pishvaee, M.S.; Piri, S. Assessing the productivity of prefabricated and in-situ construction systems using hybrid multi-criteria decision making method. J. Build. Eng. 2020, 27, 100979. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; Yepes, V.; García-Segura, T. Robust decision-making design for sustainable pedestrian concrete bridges. Eng. Struct. 2020, 209, 109968. [Google Scholar] [CrossRef]
- Qi, J.; Zhao, X.; Yang, H.C. Selection of deep excavation construction methods in building construction. In Proceedings of the 2020 IEEE 2nd International Conference on Architecture, Construction, Environment and Hydraulics (ICACEH), Hsinchu, Taiwan, 25–27 December 2020; pp. 72–75. [Google Scholar] [CrossRef]
- Saaty, T.L. How to make a decision: The analytic hierarchy process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Mardani, A.; Turskis, Z.; Jusoh, A.; Nor, K.M. Development of TOPSIS Method to Solve Complicated Decision-Making Problems—An Overview on Developments from 2000 to 2015. Int. J. Inf. Technol. Decis. Mak. 2016, 15, 645–682. [Google Scholar] [CrossRef]
- Gitinavard, H.; Pishvaee, M.S.; Jalalvand, F. A hierarchical multi-criteria group decision-making method based on TOPSIS and hesitant fuzzy information. Int. J. Appl. Decis. Sci. 2017, 10, 213–232. [Google Scholar] [CrossRef]
- Abdel-malak, F.F.; Issa, U.H.; Miky, Y.H.; Osman, E.A. Applying decision-making techniques to Civil Engineering Projects. Beni-Suef Univ. J. Basic Appl. Sci. 2017, 6, 326–331. [Google Scholar] [CrossRef]
- Pan, N.F. Selecting an appropriate excavation construction method based on qualitative assessments. Expert Syst. Appl. 2009, 36, 5481–5490. [Google Scholar] [CrossRef]
- Buckley, J.J. Fuzzy hierarchy analysis. Fuzzy Sets Syst. 1985, 17, 233–247. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process: Planning, Priority Setting; Resource Allocation, McGraw Hill: New York, NY, USA, 1980. [Google Scholar]
- Durán, O.; Aguilo, J. Computer-aided machine-tool selection based on a Fuzzy-AHP approach. Expert Syst. Appl. 2008, 34, 1787–1794. [Google Scholar] [CrossRef]
- Khader, M. A Fuzzy Hierarchical Decision Model and Its Application in Networking Datacenters and in Infrastructure Acquisitions and Design. Ph.D. Thesis, Walden University, Minneapolis, MN, USA, 2009. [Google Scholar]

| Feature | Description | Suitability | Advantages | Disadvantages | References |
|---|---|---|---|---|---|
| Diaphragm Wall | Reinforced concrete wall constructed using slurry trench excavation | - Deep excavations - Unstable soil - High water table | - High strength and stiffness - Any depth - Watertight | - Time-consuming - Expensive - Needs specialized equipment | [11,13] |
| Steel Sheet Pile | Thin, interlocked steel walls driven into the ground. | - Shallow to deep excavations - Stable soil - Low water table | - Easy installation and removal - Reusable - Suitable for limited spaces | - Difficult in hard soil/rock - Susceptible to corrosion | [1,14] |
| Secant Piles | Overlapping reinforced concrete piles form a continuous wall. | - Deep excavations - Unstable soil - High water table | - High strength and stiffness - Any depth - Watertight | - Time-consuming - Expensive - Needs specialized equipment | [15,16] |
| Soldier Pile Shoring | Vertical steel I- or H-beams with horizontal lagging. | - Shallow to deep excavations - Stable soil - Low water table | - Cost-effective - Easy installation - Suitable for limited spaces | - Lower strength/stiffness - Not ideal for high water tables | [17] |
| Verbal Judgment | Explanation | Fuzzy Number |
|---|---|---|
| Very Unimportant (1) | One criterion is significantly less important than another | (1, 1, 2) |
| Less Important (2) | One criterion is slightly less important than another | (1, 2, 3) |
| Equally Important (3) | Both criteria contribute equally to the objective | (2, 3, 4) |
| More Important (4) | One criterion is somewhat preferred over another | (3, 4, 5) |
| Very Important (5) | One criterion is strongly preferred over another | (4, 5, 5) |
| Question No. | Comparison Criteria | Question |
|---|---|---|
| Q1 | Soil Condition vs. Underground Water Condition | How does the significance of soil condition compare to that of underground water condition? |
| Q2 | Soil Condition vs. Excavation Depth | How does the significance of soil condition compare to excavation depth? |
| Q3 | Soil Condition vs. Condition of Adjacent Buildings | How does the significance of soil condition compare to the condition of adjacent buildings? |
| Q4 | Underground Water Condition vs. Excavation Depth | How does the significance of underground water condition compare to excavation depth? |
| Q5 | Underground Water Condition vs. Condition of Adjacent Buildings | How significant is underground water condition compared to the condition of adjacent buildings? |
| Q6 | Excavation Depth vs. Condition of Adjacent Buildings | How significant is excavation depth compared to the condition of adjacent buildings? |
| Pairwise Criteria | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th | 8th | 9th | 10th |
|---|---|---|---|---|---|---|---|---|---|---|
| Safety vs. cost | 4 | 4 | 3 | 3 | 3 | 4 | 5 | 4 | 4 | 3 |
| Pairwise Criteria | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th | 8th | 9th | 10th |
|---|---|---|---|---|---|---|---|---|---|---|
| Soil vs. water | 3 | 3 | 5 | 3 | 3 | 2 | 2 | 3 | 3 | 3 |
| Soil vs. depth | 3 | 5 | 5 | 3 | 3 | 4 | 3 | 3 | 3 | 4 |
| Soil vs. adjacent | 4 | 5 | 5 | 3 | 3 | 4 | 3 | 3 | 5 | 3 |
| Water vs. depth | 3 | 5 | 5 | 3 | 3 | 4 | 3 | 3 | 3 | 5 |
| Water vs. adjacent | 3 | 4 | 5 | 3 | 3 | 3 | 4 | 3 | 4 | 3 |
| Depth vs. adjacent | 3 | 4 | 5 | 3 | 3 | 4 | 3 | 3 | 3 | 4 |
| Safety | B11 | B12 | B13 | B14 | |||
|---|---|---|---|---|---|---|---|
| B11 | 1 | 2.5 | 2.5 | 3.5 | |||
| B12 | 2.5 | 1 | 2.5 | 2.5 | |||
| B13 | 2.5 | 2.5 | 1 | 2.5 | |||
| B14 | 1.5 | 2.5 | 2.5 | 1 | |||
| 7.5 | 8.5 | 8.5 | 9.5 | ||||
| Soil Condition | Water Condition | Excavated Depth | Adjacent Buildings | Construction Cost | Progress Rate | Crossing Utilities | |
|---|---|---|---|---|---|---|---|
| 0.5 | 0.281 | 0.277 | 0229 | 0.212 | 0.416 | 0.294 | 0.295 |
| Soil Condition | Water Condition | Excavated Depth | Adjacent Buildings | Construction Cost | Progress Rate | Crossing Utilities | |
|---|---|---|---|---|---|---|---|
| 0.5 | 0.157 | 0.155 | 0.128 | 0.118 | 0.183 | 0.129 | 0.129 |
| Expert No. | Role | Education | Years of Experience | Area of Expertise |
|---|---|---|---|---|
| 1 | Project Manager | MSc Civil Engineering | 15 | Project management, excavation planning |
| 2 | Construction Manager | BSc Civil Engineering | 13 | Construction supervision, site operations |
| 3 | Consultant | PhD Geotechnical Engineering | 20 | Geotechnical design, excavation support systems |
| Alternative Comparisons | Results | ||
|---|---|---|---|
| 1st Expert | 2nd Expert | 3rd Expert | |
| Diaphragm wall vs. secant pile | 2 | 2 | 3 |
| Diaphragm wall vs. soldier pile | 3 | 3 | 3 |
| Diaphragm wall vs. sheet pile | 4 | 3 | 3 |
| Secant pile vs. soldier pile | 5 | 5 | 4 |
| Secant pile vs. sheet pile | 5 | 5 | 4 |
| Soldier pile vs. sheet Pile | 3 | 3 | 3 |
| 8.89 | 9.21 | 9.87 | |
| CI | 1.63 | 1.73 | 1.95 |
| CR | 1.81 | 1.92 | 2.17 |
| Sub-Criteria | Alternatives | ||||
|---|---|---|---|---|---|
| Diaphragm Wall | Secant Pile | Solider Pile | Sheet Pile | ||
| Soil condition | 0.5 | 0.25 | 0.33 | 0.21 | 0.20 |
| Underground water condition | 0.5 | 0.24 | 0.30 | 0.25 | 0.22 |
| Excavated depth | 0.5 | 0.25 | 0.30 | 0.24 | 0.21 |
| Adjacent buildings | 0.5 | 0.25 | 0.25 | 0.25 | 0.25 |
| Construction cost | 0.5 | 0.31 | 0.27 | 0.22 | 0.20 |
| Construction progress rate | 0.5 | 0.27 | 0.32 | 0.26 | 0.15 |
| Crossing utilities | 0.5 | 0.22 | 0.28 | 0.19 | 0.32 |
| Sub-Criteria | Alternatives | ||||
|---|---|---|---|---|---|
| Diaphragm Wall | Secant Pile | Solider Pile | Sheet Pile | ||
| Soil condition | 0.5 | 0.039 | 0.052 | 0.033 | 0.031 |
| Underground water condition | 0.5 | 0.037 | 0.047 | 0.039 | 0.034 |
| Excavated depth | 0.5 | 0.032 | 0.038 | 0.031 | 0.027 |
| Adjacent buildings | 0.5 | 0.030 | 0.030 | 0.030 | 0.030 |
| Construction cost | 0.5 | 0.057 | 0.049 | 0.040 | 0.037 |
| Construction progress rate | 0.5 | 0.035 | 0.041 | 0.034 | 0.019 |
| Crossing utilities | 0.5 | 0.028 | 0.036 | 0.025 | 0.041 |
| 0.5 | 0.258 | 0.293 | 0.230 | 0.219 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wefki, H.; Elbeltagi, E.; Elgamal, A.; Alturki, M.; Alkharisi, M.K.; Elnabwy, M.T. Fuzzy AHP Approach for Enhancing Excavation Support System Selection in Building Projects: Balancing Safety and Cost-Effectiveness. Buildings 2025, 15, 1580. https://doi.org/10.3390/buildings15091580
Wefki H, Elbeltagi E, Elgamal A, Alturki M, Alkharisi MK, Elnabwy MT. Fuzzy AHP Approach for Enhancing Excavation Support System Selection in Building Projects: Balancing Safety and Cost-Effectiveness. Buildings. 2025; 15(9):1580. https://doi.org/10.3390/buildings15091580
Chicago/Turabian StyleWefki, Hossam, Emad Elbeltagi, Ahmed Elgamal, Mansour Alturki, Mohammed K. Alkharisi, and Mohamed T. Elnabwy. 2025. "Fuzzy AHP Approach for Enhancing Excavation Support System Selection in Building Projects: Balancing Safety and Cost-Effectiveness" Buildings 15, no. 9: 1580. https://doi.org/10.3390/buildings15091580
APA StyleWefki, H., Elbeltagi, E., Elgamal, A., Alturki, M., Alkharisi, M. K., & Elnabwy, M. T. (2025). Fuzzy AHP Approach for Enhancing Excavation Support System Selection in Building Projects: Balancing Safety and Cost-Effectiveness. Buildings, 15(9), 1580. https://doi.org/10.3390/buildings15091580







