Dynamic Response and Anti-Collapse Analysis of Multi-Column Demolition Mode in Frame Structures
Abstract
1. Introduction
2. Anti-Progressive Collapse Theory and Column Removal Design Scheme
2.1. Progressive Collapse Mechanism
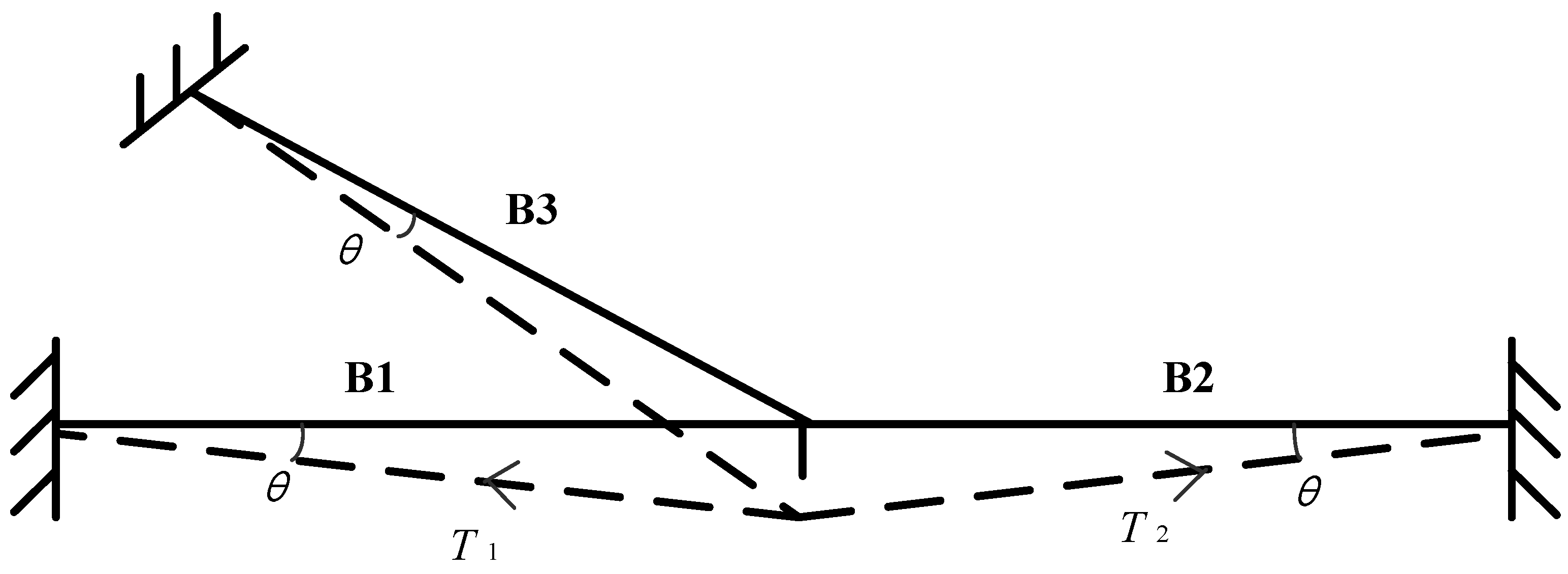
2.1.1. Beam Mechanism

2.1.2. Catenary Mechanism
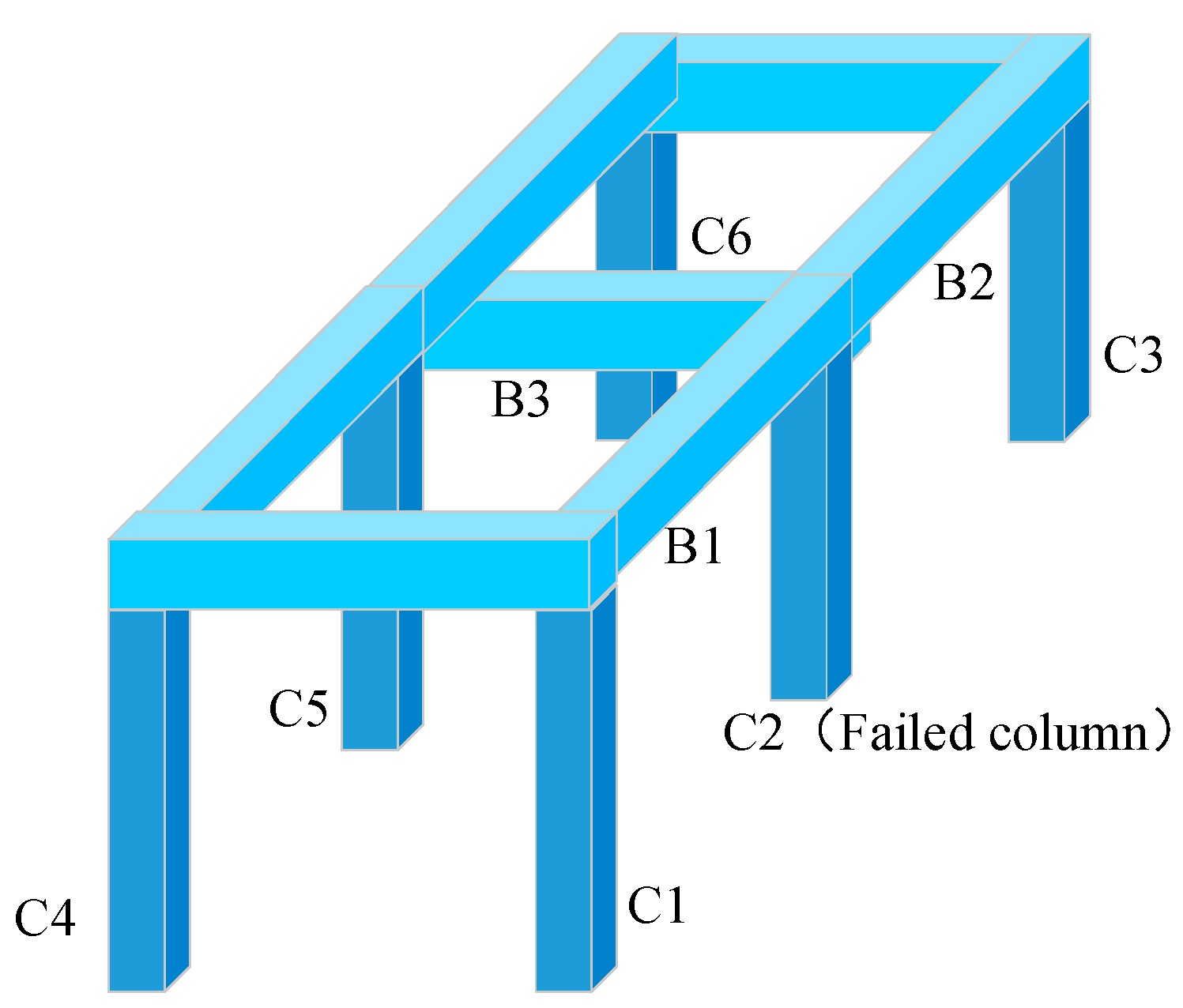
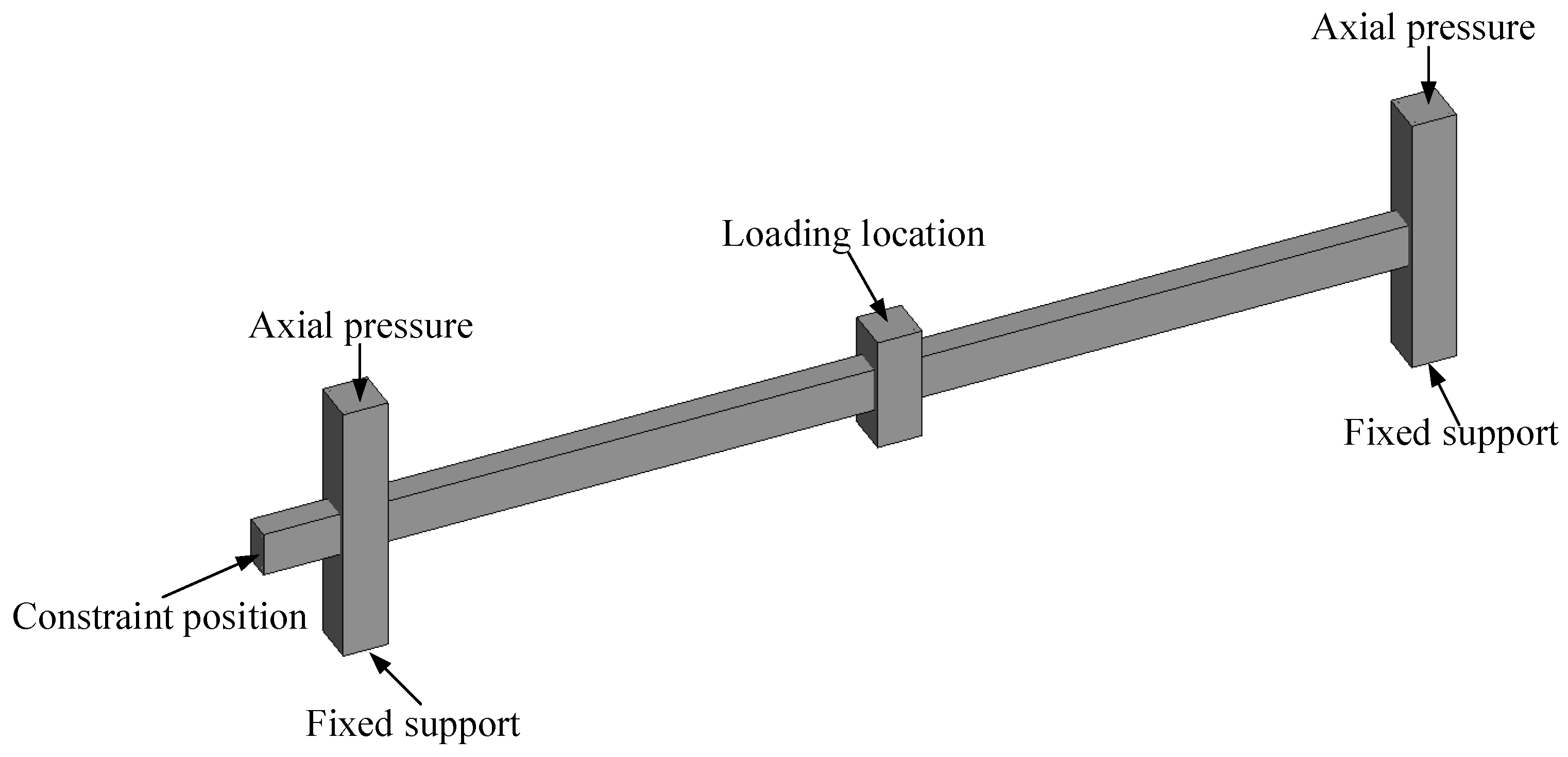
3. Design and Modeling of the Column Removal Scheme
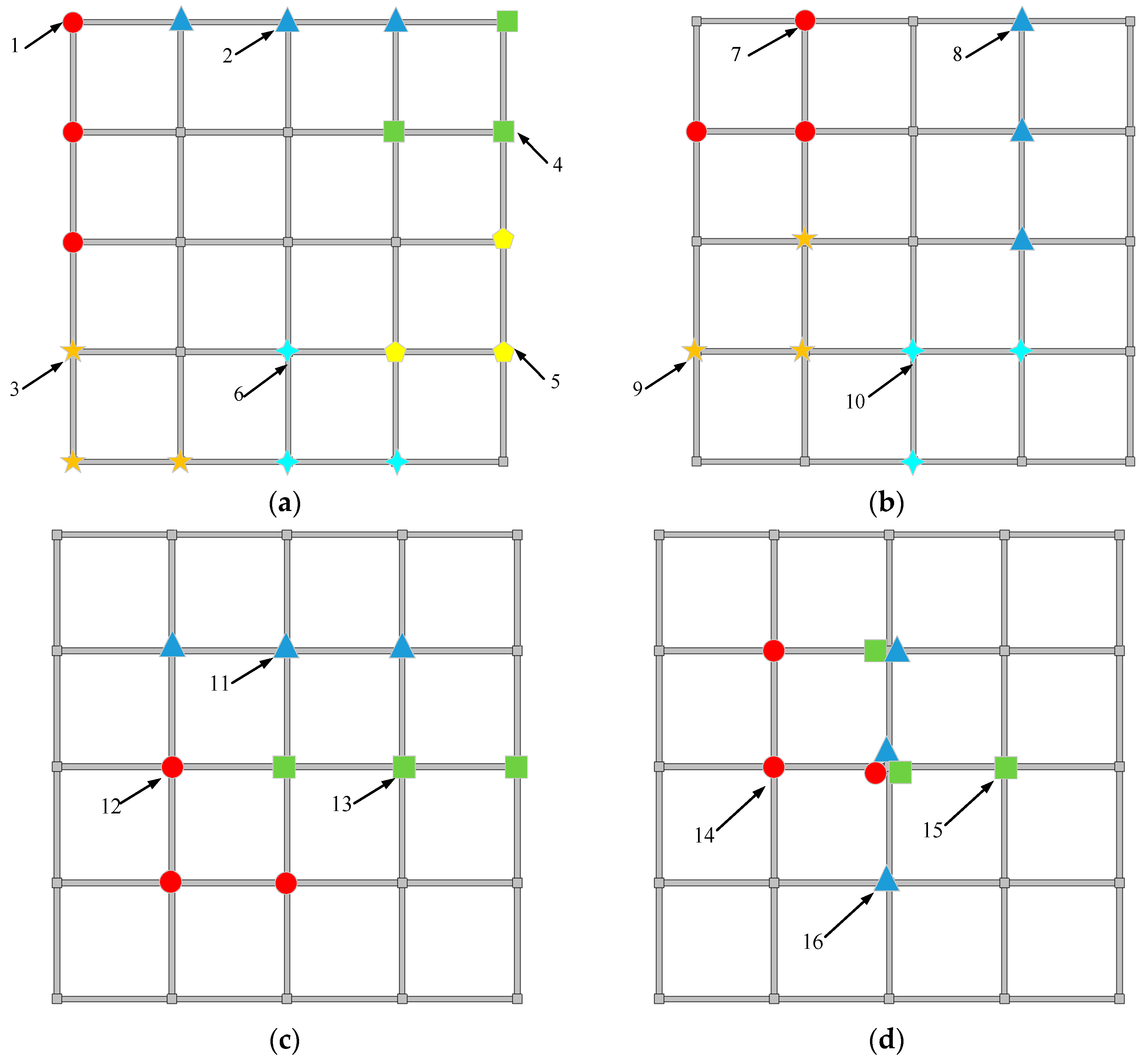
3.1. Design of the Single-Column Removal Scheme of Frame
3.2. The Design of Double-Column Removal Scheme of Frame
3.3. The Design of Three-Column Removal Scheme of Frame
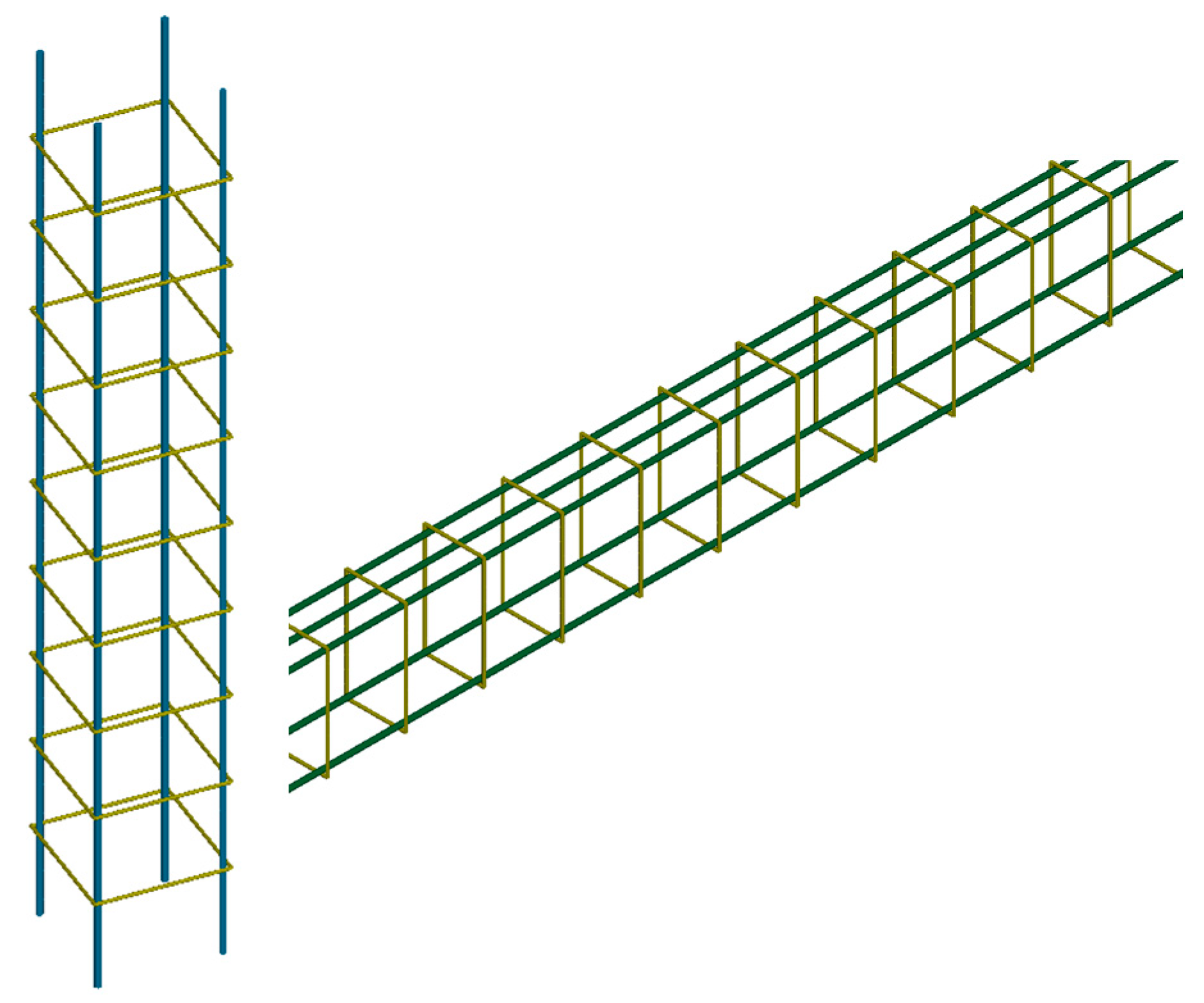
3.4. Model Establishment of the Framework
3.5. Material Model
| Density/(g/cm3) | Poisson’s Ratio | Young’s Modulus /GPa | Yield Stress/Gpa | Tangent Modulus /Gpa | Failure Strain |
|---|---|---|---|---|---|
| 7.8 | 0.3 | 200 | 0.4 | 1.92 | 0.15 |
4. Research on Multi-Column Demolition of Four-Plane Frame Structure
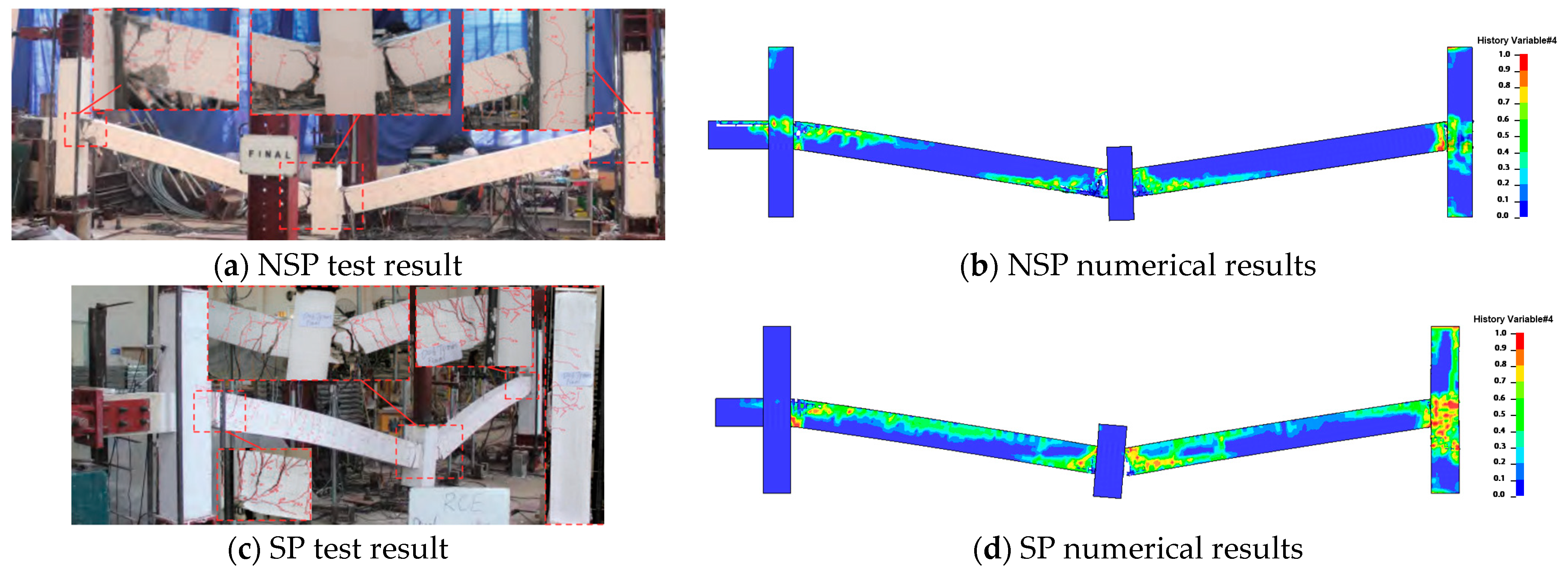
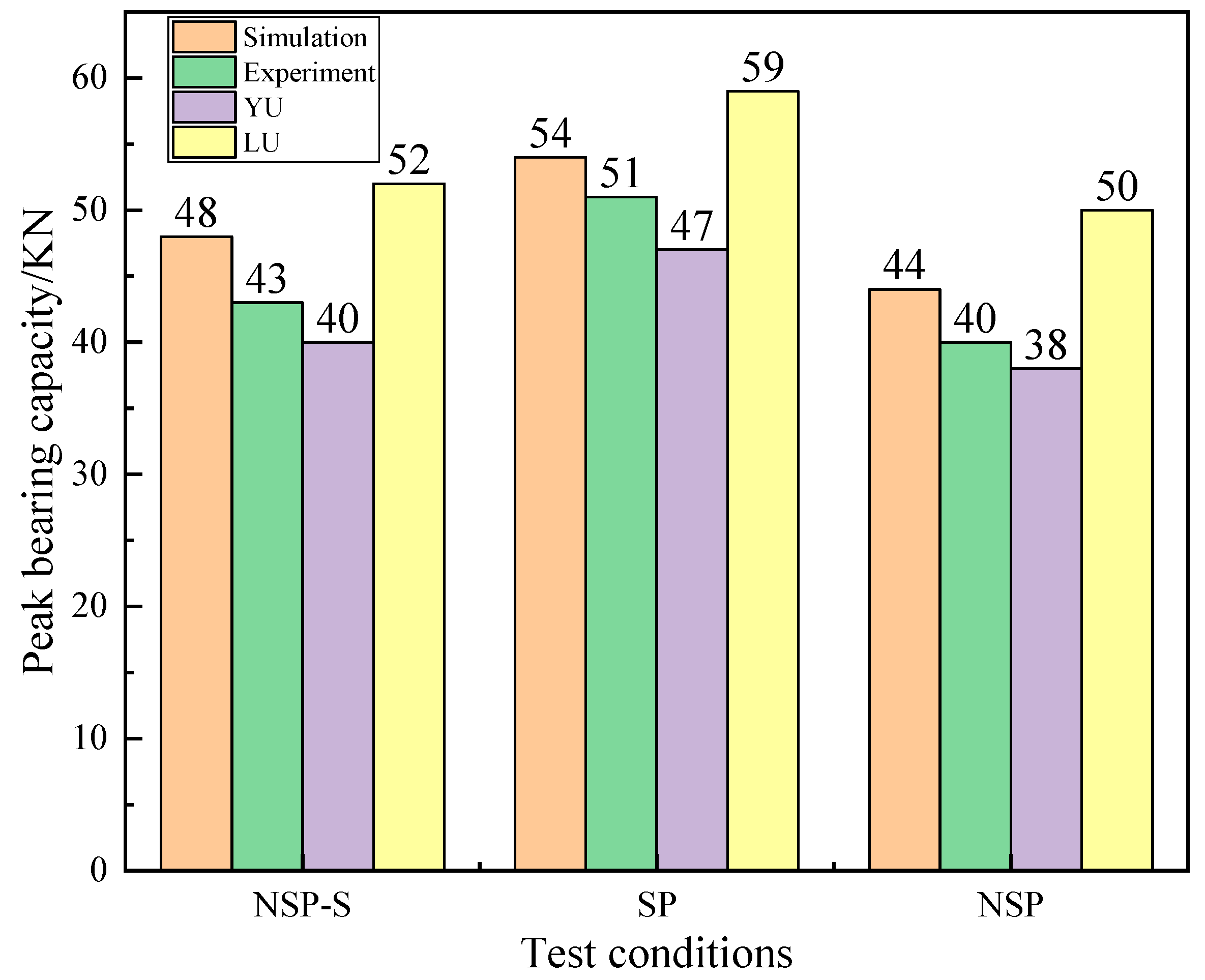
4.1. Study on Single-Column Demolition Mode
4.1.1. Failure Column Stress and Vertical Displacement Analysis
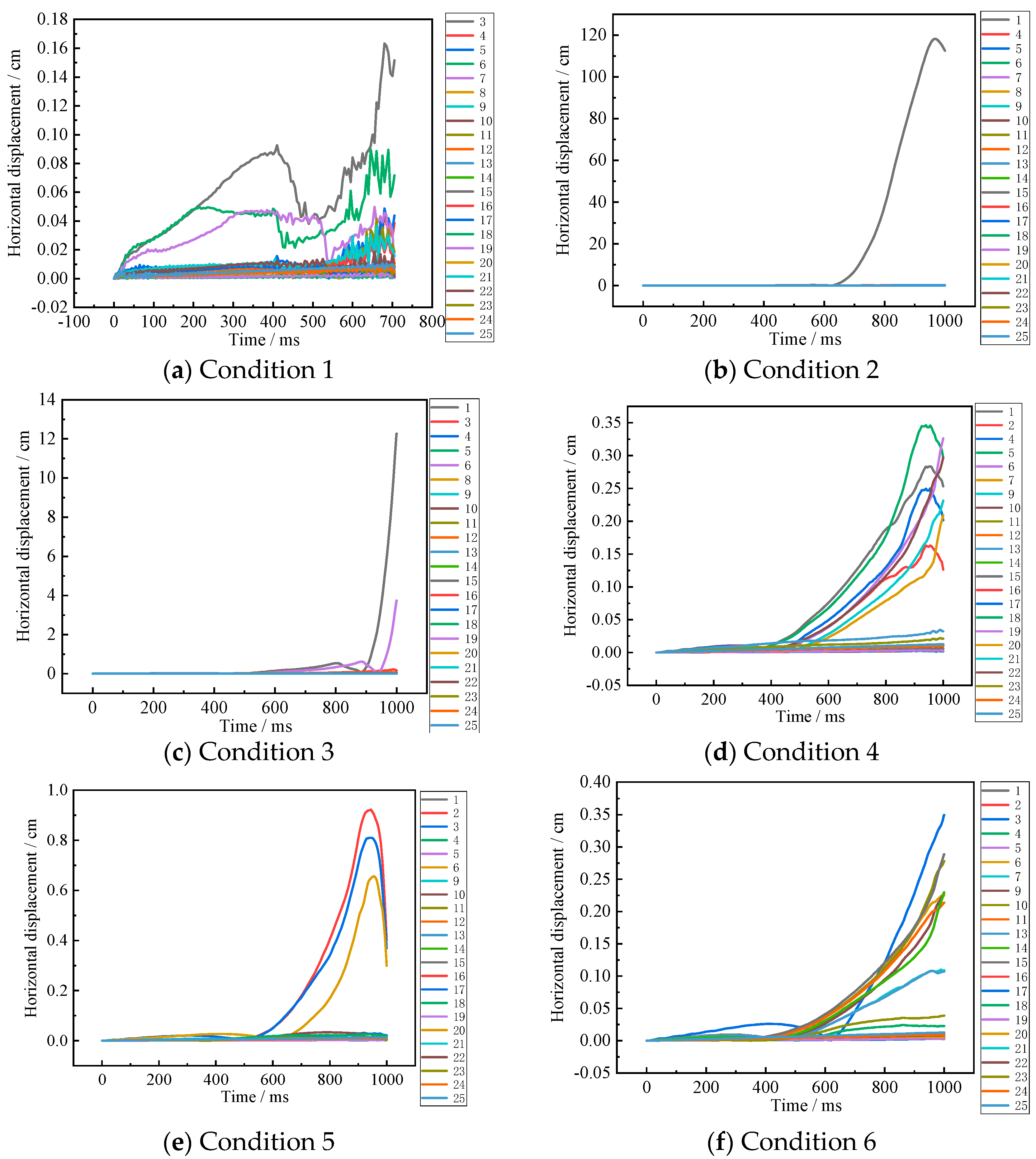
4.1.2. Horizontal XY Displacement of Column Apex (Single-Column)
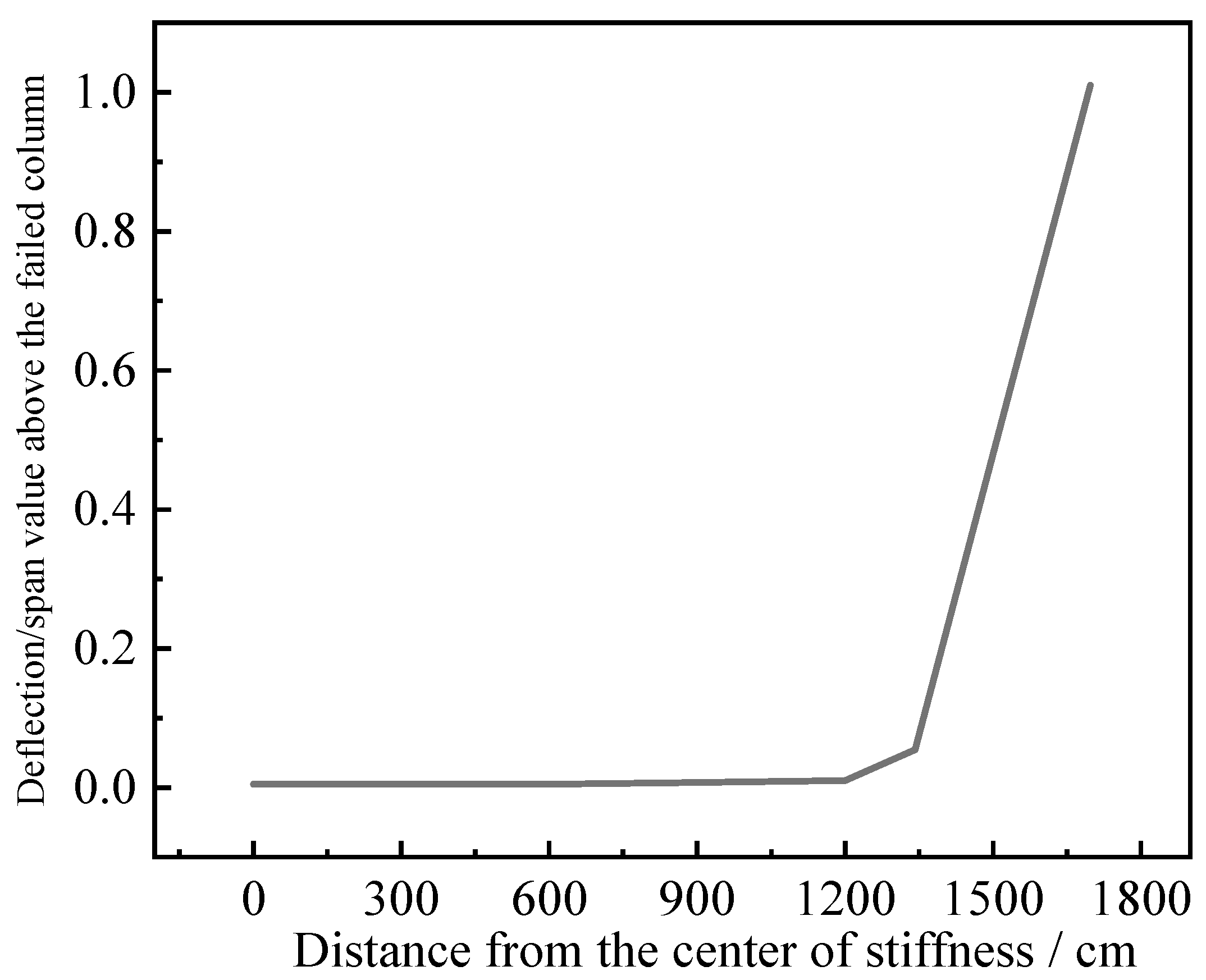
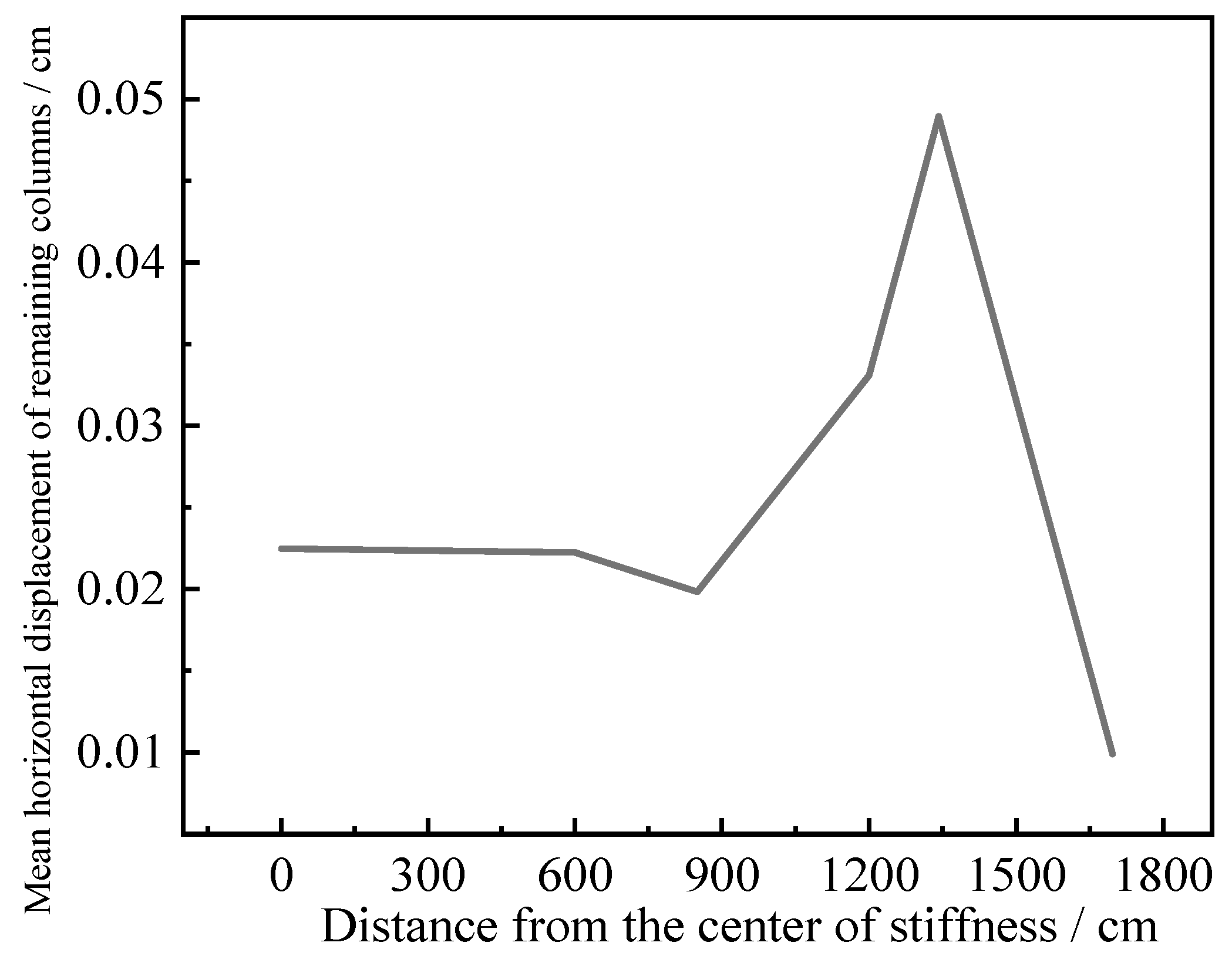
4.1.3. Response Range Analysis and Collapse Analysis Based on Single-Column Demolition Conditions
4.2. Study of the Demolition Mode of Double Columns
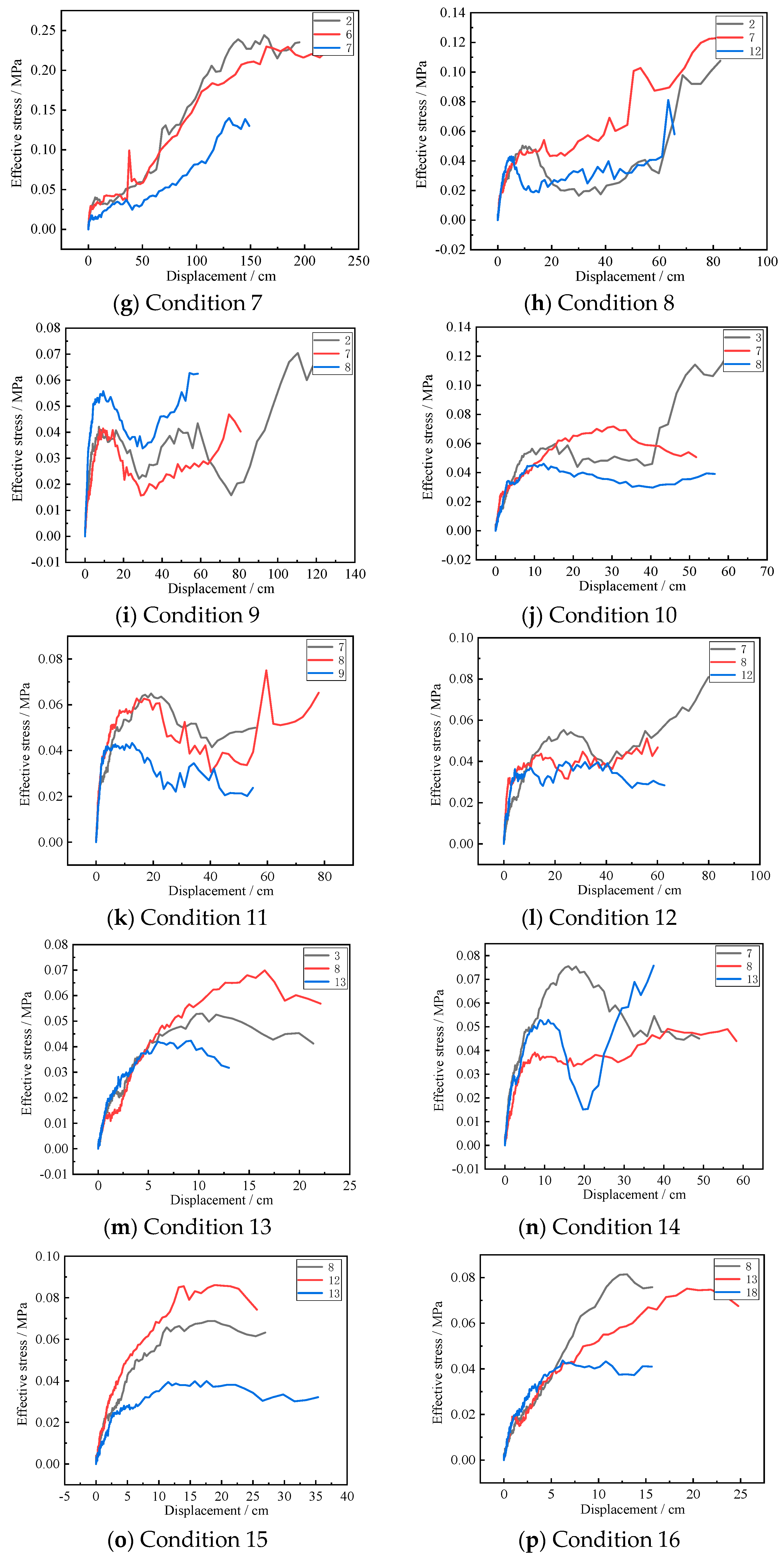
4.2.1. Substructure Resistance (Double Columns)
4.2.2. Horizontal XY Displacement of Column Apex (Double Columns)
4.2.3. Response Range Analysis and Collapse Analysis Based on Double-Column Demolition Conditions
4.3. Study of Three-Column Demolition Mode
4.3.1. Substructure Resistance (Three-Columns)
4.3.2. Horizontal XY Displacement of Column Apex (Three-Columns)
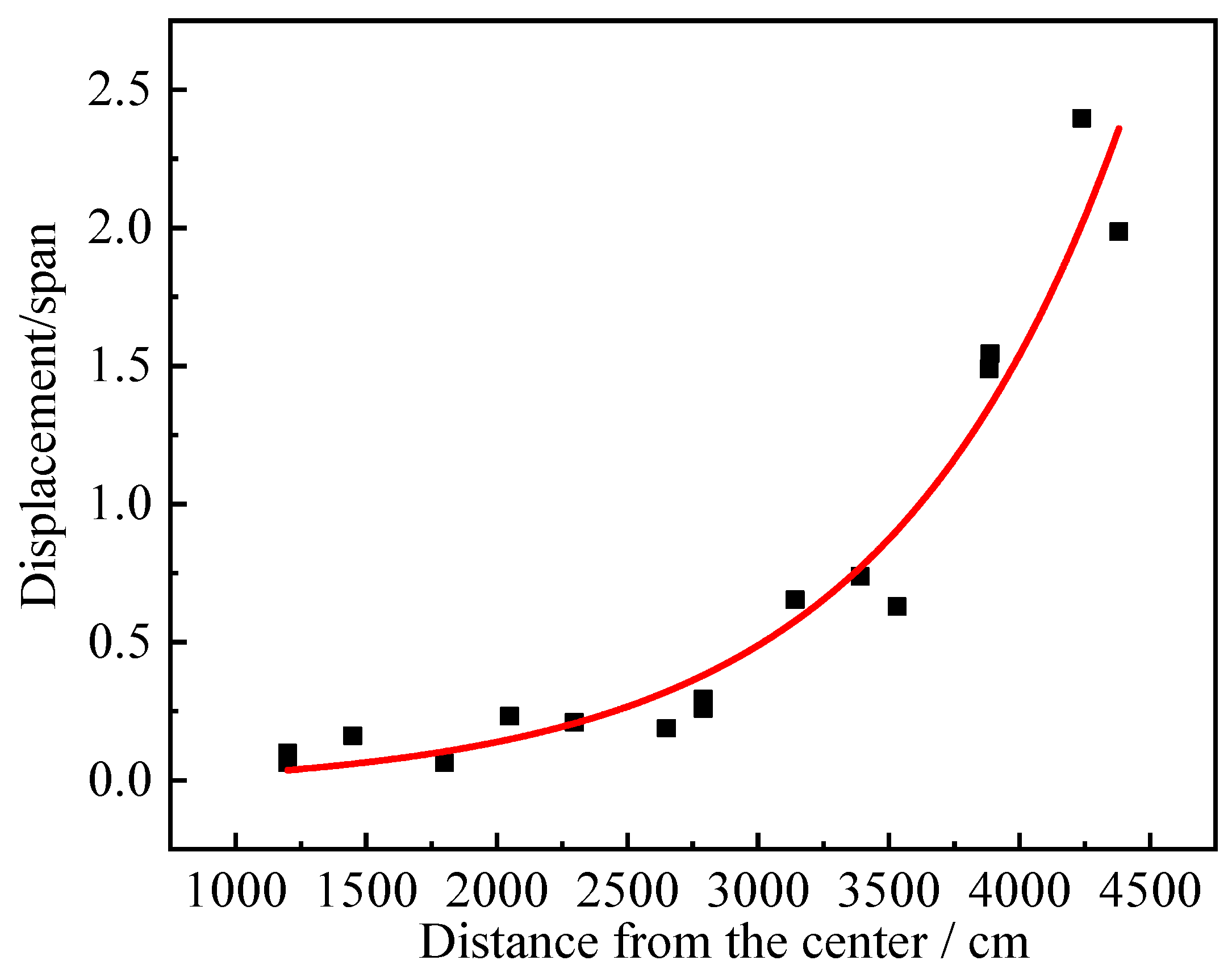
4.3.3. Response Range Analysis and Collapse Analysis Based on Three-Column Demolition Conditions
5. Conclusions
- (1)
- With the increase in the number of demolished columns, the collapse resistance of the structure decreases significantly. The column removal position affects the remaining structure by affecting the number of transfer paths of the backup bearing beam. For the demolition column mode with the same number of bearing paths, it depends on the geometric form of the remaining structure and the stiffness condition of the column. Different demolition column modes show different stresses and vertical displacements.
- (2)
- The smaller the difference between the stiffness and location conditions between the failure columns, the closer the collapse process of each failure column and the more average the collapse speed. With the increase in the number of demolished columns, the displacement and velocity of progressive collapse caused by corner columns will be greater. For the multi-column demolition mode, it will be more affected by the stiffness of the adjacent columns. The failure of three columns will bring possible progressive collapse events to the failure columns of peripheral structures such as corner columns and side columns, but the influence on the failure columns inside the structure is relatively small, and it can still resist large loads.
- (3)
- With the increase in the distance between the failure column and the center of the structure, the horizontal displacement of the structure shows a trend of increasing first and then decreasing. The conclusion of single-column demolition and double-column demolition is the same. The outer column of the structure with weak stiffness connection will become the primary goal of the collapse of the structure, and it is difficult to have an impact on the structural column with strong stiffness.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khandelwal, K.; El-Tawil, S. Pushdown resistance as a measure of robustness in progressive collapse analysis. Eng. Struct. 2011, 33, 2653–2661. [Google Scholar] [CrossRef]
- Kiakojouri, F.; De Biagi, V.; Chiaia, B.; Sheidaii, M.R. Progressive collapse of framed building structures: Current knowledge and future prospects. Eng. Struct. 2020, 206, 110061. [Google Scholar]
- Zhang, J.Z.; Jiang, B.H.; Feng, R.; Chen, R. Robustness of steel moment frames in multi-column-removal scenarios. J. Constr. Steel Res. 2020, 175, 106325. [Google Scholar] [CrossRef]
- Wang, Z.; Ye, Z.Y.; Xu, B.S. Study on Priority of Column Removal for Progressive Collapse of Reinforced Concrete Frame Structures. J. Wuhan Univ. Technol. 2024, 46, 48–54. [Google Scholar]
- Liu, C.Y.; Huang, Y. Influence of infilled wall distribution on the load of progressive collapse resistance of RC frame structures. China Sci. 2024, 19, 547–556. [Google Scholar]
- Yang, G.; Xu, D.D.; Wu, B. A Simplified Plastic Hinge Analysis Method for the Progressive Collapse Patterns of Reinforced Concrete Planar Frame Structures. J. Wuhan Univ. Technol. 2024, 46, 47–56. [Google Scholar]
- Cheng, Y.; Sun, L.; Liu, J.; Ou, C.; Xiao, Z.M. Dynamic Performance of a Remaining RC Frame with a Central-Column Failure Subjected to Impact Loads. Arab. J. Sci. Eng. 2022, 47, 12479–12496. [Google Scholar] [CrossRef]
- Tian, L.; Fu, X.W. Progressive Collapse Mechanism Analysis of High-rise Reinforced Concrete Frame Structure under Blast Loading. Sci. Technol. Eng. 2016, 16, 232–238. [Google Scholar]
- UFC 4-023-03; Design of Buildings to Resist Progressive Collapse. America Department of Defense: Washington, DC, USA, 2009.
- EN 1991-1-7; Eurocode 1-Actions on structures-Part 1-7: General actions - Accidental actions. European Committee for Standardization (CEN): Brussels, Belgium, 2006.
- Zhou, J.; Cui, J.C. Comparative study on design codes and methods for structural resistance of progressive collapse. Build. Struct. 2015, 45, 98–105. [Google Scholar]
- Li, R.R.; Yu, J.; Zhou, X.D. A vulnerability assessment framework for the disproportionate collapse of RC frame structures subjected to multiple column removal scenarios. J. Build. Eng. 2025, 100, 111659. [Google Scholar] [CrossRef]
- Yi, W.J.; He, Q.F.; Xiao, Y.; Kunnath, S.K. Experimental study on progressive collapse-resistant behavior of reinforced concrete frame structures. ACI Struct. J. 2008, 105, 433–439. [Google Scholar]
- Qiu, J.; Jiang, L.M.; Cai, X.S. Reconstruct the 3D load redistribution paths of framed structures subjected to local column failure and multi-floor fire. Structures 2024, 58, 105668. [Google Scholar] [CrossRef]
- Zhang, F.W.; Lv, X.L. Numerical simulation and analysis of different collapse patterns for RC frame structure. J. Build. Struct. 2009, 30, 119–125. [Google Scholar]
- Qian, K.; Luo, D.; He, S. Progressive collapse performance of reinforced concrete frame structures subjected to ground two-column removal scenario. J. Build. Struct. 2018, 39, 61–68. [Google Scholar]
- Wang, H.S. The Influence of the Failure of Columns to the Progressive Collapse Control for Reinforced Concrete Frame Structures Under Accidental Load. Master’s Thesis, Beijing University of Civil Engineering and Architecture, Beijing, China, 2014. [Google Scholar]
- Lv, T. Analysis of Progressive Collapse of the High-Rise Reinforced Conerete Frame Structure Under the Condition of the Double Column Failure. Master’s Thesis, Shandong Jianzhu University, Jinan, China, 2015. [Google Scholar]
- Qiao, H.Y.; Yang, Y.H.; Zhong, W.H. Progressive collapse analysis and mechanism study for multi-story frame structures with middle-column demolition. J. Vib. Shock 2018, 37, 136–143. [Google Scholar]
- Deng, X.F.; Lan, D.Q.; Jin, L. Study on Progressive Collapse Behavor of RC Frameunder a Penultimate Column Removal Scenario. Eng. Mech. 2024, 41, 12–23. [Google Scholar]
- Hei, X.D.; Sun, H.F.; Wang, B. Research on progressive collapse of steel frame after failure of inner column based on incremental dynamic analysis method. Build. Struct. 2023, 53, 6–13+43. [Google Scholar]
- Huang, M.; Huang, H.; Wang, B. Experimental Study on Progressive Collapse Behavior of HPFL-Strengthened Sub-Assemblages Subjected to Corner Column Removal. Eng. Mech. 2025. [Google Scholar] [CrossRef]
- Luo, L. Peformance and Reliability Study on Progressive Collapse of RC Frame Structures Based on Pushdown Analysis. Master’s Thesis, Nanchang University, Nanchang, China, 2016. [Google Scholar]
- Pan, L.; Liu, B.Q.; Xing, G.H. Analysis of collapse resistant behavior of RC frame structure after removal of key column of ground floor. World Earthq. Eng. 2015, 31, 170–180. [Google Scholar]
- Xu, X.H.; Qian, K.; Lv, D.G. Effects of vertical loading patterns on Pushdown analysis of structures in resisting progressive collapse. J. Build. Struct. 2015, 36, 126–130. [Google Scholar]
- Cheng, Z.H. Collapse Modes, Risk and Robustness analysis of RC Frame Structures. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2009. [Google Scholar]
- Jin, Y.; Yu, X.H.; Li, B. Probabilistic assessment of progressive collapse resistance in RC slab-incorporated frame structures: Accounting for slab effects. J. Build. Eng. 2025, 103, 112119. [Google Scholar] [CrossRef]
- Raminfar, E.; Zafarani, M.M.; Birzhandi, M.S.; Zareei, S.A. Progressive Collapse of Steel Structures Under Blast Loads Considering Soil-Structure Interaction. Shock Vib. 2025, 2025, 997912. [Google Scholar] [CrossRef]
- Qu, T.; Zeng, B.; Zhou, Z.; Huang, L.J. Experimental investigation of progressive collapse resistance of bonded local prestressed concrete frame substructures. Eng. Struct. 2025, 323, 119232. [Google Scholar] [CrossRef]
- Guo, Y.X.; Chen, K.; Dai, Z.; Yang, B.; Alqawzai, S.; Kong, D.Y. Numerical Simulation and Design of Progressive Collapse of Steel Frame Composite Structures Considering Falling-Floors Impact. J. Struct. Eng. 2024, 150, 9. [Google Scholar] [CrossRef]
- Yuzbasi, J. Experimental verification of full-scale silo structure demolition: Investigating successive column removal with finite element method and progressive collapse simulation through blast load. Struct. Concr. 2024, 25, 4408–4427. [Google Scholar] [CrossRef]
- Yu, J.; Tan, K.H. Analytical model for the capacity of compressive arch action of reinforced concrete subassemblages. Mag. Concr. Res. 2014, 66, 109–126. [Google Scholar] [CrossRef]
- Lu, X.Z.; Lin, K.Q.; Li, C.F. New analytical calculation models for compressive arch action in reinforced concrete structures. Eng. Struct. 2018, 168, 721–735. [Google Scholar] [CrossRef]


















| Symbol | Parameter | Value | Symbol | Parameter | Value |
|---|---|---|---|---|---|
| Uniaxial compressive strength | 0.035 Gpa | Compressive strain rate index | 0.032 | ||
| Tensile compressive strength ratio | 0.1 | Tensile strain rate index | 0.036 | ||
| Shear compression strength ratio | 0.18 | Reference compression strain rate | 3 × 10−8 ms−1 | ||
| G | Shear modulus | 16.7 GPa | Reference tensile strain rate | 3 × 10−9 ms−1 | |
| A | Failure surface parameters | 1.6 | Failure compression strain rate | 3 × 1022 ms−1 | |
| n | Failure surface parameters | 0.61 | Failure tensile strain rate | 3 × 1022 ms−1 | |
| Q0 | Tension compression meridian ratio parameter | 0.6805 | Compression yield surface parameters | 0.53 | |
| B | Rod angle correlation coefficient | 0.0105 | Tensile yield surface parameters | 0.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Yin, J.; Wang, Z.; Yi, J. Dynamic Response and Anti-Collapse Analysis of Multi-Column Demolition Mode in Frame Structures. Buildings 2025, 15, 1525. https://doi.org/10.3390/buildings15091525
Wang Z, Yin J, Wang Z, Yi J. Dynamic Response and Anti-Collapse Analysis of Multi-Column Demolition Mode in Frame Structures. Buildings. 2025; 15(9):1525. https://doi.org/10.3390/buildings15091525
Chicago/Turabian StyleWang, Zhenning, Jianping Yin, Zhijun Wang, and Jianya Yi. 2025. "Dynamic Response and Anti-Collapse Analysis of Multi-Column Demolition Mode in Frame Structures" Buildings 15, no. 9: 1525. https://doi.org/10.3390/buildings15091525
APA StyleWang, Z., Yin, J., Wang, Z., & Yi, J. (2025). Dynamic Response and Anti-Collapse Analysis of Multi-Column Demolition Mode in Frame Structures. Buildings, 15(9), 1525. https://doi.org/10.3390/buildings15091525






