Horizontal Bearing Characteristics of Large-Diameter Rock-Socketed Rigid Pile and Flexible Pile

Abstract

In order to study the horizontal bearing characteristics of large-diameter rock-socketed rigid pile and flexible pile, two lateral loading tests in which the pile lengths are 5.2 m and 11.07 m were carried out. Unidirectional multi-cyclic loading was applied to the piles during the tests, with the maximum load reaching 3500 kN. The measured results are compared with the calculated results of Zhang’s method, m-method and the rigid pile method in the design codes. It is indicated that if the characteristic values of the horizontal bearing capacity of the large-diameter rock-socketed rigid pile and flexible pile are determined by the same horizontal displacement of the pile head, some risk will be brought to the design of the rigid pile. Compared with the rigid pile method, the m-method is more suitable for calculating the rotation angle of the pile head. In terms of the maximum bending moment of the large-diameter rock-socketed flexible pile under the critical load, the calculated result of Zhang’s method is less than the measured result, while the calculated result of the m-method is the largest. However, for the rigid pile, both Zhang’s method and m-method underestimate the maximum bending moment of the pile body. In summary, when a large-diameter rock-socketed pile is designed, reasonable calculation method and failure discrimination standard should be chosen according to the actual conditions.

1. Introduction

In addition to the vertical load, a pile should also bear the horizontal load, such as wave load, wind load or seismic load, etc. The horizontal bearing characteristics of a pile should be studied systematically. The horizontal bearing capacity of a pile is related to the mechanical property and section size of the pile itself, as well as the horizontal resistance of the soil around the pile [1,2]. For piles with a larger diameter, the bending stiffness will be greater so that their deflection under the horizontal load will be smaller. Moreover, as the strength of the surrounding soil becomes higher, the horizontal resistance will increase and the constraint on the pile deflection will be more intense. Therefore, the relative stiffness between the pile and the surrounding soil determines the horizontal stress and deformation of the pile.

Generally, piles can be divided into rigid piles and flexible piles according to their relative stiffness to the surrounding soil. Many scholars have carried out specific research on the horizontal stress and deformation of the pile using various methods and from multiple perspectives. At first, Poulos [3] employed centrifuge model tests to study the mechanical properties of flexible piles under cyclic horizontal load in dry sand. This research revealed the effects of the cycle number and sand density on the maximum bending moment of the pile body and determined typical p–y (p is the horizontal load and y is the horizontal displacement) reaction curves for flexible piles. Alderlieste [4] conducted a series of centrifuge model tests in the laboratory and indicated that both the horizontal stiffness and bearing capacity significantly increased when the pile diameter increased. He also pointed out that the formula in the specification of the American Petroleum Institute overestimated the initial stiffness of a pile under horizontal load. Centrifuge model tests were also adopted by Zhu et al. [5] to investigate the stress and deformation characteristics of large-diameter single piles in sandy ground when static and cyclic forces were applied, respectively. A hyperbolic p–y reaction curve was obtained under static loading conditions. Akihiro et al. [6] applied two-way horizontal cyclic load to large-diameter single piles with different length–diameter ratios, and observed the stiffness degradation of the short pile (whose length–diameter ratio is smaller than five) under high-frequency loading. Through a 1 g large-scale model test, Sun et al. [7] studied the soil–pile interaction and the deformation characteristics of super large rigid piles and flexible piles in silt ground. Then, a calculation method was proposed to predict the horizontal deformation of a super-large pile under cyclic load [8]. It was further highlighted that horizontal deformation should serve as a control index for the pile design. Based on field tests and numerical simulations of large-diameter concrete-filled steel tube piles, Wang et al. [9] explained the working mechanism of a pile under horizontal load. They revealed that the horizontal bearing capacity primarily depended on the compression of the rock in front of the pile, with a pile segment socketed in rock bearing the majority of the horizontal load. Sun [10] conducted field tests in the Changbai Mountain area with a thick volcanic ash layer and measured the horizontal displacement and bearing capacity of large-diameter drilled grouting piles (1.5 m in diameter and 60 m in length). The proportional coefficient of the horizontal resistance provided by the surrounding soil was found to be 10,000 kN/m⁴, while this coefficient decreased with the horizontal load increasing. Moreover, five rock-socketed drilled grouting piles with different total lengths and embedded depths were subjected to horizontal load in situ [11]. The distribution of the horizontal displacement and bending moment along the pile body was measured and compared under different working conditions. Jiang et al. [12] assumed that the distribution of the radial earth pressure on the passive side of the pile followed a cosine function, and established an analytical solution for the horizontal bearing capacity of the rigid single pile considering the vertical friction effect. Using advanced finite element software, Gawecka et al. [13] explored the bearing capacity of energy piles in London clay. A series of numerical simulations were conducted by Wang et al. [14] to investigate the mechanical response of large-diameter rigid piles under monotonic horizontal load in medium-dense sand. The results showed that the normalized horizontal load transfer curve was independent of the pile diameter and loading eccentricity. Li et al. [15] indicated that the scour-induced unloading effect could cause stress redistribution in the surrounding soil, which consequently influenced the displacement and bearing capacity of the large-diameter pile. Liu et al. [16] simulated the single pile beneath the offshore wind turbine. With the pile diameter increasing, the horizontal displacement of the pile head reduced, while the bending moment of the pile body increased. Moreover, Wan et al. [17,18] developed an elastoplastic anisotropic constitutive model to describe the stress–strain relationship of the soil around the pile under cyclic loading conditions.

In conclusion, most of the above research focuses on the horizontal bearing characteristics of large-diameter piles that are socketed in soil, not in rock, and mainly adopts the methods of laboratory model tests and numerical simulations. Although the evolution of the mechanical properties of piles under various parameters can be investigated scientifically, laboratory test results are often affected by the model scale. Particularly for large-diameter piles, whether the measured results can truly reflect their mechanical property remains to be verified. For numerical simulation, the input parameters of the soil and structure have a significant impact on the calculated results, and the construction procedure of the pile in practical engineering is often simplified and idealized. Therefore, from both qualitative and quantitative perspectives, full-scale experimental research on large-diameter rock-socketed piles holds significant importance. However, little research in this aspect has been carried out up to now. In addition, the existing methods in the design codes for calculating the horizontal bearing capacity of piles often introduce many assumptions, but whether these assumptions align with the actual mechanical property of the rock-socketed pile needs to be deeply discussed. This paper is based on the liquefied natural gas (LNG) tank project in Zhuhai constructed by CNOOC Gas and Power Group and carries out lateral loading tests on large-diameter rock-socketed drilled grouting piles. All these piles are socketed into rock by 2 m, while the lengths from the rock-socketed surface to the pile head are different so these piles have different stiffnesses. Internal forces of the rigid pile and flexible pile are measured by many sensors to discuss the applicability of the relevant calculation methods in the design codes.

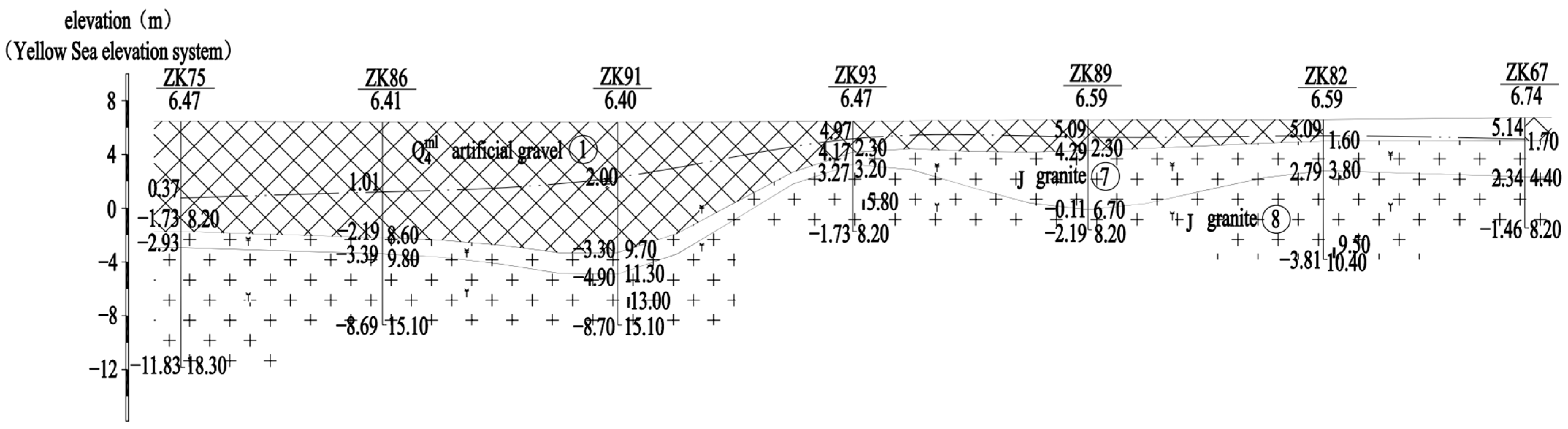
2. Test Site Conditions

The test site is located near the mountainous area of Gaolan Port, Guangdong, China. The ground condition is simple because there is only one gravel layer above the bedrock. The gravel layer is mainly composed of medium to slightly weathered granite gravel or stone blocks, and the maximum particle diameter can reach up to 1.2 m. This layer was filled in 2007 and leveled by strong compaction in 2010. The gravel and stone blocks mainly come from abandoned stone in the mountainous and hilly area near the site, and their engineering properties are relatively poor. The upper part of this layer is slightly dense to medium dense, while the lower part is partially loose.

There are two kinds of underground water: phreatic water and bedrock fissure water. The phreatic water, which stays in the particle void of the gravel layer, has a dramatically varying water level, and the water inflow is also large. The typical profile of the site is shown in Figure 1. The parameters of the bedrock are shown in

Table 1. Physical and mechanical parameters of the bedrock.

Layer No.	Name	Taking Rate of the Rock Core	Rock Quality Designation	Standard Value of the Uniaxial Compressive Strength/MPa	Hardness	Completeness
⑥	Strongly weathered granite	75%	—	—	Extremely soft	Extremely broken
⑦	Medium weathered granite	85%	14%	—	Relatively hard	Broken~relatively broken
⑧	Slightly weathered granite	98%	70%	67.1	Hard	Relatively complete~complete

.

3. Lateral Loading Tests on Large-Diameter Rock-Socketed Pile

3.1. Basic Parameters of the Pile

In this work, the test piles belong to drilled grouting piles. The concrete grade is C40. All the piles have an embedded depth of about 2 m. Other design parameters of the test piles are shown in

Table 2. Design parameters of the test piles.

Pile No.	Diameter/mm	Total Length/m	Length Above the Rock-Socketed Surface/m	Length Below the Rock-Socketed Surface/m
13#	1500	5.2	3.2	2.00
11#	1500	11.07	9.0	2.07

Note: All the test piles have the same reinforcement.

.

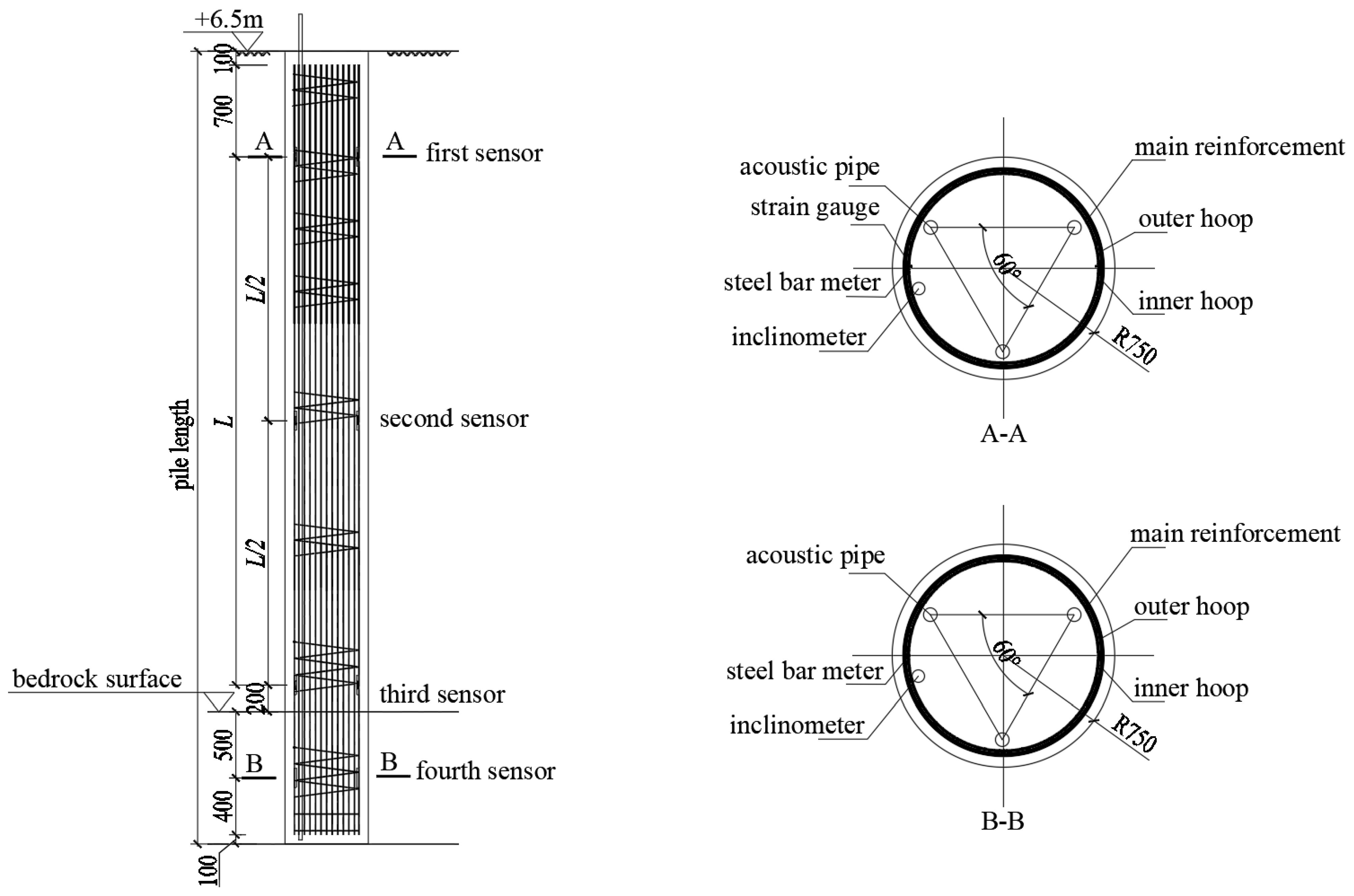
3.2. Monitoring Scheme

The following data were measured during the tests:

(1)

Load and the corresponding displacement at the loading points. Two displacement sensors were arranged symmetrically on both sides of the loading point to monitor the horizontal displacement. At the positions that were 0.5 m above these two displacement sensors, another two sensors were arranged to monitor the rotation angle of the pile head. The loading points can be found in Figure 2.

(2)

Strain and stress of the pile body. The strain and stress sensors, which were tied inside the steel cage, were arranged on both the compression side and tension side of the pile. The layout of these sensors is shown in Figure 3.

(3)

Inclination of the pile body. An inclinometer was tied on the tension side of the steel cage. The bottom of the inclinometer was parallel to the pile bottom, while the top of the inclinometer was about 1 m higher than the pile head. Due to the existence of strain and stress sensors on the tension side, the inclinometer was slightly tilted towards the other side. See Figure 3 for details.

3.3. Loading Scheme

The test piles experienced unidirectional multi-cyclic loading and unloading, and the force variation in each level was set to 350 kN. Another two piles, with the same diameter as the test piles, were constructed to provide the counterforce (see Figure 2). When each level of load was applied, we kept the load for at least four minutes and then collected the data from the displacement, stress and strain sensors. Then, the force was reduced to 0 kN, and after two minutes, the residual readings of these sensors were recorded. So far, one cycle of loading and unloading has been completed. The above process was repeated five times until the next level of load was applied. In addition, after unloading was completed for the fifth time, the inclination of the pile body was measured by the inclinometer. In order to guarantee the reliability of the measured results, the loading time should be shortened as much as possible, while the time interval of the data recording should be accurate and not interrupted. If the pile was broken during loading, the test would be stopped immediately.

Note that, because the head of the test pile was not processed specifically in this work, the concrete quality at the pile head was relatively poor. Moreover, a high level of load was applied to the pile during the tests. As a result, it was required that the loading points of the jack should keep at least 0.5 m away from the pile head, and the concrete at the loading points should be fresh and of good quality. The specific loading manner can be observed in Figure 2.

4. Results Analysis

According to the design codes, the dimensionless embedded depth of Pile 11#, α_h, is 4.6, which is larger than 2.5, so this pile belongs to the flexible pile group. On the other side, Pile 13# is rigid because its α_h = 2.37 < 2.5. This paper analyzes the horizontal bearing characteristics of large-diameter rock-socketed drilled grouting piles from the following aspects: the horizontal bearing capacity, rotation angle at the ground surface, measured and theoretical values about the bending moment of the pile body.

4.1. Horizontal Bearing Capacity

4.1.1. Horizontal Critical Load

The horizontal bearing capacity of a drilled grouting pile is usually controlled by the concrete crack under the action of tensile stress. The maximum load before the concrete on the tension side of the pile cracks and withdraws from service is called the critical load. Determining the horizontal critical load of piles is crucial for analyzing the bearing capacity, as it provides key parameters for the subsequent pile design and construction. According to the relevant design codes, the horizontal critical load of a single pile can be determined by the following discrimination standard:

(1)

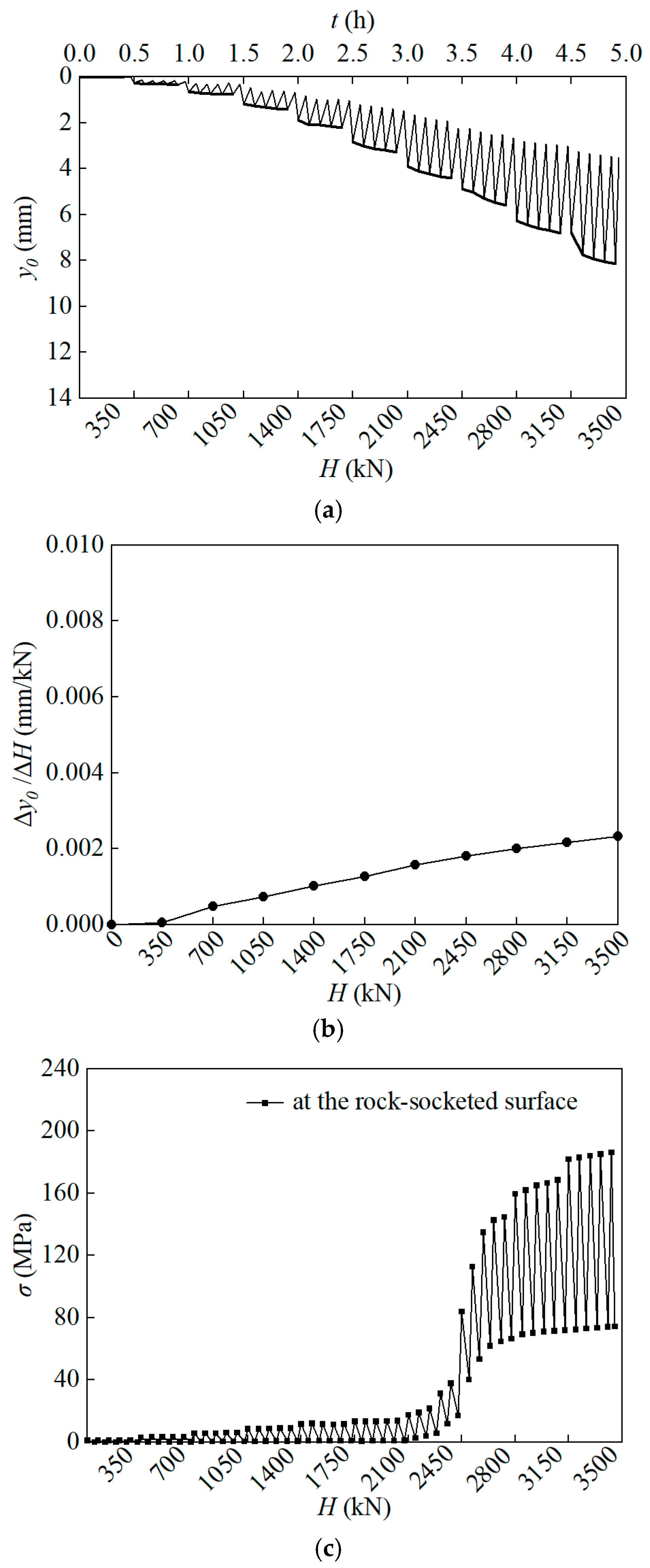
When an inflection point appears on the H–t–y₀ curve (where H is the horizontal load that is applied to the pile head, t is time and y₀ is the horizontal displacement of the pile head), the previous level of the horizontal load can be taken as the horizontal critical load. H–t–y₀ curves of Pile 11# and Pile 13# are shown in Figure 4a and Figure 5a, respectively. It can be seen that for Pile 11#, the horizontal displacement of the pile head remains negligible during the initial three load levels. A marked escalation in the displacement magnitude is observed from the fourth load level. Notably, when the horizontal load increases from 1750 kN to 2100 kN, the pile head exhibits a pronounced displacement. After that, the displacement grows almost linearly with an increase in the horizontal load. Therefore, according to the H–t–y₀ curve of Pile 11#, the inflection point corresponds to a horizontal load of 2100 kN, so the horizontal critical load is 1750 kN. Under identical load levels, the horizontal displacement at the head of Pile 13# is significantly smaller than that of Pile 11#. With the horizontal load increasing, the displacement demonstrates a gradual but sustainable growth, and there is no obvious inflection point on the H–t–y₀ curve. Hence, the horizontal critical load is supposed to be 3500 kN.

(2)

When the first inflection point appears on the H–∆y₀/∆H curve (where ∆H and ∆y₀ are increments of H and y₀, respectively) or lgH–lgy₀ curve, the corresponding horizontal load can also be taken as the horizontal critical load. Figure 4b and Figure 5b show the H–∆y₀/∆H curves of Pile 11# and Pile 13#, respectively. The slope of this curve represents the gradient of the pile head displacement with respect to the load increment. Theoretically, when plastic deformation is generated for the first time, the growth rate of the pile head displacement accelerates significantly, resulting in a sharp increase in the slope of the H–∆y₀/∆H curve. The inflection point marks the transition of the pile from elastic deformation to plastic deformation and serves as a standard for determining the horizontal critical load. This discrimination standard cross-verifies with Standard (1), thereby enhancing the accuracy and reliability of the determined results. However, from Figure 4b and Figure 5b, the inflection points on H–∆y₀/∆H curves are not obvious, because these curves are basically straight. Therefore, according to this discrimination standard, the horizontal critical loads of both piles are 3500 kN.

(3)

The horizontal load corresponding to the first inflection point on the H–σ_s curve (where σ_s is the axial tensile stress of the pile) can be taken as the horizontal critical load. Typically, this inflection point coincides with the initial yielding of the pile body material or the onset of significant plastic deformation in the surrounding soil. During this phase, the bearing capacity of the pile undergoes a substantial alteration. When the stress on the tension side of the pile reaches the maximum, H–σ_s curves of Pile 11# and Pile 13# are shown in Figure 4c and Figure 5c, respectively. Because stresses at the rock-socketed surface and at the middle part of the pile body are both very large, the stress curves at these two sections are shown in the figure. The H–σ_s curves of Pile 11# at the rock-socketed surface and at the middle part of the pile body exhibit a consistent overall trend, and the first inflection points of these two sections correspond to the same horizontal load, i.e., 3150 kN. But for Pile 13#, the maximum tensile stress appears only at the rock-socketed surface. Compared with Pile 11#, its H–σ_s curve demonstrates a more apparent inflection point. The horizontal critical load of Pile 13# is determined as 2450 kN.

Based on the above discrimination standards, three possible values for the horizontal critical load are summarized in

Table 3. Horizontal critical load of the test pile.

Pile No.	Standard (1)	Standard (2)	Standard (3)	Final Value
11#	1750 kN	3500 kN	3150 kN	1750 kN
13#	3500 kN	3500 kN	2450 kN	2450 kN

. Finally, the minimum value is taken as the horizontal critical load of the test pile.

For Pile 11#, the horizontal critical load determined by Standard (1) is significantly smaller than that determined by the other two discrimination standards. On the other hand, for Pile 13#, the horizontal critical load determined by Standard (3) is relatively smaller. This discrepancy primarily results from the fact that Standard (1) and Standard (2) are based on the horizontal displacement at the pile head, while Standard (3) relies on the stress threshold of the pile body. The horizontal critical load of a flexible pile (i.e., Pile 11#) is significantly smaller than that of a rigid pile (i.e., Pile 13#) under the same conditions of pile diameter, embedded depth and surrounding soil properties.

4.1.2. Characteristic Value of the Horizontal Bearing Capacity

In practical engineering, sensors are generally not installed on the off-site test pile body. Therefore, when determining the characteristic value of the horizontal bearing capacity, we can resort to the H–t–y₀ curve and H–∆y₀/∆H (lgH–lgy₀) curve. The load corresponding to the allowable horizontal displacement of the pile head can also be used to determine the characteristic value.

According to the relevant design codes, when the reinforcement rate of the drilled grouting pile is not less than 0.65%, it is advisable to take 0.75 times the load corresponding to the allowable horizontal displacement of the pile head as the characteristic value of the horizontal bearing capacity of a single pile. Based on this standard, the results are shown in

Table 4. Characteristic value of the horizontal bearing capacity of the test pile.

Pile No.	When Horizontal Displacement of the Pile Head Is Equal to 6 mm	When Horizontal Displacement of the Pile Head Is Equal to 10 mm
11#	1312 kN	1312 kN
13#	2100 kN	2625 kN

.

Table 4 indicates that if the allowable horizontal displacement of the pile head is set to be 6 mm, the characteristic values of the horizontal bearing capacity of both Pile 11# and Pile 13# are less than their horizontal critical loads. If the allowable displacement is set to be 10 mm, the characteristic value of the horizontal bearing capacity of Pile 11# is less than its horizontal critical load. However, the opposite case occurs with Pile 13#, which means that using this characteristic value will bring some risk to the pile design. In summary, for large-diameter rock-socketed drilled grouting piles, we should not use the same standard (i.e., the same allowable horizontal displacement of the pile head) to determine the characteristic values of the horizontal bearing capacity of a rigid pile and a flexible pile. Furthermore, because the failure position of the rigid pile is just the rock-socketed surface in some cases, it is not applicable to determine its bearing capacity by the horizontal displacement of the pile head.

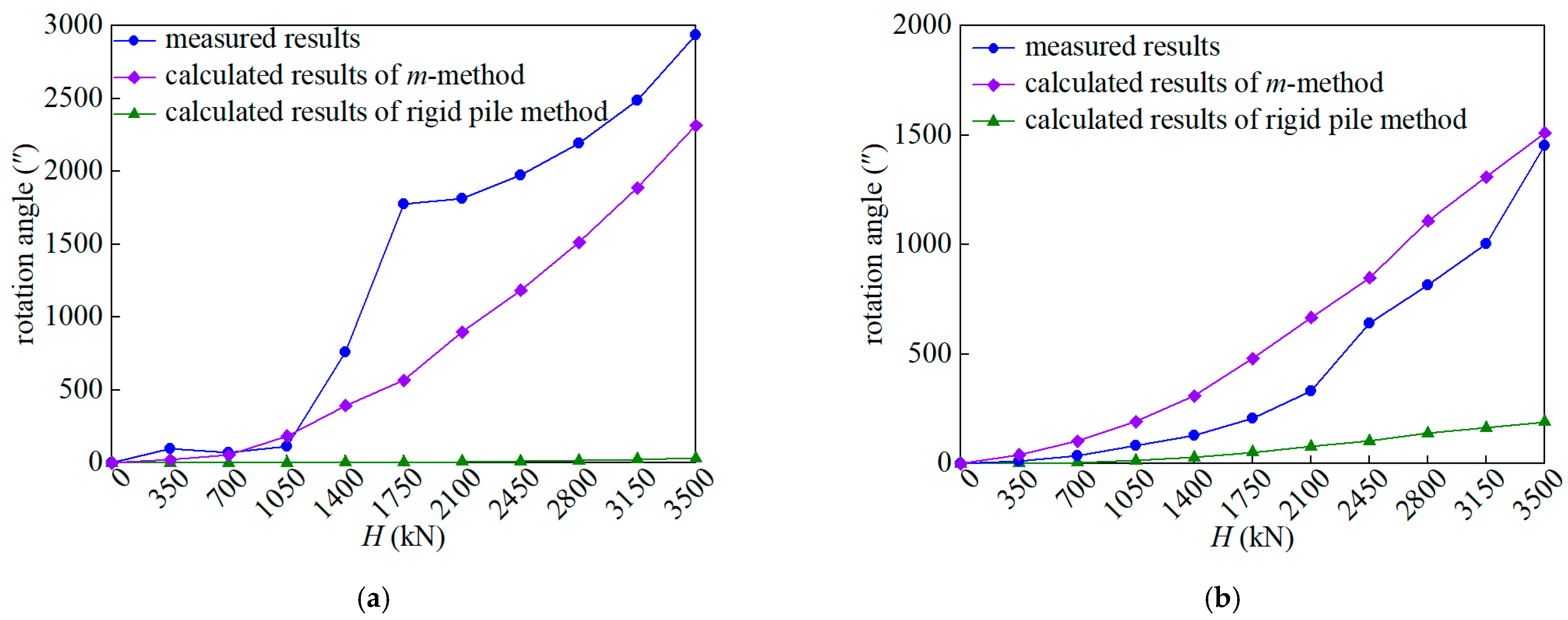
4.2. Rotation Angle of the Pile Head

The rotation angle of large-diameter rock-socketed piles at the ground surface is a critical index for evaluating the anti-overturning capacity. Under the horizontal load, the pile body undergoes measurable rotation, the magnitude of which directly determines the stability and safety of the pile. To comprehensively investigate the rotation characteristics of large-diameter rock-socketed piles, this section analyzes the rotation angle of the pile head based on the experimental data.

According to the four dial indicators installed on the pile head (see Figure 2), the rotation angle of the pile head can be measured, and its variation with the external load is shown in Figure 6. It is indicated that the rotation angle of Pile 11# experiences two abrupt changes during the whole loading process. The first change appears when the load level is 1050 kN. According to the measured results shown in Figure 4, we can conclude that this change may be caused by a measurement error. The second change corresponds to a load level of 1750 kN, which is equal to the critical load of Pile 11#. During loading, the rotation angle of Pile 13# increases monotonically, without any abrupt change, and is less than the rotation angle of Pile 11# under the same load level. In addition, the variation trend of the rotation angle of Pile 11# and Pile 13# reveals that the pile head rotation increases with the external load at an accelerating rate. The above observation indicates that under identical conditions, both rigid and flexible rock-socketed piles exhibit a consistent overall trend in the pile head rotation, yet the rigid pile has a smaller rotation angle than the flexible pile when the external load is the same.

Figure 6 also shows the foundation rotation angle calculated by the rigid pile method in Specifications for Design of Foundation of Highway Bridges and Culverts (JTG 3363-2019) [19], and the pile head rotation angle calculated using the m-method in the Technical Code for Building Pile Foundations (JGJ 94-2008) [20]. It can be seen that if the rigid pile method is adopted, the calculated rotation angles of both Pile 11# and Pile 13# are much smaller than the measured results. Furthermore, the overall variation trend of the calculated rotation angles with the external load is almost linear, which is quite different from the measured results. On the other side, based on the m-method, the calculated variation trend of both piles is basically consistent with the measured results. Specifically, the calculated values of the rotation angles of Pile 11# are smaller than the measured ones. For Pile 13#, the calculated values are relatively larger, but the absolute error is much limited. This comparison confirms that the m-method exhibits superior accuracy in predicting the rotation characteristics of both rigid and flexible rock-socketed piles.

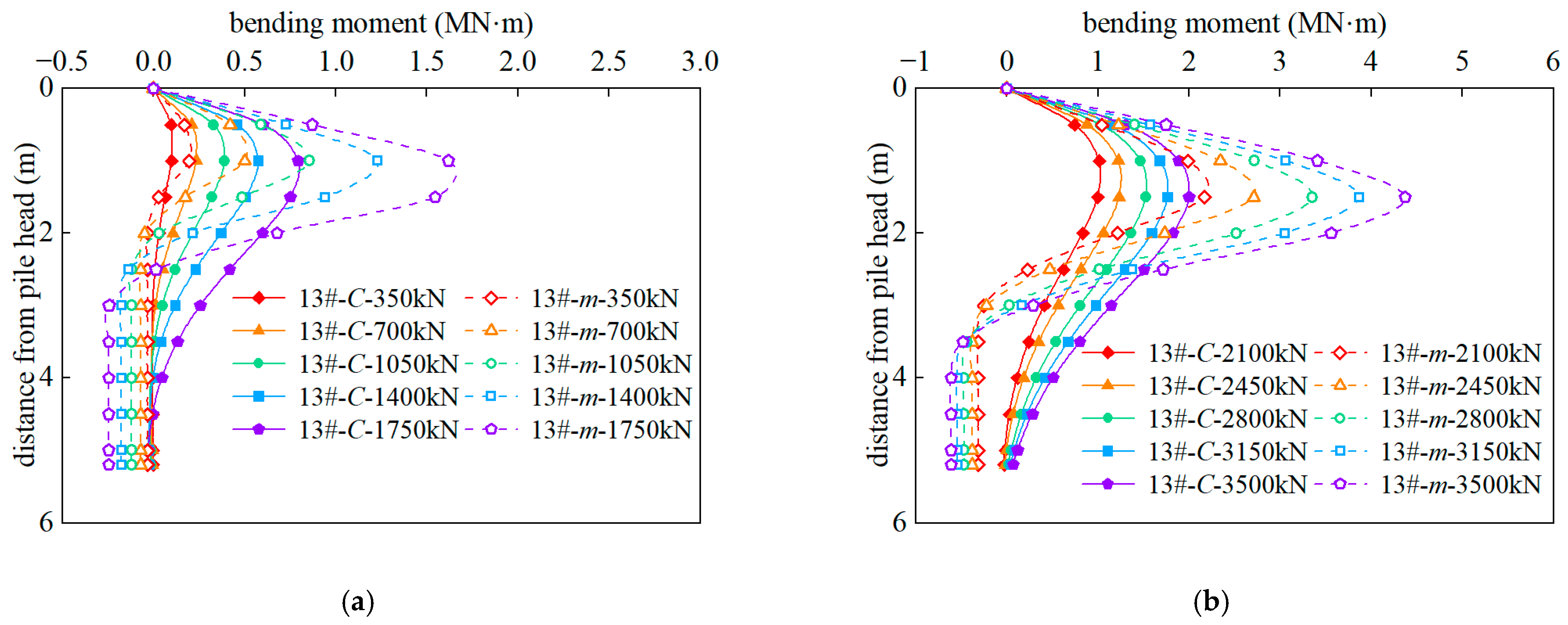
4.3. Bending Moment of the Pile Body

In the study of horizontal bearing characteristics of large-diameter rock-socketed piles, the bending moment of the pile body is another critical index. The existing research [4] has indicated that a significant difference appears in the bending moment of rigid piles and flexible piles.

4.3.1. Measured Results

Figure 7 displays the measured bending moment of Pile 11# and Pile 13#. In order to be more intuitive, the toes of these two piles are aligned. The figure shows that from the pile head to the pile toe, the bending moment first increases and then decreases, with an obvious peak at the middle part of the pile body. The maximum bending moment of Pile 11# appears above the rock-socketed surface, but the corresponding position gradually moves downward as the load level increases. This is because the surrounding soil can undertake part of the horizontal load, and the upper soil layer gets to work earlier than the lower soil layer. On the other side, the maximum bending moment of Pile 13# always appears at the rock-socketed surface. As the load level increases from 350 kN to 2800 kN, the maximum bending moment gradually increases. But when the horizontal load exceeds 2800 kN, the maximum bending moment remains basically unchanged. Before reaching the critical load, the maximum bending moment of Pile 11# is less than that of Pile 13# under the same load level because Pile 11# is a flexible pile. The above-measured results indicate that when the rock-socketed pile is loaded along the horizontal direction, the contribution of the surrounding soil is related to the stiffness and length of the pile. When the pile is stiff and short, the surrounding soil has little impact on the horizontal bearing capacity of the pile. Instead, the horizontal bearing capacity of the pile is determined by the mechanical property and section size of the pile itself. In this case, the pile works as a fixed end of the upper structure. When the pile is soft and long, its horizontal bearing capacity is mainly affected by the surrounding soil, which provides a large horizontal resistance for the pile through the soil–pile interaction. And as the external load increases, the plastic zone of the surrounding soil gradually extends towards the deeper layer.

4.3.2. Calculated Results

Zhang’s method and the m-method are commonly used to calculate the subgrade reaction in foundation engineering. They assume that the soil behaves like an elastic body so that the subgrade reaction acting on the pile is proportional to the displacement as follows:

$$q=k\left(z\right)\cdot x$$

(1)

where q is the subgrade reaction; k is called the foundation coefficient; and x is the horizontal displacement of the pile as the horizontal subgrade reaction is to be calculated in this work. In Zhang’s method, k is a constant (so that k is replaced by C to avoid confusion); while the m-method assumes that k increases proportionally where the buried depth is z and the proportionality coefficient is m.

According to the measured horizontal displacement of the pile, parameter C and parameter m can be determined first. Their values are listed in

Table 5. Foundation coefficients calculated by thes measured displacement.

Pile No.		Load/kN
		350	700	1050	1400	1750	2100	2450	2800	3150	3500
13#	Measured displacement/mm	0.22	0.61	1.27	2.25	3.88	5.78	7.69	10.73	13.00	15.27
	C/MN·m−3	1504.88	896.35	628.00	435.96	282.00	211.32	177.43	136.03	123.24	114.53
	m/MN·m−4	5481.44	3180.04	1841.32	1146.56	670.65	467.70	375.74	269.41	238.10	217.04
11#	Measured displacement/mm	0.07	0.17	0.85	2.34	3.63	6.38	8.95	11.97	15.67	20.15
	C/MN·m−3	6975.32	5360.86	1080.71	409.91	308.53	185.49	144.86	117.82	96.18	78.89
	m/MN·m−4	36,963.1	26,744.4	3595.59	1074.00	749.38	396.72	291.78	224.52	174.40	136.71

. Both C and m decrease with the external load increasing, while m is greater than C under the same load level. Then, the reaction force and bending moment of the pile body can be obtained successively. The calculated bending moment of Pile 11# and Pile 13# are shown in Figure 8 and Figure 9, respectively. Note that in the legend, Series 11#-C-350 kN denotes the bending moment of Pile 11# calculated by Zhang’s method when the horizontal load is 350 kN, while Series 11#-m-350 kN is the corresponding value calculated by the m-method. We can observe that based on these two methods, the calculated bending moment first increases and then decreases from up to down, which is consistent with the measured results. The maximum bending moment appears at the same position on the pile body. This position is within the range of 0.7~1.0d (d is the pile diameter) below the pile head, and slightly moves downwards as the load level increases. The calculated results in this aspect are quite different from the measured results. Moreover, at a depth of 4 m below the pile head, the calculated bending moment of Pile 11# has already been reduced to zero. For Pile 13#, the position where the calculated bending moment becomes zero is 2 m below the pile head. However, according to the measured results, only at the pile toe does the bending moment vanish. From the above comparison, we can deduce that the assumption of Zhang’s method and m-method about the boundary condition deviates from the actual situation of the rock-socketed pile.

When Pile 11# is under the critical load (i.e., 1750 kN), the maximum bending moment calculated using Zhang’s method (i.e., 0.78 MN·m) is less than the measured result (i.e., 1.57 MN·m), while the calculated result of the m-method (i.e., 1.82 MN·m) is the largest. But for Pile 13#, the maximum bending moment under the critical load (i.e., 2450 kN) can be arranged from small to large as follows: the calculated result of Zhang’s method (i.e., 1.23 MN·m), the calculated result of the m-method (i.e., 2.71 MN·m) and the measured result (i.e., 4.27 MN·m). Therefore, under the experimental conditions of this work, Zhang’s method underestimates the actual bending moments of both the rigid pile and flexible pile, meaning that the design will be in danger. On the other side, the calculated results of the m-method tend to be conservative for flexible piles but will bring some risk to the design of rigid piles.

5. Conclusions

This paper carries out full-scale field tests to investigate the horizontal bearing characteristics of large-diameter rock-socketed rigid piles and flexible piles. Horizontal critical load, characteristic value of the horizontal bearing capacity, rotation angle of the pile head, and bending moment of the pile body are measured during the tests. The measured results are adopted to evaluate the applicability of the calculation methods in the design codes. The main conclusions are summarized as follows:

(1)

According to the Technical Code for Building Pile Foundations (JGJ 94-2008) [20], if the allowable horizontal displacement of the pile head is set to be 10 mm for both rigid and flexible piles, the obtained characteristic value of the horizontal bearing capacity of the rigid pile is less than the critical load. Piles designed by this method will be in danger. Therefore, for the large-diameter rock-socketed drilled grouting pile, the horizontal bearing capacity should be comprehensively determined by considering the displacement of the pile head and the internal force of the pile body.

(2)

Compared with the rigid pile method, the m-method can provide a more accurate calculation for the rotation angle of the head of the large-diameter rock-socketed drilled grouting pile. Moreover, based on the m-method, the variation trend of the pile head rotation angle with the external load is more reasonable.

(3)

The maximum bending moment of the large-diameter rock-socketed drilled grouting pile calculated by Zhang’s method is significantly less than the measured value. The relative error is 50.3% for flexible piles and 71.2% for rigid piles. On the other side, the calculated value of the m-method is 15.9% greater than the measured value for flexible piles; therefore, this method tends to be slightly conservative. However, the m-method also underestimates the maximum bending moment of the rigid pile, which will bring some risk to the pile design.

Due to the deviation of the above calculation methods, subsequent work should focus on revising them to better reflect the practical engineering conditions. Different discrimination standards could be adopted when determining the horizontal bearing capacity of piles with different stiffness. It is necessary to note that the test piles in this work have identical diameters and embedded depths, and the only difference lies in the total length. This parameter configuration means that the measured results cannot demonstrate the effects of pile diameter and embedded depth (as well as properties of the pile material and surrounding soil, loading conditions, and so on), which are critical indexes during the pile design, on the horizontal bearing capacity. In summary, research on the horizontal bearing characteristics of large-diameter rock-socketed piles holds great significance in guiding engineering practice. Further investigation into this aspect is needed in the future.