Next Article in Journal
Assessing the Seismic Performance of Prefabricated Coupling Beams Using Double-Lap Sleeves: An Experimental and Numerical Investigation
Previous Article in Journal
Molecular-Scale Analysis of the Interfacial Adhesion Behavior Between Asphalt Binder and Aggregates with Distinct Chemical Compositions
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Buildings
Volume 15
Issue 23
10.3390/buildings15234385
buildings-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Effect of Horizontal Stiffeners on the Efficiency of Steel Beams in Resisting Bending and Torsional Moments: Finite Element Analysis

by
Mishal H. Aljarbou
1 and
Ahmed M. Sayed
1,2,*
1
Department of Civil and Environmental Engineering, College of Engineering, Majmaah University, Al Majmaah 11952, Saudi Arabia
2
Department of Civil Engineering, College of Engineering, Assiut University, Assiut 71511, Egypt
*
Author to whom correspondence should be addressed.
Buildings 2025, 15(23), 4385; https://doi.org/10.3390/buildings15234385
Submission received: 11 November 2025 / Revised: 26 November 2025 / Accepted: 2 December 2025 / Published: 3 December 2025
(This article belongs to the Section Building Structures)
Browse Figures
Versions Notes

Abstract

Steel beams with eccentric loads are subjected to combined bending and torsional moments that lead to lateral displacements, unwanted stresses at the top and bottom flanges, and global buckling along their length. To resist these displacements and stresses, horizontal stiffeners were used in the direction of the beam axis at locations of the beam’s web height. To conduct this study, Finite Element Modeling (FEM) was used to simulate these steel beams. The reliability of the FEM results was first verified by comparing them with the results of 25 steel beams that had been experimentally tested in previous studies, and the results showed high accuracy in modeling these steel beams. Secondly, a FEM analysis was performed on 70 steel beams, considering certain variables, namely the locations of the horizontal stiffeners relative to the beam’s web height, the width of the horizontal stiffeners, and the reduction in the spacing between the vertical stiffeners. The results showed that locating the horizontal stiffeners closer to the top or bottom flange enhances the beam’s resistance to eccentric loads. The placement of horizontal stiffeners near the flanges influences the stress distribution at their edges and the overall load capacity, with optimal locations at 10%, 20%, and 90% of the web height. Additionally, combining stiffeners at two web height locations increased capacity synergistically, though less than the sum of their individual effects. Using small-width horizontal stiffeners at low ratios of web height achieved similar efficiency to full-width stiffeners at higher ratios, allowing for material savings. Reducing the distance between vertical stiffeners by half also led to similar improvements to using steel beams with horizontal stiffeners of 20% or 90% of the web height. An interaction diagram was developed to predict the ultimate load capacity of steel beams under combined bending and torsion moments with varying horizontal stiffeners.

1. Introduction

Steel beams are among the most important elements of steel structures, and require careful attention, especially with regard to improving their efficiency in resisting different loads. These steel beams are often subjected to eccentric loads due to their presence in specific structural systems, such as the edge beams of bridges supporting a side cantilever, or their location in building facades, or any other location where they are exposed to loads that do not act along their longitudinal axis (eccentric loads). These eccentric loads generate torsional moments in addition to the basic bending moments on the cross-section, as well as shear forces. The presence of combined bending and torsional moments acting on the beam’s cross-section weakens it and reduces its efficiency in resisting external loads. Torsional moments cause undesirable lateral displacement, accelerating failure due to global buckling along the entire length of the beam. In addition, they generate atypical stresses at the edges of the upper and lower flanges of the steel beam’s cross-section. A review of the previous literature revealed that steel beams have received considerable attention in research and analysis, both experimentally and numerically, under various parameters and different loads. Many previous studies have addressed a wide range of parameters to evaluate and monitor the performance of steel beams [1,2,3,4]. Researchers have explored the behavior of these structural elements under various loading conditions, including shear forces [5,6,7,8], bending moments [9,10,11,12], axial compression loads [13,14], cyclic loads [15,16,17], torsional lateral buckling [18,19,20,21,22], and patch and concentrated transverse loading [23,24,25,26,27], as well as the effects of temperature [28,29,30]. Other studies have conducted experimental investigations on steel beams under varying parameters to determine their ultimate load-carrying capacity [31,32,33]. The results obtained were then compared with theoretical predictions from models incorporated in various existing design codes. Overall, these studies revealed that the predicted capacities from current design codes are generally lower than the experimentally measured values. Therefore, it is a safe design approach. However, these results apply mainly to beams with straight longitudinal axes subjected to non-eccentric static loads. Many previous studies have dealt with the use of stiffeners in strengthening and improving the efficiency of the flanges and webs of the cross-section of steel beams [34,35,36], and some have focused specifically on the effect of vertical stiffeners and have developed rules for calculating their effect on the ultimate strength of steel beams [37,38,39,40]. Graciano [41] performed a series of experimental tests on steel beams under non-eccentric static loads, incorporating a longitudinal web stiffener positioned within the compression zone. The findings indicated that installing the stiffener at a height equivalent to approximately 0.3 times the web depth enhanced the beam’s ultimate load capacity. However, when the spacing between the longitudinal stiffeners exceeded forty times the web thickness, no significant improvement in structural performance was observed. The study conducted by Sinur and Beg [42] addresses the design requirements of rigid intermediate transverse stiffeners in longitudinally stiffened plate girders under the influence of non-eccentric static loads. Comparative analysis of current design codes, along with experimental testing on 1.5 m deep beams and numerical simulations, revealed that both codes significantly overestimate the axial force resulting from the tensile field effect. The experimental results showed that the actual force did not exceed 56% of the calculated value. The study concludes that the performance of rigid intermediate transverse stiffeners can be ensured by satisfying a stiffness-based criterion defined by the minimum required second moment of area, which simplifies the design process without compromising structural reliability. Roudsari et al. [43] conducted a numerical study to investigate the influence of web stiffeners on the seismic performance of reduced beam section connections in steel moment-resisting frames. Using 183 nonlinear finite element models, various stiffener geometries, orientations, and configurations were analyzed for sections with radius, straight, and drilled-flange cuts. The results showed that appropriate combinations of vertical, horizontal, and diagonal stiffeners significantly improved hysteretic behavior, reduced local and lateral-torsional buckling, and enhanced energy dissipation capacity. The geometry and arrangement of stiffeners were found to have a greater impact on connection performance than their thickness, contributing to more reliable and ductile seismic behavior. Hou et al. [44] carried out experimental investigations on seven steel beam specimens with full cuts along the lower flange at mid-span. Additional specimens incorporated web damage corresponding to 15% and 28% of the web height at the cut location. The results demonstrated that damage to the web in conjunction with flange cuts in the tension zone significantly reduces both structural efficiency and ultimate load capacity. Specifically, reductions of approximately 75.76% and 57.54% in ultimate strength were observed for specimens with 15% and 28%, respectively, of web damage. Sayed et al. [45] conducted a numerical study on 116 specimens to investigate the effect of lateral out-of-plane deviations on the structural performance of steel I-beams. Findings revealed that out-of-plane deviation significantly decreases the ultimate moment capacity, with reductions of up to 60% when the offset equals the flange width of the beam’s cross-section. The reduction ratio increases linearly with out-of-plane distance and nonlinearly with section size and yield stress. Failure typically occurs due to global buckling in the upper flange, accompanied by stress concentration at the deviation point. The study by Sarfarazi et al. [46] develops a mathematical model to characterize the shear behavior of panel zones in flanged cruciform columns while explicitly accounting for axial force effects. A comprehensive parametric investigation involving 432 nonlinear finite element models examines the influence of column web and flange thicknesses, continuity plate thickness, and axial load level. The proposed relations predict yield and ultimate shear capacities with average deviations of 5.32% and 6.2%, respectively, demonstrating strong agreement with the numerical results. Findings indicate that continuity plate thickness has minimal impact, whereas axial load significantly alters panel zone response. The model offers improved accuracy and applicability over existing design approaches.
The Finite Element Method (FEM) has become an essential tool in the structural analysis of both steel and concrete structures, owing to its efficiency in reducing time, cost, and labor, as well as its ability to enhance safety in specific testing scenarios. FEM enables the analysis of structural elements that are impractical to test experimentally due to their large scale or measurement limitations. Consequently, many researchers have adopted FEM simulations to achieve reliable and precise results by modeling various structural components under diverse loading conditions and influencing parameters [47,48,49,50], especially steel beams [51,52,53,54] and with cold- or hot-formed sections [55,56,57,58]. Tao et al. [59] conducted FEM simulations on 340 steel tube specimens with varying geometries and cross-sectional shapes, including 44 rectangular, 154 square, and 142 circular sections. The numerical predictions demonstrated excellent agreement with the experimental results, achieving an average capacity ratio of 1.019 and a standard deviation of 0.072. This finding is particularly significant as it represents one of the most comprehensive verification studies conducted, involving the largest number of specimens analyzed for model validation. Sayed [60] performed an FEM simulation to verify the results by comparing the FEM results with data from previously published experimental tests on 6 steel beam specimens. The close agreement between the FEM and experimental results demonstrated the model’s high reliability, with an average of ratios of ultimate load capacity and deflection reaching 0.994 and 0.997, respectively, with a correlation coefficient of 0.997. Also, Perera and Mahendran [61] conducted FEM on six steel beam specimens that had previously been tested experimentally. The comparison between the numerical and experimental results demonstrated strong consistency in deformation patterns, moment–deflection relationships, and ultimate load capacities, yielding an average ratio of 1.03 and a coefficient of variation (COV) of 2.00%. Through this, it can be said that the use of FEM analysis systems provides great reliability and accuracy in the analysis and simulation of structural elements, especially steel beams, in predicting the ultimate load capacity of the structural element, its behavior, and the distribution of different stresses in the cross-section.
From the above, it is clear that many previous studies have addressed the effect of horizontal, vertical, and diagonal stiffeners on improving the efficiency of steel beams in resisting external loads. These studies have reached an advanced stage in the analysis process and the formulation of models for predicting the ultimate load capacity of these steel beams. However, they focused on the effect under non-eccentric loads, which generate bending moments and shear stresses, or under lateral loads. The authors did not find any studies that considered steel beams under eccentric loads, which result in both bending and torsional moments on the beam’s cross-section. This may be due to the difficulty of conducting these tests experimentally, as they require specialized machinery and equipment, or analytically, perhaps due to the large number of samples required. To improve the efficiency of steel beams under eccentric loads, a system of horizontal and vertical stiffeners is the optimal solution. To determine the effect of these stiffeners on the efficiency of steel beams under eccentric loads, and by reviewing the previous literature on the use of FEM in modeling structural elements, especially steel beams, it has been proven to be very accurate in the simulation results. Therefore, in this study, a FEM system was used to model steel beams with and without horizontal stiffeners under eccentric loading. This was carried out to determine the effect and contribution of horizontal stiffeners on the efficiency of steel beams in resisting eccentric loads. Several variables believed to influence the test results were considered, including the position of the horizontal stiffeners relative to the beam web height, variations in the width of the horizontal stiffeners, and a reduction in the spacing between the vertical stiffeners. Based on the results, an attempt will be made to develop a preliminary interaction diagram that can predict the ultimate eccentric load capacity of steel beams.

2. Finite Element Model Study

2.1. Modeling and Characteristics of Steel Materials

The ANSYS software (version 22) was used to perform FEM simulation of the steel beams. The SOLID186 element [62] was used to simulate steel beams, as this element has 3 degrees of freedom with 20 points distributed at the vertices and the midpoint of the element’s edges. This element is suitable for asymmetric meshes and can model the deformations of elastic-plastic materials. Therefore, it is suitable for simulating the various properties of steel in terms of plasticity, large deflection, higher strain capabilities, creep, and hyper-elasticity. To help obtain the true properties of the steel used in the manufacture of steel beams, the results of experimental tests available in [63] were used. Standard specimens of steel plates used in the manufacture of built-up steel beams with a thickness of 5 mm were tested. The average stress–strain relationship obtained from these specimens is listed in Table 1, and as shown in Figure 1. The average value of the modulus of elasticity for these samples was recorded as 211 GPa. A Poisson’s ratio of 0.3 for steel was used.

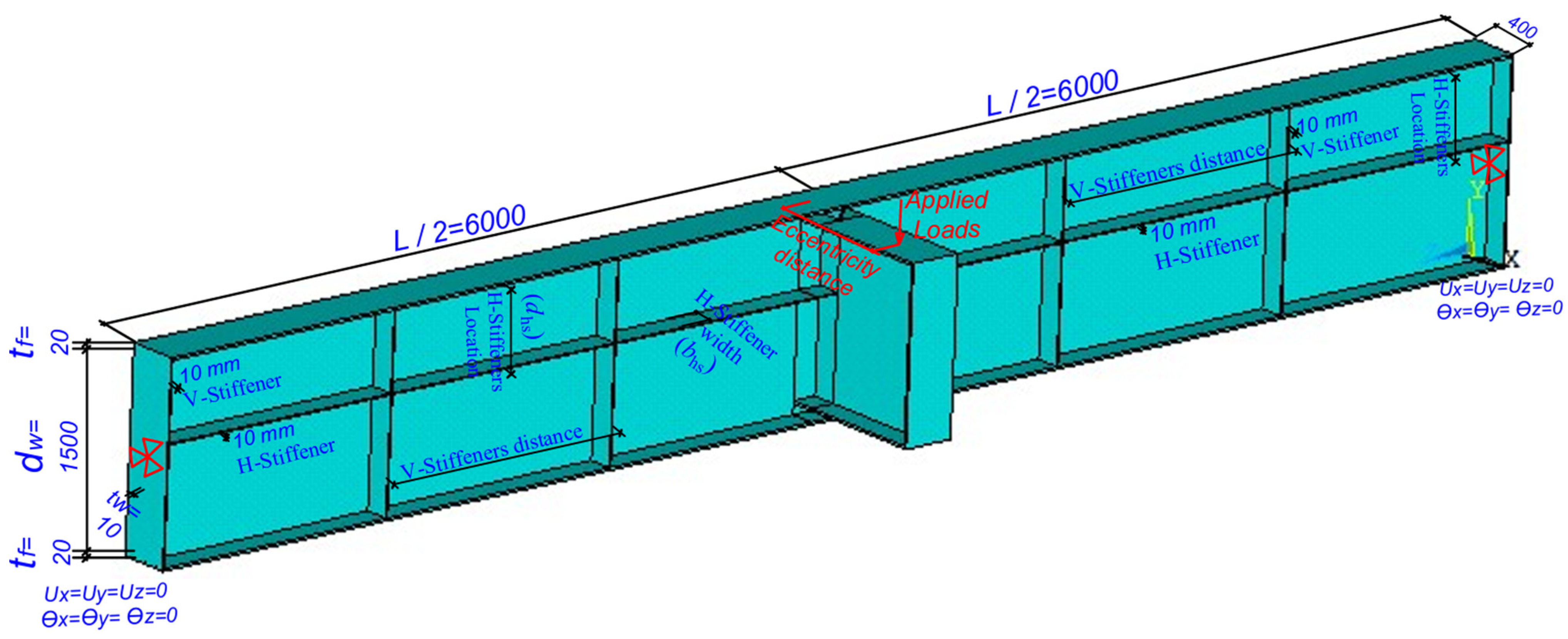
2.2. Structural Model Studies

To conduct this study, a FEM analysis system was used to simulate 95 steel beams. These steel beam specimens are divided into two main groups as follows: The first group consists of 25 specimens of experimental tests for steel beams available in previous studies [64,65,66,67,68,69], as listed in Table 2. The main objective of this group is to verify the accuracy and reliability of using FEM analysis systems in modeling this type of structural element. Therefore, this number of specimens was chosen to cover the largest possible number of different variables that affect the ultimate load capacity of the steel beams. Among these variables are the steel beam length, L, the beam flange width, bf, the flange thickness, tf, the web beam height, dw, the web thickness, tw, and the steel yield stress used, fy. Experimental tests were carried out on these steel beams in two ways: four-point loading as described in references [67,68,69] and three-point loading as described in references [64,65,66].
The second group includes 14 steel beam models, where each model was tested using FEM simulation under the influence of 5 cases of eccentricity distance measured from the longitudinal axis of the beams, bringing the total number of steel beam specimens to 70, as listed in Table 3. These steel beams were modeled using large dimensions to simulate the actual size of the beams used in steel structures. Therefore, steel beams with a total length of 12.0 m were used, and steel beams with a fixed cross-section were used. Where the height and thickness of the beam web are 1500 mm and 10 mm, respectively, while the width and thickness of the upper and lower beam flanges are 400 mm and 20 mm, respectively. Vertical stiffeners were used in all beams with a width and thickness of 195 mm and 10 mm, respectively, and horizontal stiffeners with a thickness of 10 mm were also used, with the width being used as a variable as listed in Table 3. These models contain several variables, including firstly, the use of horizontal stiffeners; therefore, steel beams with only vertical stiffeners (standard beams) were simulated, as well as steel beams with both vertical and horizontal stiffeners. Secondly, the location of the horizontal stiffeners in relation to the height of the beam web, dhs, measured from the top edge. To model this variable, distances equal to 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%, and 10% + 90% of the web height were used. Thirdly, changing the width of the horizontal stiffeners, bhs, where values of 120, 160, and 195 mm were used for this variable, with the stiffener position fixed at a distance of 20% of the beam web height. All these variables were carried out under the influence of 5 load conditions from the eccentricity of the load at distances equal to 0.0, 250, 500, 750, and 1000 mm measured from the longitudinal axis of the steel beam. All models were simulated under the influence of three-point loading, taking into account that the ends of the beam are fixed supports, thus preventing movement and rotation in the three directions X, Y, and Z, as shown in Figure 2. All these specimens were simulated to determine the extent to which all these variables affect the efficiency of steel beams in resisting combined bending and torsional moments. All the details and variables, both constant and variable, for these steel beam models are shown in Figure 2. The notation “Without-V@2m” refers to steel beams without horizontal stiffeners, utilizing vertical stiffeners at 2.0 m intervals, and the notation “H@10%+90%-V@2m” indicates steel beams with horizontal stiffeners at a distance of 10% and 90% of the beam’s web height, utilizing vertical stiffeners at 2.0 m intervals.

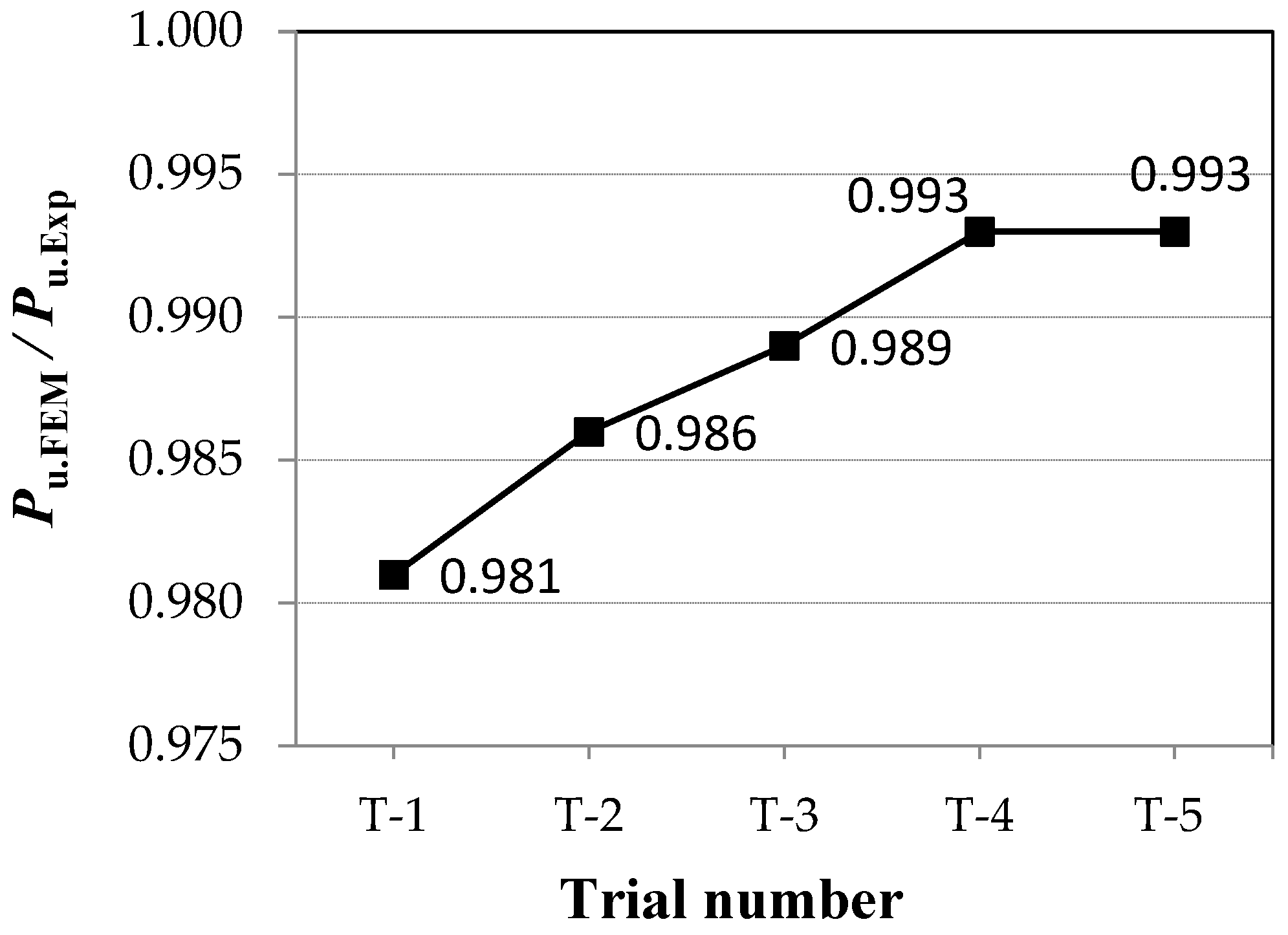
2.3. Choosing the Optimal Mesh Size for Element Convergence

Given that mesh sensitivity and element size significantly influence both the accuracy and computational efficiency of FEM simulations, a mesh convergence study was performed. The assessment was conducted using the largest specimen (length = 6000 mm), for which the experimental test (C2) was available from previous work by Xiong et al. [64]. Five mesh configurations were examined by varying the element dimensions in the height, width, and length directions. The tested element sizes were: (T1) 10 × 10 × 50 mm, (T2) 10 × 10 × 20 mm, (T3) 10 × 10 × 10 mm, (T4) 5 × 5 × 20 mm, and (T5) 5 × 5 × 10 mm. For each mesh, the ratio between the ultimate load capacity predicted by the FEM simulations and the corresponding experimental value (Pu,FEM/Pu,Exp) was calculated. These ratios were then plotted against the respective mesh configurations to identify the optimal mesh refinement, as shown in Figure 3. The results indicate that the 5 × 5 × 20 mm mesh provides the best balance between accuracy and computational time, offering the closest agreement with the experimental data while maintaining reasonable analysis time. Consequently, this mesh density was adopted for all subsequent FEM simulations, including both previously published specimens and those newly proposed in this study.

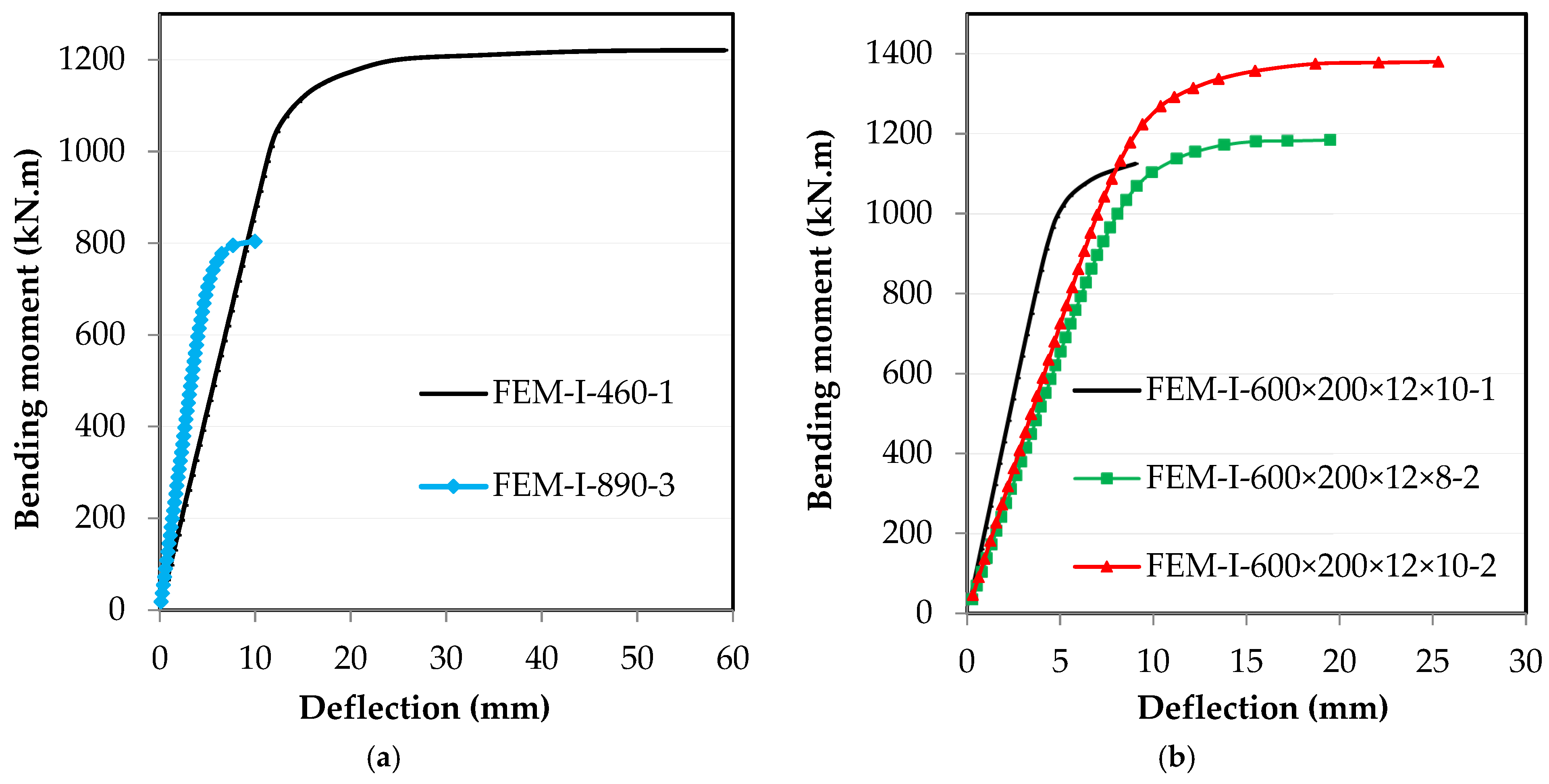
3. Verify Results from FEM

As observed in previous studies, some of which are included in the introduction section, it has been shown that the accuracy and reliability resulting from FEM simulations, when compared to the experimental test results, are very high. Specifically, by comparing the ultimate bending moment capacities of the steel beams obtained from FEM modeling with those from experimental tests, as listed in Table 4, an average ratio of 1.007 was obtained between the ultimate bending moment capacity from the FEM simulation and that from the experimental tests, with a coefficient of variation equal to 1.57% and a coefficient of correlation equal to 0.99. These values document and confirm the high accuracy of the FEM simulation results for steel beams.
Another important element that demonstrates the reliability and accuracy of the simulation results using FEM analysis is the comparison of load-deflection relationships for these steel beams. To conduct this comparison, 5 steel beams were obtained from previous studies [65,69] for which load, and deflection relationships were available at the mid-span of the steel beam length. The same relationships were obtained from the results of the FEM analysis, as shown in Figure 4. It became clear how closely matched the behavior of the steel beams resulting from FEM simulation was with the behavior resulting from experimental tests when compared with the same experimental test results for these specimens (I-460-1 and I-890-3) provided in Shi et al. [69] and specimens (I-600×200×12×10-1, I-600×200×12×10-2 and I-600×200×12×8-2) provided in the work of Saliba and Gardner [65]. To complete the verification of the simulation results, the deformation pattern and buckling failure locations were obtained and compared with those derived from experimental tests of steel beams with deformation patterns available in previous studies [69]. The degree of similarity between experimental tests and FEM analysis is an excellent match, as shown in Figure 5. A high degree of agreement is also observed between the deformation patterns resulting from the application of loads in both the FEM simulations and the experimental test results when compared with the same experimental test results for these specimens (I-460-1 and I-890-3) available in the work of Shi et al. [69], as shown in Figure 5.

4. Results and Discussion

To determine the extent to which the presence of horizontal stiffeners in the longitudinal direction of the steel beam affects its efficiency in resisting combined bending and torsional moments, the second group, which contains 70 steel beams, was simulated. The second group contains several variables, including the presence of horizontal stiffeners, the location of the horizontal stiffeners relative to the beam web height, and the width of the horizontal stiffeners. All these variables were modeled under the influence of eccentric loads measured from the longitudinal axis of the beam at mid-span. The effect of all these variables on the behavior of the steel beams was determined, as well as their impact on the stress distribution in the upper and lower flanges, and the shape and values of the vertical and lateral displacements at the mid-span of these steel beams.

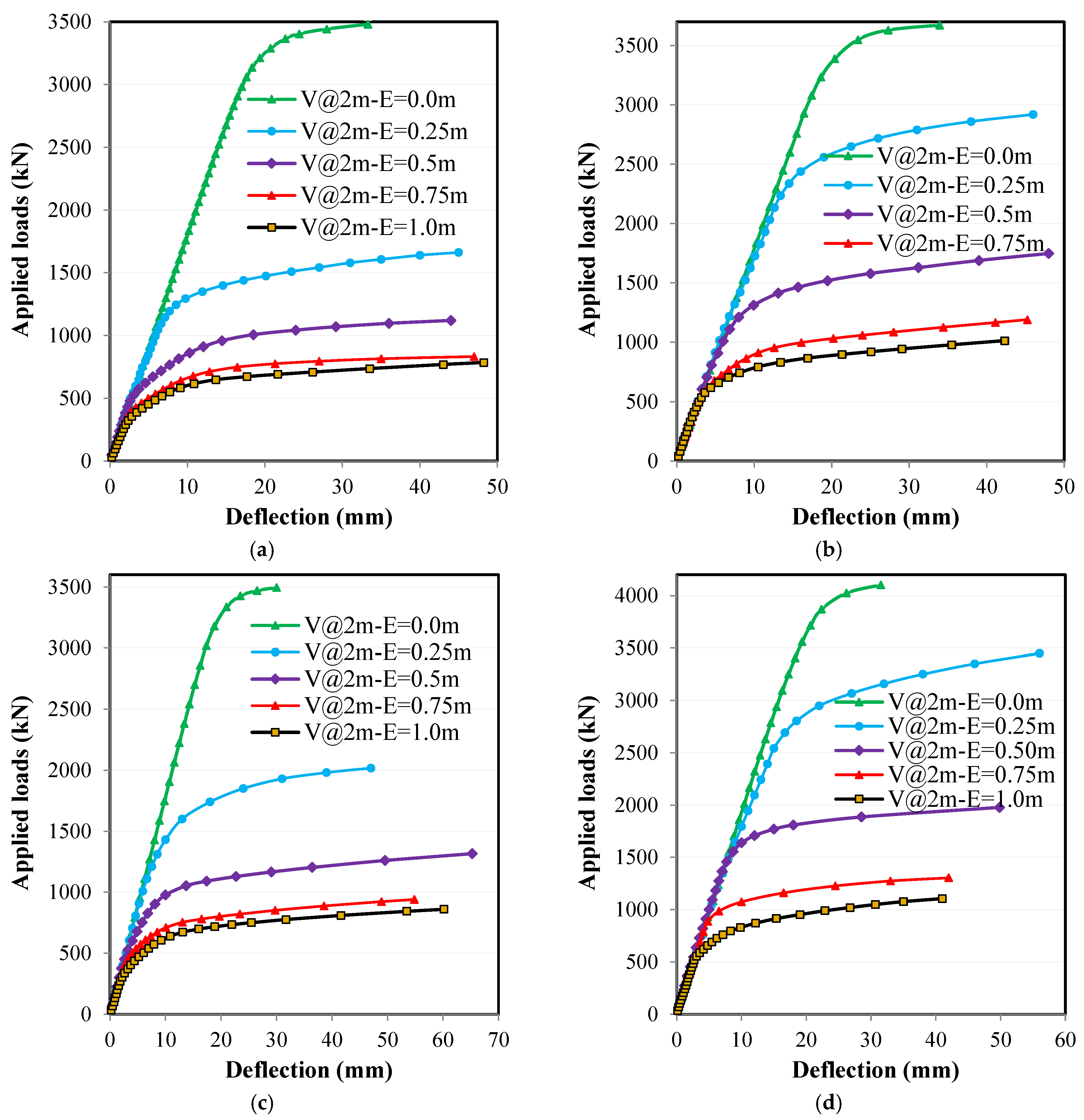
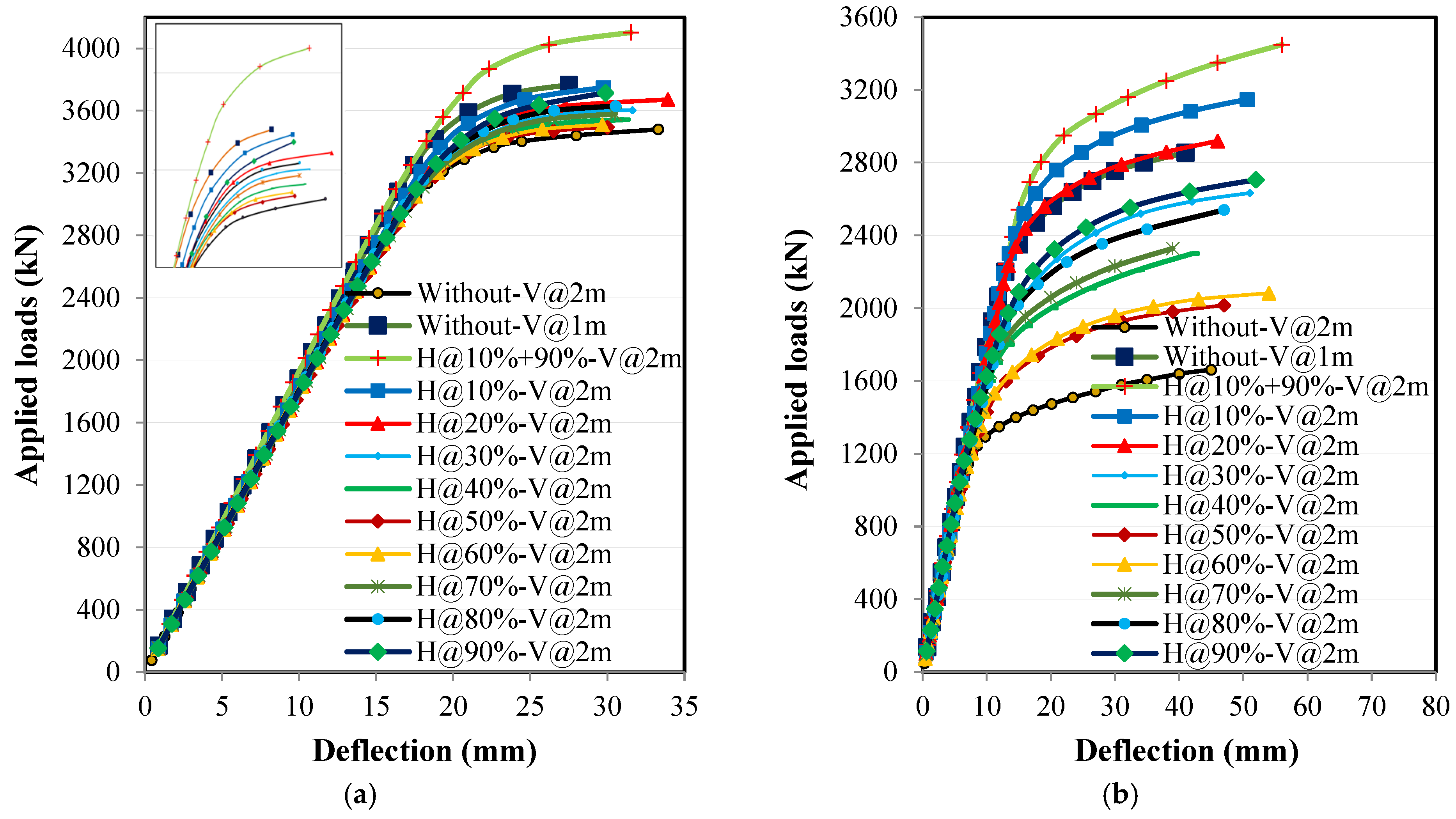
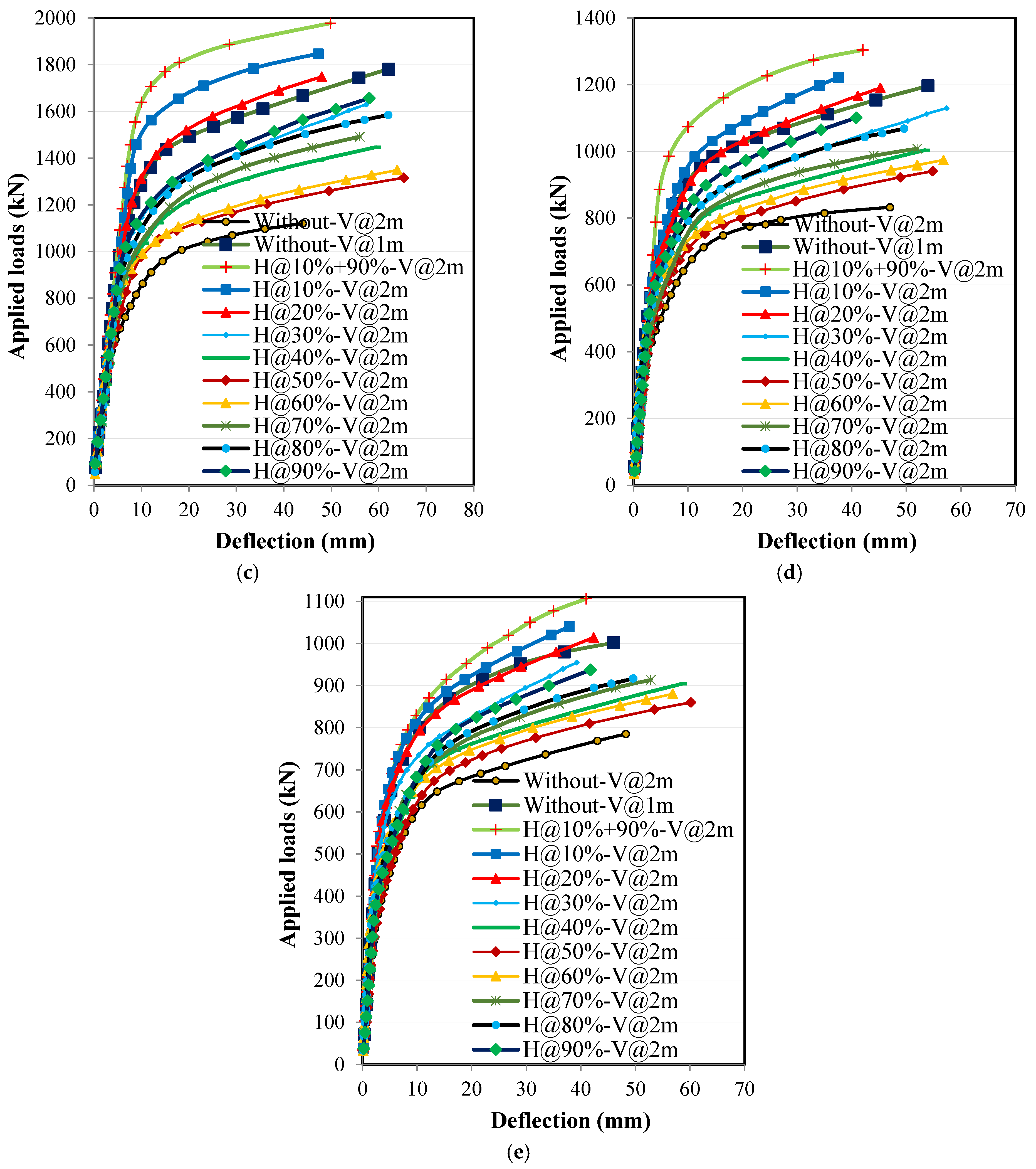
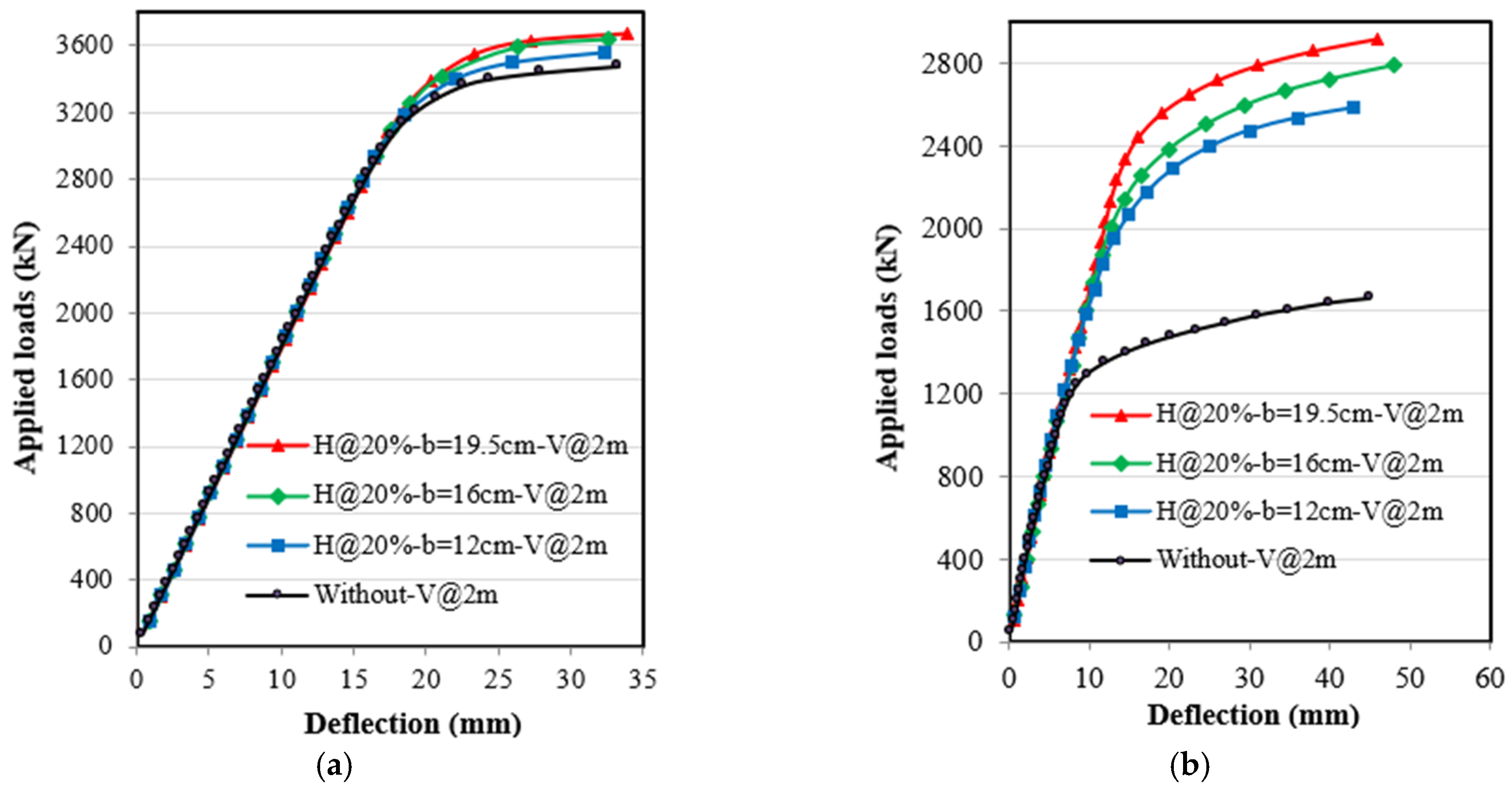
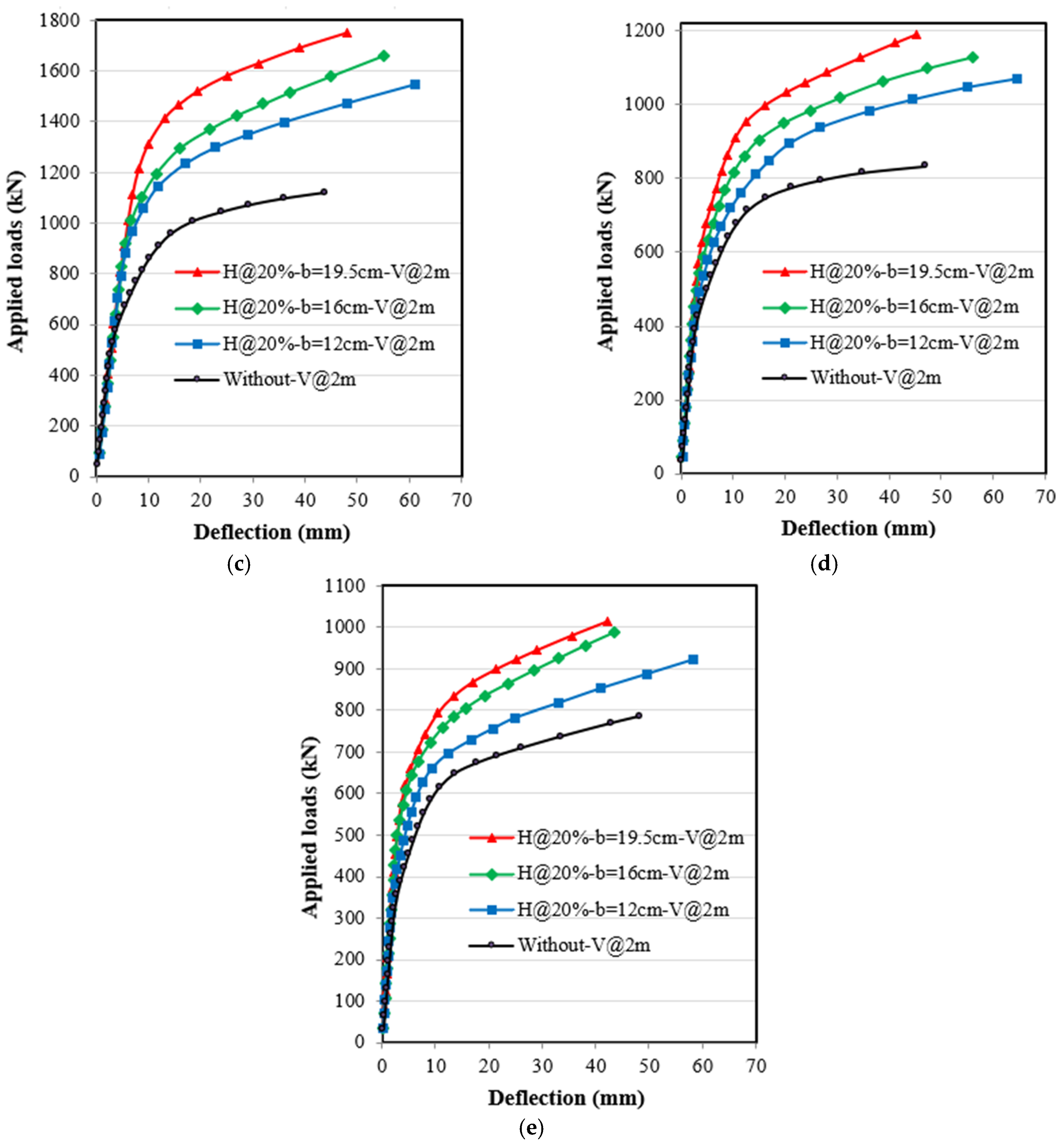
4.1. Applied Loads and Deflection Relationships

The relationship between the applied load and the corresponding deflection is one of the most important relationships that illustrates the behavior of structural elements in resisting loads. In this study, the relationship between load and deflection at the mid-span of the steel beam for each model was obtained through FEM simulation. The relationship for these models is drawn as shown in Figure 6. It was observed that the behavior pattern of the relationship between load and deflection followed the same pattern when using the same value of eccentricity distance for the load, with variations in the load value and the ultimate load capacity of the steel beams, as shown in Figure 6.
To facilitate comparison, each case of eccentricity for all beams has been grouped into a single figure, as shown in Figure 7. Figure 7 illustrates how the use of horizontal stiffeners in steel beams subjected to eccentric loads contributes to increasing their efficiency. It is evident from the relationship diagrams that the presence of horizontal stiffeners at the mid-height of the beam web has the least effect on increasing the efficiency and the ultimate load capacity of the steel beam. However, when horizontal stiffeners are located in the upper or lower part of the beam’s web height at values different from 50% of the web height, the behavior of the steel beam in resisting applied loads with eccentricity improves significantly. Although there was improvement, the presence of horizontal stiffeners in the upper half of the beam web height had a better effect than the presence of the same stiffeners in the lower half. It was observed that the beam behavior when using horizontal stiffeners at a height equal to 90% of the web height closely resembled, in most eccentricity cases, the behavior of the beam when using horizontal stiffeners at a height equal to 30% of the web height. It was also found that the best use of horizontal stiffeners is to use stiffeners at a height equal to 10% and 90% of the web height of the steel beam subjected to eccentric loading, which causes combined bending and torsional moments. The measurements also showed that using only vertical stiffeners while reducing the horizontal distance between them also improves the efficiency of the steel beam in resisting combined bending and torsional moments. However, this improvement in efficiency is equivalent to replacing the vertical stiffeners with horizontal stiffeners at a height equal to 20% of the beam’s web height. Conversely, using only vertical stiffeners with reduced spacing is better than using horizontal stiffeners at any other ratio from 30% to 90% of the web height. These results were measured in all eccentricity cases used in this study, as shown in Figure 7.
The effect of changing the width of the horizontal stiffeners on the behavior of steel beams under eccentric loads was also studied. The width of the horizontal stiffeners was changed from 195 mm to 120 mm, and the relationship between the applied load and the corresponding deflection was plotted for all eccentricity cases, as shown in Figure 8. Figure 8 clearly shows that the width of the horizontal stiffeners has a significant effect on increasing the efficiency and resistance of the steel beams to combined bending and torsional moments. The greater the stiffener width, the greater the ultimate load capacity of the steel beams in all the eccentricity cases studied. However, Figure 8 also shows that the beam’s resistance to eccentric loads is inversely proportional to the increase in eccentricity distance. As the eccentricity distance increases, the bending moments decrease, while the torsional moments increase.

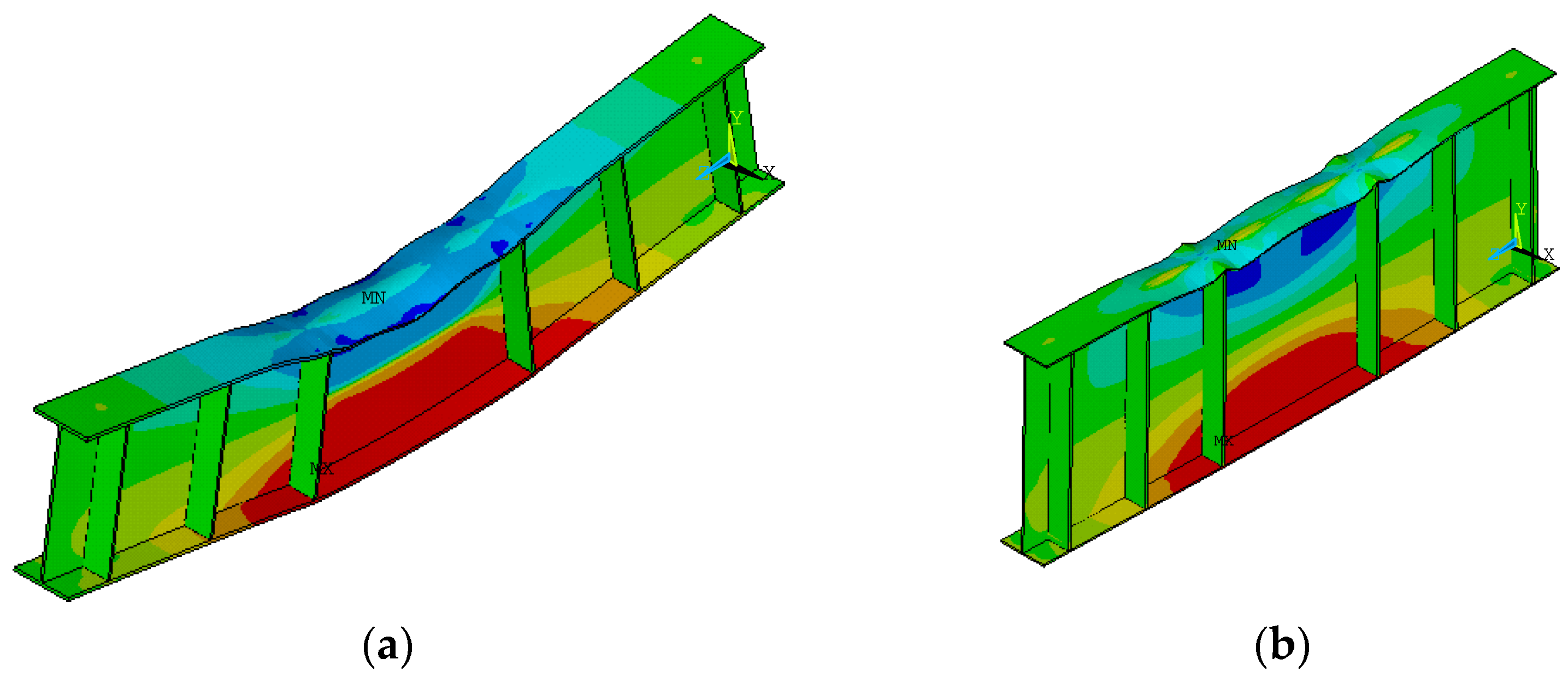
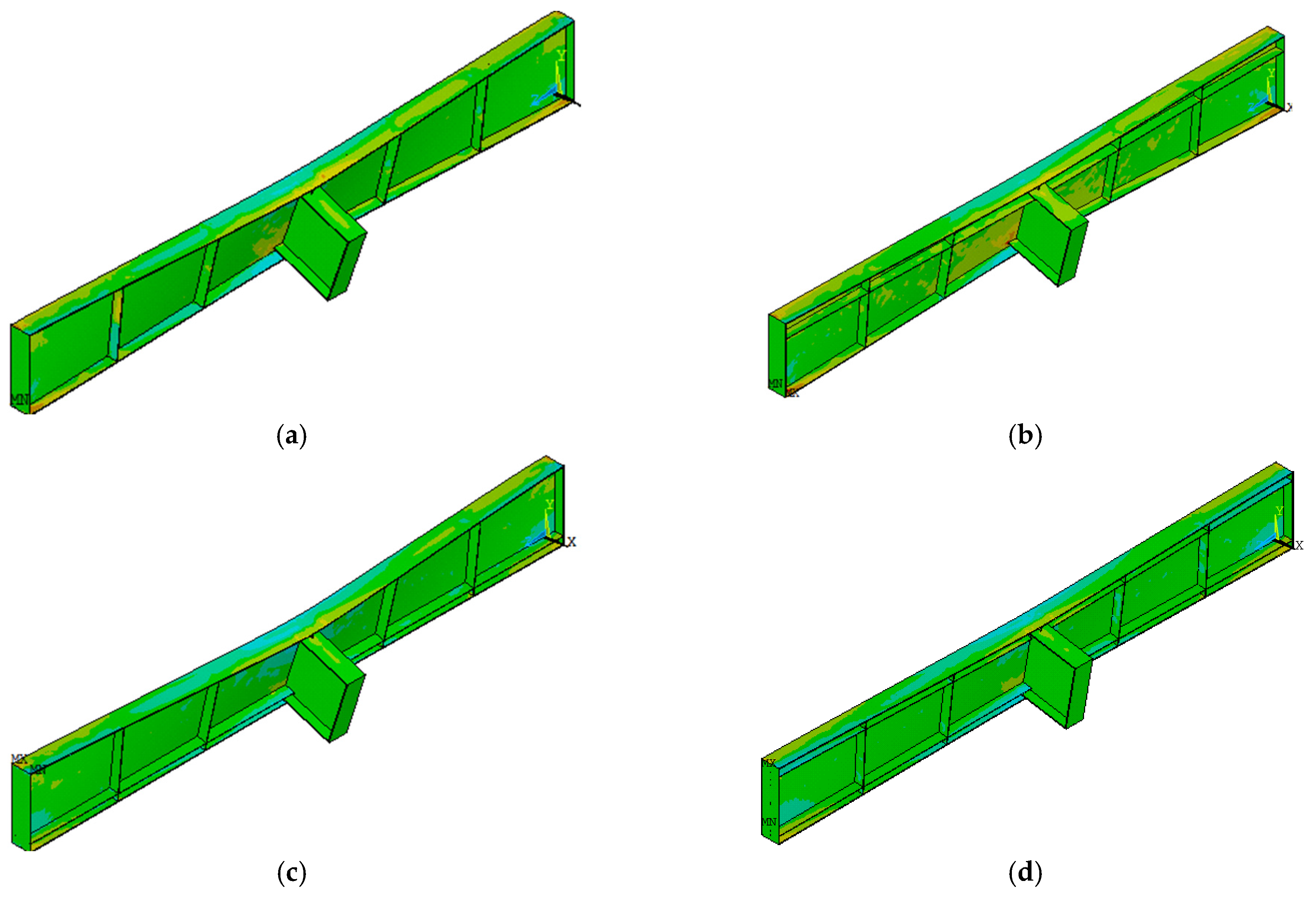
4.2. Effect of Horizontal Stiffeners on Deformation Patterns and Stress Distributions

Through the results of the FEM simulation, the stress distribution shape with deformations along the entire length of the steel beam, with or without horizontal stiffeners, under the influence of eccentric loads was obtained, as shown in Figure 9. The figure illustrates that all beams undergo lateral deformations due to the applied eccentric loads. It was observed that the upper flange undergoes lateral displacements towards the side of load application, while the lower flange experiences lateral displacement in the opposite direction of load application in all beam models, both with and without horizontal stiffeners. Figure 9a shows that in the case of steel beams without horizontal stiffeners; the upper and lower flanges move by the same amount but in opposite directions. However, from Figure 9b, when horizontal stiffeners are used at 20% of the web height, the lateral displacement decreases in the upper flange, while it increases in the lower flange. Conversely, when horizontal stiffeners are used at 90% of the web height, the lateral displacement decreases in the lower flange and increases in the upper flange, as shown in Figure 9c. This indicates that the presence of horizontal stiffeners near the flanges of the beam’s cross-section improves its ability to resist undesirable lateral deformations resulting from eccentric loading. It was observed that there are tensile and compressive stresses in the upper and lower flanges of all steel beams subjected to eccentric loads. The effect of the tensile to compressive stress zone appeared on the upper flanges, and the compressive to tensile stress zone on the lower flanges was small. As a result of these stresses and lateral displacements caused by the application of eccentric loads, the type of failure is a global buckling along the entire length of the beam, as shown in Figure 9. To more clearly define the behavior of all beams in resisting lateral displacements and the relationships between the applied loads and the stresses at the upper and lower flange edges of the cross-section, this will be discussed in detail in the following sections.

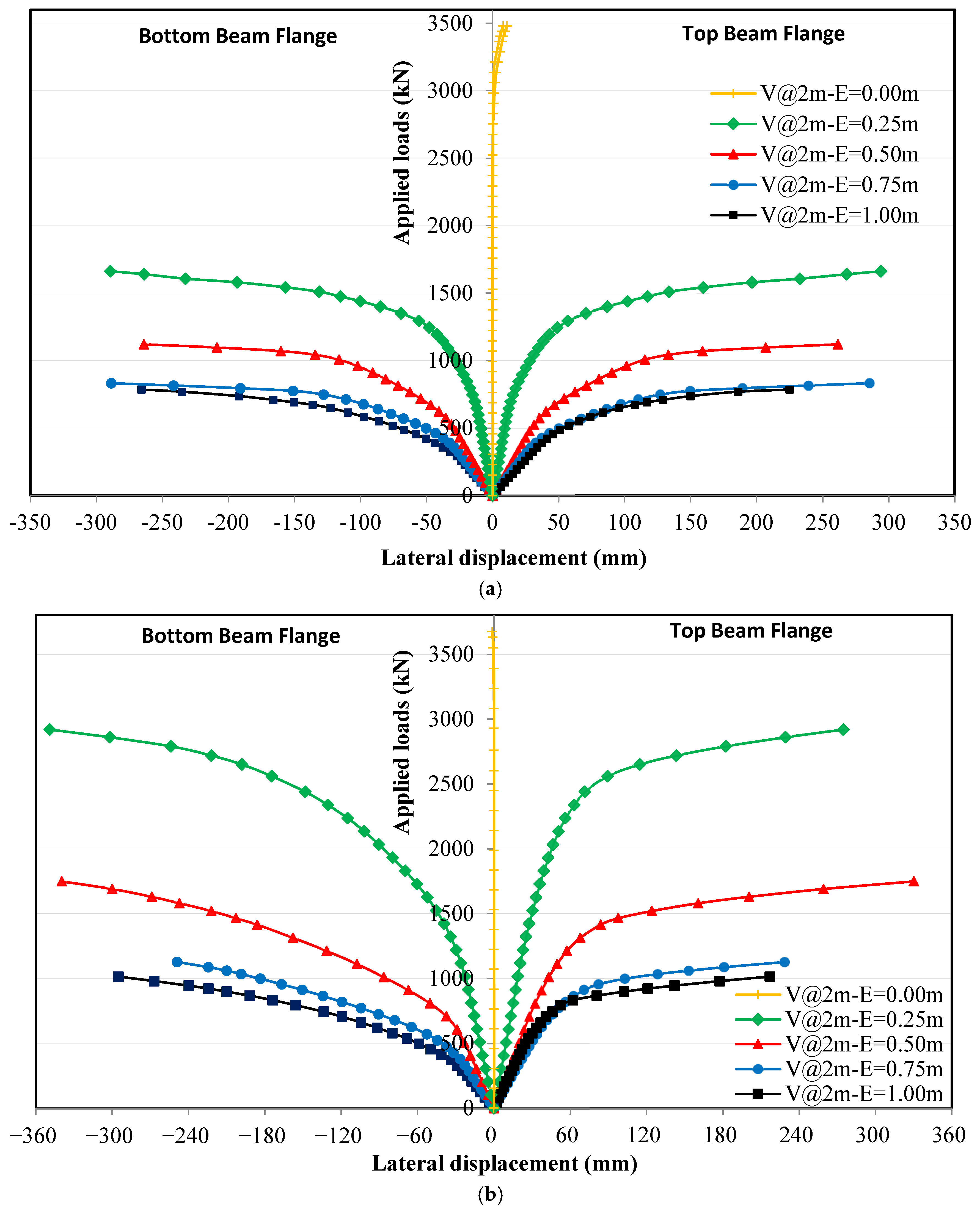
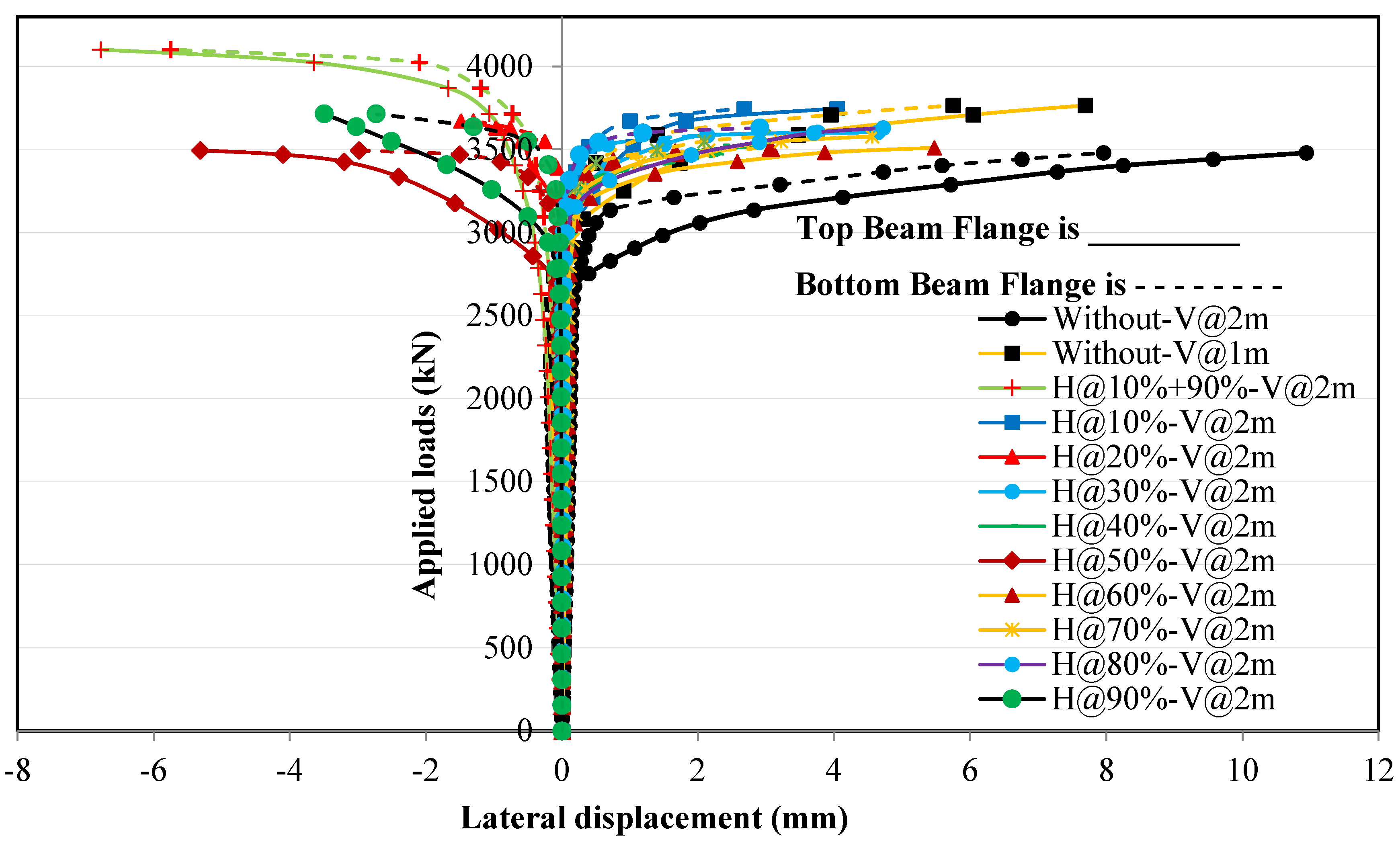
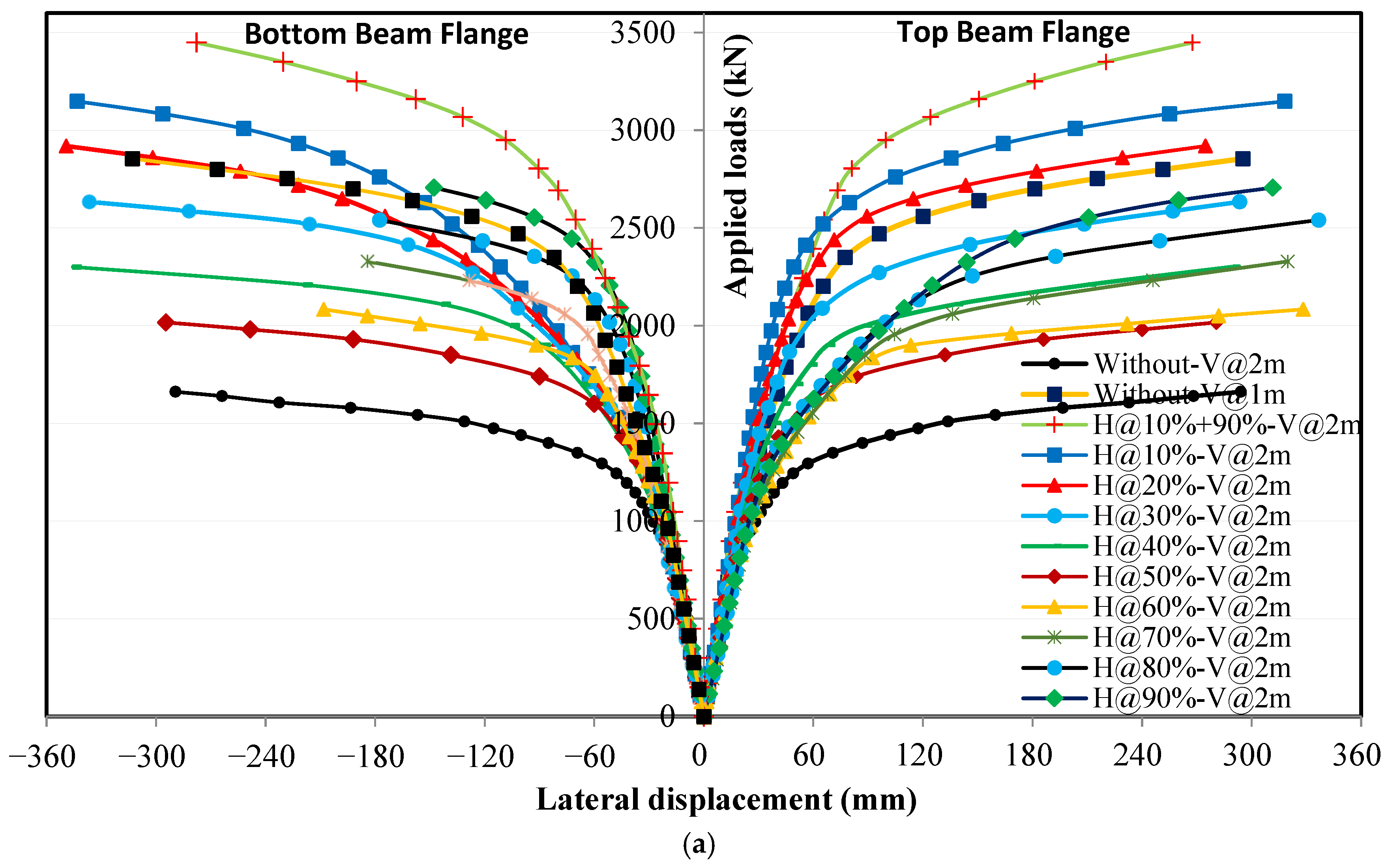
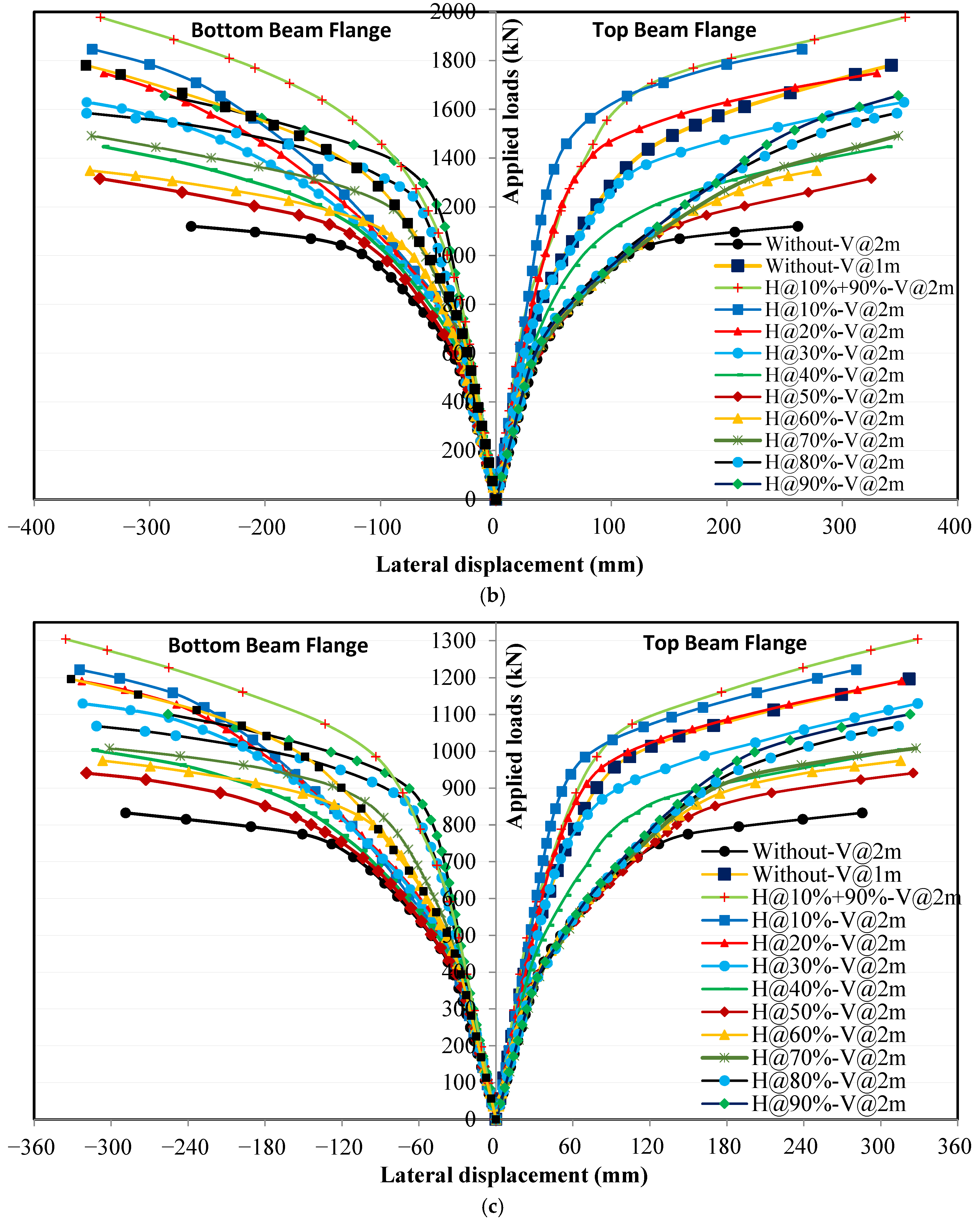
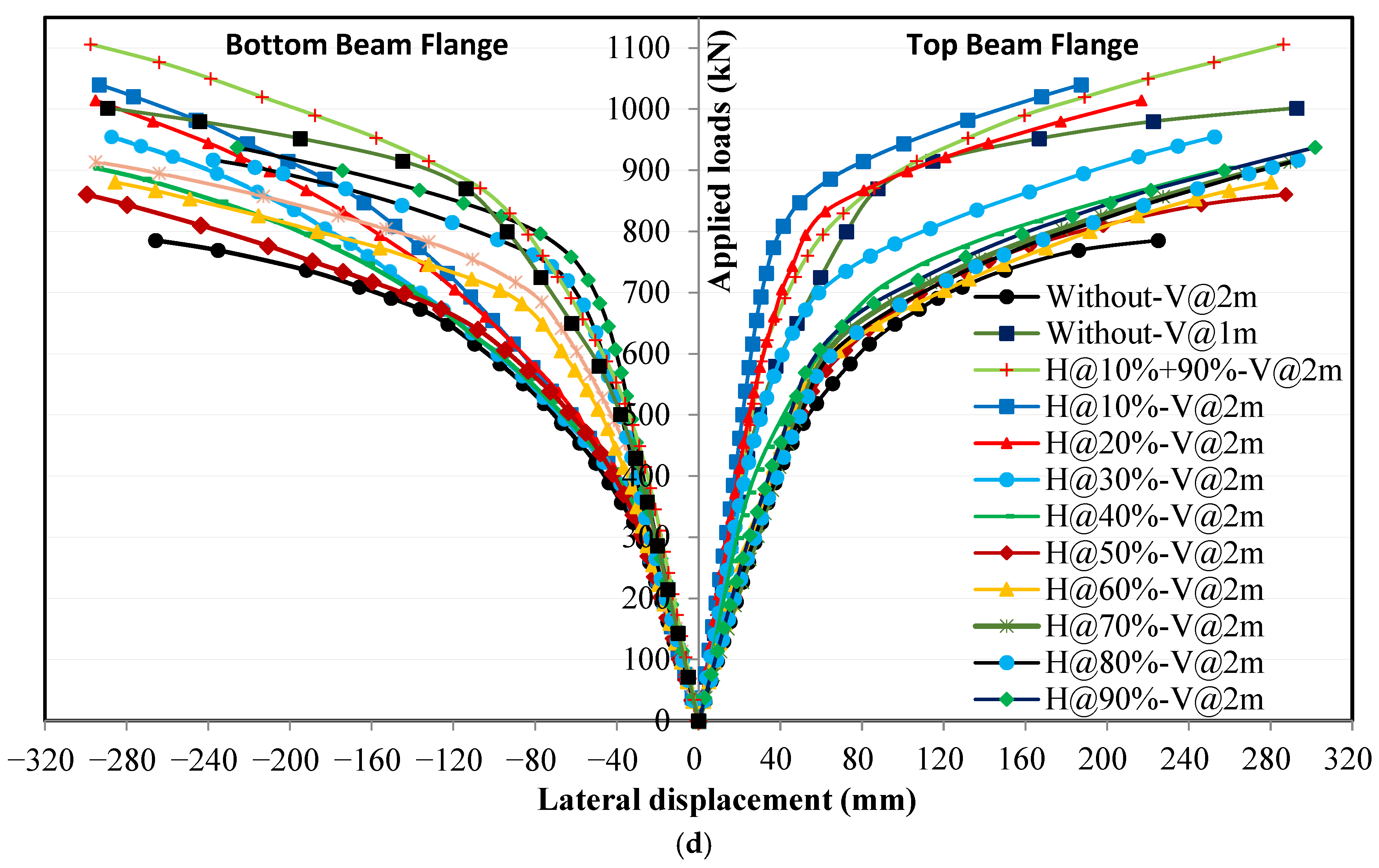
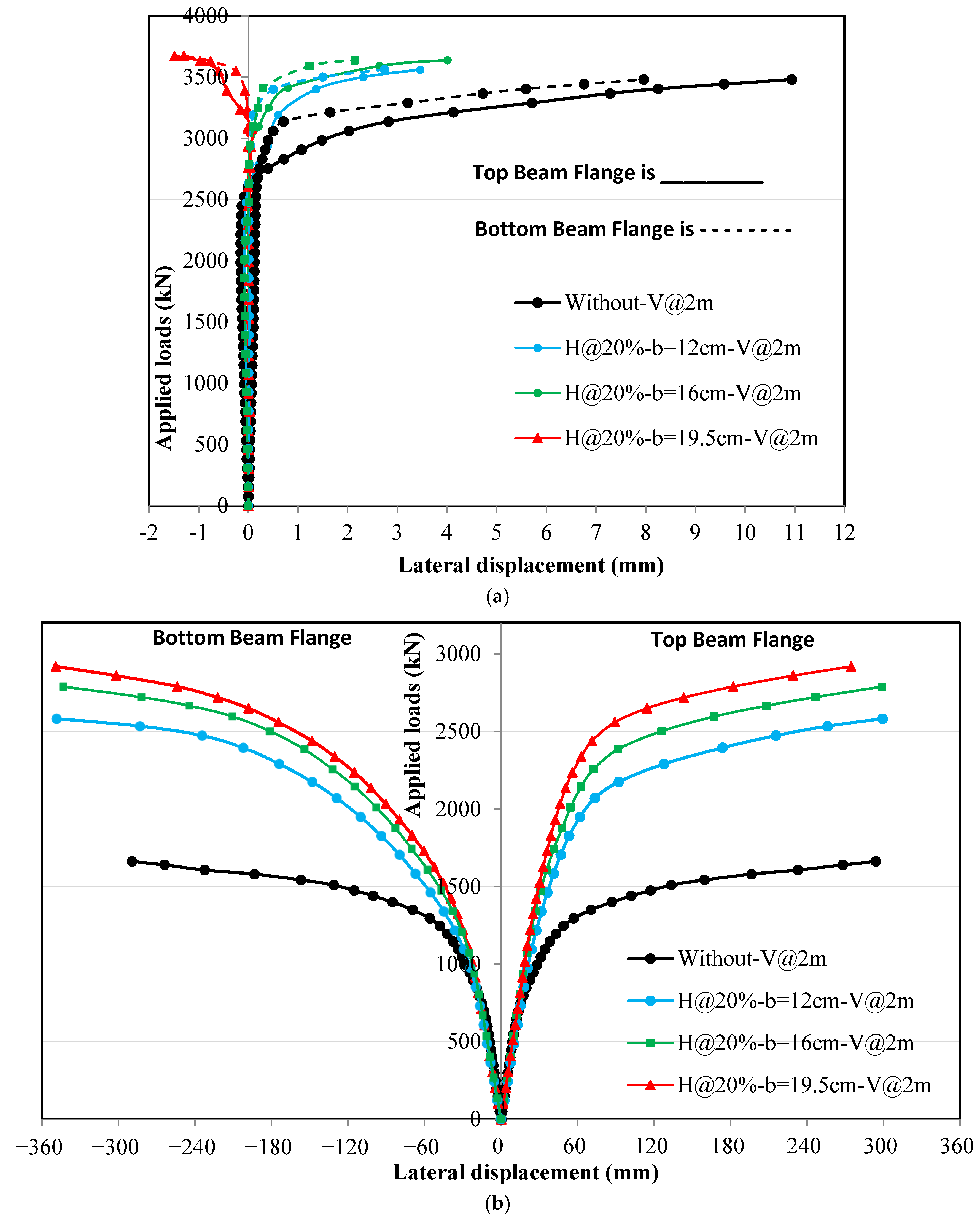
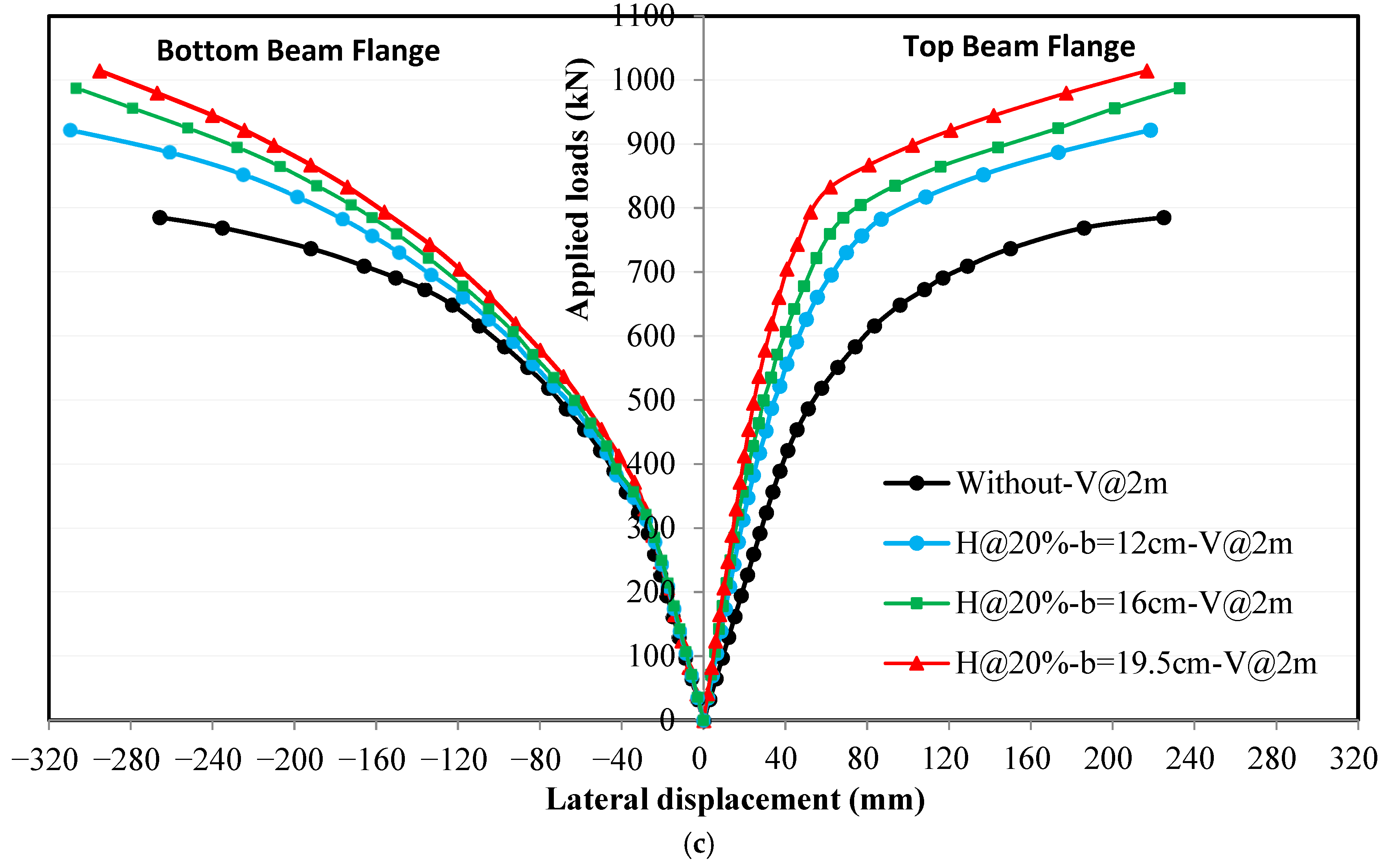
4.3. Effect of Horizontal Stiffeners on Applied Loads and Lateral Displacement Relationships

One of the most important characteristics that distinguishes the behavior of steel beams subjected to eccentric loads, which generate torsional moments, is the presence of lateral displacement in both the upper and lower flanges of the beam’s cross-section. Through the results of the FEM simulation, the lateral displacements at the mid-span of the beam were measured in both the upper and lower flanges, as shown in Figure 10. These displacements were measured in all models, both with and without horizontal stiffeners. It became clear from the measurements that all relationships between the applied load and the corresponding lateral displacement follow the same trend, with variations in the load values and the maximum capacity of the steel beam. Therefore, some models were attached for clarification, as shown in Figure 10a, where the beams are without horizontal stiffeners, and Figure 10b, for the beams with horizontal stiffeners placed at a position equal to 20% of the web height of the steel beam.
To conduct an effective comparison, all lateral displacements with applied loads were grouped into a single figure according to the eccentric distance values of the load, as shown in Figure 11, Figure 12 and Figure 13.

4.3.1. Loading Without Eccentricity

Figure 11 shows that when there is no eccentricity of the loads, the relationship between the applied load and the lateral displacement can be neglected until the end of the yielding stage of the steel used. Then, lateral displacement appears in both the upper and lower flanges, along with local buckling in the behavior of the steel beam, as previously illustrated in Figure 5. This generated lateral displacement is the strongest evidence of buckling behavior in the upper flange, and it is also followed by the lower flanges in steel beams. It was observed that the lateral displacement in the upper flange is always greater than the lateral displacement in the lower flange. These displacements are always on the same side of the steel beam in both flanges of the beam’s cross-section. It was also observed that the displacement of the upper flange begins at a lower load value compared to the lower flange, which is due to the fact that the upper flange of the cross-section is subjected to compressive stresses. These results apply to all steel beams, whether with or without horizontal stiffeners. In a beam without horizontal stiffeners, the final lateral displacement values are larger (i.e., buckling is more pronounced) compared to steel beams with horizontal stiffeners.

4.3.2. Loading with Eccentricity

Figure 12 shows the effect of eccentric loading with lateral displacement of the upper and lower flanges. It is evident that the upper flanges move laterally towards the side containing the applied load (positive displacement values), while the lower flange moves in the opposite direction to the effect of the eccentric load (negative displacement values). It was observed that the effect of the presence of horizontal stiffeners on lateral displacement is ineffective in terms of the final values of lateral displacement, but it delays its occurrence to higher levels of loads, meaning that it increases the ultimate load capacity of the steel beams. In general, the values of lateral displacements decrease at the same load level when horizontal stiffeners are used. The greatest reduction occurs when using horizontal stiffeners at 10% of the beam’s web height. This reduction decreases as the position of the horizontal stiffeners moves towards the middle of the web height, and then the percentage of reduction increases again as the position of the horizontal stiffeners exceeds the middle of the web height, as shown in Figure 12. It was observed that the relationship between the applied load and the lateral displacement in the upper flange of the steel beam containing horizontal stiffeners in the upper half of the web is mostly linear up to the yield point of the steel used in the upper flange. In contrast, the lateral displacement in the lower flange exhibits a mostly non-linear (curved) relationship. This observation indicates that lateral displacements are small in the upper flange and increase linearly until the steel begins to yield, while lateral displacement is large in the lower flange at the same load level and increases gradually until failure occurs. This trend is fully reflected in steel beams with horizontal stiffeners in the lower half of the web of the steel beam. This applies to all beam models that contain any value of eccentricity distance for applied loads. For steel beams containing horizontal stiffeners in both the upper and lower halves of the web height (10% and 90%), and for the steel beam with only vertical stiffeners with the inter-space reduced to half (Without-V@1m), the relationship between load and lateral displacement was mostly linear in both flanges, with approximately equal displacement values at the same applied load level. Figure 12 shows that the best possible results for using horizontal stiffeners are achieved when they are located in the upper half at a distance of 10% and the lower half at a distance of 90% of the web height. However, when using only vertical stiffeners with the inter-space reduced to half, the behavior was similar to that of beams with horizontal stiffeners at a distance of 20% of the web height for the upper flange or 80% for the lower flange, as shown in Figure 12.

4.3.3. Effect of Horizontal Stiffeners Width

For steel beams with or without eccentric loading, there was no difference in the behavior pattern of the load-lateral displacement relationship with changing the width of the horizontal stiffeners, except for a difference in the values of the load and the ultimate load capacity of the steel beam, as shown in Figure 13. Figure 13a illustrates the relationships when there is no load eccentricity, and the lateral displacement in both the upper and lower flanges is on the same side of the steel beam. In Figure 13b, where the load eccentricity is 250 mm, and in Figure 13c, where the load eccentricity is 1000 mm, with horizontal stiffeners placed at a distance of 20% at a distance equal to 20% of the height of the beam web, the relationship is linear for the upper flange and non-linear for the lower flange, with different values of lateral displacement at the same level of applied load. The displacement is small in the upper flange, increasing linearly in the direction of the load side until the steel reaches the yield point. Conversely, this displacement is large in the lower flange and gradually increases on the opposite side to the direction of the applied load until failure.

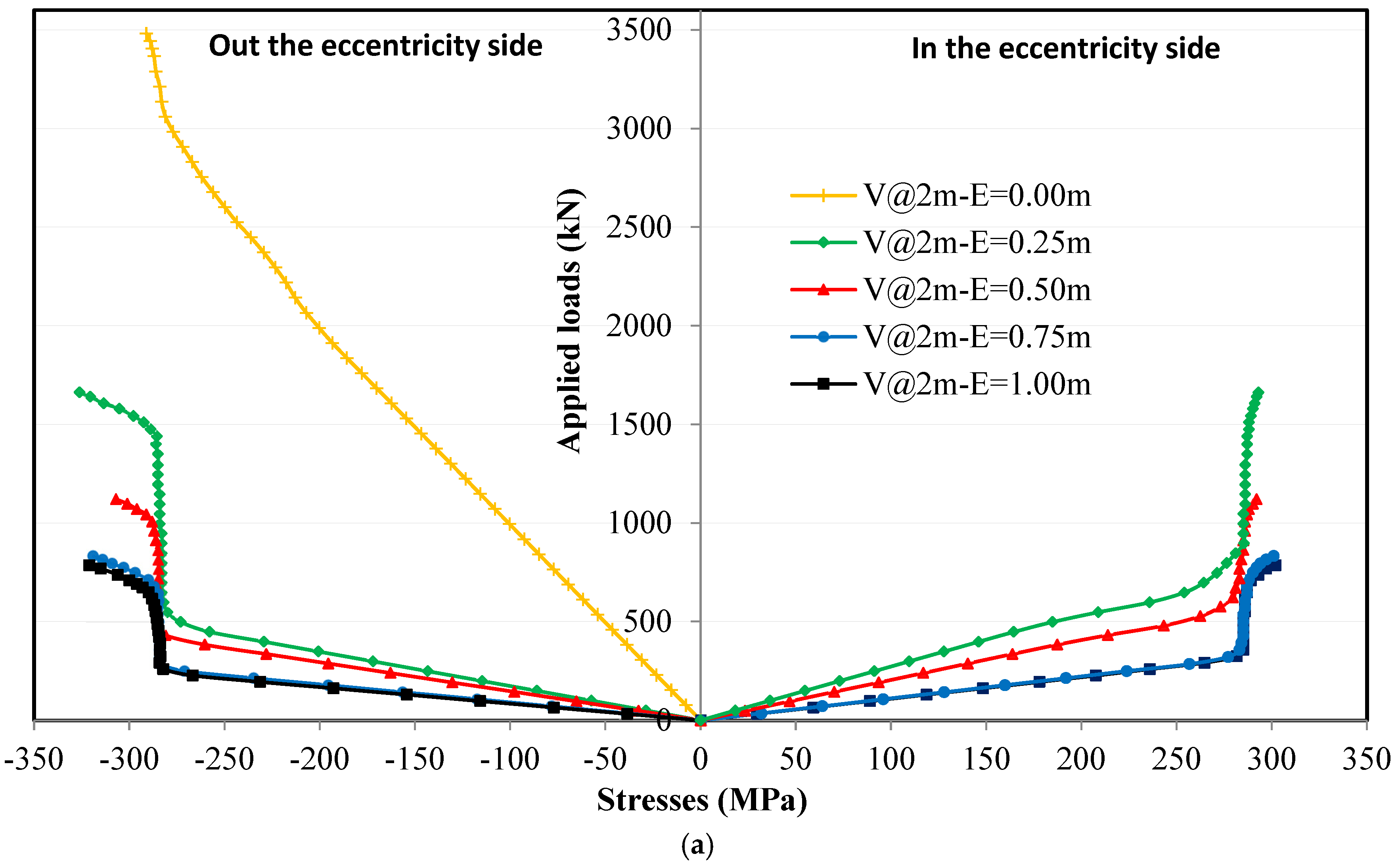
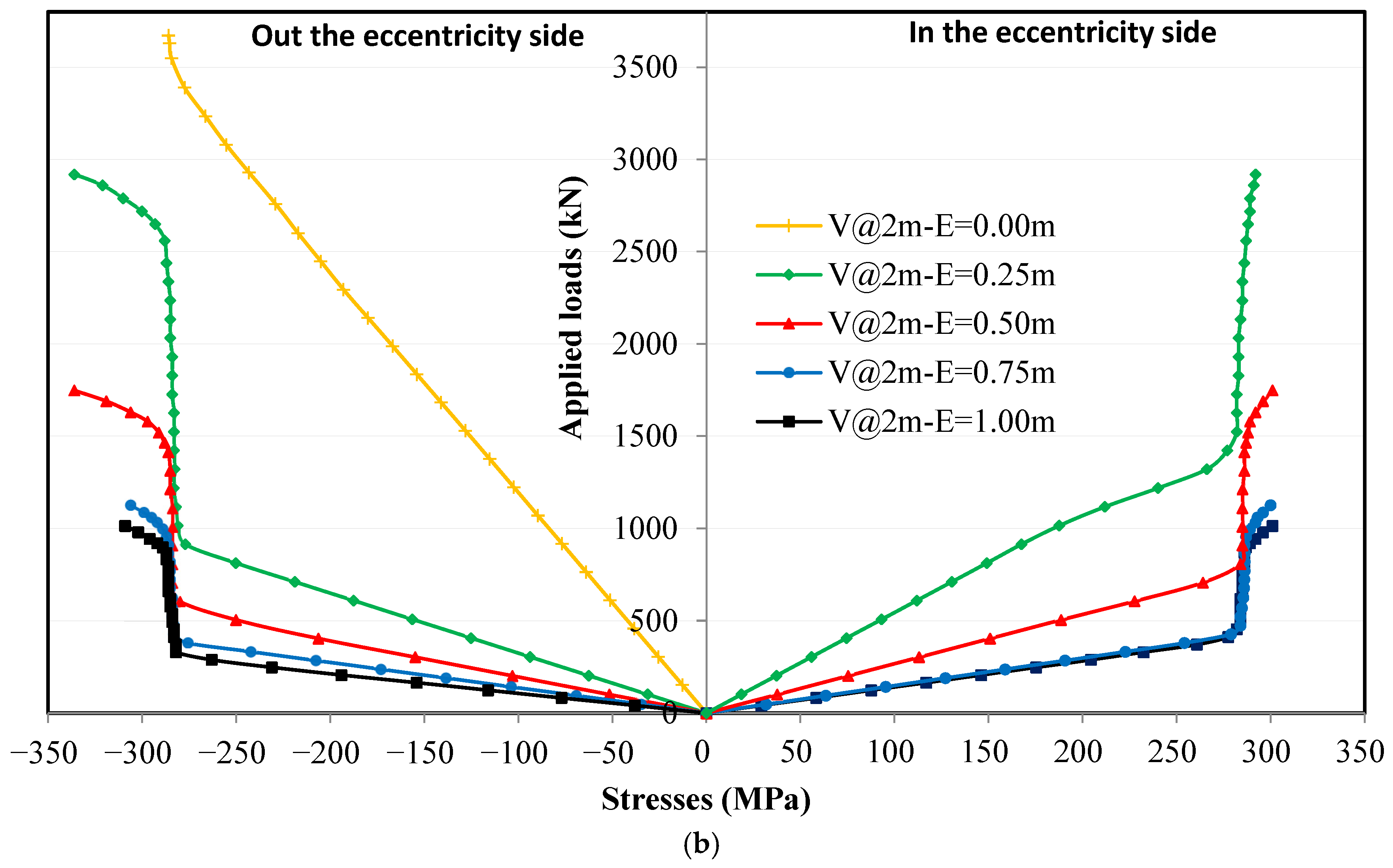
4.4. Effect of Horizontal Stiffeners on Stress Distribution in the Upper Flanges

Based on the results previously mentioned in the section on loading with lateral displacement, and as is evident in Figure 10, Figure 11, Figure 12 and Figure 13, new stresses are generated with a different distribution pattern than the prevailing pattern on both edges of the upper flange of the cross-section of the steel beam. Through FEM simulation, the stresses generated at the edges of the upper flange were measured, specifically at the edge on the side of the eccentric load application (in the eccentricity side) and the other edge on the opposite side (out the eccentricity side), for all models of the steel beams, as shown in Figure 14. It was observed that all steel beams exhibited the same pattern in stress distribution values and behavior across the upper beam flange when varying the load eccentricity, with differing values and ultimate applied load capacities. Tensile stresses were measured at the edge of the upper flange in the edge where the eccentric load was applied (which is unexpected, as the upper flange is generally subjected to compressive stresses). This is due to the lateral displacements resulting from the torsional moments resulting from the eccentricity of the load, which causes the edge to elongate towards the side on which the load is applied and to compress on the opposite side. Meanwhile, compressive stresses were measured at the edge opposite the point of load application (out the eccentricity side), as shown in Figure 14. It was also observed that the values and behavior of stress distribution converge with increasing eccentricity of the load, where they almost match the load eccentricity of 750 mm and 1000 mm.
To conduct an effective comparison, all the behavior of steel beams in terms of stress distribution in the upper flange with the corresponding load were grouped into a single figure according to the eccentric distance values of the load, as shown in Figure 15, Figure 16 and Figure 17.

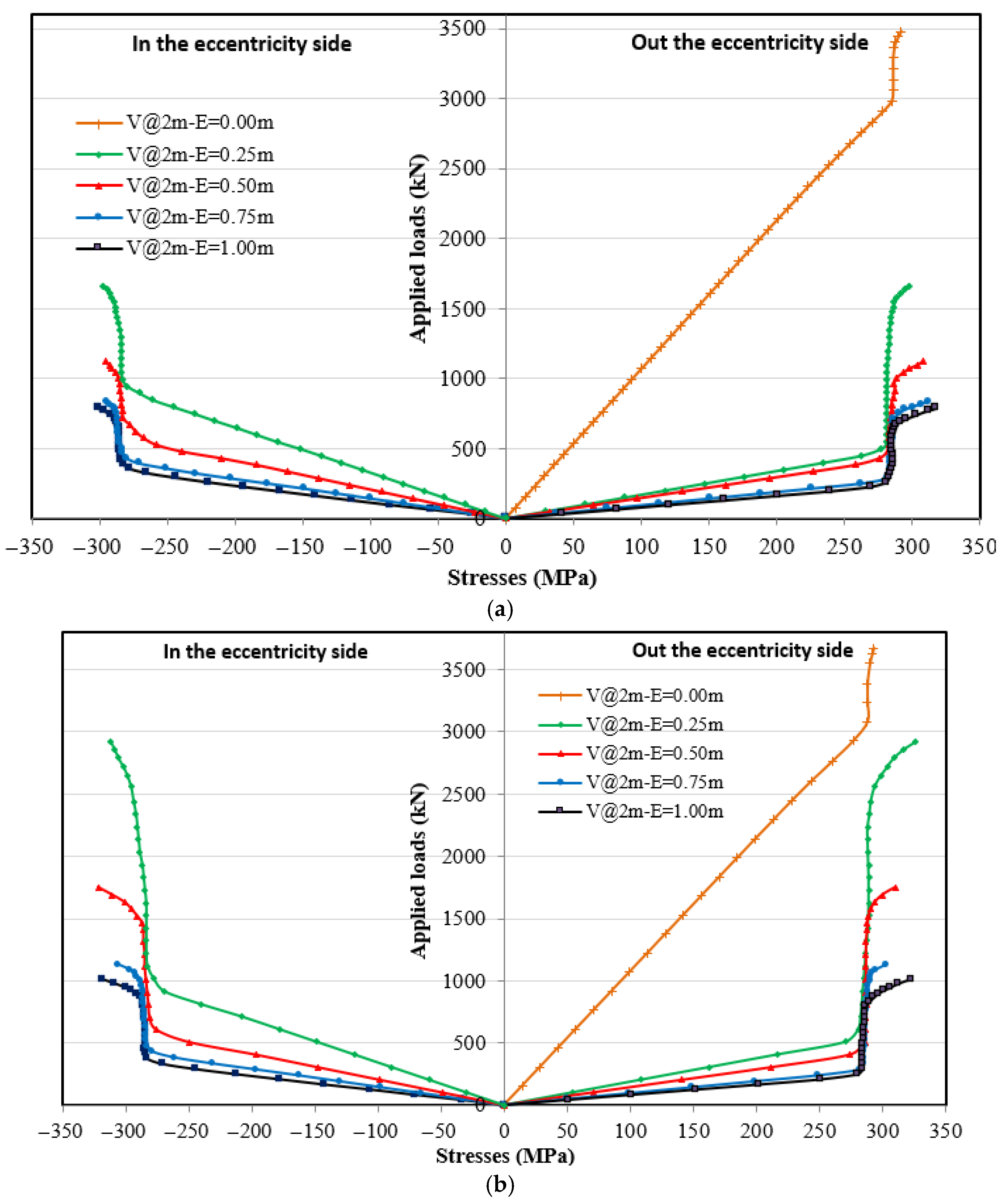
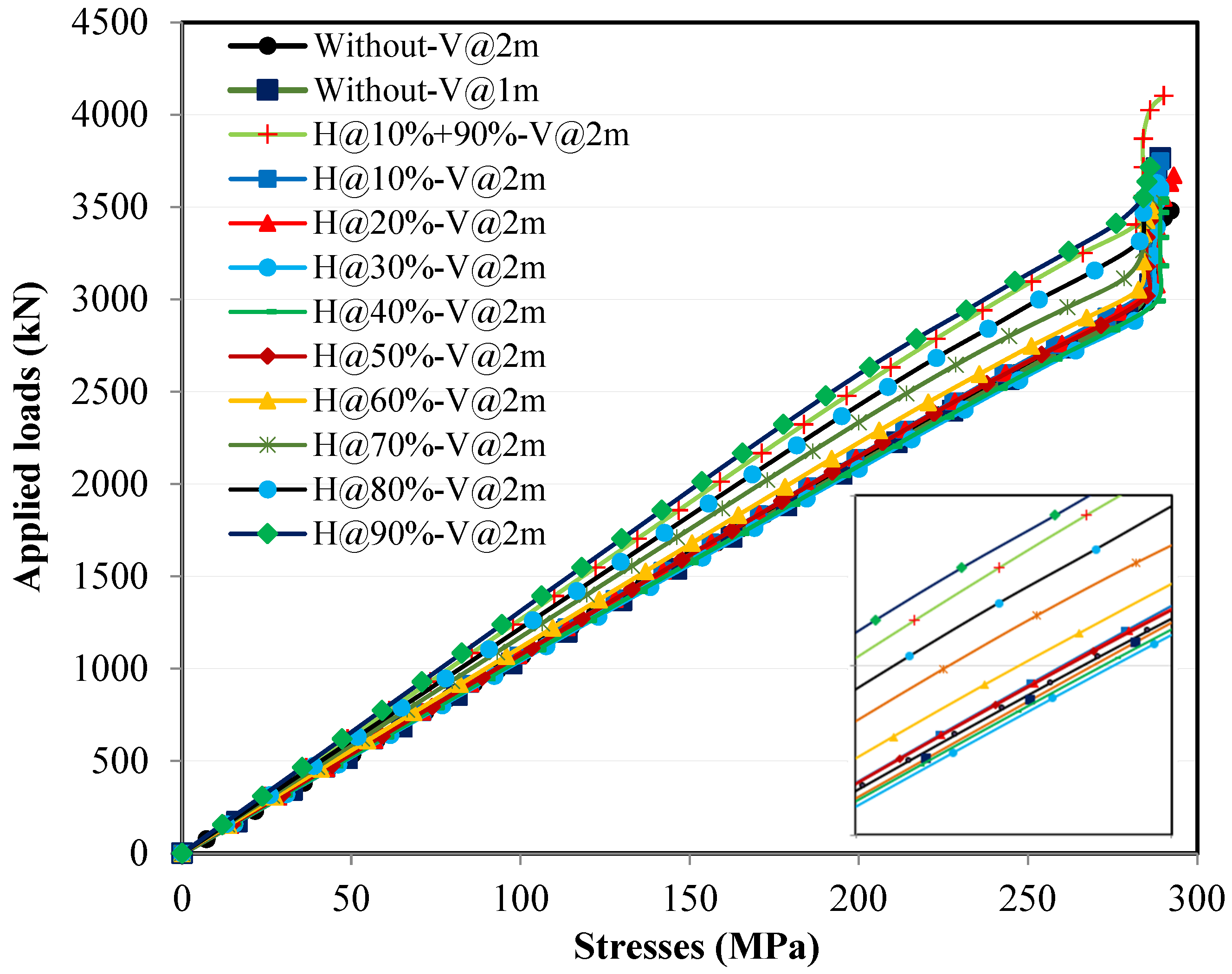
4.4.1. Loading Without Eccentricity

In the case of steel beams, whether with or without horizontal stiffeners, subjected to loads without eccentricity, the stress generated in the middle of the beam length are compressive stresses in both edges of the upper flange, as shown in Figure 15. The results show that for all steel beams, with or without horizontal stiffeners, stress distribution is linear up to the yield point of the steel used. After this point, a change in stress distribution occurs, leading to a stage of plastic deformation, followed by failure. None of the beams, whether with or without horizontal stiffeners, reached the steel’s ultimate tensile strength. Failure in these beams occurred due to buckling of the top flange, preventing the stress from reaching its maximum capacity. The highest recorded compressive stress was 293 MPa, while the steel’s ultimate tensile strength was 377 MPa. However, all beams reached stresses higher than the yield stress of the steel, which is 282 MPa, as shown in Figure 15. It was observed that the stress values in the upper flange decrease at the same level of applied load when using horizontal stiffeners in the upper half of the web height (from 10% to 40%). Also, the stress distribution values and patterns improve with the use of horizontal stiffeners in both the upper and lower halves of the beam web height, whereas no difference is observed when using only vertical stiffeners, even with the inter-spaces between them being reduced by half.

4.4.2. Loading with Eccentricity

By grouping the relationships between the load and the resulting stresses on the upper flange edges of the cross-section according to the value of eccentricity of the load, Figure 16 was obtained. The figure shows that all beams subjected to eccentric loads experience tensile stresses at the edge adjacent to the load-applied side and compressive stresses at the opposite edge. The tensile stress values at a 250 mm eccentricity do not reach the plasticity stage in steel, but with increasing eccentricity, the plasticity stage begins to appear. However, in all cases of eccentricity, the compressive stress values exceed the yielding limit and enter the plastic stage, as shown in Figure 15. The presence of horizontal stiffeners in the upper half of the web height (from 10% to 40%) improves the behavior and stress values within the upper flange, for both tensile and compressive stresses. The stress values decrease at the same load level as the horizontal stiffeners are positioned closer to the top of the web height. While no effect was observed on the stress distribution, whether tensile or compressive, when using horizontal stiffeners from the beginning of the lower half of the web height (from 50% to 90%), there was an increase in the ultimate load capacity, which increases the yield area of the steel used. At the beginning of the eccentricity values, at 250 mm, there is a large difference between the stress values on the edges of the upper flange, whether tensile or compressive, at the same level of applied load, as shown in Figure 16a. This difference decreases with increasing eccentricity distance, as shown in Figure 16d. By using horizontal stiffeners in the upper half of the beam’s web height (10%) in addition to horizontal stiffeners in the lower half (90%), the stress distribution behavior is improved, and the final compressive stress values of the steel used increase, reaching 378, 361, 351, and 345 MPa with eccentricity values of 250, 500, 750, and 1000 mm, respectively. These values are close to the steel ultimate stress, which is 377 MPa, where the highest efficiency is obtained from the steel used. When steel beams are used with only vertical stiffeners and the spacing between them is halved, the stress distribution behavior at both edges of the upper flange is improved, and these beams show results similar to beams with horizontal stiffeners at a distance of 30% of the beam’s web height.

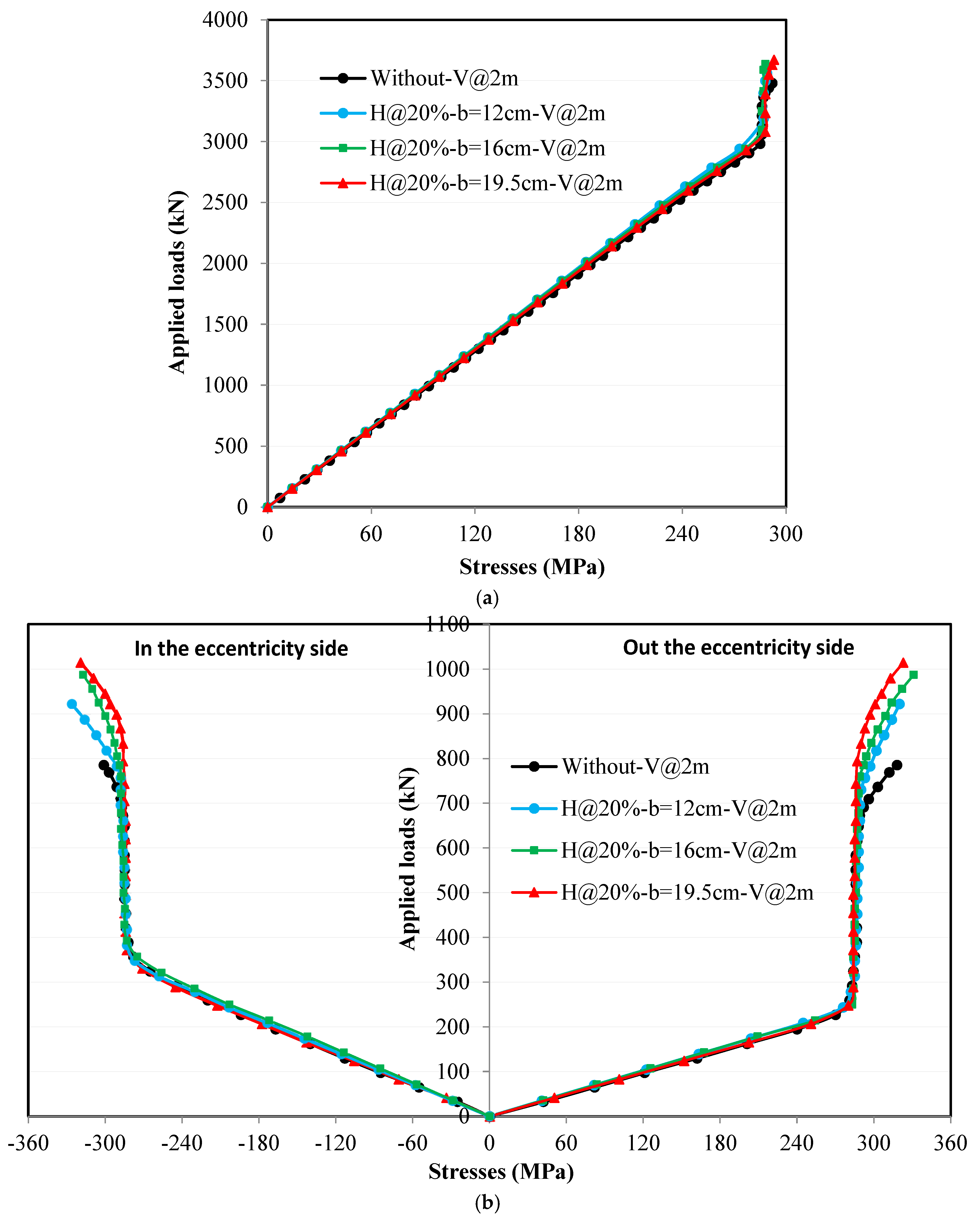
4.4.3. Effect of Horizontal Stiffeners Width

Figure 17 shows that the effect of the width of the horizontal stiffeners is strongly effective on the stress distribution behavior through the upper flange, both without eccentric loading, as shown in Figure 17a, and with eccentric loading, as shown in Figure 17b. By using horizontal stiffeners with widths of 120 mm and 160 mm, which represent 62% and 82%, respectively, of the total width of the horizontal beam stiffeners, the shape and pattern of stress distribution changed. The stress values increased at the same level of applied load with a decrease in the width of the stiffeners. From the figures, it can be observed that reducing the width of the horizontal stiffeners and placing them at a location with a low ratio of web height is similar to using full-width horizontal stiffeners placed at distances with a high ratio of beam web height.

4.4.4. Effect of Eccentricity and Horizontal Stiffeners on the Onset of Yield Stresses at the Edges of the Upper Flange

Through Figure 15, Figure 16 and Figure 17, it was observed that the load values causing tensile stresses in the upper flange edge do not correspond to the same level of load in the appearance of compressive stresses in the other edge of the same steel beam. Where there is a delay occurs in the tensile stress values compared to the compressive stress at the same level of applied load. Figure 15, Figure 16 and Figure 17 were used to determine the load values that cause the onset of yield stress in the steel used in the tensile and compression edges, and the ratios between them were calculated for each beam and these ratios were drawn, as shown in Figure 18. It was observed that all ratios were greater than 1.0, which clearly demonstrates the delay in the appearance of tensile stresses compared to compressive stresses at the same load level. Furthermore, any steel beam, even without vertical or horizontal stiffeners, possesses resistance to eccentric loads due to the presence of the upper and lower flanges in the cross-section. The larger this ratio, the stronger and more effective the effect of the stiffeners in increasing the efficiency of the steel beam in resisting eccentric loads, including torsional moments, as it works to resist lateral deformations. The figure illustrates the effect of the presence of horizontal stiffeners on the behavior and distribution of stress values on the edges of the upper flange. Using horizontal stiffeners in the upper half of the web height (from 10% to 40%), even with a reduction in the width of the stiffeners, improves stress distribution in all cases of eccentric loading. However, there was no significant change when using horizontal stiffeners at distances ranging from 50% to 90% of the web height. The highest percentage was measured when horizontal stiffeners were used in the upper half at 10%, along with the lower half at 90% of the beam’s web height. Reducing the spacing between the vertical stiffeners, even without using horizontal stiffeners, also improves the stress distribution behavior, but as mentioned earlier, it is comparable to using horizontal stiffeners at a distance of 30% of the web height.

4.5. Effect of Horizontal Stiffeners on Stress Distribution in the Lower Flanges

As shown in Figure 14, Figure 15, Figure 16 and Figure 17, the effect of horizontal stiffeners and eccentric loads on the behavior and stress distribution values at the edges of the upper flange was considered, and this was also carried out at the edges of the lower flange of the cross-section of the steel beam, as shown in Figure 19. It was observed that all steel beams exhibited the same pattern in stress distribution values and behavior across the lower beam flange when varying the load eccentricity, with differing values and ultimate applied load capacities. Compression stresses were measured at the edge of the lower flange in the edge where the eccentric load was applied (which is unexpected, as the lower flange is generally subjected to tensile stresses). This is due to the torsional moments resulting from the eccentricity of the load, which causes the edge to compress towards the side on which the load is applied and to elongate on the opposite side. Meanwhile, tensile stresses were measured at the edge opposite the point of load application (out the eccentricity side), as shown in Figure 19. It was also observed that the values and behavior of stress distribution converge with increasing eccentricity of the load, as previously documented in Figure 14.

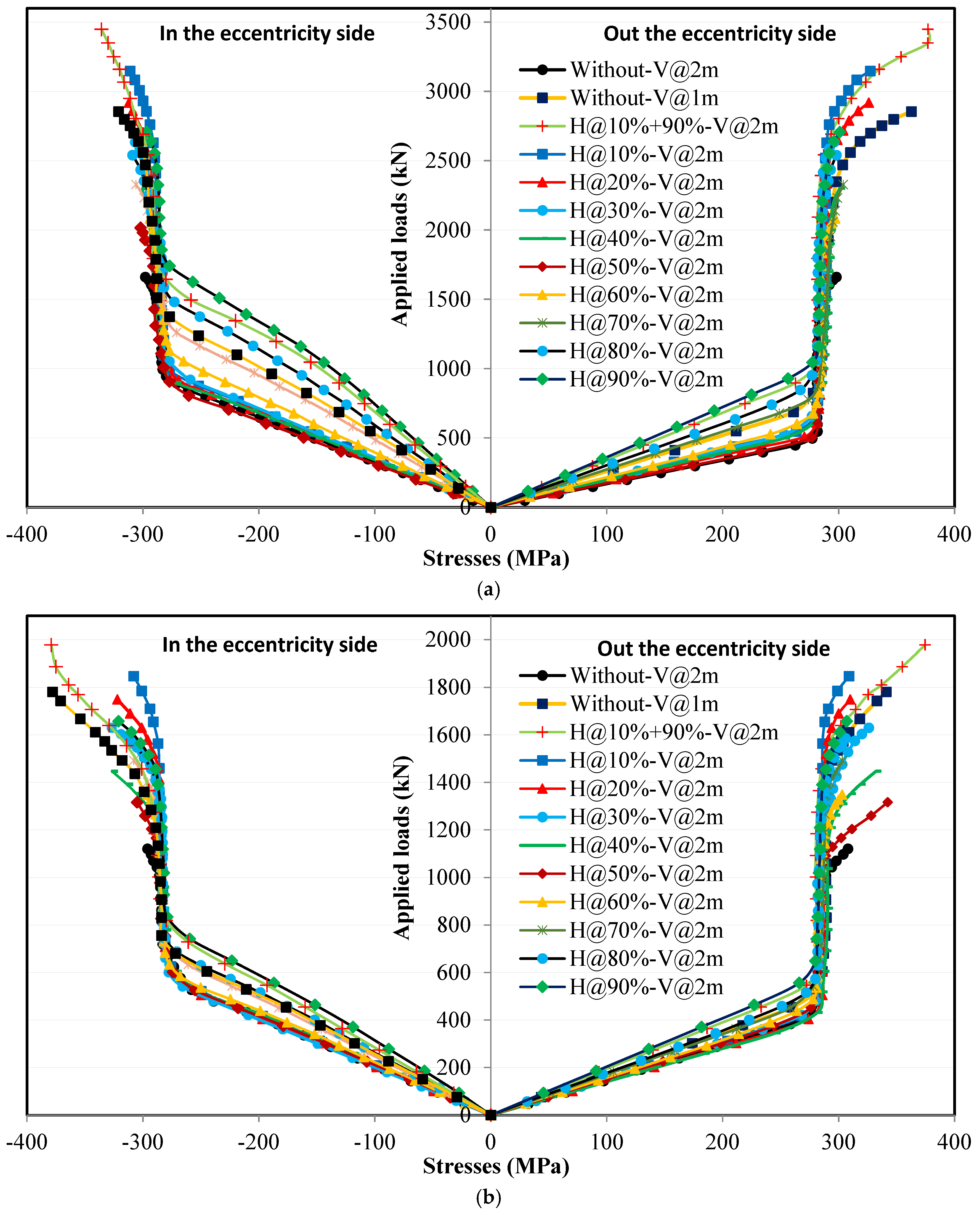
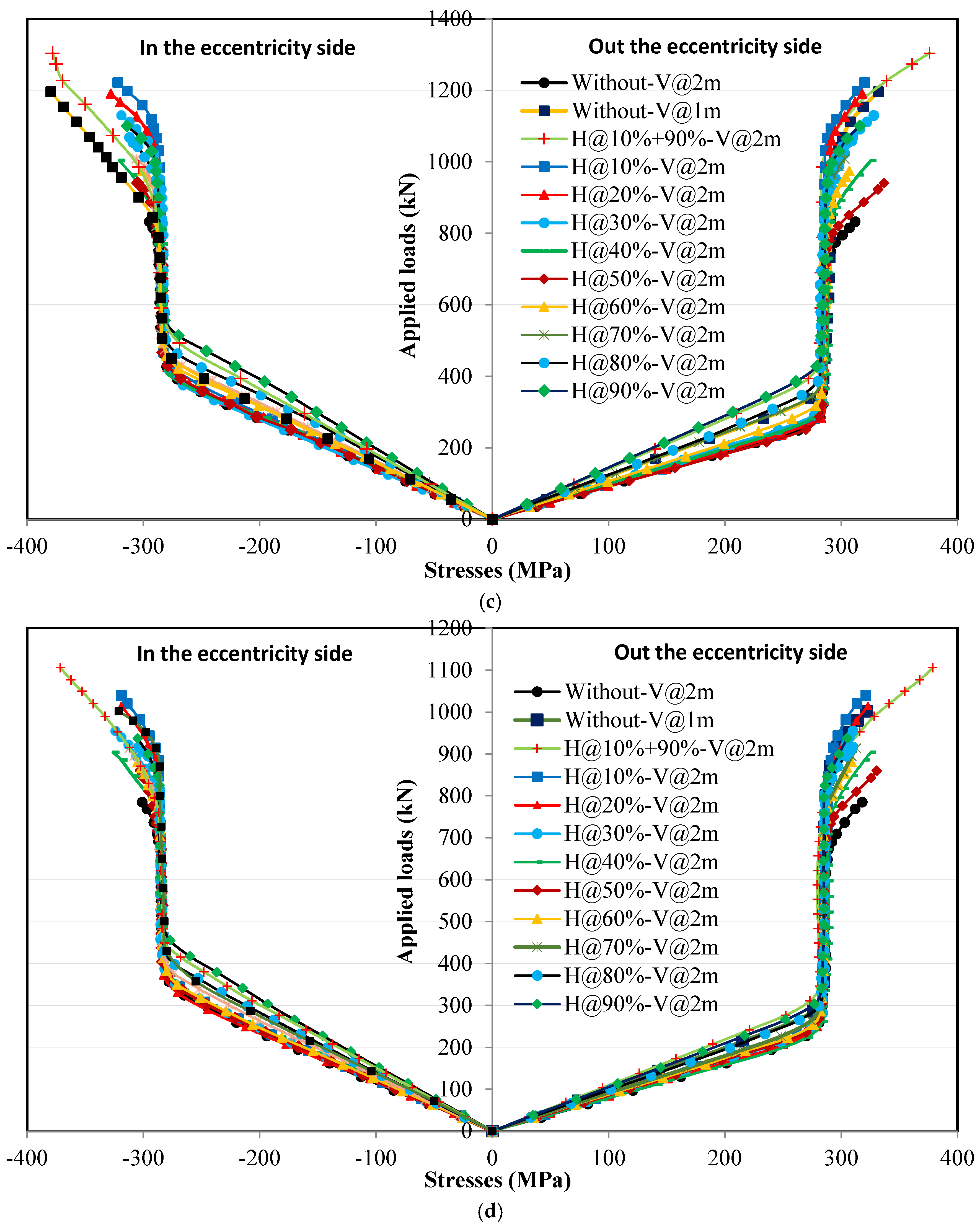
4.5.1. Loading Without Eccentricity

In the case of steel beams, whether with or without horizontal stiffeners, subjected to loads without eccentricity, the stresses generated in the middle of the beam length are tensile stresses in both edges of the lower flange, as shown in Figure 20. The results show that the behavior of stress distribution is linear up to the yield point of the steel used. After this point, a change in stress distribution occurs, leading to a stage of plastic deformation, followed by failure. None of the beams, whether with or without horizontal stiffeners, reached the steel’s ultimate tensile strength, where the highest recorded tensile stress was 293 MPa, while the steel’s ultimate tensile strength was 377 MPa. However, all beams reached stresses higher than the yield stress of the steel, which is 282 MPa, as shown in Figure 20. It was observed that the stress values in the lower flange decrease at the same level of applied load when horizontal stiffeners are used in the lower half of the web height (from 60% to 90%). Also, the stress distribution values and patterns improve with the use of horizontal stiffeners in both the upper and lower halves of the beam web height, whereas no difference is observed when using only vertical stiffeners, even with the inter-spaces between them being reduced by half.

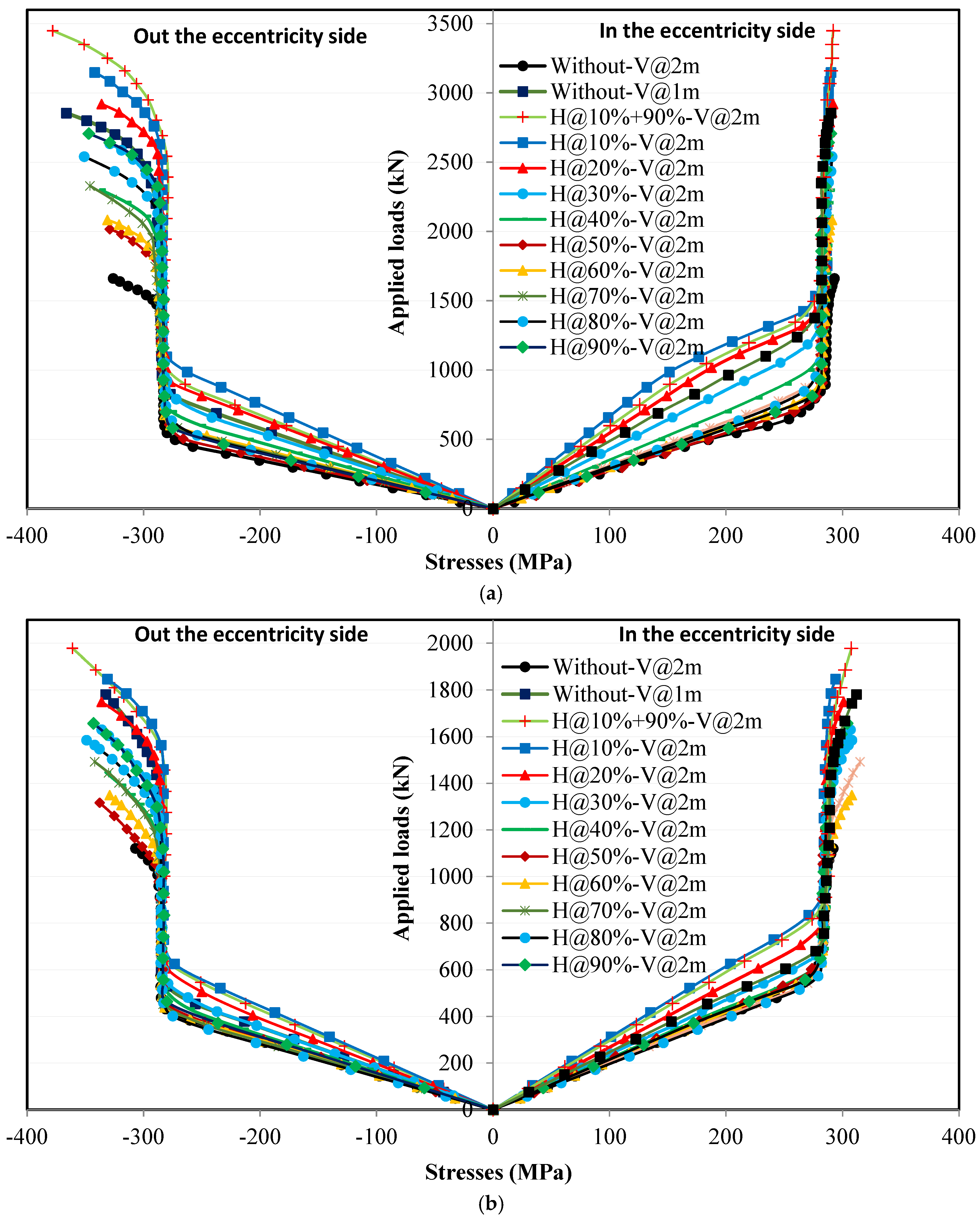
4.5.2. Loading with Eccentricity

By grouping the relationships between the load and the resulting stresses on the lower flange edges of the cross-section according to the value of eccentricity of the load, Figure 21 was obtained. The figure shows that all beams subjected to eccentric loads experience compressive stresses at the edge adjacent to the load-applied side and tensile stresses at the opposite edge. All steel beams under eccentric loads have compressive stress values at the lower flange edge that reach the beginning of the plasticity stage of the steel stresses, and these stress values increase with increasing eccentricity distance, as shown in Figure 21. The presence of horizontal stiffeners in the lower half of the web height (from 60% to 90%) improves the behavior and stress values within the lower flange. The stress values decrease at the same load level as the horizontal stiffeners are positioned closer to the bottom of the web height. While no effect was observed on the stress distribution when using horizontal stiffeners from the beginning of the upper half of the web height (from 10% to 50%), there was an increase in the ultimate load capacity, which increases the yield area of the steel used. By using horizontal stiffeners in the upper half of the beam’s web height (10%) in addition to horizontal stiffeners in the lower half (90%), the stress distribution behavior is improved, and the final tensile stress values of the steel used increase, reaching 377, 375, 376, and 379 MPa with eccentricity values of 250, 500, 750, and 1000 mm, respectively. These values are very close to the steel ultimate stress, which is 377 MPa, where the highest efficiency is obtained from the steel used. When steel beams are used with only vertical stiffeners and the spacing between them is halved, the stress distribution behavior at both edges of the lower flange is improved, and these beams show results similar to beams with horizontal stiffeners at a distance of 70% of the beam’s web height.

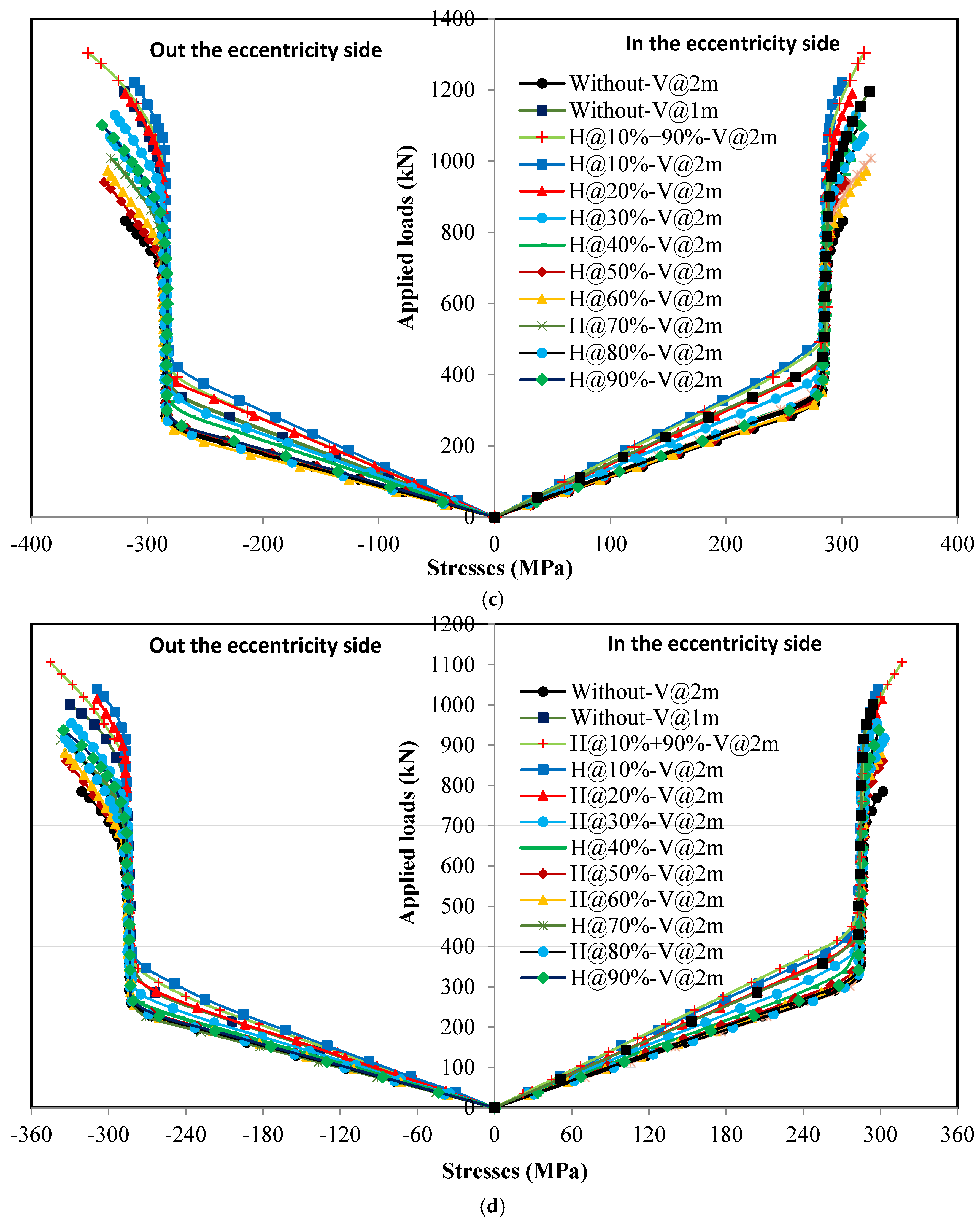
4.5.3. Effect of Horizontal Stiffeners Width

Figure 22 shows that changing the width of the horizontal stiffeners does not affect the behavior and stress distribution at the edges of the lower flange, whether without eccentric loads, as shown in Figure 22a, or with eccentric loads, as shown in Figure 22b. The reason for the lack of any noticeable effect is that these beams utilized horizontal stiffeners in the upper half of the web at a distance of 20% of the height, despite an improvement in the ultimate load capacity of the steel beam.

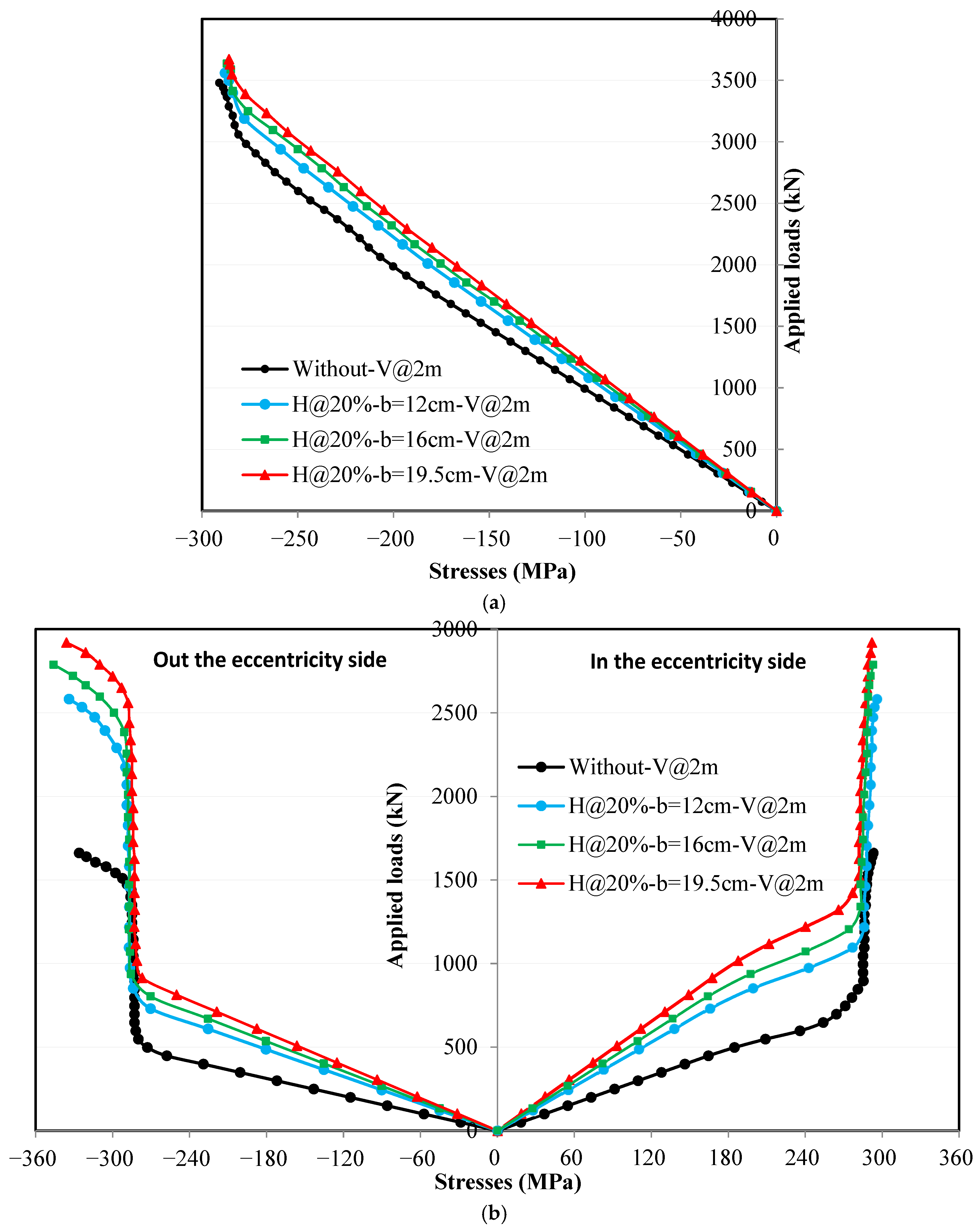
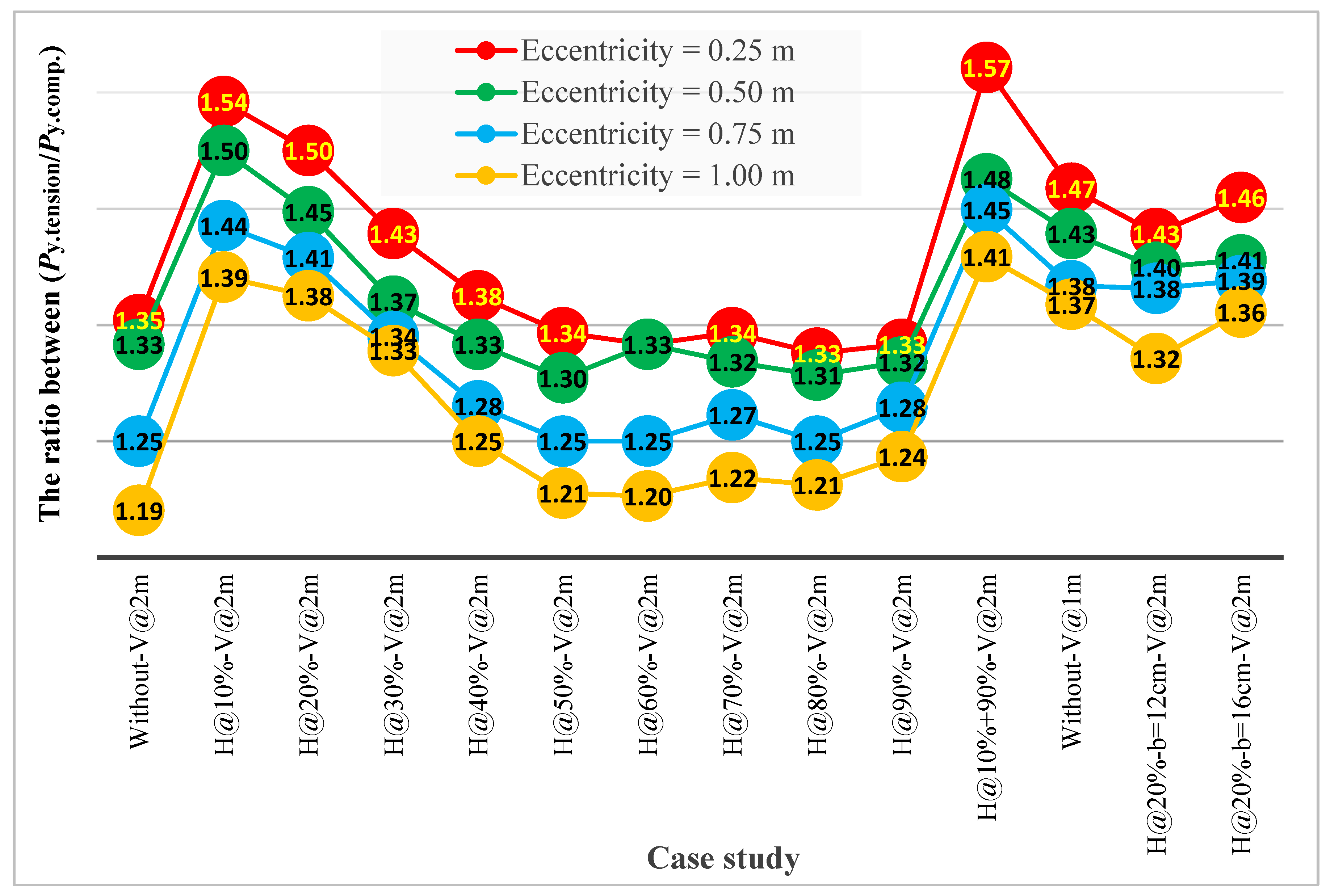
4.5.4. Effect of Eccentricity and Horizontal Stiffeners on the Onset of Yield Stresses at the Edges of the Lower Flange

Through Figure 20, Figure 21 and Figure 22, it was observed that the load values causing compressive stresses in the lower flange edge do not correspond to the same level of load in the appearance of tensile stresses in the other edge. Where there is a delay occurs in the compressive stress values compared to the tensile stress at the same level of applied load. Figure 20, Figure 21 and Figure 22 were used to determine the load values that cause the onset of yield stress in the steel used in compression and tension edges, and the ratios between them were calculated for each beam. These ratios have been plotted as shown in Figure 23. It was observed that all ratios were greater than 1.0, which clearly indicates a delay in the onset of compressive stresses compared to tensile stresses at the same load level. Using horizontal stiffeners in the lower half of the web height (from 60% to 90%) improves stress distribution in the bottom flange for all eccentric loading cases. However, there was no significant change when horizontal stiffeners were used, even with a reduction in stiffener width, at distances ranging from 10% to 50% of the web height. The highest percentage was measured when horizontal stiffeners were used in the lower half at 90% of the beam’s web height. Reducing the spacing between the vertical stiffeners, even without using horizontal stiffeners, improves the stress distribution behavior, which is comparable to using horizontal stiffeners at a distance of 70% of the web height.

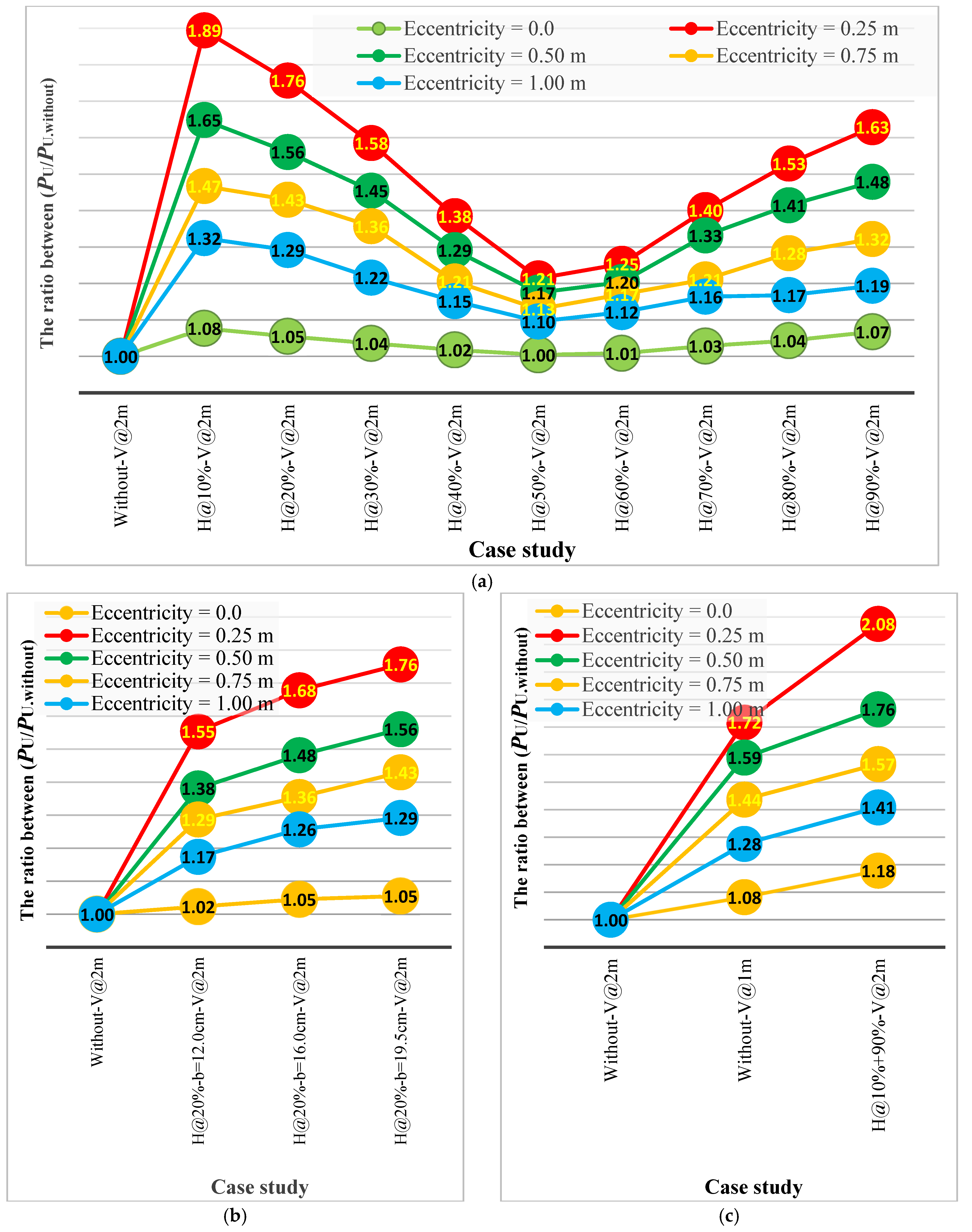
5. Effect of Horizontal Stiffeners on the Ultimate Load Capacity of Beam Under Eccentric Loads

From the results of the FEM simulation and through the relationships between the applied loads and various variables, the ultimate load capacity for all beams, with and without eccentricity, was obtained, as listed in Table 5. Using the values listed in the table, the ratio increases in the ultimate load capacity when using horizontal stiffeners was calculated by finding the ratio between the ultimate load capacity of beams with horizontal stiffeners and beams without horizontal stiffeners (reference beam), with only vertical stiffeners, and an inter-spacing of 2000 mm (Without-V@2m). The results showed that all beams that used horizontal stiffeners or in which the distance between vertical stiffeners was reduced had ratios greater than 1.0. This indicates a significant improvement in the efficiency of steel beams in resisting eccentric loads, which generate torsional moments in addition to combined bending moments.
To facilitate a clearer comparison, the table was converted into relationships, as shown in Figure 24. Figure 24a shows the relationship between the ratio increase in ultimate load capacity and the location of the horizontal stiffeners. It is evident that the best position for the horizontal stiffeners is at a distance of 10% of the beam web height in all eccentric loading cases, where the ratio increase reached 1.89, 1.65, 1.47, and 1.32 at eccentricities of 250, 500, 750, and 1000 mm, respectively. Based on these ratios, the preferred locations for using horizontal stiffeners can be arranged as follows: 10%, 20%, 90%, 30%, 80%, 70%, 40%, 60%, and finally 50% of the web height of the beam, measured from the top. It was also found that the weakest location for placing the horizontal stiffeners is in the middle of the vertical web height. The limited effectiveness of horizontal stiffeners placed at mid-depth of the web (50% of the web height) is consistent with the structural response under eccentric loading. At this location, the stiffener coincides with the neutral axis of the cross-section, resulting in a configuration that is effectively symmetric after the stiffener is added. Consequently, the rotation of the upper flanges, characterized by lateral displacement in the direction of the applied eccentric load, is counteracted by the opposite rotation of the lower flanges. Because the stiffener is positioned at the neutral axis, it contributes minimally to restraining these opposite lateral displacements and the associated torsional deformations induced by the eccentric moment. Nevertheless, a modest performance improvement was observed, ranging from approximately 10% to 21% for eccentricities between 1000 mm and 250 mm. This residual contribution is attributed to the unequal values of lateral displacement in the upper and lower flanges. In contrast, stiffeners located away from the neutral axis, either above or below the mid-depth of the web, lie within regions where rotation and lateral displacement are more pronounced, either in the direction of the applied load (10–40%) or opposite to it (60–90%). These positions enable the stiffeners to more effectively resist lateral deformation, thereby enhancing the beam’s overall capacity to resist eccentric loading. In all cases, the effectiveness of the horizontal braces decreases with increasing load eccentricity distance, as shown in Figure 24a.
Figure 24b illustrates the relationship between the ratio increase in load capacity and the changes in the width of the horizontal stiffeners. It became clear that changing the width of the horizontal stiffeners at the same location along the beam’s web height affects the ultimate load capacity of the beam in resisting eccentric loads. These ratios showed that the width of the horizontal stiffeners can be reduced to 61%, increasing the maximum eccentric load-carrying capacity and achieving better results than using full-width horizontal stiffeners when the stiffener position is between 40% and 80% of the beam’s web height. This finding allows for a reduction in the amount of material used in the horizontal stiffeners by selecting the optimal position along the web height.
Figure 24c shows the ratio increase in the ultimate load capacity when horizontal stiffeners are used in both halves of the web at distances of 10% and 90% of the web height, as well as when using beams with only vertical stiffeners while reducing the inter-spacing between them. It was found that using horizontal stiffeners in both halves of the web provides a significant improvement, being the greatest overall in resisting eccentric loads, including resistance to torsional moments combined with bending moments. The ratio increase reached 2.08, 1.76, 1.57, and 1.41 when using eccentric distances of 250, 500, 750, and 1000 mm, respectively. It was observed that using horizontal stiffeners connecting two locations at the web height provides an improvement that considers the rate of increase for each location individually, but it does not mean adding the percentages completely. In fact, it gives percentage increases higher than the highest one shown and lower than the sum of the two percentages (algebraic sum). For example, when using horizontal stiffeners with an eccentricity of 250 mm at only 10% of the web height, the ratio increase was 1.89, while when using them at only 90% of the web height, the ratio increase was 1.63. However, when using horizontal stiffeners at both locations (10% and 90%), the increase in load capacity was 2.08. The ratio increase of 2.08 was found to be greater than both 1.89 and 1.63, and at the same time, less than their algebraic sum, which is 2.52. This can be explained by examining the values and behavior of the stress distribution in the upper flanges (Figure 16) and lower flanges (Figure 21) and by determining the ultimate stress values at the failure point of the steel beam. The FEM results show that when stiffeners are placed only at 10% of the web height, the upper flange reaches a compressive stress of 342 MPa and the lower flange a tensile stress of 327 MPa under an eccentric load of 250 mm. When stiffeners are placed only at 90% of the web height, corresponding stresses reach 347 MPa and 301 MPa, respectively. In both cases, the stresses do not reach the steel’s ultimate strength of 377 MPa, and failure occurs due to global buckling over the beam’s full length. When stiffeners are installed at both 10% and 90%, the upper flange compressive stress reaches 378 MPa, and the lower flange tensile stress reaches 377 MPa, indicating tensile rupture at the lower flange as the governing failure mode, causing the solution process to stop. To further assess this behavior, the differences between the ultimate stresses in beams with and without stiffeners were calculated. Stiffeners at 10% contribute to the upper flange an increase of 49 MPa, while those at 90% add 54 MPa. If combined additively, these would yield a theoretical stress of 396 MPa, exceeding both the finite element results and the material’s allowable limit, demonstrating that such linear superposition is not physically realistic. A similar comparison was made to the loads generating these stresses. Stiffeners at 10% increased load capacity by 1486.43 kN, while those at 90% contribute 1044.74 kN. Summing these with the capacity of the unstiffened beam results in a theoretical load of 4193.25 kN. This exceeds both the FEM-predicted ultimate load of 3449.33 kN for the combined stiffener configuration and the ultimate capacity of the beam without eccentric loading, which is 4102.20 kN, such that no beam with eccentric load can exceed this limit.
Using only vertical stiffeners without horizontal stiffeners, while reducing the inter-spacing between them, provides a significant improvement in the ultimate load capacity in all eccentric loading cases. However, this improvement is equivalent to using horizontal stiffeners at a distance from the web equal to 20% or 90% of its height. The spacing between vertical stiffeners plays a crucial role in the load-resistance efficiency of steel beams. This effect depends on the type of structural element (simple-supported beam, beam with fixed support ends, or cantilever beam) and the type of load acting on it (shear load, bending moment, or torsional moment). This spacing has been incorporated into the design equations proposed in previous studies [70,71,72,73], which allow for the calculation of the ultimate load capacity of steel beams. It has also been demonstrated that reducing the ratio between the spacing of the vertical stiffeners and the total beam length increases the beam’s load-resistance efficiency. This demonstrates that using beams with horizontal stiffeners at distances of 10% or 20% of the web height is better than using only vertical stiffeners, even when reducing the inter-spacing between them by half.

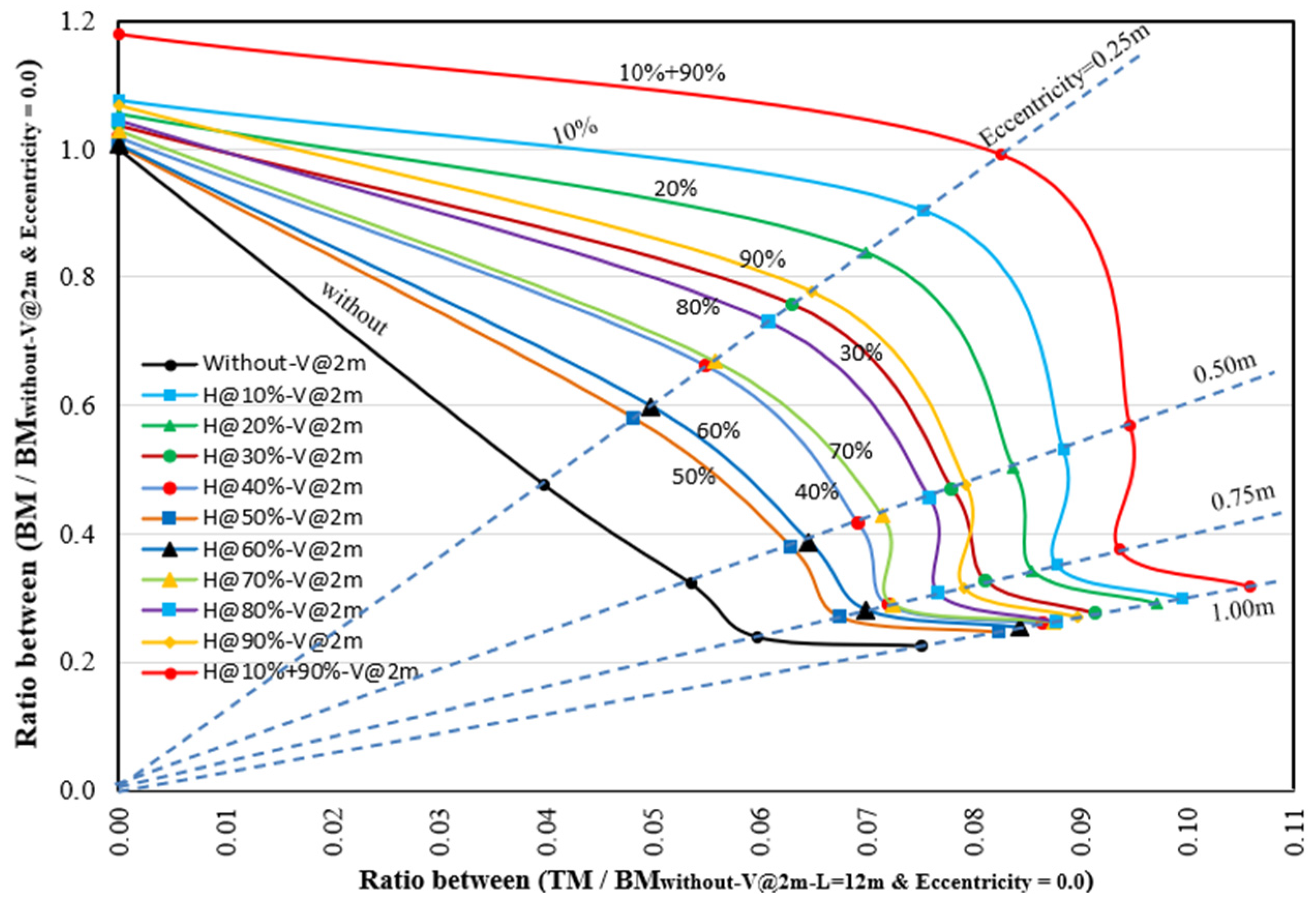
6. Predicting the Beam Capacity to Resist Combined Bending and Torsional Moments

The values listed in Table 5 show the ultimate load capacity of steel beams with varying eccentric distances and locations of the horizontal stiffeners. Using the structural system for the steel beams, where fixed supports were used at the beam ends and eccentric loads, P, were applied in the middle of the span, the bending, BM, and torsional, TM, moments were calculated based on the following equations:
B M = P × L / 8
T M = P × E c c e n t r i c i t y / 2
Using the calculated values of bending moments, BM, and torsional moments, TM, for each of the steel beam models, the ratio between the bending moments of beams with horizontal stiffeners subjected to eccentric loads and beams without horizontal stiffeners under a non-eccentric load was calculated and plotted on the vertical axis. Similarly, the ratio between the torsional moments of the same beams and the bending moments of beams without horizontal stiffeners under a non-eccentric load was calculated and plotted on the horizontal axis. Thus, the interaction diagram was obtained, as shown in Figure 25. Figure 25 illustrates the relationship between the ratios of ultimate bending moment resistance and the location of horizontal stiffeners. Straight lines were also drawn from the origin point to the points of influence of the eccentric load distances. The figure shows that as the eccentricity of the applied loads increases, the ultimate bending moment capacity of the beam decreases, while its resistance to torsional moments increases. The beam’s cross-section is subjected to two types of stresses generated by these combined moments. This figure (interaction diagram) allows for the prediction of the ultimate bending and torsional moments values of beams under the influence of eccentric loads. This is carried out by knowing the value of load eccentricity and the position of the horizontal stiffeners relative to the beam’s web height, as well as the ultimate bending moment capacity of the steel beam without horizontal stiffeners, without eccentric loading. The interaction diagram is suitable for use if the following conditions are met: the beam length is 12.0 m, there is a fixed support at the beam ends, the horizontal stiffeners are full-width and 10 mm thick, and the vertical stiffeners are spaced 2.0 m apart and 10 mm thick.

7. Conclusions

Steel beams are usually subjected to eccentric loads, which generate combined bending and torsional moments on the cross-section. These loads cause lateral displacements and unwanted stresses at the upper and lower flanges of the cross-section, ultimately leading to failure as a result of global buckling along the beam length. To resist these loads, horizontal stiffeners are added to the length of the beam axis at locations of the web height. To determine the effect of these horizontal stiffeners on the efficiency of the beam, simulations were performed using the FEM method on 70 steel beams. The reliability and accuracy of the FEM results were first verified by comparing them with the results of 25 steel beams that had been experimentally tested in previous studies, which showed very high accuracy in this simulation. Based on the variables studied in this research, the following results were obtained:
-
The closer the horizontal stiffeners are to the flange, whether the upper, lower, or both, the better the efficiency and behavior of the steel beams in resisting eccentric loads.
-
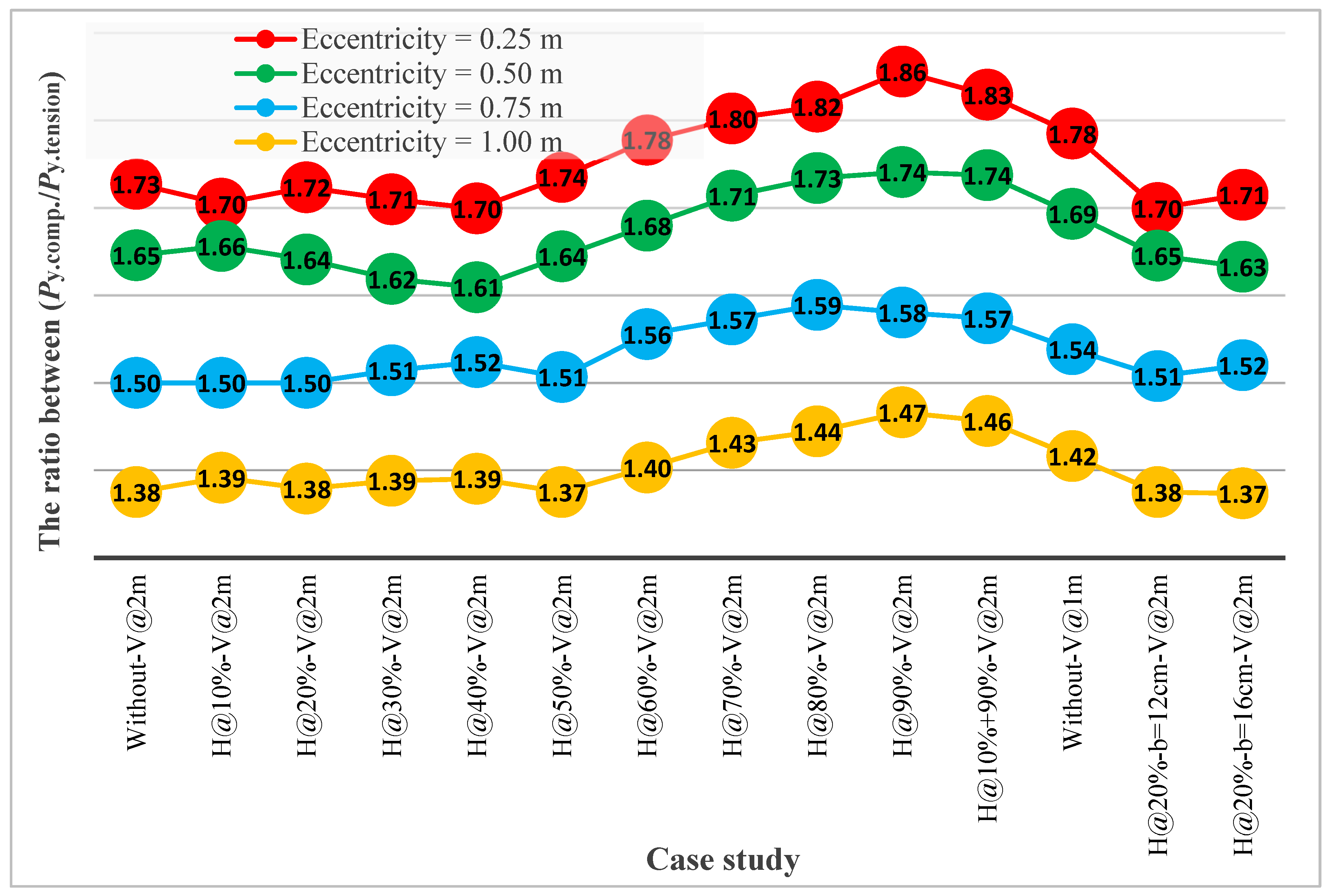
Based on the ultimate load capacity of the steel beams for eccentric loads, the order of preference for the proposed locations of the horizontal stiffeners was as follows: 10%, 20%, 90%, 30%, 80%, 70%, 40%, and 50% of the beam’s web height.
-
Using horizontal stiffeners in the upper half of the web height (from 10% to 40%) contributes to improving the behavior and stresses distribution values in the upper flange edges. However, having them at a distance greater than or equal to 50% does not improve their effectiveness.
-
Using horizontal stiffeners in the lower half of the web height (from 60% to 90%) contributes to improving the behavior and stress distribution values in the edges of the lower flange. However, having them at less than or equal to 50% does not provide any improvement.
-
Using horizontal stiffeners with a small width at low ratios of web height provides efficiency in the behavior of beams and their resistance to eccentric loads, similar to using full-width stiffeners located at large ratios of web height. That is, the amount of material used in horizontal stiffeners can be reduced by choosing the appropriate location for the web height.
-
When horizontal stiffeners are used that combine two locations of web height, the percentage increase in capacity gives a greater improvement than the percentages for the two locations separately, but less than the sum of their values.
-
Using beams with only vertical stiffeners and reducing the distances between them by half improves their behavior in resisting combined bending and torsional moments, similar to using steel beams with horizontal stiffeners at 20% or 90% of the web height. In addition, there is a noticeable improvement in the behavior and distribution of stresses along both the upper and lower flange edges.
-
The proposed interaction diagram can predict the ultimate load capacity of combined bending and torsional moments resulting from eccentric loads using horizontal stiffeners at different locations along the web height.
Based on the conclusions reached, it is evident that other variables, such as the thickness of the stiffeners, the length of the steel beam, the height of the web, connection stiffness, and other welding-induced vulnerabilities, should be considered in future studies to assess their impact on the efficiency of steel beams subjected to eccentric loads with horizontal supports. Other systems besides traditional stiffeners can also be used to resist eccentric loads, such as corrugated webs and hollow flanges.

Author Contributions

Conceptualization, A.M.S.; methodology, A.M.S. and M.H.A.; software, A.M.S.; validation, A.M.S. and M.H.A.; formal analysis, A.M.S. and M.H.A.; investigation, A.M.S.; resources, A.M.S. and M.H.A.; data curation, A.M.S.; writing—original draft preparation, A.M.S.; writing—review and editing, A.M.S. and M.H.A.; visualization, A.M.S.; supervision, A.M.S.; project administration, A.M.S. and M.H.A. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.

Acknowledgments

The author extends the appreciation to the Deanship of Postgraduate Studies and Scientific Research at Majmaah University for funding this research work through the project number (R-2025-2172).

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Lee, C.H.; Han, K.H.; Uang, C.M.; Kim, D.-K.; Park, C.-H.; Kim, J.-H. Flexural strength and rotation capacity of I-shaped beams fabricated from 800 MPa steel. J. Struct. Eng. 2013, 139, 1043–1058. [Google Scholar] [CrossRef]
  2. Thomas, S.J.; Earls, C.J. Cross-sectional compactness and bracing requirements for HPS483W girders. J. Struct. Eng. 2003, 129, 1569–1583. [Google Scholar] [CrossRef]
  3. Xu, Z.; Tong, G.; Zhang, L. Design of horizontal stiffeners for stiffened steel plate walls in compression. Thin-Walled Struct. 2018, 132, 385–397. [Google Scholar] [CrossRef]
  4. Al-Dafafea, T.; Durif, S.; Bouchaïr, A.; Fournely, E. Experimental study of beams with stiffened large web openings. J. Constr. Steel Res. 2019, 154, 149–160. [Google Scholar] [CrossRef]
  5. Hamoda, A.; Yehia, S.A.; Ahmed, M.; Sennah, K.; Abadel, A.A.; Shahin, R.I. Experimental and numerical investigation of shear strengthening of simply supported deep beams incorporating stainless steel plates. Buildings 2024, 14, 3680. [Google Scholar] [CrossRef]
  6. Elamary, A.S.; Mohamed, M.A.; Sharaky, I.A.; Mohamed, A.K.; Alharthi, Y.M.; Ali, M.A.M. Utilizing artificial intelligence approaches to determine the shear strength of steel beams with flat webs. Metals 2023, 13, 232. [Google Scholar] [CrossRef]
  7. Nikoomanesh, M.R.; Goudarzi, M.A. Experimental and numerical evaluation of shear load capacity for sinusoidal corrugated web girders. Thin-Walled Struct. 2020, 153, 106798. [Google Scholar] [CrossRef]
  8. Jáger, B.; Kövesdi, B.; Dunai, L. Numerical investigations on bending and shear buckling interaction of I-Girders with slender WEB. Thin-Walled Struct. 2019, 143, 106199. [Google Scholar] [CrossRef]
  9. Green, P.S.; Sause, R.; Ricles, J.M. Strength and ductility of HPS flexural members. J. Constr. Steel Res. 2002, 58, 907–941. [Google Scholar] [CrossRef]
  10. Earls, C.J. Uniform moment behavior of high performance steel I-shaped beams. J. Constr. Steel Res. 2001, 57, 711–728. [Google Scholar] [CrossRef]
  11. Xue, J.; Ma, S.; Chen, X.; Wu, Q.; Wang, Y.; Wang, Y.; Akbar, M.; Yang, N. Experimental investigation and design of novel hollow flange beams under bending. Buildings 2024, 14, 1413. [Google Scholar] [CrossRef]
  12. El-Mahdy, G.M.; El-Saadaway, M.M. Ultimate strength of singly symmetric I-section steel beams with variable flange ratio. Thin-Walled Struct. 2015, 87, 149–157. [Google Scholar] [CrossRef]
  13. Nascimento, S.; Pedro, J.J.O.; Kuhlmann, U. Axial forces in transverse web stiffeners of steel plate girders—A numerical investigation. Thin-Walled Struct. 2025, 217, 113778. [Google Scholar] [CrossRef]
  14. Pedro, J.J.O.; Biscaya, A.; Nascimento, S.; Kuhlmann, U. Buckling resistance of transversally stiffened steel plate girders considering M-V interaction with high compression forces. Structures 2024, 70, 107714. [Google Scholar] [CrossRef]
  15. Tan, L.; Zhou, Y.; Kong, H.; Yue, Z.; Wang, Q.; Zhou, L. Dynamic monitoring of steel beam stress based on PMN-PT sensor. Buildings 2024, 14, 2831. [Google Scholar] [CrossRef]
  16. Nasery, M.M. Investigation on behaviours along weak axes of steel beam under low velocity impact loading: Experimental and numerical. Buildings 2023, 13, 2331. [Google Scholar] [CrossRef]
  17. Narendra, P.V.R.; Singh, K.D. Elliptical hollow section steel cantilever beams under extremely low cycle fatigue flexural load—A finite element study. Thin-Walled Struct. 2017, 119, 126–150. [Google Scholar] [CrossRef]
  18. Lim, J.; Kang, Y.-J.; Lee, J.; Kim, S.; Lee, K. Experimental and analytical study of horizontally curved i-girders subjected to equal end moments. Metals 2021, 11, 1132. [Google Scholar] [CrossRef]
  19. Andrade, A.; Camotim, D. Lateral-torsional buckling of singly symmetric web-tapered beams: Theory and application. J. Eng. Mech. ASCE 2005, 131, 586–597. [Google Scholar] [CrossRef]
  20. Andrade, A.; Camotim, D.; Dinis, P.B. Lateral-torsional buckling of singly symmetric web-tapered thin-walled I-beams: 1D model vs. shell FEA. Comput. Struct. 2007, 85, 1343–1359. [Google Scholar] [CrossRef]
  21. Mascolo, I.; Modano, M.; Fiorillo, A.; Fulgione, M.; Pasquino, V.; Fraternali, F. Experimental and numerical study on the lateral-torsional buckling of steel c-beams with variable cross-section. Metals 2018, 8, 941. [Google Scholar] [CrossRef]
  22. Asgarian, B.; Soltani, M.; Mohri, F. Lateral-torsional buckling of tapered thin-walled beams with arbitrary cross-sections. Thin-Walled Struct. 2013, 62, 96–108. [Google Scholar] [CrossRef]
  23. Kövesdi, B. Patch loading resistance of slender plate girders with longitudinal stiffeners. J. Constr. Steel Res. 2018, 140, 237–246. [Google Scholar] [CrossRef]
  24. Graciano, C.; Mendes, J. Elastic buckling of longitudinally stiffened patch loaded plate girders using factorial design. J. Constr. Steel Res. 2014, 100, 229–236. [Google Scholar] [CrossRef]
  25. Chacón, R.; Mirambell, E.; Real, E. Transversally stiffened plate girders subjected to patch loading: Part 2. Additional numerical study and design proposal. J. Constr. Steel Res. 2013, 80, 492–504. [Google Scholar] [CrossRef]
  26. Dos Santos, G.B.; Gardner, L. Design recommendations for stainless steel I-sections under concentrated transverse loading. Eng. Struct. 2020, 204, 109810. [Google Scholar] [CrossRef]
  27. Graciano, C.; Johansson, B. Resistance of longitudinally stiffened I-girders subjected to concentrated loads. J. Constr. Steel Res. 2003, 59, 561–586. [Google Scholar] [CrossRef]
  28. Cai, M.; Liu, S.; Wang, F. Temperature effect of composite girders with corrugated steel webs considering local longitudinal stiffness of webs. Buildings 2024, 14, 1939. [Google Scholar] [CrossRef]
  29. Abed, F.; Abdul-Latif, A.; Yehia, A. Experimental study on the mechanical behavior of en08 steel at different temperatures and strain rates. Metals 2018, 8, 736. [Google Scholar] [CrossRef]
  30. Hu, W.; Zhang, Z.; Shi, J.; Chen, Y.; Li, Y.; Feng, Q. Refined analysis of spatial three-curved steel box girder bridge and temperature stress prediction based on WOA-BPNN. Buildings 2024, 14, 415. [Google Scholar] [CrossRef]
  31. Saliba, N.; Real, E.; Gardner, L. Shear design recommendations for stainless steel plate girders. Eng. Struct. 2014, 59, 220–228. [Google Scholar] [CrossRef]
  32. Prabaharan, V.; Akhas, P.K. Evaluating the influence of stiffener in the bending capacity of cold formed steel C-section. Innov. Infrastruct. Solut. 2025, 10, 118. [Google Scholar] [CrossRef]
  33. Perera, N.; Mahendran, M. Section moment capacity tests of hollow flange steel plate girders. J. Constr. Steel Res. 2018, 148, 97–111. [Google Scholar] [CrossRef]
  34. Young, B.; Ellobody, E.; He, J. Web crippling tests on cold-formed high strength steel channel sections having different stiffened flanges and stiffened web. Thin-Walled Struct. 2023, 190, 110995. [Google Scholar] [CrossRef]
  35. Young, B.; Ellobody, E. Experimental investigation on cold-formed steel Z-sections having different stiffened flanges undergoing web crippling. Eng. Struct. 2023, 286, 116144. [Google Scholar] [CrossRef]
  36. Lee, S.C.; Yoo, C.H.; Yoon, D.Y. Behavior of intermediate transverse stiffeners attached on web panels. J. Struct. Eng. 2002, 128, 337–345. [Google Scholar] [CrossRef]
  37. Lee, S.C.; Lee, D.S.; Yoo, C.H. Design of intermediate transverse stiffeners for shear web panels. Eng. Struct. 2014, 75, 27–38. [Google Scholar] [CrossRef]
  38. Loughlan, J.; Hussain, N. The in-plane shear failure of transversely stiffened thin plates. Thin-Walled Struct. 2014, 81, 225–235. [Google Scholar] [CrossRef]
  39. Freitas, P.; Nascimento, S.; Pedro, J.J.O. Shear buckling resistance and intermediate transverse stiffeners internal forces of full-scale steel plate girders—Experimental tests and numerical investigation. Eng. Struct. 2024, 314, 118303. [Google Scholar] [CrossRef]
  40. Kim, Y.D.; White, D.W. Transverse stiffener requirements to develop shear-buckling and postbuckling resistance of steel i-girders. J. Struct. Eng. 2013, 140, 04013098. [Google Scholar] [CrossRef]
  41. Graciano, C. Strength of longitudinally stiffened webs subjected to concentrated loading. J. Struct. Eng. 2005, 131, 268–278. [Google Scholar] [CrossRef]
  42. Sinur, F.; Beg, D. Intermediate transverse stiffeners in plate girders. Steel Constr. 2012, 5, 23–32. [Google Scholar] [CrossRef]
  43. Roudsari, M.T.; Abdollahi, F.; Salimi, H.; Azizi, S.; Khosravi, A.R. The effect of stiffener on behavior of reduced beam section connections in steel moment-resisting frames. Int. J. Steel Struct. 2015, 15, 827–834. [Google Scholar] [CrossRef]
  44. Hou, W.; Wang, L.; Shi, D. Flexural behaviour of strengthened damaged steel beams using carbon fibre-reinforced polymer sheets. Sci. Rep. 2022, 12, 10134. [Google Scholar] [CrossRef]
  45. Sayed, A.M.; Ali, N.M.; Aljarbou, M.H.; Alzlfawi, A.; Aldhobaib, S.; Alanazi, H.; Altuwayjiri, A.H. Numerical study of the effect of out-of-plane distance in the lateral direction at the mid-span of a steel beam on the sectional moment capacity. Buildings 2025, 15, 283. [Google Scholar] [CrossRef]
  46. Sarfarazi, S.; Saffari, H.; Fakhraddini, A. Shear behavior of panel zone considering axial force for flanged cruciform columns. Civ. Eng. Infrastruct. J. 2020, 53, 359–377. [Google Scholar]
  47. Kumar, S.; Gupta, P.K.; Iqbal, M.A. Experimental and numerical study on self-compacting alkali-activated slag concrete-filled steel tubes. J. Constr. Steel Res. 2024, 214, 108453. [Google Scholar] [CrossRef]
  48. Wang, Y.-B.; Li, G.-Q.; Chen, S.-W.; Sun, F.-F. Experimental and numerical study on the behavior of axially compressed high strength steel box-columns. Eng. Struct. 2014, 58, 79–91. [Google Scholar] [CrossRef]
  49. Rabi, M.; Ferreira, F.P.V.; Abarkan, I.; Limbachiya, V.; Shamass, R. Prediction of the cross-sectional capacity of cold-formed CHS using numerical modelling and machine learning. Results Eng. 2023, 17, 100902. [Google Scholar] [CrossRef]
  50. Zhang, Y.C.; Chen, Y. Experimental study and finite element analysis of square stub columns with straight ribs of concrete-filled thin-walled steel tube. J. Build. Struct. 2006, 27, 16–22. [Google Scholar]
  51. Chan, C.L.; Khalid, Y.A.; Sahari, B.B.; Hamouda, A.M.S. Finite element analysis of corrugated web beams under bending. J. Constr. Steel Res. 2002, 58, 1391–1406. [Google Scholar] [CrossRef]
  52. Shao, Y.B.; Mohamed, H.S.; Wang, L.; Wu, C.S. Experimental and numerical investigation on stiffened rectangular hollow flange beam. Int. J. Steel Struct. 2020, 20, 1564–1581. [Google Scholar] [CrossRef]
  53. Erdal, F.; Tunca, O.; Tas, S.; Ozcelik, R. Experimental and finite element study of optimal designed steel corrugated web beams. Adv. Struct. Eng. 2021, 24, 1814–1827. [Google Scholar] [CrossRef]
  54. Xue, J.; Ma, S.; Chen, X.; Wu, Q.; Akbar, M. Finite element modeling of assembling rivet-fastened rectangular hollow flange beams in bending. J. Constr. Steel Res. 2023, 211, 108177. [Google Scholar] [CrossRef]
  55. Senapati, S.; Sangle, K.K. Nonlinear static analysis of cold-formed steel frame with rigid connections. Results Eng. 2022, 15, 100503. [Google Scholar] [CrossRef]
  56. Al-Kaseasbeh, Q. Analysis of hydrocarbon fire-exposed cold-formed steel columns. Results Eng. 2023, 20, 101400. [Google Scholar] [CrossRef]
  57. Uzzaman, A.; Lim, J.B.P.; Nash, D.; Rhodes, J.; Young, B. Cold-formed steel sections with web openings subjected to web crippling under two-flange loading conditions—Part I: Tests and finite element analysis. Thin-Walled Struct. 2012, 56, 38–48. [Google Scholar] [CrossRef]
  58. Isleem, H.F.; Chukka, N.D.K.R.; Bahrami, A.; Oyebisi, S.; Kumar, R.; Qiong, T. Nonlinear finite element and analytical modelling of reinforced concrete filled steel tube columns under axial compression loading. Results Eng. 2023, 19, 101341. [Google Scholar] [CrossRef]
  59. Tao, Z.; Wang, Z.-B.; Yu, Q. Finite element modelling of concrete-filled steel stub columns under axial compression. J. Construct. Steel Res. 2013, 89, 121–131. [Google Scholar] [CrossRef]
  60. Sayed, A.M. Numerical study of the effects of flange damage on the steel beam capacity under static and fatigue flexural loads. Results Eng. 2023, 17, 100835. [Google Scholar] [CrossRef]
  61. Perera, N.; Mahendran, M. Finite element analysis and design for section moment capacities of hollow flange steel plate girders. Thin-Walled Struct. 2019, 135, 356–375. [Google Scholar] [CrossRef]
  62. ANSYS. ANSYS Help User’s Manual, Version 22; Swanson Analysis Systems, Inc.: Technology Drive Canonsburg, PA, USA, 2022. [Google Scholar]
  63. Sayed, A.M.; Alanazi, H. Performance of steel metal prepared using different welding cooling methods. Case Stud. Constr. Mater. 2022, 16, e00953. [Google Scholar] [CrossRef]
  64. Xiong, G.; Kang, S.-B.; Yang, B.; Wang, S.; Bai, J.; Nie, S.; Hu, Y.; Dai, G. Experimental and numerical studies on lateral torsional buckling of welded Q460GJ structural steel beams. Eng. Struct. 2016, 126, 1–14. [Google Scholar] [CrossRef]
  65. Saliba, N.; Gardner, L. Experimental study of the shear response of lean duplex stainless steel plate girders. Eng. Struct. 2013, 46, 375–391. [Google Scholar] [CrossRef]
  66. Yang, B.; Dong, M.; Han, Q.; Elchalakani, M.; Xiong, G. Flexural behavior and rotation capacity of welded i-beams made from 690-mpa high-strength steel. J. Struct. Eng. 2021, 147, 04020320. [Google Scholar] [CrossRef]
  67. Shokouhian, M.; Shi, Y.J. Flexural strength of hybrid steel I-beams based on slenderness. Eng. Struct. 2015, 93, 114–128. [Google Scholar] [CrossRef]
  68. Beg, D.; Hladnik, L. Slenderness limit of class 3 I cross-sections made of high strength steel. J. Constr. Steel Res. 1996, 38, 201–217. [Google Scholar] [CrossRef]
  69. Shi, Y.; Xu, K.; Shi, G.; Li, Y. Local buckling behavior of high strength steel welded I-section flexural members under uniform moment. Adv. Struct. Eng. 2018, 21, 93–108. [Google Scholar] [CrossRef]
  70. Hassanien, M.; Bahaa, M.; Sobhy, H.; Hassan, A.; Inoue, J. Effect of vertical web stiffeners on lateral torsional buckling behavior of cantilever steel I-beams. J. Appl. Mech. 2004, 7, 233–246. [Google Scholar] [CrossRef][Green Version]
  71. Takabatake, H. Lateral buckling of I beams with web stiffeners and batten plates. Int. J. Solids Struct. 1988, 24, 1003–1019. [Google Scholar] [CrossRef]
  72. Xu, Z.; Tong, G.; Zhang, L. Stiffness demand on stiffeners of vertically stiffened steel plate shear wall. J. Struct. Eng. 2020, 146, 06020005. [Google Scholar] [CrossRef]
  73. Choi, B.H.; Kang, Y.J.; Yoo, C.H. Stiffness requirements for transverse stiffeners of compression panels. Eng. Struct. 2007, 29, 2087–2096. [Google Scholar] [CrossRef]
Buildings 15 04385 g001
Figure 1. The steel stress–strain relationship for steel applied to the FEM simulation [63].
Figure 1. The steel stress–strain relationship for steel applied to the FEM simulation [63].
Buildings 15 04385 g001
Buildings 15 04385 g002
Figure 2. Steel beam geometric details, variables, and conditions used in FEM simulation.
Figure 2. Steel beam geometric details, variables, and conditions used in FEM simulation.
Buildings 15 04385 g002
Buildings 15 04385 g003
Figure 3. The relationship between the accuracy ratio in the ultimate load capacity and the size of the mesh dimensions.
Figure 3. The relationship between the accuracy ratio in the ultimate load capacity and the size of the mesh dimensions.
Buildings 15 04385 g003
Buildings 15 04385 g004
Figure 4. Applied bending moment and the mid-span deflection resulting from the FEM tests. (a) Beams according to Shi et al. [69]; (b) Beams according to Saliba and Gardner [65].
Figure 4. Applied bending moment and the mid-span deflection resulting from the FEM tests. (a) Beams according to Shi et al. [69]; (b) Beams according to Saliba and Gardner [65].
Buildings 15 04385 g004
Buildings 15 04385 g005
Figure 5. The locations of buckling failure and deformation patterns were obtained through FEM simulation tests according to Shi et al. [69]. (a) I-460-1; (b) I-890-3.
Figure 5. The locations of buckling failure and deformation patterns were obtained through FEM simulation tests according to Shi et al. [69]. (a) I-460-1; (b) I-890-3.
Buildings 15 04385 g005
Buildings 15 04385 g006
Figure 6. Applied loads and deflection relationships obtained from FEM simulation. (a) With vertical at 2.0 m and without horizontal stiffeners; (b) With horizontal stiffeners at 20%; (c) With horizontal stiffeners at 50%; (d) With horizontal stiffeners at 10% + 90%.
Figure 6. Applied loads and deflection relationships obtained from FEM simulation. (a) With vertical at 2.0 m and without horizontal stiffeners; (b) With horizontal stiffeners at 20%; (c) With horizontal stiffeners at 50%; (d) With horizontal stiffeners at 10% + 90%.
Buildings 15 04385 g006
Buildings 15 04385 g007aBuildings 15 04385 g007b
Figure 7. Applied loads and deflection relationships for horizontal stiffeners’ locations. (a) Beam without eccentricity; (b) With eccentricity = 250 mm; (c) With eccentricity = 500 mm; (d) With eccentricity = 750 mm; (e) With eccentricity = 1000 mm.
Figure 7. Applied loads and deflection relationships for horizontal stiffeners’ locations. (a) Beam without eccentricity; (b) With eccentricity = 250 mm; (c) With eccentricity = 500 mm; (d) With eccentricity = 750 mm; (e) With eccentricity = 1000 mm.
Buildings 15 04385 g007aBuildings 15 04385 g007b
Buildings 15 04385 g008aBuildings 15 04385 g008b
Figure 8. Applied loads and deflection relationships for horizontal stiffeners’ width. (a) Beam without eccentricity; (b) With eccentricity = 250 mm; (c) With eccentricity = 500 mm; (d) With eccentricity = 750 mm; (e) With eccentricity = 1000 mm.
Figure 8. Applied loads and deflection relationships for horizontal stiffeners’ width. (a) Beam without eccentricity; (b) With eccentricity = 250 mm; (c) With eccentricity = 500 mm; (d) With eccentricity = 750 mm; (e) With eccentricity = 1000 mm.
Buildings 15 04385 g008aBuildings 15 04385 g008b
Buildings 15 04385 g009
Figure 9. Deformations and stress distributions resulting from FEM simulations. (a) With a vertical at 2.0 m and without horizontal stiffeners; (b) With horizontal stiffeners at 20%; (c) With horizontal stiffeners at 90%; (d) With horizontal stiffeners at 10% and 90%.
Figure 9. Deformations and stress distributions resulting from FEM simulations. (a) With a vertical at 2.0 m and without horizontal stiffeners; (b) With horizontal stiffeners at 20%; (c) With horizontal stiffeners at 90%; (d) With horizontal stiffeners at 10% and 90%.
Buildings 15 04385 g009
Buildings 15 04385 g010
Figure 10. Applied loads and lateral displacement relationships obtained from FEM simulation. (a) With a vertical at 2.0 m and without horizontal stiffeners; (b) With horizontal stiffeners at 20%.
Figure 10. Applied loads and lateral displacement relationships obtained from FEM simulation. (a) With a vertical at 2.0 m and without horizontal stiffeners; (b) With horizontal stiffeners at 20%.
Buildings 15 04385 g010
Buildings 15 04385 g011
Figure 11. Applied loads and lateral displacement relationships for horizontal stiffeners’ locations for beam without eccentricity.
Figure 11. Applied loads and lateral displacement relationships for horizontal stiffeners’ locations for beam without eccentricity.
Buildings 15 04385 g011
Buildings 15 04385 g012aBuildings 15 04385 g012bBuildings 15 04385 g012c
Figure 12. Load and lateral displacement relationships for horizontal stiffeners’ locations. (a) With eccentricity = 250 mm; (b) With eccentricity = 500 mm; (c) With eccentricity = 750 mm; (d) With eccentricity = 1000 mm.
Figure 12. Load and lateral displacement relationships for horizontal stiffeners’ locations. (a) With eccentricity = 250 mm; (b) With eccentricity = 500 mm; (c) With eccentricity = 750 mm; (d) With eccentricity = 1000 mm.
Buildings 15 04385 g012aBuildings 15 04385 g012bBuildings 15 04385 g012c
Buildings 15 04385 g013aBuildings 15 04385 g013b
Figure 13. Load and lateral displacement relationships for horizontal stiffeners’ width. (a) Beam without eccentricity; (b) With eccentricity = 250 mm; (c) With eccentricity = 1000 mm.
Figure 13. Load and lateral displacement relationships for horizontal stiffeners’ width. (a) Beam without eccentricity; (b) With eccentricity = 250 mm; (c) With eccentricity = 1000 mm.
Buildings 15 04385 g013aBuildings 15 04385 g013b
Buildings 15 04385 g014aBuildings 15 04385 g014b
Figure 14. Load and upper flange stress distribution relationships obtained from FEM simulation. (a) With a vertical at 2.0 m and without horizontal stiffeners; (b) With horizontal stiffeners at 20%.
Figure 14. Load and upper flange stress distribution relationships obtained from FEM simulation. (a) With a vertical at 2.0 m and without horizontal stiffeners; (b) With horizontal stiffeners at 20%.
Buildings 15 04385 g014aBuildings 15 04385 g014b
Buildings 15 04385 g015
Figure 15. Load and upper flange stress distribution relationships for horizontal stiffeners’ locations for a beam without eccentricity.
Figure 15. Load and upper flange stress distribution relationships for horizontal stiffeners’ locations for a beam without eccentricity.
Buildings 15 04385 g015
Buildings 15 04385 g016aBuildings 15 04385 g016b
Figure 16. Load and upper flange stress distribution relationships for horizontal stiffeners’ locations. (a) With eccentricity = 250 mm; (b) With eccentricity = 500 mm; (c) With eccentricity = 750 mm; (d) With eccentricity = 1000 mm.
Figure 16. Load and upper flange stress distribution relationships for horizontal stiffeners’ locations. (a) With eccentricity = 250 mm; (b) With eccentricity = 500 mm; (c) With eccentricity = 750 mm; (d) With eccentricity = 1000 mm.
Buildings 15 04385 g016aBuildings 15 04385 g016b
Buildings 15 04385 g017
Figure 17. Load and upper flange stress distribution relationships for horizontal stiffeners’ width. (a) Beam without eccentricity; (b) With eccentricity = 250 mm.
Figure 17. Load and upper flange stress distribution relationships for horizontal stiffeners’ width. (a) Beam without eccentricity; (b) With eccentricity = 250 mm.
Buildings 15 04385 g017
Buildings 15 04385 g018
Figure 18. The effect of eccentricity distance and horizontal stiffeners on the ratio between loads that cause the onset of tensile and compressive to yield stress at the edges of the upper flange.
Figure 18. The effect of eccentricity distance and horizontal stiffeners on the ratio between loads that cause the onset of tensile and compressive to yield stress at the edges of the upper flange.
Buildings 15 04385 g018
Buildings 15 04385 g019
Figure 19. Load and bottom flange stress distribution relationships obtained from FEM simulation. (a) With a vertical at 2.0 m and without horizontal stiffeners; (b) With horizontal stiffeners at 20%.
Figure 19. Load and bottom flange stress distribution relationships obtained from FEM simulation. (a) With a vertical at 2.0 m and without horizontal stiffeners; (b) With horizontal stiffeners at 20%.
Buildings 15 04385 g019
Buildings 15 04385 g020
Figure 20. Load and bottom flange stress distribution relationships for horizontal stiffeners’ locations for a beam without eccentricity.
Figure 20. Load and bottom flange stress distribution relationships for horizontal stiffeners’ locations for a beam without eccentricity.
Buildings 15 04385 g020
Buildings 15 04385 g021aBuildings 15 04385 g021b
Figure 21. Load and bottom flange stress distribution relationships for horizontal stiffeners’ locations. (a) With eccentricity = 250 mm; (b) With eccentricity = 500 mm; (c) With eccentricity = 750 mm; (d) With eccentricity = 1000 mm.
Figure 21. Load and bottom flange stress distribution relationships for horizontal stiffeners’ locations. (a) With eccentricity = 250 mm; (b) With eccentricity = 500 mm; (c) With eccentricity = 750 mm; (d) With eccentricity = 1000 mm.
Buildings 15 04385 g021aBuildings 15 04385 g021b
Buildings 15 04385 g022
Figure 22. Load and bottom flange stress distribution relationships for horizontal stiffeners’ width. (a) Beam without eccentricity; (b) With eccentricity = 1000 mm.
Figure 22. Load and bottom flange stress distribution relationships for horizontal stiffeners’ width. (a) Beam without eccentricity; (b) With eccentricity = 1000 mm.
Buildings 15 04385 g022
Buildings 15 04385 g023
Figure 23. The effect of eccentric distance and horizontal stiffeners on the ratio between loads that cause the onset of compressive and tensile to yield stress at the edges of the lower flange.
Figure 23. The effect of eccentric distance and horizontal stiffeners on the ratio between loads that cause the onset of compressive and tensile to yield stress at the edges of the lower flange.
Buildings 15 04385 g023
Buildings 15 04385 g024
Figure 24. The relationship between the ultimate load capacity ratios of beams with and without horizontal stiffeners under: (a) Effect of horizontal stiffener positions; (b) Effect of the horizontal stiffeners’ width; (c) Beam with vertical stiffeners only, and beam with horizontal stiffeners in both halves of the web.
Figure 24. The relationship between the ultimate load capacity ratios of beams with and without horizontal stiffeners under: (a) Effect of horizontal stiffener positions; (b) Effect of the horizontal stiffeners’ width; (c) Beam with vertical stiffeners only, and beam with horizontal stiffeners in both halves of the web.
Buildings 15 04385 g024
Buildings 15 04385 g025
Figure 25. The relationship between the ratio of bending and torsional moments for beams with horizontal stiffeners compared to beams without stiffeners under eccentric loads (Interaction Diagram).
Figure 25. The relationship between the ratio of bending and torsional moments for beams with horizontal stiffeners compared to beams without stiffeners under eccentric loads (Interaction Diagram).
Buildings 15 04385 g025
Table 1. The stress and the corresponding strain for steel applied to the FEM simulation [63].
Table 1. The stress and the corresponding strain for steel applied to the FEM simulation [63].
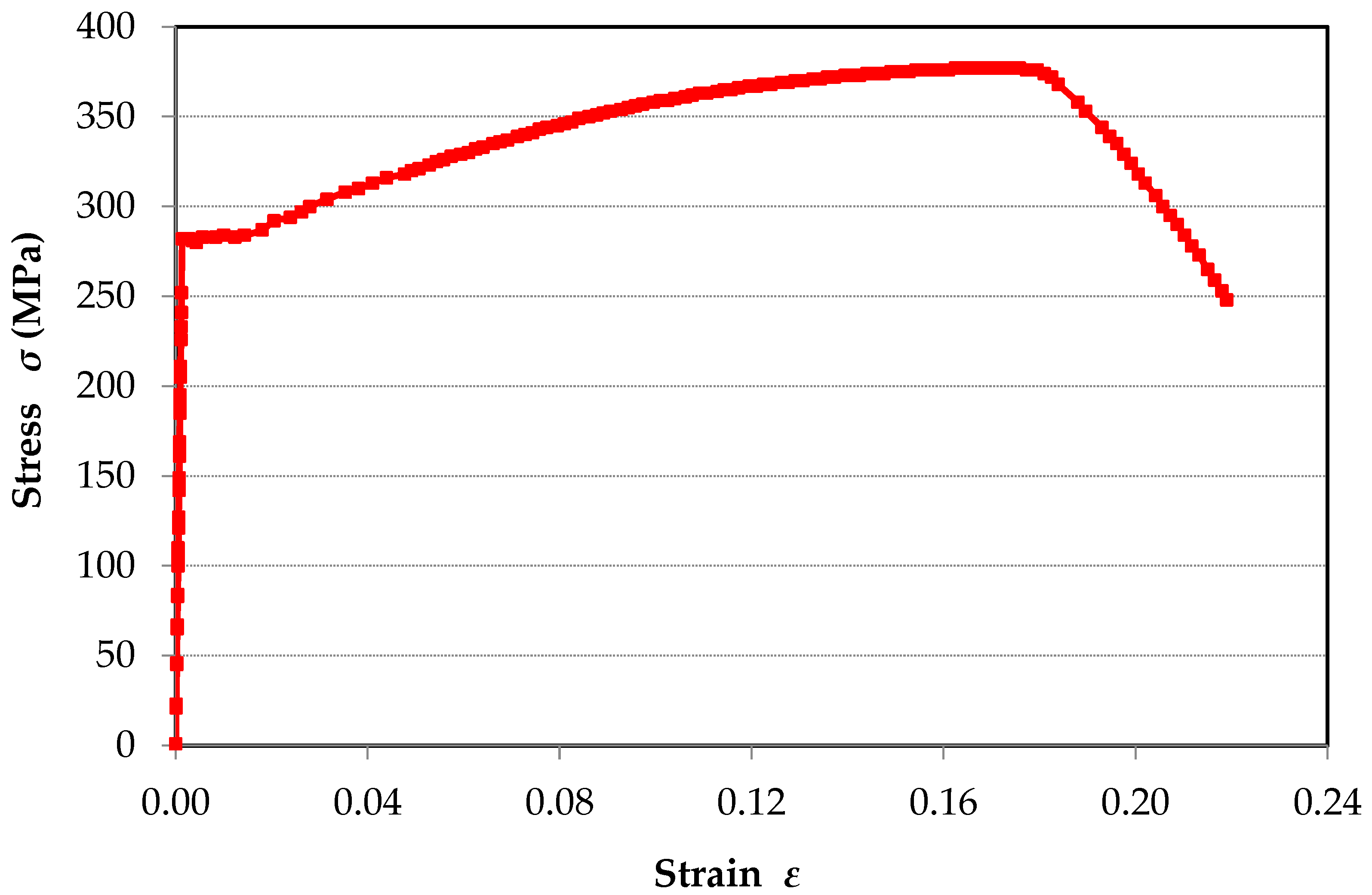
Stress (MPa)282301347369377339299
Strain0.001340.02790.08250.12620.17950.19460.2057
Table 2. Summary of previous studies on steel beams used to verify FEM simulation results.
Table 2. Summary of previous studies on steel beams used to verify FEM simulation results.
FE Model Based onBeam
Specimens		Steel Beam Dimensionsfyw
(MPa)		fyf
(MPa)
L
(mm)		a
(mm)		dw
(mm)		tw
(mm)		bf
(mm)		tf
(mm)
Xiong et al. [64]C150002500249.269.01180.1710.48541.0525.0
C260003000247.749.00179.1910.49541.0525.0
C350002500431.038.79179.1510.47541.0525.0
Saliba and Gardner [65]I-600×200×12×10-11360600599.210.2200.112.4433.0484.0
I-600×200×12×8-225601200600.08.4199.812.3431.0484.0
I-600×200×12×10-225601200600.110.6200.412.6433.0484.0
I-600×200×12×15-225601200599.015.0200.115.3564.0484.0
Yang et al. [66]Y1-335001500373.269.57178.9813.59781.0769.0
Y2-335001500372.449.63197.4713.63781.0769.0
Y6-335001500323.949.65201.4613.50781.0769.0
Y8-335001500319.159.64159.9516.10781.0754.0
Y9-335001500370.119.90159.1516.26781.0754.0
Y10-335001500369.959.81177.8116.03781.0754.0
Y12-440001200320.199.50177.4016.38781.0754.0
Y13-440001200368.89.68159.3416.35781.0754.0
Y14-440001200368.329.51182.3616.11781.0754.0
Shokouhian and Shi [67]C133991000357.47.87169.011.91442.8408.2
C234011000358.487.82263.611.85442.8408.2
Beg and Hladnik [68]B150001800222.7010.40271.0012.40775797.0
C150001800221.3010.40251.0012.60775776.0
D150001800220.9010.40220.8012.40830873.0
E150001800220.7010.40198.8012.60830797.0
Shi et al. [69]I-460-134001000520.911.96167.813.87510.5557.0
I-460-234001000610.812.08260.113.94510.5557.0
I-890-32000600661.06.17166.56.35886.0886.0
Table 3. Details of the variables in the steel beams created in this study by FEA simulation.
Table 3. Details of the variables in the steel beams created in this study by FEA simulation.
Beam
Specimens		Horizontal StiffenersVertical Stiffeners at Distance, (mm)Cases of Eccentricity Distance, (mm)
Width
bhs (mm)		Location
dhs (mm)		12345
Without-V@2m--20000.002505007501000
H@10%-V@2m19510% = 15020000.002505007501000
H@20%-V@2m19520% = 30020000.002505007501000
H@30%-V@2m19530% = 45020000.002505007501000
H@40%-V@2m19540% = 60020000.002505007501000
H@50%-V@2m19550% = 75020000.002505007501000
H@60%-V@2m19560% = 90020000.002505007501000
H@70%-V@2m19570% = 105020000.002505007501000
H@80%-V@2m19580% = 120020000.002505007501000
H@90%-V@2m19590% = 135020000.002505007501000
H@10%+90%-V@2m19510% = 150 and 90% = 135020000.002505007501000
H@20%-b=16cm-V@2m16020% = 30020000.002505007501000
H@20%-b=12cm-V@2m12020% = 30020000.002505007501000
Without-V@1m--10000.002505007501000
Table 4. Comparing the FEM simulation results with the experimental test results for steel beams from previous studies.
Table 4. Comparing the FEM simulation results with the experimental test results for steel beams from previous studies.
FE Model Based onBeam
Specimens		Mu.Exp
(kN.m)		FEM Results
Mu.FEM (kN.m)Mu.FEM /Mu.Exp
Xiong et al. [64]C1335.30344.881.029
C2326.39324.120.993
C5634.68631.400.995
Saliba and Gardner [65]I-600×200×12×10-11102.801126.051.021
I-600×200×12×8-21172.001184.331.011
I-600×200×12×10-21395.001380.120.989
I-600×200×12×15-22162.002139.760.990
Yang et al. [66]Y1-31012.231037.911.025
Y2-31117.221149.061.028
Y6-3962.23957.550.995
Y8-3955.01964.441.010
Y9-31158.331191.081.028
Y10-31230.551251.791.017
Y12-41065.001034.810.972
Y13-41184.361179.610.996
Y14-41274.401290.051.012
Shokouhian and Shi [67]C1447.91455.661.017
C2616.70613.080.994
Beg and Hladnik [68]B1703.80724.611.030
C1646.20640.700.991
D1644.40638.660.991
E1559.80567.001.013
Shi et al. [69]I-460-11225.401220.710.996
I-460-21999.702029.061.015
I-890-3797.10804.001.009
Table 5. Summary of FEM analysis results for steel beams with and without horizontal stiffeners.
Table 5. Summary of FEM analysis results for steel beams with and without horizontal stiffeners.
Beam SpecimensThe Case Study of the Eccentricity Measured from the Center Line of the Beam
Eccentricity
= 0.00		Eccentricity
= 0.25 m		Eccentricity
= 0.50 m		Eccentricity
= 0.75 m		Eccentricity
= 1.00 m
Pu (kN)Pu/Pu.woPu (kN)Pu/Pu.woPu (kN)Pu/Pu.woPu (kN)Pu/Pu.woPu (kN)Pu/Pu.wo
Without-V@2m3480.751.001662.081.001120.681.00832.881.00785.421.00
H@10%-V@2m3748.501.083148.501.891847.111.651221.961.471040.021.32
H@20%-V@2m3672.001.052919.551.761748.761.561190.801.431014.431.29
H@30%-V@2m3604.301.042634.221.581629.881.451130.081.36955.001.22
H@40%-V@2m3542.501.022300.911.381447.011.291003.951.21904.271.15
H@50%-V@2m3495.021.002017.001.211316.401.17940.881.13860.371.10
H@60%-V@2m3510.331.012083.441.251349.041.20974.641.17880.711.12
H@70%-V@2m3579.001.032328.991.401492.321.331008.451.21913.931.16
H@80%-V@2m3630.611.042541.051.531584.981.411068.551.28917.081.17
H@90%-V@2m3715.021.072706.821.631657.001.481100.891.32937.521.19
H@10%+90%-V@2m4102.201.183449.332.081977.651.761304.081.571106.171.41
H@20%-b=16cm-V@2m3637.801.052789.261.681660.561.481128.631.36987.451.26
H@20%-b=12cm-V@2m3560.401.022582.741.551547.631.381071.911.29921.941.17
Without-V@1m3766.001.082855.201.721781.101.591196.501.441001.881.28
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Aljarbou, M.H.; Sayed, A.M. Effect of Horizontal Stiffeners on the Efficiency of Steel Beams in Resisting Bending and Torsional Moments: Finite Element Analysis. Buildings 2025, 15, 4385. https://doi.org/10.3390/buildings15234385

AMA Style

Aljarbou MH, Sayed AM. Effect of Horizontal Stiffeners on the Efficiency of Steel Beams in Resisting Bending and Torsional Moments: Finite Element Analysis. Buildings. 2025; 15(23):4385. https://doi.org/10.3390/buildings15234385

Chicago/Turabian Style

Aljarbou, Mishal H., and Ahmed M. Sayed. 2025. "Effect of Horizontal Stiffeners on the Efficiency of Steel Beams in Resisting Bending and Torsional Moments: Finite Element Analysis" Buildings 15, no. 23: 4385. https://doi.org/10.3390/buildings15234385

APA Style

Aljarbou, M. H., & Sayed, A. M. (2025). Effect of Horizontal Stiffeners on the Efficiency of Steel Beams in Resisting Bending and Torsional Moments: Finite Element Analysis. Buildings, 15(23), 4385. https://doi.org/10.3390/buildings15234385

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop