Statistical Analysis of Factors Influencing Segmental Joint Opening in a Soft Soil Tunnel
Abstract
1. Introduction
- (1)
- To provide a set of field monitoring data for soil pressure, water pressure, axial force, and reinforcement stress at Ring 30 of the engineering liaison passage.
- (2)
- To systematically investigate the influence of key parameters—including earth pressure, water pressure, axial force, and reinforcement stress—on longitudinal joint deformation using multivariate linear regression analysis in conjunction with field monitoring data. This ultimately aims to derive a computational expression for the opening degree of tunnel segments’ longitudinal joints at the same location under soft soil conditions.
- (3)
- Based on field monitoring and multivariate regression analysis, to provide theoretical support and technical reference for structural safety control in similar projects by identifying factors influencing the opening of longitudinal joints in segmental construction of cross-passages in soft soil strata.
2. Engineering Background and Monitoring Scheme
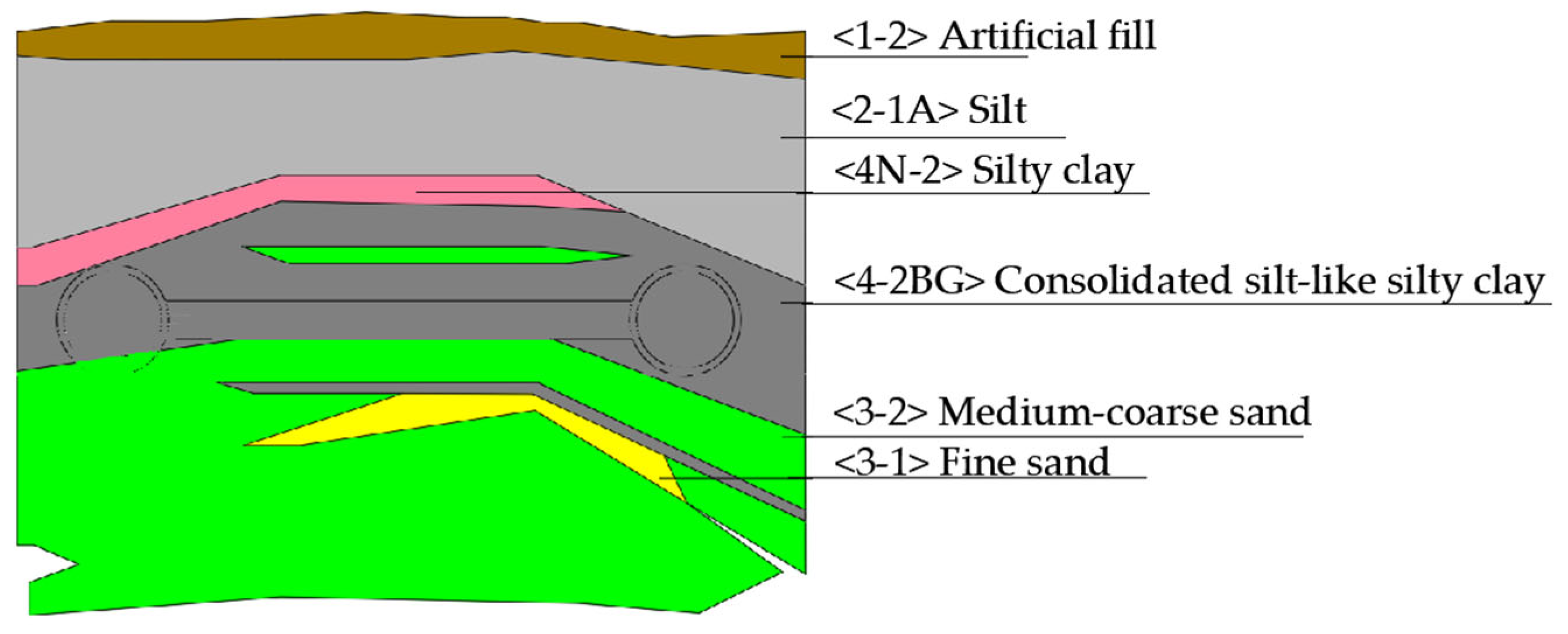
2.1. Project Overview
2.2. Monitoring Plan
2.2.1. Monitoring Content
- (1)
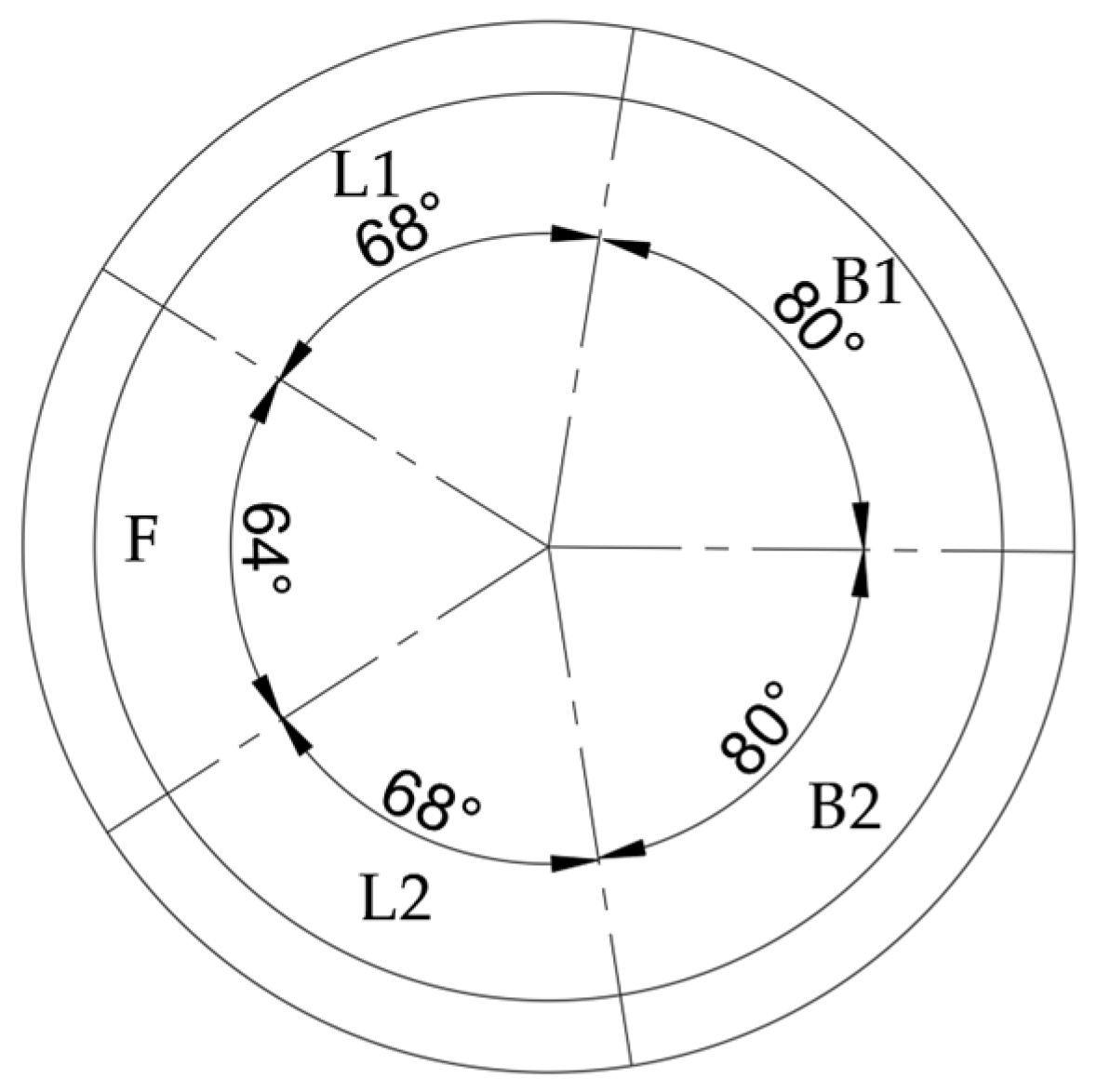
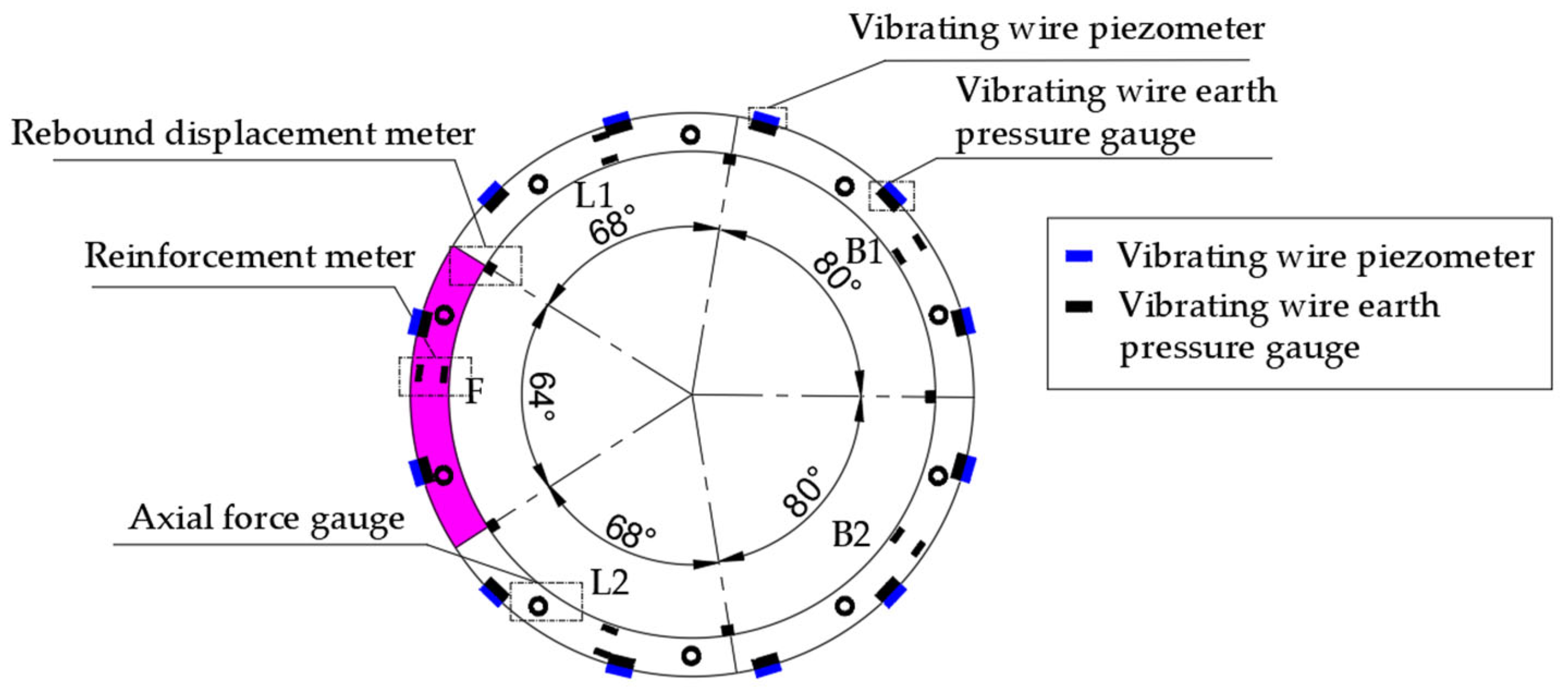
- Symmetric coverage: The shield tunnel segments are axisymmetric structures, and theoretically, the load distribution is symmetrical. By arranging 12 measurement points at 30° intervals, the overall load pattern can be captured while also effectively identifying asymmetric conditions such as actual eccentric loading.
- (2)
- Key section control: The measurement points are laid out to cover mechanically sensitive areas such as the crown, haunch, and invert, ensuring effective monitoring of maximum internal forces and deformations.
- (3)
- Model robustness assurance: The data from 12 measurement points provide enough dimensionality to meet the basic requirements of regression analysis while avoiding the complexity issues caused by too many variables, ensuring the reliability of the results of the analysis.
- (1)
- Earth pressure
- (2)
- Water pressure
- (3)
- Axial force
- (4)
- Reinforcement stress
- (5)
- Longitudinal joint opening amount
- (6)
- Sensor protection
2.2.2. Monitoring Results
3. Multivariate Regression Analysis Based on SPSS
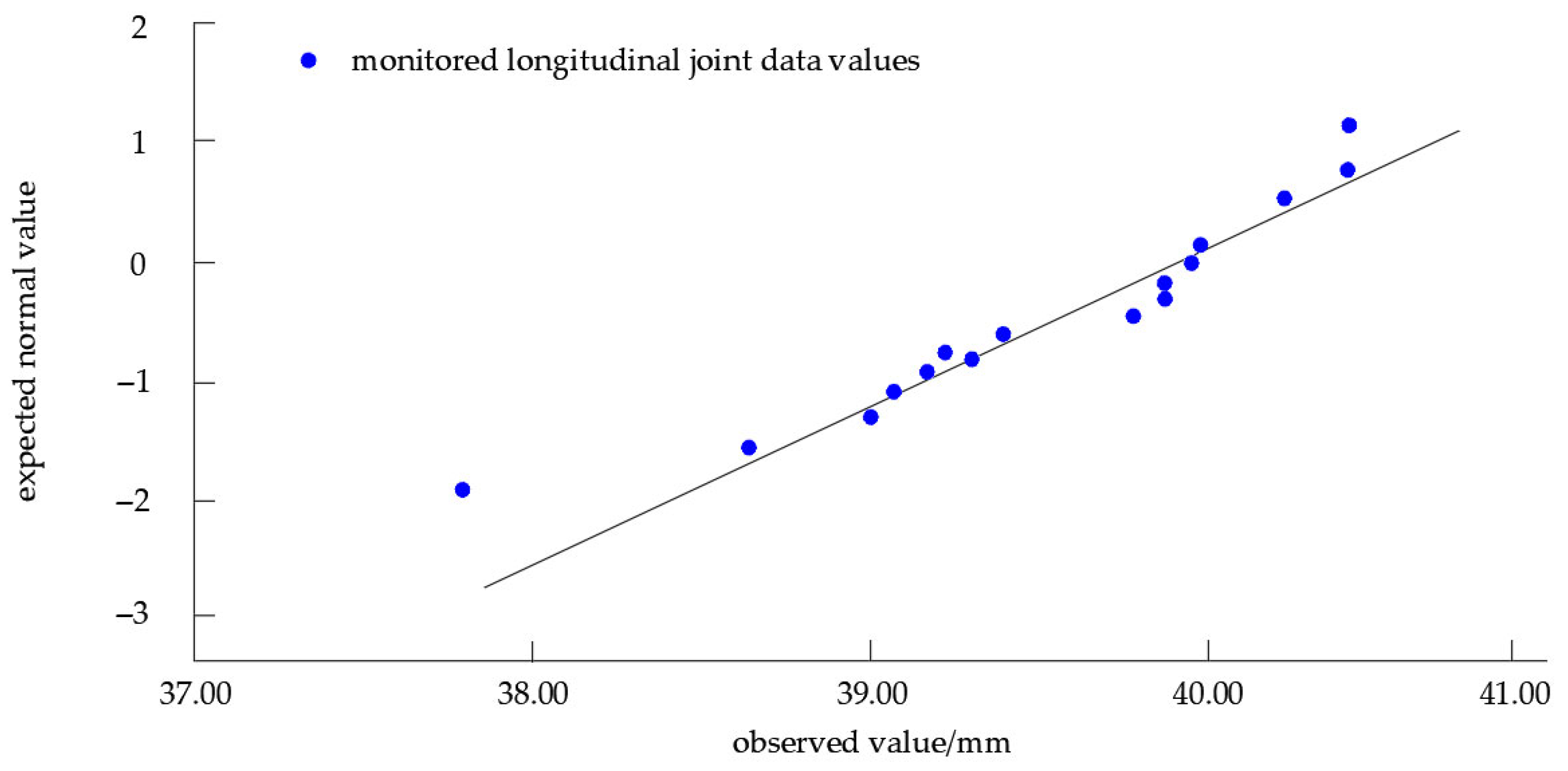
3.1. Normality Test
3.2. Stepwise Linear Regression Analysis
3.2.1. Procedure of Stepwise Linear Regression Analysis
- (1)
- Data preparation. Import the data into SPSS, ensuring each variable is in a separate column and each observation is in a separate row. Confirm the measurement scale is correctly set in the Variable View: continuous for continuous variables, ordinal for ordinal, and nominal for categorical. The data in this paper are continuous variables, so select Scale.
- (2)
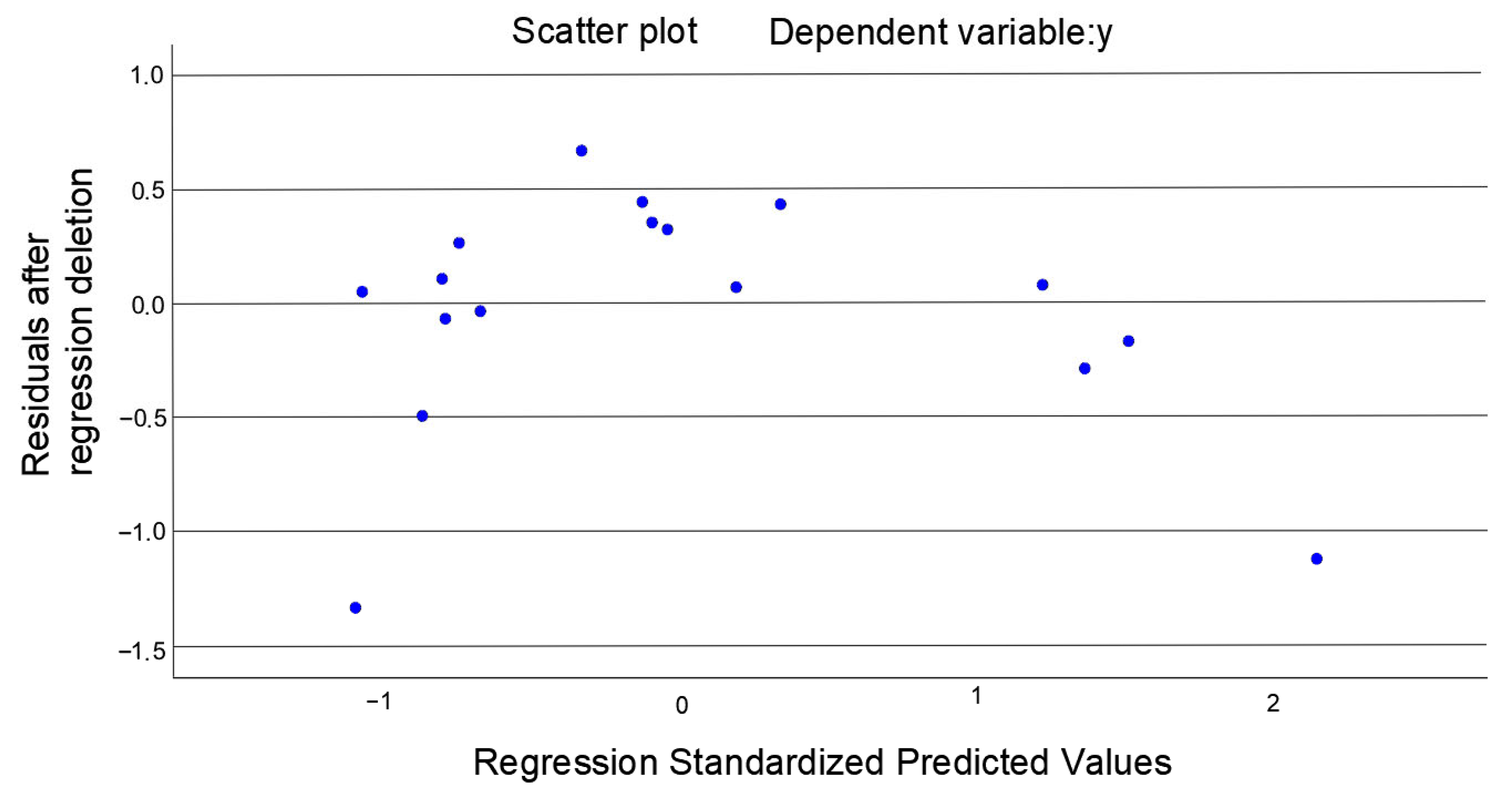
- Preliminary analysis. Preliminary analysis of residual linearity, error independence, and homoscedasticity. The Durbin–Watson statistic is 2.2, indicating good independence of residuals. The scatter plot of standardized residuals is uniformly distributed around the origin, confirming good homoscedasticity. Run descriptive statistics by selecting Analyze, Descriptive Statistics, and Frequency. Review the mean and standard deviation, and check for outliers. Run correlation analysis by selecting Analyze, Correlation, and Bivariate. Initially examine the correlations between the independent variables and the dependent variable, as well as among the independent variables themselves. Be alert to highly correlated independent variables, which indicate potential multicollinearity.
- (3)
- Variable and method selection. Select Analyze, Regression, and Linear. Place the vertical joint opening into the Dependent Variable box and select earth pressure, water pressure, axial force, and reinforcement stress in the Independent Variable box. Allow SPSS to automatically screen variables based on the statistical significance of the F-value.
- (4)
- Select required statistics. Choose to output regression coefficients B, standard errors, significance levels, R, R2, variance inflation factors, and other relevant statistics.
- (5)
- Run the multiple regression analysis.
3.2.2. Results and Analysis of Stepwise Linear Regression
4. Conclusions
- (1)
- The influence of internal forces within the segment on longitudinal joint opening is relatively minor. Within the context of the regression model developed for this specific dataset, external pressure variables were found to be statistically more significant predictors of longitudinal joint opening than measured internal force variables. Specifically, longitudinal joint opening increases with rising water pressure and decreases with increasing earth pressure. Although the statistical method excluded the significance of axial force, this contradicts engineering intuition. Analysis suggests that the result is more likely due to data characteristics or modeling limitations: during construction, axial force is affected by transient factors, resulting in noisy data and high correlation with external loads, which leads the model to prioritize more stable proxy variables. This finding indicates that the mechanical importance of axial force is not negated, but caution is required when interpreting data-driven models due to construction disturbances.
- (2)
- A stepwise linear regression analysis method was adopted, resulting in a linear regression equation for water pressure and earth pressure as , with a coefficient of determination R2; of 0.697. The error is 30.3%.
- (3)
- By fitting the monitoring data and predicted data for the 30th ring segment, the model demonstrated excellent agreement with the monitoring data. This research outcome provides a case-specific reference for structural safety control in analogous geological and construction conditions, though its generalizability requires further validation with long-term multi-ring data.
- (4)
- This study has certain limitations. The analysis primarily relies on data from a single monitoring ring during a specific construction phase, potentially failing to fully capture the complex nonlinear relationships and multi-factor interactions between water and soil pressures and structural responses in shield tunnels. These factors may affect the model’s universality and predictive accuracy under broader geological conditions or different construction scenarios. Future research should focus on establishing a large-scale, standardized database covering diverse geological conditions and the entire construction cycle. Building upon this foundation, actively incorporating nonlinear models or machine learning algorithms could enable more precise characterization of the complex mechanisms governing longitudinal joint opening.
- (5)
- It must be acknowledged that two-dimensional regression models based on single-ring data have inherent limitations in capturing the complex three-dimensional mechanical behavior of intersecting channels (such as longitudinal bending and inter-ring load transfer). Subsequent work will introduce three-dimensional numerical analysis and multi-ring synchronous monitoring to reveal its spatial mechanical mechanisms.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Pearson Coefficient | |||||||||||||||||
| TY-01 | TY-02 | SY-01 | SY-02 | ZL-01 | ZL-02 | ZL-03 | ZL-04 | YL-01 | YL-02 | YL-03 | YL-04 | YL-05 | YL-06 | YL-07 | YL-08 | y | |
| TY-01 | 1 | 0.683 ** | 0.419 | 0.526 * | −0.185 | 0.107 | 0.384 | −0.052 | 0.401 | 0.37 | 0.254 | 0.03 | 0.066 | 0.487 * | 0.640 ** | 0.316 | −0.038 |
| TY-02 | 0.683 ** | 1 | 0.119 | 0.199 | −0.585 * | 0.203 | 0.294 | 0.123 | 0.619 ** | 0.730 ** | 0.694 ** | 0.099 | −0.014 | 0.834 ** | 0.791 ** | 0.621 ** | −0.725 |
| SY-01 | 0.419 | 0.119 | 1 | 0.982 ** | 0.609 ** | 0.047 | 0.015 | −0.101 | −0.293 | −0.547 * | −0.607 ** | −0.056 | 0.549 * | −0.313 | 0.044 | −0.387 | 0.736 ** |
| SY-02 | 0.526 * | 0.199 | 0.982 ** | 1 | 0.512 * | 0.052 | 0.007 | −0.041 | −0.224 | −0.458 | −0.530 * | −0.094 | 0.504 * | −0.2 | 0.146 | −0.3 | 0.696 ** |
| ZL-01 | −0.185 | −0.585 * | 0.609 ** | 0.512 * | 1 | 0.14 | −0.176 | −0.079 | −0.469 | −0.860 ** | −0.888 ** | −0.235 | 0.261 | −0.764 ** | −0.512 * | −0.569 * | 0.598 * |
| ZL-02 | 0.107 | 0.203 | 0.047 | 0.052 | 0.14 | 1 | −0.054 | 0.405 | 0.477 | 0.1 | 0.104 | −0.581 * | −0.542 * | 0.276 | 0.326 | 0.482 | −0.202 |
| ZL-03 | 0.384 | 0.294 | 0.015 | 0.007 | −0.176 | −0.054 | 1 | −0.799 ** | 0.129 | 0.284 | 0.285 | 0.535 * | 0.103 | 0.206 | 0.052 | −0.024 | −0.097 |
| ZL-04 | −0.052 | 0.123 | −0.101 | −0.041 | −0.079 | 0.405 | −0.799 ** | 1 | 0.431 | 0.132 | 0.118 | −0.794 ** | −0.513 * | 0.292 | 0.423 | 0.557 * | −0.235 |
| YL-01 | 0.401 | 0.619 ** | −0.293 | −0.224 | −0.469 | 0.477 | 0.129 | 0.431 | 1 | 0.773 ** | 0.749 ** | −0.383 | −0.705 ** | 0.835 ** | 0.815 ** | 0.948 ** | −0.541 * |
| YL-02 | 0.37 | 0.730 ** | −0.547 * | −0.458 | −0.860 ** | 0.1 | 0.284 | 0.132 | 0.773 ** | 1 | 0.987 ** | 0.109 | −0.401 | 0.928 ** | 0.684 ** | 0.812 ** | −0.707 ** |
| YL-03 | 0.254 | 0.694 ** | −0.607 ** | −0.530 * | −0.888 ** | 0.104 | 0.285 | 0.118 | 0.749 ** | 0.987 ** | 1 | 0.125 | −0.425 | 0.907 ** | 0.632 ** | 0.796 ** | −0.710 ** |
| YL-04 | 0.03 | 0.099 | −0.056 | −0.094 | −0.235 | −0.581 * | 0.535 * | −0.794 ** | −0.383 | 0.109 | 0.125 | 1 | 0.662 ** | −0.094 | −0.282 | −0.454 | 0.053 |
| YL-05 | 0.066 | −0.014 | 0.549 * | 0.504 * | 0.261 | −0.542 * | 0.103 | −0.513 * | −0.705 ** | −0.401 | −0.425 | 0.662 ** | 1 | −0.424 | −0.38 | −0.719 ** | 0.532 * |
| YL-06 | 0.487 * | 0.834 ** | −0.313 | −0.2 | −0.764 ** | 0.276 | 0.206 | 0.292 | 0.835 ** | 0.928 ** | 0.907 ** | −0.094 | −0.424 | 1 | 0.845 ** | 0.890 ** | −0.557 * |
| YL-07 | 0.640 ** | 0.791 ** | 0.044 | 0.146 | −0.512 * | 0.326 | 0.052 | 0.423 | 0.815 ** | 0.684 ** | 0.632 ** | −0.282 | −0.38 | 0.845 ** | 1 | 0.814 ** | −0.251 |
| YL-08 | 0.316 | 0.621 ** | −0.387 | −0.3 | −0.569 * | 0.482 | −0.024 | 0.557 * | 0.948 ** | 0.812 ** | 0.796 ** | −0.454 | −0.719 ** | 0.890 ** | 0.814 ** | 1 | −0.599 * |
| y | −0.038 | −0.72 ** | 0.736 ** | 0.696 ** | 0.598 * | −0.202 | −0.097 | −0.235 | −0.541 * | −0.707 ** | −0.710 ** | 0.053 | 0.532 * | −0.557 * | −0.251 | −0.599 * | 1 |
| * denotes p < 0.05, and ** indicates p < 0.01. | |||||||||||||||||
References
- Yang, J.; Chen, W.-Z.; Li, M.; Tan, X.-J.; Yu, J.-X. Structural Health Monitoring and Response Pattern Analysis of Underwater Shield Tunnels During Operation. J. Rock Mech. Eng. 2021, 40, 902–915. [Google Scholar]
- Wang, R. Analysis of Deformation Factors and Characteristics in Shanghai’s Soft Soil Subway Tunnels. Undergr. Eng. Tunneling 2009, 7, 1–6+52. [Google Scholar]
- Han, S. Analysis of Causes and Countermeasures for Cracking in Shield Tunnel Segments. West. Explor. Eng. 2010, 22, 151–153. [Google Scholar]
- Hong, W.; Wang, F. Unified Phase-Field Simulation and Toughness Evaluation of Crack Damage Evolution in Shield Tunnels Through Saturated Soft Soil. J. Geotech. Eng. 2025, 40, 1–10. [Google Scholar]
- Zhang, W.; Yang, Q.; Li, Y.; Dong, Z.; Wang, X. Design and mechanical properties of special segment structure in mechanical connecting aisle. Structures 2024, 64, 106589. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, Y.; Zhang, S.; Gao, Y. Risk analysis of mechanical cross-passage construction using work breakdown and fault tree. Proc. Inst. Civ. Eng. Forensic Eng. 2025, 178, 8–17. [Google Scholar] [CrossRef]
- Wang, X.; Chen, C. Vibration Table Test of Prefabricated L-Shaped Column Concrete Structure. Buildings 2025, 15, 2329. [Google Scholar] [CrossRef]
- Chen, P.; Geng, P.; Chen, C. A Study on the Mechanical Model of Shield Tunnel Segment Joints Considering Joint Positive Contact Nonlinearity. Acta Civilia Ingeniae Sin. 2021, 54, 87–97. [Google Scholar]
- Sun, F.; Li, W.; Li, C. Relationship between Longitudinal joint Opening and Convergence Deformation in Cross-River Shield Tunnels. J. Undergr. Space Eng. 2023, 19, 309–318. [Google Scholar]
- Xu, C.; Wang, S.; Xia, C.; Liu, L.; Ma, Z.; Yang, J. Viscoelastic plastic interaction of tunnel support and strain-softening rock mass considering longitudinal effect. Rock Mech. Bull. 2024, 3, 100152. [Google Scholar] [CrossRef]
- Xu, C.; Wang, S.; Xia, C. Analytical prediction for time-dependent interaction of a circular tunnel excavated in strain-softening rock mass. Rock Mech. Bull. 2024, 3, 100127. [Google Scholar] [CrossRef]
- Xu, C.; Xia, C. A new large strain approach for predicting tunnel deformation in strain-softening rock mass based on the generalized Zhang-Zhu strength criterion. Int. J. Rock Mech. Min. Sci. 2021, 143, 104786. [Google Scholar] [CrossRef]
- Zhang, B. Monitoring and Analysis of Stress Characteristics in Large-Diameter Shield Tunnel Segments Crossing Rivers. Railw. Constr. Technol. 2022, 184–188. [Google Scholar]
- Mu, H.; Kun, F.; Guo, W. Study on Structural Mechanical Behavior and Failure Characteristics of Segments in Ultra-Large-Diameter Shield Tunnels. Mod. Tunn. Technol. 2025, 62, 125–134. [Google Scholar]
- Sun, F. Analysis of Causes and Prevention Measures for Segment Misalignment in Shield Construction. Sichuan Cem. 2018, 294. [Google Scholar]
- Ni, Z.; Wang, S.; Hang, S. Influence of Upper Shield Tunneling in Water-Rich Gravel Formations on the Mechanical State of Lower Segments in Diagonally Parallel Tunnels. J. Cent. South Univ. (Nat. Sci. Ed.) 2022, 53, 2996–3007. [Google Scholar]
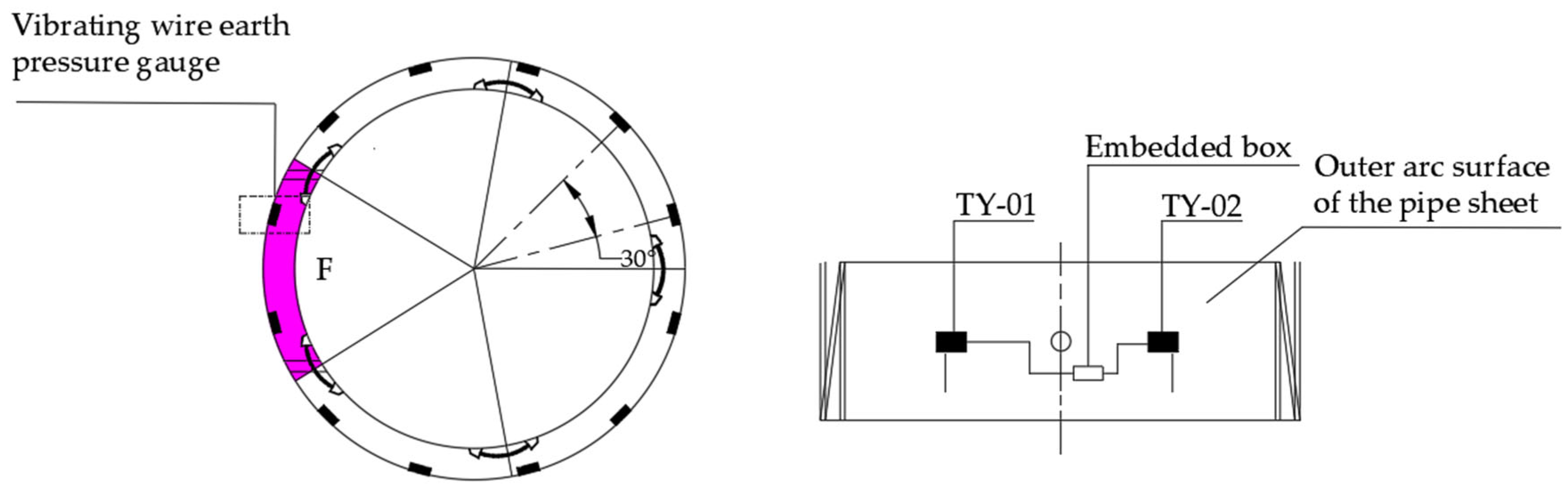

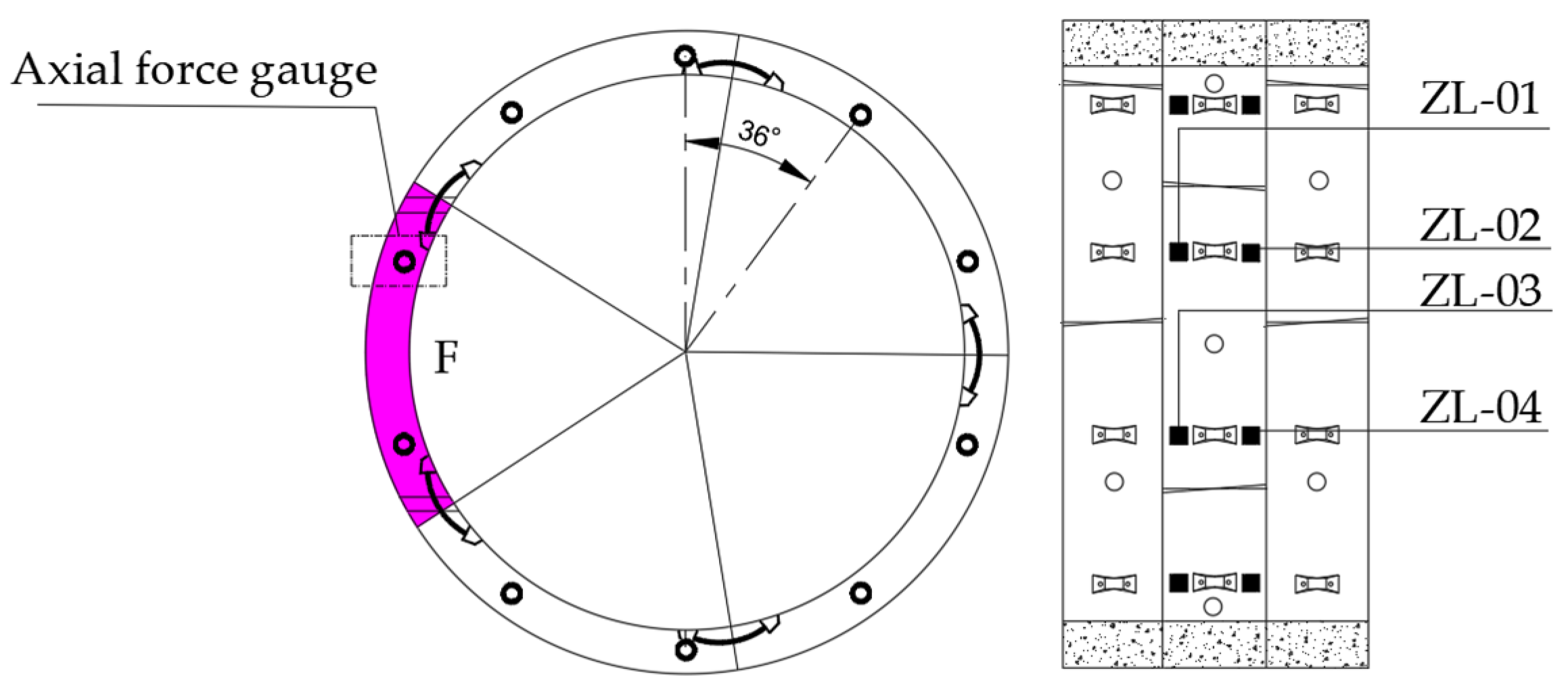
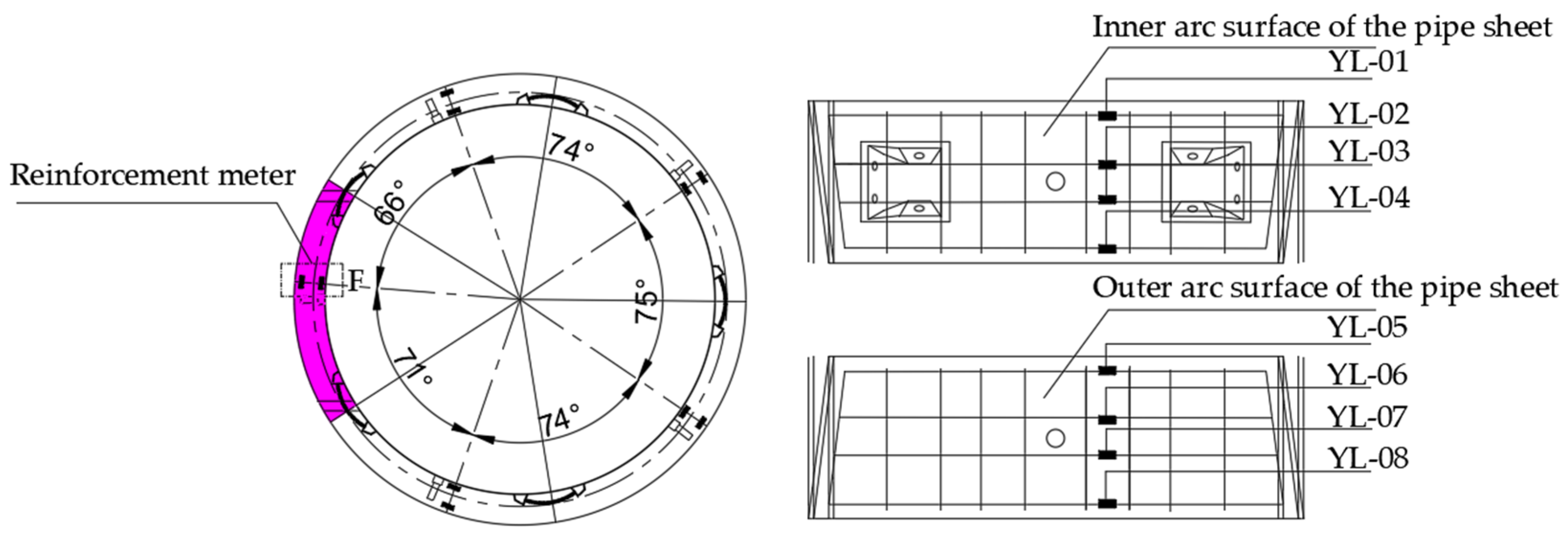
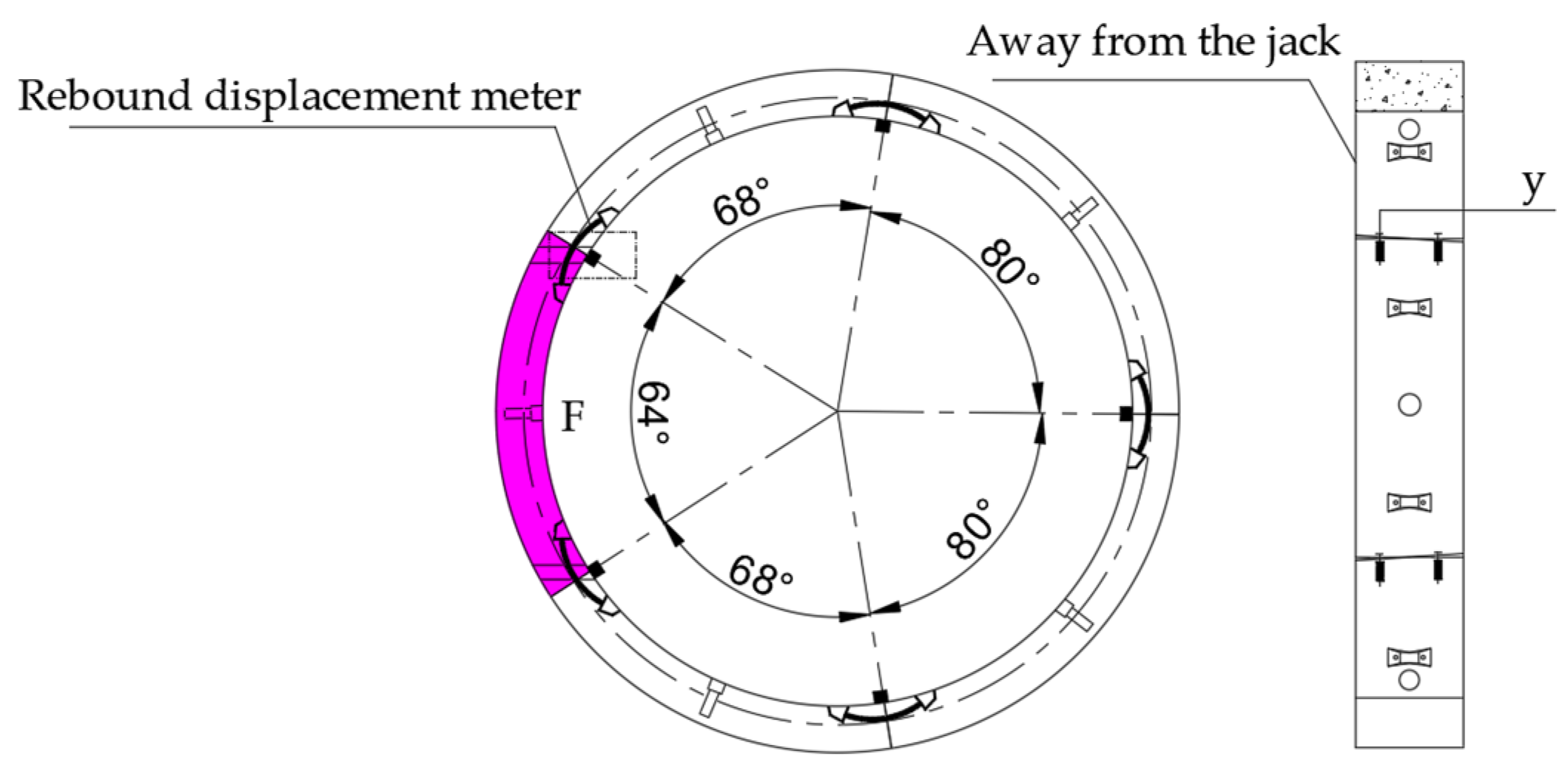

| Serial Number | Monitoring Parameters | Sensor Name | Model | Range | Resolution |
|---|---|---|---|---|---|
| 1 | Earth pressure | Vibrating wire soil pressure gauge | Gn-TY0106A | 0~1.6 (MPa) | <0.05 F.S. |
| 2 | Water pressure | Vibrating wire piezometer | Gn-SY0206 | 0~1.0 (MPa) | <0.05 F·S |
| 3 | Axial force | Axial force gauge | YBY-M | 0~500 (kN) | |
| 4 | Reinforcement stress | Vibrating wire rebar gauge | HD-GJ1040 | <800 (MPa) | <0.05 F·S |
| 5 | Longitudinal joint opening amount | Rebound displacement gauge | ATR-C | ±50 mm | ±0.1 mm |
| Date (yyyy-mm-dd) | Earth Pressure (MPa) | Water Pressure (MPa) | Axial Force Monitoring Results (KN) | |||||
|---|---|---|---|---|---|---|---|---|
| TY-01 | TY-02 | SY-01 | SY-02 | ZL-01 | ZL-02 | ZL-03 | ZL-04 | |
| 2024-10-02 | 265.74 | 269.69 | 203.85 | 203.20 | 90.21 | 16.23 | 2.32 | 47.70 |
| 2024-10-03 | 271.89 | 268.46 | 205.67 | 203.28 | 89.78 | 15.89 | 7.82 | 34.90 |
| 2024-10-04 | 269.53 | 270.36 | 201.56 | 197.04 | 89.61 | 16.06 | 7.48 | 34.11 |
| 2024-10-06 | 289.88 | 302.21 | 242.94 | 236.96 | 86.40 | 14.18 | 7.65 | 34.29 |
| 2024-10-07 | 258.26 | 267.30 | 179.29 | 174.81 | 88.35 | 13.67 | 6.53 | 34.11 |
| 2024-10-08 | 265.92 | 276.02 | 180.39 | 183.43 | 38.89 | 13.49 | 6.53 | 33.76 |
| 2024-10-09 | 270.88 | 275.54 | 181.02 | 184.50 | 38.89 | 3.50 | 6.70 | 34.11 |
| 2024-10-10 | 269.73 | 302.05 | 208.05 | 203.66 | 38.89 | 14.43 | 6.62 | 37.97 |
| 2024-10-11 | 279.23 | 288.65 | 189.13 | 192.79 | 38.89 | 14.69 | 6.36 | 37.71 |
| 2024-10-12 | 276.36 | 300.80 | 194.23 | 195.60 | 38.89 | 15.12 | 7.05 | 38.32 |
| 2024-10-14 | 271.79 | 296.98 | 183.40 | 186.73 | 38.89 | 15.37 | 6.70 | 38.41 |
| 2024-10-15 | 272.57 | 288.09 | 178.21 | 185.67 | 38.89 | 15.80 | 6.79 | 38.76 |
| 2024-10-16 | 273.82 | 290.78 | 177.71 | 184.23 | 38.89 | 15.89 | 6.87 | 38.67 |
| 2024-10-17 | 275.48 | 289.72 | 177.15 | 183.49 | 38.89 | 15.89 | 6.87 | 38.50 |
| 2024-10-18 | 277.03 | 294.41 | 175.18 | 178.69 | 38.89 | 15.97 | 6.87 | 38.58 |
| 2024-10-19 | 273.53 | 289.30 | 175.24 | 177.79 | 38.89 | 15.97 | 6.87 | 38.76 |
| 2024-10-20 | 274.66 | 293.25 | 173.84 | 177.17 | 38.89 | 16.06 | 6.96 | 38.76 |
| Date (yyyy-mm-dd) | Reinforcement Stress (MPa) | Longitudinal Joint (mm) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| YL-01 | YL-02 | YL-03 | YL-04 | YL-05 | YL-06 | YL-07 | YL-08 | y | |
| 2024-10-02 | 11.46 | 13.79 | 11.78 | 14.46 | 8.93 | 2.81 | 3.52 | 2.69 | 40.23 |
| 2024-10-03 | 11.50 | 13.98 | 12.30 | 15.18 | 8.86 | 2.73 | 3.31 | 2.34 | 40.41 |
| 2024-10-04 | 11.44 | 14.09 | 12.64 | 16.23 | 8.96 | 2.73 | 3.31 | 2.07 | 40.42 |
| 2024-10-06 | 11.40 | 14.89 | 13.13 | 16.59 | 9.85 | 3.35 | 3.73 | 2.22 | 40.54 |
| 2024-10-07 | 11.33 | 14.83 | 13.97 | 16.62 | 9.33 | 2.74 | 2.98 | 2.25 | 39.78 |
| 2024-10-08 | 10.59 | 14.76 | 14.08 | 16.98 | 9.51 | 2.87 | 3.03 | 1.71 | 39.87 |
| 2024-10-09 | 11.13 | 15.40 | 14.76 | 16.99 | 9.46 | 3.04 | 3.30 | 2.01 | 39.87 |
| 2024-10-10 | 11.86 | 15.78 | 15.86 | 16.23 | 9.35 | 3.77 | 3.99 | 2.89 | 40.16 |
| 2024-10-11 | 12.12 | 16.34 | 16.09 | 15.90 | 8.87 | 3.78 | 4.10 | 3.25 | 39.95 |
| 2024-10-12 | 12.31 | 16.27 | 16.78 | 16.06 | 8.92 | 4.03 | 4.11 | 3.41 | 39.98 |
| 2024-10-14 | 12.02 | 16.39 | 16.85 | 15.70 | 8.88 | 3.89 | 3.55 | 3.25 | 39.39 |
| 2024-10-15 | 12.03 | 16.38 | 16.57 | 15.61 | 8.83 | 4.18 | 3.92 | 3.44 | 39.17 |
| 2024-10-16 | 12.14 | 16.47 | 16.72 | 15.98 | 8.83 | 4.03 | 3.77 | 3.38 | 39.22 |
| 2024-10-17 | 12.43 | 16.53 | 16.80 | 16.10 | 8.85 | 3.90 | 3.81 | 3.24 | 39.07 |
| 2024-10-18 | 12.18 | 16.59 | 16.76 | 15.86 | 8.84 | 3.85 | 3.92 | 3.32 | 39.00 |
| 2024-10-19 | 12.20 | 16.41 | 16.77 | 15.87 | 8.84 | 3.75 | 3.75 | 3.37 | 38.64 |
| 2024-10-20 | 12.12 | 16.41 | 16.61 | 15.93 | 8.74 | 3.75 | 3.72 | 3.21 | 37.79 |
| Kolmogorov–Smirnova | Shapiro–Wilk | |||||
|---|---|---|---|---|---|---|
| Statistic | df | Significance | Statistic | df | Significance | |
| y | 0.176 | 17 | 0.167 | 0.925 | 17 | 0.180 |
| Regression Model | Model Variables | Determination Coefficient/R2 | Standard Error of Estimate | Significance Change |
|---|---|---|---|---|
| 1 | SY-01 | 0.542 | 0.512 | <0.001 |
| 2 | SY-01 TY-02 | 0.697 | 0.431 | 0.018 |
| Model | Unstandardized Coefficients | Standardized Coefficients | t | Significance | Collinearity Statistics | |||
|---|---|---|---|---|---|---|---|---|
| B | Std. Error | Beta | Tolerance | VIF | ||||
| 1 | (Constant) | 33.946 | 1.353 | - | 25.090 | <0.001 | - | - |
| SY-01 | 0.030 | 0.007 | 0.736 | 4.209 | <0.001 | 1.000 | 1.000 | |
| 2 | (Constant) | 40.348 | 2.645 | - | 15.256 | <0.001 | - | - |
| SY-01 | 0.032 | 0.006 | 0.783 | 5.287 | <0.001 | 0.986 | 1.014 | |
| TY-02 | −0.024 | 0.009 | −0.397 | −2.682 | 0.018 | 0.986 | 1.014 | |
| Model | Sum of Squares | df | Mean Square | F | Significance | |
|---|---|---|---|---|---|---|
| 1 | Regression | 4.643 | 1 | 4.643 | 17.716 | <0.001 |
| Residual | 3.931 | 15 | 0.262 | |||
| Total | 8.575 | 16 | - | |||
| 2 | Regression | 5.977 | 2 | 2.989 | 16.110 | <0.001 |
| Residual | 2.597 | 14 | 0.186 | |||
| Total | 8.575 | 16 | - | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Hao, J.; Gao, Y.; Zhang, L.; Zhang, W. Statistical Analysis of Factors Influencing Segmental Joint Opening in a Soft Soil Tunnel. Buildings 2025, 15, 4175. https://doi.org/10.3390/buildings15224175
Li S, Hao J, Gao Y, Zhang L, Zhang W. Statistical Analysis of Factors Influencing Segmental Joint Opening in a Soft Soil Tunnel. Buildings. 2025; 15(22):4175. https://doi.org/10.3390/buildings15224175
Chicago/Turabian StyleLi, Shuqiang, Jianzhong Hao, Yunchang Gao, Lei Zhang, and Wencui Zhang. 2025. "Statistical Analysis of Factors Influencing Segmental Joint Opening in a Soft Soil Tunnel" Buildings 15, no. 22: 4175. https://doi.org/10.3390/buildings15224175
APA StyleLi, S., Hao, J., Gao, Y., Zhang, L., & Zhang, W. (2025). Statistical Analysis of Factors Influencing Segmental Joint Opening in a Soft Soil Tunnel. Buildings, 15(22), 4175. https://doi.org/10.3390/buildings15224175





