Scan-to-EDTs: Automated Generation of Energy Digital Twins from 3D Point Clouds

Abstract

Digital Twins (DTs) are transforming construction and energy management sectors by integrating 3D surveying, monitoring, Building Performance Simulation (BPS), and Building Energy Simulation (BES) from the earliest design or retrofit stages. Moreover, dynamic thermal simulations further support energy performance assessments by modeling indoor conditions to meet comfort and efficiency targets. However, their reliability depends on accurate, standards-compliant 3D building models, which are costly to create. This research introduces a complete framework for automatically generating energy-focused Digital Twins (EDTs) directly from unstructured point clouds. Combining Deep Learning-based instance detection, Scan-to-BIM techniques, and computational geometry, the method produces simulation-ready models without manual intervention. The resulting EDTs streamline early-stage performance evaluation, enable scenario testing, and enhance decision making for energy-efficient retrofits, advancing smart-building design through predictive simulation.

1. Introduction

Achieving the EU’s 2050 zero-emission building target necessitates immediate, cross-sectoral intervention, as building operations globally accounted for 30% of final energy consumption and 26% of energy-related emissions in 2022, including 8% from direct sources and 18% from electricity and heat production [1]. The EU’s estimated 24 billion m² of floor area, 75% residential and 25% non-residential, consumes 64.4% of residential energy for heating and cooling [2,3], with potential reductions of up to 70% through improved insulation, heat pumps and solar integration [4].

Achieving this reduction at a large scale requires digitization across the AECOO (Architecture, Engineering, Construction, Owners and Operations) sector, where recent growth in tools supporting interoperability between Building Information Modeling (BIM) and energy simulation platforms reflects the industry’s shift toward data-driven energy optimization [5]. By automating the generation of Energy Digital Twins (EDTs) from raw spatial data, the proposed framework directly speeds up large-scale energy audits and retrofit planning, thereby contributing to the EU’s 2050 decarbonization targets by reducing modeling costs, retrofit analysis, and enabling scalable, simulation-driven optimization. Furthermore, it is well suited for building-stock mapping and for creating a complete as-is digital record of each building at different scales.

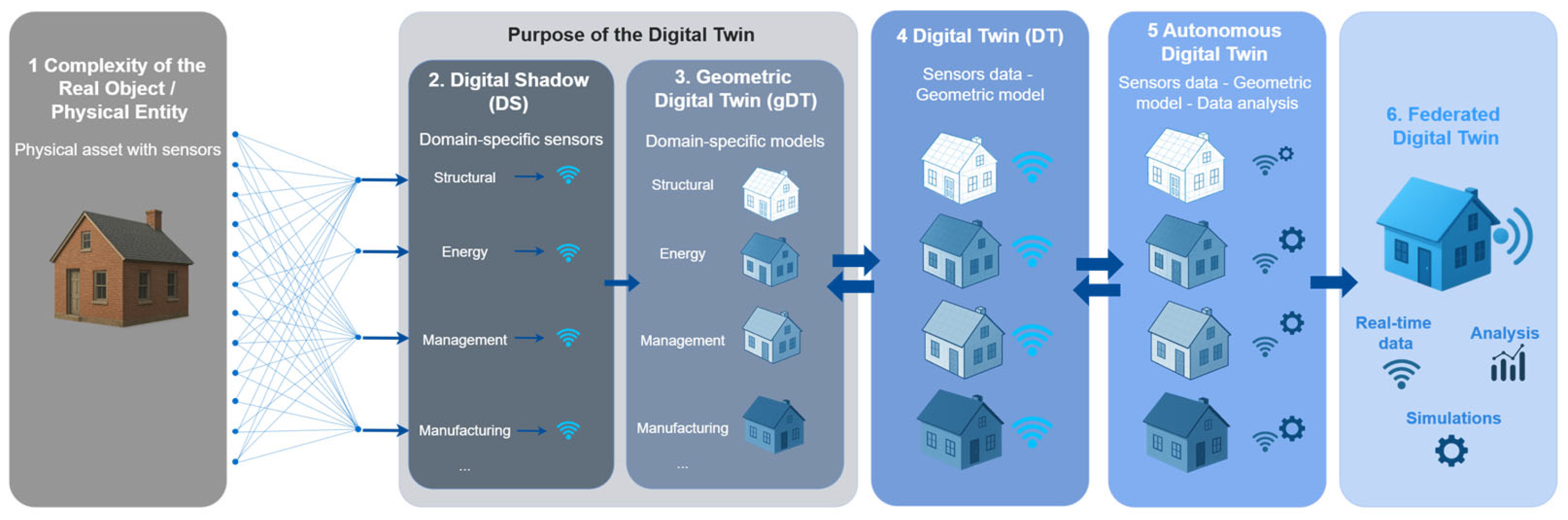
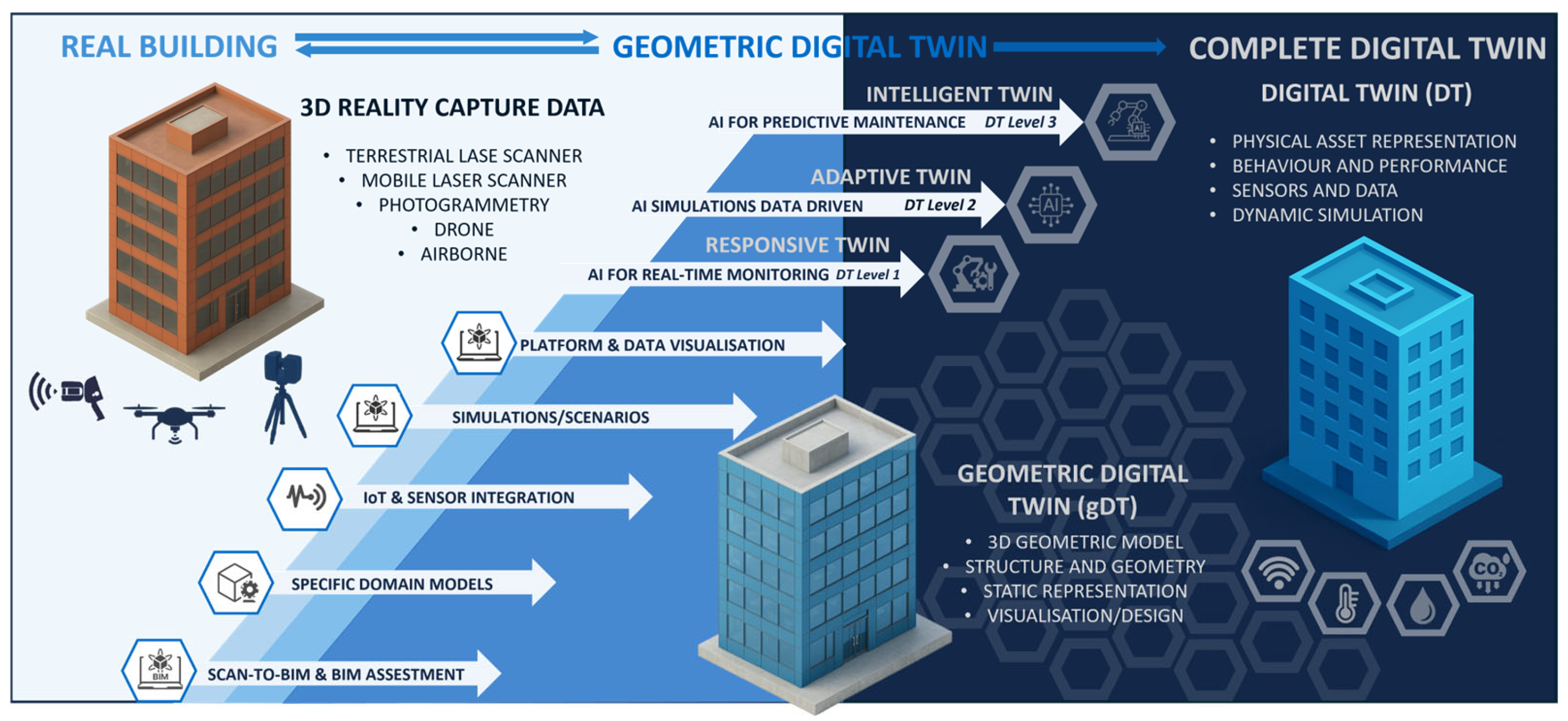
1.1. Context of the DT for Building Applications

Digital Twins (DTs) are increasingly important in building operations, integrating geometric models, real-time Digital Shadows (DSs) [6], and actuators for closed loop control to form a comprehensive virtual representation of physical systems.

In common approaches (Figure 1), the DS is the continuous stream of time-stamped measurements and events from the asset, whereas the geometric Digital Twin (gDT) is a structured 3D representation (e.g., solid, Boundary Representation (B-Rep), Constructive Solid Geometry (CSG), or Building Information Modeling (BIM)) that evolves slowly and serves as the authoritative geometric–topological–semantic index. Figure 1 shows a reference architecture widely used in the literature: the DS mirrors the physical state, while the gDT provides the spatial index from which domain-specific models, such as the structural Finite Element Model (FEM), Discrete Element Method (DEM), and Building Management System (BMS) models, are derived. The DS does not store geometry; instead, it references gDT elements via stable identifiers or coordinates.

In this research, DS data are instead embedded within the gDT schema, producing a unified representation that couples geometry with historical sensor data. A DT then links the gDT, these domain models, and the DS in a bi-directional loop for state estimation, simulation, and control. Artificial Intelligence (AI), Machine Learning (ML), Deep Learning (DL), and Physics-Informed Neural Networks (PINNs) elevate the twin to an intelligent, autonomous system capable of forecasting and self-optimization. Multiple twins can be joined to form a Federated Digital Twin (FDT) for system-level optimization. Integration with the BMS enables real-time monitoring [7,8,9], predictive maintenance [10,11,12,13], and energy optimization [14,15], further enhanced by PINN-driven Data-Driven Decision Support Systems (DDSS) [16].

However, current tools often suffer from fragmented interoperability, incompatible file formats, divergent model structures, and inconsistent communication protocols, largely due to a lack of standardization [17]. These issues cause data loss, workflow inefficiencies, and reduced analytical coherence [18,19]. Addressing these challenges requires semantic integration frameworks that unify heterogeneous data sources into high-fidelity, queryable models. Structured hierarchically and enriched with spatial reasoning and semantics, such models ground intelligent systems and support accurate, scalable, performance-oriented decision making across the building life cycle.

1.2. Aim of the Research

This research presents a holistic end-to-end framework that generates a multi-level geometric Digital Twin from surveyed point clouds, unifying (i) solid and (ii) surface B-Reps with consistent topology, in particular, watertight and 2-manifold envelopes that preserve face-edge-vertex incidence and validated zone-surface adjacencies across building, thermal-zone, and surface levels, enriched with semantic, topological, and energy data for advanced simulation within a single graph model that supports real-time IoT connection and performance optimization. Unlike prior Scan-to-BIM or DT creation approaches that rely on manual modeling or intermediate BIM translation, the proposed unified data-driven pipeline produces energy-compliant DTs directly from unstructured point clouds. The principal novelties are (i) integration of topology and energy semantics within a single model; (ii) elimination of traditional BIM steps; and (iii) complete automation from geometry to energy modeling.

The framework advances state-of-the-art DT generation by the following:

(i)

Deriving simulation-ready Energy Digital Twins (EDTs) directly from point clouds without manual steps, BIM stages, or reliance on proprietary authoring tools;

(ii)

Delivering watertight, simulation-ready models with full topology, semantics, and energy attributes for reasoning, querying and interoperability;

(iii)

Unifying solid and B-Rep representations in a single multi-level gDT and integrated graph for simulations, monitoring, IoT linking, and cross-scale navigation;

(iv)

Enabling standards-based exchange via gbXML and optional IFC to ensure interoperability while avoiding redundant steps and minimizing data loss.

2. State of the Art and Related Research

Systematic reviews [20,21,22] indicate that DTs for building energy applications are typically developed through complex, multi-phase workflows that are still evolving from conventional BIM and Building Energy Modeling (BEM) practices. Conventional workflows start with manual BIM stages, then assemble a federated BEM with Mechanical, Electrical, and Plumbing (MEP) systems. From this, an energy-analytical model is derived by defining thermal zones, constructions, loads, and schedules, and the BEM is then exported to IFC or gbXML for simulation and visualization. Monitoring and sensor integration are added later to reach a DT for interactive control and energy optimization.

Despite this progress, most DT implementations remain partially static and fragmented. Many DTs reported in the literature [23] are more accurately classified as geometric Digital Twins (gDTs), as they lack a continuous, bidirectional connection to IoT sensors. When data flow occurs only in one direction, from the physical asset to its digital representation, the model is better defined as a Digital Shadow (DS). In both cases, the absence of live, two-way communication means the system cannot respond dynamically to real-world changes, which is a defining feature of a fully realized DT.

Although the literature [23] often implies a direct BIM-to-DT link, the relationship is more complex and the connection is neither linear nor efficient. BIM models, whether manual or Scan-to-BIM generated with classification, segmentation, and reconstruction, are static, solid, and design oriented: they aid coordination and documentation but are ill-suited to lifecycle asset management and integrating heterogeneous data in BIM lowers usability and raises system complexity (Figure 2). For this reason, integrating real-time data often requires specialized tools or platforms and alternative model types. Tools like Dynamo [24] for Revit (version 2.17.0.3472, Autodesk, San Rafael, CA, USA) now support continuous and historical data flows, while platforms like Autodesk Forge enable cloud-based access and visualization, both essential for operational DTs.

Consequently, there is growing research interest in bypassing traditional BIM-based workflows by directly generating energy-oriented geometric Digital Twins (EDTs) from unstructured 3D data. The innovation of the present study lies in addressing this gap by bypassing BIM where possible and generating energy-oriented EDTs directly from raw point clouds. The following sections review the state of the art across the full workflow, from point cloud segmentation and Scan-to-BIM geometry to the generation of EDTs and a gDT ready to be enriched with real-time and historical data for monitoring and simulation.

2.1. Advancements in Semantic Segmentation: Transformers and 3D Open Vocabularies

In recent years, a wide range of point cloud classification and semantic segmentation methods have emerged, broadly categorized into image-based and point-based approaches [25]. Given the unstructured nature of 3D point clouds, traditional Convolutional Neural Networks (CNNs) have been adapted for effective point cloud processing. In segmentation, both CNNs and Transformers have evolved [26], incorporating self-attention mechanisms [27], channel-wise attention, and graph-based structures for improved sensitivity [28,29]. Hierarchical global feature aggregation [30], Point Cloud Local Auxiliary Blocks (PLABs) for neighborhood enhancement [31], edge-aware modules for fine detail [32], and multi-scale local aggregation strategies further advance performance. Kernel methods like KPConvX [33] use deformable kernels, while the Point Patch Transformer (PPT) [34], combining Points2Patches and positional encoding to capture local and global contexts for state-of-the-art performance. Emerging vocabulary free approaches [35,36] use vision-language models, and spectral clustering to merge Superpoints, enabling category-agnostic object discovery from raw 3D data [37].

2.2. Image-Based Classification and Semantic Segmentation

Semantic segmentation has also advanced rapidly in image segmentation. Key advances include the Segment Anything Model (SAM) for prompt-based, zero-shot segmentation with broad generalization [38] and GroundingDINOv2 using self-supervised, transferable features for stronger dense prediction [39]. These advances highlight self-supervised learning and transformer architectures in vision, enabling segmentation without task-specific training. Among these, K-Net [40] enhances object grouping using Transformers for better global context, while Pyramid Fusion Transformer (PFT) [41] leverages multi-scale features for top-tier performance. Models like MaskFormer [42] and Graph-Segmenter [43] further improve segmentation with boundary-aware attention and graph-based refinement.

2.3. Object Detection in Challenging Environments: Latest Strategies and Techniques

Detecting small or occluded indoor objects is challenging, especially when they are camouflaged within their surroundings, such as wall-integrated radiators, recessed lights, or embedded sensors [44]. In such settings, the goal often shifts from exact localization to detecting object presence within a Region of Interest (ROI). Region-based Convolutional Neural Networks (R-CNNs) support this by proposing candidate regions for detection and classification [45]. Multi-scale feature extraction addresses varying object sizes, while contextual recognition uses spatial cues to infer object presence. Region Proposal Networks (RPNs) suggest object locations and bounding box-based loss functions like Intersection over Union (IoU) evaluate object presence. Anchor boxes help define object sizes and shapes, and probabilistic models assign confidence scores, compensating for occlusion and partial visibility. Similar approaches are used in complex domains like forestry [46] and harvesting [47]. Finally, a promising 3D Large Language Model (LLM) has been introduced in [48], capable of processing point cloud data to generate structured 3D scene understanding for complex analysis.

2.4. Late Fusion Approaches

Late fusion is a multi-modal integration strategy where features from different data sources are processed separately and combined at the decision-making stage [49]. This preserves the unique strengths of each modality and minimizes redundancy. It is widely used in applications involving heterogeneous sensors, such as RGB cameras, LiDAR, and Global Navigation Satellite System/Inertial Measurement Unit (GNSS/IMU) [50], to enhance robustness in challenging environments [51] like tunnels [52], cluttered indoor spaces, or dense vegetation [53]. In urban-scale building segmentation, late fusion merges high-resolution satellite imagery [54], Digital Surface Models (DSMs), and ancillary data (e.g., OpenStreetMap), improving instance-level accuracy and boundary delineation. Similarly, in 3D reality capture, late fusion of features from images and point clouds across parallel networks enhances both object detection and geometric fidelity by leveraging complementary spatial and semantic cues.

2.5. Advancements in Scan-to-BIM

Automated BIM generation remains an emerging field with limited comprehensive methods, marking it as a key area of ongoing research [55]. Successful Scan-to-BIM approaches typically rely on structured classification and segmentation of raw point cloud data and, in general, they follow three main stages [56]: (i) point cloud segmentation, (ii) classification and instance segmentation, and (iii) 3D modeling and evaluation. These are essential to create BIMs of existing buildings and support applications such as indoor navigation [57], construction robotics, and Simultaneous Localization and Mapping (SLAM) technologies in the AEC sector [58].

For example, SLABIM [59] merges BIM with SLAM sensor data to enhance registration, localization, and semantic mapping in complex indoor spaces. These stages also support change detection, structural deformation monitoring [60], and quality control [61,62,63]. The use of Terrestrial and Mobile Laser Scanning (TLS or MLS) enables detailed 3D point cloud capture, despite challenges like clutter, occlusion, and reflective or transparent surfaces [64]. Recent advances include computational geometry-based methods [65], graph-based methods [66], and Reversible Jump Markov Chain Monte Carlo (RJMCMC) techniques [67] for improved 3D reconstruction. These developments aid in building semantic-rich DT for structural and energy analysis.

2.6. BIM, BEM, and Building Management Systems (BMSs)

Building Energy Models (BEMs) are increasingly critical for energy-efficient design and retrofitting, complementing BIM’s strengths in 3D visualization and construction planning. BIM–BEM integration [68,69,70] enables comprehensive model generation and accurate energy analysis, yet faces challenges like interoperability, between solid and B-Rep representation and the need for expert input. Integrating MEP systems enhances detail and enables clash detection to avoid on-site conflicts. Advances in object detection [71], extended reality [72], and ML/DL methods [15,73] support energy optimization, smart modeling [74,75], and system management via graph-based approaches [76] and HVAC optimization [77]. However, since BIM is mostly a static model, it remains underutilized in facility management, particularly during the operational phase, which accounts for over 80% of lifecycle costs. Detailed simulations at the building level, with progressive data enrichment and semantic alignment with BEM schemas (e.g., EnergyPlus .IDF or .epJSON), are supported by EnergyPlus [14], while tools like Ladybug and HoneyBee [78] extend analysis to city-wide energy modeling, district consumption, and demand forecasting [79,80], enabling data-driven urban planning.

2.7. Topologic BIM (TBIMs)

Scan-to-BIM is a complex first step toward creating DTs for building applications. Bridging BIM’s solid and heavy geometry and product-focused outputs with space-oriented simulation workflows requires semantic consistency, spatial reasoning, and topological connectivity. The TBIM methodology [81] addresses this by modeling buildings with topological abstractions, such as rooms as cells, partitions as faces, and clusters as complex cells, enriched via rule-based modeling and topological queries to assign energy properties [82,83]. TBIM reduces geometric complexity [84] while preserving semantic richness, enabling compatibility with Building Performance Simulation (BPS) tools [85]. It supports non-manifold topology, hierarchical relationships, geometry-agnostic modeling, semantic metadata, and interoperability. Rather than adhering to a single standard, TBIMs are purpose-driven representations that rely on various building ontologies, such as IFC, Building Object Typology (BOT), or Brick, depending on the target application, be it compliance checking, energy simulation, or real-time DT integration.

2.8. Digital Twins for Buildings

The DT concept originated with NASA’s Apollo 13 for real-time monitoring [86]. Currently, DTs are used in buildings, industry, manufacturing, and cities for management, maintenance, and performance optimization [87,88]. Unlike static BIM, DTs fuse real time and historical data from the physical asset and its virtual model to inform structural, energy, and operational decisions [89]. In energy applications, they improve fault detection, anomaly prediction, and efficiency, and track indoor conditions such as temperature, CO₂, and humidity for predictive maintenance [90]. Combined with AI, they run simulations that reveal inefficiencies and optimize performance in real time [3,6,8,9].

A key challenge is integrating geometry, semantics, and external datasets within a single real-time framework. Since DTs are visual and data-driven replicas of physical systems [91,92], seamless interoperability across diverse sources is essential for accurate monitoring, simulation, and decision making.

The development of DTs can be classified by functional maturity [22]:

• DT Level 1: Real-time sensor integration for monitoring, visualization, and diagnostics.
• DT Level 2: Dynamic simulation, forecasting, and optimization (also from historic data).
• DT Level 3: Analytics for failure prediction and strategic building management, contingent on historical data availability.

A key distinction between a geometric DT and a full DT (Figure 3) is the integration of real-time data and the ability to simulate behavior from that data. This enables progressively advanced capabilities: monitoring (Level 1), simulation (Level 2), and predictive maintenance (Level 3) [22,93].

These capabilities align with different DT types: Geometric (static 3D models), Behavioral (system performance), Operational (real-time and historical data), and Predictive (future state forecasting).

3. Methodology

Figure 4 introduces the pipeline that generates energy-oriented geometric digital twins (EDTs) directly from raw point clouds, extending [94] into a structured, semantically enriched, multi-level DT for monitoring and preliminary simulations.

The framework builds a geometrically accurate, topologically coherent model enriched with energy metadata through the following phases:

• Object Classification and Instance Segmentation (Section 3.1 and Section 3.2): Detect architectural components in the 3D point cloud, merging point-based and image-based outputs via late fusion [94].
• Scan-to-BIM Process (Section 3.3): Build an intermediate solid model (Figure 4, step A) with a graph representation of geometry and spatial configuration, aligning with object-level reconstruction in [94] and solid mesh representation [66].
• Scan-to-BEM Process (Section 3.4): Augment the model with energy devices, their localization, and their data for integration with building energy modeling workflows.
• Topologic Model Generation (Section 3.5): Convert the 2D Topologic Map [95] into a 3D graph-based topology with adjacencies, containment hierarchies, and watertight room enclosures, and fully closed 3D spaces with seamlessly joined surfaces, ensuring validity for energy and spatial simulations.
• Geometric Digital Twin output (Section 3.6): Derive the final multi-level gDT that integrates geometry, topology, and semantic energy attributes in a graph-based model, ready for simulation-driven DT development.

The system builds a progressively enriched graph with two hierarchical views:

• Volumetric model (Figure 4, step B) that defines watertight room level enclosures for thermal zoning, a Topologic Solid Model (TSM);
• Semantic model (Figure 4, step C) that encodes surfaces and thematic partitions with material and use metadata.

The resulting gDT (Figure 4, step D) supports hierarchical visualization, semantic queries, graph navigation, and real-time data integration. Semantic and material enrichment is achieved through Information Loading Dictionaries (ILDs), which add space-specific functional, regulatory, and energy data such as occupancy and device specifications. Coupled with IoT sensors and simulation engines, the static gDT is transformed into an operational Digital Twin.

3.1. Object Classification and Instance Segmentation: Point Clouds

For the captured point clouds, the methodology leverages the Pointcept framework that integrates PointTransformer version 3 [26,96] for classification tasks and the Segmentor module for instance segmentation, ensuring identification of building elements. During the preprocessing phase, point cloud data is subsampled to a 1 cm resolution using a Voxel Grid Filtering (VGF) approach and partitioned into smaller grid-based subsets, enhancing processing efficiency and scalability. The model is trained to detect five distinct classes, encompassing both primary elements, such as ceilings, floors, and walls, and secondary elements, including doors and windows. As highlighted in [94], the detection phase exhibits robust performance in recognizing objects with distinct geometric characteristics, such as floors and walls.

3.2. Object Classification and Instance Segmentation: Images

To address detection challenges, image-based strategies are employed to identify columns [97] and openings [98] from the point cloud. The raw point cloud is (i) rasterized into a top view projection at 1 cm resolution and (ii) aligned with the global xy axes by estimating the building’s principal orientation from the oriented bounding box (OBB) of the entire building. A YOLO detector [97] is then applied to localize columns in the raster image. For openings, (i) virtual cameras are placed 1 m orthogonal to each wall face, from which (ii) high-resolution orthographic views are rasterized using wall-aligned octree meshes. GroundingDINO [39] is applied to these projections and dimensional constraints filter and classify door and window candidates. Finally, all detections are mapped back into the 3D world space as Oriented Bounding Boxes (OBBs) via inverse transformations from the projection frames. A late-fusion scheme (from Section 3.1 and Section 3.2) based on class-wise model selection was adopted. Let $p_c^{\left(PT\right)}\left(x\right)$ denote per-class logits or probabilities from the Point Transformer on the 3D point cloud and $p_c^{\left(IMG\right)}\left(x\right)$ those obtained by reprojecting image-based detections (YOLO, GroundingDINO) onto the point cloud. On a held-out validation set, per-class performance (mIoU) is estimated and a provider ${\pi }_c\in \{\mathrm{PT}, \mathrm{IMG}\}$ is chosen for each class $c$. At inference, the fused score $s_c\left(x\right)$ for class $c$ is the following:

$$s_c\left(x\right)=\left\{\begin{array}{c}{p}_c^{\left(PT\right)}\left(x\right),if{\pi }_c=PT\\ p_c^{\left(IMG\right)}\left(x\right),if{\pi }_c=IMG\end{array}\hspace{1em}ŷ\left(x\right)=arg\hspace{0.17em}ma{x}_c\hspace{0.17em}{s}_c\left(x\right)\right.$$

(1)

where ${\pi }_c$ denotes the per-class provider selected on validation mIoU (ties broken by calibrated confidence). Image predictions are reprojected onto the point cloud to ensure spatial alignment. Spatial coherence is enforced via connected-component smoothing and majority voting within local 3D regions. Concretely, geometry-dominant classes are taken from the Point Transformer, whereas small or texture/appearance-dominant classes are sourced from YOLO/GroundingDINO. This achieves the benefits of both modalities without heuristic per-pixel weighting.

3.3. From Geometric Graph to Reconstructed Objects

The geometric model leverages the graph-structured framework [66] to extract class_id (the element category in the ontology, such as doors, walls, windows) and object_id (the unique instance identifier for the specific physical element) from the classified point cloud, systematically organizing all related information within this structure. This framework includes essential components, such as OBB and associated point data, along with georeferenced information, creating a robust foundation for spatial data representation. By extracting and processing these points [94], the various object classes are reconstructed. In the following subsections, we detail the reconstruction procedure for each class element.

Let $𝒟$ represent the complete point cloud. Following the classification phase, $𝒟$ can be described as consisting of the following components (Equation (2)):

$$\mathcal{D}=\mathcal{U}+\mathcal{F}+\mathcal{C}+\mathcal{W}+\mathcal{L}+\mathcal{O}$$

(2)

where:

• $\mathcal{F}$ represents the floor class, serving as the base to which the lower bonds of all walls are connected (Section 3.3.1);
• $\mathcal{C}$ represents the ceiling class, serving as the upper connection point for the tops of all wall elements (Section 3.3.1);
• $\mathcal{W}$ denotes the wall class, containing all identified vertical partition elements (Section 3.3.2);
• $\mathcal{L}$ refers to the column class, capturing all structural columns within the environment;
• $\mathcal{O}$ denote the sets of doors and windows, so it defines the generalized openings class (Section 3.3.3);
• $\mathcal{U}$ represents the unclassified class, encompassing all elements that do not fall into any of the defined categories above.

3.3.1. Floors ($\mathcal{F}$) and Ceiling ($\mathcal{C}$) Class

The method robustly extracts horizontal structural elements, from floors ($\mathcal{F}$) and ceilings ($\mathcal{C})point cloud classes$, from the original 3D point cloud $\mathcal{D}$, using geometric and spatial analysis. Surface normals are first estimated using local Principal Component Analysis (PCA) with a radius $r= 0.30 \mathrm{m}$. This radius defines the PCA neighborhood, where smaller values (0.10–0.15 m) capture finer detail but are more noise sensitive, while larger ones (0.50–0.60 m) yield smoother slab normals yet risk over-smoothing and merging adjacent levels. Points satisfying $\left|{\mathrm{n}}_{\mathrm{z}}\right|\ge 0.98$ are classified as horizontally aligned candidates. These are clustered using the DBSCAN [98] algorithm $\left(\mathsf{\epsilon }=0.5\hspace{0.17em}\mathrm{m},\mathrm{minPts}=30\right)$ to group co-planar regions and suppress noise. Each cluster is projected onto the xy plane and bounded by a minimum Oriented Bounding Box (mOBB), capturing its extent and orientation. Floor–ceiling pairs are identified by evaluating vertical spacing between mOBB centroids $\mathsf{\Delta }z\ge 2.0\hspace{0.17em}\mathrm{m}$ and enforcing a horizontal overlap threshold (IoU or projection overlap ≥ 85%). This stratifies the point cloud into building levels, forming the basis for semantic segmentation and volumetric reasoning.

Finally, for each pair $z_{\max }, z_{\min } \mathrm{a}\mathrm{n}\mathrm{d} z_{\mathrm{mean}}$ (Equation (3)) are stored to define vertical extents and ensure geometric connectivity between floors, ceilings, and adjoining walls.

$$z_{\mathit{mean}}=z_{\mathit{min}}+{\displaystyle \frac{z_{\mathit{max}}-z_{\mathit{min}}}{2}}.$$

(3)

3.3.2. Wall Class ($\mathcal{W}$)

The topology of walls is established through a robust workflow inspired by the methodology in [58] comprising an initial noise-filtering stage followed by a Random Sample Consensus (RANSAC)-based plane segmentation. For each wall cluster $\mathcal{W}$ = {w_i, …, w_k}, a dominant supporting plane is identified. This plane is characterized by a standard planar equation (Equation (4)) of the following form:

$$ax+by+cz+d=0\hspace{1em}$$

(4)

where the coefficients a, b, c, d are the unit normal vector of the wall plane and d is the signed distance from the origin. The coefficients are obtained by minimizing the least-squares error function (Equation (5))

$$\mathrm{E}=\sum _{i=1}^N{\displaystyle \frac{{\left(a{x}_i+b{y}_i+c{z}_i+d\right)}^2}{a^2+b^2+c^2}}$$

(5)

which corresponds to minimizing the sum of squared orthogonal distances between the plane and the observed points. Walls with a thickness below a specified threshold (tth = 0.12 m) were excluded from reconstruction, consistent with common dimensions of interior partitions in standard construction practice. The remaining walls are grouped into clusters based on two criteria: proximity and orientation similarity. For the proximity criterion, the distance between two clusters $𝒲$₁ and $𝒲$₂ is computed (Equation (6)), where $d\left(W_1,W_2\right)\le t_d$, with t_d as the distance threshold.

$$d\left({\mathcal{W}}_1,{\mathcal{W}}_2\right)=\underset{w_{1i}\in W_1,w_{2j}\in W_2}{\min }|w_{1i}-w_{2j}|$$

(6)

On the other hand, the orientation criterion evaluates the angular similarity between clusters (Equation (7)), and they are merged only when both the distance and orientation criteria are simultaneously satisfied.

$$\theta \left({\mathcal{W}}_1,{\mathcal{W}}_2\right)=\arccos \left({\displaystyle \frac{n_{W_1}\cdot n_{W_2}}{\left|n_{W_1}\right|\left|n_{W_2}\right|}}\right)$$

(7)

To analyze connections between walls, the algorithm examines intersections and spatial relationships by leveraging geometric features and computational methods. Each wall is represented by its start and end points$\left(p_{\mathrm{start}},p_{\mathrm{end}}\right)$, its normal vector $\left(\overrightarrow{n}\right)$, and orthogonal offsets $\left(p_{\perp \mathrm{start}},p_{\perp \mathrm{end}}\right)$ that define the wall’s boundaries in 3D space. The orthogonal offsets are calculated as (Equation (8)):

$$p_{\perp \mathrm{start}}=p_{\mathrm{start}}+{\displaystyle \frac{t_i}{2}}\cdot \overrightarrow{n},\hspace{1em}{p}_{\perp \mathrm{end}}=p_{\mathrm{end}}+{\displaystyle \frac{t_i}{2}}\cdot \overrightarrow{n}$$

(8)

where $t_i$ is the i-th wall thickness.

Using a nearest neighbor (NN) search, the algorithm identifies walls within a distance threshold ($t_d)$. For each wall, nearby candidates are found by comparing start and end points in 3D space. Intersections between two walls (Equation (9)) are obtained by solving the parametric line equations and equating $\overrightarrow{r_1}\left(t\right)=\overrightarrow{r_2}\left(s\right)$ and solving for the parameters ($t)$ and ($s)$. If the parameters are within the valid range ($0 \le \mathrm{t}, \mathrm{s} \le 1$), the intersection lies within the bounds of both wall segments.

$$\begin{gathered} \overrightarrow{r_1}\left(t\right)=p_{\mathrm{start},1}+t\cdot \left(\overrightarrow{p_{\mathrm{end},1}}-\overrightarrow{p_{\mathrm{start},1}}\right)\hspace{1em} \\ \overrightarrow{r_2}\left(s\right)=p_{\mathrm{start},2}+s\cdot \left(\overrightarrow{p_{\mathrm{end},2}}-\overrightarrow{p_{\mathrm{start},2}}\right) \end{gathered}$$

(9)

To refine wall relationships, orthogonal intersections are computed at endpoints using offsets$\left(p_{\perp \mathrm{start}},p_{\perp \mathrm{end}}\right)$ to detect potential overlaps or extensions. Distances from candidate intersections to wall axes are then evaluated and those exceeding the threshold ($t_{\mathrm{int}}$) are excluded, ensuring the accuracy of the connections. This ensures accurate representation of intersections, alignments, and overlaps, which are critical for reconstructing a realistic structural model (Figure 5). While transforming models from the Scan-to-BIM process into IFC format is supported, it remains optional within the proposed pipeline.

3.3.3. Openings ($\mathcal{O}$) Class: Windows and Doors

The openings reconstruction process begins with the topological reconstruction of walls. From each wall’s centroid and main axis, orthographic images $I\left(x,y\right)$ of the $\mathcal{O}$ class point cloud are generated via ray casting 1 m on both sides. These 2D projections capture wall surface details for object detection, with missing pixels filled black for consistency.

Object detection outputs bounding boxes $\left[x_{\min },{ y}_{\min }, x_{\max },{ y}_{\max }\right]$, where the corners define the detected region. Width $w=x_{\max }-x_{\min }$ and $w=x_{\max }-x_{\min }$ are calculated, incorporating a framing threshold $\left({th}_f = 0.07 \mathrm{m}\right)$. Bounding boxes are overlaid on the orthographic images to annotate doors and windows, then mapped back into 3D space using known camera positions. Openings are reconstructed by sampling between start $\left(x_1,y_1,z_1\right)$ and end $\left(x_2,y_2,z_2\right)$ points and aligned with the wall’s axis. To ensure geometric robustness in downstream operations, such as surface Boolean intersections and wall embedding, each opening is slightly thickened along the normal direction.

Finally, each opening area is computed and stored for further thermal-envelope analyses. Openings are detected in 2D with GroundingDINO (39) (Section 3.2), backprojected using known camera poses, and intersected with the wall plane to obtain the 3D aperture polygon. The operable area is then obtained by insetting this polygon by a uniform frame thickness $t_{\mathrm{f}\mathrm{r}}=0.075 \mathrm{m}$ to derive the clear glazed portion within the fixed frame.

3.4. Scan-to-BEM

To support the detection of devices and energy-related systems, a lightweight interactive tool (Figure 6) was developed featuring a 3D point cloud viewport, with navigation and class selection for lighting, radiators, HVAC, and sensors. Device instances are identified by user clicks within the scene, followed by a ray casting and nearest-neighbor search in a k-d tree to snap to the closest in-class point within a radius of $r_{\mathrm{snap}}=0.10 \mathrm{m}$. Each confirmed instance is stored as an object containing the class name, element ID, and global coordinates $\left(x,y,z\right)$ in meters.

Using the captured coordinates, each device is automatically assigned to the corresponding room or thermal zone through a point-in-solid spatial query; in cases of multiple overlaps, the assignment is made to the room with the largest volumetric intersection. A minimum inter-device distance per class (e.g., $d_{\mathrm{m}\mathrm{i}\mathrm{n}}=0.25 \mathrm{m}$ for luminaires) is enforced to prevent duplicate selections.

The final annotation can be exported as a JSON file containing class_name, element_id, and coordinates, with optional room_id and confidence fields. Additional attributes related to energy performance, such as nominal power for radiators or seasonal efficiency for HVAC units, can be integrated post export using external manufacturer libraries or Information Loading Dictionaries (ILDs).

This spatially aware annotation approach enables the precise localization and classification of energy-critical components that are often partially concealed within architectural elements, for example in recessed luminaires and embedded radiators, thereby improving the completeness and accuracy of energy performance modeling.

3.5. Topologic Map and Topologic Model

To enable accurate energy simulation and performance analysis, the workflow requires the generation of B-Rep models that comply with strict geometric and topological constraints, including [99] the following:

• Watertightness: All surfaces enclosing interior volumes must form a completely closed shell, without gaps or discontinuities.
• Consistency and Manifoldness: Shared surfaces between adjacent spaces must be consistently defined, ensuring topological correctness.

The Topologic B-Rep model, grounded in the Topologic Map [95] framework and extended into three dimensions, is specifically engineered to address current limitations by providing a structured workflow for generating watertight volumetric representations of indoor spaces, which is an essential prerequisite for accurate and reliable energy simulations. The workflow initiates with the geometric abstraction of walls using minimum Oriented Bounding Boxes (mOBBs), forming the foundational elements for topological reasoning and space reconstruction.

Let $\mathcal{W}=\{w_1,w_2,\dots ,w_n\}$ denote the set of all wall instances. Each wall $w_i$ is described as a collection of 3D points (Equation (9)) derived from the classified point cloud data, as detailed in the preceding section, while for each wall $w_i$, its mOBB is defined as a triplet as shown in Equation (11):

$$w_i=\{p_1^i,p_2^i,\dots ,p_{m_i}^i\},\hspace{1em}{p}_j^i\in R^3$$

(10)

$$\mathrm{mOBB}\left(w_i\right)=\left(R_i,c_i,e_i\right)$$

(11)

where

• $R_i\in SO\left(3\right)$ is a 3D rotation matrix is the rotation matrix of the local frame;
• $c_{i }\in R^3$ is the center of the bounding box;
• $e_i=\left(e_{x,i},e_{y,i},e_{z,i}\right)\in R^3$ represents the extents of the bounding box along each local axis.

From each mOBB, the wall centerline is obtained using the midpoints of its shorter edges as endpoints. Principal Component Analysis (PCA) on the wall points yields the dominant axis and the normal vector defines the local wall reference frame.

However, due to imperfections in the classification phase, occlusions in the surveying phase or the presence of columns at the intersection’s points, adjacent walls may not intersect and explicit joint points can be missing. A loop-based refinement computes candidate intersections, filters them using proximity thresholds and wall bounding box masks, and then consolidates vertices by snapping endpoints within a spatial tolerance, ensuring geometric consistency and topological correctness (Figure 7).

The process begins by generating wall buffers $\left(B\left(w_i;\delta \right)\right)$ for each wall instance $w_i$ in $\mathcal{W}$, where each buffer is defined as Equation (12):

$$B\left(w_i; \delta \right)=\left\{x\in R^2\hspace{0.17em}|\hspace{0.17em}\mathrm{dist}\left(x,\mathrm{centerline}\left(w_i\right)\right)\le \delta \right\}$$

(12)

where $\delta$ represents the buffer radius. Candidate connection segments are then computed from pairwise buffer intersections (Equation (13)):

$$S_{i,j}=B\left(w_i; \delta \right)\cap B\left(w_j; \delta \right), \mathrm{for} \mathrm{all} i \ne j.$$

(13)

These segments are filtered by evaluating their angular similarity, where for each pair of direction vectors $\overrightarrow{d_i}$ and $\overrightarrow{d_j}$, the angle is defined as Equations (14a) and (14b) [100]:

$${\theta }_{i,j}=\mathit{arccos}\left({\displaystyle \frac{\overrightarrow{d_i}\cdot \overrightarrow{d_j}}{\left|\overrightarrow{d_i}\right|\hspace{0.17em}\left|\overrightarrow{d_j}\right|}}\right),\hspace{1em}{\theta }_{i,j}\in \left[0,\pi \right].$$

(14a)

$${\theta }_{i,j}=\angle \left(\overrightarrow{d_i },\overrightarrow{ d_j}\right)$$

(14b)

A candidate segment is retained only if ${\theta }_{i,j}<{ϵ}_{\theta },$ where ${ϵ}_{\theta }$ is the angular tolerance (here ${ϵ}_{\theta } = 5°$). The resulting intersection points $v_k\in R^2$ are then refined by merging any pair $\left(v_a,v_b\right)$ such that $|v_a-v_b|<{ϵ}_d$, to avoid topological noise due to overly dense point distributions. Then, from the filtered and refined connections, a Doubly Connected Edge List (DCEL) is constructed by representing each segment $s_k=\left(v_a,v_b\right)$ as two half-edges. In Equation (15), the arrow notation $\left(e.g.,v_a\to v_b\right)$ denotes a directed half-edge from vertex $v_a$ to vertex $v_b$ in the topological graph. Each undirected edge is represented by two opposite half-edges

$$h{e}_k=\left(v_a\to v_b\right)\mathrm{and} h{e}_k^{’}=\left(v_b\to v_a\right),$$

(15)

which encode adjacency and orientation between connected surfaces.

These half-edges are linked by defining $h{e}_{k, next}.\mathrm{next}=h{e}_{k+1}$ and $h{e}_{k+1}.\mathrm{prev}=h{e}_k,$ forming closed loops used to generate topological faces (Equation (16)):

$$f_m=\{h{e}_m^1,h{e}_m^2,\dots ,h{e}_m^p\}, \mathrm{where} h{e}_m^p.\mathrm{next}=h{e}_m^1.$$

(16)

Perimeter walls may sometimes be discontinuous and some segments may appear open or incomplete (Figure 7a), due to the absence of closing walls or missing boundary openings. To restore enclosure, closure surfaces are introduced: auxiliary zero thickness faces inserted only to seal perimeter gaps and produce a watertight envelope for analysis; they are synthetic and excluded from structural computations. A radial ray casting algorithm then constructs the outer boundary (Figure 8):

(i)

Emit rays uniformly from the building centroid over 360° at a fixed angular step; record each ray’s farthest valid wall hit and wall ID.

(ii)

Use filter hits to remove outliers/duplicates and retain points consistent with the exterior boundaries.

(iii)

Sort the remaining points counterclockwise by polar angle about the centroid.

(iv)

Detect gaps (distance/disconnect thresholds) and insert bridging segments via a Convex-Hull–based completion to obtain a continuous boundary polygon.

This robust structure enables the definition of complex room geometries, including both convex and concave configurations, based on the previously extracted connection segments. Finally, the height boundaries of the volumetric spaces are defined based on the floor and ceiling nodes, specifically using the previously computed values $z_{min}$ and $z_{max}$ (Equation (2)), which represent the vertical extent of the enclosed room geometry.

This topological model is finally restituted in 3D, providing a coherent and watertight geometric structure that can be directly used for spatial reasoning and energy-related simulations (Figure 9).

3.6. The Multilevel Geometric Digital Twin (gDT)

The multilevel framework combines (i) volumetric (Topologic Solid model, TSM) and (ii) surface-based (B-Rep model) representations to capture the complexity of indoor environments. Both models originate from the 3D transformation of the 2D Topologic Map [101], embedding metadata within the solid nodes. In the TSM, a DCEL-based structure generates watertight 2D room volumes from segment connectivity and refined intersection logic, which are then extruded along the z axis with base and top boundaries set by the level node elevations (Equation (3)).

The (ii) B-Rep model semantically labels wall, ceiling, and floor surfaces using the Topologic Map 2D segments, while openings detected in the classification are matched to their host wall $w_i$ via geometric and orientation-aware projection. Each opening $\mathcal{O}j$ is mapped to a local 2D wall frame derived from the wall face’s principal axes and rotation matrices, filtered by area (th_Area > 0.10 m²) and subtracted by Boolean difference to yield walls with precise holes (Equation (17)).

$$W_{\mathrm{hls}}=W_i\setminus \bigcup _{j=1}^n{O}_j$$

(17)

The result is a hierarchical set of oriented polygons representing (i) plain wall surfaces, (ii) floors and ceilings, (iii) wall surfaces with openings, and (iv) individual opening geometries. Except for minor watertightness adjustments during room creation (e.g., closure walls), components retain a consistent, traceable identity (element_id) from point cloud detection through the final models.

This integrated representation forms the geometric Digital Twin (gDT), a layered, semantically enriched 3D model that unifies the following:

(i)

Volumetric Model (TSM): Watertight, room-level spatial cells (CellComplex model) for thermal zoning and energy simulation.

(ii)

Thematic Surface Model (B-Rep): Walls, floors, ceilings, and openings, each semantically annotated with material, function, and energy performance data.

(iii)

Energy System Elements and Devices: Geometric-topological representations and spatial registration of sensors and devices, enabling semantic graph-based reasoning and zone-level device mapping.

(iv)

Ancillary/Building physics data: A graph structure embedding construction layers, material properties, and performance attributes.

Finally, thanks to its multi-scale graph-based structure (Figure 10), the gDT supports semantic queries, interoperability, energy simulation and real-time deployment for smart building design, monitoring, and optimization. During faults, it pinpoints affected devices for faster diagnostics and maintenance.

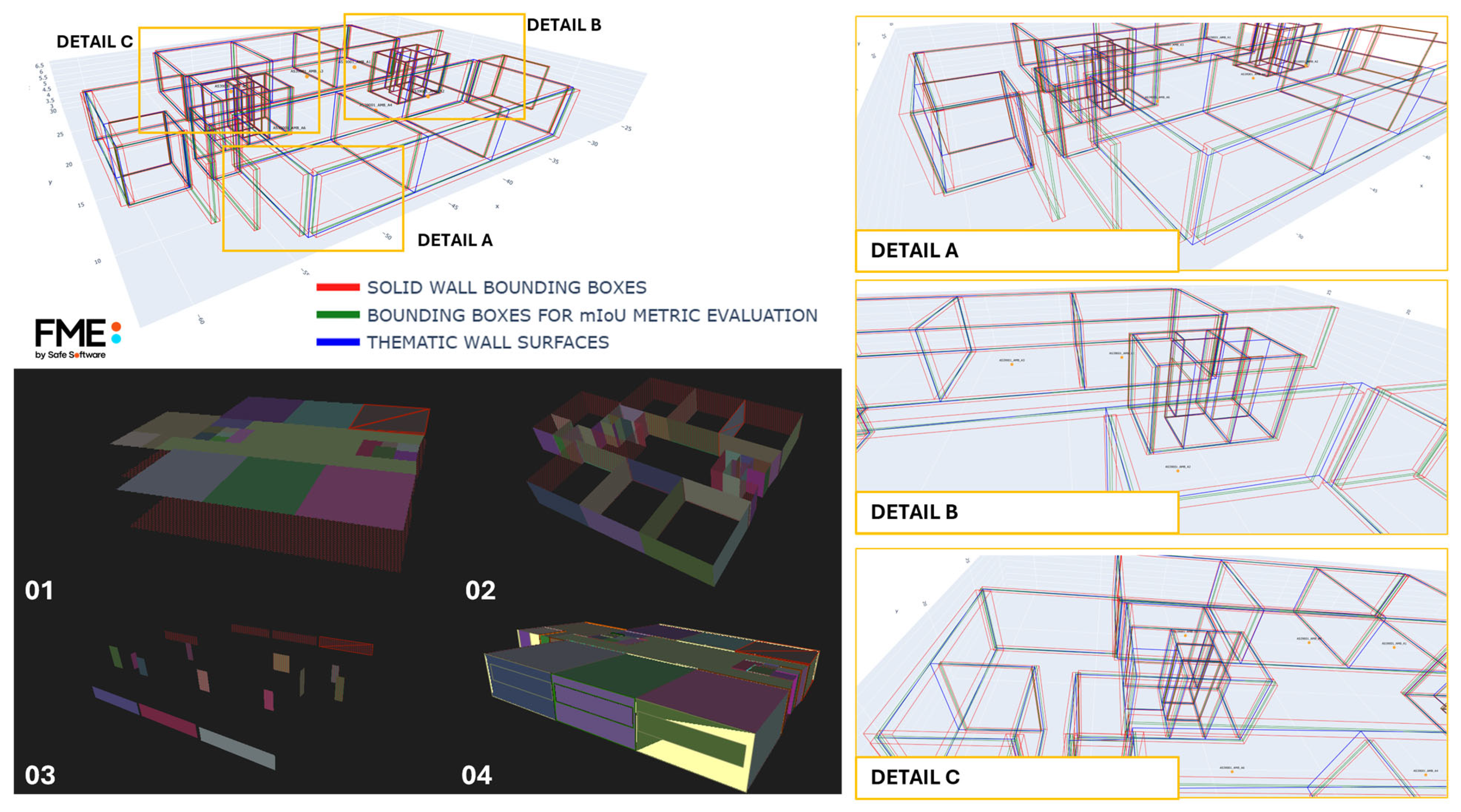
4. Results

The following sections present results from the geometric gDT framework, demonstrating spatial semantic integration, device to space mapping, and energy-oriented reasoning. To validate the method, heterogeneous datasets from Terrestrial Laser Scanning and Mobile Laser Scanning were processed, spanning residential (House 01), educational (Block N, Gent, Belgium; PEA School, Italy), and heritage contexts (Santa Chiara, Trento, Italy). The datasets have comparable point cloud densities but differ in acquisition features and sensor configurations. A summary of these characteristics, along with information on whether indoor sensor data are available, is reported in

Table 1. Summary of datasets and their key features.

	House 01	Block N	PEA School	Santa Chiara
Type of device	MLS	TLS	TLS	TLS
Density	6 mm	5mm	5 mm	5mm
Number of Floorplans	2	4	1	1
Contains indoor sensor data	✗	✗	✓	✓

, providing diverse conditions for evaluating the reconstruction pipeline.

Given the multi-stage nature of the Scan-to-EDTs framework, each step undergoes a consistent geometric assessment using oriented-bounding-box (OBB) matching with an IoU (Equation (18)) threshold (τ) and reporting Precision, Recall and F1 (Equation (19)), along with mean per-class accuracy (mAcc, Equation (20)) and mean per-class Intersection-over-Union (mIoU, Equation (21)).

$$\mathrm{IoU}={\displaystyle \frac{\left|\mathrm{A}\cap \mathrm{B}\right|}{\left|\mathrm{A}\cup \mathrm{B}\right|}}$$

(18)

where

• $\mathrm{A} \mathrm{and} \mathrm{B}$ are the predicted and ground truth (GT) oriented bounding boxes (OBBs);
• $\left|\mathrm{A}\cap \mathrm{B}\right|$ is the intersection volume;
• $\left|\mathrm{A}\cup \mathrm{B}\right|$ is the union volume.

$$F1={\displaystyle \frac{2\cdot TP}{2\cdot TP+FP+FN}}$$

(19)

where

• TP are true positives, predicted OBBs correctly matched to a GT OBB;
• FP are false positives, predicted OBBs not matched to any GT OBB;
• FN are false negatives, GT OBBs not matched by any prediction.

$${\mathrm{Acc}}_{\mathrm{c}}={\displaystyle \frac{T{P}_c}{T{P}_c+F{N}_c}},\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{mAcc}={\displaystyle \frac{1}{C}}\sum _{c=1}^C\mathrm{Ac}{\mathrm{c}}_{\mathrm{c}}$$

(20)

where $c$ indexes classes, $C$ is the number of classes; $T{P}_c$ and $F{N}_c$ are true and false negatives for class $c$ (with positives/negatives defined per class).

$$\mathrm{Io}{\mathrm{U}}_{\mathrm{c}}={\displaystyle \frac{T{P}_c}{T{P}_c+F{P}_c+F{N}_c}},\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{mIoU}={\displaystyle \frac{1}{C}}\sum _{c=1}^C\mathrm{Io}{\mathrm{U}}_{\mathrm{c}}$$

(21)

Predictions are matched one-to-one to ground truth (GT) OBBs using IoU thresholds $\tau \in 0.05, 0.10, 0.15$. A prediction with $IoU\ge \tau$ to an unmatched GT is counted as a TP; unmatched predictions are FP and unmatched GT instances are FN.

4.1. Data Classification

Semantic classification is not the primary focus of this research; nevertheless, the segmentation results are consistent with the ones reported on [94]. Point cloud segmentation uses Point Transformer v3 [26] with an internally pretrained model [94], taking point coordinates, RGB when available, and surface normals as inputs. In parallel, 2D image-based object detection follows the method in Section 3.1 and Section 3.2 and, mostly, in [94].

The two outputs are fused to ensure consistency within the 3D reconstruction workflow and results are reported in

Table 2. Classification results obtained using the Point Transformer v3 model.

Elements	Std Deviation (%)	mIoU (%)	mAcc (%)
Unclassified	5.1	78.3	85.4
Floors	2.6	94.2	96.8
Ceilings	2.7	92.7	95.6
Walls	2.4	87.5	89.4
Columns	0.7	44.1	71.5
Doors	1.1	51.6	65.3
Windows	1.6	58.8	70.2

. The table indicates strong performance for major structural elements, such as floors, ceilings, and walls, that reach mIoU > 85% and mAcc > 89%, with low variance, reflecting limited variability and good representation in training data. In contrast, columns, doors, and windows score lower (mIoU = 44.1%, 51.6%, 58.8%) due to smaller size, occlusions, and class imbalance. Late fusion of point- and image-based outputs improves consistency for windows, confirming the value of multimodal integration. Overall, accuracy is sufficient for reliable topology reconstruction and energy-zone definition in subsequent pipeline stages.

4.2. Scan-to-BIM Process: Reconstruction Results

The following section presents results of the Scan-to-BIM workflow for the solid model (Figure 4, step A). A per-class reconstruction strategy (Section 3.3) [94] reconstructs each semantic class separately, allowing class-specific geometric assumptions and constraints, such as axis alignment for walls and columns, which leads to higher precision and completeness. Performance is evaluated using mean Intersection over Union (mIoU) and F1 score, defined in Equations (17) and (18), based on the spatial overlap between predicted elements and minimum Oriented Bounding Boxes (mOBBs) extracted from a manually segmented and classified point cloud that serves as instance level semantic ground truth.

Per class metrics (walls, columns, doors, etc.) are summarized in

Table 3. Scan-to-BIM reconstruction metrics for classes.

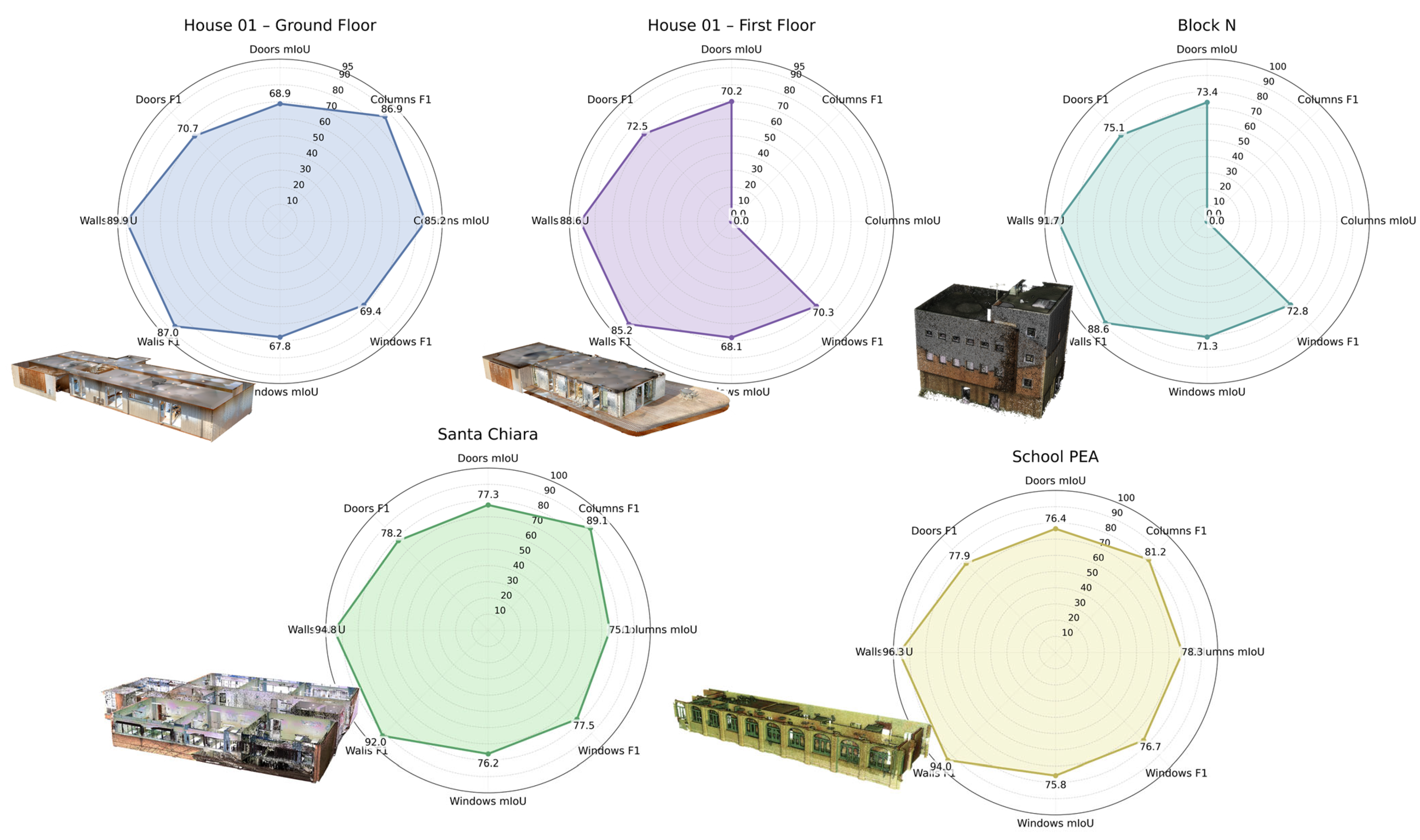
Elements	Metrics	Columns [%]	Doors [%]	Walls [%]	Windows [%]
House 01—First floor NavVis dataset	mIoU	—	70.2	88.6	68.1
	F1	—	72.5	85.2	70.3
House 01—Ground Floor NavVis dataset	mIoU	85.2	68.9	89.9	67.8
	F1	86.9	70.7	87.0	69.4
Block N KULeuven Campus	mIoU	—	73.4	91.7	71.3
	F1	—	75.1	88.6	72.8
Santa Chiara Trento, Italy	mIoU	75.1	77.3	94.8	76.2
	F1	89.1	78.2	92.0	77.5
School PEA Italy	mIoU	78.3	76.4	96.3	75.8
	F1	81.2	77.9	94.0	76.7

and visualized in Figure 11. The overall mesh-to-cloud assessment is reported in Figure 12, last column, where the color bar represents the visual error distribution (ranging from −30 cm to +30 cm). Walls, benefiting from regular geometry and strong structural features, achieve consistently high accuracy (mIoU: 88.6–96.3%; F1: 85.2–94.0%). In contrast, doors and windows, being morphologically similar, frequently occluded, and often affected by clutter, yield moderate accuracy (mIoU: 67.8–77.3%; F1: 69.4–78.2%).

Notably, columns, which are generally a structurally sparse and spatially narrow class, show precision (mIoU: 75.1–78.3%; F1: 89.0–91.2%), though they are absent in certain datasets (House 01 or Block N). Performance varies with structural diversity, noise, occlusions, and class balance, with School PEA and Santa Chiara demonstrating the most consistency. A higher F1 than mIoU indicates reliable detection with some spatial imprecision, such as OBB misalignment. For House 01, separate reconstructions of the ground and first floor plans are shown. Currently, the method supports reconstructing one floor plan at a time. However, by processing each floor individually and subsequently merging them, a complete multi-level reconstruction can still be achieved, as demonstrated for House 01 and Block N.

Overall, the average distances remain low (0.02–0.12 m), with modest standard deviations, indicating isolated rather than systemic errors, and the accuracy is adequate for energy modeling that depends mainly on walls, floors, and ceilings.

Regarding energy-related elements, detection is performed manually via the tool described in Section 3.4. As it relies on visual interpretation rather than automated inference, no quantitative metrics (e.g., Accuracy or Recall) are provided.

4.3. Topologic Solid (TSM) and B-Rep Model Results

The Topologic Solid model (TSM) and B-Rep results are shown in Figure 13. Evaluation results (

Table 4. Metrics evaluation for both TMS- and B-Rep-based models (th = 0.065 m).

Elements	Topological Solid Model (TSM)				B-Rep Model (th = 0.065 m)
	Precision	Recall	F1	mIoU	Precision	Recall	F1	mIoU
House 01—Ground Floor	0.950	0.903	0.926	0.948	0.899	0.879	0.889	0.849
House 01—First Floor	0.961	0.922	0.941	0.958	0.921	0.901	0.911	0.871
Block N—Ground Floor	0.947	0.930	0.938	0.981	0.931	0.911	0.921	0.881
Block N—First Floor	0.973	0.943	0.958	0.968	0.938	0.918	0.928	0.888
Block N—Second Floor	0.984	0.957	0.970	0.972	0.946	0.926	0.936	0.896
Block N—Third Floor	0.983	0.953	0.968	0.969	0.981	0.961	0.971	0.931
Santa Chiara—Italy	0.937	0.879	0.907	0.934	0.898	0.878	0.888	0.848
School PEA—Italy	0.930	0.867	0.897	0.927	0.887	0.867	0.877	0.837

, Figure 14) show that TSMs (step B), also referred to as the CellComplex model, consistently outperform B-Rep models (step C) across all metrics. The accuracy of the surface objects of the B-Rep models was assessed against manually generated GT models, with a particular focus on the mean Intersection over Union (mIoU) parameter. Figure 14 illustrates the evaluation bounding boxes applied for the B-Rep model comparison, using a 0.065 m threshold, specifically for the evaluation of walls only.

Both models achieve high precision (TSM: 0.93–0.98, B-Rep: 0.74–0.95), confirming geometric accuracy when overlaps occur. However, recall is lower for B-Rep models (0.57–0.90) compared to TSMs (0.87–0.96), leading to reduced F1 scores (B-Rep: 0.65–0.89, TSM: 0.90–0.97) and IoU values (B-Rep: 0.72–0.95, TSM: 0.93–0.98). These discrepancies stem from differences in modeling strategy: TSMs represent enclosed volumes, while B-Rep models are surface-based and derived from wall centerlines.

Since GT models define walls by outer surfaces, consistent with energy modeling conventions, B-Rep models, though watertight and structurally correct via DCEL, yield lower recall, F1, and IoU results under voxel-based evaluation.

This effect is most evident in complex datasets. The PEA School, with dense layouts of small rooms and fine-grained partitions, produces the lowest B-Rep scores despite structural correctness.

Likewise, the Santa Chiara dataset, with irregular historic architecture and non-orthogonal geometries, presents challenges for B-Rep modeling and DCEL completion. To account for spatial discrepancies between centerline-based wall B-Rep modeling and the ground truth (GT) external wall surfaces defined by modeling standards, a buffer threshold (th) is applied (Figure 15).

This prevents accurate reconstructions from being unfairly penalized during evaluation, especially in IoU (Equation (18)), F1 (Equation (19)), Precision (Equation (22)), and Recall (Equation (23)). In contrast, TSM defines enclosed volumes explicitly, aligning more naturally with the GT evaluation models and achieving consistently higher scores.

$$\mathit{Precision}={\displaystyle \frac{\left|\left\{p\in P\hspace{0.25em}|\hspace{0.25em}\exists g\in G,\hspace{0.25em}|p-g|<\tau \right\}\right|}{\left|P\right|}}$$

(22)

$$\mathit{Recall}={\displaystyle \frac{\left|\left\{g\in G\hspace{0.25em}|\hspace{0.25em}\exists p\in P,\hspace{0.25em}|g-p|<\tau \right\}\right|}{\left|G\right|}}$$

(23)

where

• $P$ is the set of predicted points $p\in P\hspace{0.25em};$
• $G$ is the set of ground truth points $g\in G$;
• $|p-g|$ is the Euclidean distance between $p\in P$ and $g\in G$;
• $\tau$ is the distance threshold (th).

Despite these discrepancies, the B-Rep results are adequate for energy performance applications because they preserve dimensions, structural logic, semantic clarity, and topological integrity, all of which are essential for simulation and analysis. Furthermore, the B-Rep models have been visually verified in FME^® [101] to confirm model consistency, correct surface orientation, and overall topological validity (Figure 15).

The workflow yields a multi-level DT in which the TSM and B-Rep model coexist and are linked to the graph node structure. The DT is exportable to gbXML, enabling interoperable exchange with building performance simulation environments (Figure 16).

4.4. Energy Simulations

To demonstrate the feasibility of producing a simulation-ready DTL2 (Section 2.8), a preliminary simulation was performed using the model generated by the Scan-to-EDTs workflow in EnergyPlus [14]. The simulation employs an epJSON input file generated from the model output, real-world survey data, and standard simulation parameters.

This file was created using the first version of our custom-built parser–transformer–writer algorithm (Figure 17), developed in-house to process the tailored output.

This proof of concept validates the end-to-end integration of the pipeline, as the successful execution of energy simulations from the generated outputs confirms that the reconstructed zones are geometrically watertight, and the exported epJSON models are structurally consistent with all required inputs, while further robustness improvements are still needed for large-scale deployment. The pipeline also outputs models compatible with the latest CityGML Energy ADE 3.0 (GitHub: https://github.com/tudelft3d/Energy_ADE, URL accessed on 20 August 2025) [102], showing that the semantically enriched topological model maps cleanly to other formats and can upgrade existing single-zone CityGML urban models with multi-zone BEMs toward a more fine-grained UBEM. By embedding volumetric, thematic surface and geometric representations for visualization, the approach enables DTL2 and open platforms to support real-time or historical data display. Together, these results indicate that the end-to-end Scan-to-EDTs pipeline is operational. The interface (Figure 18) supports detailed inspection of the building model, including spatial hierarchies, thermal properties, material layers, and construction details, and it enables testing of retrofit scenarios by varying U values and integrating real-time monitoring data when available.

5. Conclusions and Future Research

This research presents a scalable 3D framework that produces simulation-ready Energy Digital Twins (EDTs) directly from unstructured point clouds, eliminating intermediate manual or BIM stages. The hierarchical schema encodes room volumes, semantic surfaces, and geometric elements in a unified graph structure, ensuring watertight, topologically valid, and semantically coherent models. The resulting EDTs support energy simulation, semantic querying, graph-based navigation, and real-time device integration, with seamless export to B-Rep-based gbXML and CityGML (with Energy ADE) and, optionally, CSG-based IFC for interoperability.

Several innovative aspects distinguish this research:

• Deriving simulation-ready Energy Digital Twins (EDTs) directly from raw point clouds, using a graph-based native architecture that converts unstructured surveys into concrete, topologically consistent models without manual stages or proprietary tools.
• Delivering watertight, simulation ready models with consistent topology and semantics, including adjacency, containment, connectivity, and energy attributes, enabling reliable reasoning, efficient querying, and seamless interoperability.
• Unifying solid and B-Rep representations in a single multi-level gDT and integrated graph, enabling simulations, monitoring, IoT linking, optimization, and cross-scale navigation with consistent behavior across levels.
• Enabling standards-based exchange via gbXML, CityGML and, optionally, IFC, ensuring standards-compliant interoperability while avoiding redundant steps and minimizing data loss across energy and BIM workflows.

In the literature, this paper links (1) point cloud semantics, (2) graph-based building models, and (3) BEM interoperability (via gbXML/IFC); unlike pipelines that rely on manual BIM authoring or mesh cleanup, it directly maps survey data into an energy-aware graph that preserves adjacency, containment, and connectivity and, by supporting both solid and B-Rep in a single multi-level structure, complements Scan-to-BIM while adding a direct-to-BEM route for simulation.

While the pipeline is effective end-to-end, some components can be strengthened. The classification and instance-segmentation modules occasionally introduce label noise, which can affect the stability of the overall workflow. Despite its practical efficiency, the Scan-to-BEM pipeline still relies on interactive elements, including manual device placement, which may introduce user-dependent variability into the results. Certain geometric simplifications (e.g., deriving exterior walls from centerlines) can lead to small deviations, especially at complex façades. Finally, because this is a point-cloud-based workflow, performance remains sensitive to input coverage and quality (e.g., occlusions or sparse scans).

Future research will focus on the geometric reconstruction pipeline for energy-model compliance: (i) improving classification and instance segmentation using state-of-the-art networks; (ii) placing external walls on the true exterior face (replacing the centerline placement used in the presented workflow); (iii) optimizing the epJSON parser–transformer–writer algorithm for parameter customization; (iv) refining the linked Informational Load Dictionaries (ILDs) with explicit schema definitions and improved interoperability mappings; (v) implement better interoperability with the evolving CityGML Energy ADE [102] to inject multi-zone BEMs into single-zone city models and to export gbXML for seamless use in BPS tools; (vi) add high-fidelity IFC mapping to capture rich BIM semantics; and finally, (vii) full automation for simulation-ready BEM generation will streamline deployment across diverse energy-analysis platforms.