Investigating Damage Evolution of Concrete with Silica Fume Under Freeze–Thaw Conditions Using DIC Technology and Gray Model Approach

Abstract

Silica fume (SF) is extensively utilized for enhancing concrete properties. This study examines the impact of SF dosage on concrete frost resistance. Specimens were produced by replacing cement with SF at 5%, 10%, 20%, and 30% ratios. Mechanical testing and microscopic characterization measured variations in mass loss, relative dynamic elastic modulus, flexural strength, hydration products, and pore structure. Digital image correlation tracked failure development during flexural tests. Results indicated that SF-modified concrete showed lower mass loss, better elastic modulus retention, and improved flexural strength maintenance compared to plain concrete after identical freeze–thaw (F-T) cycles. Additionally, SF-modified concrete demonstrated reduced crack widths and slower crack expansion during bending. The 10% SF mixture, after 300 cycles, achieved optimal results characterized by 2.83% mass loss, 88.1% relative dynamic modulus, and only a 17% flexural strength reduction. Microscopic studies confirm that SF addition increases calcium silicate hydrate formation, decreases calcium hydroxide levels, and refines pore structure with higher density. These modifications enhance frost resistance. A service-life prediction model using gray model approach methodology projected that 10% SF concrete would last 2.01 times longer than unmodified concrete under F-T exposure.

1. Introduction

Science and technology are rapidly advancing, making concrete, one of the most widely used materials in construction, play a crucial role in urban planning, civil engineering, underground and underwater projects, nuclear energy endeavors, and various other sectors [1,2]. Enhancing the performance characteristics of concrete is essential for ensuring the quality, safety, and sustainable development of buildings and infrastructure [3]. However, in many cold regions, seasonal F-T cycles remain a primary cause of concrete failure [4,5].

The mineral additives of concrete exhibit outstanding filling capabilities, thereby enhancing its frost resistance [6,7]. Karaaslan [8] studied the internal texture of concrete when modified with fly ash (FA) and discovered that FA fills the voids and cracks, refines the internal texture, and enhances the material’s resistance to freezing. Oyunbileg et al. [9] analyzed the behavior of concrete enhanced with SF through macro and micro tests, concluding that SF improves both its strength and frost resistance. Similarly, Bayraktar et al. [10] investigated the role of FA in enhancing the mechanical and durability features of polypropylene fiber-reinforced concrete, concluding that a 25% FA mixture achieved the highest compressive strength and abrasion resistance during F-T testing. Zhang et al. [11] studied how FA affects the durability of prestressed damaged concrete. Their findings reveal that using 25% FA resulted in lower mass loss rates. Ma et al. [12] varied the FA content and determined that concrete with 20% FA had better frost resistance than concrete with 40% FA after F-T cycles. Blast furnace slag also contributes to improved frost resistance in concrete [13,14]. Zhao et al. [15] investigated the impact of slag content on the frost resistance of fly ash-based polymer concrete. Their research demonstrated that increasing the slag content from 10% to 50% significantly improved the frost resistance of the material. Ding et al. [16] investigated the frost resistance characteristics and pore characteristics of concrete with different proportions of blast furnace slag. Their findings revealed that higher slag substitution rates led to reduced cement hydration, increased capillary pore content, and decreased frost resistance. Yavuz et al. [17] studied the impact of SF on the mechanical properties of porous concrete after F-T cycles and found that the addition of SF improved the residual compressive strength, splitting tensile strength, and flexural strength of the concrete. Das et al. [18] used glass powder instead of fly ash to demonstrate the potential of glass powder to enhance sustainability while maintaining good mechanical and durability properties. A 30% glass powder substitution level increased the flexural and tensile properties of concrete by an average of 20%, forming a denser microstructure. Matos et al. [19] ground broken waste glass and used it as a partial cement substitute in mortar, demonstrating stronger resistance to chloride penetration, which increased with the increase in glass powder content. At the same time, the concrete with glass powder added also had much higher resistance to sulfate attack than that with fly ash added.

In recent years, researchers have conducted numerous experiments to investigate the enhancement of concrete performance through the use of SF [20,21,22,23]. Gencel et al. [24] investigated the impact of SF content on foam concrete’s compressive strength, reporting that materials with 15% SF exhibited a 46% increase in compressive strength. Saradar et al. [25] examined the influence of SF on the slump and shrinkage of lightweight concrete, revealing that the addition of SF led to a 24% reduction in slump and a 19% decrease in shrinkage rate. Furthermore, the incorporation of SF enhances the interface between fibers and the concrete matrix, thereby improving the strength of fiber-reinforced concrete; specimens with 15% SF exhibited a 218% increase in flexural strength [26]. Aghajanzadeh et al. [27] conducted research on the properties of alkali-activated slag concrete with SF, employing response surface methodology, and found that an optimal SF content of 8.1% resulted in a notable enhancement of the specimens’ properties. Xiao et al. [28] studied the impact of SF on marine anti-washout concrete and discovered that the concrete with 10% SF achieved the highest compressive strength. Buller et al. [29] examined the healing capacity of concrete containing SF and found that at an SF content of 7.5%, the crack surfaces were entirely filled.

The durability of concrete is affected by various elements, and numerous scholars have conducted research on this subject [30,31,32]. Zhou et al. [33] investigated the impact of factors on the durability of permeable concrete, predicting its lifespan in certain regions of China. Their findings indicate that the maximum utilization period of permeable concrete could reach 227.81 years. The type of salt significantly influences the resistance of concrete in a freezing environment. Guo et al. [34] utilized the Wiener random model for predicting the service life of concrete under various salt-freezing scenarios, revealing that the maximum service life under sulfate conditions is 1.26 to 1.86 times longer than when chloride conditions are applied. Qin et al. [35] assessed the durability of concrete exposed to external sulfate attack by employing a predictive model developed based on factors such as the ion diffusion coefficient. Additionally, Dudi et al. [36] found that the water/cement ratio significantly affects the prediction of concrete service life and that reducing the ratio from 0.5 to 0.4 doubled the service life.

Currently, research on enhancing the F-T resistance of concrete primarily relies on traditional macroscopic mechanical testing and microscopic structural analysis. These methods only provide final-state results and static indicators after F-T cycles, failing to reveal the crack initiation and evolution processes during F-T and loading. This study innovatively introduces DIC technology to visualize cracks and analyze the entire process from local micro strain to macro crack initiation, propagation, and ultimate failure [37,38]. Concrete specimens with varying SF dosages (0%, 5%, 10%, 20%, 30%) were prepared. By integrating DIC damage analysis, mechanical performance testing, and microstructural characterization, the optimal dosage was determined. This dynamic damage evolution perspective deepens the understanding of the mechanism by which silica fume enhances concrete durability.

2. Research Value

2.1. The Novelty

The novelty of this study lies in the pioneering combined application of DIC technology and gray system theory to elucidate the F-T damage mechanisms of SF-modified concrete from macro- to meso-scales. By quantitatively characterizing the evolution of crack width and propagation rate under flexural loading via DIC, this research provides direct experimental evidence for the frost resistance enhancement mechanism of SF. Furthermore, a high-precision service life prediction model was established based on the integrated methodology.

2.2. Research Significance

This study offers critical theoretical and data support for the durability design of concrete structures in extreme cold regions. By identifying the optimal SF content and demonstrating its remarkable anti-freezing effects, it provides clear guidance for developing high-durability, long-service-life concrete materials. The accurate life prediction model developed herein serves as a vital technical tool for durability design and service life assessment in engineering practice, underscoring the substantial application value of this research.

3. Experimental Design

3.1. Material and Mix Design

The concrete utilizes a standard Portland cement from Haixi Chemical Plant (Qinghai West Chemical Building Materials Co., Ltd., Qinghai, China.), with its composition details outlined in Table 1. Ultra-fine and highly active SF (Hebei Zhuofei mineral products Co., Ltd., Hebei, China) is used, and its chemical compositions is detailed in Table 2. The aggregate is selected with a diameter of 5–20 mm, and the aggregate is sieved into coarse aggregate (10–20 mm) and fine aggregate (5–20 mm). The sand is natural river sand, with an accuracy modulus of 2.5, and the water reducing agent is huiba brand high-efficiency water reducing agent produced by Laiyang Hongxiang building admixture factory in Shandong Province, China. The concrete mix proportion is documented in Table 3. Choosing appropriate levels of SF content (5%, 10%, 20%, and 30%) can more significantly demonstrate the effect of SF content on concrete performance [22,23,24,25,26,27,39].

Table 1. The main chemical components and ratio of cement.

Chemical Components	Al2O3	SiO2	SO3	Cl	TiO2	Fe2O3	Na2O	K2O	MgO	CaO
Content (%)	4.16	20.42	2.75	0.028	0.341	2.83	0.7	0.46	1.6	60.74

Table 2. The chemical components and proportion of SF.

Chemical Components	Al2O3	SiO2	Fe2O3	Na2O	MgO	CaO
Content (%)	1.28	91.8	2.83	0.9	0.6	1.35

Table 3. Concrete mix’s specific proportions (kg/m³).

Water	Water–Cement Ratio	Coarse Aggregate	Fine Aggregate	Sand	Water-Reducing Agent	Air-Entraining Agents
164.66	0.36	688.82	688.82	982.42	1.85	0.23

3.2. Specimen Preparation and Experimental Methods

According to the Chinese standard “Test Code for Hydraulic Concrete” (DL/T 5150-2017) [40], concrete samples of 100 × 100 × 400 mm dimensions were processed and cured for 28 days after demolding. The specimens were numbered based on the amount of SF used, with the details provided in Table 4. These F-T cycle tests were carried out using the rapid freezing method outlined in the Chinese standard “Test Method for Long-term Performance and Durability of Ordinary Concrete” (GB/T 50082-2024) [41]. During the experimental process, each F-T testing cycle was conducted for a duration of 2–4 h, with the melting phase accounting for at least one-fourth of the total cycle time. A total of 300 F-T testing cycles were executed, systematically organized into groups of 25 cycles each. Following each individual testing cycle, comprehensive analyses were performed on the concrete samples, focusing on their apparent morphology, mass degradation rate, relative dynamic modulus, and nuclear magnetic resonance characteristics. Specifically, the calculation of the mass degradation rate was formulated as Equation (1), while the relative dynamic modulus was determined using Equation (2). Upon completion of all testing cycles, flexural strength evaluations were conducted to assess the propagation characteristics of cracks within the concrete material.

$$\mathsf{\Delta }M={\displaystyle \frac{w_0-w_n}{w_0}}\times 100\%$$

(1)

$$E_{dR}={\displaystyle \frac{f_n^2}{f_0^2}}\times 100\%$$

(2)

where ΔM represents the mass loss of the specimens after n F-T cycles (%), w₀ is the mass of the specimens before the F-T cycles (g), and w_n is the mass of the specimens after n F-T cycles (g). Additionally, E_dR denotes the relative dynamic modulus of elasticity (%) of the specimen after n F-T cycles, f₀ is the self-oscillation frequency (Hz) of the specimen before the F-T cycles, and f_n is the self-oscillation frequency (Hz) of the specimen after n F-T cycles.

Table 4. Concrete specimen number and SF content.

Group Name	G0	G5	G10	G20	G30
SF content (%)	0	5	10	20	30

The 100 mm × 100 mm × 400 mm specimens, before and after 300 F-T cycles, were placed on the test platform with their surfaces dried. Prior to testing, a stochastic speckle pattern was applied to the specimen surface for DIC analysis by first spraying a white matte base coat followed by black matte paint. The system was equipped with two cameras with a resolution of 3320 × 3320 pixels. During the stable loading stage, images were captured at a frequency of 1 Hz. A subset size of 29 × 29 pixels and a step size of 5 pixels were selected. The DIC system, including high-resolution cameras and a light source, was then set up and calibrated to ensure measurement accuracy. After the test commenced, the DIC system was activated to capture images in real time during the loading process. Throughout loading, camera stability was maintained to prevent image blurring caused by vibration. Figure 1 shows the three-dimensional full-field deformation measurement system. The DIC system operates by defining subsets of pixels centered on pre-defined calculation points in the undeformed reference image. Subsequently, for corresponding regions in the deformed images, iterative algorithms like the inverse compositional Gauss–Newton are used for search and matching to precisely determine the new position of each subset center. The displacement components of these calculation points yield full-field displacement data, providing the basis for subsequent strain calculation and damage analysis. The experimental process is depicted in Figure 2. This study considered potential errors and limitations in the DIC measurements. System errors caused by lens distortion were minimized through a rigorous calibration process. Random errors due to speckle pattern quality and noise were mitigated by ensuring a high-contrast, fine-grained speckle pattern. The selection of subset and strain window sizes represents a compromise between spatial resolution and measurement noise.

Figure 1. Three-dimensional full-field deformation measurement system.

Figure 2. Experimental test equipment and procedures.

During specimen preparation, all concretes were produced following identical mixing procedures and a constant water-to-binder ratio. SF was incorporated by replacing part of the cement at equal mass. The dosages of the water-reducing agent (1.85 kg/m³) and air-entraining agent (0.23 kg/m³, Laiyang Hongxiang building admixture factory, Shandong, China) were kept constant across all mixtures to isolate the effect of SF on frost resistance. The measured air contents ranged from 2.1% to 5.2%, showing only slight variations in the air–void system, which are attributed to minor rheological differences introduced by SF rather than intentional dosage adjustments.

4. Results and Discussion

4.1. Apparent Morphology

Figure 3 illustrates the surface morphology of concrete modified with SF. Figure 3a–d illustrate the progressive deterioration of the G0 throughout the F-T cycling test. It was observed that the degree of surface degradation escalated with increasing F-T cycles. The concrete surface developed extensive surface pitting accompanied by gradual detachment of the surface mortar, which ultimately led to the formation of erosion pits. In contrast, Figure 3e–h demonstrate that SF-modified concrete specimens exhibited significantly reduced surface damage and maintained superior surface integrity. Notably, among all modified mixtures, the specimen with 10% SF content displayed the most minimal surface deterioration, characterized by only minor pitting without significant aggregate exposure. These observations conclusively demonstrate that the incorporation of 10% SF effectively enhances the frost resistance of concrete.

Figure 3. The surface morphology of concrete modified with SF. (a) G0 before F-T cycles, (b) G0 after 100 F-T cycles, (c) G0 after 200 F-T cycles, (d) G0 after 300 F-T cycles, (e) G5 after 300 F-T cycles, (f) G10 after 300 F-T cycles, (g) G20 after 300 F-T cycles, (h) G30 after 300 F-T cycles.

4.2. Mass Loss

Figure 4 illustrates how the mass loss rate of concrete modified with SF changes with the number of F-T cycles. The experiments revealed that concrete samples with different amounts of SF initially showed reduced mass loss, which was later accompanied by an increase in mass loss as the number of freezing–thawing cycles increased. The mass of each specimen reached its maximum at 50 cycles and then began to decrease. Following 200 F-T cycles, the rate of mass loss exhibited a sharp increase. This mass loss during F-T cycling consists of two components. One component of the mass loss is the deterioration of internal microcracks early in the F-T cycle. These cracks absorb water and become saturated, leading to an initial increase in weight. The second component is the spalling of mortar as well as coarse and fine aggregates from the concrete surface. The evolution of concrete mass under F-T cycling exhibits distinct phases, which can be systematically characterized. During the initial phase, the observed weight increase is primarily attributed to water absorption through existing cracks, which surpasses the compensatory mass loss caused by surface spalling, thereby leading to an overall net gain in weight. As the number of F-T cycles progressively increases, the second phase is marked by an intensification of surface spalling, resulting in a net decrease in the measured mass. In the final phase, the rate of mass loss undergoes a significant acceleration. Prior studies by Shi et al. [42] and Qiu et al. [43] also found that concrete’s mass initially increases and then decreases under F-T cyclic conditions and that the rate of mass loss accelerated after a certain number of cycles.

Figure 4. Mass loss rate of concrete modified with SF.

For the same number of cycles, the G0 specimen experienced the greatest mass loss, reaching 5.91% at 300 cycles. This was 1.41%, 3.08%, 2.19%, and 1.74% higher than the mass loss observed in the G5, G10, G20, and G30 specimens, respectively. All specimens were water-cured and maintained in a saturated condition prior to F-T testing. Therefore, during the early stage (within 50 cycles), the degree of damage was limited, and all concretes exhibited similar mass gains due to surface water absorption. This behavior mainly results from the filling of surface-connected pores and microcracks rather than internal deterioration [44,45]. The G10 specimen, although denser, showed a comparable early mass increase because the initial absorption is governed by surface wetting rather than bulk porosity. The enhancement from SF is, thus, not reflected in the early absorption stage but in its ability to resist internal stresses in subsequent cycles, preventing defect coarsening and mass loss [46]. This mechanism highlights the role of SF in improving frost resistance by enhancing interfacial bonding, reducing osmotic pressure, and densifying the matrix, while excessive SF incorporation weakens these benefits.

4.3. Modulus of Elasticity

Table 5 presents the dynamic elastic modulus of SF-modified concrete under F-T cycles. It can be observed that the dynamic elastic modulus decreases with increasing number of F-T cycles. However, the decay rate of the dynamic elastic modulus in concrete specimens incorporating SF is significantly slower than that of G0, with G10 exhibiting the best performance and the highest initial dynamic elastic modulus of 42.01 GPa before F-T cycling. After 300 F-T cycles, the retention ratios of the dynamic elastic modulus for G0, G5, G10, G20, and G30 are 70.6%, 79.4%, 85.6%, 83.3%, and 82.0%, respectively. These results indicate that the incorporation of SF not only enhances the initial dynamic elastic modulus of concrete but also significantly improves its retention capacity under F-T conditions, thereby comprehensively improving both the mechanical properties and durability of concrete.

Table 5. Dynamic elastic modulus of SF-modified concrete under F-T cycles.

	Dynamic Elastic Modulus/GPa
Number of F-T Cycles	G0	G5	G10	G20	G30
0	36.36	38.08	42.01	40.35	39.72
25	35.35	37.50	41.60	39.94	39.04
50	34.67	37.10	41.49	39.73	38.91
75	33.84	36.39	40.80	38.89	38.18
100	33.35	35.66	40.34	38.41	37.37
125	32.65	34.86	39.86	38.06	37.01
150	32.23	34.53	39.45	37.25	36.37
175	31.37	33.96	38.93	36.66	35.92
200	30.53	33.36	38.36	36.03	35.33
225	29.54	32.67	37.89	35.71	34.82
250	28.68	32.06	37.30	35.19	34.10
275	27.39	31.36	36.65	34.39	33.30
300	25.67	30.22	35.96	33.61	32.58

The relative dynamic elastic modulus of concrete modified with SF exhibited a notable variation in response to the increasing number of F-T cycles, as illustrated in Figure 5. With each additional F-T cycle, the decrement in the dynamic elastic modulus of the concrete specimens accelerated in magnitude. Notably, the relative modulus loss rates for G5, G10, G20, and G30 groups were consistently lower than those observed in the G0 control group, suggesting enhanced frost resistance. At the 300th F-T cycle, the modulus loss for G5 and G10 was 67.9% and 47.6%, respectively, relative to G0, indicating a substantial improvement in frost resistance. However, as the incorporated SF content continued to rise, the modulus loss rate exhibited an upward trend. When SF reached 30%, the modulus loss for G30 was 57.8% of G0, implying that excessive SF content did not yield significant benefits in terms of frost resistance enhancement.

Figure 5. Relative dynamic elastic modulus of concrete modified with SF.

The decrease in the dynamic elastic modulus of concrete is predominantly attributed to the progressive degradation of its internal structural integrity, which can be characterized by two distinct phases. In Stage I, with an increment in the number of F-T cycles, microcracks begin to develop in the concrete slurry. At this stage, the number of cracks is relatively low, leading to a gradual decline in the relative dynamic modulus. In Stage II, as the number of F-T cycles progresses, the quantity and dimensions of pores grow progressively, and numerous cracks begin to develop in the interface area. Consequently, undergoing F-T cycles, concrete aggregates and slurry experiences a process of deterioration, which leads to the propagation of microcracks and the degradation of its internal structure, resulting in an accelerated decline in relative dynamic modulus. Additionally, the relative dynamic elastic modules of G0 decreases rapidly in Stage II, whereas the modules for G5, G10, G20, and G30 decrease more gradually. SF’s fill performance optimizes the particle size distribution within the cementitious system of concrete, effectively minimizing large pores and reducing overall porosity. This treatment enhances the internal density of the concrete, delays the decline in relative dynamic elastic modulus under F-T cycles, and forms a gel network via its pozzolanic effect with Ca(OH)₂. This gel acts as a filler, improving internal pore structure and dispersing interconnected macropores, thereby reducing water infiltration and minimizing water content during F-T cycles, thus further slowing the decline in relative dynamic elastic modulus. Admixtures significantly enhance the internal structure of concrete, leading to a reduction in the rate of dynamic modulus decrease under F-T loading cycles, as demonstrated by Zeng et al. [47] and Lu et al. [48].

4.4. Flexural Strength

The flexural strength of concrete modified with SF is illustrated in Figure 6. The inclusion of SF significantly enhances the flexural resistance of concrete. Initially, the concrete’s strength increases with addition quantity, yet strength will eventually weaken as the quantity surpasses an optimal threshold. The minimum flexural strength of concrete without SF is 3.78 MPa. In contrast, the flexural strengths of concrete specimens G5, G10, G20, and G30 are generally higher than that of the G5. The maximum flexural strength occurs at an SF content of 10%, where it is increased by 44.6% compared to G0. Such an improvement can be attributed to the Pozzolanic reaction resulting from the interaction between SF and cement hydrates’ chemical constituents, which forms a novel slurry gel and optimizes the interface between the original cement slurry and aggregates. Analysis of the loss rates reveals that although the residual flexural strengths of G5, G10, and G20 are similar, the G10 specimens exhibited the lowest flexural strength loss rate after 300 F-T cycles, at a mere 17.12%. In comparison, the loss rates for G0, G5, G20, and G30 were 27.72%, 20.87%, 19.91%, and 20.88%, respectively. This indicates that G10 not only possesses superior initial performance but also the most robust mechanism for maintaining its mechanical integrity against F-T damage. The refined particle dimensions of SF enhance micropore uniformity in cementitious composites, strengthening concrete. However, elevated SF content proportionally diminish cement proportions, causing deficient C-S-H gel formation and subsequent strength reduction [49,50]. Research identifies 10% SF as the optimal threshold for maximizing flexural strength.

Figure 6. Flexural strength of concrete modified with SF.

4.5. Flexural Cracking Behavior

4.5.1. DIC Analysis

The flexural behavior of concrete under four-point bending, as shown in Figure 7a, demonstrates four progressive mechanical stages: initial stage (Stage I), crack initiation (Stage II), crack propagation (Stage III), and structural destabilization (Stage IV) [51,52]. During Stage I–II, displacement escalates proportionally with incremental loading until maximum load capacity is achieved. As shown in Figure 7b, untreated specimens (G0 group) registered a pre-F-T peak load of 15.34 kN, which reduced to 10.11 kN after 300 F-T cycles. Specimens modified with 10% SF exhibited superior performance, attaining 13.01 kN peak load post-cycling. Stage III reveals a pronounced reduction in load-bearing capacity across all specimens, with unmodified concrete experiencing the steepest decline. This contrast highlights SF’s effectiveness in enhancing structural stability through improved cement–aggregate interfacial bonding and densified microstructure. In Stage IV, load–displacement curves exhibit progressive deceleration until a residual strength of zero is reached, indicating complete failure of the specimen. These results confirm that F-T cycles critically impair concrete’s flexural resistance, while SF incorporation mitigates flexural strength degradation by optimizing the interfacial transition zone and concrete compactness.

Figure 7. Displacement load diagram of concrete modified with SF during bending process. (a) Sketch map. (b) Displacement load diagram of each group.

Figure 8 illustrates crack evolution mechanisms in SF-enhanced concrete samples subjected to 300 F-T cycles through maximum principal strain analysis via DIC monitoring. As shown in Figure 8a, for uncycled G0 group samples (Stage I), initial strain localization emerges near the lower part without substantial overall deformation. Stage II demonstrates progressive strain escalation propagating upward from the lower region under intensified loading. After reaching Stage III, distinct strain concentration bands appear in the strain cloud map, and the surface strain becomes noticeably concentrated and rapidly expands. In Stage IV, final failure manifests through strain accumulation developing within the central section, culminating in complete structural failure through full-section penetration.

Figure 8. Strain cloud map of concrete modified with SF during bending process. (a) G0 before F-T cycles, (b) G0 after 300 F-T cycles, (c) G5 after 300 F-T cycles, (d) G10 after 300 F-T cycles, (e) G20 after 300 F-T cycles, (f) G30 after 300 F-T cycles.

Figure 8b demonstrates significant degradation in G0 specimens after 300 F-T cycles, manifested through interconnected fracture networks and a dominant primary fracture path during failure Stage (Stage IV). The distinct trapezoidal strain concentration pattern observed through DIC corroborates complete specimen failure, confirming compromised structural integrity and diminished flexural resistance. Comparative analysis reveals consistent fracture initiation patterns across SF-reinforced specimens during initial loading (Stage I), characterized by homogeneous strain distribution. Subsequent stress redistribution in Stage II initiates localized strain accumulation at the specimen base. In Stage III, as the flexural tests progress, the specimen’s surface exhibits strain concentration that expands upwards. As depicted in Figure 8d, the width and extent of crack propagation in the G10 group specimens are smaller than those in other groups. This performance enhancement stems from SF-induced matrix densification and interfacial reinforcement, effectively retarding crack nucleation and development through enhanced energy dissipation mechanisms during bending deformation.

At the initiation of crack propagation in each stage, continuous points are selected along the horizontal direction, and the lateral displacement of each point is calculated using DIC, as shown in Figure 9. According to Figure 9a, the transverse displacement of each point in the G0 group specimen before F-T cycling is nearly identical in stages I and II, with no significant cracks observed. In Stage III, a notable difference in lateral displacement of approximately 0.32 mm is recorded near the horizontal axis at −1 mm. In the final Stage IV, the lateral displacement difference significantly increases to 0.51 mm. Figure 9b reveals comparable transverse displacement patterns in G0 specimens during Stages I and II before and after 300 F-T cycles. During flexural tests, progressive divergence between lateral and vertical displacements manifested crack initiation and propagation. Notably, Stage IV exhibited a 1.12 mm lateral displacement differential in F-T cycled specimens, demonstrating structural deterioration induced by F-T cycling. Post-300 F-T cycles, Stage IV crack sliding displacements for specimens G5, G10, G20, and G30 were 85%, 49%, 63%, and 81% of G0, respectively. These findings demonstrate SF’s efficacy in mitigating crack displacement and retarding shear crack progression during flexural failure, with optimal performance at 10% SF incorporation.

Figure 9. Lateral displacement of each point during bending process. (a) G0 before F-T cycles, (b) G0 after 300 F-T cycles, (c) G5 after 300 F-T cycles, (d) G10 after 300 F-T cycles, (e) G20 after 300 F-T cycles, (f) G30 after 300 F-T cycles.

4.5.2. Crack Behavior Analysis

Starting from the initial moment, the crack -opening width in Stages I and II is calculated at a sampling interval of 2 s per frame. Due to the rapid crack propagation in Stages III and IV, comprehensive monitoring of crack propagation enables systematic evaluation of crack width evolution and velocity parameters, the crack opening width is calculated at a sampling interval of 0.1 s per frame in these stages. Figure 10 shows the DIC calculation area and intercept position, with transect lines defined at heights of 20 mm, 50 mm, and 80 mm within the specimen area. Figure 11 illustrates the temporal evolution of the crack-opening width, where the photo sampling interval is used as a proxy for time.

Figure 10. DIC calculation area and intercept position. (The three red lines from bottom to top are ab, cd, and ef, indicating the sections used to measure lateral displacement and crack development at different heights.).

Figure 11. Process of changing the width of cracks. (a) G0 before F-T cycles, (b) G0 after 300 F-T cycles, (c) G5 after 300 F-T cycles, (d) G10 after 300 F-T cycles, (e) G20 after 300 F-T cycles, (f) G30 after 300 F-T cycles. (The red dotted rectangles indicate the areas that are enlarged in the insets, and the arrows point from the original regions to their corresponding enlarged views).

Figure 11 demonstrates dynamic variations in crack opening width during specimen failure. In Stage I, due to the absence of surface cracks on the specimen, it appears as a horizontal straight line in the figure. After entering stage II, surface cracks begin to form, leading to an increase in the width of crack openings. The comparative analysis of Figure 11a,b reveals that post-F-T cycled specimens exhibit initial crack width expansion relative to untreated counterparts, indicating that the specimens are more prone to cracking. During Stages III and IV, accelerated crack propagation culminates in structural failure, with maximum crack width measured at the designated a-b intercept upon Stage IV termination. Post-300 F-T cycles, G0 registers a peak crack width of 1.83 mm. Comparatively, G5, G10, G20, and G30 attain 63%, 39%, 48%, and 72% of G0’s maximum width, respectively. This may be due to the addition of SF, which densifies the concrete structure and consequently reduces the crack opening width.

The evolution of crack expansion rates throughout the failure progression of concrete specimens incorporating varied SF admixtures is illustrated in Figure 12. As seen in Figure 12, crack expansion initially begins at a low rate, then fluctuates and increases, before accelerating rapidly. This occurs because, in Stage I, no surface cracks are present. After Stage II, surface cracks begin to form, expand, and interconnect, causing the crack expansion rate to rise. However, the presence of aggregates hinder crack propagation, resulting in a slower rate. During Stage III–IV, crack propagation preferentially circumvents aggregate interfaces, inducing a rapid increase in the expansion rate, eventually resulting in the cracks fully penetrating the specimen.

Figure 12. Concrete crack expansion rate. (a) G0 before F-T cycles, (b) G0 after 300 F-T cycles, (c) G5 after 300 F-T cycles, (d) G10 after 300 F-T cycles, (e) G20 after 300 F-T cycles, (f) G30 after 300 F-T cycles. (The red dotted rectangles indicate the areas that are enlarged in the insets, and the arrows point from the original regions to their corresponding enlarged views.)

Taking the peak rate in Stage IV as the maximum crack expansion rate, the G0 specimen registers 1.15 mm/s expansion rate prior to F-T. After F-T cycling, the expansion rate of the G0 specimen increases to 2.23 mm/s, which is 193.9% of the rate before F-T cycling. The F-T cycles progressively degrade the concrete structure, leading to this increase. The crack expansion rates of G5, G10, G20, and G30 after the F-T cycles are 88.8%, 75.3%, 92.4%, and 92.8% of G0, respectively, indicating that the concrete achieved its best freezing resistance with a 10% SF admixture.

4.6. Microstructural Characterization of Concrete Modified with SF

4.6.1. Analysis of Hydration Products

Figure 13a shows the thermogravimetric (TG) curves of different specimens before the F-T cycles. TG curves generally exhibit four characteristic phases during thermal decomposition. Stage I ranges from room temperature to 120 °C, during which the primary loss of free water and some crystallization water occurs. Stage II spans from 120 °C to 400 °C, during which C-S-H undergoes dehydration and decomposition. Stage III ranges from 400 °C to 500 °C, where Ca(OH)₂ is the main decomposing material. Stage IV occurs above 500 °C and corresponds to the decomposition of carbonate materials. The specimen with a 5% SF admixture exhibited the least weight loss of only 13.15%.

Figure 13. TG-DTG curves of different specimens before F-T cycles. (a) TG curve, (b) DTG curve. (The arrow indicates the substance losing weight at this stage).

The derivative thermogravimetric (DTG) curves of various samples prior to the F-T cycles are displayed in Figure 13b. During Stage III, a distinct mass loss peak emerges on these curves. Interestingly, the peak area demonstrates an initial reduction followed by expansion as SF content increases. Notably, G0 specimens exhibit a larger peak area compared to G10 counterparts, suggesting greater Ca(OH)₂ quantities in the G0 group. This phenomenon results from SF’s pozzolanic activity triggering secondary hydration reactions that consume Ca(OH)₂. Table 6 presents the content of major hydration products for different specimens. As seen in Table 5, G10 contains the lowest Ca(OH)₂ content, with a weight loss of 3.70% in Stage III. G10 also contains the highest C-S-H content, with a weight loss of 12.48% in Stage II, which contributes to improved frost resistance. The content of the main hydration products is calculated as follows [53]:

$$w_{C-S-H}=b\times {\displaystyle \frac{1255.26}{26\times 18.02}}$$

(3)

$$w_{Ca{(OH)}_2}=c\times {\displaystyle \frac{74.09}{18.02}}$$

(4)

$$w_{total}={\displaystyle \frac{w-d_2}{w}}$$

(5)

Table 6. Content of hydration products in concrete.

Group Name	C-S-H (%)	Ca(OH)2 (%)	Total Loss of Water (%)
G0	9.53	7.37	20.20
G5	9.20	5.00	13.15
G10	12.48	3.70	15.13
G20	9.37	3.75	15.75
G30	7.16	4.71	20.88

In the formula, w_C-S-H is the mass of the hydration product C-S-H, b is the quality loss of stage II, c is the quality loss of stage III, w is the total mass, and d₂ is the mass at the end of stage IV.

The active SiO₂ in SF reacts with the cement hydration product, Ca(OH)₂, to generate more C-S-H gel with gelling properties. The optimization of this hydration product, namely the increase in C-S-H gel and the consumption of Ca(OH)₂, significantly enhanced the compactness and integrity of the cement matrix, which also explains why the G10 group of specimens showed the lowest flexural strength loss rate and the highest relative dynamic modulus retention rate in the F-T cycles.

4.6.2. Analysis of Air Content in Freshly Mixed Concrete and Pores in Hardened Concrete

To investigate the effect of SF on the frost resistance of concrete, the air content of fresh concrete mixtures was tested, and the results are shown in Figure 14. The air content gradually decreased with the increase in SF content and with a maximum air content of 5.2% observed in mix G0. This reduction is attributed to the extremely fine particles and high specific surface area of silica fume, which significantly increase the viscosity of the paste, thereby trapping and hindering the movement and escape of air bubbles. Additionally, the micro-filler effect of silica fume densifies the concrete matrix, directly reducing the space available for air and compromising air bubble stability, ultimately leading to a decrease in air content. This result is consistent with the findings of Mei et al. [54] that the air content of fresh concrete decreases with increasing silica fume content. It is noteworthy that excessively low air content can significantly impair frost resistance, while excessively high air content may compromise strength. Therefore, the frost resistance and durability of concrete are optimized at a moderate air content [55].

Figure 14. Air content of fresh concrete.

Figure 15 illustrates the T₂ spectral distribution profile of SF-modified concrete specimens under F-T cycling. The profile exhibits multiple distinct peaks, presenting three characteristic peaks: the primary peak corresponds to transition and cementitious pores, the secondary peak corresponds to capillary pores, and the tertiary peak represents macropores. The primary peak demonstrates the highest amplitude, with progressively reduced magnitudes observed in subsequent peaks. The classification boundaries of the T₂ relaxation time were determined by combining the characteristic inflection points in the measured spectra with reference values reported in previous NMR studies on cementitious materials. Specifically, pores were divided into four categories: gel pores (T₂ < 1 ms), transition pores (1 ms ≤ T₂ < 10 ms), capillary pores (10 ms ≤ T₂ < 100 ms), and large pores (T₂ ≥ 100 ms). These boundaries are consistent with the typical ranges used in the literature [56,57]. Overall, expanded peak areas are observed following F-T cycling, accompanied by marginally enhanced signal intensities. Throughout F-T exposure, extended F-T cycling induces a slight rightward shift in peak positions corresponding to transition and capillary pores, with more pronounced positional alterations in capillary pores. Simultaneously, the amplitude of corresponding peaks increases with cycling progression. Progressive F-T cycling induces both amplitude enhancement and rightward migration in secondary and tertiary peak inflection points, indicating elevated macropore content and capillary pore development. As shown in Figure 15a, G0 group porosity measurements throughout the 0–300 F-T cycles register 0.92%, 1.04%, 1.21%, 1.59%, 1.96%, 2.41%, and 2.85%, respectively. This phenomenon arises from cyclic phase transitions of interstitial water during F-T cycles, initiating novel pore formation while promoting existing pore coalescence. At the same time, some existing pores will gradually break down due to the expansion because of the repeated F-T cycles of water, evolving towards larger pores and gradually transforming into capillary and macropores.

Figure 15. Distribution curve of T₂ spectrum of concrete. (a) G0, (b) G5, (c) G10, (d) G20, (e) G30. (The red dotted line is the boundary of aperture Division).

A comparison of Figure 15a,c reveal that the porosity of the G10 specimen following the 300 F-T cycles corresponds to 71% of the G0 specimen. Prior to F-T exposure, the G0 specimen exhibited a substantially greater peak area relative to the G10 specimen, suggesting higher porosity in the matrix of SF-free concrete compared to its 10% SF-modified concrete. This difference is due to the fact that SF reduces pore content and promotes structural densification through a filling effect and also due to the pozzolanic reaction of SF, which involves a secondary hydration reaction with Ca(OH)₂ to produce C-S-H gel, thus optimizing the pore structure. Analysis of Figure 15d,e demonstrates that both G20 and G30 specimens display markedly expanded peak areas compared to G10, attributable to SF overdosage and inhomogeneous dispersion. These factors induce particle agglomeration, ultimately increasing void formation and microstructural defects during concrete hardening. Post-300 F-T cycles, the G0 specimen showed amplified secondary and tertiary peak areas versus G10, reflecting its inherently higher initial porosity. The F-T cycles led to the repeated freezing and expansion of pore water during freezing phases, accelerating crack propagation and pore coalescence in the G0 specimen. To verify the robustness of the pore classification, a sensitivity check was conducted by shifting the T₂ boundary values within ±20%. The results showed only minor variations in the relative proportions of each pore type, and the overall distribution trends remained unchanged. SF particles not only directly fill the micro pores but also its secondary hydration product, C-S-H gel, which further blocks the pore connectivity path, thus improving the compactness of the matrix. This optimized pore structure effectively suppresses the freezing–expansion stress of pore water during the F-T process and delays the initiation and propagation of microcracks. Therefore, the G10 group suffered the least damage in terms of mass, relative dynamic modulus of elasticity, and flexural strength during the F-T process.

The pore size distribution in cementitious materials, including gel pores, transition pores, capillary pores, and macropores, for SF-modified concrete subjected to F-T cycles is presented in Figure 16. Figure 16a demonstrates that F-T cycling reduces the relative volume of smaller pores (gel and transition pores) while increasing the proportion of larger pores (capillary pores and macropores). Initial measurements for the control group (G0) prior to F-T exposure revealed pore volume percentages of 29.01% gel pores, 45.84% transition pores, 21.12% capillary pores, and 4.03% macropores. Following the 300 F-T cycles, these values shifted to 20.31%, 45.09%, 23.02%, and 11.58%, respectively. This microstructural evolution stems from cryogenic pore solution migration towards undersaturated regions, generating hydrostatic stresses that exceed the concrete’s tensile capacity. Subsequent wall fracture and crack propagation induce cumulative damage through cyclic loading, facilitating pore coalescence and enlargement. Notably, SF incorporation effectively ameliorates pore structure degradation. Specimens containing 5%, 10%, 20%, and 30% SF exhibited post-cycling harmful pore (capillary + macropore) contents of 32.3%, 30.1%, 32.6%, and 34.4%, respectively. The improvement mechanism involves SF-enhanced matrix densification and reduced pore connectivity, which collectively inhibit pore development under F-T cyclic conditions. When the SF content is 10%, the proportion of harmful pores is the lowest after the 300 F-T cycles at only 30.1%. This indicates the existence of an optimal 10% SF dosage, at which the optimization effect of SF on the pore structure is most significant, thereby maximizing the macroscopic frost resistance of concrete. Specifically, the quality loss rate after the F-T cycles is lower while the flexural strength and relative dynamic modulus are higher.

Figure 16. Distribution diagram of concrete pore structure. (a) G0, (b) G5, (c) G10, (d) G20, (e) G30.

For the G10 specimen, the relative volume of transition pores remained remarkably stable throughout the 300 F-T cycles, in contrast to the significant reduction observed in the control group (G0). This stability is mainly attributed to the secondary pozzolanic reaction of SF, which consumes Ca(OH)₂ and C-S-H. The newly formed C-S-H products refine the pore walls and fill part of the transition pore network, effectively preventing the merging of medium pores into larger capillary pores. Furthermore, the dense interfacial transition zone formed by SF addition helps to redistribute internal stresses and reduce microcrack propagation, thus maintaining the structural integrity of transition pores under cyclic freezing and thawing [58]. This mechanism suggests that the F-T resistance improvement in SF-modified concrete is not only due to lower total porosity but also due to the stabilization of transition pores and the reduced connectivity between harmful pores. These factors jointly delay internal damage accumulation, allowing the G10 specimen to retain a denser and more resilient microstructure even after prolonged F-T exposure [59].

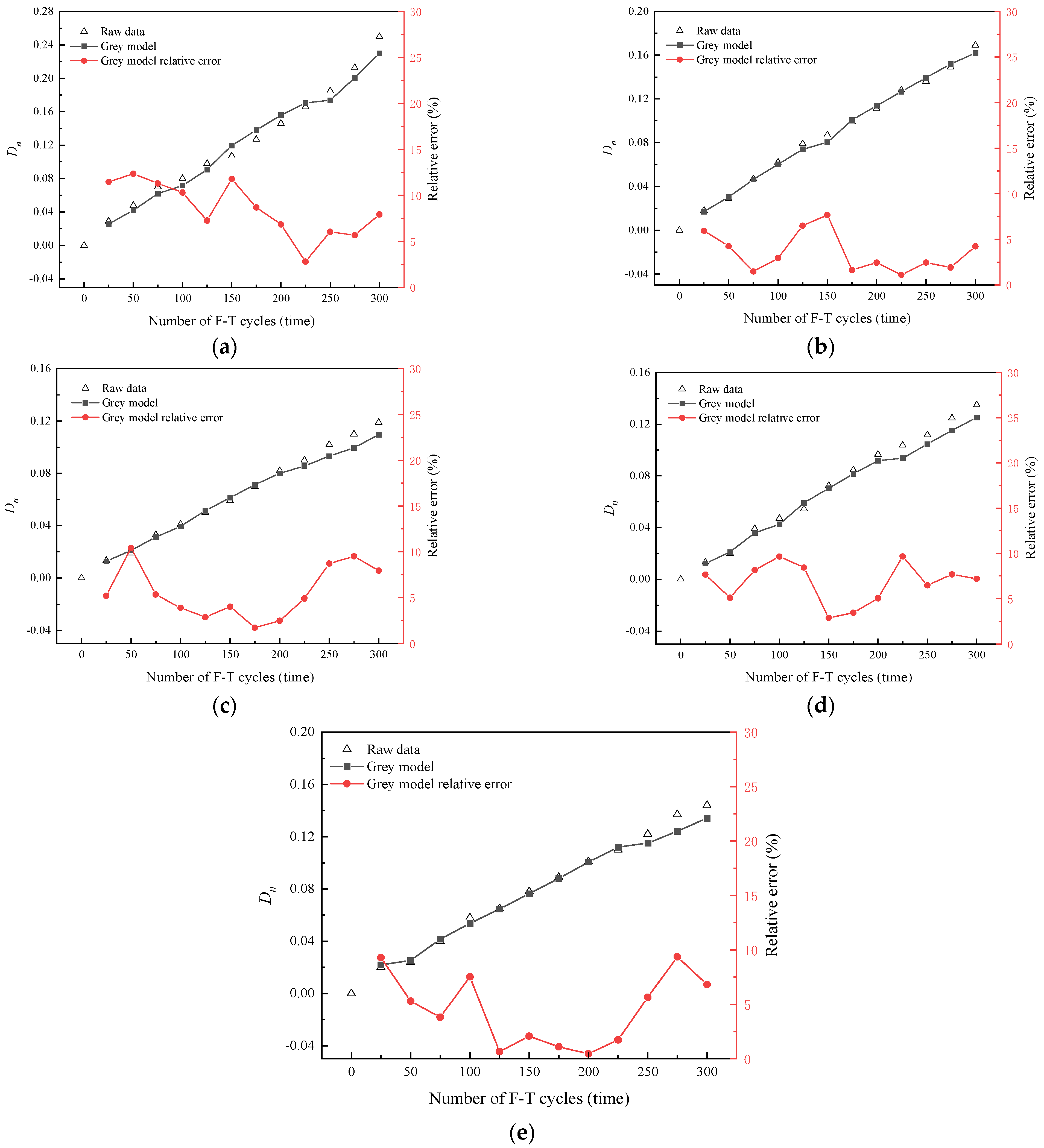
4.7. F-T Damage Model and Service Life Prediction

The F-T damage of concrete is essentially a complex physical and mechanical process involving pore water phase transition, hydrostatic pressure, osmotic pressure, and microcrack initiation and propagation. Accurate physical models with comprehensive intrinsic parameters are difficult to obtain through conventional experiments, and the damage evolution exhibits strong nonlinear characteristics, making the solution extremely complex [60,61]. Finally, the gray model approach was chosen. The core advantage of the gray model approach lies in its powerful processing ability for “poor information, small sample” datasets [62,63]. It can reveal the macroscopic trend rules inherent in the system through the generation and evolution of data sequences and achieve trend prediction of damage accumulation.

The F-T deterioration of concrete is attributed to the progressive initiation and propagation of internal microcracks. Current concrete specifications stipulate that specimens demonstrating elastic modulus reduction below 60% are deemed to have achieved complete structural failure, indicating serviceability limit attainment. As a fundamental component of the gray system theory, the gray model approach has gained significant traction in materials engineering research due to its capability to characterize system evolution through limited datasets [64,65]. This article establishes a prediction model for relative dynamic elastic modulus based on this model and conducts a service life analysis.

According to damage mechanics, the F-T damage equation D_n for concrete is

$$D_n=1-{\displaystyle \frac{E(n)}{E_0}}$$

(6)

In the formula, D_n is the damage value after n F-T cycles; E(n) is the relative dynamic modulus after n F-T cycles; E₀ is the initial relative dynamic modulus of elasticity; n is the number of F-T cycles.

Take the relative dynamic modulus of elasticity data under different F-T cycles (with 25 cycles as the detection age) as the given sequence:

$$X^{(0)}=(x^{(0)}(1),x^{(0)}(2),\dots ,x^{(0)}(n))$$

(7)

Accumulate the original sequence to obtain a new sequence $x^{\left(1\right)}$:

$$X^{(1)}=(x^{(1)}(1),x^{(1)}(2),\dots ,x^{(1)}(n))$$

(8)

In the formula, $x^{\left(1\right)}\left(k\right)=\sum _{i=1}^k{x}^{\left(0\right)}\left(i\right), k=1,2,\dots ,n.$ $x^{\left(1\right)}$ is referred to as the 1−AGO accumulation sequence of $x^{\left(0\right)}$.

$$Z^{(1)}=(z^{(1)}(1),z^{(1)}(2),\dots ,z^{(1)}(n),)$$

(9)

In the formula, if $z^{\left(1\right)}\left(k\right)={\displaystyle \frac{1}{2}}\left(x^{\left(1\right)}\left(k\right)+x^{\left(1\right)}\left(k-1\right)\right)$, then the mean form (EGM) of gray model approach is

$$x^{(0)}(k)+a{z}^{(1)}(k)=b$$

(10)

The whitening differential equation of Equation (10) is

$${\displaystyle \frac{d{x}^{(1)}}{dt}}+a{x}^{(1)}=b$$

(11)

In the formula, a is the development coefficient, b is the total amount of gray, depending on the construction form of the original sequence and background values. It can be determined by the least squares method using the vector $\mathsf{\alpha }={\left(\mathbf{a},\mathbf{b}\right)}^{\mathbf{T}}={\left({\mathbf{B}}^{\mathbf{T}}\mathbf{B}\right)}^{-1}{\mathbf{B}}^{\mathbf{T}}\mathbf{Y}$.

$$\mathbf{Y}=\left[\begin{array}{c}\begin{array}{c}{x}^{\left(0\right)}\left(2\right)\\ x^{\left(0\right)}\left(2\right)\\ ⋮\end{array}\\ x^{\left(0\right)}\left(n\right)\end{array}\right], \mathbf{B}=\left[\begin{array}{c}\begin{array}{c}-z^{\left(1\right)}\left(2\right) 1\\ -z^{\left(1\right)}\left(2\right) 1\\ ⋮ ⋮\end{array}\\ -z^{\left(1\right)}\left(n\right) 1\end{array}\right]$$

The time response equation for $X^{\left(0\right)}$ can be obtained as follows:

$${\widehat{x}}^{(0)}(k)=(1-e^a)(x^{(0)}(1)-{\displaystyle \frac{b}{a}})e^{-a(k-1)},k=1,2,\dots ,n$$

(12)

The substitution of relative dynamic elastic modulus parameters under F-T cycles into Equations (7)–(12) yields predictive formulations for modulus degradation, as presented in Equations (13)–(17):

$$\mathrm{G}0:{\widehat{x}}^{(0)}=(1-e^{0.0211})(x^{(0)}(1)-{\displaystyle \frac{100.9738}{0.0211}})e^{-0.0211(k-1)}$$

(13)

$$\mathrm{G}5:{\widehat{x}}^{(0)}=(1-e^{0.0147})(x^{(0)}(1)-{\displaystyle \frac{100.3941}{0.0147}})e^{-0.0147(k-1)}$$

(14)

$$\mathrm{G}10:{\widehat{x}}^{(0)}=(1-e^{0.0105})(x^{(0)}(1)-{\displaystyle \frac{100.5148}{0.0105}})e^{-0.0105(k-1)}$$

(15)

$$\mathrm{G}20:{\widehat{x}}^{(0)}=(1-e^{0.0122})(x^{(0)}(1)-{\displaystyle \frac{100.6089}{0.0122}})e^{-0.0122(k-1)}$$

(16)

$$\mathrm{G}30:{\widehat{x}}^{(0)}=(1-e^{0.0127})(x^{(0)}(1)-{\displaystyle \frac{100.2113}{0.0127}})e^{-0.0127(k-1)}$$

(17)

4.8. Accuracy Analysis of Prediction Models

If the measured damage values and predicted damage value sequences are $D^{\left(0\right)}\left(k\right)$ and ${\widehat{D}}^{\left(0\right)}(k)$, where k = 1, 2, …, n, the model residuals are determined through Equation (18), while relative error derivation employs Equation (19).

$$\epsilon (k)=D^{(0)}(k)-{\widehat{D}}^{(0)}(k)$$

(18)

$$q={\displaystyle \frac{\epsilon (k)}{D^{(0)}(k)}}\times 100\%$$

(19)

The damage degree parameters and associated relative errors for specimen cohorts analyzed through the gray model approach under F-T cycles are quantified in Figure 17.

Figure 17. Relative error of gray model approach for different groups of specimens. (a) G0, (b) G5, (c) G10, (d) G20, (e) G30.

The mean and variance of the original relative dynamic elastic modulus data are

$$\overline{x}={\displaystyle \frac{1}{n}}{\displaystyle {\sum }_{k=1}^n{x}^{(0)}(k)}$$

(20)

$$S_1^2={\displaystyle \frac{1}{n}}{\displaystyle {\sum }_{k=1}^n(x^{(0)}(k)}-\overline{x}{)}^2$$

(21)

The mean square deviation ratio and small probability error are

$$C={\displaystyle \frac{S_1}{S_2}}$$

(22)

$$P=p({\epsilon }^{(0)}(k)-\overline{\epsilon }<0.6745S_2)$$

(23)

The model was employed to forecast the evolution of the relative dynamic elastic modulus of concrete subjected to F-T cycles, and its predictive performance was evaluated using the mean square error ratio (C) and the small probability error (P). As summarized in Table 7, the computed C values for all groups (G0, G5, G10, G20, G30) are below 0.35, while the corresponding p values are consistently equal to 1. These results indicate that the predictive accuracy of the model attains Grade I, demonstrating a high level of reliability. Furthermore, a randomness test conducted on the residual series of the model revealed no significant autocorrelation, suggesting that the model structure is appropriately specified and that no major influencing factors have been omitted.

Table 7. Accuracy evaluation of gray model approach prediction model.

Group Name	Verification Indicators
	C	P
G0	0.1594	1
G5	0.0893	1
G10	0.0821	1
G20	0.0939	1
G30	0.089	1

Using the gray model approach model to predict the service life of concrete modified with SF, calculate the number of F-T cycles when the relative dynamic elastic modulus of the specimen reaches 60%. The average annual F-T cycles in Northeast, North, and Northwest China are 120, 84, and 118, respectively [33,66]. In natural environments, 12 F-T cycles are equivalent to one rapid indoor F-T cycle. From this, the service life of different concrete modified with SF in various regions of northern China was obtained, and the calculation results are shown in Table 8.

Table 8. Prediction of concrete service life under F-T cycles.

Group Name		G0	G5	G10	G20	G30
Indoor F-T cycle times		604	862	1215	1046	997
Prediction	Northeast China/year	60.4	86.2	121.5	104.6	99.7
	North China/year	86.3	123.1	173.6	149.4	142.4
	Northwest China/year	61.4	87.7	123.6	106.4	101.4

According to Table 8, the service life of G0 is relatively short. Taking the Northeast region as an example, the service life of G5, G10, G20, and G30 increased by 42.7%, 101.2%, 73.2%, and 65.1%, respectively, compared to G0. This indicates that the service life of concretes modified with SF is significantly improved in F-T environments, with G10 showing the best improvement in F-T durability.

The gray model predictions may be influenced by significant fluctuations or outliers in the original data, which can affect background value construction and parameter estimation. The use of 25 F-T cycles as the monitoring interval also presents a constraint. Furthermore, the model may not fully capture nonlinear behaviors, and parameter estimation via the least square method is sensitive to outliers. As shown in Table 9, compared with the prediction models used by Das et al. [39] and Wang et al. [67], the gray model used in this study has a prediction error of less than 5% for service life, indicating that the service life prediction model in this study has high accuracy.

Table 9. Comparison of different prediction models.

Number	Gray Model	Ref. [39]		Ref. [67]
	Times	Times	Deviation	Times	Deviation
G0	604	633	4.79%	587	2.81%
G5	862	892	3.43%	849	1.48%
G10	1215	1260	3.72%	1175	3.27%
G20	1046	1084	3.60%	1028	1.74%
G30	997	1030	3.26%	970	2.67%

In terms of environmental benefits, the utilization of SF as an industrial by-product conforms to the sustainable development concept of “waste resource utilization”. The addition of SF significantly improved the F-T durability of concrete, especially for the G10 group (10% dosage), which had a predicted service life of 121.5 years in Northeast China and an increase of 101.2% compared to the benchmark group G0. According to Das et al. [18], Qingyuan City in Guangdong Province, China emits 0.995 kg of CO₂ per kilogram of cement during the cement production stage. This means that the maintenance and replacement frequency of SF concrete is significantly reduced throughout the entire lifecycle of the structure, thereby reducing carbon emissions during cement production, transportation, and construction processes. In addition, the high durability of SF concrete also helps to improve the sustainability rating of building structures, which is in line with the trend of green building development.

5. Conclusions and Prospects

5.1. Conclusions

To investigate the influence of SF content on the frost resistance of concrete, this study explored the mass loss, relative dynamic elastic modulus, flexural strength characteristics, and microstructural evolution of SF-modified concrete after F-T cycles. The crack propagation behavior of SF concrete under flexural was studied using the DIC technique. Furthermore, a gray system prediction model was established to forecast the long-term durability performance under F-T cycling conditions, and the service life was estimated via numerical simulation. The main findings are summarized as follows:

(1)

The incorporation of SF can effectively improve the internal structure of concrete, enhance its relative dynamic elastic modulus and flexural strength, and reduce mass loss. Among them, the G10 specimen demonstrated the best performance. After 300 F-T cycles, the relative dynamic elastic modulus and flexural strength decreased by only 11.9% and 17%, respectively.

(2)

The flexural process of concrete exhibits four progressive mechanical stages: early stage, initiation stage, extension stage, and penetration stage. The addition of SF delayed the crack propagation rate and reduced the crack width. After 300 F-T cycles, the maximum crack width of G10 was reduced by 61% compared to G0, and the crack propagation rate decreased by 24.7%.

(3)

Microscopic experiments indicate that F-T cycles cause the expansion and interconnection of gel pores and transition pores in concrete, increasing the proportion of harmful pores. The incorporation of SF promotes cement hydration, generating a large amount of C-S-H gel that fills the pores, thereby improving the compactness of the matrix and effectively resisting F-T damage.

(4)

The accuracy of the gray system-based life prediction model meets Grade I standards, effectively characterizing the F-T damage of concrete. Under simulated severe cold climate conditions in Northeast China, the F-T resistance life of concrete with different SF contents follows the order of G10 > G20 > G30 > G5 > G0, with the predicted service life of G10 reaching 121.5 years.

5.2. Prospects

(1)

Using concrete mixed with SF in cold regions and strictly controlling the SF dosage to ensure performance can reduce carbon emissions and save costs. The gray system theory-based life prediction extends service cycles and reduces lifecycle costs.

(2)

In the future, we will study the synergistic effect of SF with fly ash or slag as well as analyze and explore the modification mechanism of other sustainable materials such as glass powder or industrial waste on the durability performance of concrete.

(3)

Future research will assess the long-term performance of G10 and G20 under combined salt and F-T exposure, with a focus on quantifying the effectiveness of their densified microstructure against salt crystallization and chemical degradation.