Simulations of Damage Scenarios in Urban Areas: The Case of the Seismic Sequence of L’Aquila 2009
Abstract
1. Introduction
2. The Case Study of L’Aquila
2.1. The Seismic Input: INGV Instrumental Intensity ShakeMaps
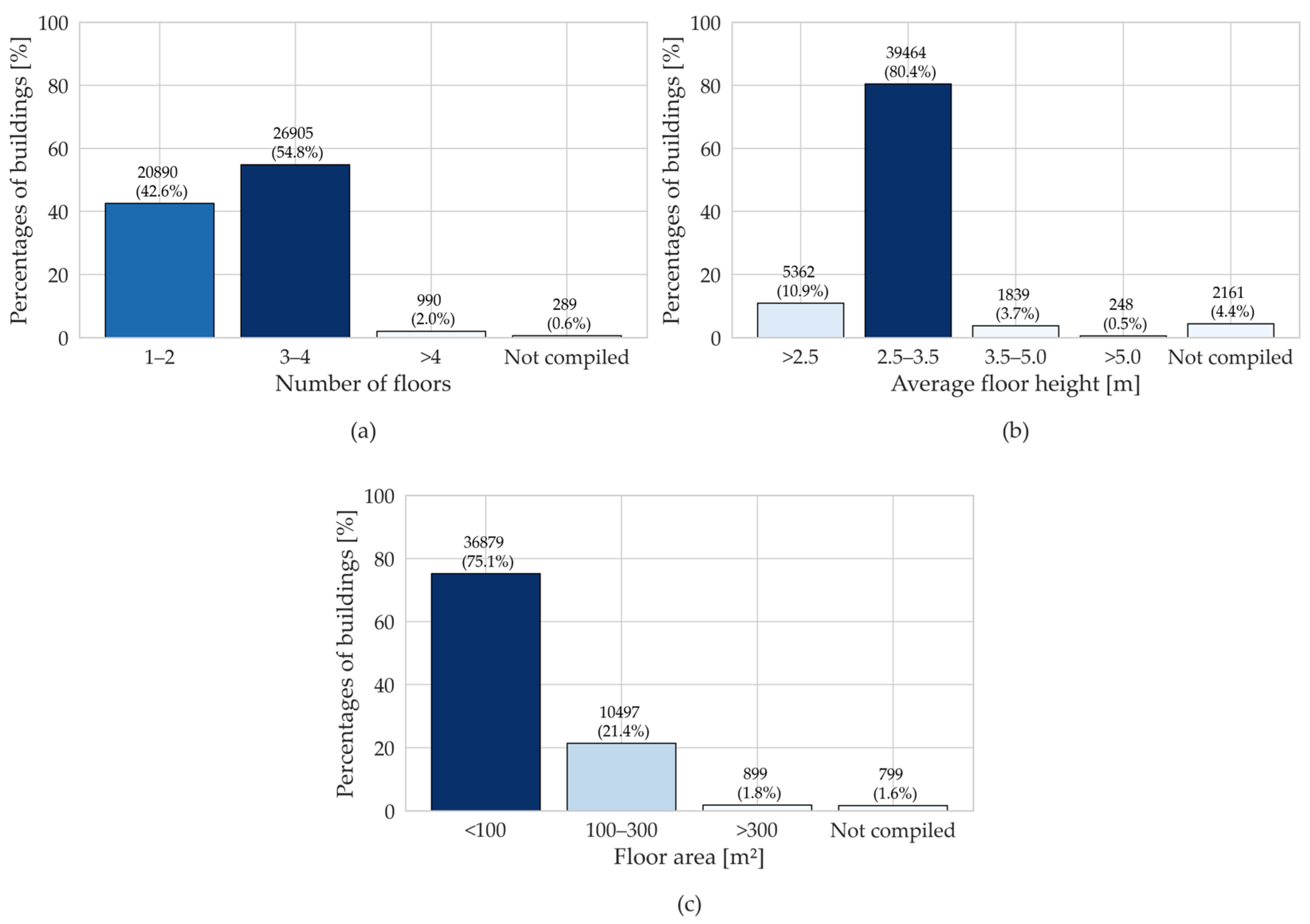
2.2. The Da.D.O. Buildings Dataset
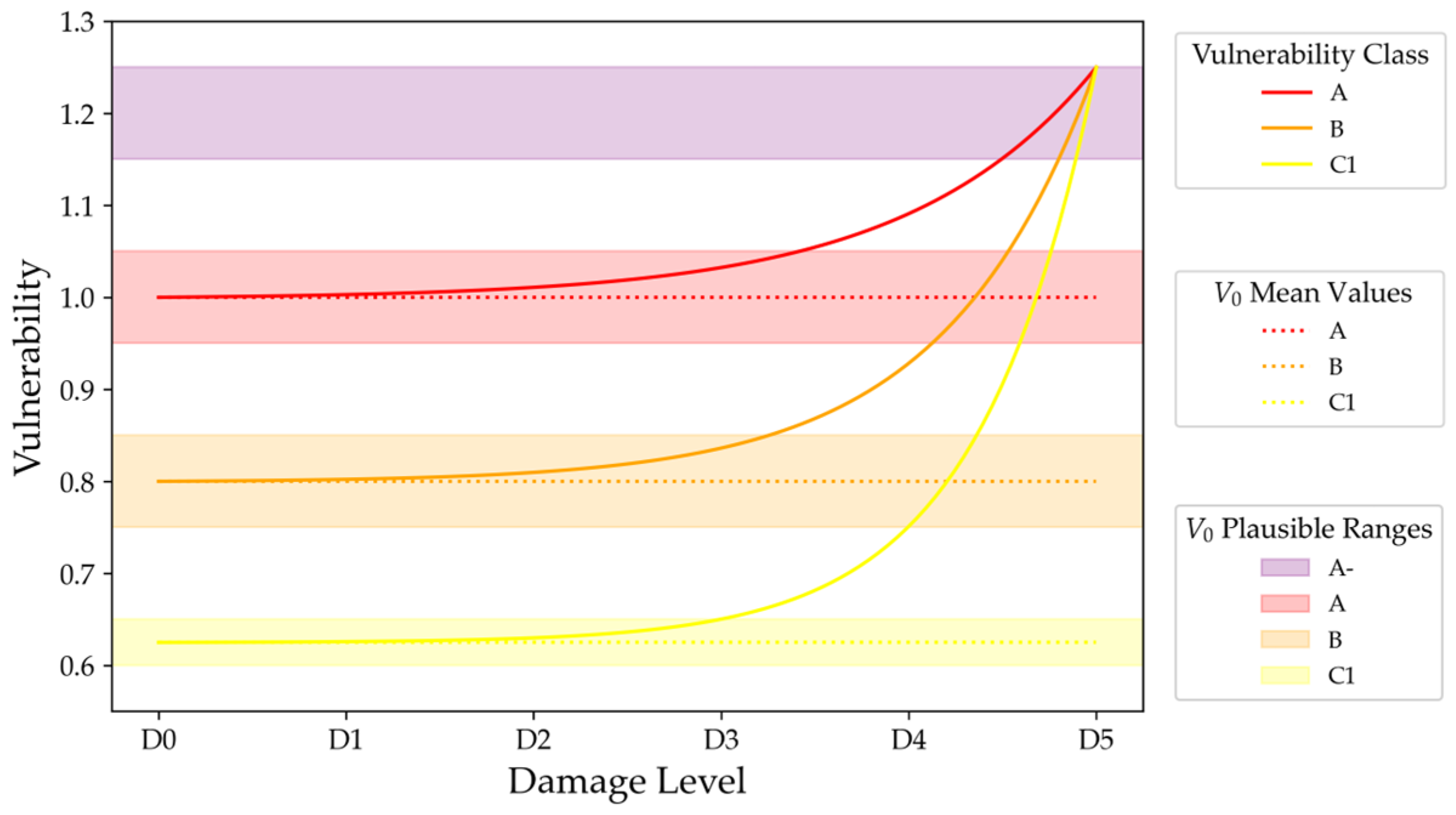
2.3. Initial Vulnerability Class and Observed Damage in the Da.D.O. Dataset
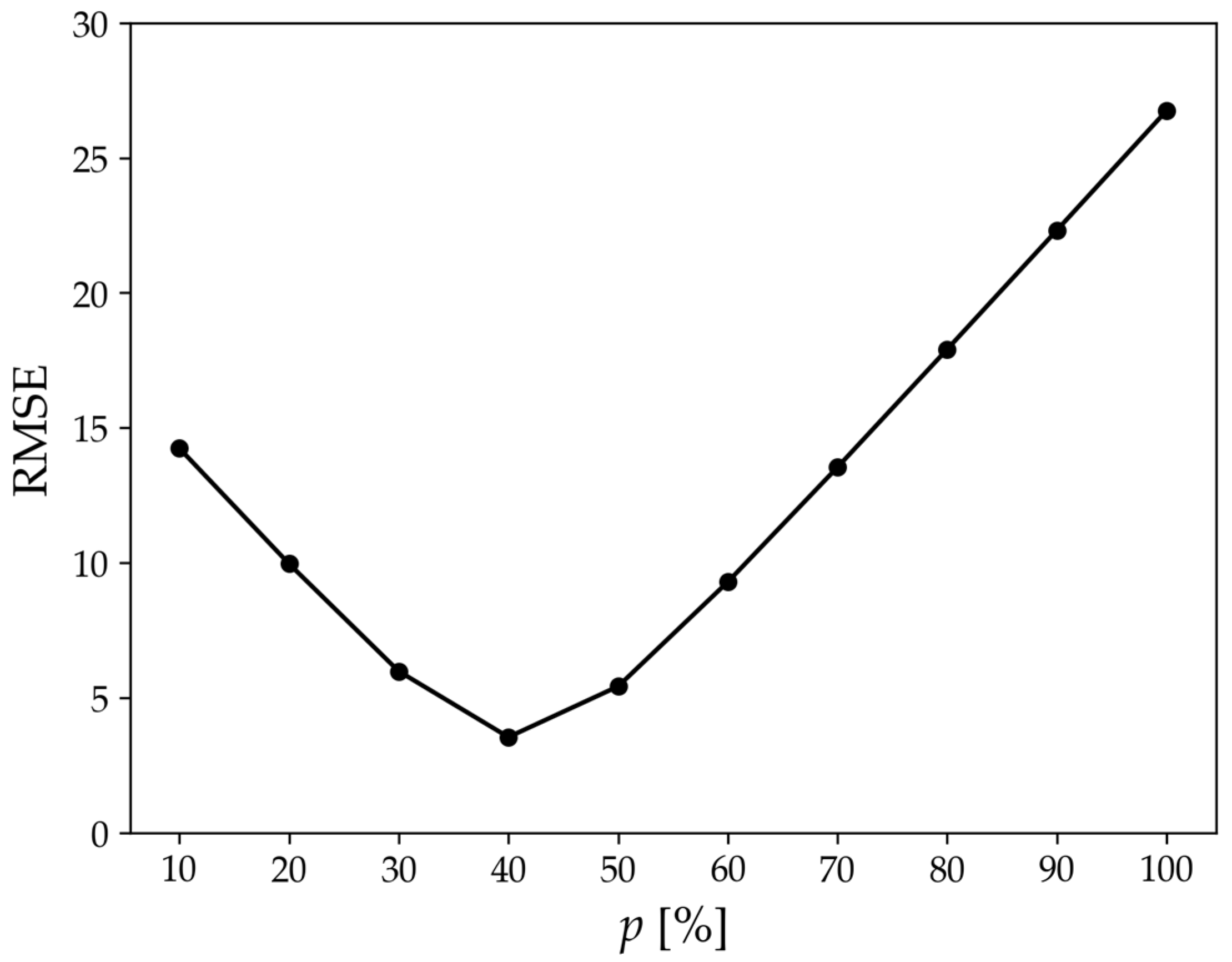
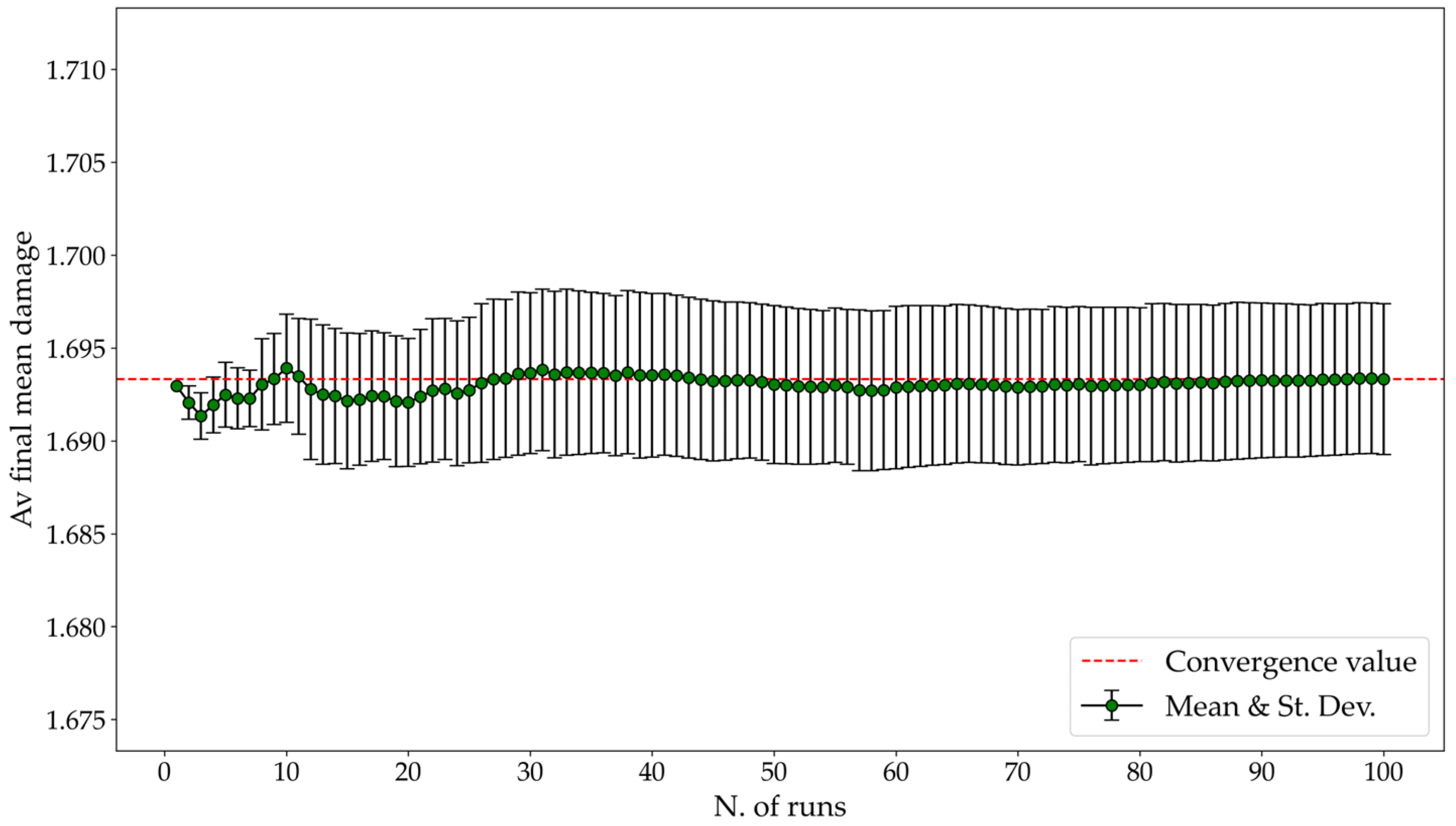
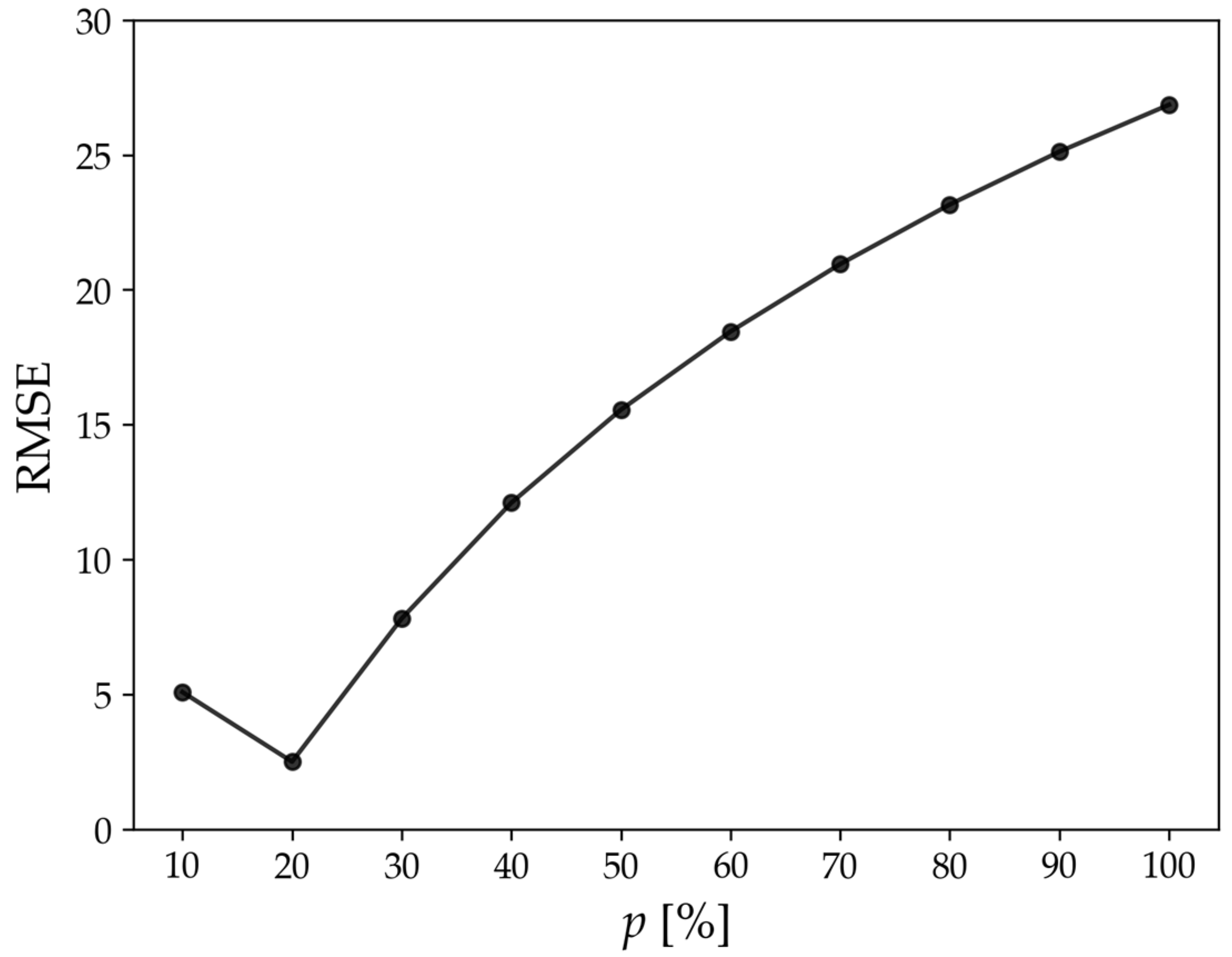
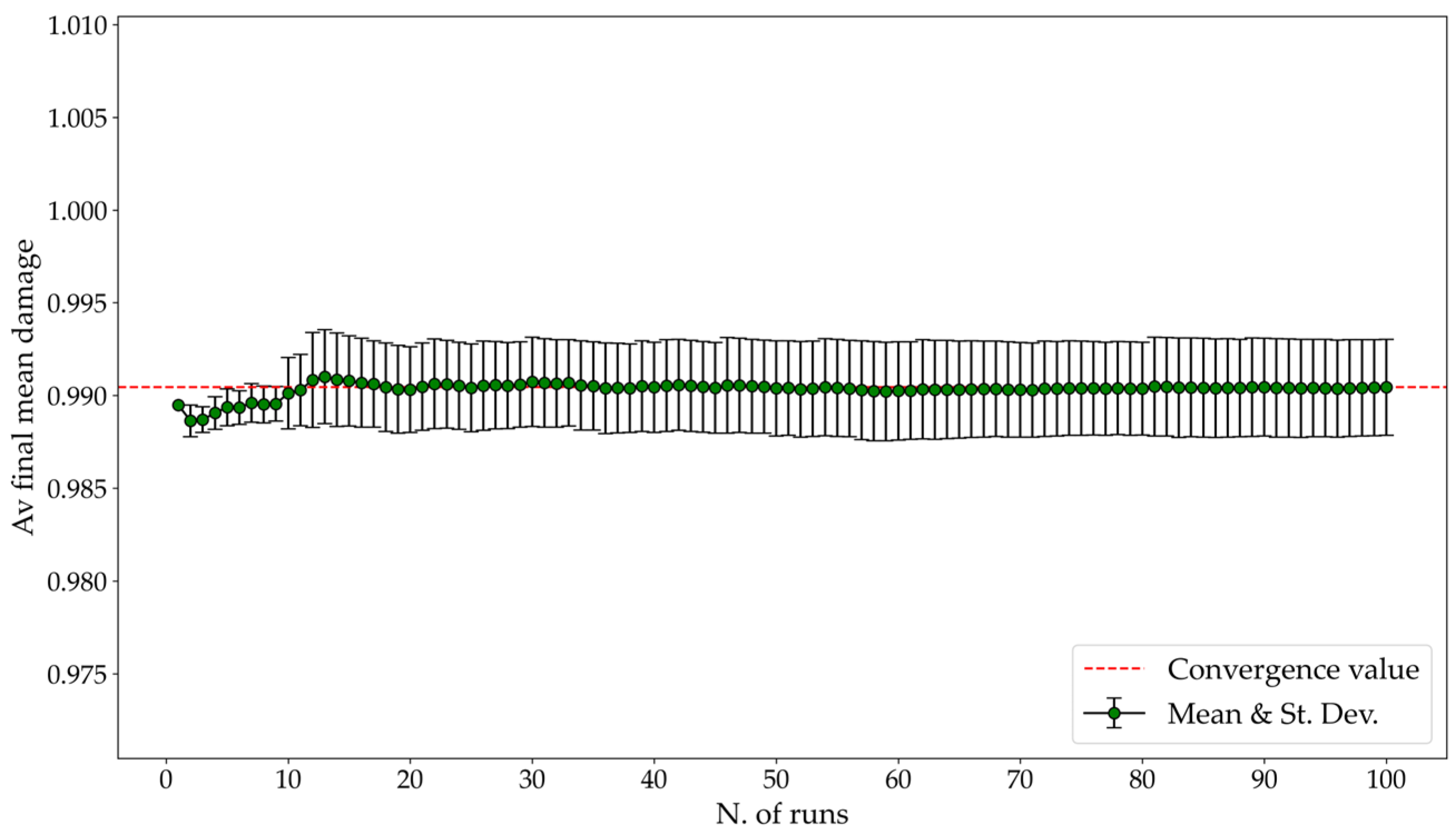
3. Simulation of Damage Evolution
4. Results and Discussion
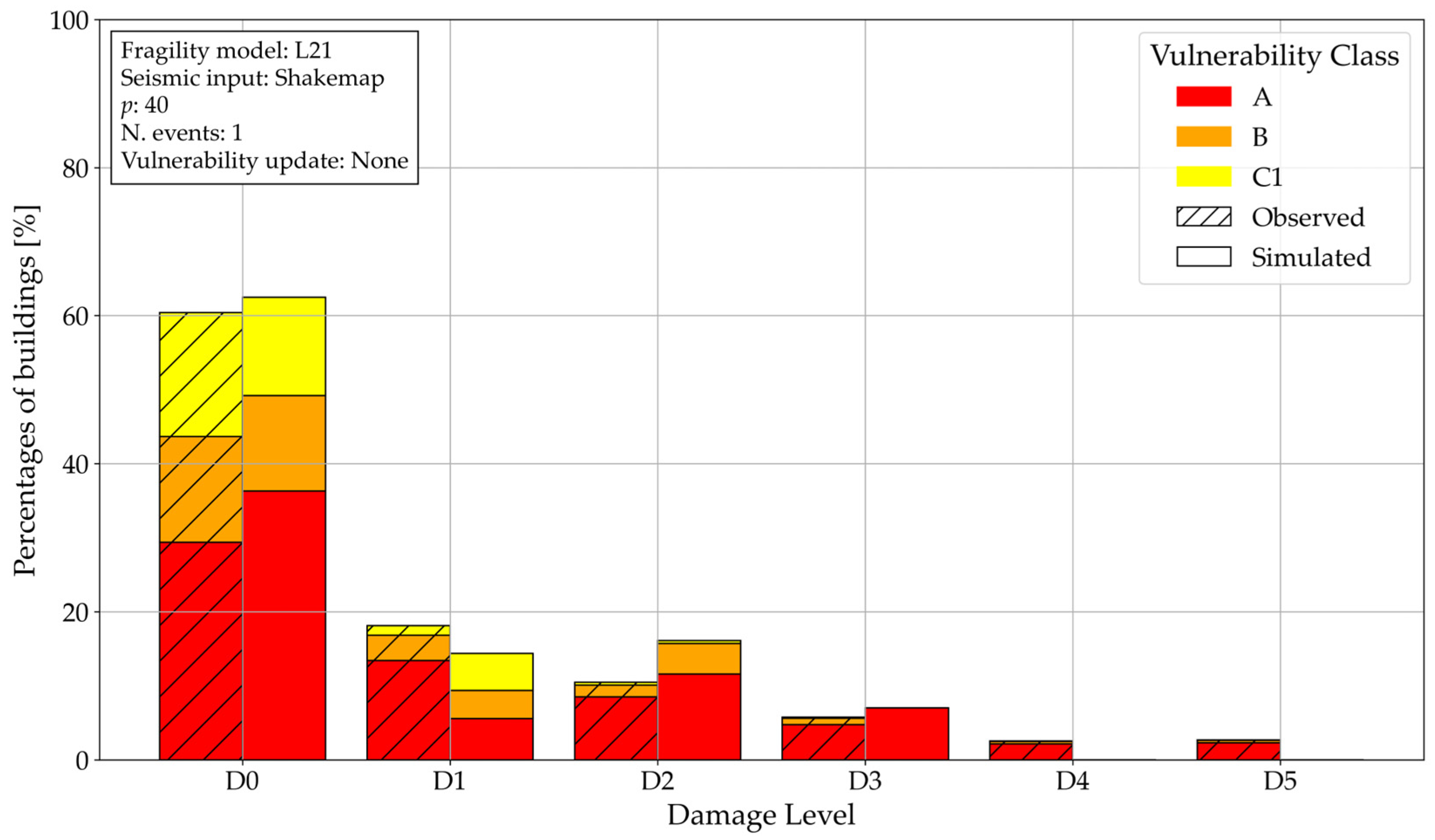
4.1. Mainshock-Only Scenario
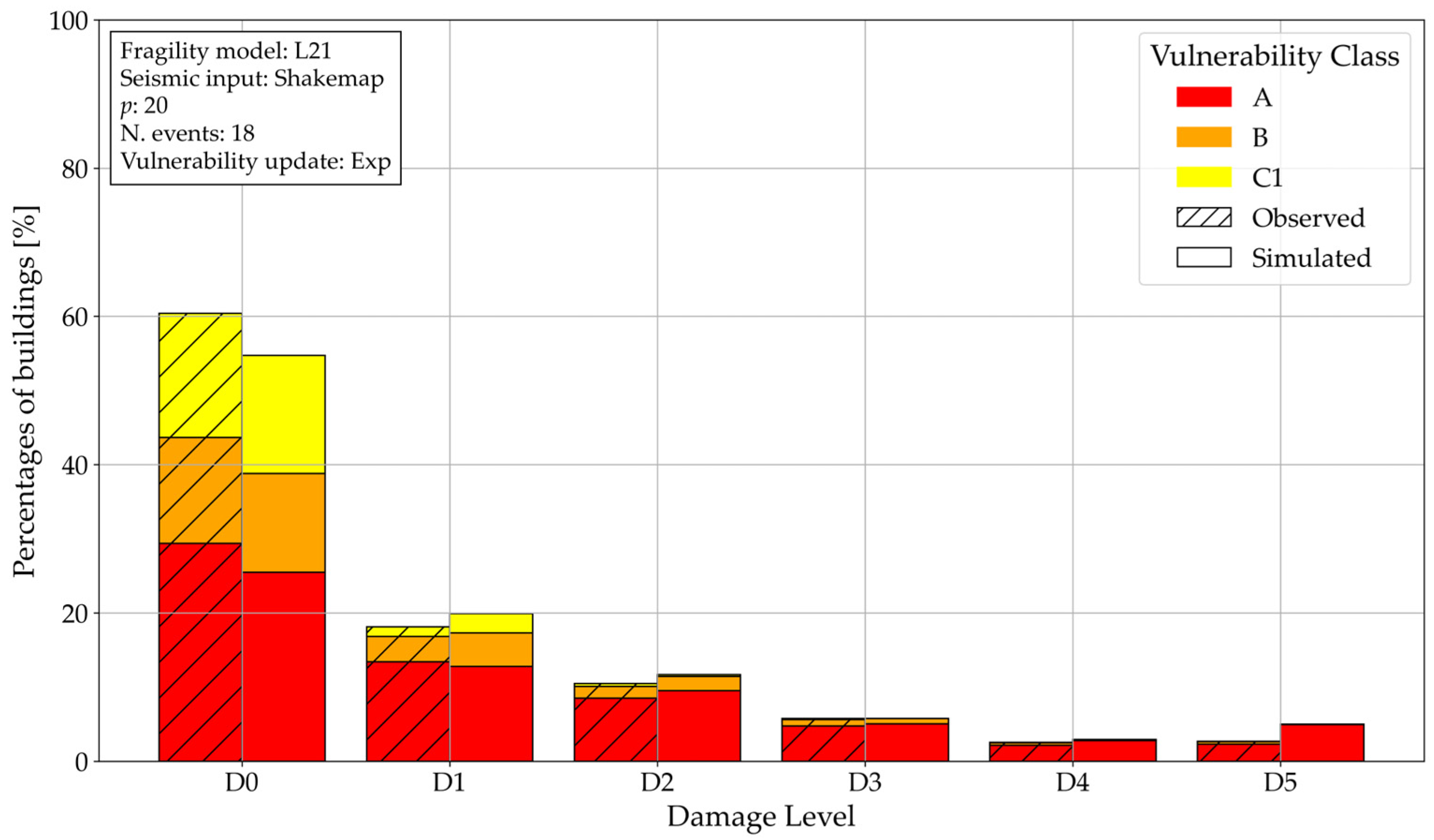
4.2. 18-Event Scenario
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AeDES | Agibilità e Danno nell’Emergenza Sismica |
| Da.D.O. | Database del Danno Osservato |
| DPM | Damage Probability Matrix |
| DPC | Department of Civil Protection |
| EMS-98 | European Macroseismic Scale |
| GEM | Global Earthquake Model Foundation |
| GMPE | Ground Motion Prediction Equation |
| GMICE | Ground Motion to Intensity Conversion Equation |
| INGV | National Institute of Geophysics and Volcanology |
| IRMA | Italian Risk Maps |
| MCS | Mercalli–Cancani–Sieberg |
| MLA | Machine Learning Algorithm |
| PBEE | Physics-Based Performance Engineering |
| PGA | Peak Ground Acceleration |
| PGM | Peak Ground Motion |
| PGV | Peak Ground Velocity |
| PSHA | Probabilistic Seismic Hazard Assessment |
| QUEST | Quick Earthquake Survey Team |
| RC | Reinforced Concrete |
| RMSE | Root Mean Squared Error |
| RVS | Rapid Visual Screening |
| SA | Spectral Acceleration |
| USGS | United States Geological Society |
| UTC | Coordinated Universal Time |
| VIM | Vulnerability Index Method |
References
- Greco, A.; Caddemi, S.; Caliò, I.; Fiore, I. A Review of Simplified Numerical Beam-like Models of Multi-Storey Framed Buildings. Buildings 2022, 12, 1397. [Google Scholar] [CrossRef]
- Greco, A.; Fiore, I.; Occhipinti, G.; Caddemi, S.; Spina, D.; Caliò, I. An Equivalent Non-Uniform Beam-Like Model for Dynamic Analysis of Multi-Storey Irregular Buildings. Appl. Sci. 2020, 10, 3212. [Google Scholar] [CrossRef]
- Fiore, I.; Caddemi, S.; Caliò, I.; Greco, A. An Inelastic Beam-Like Model for Nonlinear Dynamic Analyses of Multi-Storey Buildings. Eng. Struct. 2024, 308, 117852. [Google Scholar] [CrossRef]
- Perrone, D.; Aiello, M.A.; Pecce, M.; Rossi, F. Rapid Visual Screening for Seismic Evaluation of RC Hospital Buildings. Structures 2015, 3, 57–70. [Google Scholar] [CrossRef]
- Mouroux, P.; Le Brun, B. Risk-UE Project: An Advanced Approach to Earthquake Risk Scenarios with Application to Different European Towns. In Assessing and Managing Earthquake Risk; Oliveira, C.S., Roca, A., Goula, X., Eds.; Geotechnical, Geological and Earthquake Engineering; Springer: Dordrecht, The Netherlands, 2008; Volume 2, pp. 479–508. [Google Scholar] [CrossRef]
- Lagomarsino, S.; Giovinazzi, S. Macroseismic and Mechanical Models for the Vulnerability and Damage Assessment of Current Buildings. Bull. Earthq. Eng. 2006, 4, 415–443. [Google Scholar] [CrossRef]
- Grünthal, G. (Ed.) European Macroseismic Scale 1998; Cahiers du Centre Européen de Géodynamique et de Séismologie; Conseil de l’Europe: Luxembourg, 1998. [Google Scholar]
- Eleftheriadou, A.K.; Karabinis, A.I. Evaluation of damage probability matrices from observational seismic damage data. Earthq. Struct. 2013, 4, 299–324. [Google Scholar] [CrossRef]
- Li, S.Q.; Chen, Y.S. Analysis of the Probability Matrix Model for the Seismic Damage Vulnerability of Empirical Structures. Nat. Hazards 2020, 104, 705–730. [Google Scholar] [CrossRef]
- Surana, M.; Meslem, A.; Singh, Y.; Lang, D.H. Analytical Evaluation of Damage Probability Matrices for Hill-Side RC Buildings Using Different Seismic Intensity Measures. Eng. Struct. 2020, 207, 110254. [Google Scholar] [CrossRef]
- Rosti, A.; Rota, M.; Penna, A. Empirical fragility curves for Italian URM buildings. Bull. Earthq. Eng. 2021, 19, 3057–3076. [Google Scholar] [CrossRef]
- Da Porto, F.; Donà, M.; Rosti, A.; Rota, M.; Lagomarsino, S.; Cattari, S.; Borzi, B.; Onida, M.; De Gregorio, D.; Perelli, F.L.; et al. Comparative Analysis of the Fragility Curves for Italian Residential Masonry and RC Buildings. Bull. Earthq. Eng. 2021, 19, 3209–3252. [Google Scholar] [CrossRef]
- Ferranti, G.; Greco, A.; Pluchino, A.; Rapisarda, A.; Scibilia, A. Seismic Vulnerability Assessment at Urban Scale by Means of Machine Learning Techniques. Buildings 2024, 14, 309. [Google Scholar] [CrossRef]
- Pagani, M.; Monelli, D.; Weatherill, G.; Danciu, L.; Crowley, H.; Silva, V.; Henshaw, P.; Butler, L.; Nastasi, M.; Panzeri, L.; et al. OpenQuake Engine: An Open Hazard (and Risk) Software for the Global Earthquake Model. Seismol. Res. Lett. 2014, 85, 692–702. [Google Scholar] [CrossRef]
- Borzi, B.; Onida, M.; Faravelli, M.; Polli, D.; Pagano, M.; Quaroni, D.; Cantoni, A.; Speranza, E.; Moroni, C. IRMA Platform for the Calculation of Damages and Risks of Italian Residential Buildings. Bull. Earthq. Eng. 2021, 19, 3033–3055. [Google Scholar] [CrossRef]
- Iervolino, I.; Chioccarelli, E.; Suzuki, A. Seismic Damage Accumulation in Multiple Mainshock–Aftershock Sequences. Earthq. Eng. Struct. Dyn. 2020, 49, 1007–1027. [Google Scholar] [CrossRef]
- Lazaridis, P.C.; Kavvadias, I.E.; Demertzis, K.; Iliadis, L.; Papaleonidas, A.; Vasiliadis, L.K.; Elenas, A. Structural Damage Prediction Under Seismic Sequence Using Neural Networks. In Proceedings of the 8th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN 2021), Athens, Greece, 28–30 June 2021; ECCOMAS Proceedia: Athens, Greece, 2021; pp. 3820–3836. [Google Scholar] [CrossRef]
- Yuan, X.; Li, L.; Zhang, H.; Zhu, Y.; Chen, G.; Dagli, C. Machine Learning-Based Seismic Damage Assessment of Residential Buildings Considering Multiple Earthquake and Structure Uncertainties. Nat. Hazards Rev. 2023, 24, 04023024. [Google Scholar] [CrossRef]
- Dataset Developed by Eucentre (European Center for Training and Research in Seismic Engineering); Dolce, M.; Speranza, E.; Giordano, F.; Borzi, B.; Bocchi, F.; Conte, C.; Di Meo, A.; Faravelli, M.; Pascale, V. Da.D.O.—Uno Strumento per la Consultazione e la Comparazione del Danno Osservato Relativo ai Più Significativi Eventi Sismici in Italia dal 1976. In Atti del XVII Convegno ANIDIS “L’ingegneria Sismica in Italia”; Pisa University Press: Pisa, Italy; pp. 347–357. ISBN 978-886741-854-1. Available online: http://egeos.eucentre.it/danno_osservato/web/danno_osservato (accessed on 29 June 2024).
- Dolce, M.; Speranza, E.; Giordano, F.; Borzi, B.; Bocchi, F.; Conte, C.; Di Meo, A.; Faravelli, M.; Pascale, V. Observed Damage Database of Past Italian Earthquakes: The Da.D.O. WebGIS. Boll. Geofis. Teor. Appl. 2019, 60, 141–164. [Google Scholar] [CrossRef]
- Greco, A.; Pluchino, A.; Barbarossa, L.; Barreca, G.; Caliò, I.; Martinico, F.; Rapisarda, A. A New Agent-Based Methodology for the Seismic Vulnerability Assessment of Urban Areas. ISPRS Int. J. Geo-Inf. 2019, 8, 274. [Google Scholar] [CrossRef]
- Fischer, E.; Barreca, G.; Greco, A.; Martinico, F.; Pluchino, A.; Rapisarda, A. Seismic risk assessment of a large metropolitan area by means of simulated earthquakes. Nat. Hazards 2023, 118, 117–153. [Google Scholar] [CrossRef]
- Wald, D.J.; Quitoriano, V.; Heaton, T.H.; Kanamori, H.; Scrivner, C.W.; Worden, C.B. TriNet “ShakeMaps”: Rapid generation of peak ground motion and intensity maps for earthquakes in Southern California. Earthq. Spectra 1999, 15, 537–555. [Google Scholar] [CrossRef]
- Michelini, A.; Faenza, L.; Lauciani, V.; Malagnini, L. Shakemap implementation in Italy. Seismol. Res. Lett. 2008, 79, 688–697. [Google Scholar] [CrossRef]
- Michelini, A.; Faenza, L.; Lanzano, G.; Lauciani, V.; Jozinović, D.; Puglia, R.; Luzi, L. The new ShakeMap in Italy: Progress and advances in the last 10 years. Seismol. Res. Lett. 2020, 91, 317–333. [Google Scholar] [CrossRef]
- Sorrentino, L.; Giresini, L. Risk Assessment of Road Blockage after Earthquakes. Buildings 2024, 14, 984. [Google Scholar] [CrossRef]
- Galli, P.; Camassi, R. (Eds.) Rapporto Sugli Effetti del Terremoto Aquilano del 6 Aprile 2009; Rapporto Tecnico QUEST; DPC-INGV: Roma, Italy, 2009; 12p. (In Italian) [Google Scholar] [CrossRef]
- Chiarabba, C.; Amato, A.; Anselmi, M.; Baccheschi, P.; Bianchi, I.; Cattaneo, M.; Cecere, G.; Chiaraluce, L.; Ciaccio, M.G.; De Gori, P.; et al. The 2009 L’Aquila (Central Italy) MW 6.3 Earthquake: Main Shock and Aftershocks. Geophys. Res. Lett. 2009, 36, 2009GL039627. [Google Scholar] [CrossRef]
- Chiaraluce, L.; Valoroso, L.; Piccinini, D.; Di Stefano, R.; De Gori, P. The Anatomy of the 2009 L’Aquila Normal Fault System (Central Italy) Imaged by High Resolution Foreshock and Aftershock Locations. J. Geophys. Res. 2011, 116, B12311. [Google Scholar] [CrossRef]
- Sieberg, A. Scala MCS (Mercalli-Cancani-Sieberg). Geol. Der Erdbeben Handb. Der Geophys. 1930, 2, 552–555. [Google Scholar]
- Faenza, L. Rapid Determination of the Shakemaps for the L’Aquila Main Shock: A Critical Analysis. BGTA 2011, 52, 407–425. [Google Scholar] [CrossRef]
- Faenza, L.; Michelini, A. Regression Analysis of MCS Intensity and Ground Motion Parameters in Italy and Its Application in ShakeMap. Geophys. J. Int. 2010, 180, 1138–1152. [Google Scholar] [CrossRef]
- Bindi, D.; Pacor, F.; Luzi, L.; Puglia, R.; Massa, M.; Ameri, G.; Paolucci, R. Ground motion prediction equations derived from the Italian strong motion database. Bull. Earthq. Eng. 2011, 9, 1899–1920. [Google Scholar] [CrossRef]
- Oliveti, I.; Faenza, L.; Michelini, A. New reversible relationships between ground motion parameters and macroseismic intensity for Italy and their application in ShakeMap. Geophys. J. Int. 2022, 231, 1117–1137. [Google Scholar] [CrossRef]
- Oliveti, I.; Faenza, L.; Michelini, A. INGe: Intensity-ground motion data set for Italy. Ann. Geophys. 2022, 65, DM102. [Google Scholar] [CrossRef]
- Rossetto, T.; Peiris, N.; Alarcon, J.E.; So, E.; Sargeant, S.; Free, M.; Sword-Daniels, V.; Del Re, D.; Libberton, C.; Verrucci, E.; et al. Field observations from the Aquila, Italy earthquake of April 6, 2009. Bull. Earthq. Eng. 2009, 9, 11–37. [Google Scholar] [CrossRef]
- Lagomarsino, S.; Cattari, S.; Ottonelli, D. The heuristic vulnerability model: Fragility curves for masonry buildings. Bull. Earthq. Eng. 2021, 19, 3129–3163. [Google Scholar] [CrossRef]
- Baggio, C.; Bernardini, A.; Colozza, R.; Corazza, L.; Della Bella, M.; Di Pasquale, G.; Dolce, M.; Goretti, A.; Martinelli, A.; Orsini, G.; et al. Manuale per la Compilazione Della Scheda di 1° Livello di Rilevamento del Danno, Pronto Intervento e Agibilità per Edifici Ordinari Nell’Emergenza Post-Sismica (AeDES), 1st ed.; Dipartimento della Protezione Civile: Roma, Italy, 2002.
- Dolce, M.; Papa, F.; Pazza, A. Manuale per la Compilazione Della Scheda di 1° Livello di Rilevamento del Danno, Pronto Intervento e Agibilità per Edifici Ordinari Nell’Emergenza Post-Sismica (AeDES), 2nd ed.; Dipartimento della Protezione Civile: Roma, Italy, 2014.
- Caruso, F.; Pluchino, A.; Latora, V.; Vinciguerra, S.; Rapisarda, A. A new analysis of Self-Organized Criticality in the OFC model and in real earthquakes. Phys. Rev. E 2007, 75, 055101(R). [Google Scholar] [CrossRef]
- Caruso, F.; Latora, V.; Pluchino, A.; Rapisarda, A.; Tadić, B. Olami-Feder-Christensen Model on Different Networks. Eur. Phys. J. B 2006, 50, 243–247. [Google Scholar] [CrossRef]
- Grimaz, S.; Malisan, P. How could cumulative damage affect the macroseismic assessment? Bull. Earthq. Eng. 2017, 15, 2465–2481. [Google Scholar] [CrossRef]
- Lanzano, G.; Luzi, L.; Pacor, F.; Felicetta, C.; Puglia, R.; Sgobba, S.; D’Amico, M. A revised ground-motion prediction model for shallow crustal earthquakes in Italy. Bull. Seismol. Soc. Am. 2019, 109, 525–540. [Google Scholar] [CrossRef]
- Caicedo, D.; Tomić, I.; Karimzadeh, S.; Bernardo, V.; Beyer, K.; Lourenço, P.B. Optimal Intensity Measure and Probabilistic Seismic Demand Model for the Assessment of Historical Masonry Buildings: Application to Two Case Studies. Reliab. Eng. Syst. Saf. 2025, 261, 111149. [Google Scholar] [CrossRef]
- Gehl, P.; Seyedi, D.M.; Douglas, J. Vector-Valued Fragility Functions for Seismic Risk Evaluation. Bull. Earthq. Eng. 2013, 11, 365–384. [Google Scholar] [CrossRef]
- Muho, E.V.; Kalapodis, N.A.; Beskos, D.E. Multi-Modal and Multi-Level Structure-Specific Spectral Intensity Measures for Seismic Evaluation of Reinforced Concrete Frames. Bull. Earthq. Eng. 2024, 22, 6955–6989. [Google Scholar] [CrossRef]
- Monsalvo Franco, I.E.; Smerzini, C.; Rosti, A.; Rota, M.; Paolucci, R.; Penna, A. Seismic Fragility Curves with Unconventional Ground Motion Intensity Measures from Physics-Based Simulations. Bull. Earthq. Eng. 2025, 23, 1885–1915. [Google Scholar] [CrossRef]
- Kalapodis, N.A.; Muho, E.V.; Beskos, D.E. Structure-Specific, Multi-Modal and Multi-Level Scalar Intensity Measures for Steel Plane Frames. Soil Dyn. Earthq. Eng. 2025, 190, 109185. [Google Scholar] [CrossRef]
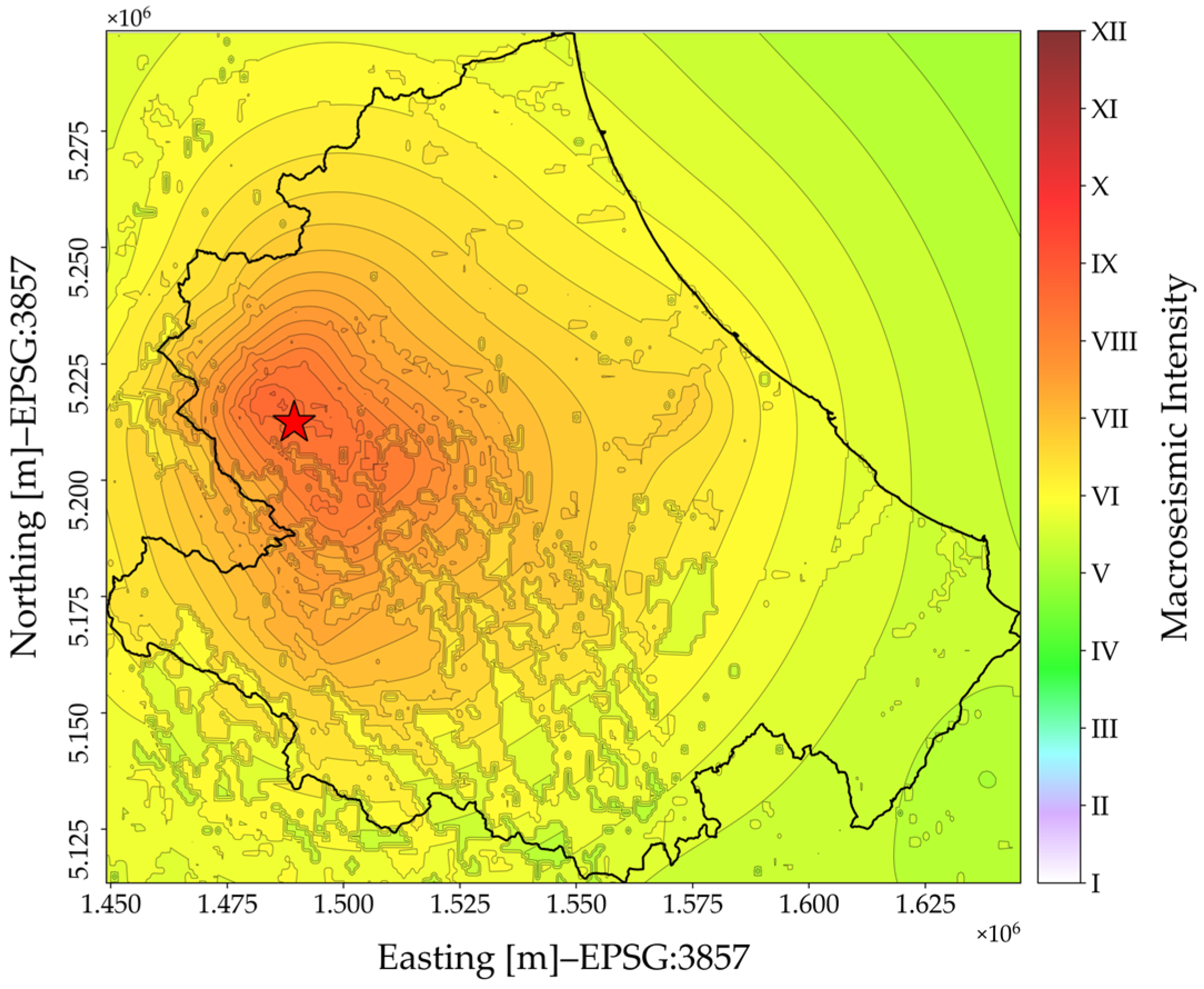
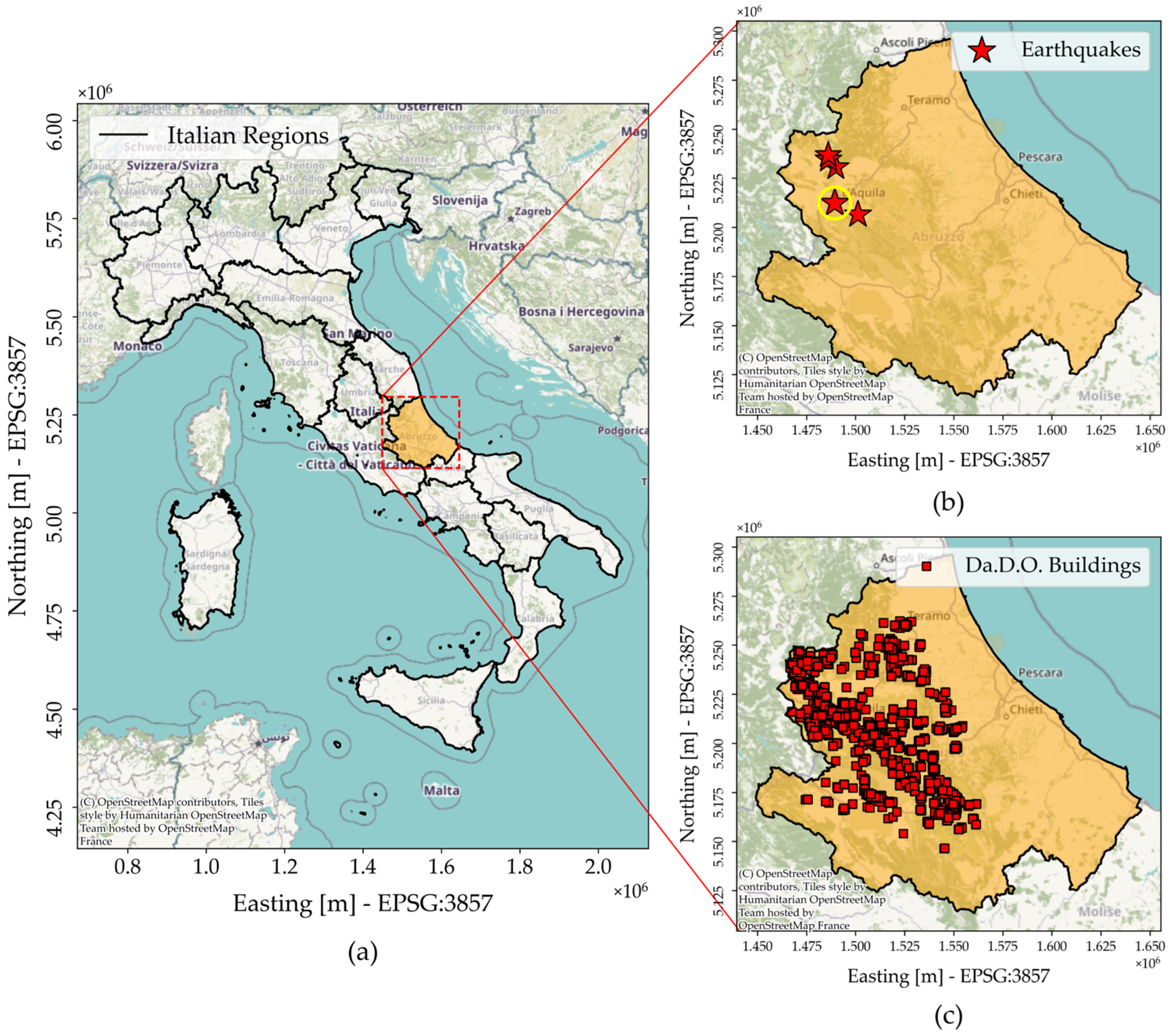
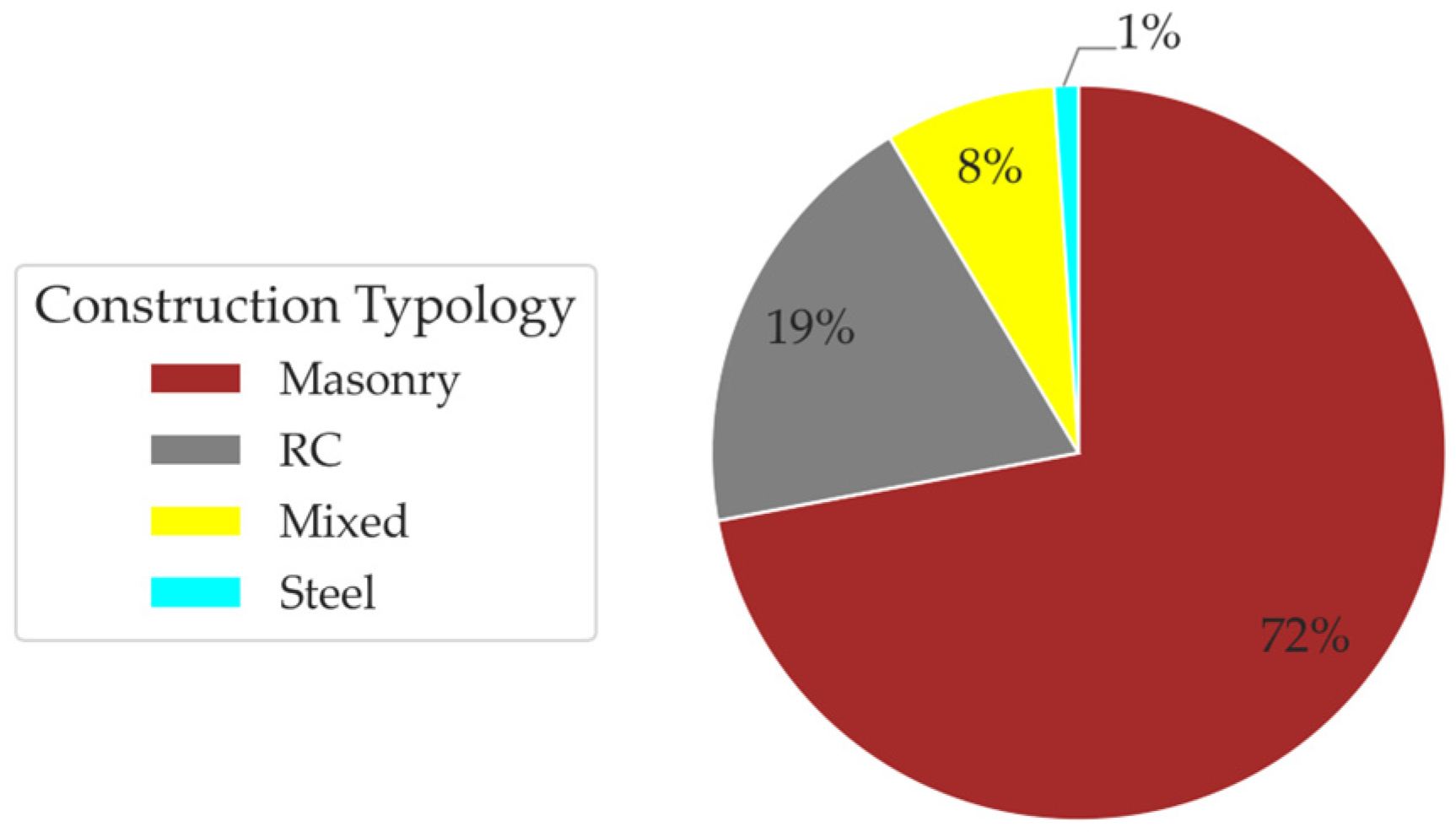
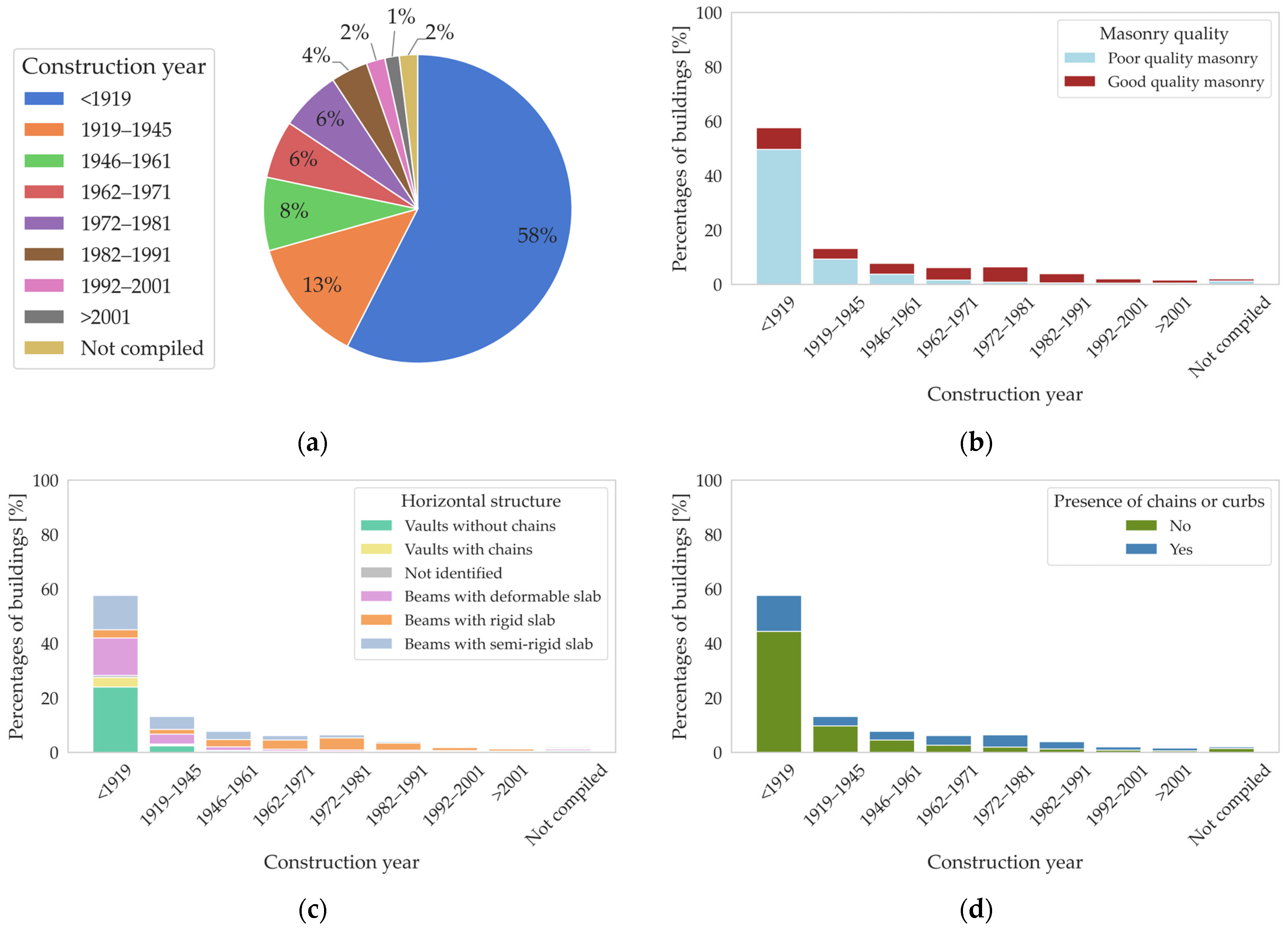



| Event Id | Date [yyyy-mm-dd] | Time UTC [hh:mm:ss] | Latitude [°] | Longitude [°] | Depth [km] | Mw | |
|---|---|---|---|---|---|---|---|
| 1 | 1895389 | 2009-04-06 | 01:32:00 | 42.342 | 13.380 | 8.3 | 6.1 |
| 2 | 1895409 | 2009-04-06 | 01:36:39 | 42.352 | 13.346 | 9.7 | 4.7 |
| 3 | 1895419 | 2009-04-06 | 01:40:50 | 42.417 | 13.402 | 11 | 4.1 |
| 4 | 1895429 | 2009-04-06 | 01:41:32 | 42.377 | 13.319 | 8.5 | 4.0 |
| 5 | 1895439 | 2009-04-06 | 01:41:37 | 42.364 | 13.456 | 8.7 | 4.3 |
| 6 | 1895449 | 2009-04-06 | 01:42:49 | 42.300 | 13.429 | 10.5 | 4.2 |
| 7 | 1895879 | 2009-04-06 | 02:37:04 | 42.360 | 13.328 | 8.7 | 4.8 |
| 8 | 1896349 | 2009-04-06 | 03:56:45 | 42.335 | 13.386 | 9.3 | 4.3 |
| 9 | 1897629 | 2009-04-06 | 07:17:10 | 42.356 | 13.383 | 9 | 4.1 |
| 10 | 1901099 | 2009-04-06 | 16:38:09 | 42.363 | 13.339 | 10 | 4.3 |
| 11 | 1903809 | 2009-04-06 | 23:15:00 | 42.463 | 13.385 | 9.7 | 5.0 |
| 12 | 1906339 | 2009-04-07 | 09:26:28 | 42.336 | 13.387 | 9.6 | 4.9 |
| 13 | 1908319 | 2009-04-07 | 17:47:00 | 42.303 | 13.486 | 17.1 | 5.4 |
| 14 | 1909629 | 2009-04-07 | 21:34:29 | 42.364 | 13.365 | 9.6 | 4.3 |
| 15 | 1916789 | 2009-04-09 | 00:52:00 | 42.489 | 13.351 | 11 | 5.2 |
| 16 | 1917479 | 2009-04-09 | 03:14:52 | 42.335 | 13.444 | 17.1 | 4.2 |
| 17 | 1917839 | 2009-04-09 | 04:32:45 | 42.445 | 13.434 | 9.8 | 4.1 |
| 18 | 1921649 | 2009-04-09 | 19:38:00 | 42.504 | 13.35 | 9.3 | 5.0 |
| Vulnerability Class | Vertical Structure | Horizontal Structure | Chains |
|---|---|---|---|
| A | Bad quality | Vaults without chains, vaults with chains, deformable slab, semi-rigid slab, unidentified | No |
| Bad quality | Vaults without chains, unidentified | Yes | |
| Good quality | Vaults without chains, vaults with chains, deformable slab, unidentified | No | |
| B | Bad quality | Rigid slab | No |
| Bad quality | Vaults with chains, deformable slab, semi-rigid slab, rigid slab | Yes | |
| Good quality | Semi-rigid slab | No | |
| Good quality | Vaults without chains, vaults with chains, deformable slab, unidentified | Yes | |
| C1 | Good quality | Rigid slab | No |
| Good quality | Semi-rigid slab, rigid slab | Yes |
| Vulnerability Class | Plausible Range |
|---|---|
| A | 0.95–1.05 |
| B | 0.75–0.85 |
| C1 | 0.60–0.65 |
| Vulnerability Class | Plausible Range |
| A- | 1.15–1.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sava, R.M.; Arcoraci, R.; Greco, A.; Pluchino, A.; Rapisarda, A. Simulations of Damage Scenarios in Urban Areas: The Case of the Seismic Sequence of L’Aquila 2009. Buildings 2025, 15, 3980. https://doi.org/10.3390/buildings15213980
Sava RM, Arcoraci R, Greco A, Pluchino A, Rapisarda A. Simulations of Damage Scenarios in Urban Areas: The Case of the Seismic Sequence of L’Aquila 2009. Buildings. 2025; 15(21):3980. https://doi.org/10.3390/buildings15213980
Chicago/Turabian StyleSava, Rosa Maria, Rosalinda Arcoraci, Annalisa Greco, Alessandro Pluchino, and Andrea Rapisarda. 2025. "Simulations of Damage Scenarios in Urban Areas: The Case of the Seismic Sequence of L’Aquila 2009" Buildings 15, no. 21: 3980. https://doi.org/10.3390/buildings15213980
APA StyleSava, R. M., Arcoraci, R., Greco, A., Pluchino, A., & Rapisarda, A. (2025). Simulations of Damage Scenarios in Urban Areas: The Case of the Seismic Sequence of L’Aquila 2009. Buildings, 15(21), 3980. https://doi.org/10.3390/buildings15213980








