A Global Performance-Based Seismic Assessment of a Retrofitted Hospital Building Equipped with Dissipative Bracing Systems

Abstract

This paper presents a global performance-based seismic assessment of an existing reinforced concrete hospital building retrofitted with dissipative bracing systems. The study aims to evaluate the overall effectiveness of different dissipative configurations, two traditional systems and one innovative low-activation solution in enhancing the seismic performance of the structure in compliance with the Italian Building Code (NTC 2018). The analyses were carried out using nonlinear static (pushover) procedures to determine the global capacity, equivalent damping, and displacement demand at the Life Safety (SLV) and Near Collapse (SLC) limit states. The retrofitting interventions were modeled assuming elastic connections between the existing RC frames and the added steel members, consistent with standard design practice in which connections are dimensioned with overstrength to avoid premature failure. The results demonstrate that the integration of dissipative systems significantly increases stiffness and damping, effectively reducing lateral displacements and improving the seismic safety index above the 60% threshold required for strategic facilities. The study highlights the importance of global assessment methodologies in guiding the seismic upgrading of hospitals and other critical infrastructures, while local detailing and device-level optimization are identified as topics for future research.

1. Introduction

Hospitals are critical infrastructures that must remain operational during and after seismic events to ensure the continuous provision of emergency medical care [1,2,3]. As strategic facilities, they play a vital role in disaster response [4,5,6], accommodating injured individuals and supporting public health efforts in the aftermath of an earthquake or earthquake sequence. The failure or partial collapse of hospital buildings can thus lead to severe consequences, including the inability to provide urgent medical assistance, increased mortality rates, and disruption of essential healthcare services. Given their fundamental role in societal resilience, hospitals must be designed or retrofitted to withstand seismic forces while maintaining functionality [7,8,9]. This necessitates not only structural integrity but also the protection of non-structural components [10,11,12,13,14,15,16], such as medical equipment, power supply systems, and communication networks, which are essential for uninterrupted hospital operations. Strengthening hospital buildings through advanced seismic mitigation strategies, such as dissipative bracing systems, enhances their ability to remain fully or partially functional, thereby improving emergency response capabilities and ensuring the safety of both patients and healthcare personnel.

Post-earthquake evaluations have consistently identified recurrent structural failure patterns across various seismic events [17,18], highlighting vulnerabilities in numerous construction types. These include reinforced concrete structures [17,19,20,21], precast components [17,22,23], lightweight concrete [24,25,26] with infill panels, and steel frameworks [17,27,28,29]. The observed deficiencies can largely be attributed to the fact that many of these buildings were originally designed based on outdated seismic standards, which did not fully account for contemporary seismic performance requirements [30,31,32].

In recent years, the use of dissipative [33,34], retrofitting [35,36,37], and base isolation techniques [38,39,40,41,42,43,44] has gained significant attention in modern structural/earthquake engineering, as these approaches offer effective strategies for mitigating the impact of seismic hazards on buildings and infrastructures. Numerous experimental and analytical studies have demonstrated that dissipative retrofitting systems can substantially enhance the seismic performance of existing reinforced concrete buildings. For example, Berman and Bruneau in 2005 experimentally verified the efficiency of metallic shear-yielding panels in dissipating seismic energy and reducing interstory drifts, while Mohammadi and Akrami in 2010 demonstrated that steel frames infilled with sliding masonry panels improve both ductility and energy dissipation capacity. Other investigations [33,34] confirmed that passive energy dissipation devices are among the most cost-effective and structurally efficient techniques for seismic retrofitting. More recent analytical and experimental research (e.g., Matteis et al. in 2004 and Foti et al. in 2010 or also Mualla et al. in 2003 [45,46,47]) further validated these findings by demonstrating consistent improvements in stiffness, damping, and overall resilience.

In this context, the dissipative devices investigated in the present study, Types A, B, and C, were selected for their proven reliability, ease of integration into existing RC frames, and favorable cost-to-benefit ratio. These systems can be installed with minimal interference to hospital operations and without major structural modification, providing a practical balance between efficiency, economic feasibility, and architectural compatibility. Their inclusion aligns with the study’s overarching goal of proposing non-invasive and economically sustainable retrofitting solutions for critical facilities that must remain functional during and after seismic events.

The increasing frequency and intensity of earthquakes worldwide have underscored the urgent need for resilient structural solutions that enhance the seismic performance of both new and existing buildings. Many hospital buildings, particularly older ones, were designed based on outdated seismic provisions [48,49], making them highly vulnerable to earthquake-induced damage [17,50]. Structural deficiencies, such as inadequate reinforcement detailing, insufficient ductility, and poor energy dissipation capacity, have been widely observed in post-earthquake damage assessments. To address these challenges, seismic retrofitting techniques have evolved to incorporate passive energy dissipation systems, which enhance a structure’s ability to withstand seismic forces while minimizing damage to both structural and non-structural components.

Dissipative bracing systems, in particular, have proven to be a cost-effective and non-invasive retrofitting solution [51,52,53], offering improved seismic resilience with minimal disruption to building functionality. These systems absorb and dissipate a significant portion of seismic energy, reducing interstory drifts and protecting primary structural elements from excessive deformation [54,55]. By integrating advanced dissipative devices, such as metallic yielding panels [45,46] and friction-based dampers [47], buildings can achieve higher safety levels while meeting modern seismic performance requirements.

This study focuses on the performance-based seismic assessment of a retrofitted hospital building in Modena, Italy, analyzing the effectiveness of different dissipative systems in improving its structural performance. Modena is located in a region that was severely affected by the earthquakes of May 20 and 29, 2012 [56], which caused extensive damage to buildings [57,58,59,60], infrastructure [61], and industrial components [23,62]. These seismic events underscored the vulnerability of existing structures and highlighted the urgent need for advanced retrofitting strategies to enhance seismic resilience, particularly in critical facilities such as hospitals. Through advanced numerical analyses, including nonlinear static (pushover) simulations [63], this research investigates the impact of traditional and innovative dissipative devices on two hospital blocks, assessing their capacity to improve seismic safety while maintaining hospital operability/functionality. The findings provide valuable insights into the practical implementation of energy dissipation technologies in critical infrastructure, contributing to the ongoing efforts to enhance the seismic resilience of healthcare facilities worldwide.

In this study, the seismic response of an existing reinforced concrete (RC) hospital building, the Policlinico of Modena (Figure 1), located in the northern-central region of Italy, was assessed through advanced numerical analyses. The research was conducted in two phases. In the first phase, the effects of two conventional dissipative systems (Type A and Type B), considered as alternative solutions one another, were evaluated when applied to one of the structural units of the hospital complex, designated as Block H (Figure 1b). In the second phase, the feasibility of implementing an innovative dissipative system, comprising a steel-element framework and labeled Type C, was examined for Block C (Figure 1b). The key distinction between the conventional and innovative systems lies in their activation thresholds: while the traditional systems require larger interstory displacements to engage, the innovative system is designed to activate at lower displacement levels, enhancing its effectiveness in mitigating seismic damage.

The assessment was carried out using three-dimensional finite element (FE) modeling and nonlinear static (pushover) analyses along the two principal structural directions. To facilitate the analysis, separate FE models were developed for Block H and Block C, into which the selected dissipative devices were integrated.

The traditional dissipative systems evaluated in Phase 1 are

• Type A: metallic panels designed to dissipate energy through shear yielding, activated by relative interstory displacements induced by seismic loading;
• Type B: passive dissipation devices embedded within infill walls, incorporating shear connections that enable controlled sliding between partitions during earthquakes.

For Block H in the first phase, the numerical model accounted for geometric nonlinearity, material inelasticity, and predefined loading conditions. The analyses were performed for both the Life Safety Limit State (SLV) and the Near Collapse (SLC) of primary structural elements. Note that the above two acronyms, namely SLV and SLC, follow the Italian nomenclature. The study included an evaluation of rotational capacity and shear resistance, along with damping calculations to compare the seismic performance of the different retrofitting solutions.

In the second phase (Phase 2), focusing on Block C, an innovative dissipative system (Type C) was analyzed using the same modeling approach. This system was specifically designed to activate at lower displacement levels, potentially offering enhanced seismic resilience by engaging earlier in the response to earthquake-induced demand. The study provides valuable insights into the comparative effectiveness of conventional and innovative dissipative technologies for improving the seismic performance of hospital buildings.

Based on the reviewed state of the art, this study addresses the following research question: How can the integration of different dissipative retrofitting systems improve the seismic performance and safety level of existing reinforced concrete hospital buildings originally designed without modern seismic provisions? To answer this question, the paper investigates two main case studies (Blocks H and C of the Modena Hospital Complex), which underwent successive retrofitting phases. Through nonlinear static (pushover) analyses, the study compares the performance of three different dissipative systems, two conventional (Types A and B) and one innovative (Type C), with the objective of quantifying their contribution to global seismic capacity, equivalent damping, and compliance with the 60% safety requirement established by Italian regulations.

2. Methodology

The research methodology adopted in this study follows a structured and sequential approach aimed at assessing the seismic performance of an existing hospital building and evaluating different retrofitting strategies with dissipative systems. The process is summarized in the following steps and consists of the following main phases:

• Data collection and structural characterization: compilation of original design documentation, in situ inspection data, and material test results, which formed the basis for defining geometry, reinforcement details, and mechanical properties of both existing and retrofitted structural components.
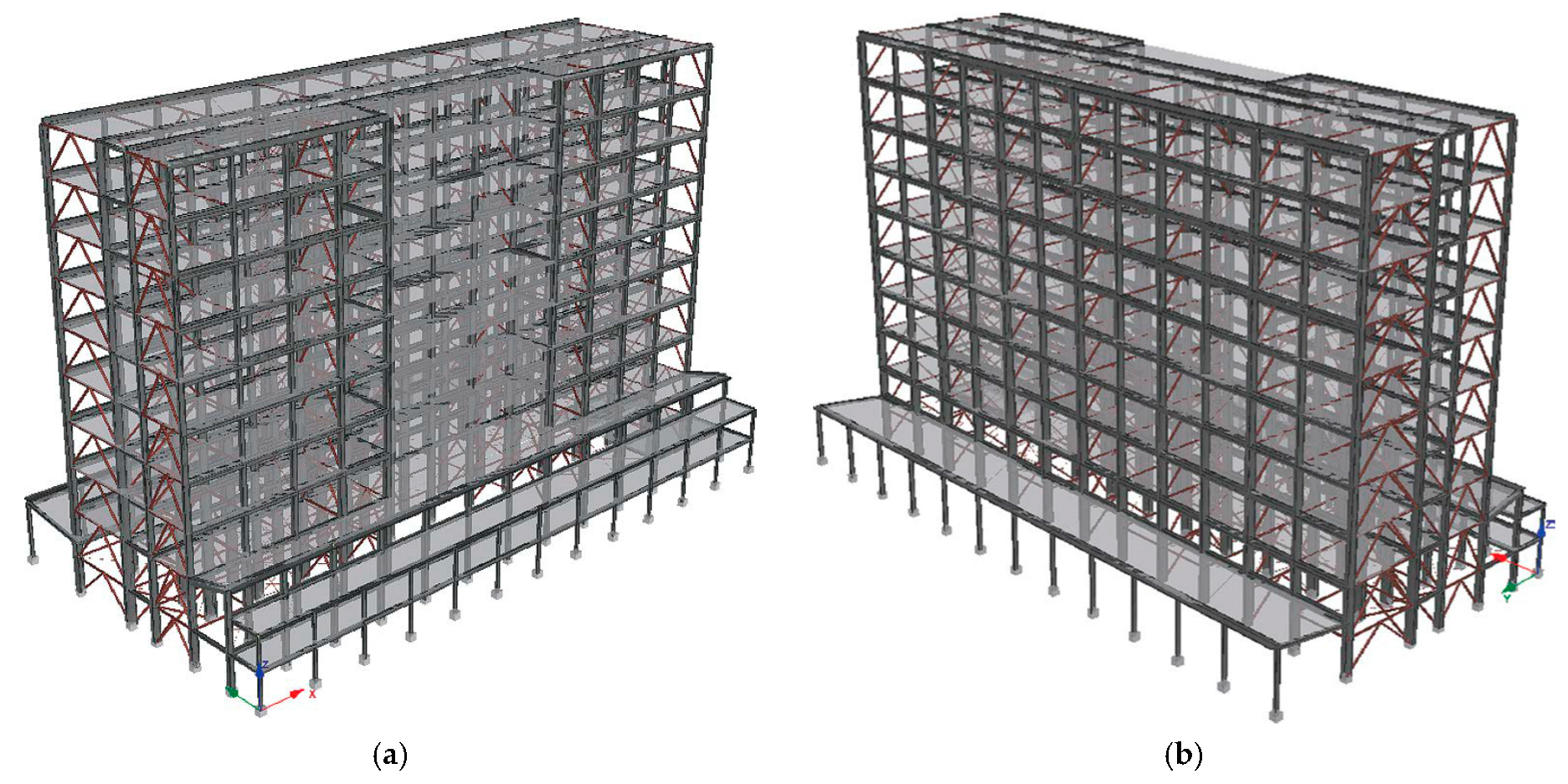
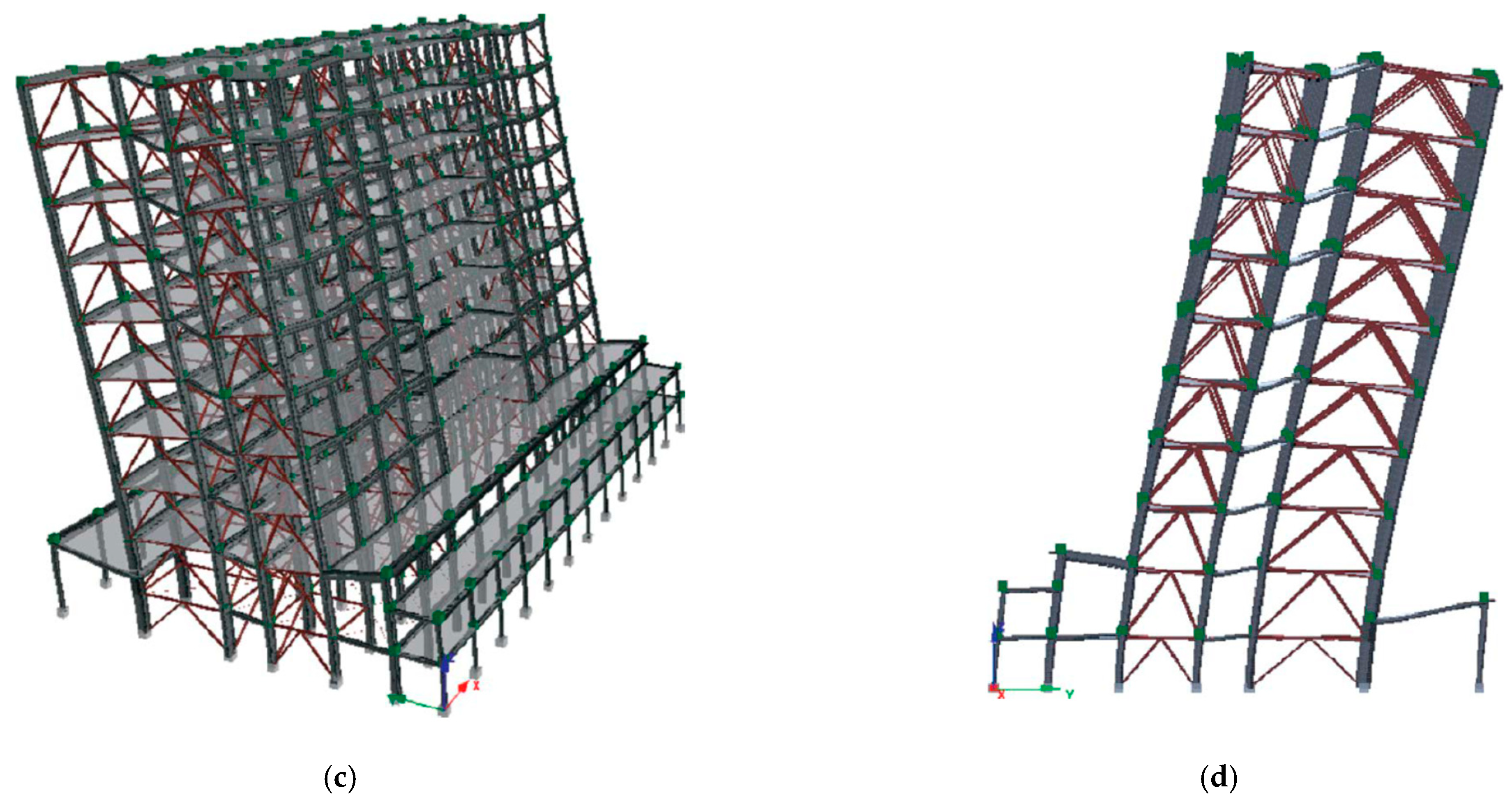
• Development of the numerical model: creation of three-dimensional finite element models of Blocks H and C using SeismoStruct, accounting for geometric and material nonlinearities, as well as previously implemented strengthening interventions (steel bracing and jacketing).
• Definition of seismic input: determination of design spectra for the Life Safety and Near Collapse limit states according to the Italian Building Code (NTC 2018), considering local site effects, soil category, and topographic amplification.
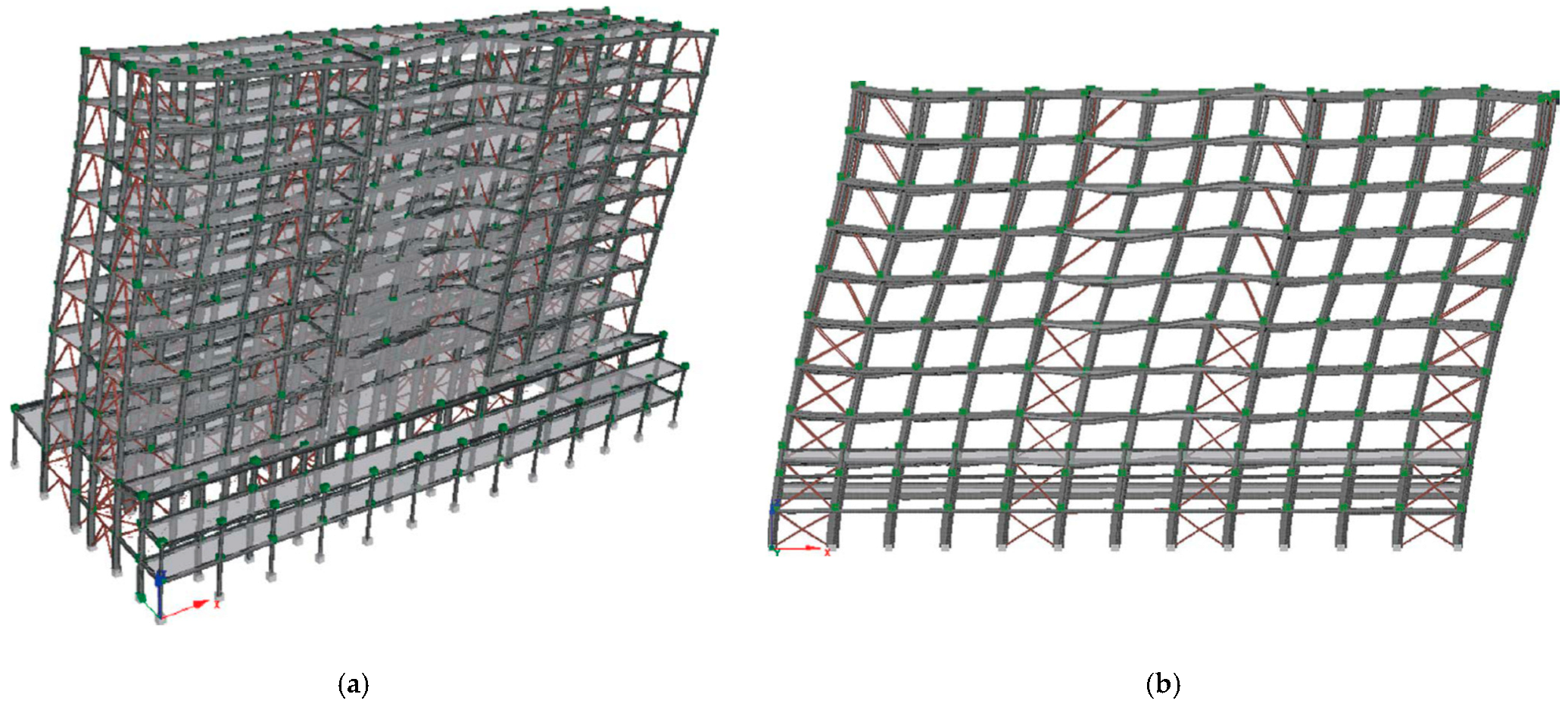
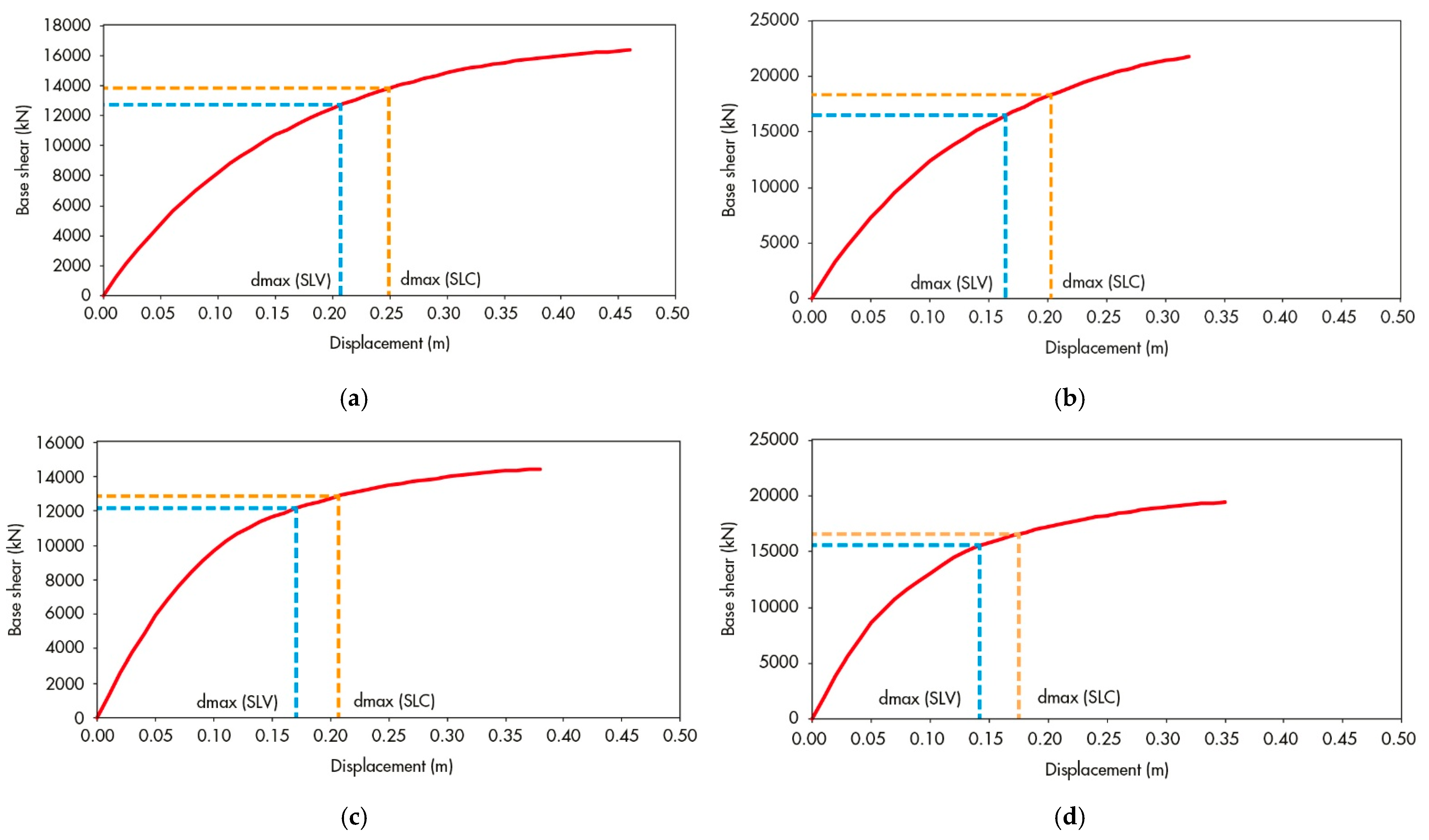
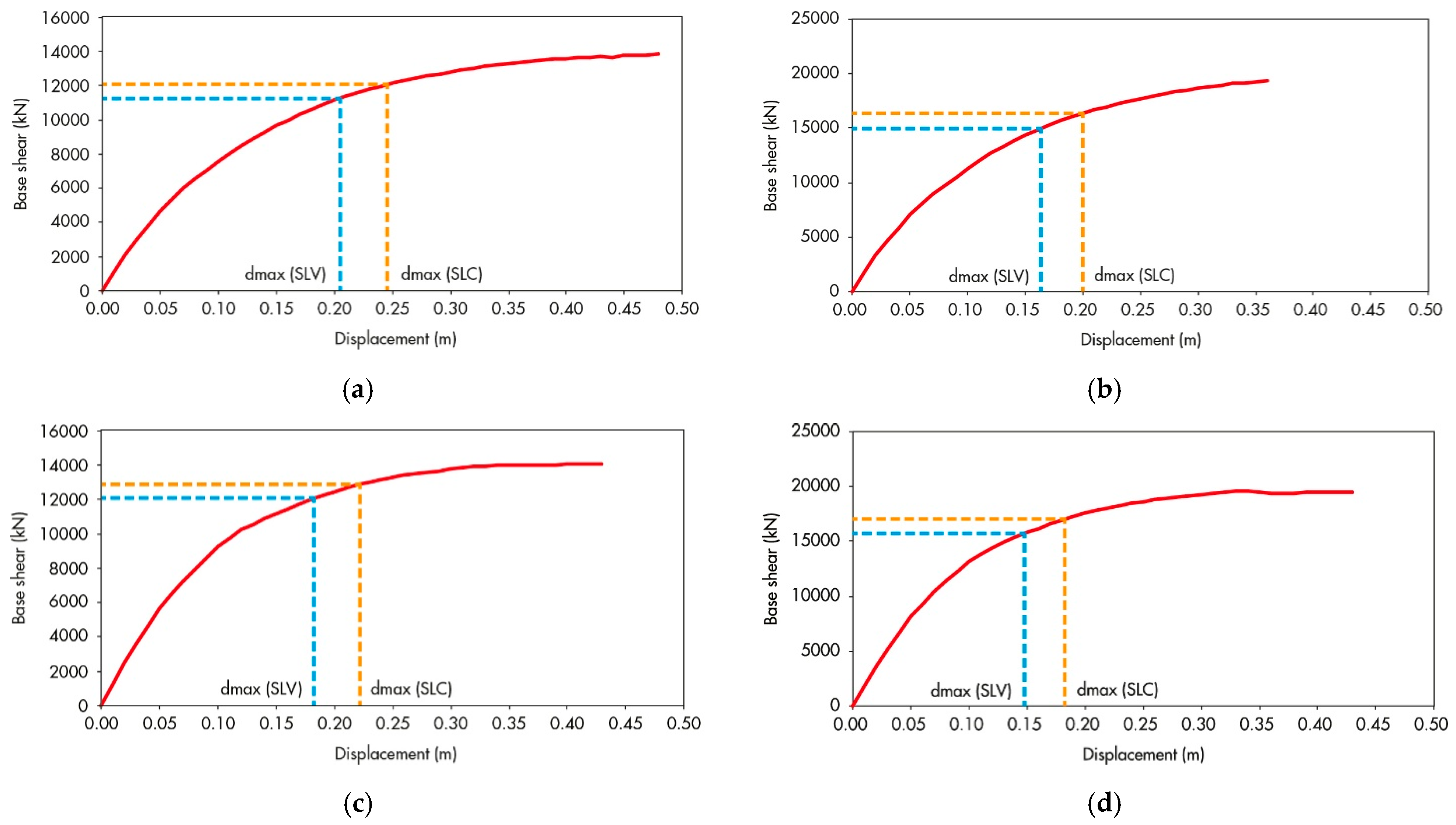
• Nonlinear static (pushover) analyses: performance evaluation of the retrofitted structures under monotonic lateral load distributions in both principal directions, following the displacement-based procedure outlined in NTC 2018 §C8.7.1.2.
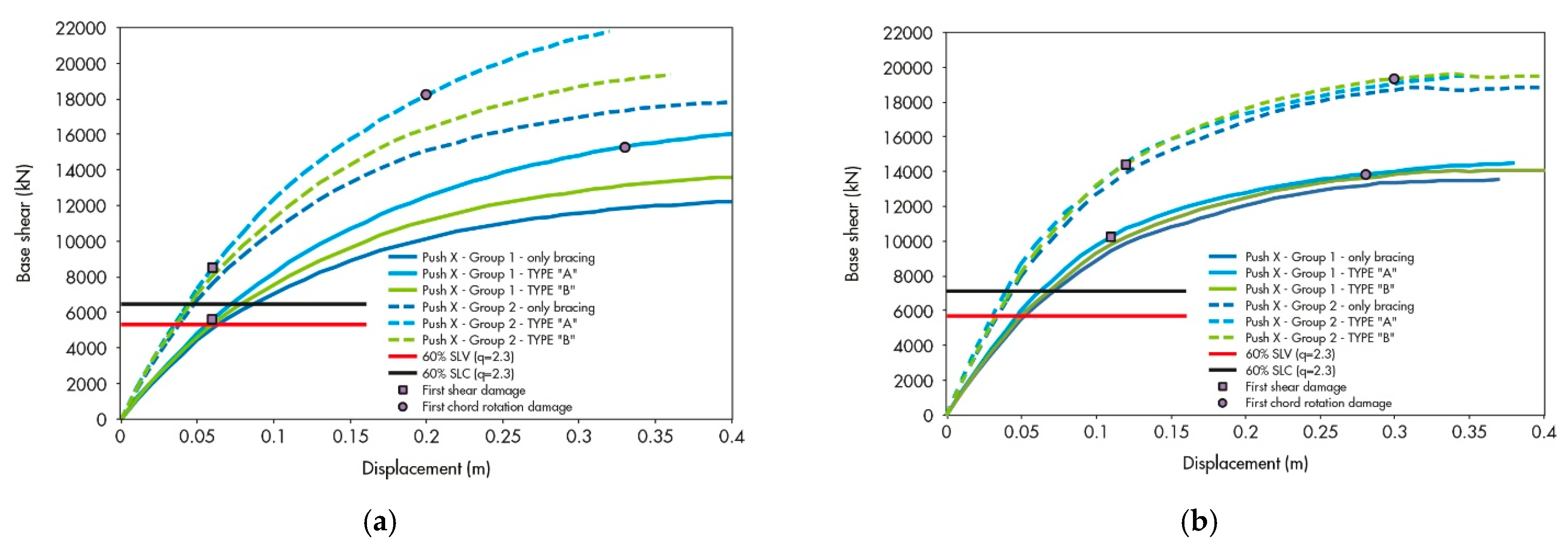
• Comparative assessment of retrofitting solutions: evaluation of three dissipative systems (Types A, B, and C), with emphasis on base shear capacity, equivalent damping, and global displacement demand, to verify compliance with the target seismic safety level of 60% required for existing hospital buildings.
• Interpretation and validation of results: critical analysis of the obtained capacity curves, equivalent viscous damping ratios, and performance indices, followed by discussion of the implications for practical design and future research.

This structured methodology ensured consistency between the analytical modeling, code-based performance verification, and practical retrofit objectives, providing a comprehensive framework for evaluating dissipative solutions in existing hospital facilities.

3. Structural Description

The examined structures are part of the Policlinico of Modena, a hospital complex located in northern-central Italy. Construction of these buildings began in the 1930s and was completed between 1951 and 1963. The structures are RC buildings characterized by irregular geometries in both plan and elevation, which can significantly influence their seismic response. The study specifically focuses on two key pavilions, Block C and Block H, identified in Figure 1b, where Block C is located on the left and Block H on the right. Both buildings extend across 11 floors, including a flat roof. The first three levels (Floors −2, −1, and 0) feature six spans and have a plan dimension of 54.9 m × 29.2 m, while the upper eight floors are structured with three spans, reducing the plan dimensions to 54.9 m × 18.5 m. The vertical floor heights are as follows: 2.95 m between the first and second floor, 3.90 m for the raised ground floor, and 3.65 m for the upper floors.

The floor slabs are composed of a clay-concrete composite, with thicknesses ranging between 24 and 27 cm. The reinforced concrete beams are approximately 52 cm × 40 cm, while columns at the basement level vary in section, with dimensions of 35 cm × 25 cm, 80 cm × 35 cm, 40 cm × 90 cm, 35 cm × 80 cm, 40 cm × 50 cm, and 40 cm × 25 cm, progressively reducing to 40 cm × 30 cm at the eighth floor. Notably, the original structural system consisted exclusively of longitudinal frames, lacking a transverse framing system, which posed significant structural limitations under seismic loads.

As a consequence of the seismic events of May 2012, a numerical analysis was conducted to evaluate the seismic vulnerability of the hospital buildings. The results highlighted structural deficiencies, necessitating targeted retrofitting interventions to enhance seismic performance. These interventions were implemented in multiple phases and included the following strategies:

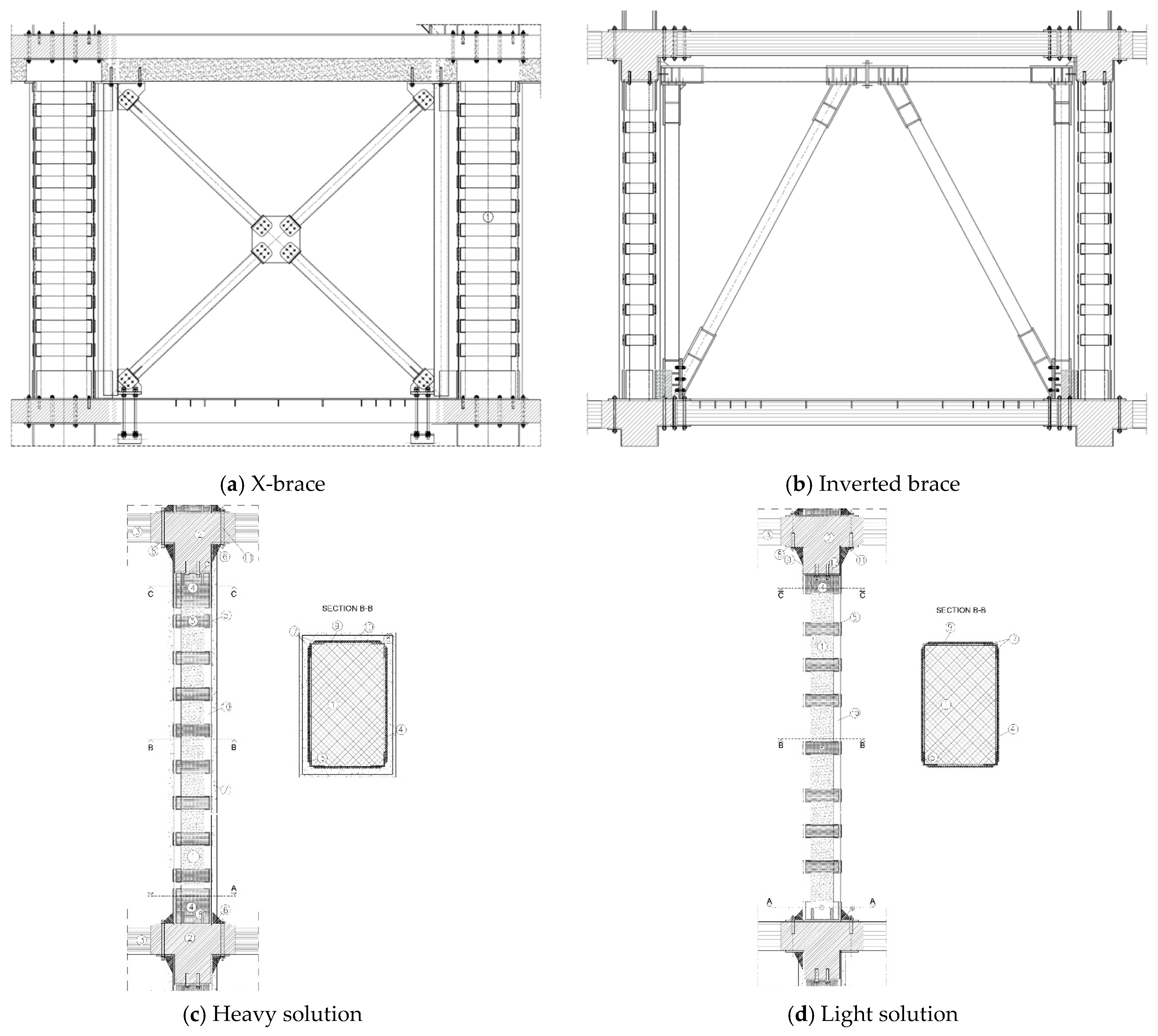
• Integration of Bracing Systems: steel bracing systems were incorporated within the existing frame bays to enhance lateral resistance in both $X$ (Figure 2a) and $Y$ (Figure 2b) orthogonal directions. Concentric braces were installed along the $X$ direction and inverted V-bracing was employed along the $Y$ direction. In both cases, the bracing elements were connected to steel columns and beams, which were firmly anchored to the existing RC frame using specialized connectors to ensure proper load transfer.
• Column Jacketing for Enhanced Load Capacity: to strengthen the reinforced concrete columns, two types of steel jacketing methods were adopted: “Light reinforcement” steel jackets (Figure 2d), designed to provide moderate confinement and stiffness; “Heavy reinforcement” (Figure 2c) steel jackets, further enhanced with fiber-reinforced concrete layers to significantly increase structural ductility and strength.
• Insertion of Horizontal Bracing Systems: to improve the global stability of the structure, horizontal bracing systems were integrated into the double-height floors through the use of steel tie rods, ensuring effective load distribution under seismic excitation.

Both longitudinal and transverse bracing systems were carefully positioned at structural extremities and central regions to optimize symmetry in the plan view and to increase torsional stiffness, reducing the risk of excessive lateral deformations during seismic events. The combined effect of these retrofitting measures significantly enhanced the seismic resilience of the hospital complex (56%), ensuring a safer environment for patients and healthcare personnel.

Thanks to the availability of the original design documentation, the records collected during the seismic strengthening phase, and the data obtained from both laboratory and in situ testing, it was possible to determine the mechanical properties of the materials used in both the original construction and the subsequent retrofitting. The material properties listed in

Table 1. Mechanical properties of original and retrofitted concrete (heavy jacket strengthening) and mechanical properties of existing and new reinforcement steels.

Concrete	Original	Retrofitted
Compressive strength [MPa]	12.97	21.20
Tensile strength [MPa]	1.30	2.10
Elastic modulus [MPa]	122	125
Strain at peak stress [m/m]	1.6927 × 104	2.1640 × 104
Unit weight [kN/m3]	24	24
Steel	Existing	New
Elastic modulus [MPa]	2.10 × 105	2.10 × 105
Yield strength [MPa]	371	355
Strain hardening parameter	0.005	0.005
Initial curvature parameter of the transition curve	20	20
Transition curve coefficient A1 (isotropic hardening in compression parameter)	18.5	18.5
Transition curve coefficient A2 A1 (isotropic hardening in compression parameter)	0.15	0.15
Transition curve coefficient A3 (isotropic hardening in tension parameter)	0	0
Transition curve coefficient A4 (isotropic hardening in tension parameter)	1	1
Ultimate strain (or buckling strain)	0.1	0.1
Unit weight [kN/m3]	78	78

are those required for implementing the Mander model [64] for concrete and the Menegotto and Pinto model [65] for steel.

4. Selected Seismic Action

Over the past two decades, Italy has experienced several major seismic events that have underscored the widespread vulnerability of buildings constructed according to outdated structural practices [30,31]. Notable earthquakes include those in San Giuliano di Puglia in 2002 [57,58], L’Aquila in 2009 [59,60], Emilia in 2012 [66,67], and Central Italy in 2016–2017 [68,69]. These events consistently revealed recurring structural deficiencies [70], particularly in the ability of buildings to effectively transfer horizontal seismic forces between structural and non-structural components [71]. The seismic event considered in this study, the May 2012 earthquake near Modena, in the northern-central region of Italy, registered a magnitude of 5.9 and serves as a striking example of such vulnerability. While the number of casualties was relatively low (27 deaths), the economic impact was devastating, with estimated direct losses exceeding €13 billion. When factoring in indirect economic consequences, the total damage is believed to have surpassed 1% of Italy’s Gross Domestic Product (GDP). This context highlights the urgency and necessity of improving seismic resilience through regulatory evolution [72]. As a result, the Italian seismic code has undergone rapid and significant development in recent years, starting from OPCM 3274 [73] and culminating in the adoption of the NTC 2018 code [74], which incorporates advanced concepts of seismic performance and modern design criteria aimed at preventing similar damage in future events.

The analyzed building is located within the Municipality of Modena, which, according to the seismic classification established by the former regulation (OPCM 3274) [73], falls within Seismic Zone 3. The design spectra for the Ultimate Limit States, namely, Life Safety (SLV) and Near Collapse (SLC), were defined in compliance with the Italian Building Code [74].

To establish the seismic action parameters, the nominal design life of the structure was set at 50 years, while the Importance Factor was defined as 2, leading to a reference period of 100 years. Using the geographic coordinates of the building (longitude 10.9247, latitude 44.6481), and considering a return period of 949 years, the basic seismic parameters were identified by interpolating the values from the four nearest grid points. For the SLV condition, the peak ground acceleration ($a_g$) was 0.213 g, the amplification factor ($F_0$) was 2.438, and the characteristic period ($T_c^{\ast }$) was 0.281 s. For the SLC condition, the corresponding values were 0.273 g, 2.413, and 0.297 s, respectively. Site amplification coefficients were also considered based on the local soil category (C) and topographic type (T1). These coefficients were calculated as $S_S$ = 1.389 and $S_T$ = 1.0 for SLV, and $S_S$ = 1.305 and $S_T$ = 1.0 for SLC. Furthermore, the corner period $T_c$, representing the beginning of the constant velocity segment of the spectrum, was computed as 0.457 s for SLV and 0.466 s for SLC.

All seismic spectra referenced in this study were developed using the equations provided in Section 3.2.3.2 of the NTC code [74], and are shown in Figure 3.

5. Results and Discussion

This section presents and interprets the numerical results obtained from the seismic assessment of the retrofitted hospital buildings, organized according to the two main analytical phases of the study. The first phase focuses on the evaluation of conventional dissipative systems (Types A and B) applied to Block H, while the second phase investigates the performance of an innovative low-activation dissipative system (Type C) implemented in Block C. The analyses were carried out using nonlinear static (pushover) procedures, as described in the methodology, and include detailed modeling assumptions, device characterization, and comparative performance evaluation. The discussion integrates the outcomes of the capacity curves, equivalent damping ratios, and energy dissipation capacities to highlight the effectiveness of each retrofit strategy in achieving the target seismic safety level prescribed by the Italian code.

5.1. Phase 1: Application of Two Dissipative Systems (Type A and Type B)

The analytical work presented in this study was motivated by the need to further improve the seismic performance of a previously retrofitted structure. Following the seismic events in the Emilia region on 20 and 29 May 2012, the building had been strengthened, reaching a safety level of approximately 56%. However, in order to comply with the minimum requirement of 60% of the seismic safety prescribed for new buildings, as stated in Article 3, paragraph 10 of Legislative Decree No. 74 of 6 June 2012 [75], additional interventions were deemed necessary.

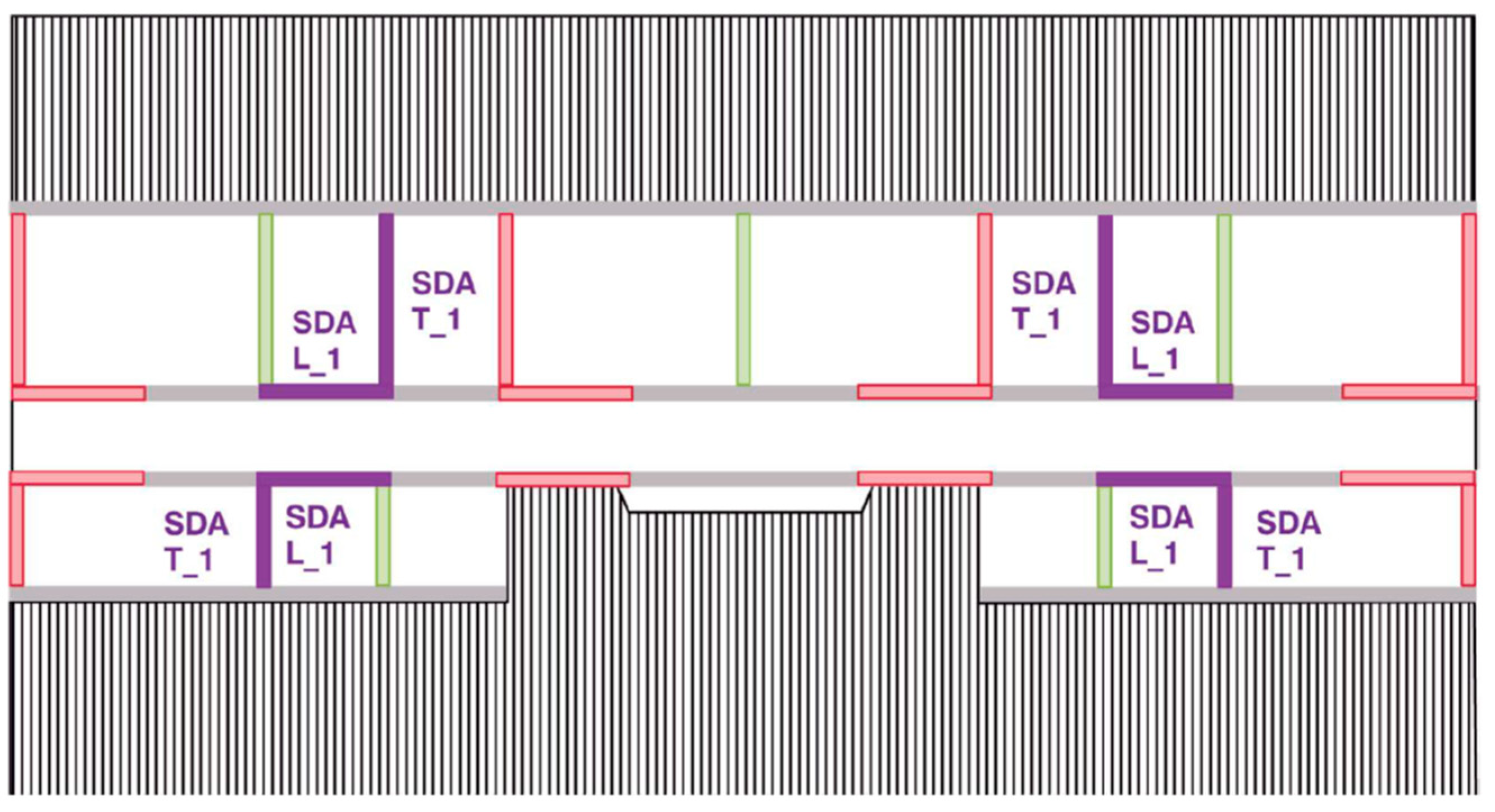
5.1.1. Overview of the Added Energy Dissipation Devices

Phase 1 of the study, described in this section, focuses on assessing the potential benefits of integrating additional dissipative panels into the already retrofitted configuration. Seismic protection devices can alter a structure’s response in several ways: by increasing the fundamental period, modifying the modal shapes, enhancing energy dissipation capacity, reducing the forces transmitted to the main structure, and introducing either permanent or temporary constraints.

The two energy dissipation systems examined in this phase are passive devices. The first, referred to as Type A, consists of metallic panels. The effectiveness of this system has been evaluated by Berman and Bruneau in [76] through a combination of experimental tests and numerical simulations. Their quasi-static tests showed that the metal panels significantly contributed to the ductility and energy dissipation of the system, while simultaneously reducing seismic demands on the surrounding RC frame. Although not a low-cost solution, this system proved to be highly effective for retrofitting existing structures in high seismicity regions, as the energy dissipated by the steel panels alone was substantial when compared to the hysteretic behavior of the bare frame. Additional findings from Berman and Bruneau’s experimental work [76] revealed that panel failure occurred due to out-of-plane buckling. Nevertheless, significant drift levels (up to 3% for the corrugated panel) were achieved, and the panels exhibited a ductile failure mechanism, along with typical pinching and sliding behaviors associated with bolted connections.

The second dissipation system, referred to as Type B, consists of a steel frame infilled with masonry blocks or ordinary concrete. Special shear connections between the infill components enable controlled sliding during seismic events. Experimental studies on steel frames infilled with masonry walls were conducted by Mohammadi and Akrami in [77]. Their proposed solution aims to control seismic demand by managing the internal force transmission and plastic deformation at critical points within the frame. They also tested similar systems with reinforced concrete infills, confirming the feasibility of the solution. The resulting force-displacement curves demonstrated a satisfactory response in terms of energy dissipation and deformation capacity.

This technology is applicable to both new constructions and existing buildings, provided that the load-bearing capacity of the existing frame is assessed after the introduction of the additional system.

Within the scope of Phase I, the configuration of the additional dissipative devices was designed to be doubly symmetric, placing them within the spans of the existing frames not already occupied by the bracing systems installed during the previous seismic retrofit. Four dissipative devices were placed along the longitudinal direction and four along the transverse direction, consistently positioned over the full height of the structure. A schematic floor plan showing the arrangement of bracing frames (in red and green) and the dissipative systems (in purple) is presented in Figure 4.

5.1.2. Structural Modeling and Analysis

The analyses of the examined structure were carried out using SeismoStruct software ver. 2024 [78], a finite element program that allows for distributed plasticity modeling and is particularly well-suited for pushover analyses [79,80,81]. Furthermore, several peer-reviewed studies have applied SeismoStruct in the context of retrofitted RC frames and columns, confirming its suitability for capturing global capacity, drift demands and energy dissipation [82,83]. The vertical and horizontal load-bearing elements were modeled using inelastic frame elements with a force-based formulation [79,80,81], defined with five integration sections and 200 fibers per section [81,84]. Additionally, the software allows for the definition of different cross-sections along the length of the same element, making it possible to model beams, even in cases of varying reinforcement, using a single finite element, thus reducing the overall number of elements and minimizing computational time. The cross-sectional properties were defined based on the original design documents provided by the client. The model also accounted for the retrofitting interventions previously carried out on the structure. Specifically, for the strengthened columns, an additional reinforcement area was introduced in the model to represent the steel angles placed at the four corners of the cross-section. The bracing elements added during the seismic retrofit (Figure 2), in both the longitudinal and transverse directions, were modeled using inelastic frame elements. To simulate pinned connections, the end moments were released in the model. The horizontal bracing systems located at the double-height level were modeled using inelastic truss elements with appropriate cross-sectional properties.

The dissipative devices were modeled using a combination of a link element in series with a diagonal truss element. The mechanical behavior of each link element was defined by assigning a bilinear force–displacement curve. The parameters used for characterizing the individual dissipative systems are reported in

Table 2. Parameters used for the mechanical characterization of the Link element (Bilinear Curve) for Type A and Type B.

Type A	Value
Initial stiffness in the positive quadrant [kPa]	93,750
Yield force in the positive quadrant [kNa]	500
Post-yield hardening ratio in the positive quadrant	0.01
Initial stiffness in the negative quadrant [kPa]	93,750
Yield force in the negative quadrant [kN]	−500
Post-yield hardening ratio in the negative quadrant	0.01
Type B	Value
Initial stiffness in the positive quadrant [kPa]	8000
Yield force in the positive quadrant [kNa]	100
Post-yield hardening ratio in the positive quadrant	0.01
Initial stiffness in the negative quadrant [kPa]	8000
Yield force in the negative quadrant [kN]	−160
Post-yield hardening ratio in the negative quadrant	0.01

. The dissipative devices were connected to the existing reinforced concrete frame through steel gusset plates and bolted anchorage systems, ensuring a direct transfer of axial forces between the RC elements and the added steel bracing members. In the numerical model, these connections were idealized using pin-ended link elements in series with diagonal truss members, thereby allowing the devices to dissipate energy through shear or axial deformation without inducing additional bending moments at the connection nodes. This simplified representation reflects the actual mechanical behavior of the retrofit joints, where rotation is released at the interface to favor the activation of the dissipative mechanism while maintaining realistic load transfer within the frame. The steel-to-concrete connections used to anchor the bracing systems and dissipative devices were designed to develop a capacity exceeding the maximum axial and shear forces transmitted during the design-level seismic demand. This ensured that the connections remained elastic, transferring forces without local damage or slippage. In the numerical model, these interfaces were represented as fully bonded nodes, an assumption justified by the overstrength design criterion adopted for the anchorage systems and by experimental evidence available in the literature.

It is worth noting that in this structural model (Figure 5), the foundation system was not explicitly modeled; instead, a fully fixed base condition was assumed.

An initial eigenvalue analysis was performed on the retrofitted structure, strengthened with steel braces and jacketing, which, in this configuration, achieves a seismic safety level of only 53%, without the addition of supplemental dissipative systems. The fundamental periods and corresponding participating masses for the main vibration modes were as follows: $T_{1x}$ = 1.10 s with participating mass $M_{1x}$ = 66% in the $X$ direction, and $T_{1y}$ = 1.00 s with $M_{1y}$ = 68% in the $Y$ direction. The deformed shapes of these primary modes are illustrated in Figure 6.

Subsequently, pushover analyses were conducted by applying gravitational loads according to the seismic load combination. The nonlinear static (pushover) analysis approach was selected following the recommendations provided by major seismic assessment guidelines, such as FEMA 356 (2000) [85], Eurocode 8 Part 3 (EN 1998-3:2018) [86], and the Italian Building Code (NTC 2018) [74]. These documents identify pushover analysis as a reliable and efficient method for evaluating the global capacity and displacement demand of existing buildings, particularly when used for performance-based assessments. The choice also reflects the practical nature of the present study, which focuses on real hospital retrofitting scenarios where professional design offices require transparent and computationally efficient tools. In contrast, nonlinear time history analysis—although more refined and suitable for academic research—requires a higher degree of input uncertainty and modeling effort, often not compatible with standard design practice. The following steps were followed:

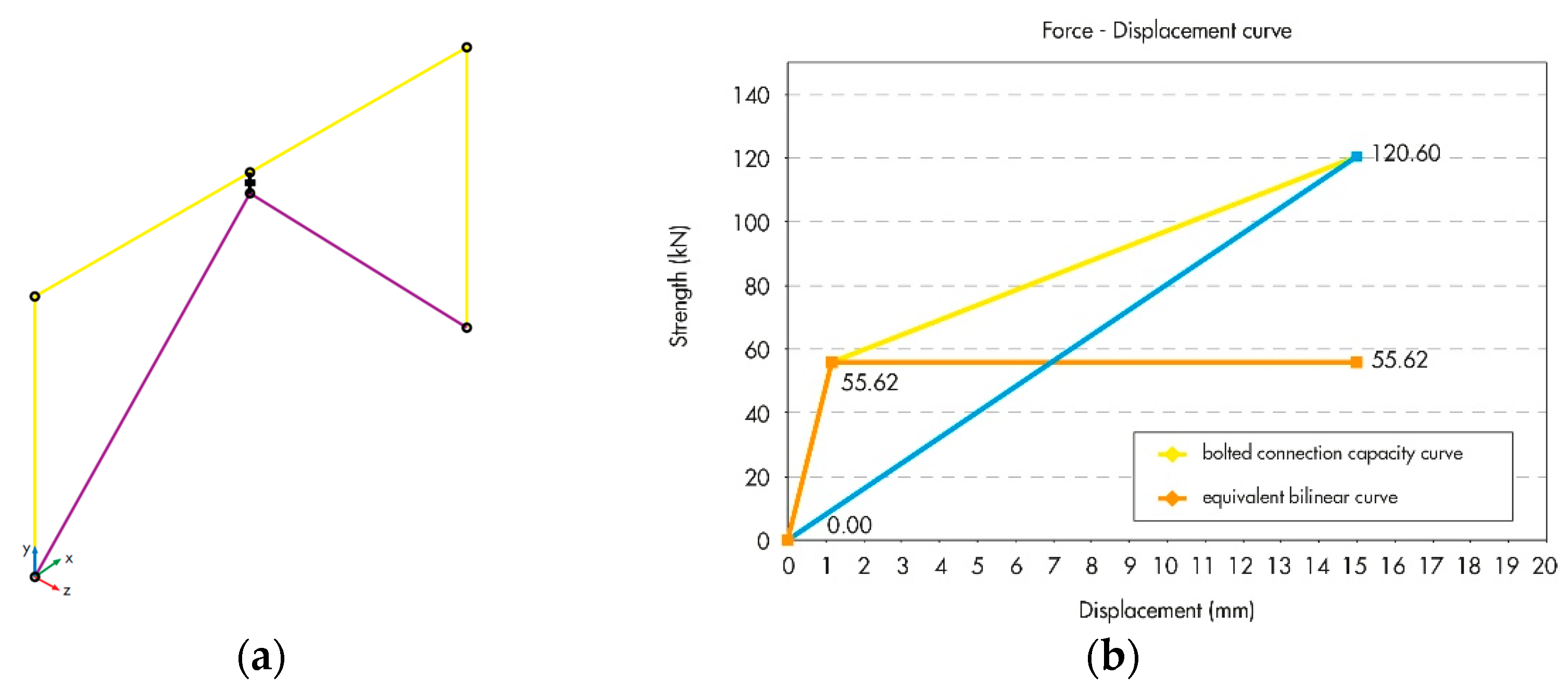
• Definition of a generalized force–displacement relationship between the resultant of applied forces (base shear, $F_b$) and the displacement ($d_c$) at the control point, located at the center of mass of the top floor;
• Derivation of an equivalent bilinear single-degree-of-freedom (SDOF) system representing the global response;
• Evaluation of the maximum displacement of the equivalent SDOF system using the displacement spectrum corresponding to the considered limit state;
• Conversion of the SDOF displacement to the actual displacement configuration of the structure;
• Verification of displacement compatibility (for ductile elements/mechanisms) and strength capacity (for brittle elements/mechanisms).

For each analysis, two distinct horizontal force distributions were applied:

• Group 1 (main distribution), as prescribed by the code [74], corresponding to a pattern proportional to the shape of the fundamental mode (4 directions $\pm X$ and $\pm Y$);
• Group 2 (alternative distribution), also permitted by the code [74], representing a uniform distribution (4 directions $\pm X$ and $\pm Y$).

The lateral forces were applied to the beam–column joints at each story level, in accordance with the distribution and modelling of seismic masses for eigen-value analysis. The capacity curves of the structure, representing the base shear ($F_b$) versus control point displacement ($d_c$), are shown in Figure 7 for Type A and Figure 8 for Type B traditional dissipative systems evaluated in Phase 1. The maximum displacement ($d_{\mathit{max}}$) induced by the seismic action for both the Life Safety Limit State (SLV) and the Collapse Limit State (SLC) was evaluated in all analyses following the procedure described in Section C.8 of the NTC [74].

The assessment procedure for existing reinforced concrete buildings involves verifying both ductile failure mechanisms [74], such as the flexural behavior of beams and columns, and brittle failure mechanisms [74], such as shear in these same elements. In accordance with the performance-based criteria set out in current seismic design codes [74], it was necessary to compute the chord rotation capacity for each primary structural member, employing the empirical formulations provided by the code. Hence, the assessment of structural failures was performed in accordance with the NTC 2018 and Eurocode 8 Part 3 framework, which evaluates both ductile (flexural) and brittle (shear) mechanisms through chord rotation and strength verifications. Since the adopted pushover procedure captures the overall progression of inelastic behavior, the analysis focuses on global limit states, Life Safety and Near Collapse, rather than on localized member failures, in line with performance-based design principles.

In this research, and in alignment with the requirements of Article 3, paragraph 10 of Legislative Decree No. 74 of 6 June 2012 [75], the seismic safety level of the existing structure was evaluated with the objective of reaching at least 60% of the safety level required for a newly constructed building. To do so, the base shear capacity of a hypothetical new structure with equivalent geometry and function was calculated and used as a benchmark. This benchmark value was subsequently compared with the seismic performance results of the existing, retrofitted building obtained through numerical analyses. As illustrated in Figure 9, the retrofitted configuration satisfies the target performance criteria. In particular, the base shear capacity of the improved structural system exceeds the corresponding demand associated with the original configuration, thereby demonstrating compliance with the minimum safety requirements established by current national regulations.

Since current building codes provide only limited guidance for the seismic performance assessment of existing structures equipped with energy dissipation devices, it was considered appropriate to calculate the total equivalent viscous damping (${\xi }_{\mathrm{t}\mathrm{o}\mathrm{t}}$) as proposed by Di Sarno et al. in [87]. Accordingly, the acceleration and displacement spectra associated with seismic demand can be reduced by applying a total damping coefficient, which is the sum of three distinct components:

• Intrinsic structural damping (${\xi }_{\mathrm{i}\mathrm{n}\mathrm{t}}$): the inherent damping of a structure in the elastic range, typically assumed to be 5%.
• Hysteretic damping (${\xi }_{\mathrm{h}\mathrm{\gamma }\mathrm{s}\mathrm{t}}$): related to the plastic behavior of the structure. This component is zero in the case of purely elastic response.
• Additional viscous damping (${\xi }_{\mathrm{v}\mathrm{i}\mathrm{s}}$): provided by the viscous dissipation systems installed in the structure. This component is zero when the structure is equipped with hysteretic or friction-based dissipative devices.

And the relation is

$${\xi }_{\mathrm{t}\mathrm{o}\mathrm{t}}={\xi }_{\mathrm{i}\mathrm{n}\mathrm{t}}+{\xi }_{\mathrm{h}\mathrm{\gamma }\mathrm{s}\mathrm{t}}+{\xi }_{\mathrm{v}\mathrm{i}\mathrm{s}}\sqrt{\mu }$$

(1)

where $\mu$ is the ductility of the system in the considered direction. For the Type A dissipative devices analyzed in this study, the total damping was calculated in accordance with Equation (1). In the case of Type B devices, however, the equation was simplified as follows:

$${\xi }_{\mathrm{t}\mathrm{o}\mathrm{t}}={\xi }_{\mathrm{i}\mathrm{n}\mathrm{t}}+ {\xi }_{\mathrm{h}\mathrm{\gamma }\mathrm{s}\mathrm{t}}$$

(2)

Table 3. Comparison of overall equivalent viscous damping values.

Pushover Curve	${\mathit{\xi }}_{\mathbf{tot}}$ (Braces) [%]	${\mathit{\xi }}_{\mathbf{tot}}$ (Type A) [%]	${\mathit{\xi }}_{\mathbf{tot}}$ (Type B) [%]
Pushover $X$ fundamental mode	24.17	31.32	23.60
Pushover $X$ uniform mode	23.21	26.73	21.63
Pushover $Y$ fundamental mode	23.96	37.44	25.30
Pushover $Y$ uniform mode	25.85	36.51	25.66

shows that the equivalent viscous damping value ${\xi }_{\mathrm{t}\mathrm{o}\mathrm{t}}$ (braces) for the configuration with structural strengthening alone is similar to that obtained for the configuration incorporating Type B dissipative devices ${\xi }_{\mathrm{t}\mathrm{o}\mathrm{t}}$ (Type B). However, it is important to note that in the case of using only steel bracing systems, a significant level of damage would be expected in primary structural elements such as beams and columns. Conversely, when Type B dampers are introduced, the seismic energy is primarily absorbed by the devices themselves, thereby preserving the integrity of the main load-bearing elements. An additional consideration is that the damping values reported in Table 3 represent theoretical values calculated as a function of the maximum ductility of the system, derived from the ultimate displacement of the equivalent bilinear curve. In reality, the developed ductility is typically lower, as it depends on the actual displacement demand, which is identified at the intersection between the elastic branch of the bilinear curve and the elastic response spectrum. As a result, the expected damping level is also lower than the theoretical estimate, in some cases by as much as 10%.

Nevertheless, the observations made above remain valid. That said, a residual uncertainty exists concerning the stability and efficiency of additional damping systems over the full duration of a seismic event. This, combined with considerations related to the activation displacement threshold of the dissipative devices, led to the extension of the study into Phase 2 of analysis, as described in the following sections.

5.2. Phase 2: Innovative Dissipative System

The “traditional” dissipative systems analyzed in the previous sections reach their yield deformation, and thus achieve maximum energy dissipation, only for relative displacements exceeding 7.5 cm. However, due to the slenderness of the existing structure, such displacements are not sustainable. The columns are susceptible to second-order (P-Δ) effects, and reaching such displacement levels could compromise the structural stability and functionality (e.g., piping systems and/or sprinklers housed in the structure). This observation prompted the need to adopt a dissipative system capable of activating at smaller displacement thresholds. As a result, an alternative solution, Type C system, was proposed. This system consists of steel diagonals with timber end connections (see Figure 10). The dissipative element is modeled as a special type of link element exhibiting a bilinear behavior with a strain-hardening plastic branch. However, for safety and conservatism, the model was idealized with the same elastic stiffness but a non-hardening plastic branch, with a maximum displacement capacity limited to 15 mm (also shown in Figure 10). Readers are thus referred to Figure 10 for the elastic perfectly plastic model assumed, and corresponding capacity values.

The elastic stiffness of the bilinear model and the secant stiffness of the equivalent linear system can be calculated accordingly: $k_e={\displaystyle \frac{F_y}{d_y}}={\displaystyle \frac{55.62}{0.118}}=470.3 \mathrm{kN}/\mathrm{cm}$ and $k_{sec}={\displaystyle \frac{F_u}{d_u}}={\displaystyle \frac{120.6}{1.5}}=80.4 \mathrm{kN}/\mathrm{cm}$. The purpose of introducing these Type C bracing grids is to enhance the structure’s energy dissipation capacity, and thereby its equivalent damping, to a level sufficient to meet the 60% seismic safety requirement for existing buildings compared to new constructions. To provide a first-order estimation of the benefit introduced by these devices, and given the limited guidance in current codes regarding the seismic performance assessment of existing structures with supplemental dampers, a simplified, though approximate, calculation of the total equivalent damping provided by a single grid was carried out. Hence, to approximate the total energy dissipated by the building in a given direction, the energy dissipated by a single bracing grid was multiplied by the number of grids per floor and by the number of floors. The resulting estimates of energy dissipation along the two orthogonal directions are summarized in

Table 4. Preliminary estimation of the energy dissipated by the entire building along the transverse and longitudinal directions.

Pushover Curve	Unitary Energy [kN/mm]	Number of Grids	Number of Floors	Total Energy Dissipated [kN/mm]
Transverse direction	1383.3	8	10	110,667
Longitudinal direction	1282.1	4	10	51,282

.

The hysteretic damping component, associated with the cycle at maximum amplitude was calculated following the approach of Priestley et al. in [88]. Finally, capacity versus demand comparisons are shown in Figure 11, which displays both the elastic spectrum for the Collapse Prevention Limit State (SLC) scaled to 60% (in red), and the same spectrum adjusted to account for the additional damping provided by the new devices (in blue). The results clearly indicate that the unretrofitted structure does not meet the seismic performance requirements under the reduced spectrum. However, the addition of supplemental dissipative grids improves the seismic performance, making the structure compliant with the 60% safety level at the SLC.

A synthesis of the obtained results shows that all retrofitting strategies significantly improved the global seismic performance of the hospital structures. The introduction of dissipative devices led to a marked increase in base shear capacity (up to +30%) and equivalent damping (up to 37%), while the maximum lateral displacements were correspondingly reduced. Among the investigated configurations, the innovative low-activation Type C system demonstrated the most balanced behavior, achieving early energy dissipation and better control of interstory drifts. Overall, the retrofitted structures met or exceeded the 60% seismic safety level required for existing hospitals, confirming the effectiveness of the proposed dissipative solutions.

6. Conclusions

This study presented a performance-based seismic assessment of a reinforced concrete hospital complex retrofitted with steel bracing and dissipative systems, with the aim of verifying compliance with the 60% minimum safety level prescribed for existing public buildings in Italy. The investigation was carried out through nonlinear static (pushover) analyses on two representative blocks (H and C) of the Policlinico of Modena, considering both conventional and innovative energy-dissipating solutions.

The results obtained from Phase 1 demonstrated that the addition of traditional dissipative systems (Types A and B) is effective in improving the global seismic response of the building. In particular, the introduction of metallic shear-yielding panels (Type A) and infill-based sliding systems (Type B) led to an appreciable increase in base-shear capacity and a noticeable enhancement of the equivalent viscous damping, up to 37% for the most favorable configurations. These systems allow the main structural members to remain largely within their elastic range, thereby limiting damage concentration in critical RC elements.

Nevertheless, due to the slenderness and irregularity of the existing structure, both traditional systems reach their maximum energy dissipation capacity only at relatively high interstory displacements (around 7.5 cm), which may induce second-order effects and threaten the functionality of non-structural components. To overcome this limitation, Phase 2 investigated an innovative dissipative concept (Type C) designed to activate at smaller deformation levels. The inclusion of these low-activation devices further increased the global damping and allowed the structure to achieve the target safety level of 60% at the Near-Collapse (SLC) limit state.

The seismic performance improvement index, defined as the ratio between the anchoring accelerations ($a_g/g$) corresponding to the maximum earthquakes that can be sustained in safe conditions after and before retrofitting, was found to be $I_m$ = 0.129/0.113 = 1.14.

It is worth emphasizing that in hospital buildings, the control of interstory displacements plays a crucial role not only in protecting the structural system but also in preserving the functionality of nonstructural components, including medical equipment, piping, and electrical or communication networks. The retrofit strategies adopted in this study, combining steel bracing systems with dissipative devices, result in a significant increase in global stiffness and equivalent damping, which effectively reduces lateral deformations under seismic loading. The early activation of the dissipative systems, particularly in the innovative Type C configuration, further contributes to limiting drift demands, thereby enhancing the operational continuity of the hospital and ensuring post-earthquake serviceability.

A more robust validation of the methods adopted in Phase 2 of this study could be achieved through refined analyses, particularly by investigating the cyclic response of the structure under repeated seismic loading.

From a practical perspective, the adopted methodology, based on code-recommended pushover analysis and validated numerical modeling, proves to be a suitable and cost-effective approach for design offices and public agencies involved in the seismic upgrading of healthcare facilities.

The present study is subject to certain limitations that suggest valuable directions for future research. The analyses were performed using nonlinear static (pushover) procedures, which, while fully compliant with current design codes and widely used in engineering practice, do not capture the cyclic deterioration or dynamic interaction effects that could emerge under strong ground motions. In addition, the investigation focused on a single hospital complex, and although the results are representative, extending the methodology to a broader set of case studies with varying geometries and structural typologies would enhance the generality of the conclusions.

Future research will focus on extending the present investigation through cyclic and nonlinear time history analyses to validate the hysteretic behavior of the proposed dissipative systems under repeated seismic excitation and to further refine their design for critical infrastructures.