Microscopic Numerical Simulation of Compressive Performance of Steel-Recycled PET Hybrid Fiber Recycled Concrete
Abstract
1. Introduction
2. Establishment and Verification of Microscopic Numerical Model
2.1. Generation of Random Coarse Aggregate and Interface Transition Zone
2.2. Generation and Deployment of Two Types of Fibers
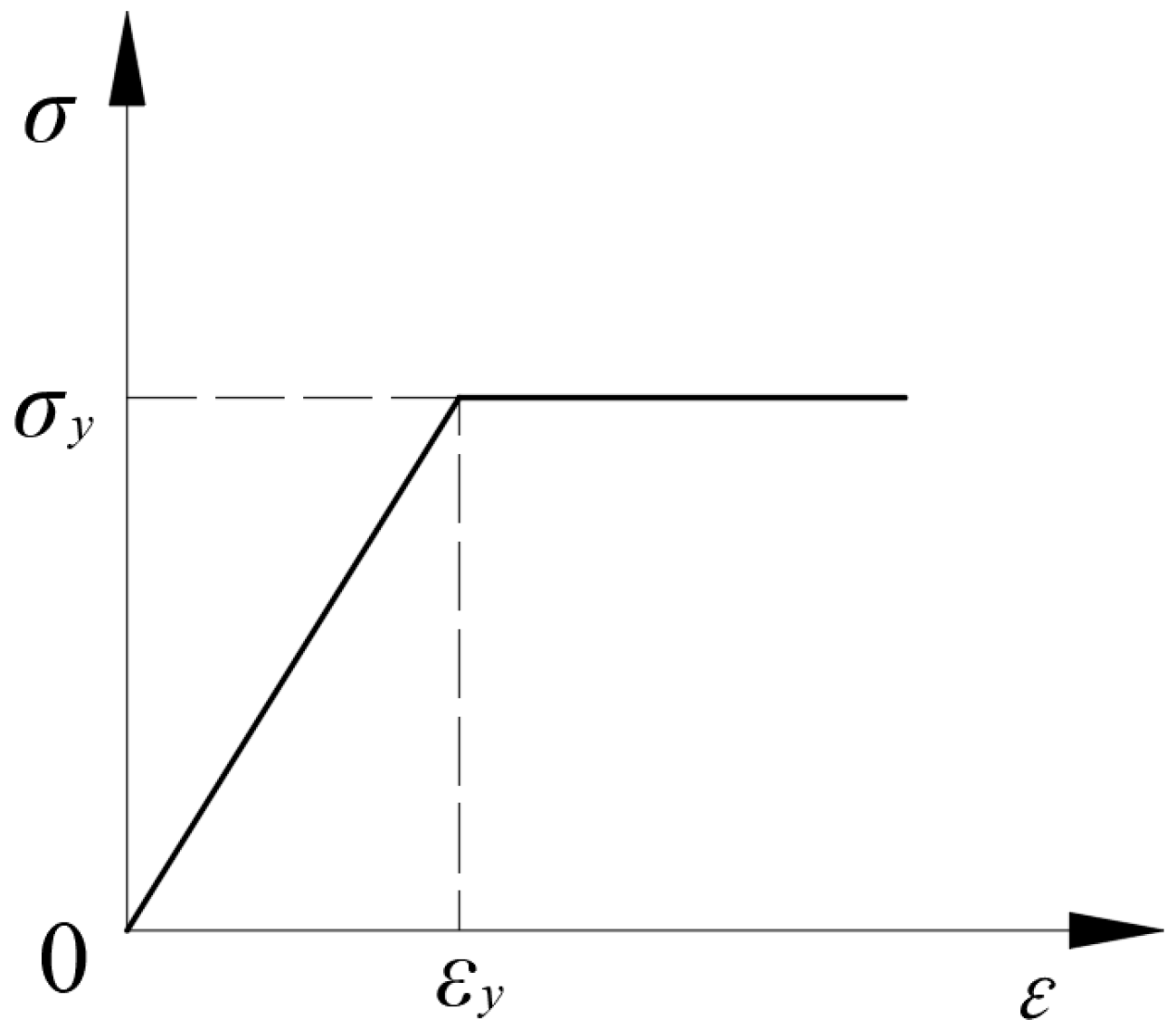
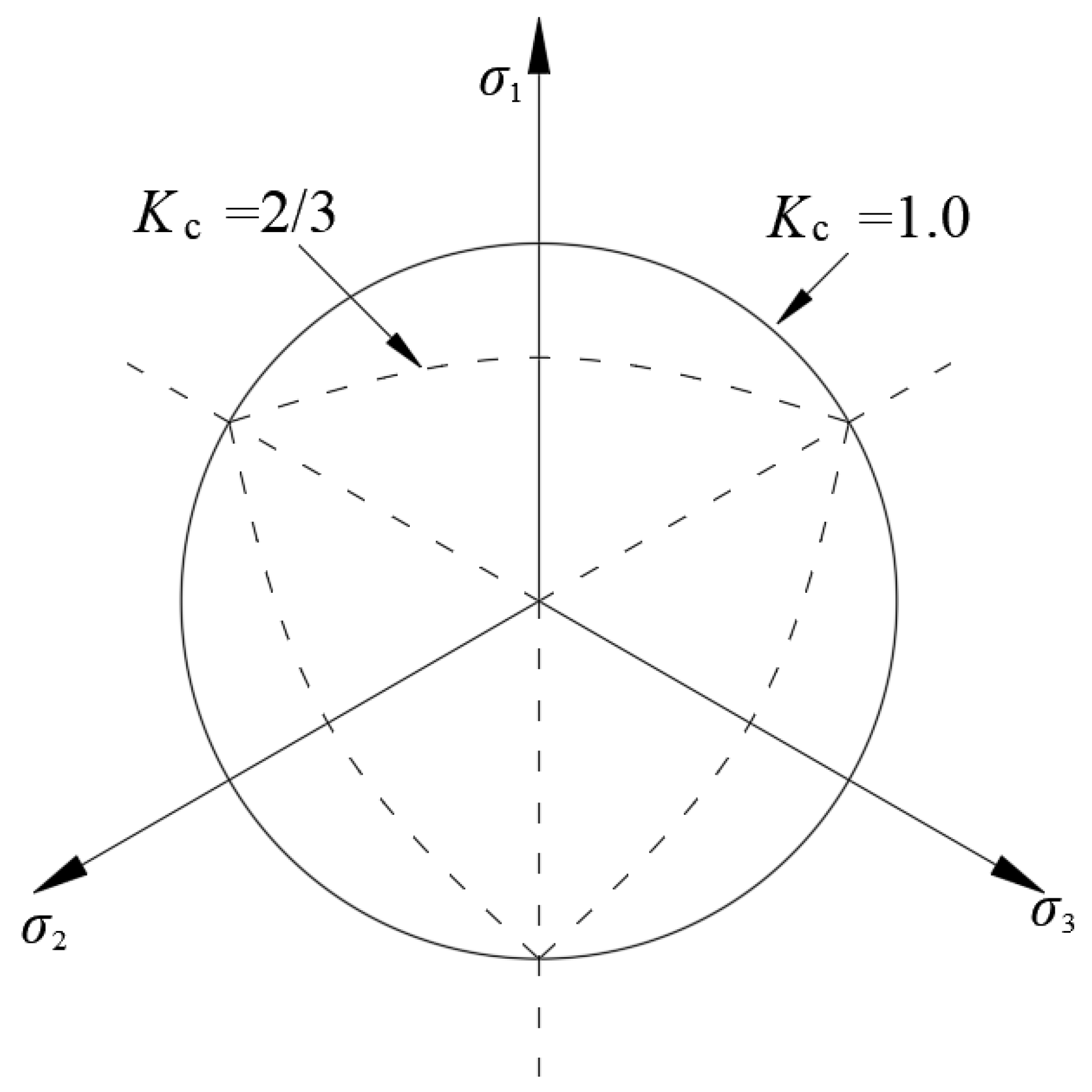
2.3. Selection of Constitutive Models
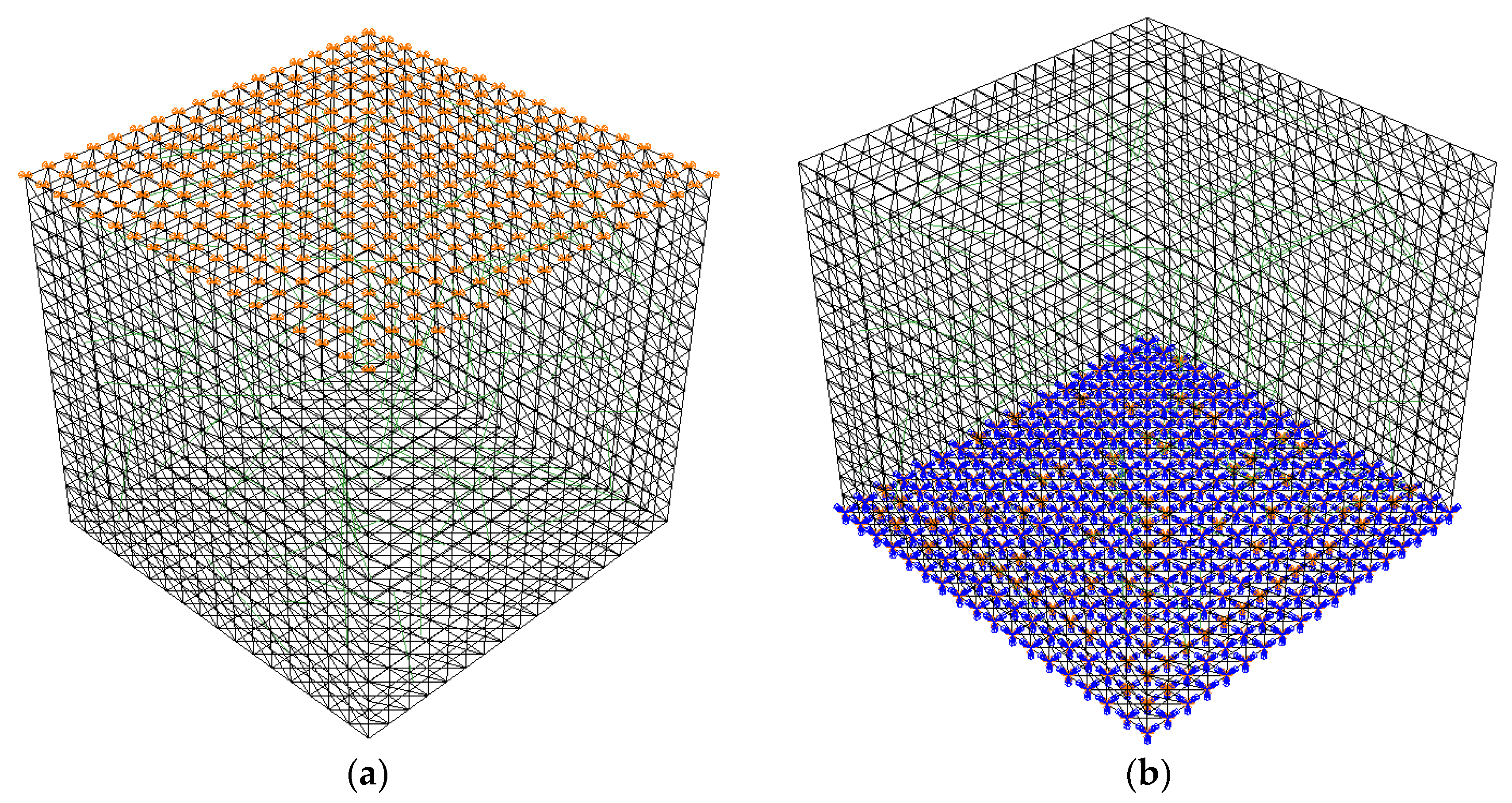
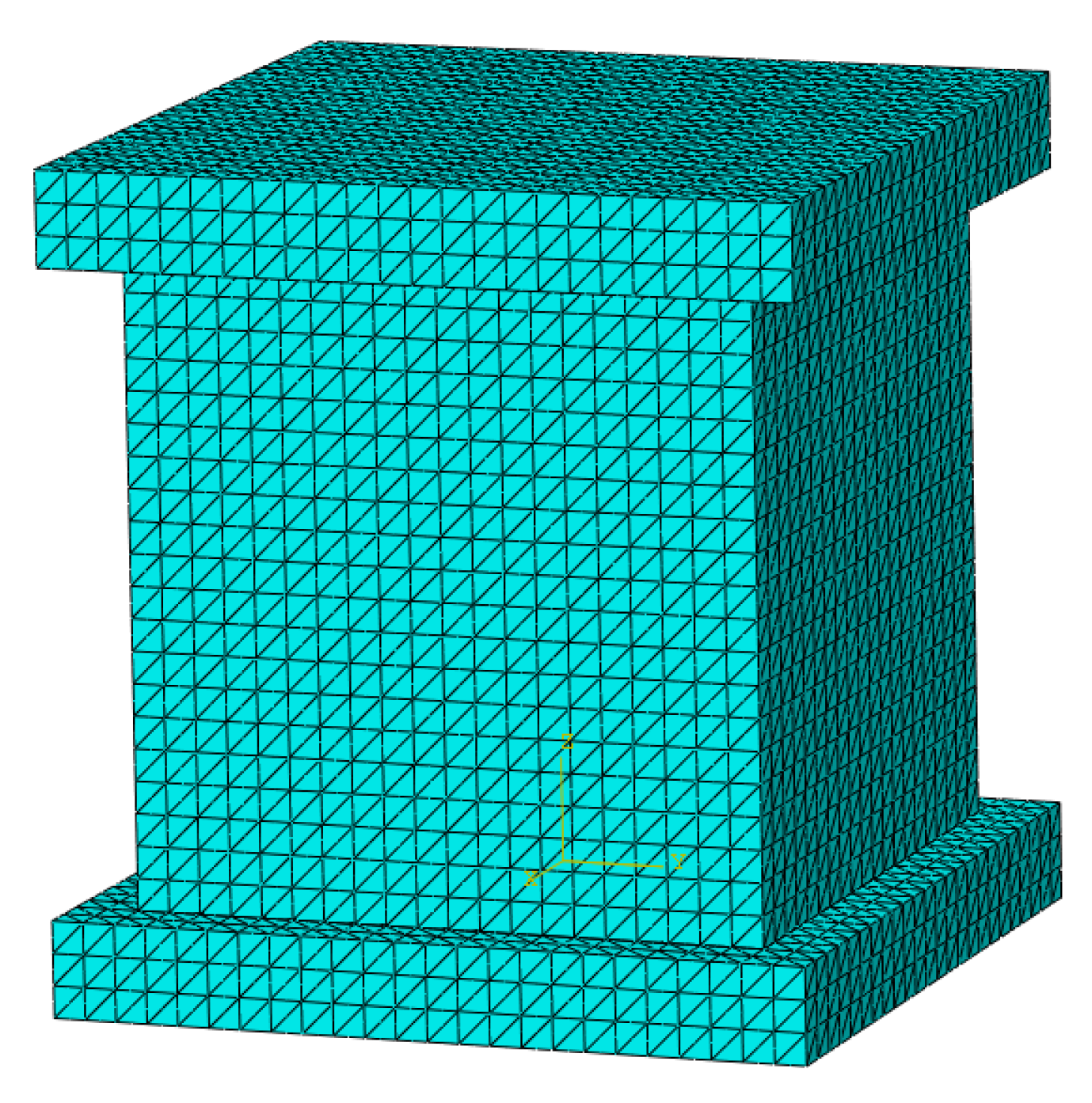
2.4. Grid Division and Boundary Condition Setting
2.5. Parameter Tuning
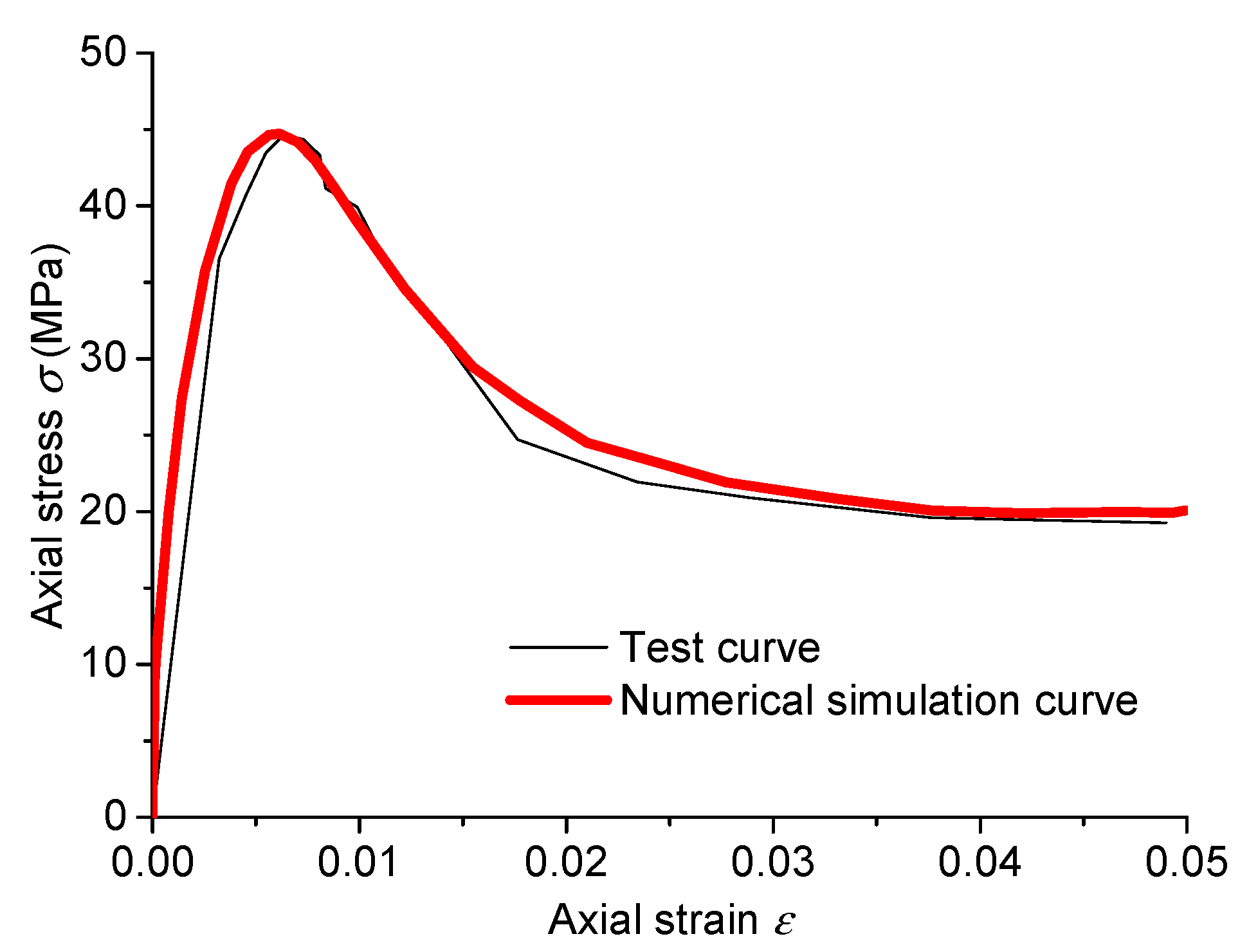
2.6. Model Validation
3. Parameter Sensitivity Analysis and Analysis of Simulated Results
3.1. Parameter Sensitivity Analysis
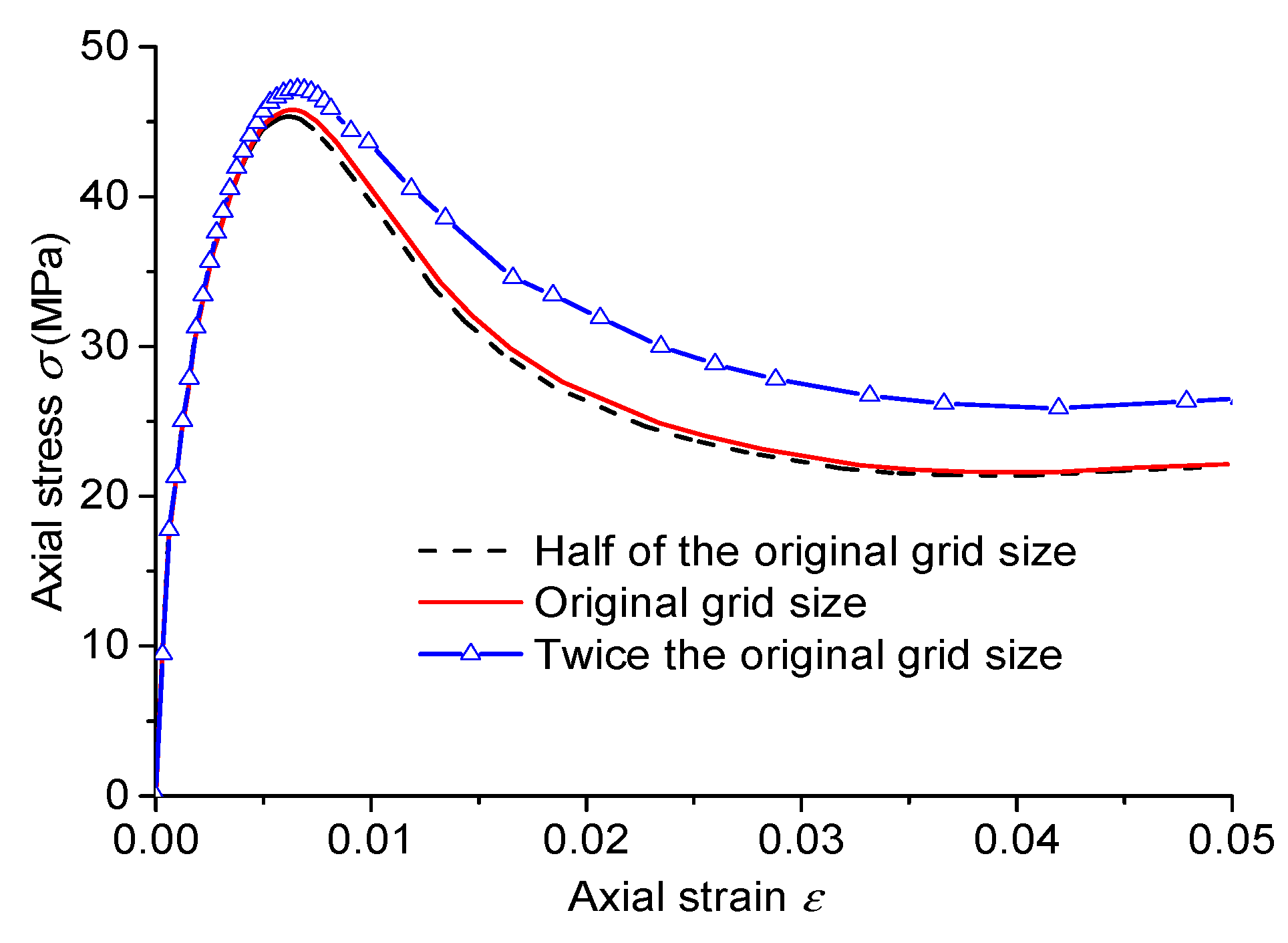
3.1.1. Sensitivity Analysis with Different Mesh Sizes
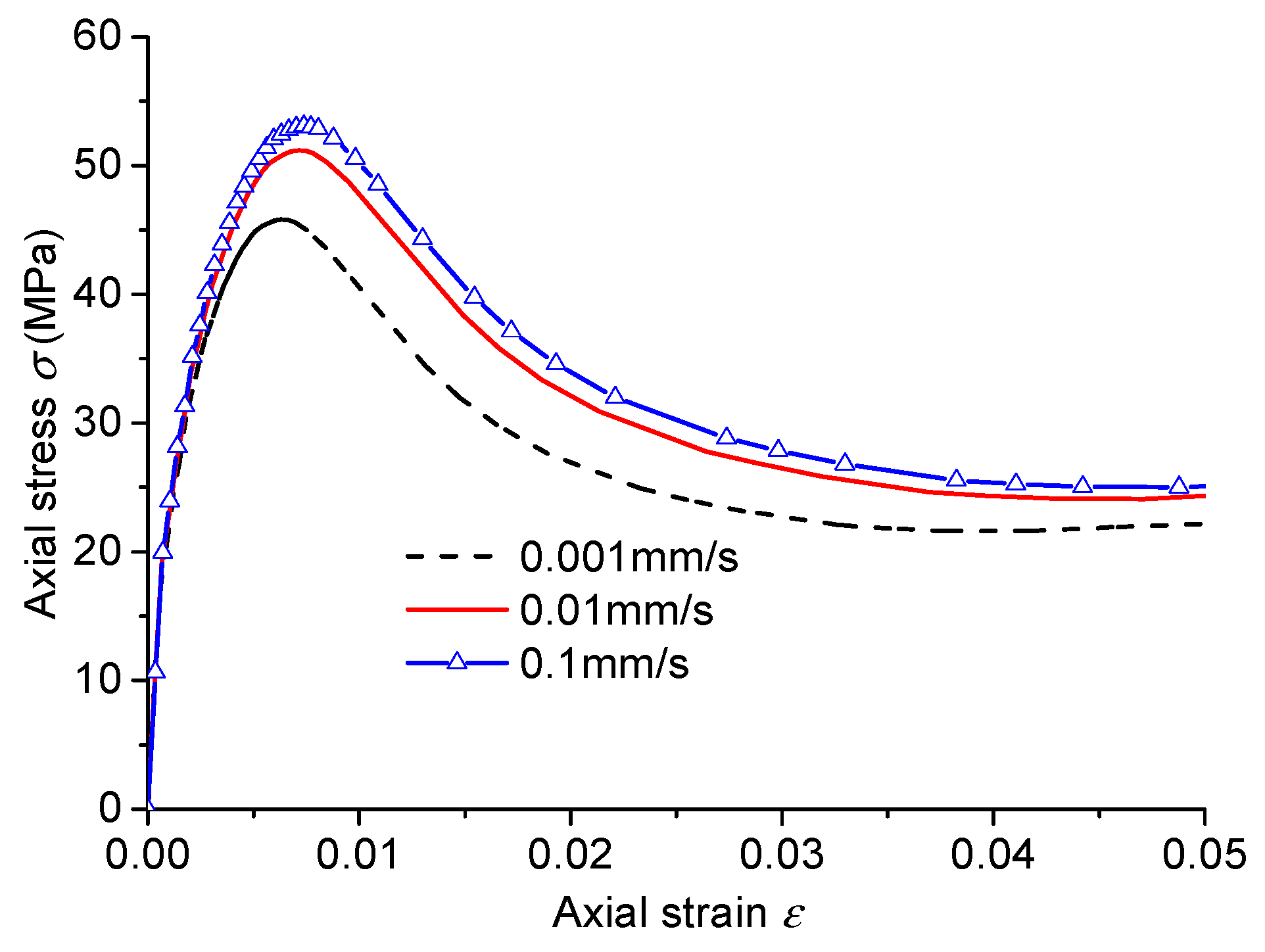
3.1.2. Sensitivity Analysis with Different Loading Rates
3.1.3. Sensitivity Analysis with Different Boundary Conditions
3.2. Analysis of Simulated Results
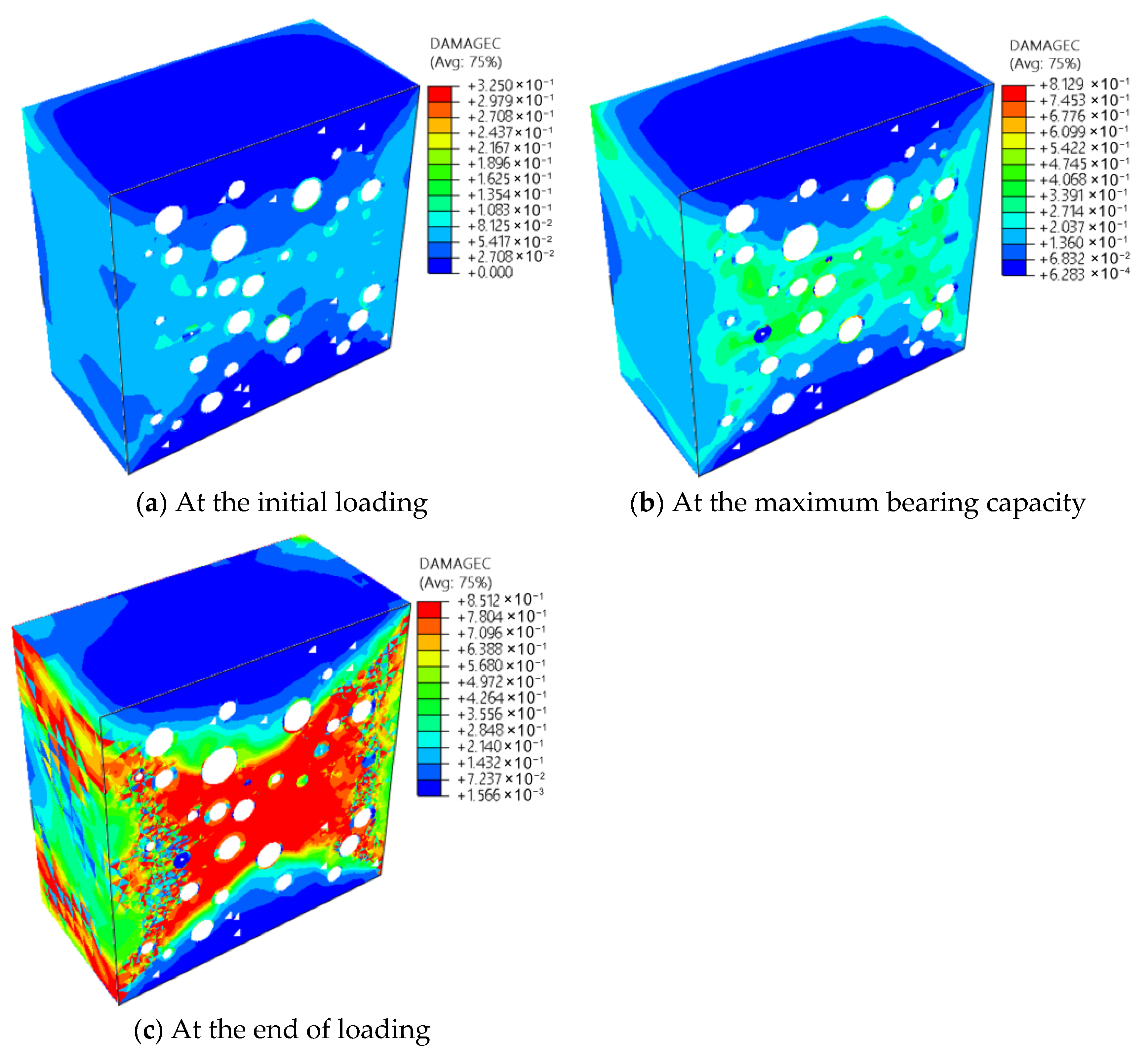
3.2.1. Stress Distribution Law
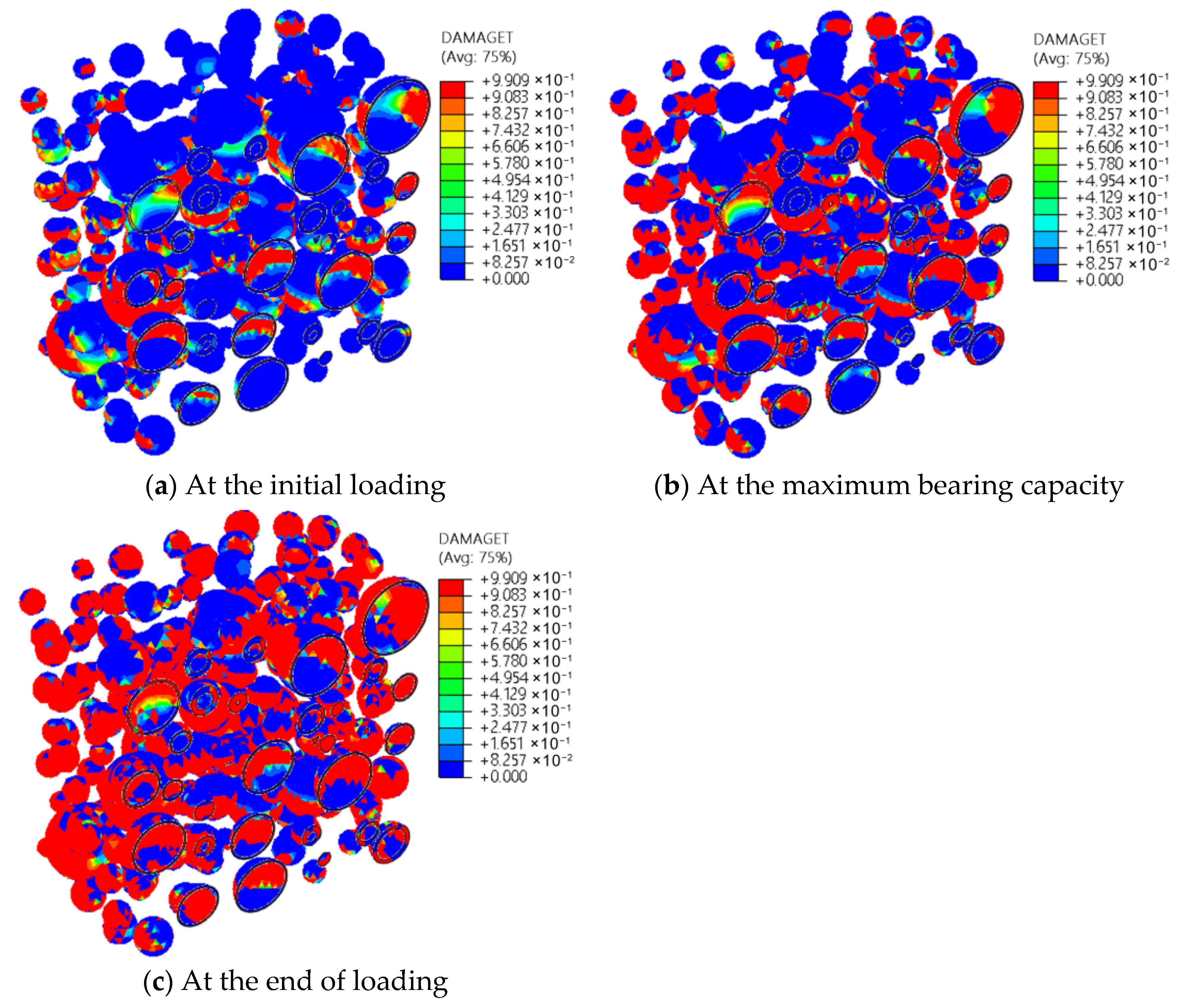
3.2.2. Evolution Law of Specimen Damage
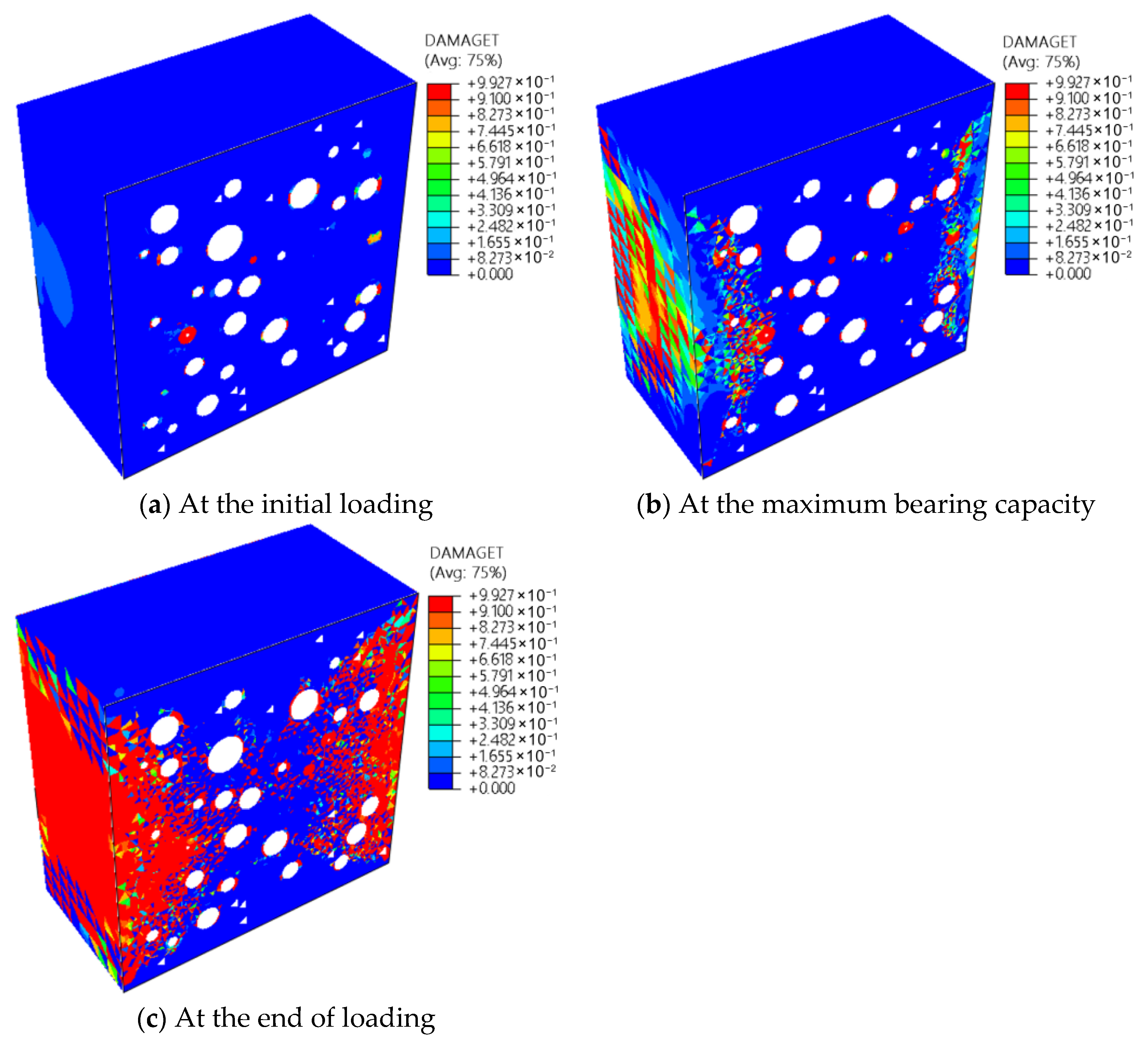
3.2.3. Evolution Law of ITZ Damage
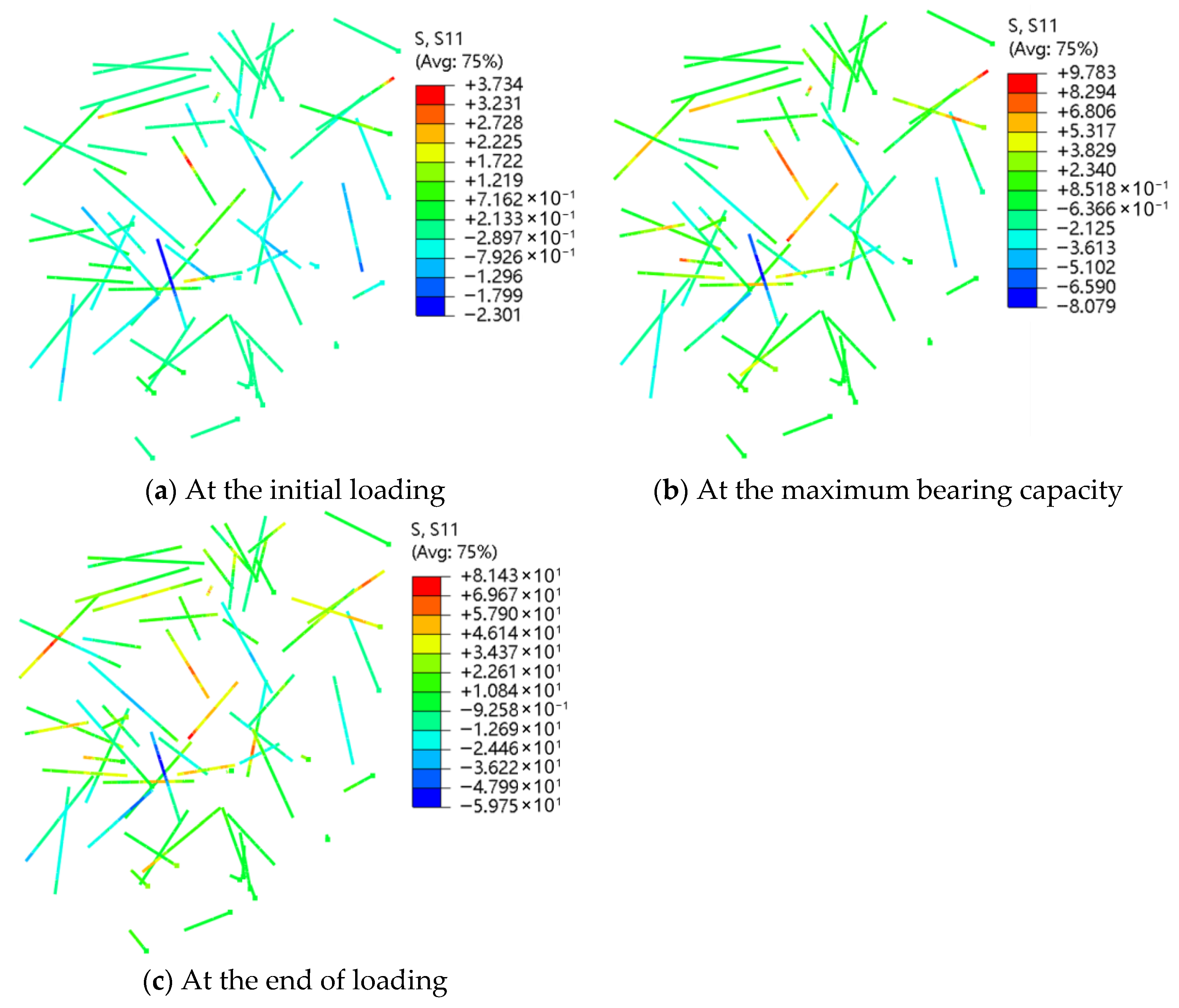
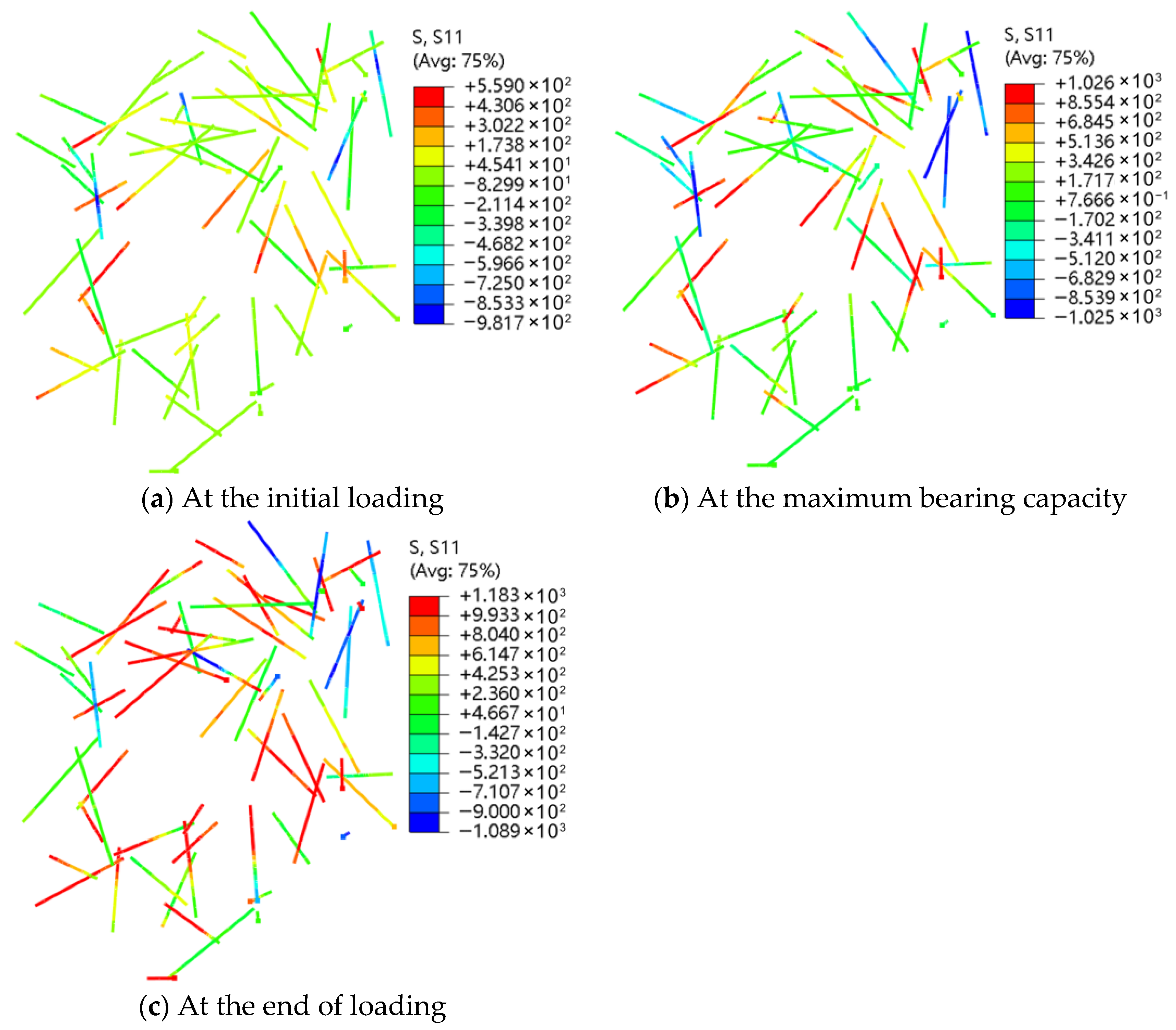
3.2.4. Force Characteristics of Fibers
4. Conclusions
- (1)
- The simulation results show that smaller mesh sizes yield more stable and accurate results, though with longer computation times. The loading rate has a pronounced effect: higher rates increase peak stress, peak strain, and residual stress. Stronger top and bottom surface constraints also lead to higher calculated values of these parameters.
- (2)
- Under vertical compression, the first form of compressive and tensile damage occurs in the ITZ, subsequently spreading into the mortar. At final loading, compressive damage is mainly concentrated inside the specimen, forming a distinct X-shaped damage zone, while tensile damage develops around the specimen perimeter.
- (3)
- Larger RCA particle sizes result in more severe ITZ damage. For engineering practice, smaller RCA particles should be used, or larger RCAs should be crushed to finer fractions to enhance RAC strength.
- (4)
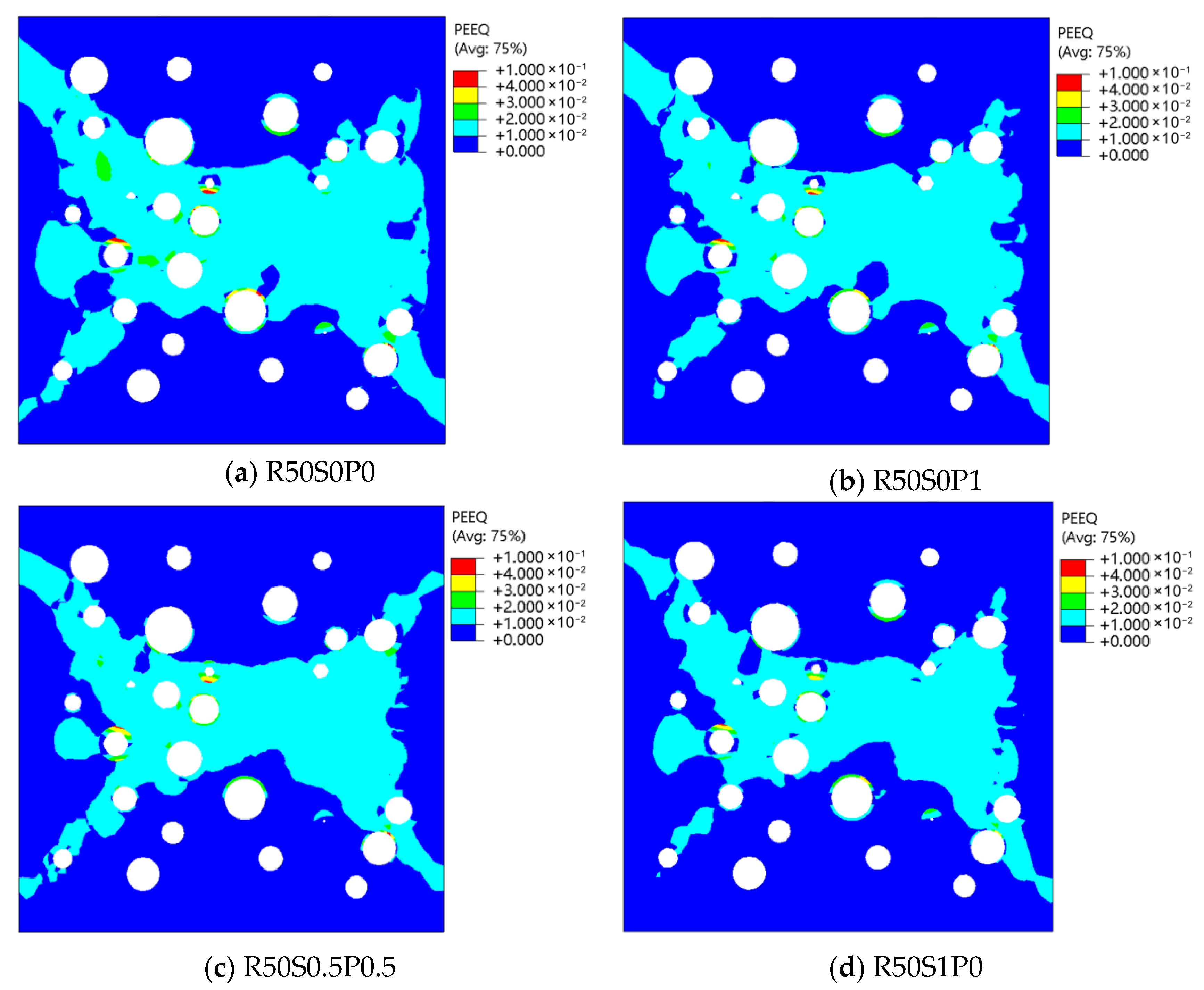
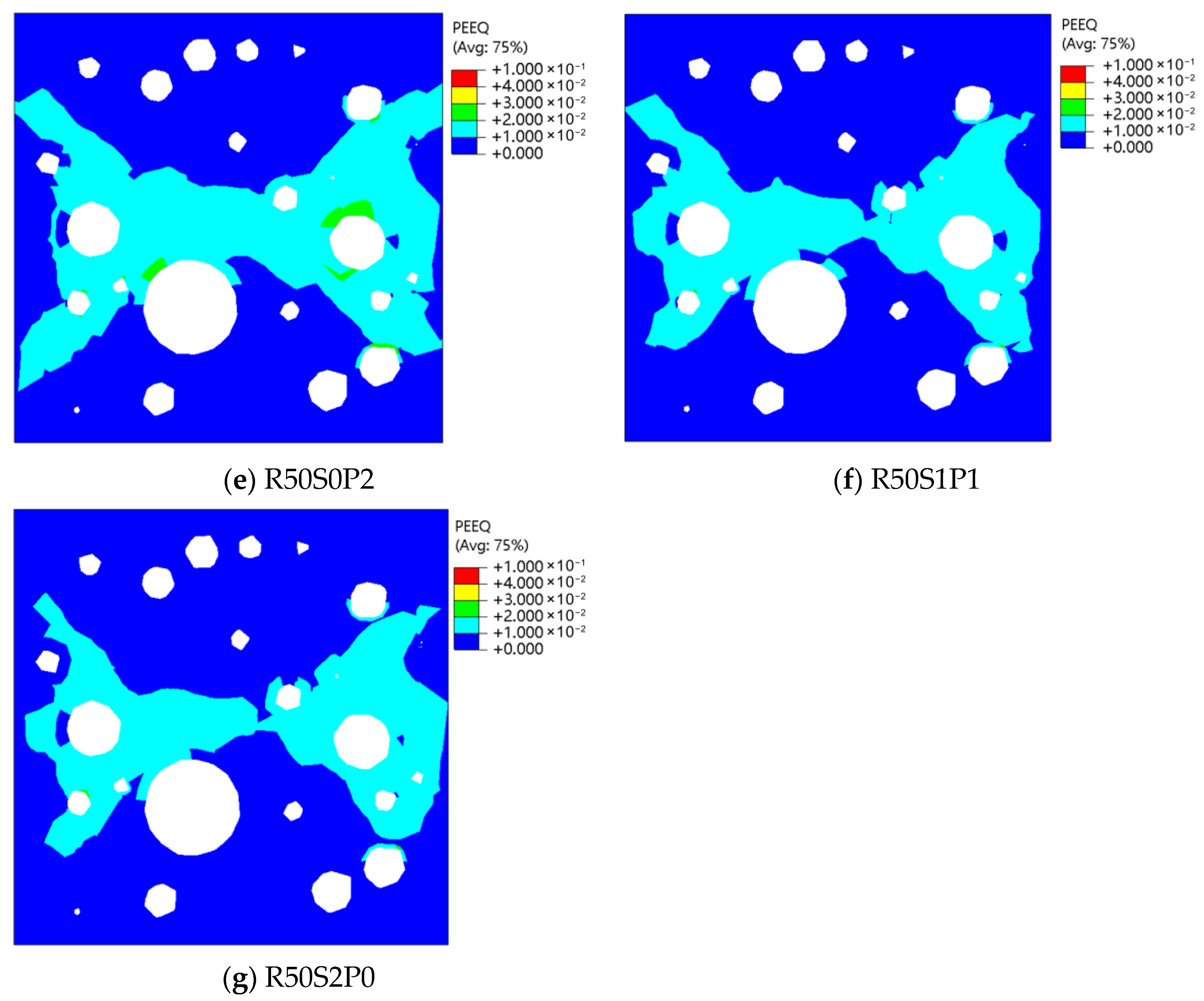
- With increasing fiber content, the area of PEEQ regions above the threshold decreases, though this trend slows beyond 1.0% total fiber content. Initially, SF bears higher tensile stress, while rPETF stress is low. After peak load, SF stress increases gradually, whereas rPETF stress rises sharply.
- (5)
- The proposed mesoscopic model reliably reflects stress, strain, and damage evolution in SRPRAC and can serve as a tool for parameter optimization.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| RCA | recycled coarse aggregate |
| NCA | natural coarse aggregate |
| RAC | recycled aggregate concrete |
| NAC | natural aggregate concrete |
| ITZ | interfacial transition zone |
| PET | polyethylene terephthalate |
| rPETF | recycled PET fibers |
| SF | steel fibers |
| SRPRAC | steel-recycled polyethylene terephthalate hybrid fiber recycled concrete |
References
- Gao, D.; Zhang, L.; Nokken, M. Compressive behavior of steel fiber reinforced recycled coarse aggregate concrete designed with equivalent cubic compressive strength. Constr. Build. Mater. 2017, 141, 235–244. [Google Scholar] [CrossRef]
- Sun, L.; Hao, Q.; Zhao, J.; Wu, D.; Yang, F. Stress strain behavior of hybrid steel-PVA fiber reinforced cementitious composites under uniaxial compression. Constr. Build. Mater. 2018, 188, 349–360. [Google Scholar] [CrossRef]
- Akca, K.R.; Cakir, O.; Ipek, M. Properties of polypropylene fiber reinforced concrete using recycled aggregates. Constr. Build. Mater. 2015, 98, 620–630. [Google Scholar] [CrossRef]
- Ajamu, S.O.; Ige, J.A.; Oyinkanola, T.M. Effect of waste (PET) bottle fibers on the properties of concrete. Int. J. Res. Eng. Technol. 2018, 6, 1–8. [Google Scholar]
- Kassa, R.B.; Kanali, C.; Ambassah, N. Flexural performance evaluation of polyethylene terephthalate fibre reinforced concrete with fly ash as a partial cement replacement. Int. J. Eng. Res. Technol. 2019, 12, 1417–1422. [Google Scholar]
- Soe, K.T.; Zhang, Y.X.; Zhang, L.C. Material properties of a new hybrid fibre-reinforced engineered cementitious composite. Constr. Build. Mater. 2013, 43, 399–407. [Google Scholar] [CrossRef]
- Maalej, M.; Quek, S.T.; Ahmed, S.F.U. Review of potential structural applications of hybrid fiber engineered cementitious composites. Constr. Build. Mater. 2012, 36, 216–227. [Google Scholar] [CrossRef]
- Ahmed, S.F.U.; Maalej, M.; Paramasivam, P. Flexural responses of hybrid steel-polyethylene fiber reinforced cement composites containing high volume fly ash. Constr. Build. Mater. 2007, 21, 1088–1097. [Google Scholar] [CrossRef]
- Carneiroa, J.A.; Limaa, P.R.L.; Leite, M.B.; Filho, R.D.T. Compressive stress-strain behavior of steel fiber reinforced-recycled aggregate concrete. Cem. Concr. Compos. 2014, 46, 65–72. [Google Scholar] [CrossRef]
- Debora, M.C.; Albert, D.L.F.; Sergio, H.P.C. Fatigue of cracked high performance fiber reinforced concrete subjected to bending. Constr. Build. Mater. 2019, 220, 444–455. [Google Scholar] [CrossRef]
- Selvi, M.T.; Thandavamoorthy, T.S. Mechanical and durability properties of steel and polypropylene fibre reinforced concrete. Int. J. Earth Sci. Eng. 2014, 7, 696–703. [Google Scholar]
- Liang, X.W.; Wu, C. Meso-scale modelling of steel fibre reinforced concrete with high strength. Constr. Build. Mater. 2018, 165, 187–198. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, H.; Zhang, X.; Ren, F.; Li, Y.; Yang, Z. Experimental, analytical and numerical studies of interfacial bonding properties between silane-coated steel fibres and mortar. Buildings 2021, 11, 398. [Google Scholar] [CrossRef]
- Guo, S.L.; Zheng, D.J.; Zhao, L.H.; Lu, Q.; Liu, X.K. Mechanical test and constitutive model of recycled plastic fiber reinforced recycled concrete. Constr. Build. Mater. 2022, 348, 128578. [Google Scholar] [CrossRef]
- Peng, Y.; Chu, H.; Pu, J. Numerical simulation of recycled concrete using convex aggregate model and base force element method. Adv. Mater. Sci. Eng. 2016, 2016, 5075109. [Google Scholar] [CrossRef]
- Xiao, J.; Li, W.; Corr, D.J. Effects of interfacial transition zones on the stress–strain behavior of modeled recycled aggregate concrete. Cem. Concr. Res. 2013, 52, 82–99. [Google Scholar] [CrossRef]
- Xu, Y.; Geng, F.; Luan, H.; Chen, J.; Yang, H.; Gao, P. Three-dimensional mesoscopic DEM modeling and compressive behavior of macroporous recycled concrete. Buildings 2025, 15, 2655. [Google Scholar] [CrossRef]
- Qi, L.; Yu, B.; Yu, M.; Zhang, M. Simulation-based analysis of micro-damage to recycled concrete-containing brick coarse aggregates. Buildings 2023, 13, 2297. [Google Scholar] [CrossRef]
- Zhang, L.; Li, X.; Li, C.; Zhao, J.; Cheng, S. Mechanical properties of fully recycled aggregate concrete reinforced with steel fiber and polypropylene fiber. Materials 2024, 17, 1156. [Google Scholar] [CrossRef]
- Jayasuriya, A.; Bandelt, M.; Adamsm, P. Stochastic mesoscopic modeling of concrete systems containing recycled concrete aggregates using monte carlo methods. ACI Mater. J. 2022, 119, 3–18. [Google Scholar] [CrossRef]
- Meng, Q.P.; Wu, Y.Q.; Xiao, J.Z. The effect of micro-structural uncertainties of recycled aggregate concrete on its global stochastic properties via finite pixel-element Monte Carlo simulation. Front. Struct. Civ. Eng. 2018, 12, 16. [Google Scholar] [CrossRef]
- Ren, Q.F.; Pacheco, J.; de Brito, J. Mesoscale modeling of recycled aggregate concrete: A parametric analysis of the quality and shape of aggregate. Struct. Concr. 2025, 26, 1636–1653. [Google Scholar] [CrossRef]
- Lu, Y.; Song, Z.H.; Tu, Z.G. Analysis of dynamic response of concrete using a mesoscale model in Corporating 3D effects. Int. J. Prot. Struct. 2010, 1, 197–218. [Google Scholar] [CrossRef]
- Sun, M.Z.; Zhu, J.P. 3d concave-convex aggregate modeling based on python-abaqus and influence analysis of different shapes of aggregates. Sci. Technol. Eng. 2024, 24, 10022–10031. [Google Scholar]
- Ye, Y.; Yu, H.; Luo, W.; Lu, Q. Analysis of impact of different modeling techniques on concrete mesoscopic simulation. J. Three Gorges Univ. (Nat. Sci. Ed.) 2016, 38, 33–36. [Google Scholar]
- Deng, C. Microscopic Numerical Simulation Analysis of Recycled Concrete. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2020. [Google Scholar]
- Walraven, J.C.; Reinhard, H.W. Theory and experiments on the mechanics behavior of cracks in plane and reinforced concrete subject to shear loading. Heron 1991, 26, 26–33. [Google Scholar]
- Hong, C.; Ji, W. Scalable data-driven micromechanics model trained with pairwise fiber data for composite materials with randomly distributed fibers. Eng. Comput. 2024, 41, 801–814. [Google Scholar] [CrossRef]
- Yin, D.; Zhang, M.; Xiong, B.; Zhang, S. Study on the physical and mechanical properties of concrete interfacial transition zones (ITZ) with consideration of positional effects. Constr. Build. Mater. 2025, 486, 141985. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Chen, X.Y.; Liu, A.X.; Zhou, J. Properties characterization of interfacial transition zone of recycled concrete for reducing the resource waste and environmental pollution. IOP Conf. Ser. Earth Environ. Sci. 2021, 804, 022097. [Google Scholar] [CrossRef]
- Zheng, J.C.; Zhu, L.; Peng, G.; Song, Z.L. Numerical simulation of concrete axial tensile performance based on mesomechanics. Eng. J. Wuhan Univ. 2013, 46, 188–193. [Google Scholar]
- Yi, Y.; Xiao, Y.X.; Yu, K. Establishment and numerical simulation of mesoscopic models of concrete with arbitrary polygonal aggregates. J. Shandong Univ. (Eng. Sci.) 2025, 55, 97–107. [Google Scholar]
- Zhou, J.H.; Wang, X.T.; Guo, Y.Q.; Kang, T.B. Finite element analysis on the compressive strength of recycled concrete. Concrete 2017, 10, 699–720. [Google Scholar]
- Zhang, H.R.; Zhao, Y.X.; Meng, T.; Shah, S.P. The modification effects of a nano-silica slurry on microstructure, strength, and strain development of recycled aggregate concrete applied in an enlarged structural test. Constr. Build. Mater. 2015, 95, 721–735. [Google Scholar] [CrossRef]
- Xu, L.; Deng, F.; Chi, Y. Nano-mechanical behavior of the interfacial transition zone between steel-polypropylene fiber and cement paste. Constr. Build. Mater. 2017, 145, 619–638. [Google Scholar] [CrossRef]
- Jankowiak, T.; Lodygowski, T. Identification of parameters of concrete damage plasticity constitutive model. Found. Civ. Environ. Eng. 2005, 6, 53–69. [Google Scholar]
- Kmiecik, P.; Kaminski, M. Modelling of reinforced concrete structures and composite structures with concrete strength degradation taken into consideration. Arch. Civ. Mech. Eng. 2011, 11, 623–636. [Google Scholar] [CrossRef]
- Du, P. Study on Meso-Scale Numerical Simulation and Influence Factors of Recycled Concrete. Master’s Thesis, Dalian University of Technology, Dalian, China, 2023. [Google Scholar]
- Yao, Z.L.; Duan, D.X. Numerical simulation of recycled concrete under uniaxial compression based on random aggregate model. J. Xi’an Univ. Technol. 2018, 34, 475–480. [Google Scholar]
- Maruthachalam, D.; Muthukumar, J. Mechanical Performance of Recycled PET Fiber Reinforced Concrete with Low Volume Fraction. Int. J. Struct. Civ. Eng. Res. 2013, 2, 101–108. [Google Scholar]
- Liu, W.; Xu, M.; Chen, Z.F. Parameters calibration and verification of concrete damage plasticity model of abaqus. Ind. Build. 2014, 44, 167–171. [Google Scholar]
- Guan, X.; Niu, D.T.; Wang, J.B.; Jiang, L. Study on freeze-thaw damage constitutive model of concrete considering plastic strain and damage threshold. J. Disaster Prev. Mitig. Eng. 2015, 35, 777–784. [Google Scholar]








| No. | SF (kg) | rPETF (kg) | Cement (P.O.42.5) (kg) | NCA (kg) | RCA (kg) | Natural Sand (kg) | Water (kg) | Water Reducer (kg) |
|---|---|---|---|---|---|---|---|---|
| R50S0.5P0.5 | 39.3 | 7 | 453.5 | 587 | 587 | 587 | 224 | 4.5 |
| Type | Length (mm) | Equivalent Diameter (mm) | Density (kg/m3) | E (GPa) | Poisson’s Ratio | Tensile Strength (MPa) | Compressive Strength (MPa) |
|---|---|---|---|---|---|---|---|
| rPETF | 36 | 0.82 | 1400 | 4.3 | 0.35 | 89 | 89 |
| SF | 36 | 0.75 | 7850 | 210 | 0.3 | 1200 | 1200 |
| Material Name | E (GPa) | Poisson’s Ratio | Density (kg/m3) | Tensile Strength (MPa) | Compressive Strength (MPa) |
|---|---|---|---|---|---|
| Mortar | 35 | 0.2 | 2400 | 2.8 | 34.8 |
| NCA | 80 | 0.16 | 2200 | / | / |
| RCA | 50 | 0.16 | 2100 | / | / |
| NCAITZ | 28 | 0.2 | 2200 | 2.5 | 27.9 |
| RCAITZ | 21 | 0.2 | 2100 | 2.1 | 20.9 |
| Material Name | ψ | e | fb0/fc0 | Kc | w |
|---|---|---|---|---|---|
| Mortar | 38 | 0.1 | 1.16 | 0.667 | 1 × 10−5 |
| NACITZ | 33 | 0.1 | 1.16 | 0.667 | 1 × 10−5 |
| RCAITZ | 30 | 0.1 | 1.16 | 0.667 | 1 × 10−5 |
| Type | Total Fiber Content (%) | Steel Fibers Content (%) | rPET Fibers Content (%) | RCA Replacement Rate (%) |
|---|---|---|---|---|
| R50S0P0 | 0 | 0 | 0 | 50 |
| R50S0P1 | 1 | 0 | 1 | 50 |
| R50S0.5P0.5 | 1 | 0.5 | 0.5 | 50 |
| R50S1P0 | 1 | 1 | 0 | 50 |
| R50S0P2 | 2 | 0 | 2 | 50 |
| R50S1P1 | 2 | 1 | 1 | 50 |
| R50S2P0 | 2 | 2 | 0 | 50 |
| Type | Total Fiber Content (%) | SF Content (%) | rPETF Content (%) | Area Ratio |
|---|---|---|---|---|
| R50S0P0 | 0.0 | 0.0 | 0.0 | 1.000 |
| R50S0P1 | 1.0 | 0.0 | 1.0 | 0.837 |
| R50S0.5P0.5 | 1.0 | 0.5 | 0.5 | 0.750 |
| R50S1P0 | 1.0 | 1.0 | 0.0 | 0.691 |
| R50S0P2 | 2.0 | 0.0 | 2.0 | 0.832 |
| R50S1P1 | 2.0 | 1.0 | 1.0 | 0.673 |
| R50S2P0 | 2.0 | 2.0 | 0.0 | 0.666 |
| Type | Peak Strain | Peak Stress (MPa) | Residual Stress (MPa) | Time Consumption Multiple |
|---|---|---|---|---|
| Half of the original grid size | 0.00632 | 45.9 | 23.0 | 7.5 |
| Original grid size | 0.00649 | 46.3 | 23.3 | 1.0 |
| Twice the original grid size | 0.00657 | 47.2 | 26.5 | 0.8 |
| Type | Peak Strain | Peak Stress (MPa) | Residual Stress (MPa) |
|---|---|---|---|
| 0.001 | 0.0063 | 45.8 | 22.1 |
| 0.01 | 0.00712 | 51.2 | 24.1 |
| 0.1 | 0.00737 | 53.1 | 24.8 |
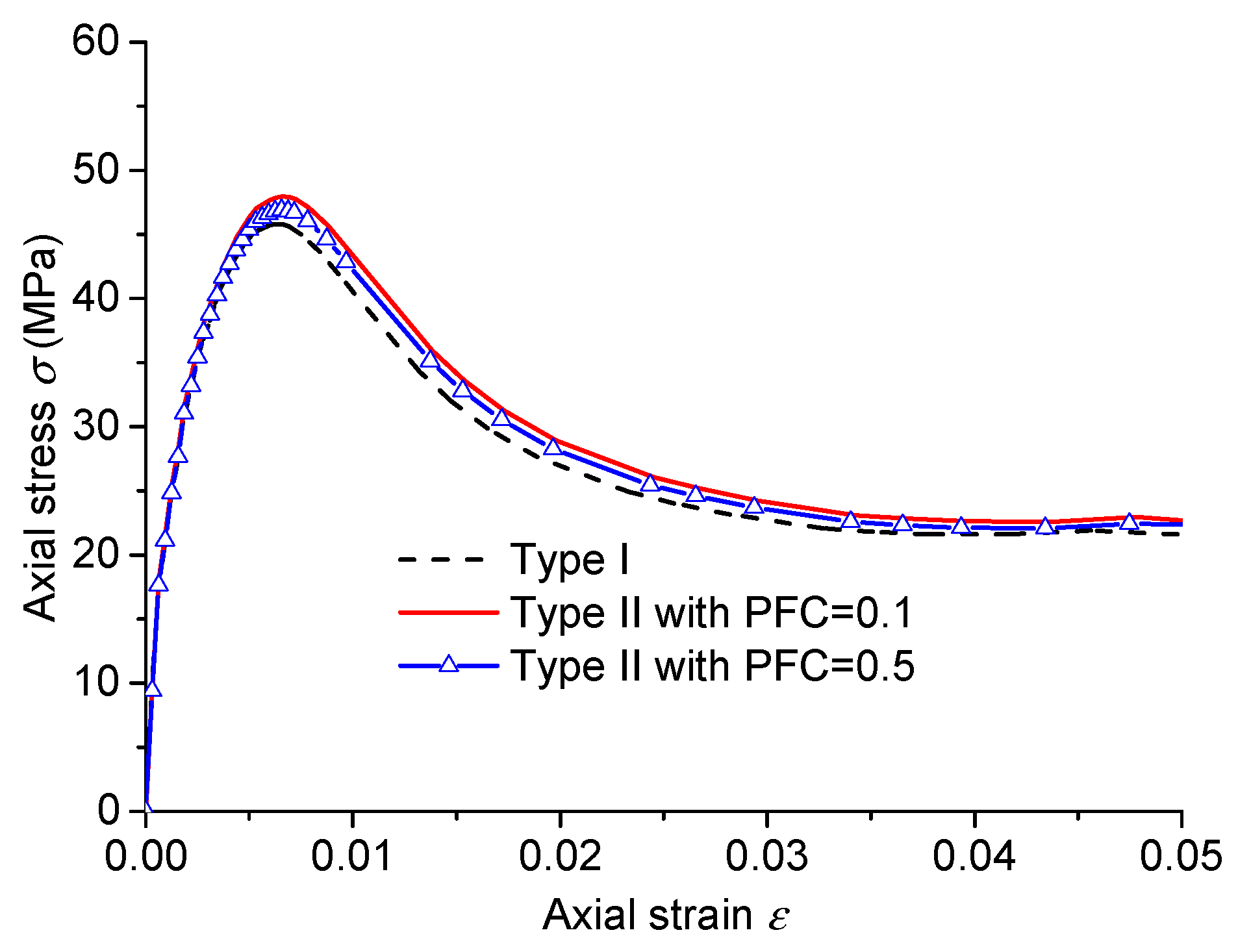
| Type | Peak Strain | Peak Stress (MPa) | Residual Stress (MPa) | Time Consumption Multiple |
|---|---|---|---|---|
| Type I | 0.0063 | 45.8 | 21.6 | 1.0 |
| Type II with PFC = 0.1 | 0.0066 | 48.0 | 22.4 | 11.3 |
| Type II with PFC = 0.5 | 0.0066 | 46.9 | 22.3 | 7.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, S.; Lu, Q.; Czech, K.R.; Krassowska, J. Microscopic Numerical Simulation of Compressive Performance of Steel-Recycled PET Hybrid Fiber Recycled Concrete. Buildings 2025, 15, 3893. https://doi.org/10.3390/buildings15213893
Guo S, Lu Q, Czech KR, Krassowska J. Microscopic Numerical Simulation of Compressive Performance of Steel-Recycled PET Hybrid Fiber Recycled Concrete. Buildings. 2025; 15(21):3893. https://doi.org/10.3390/buildings15213893
Chicago/Turabian StyleGuo, Shaolong, Qun Lu, Krzysztof Robert Czech, and Julita Krassowska. 2025. "Microscopic Numerical Simulation of Compressive Performance of Steel-Recycled PET Hybrid Fiber Recycled Concrete" Buildings 15, no. 21: 3893. https://doi.org/10.3390/buildings15213893
APA StyleGuo, S., Lu, Q., Czech, K. R., & Krassowska, J. (2025). Microscopic Numerical Simulation of Compressive Performance of Steel-Recycled PET Hybrid Fiber Recycled Concrete. Buildings, 15(21), 3893. https://doi.org/10.3390/buildings15213893








