Construction and Application of a Multi-Dimensional Quality Gain–Loss Function for Dam Concrete Based on Gaussian Process
Abstract
1. Introduction
2. Multivariate Quality Gain–Loss Function Based on Artiles-León
3. Traditional Multivariate Quality Gain–Loss Function
4. Multi-Dimensional Quality Gain–Loss Function Based on Gaussian Process
4.1. Principle of GPR Model
4.2. Signal-to-Noise Ratio (SNR)
4.3. Multi-Dimensional Quality Gain–Loss Function Based on Gaussian Process
5. Case Analysis
5.1. Project Overview
5.2. Multi-Dimensional Quality Gain–Loss Function Based on Gaussian Process Analyze
5.2.1. Construction of Gaussian Process Regression Model
5.2.2. Construction of Multi-Dimensional Quality Gain–Loss Function
5.3. Multi-Dimensional Quality Gain–Loss Calculation and Comparative Analysis
5.3.1. Multi-Dimensional Quality Gain–Loss Calculation
- Model 1 Multiple quality gain–loss calculations based on Artiles-León
- Model 2 Traditional multivariate quality gain–loss calculation
- Model 3 Multi-dimensional quality gain–loss calculation based on the Gaussian process
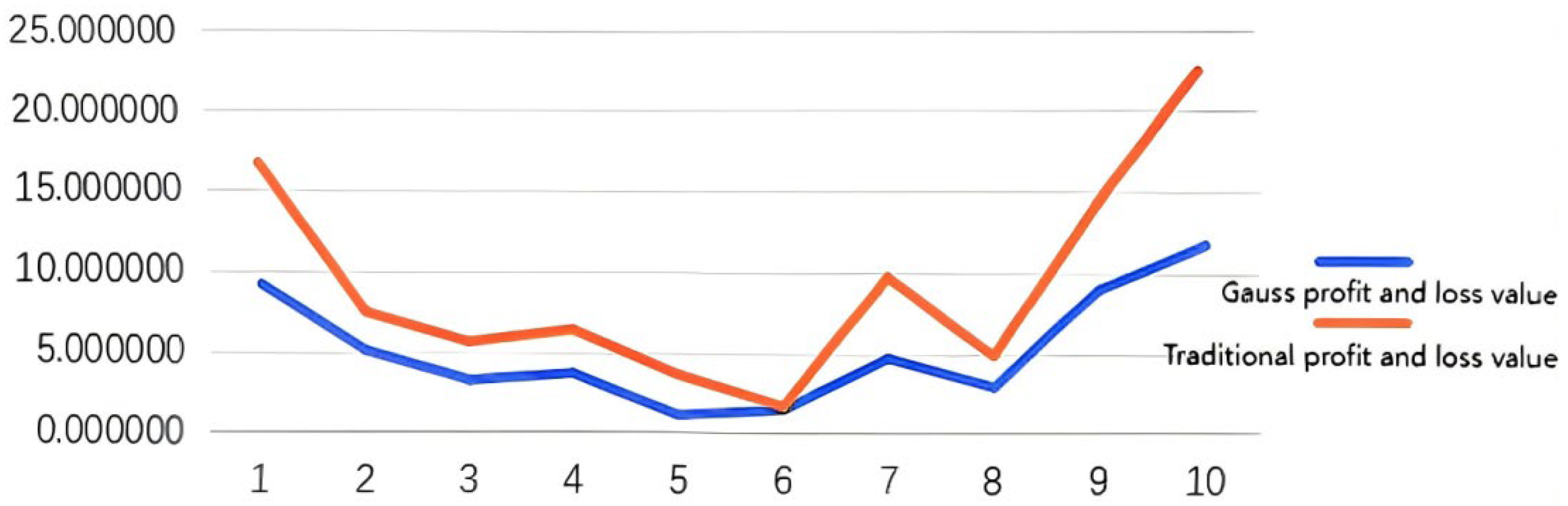
5.3.2. Comparative Analysis
6. Conclusions
- (1)
- By comparing the gain–loss values from the proposed function model with those obtained using the traditional multivariate quality gain–loss function and the dimensionless standardized multivariate function of Artiles-León, it is demonstrated that the proposed model exhibits clear advantages in addressing quality gain–loss problems under multiple quality characteristics and influencing factors.
- (2)
- As an extension of the conventional quality gain–loss function, the multivariate and multidimensional quality gain–loss function, when integrated with the Gaussian process framework, not only accounts for interactions among multiple quality characteristics but also enables simultaneous evaluation of control effectiveness across different types of quality characteristics. This integration broadens the application scope of the quality gain–loss function in dam concrete construction quality control.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Gan, Y.F.; Li, Q.B.; Hu, Y. Dry curing strength and microstructure of concrete of Baihetan dam. J. Hydroelectr. Eng. 2022, 41, 42–49. [Google Scholar]
- Fan, X.Q.; Liu, J.D.; Ge, F.; Tang, L.; Han, H. Comparative study on mechanical properties of concrete for a hydraulic complex project. Hydro-Sci. Eng. 2023, 2, 129–137. [Google Scholar]
- Dong, Y.; Zhou, Z.C.; Li, P.X.; Liu, C. Long-term effectiveness of preventive measures against alkali-aggregate reaction of Jinping-I dam concrete. J. Yangtze River Sci. Res. Inst. 2022, 39, 140–144, 152. [Google Scholar]
- Li, R.Q.; Pai, L.F.; Wu, H.G. Research and simulation of hydration heat of special-shaped mass concrete. Sci. Technol. Eng. 2021, 21, 10452–10460. [Google Scholar]
- Lyu, G.E.; Tang, Q.Y.; Wang, D.S.; Li, T.; Zhu, Y.; Chen, D. Calculation method of heat damage by hydration of mass concrete. J. Hohai Univ. (Nat. Sci.) 2024, 52, 29–34. [Google Scholar]
- Wang, X.G.; Peng, Y.F.; Yang, M.G. Research on hydration heat of mass concrete at arch support and temperature control measures for a high-speed railway tied-arch bridge. J. Railw. Sci. Eng. 2020, 17, 549–555. [Google Scholar]
- Tasri, A.; Susilawati, A. Effect of cooling water temperature and space between cooling pipes of post-cooling system on temperature and thermal stress in mass concrete. J. Build. Eng. 2019, 24, 100731. [Google Scholar] [CrossRef]
- El-Mir, A.; Assaad, J.J.; Nehme, S.G.; El-Hassan, H. Correlating strength and durability to time-temperature profiles of high-performance mass concrete. Case Stud. Constr. Mater. 2022, 16, e01055. [Google Scholar] [CrossRef]
- Van Tran, M.; Chau, V.N.; Nguyen, P.H. Prediction and control of temperature rise of massive reinforced concrete transfer slab with embedded cooling pipe. Case Stud. Constr. Mater. 2023, 18, e01817. [Google Scholar] [CrossRef]
- Qiao, Y.; Yang, N.; Tan, P.; Peng, H.; Wu, W.; Zhou, D.; Wang, X. Engineering application and factors affecting infrared temperature measurements of mass concrete surfaces. J. Tsinghua Univ. (Sci. Technol.) 2021, 61, 730–737. [Google Scholar]
- Yang, N.; Liu, Y.; Qiao, Y.; Tan, Y.; Zhu, Z. Intelligent spray control for the concrete curing of mass concrete bins. J. Tsinghua Univ. (Sci. Technol.) 2021, 61, 724–729. [Google Scholar]
- Deng, K.D.; Qiang, S.; Jiang, Y.B.; Xu, C.L. Research on unmanned transportation and pouring system model for hydraulic mass concrete construction. Int. J. Hydroelectr. Energy 2022, 40, 175–179. [Google Scholar]
- Cui, W.; Liu, W.; Guo, R.; Wan, D.; Yu, X.; Ding, L.; Tao, Y. Geometrical quality inspection in 3D concrete printing using AI-assisted computer vision. Mater. Struct. 2025, 58, 68. [Google Scholar] [CrossRef]
- Cui, W.; Ji, D.; Shen, L.; Su, S.; Shi, X.; Liu, J.; Bai, Z.; Sun, Y.; Gong, J.; Tao, Y. A neural network-based model for assessing 3D printable concrete performance in robotic fabrication. Results Eng. 2025, 27, 105970. [Google Scholar] [CrossRef]
- Wang, B.; Li, Q.; Li, P.; Zhang, P.; Fan, T. Quality gain-loss transmission in dam concrete construction: A CF-GERT-based approach. Int. J. Ind. Eng. Comput. 2025, 16, 963–978. [Google Scholar] [CrossRef]
- Cao, Y.-L.; Mao, J.; Yang, J.-X.; Wu, Z.-T.; Wu, L.-Q. Robust tolerance design based on fuzzy quality loss. J. Zhejiang Univ. (Eng. Sci.) 2004, 38, 1–4, 10. [Google Scholar] [CrossRef]
- Wang, B.P.; Zhang, H.; Jing, D.Y. Study on section curve quality loss function model. Trans. Chin. Soc. Agric. Mach. 2007, 38, 150–152. [Google Scholar]
- Zhao, Y.M.; Liu, D.S.; Zhang, J.; Liu, Q. Quality loss cost model and its application to products with multi-quality characteristics. J. Cent. South Univ. (Sci. Technol.) 2012, 43, 1753–1763. [Google Scholar]
- Yang, C.M.; Duan, S.Q. Robust synthesis of function mechanisms by using asymmetric quality loss models. J. Xihua Univ. (Nat. Sci.) 2016, 35, 30–33. [Google Scholar]
- Zeybek, M.; Köksoy, O. Optimization of correlated multi-response quality engineering by the upside-down normal loss function. Eng. Optim. 2016, 48, 1419–1431. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Song, M.S.; Han, Z.J.; Chen, X.L. Design of quality loss function under the smaller the better characteristic without neglecting the linear term. Ind. Eng. J. 2011, 14, 81–83, 89. [Google Scholar]
- Zhang, Y.Y.; Song, M.S.; Han, Z.J. Designing of the quality loss function of the larger the better characteristic under not neglecting the linear term. J. Appl. Stat. Manag. 2013, 32, 486–491. [Google Scholar]
- Pignatiello, J.J. Strategies for robust multi-response quality engineering. IIE Trans. 1993, 25, 5–15. [Google Scholar] [CrossRef]
- Artiles-León, N. A pragmatic approach to multiple-response problems using loss functions. Qual. Eng. 1996, 9, 213–220. [Google Scholar] [CrossRef]
- Lee, C.L.; Tang, G.R. Tolerance design for products with correlated characteristics. Mech. Mach. Theory 2000, 35, 1675–1687. [Google Scholar] [CrossRef]
- Ai, Y.T.; Tian, J.; Gao, H.C. Study on assembly quality optimization technology based on multivariate quality loss and genetic algorithm. China Mech. Eng. 2012, 23, 1161–1164. [Google Scholar]
- Tansel, I.Y.; Yildirim, S. Moora-based Taguchi optimisation for improving product or process quality. Int. J. Prod. Res. 2013, 51, 3321–3341. [Google Scholar] [CrossRef]
- Wu, J.J.; Xie, Z.W.; Huang, Y.L. A new method for multi-response robust optimization based on improved quality loss function. Mech. Sci. Technol. Aerosp. Eng. 2017, 36, 519–526. [Google Scholar]
- Zhong, H.M.; Wu, H.C. Multi-response robust design based on comprehensive weight and quality loss. Mech. Sci. Technol. Aerosp. Eng. 2017, 36, 903–908. [Google Scholar]
- Wang, B.; Fan, T.Y.; Tian, J. Designing a quality gain-loss function for larger-the-better characteristic and smaller-the-better characteristic under not neglecting the linear term loss and keeping compensation amount constant. Math. Pract. Theory 2019, 49, 153–160. [Google Scholar]
- Wang, B.; Zhou, H.G.; Li, Z.Y.; Nie, X.T. Tolerance optimization for quality characteristics of the dam concrete construction based on quality gain-loss function. Math. Pract. Theory 2016, 46, 90–99. [Google Scholar]
- Wang, B.; Li, Q.; Liu, C.; Chen, Z.; Nie, X. Establishment and application of a grey quality gain–loss function model. Processes 2022, 10, 495. [Google Scholar] [CrossRef]
- Wang, B.; Li, Q.; Yang, Q.; Lu, J.; Nie, X. Improvement of quadratic exponential quality gain–loss function and optimization of engineering specifications. Processes 2023, 11, 2225. [Google Scholar] [CrossRef]
- Wang, B.; Zhou, H.; Li, Z.; Fan, T.; Nie, X. Quality gain-loss function and its empirical analysis in dam concrete construction. J. Coast. Res. 2020, 104, 842–848. [Google Scholar] [CrossRef]
- Wang, B.; Li, X.; Shi, J.; Li, Q.; Nie, X. The establishment and application of quality gain-loss function when the loss of primary and cubic term is not ignored and the compensation quantity is constant. PLoS ONE 2023, 18, e295949. [Google Scholar] [CrossRef]
- Zhang, Y.; Su, G.S.; Yan, L.B. Strength prediction of high strength concrete using Gaussian process machine learning. Concrete 2011, 11, 18–20. [Google Scholar]
- Luo, Y.Y. A Gaussian process based model for predicting deformations of dams. J. Zhejiang Univ. Technol. 2016, 44, 543–546. [Google Scholar]
- Zhai, C.H.; Wang, J.J.; Feng, Z.B. Robust parameter design of multiple responses based on Gaussian process model. Syst. Eng. Electron. 2021, 43, 3683–3693. [Google Scholar]
- Liu, M.H.; Wang, X.L.; Wang, J.J. Study on improved multi-output prediction model for compaction characteristics of earth-rock dam materials. J. Hydroelectr. Eng. 2022, 41, 63–73. [Google Scholar]
- Ma, J.T.; Kang, F.; Jiang, C.L.; Xiang, Z.L.; Wang, Y.F. Jaya-Gaussian process regression model for parameter inversion of high arch dams. Adv. Sci. Technol. Water Resour. 2022, 42, 74–79. [Google Scholar]
- Mao, Y.X.; Zhang, Y.; Jia, B.J. Application research of medium and long term runoff forecast of hydropower station based on data mining. In Proceedings of the China Hydropower Engineering Society Automation Committee 2022 Annual Meeting and the National Hydropower Plant Intelligent Application Academic Exchange Meeting, Nanjing, China, 7–9 August 2022. [Google Scholar]
- Huang, L.; Chen, S.; Li, C.; Si, Z.; Zhang, F. Application of Gaussian process regression model based on wavelet denoising in settlement prediction of CFRD. J. Water Resour. Water Eng. 2023, 34, 144–150. [Google Scholar]
- Liu, W.Q.; Chen, B. Prediction model of dam deformation driven by NGO-GPR and projection pursuit. J. Hydroelectr. Eng. 2023, 42, 126–136. [Google Scholar]
- Li, H.K.; Ke, X.Y.; Huang, W.; Liu, S.P.; Tang, Y.Y. Inversion study of soft foundation sluice bottom plate emptying based on a GPR surrogate model and a GA-APSO hybrid optimization algorithm. J. Vib. Shock 2023, 42, 1–10. [Google Scholar]
- Li, W.H.; Lou, J.K.; Li, X. Combined kernel function-based gaussian process dam deformation prediction method. Yelloe River 2023, 45, 137–140. [Google Scholar]
- Chen, X.H.; Hu, Y.; Wang, Y.J.; Zhu, X.Z. Dam deformation interval prediction model based on XGBoost. J. Hydroelectr. Eng. 2024, 43, 121–136. [Google Scholar]


| Evaluation Index | RMSE | R2 | MSE | RPD | MAE | MAPE |
|---|---|---|---|---|---|---|
| Evaluation result | 0.026716 | 0.96074 | 0.00071375 | 5.9686 | 0.018491 | 0.068282 |
| Serial Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| x1 (m3/h) | 130 | 130 | 130 | 128 | 126 | 125 | 125 | 123 | 120 | 120 |
| x2 (h) | 3 | 3 | 4 | 3 | 3 | 3 | 3.5 | 4 | 4 | 4 |
| x3 (°C) | 8 | 10 | 10 | 7 | 9 | 10 | 8 | 7 | 7 | 8 |
| y1 (xi) | 0.12 | 0.18 | 0.22 | 0.10 | 0.15 | 0.18 | 0.11 | 0.17 | 0.18 | 0.20 |
| Group | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| y1 (xi) | 0.12 | 0.18 | 0.22 | 0.10 | 0.15 | 0.18 | 0.11 | 0.17 | 0.18 | 0.20 |
| y2 (%) | 1 | 0.5 | 1 | 1.5 | 0.5 | 0.5 | 1 | 1 | 0.5 | 1 |
| y3 (cm) | 3 | 4 | 6 | 4 | 2 | 3 | 5 | 3 | 6 | 4 |
| Conditions | Condition 1 | Condition 2 | Condition 3 | Condition 4 | Condition 5 | Condition 6 |
|---|---|---|---|---|---|---|
| y1 (xi) | 0 | 0 | 0.25 | 0 | 0.25 | 0.25 |
| y2 (%) | 0 | 0.015 | 0 | 0.015 | 0 | 0.015 |
| y3 (cm) | 2 | 4 | 4 | 2 | 2 | 4 |
| Compensating quantity (yuan/m3) | −3 | −640y2 | −2.4 | / | / | / |
| Gain–loss value (yuan/m3) | 11 | −0.7 | 5.2 | 11 | 18.5 | 12.5 |
| Group | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| y1 (xi) | 0.12 | 0.18 | 0.22 | 0.1 | 0.15 | 0.18 | 0.11 | 0.17 | 0.18 | 0.2 |
| y2 (%) | 0.01 | 0.005 | 0.009 | 0.014 | 0.005 | 0.006 | 0.01 | 0.01 | 0.005 | 0.011 |
| y3 (cm) | 3 | 4 | 4.5 | 3.5 | 2.8 | 3.2 | 5 | 2.5 | 5.5 | 5.7 |
| Group | y1 (xi) | y2 (%) | y3 (cm) | Model 1 | Model 2 | Model 3 |
|---|---|---|---|---|---|---|
| 1 | 0.17 | 0.01 | 2.5 | 25.081996 | 16.672565 | 9.156532 |
| 2 | 0.15 | 0.005 | 2.8 | 28.948889 | 7.454505 | 5.072680 |
| 3 | 0.12 | 0.01 | 3 | 33.897795 | 5.545830 | 3.197272 |
| 4 | 0.18 | 0.006 | 3.2 | 40.527040 | 6.377674 | 3.681192 |
| 5 | 0.1 | 0.014 | 3.5 | 50.017889 | 3.652830 | 1.094740 |
| 6 | 0.18 | 0.005 | 4 | 64.083929 | 1.684948 | 1.476712 |
| 7 | 0.22 | 0.009 | 4.5 | 85.221640 | 9.682627 | 4.698132 |
| 8 | 0.11 | 0.01 | 5 | 99.107715 | 4.870369 | 2.914648 |
| 9 | 0.18 | 0.005 | 5.5 | 122.508928 | 14.358974 | 8.996212 |
| 10 | 0.2 | 0.011 | 5.7 | 130.610222 | 22.515333 | 11.753320 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Li, Q.; Pei, L.; Li, P.; Li, H.; Nie, X.; Fan, T. Construction and Application of a Multi-Dimensional Quality Gain–Loss Function for Dam Concrete Based on Gaussian Process. Buildings 2025, 15, 3851. https://doi.org/10.3390/buildings15213851
Wang B, Li Q, Pei L, Li P, Li H, Nie X, Fan T. Construction and Application of a Multi-Dimensional Quality Gain–Loss Function for Dam Concrete Based on Gaussian Process. Buildings. 2025; 15(21):3851. https://doi.org/10.3390/buildings15213851
Chicago/Turabian StyleWang, Bo, Qikai Li, Liang Pei, Pengyuan Li, Hongxiang Li, Xiangtian Nie, and Tianyu Fan. 2025. "Construction and Application of a Multi-Dimensional Quality Gain–Loss Function for Dam Concrete Based on Gaussian Process" Buildings 15, no. 21: 3851. https://doi.org/10.3390/buildings15213851
APA StyleWang, B., Li, Q., Pei, L., Li, P., Li, H., Nie, X., & Fan, T. (2025). Construction and Application of a Multi-Dimensional Quality Gain–Loss Function for Dam Concrete Based on Gaussian Process. Buildings, 15(21), 3851. https://doi.org/10.3390/buildings15213851





