Predicting the Properties of Polypropylene Fiber Recycled Aggregate Concrete Using Response Surface Methodology and Machine Learning
Abstract
1. Introduction
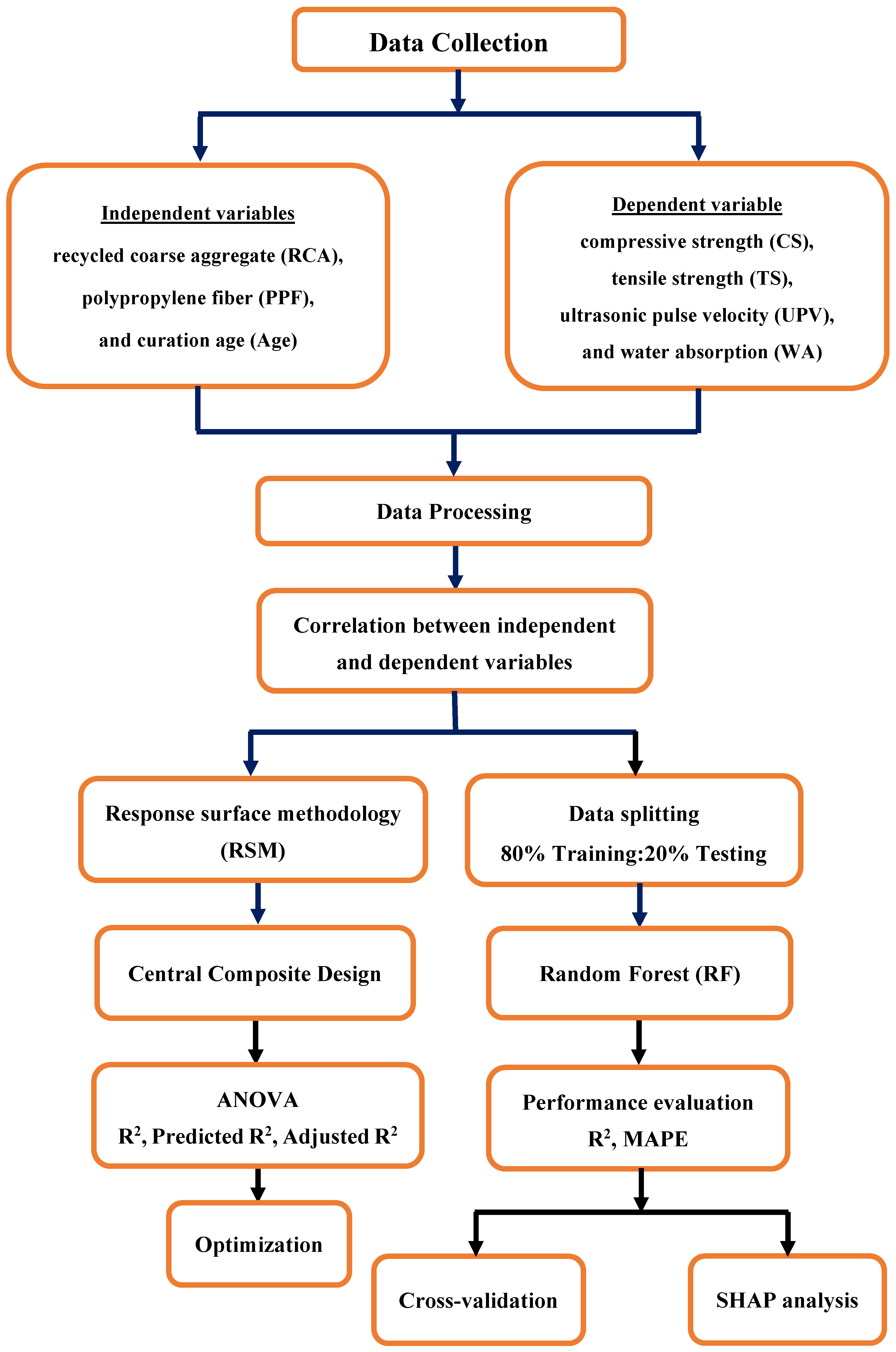
2. Experimental Data and Methods
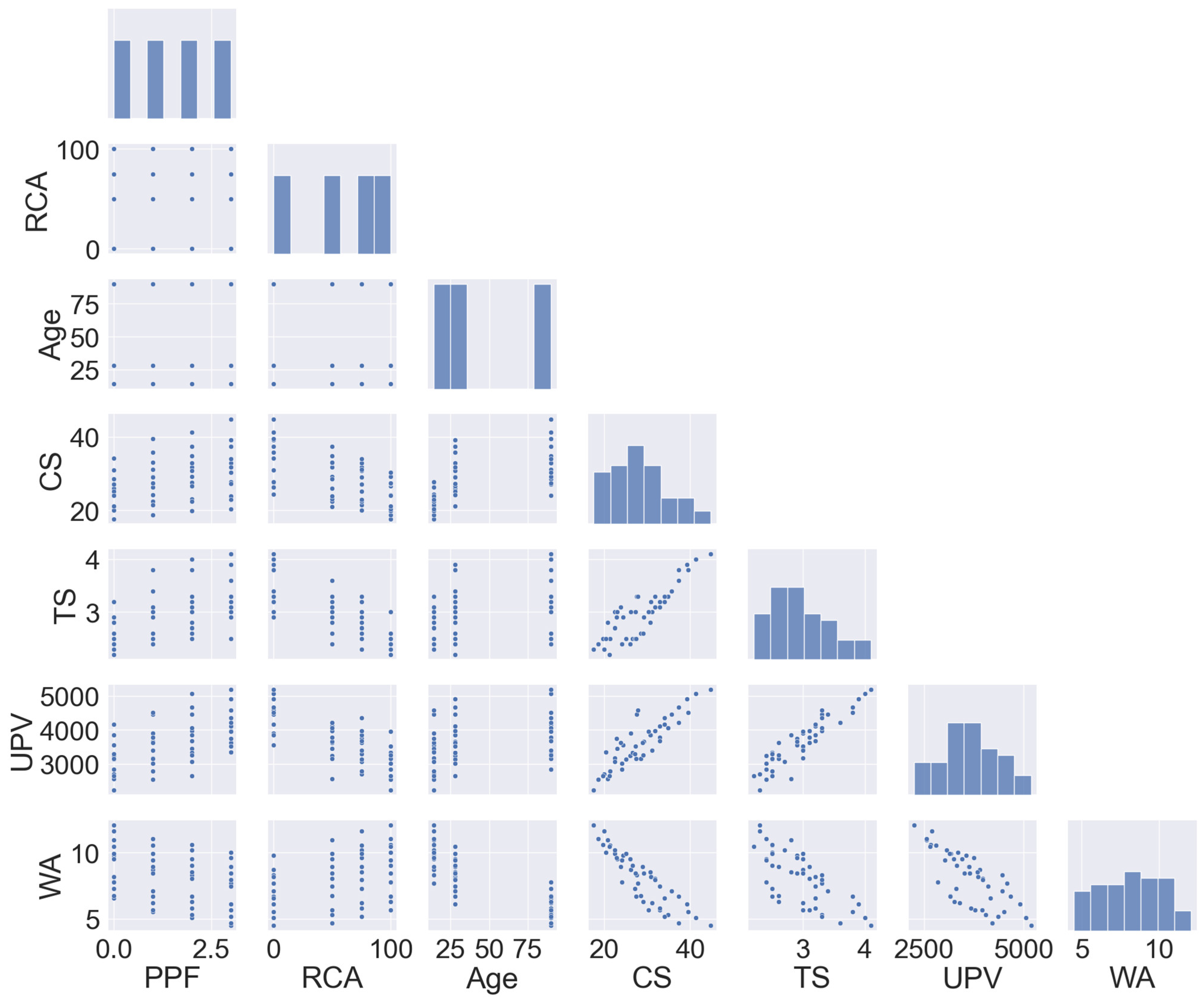
2.1. Experimental Dataset
2.2. Processing of Data for Use
2.2.1. Outlier Removal
2.2.2. Feature Scaling
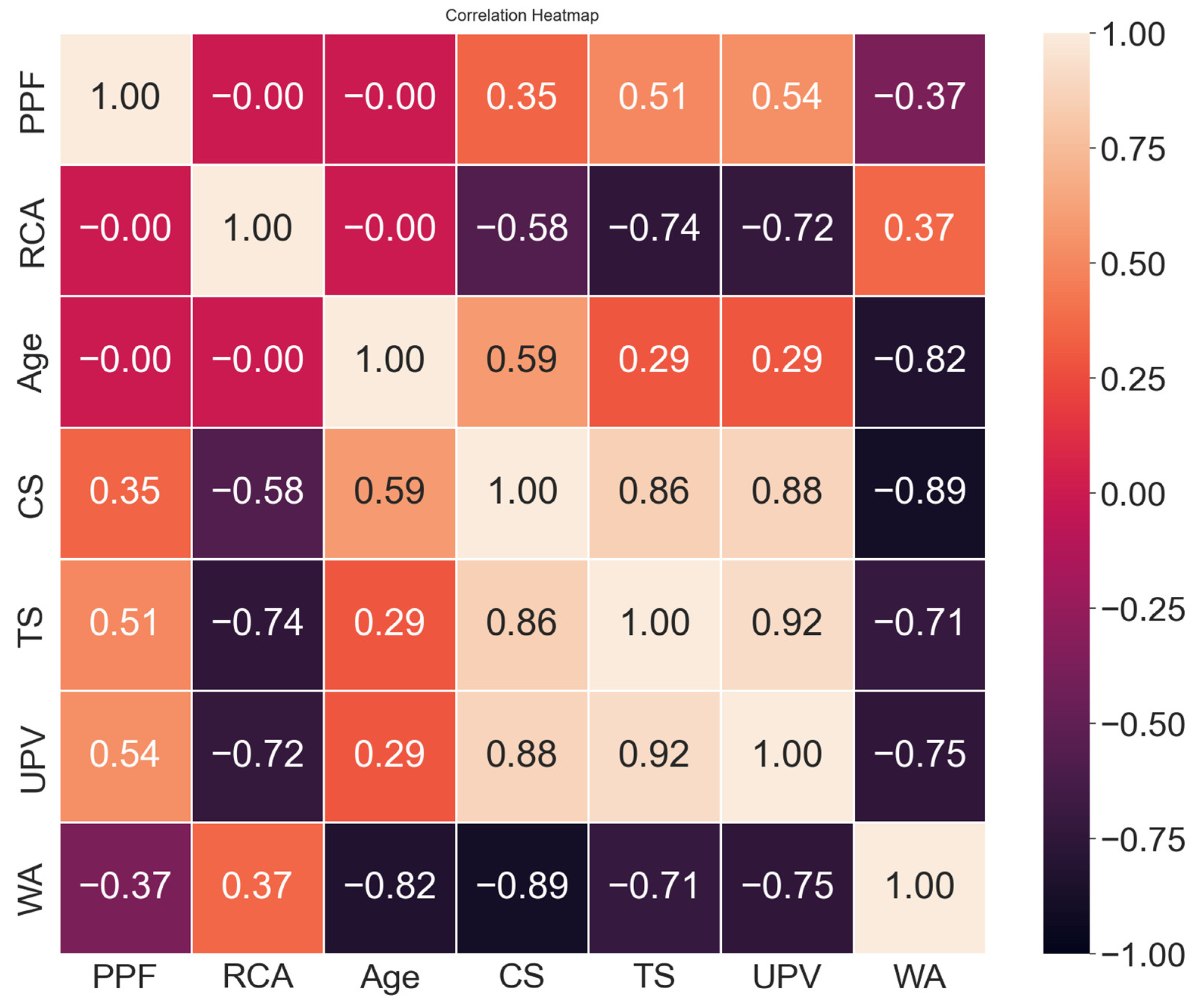
2.3. Correlation Coefficients
2.4. Response Surface Methodology (RSM)
2.5. Machine Learning (ML) Techniques
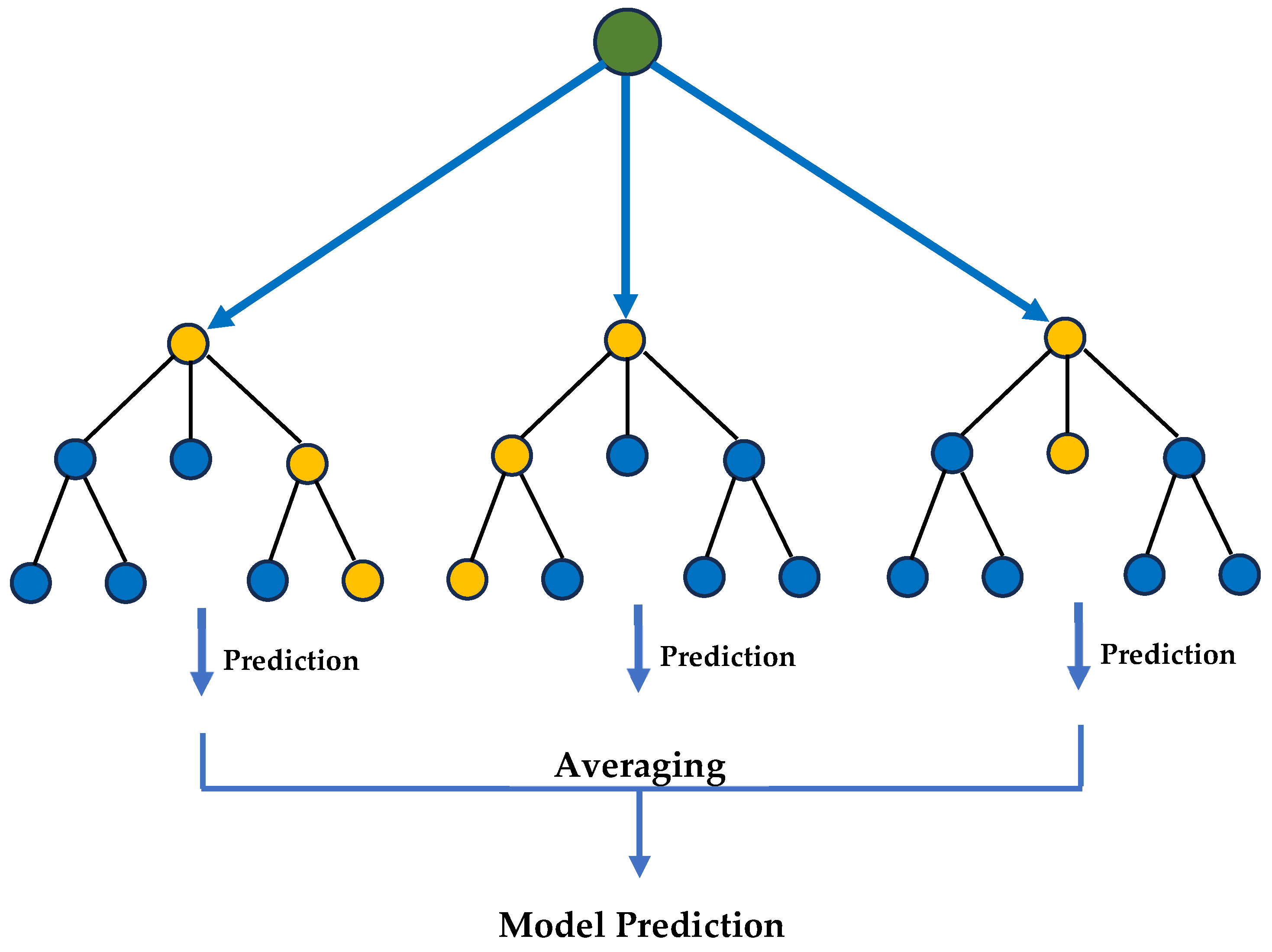
2.5.1. Random Forest (RF)
2.5.2. Efficiency of the Model
3. Results
3.1. Response Surface Methodology Results
3.1.1. Analysis of Variance (ANOVA)
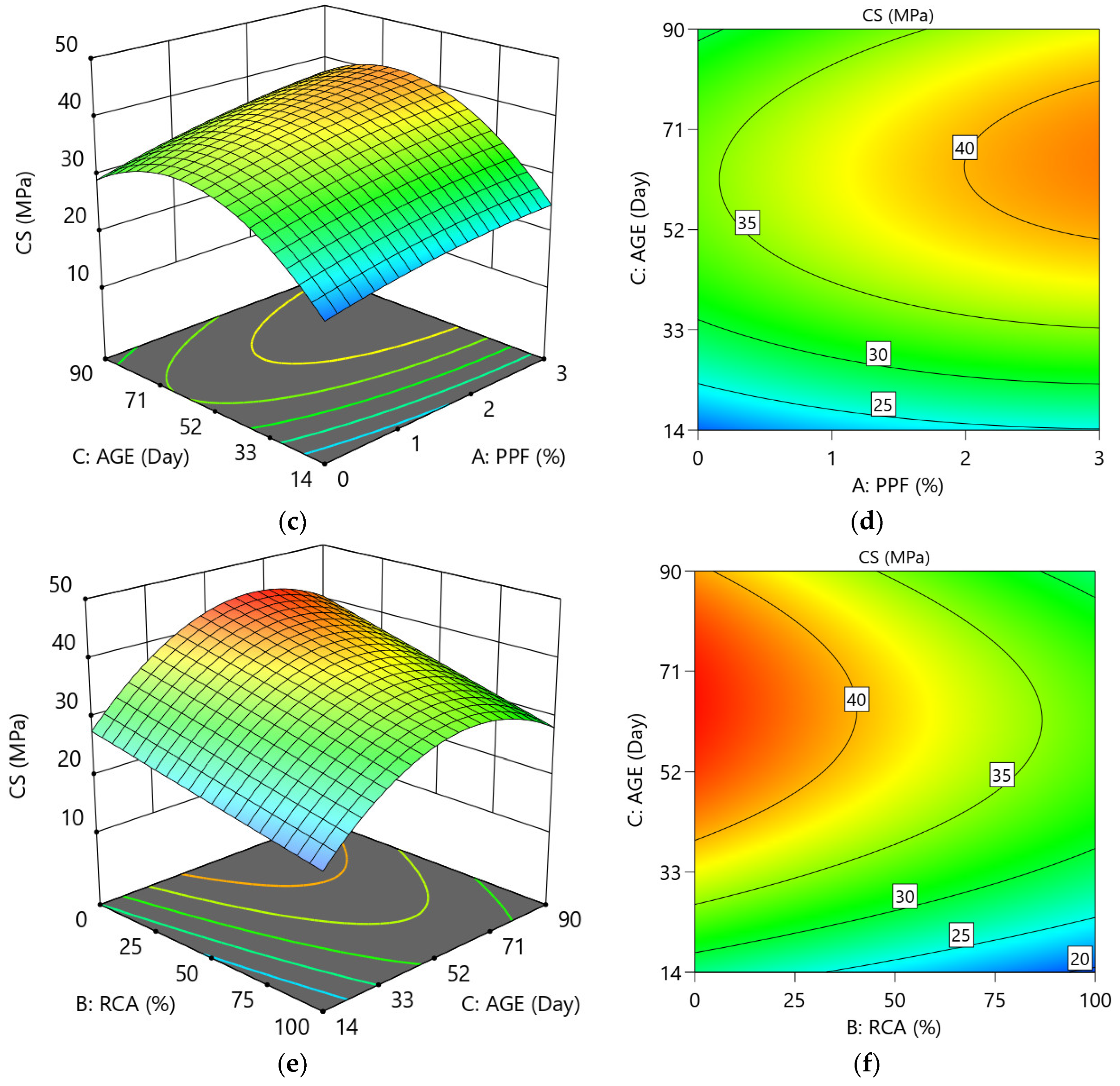
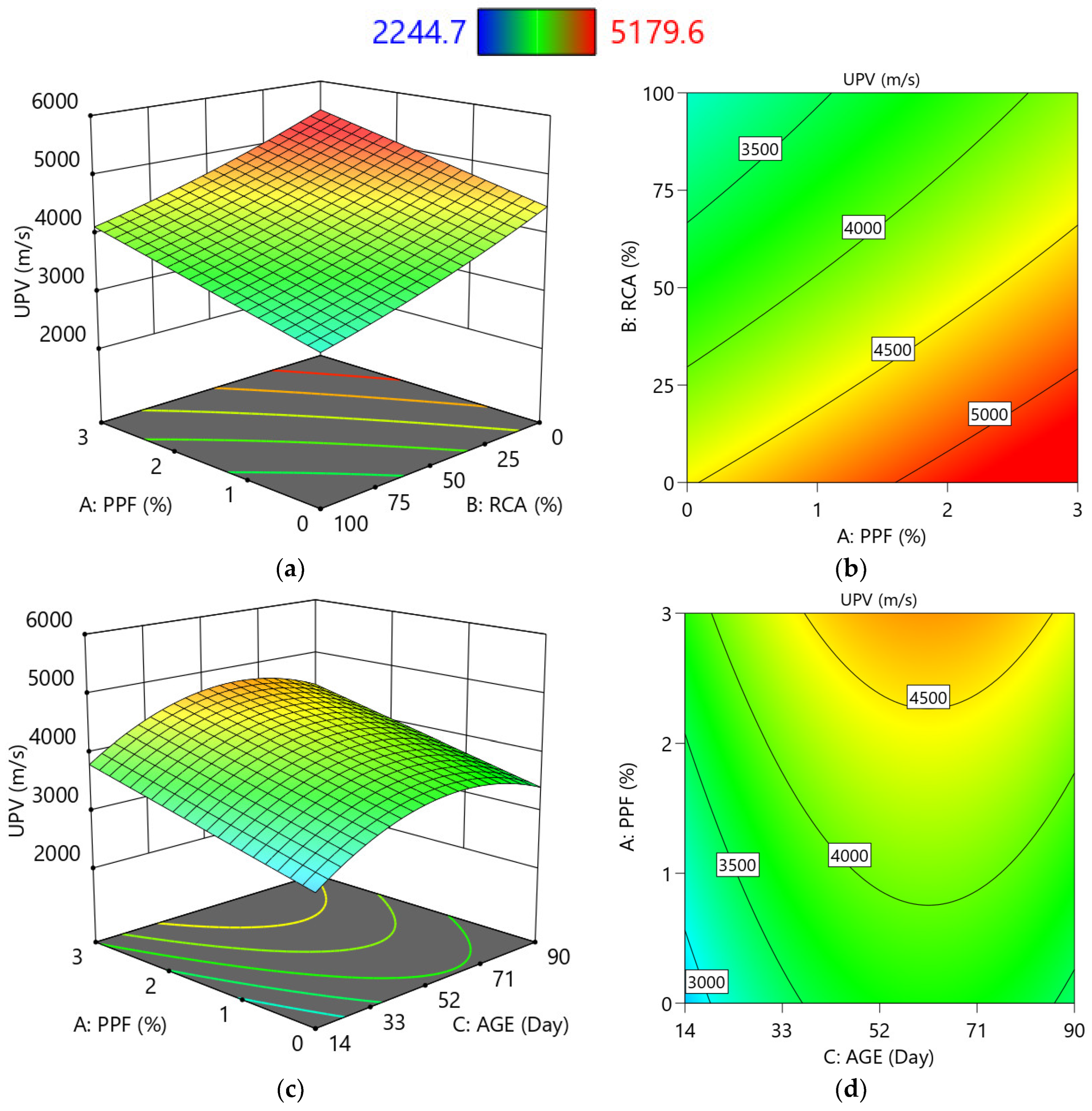
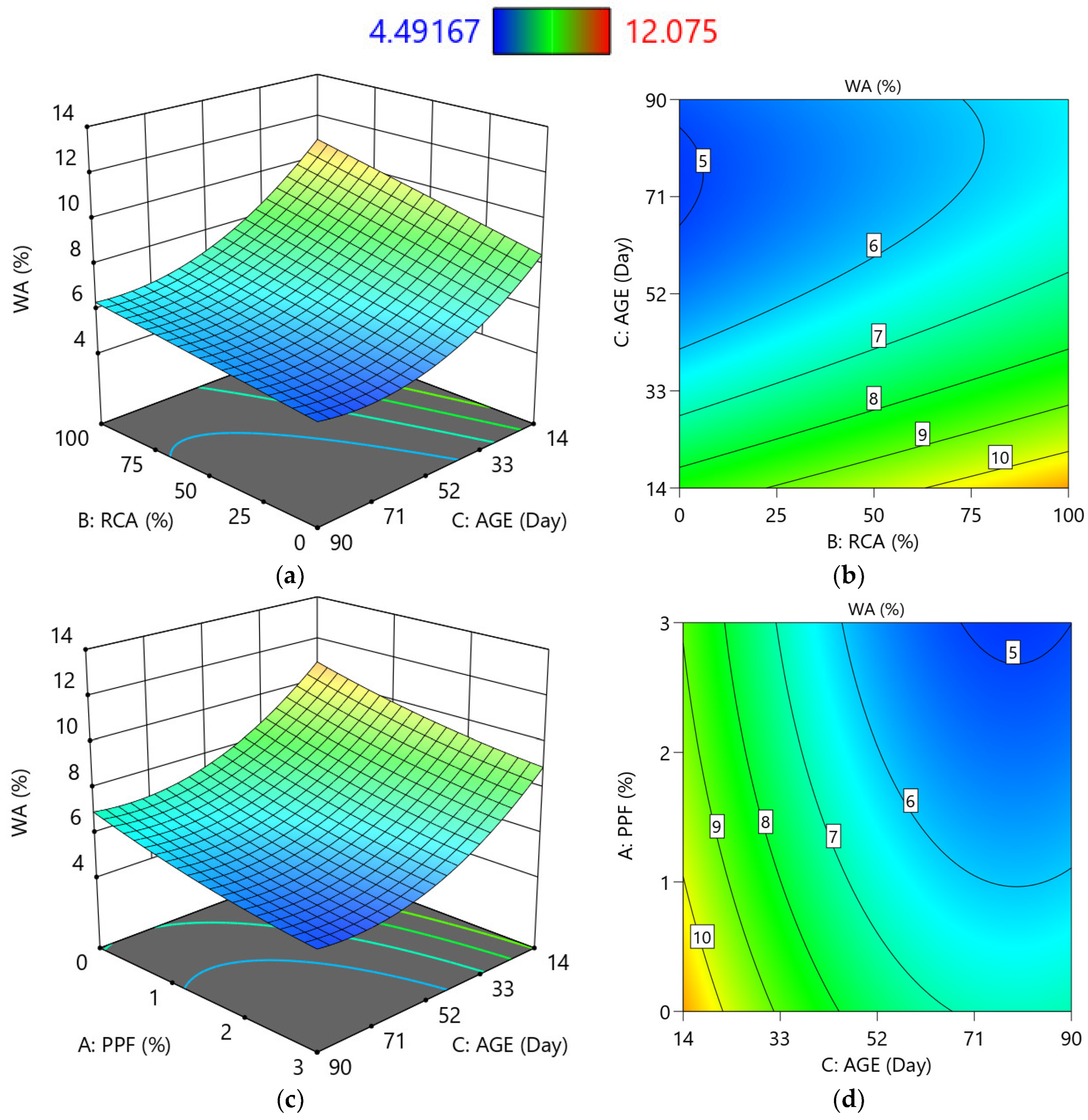
3.1.2. Response Surface Contour Plots
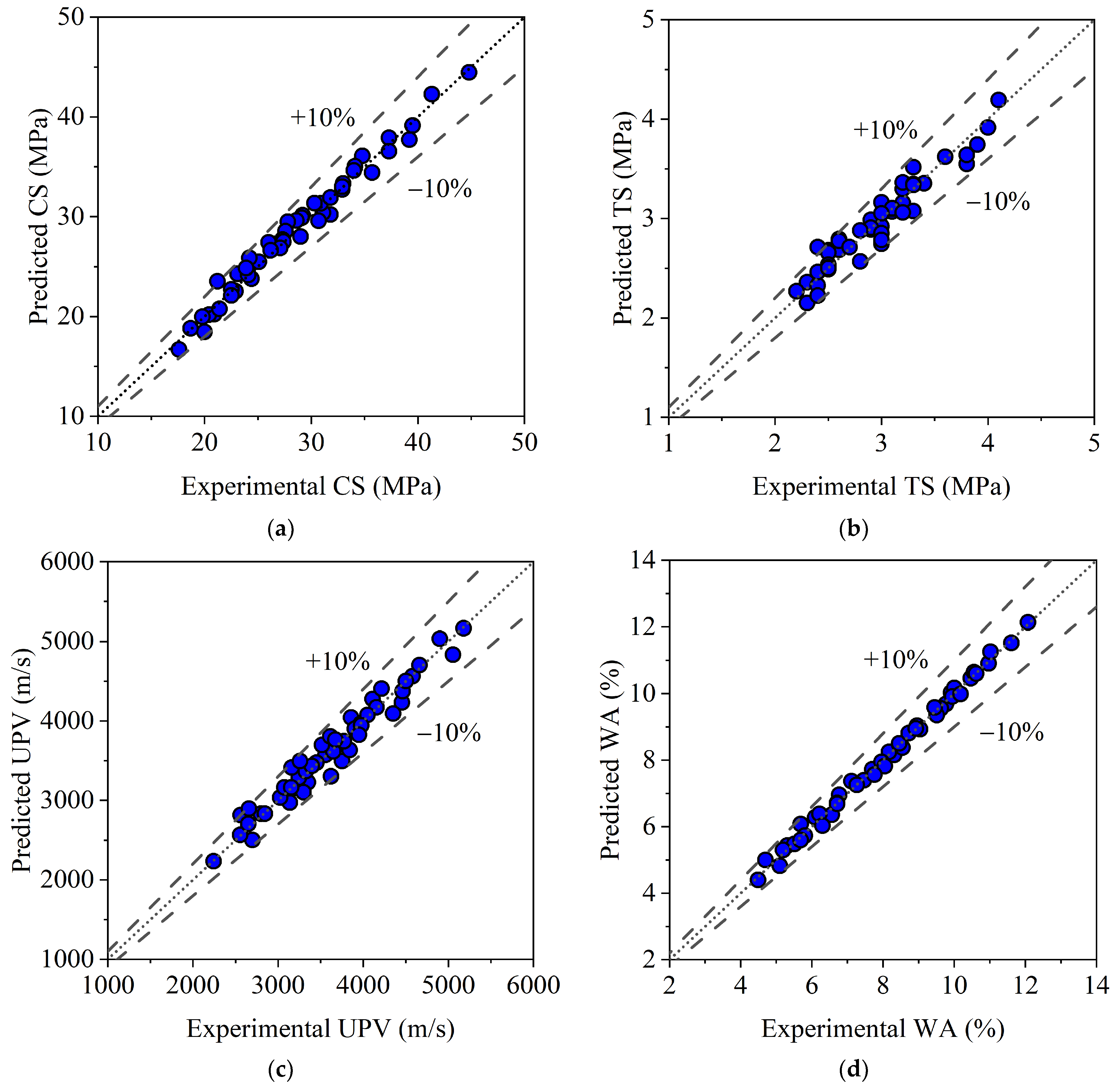
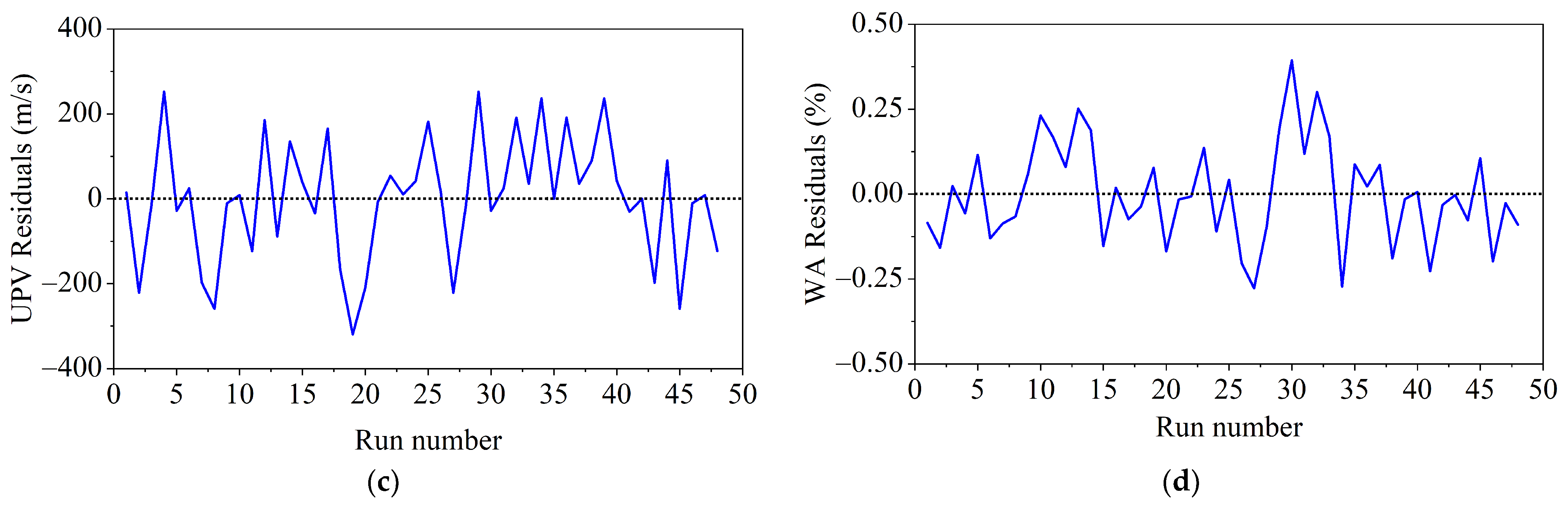
3.2. ML Prediction Models
3.2.1. Optimization of Hyperparameter
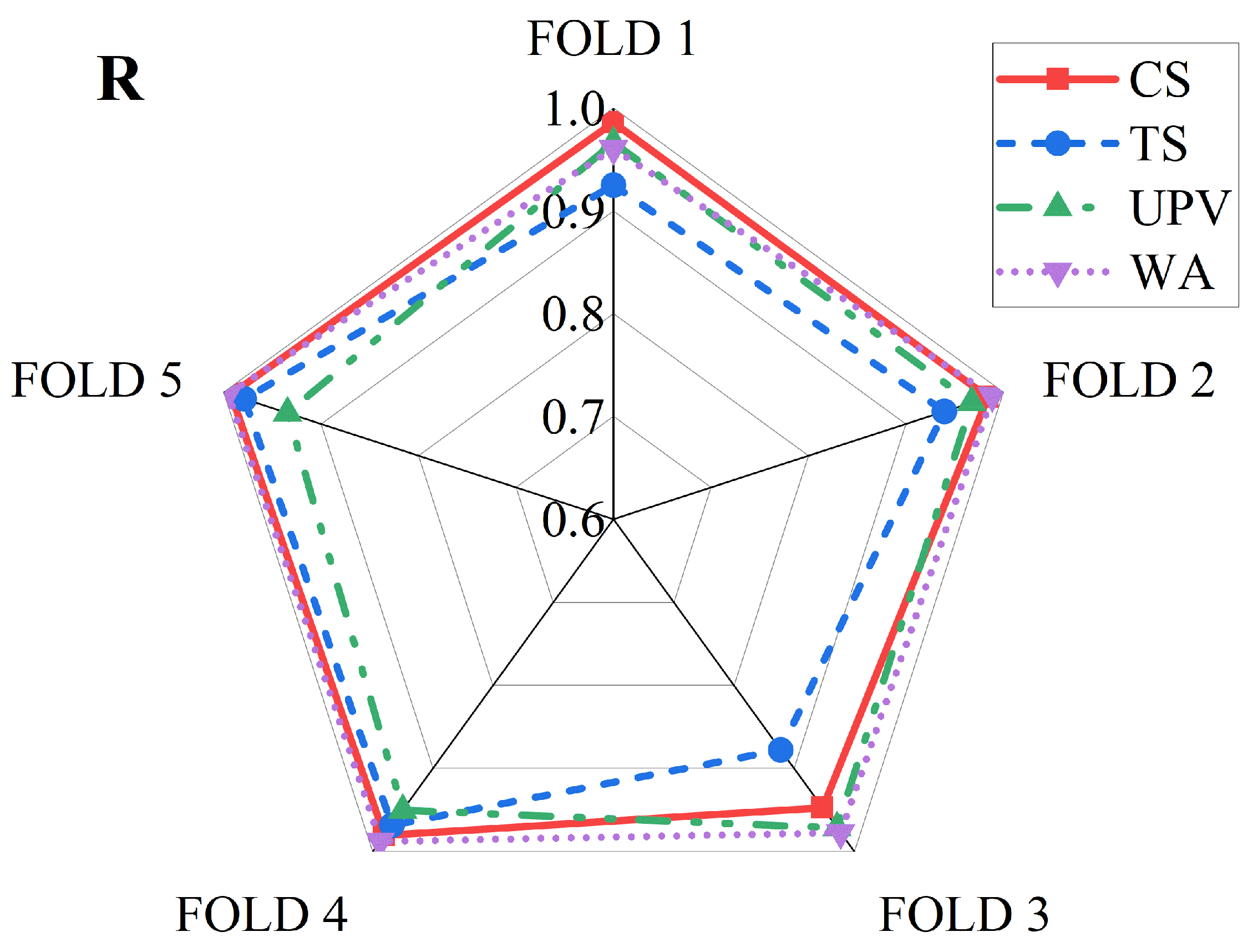
3.2.2. K-Fold Cross Validation (KCV)
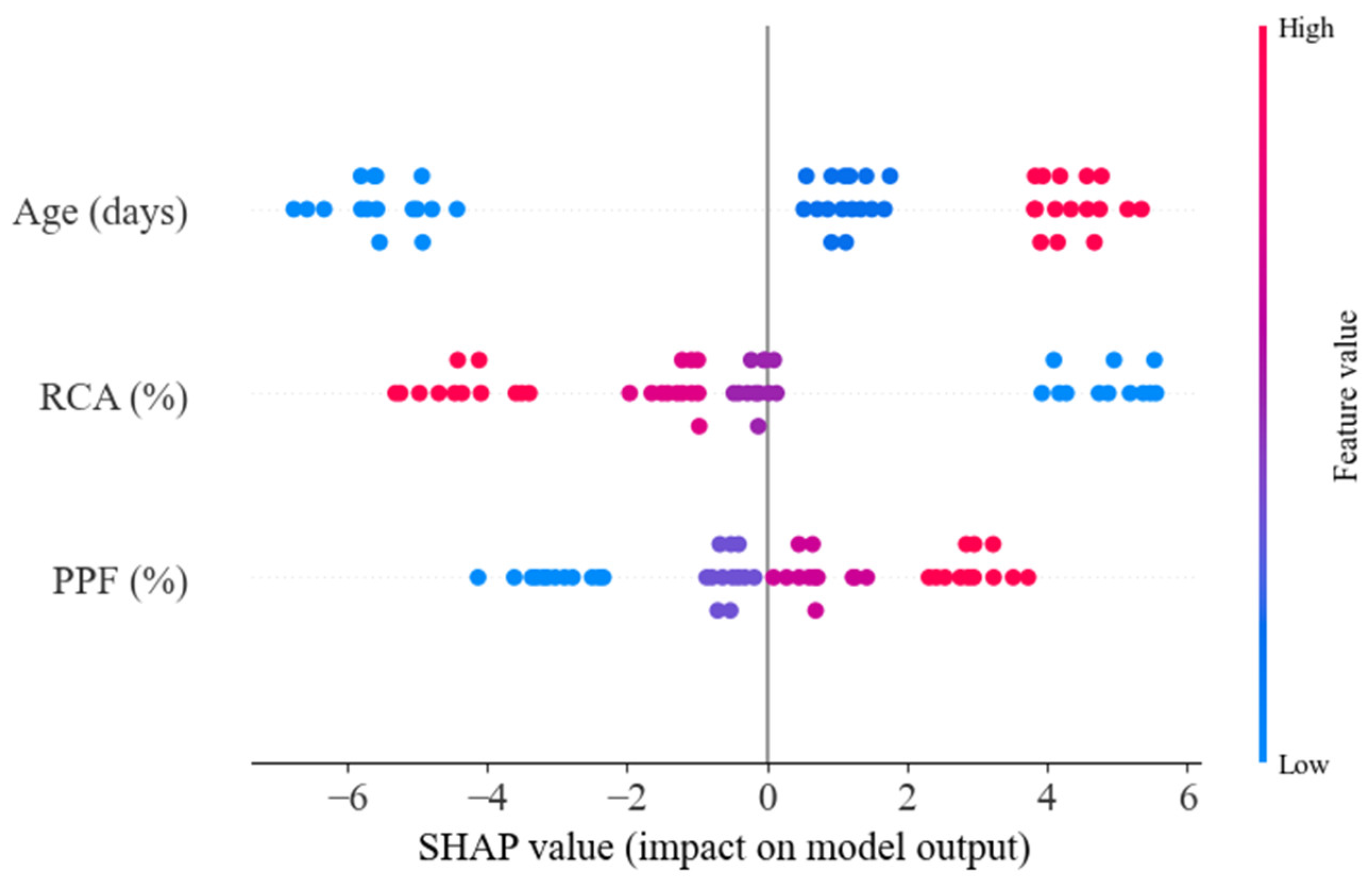
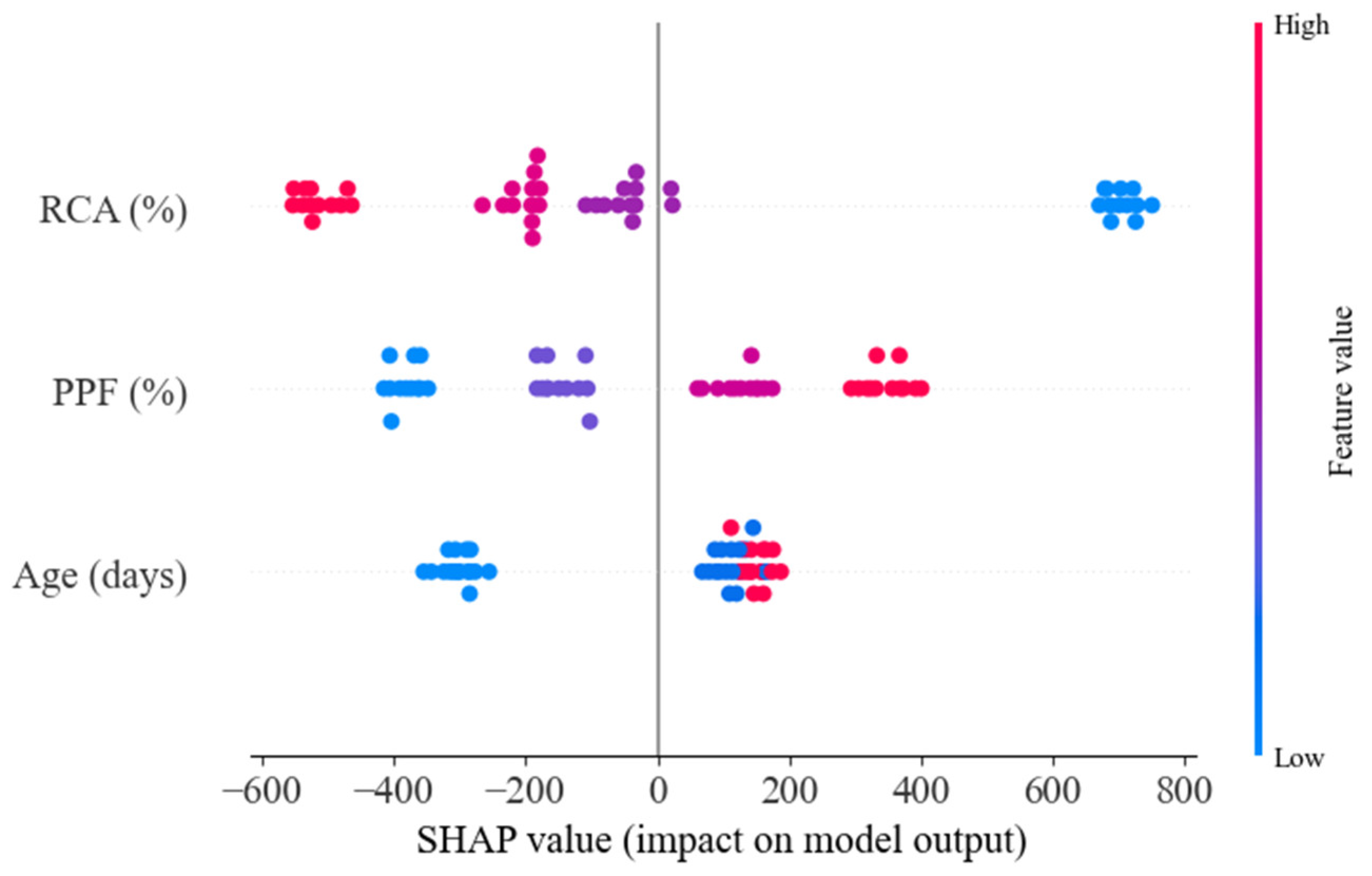
3.2.3. Feature Importance
3.2.4. Enhanced Explainability of the Developed RF Models
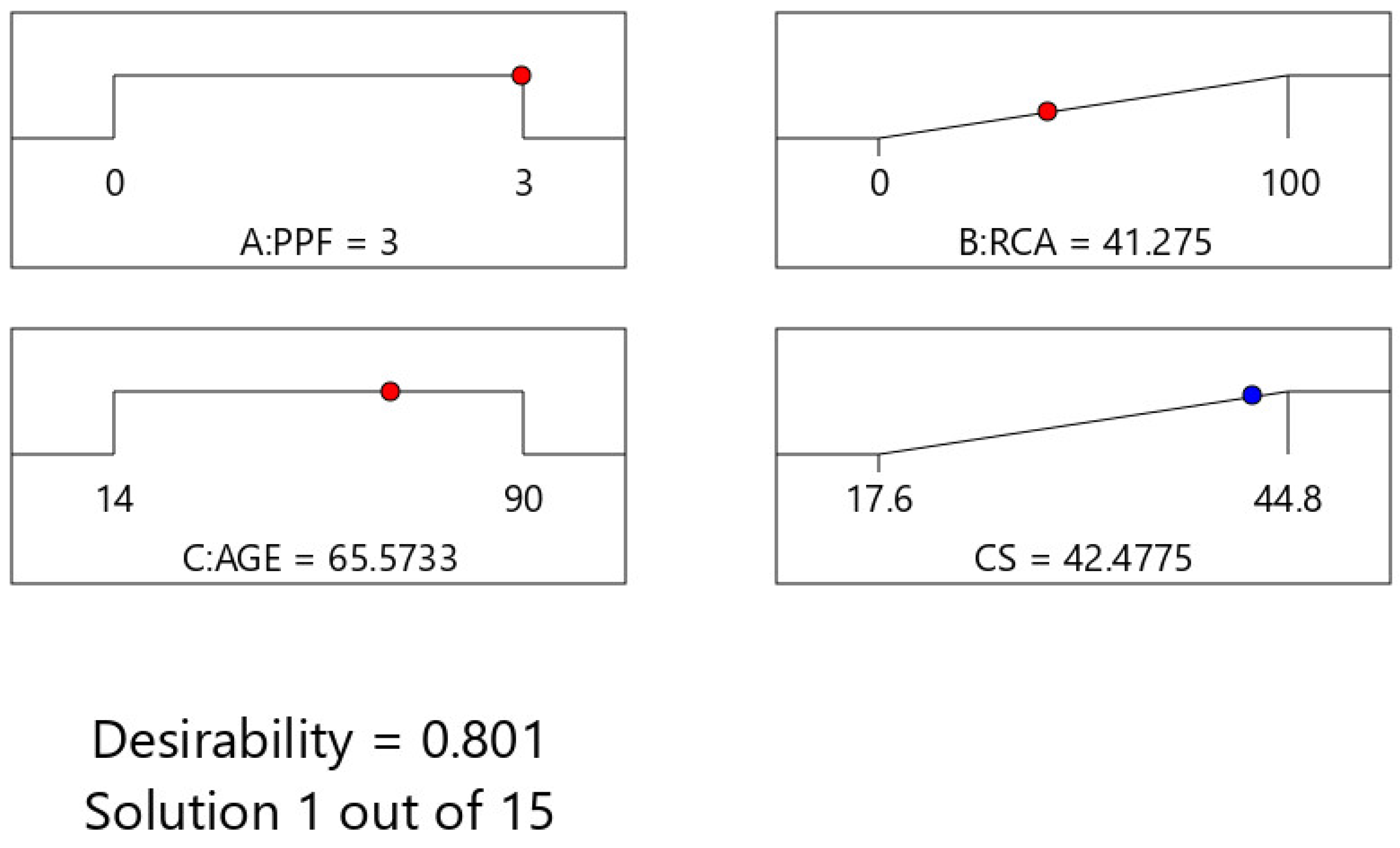
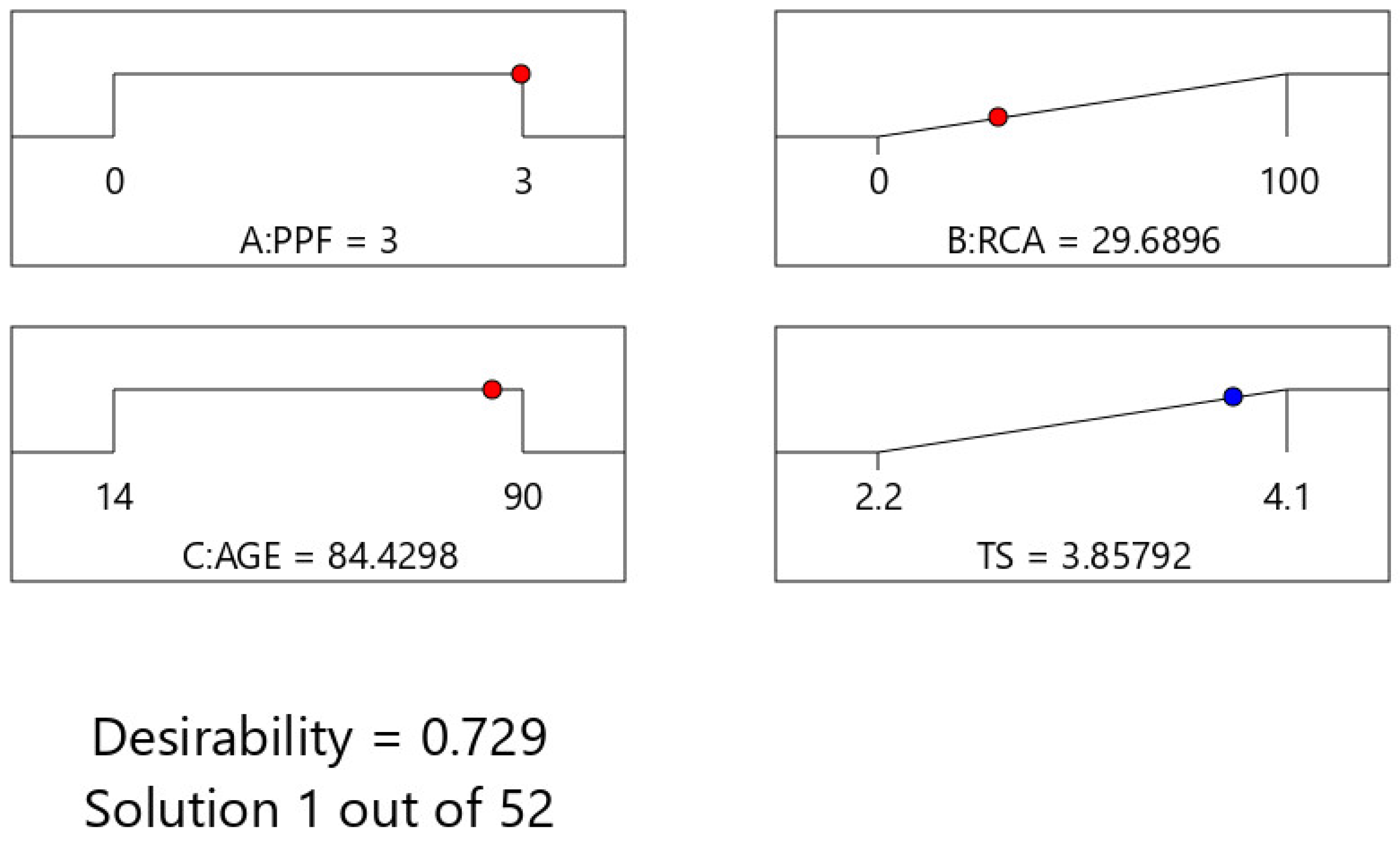
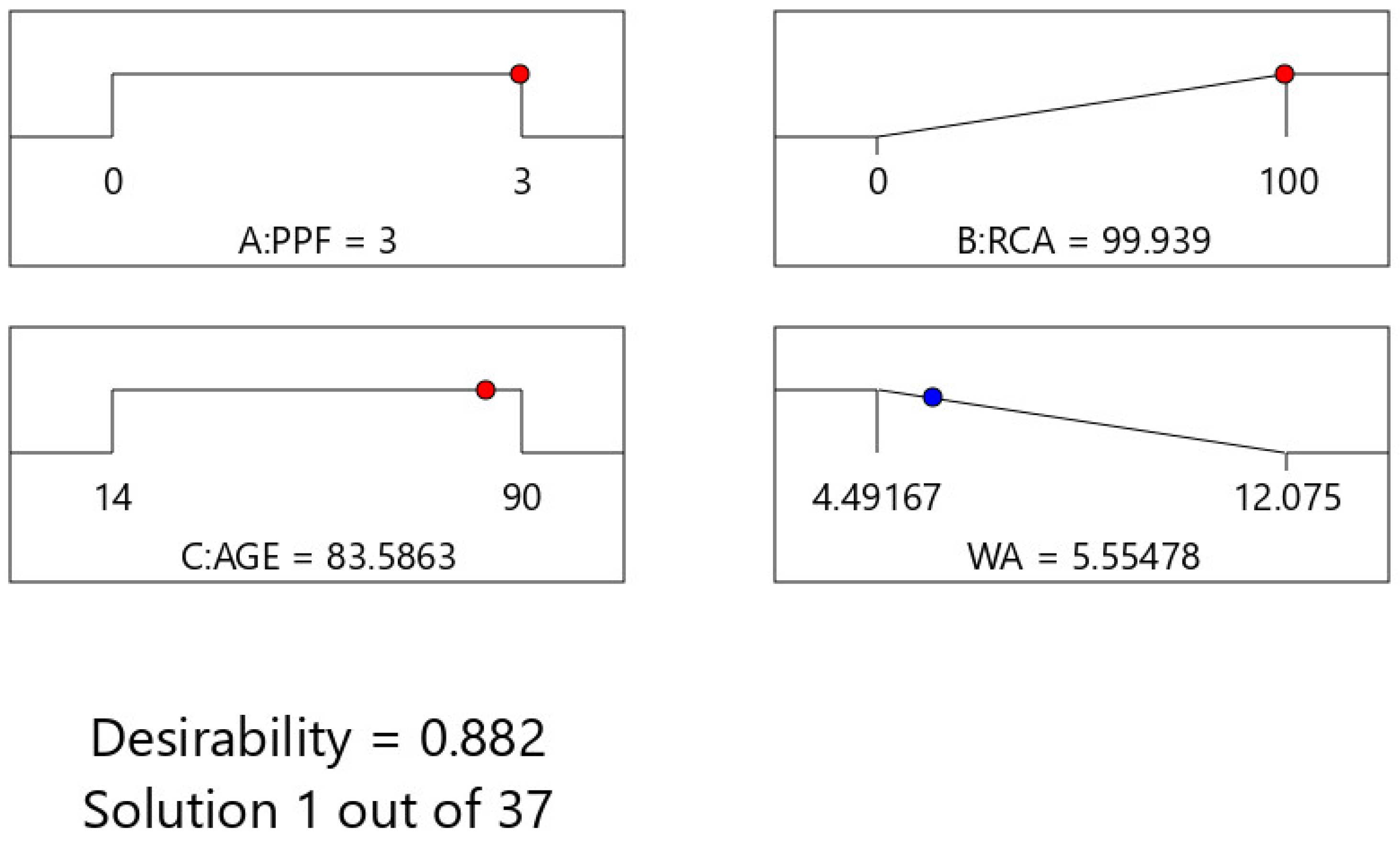
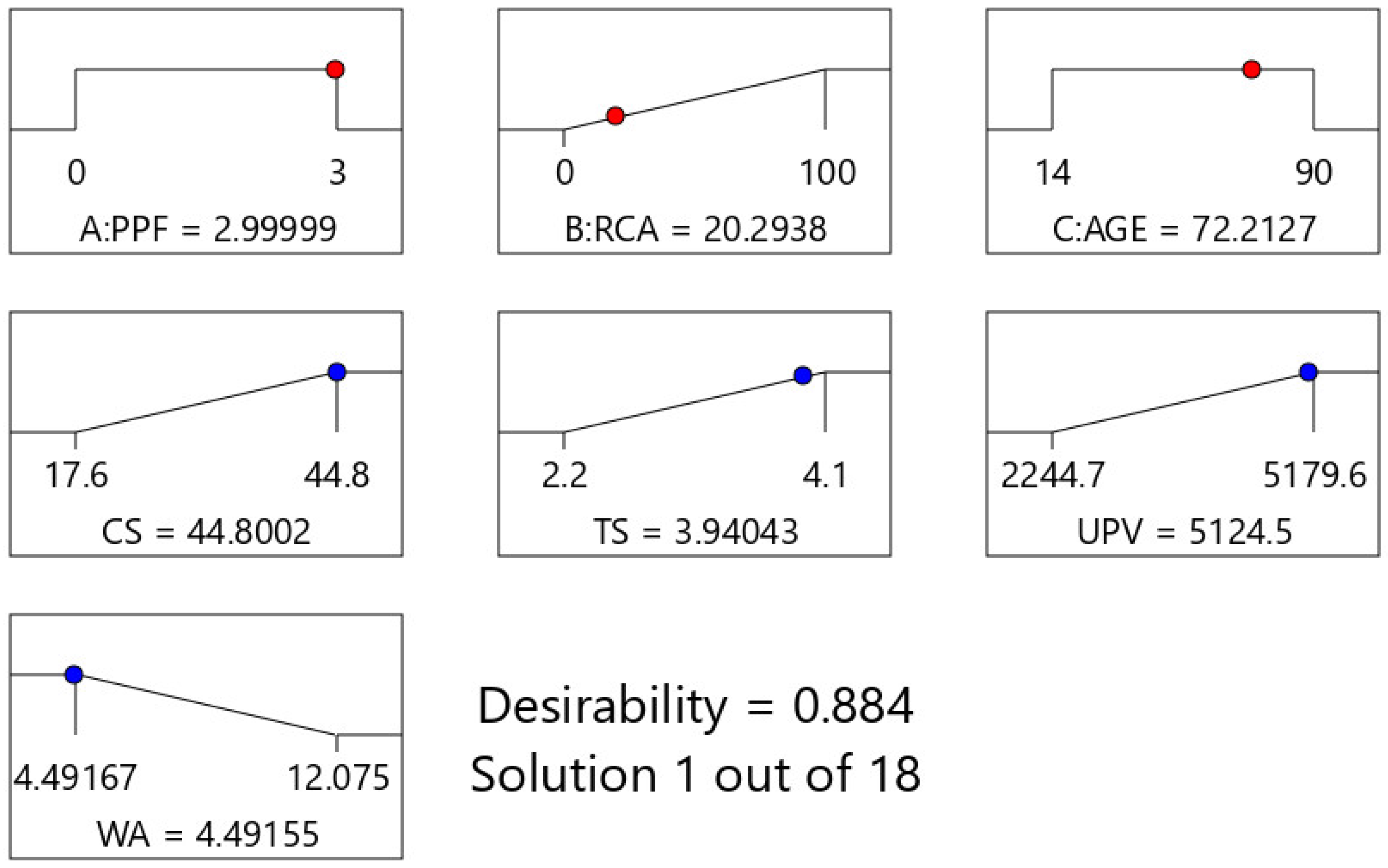
3.3. Optimization of Engineering Properties of Concrete by RSM
4. Discussion
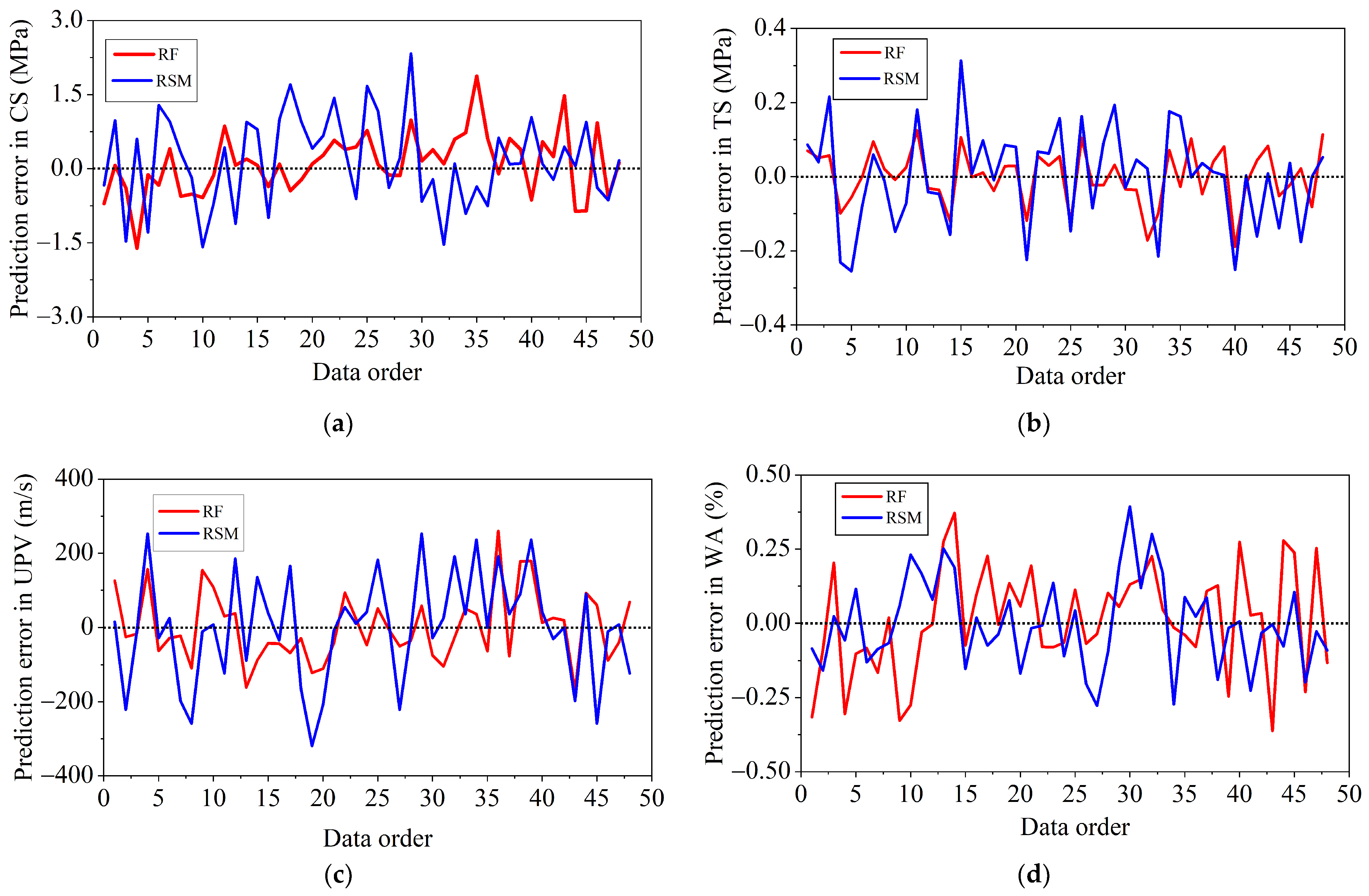
4.1. Comparison of RSM and Machine Learning
4.2. Comparison of Developed Models and Previously Developed Models
4.3. Practical Implications
5. Conclusions
- Increasing the RCA ratio resulted in decreased CS, TS, and UPV while increasing WA. Conversely, the inclusion of PPF improved CS, TS, and UPV, and decreased WA. Additionally, as the concrete age increased, the WA of RCA-concrete decreased.
- The regression models developed for predicting the engineering characteristics of RCA-concrete containing PPF exhibited R2 values of 0.9803, 0.9234, 0.9569, and 0.9943 for CS, TS, UPV, and WA, respectively. These models demonstrated adequate precision (64.781, 37.540, 54.238, and 125.86) and p-values below 0.05, indicating a high level of correlation.
- The optimal conditions for all responses were achieved at a PPF of 3% by volume of concrete, an AGE of 83.6 days, and a near-maximum RCA value of 100%, highlighting optimal reuse of recycled aggregate with an overall desirability of 0.882.
- The ML model established a strong correlation between the experimental and predicted data, with R2 values ranging between 0.9690 and 0.9959, extremely near unity, indicating high power of the prediction models, and the developed models accurately represent the trend in the dataset.
- Based on RF models’ results, MAPE values for CS, TS, UPV, and WA were (1.46, 2.01, 1.95, and 1.7%) for the train dataset, and (2.53, 2.23, 2.74, and 2.51%) for the test dataset. This means that all the prediction models had error rates of less than 5%.
- The SHAP analyses demonstrate that curing age is the dominant factor influencing CS, UPV, and WA, demonstrating its critical role in microstructural development. In contrast, TS is primarily governed by RCA and PPF content. These distinct feature importance patterns underscore the need for property-specific optimization strategies when designing sustainable concrete containing recycled materials.
- This study developed a robust and accurate predictive tool for engineers and researchers. The RF model and QM from RSM can be utilized to optimize sustainable concrete mix designs containing RCA and PPF without the immediate need for extensive laboratory trials. This accelerates the mix design process, reduces material costs, and promotes the wider adoption of sustainable construction practices.
- The predictive models developed in this study are validated for their high accuracy within the experimental range of the utilized dataset.
6. Limitations and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RCA | recycled coarse aggregate |
| PPF | polypropylene fiber |
| ML | machine learning |
| RSM | response surface methodology |
| RF | random forest |
| ANOVA | analysis of variance |
| ITZ | interfacial transition zone |
| CCD | central composite design |
| NCA | natural coarse aggregate |
| RA | recycled aggregate |
| AGE | concrete age |
| CS | compressive strength |
| TS | tensile strength |
| UPV | ultrasonic pulse velocity |
| WA | water absorption |
| R | Pearson correlation coefficient |
| R2 | coefficient of determination |
| MAPE | mean absolute percentage error |
| D | overall desirability D |
| QM | quadratic model |
| KCV | K-fold Cross Validation |
Appendix A
| Response | Source | Sum of Squares | df | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|---|
| Compressive Strength (CS) | Model | 1868.68 | 8 | 233.59 | 242.05 | <0.0001 | significant |
| A-PPF | 256.01 | 1 | 256.01 | 265.28 | <0.0001 | ||
| B-RCA | 649.79 | 1 | 649.79 | 673.33 | <0.0001 | ||
| C-Age | 919.7 | 1 | 919.7 | 953.01 | <0.0001 | ||
| AB | 4.43 | 1 | 4.43 | 4.6 | 0.0384 | ||
| AC | 17.17 | 1 | 17.17 | 17.79 | 0.0001 | ||
| BC | 19.85 | 1 | 19.85 | 20.57 | <0.0001 | ||
| A2 | 10.83 | 1 | 10.83 | 11.22 | 0.0018 | ||
| C2 | 284.41 | 1 | 284.41 | 294.71 | <0.0001 | ||
| Residual | 37.64 | 39 | 0.965 | ||||
| Cor Total | 1906.32 | 47 | |||||
| Tensile Strength (TS) | Model | 10.03 | 6 | 1.67 | 82.4 | <0.0001 | significant |
| A-PPF | 2.9 | 1 | 2.9 | 143.13 | <0.0001 | ||
| B-RCA | 6.04 | 1 | 6.04 | 297.95 | <0.0001 | ||
| C-AGE | 1.1 | 1 | 1.1 | 54.19 | <0.0001 | ||
| AC | 0.1122 | 1 | 0.1122 | 5.53 | 0.0235 | ||
| BC | 0.115 | 1 | 0.115 | 5.67 | 0.022 | ||
| C2 | 0.1001 | 1 | 0.1001 | 4.94 | 0.0319 | ||
| Residual | 0.8315 | 41 | 0.0203 | ||||
| Cor Total | 10.86 | 47 | |||||
| Ultrasonic Pulse Velocity (UPV) | Model | 2.18 × 107 | 5 | 4.36 × 106 | 186.72 | <0.0001 | significant |
| A-PPF | 6.57 × 106 | 1 | 6.57 × 106 | 281.23 | <0.0001 | ||
| B-RCA | 1.16 × 107 | 1 | 1.16 × 107 | 495.93 | <0.0001 | ||
| C-AGE | 2.88 × 106 | 1 | 2.88 × 106 | 123.33 | <0.0001 | ||
| B2 | 7.44 × 104 | 1 | 7.44 × 104 | 3.19 | 0.0815 | ||
| C2 | 1.22 × 106 | 1 | 1.22 × 106 | 52.24 | <0.0001 | ||
| Residual | 9.81 × 105 | 42 | 23.4 × 103 | ||||
| Cor Total | 2.28 × 107 | 47 | |||||
| Water Absorption (WA) | Model | 185.21 | 6 | 30.87 | 1191.77 | <0.0001 | significant |
| A-PPF | 25.69 | 1 | 25.69 | 991.71 | <0.0001 | ||
| B-RCA | 20.57 | 1 | 20.57 | 794.28 | <0.0001 | ||
| C-AGE | 121.78 | 1 | 121.78 | 4701.78 | <0.0001 | ||
| BC | 1.94 | 1 | 1.94 | 74.72 | <0.0001 | ||
| A2 | 0.6 | 1 | 0.6 | 23.17 | <0.0001 | ||
| C2 | 6.45 | 1 | 6.45 | 248.85 | <0.0001 | ||
| Residual | 1.06 | 41 | 0.0259 | ||||
| Cor Total | 186.27 | 47 |
References
- Alharthai, M.; Ali, T.; Qureshi, M.Z.; Ahmed, H. The Enhancement of Engineering Characteristics in Recycled Aggregates Concrete Combined Effect of Fly Ash, Silica Fume and PP Fiber. Alex. Eng. J. 2024, 95, 363–375. [Google Scholar] [CrossRef]
- Behera, M.; Bhattacharyya, S.K.; Minocha, A.K.; Deoliya, R.; Maiti, S. Recycled Aggregate from C&D Waste & Its Use in Concrete—A Breakthrough towards Sustainability in Construction Sector: A Review. Constr. Build. Mater. 2014, 68, 501–516. [Google Scholar] [CrossRef]
- Tam, V.W.Y.; Soomro, M.; Evangelista, A.C.J. A Review of Recycled Aggregate in Concrete Applications (2000–2017). Constr. Build. Mater. 2018, 172, 272–292. [Google Scholar] [CrossRef]
- Kisku, N.; Joshi, H.; Ansari, M.; Panda, S.K.; Nayak, S.; Dutta, S.C. A Critical Review and Assessment for Usage of Recycled Aggregate as Sustainable Construction Material. Constr. Build. Mater. 2017, 131, 721–740. [Google Scholar] [CrossRef]
- Silva, R.V.; de Brito, J.; Dhir, R.K. Properties and Composition of Recycled Aggregates from Construction and Demolition Waste Suitable for Concrete Production. Constr. Build. Mater. 2014, 65, 201–217. [Google Scholar] [CrossRef]
- Katz, A. Properties of Concrete Made with Recycled Aggregate from Partially Hydrated Old Concrete. Cem. Concr. Res. 2003, 33, 703–711. [Google Scholar] [CrossRef]
- Tam, V.W.Y.; Tam, C.M.; Le, K.N. Removal of Cement Mortar Remains from Recycled Aggregate Using Pre-Soaking Approaches. Resour. Conserv. Recycl. 2007, 50, 82–101. [Google Scholar] [CrossRef]
- Kou, S.; Poon, C.; Agrela, F. Comparisons of Natural and Recycled Aggregate Concretes Prepared with the Addition of Different Mineral Admixtures. Cem. Concr. Compos. 2011, 33, 788–795. [Google Scholar] [CrossRef]
- Kapoor, K.; Singh, S.P.; Singh, B. Durability of Self-Compacting Concrete Made with Recycled Concrete Aggregates and Mineral Admixtures. Constr. Build. Mater. 2016, 128, 67–76. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Y.; Sun, H.; Wu, S. Transient Dynamic Behavior of Polypropylene Fiber Reinforced Mortar under Compressive Impact Loading. Constr. Build. Mater. 2016, 111, 30–42. [Google Scholar] [CrossRef]
- Fallah, S.; Nematzadeh, M. Mechanical Properties and Durability of High-Strength Concrete Containing Macro-Polymeric and Polypropylene Fibers with Nano-Silica and Silica Fume. Constr. Build. Mater. 2017, 132, 170–187. [Google Scholar] [CrossRef]
- Yan, P.; Chen, B.; Afgan, S.; Aminul Haque, M.; Wu, M.; Han, J. Experimental Research on Ductility Enhancement of Ultra-High Performance Concrete Incorporation with Basalt Fibre, Polypropylene Fibre and Glass Fibre. Constr. Build. Mater. 2021, 279, 122489. [Google Scholar] [CrossRef]
- Imran, H.; Al-Abdaly, N.M.; Shamsa, M.H.; Shatnawi, A.; Ibrahim, M.; Ostrowski, K.A. Development of Prediction Model to Predict the CompressiveStrength of Eco-Friendly Concrete Using MultivariatePolynomial Regression Combined with Stepwise Method. Materials 2022, 15, 317. [Google Scholar] [CrossRef]
- Unamba, U.K.; Nwajagu, E.S.; Abutu, J.; Agbo-Anike, O.J. Predictive Model of the Compressive Strength of Concrete Containing Coconut Shell Ash as Partial Replacement of Cement Using Multiple Regression Analysis. Int. J. Innov. Sci. Res. Technol. 2021, 6, 600–608. [Google Scholar]
- Haque, M.; Ray, S.; Mita, A.F.; Mozumder, A.; Karmaker, T.; Akter, S. Prediction and Optimization of Hardened Properties of Concrete Prepared with Granite Dust and Scrapped Copper Wire Using Response Surface Methodology. Heliyon 2024, 10, e24705. [Google Scholar] [CrossRef] [PubMed]
- Patil, S.; Ramesh, B.; Sathish, T.; Saravanan, A. RSM-Based Modelling for Predicting and Optimizing the Rheological and Mechanical Properties of Fibre-Reinforced Laterized Self-Compacting Concrete. Heliyon 2024, 10, e25973. [Google Scholar] [CrossRef]
- Zamir Hashmi, S.R.; Khan, M.I.; Khahro, S.H.; Zaid, O.; Shahid Siddique, M.; Md Yusoff, N.I. Prediction of Strength Properties of Concrete Containing Waste Marble Aggregate and Stone Dust—Modeling and Optimization Using RSM. Materials 2022, 15, 8024. [Google Scholar] [CrossRef]
- Habibi, A.; Ramezanianpour, A.M.; Mahdikhani, M. RSM-Based Optimized Mix Design of Recycled Aggregate Concrete Containing Supplementary Cementitious Materials Based on Waste Generation and Global Warming Potential. Resour. Conserv. Recycl. 2021, 167, 105420. [Google Scholar] [CrossRef]
- Ofuyatan, O.M.; Agbawhe, O.B.; Omole, D.O.; Igwegbe, C.A.; Ighalo, J.O. RSM and ANN Modelling of the Mechanical Properties of Self-Compacting Concrete with Silica Fume and Plastic Waste as Partial Constituent Replacement. Clean. Mater. 2022, 4, 100065. [Google Scholar] [CrossRef]
- Mohammed, N. Characterization of Sustainable Concrete Made from Wastewater Bottle Caps Using a Machine Learning and RSM-CCD: Towards Performance and Optimization. In AToMech1-2023 Supplement; Materials Research Forum LLC: Millersville, PA, USA, 2023; pp. 38–46. [Google Scholar]
- Chong, B.W.; Shi, X. Meta-Analysis on PET Plastic as Concrete Aggregate Using Response Surface Methodology and Regression Analysis. J. Infrastruct. Preserv. Resil. 2023, 4, 2. [Google Scholar] [CrossRef]
- Pereira, F.; Mitchell, T.; Botvinick, M. Machine Learning Classifiers and FMRI: A Tutorial Overview. Neuroimage 2009, 45, S199–S209. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.; Manan, A.; Umar, M.; Mehmood, M.; Onyelowe, K.C.; Arunachalam, K.P. Enhancing Concrete Strength for Sustainability Using a Machine Learning Approach to Improve Mechanical Performance. Sci. Rep. 2025, 15, 23067. [Google Scholar] [CrossRef] [PubMed]
- Manan, A.; Pu, Z.; Majdi, A.; Alattyih, W.; Elagan, S.K.; Ahmad, J. Sustainable Optimization of Concrete Strength Properties Using Artificial Neural Networks: A Focus on Mechanical Performance. Mater. Res. Express 2025, 12, 025504. [Google Scholar] [CrossRef]
- Yuan, X.; Tian, Y.; Ahmad, W.; Ahmad, A.; Usanova, K.I.; Mohamed, A.M.; Khallaf, R. Machine Learning Prediction Models to Evaluate the Strength of Recycled Aggregate Concrete. Materials 2022, 15, 2823. [Google Scholar] [CrossRef]
- Shang, M.; Li, H.; Ahmad, A.; Ahmad, W.; Ostrowski, K.A.; Aslam, F.; Joyklad, P.; Majka, T.M. Predicting the Mechanical Properties of RCA-Based Concrete Using Supervised Machine Learning Algorithms. Materials 2022, 15, 647. [Google Scholar] [CrossRef]
- Alkharisi, M.K.; Dahish, H.A. The Application of Response Surface Methodology and Machine Learning for Predicting the Compressive Strength of Recycled Aggregate Concrete Containing Polypropylene Fibers and Supplementary Cementitious Materials. Sustainability 2025, 17, 2913. [Google Scholar] [CrossRef]
- Roy, T.; Das, P.; Jagirdar, R.; Shhabat, M.; Abdullah, M.S.; Kashem, A.; Rahman, R. Prediction of Mechanical Properties of Eco-Friendly Concrete Using Machine Learning Algorithms and Partial Dependence Plot Analysis. Smart Constr. Sustain. Cities 2025, 3, 2. [Google Scholar] [CrossRef]
- Dhengare, S.; Waghe, U.; Yenurkar, G.; Shyamala, A. A Comprehensive Model for Concrete Strength Prediction Using Advanced Learning Techniques. Discov. Appl. Sci. 2025, 7, 551. [Google Scholar] [CrossRef]
- Yu, L. Strength Properties Prediction of RCA Concrete via Hybrid Regression Framework. J. Eng. Appl. Sci. 2024, 71, 6. [Google Scholar] [CrossRef]
- Al-Shamasneh, A.R.; Mahmoodzadeh, A.; Karim, F.K.; Saidani, T.; Alghamdi, A.; Alnahas, J.; Sulaiman, M. Application of Machine Learning Techniques to Predict the Compressive Strength of Steel Fiber Reinforced Concrete. Sci. Rep. 2025, 15, 30674. [Google Scholar] [CrossRef]
- Tipu, R.K.; Panchal, V.R.; Pandya, K.S. Prediction of Concrete Properties Using Machine Learning Algorithm. J. Phys. Conf. Ser. 2022, 2273, 012016. [Google Scholar] [CrossRef]
- Zhu, Y.; Ahmad, A.; Ahmad, W.; Vatin, N.I.; Mohamed, A.M.; Fathi, D. Predicting the Splitting Tensile Strength of Recycled Aggregate Concrete Using Individual and Ensemble Machine Learning Approaches. Crystals 2022, 12, 569. [Google Scholar] [CrossRef]
- Anaconda Inc. Anaconda Individual Edition, Anaconda Website. Available online: https://www.anaconda.com/products/individual (accessed on 14 January 2025).
- Montgomery, D.C. Design and Analysis of Experiments, 10th ed.; Wiley: Hoboken, NJ, USA, 2019; ISBN 9781118146927. [Google Scholar]
- Junaid, M.; Jiang, C.; Eltwati, A.; Khan, D.; Alamri, M.; Eisa, M.S. Statistical Analysis of Low-Density and High-Density Polyethylene Modified Asphalt Mixes Using the Response Surface Method. Case Stud. Constr. Mater. 2024, 21, e03697. [Google Scholar] [CrossRef]
- Adamu, M.; Trabanpruek, P.; Limwibul, V.; Jongvivatsakul, P.; Iwanami, M.; Likitlersuang, S. Compressive Behavior and Durability Performance of High-Volume Fly-Ash Concrete with Plastic Waste and Graphene Nanoplatelets by Using Response-Surface Methodology. J. Mater. Civ. Eng. 2022, 34, 04022222. [Google Scholar] [CrossRef]
- Mohammed, B.S.; Adamu, M. Mechanical Performance of Roller Compacted Concrete Pavement Containing Crumb Rubber and Nano Silica. Constr. Build. Mater. 2018, 159, 234–251. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Jaglan, A.; Singh, R.R. Recycled Aggregate Concrete Incorporating GGBS and Polypropylene Fibers Using RSM and Machine Learning Techniques. Buildings 2024, 15, 66. [Google Scholar] [CrossRef]








| Reference | Sample Size | Study Target | Used ML Techniques | Input Variables | Main Results |
|---|---|---|---|---|---|
| Khan et al. (2025) [23] | 583 | Predicting compressive strength (CS) and split tensile strength (STS). | Extreme Gradient Boosting (XGBoost), Decision Tree, and K-Nearest Neighbors (KNN) | RCA replacement level (RL), water-to-cement ratio (w/c), aggregate-to-cement ratio (A:C), sand-to-cement ratio (S:C), bulk density of RCA (RCA-D), bulk density of natural aggregate (NA-D), RCA particle size (RCA-S), natural aggregate size (NA-S), and the age of the concrete | XGBoost demonstrated the best performance, achieving test R2 values of 0.86 for CS and 0.88 for STS, with RMSEs of 8.32 MPa and 0.55 MPa, respectively |
| Manan et al. (2025) [24] | 358 data points | Predict compressive strength (CS), tensile strength (TS), and modulus of elasticity (MOE) of recycled aggregate concrete (RAC) | Artificial Neural Network (ANN) with K-fold cross-validation and SHAP analysis | RCA replacement level (RL), Water-to-cement ratio (W/C), Aggregate-to-cement ratio (A:C), Sand-to-cement ratio (S:C), Cement content (C), Bulk density of RCA (RCA-D), Bulk density of NA (NA-D), RCA aggregate size (RCA-S) | Training R2: Fc: 0.93, STS: 0.92, MOE: 0.99 Testing R2: Fc: 0.75, STS: 0.78, MOE: 0.67 SHAP analysis: Cement content and natural aggregate density (NA-D) were most influential for compressive strength; NA-D and RCA-D for tensile strength and MOE Model validated with K-fold cross-validation; moderate overfitting observed in testing |
| Shang et al. (2022) [26] | 344 data points | Predict compressive strength (CS) and splitting tensile strength (STS) of recycled coarse aggregate (RCA) concrete | Decision Tree (DT), AdaBoost (Ensemble) | Cement, Water, Fine aggregate, Natural coarse aggregate (NCA), RCA, Superplasticizers (SP), Maximum size of RCA, Density of RCA, Water absorption of RCA | AdaBoost: CS: R2 = 0.95, STS: R2 = 0.92 Decision Tree: CS: R2 = 0.93, STS: R2 = 0.90 AdaBoost showed lower errors (MAE, MSE, RMSE) than DT Sensitivity analysis: Cement was most influential for CS (36.8%) and STS (41.2%) |
| Alkharisi & Dahish (2025) [27] | 529 data points | Compressive strength of recycled aggregate concrete with PPF, FA, and SF | RSM (CCD), M5P, Random Forest (RF), XGBoost | Cement, NFA, NCA, RA, FA, SF, PPF, W/C, SP, AGE | XGBoost performed best: R2 = 0.979 (train), 0.9485 (test), MAE = 1.149 MPa, RMSE = 2.324 MPa, MAPE = 3.19%; optimal mix: 100% RA, 1.13% PPF, 7.9% FA, 5.3% SF |
| Roy et al. (2025) [28] | 480 (CS), 110 (STS) | CS and STS of RHA concrete | GPR, RFR, DTR | Age, Cement, RHA, Coarse Aggregate, Sand, Water, Superplasticizer | DTR best: CS R2 = 0.9646, STS R2 = 0.9691 |
| Dhengare et al. (2025) [29] | 500 samples | Compressive/tensile strength of sustainable concrete | PCA + CNN + RFR + SVR (Hybrid) | Cement, aggregates, bagasse ash, copper slag, eggshell powder, curing time, etc. | MAE: 2.0 MPa, R2: 0.95 |
| Yu (2024) [30] | 344 samples | Predict CS of High-Performance Concrete (HPC) | Support Vector Regression (SVR) optimized with SMA, ESMA, and AOSMA | Cement, Water, Fine Aggregate, NCA, RCA, SRCA, DRCA, WRCA, Superplasticizer, Chemical Admixtures | The SVR-ESMA hybrid model performed best (Test R2: 0.9894, Test MAE: 0.8506 MPa), significantly outperforming other SVR-optimizer combinations. |
| Al-Shamasneh et al. (2025) [31] | 600 | Predicting CS of steel fiber reinforced concrete (SFRC) | support vector regression (SVR), Gaussian process regression (GPR), random forest regression (RFR), extreme gradient boosting regression (XGBR), artificial neural networks (ANN), and K-nearest neighbors (KNN) | fiber characteristics (type, content, length, diameter), water-to-cement (w/c) ratio, aggregate size, curing time, silica fume, and superplasticizer | Prediction performance was best for GPR as it achieved the highest R2 value of 0.93 and lowest RMSE of 16.54, with XGBR, SVR, and RFR |
| Tipu et al. (2022) [32] | 1133 (CS), 642 (chloride) | Compressive strength & chloride penetration depth | DT, RF, SVR, GBR, ANN + PSO tuning | Cement, slag, fly ash, water, aggregates, superplasticizer, age, exposure conditions | RF & GBR best: R2 = 0.96, RMSE = 3.97–4.03 MPa |
| Zhu et al. (2022) [33] | 166 | Predicting tensile strength (TS) of concrete containing recycled aggregate (RA) | The gene expression programming (GEP), artificial neural network (ANN), and bagging techniques | cement, fine aggregate, natural coarse aggregate (NCA), water, recycled coarse aggregate (RCA), the maximum size of RA, superplasticizers, the density of RA, and water absorption of RA | The bagging model outperformed the GEP and ANN models in terms of performance. |
| PPF (%) | RCA (%) | Age (Days) | CS (MPa) | TS (MPa) | UPV (m/s) | WA (%) | |
|---|---|---|---|---|---|---|---|
| Mean | 1.5 | 56.25 | 44 | 28.5 | 2.9563 | 3633.7 | 8.104 |
| Std. Deviation | 1.1299 | 37.367 | 33.37 | 6.369 | 0.48065 | 696.2 | 1.991 |
| Skewness | 0 | −0.449 | 0.633 | 0.455 | 0.557 | 0.222 | −0.021 |
| Kurtosis | −1.377 | −1.148 | −1.533 | −0.288 | −0.285 | −0.449 | −0.977 |
| Minimum | 0 | 0 | 14 | 17.6 | 2.2 | 2244.7 | 4.49 |
| Maximum | 3 | 100 | 90 | 44.8 | 4.1 | 5179.6 | 12.08 |
| MODEL | R2 | Adjusted R2 | Predicted R2 | Adequate Precision | SD | Mean | CV % |
|---|---|---|---|---|---|---|---|
| Compressive Strength (CS) | 0.9803 | 0.9762 | 0.969 | 64.781 | 0.9824 | 28.5 | 3.45 |
| Tensile Strength (TS) | 0.9234 | 0.9122 | 0.8928 | 37.54 | 0.1424 | 2.96 | 4.82 |
| Ultra-sonic Pulse Velocity (UPV) | 0.9569 | 0.9518 | 0.9441 | 54.238 | 152.82 | 3633.7 | 4.21 |
| Water Absorption (WA) | 0.9943 | 0.9935 | 0.9922 | 125.86 | 0.1609 | 8.1 | 1.99 |
| Hyperparameter | Range | Optimized Values | |||
|---|---|---|---|---|---|
| CS | TS | UPV | WA | ||
| n_estimators | 10–100 | 10 | 19 | 13 | 34 |
| max_depth | 5–20 | 14 | 13 | 6 | 19 |
| min_samples_split | 2–10 | 2 | 2 | 3 | 2 |
| min_samples_leaf | 1–5 | 1 | 1 | 1 | 1 |
| max_features | ‘auto’, ‘sqrt’, ‘log2’ | sqrt | log2 | sqrt | log2 |
| Output | Data Set | R2 | MAPE |
|---|---|---|---|
| CS | Train | 0.9955 | 1.46 |
| Test | 0.9866 | 2.53 | |
| TS | Train | 0.9810 | 2.01 |
| Test | 0.9784 | 2.23 | |
| UPV | Train | 0.9913 | 1.95 |
| Test | 0.9690 | 2.74 | |
| WA | Train | 0.9959 | 1.70 |
| Test | 0.9895 | 2.51 |
| Order | Features | |||||||
|---|---|---|---|---|---|---|---|---|
| CS | TS | UPV | WA | |||||
| 1 | Age | 0.490 | RCA | 0.526 | RCA | 0.518 | Age | 0.638 |
| 2 | RCA | 0.324 | PPF | 0.321 | PPF | 0.315 | PPF | 0.192 |
| 3 | PPF | 0.186 | Age | 0.153 | Age | 0.168 | RCA | 0.171 |
| CS | TS | UPV | WA | |||||
|---|---|---|---|---|---|---|---|---|
| RSM | RF | RSM | RF | RSM | RF | RSM | RF | |
| R2 | 0.9803 | 0.9955 | 0.9234 | 0.9810 | 0.9569 | 0.9913 | 0.9943 | 0.9959 |
| MAPE (%) | 2.77 | 1.46 | 3.55 | 2.01 | 3.16 | 1.95 | 1.91 | 1.7 |
| Model | RF | Gradient Boosting Machine [40] | Stacked Ensemble Learning [40] | XGBoost [27] | M5P [27] |
|---|---|---|---|---|---|
| R2 | 0.9866 | 0.98961 | 0.95443 | 0.94854 | 0.8949 |
| Model | RF | Gradient Boosting Machine [40] | Stacked Ensemble Learning [40] | XGBoost [27] | M5P [27] |
|---|---|---|---|---|---|
| MAPE (%) | 2.53 | 5.49104 | 5.50887 | 6.45328 | 12.3862 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dahish, H.A.; Alkharisi, M.K. Predicting the Properties of Polypropylene Fiber Recycled Aggregate Concrete Using Response Surface Methodology and Machine Learning. Buildings 2025, 15, 3709. https://doi.org/10.3390/buildings15203709
Dahish HA, Alkharisi MK. Predicting the Properties of Polypropylene Fiber Recycled Aggregate Concrete Using Response Surface Methodology and Machine Learning. Buildings. 2025; 15(20):3709. https://doi.org/10.3390/buildings15203709
Chicago/Turabian StyleDahish, Hany A., and Mohammed K. Alkharisi. 2025. "Predicting the Properties of Polypropylene Fiber Recycled Aggregate Concrete Using Response Surface Methodology and Machine Learning" Buildings 15, no. 20: 3709. https://doi.org/10.3390/buildings15203709
APA StyleDahish, H. A., & Alkharisi, M. K. (2025). Predicting the Properties of Polypropylene Fiber Recycled Aggregate Concrete Using Response Surface Methodology and Machine Learning. Buildings, 15(20), 3709. https://doi.org/10.3390/buildings15203709






