Experimental Study on the Seismic Behavior of CFST Self-Centering Rocking Bridge Piers
Abstract
1. Introduction
2. Experimental Program
2.1. Design of the Specimen
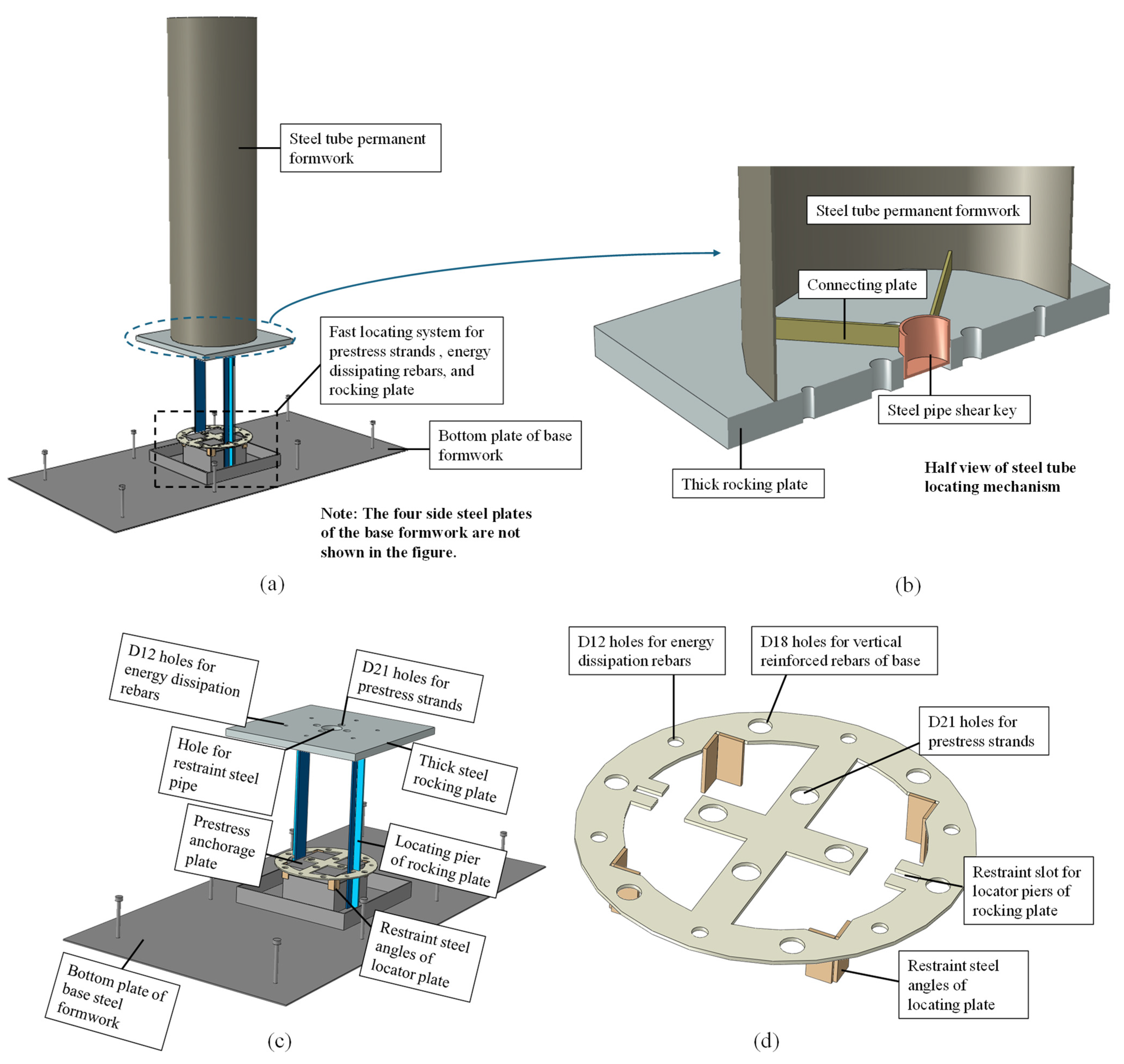
2.2. Fast Construction Design
2.3. Construction of the Specimen
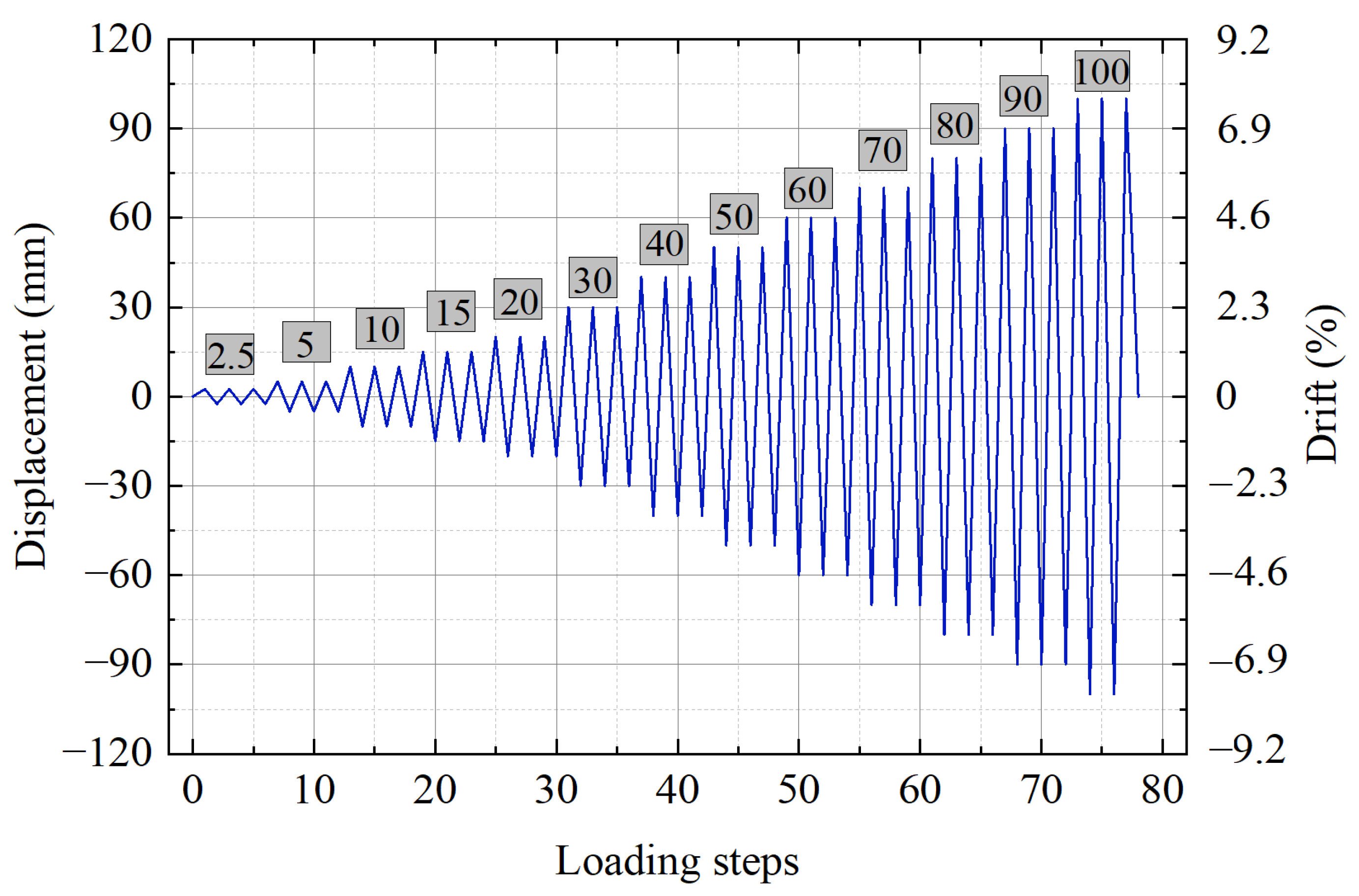
2.4. Experimental Setup and Loading Protocol
3. Experimental Results and Discussion
3.1. Loading Process and Failure Mode
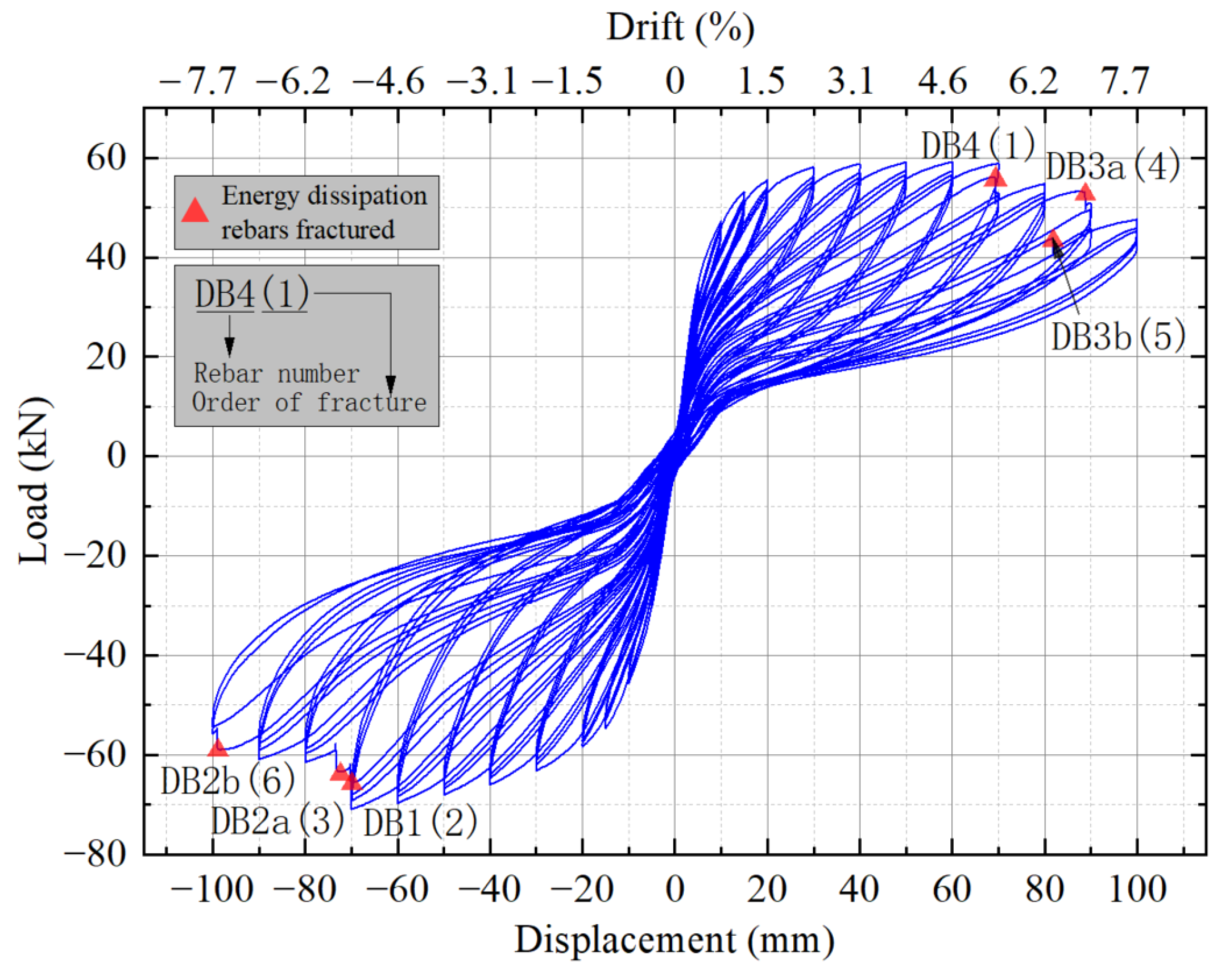
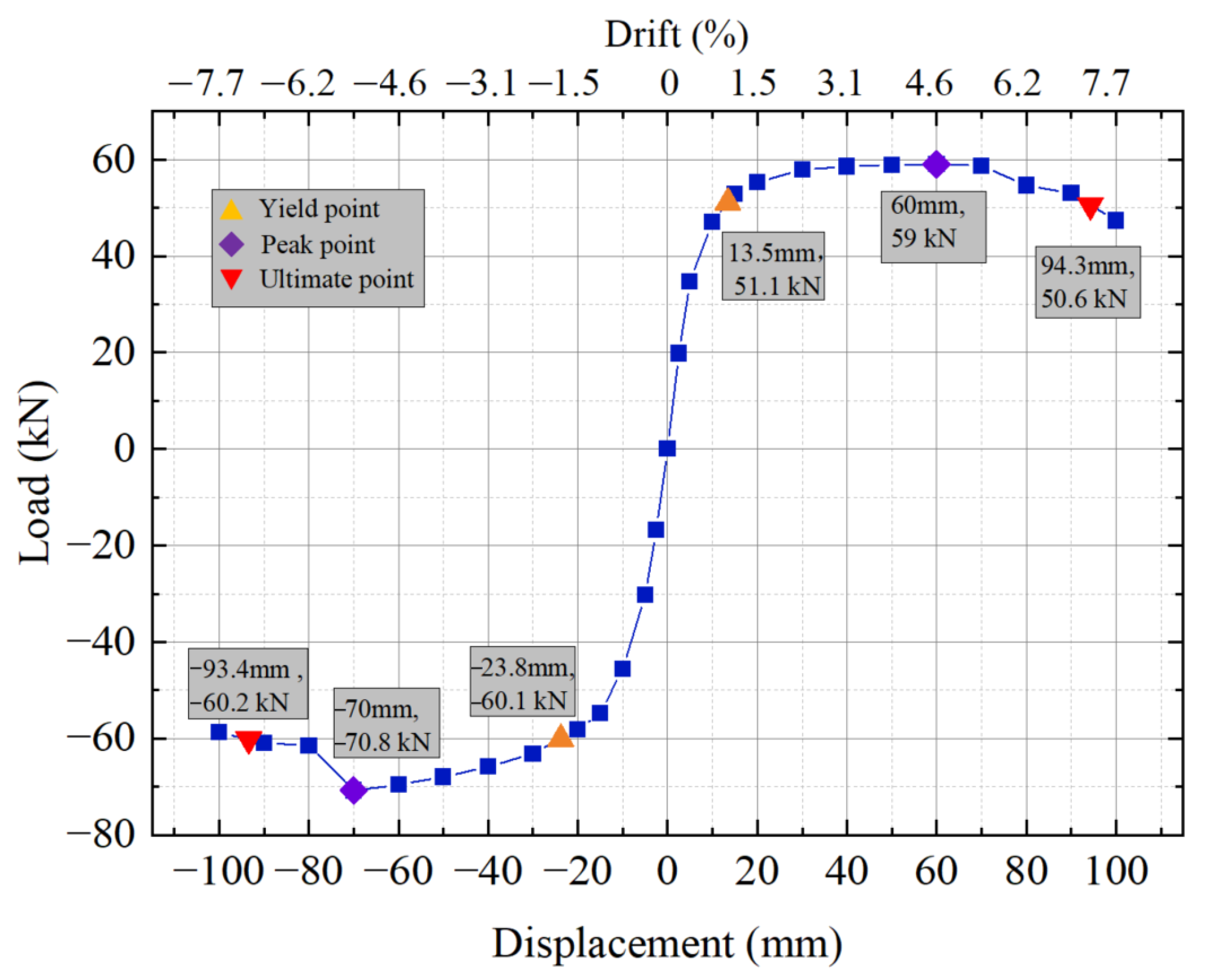
3.2. Hysteresis Behavior
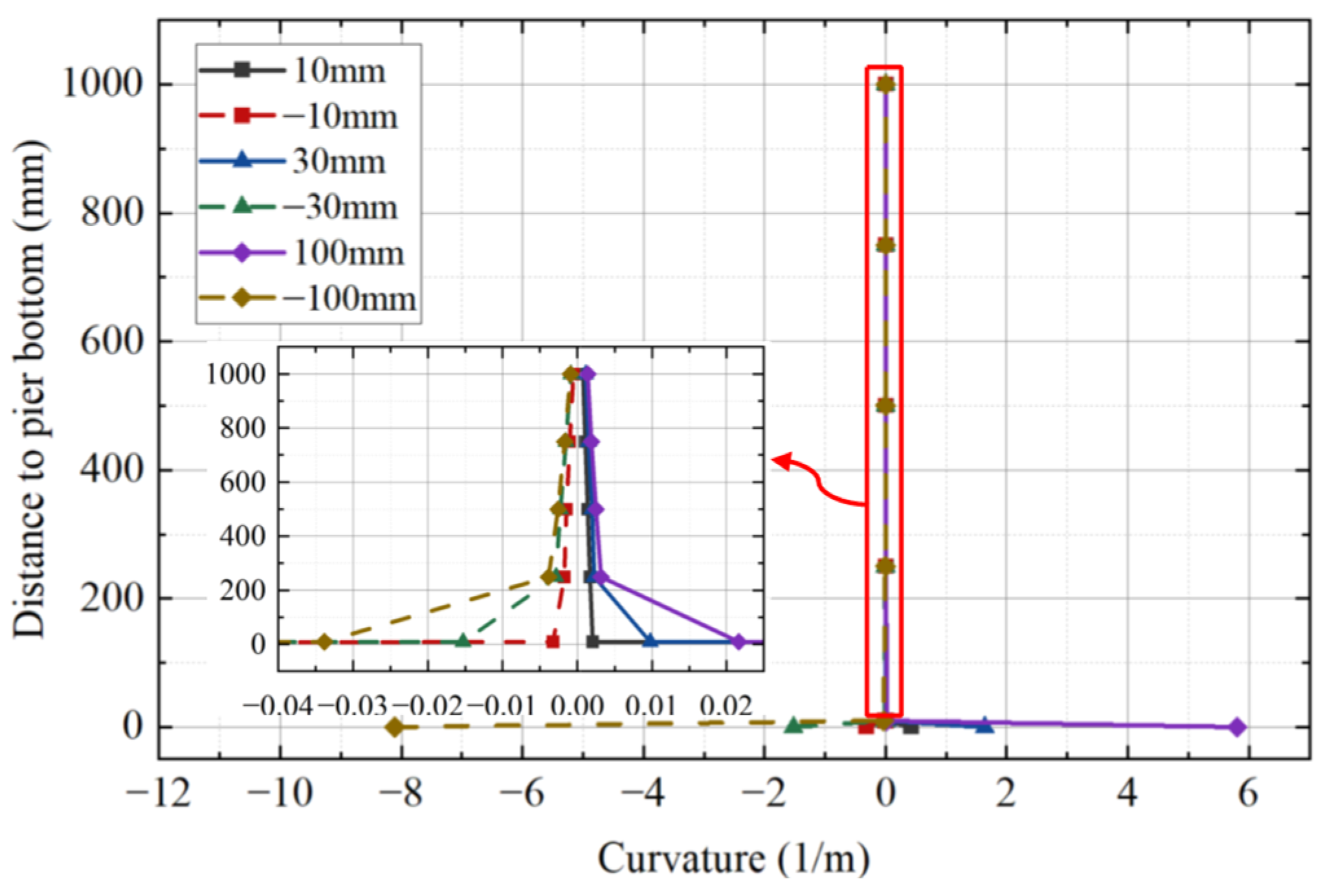
3.3. Curvature Distribution
3.4. Strand Response
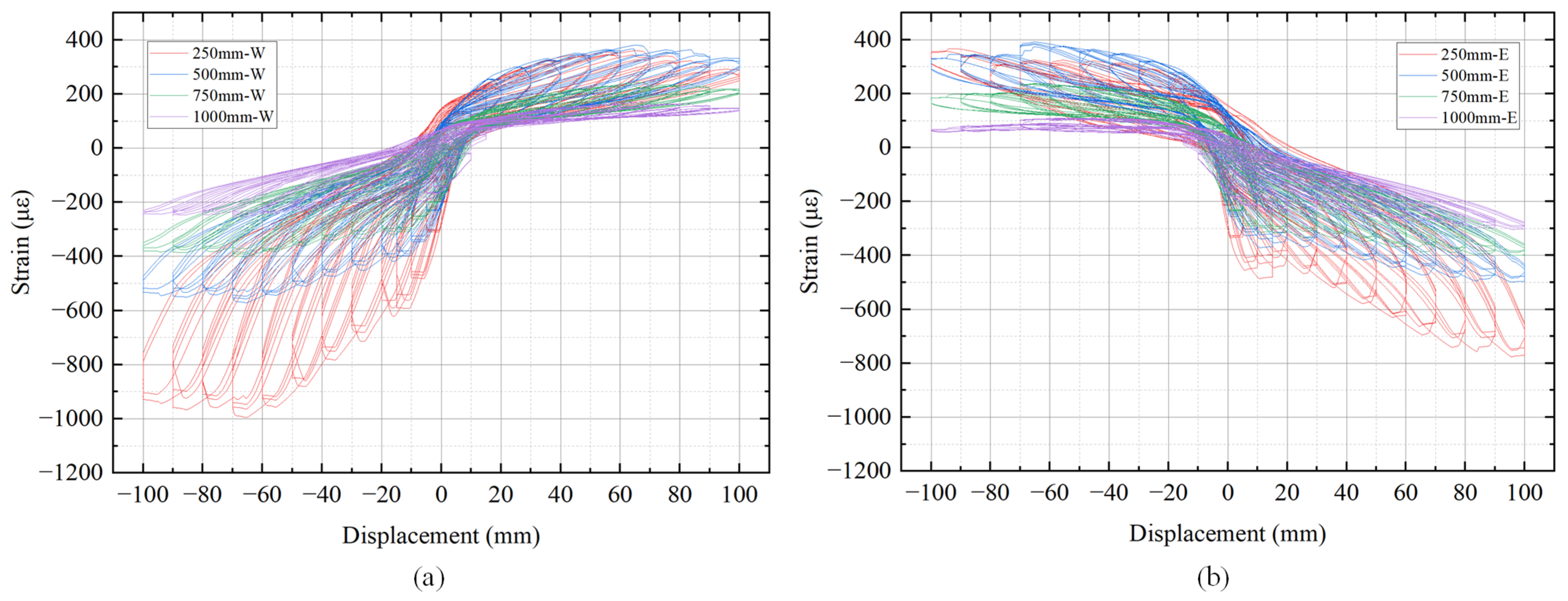
3.5. Strain Response of Steel Tube
4. Conclusions
- (1)
- This study proposed the structural details and a fast construction system for CFST self-centering rocking piers, which are suitable for rapid construction on steep mountainous slopes. Detailed descriptions were provided for the specimen fabrication, installation, loading process, and the placement of the measurement equipment.
- (2)
- During loading, the specimen exhibited stable rocking behavior. At the final level of a 7.7% drift, the buckling of the steel tube at the pier bottom of the specimen was minor, and there was a potential minor crushing of concrete at the compressed edge. All the energy-dissipating rebars fractured. All the prestressing strands were not yielded. A prestress loss was observed, with losses increasing in the tendons positioned further from the neutral axis.
- (3)
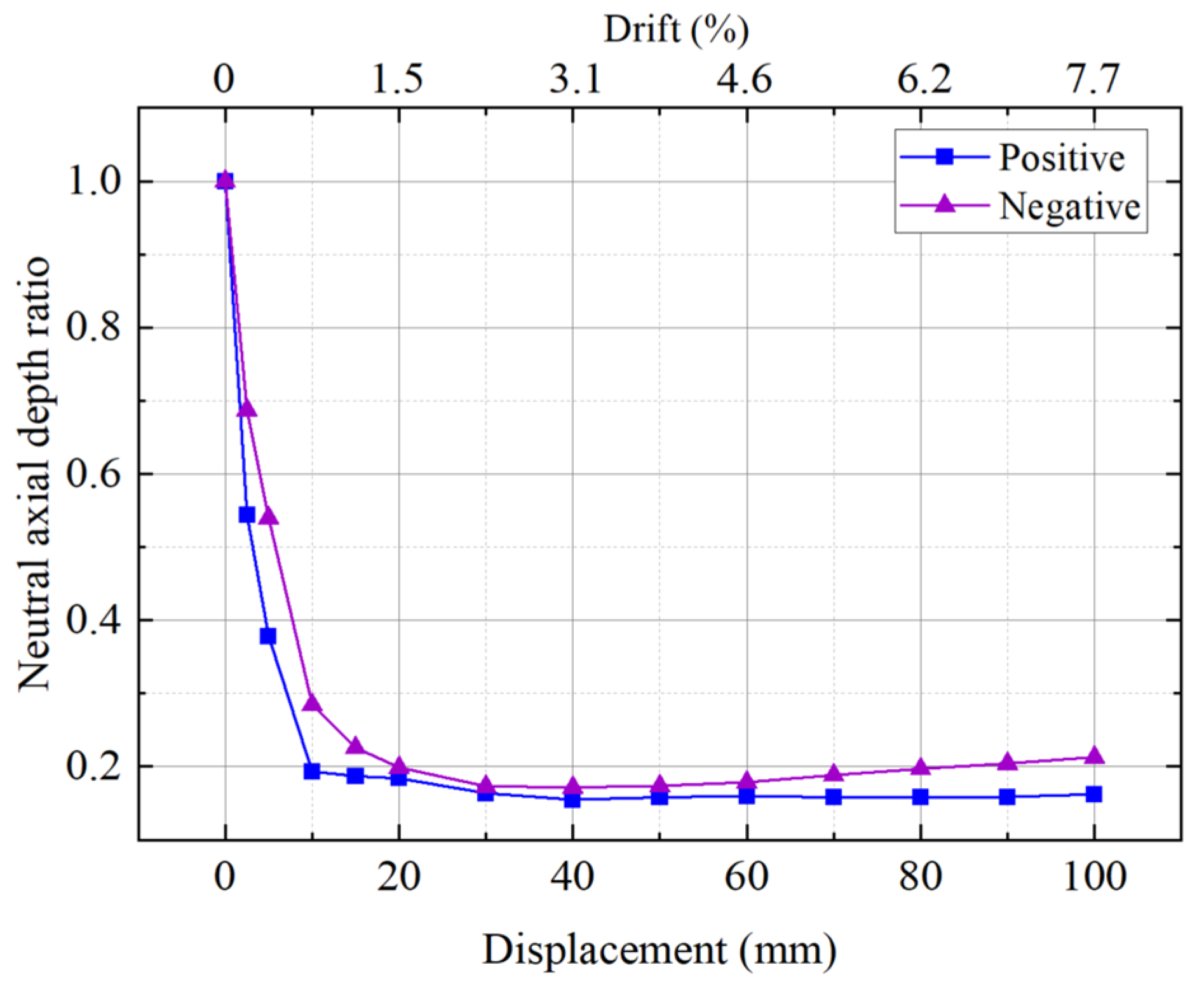
- After yielding, the specimen retained a positive tangent stiffness, maintaining a sufficient load-bearing capacity. After pier rocking, the neutral axis depth ratio at the pier bottom rapidly dropped to below 0.2. The fracture of all the energy-dissipating rebars had a minimal impact on the load-bearing capacity but significantly affected the energy-dissipation capacity.
- (4)
- The specimen’s hysteresis curves showed a prominent flag-shaped behavior. At the 7.7% drift level, the maximum residual drift was 0.17%, indicating excellent self-centering performance.
- (5)
- The cross-sectional curvature distribution along the specimen was extremely nonlinear, with a pronounced concentration at the pier bottom. The rocking gap provided most of the lateral displacement, preventing large deformations in the pier. This design significantly reduced damage to the pier.
Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yuan, W.; Wang, X.; Guo, A.; Li, C.; Dong, Z.; Wu, X. Cyclic performance of RC bridge piers retrofitted with UHPC jackets: Experimental investigation. Eng. Struct. 2022, 259, 114139. [Google Scholar] [CrossRef]
- Bruneau, M. Performance of steel bridges during the 1995 Hyogoken–Nanbu (Kobe, Japan) earthquake—A North American perspective. Eng. Struct. 1998, 20, 1063–1078. [Google Scholar] [CrossRef]
- Ji, Z.; Li, Z.; Zhang, Y.; Gao, M.; Li, T.; Sun, J.; Luo, Q. Long-period ground motion simulation and pulse probability distribution characteristics of the Kumamoto MW 7.1 earthquake in Japan. Earthq. Spectra. 2024, 87552930241276395. [Google Scholar] [CrossRef]
- Ji, Z.; Li, Z.; Zhang, Y.; Quanbo, L.; Sun, J.; Ju, C.; Zhang, Y. Statistical Analysis of Characteristic Parameters and Probability Distribution of Near-Fault Velocity Pulses—A Case Study on the 1999 Mw 7.6 Chi-Chi Earthquake. Seismol. Res. Lett. 2024, 95, 3433–3448. [Google Scholar] [CrossRef]
- Memari, A.M.; Harris, H.G.; Hamid, A.A.; Scanlon, A. Ductility evaluation for typical existing R/C bridge columns in the eastern USA. Eng. Struct. 2005, 27, 203–212. [Google Scholar] [CrossRef]
- Khalaf, S.; Abed, F.; Alhoubi, Y. Flexural behavior of circular concrete filled steel tubes with partially incorporated demolished concrete lumps. Compos. Part C Open Access 2023, 10, 100346. [Google Scholar] [CrossRef]
- Wang, R.; Han, L.-H.; Nie, J.-G.; Zhao, X.-L. Flexural performance of rectangular CFST members. Thin-Walled Struct. 2014, 79, 154–165. [Google Scholar] [CrossRef]
- Kawashima, K. Damage of bridges due to the 2011 Great East Japan Earthquake. J. Jpn. Assoc. Earthq. Eng. 2012, 12, 4_319–4_338. [Google Scholar] [CrossRef]
- Dong, B.; Pan, J.; Cai, J.; Xu, L. Mechanical behaviour of a new ECC-encased CFST column to RC beam connection under cyclic loading. Eng. Struct. 2021, 234, 111915. [Google Scholar] [CrossRef]
- Dong, H.; Han, Q.; Du, X.; Zhou, Y. Review on seismic resilient bridge structures. Adv. Struct. Eng. 2022, 25, 1565–1582. [Google Scholar] [CrossRef]
- Cimellaro, G.P.; Reinhorn, A.M.; Bruneau, M. Seismic resilience of a hospital system. Struct. Infrastruct. Eng. 2010, 6, 127–144. [Google Scholar] [CrossRef]
- Samadian, D.; Ghafory-Ashtiany, M.; Naderpour, H.; Eghbali, M. Seismic resilience evaluation based on vulnerability curves for existing and retrofitted typical RC school buildings. Soil Dyn. Earthq. Eng. 2019, 127, 105844. [Google Scholar] [CrossRef]
- Kolli, S.; Dammala, P.K.; Bhattacharya, S.; Fan, C.; Wang, T.; Cui, L. Offshore wind farms as additional coolant power sources to enhance seismic resilience of nuclear power plants–A case study. Nucl. Eng. Des. 2023, 405, 112204. [Google Scholar] [CrossRef]
- Capacci, L.; Biondini, F.; Frangopol, D.M. Resilience of aging structures and infrastructure systems with emphasis on seismic resilience of bridges and road networks. Resilient Cities Struct. 2022, 1, 23–41. [Google Scholar] [CrossRef]
- Bu, Z.-Y.; Ou, Y.-C.; Song, J.-W.; Zhang, N.-S.; Lee, G.C. Cyclic loading test of unbonded and bonded posttensioned precast segmental bridge columns with circular section. J. Bridge Eng. 2016, 21, 04015043. [Google Scholar] [CrossRef]
- Thonstad, T.; Mantawy, I.M.; Stanton, J.F.; Eberhard, M.O.; Sanders, D.H. Shaking table performance of a new bridge system with pretensioned rocking columns. J. Bridge Eng. 2016, 21, 04015079. [Google Scholar] [CrossRef]
- Mashal, M.; Palermo, A. Low-damage seismic design for accelerated bridge construction. J. Bridge Eng. 2019, 24, 04019066. [Google Scholar] [CrossRef]
- Zhou, Y.-L.; Han, Q.; Du, X.-L.; Jia, Z.-l. Shaking table tests of post-tensioned rocking bridge with double-column bents. J. Bridge Eng. 2019, 24, 04019080. [Google Scholar] [CrossRef]
- El-Hawat, O.; Fatahi, B.; Taciroglu, E. Novel post-tensioned rocking piles for enhancing the seismic resilience of bridges. Earthq. Eng. Struct. Dyn. 2022, 51, 393–417. [Google Scholar] [CrossRef]
- Jafari, A.; Sadeghi, M.; Alaee, F.J.; Bengar, H.A. Determining the optimal layout of energy-dissipating mechanisms for hybrid self-centering walls. In Structures; Elsevier: Amsterdam, The Netherlands, 2024; Volume 60, p. 105854. [Google Scholar]
- Sun, Y.; Cai, G. Seismic behavior of circular concrete columns reinforced by low bond ultrahigh strength rebars. J. Struct. Eng. 2023, 149, 04023126. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, H.; He, J. Seismic behaviors and resilient capacity of CFRP-confined concrete columns with partially debonded high-strength steel rebars. Compos. Struct. 2019, 222, 110912. [Google Scholar] [CrossRef]
- Wang, J.; Sun, Y.; Takeuchi, T.; Koyama, T. Seismic behavior of circular fly ash concrete columns reinforced with low-bond high-strength steel rebar. Structures 2020, 27, 1335–1357. [Google Scholar] [CrossRef]
- Luo, J.; Yuan, S.; Zhao, J.; Sun, Y. Seismic behavior of concrete columns reinforced with weakly bonded ultra-high strength rebars and confined by steel tubes. Materials 2023, 16, 6868. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Wang, W.; Gao, C.; Li, S.; Wang, J.; Qi, J. Shape memory alloy-reinforced UHPC tube confined bridge piers for enhancing the seismic resistance of highway bridges. Eng. Struct. 2024, 302, 117411. [Google Scholar] [CrossRef]
- Li, S.; Wang, J.q.; Alam, M.S. Seismic performance assessment of a multispan continuous isolated highway bridge with superelastic shape memory alloy reinforced piers and restraining devices. Earthq. Eng. Struct. Dyn. 2021, 50, 673–691. [Google Scholar] [CrossRef]
- Billah, A.M.; Alam, M.S. Plastic hinge length of shape memory alloy (SMA) reinforced concrete bridge pier. Eng. Struct. 2016, 117, 321–331. [Google Scholar] [CrossRef]
- Zhou, L.; Alam, M.S. Seismic reliability-based assessment and design optimization of shape memory alloy bars in concrete bridge piers. Eng. Struct. 2025, 322, 119226. [Google Scholar] [CrossRef]
- Raza, S.; Shafei, B.; Saiidi, M.S.; Motavalli, M.; Shahverdi, M. Shape memory alloy reinforcement for strengthening and self-centering of concrete structures—State of the art. Constr. Build. Mater. 2022, 324, 126628. [Google Scholar] [CrossRef]
- Rahmzadeh, A.; Alam, M.S. Feasibility of using superelastic shape memory alloy in plastic hinge regions of steel bridge columns for seismic applications. Earthq. Eng. Struct. Dyn. 2024, 53, 2988–3008. [Google Scholar] [CrossRef]
- Zhang, Y.; Lei, H.; Dong, Z.; Li, T.; Ma, F.; Liu, H.; Deng, M. Cyclic response of precast concrete columns connected with cast-in-place UHPC in plastic hinge region. J. Build. Eng. 2023, 65, 105793. [Google Scholar] [CrossRef]
- Guan, D.; Chen, Z.; Liu, J.; Lin, Z.; Guo, Z. Seismic performance of precast concrete columns with prefabricated UHPC jackets in plastic hinge zone. Eng. Struct. 2021, 245, 112776. [Google Scholar] [CrossRef]
- Ding, Y.; Zeng, B.; Zhou, Z.; Wei, Y.; Zhu, M. Seismic retrofitting of RC columns using stainless steel grid-reinforced UHPC jackets in plastic hinge zone. J. Build. Eng. 2024, 84, 108637. [Google Scholar] [CrossRef]
- Zhou, M.; Song, J.; Yin, S.; Zhu, G.; Lu, W.; Lee, G.C. Cyclic performance of severely earthquake-damaged RC bridge columns repaired using grouted UHPC jacket. Eng. Struct. 2023, 280, 115615. [Google Scholar] [CrossRef]
- Zhang, R.; Zhao, R.; Liu, Z.; Chen, K.; Hu, P.; Liu, Z. Cyclic behavior of existing flexure-dominated RC bridge columns retrofitted by ECC jackets in the region of plastic hinge. Eng. Struct. 2022, 269, 114820. [Google Scholar] [CrossRef]
- Qian, H.; Ye, Y.; Yan, C.; Jin, G.; Li, C.; Shi, Y. Experimental study on the seismic performance of self-centering bridge piers incorporating ECC and superelastic SMA bars in the plastic hinge regions. In Structures; Elsevier: Amsterdam, The Netherlands, 2022; Volume 46, pp. 1955–1967. [Google Scholar]
- Ding, M.; Xu, W.; Wang, J.; Chen, Y.; Fang, R. Analytical study on seismic performance of ECC shell-RC column and its plastic hinge forming mechanism. In Structures; Elsevier: Amsterdam, The Netherlands, 2023; Volume 58, p. 105489. [Google Scholar]
- Li, X.; Chen, K.; Hu, P.; He, W.; Xiao, L.; Zhang, R. Effect of ECC jackets for enhancing the lateral cyclic behavior of RC bridge columns. Eng. Struct. 2020, 219, 110714. [Google Scholar] [CrossRef]
- Di, J.; Fan, J.; Zhou, X.; Zhao, L.; Han, B.; Qin, F.; Zhang, Z. Hysteretic behavior of composite bridge columns with plastic hinge enhanced by engineered cementitious composite jacket for seismic resistance. Eng. Struct. 2022, 251, 113532. [Google Scholar] [CrossRef]
- Ichikawa, S.; Matsuzaki, H.; Moustafa, A.; ElGawady, M.A.; Kawashima, K. Seismic-resistant bridge columns with ultrahigh-performance concrete segments. J. Bridge Eng. 2016, 21, 04016049. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, J.; Li, T.; Deng, M. Mechanical behavior of RC columns strengthened with thin UHPC jacket under cyclic loads. J. Build. Eng. 2022, 49, 104065. [Google Scholar] [CrossRef]
- Meng, Q. Research on efficiency of RC piers seismic strengthened by Precast SFC shell Segments. J. Vib. Shock 2018, 37, 19–27. [Google Scholar]
- Luo, X.; Meng, Q. Numerical Simulation Analysis of Damage Development in RC Bridge Piers with High-Performance Plastic Hinges. J. Southwest Univ. Sci. Technol. 2022, 37, 35–43. [Google Scholar]
- Wang, Z.; Wang, J.-Q.; Tang, Y.-C.; Liu, T.-X.; Gao, Y.-F.; Zhang, J. Seismic behavior of precast segmental UHPC bridge columns with replaceable external cover plates and internal dissipaters. Eng. Struct. 2018, 177, 540–555. [Google Scholar] [CrossRef]
- Nikoukalam, M.; Sideris, P. Resilient bridge rocking columns with polyurethane damage-resistant end segments and replaceable energy-dissipating links. J. Bridge Eng. 2017, 22, 04017064. [Google Scholar] [CrossRef]
- Zhu, Y.; Wu, J.; Zhang, J.; Xie, L.; Wei, Y.; Tong, C. Experimental and theoretical investigations of post-tensioned precast reinforced concrete bridge pier with external replaceable energy dissipaters. Eng. Struct. 2023, 294, 116719. [Google Scholar] [CrossRef]
- Ma, G.; Hou, C.; Hwang, H.-J.; Chen, L.; Zhang, Z. Seismic behavior of repairable columns with UHPC segments and replaceable buckling-restrained energy dissipaters. Eng. Struct. 2024, 300, 117176. [Google Scholar] [CrossRef]
- Zhang, D.; Li, N.; Li, Z.-X. Seismic performance of precast segmental concrete-filled steel-tube bridge columns with internal and external energy dissipaters. J. Bridge Eng. 2021, 26, 04021085. [Google Scholar] [CrossRef]
- Tazarv, M.; Saiid Saiidi, M. Low-damage precast columns for accelerated bridge construction in high seismic zones. J. Bridge Eng. 2016, 21, 04015056. [Google Scholar] [CrossRef]
- Zhang, Q.; Alam, M.S. State-of-the-art review of seismic-resistant precast bridge columns. J. Bridge Eng. 2020, 25, 03120001. [Google Scholar] [CrossRef]
- Tazarv, M.; Saiidi, M.S. UHPC-filled duct connections for accelerated bridge construction of RC columns in high seismic zones. Eng. Struct. 2015, 99, 413–422. [Google Scholar] [CrossRef]
- GB/T 1591-2018; High Strength Low Alloy Structural Steels. Standardization Administration of China: Beijing, China, 2018.
- GB 1499.2-2024; Steel for the Reinforcement of Concrete-Part 2: Hot Rolled Ribbed Bars. Standardization Administration of China: Beijing, China, 2024.
- GB 50010-2010; Code for Design of Concrete Structures. The China Architecture & Building Press: Beijing, China, 2015.
- Park, R. State-of-the-art report: Ductility evaluation from laboratory and analytical testing. In Proceedings of the 9th World Conference on Earthquake Engineering, Kyoto, Japan, 2–9 August 1998. [Google Scholar]
- Specifications for Highway Bridges Part V Seismic Design; Japan Road Association: Tokyo, Japan, 2019.
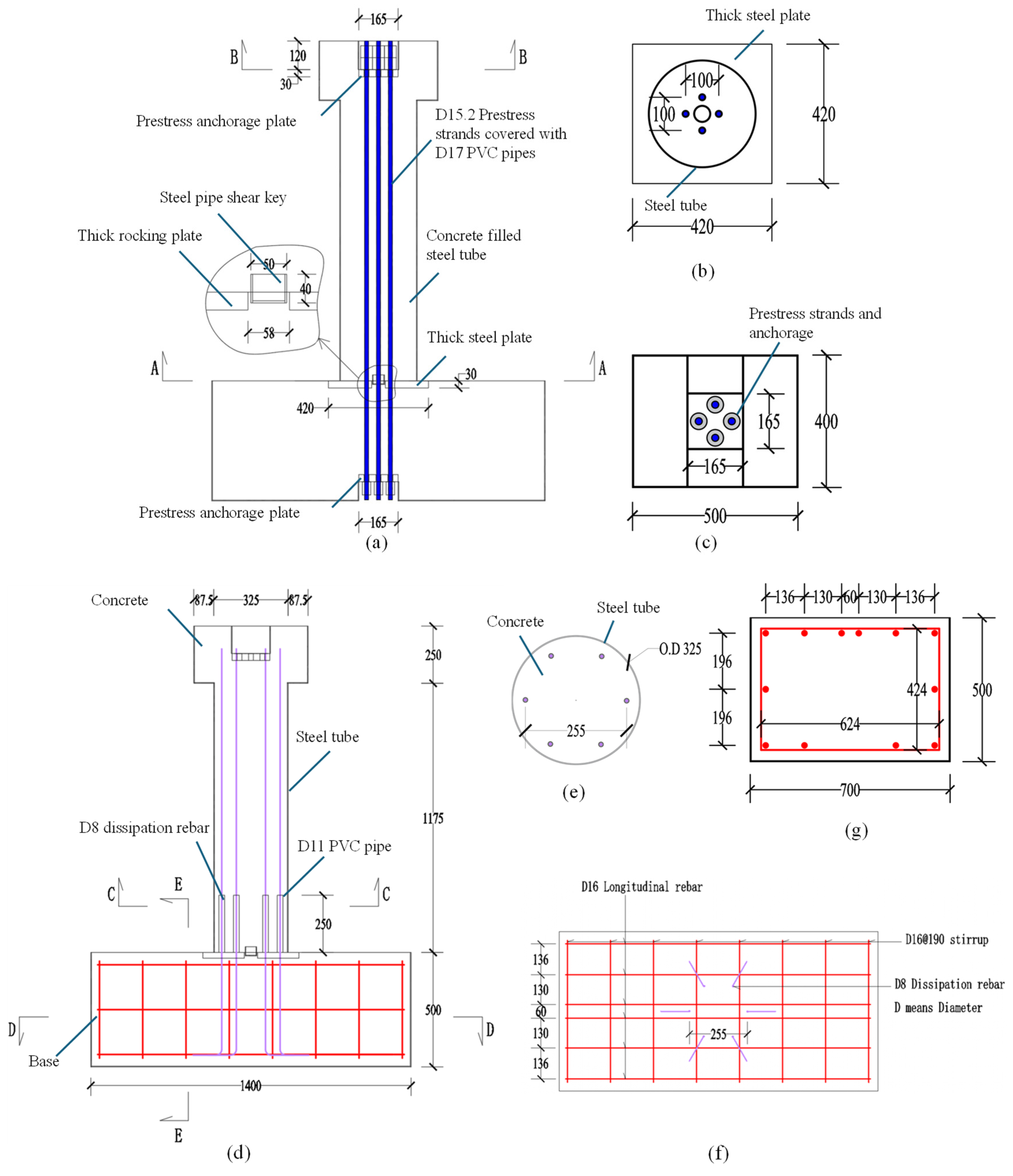














| Item | Yield Strength (MPa) | Ultimate Strength (MPa) | Elongation After Fracture (%) |
|---|---|---|---|
| D16 HRB400E rebars | 448.9 | 637.6 | 24.5 |
| D8 HRB400E rebars | 428.1 | 617.3 | 28.2 |
| D15.2 prestress steel strands | 1836.5 | 2062.5 | 7.5 |
| 3 mm thick Q355 steel plates | 445.4 | 697.9 | 23.6 |
| Item | Details (Unit: mm) |
|---|---|
| Base reinforcement | D16 longitudinal rebar × 12 D16 stirrup × 8 |
| Rocking pier reinforcement | D8 energy dissipation rebar × 6 each covered with a D11 PVC pipe, covering distance of 250 mm, in the pier near the bottom |
| Prestress strands | D15.2 prestress steel strand × 4 full length covered with a D17 PVC pipe for each |
| Strands Number | Strands Area (mm2) | Tensile Force (kN) | Tensile Stress (MPa) |
|---|---|---|---|
| S1 | 140 | 51.95 | 371.08 |
| S2 | 140 | 54.18 | 386.99 |
| S3 | 140 | 51.13 | 365.23 |
| S4 | 140 | 50.55 | 361.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, W.; Zou, Y.; Luo, X.; Song, J.; Li, H. Experimental Study on the Seismic Behavior of CFST Self-Centering Rocking Bridge Piers. Buildings 2025, 15, 267. https://doi.org/10.3390/buildings15020267
Lu W, Zou Y, Luo X, Song J, Li H. Experimental Study on the Seismic Behavior of CFST Self-Centering Rocking Bridge Piers. Buildings. 2025; 15(2):267. https://doi.org/10.3390/buildings15020267
Chicago/Turabian StyleLu, Wei, Yu Zou, Xingyu Luo, Jun Song, and Haiqing Li. 2025. "Experimental Study on the Seismic Behavior of CFST Self-Centering Rocking Bridge Piers" Buildings 15, no. 2: 267. https://doi.org/10.3390/buildings15020267
APA StyleLu, W., Zou, Y., Luo, X., Song, J., & Li, H. (2025). Experimental Study on the Seismic Behavior of CFST Self-Centering Rocking Bridge Piers. Buildings, 15(2), 267. https://doi.org/10.3390/buildings15020267






