Analysis on DDBD Method of Precast Frame with UHPC Composite Beams and HSC Columns
Abstract
1. Introduction
2. Performance Levels and Quantification Index for UHPC-HSC Frame Structure
3. Fundamentals of DDBD
3.1. Determination of Target Displacement
3.2. Equivalent Procedure for MDOF
3.3. Displacement Response Spectrum
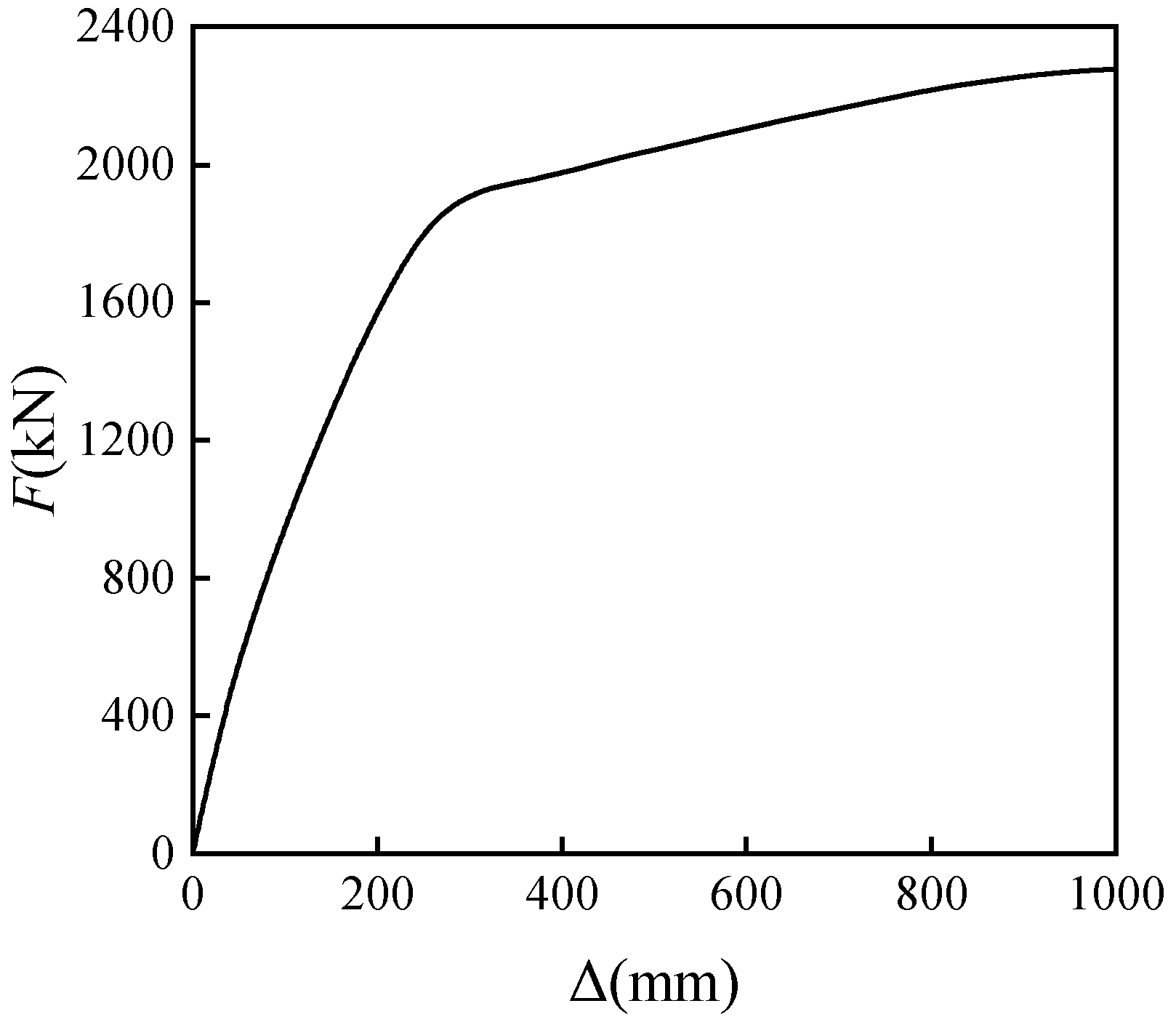
4. Design Procedure for Precast UHPC-HSC Frame Structures Based on DDBD
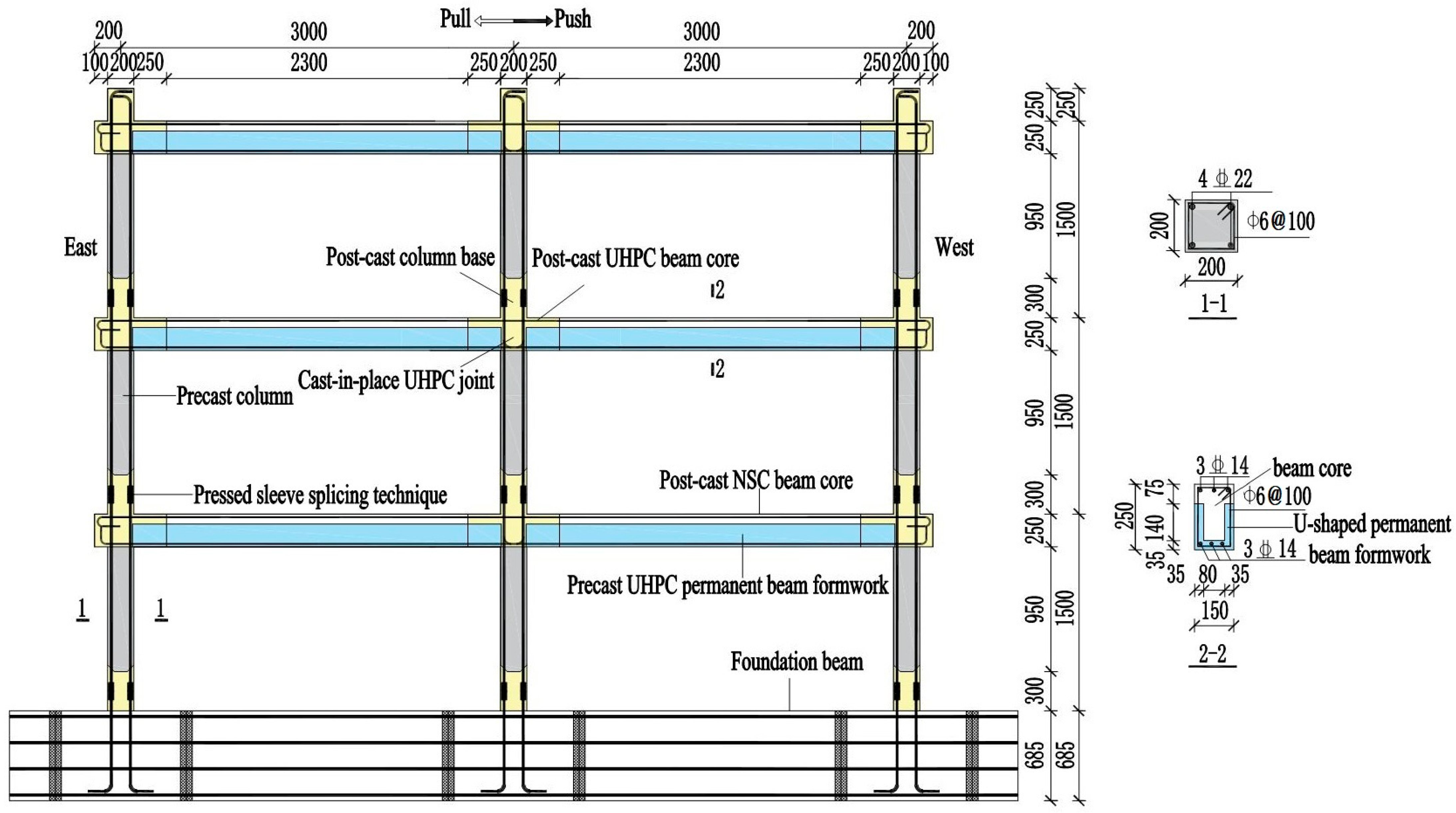
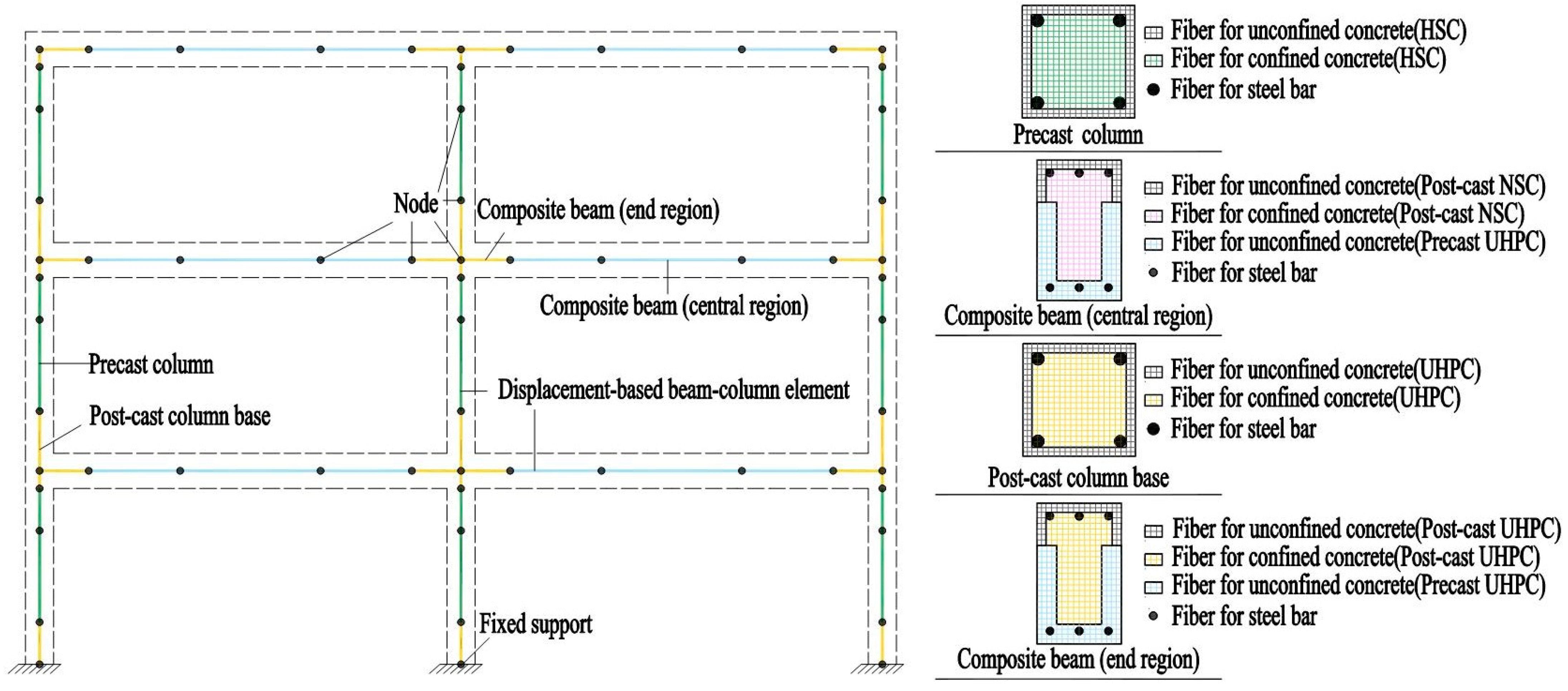
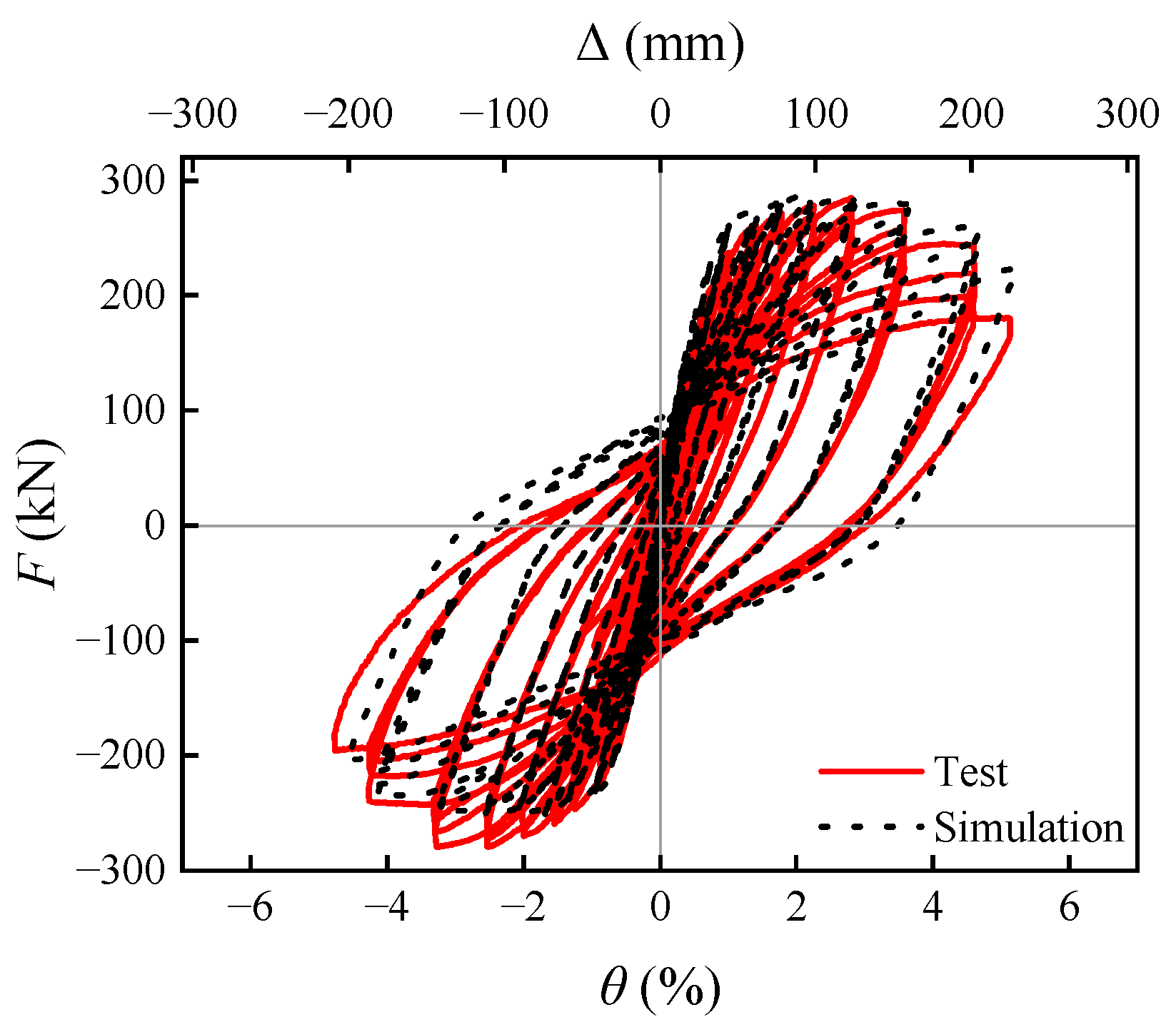
5. Modeling Methodology and Experimental Validation
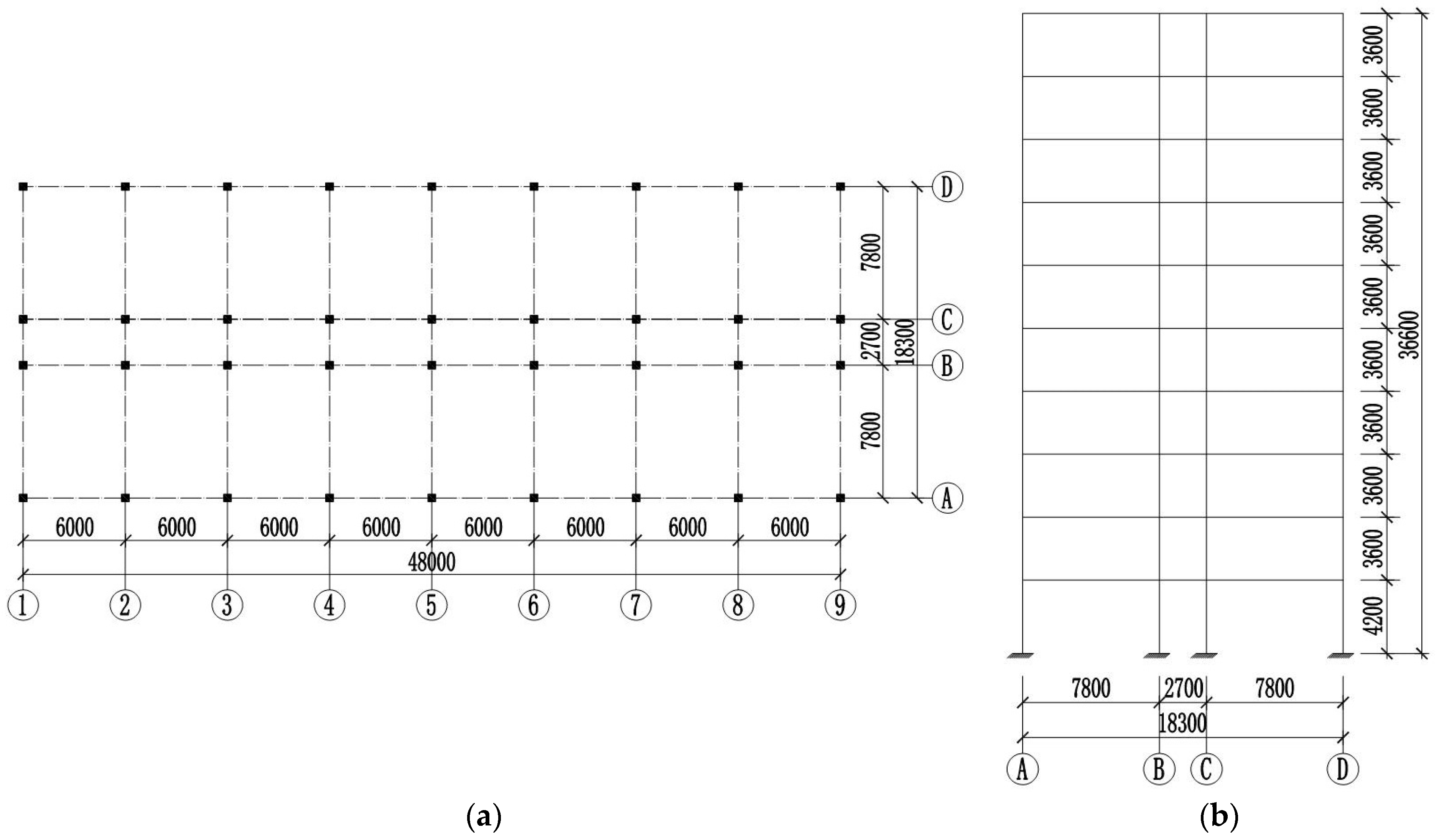
6. Case Study and Analysis of UHPC-HSC Frame Structure
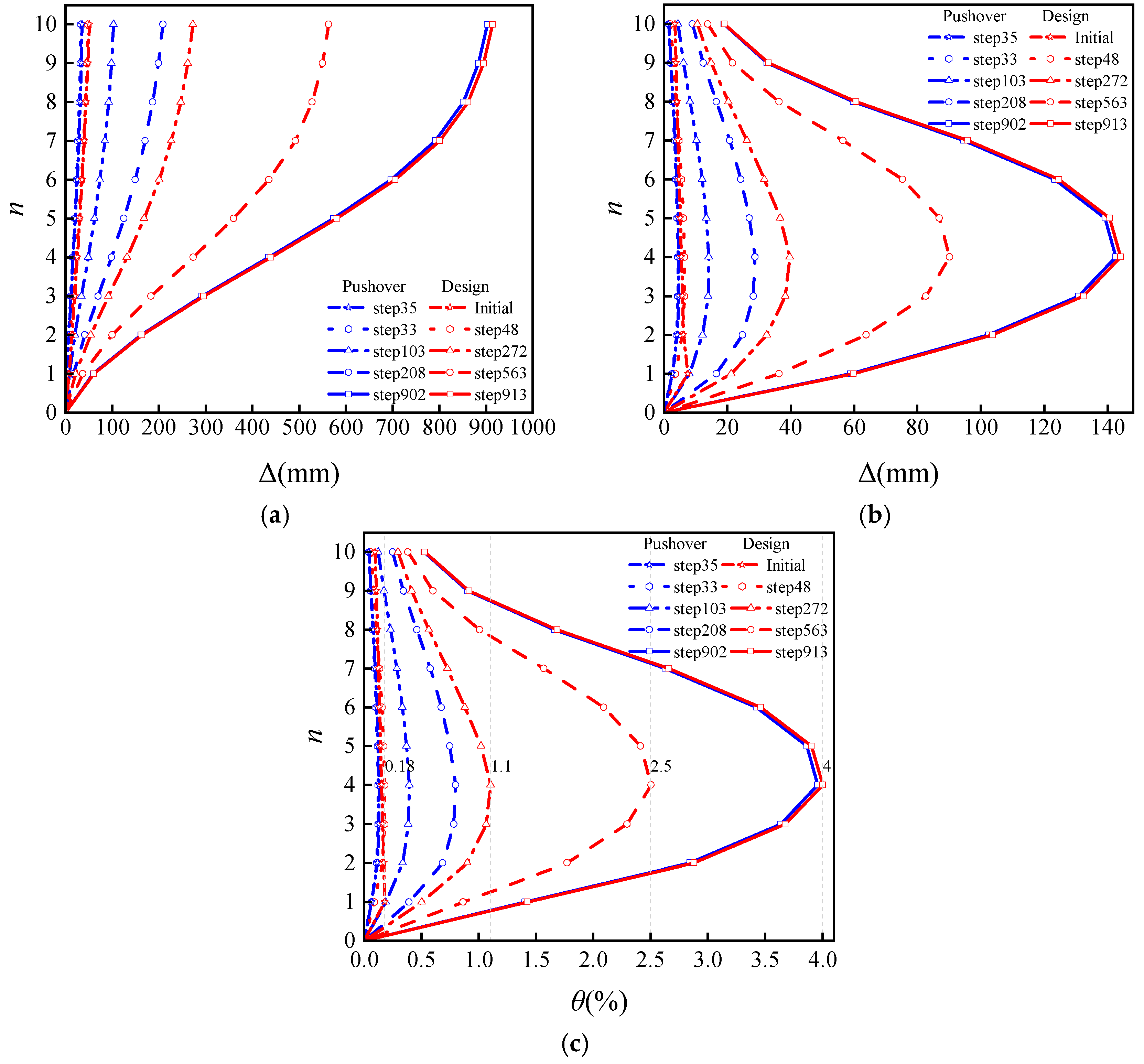
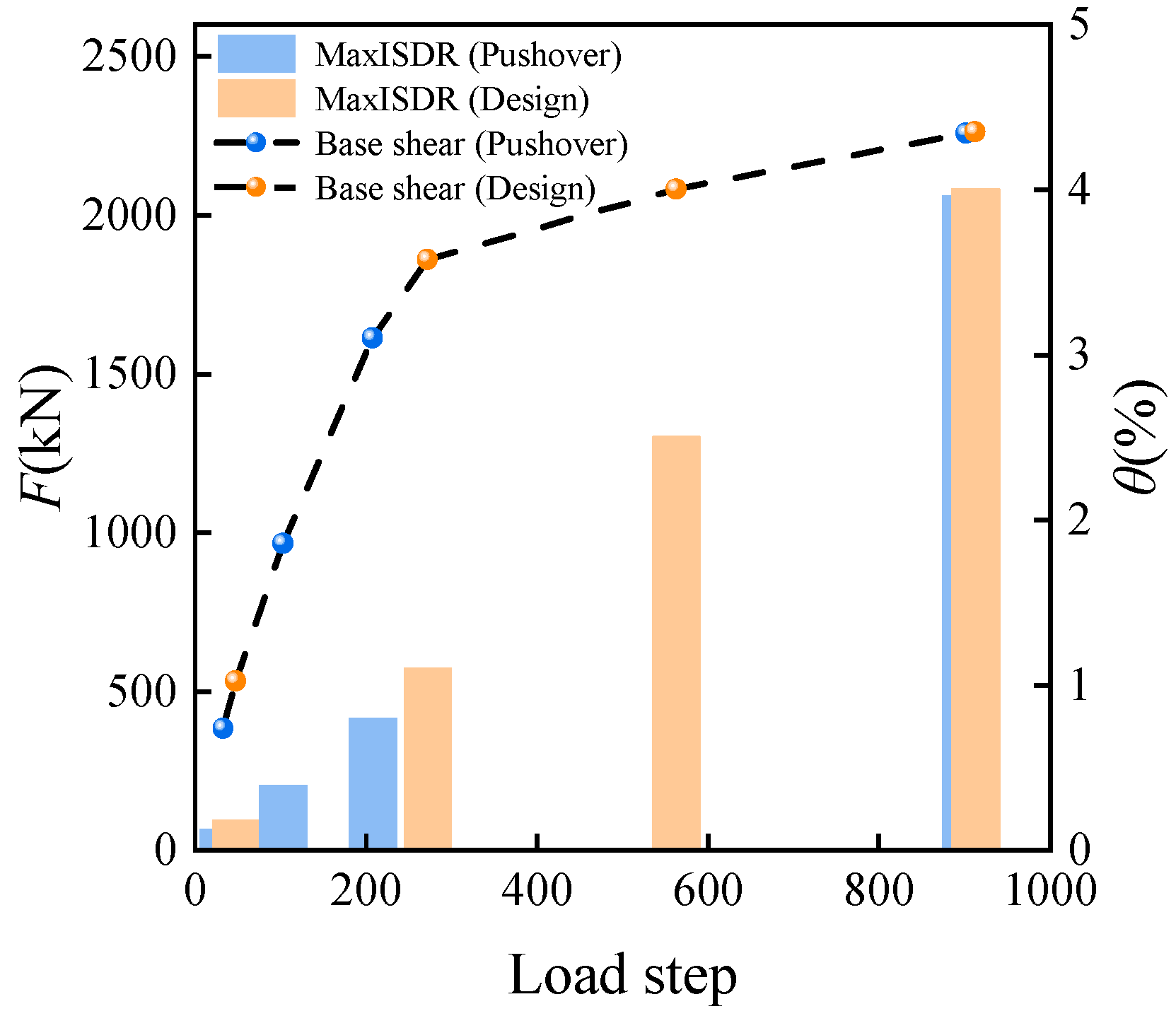
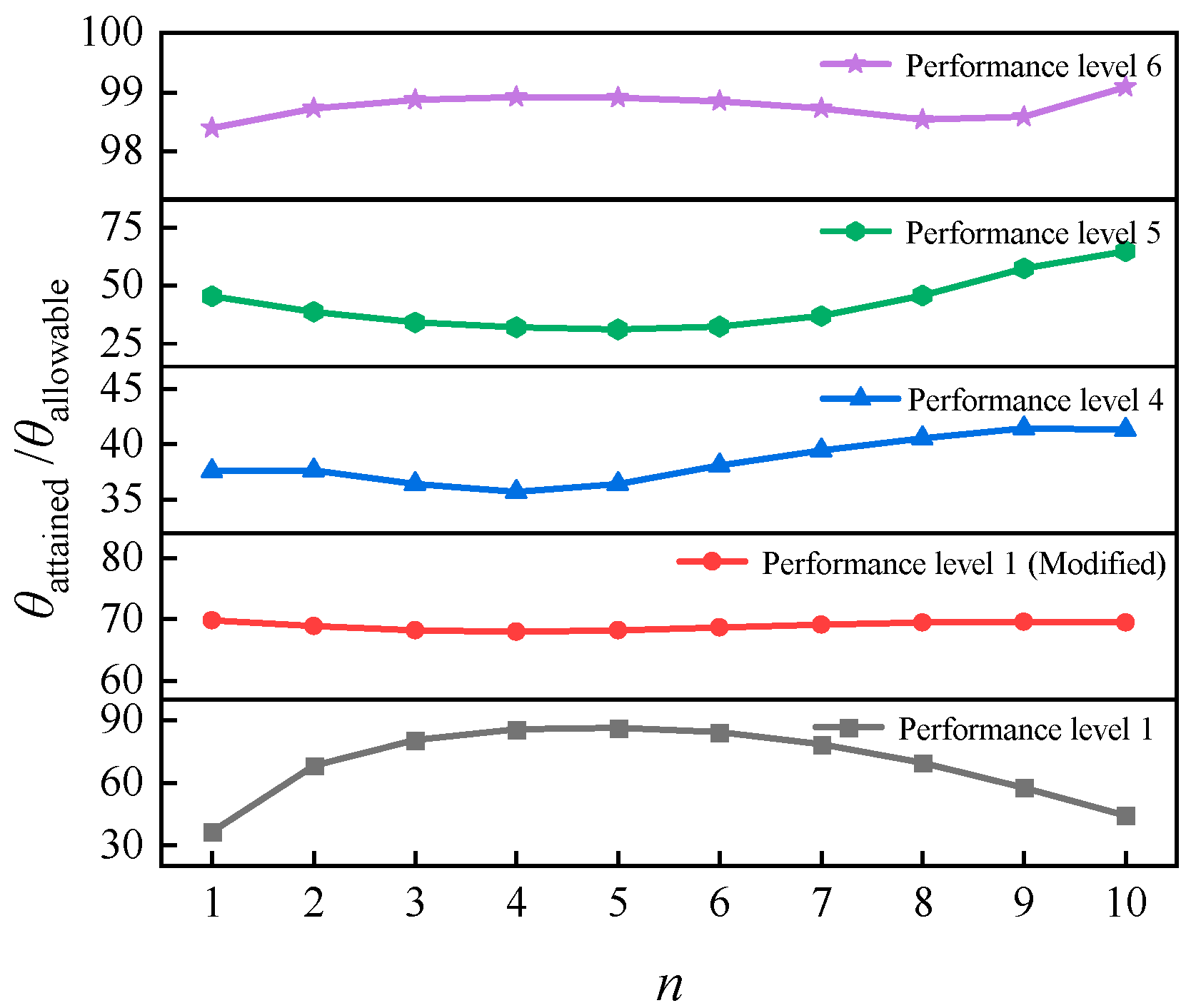
6.1. Designed for “Performance Level 1”
6.2. Verified for “Performance Level 4”
6.3. Verified for “Performance Level 5”
6.4. Verified for “Performance Level 6”
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notation
| Lateral displacement of i mass particle in the MDOF system | |
| Modal shape coefficients of each story | |
| Target displacement of the weak story | |
| Modal shape coefficients of the weak story | |
| Height of the ith story | |
| Total height of the structure | |
| Number of stories | |
| Lateral displacement reduction factor | |
| Lateral displacement shape factor | |
| Function of time | |
| Amplitude | |
| Circular frequency | |
| Acceleration of i mass particle in the MDOF system | |
| Effective displacement of the equivalent SDOF system | |
| Effective acceleration of the equivalent SDOF system | |
| Horizontal seismic action of i mass particle | |
| Base shear | |
| Effective mass of the equivalent SDOF system | |
| Lateral load at the roof story (), at other stories () | |
| Effective height of the equivalent SDOF system | |
| Effective stiffness of the equivalent SDOF system | |
| Effective period of the equivalent SDOF system | |
| Equivalent viscous damping ratio of the equivalent SDOF system | |
| Elastic damping ratio | |
| Hysteretic damping ratio | |
| Design ductility demand | |
| Yield displacement | |
| Yield rotation | |
| Contribution of each beam to the overturning moment ( and are the moment capacity contributions of the exterior and interior beams, respectively.) | |
| Yield strain of steel bar in the beam | |
| Span of the beam ( and are the span of the exterior and interior beams, respectively.) | |
| Depth of the beam ( and are the depth of the exterior and interior beams, respectively.) | |
| Seismic influence coefficient | |
| Natural vibration period () | |
| Peak seismic influence coefficient | |
| Damping modification factor (,when , .) | |
| Damping ratio () | |
| Site-specific characteristic period | |
| Decay exponent for the nonlinear descending segment () | |
| Slope reduction factor for the linear descending segment (, when , .) | |
| θ | Interstory drift ratio (ISDR) |
| [θ] | Limit values of interstory drift ratio |
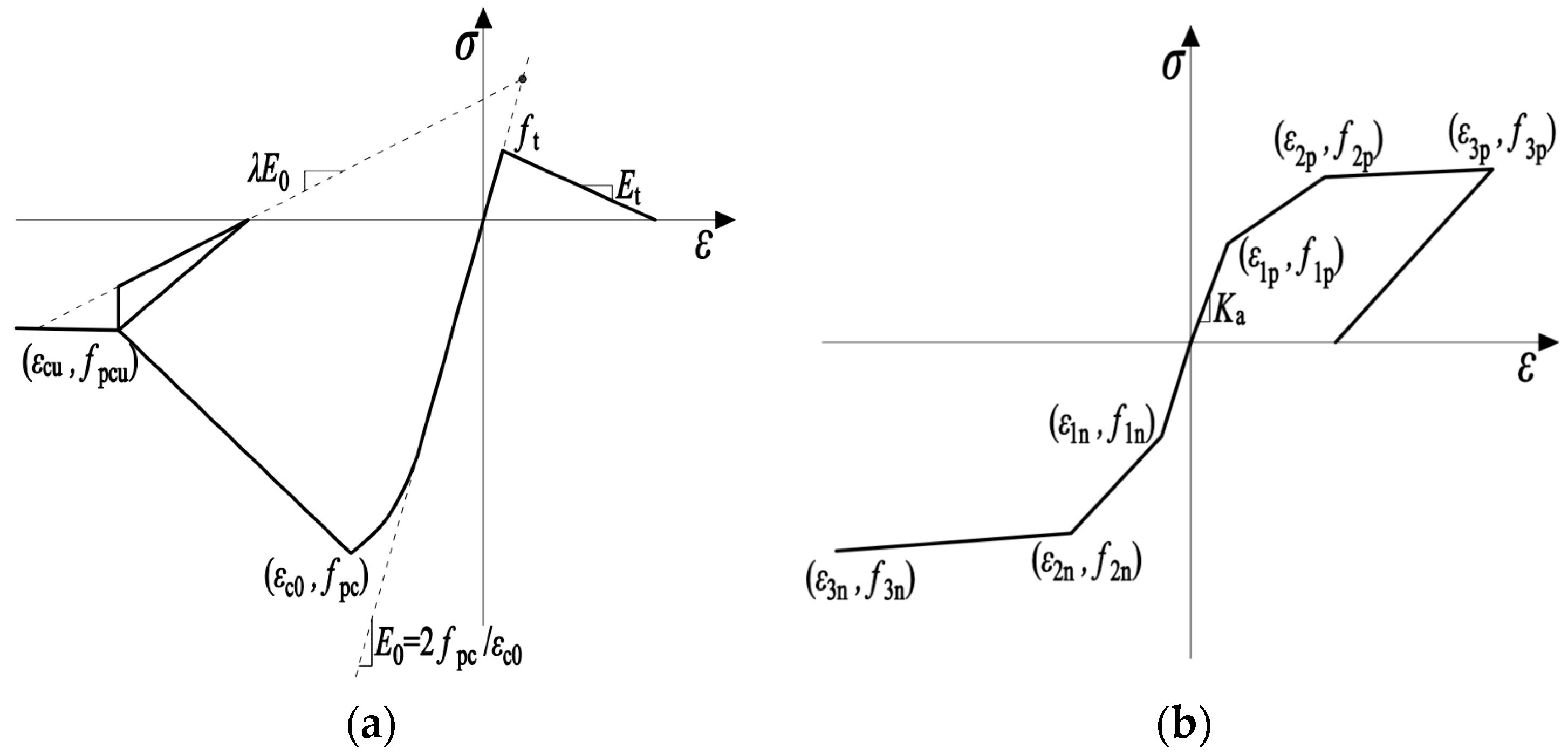
| Concrete compressive stress | |
| Confinement effectiveness factor | |
| Cylinder compressive strength of concrete | |
| Concrete compressive strain | |
| Initial elastic modulus of concrete () | |
| Peak compressive strain of concrete | |
| Slope of the strain-softening branch | |
| Ultimate compressive strain of concrete | |
| Volumetric stirrup ratio | |
| Yield strength of stirrups | |
| Width of confined concrete core | |
| Spacing of stirrups | |
| Confinement stress provided by steel fibers | |
| Number of steel fibers per unit area | |
| Average pullout strength of steel fibers | |
| Fiber orientation factor (can be taken as 3/8) | |
| Volume fraction of steel fibers | |
| Length of steel fibers | |
| Diameter of steel fibers | |
| Bond strength of the matrix | |
| Concrete tensile stress | |
| Concrete tensile strain | |
| Peak tensile strain of concrete | |
| Tensile strength of concrete | |
| Modulus of the descending branch | |
| Ultimate tensile strain of concrete | |
| Ultimate compressive strength of concrete | |
| Yield strength of longitudinal bars | |
| Yield Strain of longitudinal bars | |
| Peak strength of longitudinal bars | |
| Maximum force strain of longitudinal bars | |
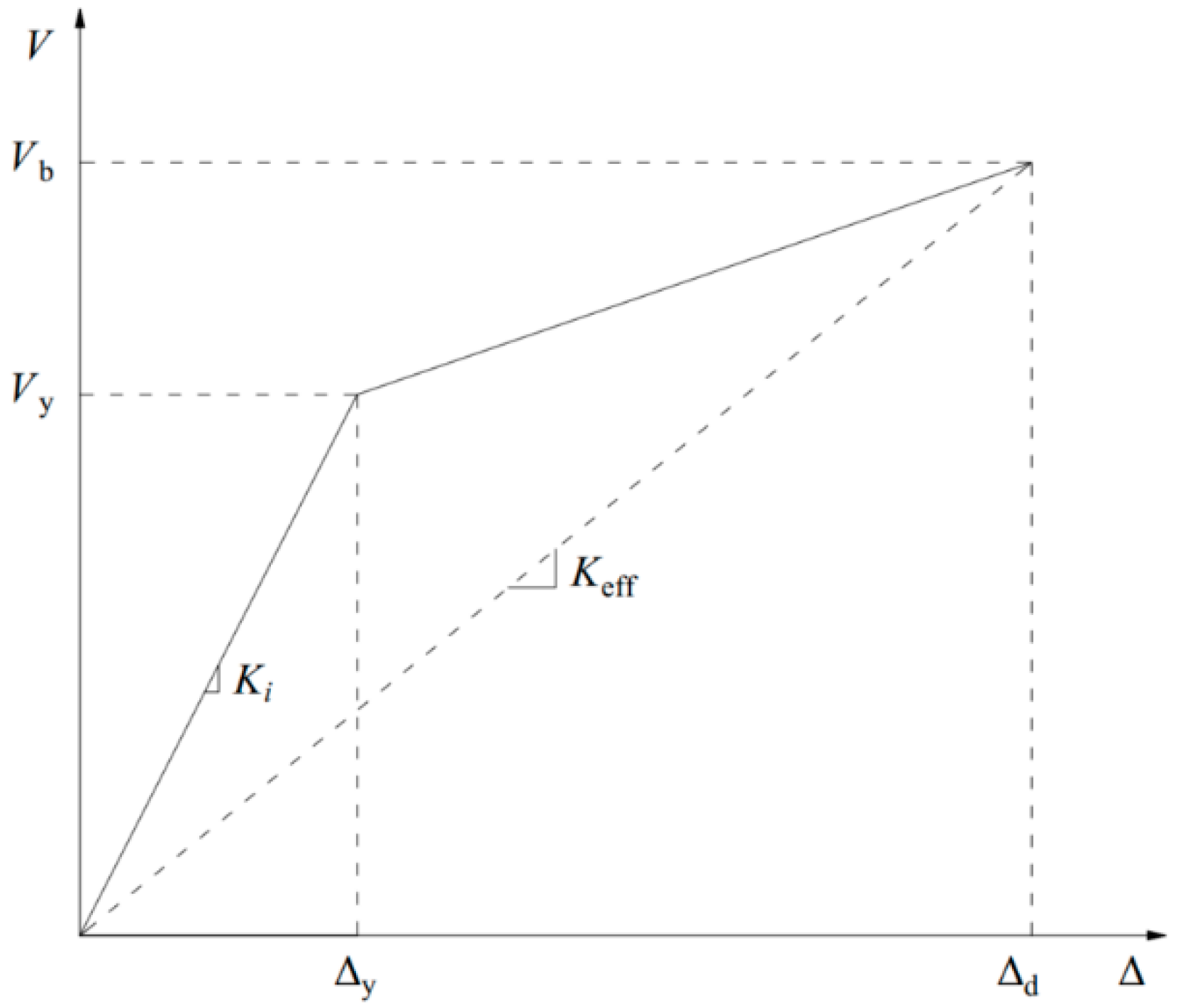
| Yield load | |
| Peak load | |
| Ultimate load | |
| Secant stiffness | |
| Cumulative energy dissipation |
Appendix A
References
- Hoque, M.A.; Mukhlis, M.R.; Bhuiyan, M.A.R. Seismic response of multi-span continuous irregular bridges using displacement-based and conventional force-based methods. Int. J. Civ. Eng. 2021, 19, 837–850. [Google Scholar] [CrossRef]
- Priestley, M.J.N.; Kowalsky, M.J. Direct displacement-based seismic design of concrete buildings. Bull. N. Z. Natl. Soc. Earthq. Eng. 2000, 33, 421–441. [Google Scholar] [CrossRef]
- Al-Mashaykhi, M.; Rajeev, P.; Wijesundara, K.; Hashemi, M. Displacement profile for displacement based seismic design of concentric braced frames. J. Constr. Steel Res. 2019, 155, 233–248. [Google Scholar] [CrossRef]
- Fakhraddini, A.; Hamed, S.; Fadaee, M.J. Peak displacement patterns for the performance-based seismic design of steel eccentrically braced frames. Earthq. Eng. Eng. Vib. 2019, 18, 379–393. [Google Scholar] [CrossRef]
- Arab, M.; Riahi, H.; Daei, M. Optimum displacement profile for the direct displacement-based design of steel moment-resisting frames. Structures 2022, 44, 323–342. [Google Scholar] [CrossRef]
- Xie, C.D.; Wang, X.T.; Vasdravellis, G.; Liang, W. Displacement profile for direct-displacement based seismic design of dual frame-wall resilient system. J. Constr. Steel Res. 2024, 214, 108495. [Google Scholar] [CrossRef]
- Kalapodis, N.A.; Muho, E.V.; Qian, J.; Zhou, Y. Assessment of seismic inelastic displacement profiles of steel MRFs by means of modal behavior factors. Soil Dyn. Earthq. Eng. 2023, 175, 108218. [Google Scholar] [CrossRef]
- Xu, G.; Guo, T.; Li, A.Q. Equivalent linearization method for seismic analysis and design of self-centering structures. Eng. Struct. 2022, 271, 114900. [Google Scholar] [CrossRef]
- Muho, E.V.; Qian, J.; Beskos, D.E. A direct displacement-based seismic design method using a MDOF equivalent system: Application to R/C framed structures. Bull. Earthq. Eng. 2020, 18, 4157–4188. [Google Scholar] [CrossRef]
- Kalapodis, N.A.; Muho, E.V.; Beskos, D.E. Seismic design of plane steel MRFS, EBFS and BRBFS by improved direct displacement-based design method. Soil Dyn. Earthq. Eng. 2022, 153, 107111. [Google Scholar] [CrossRef]
- Wu, X.Y.; Chen, L.W.; Yuan, X.M. Characteristics of long-period displacement spectra based on strong ground-motion records. J. Build. Struct. 2021, 42, 195–205. [Google Scholar]
- Orellana, M.A.; Ruiz, S.E.; Rodríguez-Castellanos, A. Displacement spectra damping factors for preliminary design of structures with hysteretic energy-dissipation device. J. Earthq. Eng. 2022, 26, 6260–6283. [Google Scholar] [CrossRef]
- Li, A.Q.; Zhang, G.D.; Wu, Y.F. Constant-ductility displacement spectra of generalized flag-shaped hysteretic model subjected to near-fault pulse-like earthquakes. J. Build. Struct. 2021, 42, 205–212. [Google Scholar]
- Zhao, G.C.; Xu, L.J.; Zhu, X.J.; Xie, L. A displacement design spectral method adapted to the Chinese seismic design code. J. Vib. Shock. 2023, 42, 266–274. [Google Scholar]
- Alimohammadi, D.; Abadi, E.I.Z. Assessment of collapse safety margin for DDBD and FBD-designed RC frame buildings. Struct. Eng. Mech. 2022, 83, 229–244. [Google Scholar]
- Palsanawala, T.N.; Gondaliya, K.M.; Bhaiya, V.; Vasanwala, S.A. Seismic vulnerability assessment of RC frame buildings designed using the DDBD approach: A parametric study. J. Vib. Eng. Technol. 2024, 12, 2319–2334. [Google Scholar]
- Zhang, C.Y.; Tian, Y. Simplified performance-based optimal seismic design of reinforced concrete frame buildings. Eng. Struct. 2019, 185, 15–25. [Google Scholar] [CrossRef]
- Giannakouras, P.; Zeris, C. Seismic performance of irregular RC frames designed according to the DDBD approach. Eng. Struct. 2019, 182, 427–445. [Google Scholar] [CrossRef]
- Zhou, Y.; Gu, A. Displacement-based seismic design of self-centering shear walls under four-level seismic fortifications. J. Build. Struct. 2019, 40, 118–126. [Google Scholar]
- Zhou, Y.; Xiao, Y.; Gu, A. Self-centering braced rocking frame systems and displacement-based seismic design method. J. Build. Struct. 2019, 40, 17–26. [Google Scholar]
- Zeng, M.R.; Lu, L.; Xia, W.Q.; Hu, Y. Performance-based seismic design method of a reinforced concrete self-centering frame with beam-end spring joints. Eng. Mech. 2024, 41, 266–274. [Google Scholar]
- Chu, L.S.; Liu, J.; Wang, S.W.; Zhao, J. Direct displacement-based seismic design method of SRC column-steel beam hybrid frames. Eng. Mech. 2018, 35, 100–110. [Google Scholar]
- Chu, L.S.; He, Y.X.; Zhao, J.; Chen, Z.Q. Study on displacement-based seismic design method of CFRP-reinforced concrete shear wall. Build. Struct. 2021, 51, 57–65. [Google Scholar]
- Ma, X.F. Investigation on direct displacement based design method of a hybrid RC frame system with stiffened masonry wall. Build. Struct. 2020, 50, 478–484. [Google Scholar]
- Zhang, X.G.; Liu, X.Y.; Zhang, S.P.; Wang, J.; Fu, L.; Yang, J.; Huang, Y. Analysis on displacement-based seismic design method of recycled aggregate concrete-filled square steel tube frame structures. Struct. Concr. 2023, 24, 3461–3475. [Google Scholar] [CrossRef]
- Men, J.J.; Huo, W.W.; Lan, T.; Lei, M.K.; Shi, Q.X. Seismic design method of RCS hybrid frame structure with replaceable members based on stiffness and displacement. Eng. Mech. 2021, 38, 169–178. [Google Scholar]
- Cosgun, C. Machine learning for the prediction of evaluation of existing reinforced concrete structures performance against earthquakes. Structures 2023, 50, 1994–2003. [Google Scholar] [CrossRef]
- Lazaridis, P.C.; Kavvadias, I.E.; Demertzis, K.; Iliadis, L.; Vasiliadis, L.K. Structural damage prediction of a reinforced concrete frame under single and multiple seismic events using machine learning algorithms. Appl. Sci. 2022, 12, 3845. [Google Scholar] [CrossRef]
- Ahmadi, M.; Ebadi-Jamkhaneh, M. Seismic Upgrading of existing steel buildings built on soft soil using passive damping systems. Buildings 2023, 13, 1587. [Google Scholar] [CrossRef]
- Jayawardana, J.; Sandanayake, M.; Jayasinghe, J.; Kulatunga, A.K.; Zhang, G. A comparative life cycle assessment of prefabricated and traditional construction-A case of a developing country. J. Build. Eng. 2023, 72, 106550. [Google Scholar] [CrossRef]
- Wang, J.X.; Li, H.J.; Gao, S. Analysis and evaluation on residual impact resistance of CFST composite frames under column removal scenario. Thin-Walled Struct. 2025, 206, 112624. [Google Scholar] [CrossRef]
- Fan, D.; Zhu, J.; Fan, M.; Lu, J.-X.; Chu, S.; Dong, E.; Yu, R. Intelligent design and manufacturing of ultra-high performance concrete (UHPC)-A review. Constr. Build. Mater. 2023, 385, 131495. [Google Scholar] [CrossRef]
- Ju, Y.Z.; Zhang, H.J.; Wang, D.H.; Kong, X.; Ma, Y.; Zhang, X.; Bai, J. Effect of mineral admixtures on the resistance to sulfate attack of reactive powder concrete. J. Clean. Prod. 2024, 440, 140769. [Google Scholar] [CrossRef]
- Hung, C.C.; El-Tawil, S.; Chao, S.H. A review of developments and challenges for UHPC in structural engineering: Behavior, analysis, and design. J. Struct. Eng. 2021, 147, 03121001. [Google Scholar] [CrossRef]
- Lee, N.K.; Koh, K.T.; Kim, M.O.; Ryu, G. Uncovering the role of micro silica in hydration of ultra-high performance concrete (UHPC). Cem. Concr. Res. 2018, 104, 68–79. [Google Scholar] [CrossRef]
- Guo, P.W.; Jiang, Z.; Meng, W.N.; Bao, Y. Multi-agent collaboration for knowledge-guided data-driven design of ultra-high-performance concrete (UHPC) incorporating solid wastes. Cem. Concr. Res. 2025, 164, 106230. [Google Scholar] [CrossRef]
- Zhang, W.; Zheng, D.W.; Huang, Y.Q.; Kang, S. Experimental and simulative analysis of flexural performance in UHPC-RC hybrid beams. Constr. Build. Mater. 2024, 436, 136889. [Google Scholar] [CrossRef]
- Wang, X.Y.; Ju, Y.Z.; Wang, D.H.; Xing, G.; Zhang, X.; Han, Y.; Song, Y. A simplified calculation model for maximum diagonal crack width of UHPC-NC composite beams. Mech. Adv. Mater. Struct. 2024, 2422576. [Google Scholar] [CrossRef]
- Gao, S.; Liu, L. Effects of freeze-thaw cycles on axial compression behaviors of UHPC-RC composite columns. Materials 2024, 17, 1843. [Google Scholar] [CrossRef]
- Yu, J.B.; Xia, Y.F.; Guan, D.Z.; Guo, X. Seismic behavior and restoring force model of precast beam-column connections with locally reactive powder concrete. J. Build. Eng. 2024, 82, 108296. [Google Scholar] [CrossRef]
- Ju, Y.Z.; Kong, X.S.; Wang, D.H.; Han, Y.; Song, Y. Seismic performance of precast interior joints with UHPC composite beams and HSC columns. Structures 2025, 75, 108741. [Google Scholar] [CrossRef]
- Zhang, X.L.; Wang, B.X.; Ju, Y.Z.; Wang, D.; Han, Y.; Song, Y. Seismic performance of precast frame with UHPC composite beams and HSC column under cyclic loadings. Eng. Struct. 2024, 302, 117429. [Google Scholar] [CrossRef]
- JGJ 3-2010; Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Technical Specification for Concrete Structures of Tall Building. China Architecture and Building Press: Beijing, China, 2010.
- T/CECA 20024-2022; China Engineering and Consulting Association. Standard for Performance-Based Seismic Design of Building Structures. China Architecture and Building Press: Beijing, China, 2022.
- FEMA 356; Prestandard and Commentary for the Seismic Rehabilitation of Buildings. Federal Emergency Management Agency: Washington, DC, USA, 2000.
- GB 18306-2015; National Standardization Administrationseismic Ground Motion Parameters Zonation Map of China. Standards Press of China: Beijing, China, 2015.
- GB 50011-2010; Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Code for Seismic Design of Buildings. China Architecture and Building Press: Beijing, China, 2016.
- SEAOC, Version 2000; Performance-Based Seismic Engineering of Buildings. Structural Engineers Association of California: Sacramento, CA, USA, 1995.
- Chen, G.; Nie, X.X.; Zheng, Q.Z.; Chen, W.; Jiang, H. Experimental study of seismic performance of assembled concrete frames with UHPC connections. Structures 2024, 63, 106353. [Google Scholar] [CrossRef]
- Zheng, Q.Z.; Liu, Y.Y.; Long, L.B.; Chen, G.; Ma, Y. Experimental research on seismic behavior of precast concrete frame connected with UHPC. Ind. Constr. 2019, 49, 85–91. [Google Scholar]
- Peng, C.F.; Zheng, Q.Z.; Long, L.B. Study on seismic performance of precast column connected with UHPC material. Build. Constr. 2016, 38, 1711–1713. [Google Scholar]
- Zhang, Y.X.; Lei, H.; Dong, Z.F.; Li, T.; Ma, F.; Liu, H.; Deng, M. Cyclic response of precast concrete columns connected with cast-in-place UHPC in plastic hinge region. J. Build. Eng. 2023, 65, 105793. [Google Scholar]
- Xu, W.J.; Shao, X.D.; Ma, B.; Li, J.Z.; Wang, R.L. Technical and experimental studies of precast bridge piers with the UHPC connection. China Civ. Eng. J. 2022, 55, 105–116+127. [Google Scholar]
- Priestley, M.J.N.; Calvi, G.M.; Kowalsky, M.J. Displacement-Based Seismic Design of Structures; IUSS Press: Pavia, Italy, 2007. [Google Scholar]
- Scott, B.D.; Park, R.; Priestley, M.J.N. Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rates. ACI J. 1982, 79, 13–27. [Google Scholar]
- Aoude, H. Structural Behaviour of Steel Fibre Reinforced Concrete Members; McGill University: Montreal, QC, Canada, 2007. [Google Scholar]
- Ren, L.; Liu, Q.Y.; Liao, Y.Z. Seismic performance of concrete piers strengthened with UHPC. J. Shenyang Jianzhu Univ. (Nat. Sci.) 2023, 39, 243–251. [Google Scholar]
- Mohd Yassin, M.H. Nonlinear Analysis of Prestressed Concrete Structures Under Monotonic and Cyclic Loads; University of California: Berkeley, CA, USA, 1994. [Google Scholar]
- Mazzoni, S.; McKenna, F.; Scott, M.H.; Fenves, G.L. OpenSEES Command Language Manual; University of California: Berkeley, CA, USA, 2009. [Google Scholar]

| Performance Objective | A | B | C | D | ||
|---|---|---|---|---|---|---|
| Performance Level | ||||||
| Seismic Design Level | ||||||
| Frequent earthquake | 1 | 1 | 1 | 1 | ||
| Design earthquake | 1 | 2 | 3 | 4 | ||
| Rare earthquake | 2 | 3 | 4 | 5 | ||
| Extremely rare earthquake | 3 | 4 | 5 | 6 | ||
| No. | Reference | Specimen Type | Specimen ID | ISDR | ||
|---|---|---|---|---|---|---|
| Yield Point | Peak Point | Ultimate Point | ||||
| 1 | Zhang [42] | Frame | Whole frame | 1.14% | 2.67% | 4.45% |
| 1st interstory | 0.98% | 2.68% | 4.66% | |||
| 2nd interstory | 1.37% | 3.04% | 4.78% | |||
| 3rd interstory | 1.06% | 2.30% | 3.93% | |||
| 2 | Chen [49] | Frame | PC | 1.16% | 2.09% | — |
| 3 | Zheng [50] | Frame | PC | 1.17% | 2.22% | — |
| Mean | 1.15% | 2.50% | 4.46% | |||
| Standard Deviation | 0.13% | 0.36% | 0.33% | |||
| 4 | Peng [51] | Column | UHPC160 | 1.41% | 4.58% | 4.91% |
| UHPC240 | 1.44% | 3.26% | 5.02% | |||
| UHPC320 | 1.73% | 2.66% | 4.73% | |||
| UHPC400 | 1.63% | 2.54% | 4.91% | |||
| UHPC480 | 1.27% | 2.63% | 4.15% | |||
| 5 | Zhang [52] | Column | U6-50-H | 0.68% | 1.65% | 2.80% |
| U8-50-H | 0.52% | 1.65% | 3.15% | |||
| U12-50-H | 0.74% | 2.10% | 4.76% | |||
| U8-50-L | 0.71% | 1.65% | 2.57% | |||
| U8-150-H | 0.61% | 1.70% | 2.69% | |||
| 6 | Xu [53] | Bridge piers | Tall pier | 1.29% | 2.48% | 5.62% |
| Short pier | 1.09% | 3.06% | 5.10% | |||
| Mean | 1.09% | 2.50% | 4.20% | |||
| Standard Deviation | 0.43% | 0.87% | 1.09% | |||
| Performance Level | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Damage degree | No damage | Slight damage | Light damage | Moderate damage | Significant damage | Severe damage |
| ISDR | 0.18% | 0.20% | 0.55% | 1.1% | 2.5% | 4% |
| Concrete | Longitudinal Bars | ||||||
|---|---|---|---|---|---|---|---|
| Parameters | Pre-Cast UHPC | Post-Cast UHPC | Pre-Cast HSC | Pre-Cast NSC | Parameters | In Beam | In Column |
| fc′ (MPa) | 108.2 | 86.8 | 57.4 | 37.2 | fy (MPa) | 449.94 | 447.34 |
| E0 (GPa) | 43.3 | 40.6 | 36.1 | 32.9 | εy | 0.002239 | 0.002246 |
| fcu (MPa) | 21.64 | 17.36 | 11.48 | 7.44 | fu (MPa) | 649.85 | 610.52 |
| ft′ (MPa) | 6.2 | 5.6 | 2.85 | 2.39 | εu | 0.12565 | 0.13672 |
| Test | Simulation | Percentage Deviation | |
|---|---|---|---|
| Fy (kN) | 242.41 | 240.90 | −0.62% |
| Fp (kN) | 281.92 | 271.31 | −3.76% |
| Fu (kN) | 239.63 | 230.61 | −3.76% |
| Kj (kN/mm) | 11.09 | 11.98 | 8.03% |
| E (kN·m) | 255.92 | 249.68 | −2.44% |
| Seismic Design Level | Performance Level | Damage Degree | Limit Value of ISDR |
|---|---|---|---|
| Frequent earthquake | 1 | No damage | 0.18% |
| Design earthquake | 4 | Moderate damage | 1.1% |
| Rare earthquake | 5 | Significant damage | 2.5% |
| Extremely rare earthquake | 6 | Severe damage | 4% |
| Story | Hi (m) | mi (t) | δi | Δi (m) | miΔi (t·m) | miΔi2 (t·m) | miΔiHi (t·m2) | Fi (kN) | Vi (kN) |
|---|---|---|---|---|---|---|---|---|---|
| 10 | 36.6 | 112.91 | 1.0000 | 0.0509 | 5.7437 | 0.2922 | 210.2198 | 57.4898 | 57.4898 |
| 9 | 33.0 | 129.23 | 0.9312 | 0.0474 | 6.1218 | 0.2900 | 202.0193 | 61.2741 | 118.7639 |
| 8 | 29.4 | 129.23 | 0.8560 | 0.0435 | 5.6271 | 0.2450 | 165.4369 | 56.3227 | 175.0866 |
| 7 | 25.8 | 129.23 | 0.7743 | 0.0394 | 5.0900 | 0.2005 | 131.3224 | 50.9468 | 226.0335 |
| 6 | 22.2 | 129.23 | 0.6861 | 0.0349 | 4.5105 | 0.1574 | 100.1335 | 45.1466 | 271.1800 |
| 5 | 18.6 | 129.23 | 0.5915 | 0.0301 | 3.8886 | 0.1170 | 72.3284 | 38.9219 | 310.1019 |
| 4 | 15.0 | 129.23 | 0.4905 | 0.0249 | 3.2243 | 0.0804 | 48.3648 | 32.2728 | 342.3747 |
| 3 | 11.4 | 129.23 | 0.3830 | 0.0195 | 2.5176 | 0.0490 | 28.7009 | 25.1993 | 367.5741 |
| 2 | 7.8 | 129.23 | 0.2690 | 0.0137 | 1.7685 | 0.0242 | 13.7944 | 17.7014 | 385.2755 |
| 1 | 4.2 | 130.53 | 0.1486 | 0.0076 | 0.9868 | 0.0075 | 4.1445 | 9.8770 | 395.1525 |
| ∑ | 1277.32 | 0.3118 | 39.4790 | 1.4632 | 976.4650 | 395.1525 |
| Loading Step | 33 | 35 | ||||
| Base Shear | 384.30 kN | 405.24 kN | ||||
| Story | Absolute Displacement (mm) | Interstory Displacement (mm) | Interstory Drift Ratio (%) | Absolute Displacement (mm) | Interstory Displacement (mm) | Interstory Drift Ratio (%) |
| 10 | 32.961 | 1.463 | 0.041 | 34.960 | 1.550 | 0.043 |
| 9 | 31.498 | 2.079 | 0.058 | 33.409 | 2.203 | 0.061 |
| 8 | 29.420 | 2.727 | 0.076 | 31.206 | 2.890 | 0.080 |
| 7 | 26.693 | 3.326 | 0.092 | 28.316 | 3.526 | 0.098 |
| 6 | 23.367 | 3.818 | 0.106 | 24.791 | 4.049 | 0.112 |
| 5 | 19.549 | 4.176 | 0.116 | 20.741 | 4.432 | 0.123 |
| 4 | 15.374 | 4.417 | 0.123 | 16.309 | 4.691 | 0.130 |
| 3 | 10.956 | 4.403 | 0.122 | 11.618 | 4.674 | 0.130 |
| 2 | 6.554 | 3.949 | 0.110 | 6.944 | 4.187 | 0.116 |
| 1 | 2.605 | 2.605 | 0.062 | 2.757 | 2.757 | 0.066 |
| Loading step | 48 | 103 | ||||
| Base shear | 532.81 kN | 967.35 kN | ||||
| Story | Absolute displacement (mm) | Interstory displacement (mm) | Interstory drift ratio (%) | Absolute displacement (mm) | Interstory displacement (mm) | Interstory drift ratio (%) |
| 10 | 47.950 | 2.106 | 0.059 | 102.953 | 4.385 | 0.122 |
| 9 | 45.844 | 2.989 | 0.083 | 98.568 | 6.206 | 0.172 |
| 8 | 42.855 | 3.927 | 0.109 | 92.362 | 8.259 | 0.229 |
| 7 | 38.928 | 4.814 | 0.134 | 84.103 | 10.318 | 0.287 |
| 6 | 34.114 | 5.561 | 0.154 | 73.786 | 12.079 | 0.336 |
| 5 | 28.553 | 6.123 | 0.170 | 61.707 | 13.382 | 0.372 |
| 4 | 22.429 | 6.505 | 0.181 | 48.325 | 14.188 | 0.394 |
| 3 | 15.925 | 6.461 | 0.179 | 34.136 | 13.952 | 0.388 |
| 2 | 9.464 | 5.735 | 0.159 | 20.185 | 12.226 | 0.340 |
| 1 | 3.729 | 3.729 | 0.089 | 7.959 | 7.959 | 0.189 |
| Loading step | 208 | 272 | ||||
| Base shear | 1612.90 kN | 1860.26 kN | ||||
| Story | Absolute displacement (mm) | Interstory displacement (mm) | Interstory drift ratio (%) | Absolute displacement (mm) | Interstory displacement (mm) | Interstory drift ratio (%) |
| 10 | 208.159 | 8.951 | 0.249 | 272.255 | 10.618 | 0.295 |
| 9 | 199.209 | 12.443 | 0.346 | 261.638 | 14.972 | 0.416 |
| 8 | 186.765 | 16.593 | 0.461 | 246.666 | 20.387 | 0.566 |
| 7 | 170.172 | 20.773 | 0.577 | 226.279 | 26.155 | 0.727 |
| 6 | 149.399 | 24.251 | 0.674 | 200.124 | 31.727 | 0.881 |
| 5 | 125.148 | 26.942 | 0.748 | 168.397 | 36.729 | 1.020 |
| 4 | 98.205 | 28.741 | 0.798 | 131.667 | 39.713 | 1.103 |
| 3 | 69.464 | 28.214 | 0.784 | 91.954 | 38.324 | 1.065 |
| 2 | 41.250 | 24.724 | 0.687 | 53.631 | 32.467 | 0.902 |
| 1 | 16.526 | 16.526 | 0.393 | 21.163 | 21.163 | 0.504 |
| Loading step | 563 | 902 | ||||
| Base shear | 2083.33 kN | 2257.95 kN | ||||
| Story | Absolute displacement (mm) | Interstory displacement (mm) | Interstory drift ratio (%) | Absolute displacement (mm) | Interstory displacement (mm) | Interstory drift ratio (%) |
| 10 | 563.480 | 13.829 | 0.384 | 902.819 | 18.886 | 0.525 |
| 9 | 549.651 | 21.657 | 0.602 | 883.933 | 32.540 | 0.904 |
| 8 | 527.993 | 36.359 | 1.010 | 851.392 | 59.803 | 1.661 |
| 7 | 491.635 | 56.498 | 1.569 | 791.590 | 94.599 | 2.628 |
| 6 | 435.136 | 75.297 | 2.092 | 696.991 | 123.250 | 3.424 |
| 5 | 359.839 | 86.880 | 2.413 | 573.740 | 139.078 | 3.863 |
| 4 | 272.959 | 90.129 | 2.504 | 434.662 | 142.587 | 3.961 |
| 3 | 182.830 | 82.668 | 2.296 | 292.075 | 130.847 | 3.635 |
| 2 | 100.162 | 63.780 | 1.772 | 161.228 | 102.327 | 2.842 |
| 1 | 36.382 | 36.382 | 0.866 | 58.901 | 58.901 | 1.402 |
| Loading step | 913 | |||||
| Base shear | 2261.38 kN | |||||
| Story | Absolute displacement (mm) | Interstory displacement (mm) | Interstory drift ratio (%) | |||
| 10 | 913.827 | 19.060 | 0.529 | |||
| 9 | 894.767 | 33.005 | 0.917 | |||
| 8 | 861.762 | 60.690 | 1.686 | |||
| 7 | 801.072 | 95.820 | 2.662 | |||
| 6 | 705.252 | 124.676 | 3.463 | |||
| 5 | 580.577 | 140.606 | 3.906 | |||
| 4 | 439.971 | 144.138 | 4.004 | |||
| 3 | 295.832 | 132.334 | 3.676 | |||
| 2 | 163.499 | 103.637 | 2.879 | |||
| 1 | 59.862 | 59.862 | 1.425 | |||
| Story | Hi (m) | mi (t) | Δi (m) | miΔi (t·m) | miΔi2 (t·m) | miΔiHi (t·m2) | Fi (kN) | Vi (kN) |
|---|---|---|---|---|---|---|---|---|
| 10 | 36.6 | 112.91 | 0.0480 | 5.4141 | 0.2596 | 198.1568 | 56.2690 | 56.2690 |
| 9 | 33.0 | 129.23 | 0.0458 | 5.9247 | 0.2716 | 195.5142 | 61.5752 | 117.8442 |
| 8 | 29.4 | 129.23 | 0.0429 | 5.5384 | 0.2373 | 162.8276 | 57.5602 | 175.4044 |
| 7 | 25.8 | 129.23 | 0.0389 | 5.0308 | 0.1958 | 129.7954 | 52.2855 | 227.6899 |
| 6 | 22.2 | 129.23 | 0.0341 | 4.4087 | 0.1504 | 97.8728 | 45.8195 | 273.5094 |
| 5 | 18.6 | 129.23 | 0.0286 | 3.6900 | 0.1054 | 68.6343 | 38.3504 | 311.8598 |
| 4 | 15.0 | 129.23 | 0.0224 | 2.8987 | 0.0650 | 43.4798 | 30.1257 | 341.9855 |
| 3 | 11.4 | 129.23 | 0.0159 | 2.0580 | 0.0328 | 23.4612 | 21.3888 | 363.3743 |
| 2 | 7.8 | 129.23 | 0.0095 | 1.2230 | 0.0116 | 9.5397 | 12.7110 | 376.0853 |
| 1 | 4.2 | 130.53 | 0.0037 | 0.4868 | 0.0018 | 2.0444 | 5.0589 | 381.1442 |
| ∑ | 1277.32 | 0.2898 | 36.6731 | 1.3313 | 931.3263 | 381.1442 |
| Story | Hi (m) | mi (t) | Δi (m) | miΔi (t·m) | miΔi2 (t·m) | miΔiHi (t·m2) | Fi (kN) | Vi (kN) |
|---|---|---|---|---|---|---|---|---|
| 10 | 36.6 | 112.91 | 0.2723 | 30.7406 | 8.3693 | 1125.1062 | 140.1657 | 140.1657 |
| 9 | 33.0 | 129.23 | 0.2616 | 33.8126 | 8.8467 | 1115.8170 | 154.1730 | 294.3387 |
| 8 | 29.4 | 129.23 | 0.2467 | 31.8778 | 7.8632 | 937.2063 | 145.3507 | 439.6894 |
| 7 | 25.8 | 129.23 | 0.2263 | 29.2431 | 6.6171 | 754.4709 | 133.3374 | 573.0268 |
| 6 | 22.2 | 129.23 | 0.2001 | 25.8629 | 5.1758 | 574.1562 | 117.9251 | 690.9519 |
| 5 | 18.6 | 129.23 | 0.1684 | 21.7627 | 3.6648 | 404.7856 | 99.2296 | 790.1815 |
| 4 | 15.0 | 129.23 | 0.1317 | 17.0160 | 2.2404 | 255.2396 | 77.5865 | 867.7680 |
| 3 | 11.4 | 129.23 | 0.0920 | 11.8837 | 1.0928 | 135.4742 | 54.1852 | 921.9532 |
| 2 | 7.8 | 129.23 | 0.0536 | 6.9309 | 0.3717 | 54.0613 | 31.6024 | 953.5557 |
| 1 | 4.2 | 130.53 | 0.0212 | 2.7624 | 0.0585 | 11.6020 | 12.5955 | 966.1511 |
| ∑ | 1277.32 | 1.6738 | 211.8926 | 44.3001 | 5367.9194 | 966.1511 |
| Story | Hi (m) | mi (t) | Δi (m) | miΔi (t·m) | miΔi2 (t·m) | miΔiHi (t·m2) | Fi (kN) | Vi (kN) |
|---|---|---|---|---|---|---|---|---|
| 10 | 36.6 | 112.91 | 0.5635 | 63.6231 | 35.8503 | 2328.6037 | 229.8549 | 229.8549 |
| 9 | 33.0 | 129.23 | 0.5497 | 71.0339 | 39.0438 | 2344.1187 | 256.6285 | 486.4834 |
| 8 | 29.4 | 129.23 | 0.5280 | 68.2350 | 36.0276 | 2006.1090 | 246.5167 | 733.0001 |
| 7 | 25.8 | 129.23 | 0.4916 | 63.5362 | 31.2366 | 1639.2345 | 229.5412 | 962.5413 |
| 6 | 22.2 | 129.23 | 0.4351 | 56.2347 | 24.4698 | 1248.4101 | 203.1625 | 1165.7037 |
| 5 | 18.6 | 129.23 | 0.3598 | 46.5037 | 16.7338 | 864.9683 | 168.0067 | 1333.7104 |
| 4 | 15.0 | 129.23 | 0.2730 | 35.2758 | 9.6288 | 529.1365 | 127.4429 | 1461.1533 |
| 3 | 11.4 | 129.23 | 0.1828 | 23.6280 | 4.3199 | 269.3593 | 85.3623 | 1546.5156 |
| 2 | 7.8 | 129.23 | 0.1002 | 12.9444 | 1.2965 | 100.9662 | 46.7650 | 1593.2806 |
| 1 | 4.2 | 130.53 | 0.0364 | 4.7489 | 0.1728 | 19.9454 | 17.1566 | 1610.4372 |
| ∑ | 1277.32 | 3.5201 | 445.7636 | 198.7800 | 11,350.8516 | 1610.4372 |
| Story | Hi (m) | mi (t) | Δi (m) | miΔi (t·m) | miΔi2 (t·m) | miΔiHi (t·m2) | Fi (kN) | Vi (kN) |
|---|---|---|---|---|---|---|---|---|
| 10 | 36.6 | 112.91 | 0.9138 | 103.1811 | 94.2897 | 3776.4294 | 321.8074 | 321.8074 |
| 9 | 33.0 | 129.23 | 0.8948 | 115.6349 | 103.4663 | 3815.9522 | 360.6490 | 682.4565 |
| 8 | 29.4 | 129.23 | 0.8618 | 111.3696 | 95.9741 | 3274.2650 | 347.3460 | 1029.8024 |
| 7 | 25.8 | 129.23 | 0.8011 | 103.5263 | 82.9320 | 2670.9779 | 322.8839 | 1352.6863 |
| 6 | 22.2 | 129.23 | 0.7053 | 91.1430 | 64.2788 | 2023.3748 | 284.2622 | 1636.9485 |
| 5 | 18.6 | 129.23 | 0.5806 | 75.0306 | 43.5610 | 1395.5694 | 234.0099 | 1870.9585 |
| 4 | 15.0 | 129.23 | 0.4400 | 56.8594 | 25.0165 | 852.8916 | 177.3366 | 2048.2951 |
| 3 | 11.4 | 129.23 | 0.2958 | 38.2318 | 11.3102 | 435.8423 | 119.2396 | 2167.5346 |
| 2 | 7.8 | 129.23 | 0.1635 | 21.1297 | 3.4547 | 164.8117 | 65.9006 | 2233.4352 |
| 1 | 4.2 | 130.53 | 0.0599 | 7.8137 | 0.4677 | 32.8175 | 24.3698 | 2257.8050 |
| ∑ | 1277.32 | 5.7164 | 723.9201 | 524.7510 | 18,442.9318 | 2257.8050 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Duan, K.; Ju, Y.; Wang, X. Analysis on DDBD Method of Precast Frame with UHPC Composite Beams and HSC Columns. Buildings 2025, 15, 3546. https://doi.org/10.3390/buildings15193546
Zhang X, Duan K, Ju Y, Wang X. Analysis on DDBD Method of Precast Frame with UHPC Composite Beams and HSC Columns. Buildings. 2025; 15(19):3546. https://doi.org/10.3390/buildings15193546
Chicago/Turabian StyleZhang, Xiaolei, Kunyu Duan, Yanzhong Ju, and Xinying Wang. 2025. "Analysis on DDBD Method of Precast Frame with UHPC Composite Beams and HSC Columns" Buildings 15, no. 19: 3546. https://doi.org/10.3390/buildings15193546
APA StyleZhang, X., Duan, K., Ju, Y., & Wang, X. (2025). Analysis on DDBD Method of Precast Frame with UHPC Composite Beams and HSC Columns. Buildings, 15(19), 3546. https://doi.org/10.3390/buildings15193546






