Damage Identification of Corroded Reinforced Concrete Beams Based on SSA-ELM
Abstract
1. Introduction
- (1)
- Development of a Damage Identification Model Integrating Dynamic Characteristics: The proposed algorithm uses natural frequencies and modal shapes as input features to directly output key damage indicators, such as corrosion rate, remaining load-bearing capacity, and remaining stiffness, allowing for precise identification of corrosion-induced damage in beams.
- (2)
- Innovative Integration of Dynamic and Static Feature Identification for Structural Performance Degradation: By combining dynamic (modal and frequency) with static (load-bearing capacity and stiffness) performance characteristics, this method identifies changes in load-bearing capacity and stiffness due to corrosion, offering a novel approach for non-destructive testing of RC structures.
- (3)
- Development of an Integrated Application Platform: To facilitate result visualization and practical engineering applications, a supporting graphical user interface (GUI) was developed on the MATLAB R2024a platform.
2. Damage Identification Method Based on Improved Extreme Learning Machine
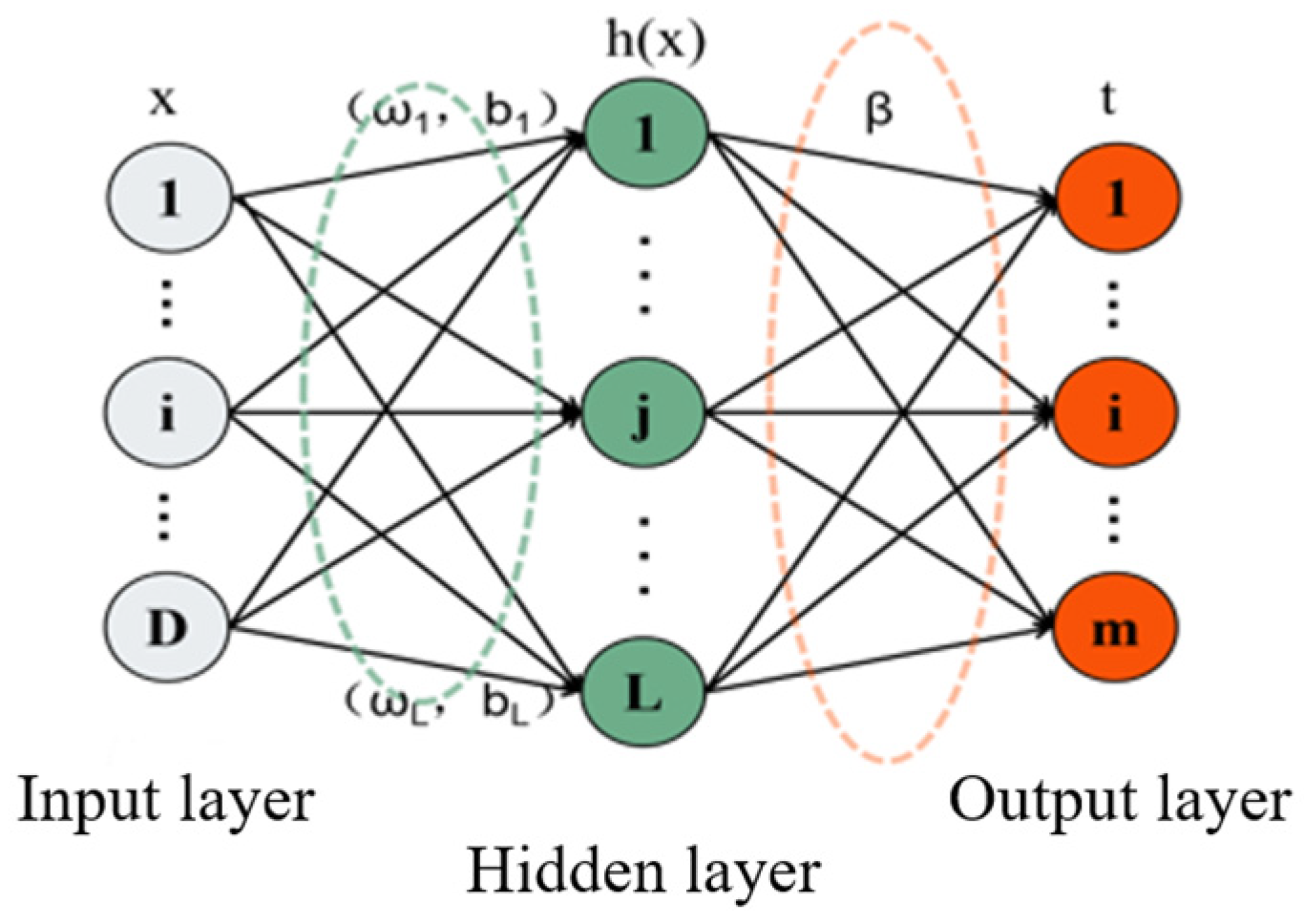
2.1. Extreme Learning Machine (ELM)
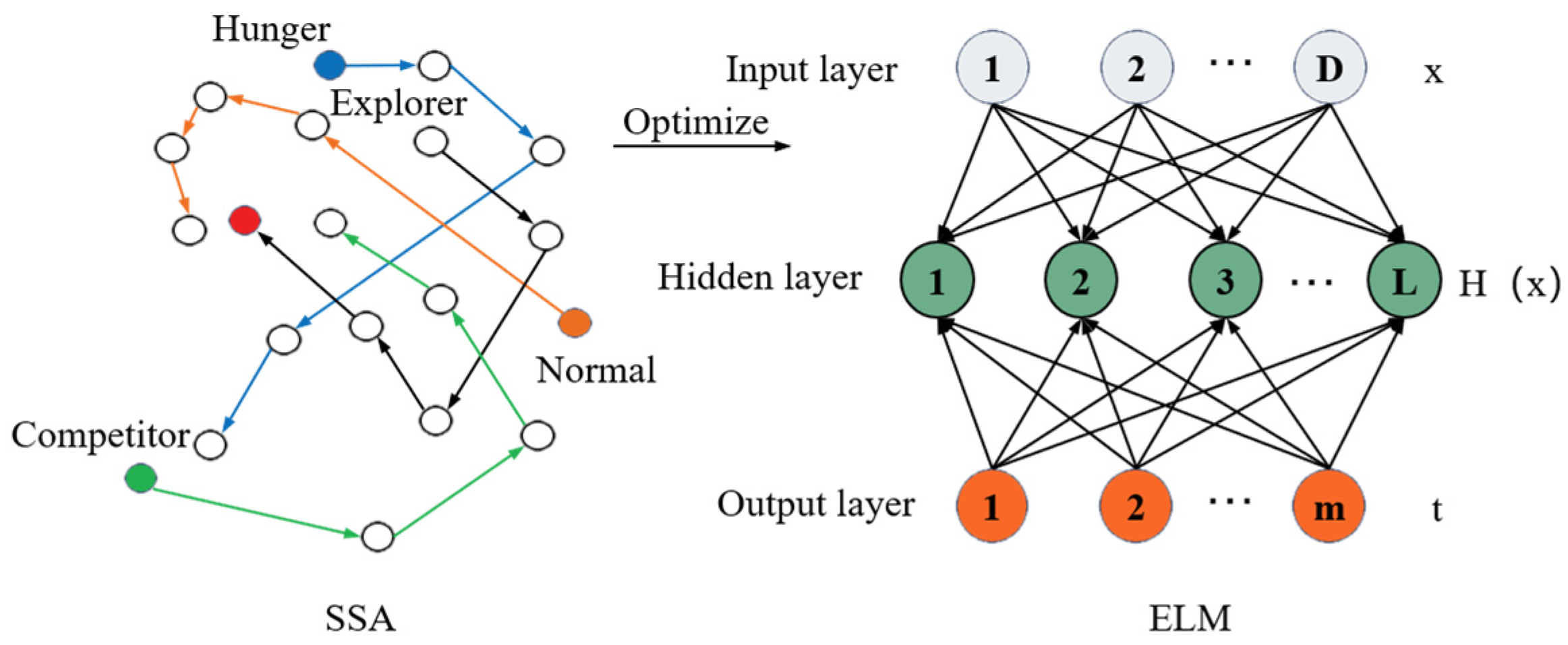
2.2. Optimization Mechanism and Parameter Tuning Strategy of Sparrow Search Algorithm (SSA)
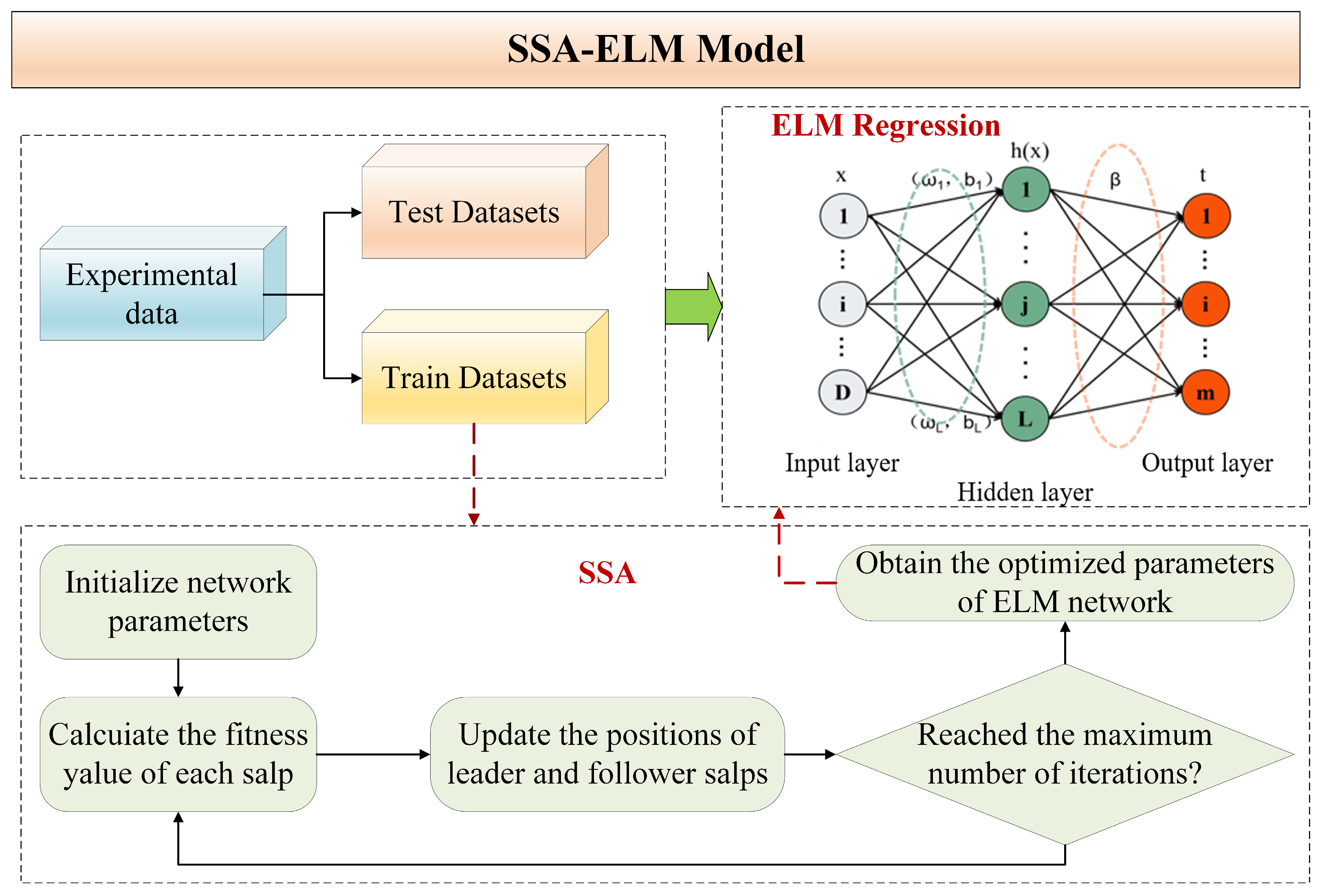
2.3. Damage Identification Method Based on SSA-ELM
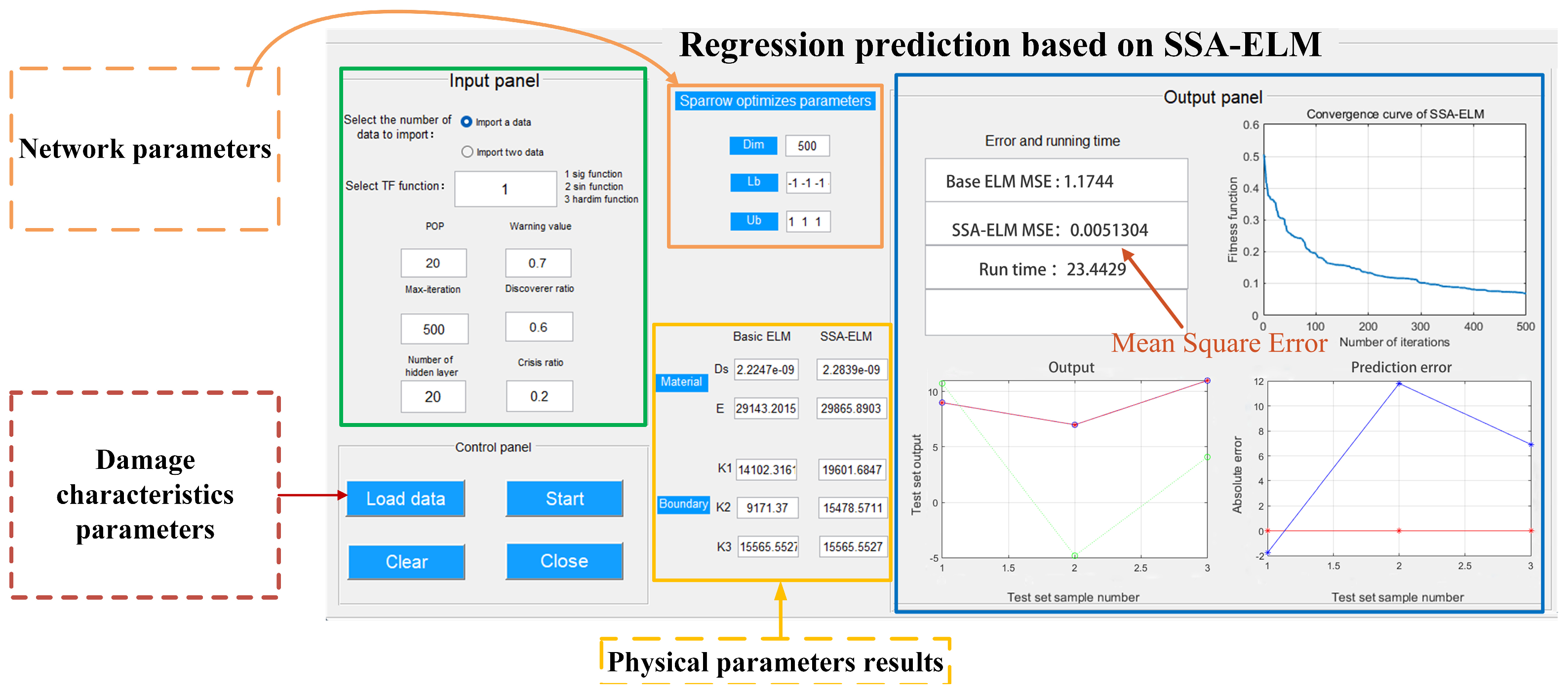
2.4. Practical and Scalable System Framework
3. Finite Element Simulation Verification
3.1. Finite Element Model
3.2. Stiffness Parameter Modulation
- (1)
- Impact on Detection Accuracy
- (2)
- Impact on Convergence Efficiency
- (3)
- Parameter Optimization Strategy
3.3. Performance Evaluation of SSA-ELM Using Simulated Values
4. Experimental Study
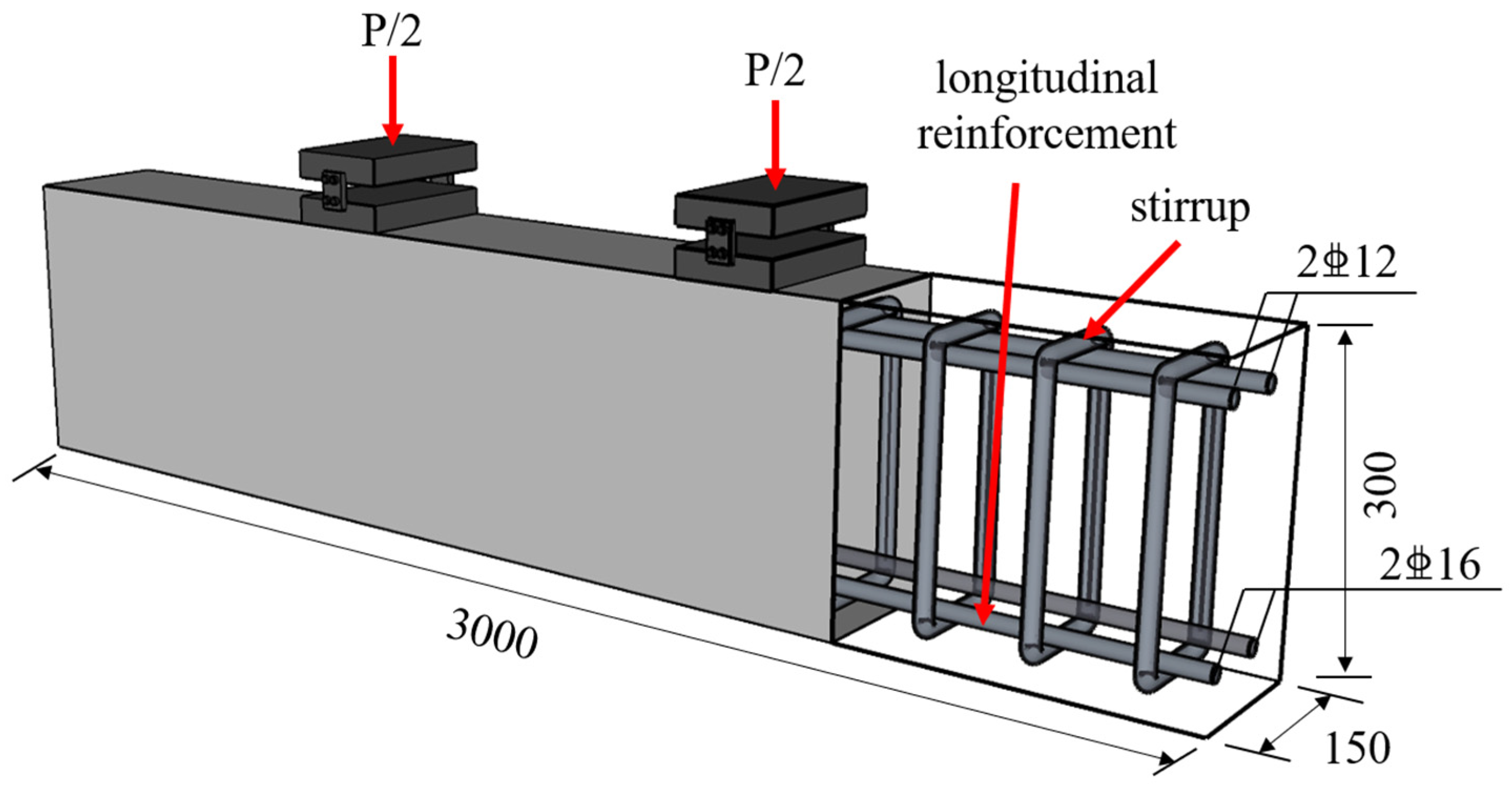
4.1. Preparation of RC Beam Components
4.2. Accelerated Corrosion Test
- (1)
- After specimen fracture, longitudinal reinforcement sections were extracted at 400 mm intervals along the axial direction. Each segment was precisely positioned using a total station and systematically cataloged to maintain spatial correspondence.
- (2)
- Steel segments underwent multi-stage abrasion: initial treatment with 80-grit sandpaper removed concrete adherent, followed by 600-grit sandpaper for surface rust elimination. Three repeated weighings were conducted using an analytical balance with 0.1 mg precision, with the mean value recorded as post-corrosion mass (m).
- (3)
- Mass loss rate (ηs) was calculated using the Equation (11):
- (4)
- Simultaneous electrochemical verification was performed via the Linear Polarization Resistance (LPR) method, enabling cross-validation with gravimetric results to ensure data reliability.
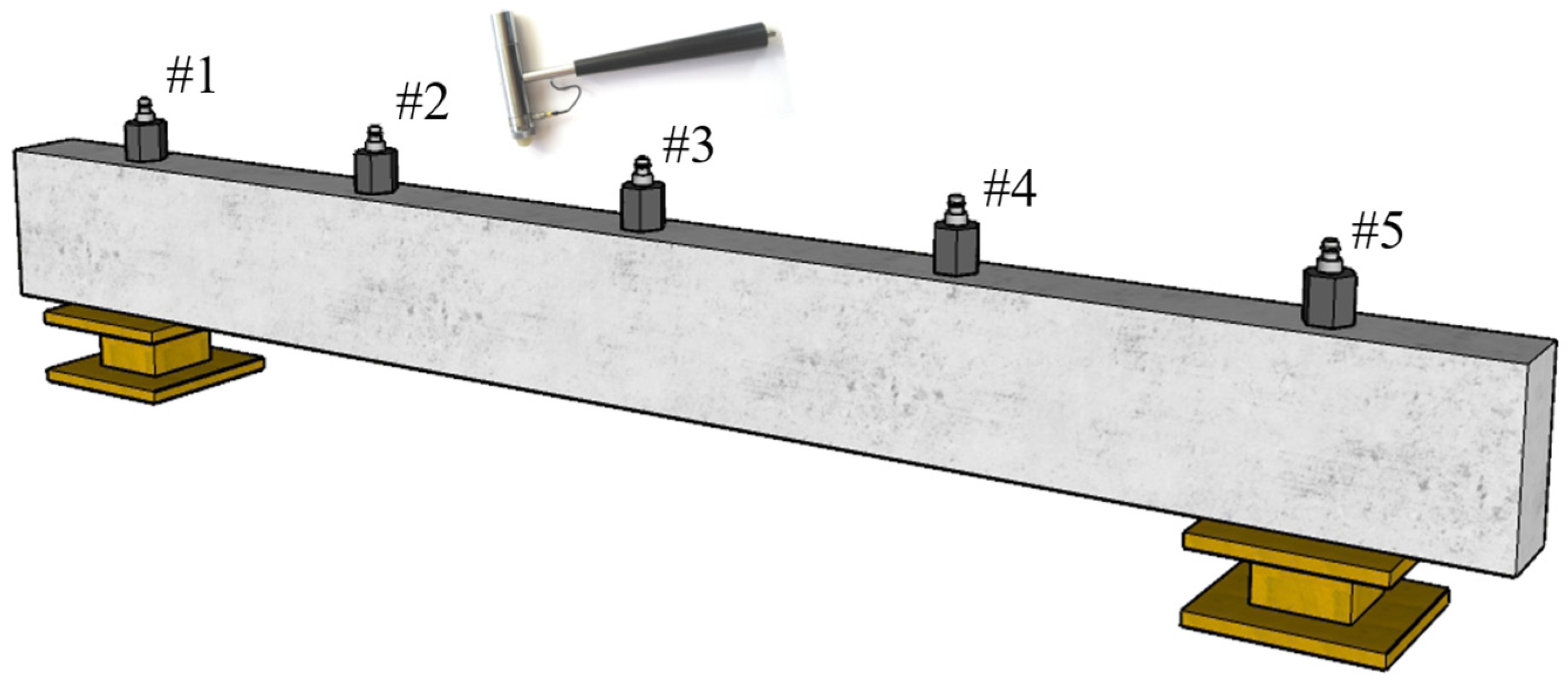
4.3. Dynamic and Static Load Tests
5. Results Analysis and Discussion
5.1. Analysis of Static Loading Test Results
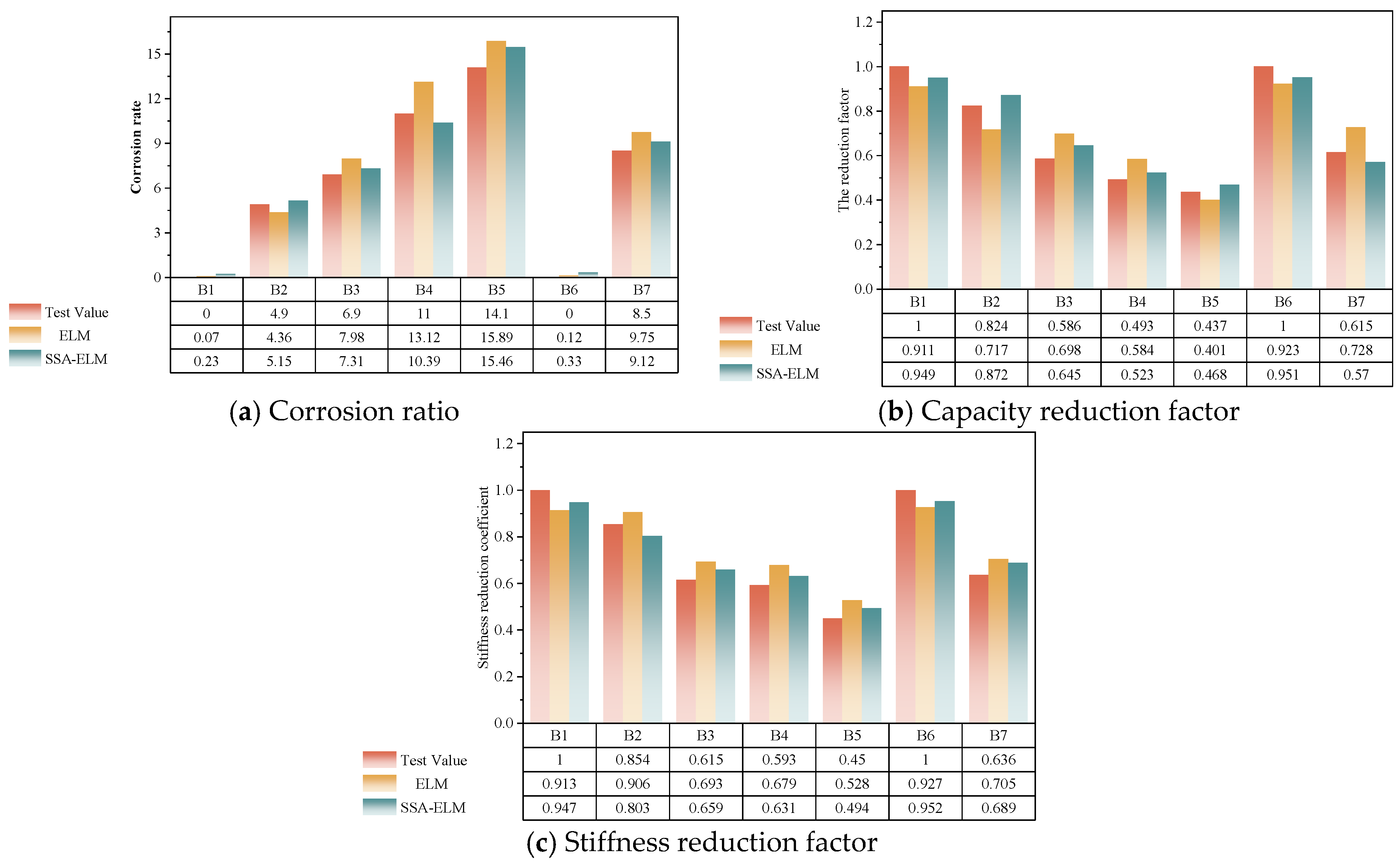
5.2. Damage Identification of Three Indexes
6. Summary
6.1. Conclusions
- (1)
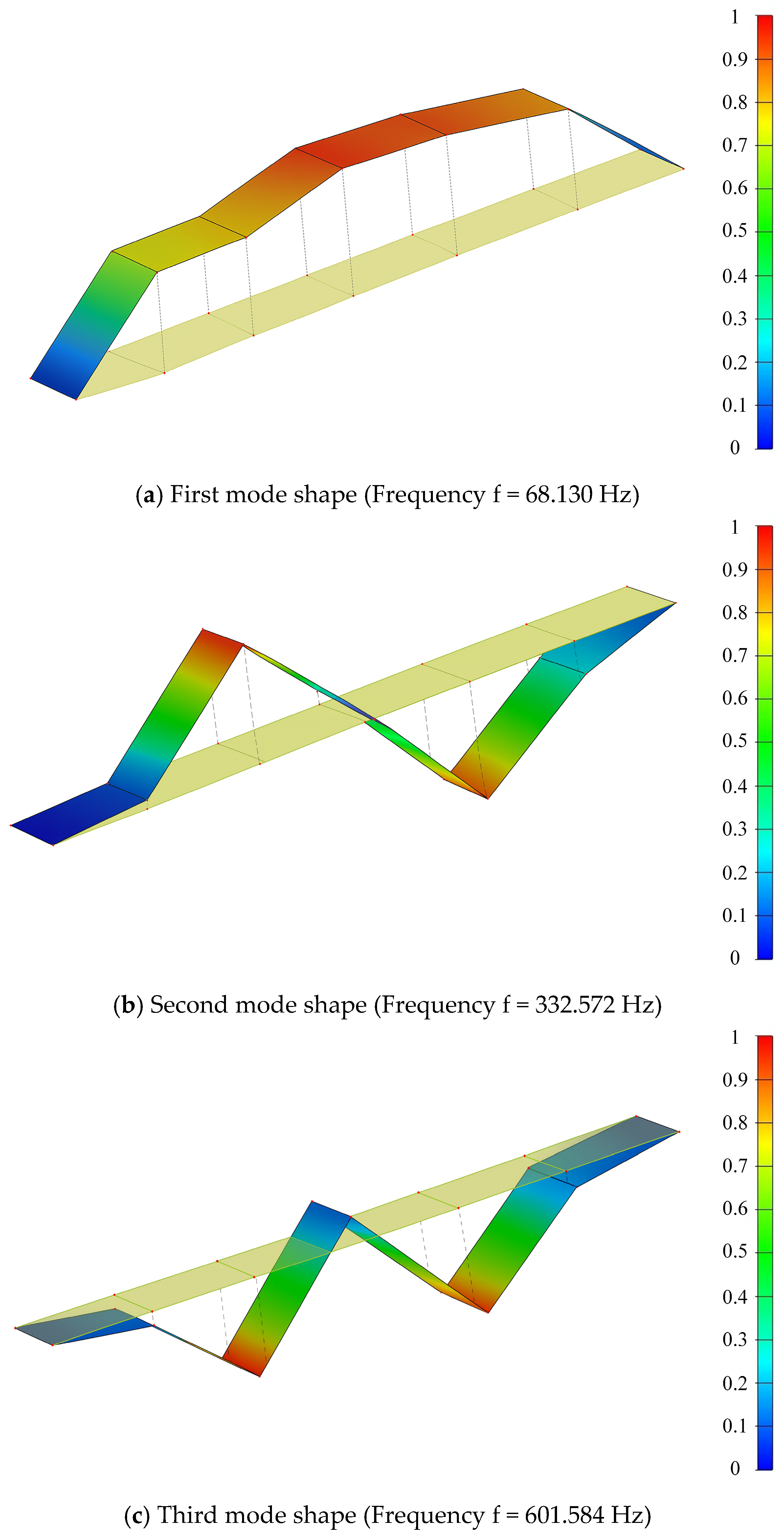
- This study quantitatively shows that corrosion severity significantly degrades the dynamic properties of reinforced concrete beams. The experimental results indicate a decrease in natural frequencies by up to 45% at a 14.1% mass loss ratio (ηs), with the third mode exhibiting the highest sensitivity. Modal Assurance Criterion (MAC) values show a decay of over 30%, reflecting a progressive loss of vibrational coherence as corrosion intensifies.
- (2)
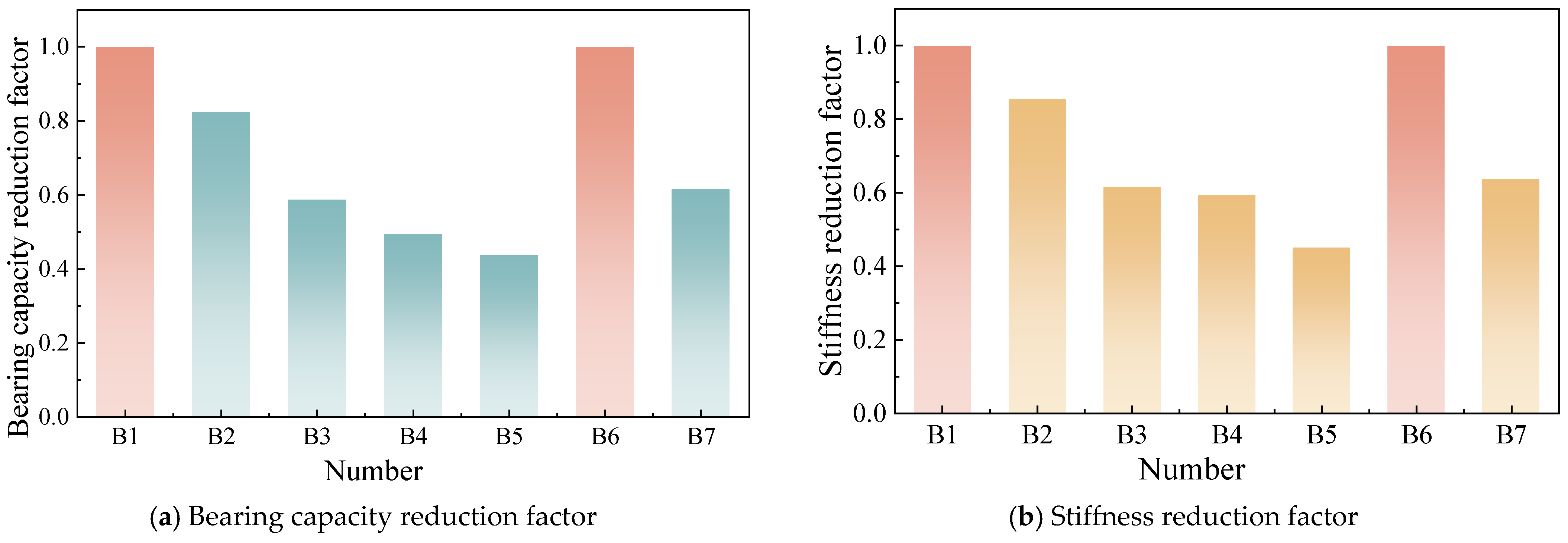
- Static load tests reveal substantial mechanical deterioration, with yield capacity dropping by 48.2% (from 110 kN to 57 kN) and ultimate load reducing by 49.6% at ηs = 14.1%. Notably, a 30 mm concrete cover enhances flexural capacity by 15–20% compared to the standard 20 mm cover, emphasizing the critical protective role of the concrete cover in mitigating corrosion effects.
- (3)
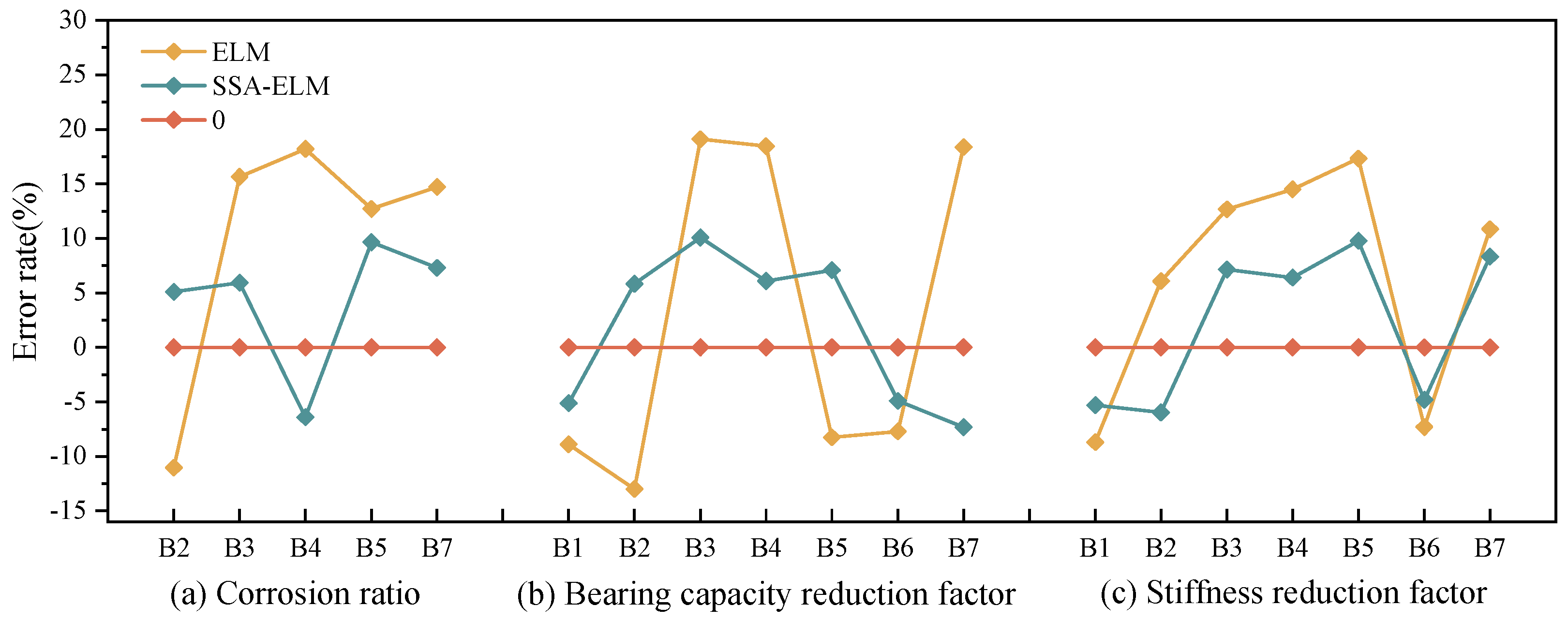
- The SSA-ELM algorithm demonstrated high precision in damage identification, with prediction errors for mass corrosion ratio (ηs), flexural capacity reduction (α), and stiffness reduction (β) ranging from 5 to 10%. This represents a 50% improvement in accuracy over conventional ELM, which showed errors between 9 and 20%. Quantitative validation revealed a 74–83% reduction in mean squared error (e.g., α MSE: 0.0021 vs. 0.0086 for ELM), maintaining robustness even under 10% Gaussian noise.
- (4)
- For practical implementation, a MATLAB-based GUI with Docker containerization enables real-time corrosion parameter identification. This deployable system offers controlled error assessment of ηs, α, and β, positioning SSA-ELM as a valuable tool for post-damage rehabilitation and structural safety management.
6.2. Limitations
- (1)
- Experimental dataset constrained by small sample size, low replication counts, and narrow corrosion rate range (0–14.1%). Lack of systematic investigation on protective layer thickness effects and higher corrosion grades (20–30%).
- (2)
- Focus on macroscopic damage identification rather than localized pitting, cross-sectional loss distribution, or multi-scale (macro–micro-electrochemical) correlation modeling.
- (3)
- Machine learning models (e.g., SSA-ELM) show limited nonlinear behavior capture at low corrosion rates (0–2%) and insufficient integration of physical mechanisms (e.g., stress distribution and crack propagation).
- (4)
- Accelerated corrosion tests lack multi-factor coupling analysis of chloride concentration, temperature–humidity cycles, and other environmental variables.
6.3. Future Works
- (1)
- Develop a physics-informed data-driven feature framework integrating corrosion stress distribution, electrochemical impedance, and nonlinear statistical features. Enhance low-corrosion-rate prediction accuracy through SHAP-based feature selection and orthogonal experimental design.
- (2)
- Establish cross-scale correlation models using SEM-EDS (nanoscale morphology), industrial CT (3D pit reconstruction), and EIS-LPR (electrochemical dynamics).
- (3)
- Construct a multi-physics experimental platform incorporating chloride ingress, temperature–humidity cycles, and electrochemical monitoring.
- (4)
- Conduct gradient tests (5–50mm) combined with COMSOL simulations to quantify chloride penetration-thickness interactions.
- (5)
- Optimize SSA with hybrid strategies (simulated annealing, PSO) and develop a digital twin-based SHM platform for real-time boundary condition updating.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Al-Kheetan, M.J. Properties of Lightweight Pedestrian Paving Blocks Incorporating Wheat Straw: Micro-to Macro-Scale Investigation. Results Eng. 2022, 16, 100758. [Google Scholar] [CrossRef]
- Seguel, F.; Meruane, V. Damage Assessment in a Sandwich Panel Based on Full-Field Vibration Measurements. J. Sound Vib. 2018, 417, 1–18. [Google Scholar] [CrossRef]
- Lu, J.; Liu, J.; Yang, H.; Wan, X.; Gao, J.; Zhang, J.; Li, P. Experimental Investigation on the Mechanical Properties and Pore Structure Deterioration of Fiber-Reinforced Concrete in Different Freeze-Thaw Media. Constr. Build. Mater. 2022, 350, 128887. [Google Scholar] [CrossRef]
- Yu, L.; Francois, R.; Dang, V.H.; L’Hostis, V.; Gagne, R. Structural Performance of RC Beams Damaged by Natural Corrosion under Sustained Loading in a Chloride Environment. Eng. Struct. 2015, 96, 30–40. [Google Scholar] [CrossRef]
- Jones, S.; Martys, N.; Lu, Y.; Bentz, D. Simulation Studies of Methods to Delay Corrosion and Increase Service Life for Cracked Concrete Exposed to Chlorides. Cem. Concr. Compos. 2015, 58, 59–69. [Google Scholar] [CrossRef]
- Ali, M.S.; Ji, C.; Mirza, M.S. Durable Design of Reinforced Concrete Elements against Corrosion—ScienceDirect. Constr. Build. Mater. 2015, 93, 317–325. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M.Q. Computer Vision for SHM of Civil Infrastructure: From Dynamic Response Measurement to Damage Detection—A Review. Eng. Struct. 2018, 156, 105–117. [Google Scholar] [CrossRef]
- Kot, P.; Muradov, M.; Gkantou, M.; Kamaris, G.S.; Yeboah, D. Recent Advancements in Non-Destructive Testing Techniques for Structural Health Monitoring. Appl. Sci. 2021, 11, 2750. [Google Scholar] [CrossRef]
- Doebling, S.W.; Farrar, C.R.; Prime, M.B.; Shevitz, D.W. Damage Identification and Health Monitoring of Structural and Mechanical Systems from Changes in Their Vibration Characteristics: A Literature Review; Los Alamos National Laboratory Report LA-13070-MS; USDOE: Washington, DC, USA, 1996; Volume 30, pp. 2043–2049.
- Sohn, H.; Farrar, C.R.; Hemez, F.M.; Czarnecki, J.J. A Review of Structural Health Review of Structural Health Monitoring Literature 1996–2001; Data Acquisition; Los Alamos National Laboratory: Los Alamos, NM, USA, 2002.
- Rytter, A.; Brincker, R.; Pilegaard, L. Vibrational Based Inspection of Civil Engineering Structures. Ph.D. Thesis, Aalborg University, Aalborg, Denmark, 1991. [Google Scholar]
- Zhang, Y.; Wang, L.; Xiang, Z. Damage Detection by Mode Shape Squares Extracted from a Passing Vehicle. J. Sound Vib. 2012, 331, 291–307. [Google Scholar] [CrossRef]
- Dongming, F.; Feng, M.Q. Output-only Damage Detection Using Vehicle-induced Displacement Response and Mode Shape Curvature Index. Struct. Control. Health Monit. 2016, 23, 1088–1107. [Google Scholar]
- Zhao, J.; Zhang, L. Structural Damage Identification Based on the Modal Data Change. Int. J. Eng. Manuf. 2012, 2, 59–66. [Google Scholar] [CrossRef]
- Capecchi, D.; Ciambella, J.; Pau, A.; Vestroni, F. Damage Identification in a Parabolic Arch by Means of Natural Frequencies, Modal Shapes and Curvatures. Mecc. J. Ital. Assoc. Theor. Appl. Mech. 2016, 51, 2847–2859. [Google Scholar] [CrossRef]
- Xiao, F.; Mao, Y.; Tian, G.; Chen, G.S.; Shi, X. Partial-Model-Based Damage Identification of Long-Span Steel Truss Bridge Based on Stiffness Separation Method. Struct. Control. Health Monit. 2024, 2024, 5530300. [Google Scholar] [CrossRef]
- Mao, Y.; Xiao, F.; Tian, G.; Xiang, Y. Sensitivity Analysis and Sensor Placement for Damage Identification of Steel Truss Bridge. Structures 2025, 73, 108310. [Google Scholar] [CrossRef]
- Fan, C.; Zheng, Y.; Wang, S.; Ma, J. Prediction of Bond Strength of Reinforced Concrete Structures Based on Feature Selection and GWO-SVR Model. Constr. Build. Mater. 2023, 400, 132602. [Google Scholar] [CrossRef]
- Xu, J.G.; Zhang, J.; Hou, S.T.; Wu, G.; Hong, W. Seismic Performance Assessment of Corroded RC Columns Based on Data-Driven Machine-Learning Approach. Eng. Struct. 2022, 255, 113936. [Google Scholar] [CrossRef]
- Jiang, K.; Liang, Y.; Zhao, O. Machine-Learning-Based Design of High Strength Steel Bolted Connections. Thin-Walled Struct. 2022, 179, 109575. [Google Scholar] [CrossRef]
- Liu, H.; Chen, C.; Guo, Z.; Xia, Y.; Li, S. Overall Grouting Compactness Detection of Bridge Prestressed Bellows Based on RF Feature Selection and the GA-SVM Model. Constr. Build. Mater. 2021, 301, 124323. [Google Scholar] [CrossRef]
- Zenzen, R.; Belaidi, I.; Khatir, S.; Abdel Wahab, M. A Damage Identification Technique for Beam-like and Truss Structures Based on FRF and Bat Algorithm. Comptes Rendus Méc. 2018, 346, 1253–1266. [Google Scholar] [CrossRef]
- Gerist, S.; Maheri, M.R. Structural Damage Detection Using Imperialist Competitive Algorithm and Damage Function. Appl. Soft Comput. 2019, 77, 1–23. [Google Scholar] [CrossRef]
- Kim, N.I.; Kim, S.; Lee, J. Vibration-Based Damage Detection of Planar and Space Trusses Using Differential Evolution Algorithm. Appl. Acoust. 2019, 148, 308–321. [Google Scholar] [CrossRef]
- Avci, O.; Abdeljaber, O.; Kiranyaz, S.; Hussein, M.; Gabbouj, M.; Inman, D.J. A Review of Vibration-Based Damage Detection in Civil Structures: From Traditional Methods to Machine Learning and Deep Learning Applications. Mech. Syst. Signal Process. 2020, 147, 107077. [Google Scholar] [CrossRef]
- Fan, C.; Zheng, Y.; Wen, Y.; Sun, M. Classification and Prediction of Deformed Steel and Concrete Bond-Slip Failure Modes Based on SSA-ELM Model. Structures 2023, 57, 105131. [Google Scholar] [CrossRef]
- Razak, H.A.; Choi, F.C. The Effect of Corrosion on the Natural Frequency and Modal Damping of Reinforced Concrete Beams. Eng. Struct. 2001, 23, 1126–1133. [Google Scholar] [CrossRef]
- Park, H.W.; Lim, T. Investigating a Common Premise in Structural Health Monitoring: Are Higher Modal Frequencies More Sensitive to an Incipient Crack on a Beam than Lower Ones? Eng. Struct. 2018, 176, 385–395. [Google Scholar] [CrossRef]
- Jarek, A.; Dos Santos, A.T.; Bragana, M.O.G.P.; Pinkoski, I.M.; Neri, M.A.T.; Diniz, J.H.O.T.; Gomes, R.A.N. Experimental and Numerical Investigations to Evaluate the Structural Integrity of Concrete Beams Exposed to an Aggressive Coastal Environment. Structures 2022, 37, 795–806. [Google Scholar] [CrossRef]
- Capozucca, R. Detection of Damage Due to Corrosion in Prestressed RC Beams by Static and Dynamic Tests. Constr. Build. Mater. 2008, 22, 738–746. [Google Scholar] [CrossRef]
- Zhang, R.; Chang, H.; Li, Z.; Song, X.; Yang, J.; Xia, J. Corrosion Damage Identification of Towering Steel Headframe Based on Parametric Modeling and Data Fusion. Buildings 2022, 12, 1215. [Google Scholar] [CrossRef]
- Zeng, B.; Wang, Y.; Gong, F.; Maekawa, K. Corrosion-Induced Cracking Pattern Analysis of RC Beam under Sustained Load Considering the Poromechanical Characteristics of Corrosion Products. Buildings 2022, 12, 2256. [Google Scholar] [CrossRef]
- Kong, W.; Hou, P.; Liang, X.; Gao, F.; Liu, Q. An Interpretable Rockburst Prediction Model Based on SSA-CatBoost. Tunn. Undergr. Space Technol. 2025, 164, 106820. [Google Scholar] [CrossRef]
- Selselejoo, M.; Ahmadifar, H. DT-GWO: A Hybrid Decision Tree and GWO-Based Algorithm for Multi-Objective Task Scheduling Optimization in Cloud Computing. Sustain. Comput. Inform. Syst. 2025, 47, 101138. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, S.; Zhang, G.; Wang, Q.; Qin, Y.; Zhai, D.; Yang, Z.; Li, P. GA-OMTL: Genetic Algorithm Optimization for Multi-Task Neural Architecture Search in NIR Spectroscopy. Expert Syst. Appl. 2025, 290, 128517. [Google Scholar] [CrossRef]
- Ding, S.; Zhao, H.; Zhang, Y.; Xu, X.; Nie, R. Extreme Learning Machine: Algorithm, Theory and Applications. Artif. Intell. Rev. 2015, 44, 103–115. [Google Scholar] [CrossRef]
- Wang, M.; Zhao, G.; Wang, S. Hybrid Random Forest Models Optimized by Sparrow Search Algorithm (SSA) and Harris Hawk Optimization Algorithm (HHO) for Slope Stability Prediction. Transp. Geotech. 2024, 48, 101305. [Google Scholar] [CrossRef]
- Bagheri, M.; Jamkhaneh, M.E.; Samali, B. Effect of Seismic Soil-Pile-Structure Interaction on Mid- and High-Rise Steel Buildings Resting on a Group of Pile Foundations. Int. J. Geomech. 2018, 18, 04018103.1–04018103.27. [Google Scholar] [CrossRef]
- Yan, L.; Liu, L.; Liu, C. Bonding Performances of Polypropylene Fiber Reinforced Concrete Beam-Type Specimen at Corrosion Conditions: Experimental and Simulation Study. J. Build. Eng. 2025, 105, 112479. [Google Scholar] [CrossRef]
- Liu, C.W.; Zhang, X.D.; Huang, X.H.; Sun, S.Q. Finite-Element Model Modification for Investigating the Dynamic Behavior of Fire-Exposed Reinforced Concrete Beams with Corrosion. J. Struct. Eng. 2024, 150, 04024121. [Google Scholar] [CrossRef]
- Kanakubo, T. Impact of Corrosion on the Bond Strength between Concrete and Rebar: A Systematic Review. Materials 2022, 15, 7016. [Google Scholar] [CrossRef]
- El Maaddawy, T.A.; Soudki, K.A. Effectiveness of Impressed Current Technique to Simulate Corrosion of Steel Reinforcement in Concrete. J. Mater. Civ. Eng. 2003, 15, 41–47. [Google Scholar] [CrossRef]
- Zhang, Y.; Cheng, Y.; Tan, G.; Lyu, X.; Yang, S. Natural Frequency Response Evaluation for RC Beams Affected by Steel Corrosion Using Acceleration Sensors. Sensors 2020, 20, 5335. [Google Scholar] [CrossRef]
- Asgari, A.; Bagheri, M.; Hadizadeh, M. Advanced Seismic Analysis of Soil-Foundation-Structure Interaction for Shallow and Pile Foundations in Saturated and Dry Deposits: Insights from 3D Parallel Finite Element Modeling. Structures 2024, 69, 107503. [Google Scholar] [CrossRef]
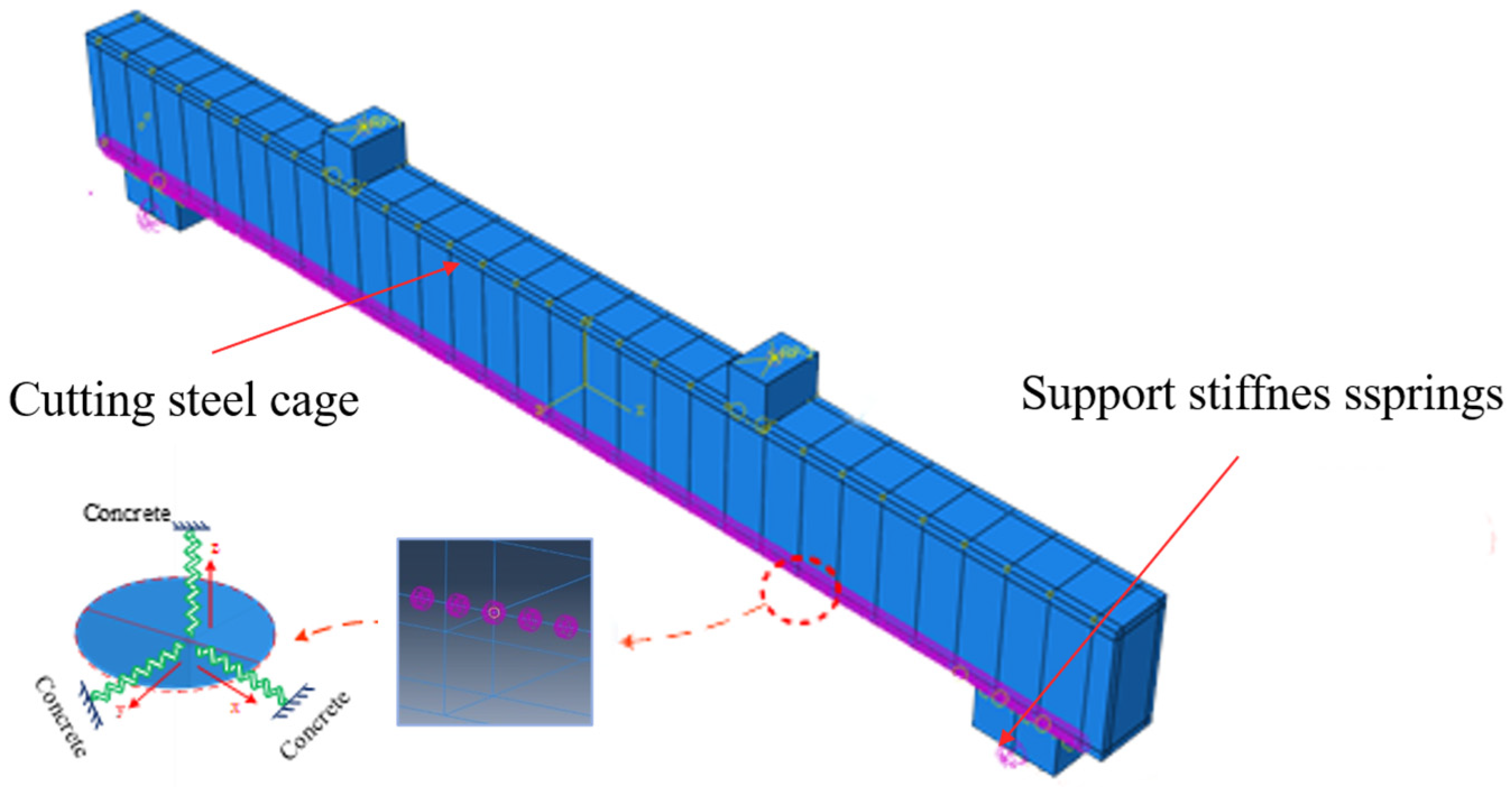

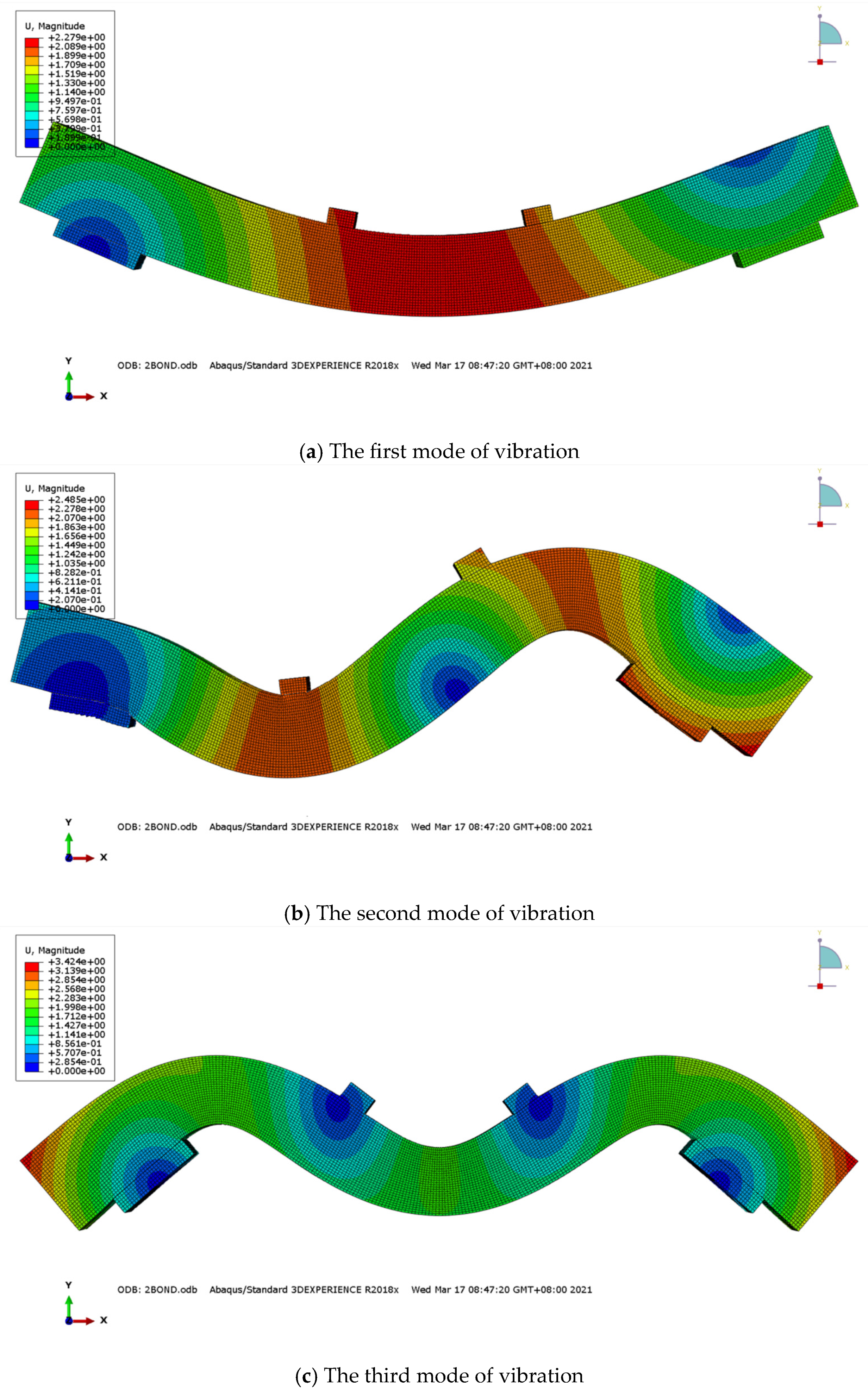






| Physical Parameter | Modulus of Elasticity for Concrete | Concrete Density | Left Bearing Offset | Right Bearing Offset | Bonding Spring Stiffness | Vertical Stiffness of Left Bearing | Vertical Stiffness of Right Support |
|---|---|---|---|---|---|---|---|
| Symbol | E | DS | D1 | D2 | K1 | K2 | K3 |
| Unit | N/mm2 | Kg/mm3 | mm | mm | N/mm | N/mm | N/mm |
| Initial value | 32,000 | 2500 | 0.1 | 0.1 | 15,000 | 15,000 | 15,000 |
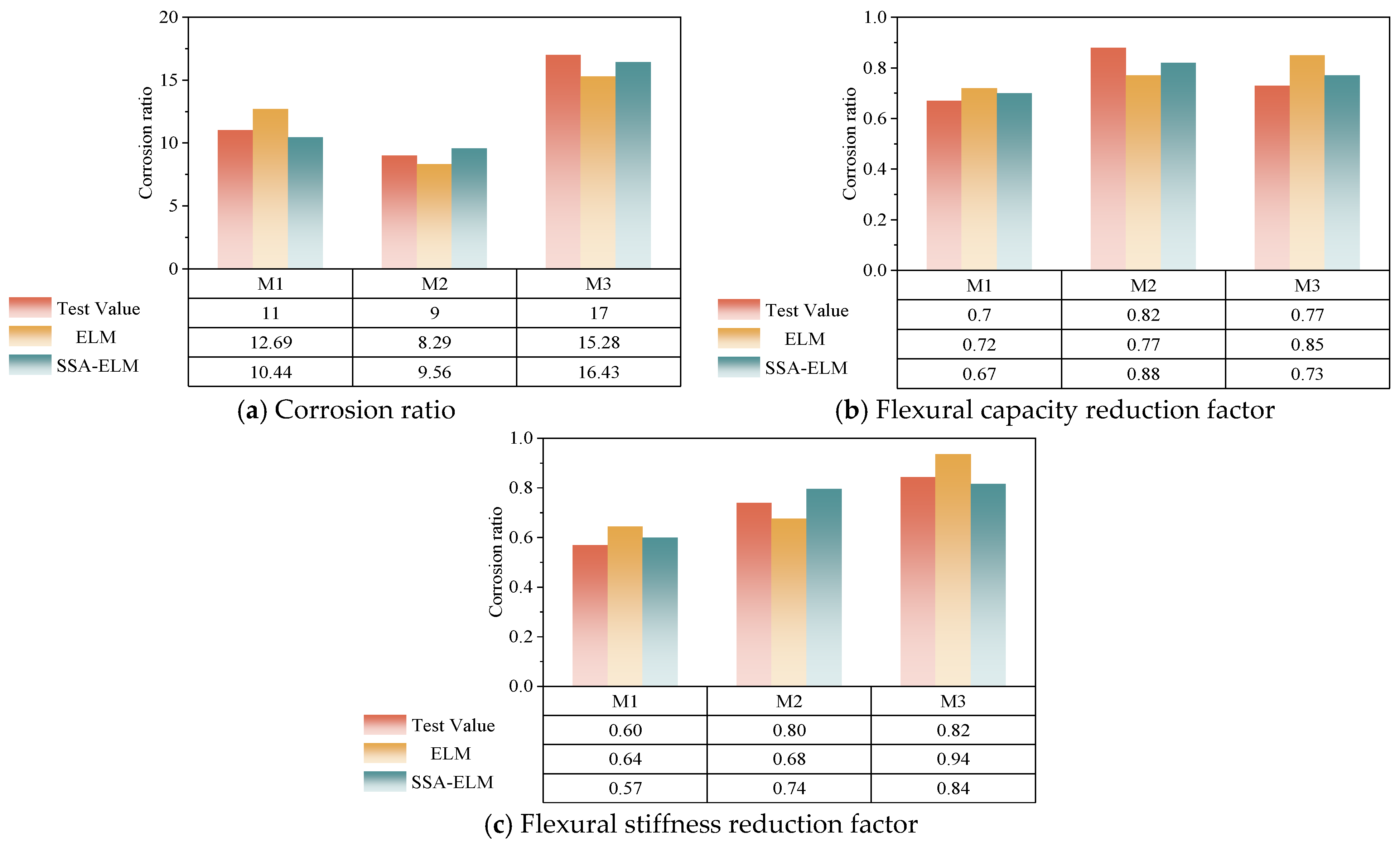
| Number | Corrosion Ratio | Flexural Capacity Reduction Factor | Flexural Stiffness Reduction Factor |
|---|---|---|---|
| M1 | 11 | 0.6652 | 0.5996 |
| M2 | 9 | 0.8824 | 0.7958 |
| M3 | 17 | 0.7258 | 0.8151 |
| Corrosion Ratio (%) | Flexural Capacity Reduction Factor | Flexural Stiffness Reduction Factor | ||||
|---|---|---|---|---|---|---|
| ELM | SSA-ELM | ELM | SSA-ELM | ELM | SSA-ELM | |
| MSE | 2.1062 | 0.3174 | 0.0111 | 0.0024 | 0.0061 | 0.0017 |
| Specimen Number | Stirrup | Longitudinal Reinforcement | Cover Thickness (mm) | Corrosion Ratio of Longitudinal Reinforcement |
|---|---|---|---|---|
| B1 | A8@100 | 2C16 | 20 | 0 |
| B2 | 0.05 | |||
| B3 | 0.1 | |||
| B4 | 0.15 | |||
| B5 | 0.2 | |||
| B6 | A8@100 | 2C16 | 30 | 0 |
| B7 | 0.1 |
| Specimen Number | Target Corrosion Ratio | Protective Layer Thickness (mm) | Rebar Diameter (mm) | Duration of Electrification (day) | Actual Corrosion Ratio | Absolute Error (%) |
|---|---|---|---|---|---|---|
| B1 | 0 | 20 | 16 | 0 | 0 | 0 |
| B2 | 0.05 | 31.5 | 0.049 | 0.1 | ||
| B3 | 0.1 | 63 | 0.069 | 3.1 | ||
| B4 | 0.15 | 94.5 | 0.110 | 4 | ||
| B5 | 0.2 | 126 | 0.141 | 5.9 | ||
| B6 | 0 | 30 | 0 | 0 | 0 | |
| B7 | 0.1 | 63 | 0.085 | 1.5 |
| Beam Number | Design Corrosion Ratio (%) | Actual Corrosion Ratio (%) | Absolute Error (%) | Yield Load (kN) | Ultimate Load (kN) |
|---|---|---|---|---|---|
| B1 | 0 | 0 | 0 | 110 | 121 |
| B2 | 5 | 4.9 | 0.1 | 90 | 101 |
| B3 | 10 | 6.9 | 3.1 | 76 | 89 |
| B4 | 15 | 11.0 | 4 | 64 | 69 |
| B5 | 20 | 14.1 | 5.9 | 57 | 61 |
| B6 | 0 | 0 | 0 | 100 | 126 |
| B7 | 10 | 8.5 | 1.5 | 95 | 115 |
| Corrosion Ratio | Flexural Capacity Reduction Factor | Flexural Stiffness Reduction Factor | ||||
|---|---|---|---|---|---|---|
| ELM | SSA-ELM | ELM | SSA-ELM | ELM | SSA-ELM | |
| MSE | 1.4749 | 0.0424 | 0.0086 | 0.0021 | 0.0057 | 0.0023 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, L.; Gao, X.; Ba, P.; Zheng, C.; Liu, C. Damage Identification of Corroded Reinforced Concrete Beams Based on SSA-ELM. Buildings 2025, 15, 2937. https://doi.org/10.3390/buildings15162937
Tian L, Gao X, Ba P, Zheng C, Liu C. Damage Identification of Corroded Reinforced Concrete Beams Based on SSA-ELM. Buildings. 2025; 15(16):2937. https://doi.org/10.3390/buildings15162937
Chicago/Turabian StyleTian, Libin, Xuyang Gao, Panfeng Ba, Chunying Zheng, and Caiwei Liu. 2025. "Damage Identification of Corroded Reinforced Concrete Beams Based on SSA-ELM" Buildings 15, no. 16: 2937. https://doi.org/10.3390/buildings15162937
APA StyleTian, L., Gao, X., Ba, P., Zheng, C., & Liu, C. (2025). Damage Identification of Corroded Reinforced Concrete Beams Based on SSA-ELM. Buildings, 15(16), 2937. https://doi.org/10.3390/buildings15162937





