Effects of High Temperature on the Interfacial Mechanical Properties of Rubber and Calcium Silicate Hydrate: Nanoscale Insights
Abstract
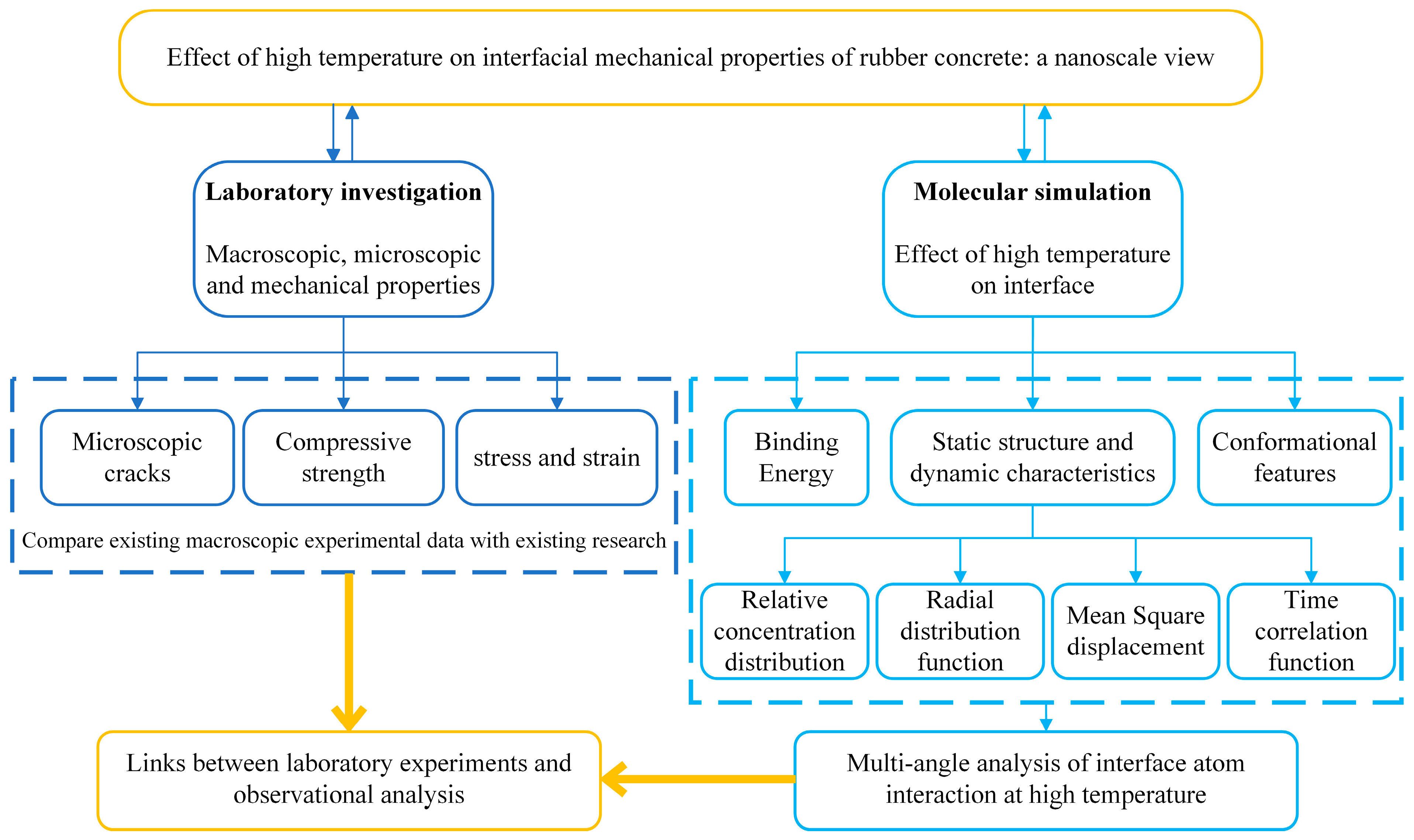
1. Introduction
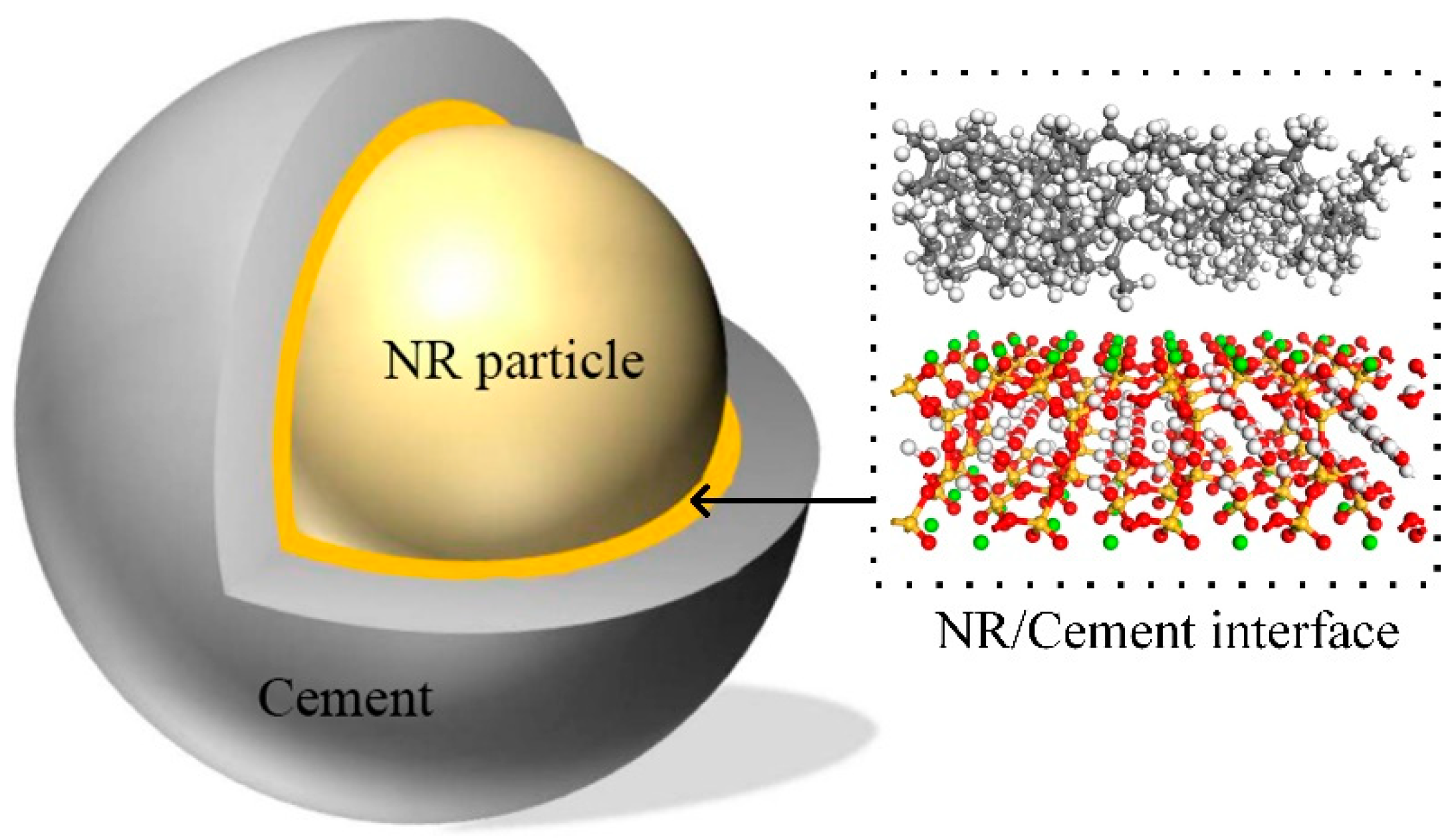
2. Simulation Method
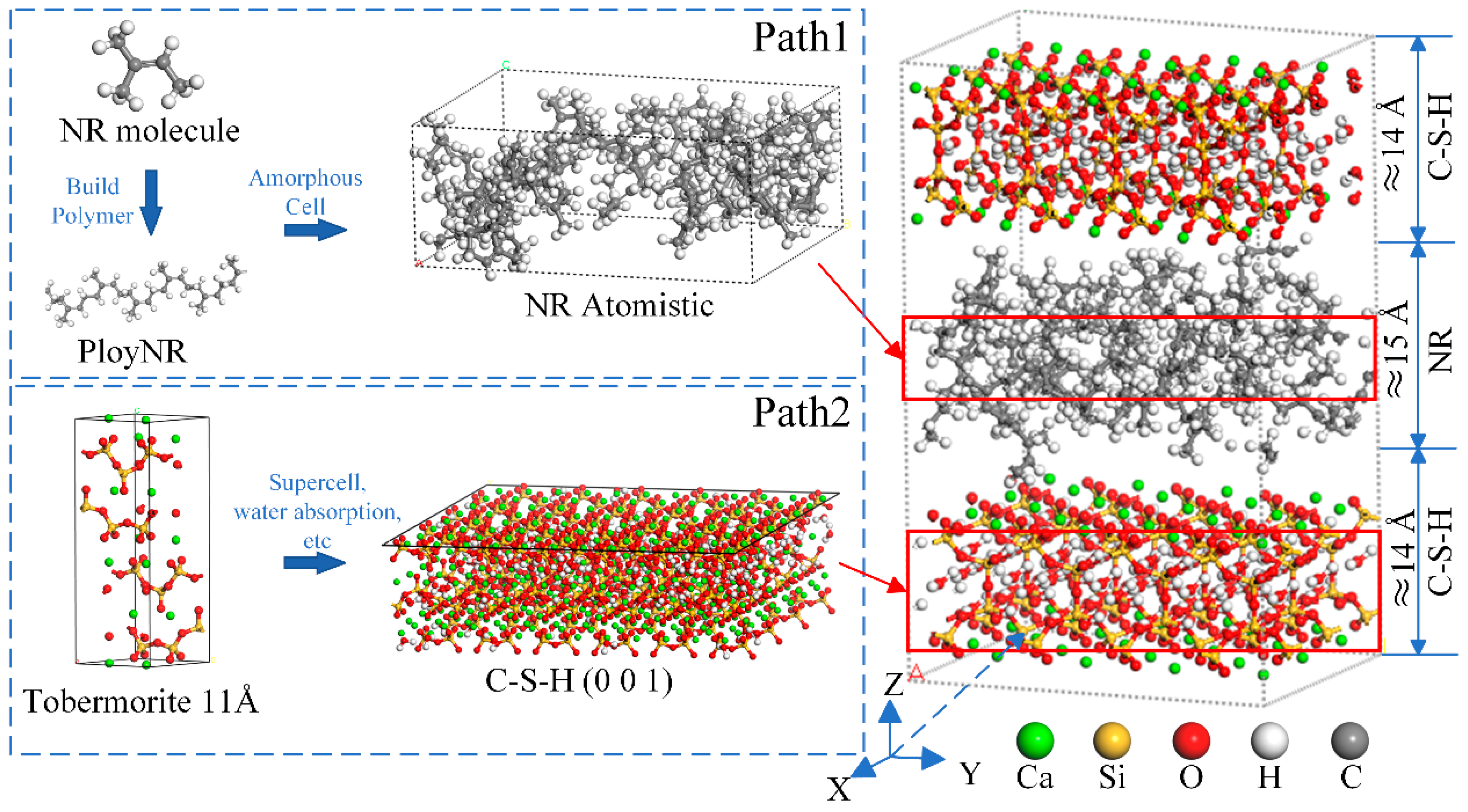
2.1. Model Construction
2.2. Simulation Details
2.3. Model Verification
3. Results and Discussion
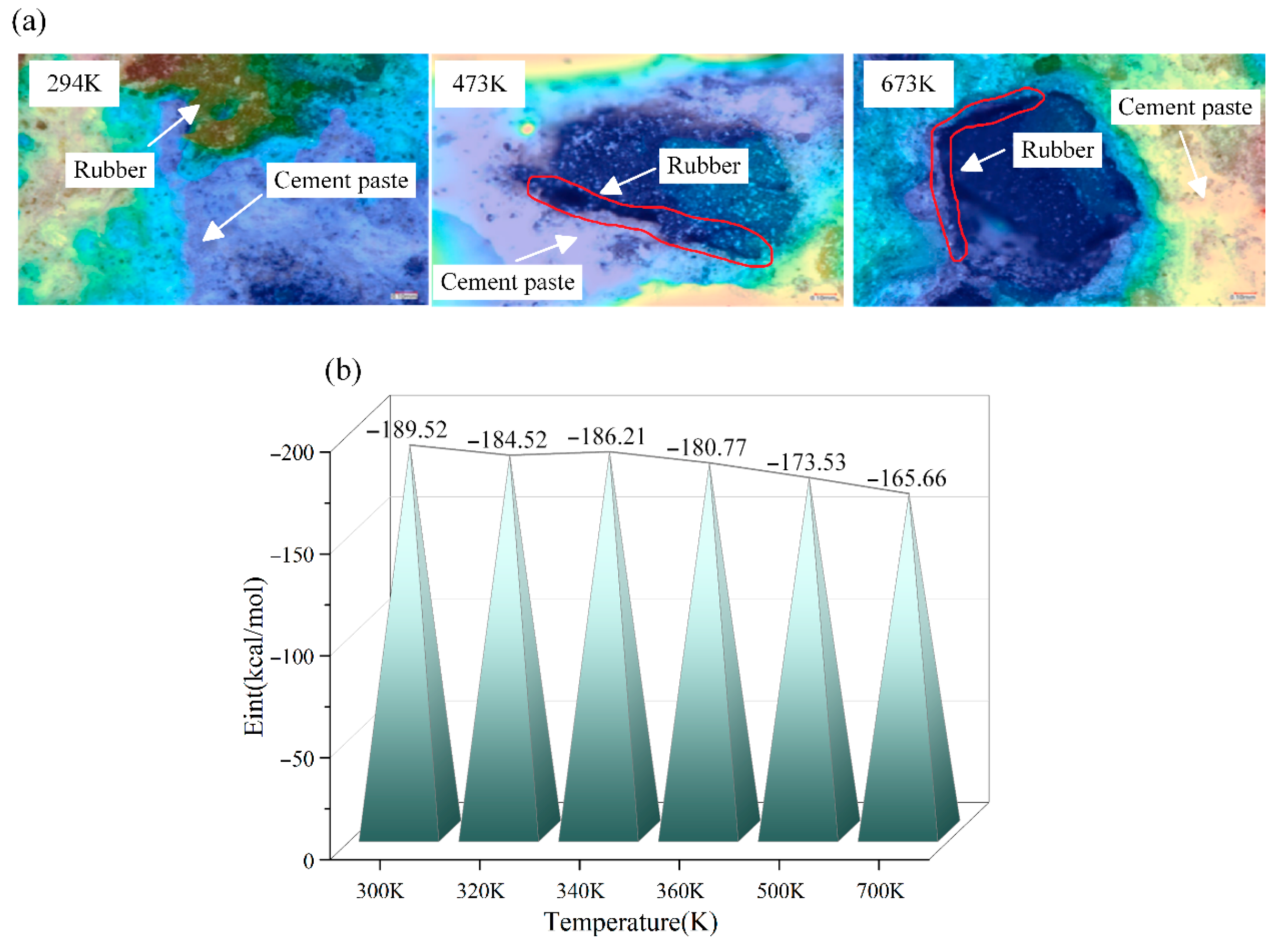
3.1. Binding Energy
3.2. Radius of Gyration
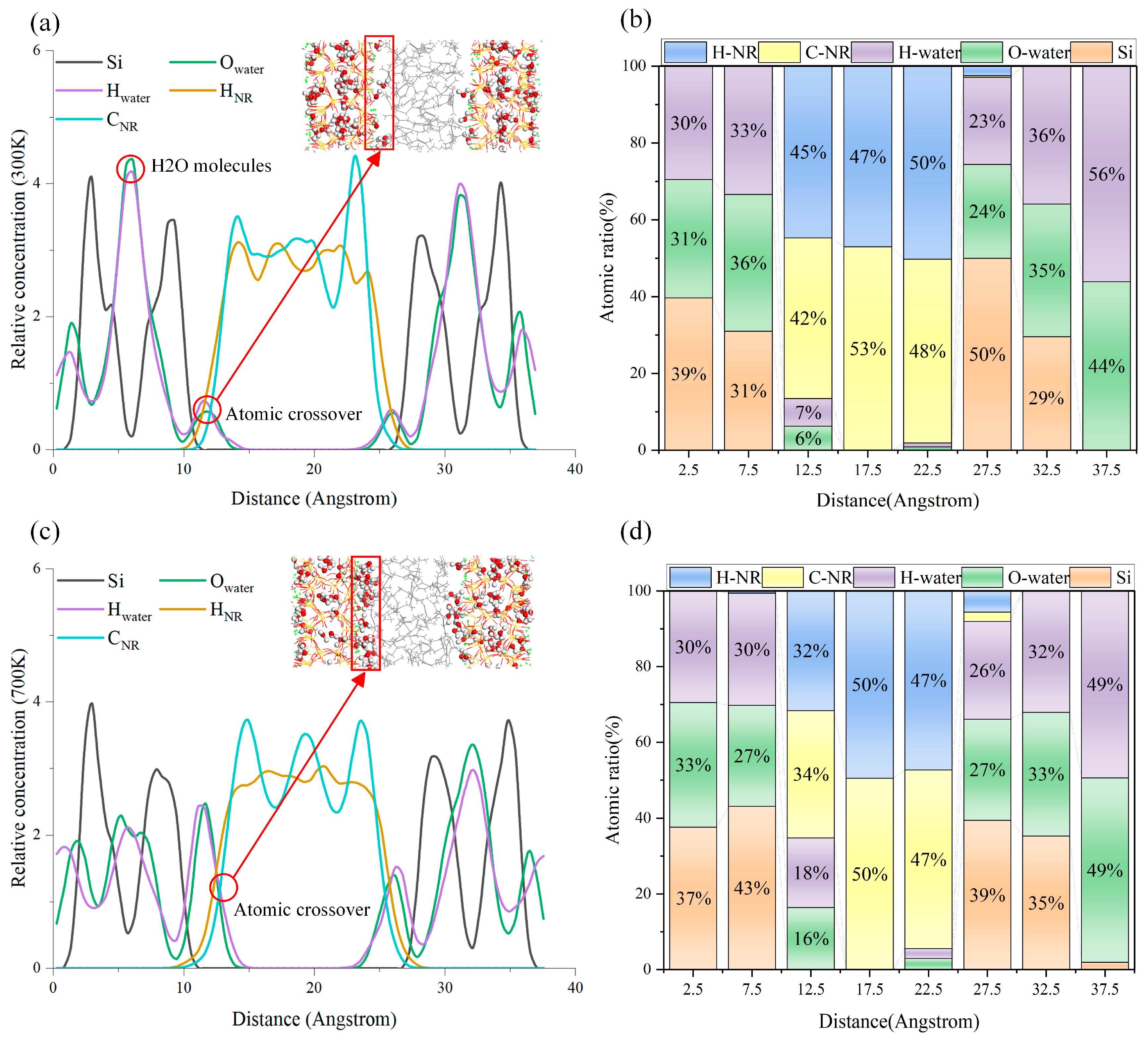
3.3. Interface Structure and Chemical Bond Analysis
3.3.1. RCD
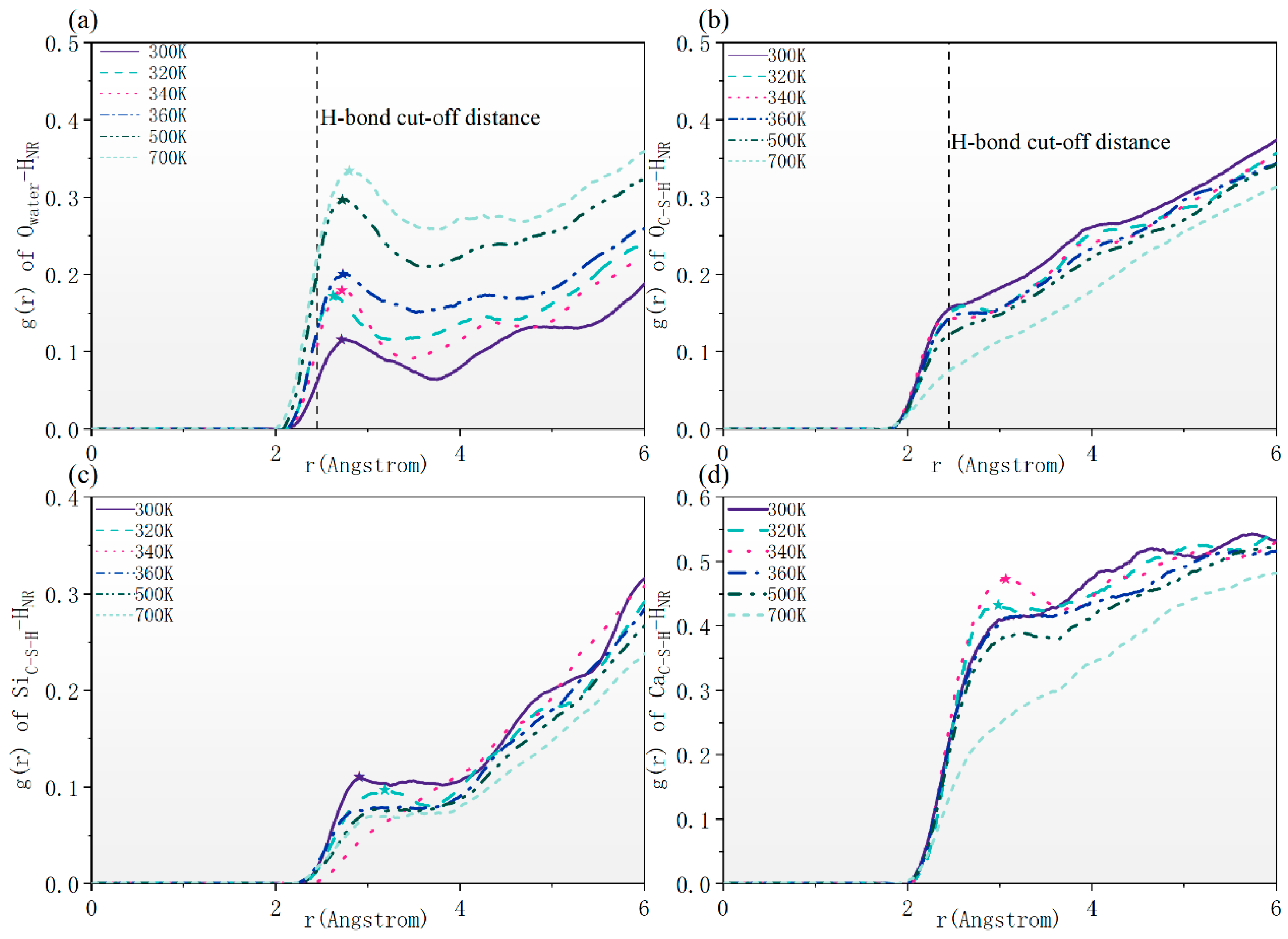
3.3.2. RDF
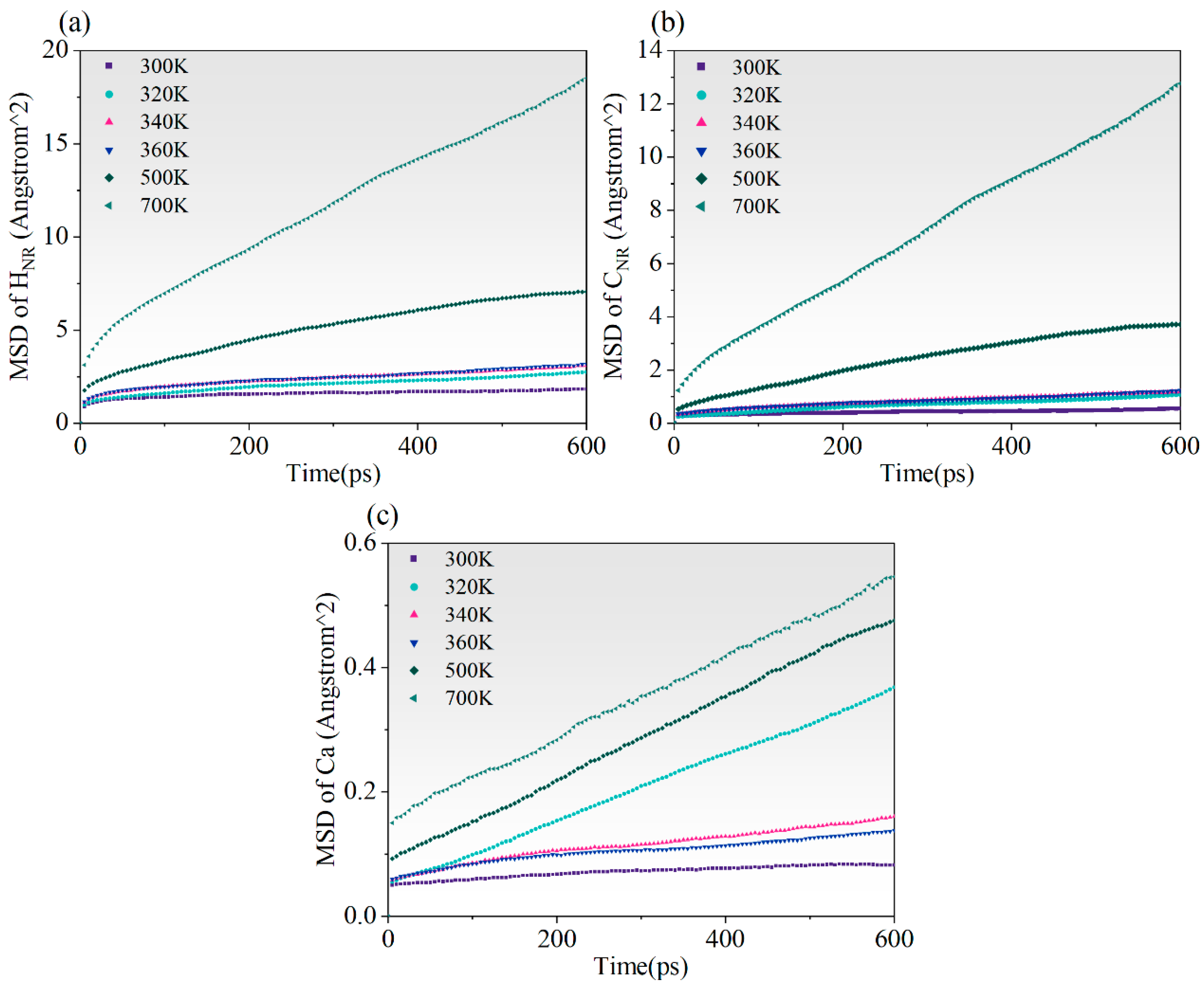
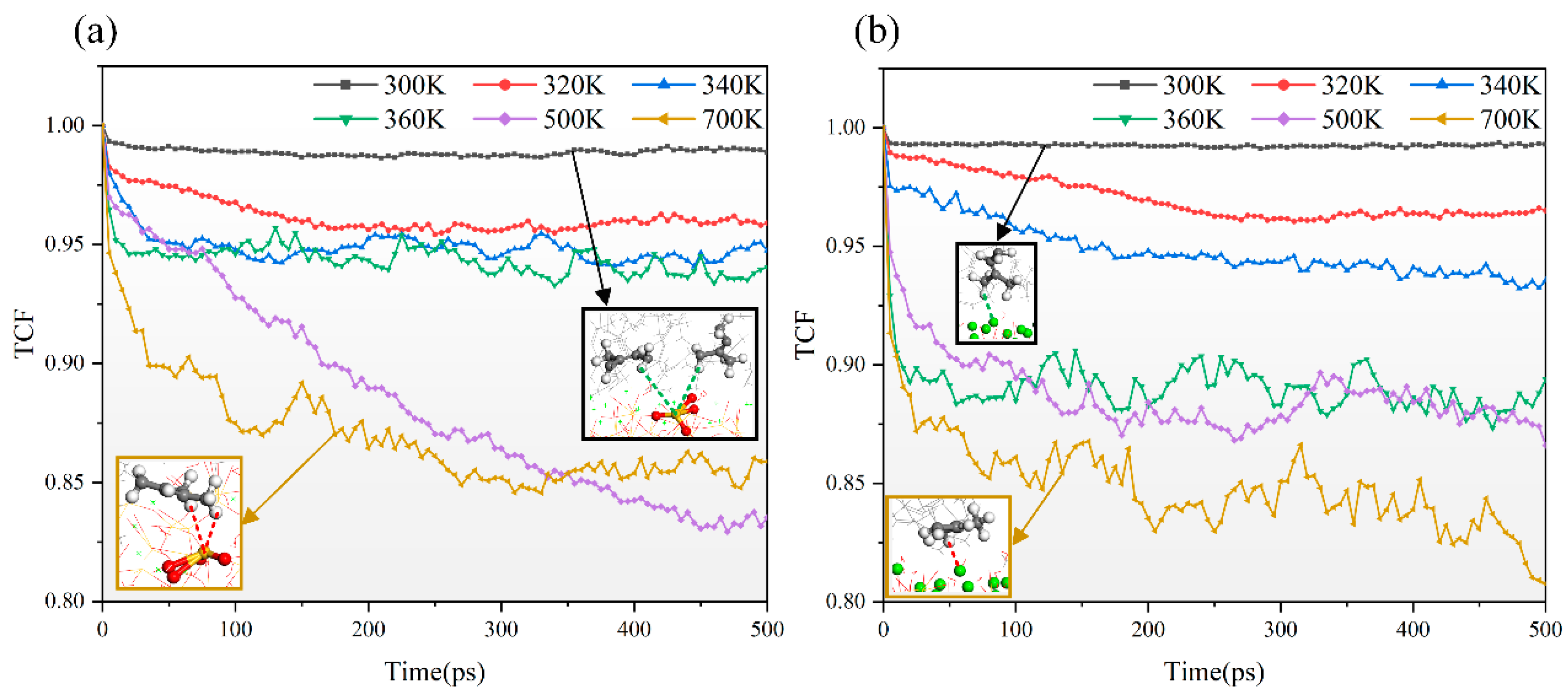
3.4. NR/C-S-H Dynamic Behavior
3.4.1. MSD
3.4.2. TCF
4. Conclusions
- (1)
- NR and C-S-H have good interfacial compatibility, but high temperatures reduce the binding energy, leading to noticeable cracking at the two-phase interface. Additionally, C-S-H has a stable skeleton with its atoms being less affected by temperature. However, atoms in NR are significantly affected by temperature; the higher the temperature, the faster the atomic movement and the poorer the stability. Notably, the number of available rubber sites on the substrate decreases at high temperatures, reducing the stability of Si-HNR and Ca-HNR bonds, and leading to a decrease in the peak stress of the material.
- (2)
- Under high temperatures, the rotation of chemical bonds in rubber molecules causes an increase in the radius of gyration, resulting in a looser molecular state. At 300 K, the radius of gyration is relatively small, and the molecular chains within the system are relatively compact. Additionally, within the temperature range of 300 K-500 K, the reduction in cohesive energy does not reach the threshold to alter the conformation of molecular chains, limiting their expansion.
- (3)
- High temperatures have little impact on the RCD. Water molecules aggregate at the two-phase interface under high temperatures, hindering the formation of chemical bonds between NR and the matrix. NR cannot form hydrogen bonds with C-S-H. Silicon atoms connect rubber to the substrate by forming HNR-Si bond chains. However, high temperatures increase the bond length of chemical bonds and reduce their bonding strength, leading to a decrease in RC compressive strength.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ince, C.; Shehata, B.M.H.; Derogar, S.; Ball, R.J. Towards the development of sustainable concrete incorporating waste tyre rubbers: A long-term study of physical, mechanical & durability properties and environmental impact. J. Clean. Prod. 2022, 334, 130223. [Google Scholar] [CrossRef]
- Yu, Y.; Jin, Z.; Shen, D.; An, J.; Sun, Y.; Li, N. Microstructure evolution and impact resistance of crumb rubber concrete after elevated temperatures. Constr. Build. Mater. 2023, 384, 131340. [Google Scholar] [CrossRef]
- Nyarko, M.H.; Nyarko, E.K.; Ademović, N.; Miličević, I.; Šipoš, T.K. Modelling the Influence of Waste Rubber on Compressive Strength of Concrete by Artificial Neural Networks. Materials 2019, 12, 561. [Google Scholar] [CrossRef]
- Ehsan, M.; Mahdi, K. Recycling of landfill waste tyre in construction materials: Durability of concrete made with chipped rubber. Constr. Build. Mater. 2023, 409, 134114. [Google Scholar] [CrossRef]
- Peng, Y.; Zhao, G.; Qi, Y.; Zeng, Q. In-situ assessment of the water-penetration resistance of polymer modified cement mortars by μ-XCT, SEM and EDS. Cem. Concr. Compos. 2020, 114, 103821. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, Z.; Hu, Y.; Wang, X. Bearing Strength of Crumb Rubber Concrete under Partial Area Loading. Materials 2020, 13, 2446. [Google Scholar] [CrossRef]
- Wang, X.; Chen, C. Vibration Table Test of Prefabricated L-Shaped Column Concrete Structure. Buildings 2025, 15, 2329. [Google Scholar] [CrossRef]
- Fadiel, A.A.M.; Abu-Lebdeh, T.; Munteanu, I.S.; Niculae, E.; Petrescu, F.I.T. Mechanical Properties of Rubberized Concrete at Elevated Temperatures. J. Compos. Sci. 2023, 7, 283. [Google Scholar] [CrossRef]
- Elsayed, M.; Almutairi, A.D.; Azzam, E.O.A.; Dahish, H.A.; Gomaa, M.S. Performance of rubberized reinforced concrete columns at ambient and high temperatures. Case Study Constr. Mater. 2023, 19, e02605. [Google Scholar] [CrossRef]
- Yan, L.; Liang, J.; Li, W. Axial Compression Behavior of Rubberized Concrete-Filled Square Steel Tubular Columns after Exposed to High Temperatures. Adv. Mater. Sci. Eng. 2022, 2022, 1506483. [Google Scholar] [CrossRef]
- Su, Q.; Xu, J. Durability and mechanical properties of rubber concrete incorporating basalt and polypropylene fibers: Experimental evaluation at elevated temperatures. Constr. Build. Mater. 2023, 368, 130445. [Google Scholar] [CrossRef]
- Gupta, T.; Siddique, S.; Sharma, R.K.; Chaudhary, S. Effect of elevated temperature and cooling regimes on mechanical and durability properties of concrete containing waste rubber fiber. Constr. Build. Mater. 2017, 137, 35–45. [Google Scholar] [CrossRef]
- Han, Y.; Lv, Z.; Bai, Y.; Han, G.; Li, D. Experimental Study on the Mechanical Properties of Crumb Rubber Concrete after Elevated Temperature. Polymers 2023, 15, 3102. [Google Scholar] [CrossRef]
- Mousavimehr, M.; Nematzadeh, M. Predicting post-fire behavior of crumb rubber aggregate concrete. Constr. Build. Mater. 2019, 229, 116834. [Google Scholar] [CrossRef]
- Al-Kheetan, M.J. Properties of lightweight pedestrian paving blocks incorporating wheat straw: Micro-to macro-scale investigation. Results Eng. 2022, 16, 100758. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, W.; Wang, S. Multiscale analysis of recycled coarse aggregate concrete under the synergistic action of KH560 and PVA fibers. Constr. Build. Mater. 2024, 419, 135433. [Google Scholar] [CrossRef]
- Wang, W.; Feng, Y.; Li, X. EVA/KH560 synergistically modified recycled concrete mechanical properties—Experiment and molecular dynamics simulations. J. Mol. Graph. Model. 2024, 126, 108641. [Google Scholar] [CrossRef]
- Huang, H.; Luo, J.; Peng, C.; Sun, T.; Deng, T.; Hu, J.; Anvarovna, K.G.; Ugli, N.A.D.; Hou, D.; Wei, J.; et al. Interfacial bond between modified micro carbon fiber and high-strength cement paste in UHPC: Bond-slip tests and molecular dynamic simulation. Cem. Concr. Compos. 2023, 142, 105168. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, Q.; Yang, X. Study on micro-mechanical properties of EVA modified rubber-cementitious materials based on molecular dynamics simulation. Constr. Build. Mater. 2024, 416, 135132. [Google Scholar] [CrossRef]
- Kang, J.; Liu, Y.; Yuan, J.; Chen, C.; Wang, L.; Yu, Z. Effectiveness of surface treatment on rubber particles towards compressive strength of rubber concrete: A numerical study on rubber-cement interface. Constr. Build. Mater. 2022, 350, 128820. [Google Scholar] [CrossRef]
- Han, Q.; Wang, N.; Zhang, J.; Yu, J.; Hou, D.; Dong, B. Experimental and computational study on chloride ion transport and corrosion inhibition mechanism of rubber concrete. Constr. Build. Mater. 2020, 268, 121105. [Google Scholar] [CrossRef]
- Yu, J.; Hou, D.; Zhang, J. Molecular dynamics study on ultra-confined NaCl solution in the silane coupling agent modified rubber calcium silicate hydrate nano-pore. Constr. Build. Mater. 2020, 270, 121418. [Google Scholar] [CrossRef]
- Li, L.; Qin, D.; Xu, Z.; Feng, Y. Study on Strengthening Mechanism of Epoxy Resin/Rubber Concrete Interface by Molecular Dynamics Simulation. Adv. Civ. Eng. 2022, 2022, 5100758. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, W.; Wang, S. PVA fiber/cement-based interface in silane coupler KH560 reinforced high performance concrete—Experimental and molecular dynamics study. Constr. Build. Mater. 2023, 395, 132184. [Google Scholar] [CrossRef]
- Pellenq, R.J.M.; Kushima, A.; Shahsavari, R.; Van Vliet, K.J.; Buehler, M.J.; Yip, S.; Ulm, F.J. A realistic molecular model of cement hydrates. Proc. Natl. Acad. Sci. USA 2009, 106, 16102–16107. [Google Scholar] [CrossRef]
- Tang, S.; Wang, Y.; Geng, Z.; Xu, X.; Yu, W.; A, H.; Chen, J. Structure, Fractality, Mechanics and Durability of Calcium Silicate Hydrates. Fractal Fract. 2021, 5, 47. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, M.; Tong, X.; Wang, S.; Kang, X. Molecular insights into the interactions between chloride liquids and C-S-H nanopore surfaces under electric field-induced transport. J. Mol. Liq. 2022, 364, 119942. [Google Scholar] [CrossRef]
- Kovačević, G.; Persson, B.; Nicoleau, L.; Nonat, A.; Veryazov, V. Atomistic modeling of crystal structure of Ca1.67SiHx. Cem. Concr. Res. 2015, 67, 197–203. [Google Scholar] [CrossRef]
- Hou, D.; Ma, H.; Zhu, Y.; Li, Z. Calcium silicate hydrate from dry to saturated state: Structure, dynamics and mechanical properties. Acta Mater. 2014, 67, 81–94. [Google Scholar] [CrossRef]
- Puibasset, J.; Pellenq, R.J.-M. Grand canonical monte carlo simulation study of water adsorption in silicalite at 300 K. J. Phys. Chem. B 2008, 112, 6390–6397. [Google Scholar] [CrossRef]
- Hou, D.; Zhang, J.; Li, Z.; Zhu, Y. Uniaxial tension study of calcium silicate hydrate (C–S–H): Structure, dynamics and mechanical properties. Mater. Struct. 2015, 48, 3811–3824. [Google Scholar] [CrossRef]
- Hou, D.; Zhang, W.; Sun, J.; Zhang, J. Structure, dynamics and mechanical properties evolution of calcium-silicate-hydrate induced by Fe ions: A molecular dynamics study. Constr. Build. Mater. 2021, 287, 122875. [Google Scholar] [CrossRef]
- Hou, D.; Wu, C.; Yang, Q.; Zhang, W.; Lu, Z.; Wang, P.; Li, J.; Ding, Q. Insights on the molecular structure evolution for tricalcium silicate and slag composite: From 29 Si and 27 Al NMR to molecular dynamics. Compos. Part B 2020, 202, 108401. [Google Scholar] [CrossRef]
- Bahraq, A.A.; Al-Osta, M.A.; Obot, I.B.; Al-Amoudi, O.S.B.; Saleh, T.A.; Maslehuddin, M. Improving the adhesion properties of cement/epoxy interface using graphene-based nanomaterials: Insights from molecular dynamics simulation. Cem. Concr. Compos. 2022, 134, 104801. [Google Scholar] [CrossRef]
- Wang, Z.; Su, M.; Duan, X.; Yao, X.; Han, X.; Song, J.; Ma, L. Molecular Dynamics Simulation of the Thermomechanical and Tribological Properties of Graphene-Reinforced Natural Rubber Nanocomposites. Polymers 2022, 14, 5056. [Google Scholar] [CrossRef]
- Zhang, X.; Fu, Q.; Luo, Y.; Wang, J.; Jia, H. A combined experimental and molecular dynamics simulation study on customizing surface chemistry of graphene oxide toward high-performance natural rubber composites. Polym. Int. 2022, 72, 790–797. [Google Scholar] [CrossRef]
- Sun, H. COMPASS: An ab Initio Force-Field Optimized for Condensed-Phase Applications Overview with Details on Alkane and Benzene Compounds. J. Phys. Chem. B 1998, 102, 7338–7364. [Google Scholar] [CrossRef]
- Bahraq, A.A.; Al-Osta, M.A.; Al-Amoudi, O.S.B.; Saleh, T.A.; Obot, I.B. Atomistic simulation of polymer-cement interactions: Progress and research challenges. Constr. Build. Mater. 2022, 327, 126881. [Google Scholar] [CrossRef]
- Xu, J.; Chen, X.; Yang, G.; Niu, X.; Chang, F.; Lacidogna, G. Review of research on micromechanical properties of cement-based materials based on molecular dynamics simulation. Constr. Build. Mater. 2021, 312, 125389. [Google Scholar] [CrossRef]
- Feng, Y.; Qin, D.; Zhao, C.; Li, Y. Multiscale Enhancement Mechanisms of EVA on EPS-Cement Composites. J. Mater. Civil. Eng. 2023, 35, 04023102. [Google Scholar] [CrossRef]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Bereau, T. Multi-timestep Integrator for the Modified Andersen Barostat. Phys. Proc. 2015, 68, 7–15. [Google Scholar] [CrossRef][Green Version]
- Tang, S.; Aa, H.; Chen, J.; Yu, P.; Chen, E.; Deng, H.; He, Z. The interactions between water molecules and C-S-H surfaces in loads-induced nanopores: A molecular dynamics study. Appl. Surf. Sci. 2019, 496, 143744. [Google Scholar] [CrossRef]
- Dharmawardhana, C.C.; Misra, A.; Aryal, S.; Rulis, P.; Ching, W.Y. Role of interatomic bonding in the mechanical anisotropy and interlayer cohesion of CSH crystals. Cem. Concr. Res. 2013, 52, 123–130. [Google Scholar] [CrossRef]
- Srivastava, A.; Sharma, S.; Patel, P.R. Atomistic Modeling of Mechanical Properties and Creep Behavior of Graphene Oxide Reinforced Natural Rubber Composites. Macromol. Theor. Simul. 2022, 32, 2200053. [Google Scholar] [CrossRef]
- Wang, X.; Wang, B.; Yuan, Y.; Yang, T.; Dong, G.; Shi, C. Study on the Effect of EICP Combined with Nano-SiO2 and Soil Stabilizer on Improving Loess Surface Strength. Buildings 2025, 15, 1998. [Google Scholar] [CrossRef]
- Yu, C.; Hu, K.; Yang, Q.; Wang, D.; Zhang, W.; Chen, G.; Kapyelata, C. Analysis of the Storage Stability Property of Carbon Nanotube/Recycled Polyethylene-Modified Asphalt Using Molecular Dynamics Simulations. Polymers 2021, 13, 1658. [Google Scholar] [CrossRef]
- Zang, Y.; Yang, Q.; Wang, P.; Wang, X.; Hou, D.; Zhao, T.; Chen, J. Molecular dynamics simulation of calcium silicate hydrate/tannic acid interfacial interactions at different temperatures: Configuration, structure and dynamic. Constr. Build. Mater. 2022, 326, 126820. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, W.; Wang, S.; Niu, Z.; Li, L. Multi-scale analysis of mechanical properties of KH-560 coupling agent modified PVA fiber-rubber concrete. Compos. Interface 2023, 30, 983–1010. [Google Scholar] [CrossRef]
- Qi, C.; Manzano, H.; Spagnoli, D.; Chen, Q.; Fourie, A. Initial hydration process of calcium silicates in Portland cement: A comprehensive comparison from molecular dynamics simulations. Cem. Concr. Res. 2021, 149, 106576. [Google Scholar] [CrossRef]
- Liu, Q.; Ding, G.; Zhang, Z.; Fu, C.; Oeser, M. Investigation on bitumen-epoxy interface in cold mixed epoxy bitumen using experimental observation and molecular dynamics simulation. Constr. Build. Mater. 2021, 303, 124490. [Google Scholar] [CrossRef]
- Peng, Z.; Zhou, Y.; Wang, J.; Chen, L.; Miao, C. The impediment and promotion effects and mechanisms of lactates on the hydration of supersulfated cements—Aiming at a performance enhancement. J. Clean. Prod. 2022, 341, 130751. [Google Scholar] [CrossRef]
- Zhang, J.; Li, W.; Yan, Y.; Wang, Y.; Liu, B.; Shen, Y.; Chen, H.; Liu, H. Molecular insight into nanoscale water films dewetting on modified silica surfaces. Phys. Chem. Chem. Phys. 2015, 17, 451. [Google Scholar] [CrossRef] [PubMed]
- Obot, I.B.; Bahraq, A.A.; Alamri, A.H. Density functional theory and molecular dynamics simulation of the corrosive particle diffusion in pyrimidine and its derivatives films. Comp. Mater. Sci. 2022, 210, 111428. [Google Scholar] [CrossRef]
- Yu, C.; Hu, K.; Yang, Q.; Chen, Y. Multi-scale observation of oxidative aging on the enhancement of high-temperature property of SBS-modified asphalt. Constr. Build. Mater. 2021, 313, 125478. [Google Scholar] [CrossRef]
- Lu, Z.; Yu, J.; Yao, J.; Hou, D. Experimental and molecular modeling of polyethylene fiber/cement interface strengthened by graphene oxide. Cem. Concr. Compos. 2020, 112, 103676. [Google Scholar] [CrossRef]



| C-S-H | Comparison Value | NR | Comparison Value | NR/C-S-H | Comparison Value | |
|---|---|---|---|---|---|---|
| Density (g/cm3) | 2.6 | 2.44 [43], 2.604 [24] | 0.864 | 0.897 [34] | ||
| Young’s modulus (GPa) | 90.25 | 77.0–129.7 [33,44] | 1.836 | 1.893 [45] | ||
| Bulk modulus (GPa) | 34.76 | 34.68 [22] | ||||
| Shear modulus (GPa) | 15.75 | 12.35 [22] |
| Temperature | ETotal (kcal/mol) | EP (kcal/mol) | EK (kcal/mol) | ||
|---|---|---|---|---|---|
| Total | vdW | Elec | |||
| 300 K | −101,283 | −102,806 | 10,504 | −125,821 | 1523.403 |
| 320 K | −101,056 | −102,692 | 10,580 | −125,786 | 1635.868 |
| 340 K | −100,725 | −102,463 | 10,503 | −125,127 | 1738.107 |
| 360 K | −100,757 | −102,597 | 10,604 | −125,958 | 1840.353 |
| 500 K | −99,738 | −102,294 | 10,743 | −126,928 | 2556.043 |
| 700 K | −98,097 | −101,676 | 10,906 | −127,854 | 3578.466 |
| Temperature | HNR | CNR | Ca |
|---|---|---|---|
| 300 K | 0.08 | 0.04 | 0.008 |
| 320 K | 0.23 | 0.138 | 0.041 |
| 340 K | 0.247 | 0.131 | 0.018 |
| 360 K | 0.241 | 0.115 | 0.022 |
| 500 K | 0.397 | 0.256 | 0.043 |
| 700 K | 1.835 | 1.473 | 0.063 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Du, Y.; Li, L.; Mei, Y.; Wang, C. Effects of High Temperature on the Interfacial Mechanical Properties of Rubber and Calcium Silicate Hydrate: Nanoscale Insights. Buildings 2025, 15, 2825. https://doi.org/10.3390/buildings15162825
Zhang X, Du Y, Li L, Mei Y, Wang C. Effects of High Temperature on the Interfacial Mechanical Properties of Rubber and Calcium Silicate Hydrate: Nanoscale Insights. Buildings. 2025; 15(16):2825. https://doi.org/10.3390/buildings15162825
Chicago/Turabian StyleZhang, Xuejing, Yongkang Du, Lei Li, Yuan Mei, and Chao Wang. 2025. "Effects of High Temperature on the Interfacial Mechanical Properties of Rubber and Calcium Silicate Hydrate: Nanoscale Insights" Buildings 15, no. 16: 2825. https://doi.org/10.3390/buildings15162825
APA StyleZhang, X., Du, Y., Li, L., Mei, Y., & Wang, C. (2025). Effects of High Temperature on the Interfacial Mechanical Properties of Rubber and Calcium Silicate Hydrate: Nanoscale Insights. Buildings, 15(16), 2825. https://doi.org/10.3390/buildings15162825







