ANN and RF Optimized by Hunter–Prey Algorithm for Predicting Post-Blast RC Column Morphology
Abstract
1. Introduction
2. FE Simulation and Database Establishment
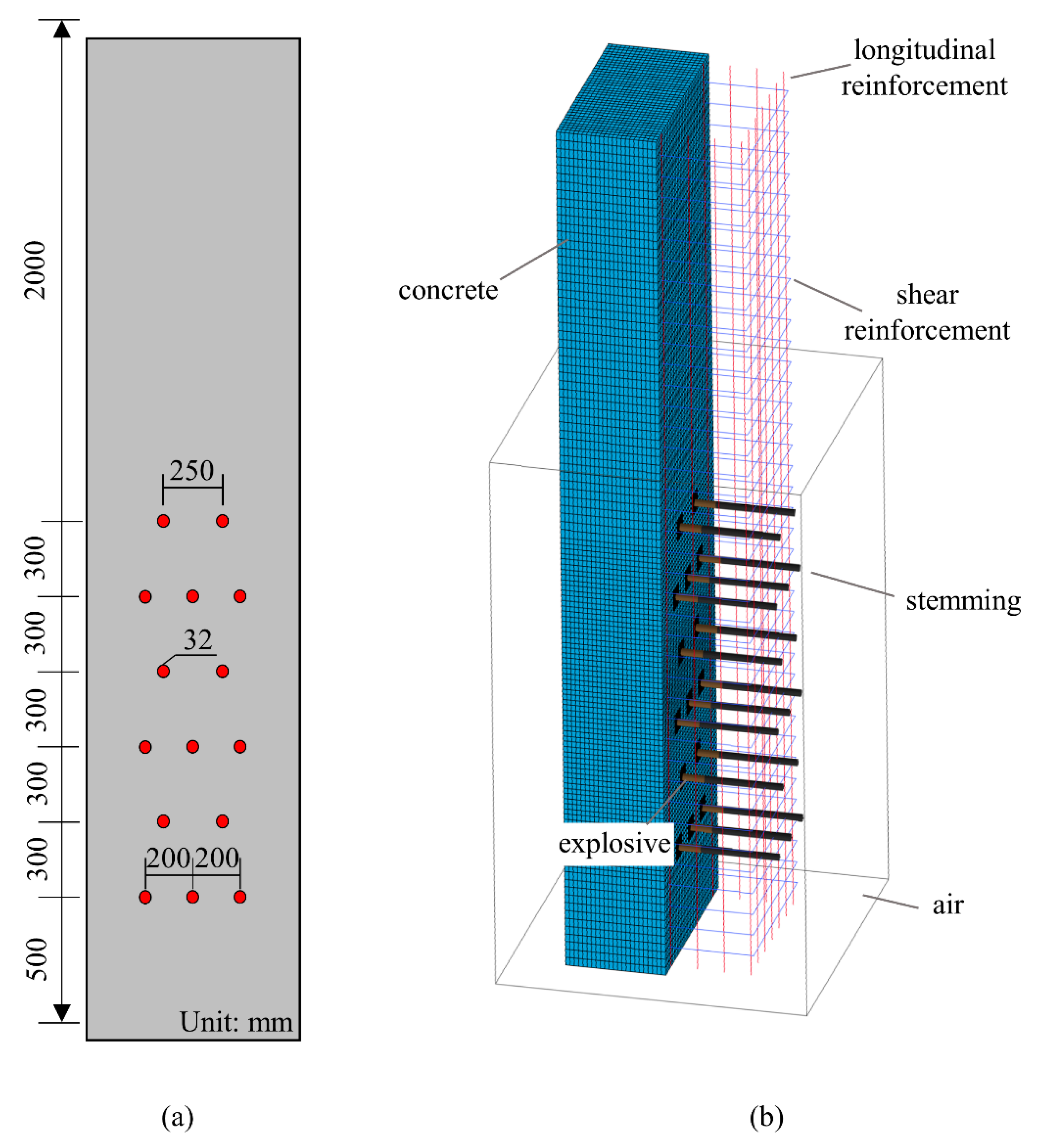
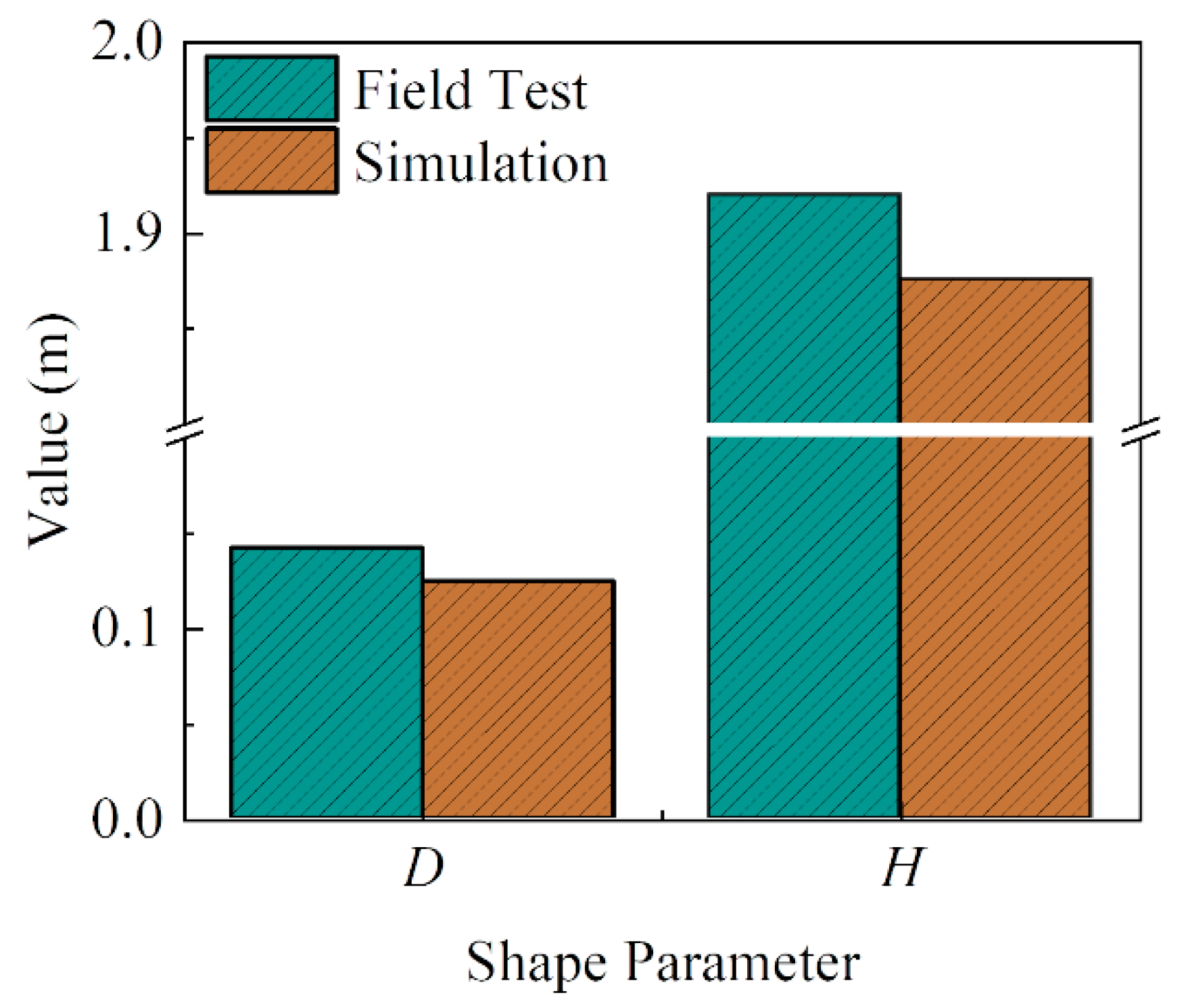
2.1. The Establishment and Calibration of FE Model
2.2. Numerical Simulation of the Post-Blast Deformation Morphology of Longitudinal Reinforcement
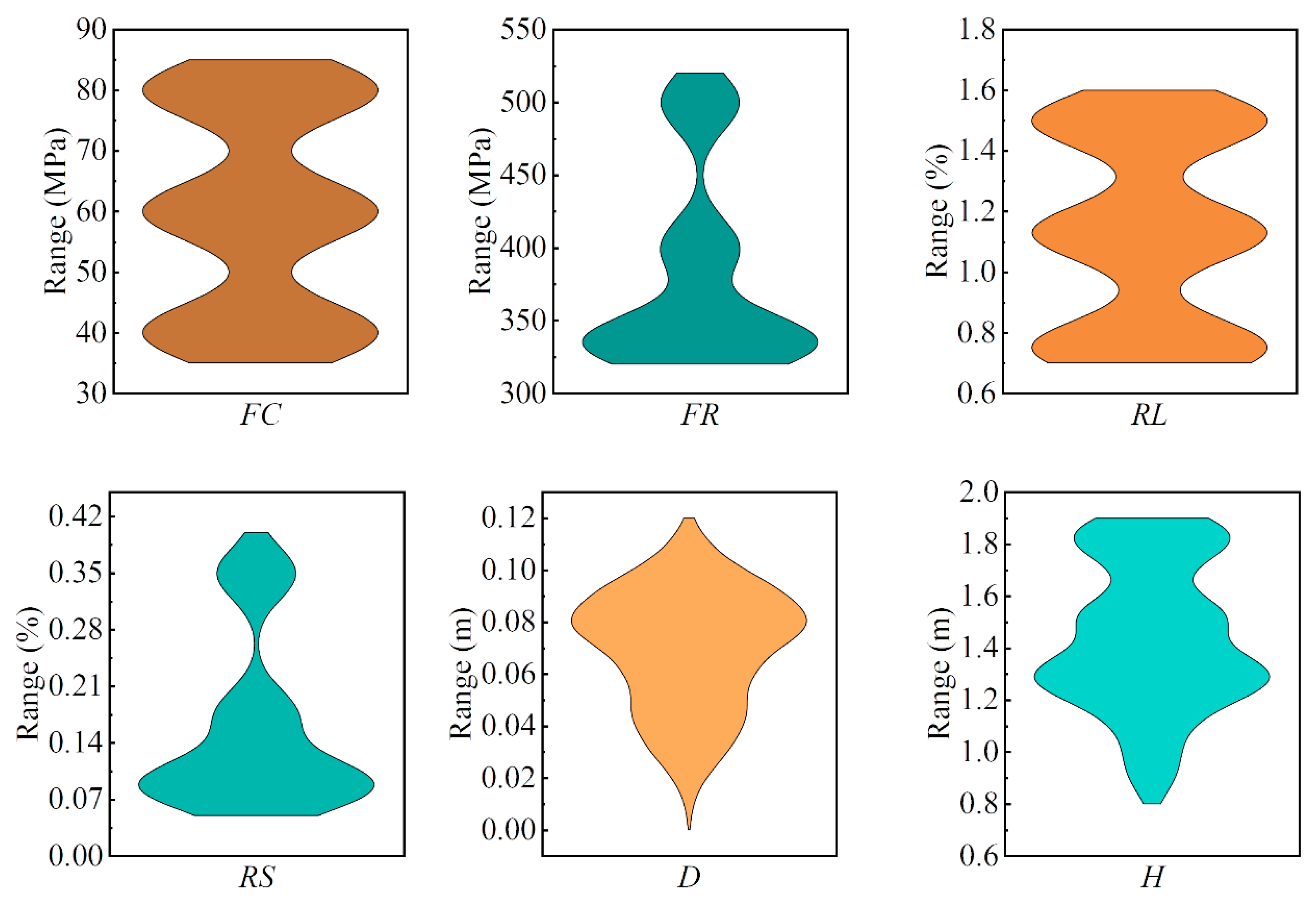
2.3. Data Collection and Database Establishment
3. Intelligence Algorithms
3.1. ANN Algorithm
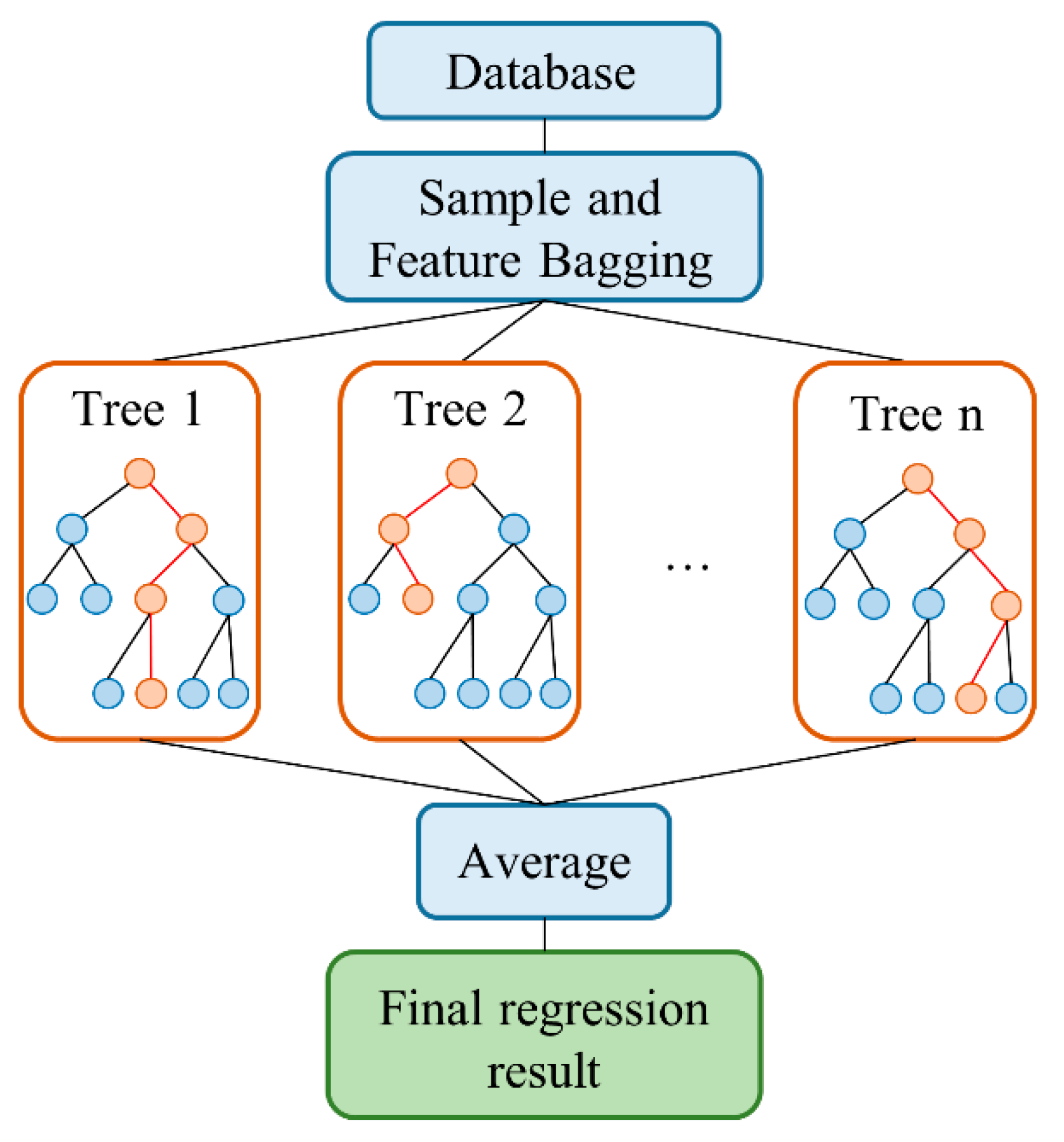
3.2. RF Algorithm
3.3. HPO Algorithm
- (1)
- Hunter behavior: initially, hunters move randomly within the search space to explore potential solutions. As optimization progresses, hunters adaptively adjust their movement and gradually converge toward prey. Although the prey population is typically dispersed, hunters strategically identify outlier prey—those positioned farthest from the population’s average location—as primary targets. Once a target is identified, hunters actively pursue and attack it, mimicking the convergence toward optimal solutions. The hunter search mechanism is given by Equation (2):
- (2)
- Prey behavior: before detecting hunters, prey moves randomly in search of food, exploring different regions of the solution space. Upon sensing the presence of hunters, prey respond collectively by fleeing toward safer locations, which are defined as the points farthest from hunters [51]. This escape mechanism enhances solution diversity and prevents premature convergence by maintaining a wide search distribution. The updated position of the prey is shown in Equation (3).
4. Intelligence Model Establishment and Evaluation
4.1. Model Establishment
4.2. Evaluation Indices
5. Results and Discussion
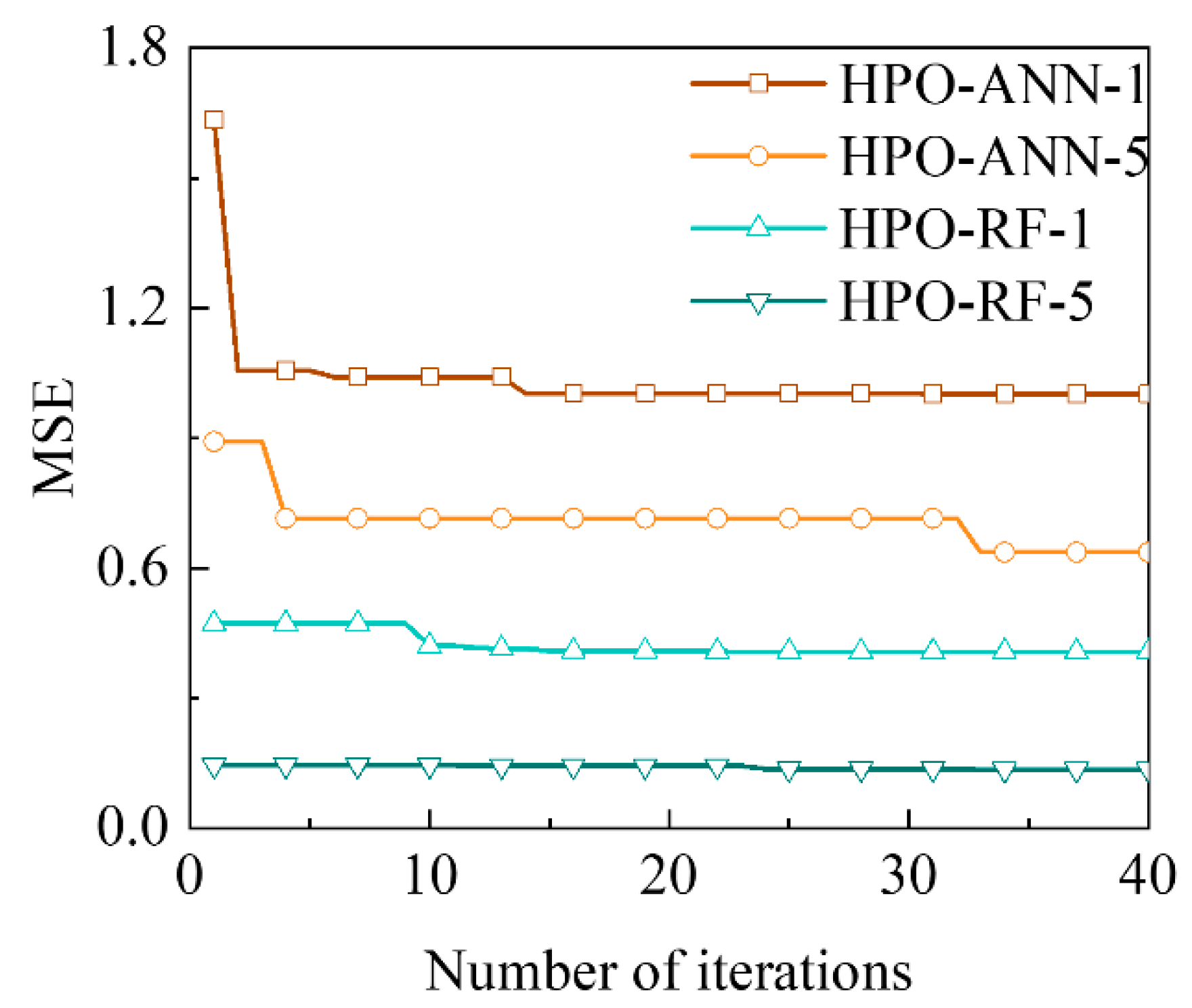
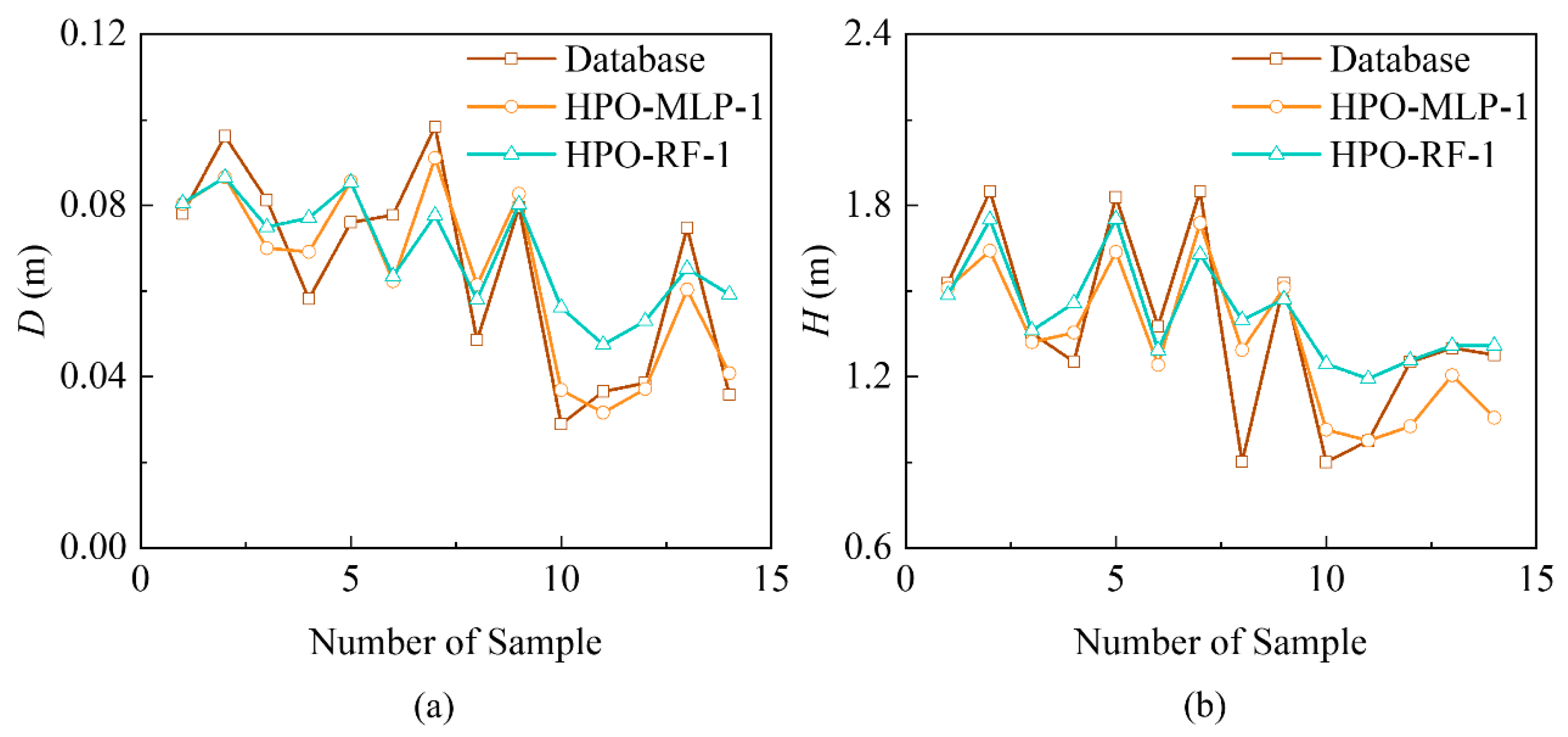
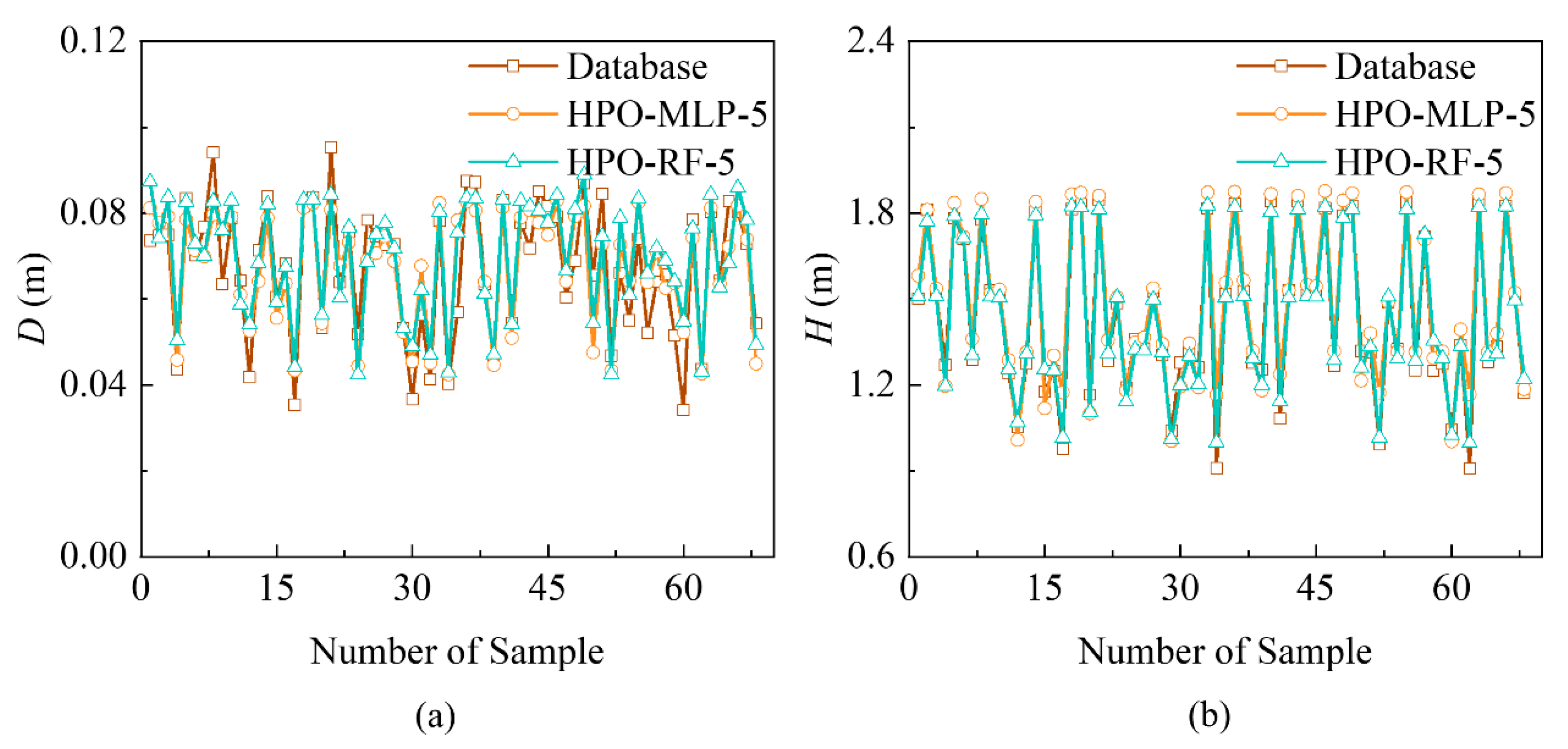
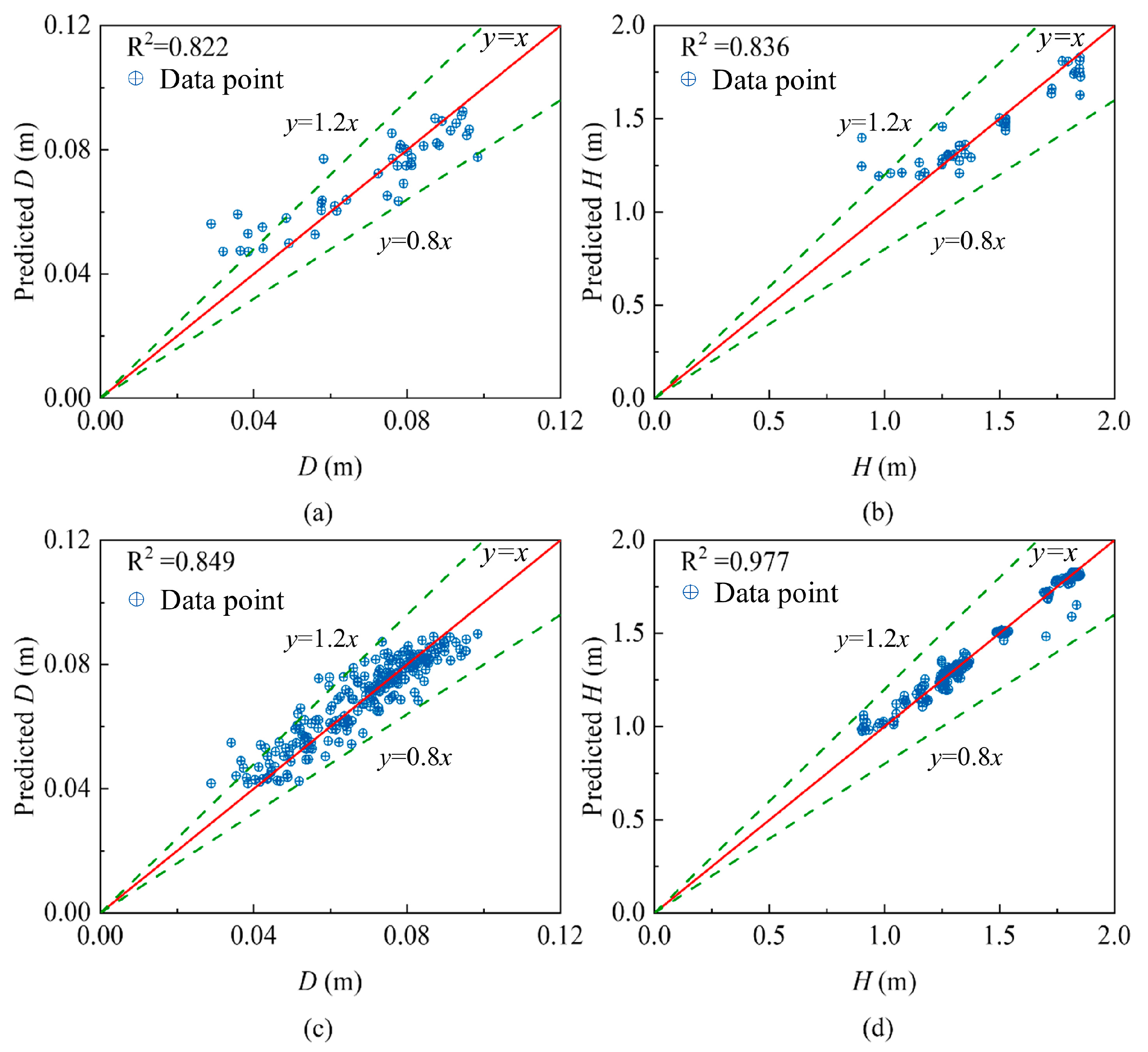
5.1. Performance of Intelligence Models
5.2. Comprehensive Evaluation of Intelligent Models
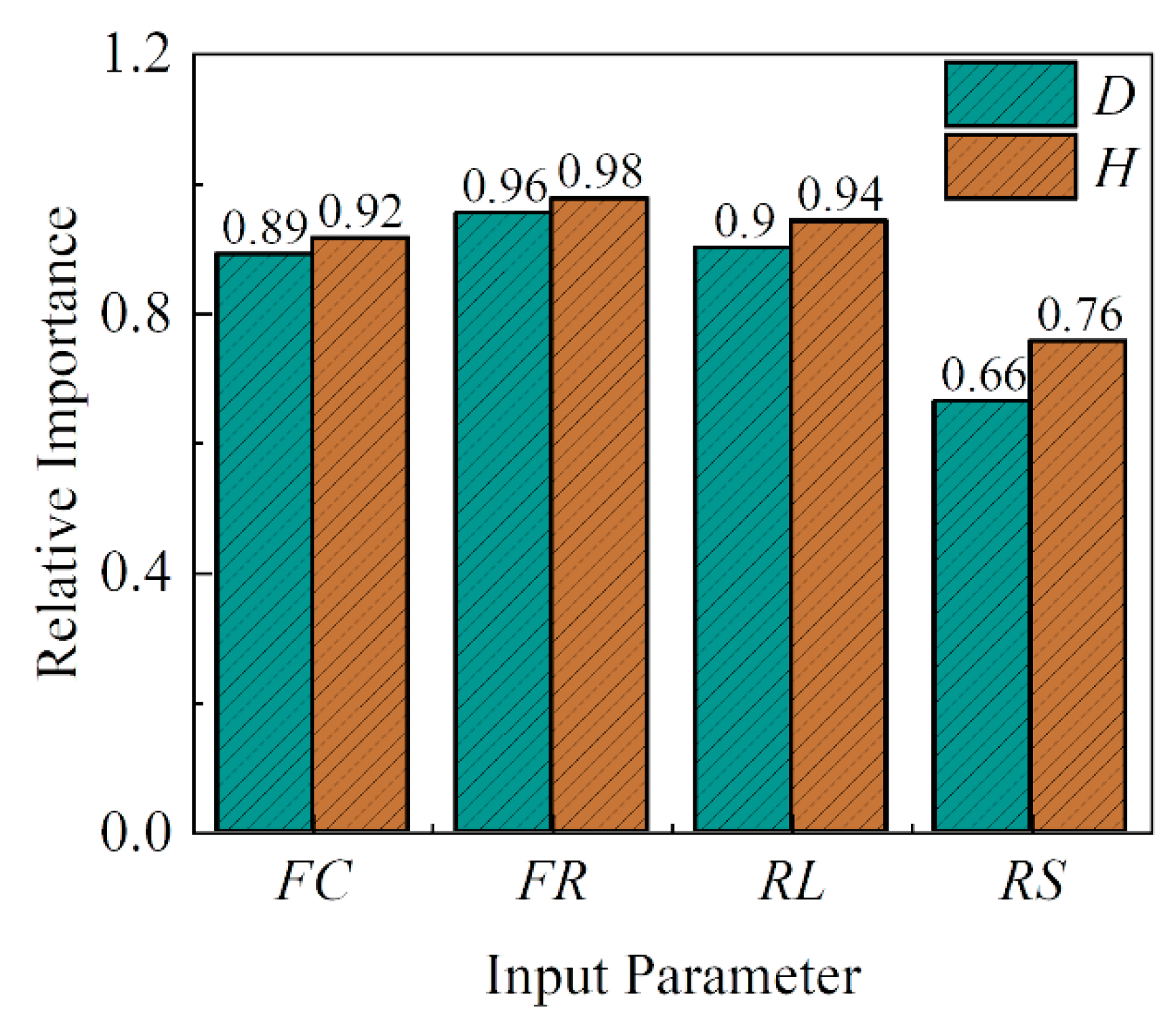
5.3. Sensitivity Analysis
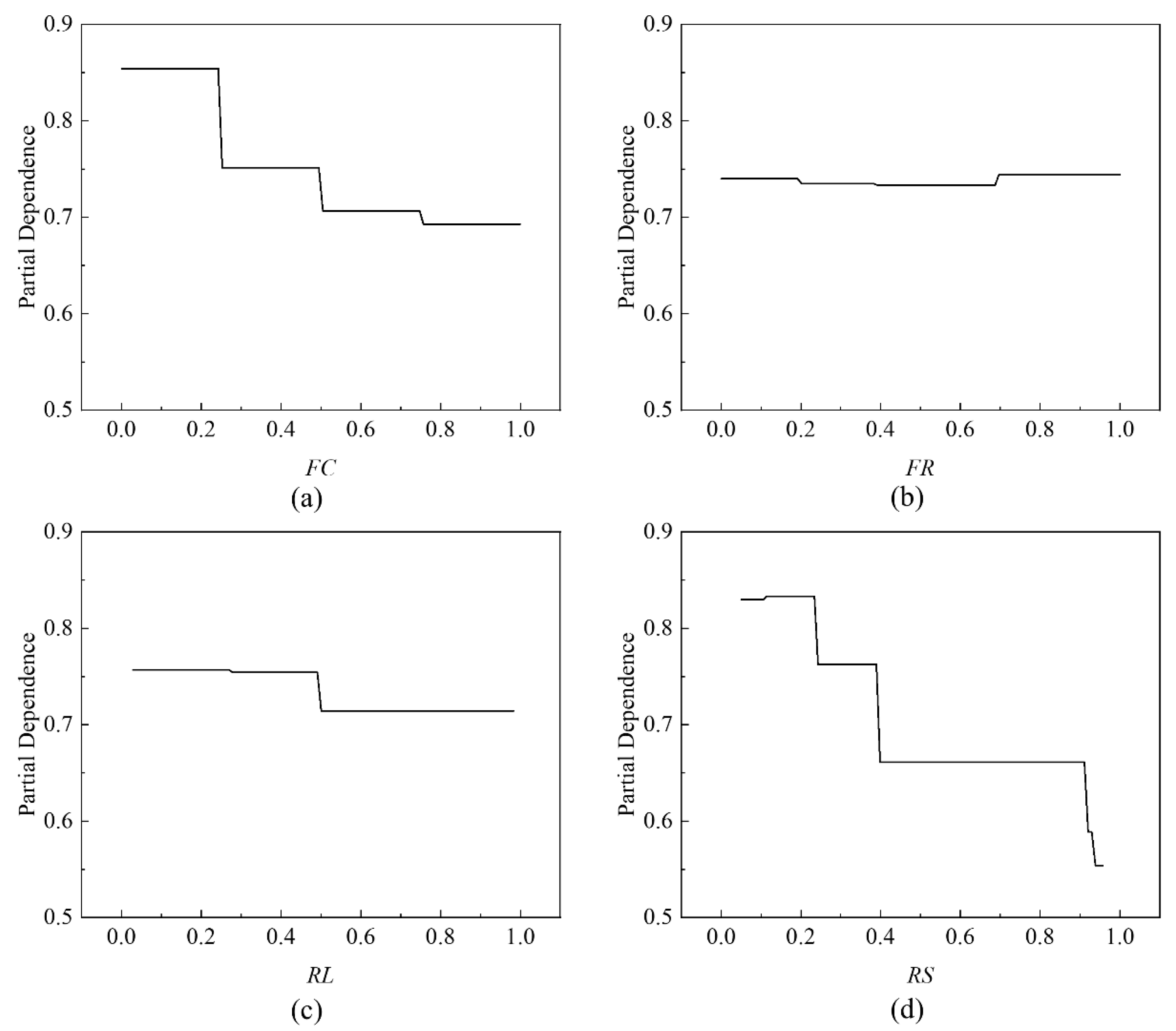
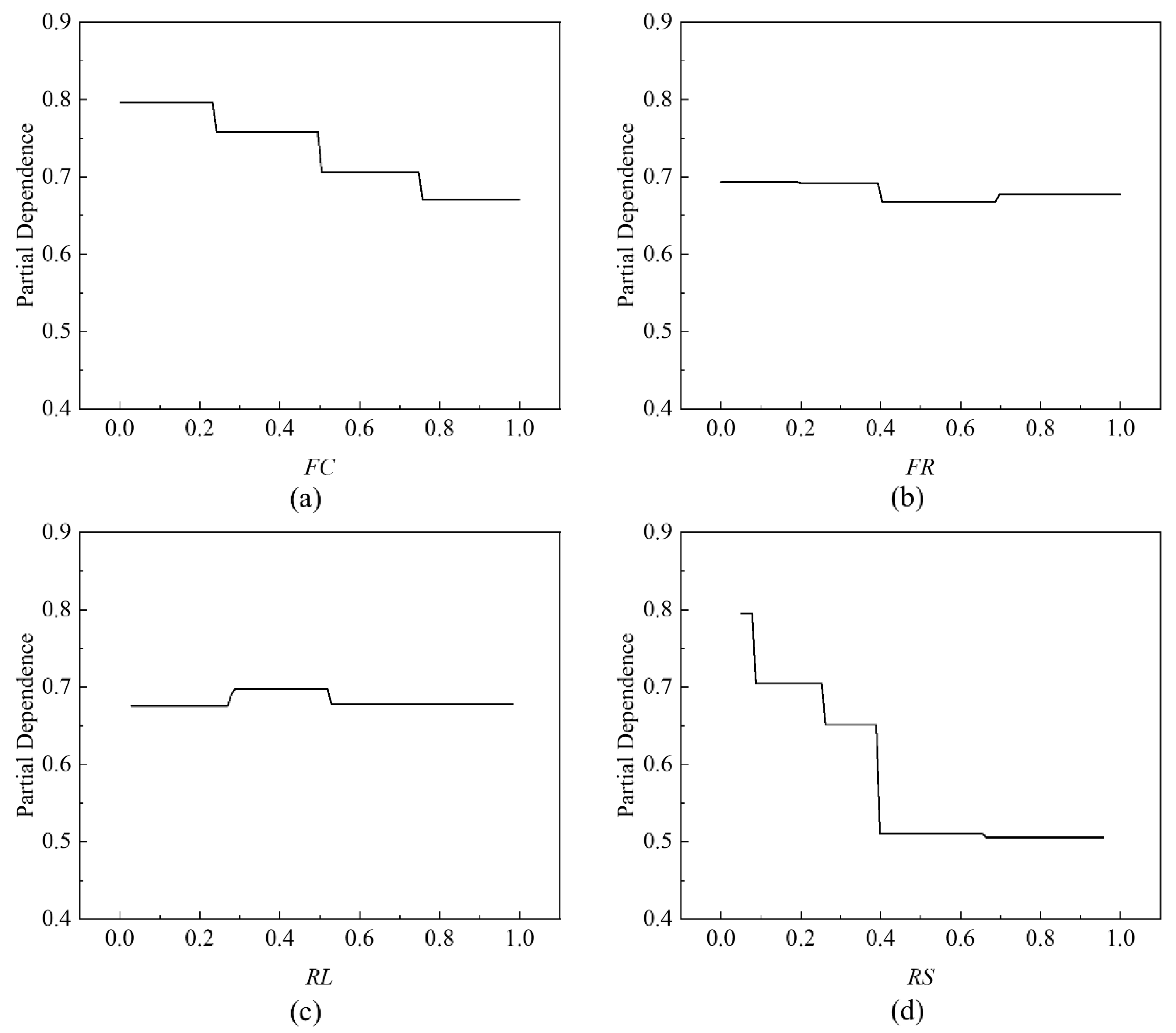
5.4. Partial Dependence Plot (PDP) Analysis
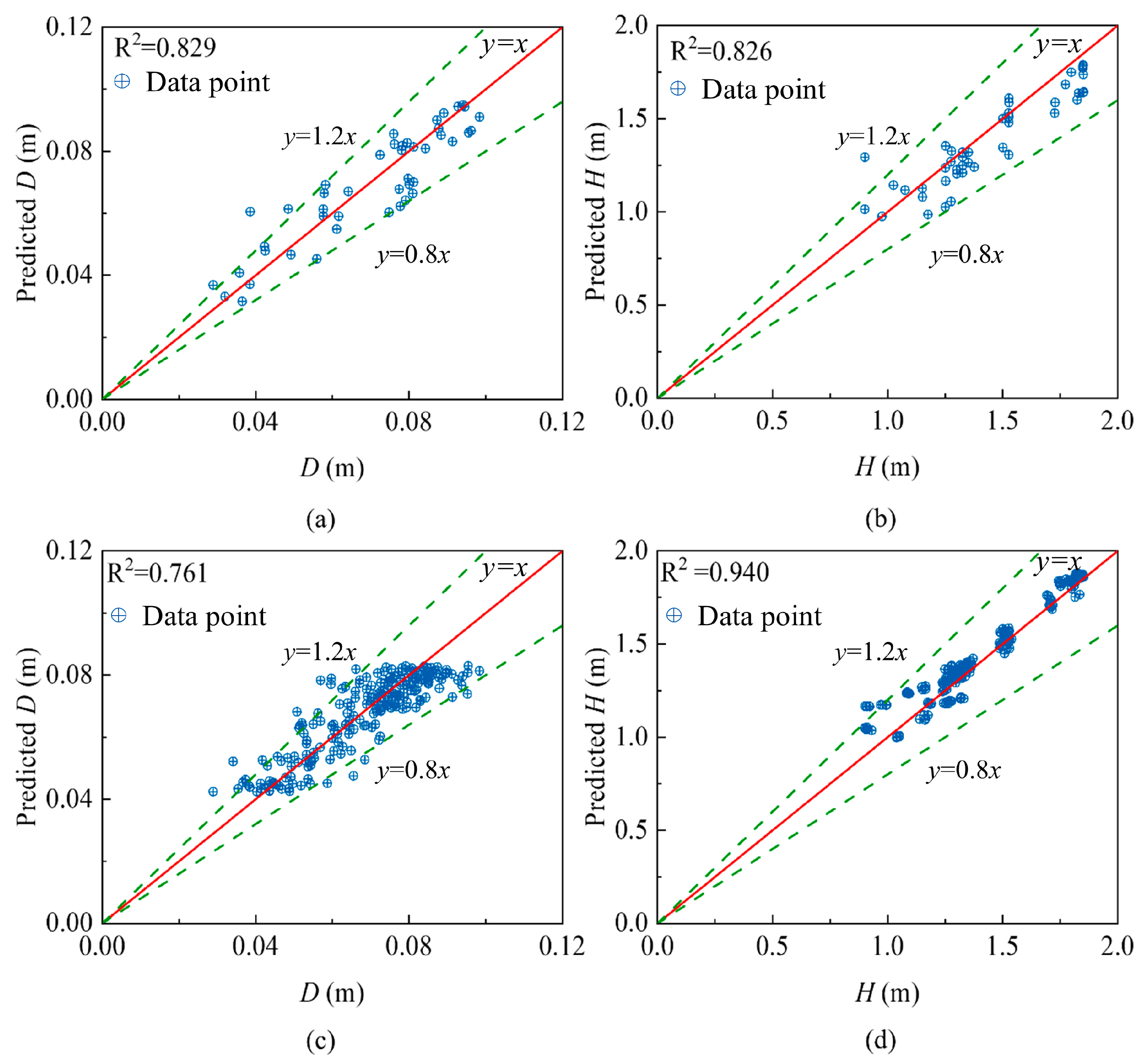
5.5. Overfitting Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, J.; Jia, Y.; Xie, X.; Yao, Y. Design Criteria for the Folding Implosion of High-Rise RC Buildings. Eng. Struct. 2018, 233, 111933. [Google Scholar] [CrossRef]
- Fang, C.; Linzell, D.G. Examining Progressive Collapse Robustness of a High-Rise Reinforced Concrete Building. Eng. Struct. 2021, 248, 113274. [Google Scholar] [CrossRef]
- Chai, Y.; Luo, N.; Zhang, H.; Duan, Y.; Mou, G.; Sun, W.; Dong, J. Application of Controlled Blasting Demolition Technology in Ultra-High Coaxial Thin-Walled Steel Inner Cylinder Reinforced Concrete Chimney. Case Stud. Constr. Mater. 2023, 18, e01936. [Google Scholar] [CrossRef]
- Sun, J.; Jia, Y.; Yao, Y.; Xie, X. Experimental Investigation of Stress Transients of Blasted RC Columns in the Blasting Demolition of Buildings. Eng. Struct. 2020, 210, 110417. [Google Scholar] [CrossRef]
- Yan, Y.; Hou, X.; Zheng, W.; Fei, H. The Damage Response of RC Columns with Considering Different Longitudinal and Shear Reinforcement under Demolition Blasting. J. Build. Eng. 2022, 62, 105396. [Google Scholar] [CrossRef]
- Zhang, Z.X. Rock Fracture and Blasting: Theory and Applications, 1st ed.; Butterworth-Heinemann: Oxford, UK, 2016; ISBN 0128027045. [Google Scholar]
- Uenishi, K.; Takahashi, H.; Yamachi, H.; Sakurai, S. PC-Based Simulations of Blasting Demolition of RC Structures. Constr. Build. Mater. 2010, 24, 2401–2410. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Z. Residual Axial Capacity of Square Recycled Aggregate Concrete-Filled Steel Tube Columns After Blast Loads. J. Build. Eng. 2022, 47, 103865. [Google Scholar] [CrossRef]
- Wu, K.C.; Li, B.; Tsai, K.C. Residual Axial Compression Capacity of Localized Blast-Damaged RC Columns. Int. J. Impact Eng. 2011, 38, 29–40. [Google Scholar] [CrossRef]
- Bao, X.; Li, B. Residual Strength of Blast Damaged Reinforced Concrete Columns. Int. J. Impact Eng. 2010, 37, 295–308. [Google Scholar] [CrossRef]
- Roller, C.; Mayrhofer, C.; Riedel, W.; Thoma, K. Residual Load Capacity of Exposed and Hardened Concrete Columns under Explosion Loads. Eng. Struct. 2013, 55, 66–72. [Google Scholar] [CrossRef]
- Sun, J.; Xie, X.; Wang, K.; Jia, Y.; Liu, C. Initial Bending Instability Model of Exposed Reinforcing Bars in Demolition Projects. Blasting 2015, 32, 1–4+27. [Google Scholar]
- Fujikake, K.; Aemlaor, P. Damage of Reinforced Concrete Columns under Demolition Blasting. Eng. Struct. 2013, 55, 116–125. [Google Scholar] [CrossRef]
- Kuzkin, V.A.; Dannert, M.M. Buckling of A Column under A Constant Speed Compression: A Dynamic Correction to the Euler Formula. Acta Mech. 2016, 227, 1645–1652. [Google Scholar] [CrossRef]
- Yao, Y. Instability and Failure Mechanism of High-Rise Buildings in Blasting Demolition Projects. Ph.D. Thesis, Hohai University, Nanjing, China, 2019. [Google Scholar]
- Kyei, C.; Braimah, A. Effects of Transverse Reinforcement Spacing on the Response of Reinforced Concrete Columns Subjected to Blast Loading. Eng. Struct. 2017, 142, 148–164. [Google Scholar] [CrossRef]
- Li, M.; Zong, Z.; Wu, G.; Zhang, X.; Yuan, S.; Tang, B. Residual Axial Capacity of Circular Reinforced Concrete Columns Subjected to Contact Explosions. Adv. Struct. Eng. 2022, 25, 1622–1635. [Google Scholar] [CrossRef]
- Shi, Y.; Hu, Y.; Chen, L.; Li, Z.X.; Xiang, H. Experimental Investigation into the Close-in Blast Performance of RC Columns with Axial Loading. Eng. Struct. 2022, 268, 114688. [Google Scholar] [CrossRef]
- Thai, D.K.; Kim, S.E. Numerical Investigation of the Damage of RC Members Subjected to Blast Loading. Eng. Fail. Anal. 2018, 92, 350–367. [Google Scholar] [CrossRef]
- Fakharian, P.; Rezazadeh Eidgahee, D.; Akbari, M.; Jahangir, H.; Ali Taeb, A. Compressive Strength Prediction of Hollow Concrete Masonry Blocks Using Artificial Intelligence Algorithms. Structures 2023, 47, 1790–1802. [Google Scholar] [CrossRef]
- Miao, X.; Chen, B.; Zhao, Y. Prediction of Compressive Strength of Glass Powder Concrete Based on Artificial Intelligence. J. Build. Eng. 2024, 91, 109377. [Google Scholar] [CrossRef]
- Wang, Q.; Hussain, A.; Farooqi, M.U.; Deifalla, A.F. Artificial Intelligence-Based Estimation of Ultra-High-Strength Concrete’s Flexural Property. Case Stud. Constr. Mater. 2022, 17, e01243. [Google Scholar] [CrossRef]
- Zhang, J.; Li, D.; Wang, Y. Predicting Uniaxial Compressive Strength of Oil Palm Shell Concrete Using A Hybrid Artificial Intelligence Model. J. Build. Eng. 2020, 30, 101282. [Google Scholar] [CrossRef]
- Asteris, P.G.; Lourenço, P.B.; Roussis, P.C.; Elpida Adami, C.; Armaghani, D.J.; Cavaleri, L.; Chalioris, C.E.; Hajihassani, M.; Lemonis, M.E.; Mohammed, A.S.; et al. Revealing the Nature of Metakaolin-Based Concrete Materials Using Artificial Intelligence Techniques. Constr. Build. Mater. 2022, 322, 126500. [Google Scholar] [CrossRef]
- Nguyen, T.; Ly, K.D.; Nguyen-Thoi, T.; Nguyen, B.P.; Doan, N.P. Prediction of Axial Load Bearing Capacity of PHC Nodular Pile Using Bayesian Regularization Artificial Neural Network. Soils Found. 2022, 62, 101203. [Google Scholar] [CrossRef]
- Zhang, G.; Ali, Z.H.; Aldlemy, M.S.; Mussa, M.H.; Salih, S.Q.; Hameed, M.M.; Al-Khafaji, Z.S.; Yaseen, Z.M. Reinforced Concrete Deep Beam Shear Strength Capacity Modelling Using an Integrative Bio-Inspired Algorithm with An Artificial Intelligence Model. Eng. Comput. 2022, 38, 15–28. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Nguyen, D.T.; Nguyen, D.H.; Tran, D.H. Evaluation of Residual Strength of Corroded Reinforced Concrete Beams Using Machine Learning Models. Arab. J. Sci. Eng. 2022, 47, 9985–10002. [Google Scholar] [CrossRef]
- Asteris, P.G.; Koopialipoor, M.; Armaghani, D.J.; Kotsonis, E.A.; Lourenço, P.B. Prediction of Cement-Based Mortars Compressive Strength Using Machine Learning Techniques. Neural Comput. Appl. 2021, 33, 13089–13121. [Google Scholar] [CrossRef]
- Debnath, P.; Dey, A.K. Prediction of Bearing Capacity of Geogrid-Reinforced Stone Columns Using Support Vector Regression. Int. J. Geomech. 2018, 18, 04017147. [Google Scholar] [CrossRef]
- Mohammed, H.R.M.; Ismail, S. Proposition of New Computer Artificial Intelligence Models for Shear Strength Prediction of Reinforced Concrete Beams. Eng. Comput. 2022, 38, 3739–3757. [Google Scholar] [CrossRef]
- Yang, L.; Qi, C.; Lin, X.; Li, J.; Dong, X. Prediction of Dynamic Increase Factor for Steel Fibre Reinforced Concrete Using a Hybrid Artificial Intelligence Model. Eng. Struct. 2019, 189, 309–318. [Google Scholar] [CrossRef]
- GB 50010-2010; Code for Design of Concrete Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China (MOHURD): Beijing, China, 2010.
- Riedel, W.; Mayrhofer, C.; Thoma, K.; Stolz, A. Engineering and Numerical Tools for Explosion Protection of Reinforced Concrete. Int. J. Prot. Struct. 2010, 1, 85–102. [Google Scholar] [CrossRef]
- Borrvall, T.; Riedel, W. The RHT Concrete Model in LS-DYNA. In Proceedings of the 8th European LS-DYNA Users Conference, Strasbourg, France, 23–24 May 2011. [Google Scholar]
- Hallquist, J.O. LS-DYNA Keyword User’s Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2007. [Google Scholar]
- Xin, C.L. Handbook of Common Material Parameters for Finite Element Analysis, 1st ed.; Machine Press: Beijing, China, 2019. [Google Scholar]
- Li, T.; Niu, X.; Fei, A.; Zhu, C.; Wang, M. Numerical Simulation for the Matching Effect of Rock Parameters on Explosives and Rocks. IOP Conf. Ser. Earth Environ. Sci. 2019, 304, 052110. [Google Scholar] [CrossRef]
- Sachpazis, C.I. Correlating Schmidt Hardness with Compressive Strength and Young’s Modulus of Carbonate Rocks. Bull. Eng. Geol. Environ. 1990, 42, 75–83. [Google Scholar] [CrossRef]
- Wei, H.; Chen, J.; Zhu, J.; Yang, X.; Chu, H. A Novel Algorithm of Nested-ELM for Predicting Blasting Vibration. Eng. Comput. 2022, 38, 1241–1256. [Google Scholar] [CrossRef]
- Abbaszadeh Shahri, A.; Pashamohammadi, F.; Asheghi, R.; Abbaszadeh Shahri, H. Automated Intelligent Hybrid Computing Schemes to Predict Blasting Induced Ground Vibration. Eng. Comput. 2022, 38, 3335–3349. [Google Scholar] [CrossRef]
- Mikołajczyk, A.; Grochowski, M. Data Augmentation for Improving Deep Learning in Image Classification Problem. In Proceedings of the 2018 International Interdisciplinary PhD Workshop, Świnouście, Poland, 9–12 May 2018; pp. 117–122. [Google Scholar] [CrossRef]
- Erichson, N.B.; Lim, S.H.; Xu, W.; Utera, F.; Cao, Z.; Mahoney, M.W. NoisyMix: Boosting Model Robustness to Common Corruptions. Proc. Mach. Learn. Res. 2024, 238, 4033–4041. [Google Scholar] [CrossRef]
- Rong, K.; Xu, X.; Wang, H.; Yang, J. Prediction of the Mean Fragment Size in Mine Blasting Operations by Deep Learning and Grey Wolf Optimization Algorithm. Earth Sci. Inform. 2024, 17, 2903–2919. [Google Scholar] [CrossRef]
- Iwana, B.K.; Uchida, S. An empirical survey of data augmentation for time series classification with neural networks. PLoS ONE 2021, 16, e0254841. [Google Scholar] [CrossRef]
- Hosseini, S.A.; Tavana, A.; Abdolahi, S.M.; Darvishmaslak, S. Prediction of Blast-Induced Ground Vibrations in Quarry Sites: A Comparison of GP, RSM and MARS. Soil. Dyn. Earthq. Eng. 2019, 119, 118–129. [Google Scholar] [CrossRef]
- Shang, Y.; Nguyen, H.; Bui, X.N.; Tran, Q.H.; Moayedi, H. A Novel Artificial Intelligence Approach to Predict Blast-Induced Ground Vibration in Open-Pit Mines Based on the Firefly Algorithm and Artificial Neural Network. Nat. Resour. Res. 2020, 29, 723–737. [Google Scholar] [CrossRef]
- Enayatollahi, I.; Aghajani Bazzazi, A.; Asadi, A. Comparison Between Neural Networks and Multiple Regression Analysis to Predict Rock Fragmentation in Open-Pit Mines. Rock. Mech. Rock. Eng. 2014, 47, 799–807. [Google Scholar] [CrossRef]
- Zhou, Z.H. Machine Learning; Tsinghua University Press: Beijing, China, 2016; ISBN B01ED31E04. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Naruei, I.; Keynia, F.; Molahosseini, A.S. Hunter–Prey Optimization: Algorithm and Applications. Soft Comput. 2021, 26, 1279–1314. [Google Scholar] [CrossRef]
- Berryman, A. The Origins and Evolution of Predator-Prey Theory. Ecology 1992, 73, 1530–1535. [Google Scholar] [CrossRef]
- Li, E.; Yang, F.; Ren, M.; Zhang, X.; Zhou, J.; Khandelwal, M. Prediction of Blasting Mean Fragment Size Using Support Vector Regression Combined with Five Optimization Algorithms. J. Rock. Mech. Geotech. Eng. 2021, 13, 1380–1397. [Google Scholar] [CrossRef]
- Monjezi, M.; Amiri, H.; Farrokhi, A.; Goshtasbi, K. Prediction of Rock Fragmentation Due to Blasting in Sarcheshmeh Copper Mine Using Artificial Neural Networks. Geotech. Geol. Eng. 2010, 28, 423–430. [Google Scholar] [CrossRef]
- Bahrami, A.; Monjezi, M.; Goshtasbi, K.; Ghazvinian, A. Prediction of Rock Fragmentation Due to Blasting Using Artificial Neural Network. Eng. Comput. 2011, 27, 177–181. [Google Scholar] [CrossRef]
- Amoako, R.; Jha, A.; Zhong, S. Rock Fragmentation Prediction Using an Artificial Neural Network and Support Vector Regression Hybrid Approach. Mining 2022, 2, 233–247. [Google Scholar] [CrossRef]
- Ding, X.; Hasanipanah, M.; Nikafshan Rad, H.; Zhou, W. Predicting the Blast-Induced Vibration Velocity Using A Bagged Support Vector Regression Optimized with Firefly Algorithm. Eng. Comput. 2021, 37, 2273–2284. [Google Scholar] [CrossRef]
- Khosla, C.; Saini, B.S. Enhancing Performance of Deep Learning Models with Different Data Augmentation Techniques: A Survey. In Proceedings of the 2020 International Conference on Intelligent Engineering and Management (ICIEM), London, UK, 17–19 June 2020; pp. 79–85. [Google Scholar] [CrossRef]
- Ross, T.J. Fuzzy Logic with Engineering Applications; Wiley: New York, NY, USA, 2010; ISBN 1119235863. [Google Scholar]


| No. | Compressive Strength of Concrete (MPa) | Yield Strength of Reinforcement (MPa) | Ratio of Longitudinal Reinforcement (%) | Ratio of Shear Reinforcement (%) | No. | Compressive Strength of Concrete (MPa) | Yield Strength of Reinforcement (MPa) | Ratio of Longitudinal Reinforcement (%) | Ratio of Shear Reinforcement (%) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 40 | 335 | 0.75 | 0.087 | 24 | 60 | 400 | 1.13 | 0.087 |
| 2 | 40 | 335 | 0.75 | 0.175 | 25 | 60 | 500 | 1.13 | 0.087 |
| 3 | 40 | 335 | 0.75 | 0.349 | 26 | 80 | 335 | 1.13 | 0.087 |
| 4 | 40 | 400 | 0.75 | 0.087 | 27 | 80 | 335 | 1.13 | 0.175 |
| 5 | 40 | 500 | 0.75 | 0.087 | 28 | 80 | 335 | 1.13 | 0.349 |
| 6 | 60 | 335 | 0.75 | 0.087 | 29 | 80 | 400 | 1.13 | 0.087 |
| 7 | 60 | 335 | 0.75 | 0.175 | 30 | 80 | 500 | 1.13 | 0.087 |
| 8 | 60 | 335 | 0.75 | 0.349 | 31 | 40 | 335 | 1.50 | 0.087 |
| 9 | 60 | 400 | 0.75 | 0.087 | 32 | 40 | 335 | 1.50 | 0.175 |
| 10 | 60 | 500 | 0.75 | 0.087 | 33 | 40 | 335 | 1.50 | 0.349 |
| 11 | 80 | 335 | 0.75 | 0.087 | 34 | 40 | 400 | 1.50 | 0.087 |
| 12 | 80 | 335 | 0.75 | 0.175 | 35 | 40 | 500 | 1.50 | 0.087 |
| 13 | 80 | 335 | 0.75 | 0.349 | 36 | 60 | 335 | 1.50 | 0.087 |
| 14 | 80 | 400 | 0.75 | 0.087 | 37 | 60 | 335 | 1.50 | 0.175 |
| 15 | 80 | 500 | 0.75 | 0.087 | 38 | 60 | 335 | 1.50 | 0.349 |
| 16 | 40 | 335 | 1.13 | 0.087 | 39 | 60 | 400 | 1.50 | 0.087 |
| 17 | 40 | 335 | 1.13 | 0.175 | 40 | 60 | 500 | 1.50 | 0.087 |
| 18 | 40 | 335 | 1.13 | 0.349 | 41 | 80 | 335 | 1.50 | 0.087 |
| 19 | 40 | 400 | 1.13 | 0.087 | 42 | 80 | 335 | 1.50 | 0.175 |
| 20 | 40 | 500 | 1.13 | 0.087 | 43 | 80 | 335 | 1.50 | 0.349 |
| 21 | 60 | 335 | 1.13 | 0.087 | 44 | 80 | 400 | 1.50 | 0.087 |
| 22 | 60 | 335 | 1.13 | 0.175 | 45 | 80 | 500 | 1.50 | 0.087 |
| 23 | 60 | 335 | 1.13 | 0.349 | / | / | / | / | / |
| No. | Model Name | Algorithm | Database Scale |
|---|---|---|---|
| 1 | HPO-ANN-1 | HPO-ANN | 45 |
| 2 | HPO-ANN-5 | HPO-ANN | 225 |
| 3 | HPO-RF-1 | HPO-RF | 45 |
| 4 | HPO-RF-5 | HPO-RF | 225 |
| Model Name | Model Rank | Total Score | Rank | |||||
|---|---|---|---|---|---|---|---|---|
| Training | Testing | |||||||
| MSE | MAE | R2 | MSE | MAE | R2 | |||
| HPO-ANN-1 | 0.013 (1) | 0.088 (1) | 0.819 (1) | 0.025 (2) | 0.130 (2) | 0.767 (2) | 9 | 4 |
| HPO-ANN-5 | 0.008 (2) | 0.069 (2) | 0.840 (2) | 0.009 (3) | 0.071 (3) | 0.839 (3) | 15 | 2 |
| HPO-RF-1 | 0.006 (3) | 0.061 (3) | 0.911 (3) | 0.043 (1) | 0.163 (1) | 0.591 (1) | 12 | 3 |
| HPO-RF-5 | 0.004 (4) | 0.041 (4) | 0.931 (4) | 0.007 (4) | 0.057 (4) | 0.865 (4) | 24 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rong, K.; Jia, Y.; Yao, Y.; Sun, J.; Yu, Q.; Tang, H.; Yang, J.; Xie, X. ANN and RF Optimized by Hunter–Prey Algorithm for Predicting Post-Blast RC Column Morphology. Buildings 2025, 15, 2351. https://doi.org/10.3390/buildings15132351
Rong K, Jia Y, Yao Y, Sun J, Yu Q, Tang H, Yang J, Xie X. ANN and RF Optimized by Hunter–Prey Algorithm for Predicting Post-Blast RC Column Morphology. Buildings. 2025; 15(13):2351. https://doi.org/10.3390/buildings15132351
Chicago/Turabian StyleRong, Kai, Yongsheng Jia, Yingkang Yao, Jinshan Sun, Qi Yu, Hongliang Tang, Jun Yang, and Xianqi Xie. 2025. "ANN and RF Optimized by Hunter–Prey Algorithm for Predicting Post-Blast RC Column Morphology" Buildings 15, no. 13: 2351. https://doi.org/10.3390/buildings15132351
APA StyleRong, K., Jia, Y., Yao, Y., Sun, J., Yu, Q., Tang, H., Yang, J., & Xie, X. (2025). ANN and RF Optimized by Hunter–Prey Algorithm for Predicting Post-Blast RC Column Morphology. Buildings, 15(13), 2351. https://doi.org/10.3390/buildings15132351






