A Hybrid RBF-PSO Framework for Real-Time Temperature Field Prediction and Hydration Heat Parameter Inversion in Mass Concrete Structures
Abstract
1. Introduction
- 1.
- A hybrid RBF-PSO framework integrating Dynamic Time Warping (DTW) and feature penalties to resolve phase misalignments while maintaining critical metrics (e.g., peak temperature), reducing prediction errors by 74% compared to conventional methods (Section 4.3).
- 2.
- A sensitivity-driven phased optimization prioritizing dominant parameters (e.g., Q∞) identified through Sobol analysis, cutting computational costs by 49%.
2. Methodology: Particle Swarm Optimization with RBF Surrogate Model
2.1. Particle Swarm Optimization (PSO)
2.1.1. Algorithm Implementation
2.1.2. Exploration–Exploitation Balance
- (1)
- Dynamic Inertia Weight:
- (2)
- Acceleration Coefficients:
- (3)
- Velocity Clamping:
2.2. Radial Basis Function (RBF) Surrogate Mode
2.3. RBF-PSO
- (1)
- Initialization:
- (2)
- Preliminary Evaluation:
- (3)
- Iterative Optimization:
- (4)
- Termination Condition:
- (5)
- Output of Optimal Solution:
| Algorithm 1. RBF-PSO Hybrid Optimization |
| Require: Parameter ranges, FEA model, objective function F Ensure: Optimized parameters 1: Initialize swarm particles (position, velocity) 2: Generate LHS samples → Perform FEA → Build initial RBF model 3: while termination condition not met do 4: for each particle i do 5: Predict F via RBF model 6: Update velocity (Equation (1)) and position (Equation (2)) 7: end for 8: Select particles with high uncertainty () 9: Perform FEA on selected particles → Update RBF model 10: Update pbest and gbest 11: end while 12: Return gbest parameters |
2.4. Complexity Analysis
3. Principle of Parameter Inversion for Mass Concrete Based on RBF-PSO
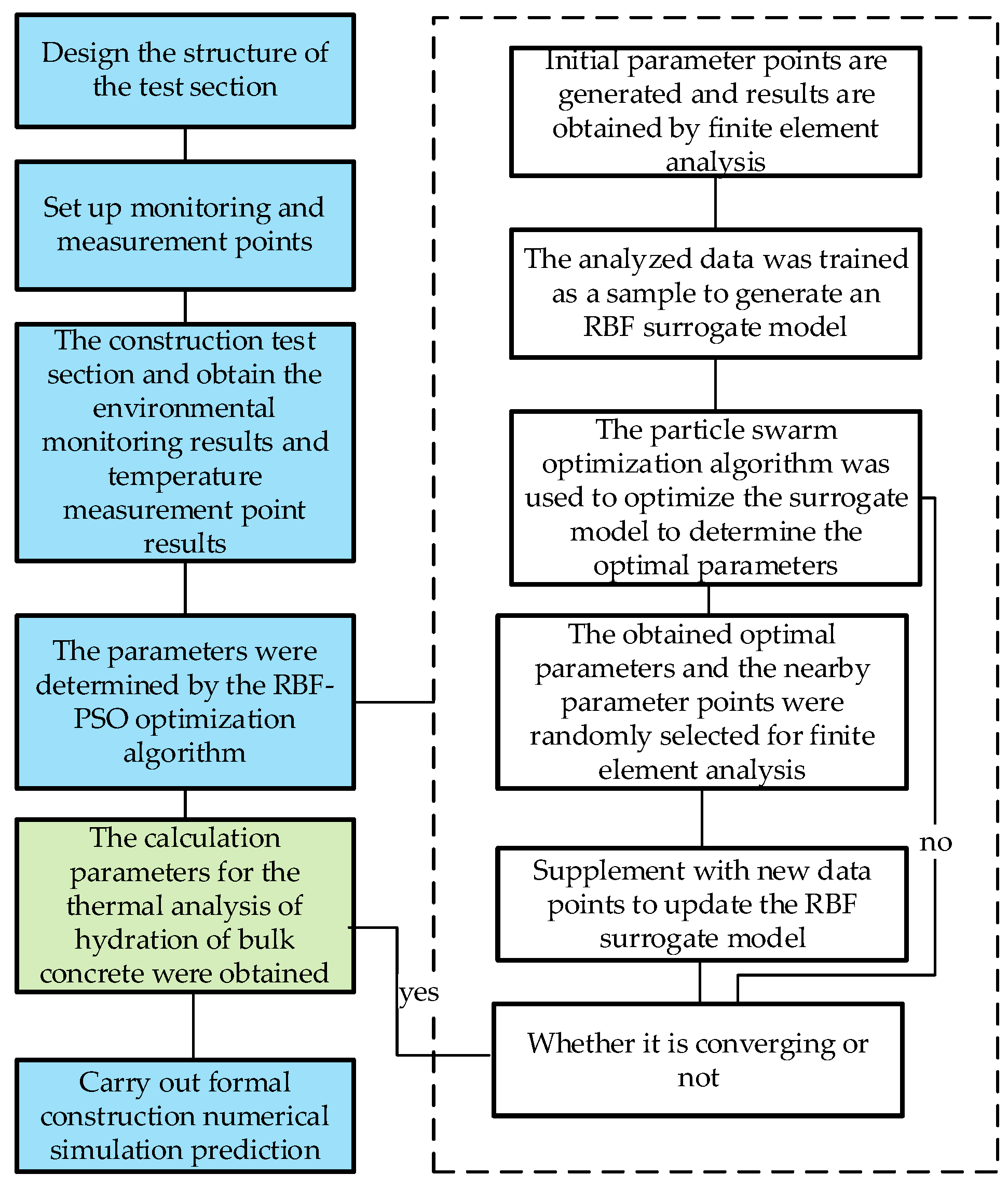
3.1. Method Framework Design
3.2. Experimental Section Monitoring and Numerical Modeling
- (1)
- Spatial Dimension: High-precision temperature sensors are placed on the top surface, bottom surface, and at the midpoint of the thickness.
- (2)
- Temporal Dimension: Temperature time series data are continuously collected at 10-min intervals.
- (3)
- Environmental Parameters: Wind speed, humidity, and curing conditions (insulation layer thickness, water storage depth, etc.) are recorded simultaneously.
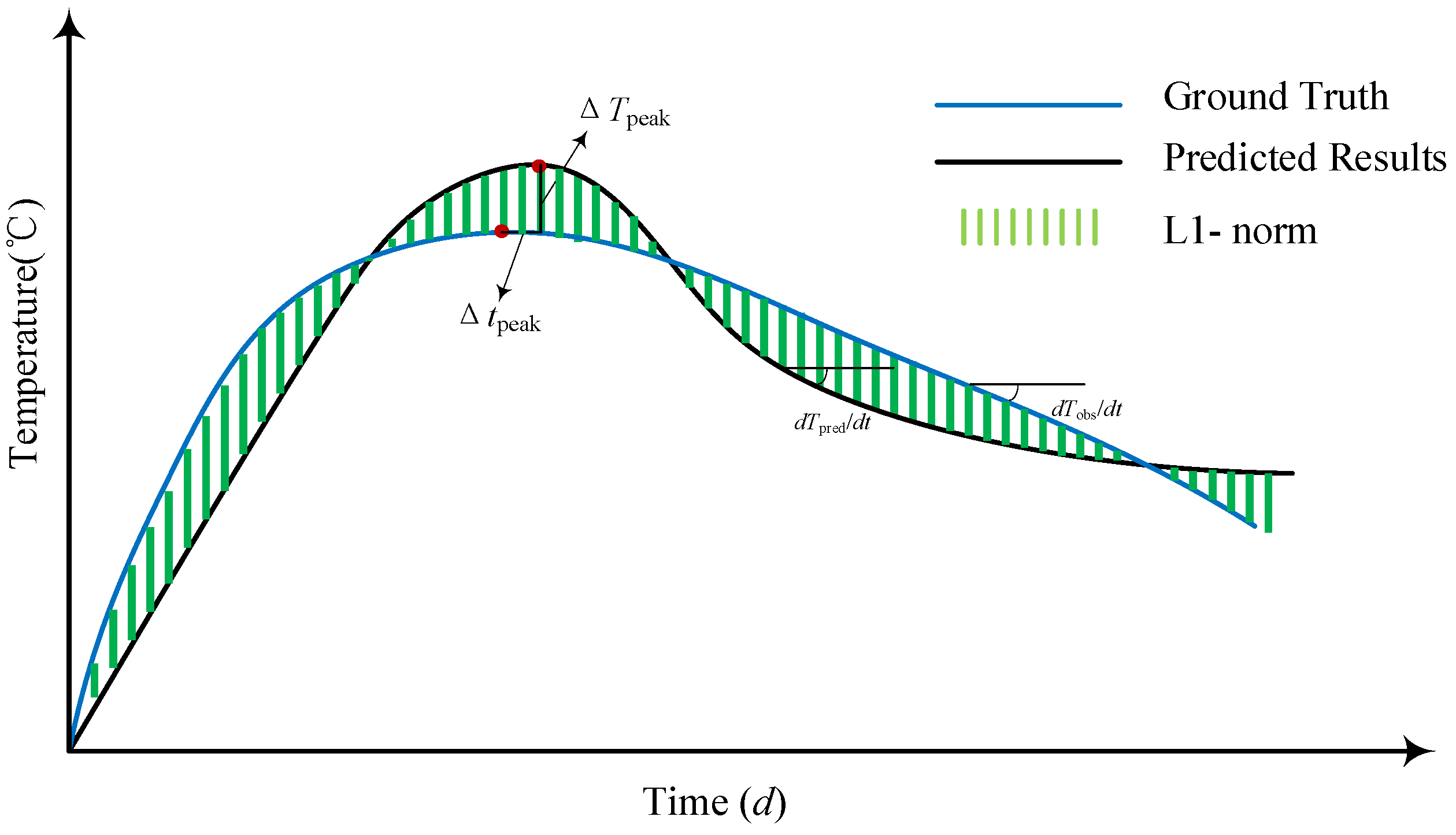
3.3. Objective Function Design and Optimization Mechanism
- (1)
- L1-Norm Cumulative Difference:
- (2)
- Key Feature Composite Index:
- a.
- Normalize the feature deviations across all samples.
- b.
- Compute the information entropy Ej for each feature, as follows:
- c.
- Derive weights , then assign α = w1, β = w2, γ = w3.
- (3)
- Dynamic Time Warping Enhanced Index:
- a.
- A grid search was performed over λ∈[0.1, 2.0], using 20% of the LHS samples.
- b.
- Optimal λ = 0.8 was selected by minimizing the MAE on validation data.
3.4. RBF-PSO Cooperative Optimization Process
- (1)
- Parameter Space Sampling and Finite Element Calculation: A Latin hypercube design is used to generate an initial set of parameter samples. These are substituted into the finite element model to calculate the spatiotemporal distribution of the temperature field. The variables include the following:
- (2)
- Hydration Heat Release Characteristic Parameters:
- (1)
- Objective Function Evaluation: The predicted temperature curve Tpred (t) is compared to the measured curve Tobs(t), and the objective function value is calculated.
- (2)
- Surrogate Model Training: An RBF surrogate model is constructed using the parameter samples as the input and the objective function values as the output, establishing a parameter response mapping relationship.
- (3)
- PSO Surrogate Optimization: Particle Swarm Optimization is performed on the response surface defined by the surrogate model to obtain the current optimal parameter solution.
- (4)
- Active Learning Update: The optimal solution and its neighboring perturbed solutions are used as new sample points, triggering finite element verification and updating the training dataset.
- (5)
- Convergence Determination: The iteration terminates when the relative change rate of the objective function value of the optimal solution in three consecutive generations is less than 0.5%. The final calibrated parameters are then output.
4. Comparative Analysis of Objective Functions
4.1. Experimental Design and Data Acquisition
4.2. Inversion Parameter Settings
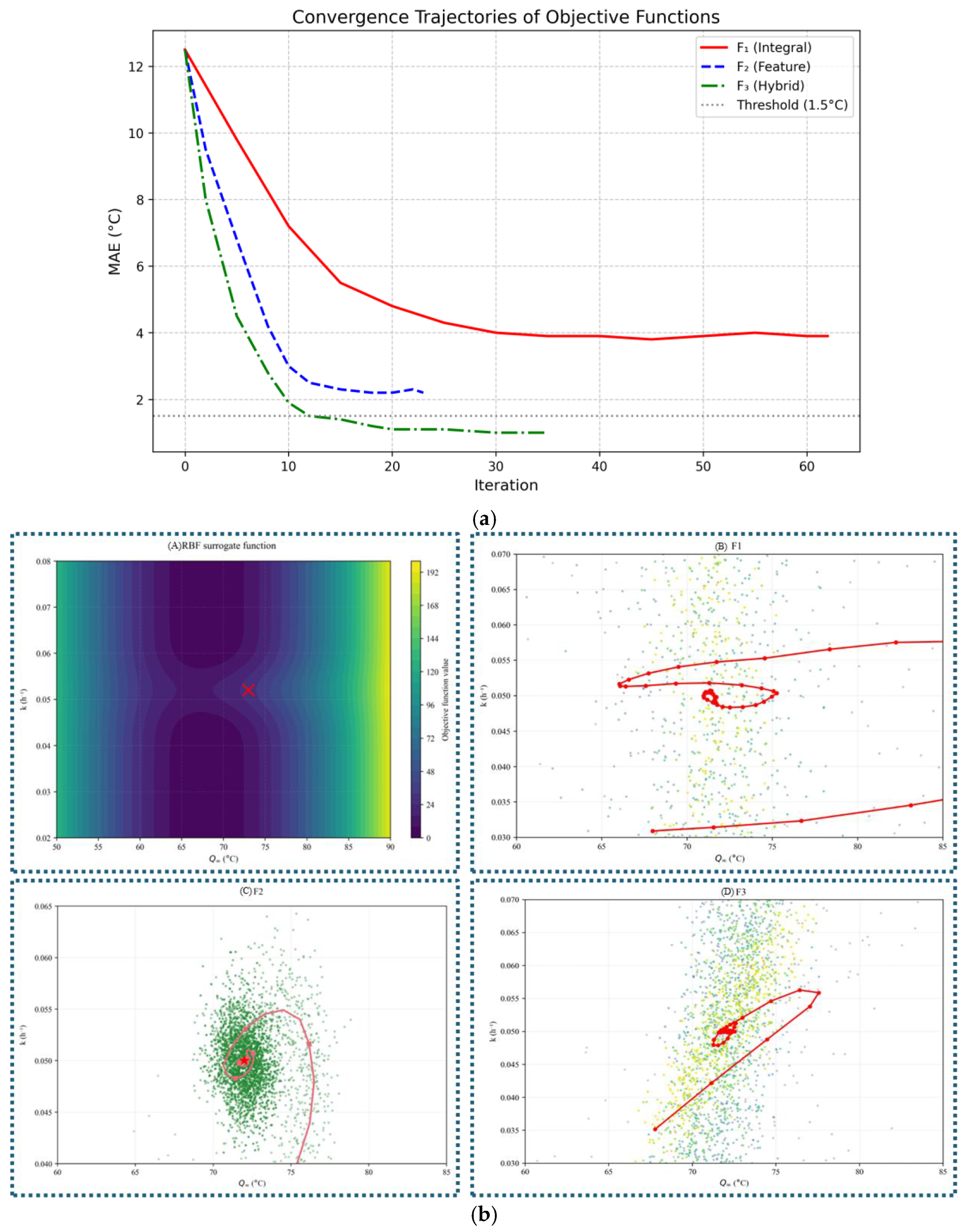
4.3. Optimization Process Comparison
4.4. Comparative Analysis of Optimization Efficiency
4.4.1. Methodology of the Comparative Analysis
- (1)
- Case Configuration:
- ◆
- Specimen: C40 concrete block (Section 4.1)
- ◆
- Parameter space: Q∞∈[50, 90], k∈[0.02, 0.08], m∈[0.8, 1.2], kconv∈[0.5, 3.0], b∈[0, 1]
- ◆
- Objective function: Hybrid F3 (Equation (10))
- ◆
- Initial point:θ0 = [65, 0.04, 1.0, 1.5, 0.5]
- (2)
- Compared Methods:
- RBF-PSO (Proposed):
- ◆
- Surrogate: RBF network with Gaussian kernels
- ◆
- Optimizer: PSO with dynamic inertia (Equation (3))
- ◆
- Initial samples: 20 (LHS design)
- ◆
- Max iterations: 10
- Total FEM calls: 70
- Standard PSO:
- ◆
- Pure PSO without surrogate
- ◆
- Population: 50 particles
- ◆
- Max iterations: 100
- CMA-ES (State-of-the-Art):
- ◆
- Covariance Matrix Adaptation Evolution Strategy
- ◆
- Population size: 20
- ◆
- Generations: 50
- Evaluation Metrics:
- ◆
- FEM call count
- ◆
- Wall-clock time (hours)
- ◆
- Final objective value: F3∗
- ◆
- Parameter error:
- ◆
- Acceleration ratio:
4.4.2. Results and Discussion
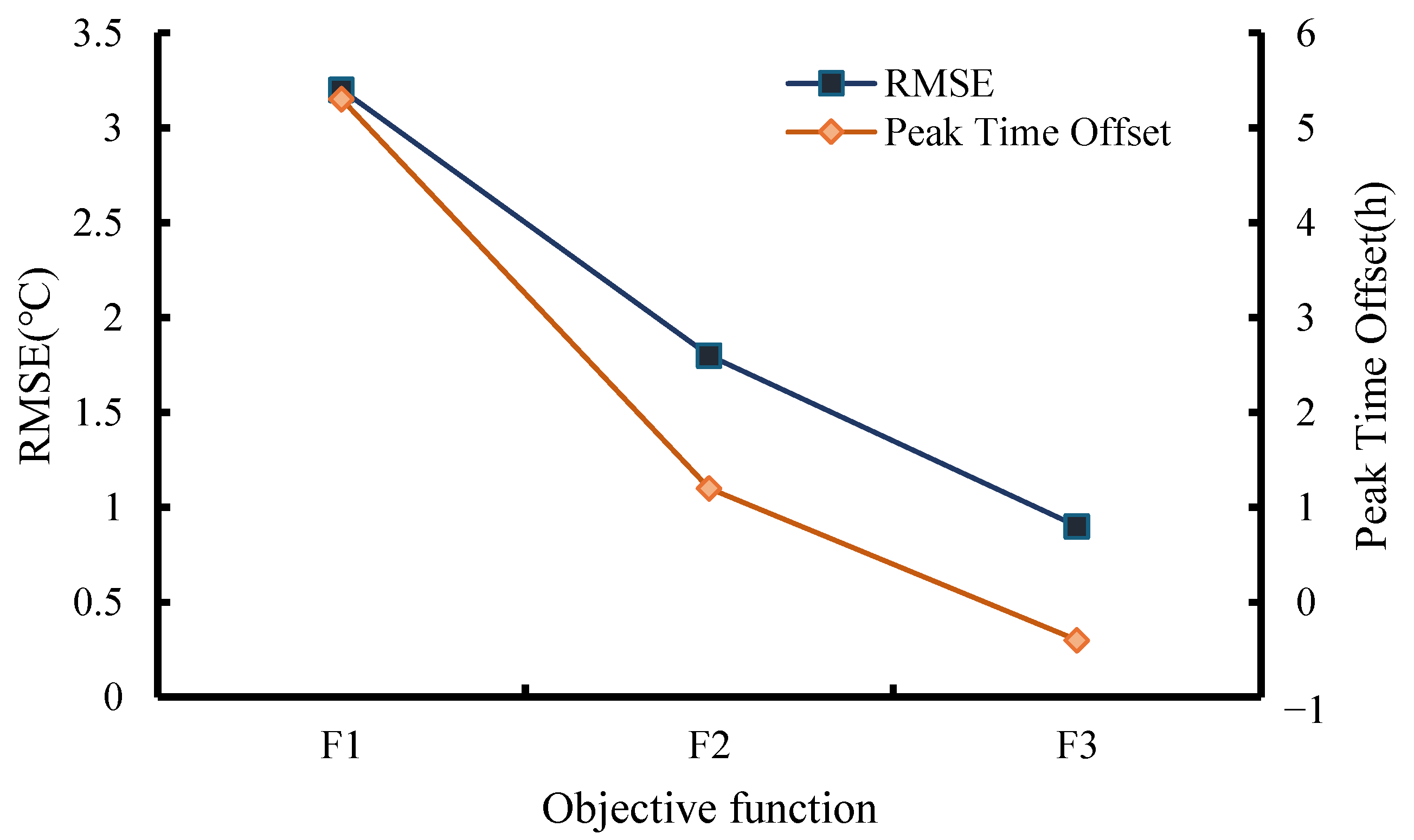
4.5. Discussion
- (1)
- Accuracy–Efficiency Trade-off in Integral-Type Objective Function (F1)
- (2)
- Local Focus and Phase Mismatch in Feature-Driven Objective Function (F2)
- (3)
- Synergistic Optimization in Hybrid Objective Function (F3)
- (4)
- Implications for Engineering Inversion
- (5)
- Surrogate-Optimizer Synergy for Transformative Efficiency
5. Parameter Sensitivity and Interaction Effect Analysis
5.1. Sensitivity Analysis of FEM Parameters
5.1.1. Sensitivity Analysis Methodology
5.1.2. Sensitivity Analysis Results
5.2. Sensitivity Analysis of Objective Function Weights
5.2.1. Methodology of the Sensitivity Analysis
5.2.2. Analysis Results
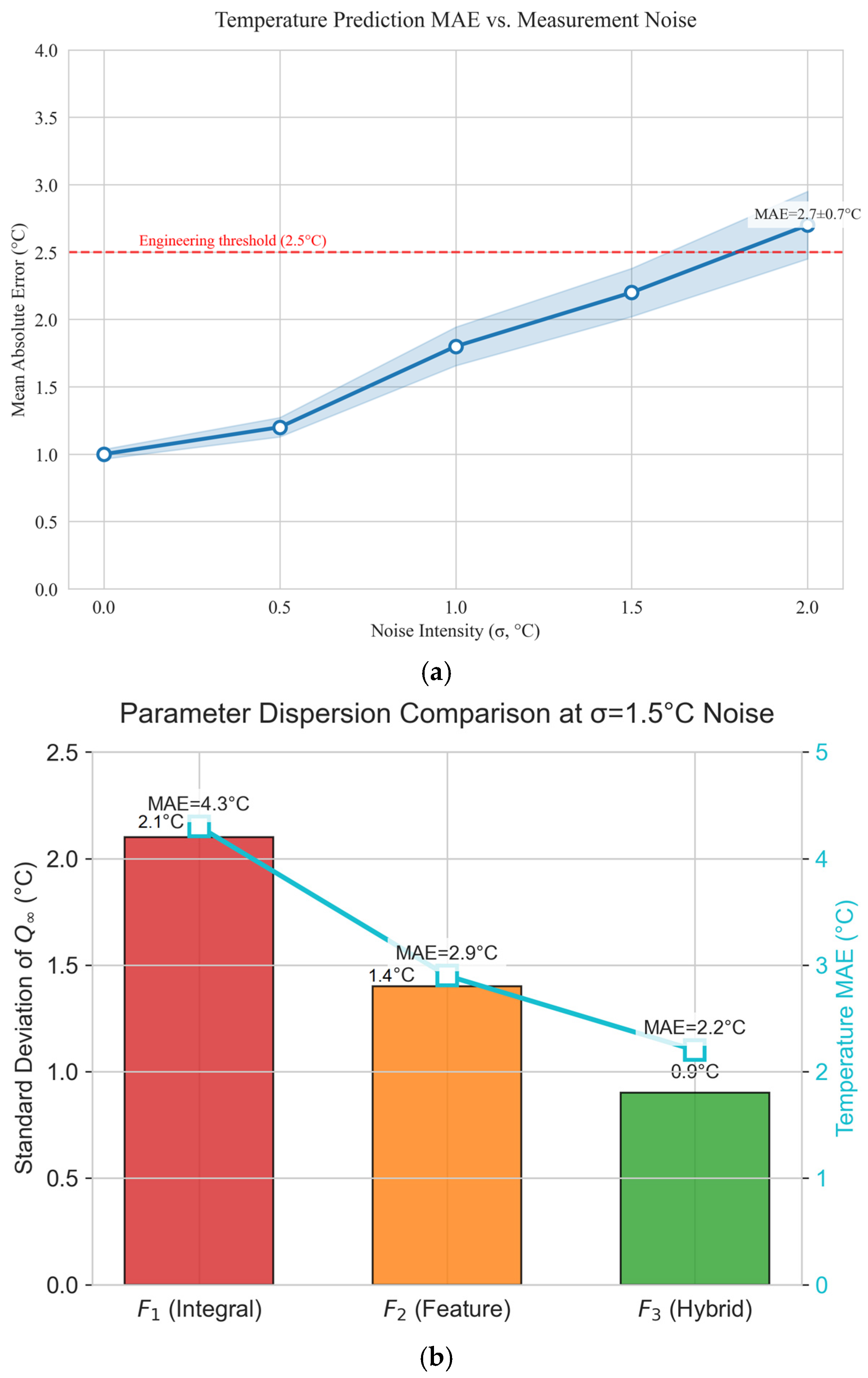
5.3. Robustness Analysis Under Measurement Noise
5.3.1. Methodology
- Low noise (): High-precision platinum RTDs
- Medium noise (): Industrial thermocouples
- High noise (): Low-cost sensors in harsh environments
5.3.2. Results and Discussion
- (1)
- Parameter Inversion Stability
- (2)
- Prediction Accuracy Degradation
- (3)
- Objective Function Noise Immunity
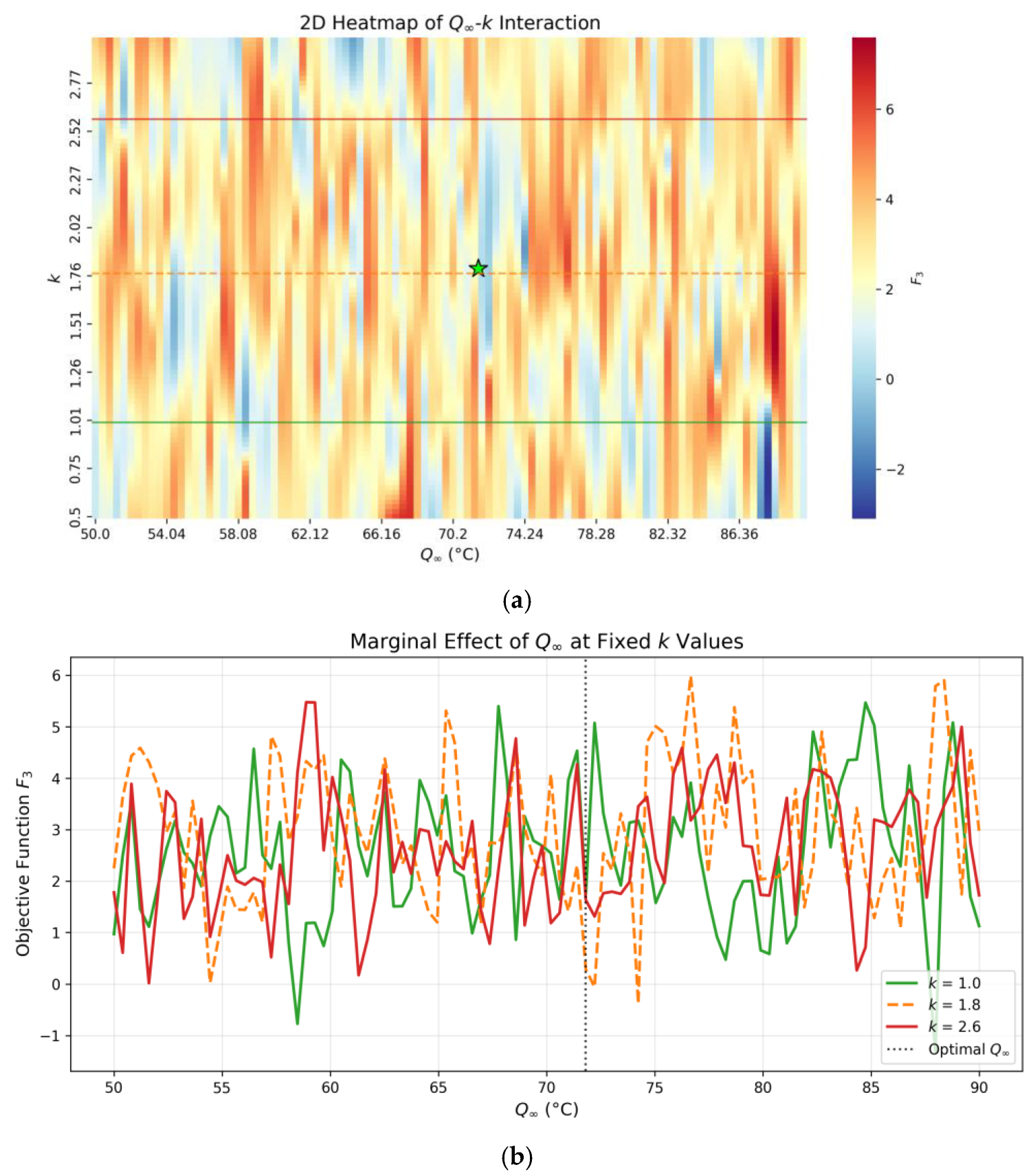
5.4. Analysis of Interaction Mechanisms
- (1)
- Non-Linear Antagonistic Relationship (Figure 8a):
- (2)
- Dominant Synergistic Coupling (Figure 8b):
- (3)
- Boundary Condition Modulation:
6. Conclusions and Limitations
6.1. Conclusions
- (1)
- Hybrid Objective Function Superiority: The hybrid-type F3, integrating Dynamic Time Warping (DTW) and feature penalty terms, demonstrated an optimal performance in balancing global curve morphology and local feature accuracy. It achieved a 74% reduction in the prediction error (MAE = 1.0 °C) compared to F1 and improved parameter identification precision (e.g., <2% error in Q∞), validating its robustness against spatiotemporal uncertainties.
- (2)
- Efficiency-Accuracy Trade-offs: While F2 reduced computational costs by 63% through feature-focused optimization, its neglect of temporal elasticity led to phase errors. Conversely, F1’s global integral strategy incurred prohibitive computational demands (498 FEM calls) without guaranteeing critical feature alignment, highlighting the necessity of hybrid designs.
- (3)
- Parameter Sensitivity Hierarchy: Sobol sensitivity analysis revealed Q∞ as the dominant parameter (78% total variance contribution), followed by synergistic k–m interactions (ΔSTi= 0.17), and the indirect coupling of kconv with boundary constraints. These insights guide phased optimization—prioritizing Q∞-k calibration while tolerating relaxed kconv precision—to balance accuracy and efficiency.
- (4)
- Engineering Applicability: The proposed framework successfully established a closed-loop inversion system (“monitoring→simulation→surrogate modeling→optimization”), enabling real-time temperature prediction and dynamic curing strategy adjustments. Calibrated parameters enhanced the accuracy of finite element models, providing reliable digital tools for heat stress risk mitigation in mass concrete projects.
- (5)
- Computational Superiority: Benchmarking against non-surrogate optimizers (PSO, CMA-ES) demonstrated a 2.8–4.6× acceleration in convergence (5.2 h, 70 FEM calls) while maintaining <2% parameter errors, validating the necessity of surrogate integration for field deployment.
- (6)
- Noise Resilience: Explicit robustness analysis under simulated sensor noise (σ = 0.5–2.0 °C) confirmed stable parameter identification and prediction accuracy (MAE < 1.3 °C at σ = 2.0 °C), ensuring operational reliability in practical monitoring scenarios.
6.2. Limitations and Generalizability
- (1)
- High-Dimensional Parameter Spaces: The current RBF-PSO framework may face scalability challenges in problems with >10 parameters due to the “curse of dimensionality,” requiring adaptive sampling strategies.
- (2)
- Real-Time Applications: While the method reduces computational costs by 49% compared to brute-force FEA, its iterative nature (35 iterations for convergence) may limit real-time deployment in ultra-fast curing environments.
- (3)
- Data Sparsity: The surrogate model’s accuracy degrades when fewer than 50 LHS samples are available, necessitating domain-specific pre-training or transfer learning for small datasets.
- (4)
- Crack and Inhomogeneity Modeling: The current framework focuses on intact concrete conditions, excluding fracture-induced thermal perturbations. While justified for early-age bulk hydration monitoring (sensors embed beyond crack-affected zones), future extensions will incorporate phase-field fracture coupling for aging infrastructure.
- (5)
- Boundary Condition Simplification: Insulation properties (λ) are treated as fixed references rather than calibrated variables, potentially limiting their adaptability to degraded insulation. A coupled inversion module for time-varying boundary properties is under development.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wen, T.-H.; Yuen, T.Y.P.; Li, V.K.S.; Yeung, A.T. A case study on early-age cracking of high-strength concrete construction by coupled thermal-mechanical analysis and field monitoring. Case Stud. Constr. Mater. 2024, 21, e03436. [Google Scholar] [CrossRef]
- Lyu, Y.; Liu, Y.; Liu, J.; Ma, Z. Research on hydration-caused thermal cracking risk of steel-concrete composite bridge pylons. J. Constr. Steel Res. 2023, 211, 108165. [Google Scholar] [CrossRef]
- Zhao, Z.; Xie, C.; Liu, Y.; Zhao, Z.; Ouyang, Y.; Song, Y.; Shi, T. Early-age thermal cracking performance of carbon nanotube modified face slab concrete. Constr. Build. Mater. 2024, 433, 136666. [Google Scholar] [CrossRef]
- Zhou, H.; Tian, X.; Wu, J. Cracking and thermal resistance in concrete: Coupled thermo-mechanics and phase-field modeling. Theor. Appl. Fract. Mech. 2024, 130, 104285. [Google Scholar] [CrossRef]
- Zhang, H.; Su, C.; Chen, X.; Song, Z.; Zhan, W. Calculation of Mass Concrete Temperature and Creep Stress under the Influence of Local Air Heat Transfer. CMES Comput. Model. Eng. Sci. 2024, 140, 2977–3000. [Google Scholar] [CrossRef]
- Wang, S.; Duan, J.; Zhang, Y.; He, S.; Hao, X. Optimization of cooling system parameters with temperature field of mass concrete during hydration. Case Stud. Therm. Eng. 2024, 64, 105456. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, J.; Lu, S.; Liang, G.; Peng, C. Multi-scale performance of large-volume concrete under dual control of temperature and deformation. Constr. Build. Mater. 2024, 454, 139116. [Google Scholar] [CrossRef]
- Cai, Y.; Wang, F.; Zhao, Z.; Lyu, Z.; Wang, Y.; Zou, P. Early-Hydration heat and influencing factor analysis of Large-Volume concrete box girder based on equivalent age. Structures 2023, 50, 1699–1713. [Google Scholar] [CrossRef]
- Wu, H.; Hu, X.; Liu, J. Investigations of the hydration heat of large-volume precast concrete bent caps using layered pouring and a new temperature control measure. Case Stud. Constr. Mater. 2024, 20, e03296. [Google Scholar] [CrossRef]
- Almeida Del Savio, A.; La Torre Esquivel, D.; Pasquel Carbajal, E.; de Andrade Silva, F. Experimental and analytical study of temperatures developed by the heat of hydration of high-strength self-compacting mass concrete. Case Stud. Constr. Mater. 2025, 22, e04098. [Google Scholar] [CrossRef]
- Xie, Y.; Du, W.; Xu, Y.; Peng, B.; Qian, C. Temperature field evolution of mass concrete: From hydration dynamics, finite element models to real concrete structure. J. Build. Eng. 2023, 65, 105699. [Google Scholar] [CrossRef]
- Li, X.; Yu, Z.; Chen, K.; Deng, C.; Yu, F. Investigation of temperature development and cracking control strategies of mass concrete: A field monitoring case study. Case Stud. Constr. Mater. 2023, 18, e02144. [Google Scholar] [CrossRef]
- Zhang, H.; Su, C.; Song, Z.; Shen, Z.; Lei, H. Calculation of Mass Concrete Temperature Containing Cooling Water Pipe Based on Substructure and Iteration Algorithm. CMES Comput. Model. Eng. Sci. 2023, 138, 813–826. [Google Scholar] [CrossRef]
- Lingye, L.; Wenwen, L.; Zhang, C.; Pengfei, Z.; Tian, W. Influence of temperature rising inhibitor on temperature and stress field of mass concrete. Case Stud. Constr. Mater. 2023, 18, e01888. [Google Scholar] [CrossRef]
- Abualigah, L. Particle Swarm Optimization: Advances, Applications, and Experimental Insights. Comput. Mater. Contin. 2025, 82, 1539–1592. [Google Scholar] [CrossRef]
- Deng, S.; Xie, M.; Wang, B.; Zhang, S.; Guan, S.; Li, M. Particle Swarm Optimization Algorithm for Feature Selection Inspired by Peak Ecosystem Dynamics. Comput. Mater. Contin. 2025, 82, 2723–2751. [Google Scholar] [CrossRef]
- Hao, R.; Hu, Z.; Xiong, W.; Jiang, S. A composite particle swarm optimization algorithm with future information inspired by non-equidistant grey predictive evolution for global optimization problems and engineering problems. Adv. Eng. Softw. 2025, 202, 103868. [Google Scholar] [CrossRef]
- Guo, Q.; Yang, X.; Li, K.; Li, D. Parameters identification of magnetorheological damper based on particle swarm optimization algorithm. Eng. Appl. Artif. Intell. 2025, 143, 110016. [Google Scholar] [CrossRef]
- Liu, B.; Qian, B.; Liang, Y.; Dai, P.; Li, R.; Wei, Q. Fast and accurate auto-disturbances-rejection temperature control system based on particle swarm optimized fuzzy control: Applied for particle three-dimensional (3D) printing prosthetic orthotic plate. Addit. Manuf. 2025, 101, 104704. [Google Scholar] [CrossRef]
- Mohapatra, P.; Ray, A.; Jena, S.; Padhiari, B.M.; Kuanar, A.; Nayak, S.; Mohanty, S. Artificial neural network based prediction and optimization of centelloside content in Centella asiatica: A comparison between multilayer perceptron (MLP) and radial basis function (RBF) algorithms for soil and climatic parameter. South Afr. J. Bot. 2023, 160, 571–585. [Google Scholar] [CrossRef]
- Mazloum, J.; Hadian Siahkal-Mahalle, B. An efficient operator-splitting radial basis function-generated finite difference (RBF-FD) scheme for image noise removal based on nonlinear total variation models. Eng. Anal. Bound. Elem. 2022, 143, 740–754. [Google Scholar] [CrossRef]
- Sahoo, M.; Dey, S.; Sahoo, S.; Das, A.; Ray, A.; Nayak, S.; Subudhi, E. MLP (multi-layer perceptron) and RBF (radial basis function) neural network approach for estimating and optimizing 6-gingerol content in Zingiber officinale Rosc. in different agro-climatic conditions. Ind. Crops Prod. 2023, 198, 116658. [Google Scholar] [CrossRef]
- Budiana, E.P.; Pranowo; Indarto. Deendarlianto Meshless numerical model based on radial basis function (RBF) method to simulate the Rayleigh–Taylor instability (RTI). Comput. Fluids 2020, 201, 104472. [Google Scholar] [CrossRef]
- Jin, H.; Wang, M.; Xiang, H.; Liu, X.; Wang, C.; Fu, D. A PSO-RBF prediction method on flow corrosion of heat exchanger using the industrial operations data. Process Saf. Environ. Prot. 2024, 183, 11–23. [Google Scholar] [CrossRef]
- Abbasi, E.; Ghatee, M.; Shiri, M.E. FRAN and RBF-PSO as two components of a hyper framework to recognize protein folds. Comput. Biol. Med. 2013, 43, 1182–1191. [Google Scholar] [CrossRef]
- Liu, X.; Wang, S.; Liu, B.; Liu, Q.; Zhou, Y.; Chen, J.; Luo, J. Cement-based grouting material development and prediction of material properties using PSO-RBF machine learning. Constr. Build. Materials 2024, 417, 135328. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, H. Research on the water quality detection method based on fluorescence spectrometry and PSO-RBF network. Measurement 2023, 218, 113197. [Google Scholar] [CrossRef]
- Zhao, D.; Shao, Y.; Hu, H.; Hu, G.; Wang, Y. RBF-PSO-IS: An innovative metamodeling for reliability analysis of bridge’s vortex-induced vibration. Structures 2023, 55, 59–70. [Google Scholar] [CrossRef]

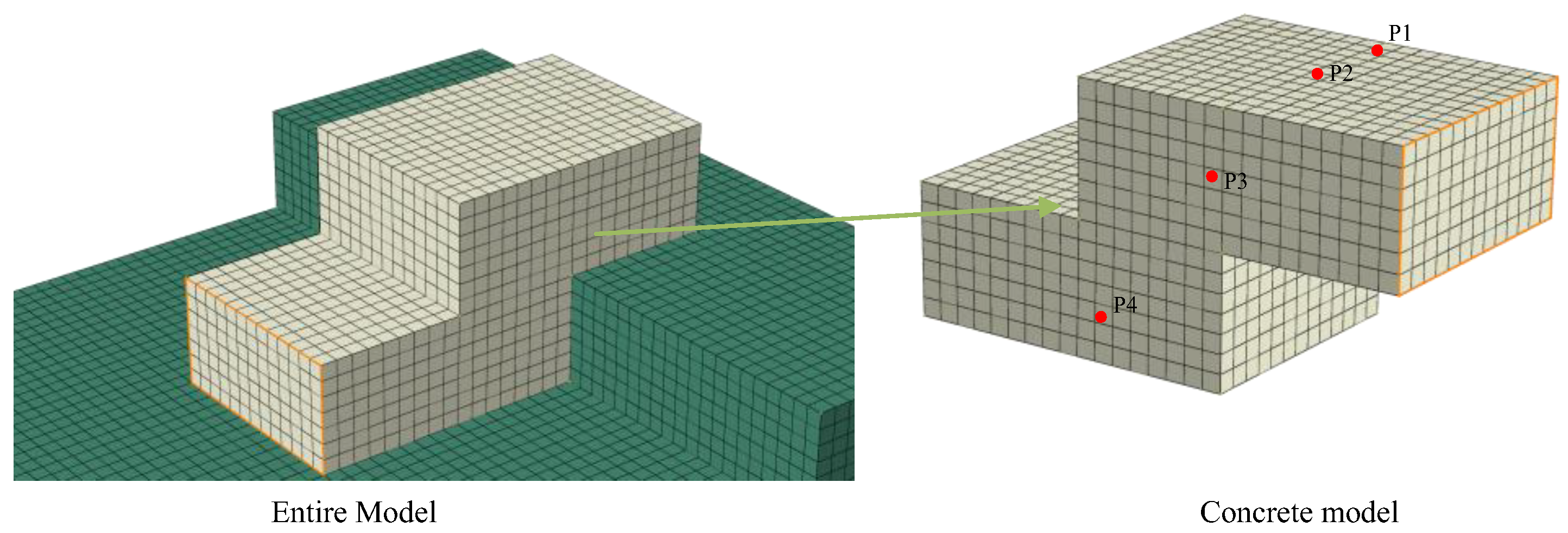
| Sensor | Peak Temperature (°C) | Peak Time (h) | Cooling Rate (°C/h) |
|---|---|---|---|
| P1 | 68.3 | 36.2 | 0.82 |
| P2 | 65.7 | 38.5 | 0.76 |
| P3 | 72.1 | 40.8 | 0.68 |
| P4 | 61.9 | 34.7 | 0.91 |
| Objective Function | Iteration Times | Total FEM Calls |
|---|---|---|
| F1 | 62 | 498 |
| F2 | 23 | 187 |
| F3 | 35 | 254 |
| Parameters | Reference Value | F1 (μ ± σ) | F2 (μ ± σ) | F3 (μ ± σ) |
|---|---|---|---|---|
| 72.1 | 69.2 ± 1.2 | 71.5 ± 0.8 | 71.7 ± 0.3 | |
| k | 0.05 | 0.047 ± 0.005 | 0.05 ± 0.002 | 0.049 ± 0.002 |
| m | 1.01 | 0.99 ± 0.07 | 0.99 ± 0.05 | 1.02 ± 0.01 |
| kconv | 1.8 | 1.66 ± 0.12 | 1.75 ± 0.05 | 1.81 ± 0.04 |
| b | 0.5 | 0.7 ± 0.15 | 0.54 ± 0.08 | 0.49 ± 0.03 |
| Objective Function | P1 | P2 | P3 | P4 | Mean Value |
|---|---|---|---|---|---|
| F1 | 4.1 | 3.8 | 3.2 | 4.5 | 3.9 |
| F2 | 2.3 | 2.1 | 1.8 | 2.6 | 2.2 |
| F3 | 1 | 0.9 | 0.9 | 1.2 | 1 |
| Method | FEM Calls | Time (h) | F3* | ε (%) | Speedup (η) |
|---|---|---|---|---|---|
| RBF-PSO (Proposed) | 70 | 5.2 | 2.1 | 1.8 | 1.0 (ref) |
| Standard PSO | 1923 | 24.0 | 8.7 | 12.3 | 0.22 |
| CMA-ES | 1014 | 14.6 | 3.9 | 2.7 | 0.36 |
| Parameter | Main Effect Si | Total Effect STi |
|---|---|---|
| Q∞ | 0.62 | 0.78 |
| k | 0.18 | 0.35 |
| m | 0.12 | 0.29 |
| kconv | 0.08 | 0.21 |
| Parameter | Baseline Value | Perturbation | MAE (°C) | ΔMAE (%) |
|---|---|---|---|---|
| α | 0.42 | 20% | 1.03 | 3.00% |
| −20% | 0.98 | −2.00% | ||
| β | 0.31 | 20% | 1.05 | 5.00% |
| −20% | 0.95 | −5.00% | ||
| γ | 0.27 | 20% | 1.02 | 2.00% |
| −20% | 0.99 | −1.00% | ||
| λ | 0.8 | 20% | 1.12 | 12.00% |
| −20% | 1.08 | 8.00% |
| Parameter | Baseline | σ = 0.5 °C | σ = 1.0 °C | σ = 2.0 °C |
|---|---|---|---|---|
| Q∞ (°C) | 71.7 ± 0.3 | 71.5 ± 0.5 | 71.2 ± 0.8 | 70.6 ± 1.6 |
| k (h⁻1) | 0.049 ± 0.002 | 0.048 ± 0.004 | 0.047 ± 0.006 | 0.043 ± 0.011 |
| kconv | 1.81 ± 0.04 | 1.78 ± 0.08 | 1.72 ± 0.15 | 1.63 ± 0.28 |
| b | 0.49 ± 0.03 | 0.51 ± 0.07 | 0.55 ± 0.12 | 0.62 ± 0.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, S.; Lin, L.; Mao, W.; Wang, Y.; Liu, J.; Yuan, Y. A Hybrid RBF-PSO Framework for Real-Time Temperature Field Prediction and Hydration Heat Parameter Inversion in Mass Concrete Structures. Buildings 2025, 15, 2236. https://doi.org/10.3390/buildings15132236
Zheng S, Lin L, Mao W, Wang Y, Liu J, Yuan Y. A Hybrid RBF-PSO Framework for Real-Time Temperature Field Prediction and Hydration Heat Parameter Inversion in Mass Concrete Structures. Buildings. 2025; 15(13):2236. https://doi.org/10.3390/buildings15132236
Chicago/Turabian StyleZheng, Shi, Lifen Lin, Wufeng Mao, Yanhong Wang, Jinsong Liu, and Yili Yuan. 2025. "A Hybrid RBF-PSO Framework for Real-Time Temperature Field Prediction and Hydration Heat Parameter Inversion in Mass Concrete Structures" Buildings 15, no. 13: 2236. https://doi.org/10.3390/buildings15132236
APA StyleZheng, S., Lin, L., Mao, W., Wang, Y., Liu, J., & Yuan, Y. (2025). A Hybrid RBF-PSO Framework for Real-Time Temperature Field Prediction and Hydration Heat Parameter Inversion in Mass Concrete Structures. Buildings, 15(13), 2236. https://doi.org/10.3390/buildings15132236





