Numerical Study of Surrounding Rock Damage in Deep-Buried Tunnels for Building-Integrated Underground Structures
Abstract
1. Introduction
2. Numerical Model
2.1. Blasting Load
2.2. Rock Mass
2.3. Description of Rock Damage Model
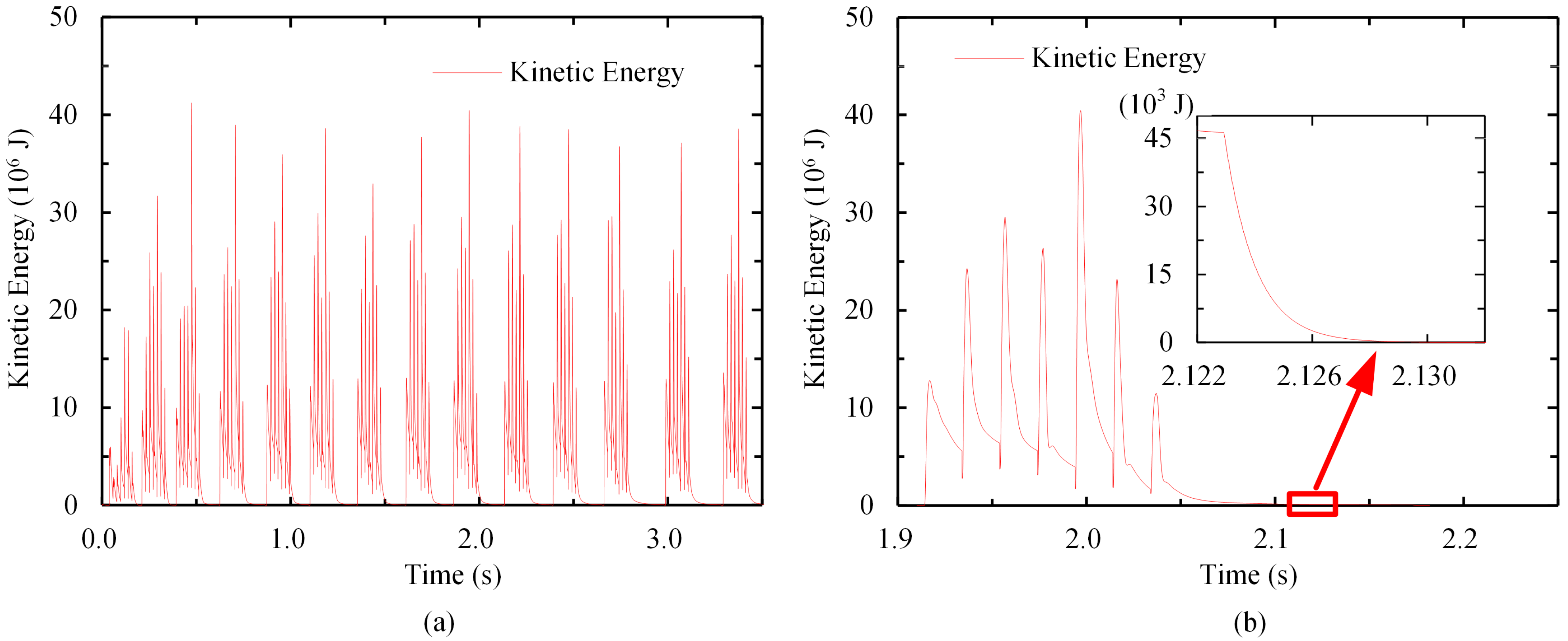
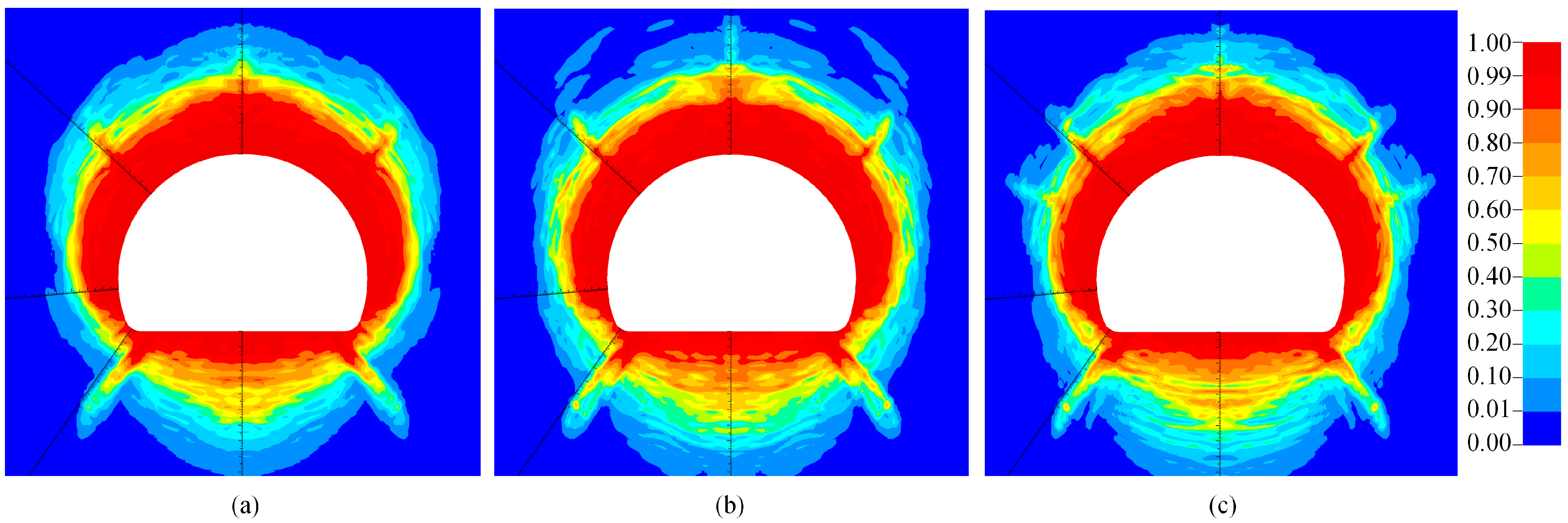
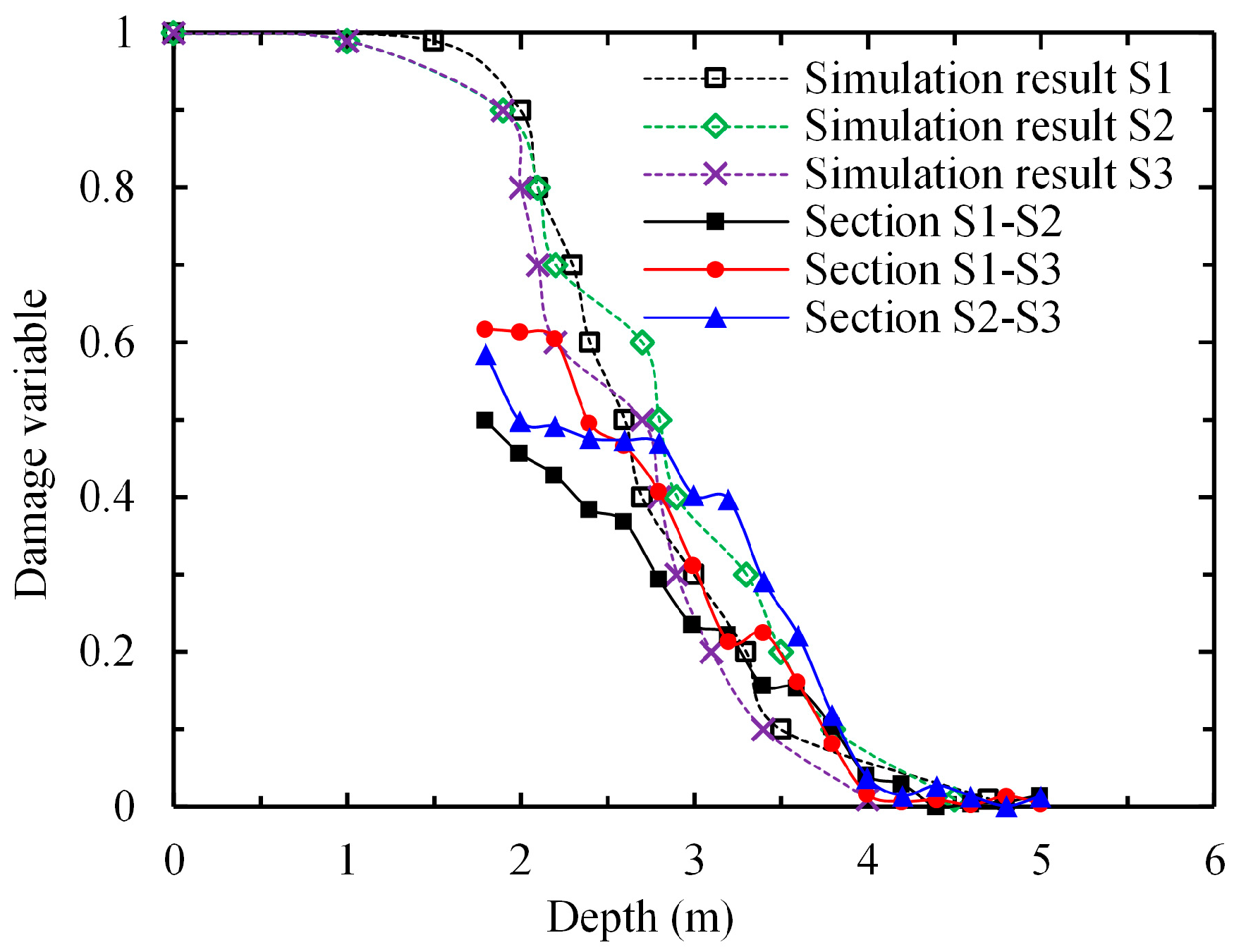
3. Model Validation
4. Results
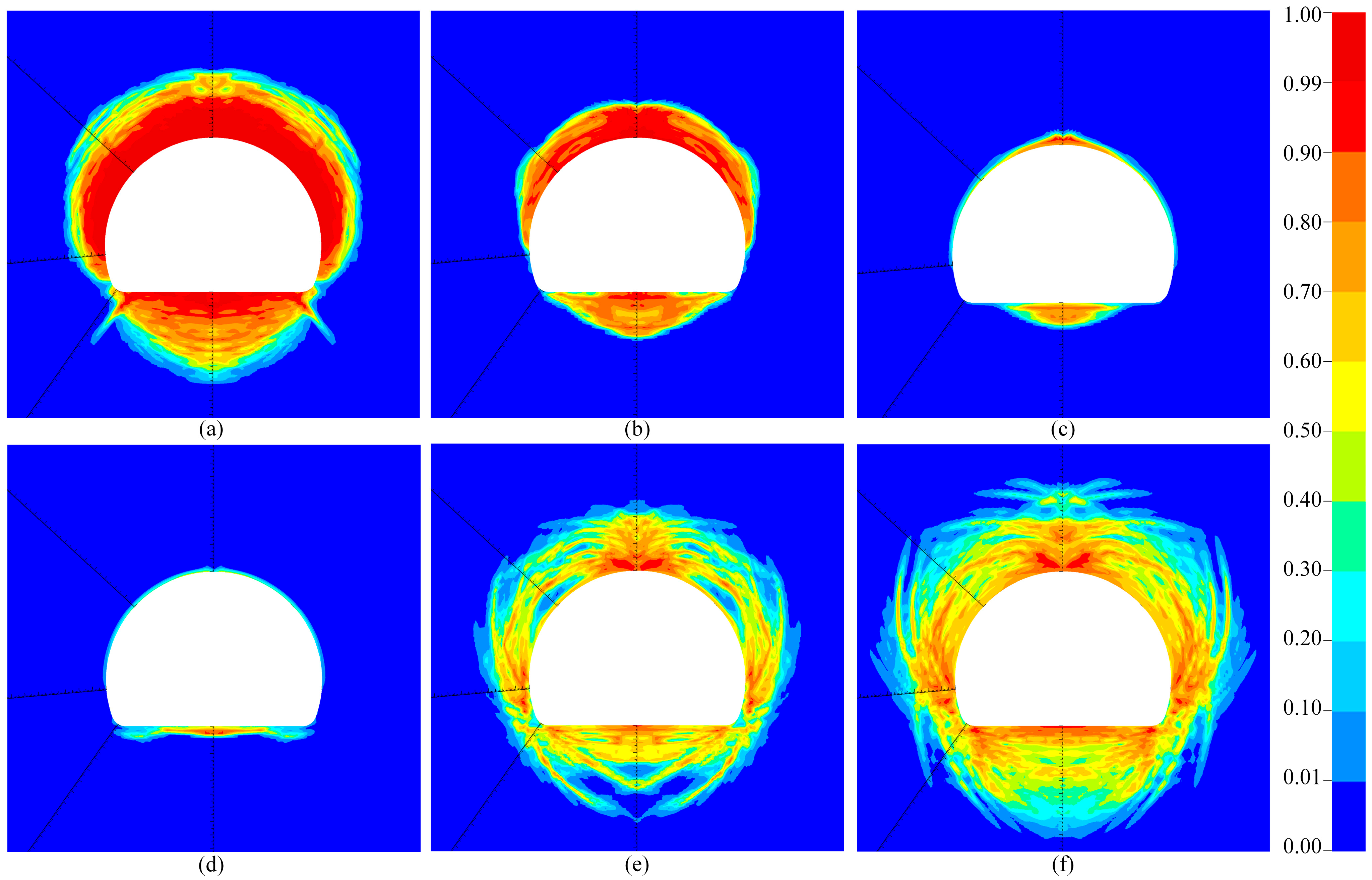
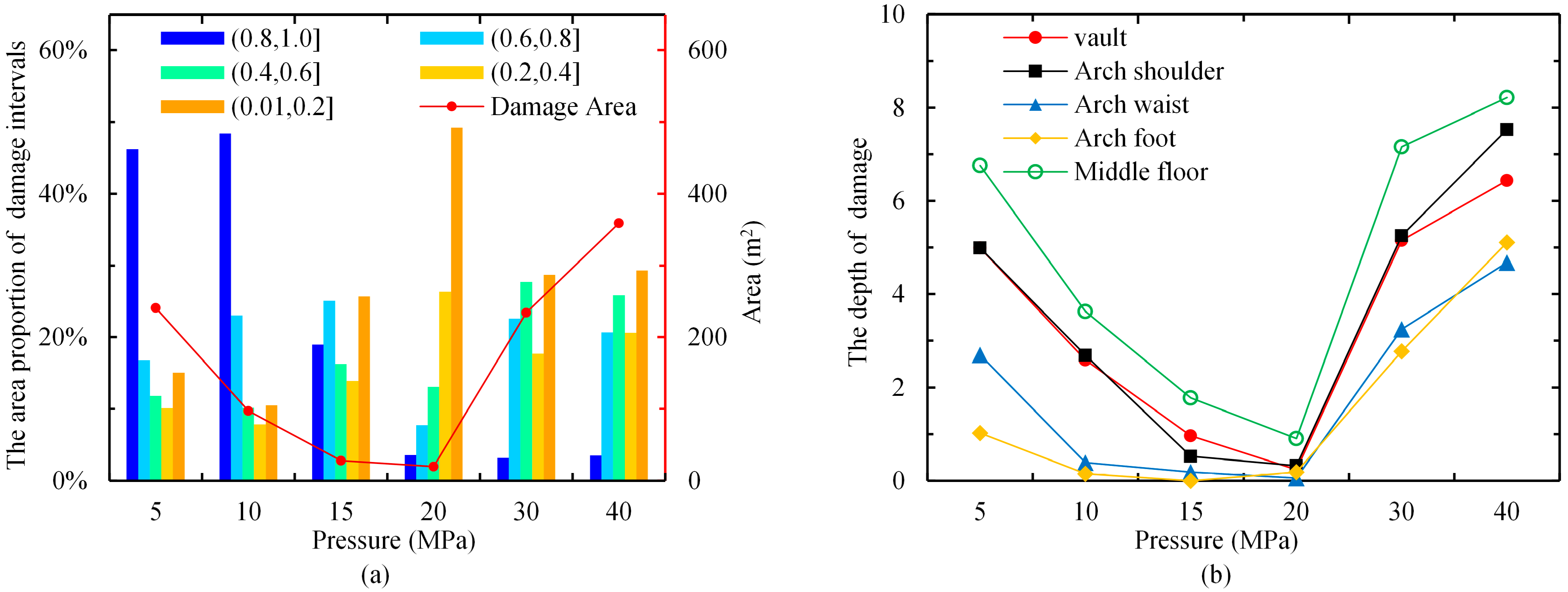
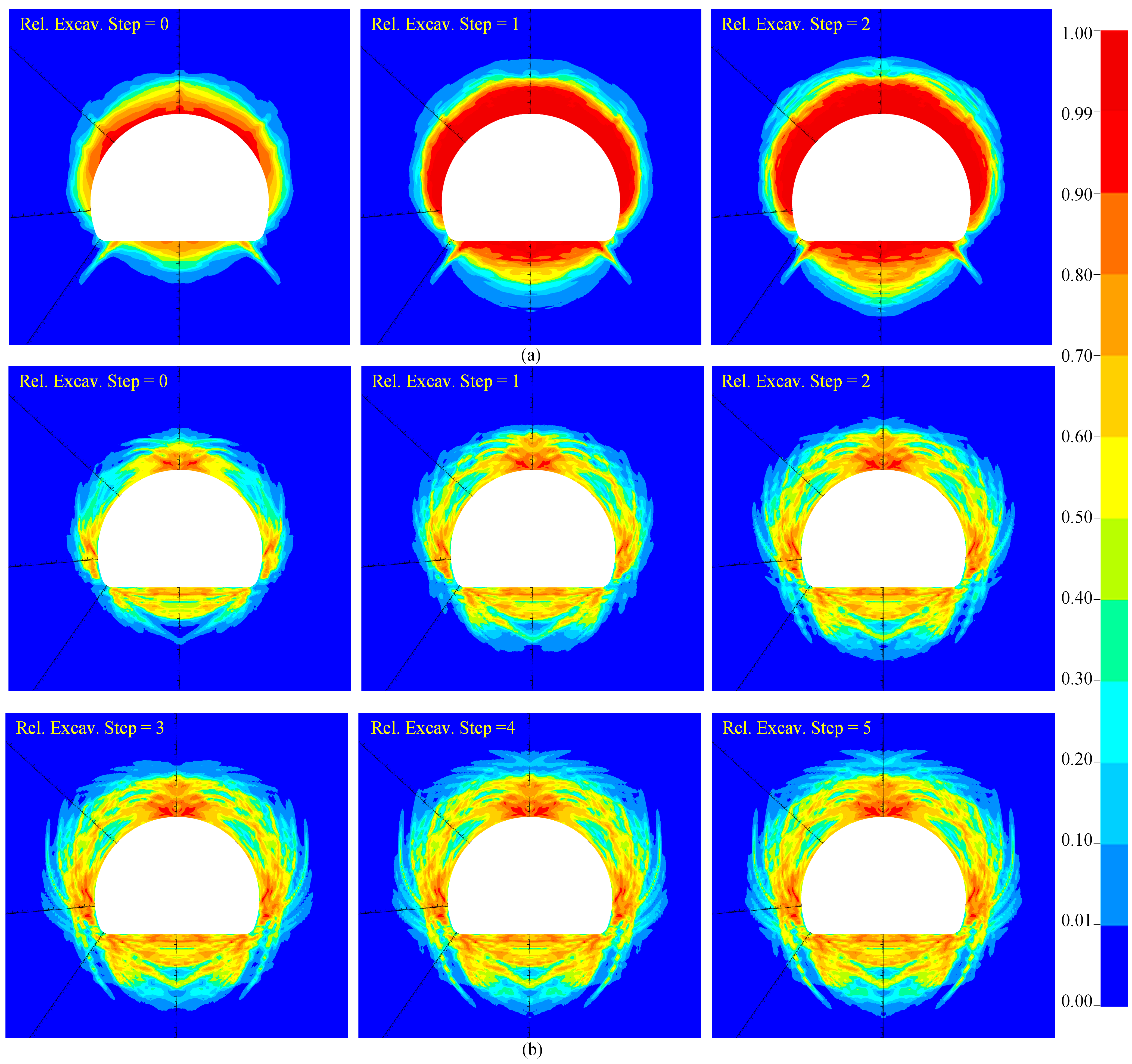
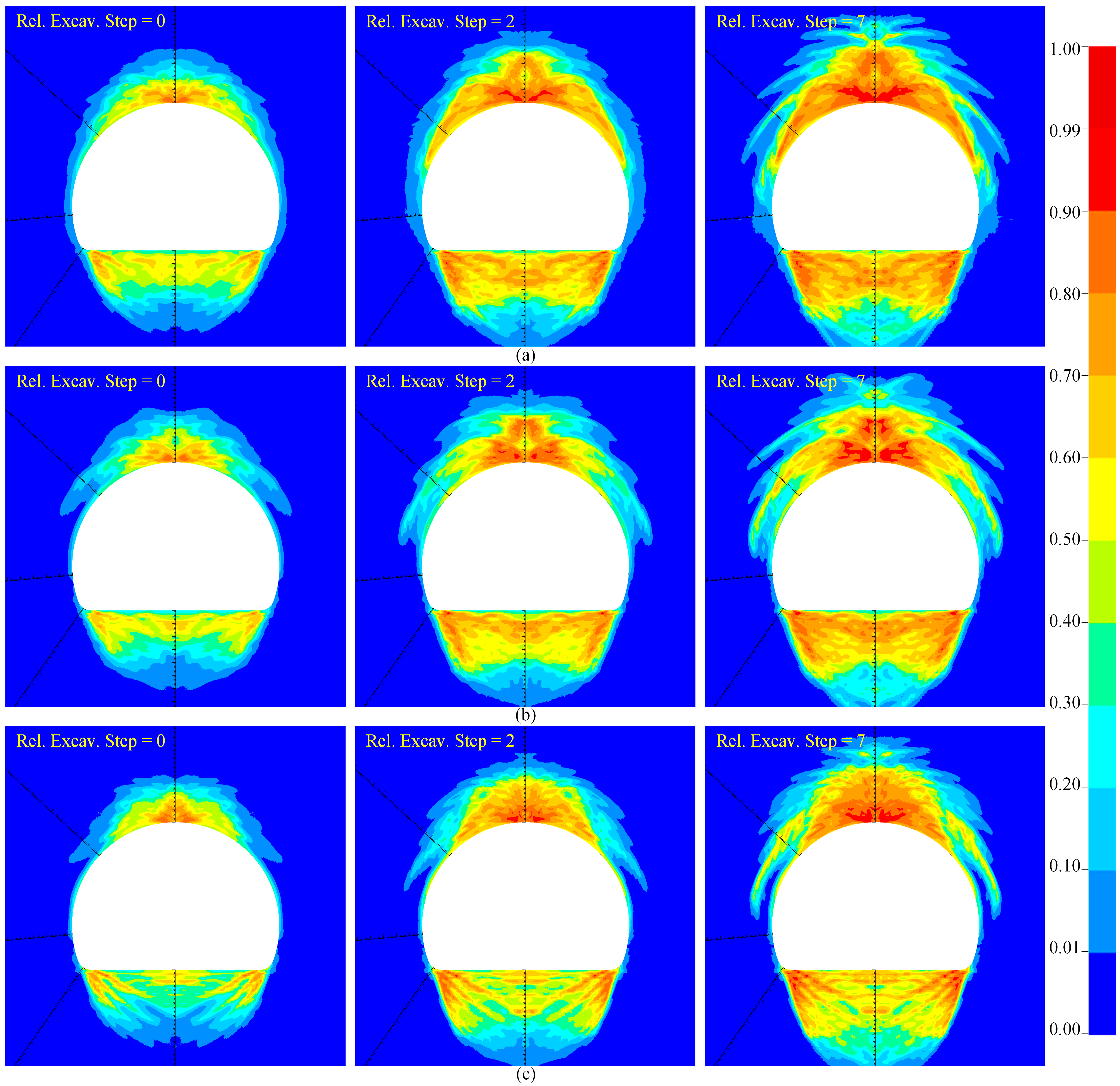
4.1. Damage Distribution Under Different Hydrostatic Pressures
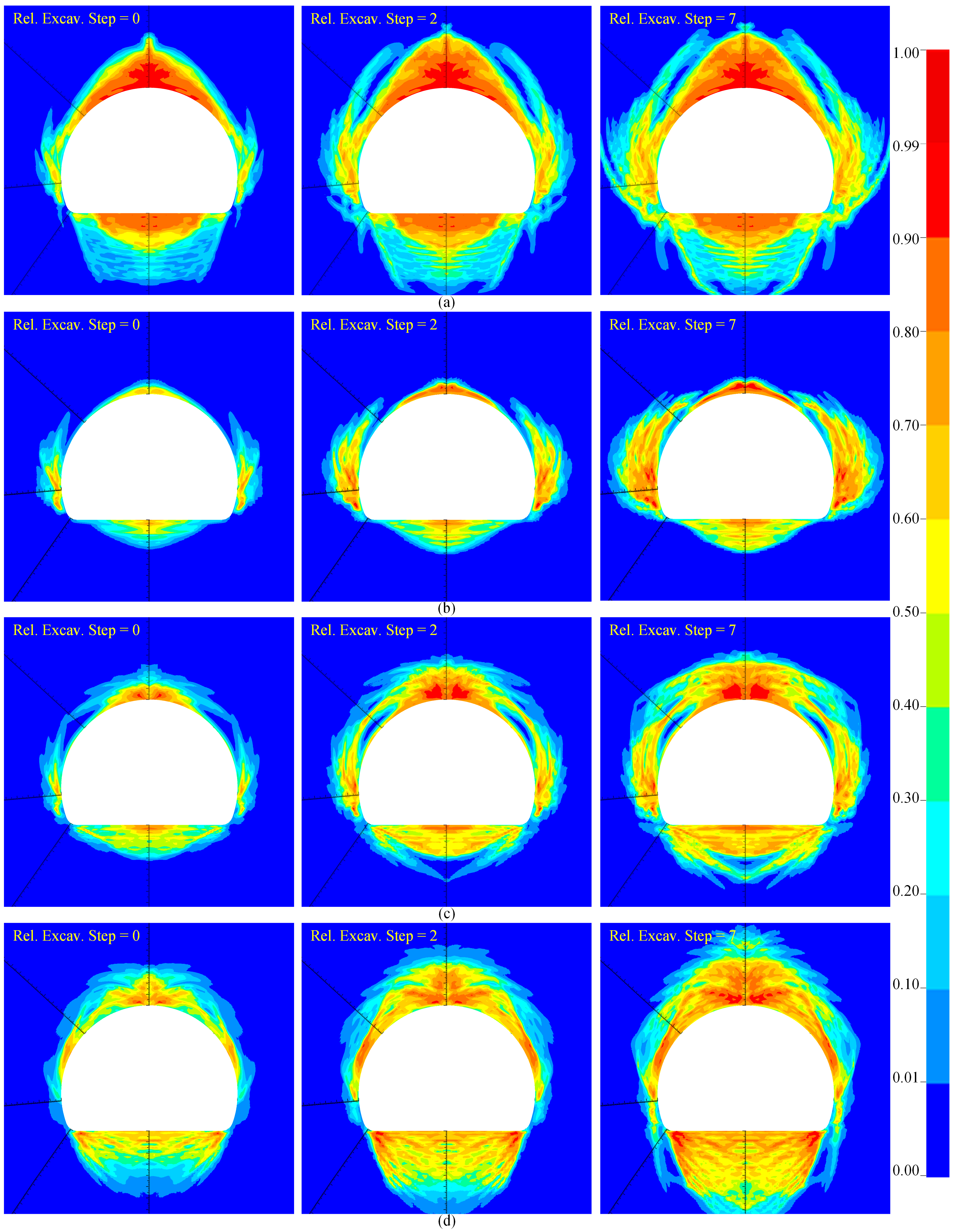
4.2. Rock Damage Under Different Lateral Pressures
4.2.1. Influence of Different Lateral Pressure Coefficients on Surrounding Rock Damage
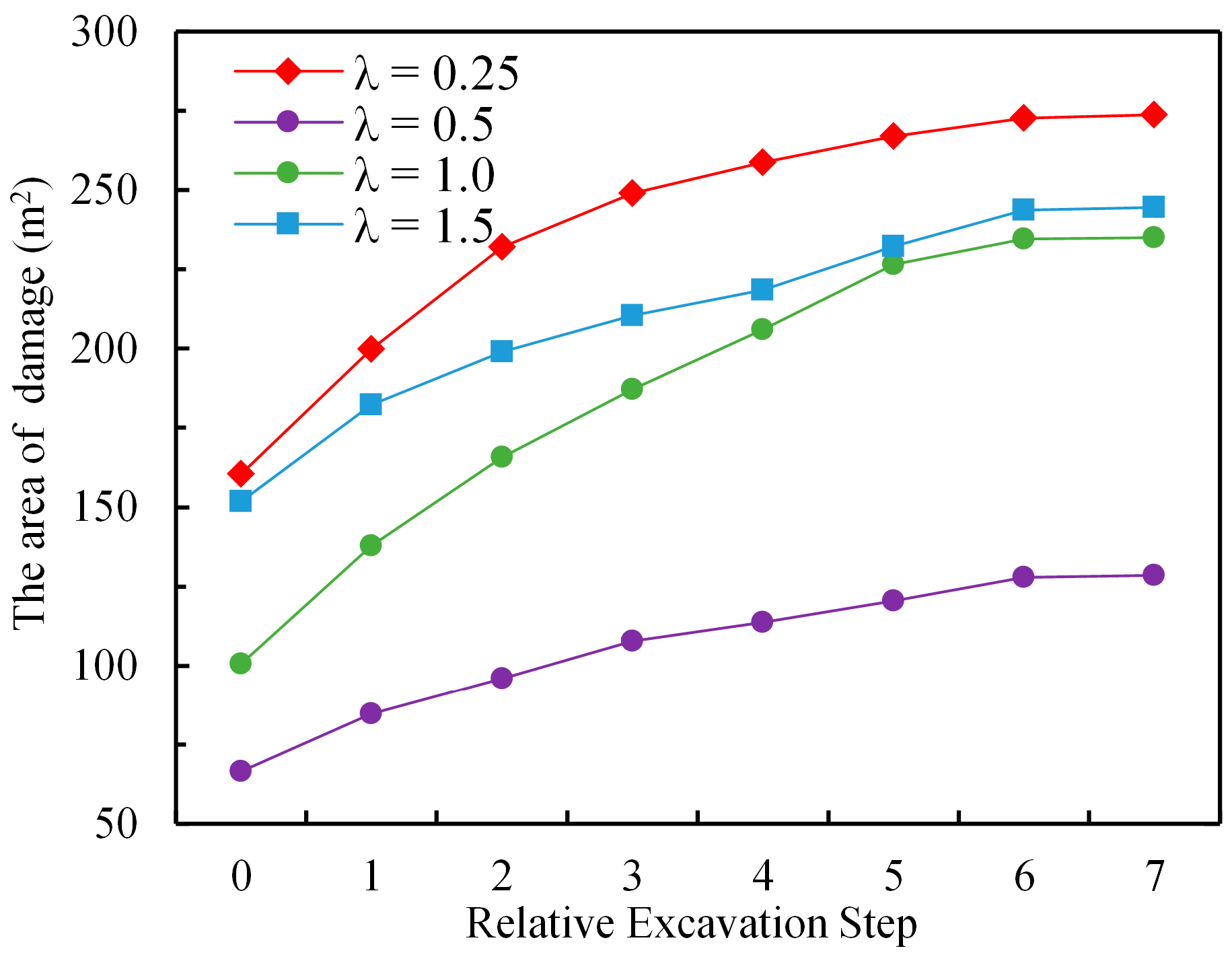
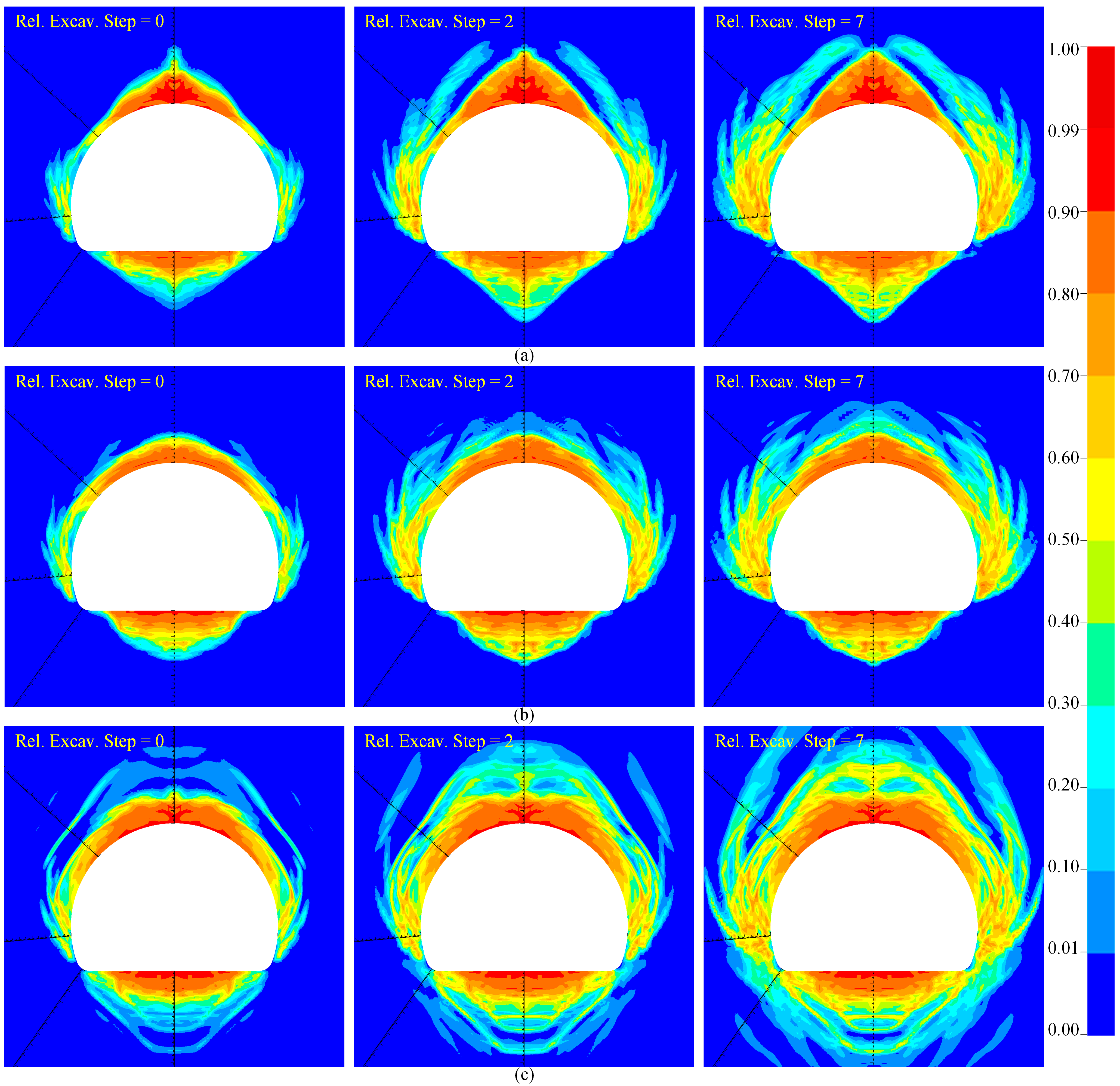
4.2.2. Influence of Different σh on Surrounding Rock Damage
5. Discussion
6. Conclusions
- (1)
- With increasing hydrostatic pressure, the extent of the damage zone in the surrounding rock initially decreases and then expands. Under low hydrostatic pressure, blasting-induced damage dominates. As hydrostatic pressure increases, it suppresses the spread of blasting damage, thereby reducing the extent of the damage. With a further increase in stress, unloading-induced shear failure becomes dominant, resulting in a progressive expansion of the damage zone.
- (2)
- At lower hydrostatic pressure, a larger proportion of the damaged zone exhibits damage values exceeding 0.8 compared with higher pressure scenarios. For this horseshoe-shaped tunnel, the damage depth is greatest at the vault and floor and minimal at the arch waist under hydrostatic pressure. When the hydrostatic pressure is less than 20 MPa, the surrounding rock stabilizes at a distance greater than 12.6 m from the tunnel face, whereas at hydrostatic pressures of 30 MPa and 40 MPa, this distance increases to 29.4 m.
- (3)
- When σH = σh and σv = 30 MPa, under low lateral pressure coefficients, damage primarily involves tensile failure at the vault and floor and shear failure at the arch waist. As the lateral pressure coefficient increases, shear failure at the arch waist diminishes, while the extent of tensile failure at the vault and floor decreases, gradually transitioning into shear failure, which then intensifies. Overall, the damaged area decreases initially and then increases as the lateral pressure coefficient rises.
- (4)
- When σH < σv = 30 MPa and σh < σv, the damage characteristics resemble those under low lateral pressure: tensile failure occurs at the vault and floor, and shear failure at the arch waist and arch shoulder. However, when σh ≥ σv, shear failure intensifies at the arch waist, forming multiple long shear damage zones. When σH > σv = 30 MPa, increases in σh have a limited influence on the extent of the damage. Thus, when the horizontal stress perpendicular to the tunnel exceeds the vertical stress, the axial stress has a negligible effect on the extent of surrounding rock damage.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hong, Z.; Tao, M.; Wu, C.; Zhou, J.; Wang, D. The Spatial Distribution of Excavation Damaged Zone around Underground Roadways during Blasting Excavation. Bull. Eng. Geol. Environ. 2023, 82, 155. [Google Scholar] [CrossRef]
- Li, S.; Ling, T.; Liu, D.; Liang, S.; Zhang, R.; Huang, B.; Liu, K. Determination of Rock Mass Parameters for the RHT Model Based on the Hoek–Brown Criterion. Rock Mech. Rock Eng. 2023, 56, 2861–2877. [Google Scholar] [CrossRef]
- Cui, Y.; Wu, B.; Meng, G.; Xu, S. Research on Blasting Cumulative Dynamic Damage of Surrounding Rock in Step Construction Tunnel. Sci. Rep. 2023, 13, 1974. [Google Scholar] [CrossRef] [PubMed]
- Ji, L.; Yao, Y.; Zhou, C.; Zhang, Z.; Cao, H.; Wu, T. Research on Cumulative Damage Effects and Safety Criterion of Surrounding Rock in Bench Blasting of a Large Cross-Section Tunnel. Alex. Eng. J. 2024, 108, 626–639. [Google Scholar] [CrossRef]
- Martino, J.B.; Chandler, N.A. Excavation-Induced Damage Studies at the Underground Research Laboratory. Int. J. Rock Mech. Min. Sci. 2004, 41, 1413–1426. [Google Scholar] [CrossRef]
- Yang, J.H.; Yao, C.; Jiang, Q.H.; Lu, W.B.; Jiang, S.H. 2D Numerical Analysis of Rock Damage Induced by Dynamic In-Situ Stress Redistribution and Blast Loading in Underground Blasting Excavation. Tunn. Undergr. Space Technol. 2017, 70, 221–232. [Google Scholar] [CrossRef]
- Yang, J.; Lu, W.; Hu, Y.; Chen, M.; Yan, P. Numerical Simulation of Rock Mass Damage Evolution during Deep-Buried Tunnel Excavation by Drill and Blast. Rock Mech. Rock Eng. 2015, 48, 2045–2059. [Google Scholar] [CrossRef]
- Ji, L.; Zhou, C.; Lu, S.; Jiang, N.; Gutierrez, M. Numerical Studies on the Cumulative Damage Effects and Safety Criterion of a Large Cross-Section Tunnel Induced by Single and Multiple Full-Scale Blasting. Rock Mech. Rock Eng. 2021, 54, 6393–6411. [Google Scholar] [CrossRef]
- Yan, P.; Lu, W.; Chen, M.; Hu, Y.; Zhou, C.; Wu, X. Contributions of In-Situ Stress Transient Redistribution to Blasting Excavation Damage Zone of Deep Tunnels. Rock Mech. Rock Eng. 2015, 48, 715–726. [Google Scholar] [CrossRef]
- Kipp, M.E.; Grady, D.E. Numerical Studies of Rock Fragmentation; Sandia National Laboratories: Albuquerque, NM, USA, 1980.
- Grady, D.E.; Kipp, M.E. Mechanisms of Dynamic Fragmentation: Factors Governing Fragment Size. Mech. Mater. 1985, 4, 311–320. [Google Scholar] [CrossRef]
- Taylor, L.M.; Chen, E.-P.; Kuszmaul, J.S. Microcrack-Induced Damage Accumulation in Brittle Rock under Dynamic Loading. Comput. Methods Appl. Mech. Eng. 1986, 55, 301–320. [Google Scholar] [CrossRef]
- Kuszmaul, J.S. A New Constitutive Model for Fragmentation of Rock Under Dynamic Loading; Sandia National Laboratories: Albuquerque, NM, USA, 1987.
- Thorne, B.J.; Hommert, P.J.; Brown, B. Experimental and Computational Investigation of the Fundamental Mechanisms of Cratering; Sandia National Laboratories: Albuquerque, NM, USA, 1990. [CrossRef]
- Krajcinovic, D.; Silva, M.A.G. Statistical Aspects of the Continuous Damage Theory. Int. J. Solids Struct. 1982, 18, 551–562. [Google Scholar] [CrossRef]
- Xie, L.X.; Lu, W.B.; Zhang, Q.B.; Jiang, Q.H.; Wang, G.H.; Zhao, J. Damage Evolution Mechanisms of Rock in Deep Tunnels Induced by Cut Blasting. Tunn. Undergr. Space Technol. 2016, 58, 257–270. [Google Scholar] [CrossRef]
- Lyu, G.; Zhou, C.; Jiang, N. Experimental and Numerical Study on Tunnel Blasting Induced Damage Characteristics of Grouted Surrounding Rock in Fault Zones. Rock Mech. Rock Eng. 2023, 56, 603–617. [Google Scholar] [CrossRef]
- Johnson, G.R.; Holmquist, T.J. Response of Boron Carbide Subjected to Large Strains, High Strain Rates, and High Pressures. J. Appl. Phys. 1999, 85, 8060–8073. [Google Scholar] [CrossRef]
- Liu, K.; Wu, C.; Li, X.; Li, Q.; Fang, J.; Liu, J. A Modified HJC Model for Improved Dynamic Response of Brittle Materials under Blasting Loads. Comput. Geotech. 2020, 123, 103584. [Google Scholar] [CrossRef]
- Yilmaz, O.; Unlu, T. Three Dimensional Numerical Rock Damage Analysis under Blasting Load. Tunn. Undergr. Space Technol. 2013, 38, 266–278. [Google Scholar] [CrossRef]
- Wang, Z.L.; Konietzky, H. Modelling of Blast-Induced Fractures in Jointed Rock Masses. Eng. Fract. Mech. 2009, 76, 1945–1955. [Google Scholar] [CrossRef]
- Li, X.; Cao, W.; Zhou, Z.; Zou, Y. Influence of Stress Path on Excavation Unloading Response. Tunn. Undergr. Space Technol. 2014, 42, 237–246. [Google Scholar] [CrossRef]
- Zou, X.-W.; Zhou, T.; Li, G.; Hu, Y.; Deng, B.; Yang, T. Intelligent Inversion Analysis of Surrounding Rock Parameters and Deformation Characteristics of a Water Diversion Surge Shaft. Designs 2024, 8, 116. [Google Scholar] [CrossRef]
- Ma, W.-B.; Zou, W.-H.; Zhang, J.-L.; Li, G. Prediction of Shear Strength in Anisotropic Structural Planes Considering Size Effects. Designs 2025, 9, 17. [Google Scholar] [CrossRef]
- Xu, X.; Wu, Z.; Weng, L.; Chu, Z.; Liu, Q.; Zhou, Y. Numerical Investigation of Geostress Influence on the Grouting Reinforcement Effectiveness of Tunnel Surrounding Rock Mass in Fault Fracture Zones. J. Rock Mech. Geotech. Eng. 2024, 16, 81–101. [Google Scholar] [CrossRef]
- Xu, X.; Wu, Z.; Weng, L.; Chu, Z.; Liu, Q.; Wang, Z. Investigating the Impacts of Reinforcement Range and Grouting Timing on Grouting Reinforcement Effectiveness for Tunnels in Fault Rupture Zones Using a Numerical Manifold Method. Eng. Geol. 2024, 330, 107423. [Google Scholar] [CrossRef]
- Ma, G.W.; An, X.M. Numerical Simulation of Blasting-Induced Rock Fractures. Int. J. Rock Mech. Min. Sci. 2008, 45, 966–975. [Google Scholar] [CrossRef]
- Lu, W.; Yang, J.; Chen, M.; Zhou, C. An Equivalent Method for Blasting Vibration Simulation. Simul. Model. Pract. Theory 2011, 19, 2050–2062. [Google Scholar] [CrossRef]
- Yang, J.; Xia, Y.; Chen, Z.; Chen, D.; Pei, Y.; Zhu, W. Dynamic Behavior of Road High Cutting Rock Slope under the Influence of Blasting for Excavation. Procedia Earth Planet. Sci. 2012, 5, 25–31. [Google Scholar] [CrossRef]
- Yang, J.; Lu, W.; Jiang, Q.; Yao, C.; Jiang, S.; Tian, L. A Study on the Vibration Frequency of Blasting Excavation in Highly Stressed Rock Masses. Rock Mech. Rock Eng. 2016, 49, 2825–2843. [Google Scholar] [CrossRef]
- Lu, W.; Yang, J.; Yan, P.; Chen, M.; Zhou, C.; Luo, Y.; Jin, L. Dynamic Response of Rock Mass Induced by the Transient Release of In-Situ Stress. Int. J. Rock Mech. Min. Sci. 2012, 53, 129–141. [Google Scholar] [CrossRef]
- Persson, P.-A.; Holmberg, R.; Lee, J. Rock Blasting and Explosives Engineering; CRC Press: Boca Raton, FL, USA, 2018; ISBN 0203740513. [Google Scholar] [CrossRef]
- Martin, C.D.; Kaiser, P.K.; McCreath, D.R. Hoek-Brown Parameters for Predicting the Depth of Brittle Failure around Tunnels. Can. Geotech. J. 1999, 36, 136–151. [Google Scholar] [CrossRef]
- Hoek, E.; Carranza-Torres, C.; Corkum, B. Hoek-Brown Failure Criterion-2002 Edition. Proc. NARMS-Tac 2002, 1, 267–273. [Google Scholar] [CrossRef]
- Zhang, Q.B.; Zhao, J. A Review of Dynamic Experimental Techniques and Mechanical Behaviour of Rock Materials. Rock Mech. Rock Eng. 2014, 47, 1411–1478. [Google Scholar] [CrossRef]
- Xie, L.X.; Lu, W.B.; Zhang, Q.B.; Jiang, Q.H.; Chen, M.; Zhao, J. Analysis of Damage Mechanisms and Optimization of Cut Blasting Design under High In-Situ Stresses. Tunn. Undergr. Space Technol. 2017, 66, 19–33. [Google Scholar] [CrossRef]
- Livermore Software Technology Corporation (LSCT). LS-DYNA, version 971; Keyword User’s Manual; Livermore Software Technology Corporation (LSCT): Livermore, CA, USA, 2012; Volume I. [Google Scholar]
- Zhu, B.; Zhou, C.; Jiang, N. Dynamic Response Characteristics and Safety Control of Mortar Bolts under the Action of Tunnel Blasting Excavation. J. Vib. Eng. 2023, 36, 235–246. [Google Scholar] [CrossRef]
- Mustapha, S.; Ye, L. Leaky and Non-Leaky Behaviours of Guided Waves in CF/EP Sandwich Structures. Wave Motion 2014, 51, 905–918. [Google Scholar] [CrossRef]
- Ji, L.; Zhou, C.; Lu, S.; Jiang, N.; Li, H. Modeling Study of Cumulative Damage Effects and Safety Criterion of Surrounding Rock under Multiple Full-Face Blasting of a Large Cross-Section Tunnel. Int. J. Rock Mech. Min. Sci. 2021, 147, 104882. [Google Scholar] [CrossRef]
- Marburg, S. Six Boundary Elements per Wavelength: Is That Enough? J. Comput. Acoust. 2002, 10, 25–51. [Google Scholar] [CrossRef]
- Bagheri, M.; Jamkhaneh, M.E.; Samali, B. Effect of seismic soil–pile–structure interaction on mid-and high-rise steel buildings resting on a group of pile foundations. Int. J. Geomech. 2018, 18, 04018103. [Google Scholar] [CrossRef]
- Yang, J.; Liu, K.; Li, X.; Liu, Z. Stress initialization methods for dynamic numerical simulation of rock mass with high in-situ stress. J. Cent. South Univ. 2020, 27, 3149–3162. [Google Scholar] [CrossRef]
- Li, X.; Zhu, Z.; Wang, M.; Wan, D.; Zhou, L.; Liu, R. Numerical Study on the Behavior of Blasting in Deep Rock Masses. Tunn. Undergr. Space Technol. 2021, 113, 103968. [Google Scholar] [CrossRef]
- Zhu, W.C.; Wei, J.; Zhao, J.; Niu, L.L. 2D Numerical Simulation on Excavation Damaged Zone Induced by Dynamic Stress Redistribution. Tunn. Undergr. Space Technol. 2014, 43, 315–326. [Google Scholar] [CrossRef]
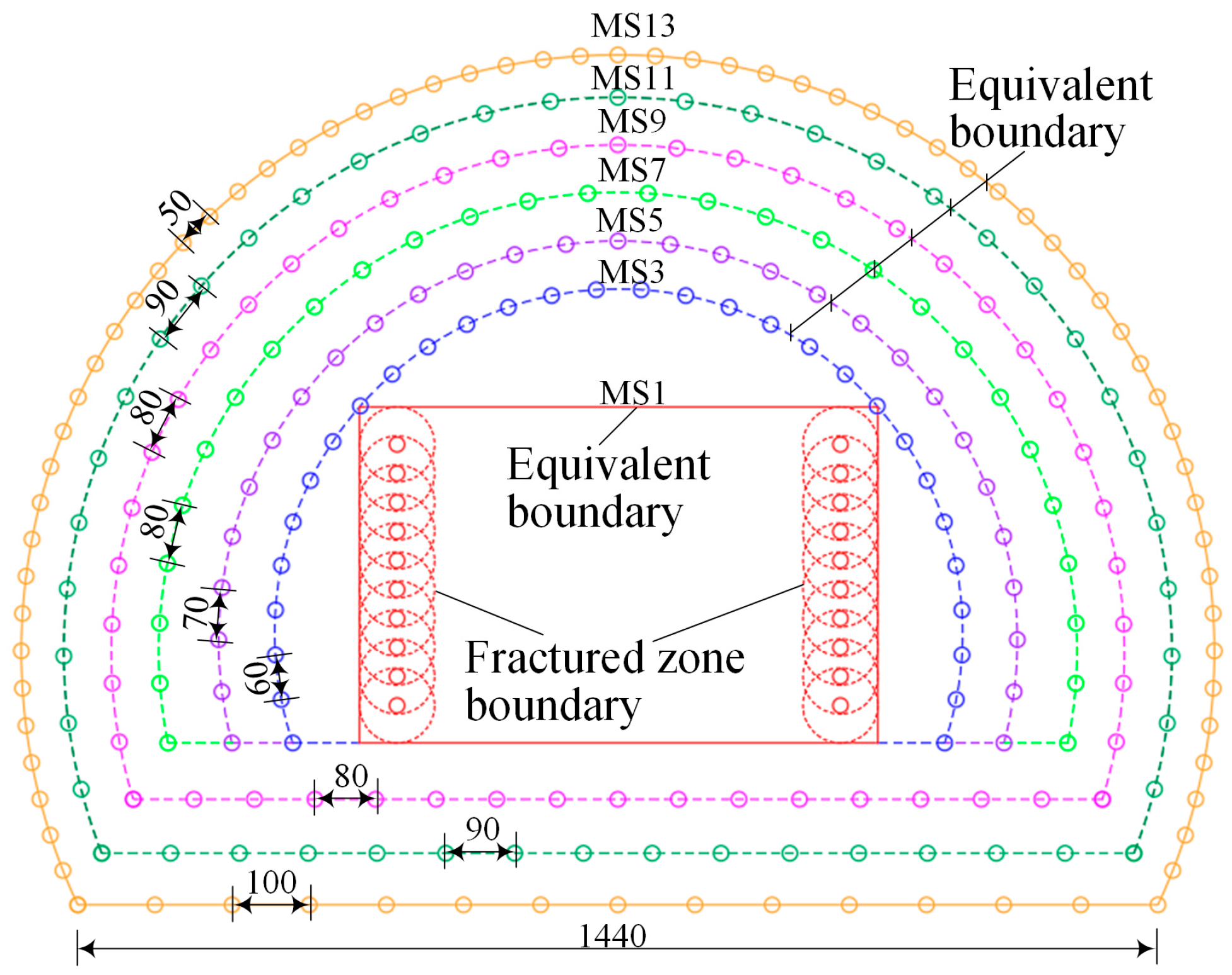





| Blast hole Type | Cutting Holes | Breaking Holes | Smooth Holes | Bottom Holes | ||||
|---|---|---|---|---|---|---|---|---|
| Detonator series | MS1 | MS3 | MS5 | MS7 | MS9 | MS11 | MS13 | MS13 |
| Peak Pc (MPa) | 78 | 52 | 45 | 39 | 39 | 35 | 12 | 32 |
| tr (ms) | 0.75 | 0.7 | 0.65 | 0.6 | 0.55 | 0.5 | 0.7 | 0.5 |
| Density (kg/m3) | Elastic Modulus (GPa) | Poisson’s Ratio | Static Tensile Strength (MPa) | Friction Angle (°) | Cohesion (MPa) |
|---|---|---|---|---|---|
| 2700 | 45 | 0.2 | 8 | 36 | 28 |
| Shear Modulus G/GPa | Poisson’s Ratio μ | Uniaxial Compressive Strength σrc/MPa | Hoek–Brown Criterion Parameter mb | Hoek–Brown Criterion Parameter s | Hoek–Brown Criterion Parameter a |
|---|---|---|---|---|---|
| 17.86 | 0.2 | 109.91 | 6.73 | 0.007 | 0.504 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Density (kg/m3) | 2700 | 0.512 | |
| Shear modulus (GPa) | 17.86 | 2.4 | |
| Poisson’s ratio | 0.2 | 0.026 | |
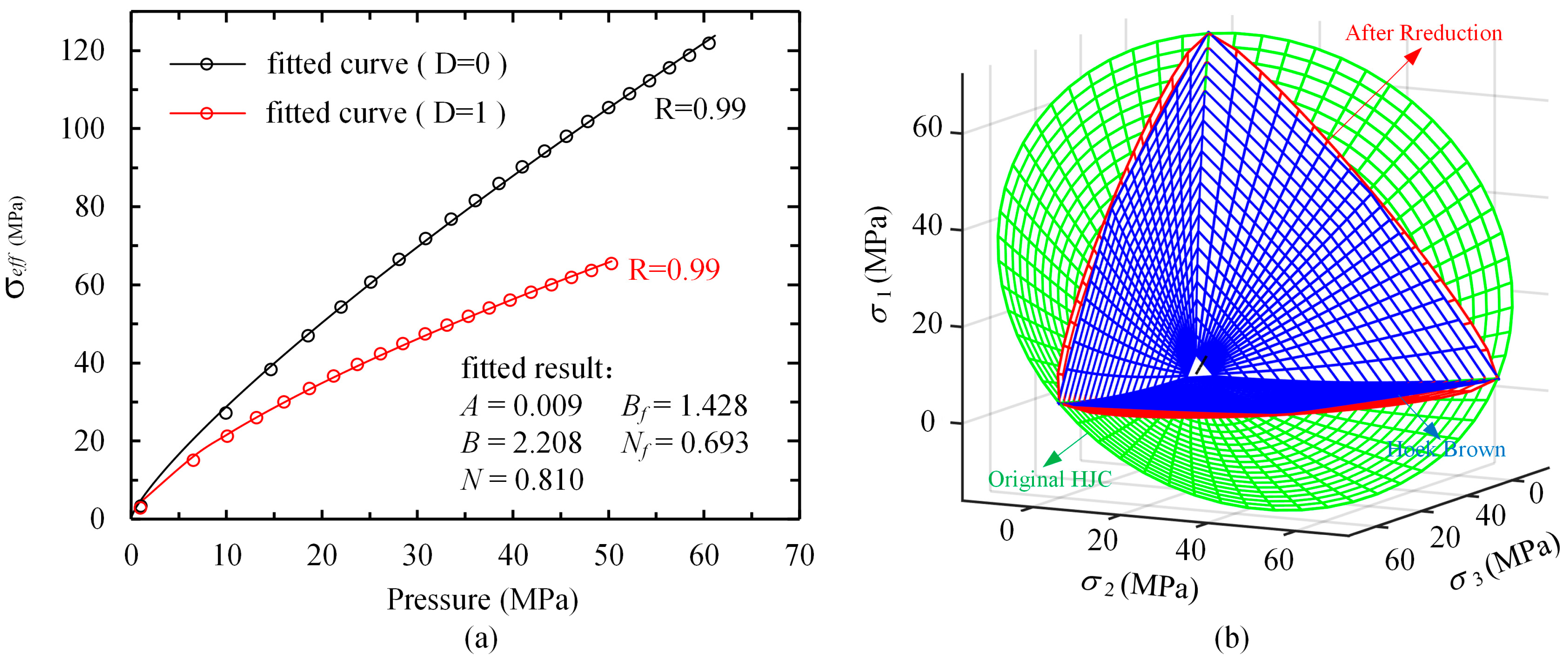
| A | 0.009 | 0.007 | |
| B | 2.208 | (s−1) | 3 × 10−5 |
| N | 0.910 | (s−1) | 3 × 10−6 |
| Bf | 1.428 | (s−1) | 30 |
| Nf | 0.693 | (s−1) | 0.1 |
| T (MPa) | 1.1 | Q0 | 0.60 |
| EFMIN | 0.007 | B0 | 0.01 |
| D1 | 0.04 | 0.5 | |
| D2 | 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Zhang, C.; Chen, W.; He, C.; Liu, Y.; Chu, Z. Numerical Study of Surrounding Rock Damage in Deep-Buried Tunnels for Building-Integrated Underground Structures. Buildings 2025, 15, 2168. https://doi.org/10.3390/buildings15132168
Zhang P, Zhang C, Chen W, He C, Liu Y, Chu Z. Numerical Study of Surrounding Rock Damage in Deep-Buried Tunnels for Building-Integrated Underground Structures. Buildings. 2025; 15(13):2168. https://doi.org/10.3390/buildings15132168
Chicago/Turabian StyleZhang, Penglin, Chong Zhang, Weitao Chen, Chunhui He, Yang Liu, and Zhaofei Chu. 2025. "Numerical Study of Surrounding Rock Damage in Deep-Buried Tunnels for Building-Integrated Underground Structures" Buildings 15, no. 13: 2168. https://doi.org/10.3390/buildings15132168
APA StyleZhang, P., Zhang, C., Chen, W., He, C., Liu, Y., & Chu, Z. (2025). Numerical Study of Surrounding Rock Damage in Deep-Buried Tunnels for Building-Integrated Underground Structures. Buildings, 15(13), 2168. https://doi.org/10.3390/buildings15132168






