Analysis of Pile–Soil Interaction Mechanisms for Wind Turbine Tower Foundations in Collapsible Loess Under Multi-Hazard Coupled Loading
Abstract
1. Introduction
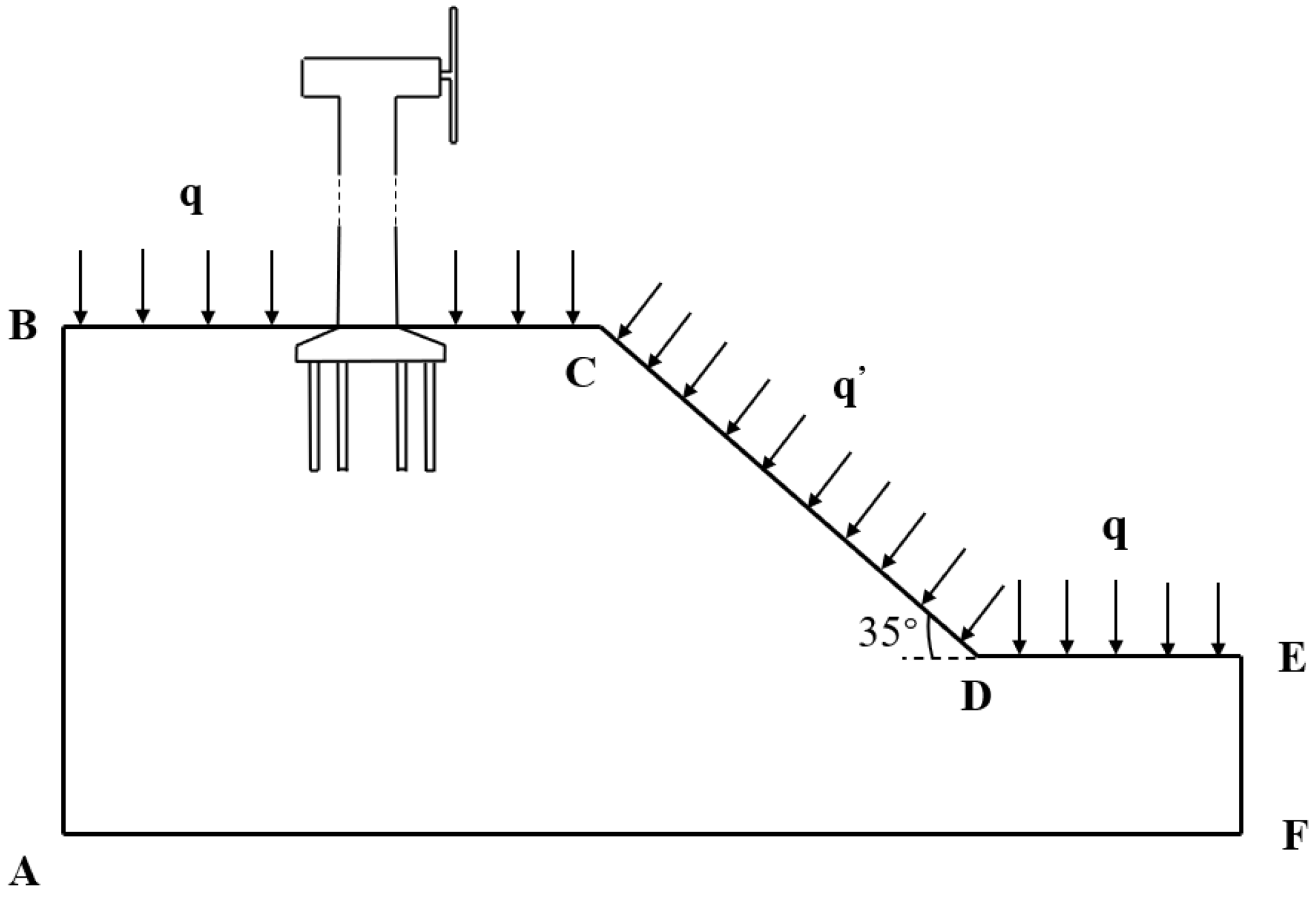
2. Engineering Background
3. Numerical Analysis
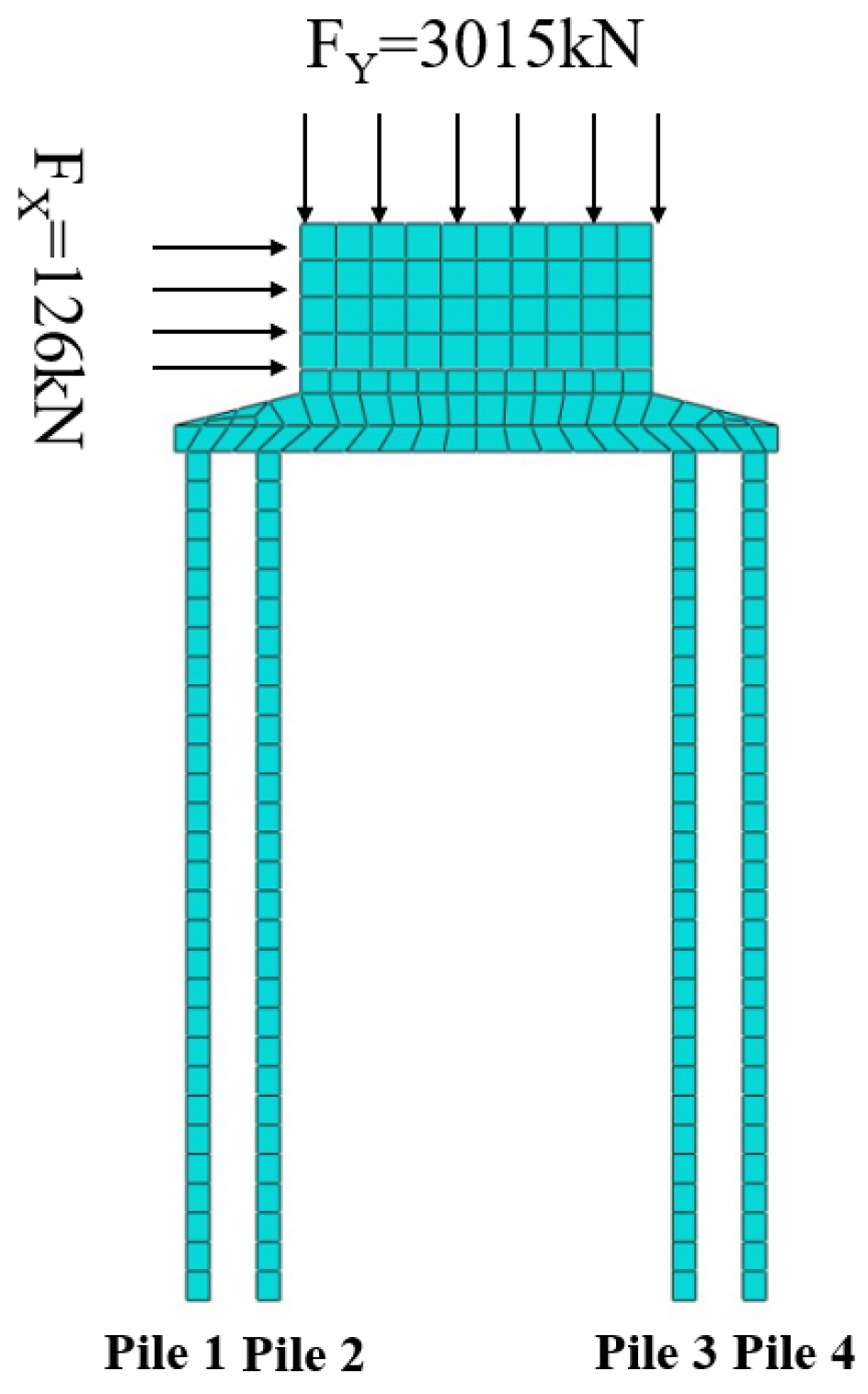
3.1. Model Construction
3.2. Axial Stress Analysis and Verification for Wind Turbine Foundation Systems
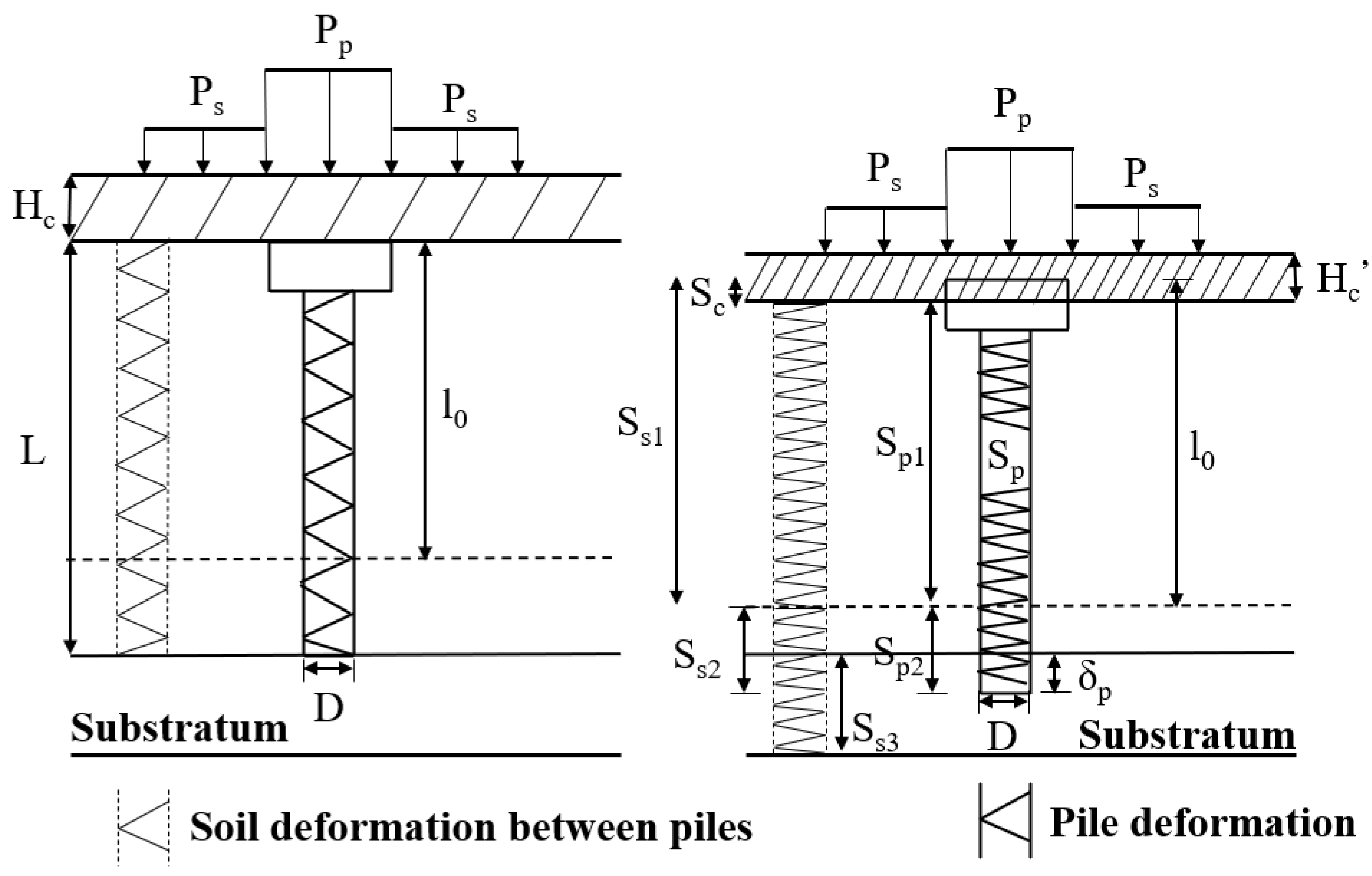
3.2.1. Derivation of Theoretical Calculation Formula for Axial Stress of Wind Turbine Foundation Systems
- (1)
- It is assumed that the foundation soil is a semi-infinite elastic body without considering the boundary effect. If the foundation is composed of multi-layer soil, the relevant parameters shall be weighted and averaged according to the thickness of each soil layer, while ignoring the impact of construction on soil uniformity.
- (2)
- The load is uniformly distributed and acts on the pile cap and soil surface under the adjustment of the cushion.
- (3)
- We regard the cushion layer as a homogeneous elastomer.
- (4)
- The piles are arranged at equal intervals, and the geometric properties and mechanical properties of the piles are completely consistent. The pile material is regarded as a linear elastic body, which satisfies Hooke’s law.
- (5)
- Ignoring the high-frequency vibration effect of dynamic load, the quasi-static analysis method is used to carry out the research.
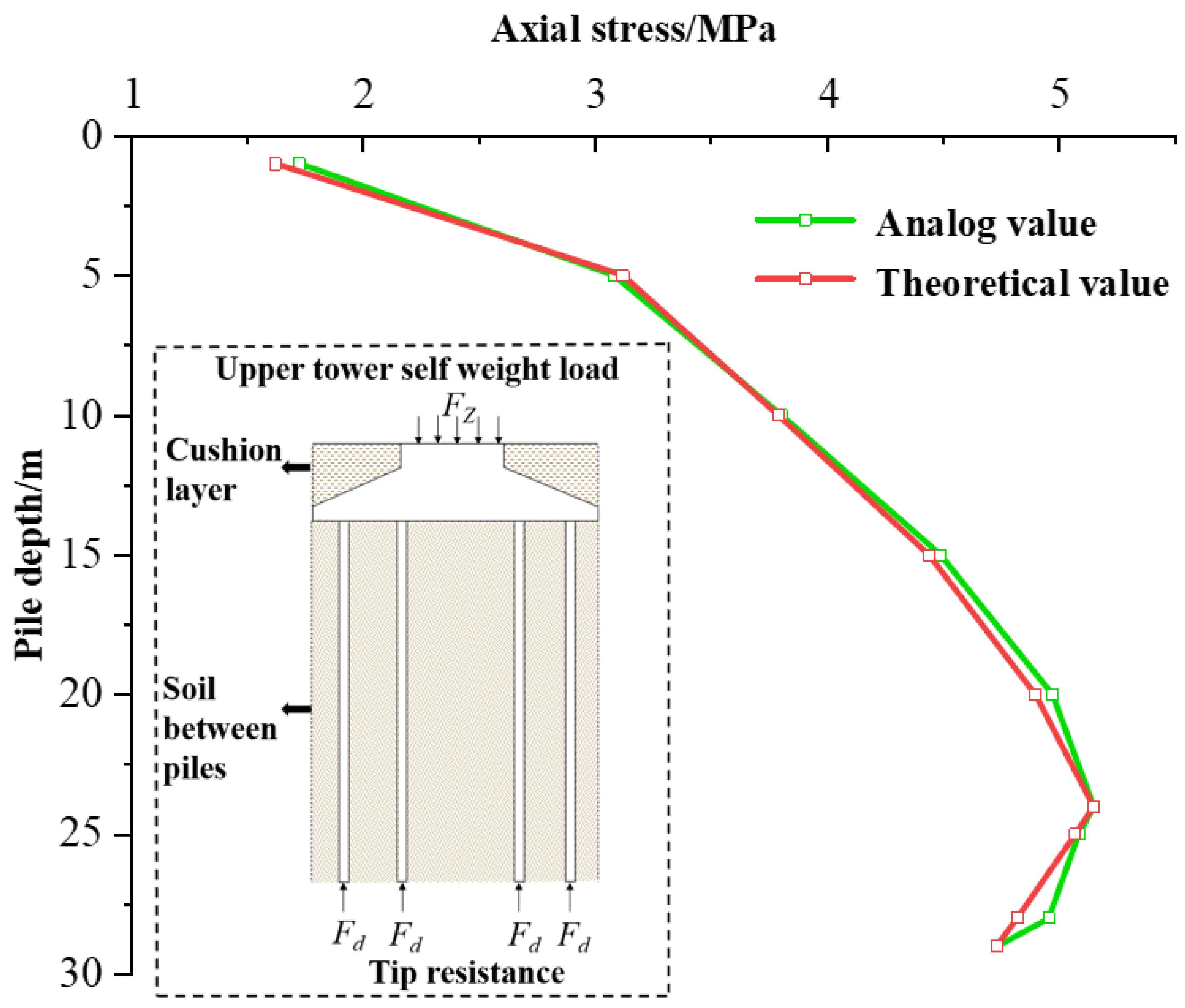
3.2.2. Axial Stress Verification for Wind Turbine Foundation Systems
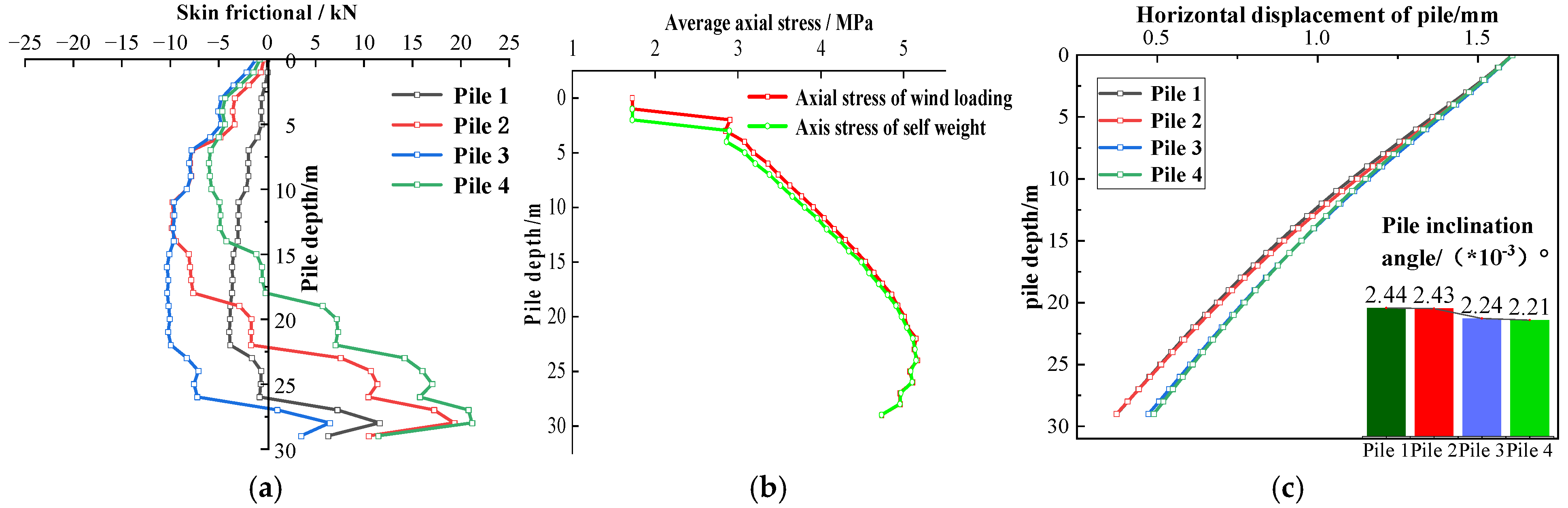
3.3. Analysis of Pile–Soil Interaction Mechanisms Under Single-Load Conditions
3.3.1. Analysis of Pile–Soil Interaction Mechanisms Under Wind Load Conditions
- (1)
- Above the neutral point, the continuous pushing effect of wind load causes the pile to have an upward pulling trend, and the pile is subjected to the downward dragging force of the surrounding soil, resulting in an accumulated increase in the negative skin friction. The maximum negative skin friction of the pile group occurred at pile 3, reaching a peak value of 10.23 kN.
- (2)
- At the neutral plane depth, the direction of skin friction reverses. At this stage, the pile end begins to press into the deep, compacted soil layer, resulting in a rapid increase in the positive skin friction. The maximum positive skin friction of the pile group was observed at pile 4, reaching a peak value of 21.18 kN.
- (3)
- Finally, due to the sudden release of soil stress near the bottom of the pile, the skin friction sharply decreases. Notably, the neutral point depths of piles 3 and 4 near the slope are the deepest at 26.5 m and the shallowest at 18 m, respectively.
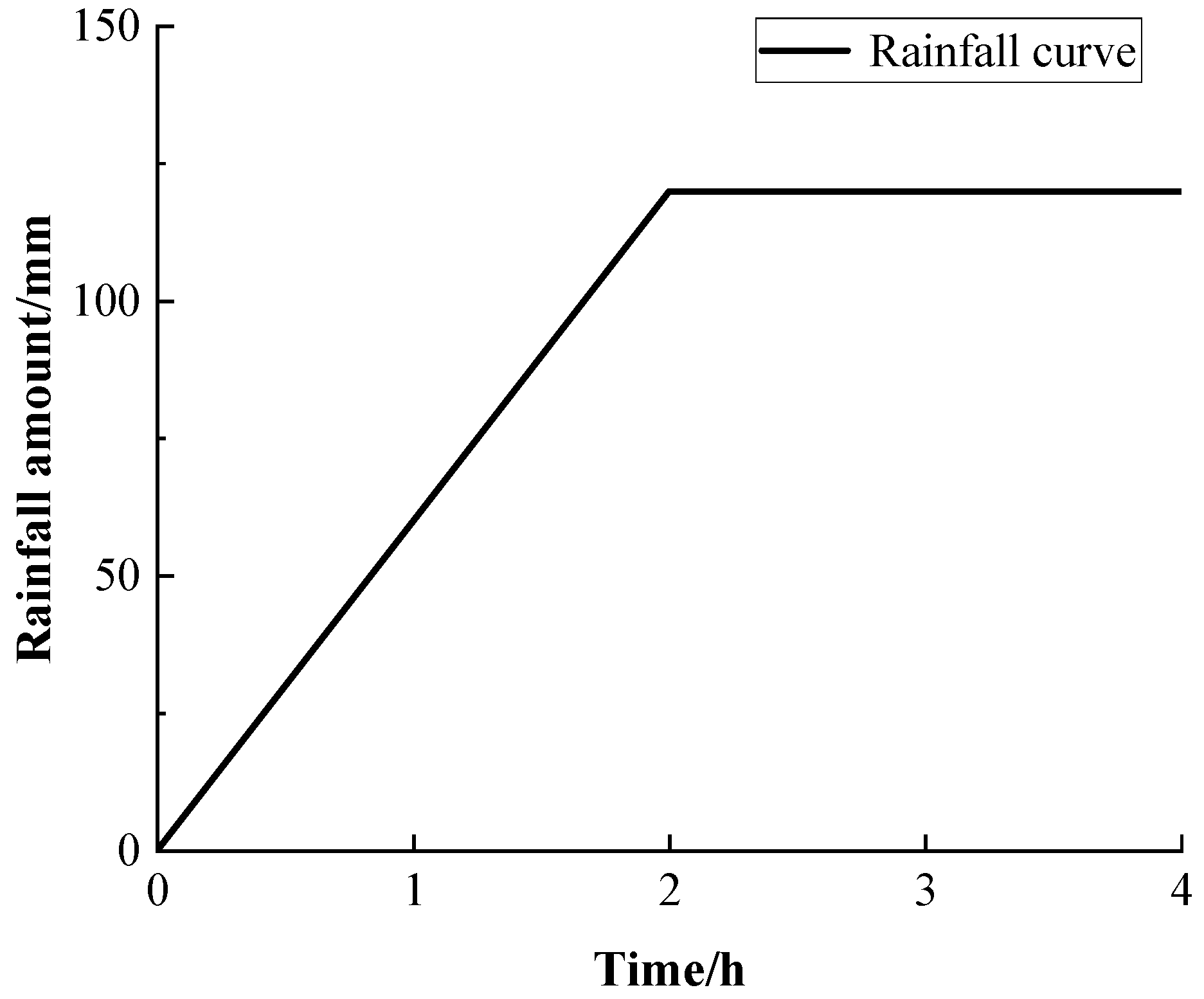
3.3.2. Analysis of Pile–Soil Interaction Mechanisms Under Extreme Rainfall Conditions
3.3.3. Analysis of Pile–Soil Interaction Mechanisms Under Seismic Load Conditions
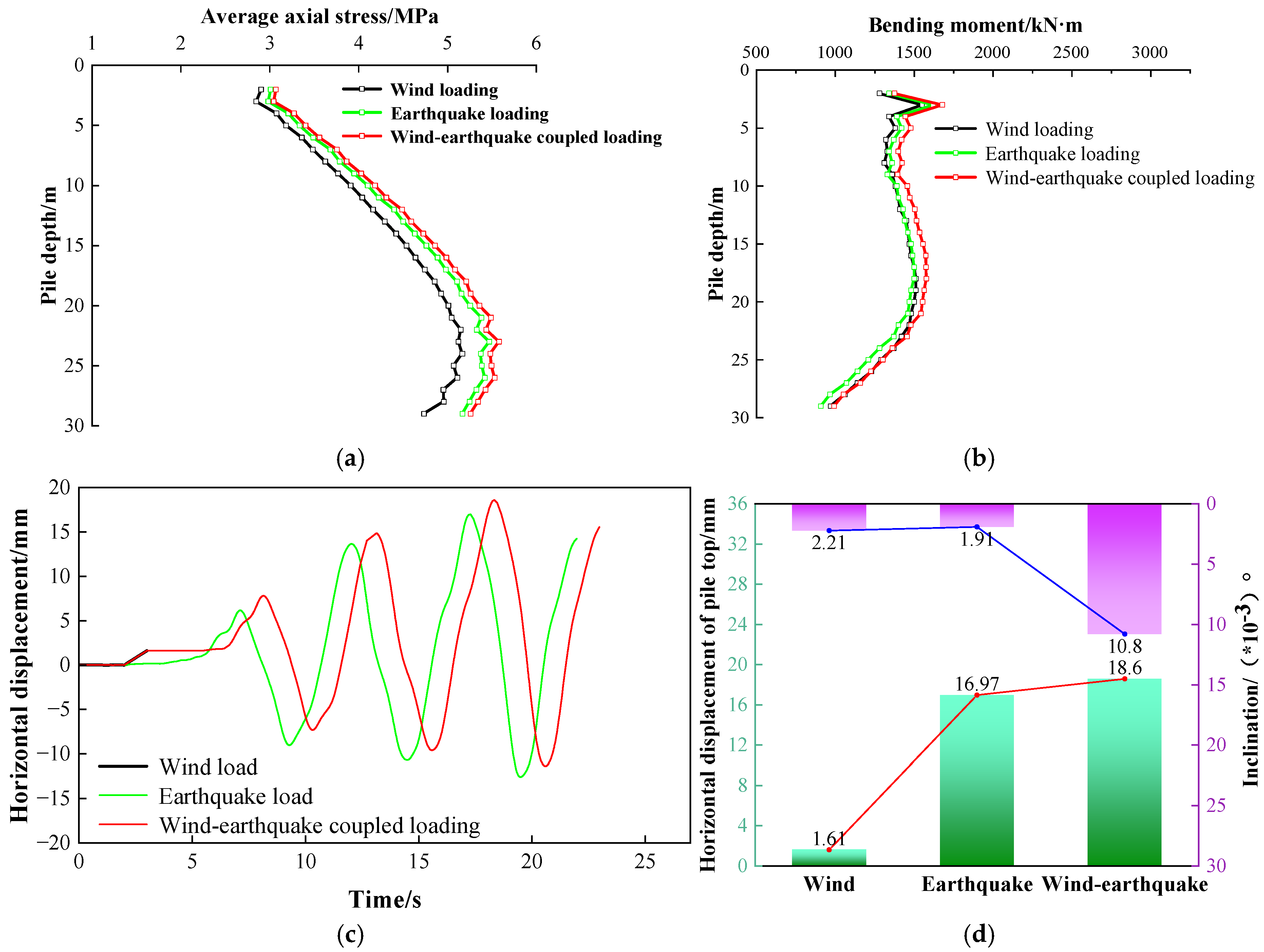
3.4. Analysis of Pile–Soil Interaction Mechanisms Under Coupled Loading Conditions
4. Conclusions
- (1)
- The distinct pile–soil interaction mechanisms under single-load conditions are as follows: wind loads cause progressive pile inclination through sustained lateral thrust, rainfall loading reveals time-dependent coupling effects, where prolonged duration increases shallow soil saturation and progressively reduces pile group bearing capacity, and seismic loading induces staged soil stiffness evolution (“softening-recovery”) via rapid seismic wave fluctuations.
- (2)
- The load-coupling effect reveals significant nonlinearity in both resistance and displacement responses, reducing structural stability through two mechanisms: reducing safety reserves via resistance attenuation (e.g., 2.28–20.17% reduction in peak positive skin friction under coupled loading) and displacement amplification (e.g., 1.85-fold nonlinear increase in pile-top horizontal displacement for wind–earthquake coupling versus seismic-only conditions).
- (3)
- The analysis confirms that seismic loading, whether it occurs independently or as part of coupled loading conditions, poses significant stability risks to pile foundations. Consequently, seismic design measures for wind turbine towers require particular emphasis in engineering practice.
- (4)
- Through site-specific simulations of the 100 MW wind farm in the Ansai loess hilly area, it is indicated that, during the construction of wind turbine tower foundations on this loess hilly site, the pile length should be 29 m for gentle slopes (with a gradient <35°) and 32–35 m for steep slopes (with a gradient >45°) to enhance the end bearing capacity and control the nonlinear displacement growth primarily caused by seismic loads. Additionally, the concrete of the pile foundations needs to be upgraded from C30 to C35 to enable them to bear an axial stress of 5.63 MPa under critical conditions.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, C.; Zhao, F.; Qi, S.; Sun, W. On interaction between single pile and soil and mechanism of load transferring. J. Eng. Geol. 2004, 12, 406–410. [Google Scholar]
- Alsharedah, Y.; Newson, T.; El Naggar, M.H. A 3-D modelling of monopile behaviour under laterally applied loading. Geomech. Geophys. Geo-Energy Geo-Resour. 2024, 10, 173. [Google Scholar] [CrossRef]
- Zuo, H.; Bi, K.; Hao, H. Dynamic analyses of operating offshore wind turbines including soil-structure interaction. Eng. Struct. 2018, 157, 42–62. [Google Scholar] [CrossRef]
- Liu, Z.; Li, P.; Zhang, H.; Han, Q.; Qin, C.; Fan, S.; Xu, Z. Research on the Effect of Aerodynamic Imbalance on Fatigue Performance of a Wind Turbine Foundation with Embedded Steel Ring. Buildings 2024, 14, 1141. [Google Scholar] [CrossRef]
- Xia, S.R. Stability Study of Transmission Tower Foundation System under Strong Wind. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2018. [Google Scholar]
- Lu, S.; Hu, Z.; Yu, H.; Fan, W.; Fu, C.; Wu, D. Changes of extreme precipitation and its associated mechanisms in Northwest China. Adv. Atmos. Sci. 2021, 38, 1665–1681. [Google Scholar] [CrossRef]
- Du, W.; Kang, S.; Qin, X.; Ji, Z.; Sun, W.; Chen, J.; Yang, J.; Chen, D. Can summer monsoon moisture invade the Jade Pass in Northwestern China? Clim. Dyn. 2020, 55, 3101–3115. [Google Scholar] [CrossRef]
- Gu, W.; Chen, L.J.; Wang, Y.G.; Gao, H.; Wang, L.; Liu, Y.Y. Extreme precipitation over northern China in autumn 2021 and joint contributions of tropical and mid-latitude factors. Adv. Clim. Change Res. 2022, 13, 835–842. [Google Scholar] [CrossRef]
- Zhen, J.; Yang, X.; Wang, B.; Fan, H.; Meng, M. Study on the destruction of backfilled loess slopes by short-term extreme rainfall erosion. Bull. Eng. Geol. Environ. 2023, 82, 406. [Google Scholar] [CrossRef]
- Bian, H.; Wei, J. Bearing Characteristics and Negative Skin Friction Preventive Measures for Highway Bridge Pile Foundations in Collapsible Loess Areas Under Water Immersion. Water 2024, 16, 3587. [Google Scholar] [CrossRef]
- Tang, K.; Liu, D.; Xie, S.; Qiu, J.; Lai, J.; Liu, T.; Fang, Y. Analysis of loess water migration regularity and failure response of tunnel structure under rainfall environment. Bull. Eng. Geol. Environ. 2024, 83, 251. [Google Scholar] [CrossRef]
- Alotta, G.; Biondo, C.; Giaralis, A.; Failla, G. Seismic protection of land-based wind turbine towers using the tuned inerter damper. Structures 2023, 51, 640–656. [Google Scholar] [CrossRef]
- Huang, H.S. Simulations of 10MW wind turbine under seismic loadings. Compos. Struct. 2022, 279, 114686. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Li, J.; Liu, D.; Zhang, Y.; Jiang, D. Field Test Study of Performance of Bored Piles in Collapsible Loess. Appl. Sci. 2023, 13, 13113. [Google Scholar] [CrossRef]
- Gao, D.; Zhao, K.; Ma, B.; Han, Z.; Fan, J.; Akhtar, M.M. Research on the bearing behavior of single pile in self-weight collapsible loess areas. PLoS ONE 2023, 18, e0290878. [Google Scholar] [CrossRef]
- Liu, X.; Li, M.; Liao, H.; Huang, B.; Liu, S. Mechanical Properties of Adjacent Pile Bases in Collapsible Loess under Metro Depot. Appl. Sci. 2024, 14, 5819. [Google Scholar] [CrossRef]
- Hou, J.; Lu, Y.; Wang, J.; Yu, K. Calculation Model of Compaction Coefficient of Soil among SP−PSC Pile Group on Collapsible Loess Foundation. Appl. Sci. 2023, 13, 4003. [Google Scholar] [CrossRef]
- Yan, D.; Yu, J.; Wang, Y.; Zhou, L.; Tian, Y.; Zhang, N. Soil particle modeling and parameter calibration based on discrete element method. Agriculture 2022, 12, 1421. [Google Scholar] [CrossRef]
- Wen, H.; Deng, S.; Zhang, W.; Cheng, Q.; Wu, J.; Hu, D.; Feng, G.-L. A simplified approach to estimating the collapsible behavior of loess. Adv. Civil Eng. 2020, 2020, 3712595. [Google Scholar] [CrossRef]
- Xie, Y.; Yuan, C.; Bai, W. A Simplified Analysis Method for Seismic Response of Pile Foundation. Appl. Sci. 2023, 13, 12398. [Google Scholar] [CrossRef]
- Yang, Y.; Zhu, L.; Ma, H. Research on Vertical Bearing Capacity of Ram-compacted Pile with Vibrating Gravel Base in Collapsible Loess Foundation. In Proceedings of the 2017 2nd International Conference on Materials Science, Machinery and Energy Engineering (MSMEE 2017), Dalian, China, 13–14 May 2017; Atlantis Press: Dordrecht, The Netherlands, 2017; pp. 1062–1070. [Google Scholar]
- Given, J.; Soga, K. Comparison of Simple and Advanced Constitutive Models with Column Collapse Simulations in the Material Point Method. In Proceedings of the Geo-Congress, Los Angeles, CA, USA, 26–29 March 2023; pp. 30–39. [Google Scholar]
- Qiu, Y.; Wang, J.; Zhang, C.; Hua, L.; Zhou, Z. Numerical simulation study on the impact of excavation on existing Subway stations based on BIM-FEM framework. Buildings 2024, 14, 1444. [Google Scholar] [CrossRef]
- Alisawi, A.T.; Collins, P.E.F.; Cashell, K.A. Novel Methodology for Scaling and Simulating Structural Behaviour for Soil–Structure Systems Subjected to Extreme Loading Conditions. Appl. Sci. 2023, 13, 8626. [Google Scholar] [CrossRef]
- Tan, W.; Lei, Z.; Wang, Y.; Liu, J.; Lai, P.; Mei, Y.; Liu, W.; Zhou, D. Analyzing the Impact of Deep Excavation on Retaining Structure Deformation Based on Element Tracking. Buildings 2024, 14, 3069. [Google Scholar] [CrossRef]
- Miao, L.C.; Wang, F.; Lv, W.H. Calculation method of pile-soil stress ratio of rigid pile composite foundation. J. Undergr. Space Eng. 2014, 10, 1270–1274+1280. [Google Scholar]
- Gong, K.; Chen, X. Improved modeling of equivalent static loads on wind turbine towers. Wind Struct. 2015, 20, 609–622. [Google Scholar] [CrossRef]
- Freebury, G.; Musial, W. Determining equivalent damage loading for full-scale wind turbine blade fatigue tests. In Proceedings of the 2000 ASME Wind Energy Symposium, Reno, NV, USA, 10–13 January 2000; Volume 50. [Google Scholar]
- Gao, G.; Shu, H.; Yi, Z.; Yang, S.; Dai, J.; Zhang, F. A Scaled Numerical Simulation Model for Structural Analysis of Large Wind Turbine Blade. Energies 2024, 17, 4849. [Google Scholar] [CrossRef]
- GB 18306-2015; Seismic Ground Motion Parameters Zonation Map of China. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China; Standardization Administration of China: Beijing, China, 2015.
- Liu, X.; Meng, Q.; Xu, L.; Liu, Y.; Tian, X. Modular Steel Buildings Based on Self-Locking-Unlockable Connections Seismic Performance Analysis. Buildings 2025, 15, 678. [Google Scholar] [CrossRef]
- Li, S.; Liu, J.; Bao, X.; Jia, Y.; Chen, Y.; Xiao, L. Implementation of artificial boundary substructure seismic input method in ABAQUS. Nat. Disasters 2020, 29, 133–141. [Google Scholar]
- Katsanos, E.I.; Sextos, A.G.; Manolis, G.D. Selection of earthquake ground motion records: A state-of-the-art review from a structural engineering perspective. Soil Dyn. Earthq. Eng. 2010, 30, 157–169. [Google Scholar] [CrossRef]
- Wang, G. A ground motion selection and modification method capturing response spectrum characteristics and variability of scenario earthquakes. Soil Dyn. Earthq. Eng. 2011, 31, 611–625. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, Y.; Hu, J. Statistical analysis of earthquake-induced bending moment in fixed-head piles embedded in soft clay. J. Eng. Mech. 2017, 143, 04017059. [Google Scholar] [CrossRef]
- Wang, R.; Hu, Z.; Hao, Z.; Chen, L.; Shi, G.; Hou, R.; Zuo, R. Seismic Vulnerability Analysis of Long-Span Prestressed Concrete Composite Box Girder Bridge with Corrugated Steel Webs under Construction. Buildings 2023, 13, 1598. [Google Scholar] [CrossRef]
- Hasanoğlu, S.; Güllü, A.; Dindar, A.A.; Müderrisoğlu, Z.; Özkaynak, H.; Bozer, A. Optimal selection and scaling of ground motion records compatible with input energy and acceleration spectra. Earthq. Eng. Struct. Dyn. 2024, 53, 2382–2404. [Google Scholar] [CrossRef]
- He, Q.; Li, X.; Dong, D.; Li, Y.; Yang, Y. Research on Peak Acceleration and Spectral Attenuation Characteristics of Near Field Vibration. J. Geotech. Eng. 2015, 37, 2014–2023. [Google Scholar]
- Shi, J.; Zhang, L.; Ma, T.; Zhai, Y. Study on the cumulative damage effect of concrete gravity dams considering the duration of strong earthquake energy. J. Water Resour. Water Eng. 2020, 31, 174–179. [Google Scholar]
- Wang, S.; Yu, R.; Li, X. The Influence of Seismic Time Frequency Characteristics on Seismic Response of Soil Sites. J. Civil Eng. 2021, 54, 101–113. [Google Scholar]
- Li, Q.; Qing, Y.; Cui, K.; Zhnag, D.; Li, P. Research progress on dynamic characteristics and constitutive models of soil under long-term cyclic loading. J. Southwest Jiaotong Univ. 2024, 59, 377–391. [Google Scholar]
- Qiao, F.; Chang, C.; Bo, J.; Wang, L.; Wang, J. Study on the dynamic characteristics of loess. Sustainability 2023, 15, 5428. [Google Scholar] [CrossRef]
- Yan, W.; Tian, X.; Wu, Z.; Wang, P.; Kang, L. Seismic effects of loess slopes using physical modeling and numerical simulation. Front. Earth Sci. 2023, 10, 1058701. [Google Scholar]
- NB/T 10311-2019; Technical Specification for Design of Foundation of Wind Turbine Generators in Wind Farms. National Energy Administration of the People’s Republic of China: Beijing, China, 2019.
- GB 50025-2018; Code for Construction in Collapsible Loess Areas. Ministry of Housing and Urban–Rural Development of the People’s Republic of China: Beijing, China, 2018.

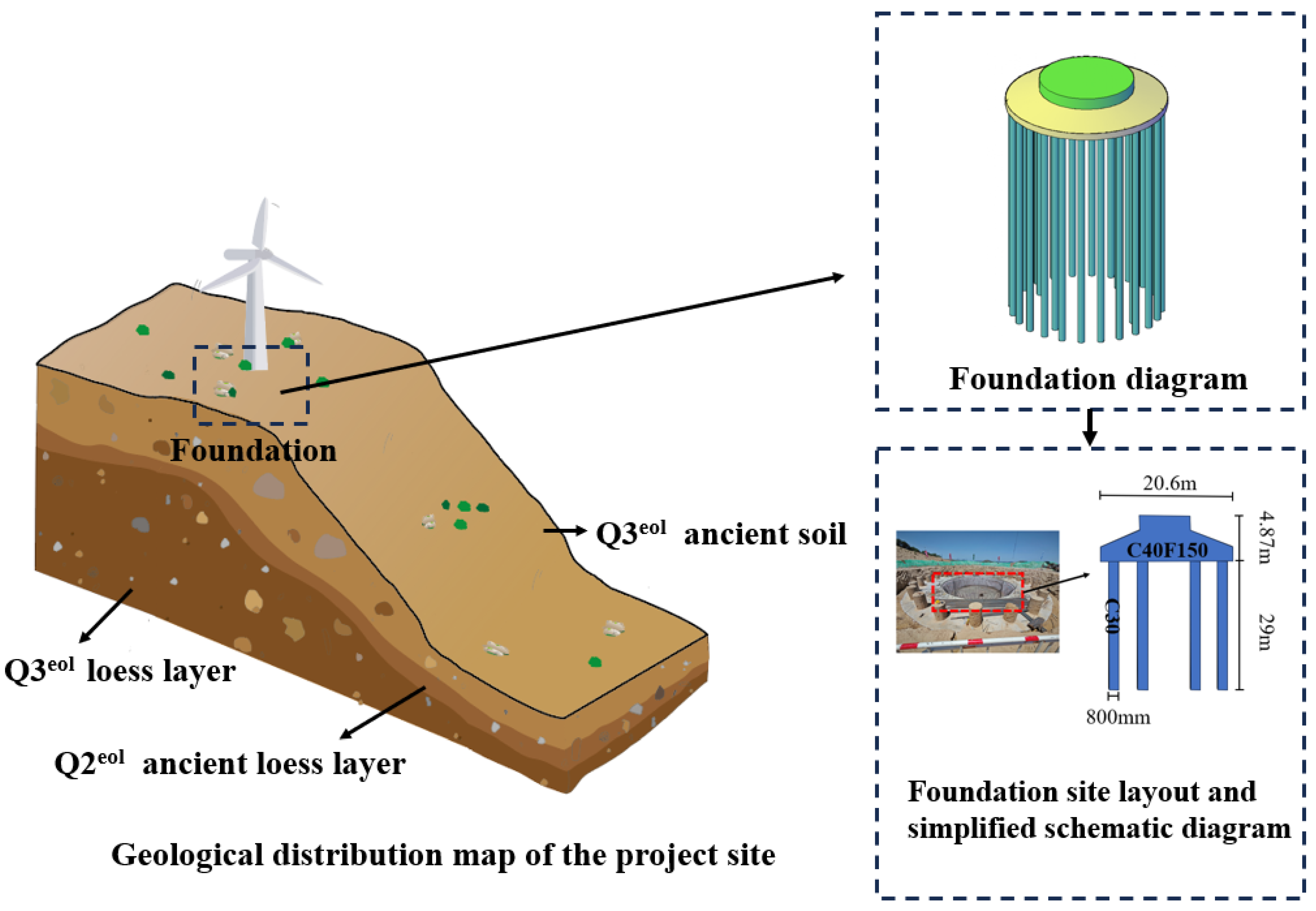


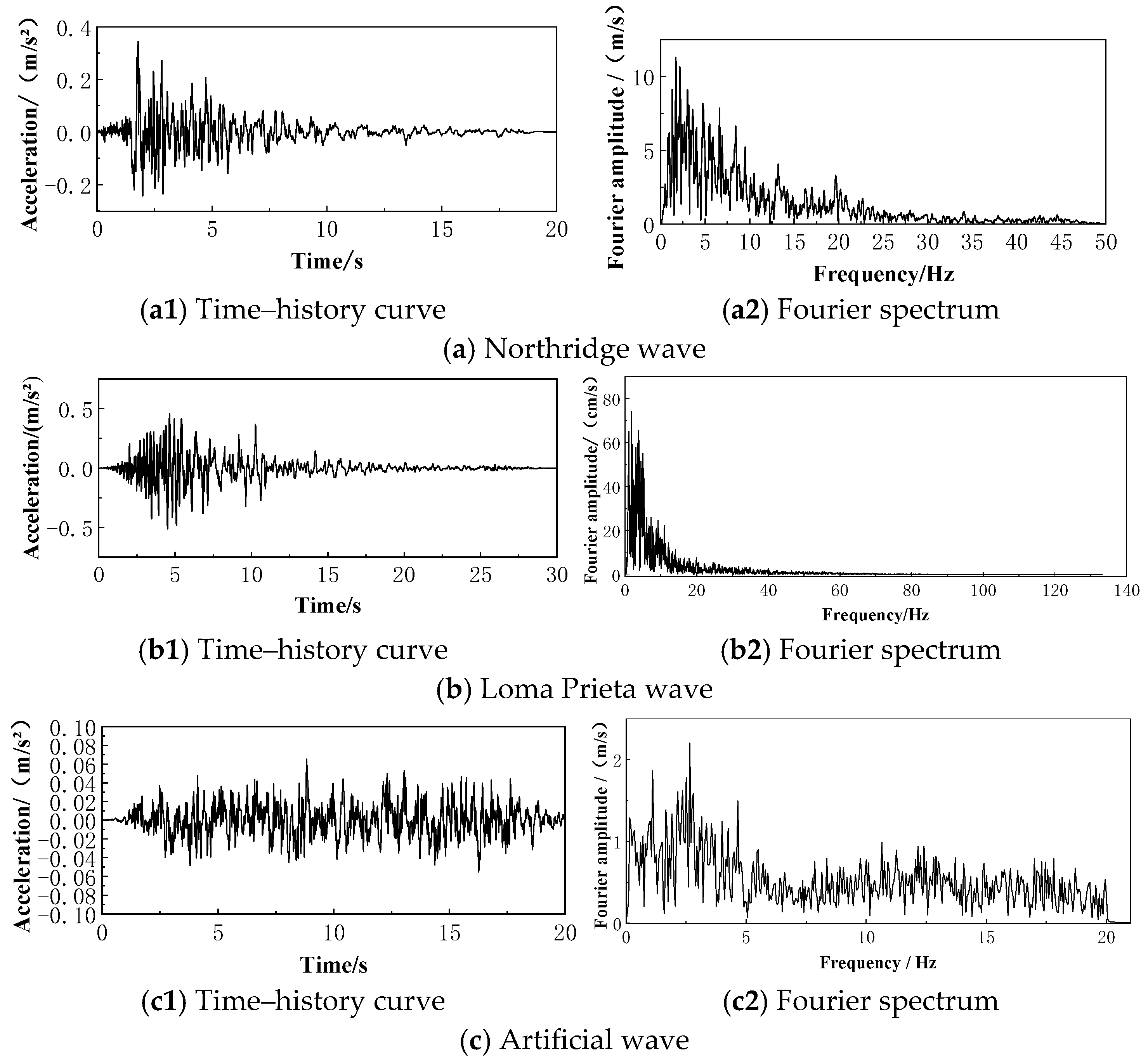
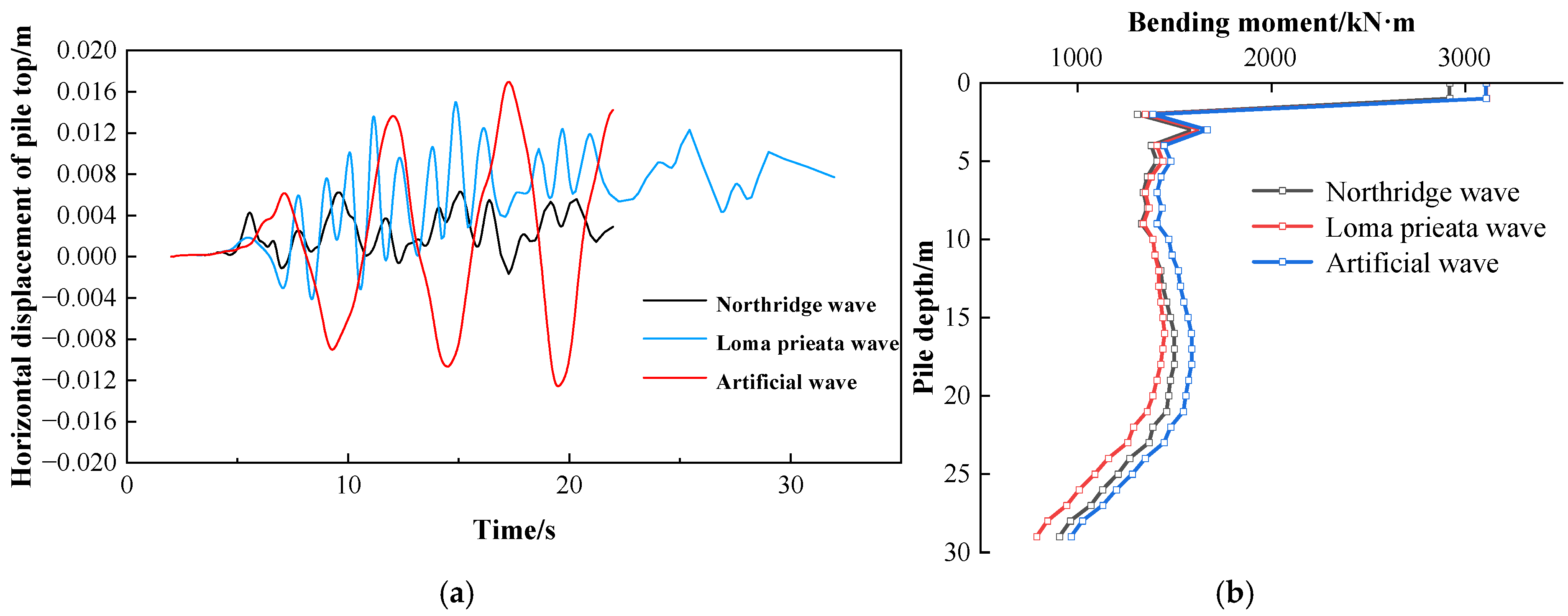
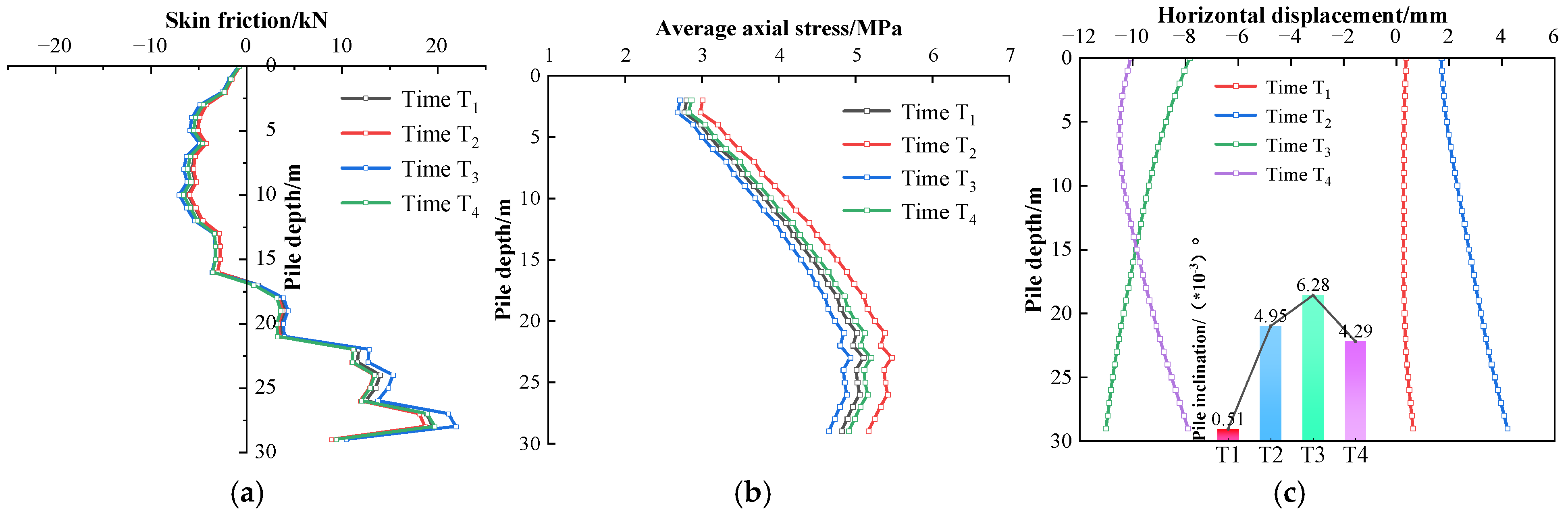
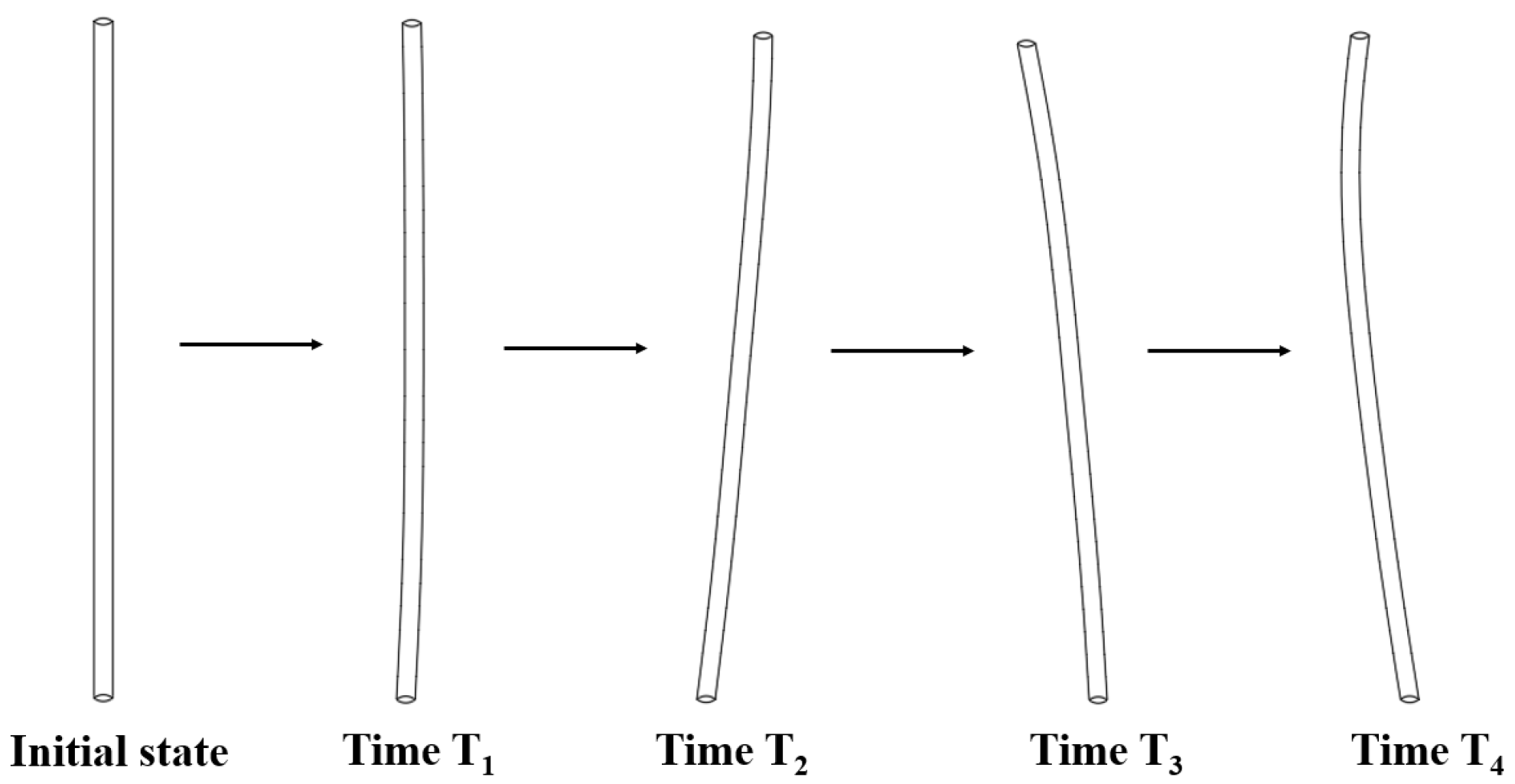


| Aspect | Prior Studies | This Study |
|---|---|---|
| Hazard scope | Single load (Wind or Rain or Quake) [1,2,3,4,5,9,10,11,12,13] | Wind, extreme rainfall, seismic mutual coupling load |
| Geological Focus | Generic soils [2,3], Saturated loess [10] | Explicitly accounts for loess’ unique wet-collapsible deformation and seismic liquefaction |
| Innovation Aim | General structural response [12] | Pile–soil interaction mechanisms for wind turbine stability |
| Design output | Qualitative resilience [12], Empirical safety factors [5] | Parametric safety thresholds |
| Natural Unit Weight (kN/m3) | Compression Modulus (MPa) | Cohesion (kPa) | Friction Angle (°) | |
|---|---|---|---|---|
| Q3eol loess layer | 15.60 | 9.20 | 26 | 20 |
| Q3eol ancient soil | 17.45 | 11.08 | 30 | 21 |
| Q2eol ancient loess layer | 16.64 | 9.93 | 33 | 22 |
| Material | Density (kg/m3) | Modulus of Elasticity (MPa) | Poisson’s Ratio | Friction Angle (°) | Cohesion (kPa) |
|---|---|---|---|---|---|
| Upper soil | 1590 | 10 | 0.3 | 25 | 35.5 |
| Lower soil | 1700 | 10 | 0.3 | 30 | 38 |
| Wind turbine tower foundation | 2400 | 32,500 | 0.25 | - | - |
| Depth | Theoretical Value (MPa) | Analog Value (MPa) | Relative Error |
|---|---|---|---|
| 0–12 m | 0.82–5.01 | 0.80–4.95 | ≤2.1% |
| 12–24 m | 5.01–5.15 | 4.95–5.12 | ≤2.15% |
| 24–29 m | 5.15–4.72 | 5.12–4.70 | ≤2.08% |
| Comparison Items | Wind Load | Extreme Rainfall Load | Seismic Load |
|---|---|---|---|
| Neutral point position (m) | 18.00 | 18.00 | 17.00 |
| Maximum lateral skin friction (kN) | 21.18 | 24.13 | 21.92 |
| Maximum horizontal displacement (mm) | 1.61 | 2.01 | 10.07 |
| Maximum axial stress of pile groups (kN) | 5.15 | 5.26 | 5.47 |
| Mechanism of action | Continuous pushing leads to gradual tilting of the pile body | Time-dependent coupling effects dominate | The staged evolution of soil stiffness featuring initial softening followed by recovery |
| Trend of lateral skin friction variation | The pile near the slope has the highest skin friction | Initial increase followed by decrease | initial decrease followed by an increase and subsequent reduction |
| Axial stress response characteristics | Significant increase in shallow layers | progressive linear decay | dynamic oscillatory variation |
| Cumulative displacement mode | progressive tilting mode | S-shaped transition from I-shaped, and shallow dominated | hysteretic response |
| Evolution of soil stiffness | Weakening of lateral confinement → Deep-layer stiffness compensation | rapid shallow-layer degradation → gradual deep-layer evolution | stiffness softening → particle restructuring recovery → dynamic equilibrium [41,42,43] |
| Load Combination | Wind | Extreme Rainfall | Earthquake | Wind–Rainfall Coupled | Wind–Earthquake Coupled | Rainfall–Earthquake Coupled | |
|---|---|---|---|---|---|---|---|
| Pile Response Parameters | |||||||
| Maximum positive skin friction (kN) | 21.18 | 24.13 | 21.92 | 20.90 | 20.29 | 17.89 | |
| Maximum average axial stress of pile group (MPa) | 5.15 | 5.26 | 5.47 | 5.16 | 5.58 | 5.63 | |
| Peak horizontal displacement of pile (mm) | 1.61 | 2.01 | 10.07 | 3.63 | 18.6 | 18.35 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, K.; Chai, S.; Zhao, L.; Yue, S.; Dang, H.; Liu, X. Analysis of Pile–Soil Interaction Mechanisms for Wind Turbine Tower Foundations in Collapsible Loess Under Multi-Hazard Coupled Loading. Buildings 2025, 15, 2152. https://doi.org/10.3390/buildings15132152
Fan K, Chai S, Zhao L, Yue S, Dang H, Liu X. Analysis of Pile–Soil Interaction Mechanisms for Wind Turbine Tower Foundations in Collapsible Loess Under Multi-Hazard Coupled Loading. Buildings. 2025; 15(13):2152. https://doi.org/10.3390/buildings15132152
Chicago/Turabian StyleFan, Kangkai, Shaobo Chai, Lang Zhao, Shanqiu Yue, Huixue Dang, and Xinyuan Liu. 2025. "Analysis of Pile–Soil Interaction Mechanisms for Wind Turbine Tower Foundations in Collapsible Loess Under Multi-Hazard Coupled Loading" Buildings 15, no. 13: 2152. https://doi.org/10.3390/buildings15132152
APA StyleFan, K., Chai, S., Zhao, L., Yue, S., Dang, H., & Liu, X. (2025). Analysis of Pile–Soil Interaction Mechanisms for Wind Turbine Tower Foundations in Collapsible Loess Under Multi-Hazard Coupled Loading. Buildings, 15(13), 2152. https://doi.org/10.3390/buildings15132152







