Next Article in Journal
Safety Risk Assessment of Double-Line Tunnel Crossings Beneath Existing Tunnels in Complex Strata
Previous Article in Journal
Research on the Factors Influencing Broken-Bridge Aluminum Exterior Windows with the Goal of Thermal Performance Improvement
Previous Article in Special Issue
The Effect of Cementitious Capillary Crystalline Waterproof Materials on the Hydration, Microstructure, and Mechanical Properties of Cement Pastes
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Buildings
Volume 15
Issue 12
10.3390/buildings15122102
buildings-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Fatigue Bond Behavior of Steel Rebars in Recycled Aggregate Concrete Containing Recycled Rubber

by
Wei Wei
1,2,
Shanming Cai
2 and
Yufu Li
1,*
1
Guangdong Construction Polytechnic, Guangzhou 510440, China
2
School of Civil and Transportation Engineering, Guangdong University of Technology, Guangzhou 510006, China
*
Author to whom correspondence should be addressed.
Buildings 2025, 15(12), 2102; https://doi.org/10.3390/buildings15122102
Submission received: 18 March 2025 / Revised: 4 June 2025 / Accepted: 6 June 2025 / Published: 17 June 2025
(This article belongs to the Special Issue New Concrete Materials: Performance Analysis and Research—2nd Edition)
Browse Figures
Versions Notes

Abstract

Recycled aggregate concrete (RAC) containing recycled rubber gains increasing attention for reinforced concrete structures, owing to its benefits in resource-saving and environmental protection. Bonding between rebars and concrete is critical to ensure the composite action in reinforced concrete members. Nevertheless, previous studies on such concrete mainly focused on material aspects. Bonding behavior for rubber RAC is not clear and needs further research. This study aims to clarify the effects of recycled aggregate and rubber on the monotonic and fatigue bond behavior of deformed steel rebar in concrete and to propose predictive models. Pullout tests under monotonic, fatigue, and post-fatigue monotonic loadings are conducted on a total of 21 monotonic and 30 fatigue specimens, including normal concrete, RAC, and rubber RAC. Four types of failure modes are identified for the tested specimens. Effects of the replacement rate of recycled aggregate, rubber, and load level on the fatigue behavior, such as fatigue life, slip-loading cycle curves, slip development, and residual bond strength, are investigated. With the addition of recycled aggregate and rubber, the monotonic bond strength is increased by 60%. Based on the experimental results, theoretical formulas are proposed to predict the monotonic bond strength, fatigue life, and the slip under fatigue loading. The predictive models are verified by the experimental results, for example, the average and COV of the predicted-to-experimental bond strength ratio are 1.0 and 0.11, which proves the reasonability of the proposed models.

1. Introduction

Recycled aggregate concrete (RAC) is a type of concrete that is produced by using recycled aggregates, which are derived from demolition waste (e.g., crushed concrete). In RAC, these recycled aggregates partially or fully replace natural aggregates. RAC has both environmental and economic benefits, such as reduced landfill use and carbon footprint [1,2]. In recent decades, recycled rubber concrete (RBC) that contains rubber particles has been proposed to address the environmental problems induced by the disposal of end-of-life rubber products, such as tires [3]. Existing studies [4,5] indicated that the addition of rubber particles reduces the strength and Young’s modulus of concrete but could increase its ductility. Rubber concrete shows enhanced ductility and impact resistance, reduced density, improved thermal and acoustic insulation, and enhanced crack control capability, making it a suitable choice in the applications of pavements, shock-absorbing floors, earthquake-resistant structures, and speed bumpers [5,6,7,8,9]. A combined usage of recycled aggregates and rubber particles in concrete could bring great environmental benefits to the concrete industry.
The bond between concrete and reinforcing steel is vital for reinforced concrete structures. It ensures effective load transfer, allowing the steel to carry tensile forces that concrete cannot [10,11]. This bond maintains strain compatibility and structural integrity by preventing slippage, controlling crack formation, and enhancing ductility. Currently, very limited studies on the bond behavior of steel rebars in rubber RAC have been conducted, but extensive investigations have been reported regarding the bond behavior of steel rebars in RAC or rubber concrete and FRP rebars in concrete [12,13,14,15,16,17]. The bond is achieved by the mechanisms of adhesion, interlocking, and friction, which could be affected by various factors, such as concrete strength, rebar diameter, concrete cover, embedment length, rebar surface morphology, and confinement [18]. Previous studies [19,20,21] have shown that the bond performance between RAC and rebars differs somewhat from that of conventional concrete, and the bond strength greatly depends on the replacement rate of recycled aggregates. Gesoglu et al. [22] found through experimental research that the shape and content of rubber affect the bond strength. For specimens with a rubber content of less than 5%, the bond strength is essentially the same as that of ordinary concrete of the same strength grade. However, for specimens with a rubber content greater than 5%, the bond strength decreases more noticeably as the rubber content increases. Tusher et al. [12] and Hall and Najim [23] generally found a decreasing trend of bond strength with the increase in rubber content, but an increasing trend was also reported in a few specimens, demonstrating the complexity of the bond behavior for rubber concrete [12,15,16,17,24]. Besides experimental studies, various theoretical models have been proposed to predict the bond stress-slip relationship of steel rebars in concrete (e.g., [24,25,26,27]). Most of the predictive formulas are experiment-based, and the coefficients in those formulas were determined by regression analysis on experimental data. Some design guidelines [28,29] offer methods to predict the monotonic bond strength, but the effects of recycled aggregate and rubber are not considered in those methods.
Reinforced concrete structures, such as bridges, are likely subjected to fatigue loading that may cause fatigue failure of structures [30,31]. Verna and Stelson [32] found that flexural members under fatigue loading are prone to bond fatigue failure. Bond fatigue failure is one of the main forms of fatigue failure in concrete structures. Therefore, it is needed to have an adequate understanding of the fatigue bonding behavior, especially for new types of concrete (e.g., RAC, rubber concrete, seawater sea-sand concrete) [33]. Some studies [33,34,35,36,37,38,39] have been reported on the fatigue bond behavior of rebars in concrete, as well as theoretical models for bond prediction. In general, the slip increases with the number of cycles. An increase in stress levels significantly shortens the bond fatigue life of reinforced concrete. Lin et al. [40] found that as long as bond fatigue failure does not occur, cyclic loading has little effect on bond strength and peak slip. Oh and Kim [41] developed a bond stress-slip constitutive model for non-corroded specimens after repeated loading based on pull-out test results. In this model, bond fatigue failure occurred when the slip under cyclic loading reaches the slip corresponding to the static ultimate bond strength. Lindorf et al.’s [42] experimental results showed that the wider the longitudinal cracks along the reinforcement direction, the more likely bond fatigue failure would occur. An S-N curve model was developed by Lindorf and Curbach [42,43]. Al-Hammoud et al. [44] and Rteil et al. [45] reported fatigue bond failure in reinforced concrete beam specimens, which was characterized as the shear-off of the concrete ribs in contact with rebars. Furthermore, some studies were conducted on the fatigue behavior of RAC and rubber concrete under bending or compressive loads. Arora and Singh [46] found that RAC had higher variability in fatigue life distribution and lower fatigue resistance than normal concrete under bending. Xiao et al. [47] claimed that the fatigue performance difference is insignificant between RAC and normal concrete under compression and bending cycles. Liu et al. [48] investigated the fatigue of rubber concrete and found that the addition of rubber particles could greatly improve fatigue life and deformation capability by absorbing energy and inhibiting crack expansion. However, to the authors’ best knowledge, no studies were reported on the fatigue bond behavior of deformed steel rebars in rubber RAC. The effect of recycled aggregates and rubber particles on the fatigue bond behavior is still not clear, and there is a lack of a fatigue model for such types of concrete. In addition, current standards for fatigue design are based on conventional concrete. Their applicability still needs further verification due to the replacement of natural aggregates with recycled aggregates and rubber.
To fill the above-mentioned knowledge gaps, this paper aims to clarify and understand the effects of recycled aggregates and rubber on the fatigue bond behavior, and propose formulas to predict such behavior (i.e., bond strength, slip, and fatigue life). An experimental and theoretical study on the fatigue bond behavior of deformed steel bars in rubber RAC is presented. Pullout tests, including monotonic, fatigue, and post-fatigue monotonic tests, were conducted on single bars embedded in concrete blocks to obtain the failure modes, stress-slip curves, bond strength, slip-loading cycle curves, and stress level-fatigue life relationships. Effects of recycled aggregate content and rubber content on the fatigue and post-fatigue behavior were investigated. Finally, empirical formulas were proposed to predict the monotonic bond strength, the slip-loading cycle, and stress level-fatigue life relationships. This research will contribute to enrich the data bank regarding the bond fatigue behavior between rebar and rubber RAC, clarifying the effects of RA and rubber on the bond behavior, offering a method to predict the fatigue bond life, and promoting the application of such concrete.

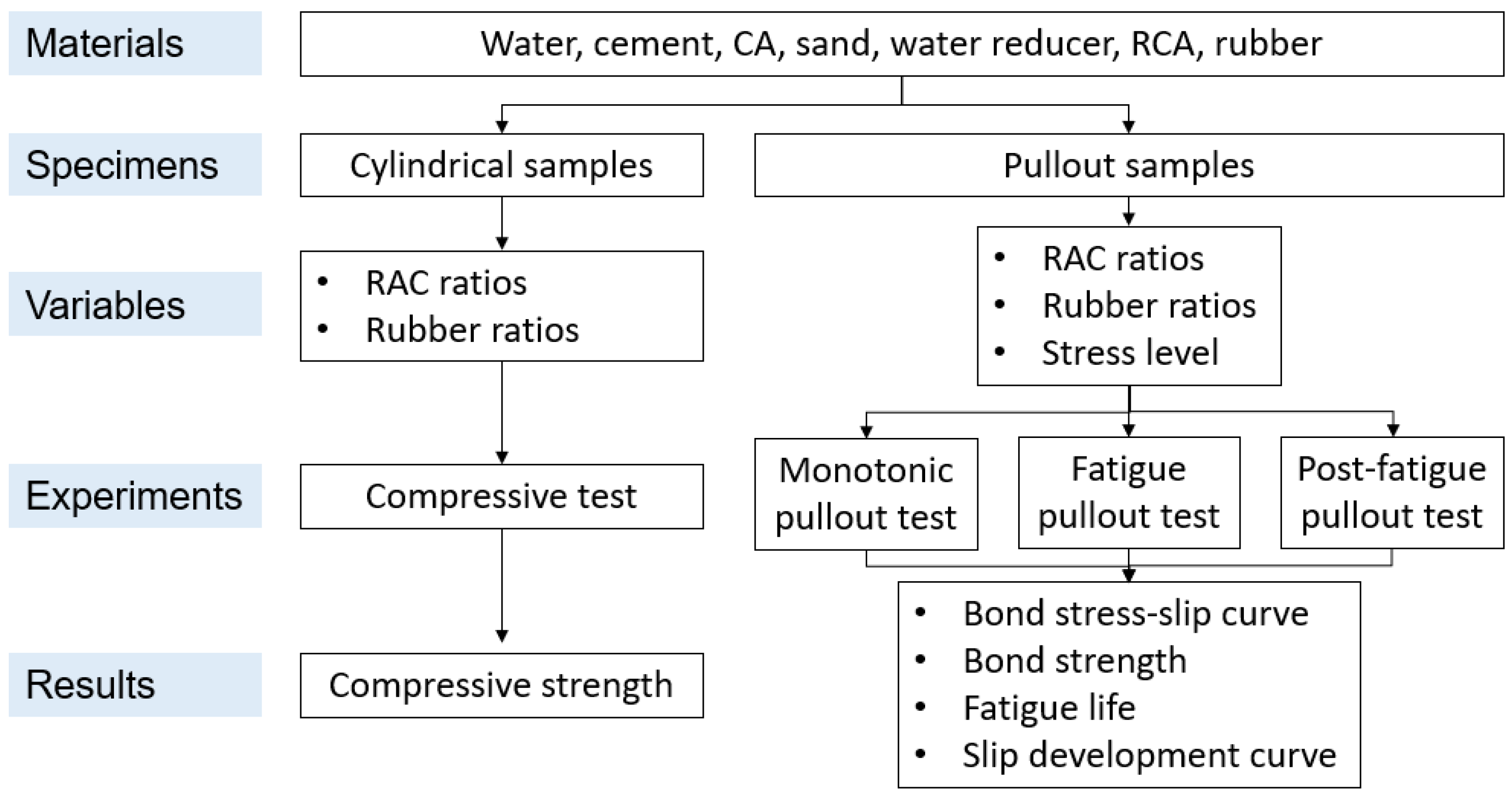
2. Experimental Program

2.1. Materials

2.1.1. Concrete

In this study, the replacement rates of recycled coarse aggregate were set at 0%, 25%, 50%, and 100%, and the rubber replacement rate was 5%. Ordinary Portland cement with a strength grade of 42.5 MPa was used to prepare the concrete. According to “ Pebble and crushed stone for construction” (GB/T 14685-2011 [29]) and “Sand for Construction” (GB/T 14684-2011 [49]), the fineness modulus and apparent density of river sand were measured to be 2.75 and 2665 kg/m3, respectively, with a maximum particle size of 5 mm. Both natural and recycled aggregates were used for concrete, and they had similar continuous grading with particle sizes ranging from 5 to 10 mm. The apparent density of the natural coarse aggregate was 2522 kg/m3, with a water absorption rate of 1.86%, and a crushing value index of 7.8%. The recycled coarse aggregate had an apparent density of 2559 kg/m3, a water absorption rate of 7.26%, and a crushing value index of 16.3%. The rubber was made from crushed waste tires, with a particle size of 40 mesh, and a density of 1000 kg/m3. A polycarboxylate high-performance water reducer was used to improve concrete workability. Figure 1 shows the raw materials used in this study. Table 1 shows the mixture proportions for concrete used in this study, including normal concrete, recycled coarse aggregate, and rubber RAC, which is determined by a density-based method. It is necessary to mention that the total absolute volume might not be equal to 1.0 m3. Nevertheless, this paper is more like a comparative study, and the absolute values in Table 1 will affect the findings and columns obtained from the experiments. The mixture in Table 1 was labeled as “RA”, followed by the recycled aggregate replacement percentage, and “RB”, followed by the recycled rubber aggregate replacement percentage. For example, RA25RB5 refers to a concrete mixture with recycled aggregate and rubber replacement rates being 25%, 5%, respectively.
When casting specimens, three concrete cylinders (150 mm in diameter and 300 mm in height) were prepared for each mixture to measure concrete properties. All the samples were cured in a standard environment (i.e., relative humidity > 95% and temperature = 20 °C) before the testing date. An axial compressive test was conducted on the cylinders according to GB/T 50081-2002 [50] to measure the compressive strength (fc’) and Young’s modulus (Ec), and the average values are listed in Table 1.

2.1.2. Steel Rebars

HRB400 deformed steel bars with a nominal diameter of 12 mm were adopted in this study. The equivalent diameter was measured as 11.23 mm by measuring the volume (via water displacement method) and the length of the rebar samples. Tensile coupon tests were conducted in a universal testing machine to measure the mechanical properties, and five samples were tested. The measured average properties are as follows: yield strength fy = 426.7 MPa, ultimate strength fu = 610.0 MPa, and Young’s modulus Es = 208 GPa. In addition, parameters of the ribs of steel bars were measured by the photograph method, and the thickness and center-to-center spacing of the ribs were 2.5 mm and 7.8 mm, respectively.

2.2. Specimens

In practical engineering, the fatigue bond performance between steel reinforcement and concrete is influenced by many factors. This paper mainly considers the impact of the following three factors on fatigue bond performance: (1) replacement rate of recycled coarse aggregate (0%, 25%, 50%, and 100%); (2) rubber replacement rate (0% and 5%); (3) fatigue stress levels (0.85, 0.75, and 0.65). Based on the parameters designed for this experiment, a total of 16 groups of pull-out specimens were tested, including 5 groups for monotonic pull-out tests (Table 2) and 11 groups for fatigue bond tests (Table 3). Each group of specimens includes 3 to 5 replicate specimens, depending on the variations in the experimental results. Label of the specimens includes: “RA” followed by recycled aggregate replacement ratio, “RB” followed by rubber content, stress level ratio (applicable for fatigue bond test), and specimen number. For example, RA25RB5-0.85-2 represents the 2nd specimen in the group with recycled aggregate replacement ratio of 25%, rubber content of 5%, and stress level of 0.85.
The pullout specimen is shown in Figure 2, which consists of a 550 mm long steel bar and a concrete cube. The authors’ previous trial tests indicated that split failure was likely to occur in specimens with a 150 mm × 150 mm ×150 mm cube size; a complete bond stress-slip curve was not obtained. Therefore, a dimension of 200 mm × 200 mm ×200 mm was selected for the concrete cube in this study, which was also in compliance with GB/T 50152-2012 [51]. Reis et al.’s [52] review on pullout tests indicated that such a dimension is common and appropriate for pullout tests to avoid the split failure in concrete. As shown in Figure 2a, the specimen is divided into four parts, i.e., the free end, bonding region in which the rebar is in contact with the concrete, deformed part, and loading end. The bonding length is 60 mm, which is 5 times the rebar diameter. It is noted that about 50% of the tested specimens in the literature adopted an embedment depth of 5 d~6.5 d to ensure the failure mode was debonding [52], where d is the rebar diameter.
During the specimen preparation process, a PVC pipe with an outer diameter of 15 mm was used to cover the steel rebar outside the bonded section, isolating the non-bonded section of concrete from the rebar. Plastic caps with a central hole were used to seal both ends of the PVC pipe to prevent concrete from entering the non-bonded section during casting, while also ensuring that the rebar is centrally positioned within the specimen, as shown in Figure 2b. After the pull-out specimens were cast, they were cured under standard conditions of 20 ± 2 °C and relative humidity > 95% for 28 days.

2.3. Experimental Setup

Both monotonic and fatigue tests were conducted on an MTS370 fatigue machine, and Figure 3 shows the experimental setup of the pullout test. The steel frame is connected to the actuator of the testing machine by a ball joint, ensuring a uniaxial tension. The center of the steel plate in the steel frame has an opening through which the rebar at the loading end of the pull-out specimen passes. The end of the rebar is gripped by the lower jaw of the MTS testing machine. The pull-out specimen is centrally placed on the steel tube to ensure it is in a horizontal position. Additionally, gypsum is applied to the contact surface between the concrete cube of the specimen and the bearing surface to effectively reduce the impact of additional friction on the test results.
The loading rate of the monotonic test was set as 1.2 mm/min. For the fatigue test, the loading frequency is set at 2 Hz. The loading regime for the fatigue test is shown in Figure 4: (1) a static load is first applied to Fmean, which is the average of the fatigue upper load limit Fmax and lower limit Fmin; (2) cyclic loading is performed in a sinusoidal waveform between Fmax and Fmin until fatigue failure occurs. The fatigue upper load limit (Fmax) is equal to the static ultimate pull-out force, which is obtained from the monotonic pull-out test multiplied by the stress level. The fatigue lower load limit is the fatigue upper load limit multiplied by a stress ratio of 0.2 (i.e., Fmin = 0.2 Fmax). In this experiment, if the specimen reaches 200,000 cycles without fatigue failure, the fatigue test is terminated. A monotonic pullout test was then conducted on such specimens to measure their residual properties. All the experimental data, such as load and displacement, were collected simultaneously with a sampling frequency of 8 Hz.
Previous studies indicated that the bond stress is non-uniform along the rebar, and a bond length of 5 times of rebar diameter (i.e., 60 mm in this study) could minimize the stress non-uniformity [33]. In this study, it is assumed that the bond stress is uniformly distributed, which is converted from the applied force by Equation (1). Considering the deformation of steel rebar, the slip is calculated by Equation (2).
τ = F π d l a ,
s = s ′ E f A − L F E f A + F ,
where F is the applied force, d is the equivalent diameter of rebar, la is the bond length, s’ is the displacement from the test machine, Ef is the Young’s modulus of steel rebar, A is the cross-sectional area of the rebar, and L is the length of deformed part of the rebar.
In summary, a flow chart is presented in Figure 5 to illustrate the experimental program, including raw materials, specimens, variables, experimental types, and expected results.

3. Results and Discussions

3.1. Monotonic Behavior

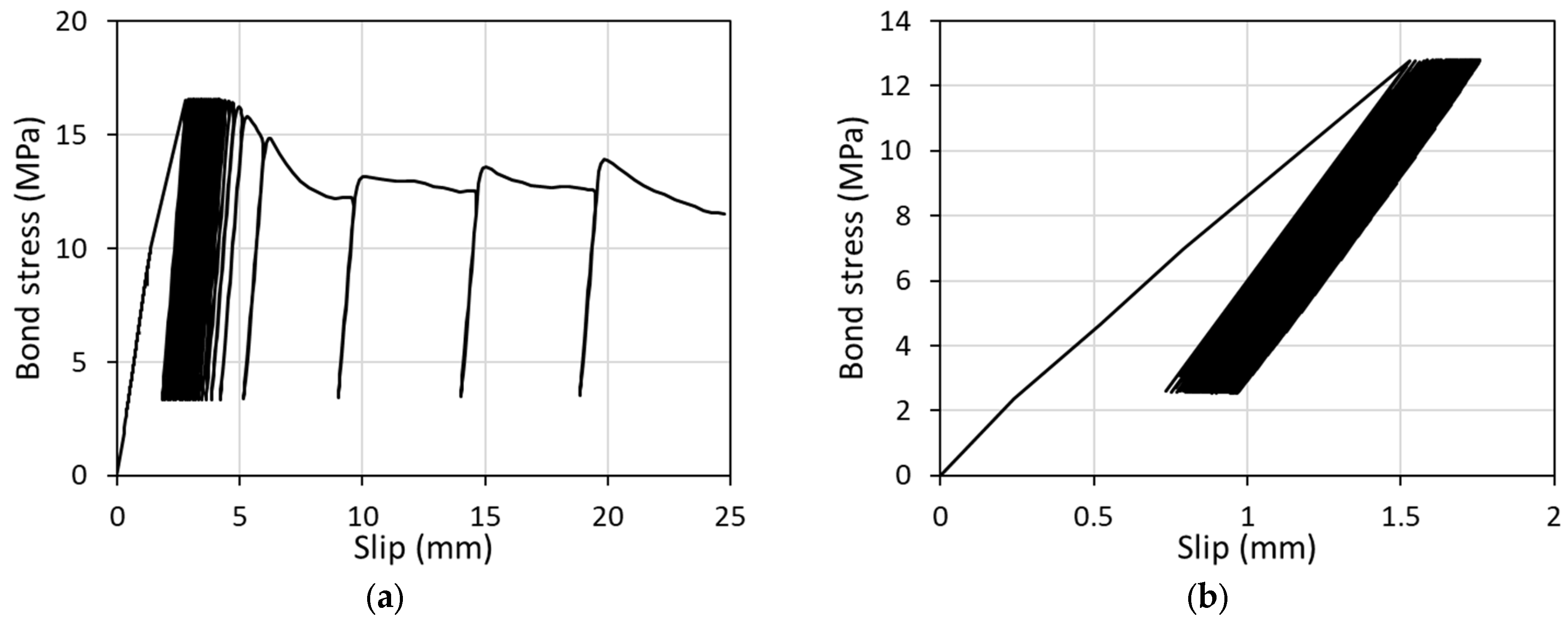
3.1.1. Bond Stress-Slip Curves and Failure Modes

The experimental bond stress-slip curves of the monotonic specimens are shown in Figure 6a–e, whereas Figure 6f shows the idealized bond stress-slip relationship that is categorized by the failure modes. In general, the bond stress-slip curves could be classified into four types (Figure 6f), i.e., (1) bond failure: the rebar was pulled out from the concrete cube with the rebar being in the elastic region (Figure 7a); (2) combined bond failure and rebar yielding: the rebar was pulled out from the concrete cube with the rebar being in the yielding region (Figure 7b); (3) combined bond failure and rebar hardening: the rebar was pulled out from the concrete cube with the rebar being in the strain hardening region (Figure 7c); and (4) rebar fracture: the rebar fractured before bond failure (Figure 7d).
In general, bond stress-slip curves in the same group showed some deviations, e.g., group RA0RB0 and RA50RB0, probably due to the inherent variation in the experimental results. Pullout failure occurred in specimens of group RA0RB0, RA25RB0, and RA25RB5 (Figure 6), and their bond stress-slip curves exhibit a similar pattern. The curve increases linearly in the initial stage, and exhibits nonlinearity before reaching the peak bond stress at a slip of 3~5 mm. Thereafter, stress decreases gradually, indicating a deterioration of the mechanical bonding between rebar and concrete. With a further increase in slip, the bond stress is mainly contributed by the friction, and it either remains stable or slightly increases. The slight regain of the bond stress is likely due to the reformation of mechanical interlocking. For these specimens, stress in the steel rebar is lower than its yield stress, and the rebar’s deformation is insignificant.
For the group RA50RB0, yielding of the rebar occurred earlier than the pullout failure. Pullout failure of specimen RA50RB0-1 occurred in the yielding stage of the rebar, whereas the pullout failure occurred in the strain hardening stage of the rebar for specimens RA50RB0-2 and RA50RB0-3, resulting in different bond stress-slip curves. This is caused by the variation in the bond strengths among the specimens. As shown in Figure 6d, the flat portion of the curve is induced by the rebar yielding. The slip actually consisted of the relative movement between the rebar and concrete and the deformation of the rebar itself.
Specimens in group RA100RB0 (i.e., 100% recycled aggregate) failed due to the fracture of the rebars (Figure 6e), indicating the rebar fracture strength is lower than the bond strength, which is not the intended failure mode for the pullout test in this study. In future studies, the bond length will be shortened to reduce the bond strength and to isolate the target bond failure. The bond stress-slip curves show a similar pattern to the stress–strain curves of steel rebar under tension. The slip in Figure 6e mainly consists of the deformation of the rebar instead of the slippage between rebar and concrete, which may be more appropriate to denote the abscissa axis of Figure 6e as “displacement”. Therefore, the actual bond strength of group RA100RB0 is higher than the peak stress of the curves in Figure 6e.

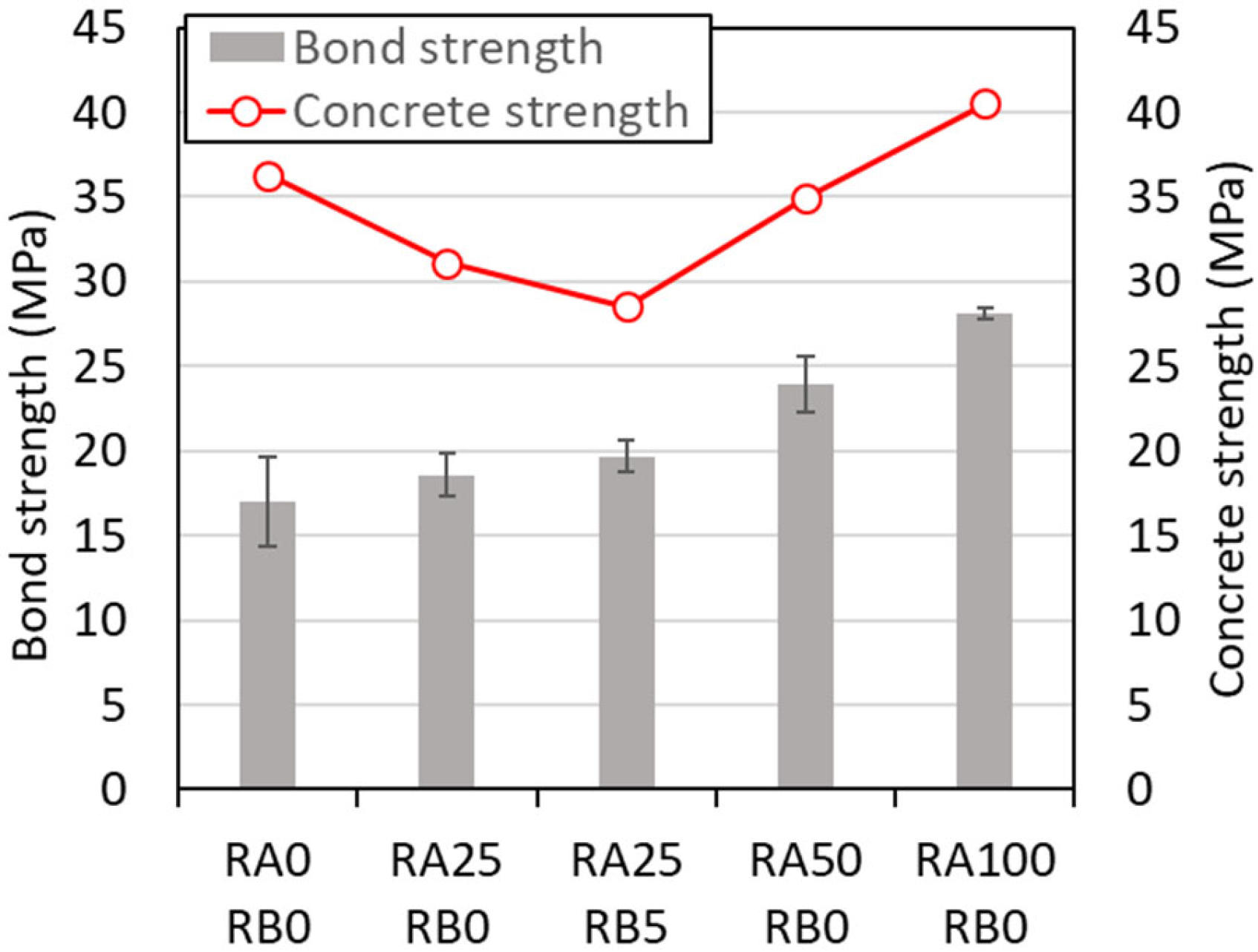
3.1.2. Bond Strength

The average bond strength of each group is listed in Table 2 and plotted in Figure 8, in which the error bar represents the standard deviation. It is noted that the actual bond strength of group RA100RB0 is higher than the value shown in Figure 8, as the specimens in this group failed by rebar fracture instead of debonding. The average concrete compressive strength is also plotted in Figure 8 in red color.
With the increase in recycled aggregate content, concrete strength decreases first (from 0% to 25%) and then increases (from 25% to 50% and 100%), whereas the bond strength increases. For specimens RA25RB5, RA50RB0, and RA100RB0, the bond strength is proportional to the concrete strength. With the addition of rubbers (RA25RB0 vs. RA25RB5), concrete strength decreases, which is in alignment with previous studies on rubber concrete [53], but the bond strength increases. In Tusher et al.’s [12] study, both strength gain and reduction were observed after adding rubbers. A consensus has still not been reached regarding the effect of rubber on bond strength. Such a phenomenon is probably caused by the combined effects of the decrease in concrete strength (i.e., detrimental to bond strength) and the addition of rubber that may enhance the friction between rebar and concrete (i.e., beneficial to bond strength). By comparing RA0RB0 with RA25RB0, concrete strength decreases with the addition of recycled aggregate, but the bond strength slightly increases. A possible reason is the variation in experiment results. Although five repeated specimens were tested for those groups, variation in the bond strengths is still significant, as evidenced by the error bars in Figure 8, probably due to the complexity of bonding mechanisms and uncertainty of the interface condition between the rebar and concrete (e.g., distribution of aggregates in concrete and the quality of concrete casting). In addition, the quality of concrete casting (e.g., aggregate distribution, compactness of concrete) may also lead to bond strength variability.

3.2. Fatigue Behavior

3.2.1. Bond Stress-Slip Curves and Failure Modes

Because a rebar fracture occurred for group RA100RB0 and the actual bond strength was not measured for such group, this group was excluded from the fatigue test. Group RA0RB0, RA25RB0, RA25RB5, and RA50RB0 were tested, and the specimen details are shown in Table 3, in which fatigue life and failure modes were also presented. Some specimens did not fail after 200,000 cycles. A monotonic pullout test was then conducted on such specimens to measure the post-fatigue behavior, which will be discussed in the subsequent section.
Figure 9 shows the typical bond stress-slip curves of specimens under fatigue loading, including a specimen that failed due to fatigue and a specimen that did not fail. For specimens that failed during fatigue loading, the skeleton curves are generally similar to the curves under monotonic loading. During the fatigue loading process, the unloading and reloading curves are linear, and the deterioration of the curve slope (i.e., stiffness) is not obvious.
As shown in Table 3, specimens in group RA0RB0, group RA25RB0 with low stress levels (i.e., 0.65 and 0.75), and group RA50RB0 (stress level = 0.75) did not fail during fatigue loading. The other specimens (i.e., group RA25RB0 with stress ratio = 0.85, and RA25RB5) failed either by debonding or rebar fracture during the loading process. The fatigue fracture of the rebar (i.e., RA25RB5-0.65-1 and RA25RB5-0.75-4) is probably due to the poor quality of the rebars. As expected, fatigue failure is more likely to occur for specimens with high stress levels. In addition, RAC is more prone to fatigue failure than normal concrete, which is likely due to weaker interfacial transition zones (ITZ) in RAC than those of normal concrete and the possible micro-deficiencies in RA. It is found that RAC with recycled rubber is most prone to fatigue failure due to the poor bonding between rubber and paste in concrete, as well as the deformable nature of rubber. Based on this study’s experimental results, the recycled aggregate and rubber are detrimental to the fatigue bond performance. It is needed to mention that the absolute fatigue loads on RAC specimens are higher than those of normal concrete, as the bond strength of RAC is higher than normal concrete, as discussed in Figure 8.

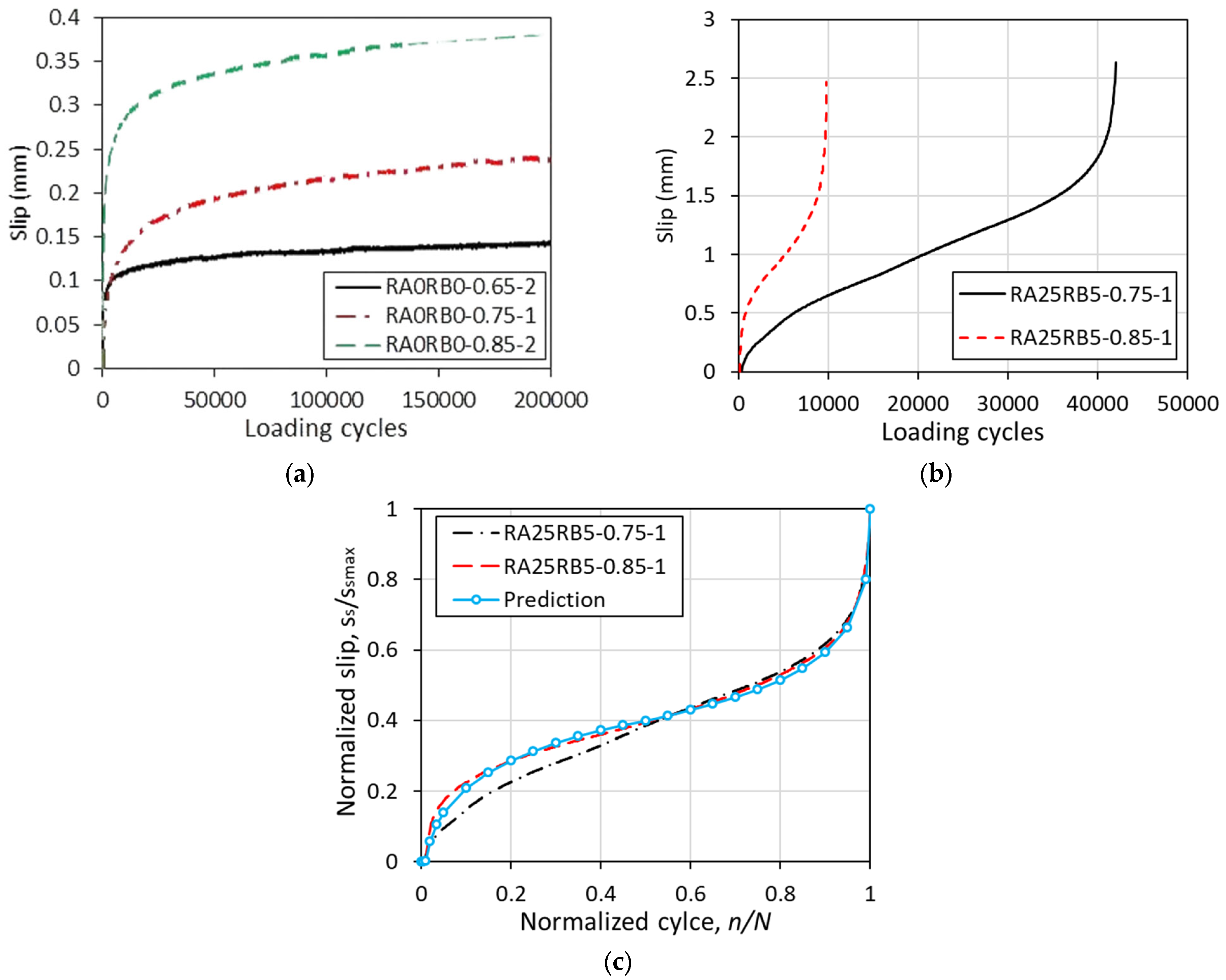
3.2.2. Slip Development

Figure 10 shows the slip development of some typical specimens during the fatigue loading process, in which the slip is read from the unloading point in each cycle. Shapes of the slip-loading cycles vary greatly, depending on whether fatigue failure occurs.
For specimens that did not fail during fatigue loading (Figure 10a), the slip curve contains a fast increase portion and a steady increase portion. For specimens in the same group, the slip of the specimens with a high stress level is larger than that with a low stress ratio, which agrees with existing studies [54]. On the other hand, the slip curve consists of three portions (i.e., fast, slow, and fast increase) for specimens having fatigue failure (Figure 10b). In general, the shape of the slip curves depends on the failure modes. Concrete type and stress level only affect the absolute values of the slip during the fatigue loading process. Figure 10c shows the development of the normalized slip, in which ssmax is the slip at fatigue failure, n is the loading cycle, and N is the fatigue life. It is found that the normalized slip curves are independent of the stress level.

3.2.3. Fatigue Life

As shown in Table 3, fatigue failure occurred for specimen groups RA25RB0 and RA25RB5 with various stress levels. Figure 11 shows the stress level—loading cycle relationship of the specimens in those groups, in which the horizontal axis is on a logarithmic scale.
As shown in Figure 11, great variation exists for the fatigue life of the specimens under different stress levels. Owing to the limited data and data deviation, it is difficult to draw a conclusion regarding the effect of rubber on the fatigue life. In general, with the increase in stress level, the fatigue life decreases. It is necessary to mention that fatigue failure did not happen for group RA0RB0 and RA50RB0, and their fatigue life is infinite.

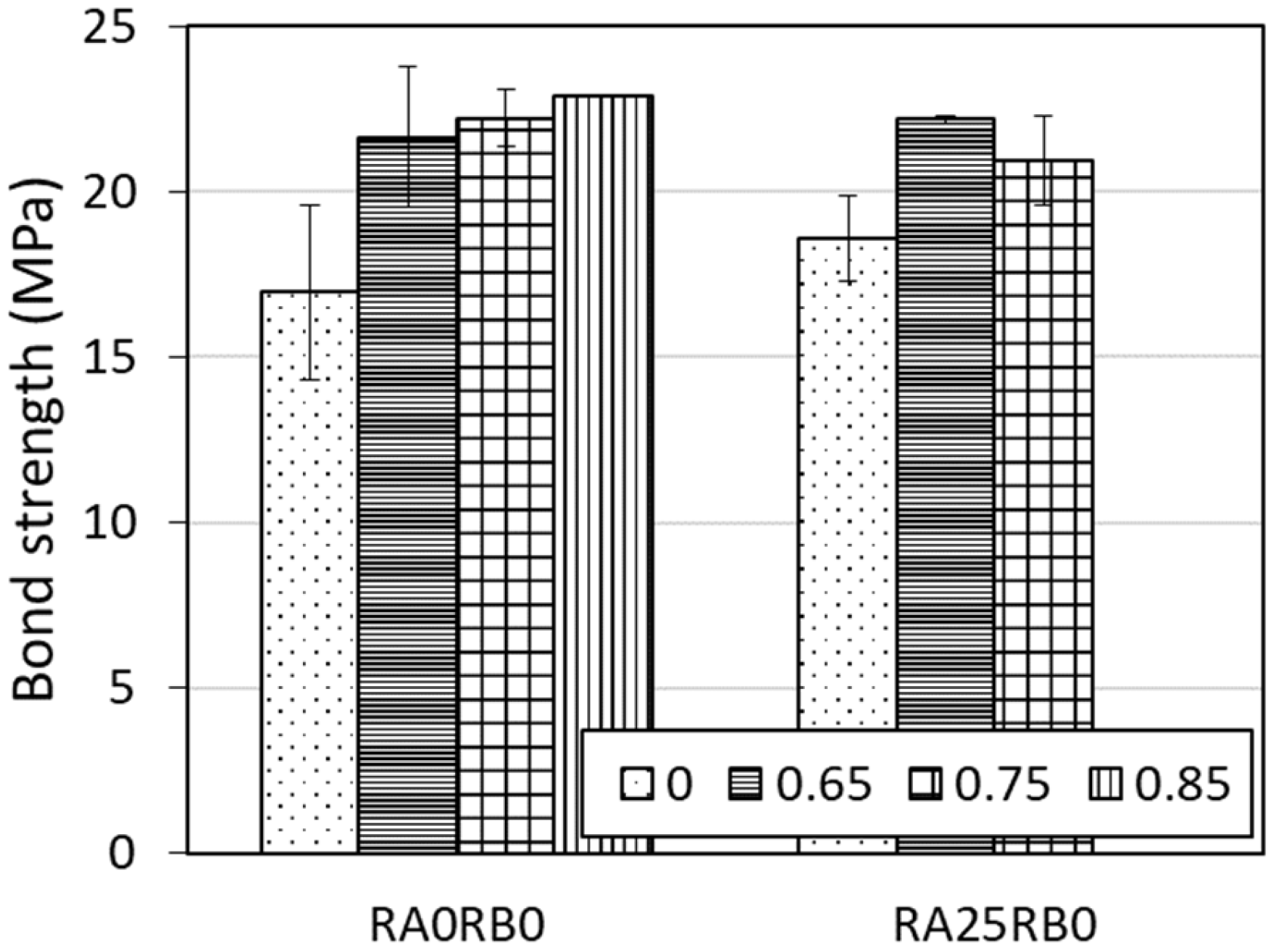
3.3. Post-Fatigue Monotonic Behavior

Post-fatigue monotonic pullout test was conducted on the specimens that did not fail due to fatigue (e.g., group RA0RB0, RA25RB0, and RA50RB0). The failure mode and bond strength are listed in Table 3. Only a few specimens failed by debonding (e.g., RA0RB0-0.65-1 and RA25RB0-0.75-2), and the other specimens failed due to yielding and bond failure or rebar fracture. The failure modes of the specimens subjected to fatigue history differed from their corresponding specimens without fatigue history, indicating an increase in the bond strength. Figure 12 shows the bond strengths of specimens in group RA0RB0 and RA25RB0, in which legend “0” means specimens without fatigue history, and legends “0.65, 0.75, and 0.85” refer to specimens subjected to fatigue history with the prespecified stress level. It is interesting to find that the bond strength was enhanced after experiencing fatigue history (i.e., residual bond strength is higher than monotonic bond strength). As shown in Figure 12, the effect of stress level and recycled aggregate content on the residual bond strength is not obvious.
The unexpected increase in bond strength after fatigue loading might be due to a further curing of the concrete during the fatigue loading process (about 12 days). Monotonic tests of specimens were conducted within one day, but the total during the fatigue test on a group of specimens took 1~3 months (depending on whether fatigue failure happened). Therefore, a substantial strength enhancement due to the increase in curing time was possible. The fatigue strength is the combined effect of beneficial curing and detrimental damage accumulation. Future studies may need to consider this effect by testing the specimens after sufficient curing time to minimize the strength change with curing age. Deviation of experimental results that are induced by, for example, variation in concrete casting quality, experimental setup errors, etc., is another reason for the unexpected bond strength increase.
As many factors (e.g., stress level, cover depth, rebar surface, rebar strength, embedment length, concrete strength, concrete type, loading frequency, and sample size) could affect the bond behavior, the monotonic and fatigue bond performance of rebars in concrete is quite complicated. Currently, predictions for bond performance, such as bond strength, fatigue life, and strain development, are mostly empirical, which may lack versatility. Nevertheless, owing to the intensive advances in artificial intelligence and deep learning algorithms [55,56,57,58], these techniques enable to achievement of a more versatile design method for predicting bonding behavior. Research on applying such AI tools in predicting structural performance that involves a large quantity of variables is promising.

4. Predictive Models

4.1. Monotonic Bond Strength Model

Currently, various models have been proposed to predict the monotonic bond strength of steel rebar in concrete, such as [59,60,61]. The factors, including concrete strength, rebar diameter, cover depth, replacement rate of recycled aggregate, embedment length, and coarse aggregate density, are partially or fully considered in those models. This study proposed a modified version of the formula in Model Code 2020 [29], in which the bond strength is proportional to the square root of concrete strength, and the modified coefficients were determined based on the experimental results discussed in Section 3.1. The monotonic bond strength (τmax) is predicted as follows:
τ m a x = ( 1.5 γ + 3 ) f c ′ ,
where fc’ is the compressive strength of concrete and γ is the replacement rate of the recycled aggregate. The constants in Equation (3) are determined by regression analysis on the experimental data. Owing to the limited data on rubber RAC, the influencing trend of rubber content on τmax is still not clear, and Equation (3) does not consider the effect of rubber content. A comparison of the predicted and experimental monotonic bond strength is shown in Figure 13a and Table 4, in which the average and COV of the prediction-to-experiment ratio are 1.0 and 0.11, respectively. A good match of them indicates the reasonability of the proposed formula. Figure 13b shows the comparison of the proposed (i.e., Equation (3)) to some existing methods in predicting the monotonic bond strength, in which formulas in the fib Model Code [29] and Seara-Paz et al. [60] are shown in Equations (4) and (5), respectively.
τ m a x = 2.5 f c ′ ,
τ m a x = 2.5 f c ′ ( 1 − 0.124 γ ) ,
where fc’ is the compressive strength of concrete and γ is the replacement rate of the recycled aggregate. The proposed method exhibits the best accuracy.
To further verify the rationale of the proposed formula, Kim et al.’s pullout test [56] on deformed steel rebar in 150 × 150 × 150 mm RAC cubes was adopted for validation. The replacement ratios of RA were 0%, 30%, 60%, and 100%. A comparison of the predicted and experimental bond strengths is shown in Figure 13a and Table 4, in which the average prediction-to-experiment ratio is 0.93 with a COV of 0.18. In addition, the performance of the fib Model Code [29] and Seara-Paz et al. [60]’s prediction of the bond strength of Kim et al.’s [56] specimens are also presented in Table 4, which shows a significant underestimation.

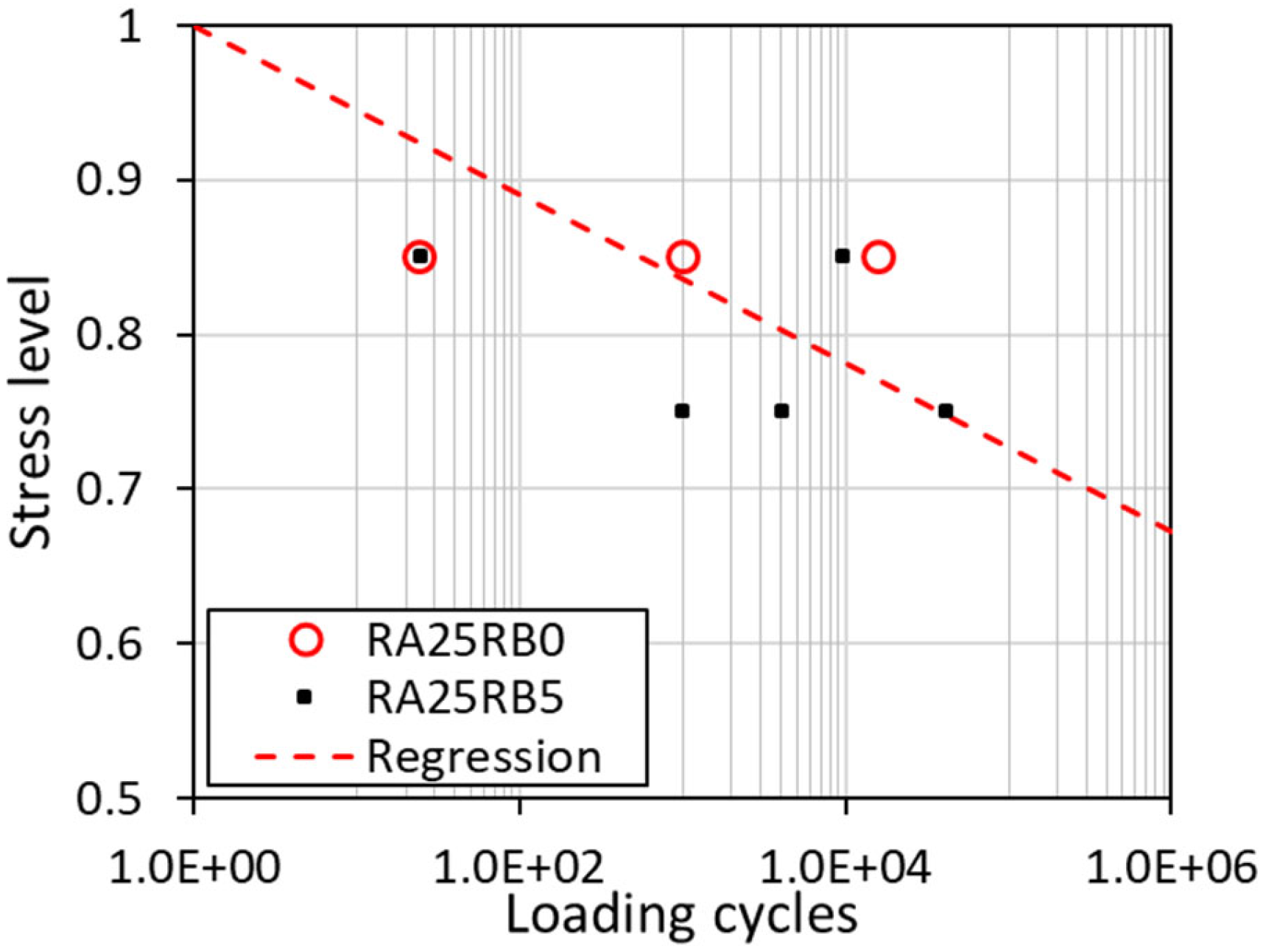
4.2. Stress Level—Fatigue Life Model

Existing studies on fatigue bond behavior commonly assume a linear relationship between the stress level and the common logarithm of fatigue life. As discussed in Section 3.2, the effect of recycled rubber on fatigue life is insignificant. Therefore, an empirical equation is proposed as shown in Equation (6), and the constants were determined by regressing the available experimental data of this study (as plotted in Figure 11):
τ τ m a x = 1 − 0.0546 l g ( N ) ,
where τ is the stress level for fatigue loading, τmax is the monotonic bond strength that could be determined by Equation (3), and N is the fatigue life. It is needed to highlight that, as experimental data for regression analysis is currently very limited, Equation (4) is applicable to both RAC and rubber RAC. Nevertheless, more research on the fatigue behavior of steel rebar in recycled rubber concrete is required to expand the database and refine the proposed empirical formula.

4.3. Slip Model Under Fatigue Loading

Besides the predictive model for fatigue life, it is important to predict the development of slip during the fatigue loading process. As discussed in Section 3.2.3, the normalized slip curve is independent on the stress level, and ss/smax is only related to the ratio of loading cycle to fatigue life (n/N). By analyzing the slip-loading cycle curves, power functions are adopted to predict slip development as shown in Equation (7)
s s = s s m a x · n N 0.15 − 0.5 ≥ 0 ,     if   n N ≤ 0.5 s s m a x · 1.3 − 1 − n N 0.15 ≤ s s m a x ,     if   n N > 0.5
where n is the loading cycle, N is the fatigue life that could be predicted by Equation (4), ssmax is the slip at fatigue failure that could be approximately taken as the slip at bond strength under monotonic loading, and ss is the slip at loading cycle n. It is necessary to mention that the constants in Equation (7) were determined by regression analysis on the experimental curves. A comparison of the experimental and predicted slip curves is shown in Figure 10c, which shows a good match between them.

5. Conclusions

This paper presents experimental and theoretical studies on the monotonic and fatigue bond behavior of steel rebars embedded in RAC and rubber RAC. The following conclusions could be drawn:
(1)
Four failure modes, including bond failure, bond failure and rebar yielding, bond failure and rebar hardening, and rebar fracture, were identified for the pullout specimens.
(2)
With the increase in recycled aggregate content and rubber content, the monotonic bond strength of the tested specimens showed an increasing trend, which is likely due to the increase in concrete strength and the beneficial effects of rubber on bonding behavior.
(3)
With the addition of recycled aggregate (from 0 to 25% replacement ratio) and rubber (from 0 to 5%), the specimens became more prone to fatigue failure than the specimens with natural aggregate concrete. It is suggested to use RAC and rubber concrete in low-fatigue applications and limit the replacement ratio of rubber to 5%.
(4)
For specimens that failed due to fatigue debonding, the normalized slip curves of the specimens under fatigue loading are independent of the stress level.
(5)
Fatigue history does not deteriorate bond strength, and even an increase in bond strength is observed, which is likely caused by the development of concrete strength induced by further curing during the fatigue loading period.
(6)
Theoretical models were proposed to predict the monotonic bond strength, fatigue life, and slip under fatigue loading. The predictions agreed well with the experimental results, indicating the reasonability of the proposed formulas.
It is necessary to emphasize that the parameters investigated in this study only include recycled aggregate and rubber replacement ratios and stress levels. Nevertheless, other factors, such as rebar diameter, cover depth, embedment length, location of rebar, quantity of rebar, and sample size, also play significant roles in affecting the fatigue bond behavior. Therefore, it is suggested to cover more parameters in future studies. As some tested specimens failed by rebar yielding or fracture instead of debonding, it is suggested to reduce the embedment length or strength grade of rebars to isolate the pullout failure mode. In addition, analysis on the microstructure, such as SEM, porosity analysis, will contribute to an in-depth understanding of the bond mechanism, which is also suggested for future studies.

Author Contributions

Conceptualization, W.W.; methodology, Y.L.; software, S.C.; validation, W.W., Y.L. and S.C.; formal analysis, S.C.; investigation, SC.; resources, Y.L.; data curation, Y.L.; writing—original draft preparation, W.W.; writing—review and editing, Y.L.; visualization, S.C.; supervision, W.W.; project administration, Y.L.; funding acquisition, W.W. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Characteristic Innovation Project of Department of Education of Guangdong Provincial (2021KTSCX211) and the High-level Talent Research Project of Guangdong Construction Polytechnic (GCC2021-02).

Data Availability Statement

Data is contained within the article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Lv, H.; Xiong, Z.; Li, H.; Liu, J.; Xu, G.; Chen, H. Investigating the mechanical properties and water permeability of recycled pervious concrete using three typical gradation schemes. Buildings 2025, 15, 358. [Google Scholar] [CrossRef]
  2. Xiao, J.-Z.; Li, J.-B.; Zhang, C. Onrelationships between the mechanical properties of recycled aggregate concrete: An overview. Mater. Struct. 2006, 39, 655–664. [Google Scholar] [CrossRef]
  3. Wang, J.; Liu, F.; Luo, Z.; He, M.; Chen, G.; Xiong, Z. Behaviour of FRP-rubber concrete-steel double-skin tubular slender columns under eccentric compression: An experimental and theoretical study. J. Build. Eng. 2025, 104, 112265. [Google Scholar] [CrossRef]
  4. Mei, J.; Xu, G.; Ahmad, W.; Khan, K.; Amin, M.N.; Aslam, F.; Alaskar, A. Promoting sustainable materials using recycled rubber in concrete: A review. J. Clean. Prod. 2022, 373, 133927. [Google Scholar] [CrossRef]
  5. Roychand, R.; Gravina, R.J.; Zhuge, Y.; Ma, X.; Youssf, O.; Mills, J.E. A comprehensive review on the mechanical properties of waste tire rubber concrete. Constr. Build. Mater. 2020, 237, 117651. [Google Scholar] [CrossRef]
  6. Pan, D.; Liu, F.; Li, L. The Application and Research Overview of Rubber Concrete. Chn. Rub. Indus. 2007, 54, 182–185. (In Chinese) [Google Scholar] [CrossRef]
  7. Aghamohammadi, O.; Mostofinejad, D.; Mostafaei, H.; Abtahi, S.M. Mechanical properties and impact resistance of concrete pavement containing crumb rubber. Int. J. Geomech. 2024, 24, 04023242. [Google Scholar] [CrossRef]
  8. Yang, Y.; Wang, Z. Applications research in engineering of roller compacted rubcrete. Concrete 2021, 139–141. (In Chinese) [Google Scholar] [CrossRef]
  9. Siddika, A.; Al Mamun, M.A.; Alyousef, R.; Amran, Y.M.; Aslani, F.; Alabduljabbar, H. Properties and utilizations of waste tire rubber in concrete: A review. Constr. Build. Mater. 2019, 224, 711–731. [Google Scholar] [CrossRef]
  10. Karabulut, M. Nonlinear Load-Deflection Analysis of Steel Rebar-Reinforced Concrete Beams: Experimental, Theoretical and Machine Learning Analysis. Buildings 2025, 15, 432. [Google Scholar] [CrossRef]
  11. Karabulut, M. Machine Learning-Driven Flexural Performance Prediction and Experimental Investigation of Glass Fiber-Reinforced Polymer Bar-Reinforced Concrete Beams. Polymers 2025, 17, 713. [Google Scholar] [CrossRef] [PubMed]
  12. Tusher, T.H.; Ahmed, K.S.; Sarker, M.S.B.I. Bond behavior of deformed rebar in concrete containing recycled brick aggregate and waste rubber. J. Build. Eng. 2024, 92, 109729. [Google Scholar] [CrossRef]
  13. Su, T.; Wang, C.; Cao, F.; Zou, Z.; Wang, C.; Wang, J.; Yi, H. An overview of bond behavior of recycled coarse aggregate concrete with steel bar. Rev. Adv. Mater. Sci. 2021, 60, 127–144. [Google Scholar] [CrossRef]
  14. Gong, Y.; Jiang, T.; Sun, L.; Jiang, W.; Zhang, Q.; Liu, S.; Tian, L. Constitutive model of bond-slip between rubber granule–basalt fiber composite modified concrete and rebar. App. Sci. 2023, 13, 12726. [Google Scholar] [CrossRef]
  15. Zhang, W.; Lin, J.; Huang, Y.; Lin, B.; Liu, X. State of the art regarding interface bond behavior between FRP and concrete based on cohesive zone model. Structures 2025, 74, 108528. [Google Scholar] [CrossRef]
  16. Sun, L.; Wang, C.; Zhang, C.; Yang, Z.; Li, C.; Qiao, P. Experimental investigation on the bond performance of sea sand coral concrete with FRP bar reinforcement for marine environments. Adv. Struct. Eng. 2023, 26, 533–546. [Google Scholar] [CrossRef]
  17. Zhang, W.; Liu, X.; Huang, Y.; Tong, M.N. Reliability-based analysis of the flexural strength of concrete beams reinforced with hybrid bfrp and steel rebars. Arch. Civ. Mech. Eng. 2022, 22, 171. [Google Scholar] [CrossRef]
  18. Kim, S.; Yun, H. Influence of recycled coarse aggregates on the bond behavior of deformed bars in concrete. Eng. Struct. 2013, 48, 133–143. [Google Scholar] [CrossRef]
  19. Ajdukiewicz, A.; Kliszczewicz, A. Influence of recycled aggregates on mechanical properties of HS/HPC. Cem. Concr. Compos. 2002, 24, 269–279. [Google Scholar] [CrossRef]
  20. Prince, M.J.R.; Singh, B. Bond behaviour of deformed steel bars embedded in recycled aggregate concrete. Constr. Build. Mater. 2013, 49, 852–862. [Google Scholar] [CrossRef]
  21. Corinaldesi, V.; Moriconi, G. Influence of mineral additions on the performance of 100% recycled aggregate concrete. Constr. Build. Mater. 2009, 23, 2869–2876. [Google Scholar] [CrossRef]
  22. Gesoglu, M.; Güneyisi, E.; Hansu, O.; İpek, S.; Asaad, D. Influence of waste rubber utilization on the fracture and steel–concrete bond strength properties of concrete. Constr. Build. Mater. 2015, 101, 1113–1121. [Google Scholar] [CrossRef]
  23. Hall, M.R.; Najim, K.B. Structural behaviour and durability of steel-reinforced structural Plain/Self-Compacting Rubberised Concrete (PRC/SCRC). Constr. Build. Mater. 2014, 73, 490–497. [Google Scholar] [CrossRef]
  24. Gao, D.; Li, Z.; Yu, Z. Uniaxial tensile stress-strain constitutive relationship of 3D/4D/5D steel fiber-reinforced concrete. Constr. Build. Mater. 2025, 470, 140539. [Google Scholar] [CrossRef]
  25. Harajli, M.H. Development/splice strength of reinforcing bars embedded in plain and fiber reinforced concrete. ACI Mater. J. 1994, 91, 511–520. [Google Scholar] [CrossRef]
  26. Prince, M.; Singh, B. Bond behaviour of normal-and high-strength recycled aggregate concrete. Struct. Concr. 2015, 16, 56–70. [Google Scholar] [CrossRef]
  27. Xiao, J.; Falkner, H. Bond behaviour between recycled aggregate concrete and steel rebars. Constr. Build. Mater. 2007, 21, 395–401. [Google Scholar] [CrossRef]
  28. Australian Standard AS 3600; Concrete Structures. Australian Business Licence and Information Service: Canberra, Australia, 2018.
  29. International Federation of Structural Concrete. The Fib Model Code for Concrete Structures; International Federation of Structural Concrete: Lausanne, Switzerland, 2020. [Google Scholar]
  30. Luo, J.; Wu, G.; Zhao, G.; Ma, Y.; Fang, Z.; Fang, S. Experimental and numerical analysis on shear performance of single embedded nut bolted shear connectors in prefabricated steel-UHPC composite structures under cyclic loading. Structures 2025, 73, 108446. [Google Scholar] [CrossRef]
  31. Kachkouch, F.Z.; Noberto, C.C.; Babadopulos, L.F.d.A.L.; Melo, A.R.S.; Machado, A.M.L.; Sebaibi, N.; Boukhelf, F.; Mendili, Y.E. Fatigue behavior of concrete: A literature review on the main relevant parameters. Constr. Build. Mater. 2022, 338, 127510. [Google Scholar] [CrossRef]
  32. Verna, J.R.; Stelson, T.E. Failure of small reinforced concrete beams under repeated loads. ACI J. Proc. 1962, 59, 1489–1504. [Google Scholar]
  33. Xiong, Z.; Mai, G.; Qiao, S.; He, S.; Zhang, B.; Wang, H.; Zhou, K.; Li, L. Fatigue bond behaviour between basalt fibre-reinforced polymer bars and seawater sea-sand concrete. Ocean Coast. Manag. 2022, 218, 106038. [Google Scholar] [CrossRef]
  34. Shi, J.W.; Wu, Q.Q.; Li, B.; Liu, Y.; Cao, W.H.; Wang, H.T. Fatigue bond behavior of FRP-to-concrete joints with various bonding adhesives. Eng. Struct. 2024, 301, 117311. [Google Scholar] [CrossRef]
  35. Zou, R.; Liu, F.; Xiong, Z.; He, S.; Li, L.; Wei, W. Experimental study on fatigue bond behaviour between basalt fibre-reinforced polymer bars and recycled aggregate concrete. Constr. Build. Mater. 2021, 270, 121399. [Google Scholar] [CrossRef]
  36. Jiang, N.; Liu, Y.; Deng, Y.; Wang, D.; Lu, N.; Yu, F. Investigation of bond behavior between steel bar and concrete under coupled effect of fatigue loading and corrosion. J. Mater. Civ. Eng. 2023, 35, 04023366. [Google Scholar] [CrossRef]
  37. Tilly, G. Fatigue of steel reinforcement bars in concrete: A review. Fatigue Fract. Eng. Mater. Struct. 1979, 2, 251–268. [Google Scholar] [CrossRef]
  38. Zhang, W.; Zhang, Y.; Li, H.; Gu, X. Experimental investigation of fatigue bond behavior between deformed steel bar and concrete. Cem. Concr. Compos. 2020, 108, 103515. [Google Scholar] [CrossRef]
  39. Rezazadeh, M.; Carvelli, V. A damage model for high-cycle fatigue behavior of bond between FRP bar and concrete. Int. J. Fatigue 2018, 111, 101–111. [Google Scholar] [CrossRef]
  40. Lin, H.; Zhao, Y.; Ožbolt, J.; Hans-Wolf, R. The bond behavior between concrete and corroded steel bar under repeated loading. Eng. Struct. 2017, 140, 390–405. [Google Scholar] [CrossRef]
  41. Oh, B.; Kim, S. Realistic models for local bond stress-slip of reinforced concrete under repeated loading. J. Struct. Eng. 2007, 133, 216–224. [Google Scholar] [CrossRef]
  42. Lindorf, A.; Lemnitzer, L.; Curbach, M. Experimental investigations on bond behaviour of reinforced concrete under transverse tension and repeated loading. Eng. Struct. 2009, 31, 1469–1476. [Google Scholar] [CrossRef]
  43. Lindorf, A.; Curbach, M. S–N curves for fatigue of bond in reinforced concrete structures under transverse tension. Eng. Struct. 2010, 32, 3068–3074. [Google Scholar] [CrossRef]
  44. Al-Hammoud, R.; Soudki, K.; Topper, T. Bond analysis of corroded reinforced concrete beams under monotonic and fatigue loads. Cem. Concr. Compos. 2010, 32, 194–203. [Google Scholar] [CrossRef]
  45. Rteil, A.; Soudki, K.; Topper, T. Mechanics of bond under repeated loading. Constr. Build. Mater. 2011, 25, 2822–2827. [Google Scholar] [CrossRef]
  46. Arora, S.; Singh, S.P. Analysis of flexural fatigue failure of concrete made with 100% coarse recycled concrete aggregates. Constr. Build. Mater. 2016, 102, 782–791. [Google Scholar] [CrossRef]
  47. Xiao, J.; Li, H.; Yang, Z. Fatigue behavior of recycled aggregate concrete under compression and bending cyclic loadings. Constr. Build. Mater. 2013, 38, 681–688. [Google Scholar] [CrossRef]
  48. Liu, F.; Zheng, W.; Li, L.; Feng, W.; Ning, G. Mechanical and fatigue performance of rubber concrete. Constr. Build. Mater. 2013, 47, 711–719. [Google Scholar] [CrossRef]
  49. GB/T 14684-2011; Sand for Construction. Standardization Administration of China: Beijing, China, 2011.
  50. GB/T 50081-2002; Standard for Test Method of Mechanical Properties on Ordinary Concrete. Standardization Administration of China: Beijing, China, 2002.
  51. GB/T 50152-2012; Standard for Test Method of Concrete Structures. Standardization Administration of China: Beijing, China, 2012.
  52. Reis, E.; Azevedo, R.C.D.; Christoforo, A.; Poggiali, F.; Bezerra, A.C.S. Bonding of steel bars in concrete: A systematic review of the literature. Structures 2023, 49, 508–519. [Google Scholar] [CrossRef]
  53. Strukar, K.; Šipoš, T.K.; Miličević, I.; Bušić, R. Potential use of rubber as aggregate in structural reinforced concrete element—A review. Eng. Struct. 2019, 188, 452–468. [Google Scholar] [CrossRef]
  54. Li, Q.-H.; Luo, A.-M.; Huang, B.-T.; Wang, G.-Z.; Xu, S.-L. Bond behavior between steel bar and strain-hardening fiber-reinforced cementitious composites under fatigue loading. Eng. Struct. 2024, 314, 118354. [Google Scholar] [CrossRef]
  55. Fang, T.; Hui, Z.; Rey, W.P.; Yang, A.; Liu, B.; Xie, Z. Digital Restoration of Historical Buildings by Integrating 3D PC Reconstruction and GAN Algorithm. J. Artif. Intell. Technol. 2024, 4, 179–187. [Google Scholar] [CrossRef]
  56. Chattopadhyay, S. Decoding medical diagnosis with machine learning classifiers. Medinformatics 2024. [Google Scholar] [CrossRef]
  57. Touil, M.; Bahatti, L.; Elmagri, A. Automatic sleep quality analysis using an artificial intelligence algorithm and eeg signal processing. J. Artif. Intell. Technol. 2024, 4, 153–159. [Google Scholar] [CrossRef]
  58. El Aeraj, O.; Leghris, C. Intrusion Detection System Based on an Intelligent Multilayer Model Using Machine Learning. J. Artif. Intell. Technol. 2024, 4, 332–341. [Google Scholar]
  59. Kim, S.; Yun, H.; Park, W.; Jang, Y. Bond strength prediction for deformed steel rebar embedded in recycled coarse aggregate concrete. Mater. Des. 2015, 83, 257–269. [Google Scholar] [CrossRef]
  60. Seara-Paz, S.; González-Fonteboa, B.; Eiras-López, J.; Herrador, M. Bond behavior between steel reinforcement and recycled concrete. Mater. Struct. 2014, 47, 323–334. [Google Scholar] [CrossRef]
  61. Wardeh, G.; Ghorbel, E.; Gomart, H.; Fiorio, B. Experimental and analytical study of bond behavior between recycled aggregate concrete and steel bars using a pullout test. Struct. Concr. 2017, 18, 811–825. [Google Scholar] [CrossRef]
Buildings 15 02102 g001
Figure 1. Raw materials for concrete.
Figure 1. Raw materials for concrete.
Buildings 15 02102 g001
Buildings 15 02102 g002aBuildings 15 02102 g002b
Figure 2. Pullout specimen: (a) after concrete casting; (b) mold for concrete casting; (c) specimen ready for test; (d) mixing of concrete.
Figure 2. Pullout specimen: (a) after concrete casting; (b) mold for concrete casting; (c) specimen ready for test; (d) mixing of concrete.
Buildings 15 02102 g002aBuildings 15 02102 g002b
Buildings 15 02102 g003
Figure 3. Experimental setup.
Figure 3. Experimental setup.
Buildings 15 02102 g003
Buildings 15 02102 g004
Figure 4. Loading regime for fatigue test.
Figure 4. Loading regime for fatigue test.
Buildings 15 02102 g004
Buildings 15 02102 g005
Figure 5. Flow chart for experimental program.
Figure 5. Flow chart for experimental program.
Buildings 15 02102 g005
Buildings 15 02102 g006aBuildings 15 02102 g006b
Figure 6. Bond stress-slip curves of monotonic tests.
Figure 6. Bond stress-slip curves of monotonic tests.
Buildings 15 02102 g006aBuildings 15 02102 g006b
Buildings 15 02102 g007
Figure 7. Failure modes: (a) pullout failure; (b) bond failure and yielding; (c) bond failure and hardening; (d) fracture.
Figure 7. Failure modes: (a) pullout failure; (b) bond failure and yielding; (c) bond failure and hardening; (d) fracture.
Buildings 15 02102 g007
Buildings 15 02102 g008
Figure 8. Static bond strength.
Figure 8. Static bond strength.
Buildings 15 02102 g008
Buildings 15 02102 g009
Figure 9. Bond stress-slip curves of typical fatigue specimens: (a) specimen having fatigue failure; (b) specimen that did not fail by fatigue loading.
Figure 9. Bond stress-slip curves of typical fatigue specimens: (a) specimen having fatigue failure; (b) specimen that did not fail by fatigue loading.
Buildings 15 02102 g009
Buildings 15 02102 g010
Figure 10. Slip-loading cycles curves of typical specimens: (a) specimens having fatigue failure; (b) specimens that did not fail by fatigue loading; (c) verification.
Figure 10. Slip-loading cycles curves of typical specimens: (a) specimens having fatigue failure; (b) specimens that did not fail by fatigue loading; (c) verification.
Buildings 15 02102 g010
Buildings 15 02102 g011
Figure 11. Fatigue life.
Figure 11. Fatigue life.
Buildings 15 02102 g011
Buildings 15 02102 g012
Figure 12. Residual bond strength of specimens with various stress levels.
Figure 12. Residual bond strength of specimens with various stress levels.
Buildings 15 02102 g012
Buildings 15 02102 g013
Figure 13. Comparison of the predicted and experimental monotonic bond strengths: (a) proposed method; (b) proposed and existing methods.
Figure 13. Comparison of the predicted and experimental monotonic bond strengths: (a) proposed method; (b) proposed and existing methods.
Buildings 15 02102 g013
Table 1. Concrete mixture and properties.
Table 1. Concrete mixture and properties.
MixtureWater
(kg/m3)		Water Reducer
(kg/m3)		Cement
(kg/m3)		Sand
(kg/m3)		Rubber
(kg/m3)		Natural CA
(kg/m3)		Recycled CA
(kg/m3)		fc’
(MPa)		Ec
(GPa)
RA0RB02343.842576201018036.370.5
RA25RB02343.84257620763.5254.531.166.4
RA25RB52343.8425723.919.1763.5254.528.563.9
RA50RB02343.8425762050950935.062.8
RA100RB02343.842576200101840.558.5
Note: CA = coarse aggregate.
Table 2. Specimens for the monotonic test.
Table 2. Specimens for the monotonic test.
GroupSpecimenRA RatioRubber RatioBond Strength (MPa)Failure Modes
IndividualGroup
RA0RB0RA0RB0-10015.017.0Bond failure
RA0RB0-220.4(2.6) aBond failure
RA0RB0-315.0 Bond failure
RA0RB0-414.5 Bond failure
RA0RB0-519.9 Bond failure
RA25RB0RA25RB0-125%017.318.6Bond failure
RA25RB0-220.1(1.3)Bond failure
RA25RB0-320.0 Bond failure
RA25RB0-417.1 Bond failure
RA25RB0-518.5 Bond failure
RA25RB5RA25RB5-125%5%21.119.7Bond failure
RA25RB5-219.0(0.9)Bond failure
RA25RB5-319.1 Bond failure
RA25RB5-420.5 Bond failure
RA25RB5-518.7 Bond failure
RA50RB0RA50RB0-150%021.723.9Bond failure and yielding
RA50RB0-224.3(1.7)Bond failure and hardening
RA50RB0-325.8 Bond failure and hardening
RA100RB0RA100RB0-1100%028.528.1Rebar fracture
RA100RB0-228.1(0.3)Rebar fracture
RA100RB0-327.8 Rebar fracture
a: The value in parentheses is the standard deviation.
Table 3. Specimens for the fatigue test.
Table 3. Specimens for the fatigue test.
GroupSpecimenStress RatioFatigue TestPost-Fatigue Pullout Test
Failure ModeFatigue LifeFailure ModeBond Strength (MPa)
RA0
RB0		RA0RB0-0.65-10.65N/AN/ABond failure19.0
RA0RB0-0.65-20.65N/AN/AYielding and bond failure24.2
RA0RB0-0.65-30.65N/AN/AYielding and bond failure21.8
RA0RB0-0.75-10.75N/AN/AYielding and bond failure22.0
RA0RB0-0.75-20.75N/AN/AYielding and bond failure23.3
RA0RB0-0.75-30.75N/AN/AYielding and bond failure21.2
RA0RB0-0.85-10.85Frame failureN/AN/AN/A
RA0RB0-0.85-20.85N/AN/AYielding and bond failure22.9
RA0RB0-0.85-40.85N/AN/ARebar fractureN/A
RA25
RB0		RA25RB0-0.65-10.65N/AN/AYielding and bond failure22.1
RA25RB0-0.65-20.65N/AN/AYielding and bond failure22.3
RA25RB0-0.65-30.65N/AN/ARebar fractureN/A
RA25RB0-0.75-10.75N/AN/AYielding and bond failure22.3
RA25RB0-0.75-20.75N/AN/ABond failure19.6
RA25RB0-0.75-40.75N/AN/ARebar fractureN/A
RA25RB0-0.85-20.85Bond failure15,920N/AN/A
RA25RB0-0.85-30.85Bond failure1000N/AN/A
RA25RB0-0.85-40.85Bond failure24N/AN/A
RA25
RB5		RA25RB5-0.65-10.65Rebar fractureN/AN/AN/A
RA25RB5-0.65-20.65N/AN/AYielding and bond failure22.7
RA25RB5-0.75-10.75Bond failure42,150N/AN/A
RA25RB5-0.75-20.75Bond failure1000N/AN/A
RA25RB5-0.75-30.75Bond failure4119N/AN/A
RA25RB5-0.75-40.75Rebar fractureN/AN/AN/A
RA25RB5-0.85-10.85Bond failure9704N/AN/A
RA25RB5-0.85-20.85Bond failure64,648N/AN/A
RA25RB5-0.85-30.85Bond failure25N/AN/A
RA50
RB0		RA50RB0-0.75-10.75N/AN/ARebar fractureN/A
RA50RB0-0.75-20.75N/AN/AYielding and bond failure22.4
RA50RB0-0.75-30.75N/AN/ARebar fractureN/A
Table 4. Validation for the bond strength prediction.
Table 4. Validation for the bond strength prediction.
Specimenfc’
(MPa)		τmax,t
(MPa)		Proposed Modelfib Model Code [29] Seara-Paz et al. [60]
τmax,p
(MPa)		 τ m a x , p τ m a x , t τmax,p
(MPa)		 τ m a x , p τ m a x , t τmax,p
(MPa)		 τ m a x , p τ m a x , t
This study
RA0RB0-136.315.018.11.2115.11.0015.11.00
RA0RB0-236.320.418.10.8915.10.7415.10.74
RA0RB0-336.315.018.11.2115.11.0115.11.01
RA0RB0-436.314.518.11.2515.11.0415.11.04
RA0RB0-536.319.918.10.9115.10.7615.10.76
RA25RB0-131.117.318.81.0913.90.8113.50.78
RA25RB0-231.120.118.80.9413.90.7013.50.67
RA25RB0-331.120.018.80.9413.90.7013.50.68
RA25RB0-431.117.118.81.1013.90.8213.50.79
RA25RB0-531.118.518.81.0213.90.7513.50.73
RA25RB5-128.521.118.00.8513.30.6312.90.61
RA25RB5-228.519.018.00.9513.30.7012.90.68
RA25RB5-328.519.118.00.9513.30.7012.90.68
RA25RB5-428.520.518.00.8813.30.6512.90.63
RA25RB5-528.518.718.00.9613.30.7112.90.69
RA50RB0-13521.722.21.0214.80.6813.90.64
RA50RB0-23524.322.20.9114.80.6113.90.57
RA50RB0-33525.822.20.8614.80.5713.90.54
RA100RB0-140.528.528.61.0015.90.5613.90.49
RA100RB0-240.528.128.61.0215.90.5713.90.50
RA100RB0-340.527.828.61.0315.90.5713.90.50
Mean 1.00 0.73 0.70
COV 0.11 0.19 0.22
Kim et al. [59]
PLA029.2621.716.20.7513.50.6213.50.62
PLA3026.5217.717.81.0112.90.7312.40.70
PLA6028.5319.220.81.0913.40.7012.40.64
PLA10027.0818.723.41.2513.00.6911.40.61
PMA033.4225.317.30.6814.50.5714.50.57
PMA3031.4621.919.40.8814.00.6413.50.62
PMA6030.6621.621.61.0013.80.6412.80.59
PMA10029.4920.924.41.1713.60.6511.90.57
PHA044.1329.419.90.6816.60.5616.60.56
PHA3039.529.921.70.7215.70.5315.10.51
PHA6043.828.825.80.9016.50.5815.30.53
PHA10042.4428.829.31.0216.30.5614.30.49
Mean 0.93 0.62 0.59
COV 0.20 0.10 0.10
Note: fc’ = compressive concrete strength; τmax,t = experimental bond strength; τmax,p = predicted bond strength.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Wei, W.; Cai, S.; Li, Y. Fatigue Bond Behavior of Steel Rebars in Recycled Aggregate Concrete Containing Recycled Rubber. Buildings 2025, 15, 2102. https://doi.org/10.3390/buildings15122102

AMA Style

Wei W, Cai S, Li Y. Fatigue Bond Behavior of Steel Rebars in Recycled Aggregate Concrete Containing Recycled Rubber. Buildings. 2025; 15(12):2102. https://doi.org/10.3390/buildings15122102

Chicago/Turabian Style

Wei, Wei, Shanming Cai, and Yufu Li. 2025. "Fatigue Bond Behavior of Steel Rebars in Recycled Aggregate Concrete Containing Recycled Rubber" Buildings 15, no. 12: 2102. https://doi.org/10.3390/buildings15122102

APA Style

Wei, W., Cai, S., & Li, Y. (2025). Fatigue Bond Behavior of Steel Rebars in Recycled Aggregate Concrete Containing Recycled Rubber. Buildings, 15(12), 2102. https://doi.org/10.3390/buildings15122102

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop