Abstract
Machine learning (ML) models in material science and construction engineering have significantly improved predictive accuracy and decision making. However, the practical implementation of these models often requires technical expertise, limiting their accessibility for engineers and practitioners. A user-friendly graphical user interface (GUI) can be an essential tool to bridge this gap. In this study, a sustainable approach to improve the compressive strength (C.S) of plastic-based mortar mixes (PMMs) by replacing cement with industrial waste materials was investigated using ML models such as support vector machine, AdaBoost regressor, and extreme gradient boosting. The significance of key mix parameters was further analyzed using SHapley Additive exPlanations (SHAPs) to interpret the influence of input variables on model predictions. To enhance the usability and real-world application of these ML models, a GUI was developed to provide an accessible platform for predicting the C.S of PMMs based on input material proportions. The ML models demonstrated strong correlations with experimental results, and the insights from SHAP analysis further support data-driven mix design strategies. The developed GUI serves as a practical and scalable decision support system, encouraging the adoption of ML-based approaches in sustainable construction engineering.
1. Introduction
Solid waste is produced at an enormous rate on a global scale. Infectious, combustible, acidic, and chemically reactive substances are abundant in this garbage. Landfilling these objects on a regular basis is harmful to ecosystems and people’s health [1,2]. The remains of plastic, which do not biodegrade, constitute a substantial portion of solid waste and pose a serious danger to the environment. The majority of the ever-increasing amount of plastic waste comes from disposable containers and leftover building materials. Burial, burning, and recycling are the current options for dealing with this trash, but none of these are particularly sustainable. Recycling is still the most popular way [3]. Health risks are a direct result of contamination and pollution, both of which are worsened by improper waste management at landfills [4]. Researchers have studied the use of recycled plastic waste in construction materials. Figure 1 shows the results of an investigation into the potential for using plastic waste as aggregates in environmentally friendly building materials. The researchers looked at plastic’s chemical inertness, lightweight nature, and flexibility [5,6,7,8,9]. Their limited applicability is a result of the fact that plastic-based mortar and concrete exhibit differing strength qualities under different conditions. This insists on extensive exploration to fully recognize and optimize their performance across diverse purposes.
Figure 1.
The benefits of reusing plastic in concrete [10].
Supplementary cementitious materials (SCMs) have been considerably explored in recent decades as substitutes for conventional binders. These include silica fume (Si-F), glass powder (Gl-P), marble powder (Ma-P), rice husk ash, bagasse ash, slags, and various other materials [11,12,13,14,15]. Cement can undergo both hydraulic and pozzolanic hydration in a pore solution when SCMs are present [16,17]. An effective method to promote environmentally friendly construction is to incorporate industrial wastes as SCMs in building materials [18,19,20,21]. This strategy has the potential to reduce the reliance on cement, mitigate carbon monoxide emissions, and enhance the economic efficiency of waste management [22]. Furthermore, studies have shown that using SCMs derived from industrial waste can enhance the strength of cementitious composites [23,24,25].
Common industrial byproducts like Gl-P, Si-F, and Ma-P can be transformed into SCMs. As a filler material, Si-F improves matrix compaction by penetrating the spaces between cement grains, made possible by its small particle size [26,27]. Being highly reactive with Ca(OH)2, which is produced during cement hydration, Si-F has the potential to partially replace cement [28,29]. By interacting with and consuming the Ca(OH)2 formed during cement hydration, Si-F oxides integrated into cementitious composites may reduce bleeding, porosity, and permeability [30]. The yearly disposal of glass bottles is the main cause of the excess of glass garbage that ends up in landfills [31]. By chemical composition, glass exhibits greater durability associated with other kinds of debris, like wood and plastic. Glass remains structurally intact even after prolonged burial [32]. The recycling of discarded glass into construction materials is feasible. Utilizing crushed glass waste, cementitious composites can partially replace sand and cement [33,34]. Research suggests that the strength of cementitious composites can be considerably improved by using powdered glass [24]. The same is true for recycling Ma-P; research has shown that it may strengthen materials and produce more environmentally friendly alternatives to cement and fine aggregate [35]. No prior research has examined the impact of Si-F, Ma-P, and Gl-P on plastic mortar, a type of cement mortar that incorporates waste plastic as a partial sand substitute.
The importance of compressive strength (C.S) has motivated an elaborate study on cement-based materials (CBMs) [36,37,38]. The key information about the characteristics of the CBMs can be found in its C.S. C.S of mortar and concrete mostly dictates its mechanical and durability properties [39,40]. The development of statistical models for strength of materials is motivated by the analyst’s urge to reduce the necessity and expenses associated with unnecessary testing. The material’s attributes obtained from the regression study are replicated using several conventional models, including the optimal curve. Traditional regression methods may incorrectly infer the material’s intrinsic behavior from CBMs due to its nonlinear character [41,42,43]. The application of supervised machine learning (ML), a methodology of artificial intelligence, is facilitating the development of increasingly complex models in the specified field [44,45,46,47]. These algorithms are subjected to extensive testing to ensure they accurately predict outcomes by utilizing input properties. Predicting CBM traits using machine learning methods is becoming more common [48].
Improvements in computational technology have made it possible to simulate the technical qualities of many materials with greater accuracy. To achieve accurate predictions, you need machine learning models that are powered by data. The complicated morphology and inherent unpredictability of construction materials make it challenging to provide accurate quality assessments. Estimating the technical qualities of building materials is one prominent application of machine learning techniques. Machine learning algorithms have been applied to analyze various traditional and modern types of mortar and concrete, including fiber-reinforced concrete, lightweight concrete, concrete with phase change materials, recycled aggregate concrete, self-compacting concrete, and many others [49,50,51,52,53,54]. Resilient machine learning models outperform traditional physical and empirical methods in forecasting certain engineering properties of concrete, according to multiple academic studies. Computing difficulties must be overcome in order to accurately forecast concrete qualities. This study focuses on the intricate mechanisms that are responsible for the hydration of cement and the production of morphology, as well as the nonlinear temporal and dependent on temperature characteristics of cement paste [55,56,57]. Utilizing input data on the ratios of mixtures and the conditions during which curing occurs, machine learning models may be taught to precisely forecast desired characteristics. The utilization of machine learning models offers several benefits, such as their capacity to provide precise and flexible predictions, their minimal computational demands, and their replicability.
A dependable computational framework for C.S prediction of plastic-based mortar mixes (PMMs) may be developed with the assistance of appropriately trained ML algorithms, according to research. Examining the C.S of PMMs is the goal of this work, which employs multiple strong ML models. A dataset with 408 points has been assembled from a publicly available scholarly journal. Using support vector machines (SVMs), AdaBoost regressors (ABRs), and extreme gradient boosting (XGB), regression models were built to forecast the C.S of PMMs. The models were validated using mathematical testing using K-fold and statistical checks. SHapley Additive exPlanations (SHAPs) analysis was used to analyze the variables’ impact on the prediction. The goal of developing this graphical user interface (GUI) was to improve the efficiency and precision of PMM analysis by automating the compressive strength calculations through the integration of input factors. The construction sector may experience the impact of newly developed methods and methodologies for the regulated study of material properties with minimal human involvement.
2. Methodology
2.1. Data Collection
Building strong, generalizable machine learning models requires a collection of trustworthy databases. A recently published article [58] obtained detailed data records for C.S, which contain 408 points, which is provided in Table A1. Data collection was not haphazard; rather, it was predicated on including relevant attributes and relying on reliable data sources. Ordinary Portland cement (OPC), marble powder (Ma-P), sand (Sd), plastic (PW), silica fume (Si-F), and glass powder (Gl-P) were the six input variables used in the databases to create plastic-based mortar mixes (PMMs), with C.S serving as the output variable. A minimum of 5 records per input variable has been suggested as the optimal ratio for producing reliable predictions in the literature [59]. Using a dataset with 406 points for C.S and six different input variables (equal to 408/6 = 68) significantly improves the observed ratio in this investigation. Hence, the recorded databases are trustworthy and suitable for model building.
At random, two subsets were created from the whole case database (i.e., C.S). For training purposes, 70 percent of the total data records (258 samples for C.S) were utilized. The remaining records, which make up 30% of the dataset overall (122 samples for C.S), were utilized for validation and testing. In addition, the findings of the statistical analysis performed on the database are presented in Table 1. The specific density (Sd) varies between 320 and 920 kg/m3, while the OPC varies between 577.50 and 825 kg/m3. For all C.S cases, the Si-F, Ma-P, and Gl-P concentration ranges from zero to 26 kg/m3. The largest plastic content that was employed was 310 kg/m3, in a similar vein. Further statistical measurements encompass information regarding the average, dispersion, kurtosis, and skewness of every input and output.

Table 1.
C.S database statistical summary.
Furthermore, to assess the possible impact of input components on output, the Pearson correlation (R) matrix was utilized. A visual representation of this is presented in Figure 2 for C.S. Relationships with R-values that are closer to 0 are considered to be weak, but R-values that fall between −1 and +1 are considered to be strongly negative or positively associated. The results revealed a maximum R-value of 0.15, suggesting a weak linear association between individual inputs and C.S. However, this weak correlation does not necessarily indicate a lack of influence. Pearson’s method is limited to capturing only linear dependencies and fails to detect nonlinear or interactive effects among variables [60]. For instance, some inputs may have a low individual R-value but can still significantly impact the output in combination with other variables or through nonlinear relationships. This apparent conflict is better understood when model-based interpretability tools such as SHAP are applied. SHAP values reveal how each input contributes to the model’s prediction, accounting for complex interactions and nonlinear behavior. In this study, inputs like OPC and Si-F showed a meaningful positive contribution to C.S in SHAP analysis despite their low Pearson R-values. This reinforces the importance of supplementing traditional statistical correlation with advanced ML interpretability techniques to achieve a more comprehensive understanding of input-output relationships.
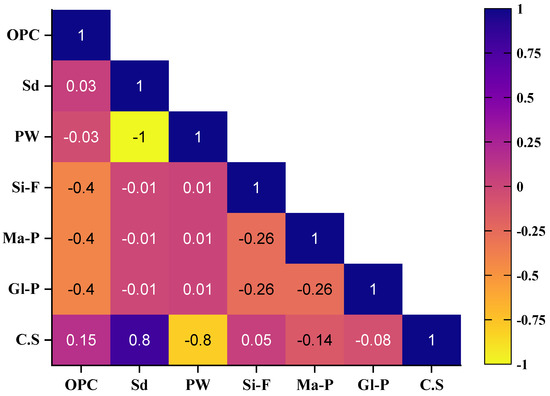
Figure 2.
Correlation matrices for the C.S database.
There is a significant relationship between the efficiency of the model and the distribution of the variables that are used as inputs. To better understand the proportionate distribution of inputs in comprehensive databases for C.S, Figure 3 shows 3D histogram prism charts. The data points clearly show a random distribution among the polyhedral shapes. In addition, 3D prism charts can draw attention to noteworthy data clusters, patterns, or outliers, revealing trends or potential problem areas. A notable characteristic of the dataset is the absence of clusters or outliers, which suggests that the data points conform to a rather normal distribution. Within the domain of machine learning models, this attribute holds significant importance.

Figure 3.
Three-dimensional histograms of the C.S database input variable frequencies.
2.2. Machine Learning Modeling
The primary result of the six experimental variables was the compressive strength (C.S) of PMMs. To predict the C.S of PMMs, state-of-the-art ML techniques such as SVM, ABR, and XGB were employed. It was much simpler to assess outcomes after analyzing input data with machine learning approaches. For training, the machine learning algorithms were given 70% of the dataset, while 30% was kept for testing. The models were evaluated using an R2 score of the expected results; a small R2 number indicates a considerable difference [61], while a large value indicates that the anticipated and observed results are highly consistent with one another. Multiple methods, including statistical tests and error evaluations, were employed to validate the model’s accuracy. An event model diagram that has been simplified is shown in Figure 4.

Figure 4.
Synopsis of the research procedure.
2.2.1. SVM Algorithm
Two applications of supervised machine learning are classification and regression. Support vector machines (SVMs) are a type of machine learning that falls under this category. The support vector machine (SVM) categorization utilizes data points as fixed points inside an ordered space to maximize the differentiation between distinct groups. Building a hyperplane that separates the categories is the primary goal in order to maximize the space between them. By separating the data points into their own categories, accurate classification is made possible. SVMs provide great predictive accuracy across multiple domains and are especially successful in managing complicated datasets. Kernel functions exhibit the capability to accommodate nonlinear interactions. In Figure 5, the supplemental instances are methodically arranged according to their orientation with respect to the provided vector. The approach employed to build the model using the support vector machine (SVM) is illustrated in Figure 6. To ensure an accurate evaluation of the material’s strength, the model considers several parameters. We employed a specific optimization method to adjust the parameters of the support vector machine model.
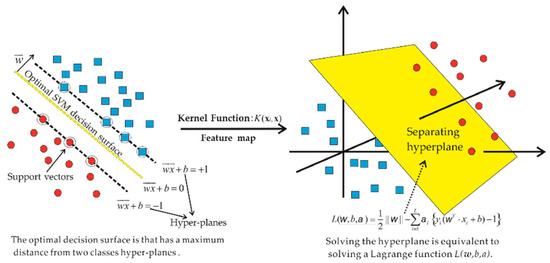
Figure 5.
SVM model calibration [62].

Figure 6.
Support vector machine process flowchart [63].
2.2.2. AdaBoost Regressor-ABR
Machine learning experts use the ensemble technique to train several models with a single learning algorithm [64]. In order to complete a single classification, an ensemble of algorithms works together. A large group of students, sometimes hundreds or even thousands strong, work together toward a shared goal in order to find a solution. As a controlled machine learning approach, ensemble learning is utilized in the ABR procedure. Also, it is called adaptive boosting because, after processing each instance, the weights are rearranged to provide more weight to the cases with incorrect labels. Supervised machine learning makes heavy use of boosting techniques to smooth the data and eliminate noise. In order to fortify the weak student, the aforementioned methods are employed. The training process involves using new input data with an endless number of decision trees (DTs). During development, a major objective is to clean up the incorrectly categorized data from the initial model. These numbers are the only input to another mathematical model. Following the generation of the required number of primary learners, the aforementioned approach will be reiterated. The ABR significantly enhances the performance of decision trees on binary classification problems. Furthermore, its secondary objective is to enhance the efficiency of other machine learning techniques. Employing this strategy will help your apprehensive learner to regain composure. Ensemble methods have extensive application in civil engineering for the prediction of the mechanical properties of concrete. The complete procedure for predicting the required ABR algorithmic outcome is illustrated in Figure 7.

Figure 7.
AdaBoost algorithm chart showing whole prediction process [65].
2.2.3. Extreme Gradient Boosting-XGB
The tree-based ensemble information theory of the XGB technique, devised by Chen and Guestrin, makes it a reliable tool for data science researchers [66]. The gradient boosting regressor architecture, upon which XGB is constructed, utilizes a range of functions to estimate targets as specified by Equation (1) [67].
The variable denotes the level of expertise required to enhance accuracy and forestall over-fitting by establishing connections between additional trees. The variable represents the expected outcome when employing the ith datapoint and as the check trajectory. The variable represents the sum of estimators for discrete tree topologies, whereas assumes a range of k from 1 to n. One primary challenge in machine learning is in developing models that exhibit little excessive fitting of the data. The following trees are specifically constructed to correct the residuals that result from the null hypothesis, which serves as the initial assumption. A fundamental difficulty in machine learning is in constructing models that demonstrate little overfitting of the data. The trees illustrated here are specifically intended to correct the residuals that result from the idea of a null, which serves as the initial reference. This iterative correction scheme enhances the accuracy of the model’s predictions. XGB employs regularization techniques such as tree cutting and weight management to mitigate overfitting. Furthermore, to enhance the generality of the model, it incorporates a shrinkage parameter that mitigates the influence of individual trees. Equation (2) establishes a connection between the kth forecaster and the procedure at the kth level. The estimated kth is calculated by comparing the conforming created with the kth identical forecaster. Denoted as , the expected value at the kth level is obtained by combining the learning rate and the prediction of the kth weak learner in the kth level approach. An equation demonstrating the repetitive nature of the boosting process reveals that the residuals of the gathered ensemble are adjusted up to the k−1-th level by training the subsequent weak learner.
The process of lowering the kth objective function of the decision tree, as expressed in Equation (3), fallouts in a leaf with a weight of .
In order to improve the model and cut down on excessive fitting, the following regulatory restrictions have been put into place: signifies the subset of leaf masses, denotes the level of complexity, denotes a coefficient that persists over time, and denotes the mass of a leaf. The parameters and provide a concise summary of the initial gradient leaf loss function as well as its predecessor by making use of the entire dataset. The formation of the kth tree requires the partitioning of a solitary leaf into many smaller leaves. Using a sophisticated collection of variables, this framework is constructed and is shown in Equation (4).
represents the gain variables, and denote the right leaf, & denote the left leaf, and so on. Commonly, the gain parameter is ignored in favor of the division criterion. The gain governs an indirect regulatory control variable denoted as . To halt the leaf convolution process, one might reduce the gain parameter by increasing the regularization value. However, adding the training data would have a detrimental effect on the model’s performance. The hierarchical structure of the XGB tree algorithm is depicted in Figure 8.

Figure 8.
Simple flowchart of XGB procedure [68].
2.3. Validation of Models
Quantitative analysis and K-fold testing were performed to verify the accuracy of the machine learning algorithms used. These approaches are commonly used by researchers to verify the precision of machine learning models [69,70]. Another often used technique for assessing the effectiveness of an investigation is K-fold investigation, that entails dividing a random dataset into 10 distinct sections [71]. Figure 9 illustrates the utilization of nine classes for the purpose of training machine learning models, with just one class designated exclusively for the validation of those models. By reducing errors and increasing the R2 value, the machine learning approach becomes more accurate. Furthermore, it is important to carry out this task 10 times before any advantages become apparent. This effort is greatly responsible for the incredible precision of the model. For statistical purposes, the accuracy of each machine learning approach was measured using a formal error evaluation. Mean absolute percentage error, root mean squared error, and mean absolute error were some of the metrics utilized in this assessment. In order to statistically evaluate the machine learning systems’ prediction abilities, regression Equations (5)–(9) were utilized.
In earlier discussions, a variety of equations were brought forward. The observed value , predicted value , mean of the observed values, mean of the predicted values , and the total number of data points are all variables in these equations. One important measure for evaluating a model’s predictive power is the correlation coefficient, abbreviated as r. When the R-value is high, it means that the anticipated and observed values are highly related [72]. The numerical value of component R remains unchanged regardless of division or multiplication. However, because it is generated by comparing the real data with the projected results, R2 offers a more accurate assessment of the actual value. Greater R2 values, approaching 1, suggest a more efficient and successful process of constructing the model [73,74]. The proposed model demonstrates superior performance with a reduced number of errors, similar to the significant enhancements shown in MAE and RMSE performance as errors increase. Nevertheless, both approaches ultimately converge to zero as the number of errors rises [75,76]. Nevertheless, MAE excels in continuous and smooth databases, as demonstrated by further investigation [77]. This model tends to perform more effectively when the magnitudes of the previously computed mistakes are smaller.
Statistical validation is a robust method for evaluating the predictive capability of a model, and another approach is to utilize a Taylor diagram. This image is useful for evaluating the accuracy and reliability of the models generated from the data by comparing their departures from the truth or point of reference [78,79]. In this graph, the x-axis and y-axis represent the standard deviation, the radial lines represent the correlation coefficient, and the circular lines located at the real value point represent the root mean squared error (RSME). These three criteria can be used to assess the optimal placement of a hypothetical model. The model that has the highest performance in terms of prediction accuracy is considered the most reliable [78].


Figure 9.
Schematic of the K-fold computational method [80].
3. Analysis and Interpretation of Model Results
3.1. C.S-SVM Model
Using six distinct factors as inputs, an SVM model was built to forecast PMM’s C.S Figure 10 displays the outcomes. With very little variation between test and estimated values, the SVM model demonstrates outstanding accuracy, as shown in Figure 10a, which compares estimated and test results. The R2 value of 0.871 indicates a high level of alignment between the test and projected results, suggesting that the SVM approach is highly effective in determining the C.S of PMMs. The typical distribution of experimental, expected, and divergent values (errors) obtained by the SVM technique is depicted in Figure 10b. On average, the inaccuracy was 1.02 MPa, although it ranged from 0.01 MPa to 2.46 MPa. There were 68 instances with error values less than 1.0 MPa, 40 cases with values between 1.0 and 2.0 MPa, and 15 cases with values greater than 2.0 MPa, as shown in Figure 11. There was a consistent normal distribution pattern across all of these instances. It appears that the SVM method successfully predicted the C.S of PMMs based on the distribution of divergent data (errors).

Figure 10.
(a) C.S-SVM forecasted vs. test strength correlation and (b) scatter of model predictions, true values, and error margins.
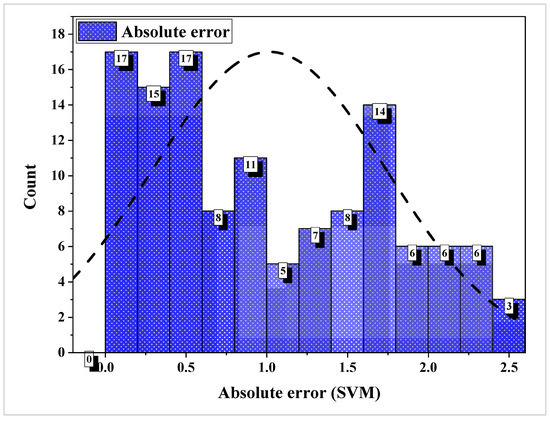
Figure 11.
Frequency plot of C.S SVM model errors.
3.2. C.S-ABR Model
The findings of the ABR technique’s prediction of the PMM’s C.S are shown in Figure 12. The correlation between the real and expected C.S is shown in Figure 12a. Because it produced more consistent outcomes between predictions and observations, the ABR technique outperformed the SVM model in this investigation. An R2 of 0.910 indicates that the ABR model is the more accurate one. Testing, estimated, and deviating values acquired using the ABR method are shown in Figure 12b together with the distribution of their respective errors. According to the results, the error levels were as follows: 0.00 MPa at the bottom, 0.772 MPa in the middle, and 2.455 MPa at the top. Figure 13 shows that out of all the errors, 82 were below 1.0 MPa, 32 were between 1.0 and 2.0 MPa, and just 9 were above 2.0 MPa, according to the frequency distribution of errors across different sizes’ study. Due to its superior accuracy, the ABR model surpasses the SVM model in terms of error dispersion. Following twenty sub-model optimizations of the AdaBoost procedure, the ABR model outperforms the SVM model in determining the optimal output value.

Figure 12.
(a) C.S-ABR forecasted vs. test strength correlation and (b) scatter of model predictions, true values, and error margins.

Figure 13.
Frequency plot of C.S ABR model errors.
3.3. C.S-XGB Model
Figure 14 displays the outcomes of PMM’s C.S forecasts that were made using the XGB algorithm. The anticipated and measured C.S are correlated, as shown in Figure 14a. It became evident that the XGB method was superior by comparing anticipated and actual outcomes. The XGB model’s R2 score of 0.940 demonstrates its higher accuracy when compared to SVM and ABR-based C.S models. Figure 14b reveals the spreading of actual, estimated, and erroneous data according to the XGB method. There was a maximum variance of 2.486 MPa and a standard deviation of 0.593 MPa. In Figure 15, it can be seen that out of a total of 102 data points, 13 were within the range of 1.0 to 2.0 MPa, and 9 were greater than 2.0 MPa, according to the error distribution analysis. By analyzing error dispersion, the XGB technique was found to be more effective than the SVM and ABR models. Examining the XGB method in comparison to the SVM and ABR methodologies reveals its superiority in predicting the C.S of PMMs. However, the SVM and ABR models stand out for their exceptional accuracy. All of the models’ cross-validation methods and R2 values demonstrated that they could accurately predict the C.S of PMMs; therefore, it seems like any of them can be used for the job. Many consider XGB to be the best option due to its exceptional performance with high-dimensional data and nonlinear interactions. It also averages out several decision trees, which helps with overfitting. Regressor models using SVM and AdaBoost could not be as resistant to overfitting and could have trouble with complicated data relationships.

Figure 14.
(a) C.S-XGB forecasted vs. test strength correlation and (b) scatter of model predictions, true values, and error margins.
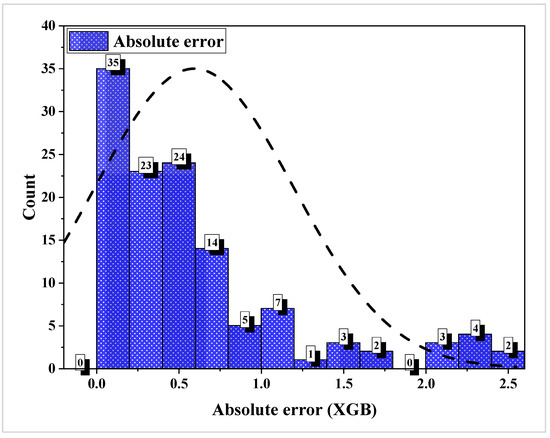
Figure 15.
Frequency plot of C.S XGB model errors.
3.4. Model’s Validation Using Statistical and K-Fold Analysis
The findings of the error and efficacy computations (MAPE, NSE, RMSE, R, and MAE) obtained using Equations (5)–(9) are presented in Table 2. Predicting C.S with SVM yielded an MAE of 1.017 MPa, ABR 0.773 MPa, and XGB 0.593 MPa. The results showed that MAPE for SVM was 2.80%, ABR was 2.10%, and XGB was 1.60%. Not only that, but we also found NSE values of 0.859 for SVM, 0.907 for ABR, and 0.936 for XGB. The XGB approach surpasses the SVM and ABR models by virtue of its significantly lower error and effectiveness rates. Table 3 presents the results of the R2, RMSE, and MAE tests conducted to validate the K-fold technique. The outcomes of K-fold tests conducted on several machine learning algorithms for C.S prediction are displayed in Figure 16. With an MAE value ranging from 1.22 to 2.08 MPa, the SVM technique generated a C.S estimate with an average of 1.57 MPa. With a range of 1.35 to 2.07 MPa, the MAE for the ABR is on average about 1.60 MPa. Averaging 41.54 MPa, the Mean Absolute Error (MAE) for XGB varied between 1.29 and 1.84 MPa. The mean root mean squared error (RMSE) when using support vector machine (SVM) was 1.92 MPa, when using the artificial neural network (ABR) was 1.87 MPa, and when using cross-validation (XGB) was 1.80 MPa. R2 values of 0.91 and 0.94, respectively, for ABR and XGB, were lower than SVM’s value of 0.88. An enhanced XGB model for PMM’s C.S prediction would be shown by a lower error rate and a higher R2. Coupling these mistakes with R2 values derived by the K-fold method provided further evidence of the XGB model’s enhanced accuracy. It should be mentioned that the SVM model does attain a fair level of accuracy. Therefore, SVM, ABR, and XGB models may be able to produce more precise C.S estimates for PMMs.

Table 2.
Analysis of errors using statistics.

Table 3.
K-fold model study utilizing MAE, RMSE, and R2.

Figure 16.
K-fold scrutiny results.
In addition to the error-based analysis mentioned above, a Taylor diagram provides an intriguing technique of comparing the corresponding model performance in predicting the provided output. A Taylor diagram is a helpful tool for comparing several ML models using standard deviation and R2. One technique to check if the algorithm is accurate is to calculate how far it is from the reference point. Near the actual data point is where a correct algorithm will lie, and the opposite is also true. As seen in the Taylor plot comparing the algorithms used in this study (Figure 17), XGB has the highest accuracy since its point is closest to the reference point. Since the ABR point is more closely aligned with the real data’s standard deviation line than the SVM point is, it can be inferred that the ABR values differ less from the actual values than the SVM values. According to the Taylor plot, the order of accuracy is as follows: XGB > ABR > SVM.

Figure 17.
Taylor plot-based comparison of developed models.
3.5. SHAP Analysis
The influence of various raw materials on the compressive strength (C.S) of PMMs was examined. By applying the SHAP network decoder to the entire dataset, a deeper understanding of the overall feature impacts and the specific contributions of individual inputs through local SHAP values was achieved. Figure 18 presents violin SHAP plots illustrating how each raw material affects the C.S of PMMs. In these plots, SHAP values along the x-axis represent each feature’s relative impact, while color gradients reflect the magnitude of the input variables. The SHAP analysis revealed that Sd, OPC, and Si-F had a positive correlation with the compressive strength of PMMs. A strong positive influence on strength is shown by a concentration of intense red spots on the positive axis, whereas a smaller number of low-intensity blue spots can be seen on the negative axis. Consequently, strength is likely to be enhanced by improving these characteristics. The relationship between Gl-P and Ma-P content and the C.S of PMMs exhibited a balanced trend, as demonstrated by the SHAP plot in Figure 18. The plot indicates that an initial increase in the content of these variables leads to a rise in strength, followed by a decline as their content continues to increase. The results regarding the effects of PW were inconclusive, primarily due to limited data variability. A larger dataset with greater diversity and the inclusion of additional input variables could provide more robust and definitive conclusions. Expanding the dataset would likely capture a broader range of impacts, strengthening the reliability of the findings.

Figure 18.
Visualization of influential factors using SHAP.
Figure 19 graphically illustrates the impact of raw materials on the strength of PMMs. The effect and interaction of Sd are depicted in Figure 19a. The C.S of PMMs improves consistently with higher Sd concentration, as seen in the graph. Figure 19b–d clearly demonstrate that the strength of PMMs grows dramatically when the content of OPC, Si-F, and Gl-P increases up to the values of 700, 100, and 80 kg/m3, respectively. Beyond these values, the strength of PMMs experiences a major decrease. Furthermore, the interaction between Ma-P content and the compressive strength (C.S) of PMMs, as shown in Figure 19e, remained consistent with initial increases in Ma-P content up to 120 kg/m3. Beyond this threshold, the compressive strength dropped significantly as the Ma-P content continued to increase. Figure 19f demonstrates that the variable PW has only a marginal impact on the C.S of PMMs. This is because the variations in these variables are quite small. The results of the SHAP statistical analysis are drastically affected by the study’s sample size and the raw materials used. Results may vary depending on how you tweak the input settings or adjust the sample size.


Figure 19.
Interaction of PMMs C.S input variables: (a) Sd; (b) OPC; (c) Si-F; (d) Gl-P; (e) Ma-P; (f) PW.
3.6. Graphical User Interface for PMMs Strength
The graphical user interface (GUI) is a user-friendly, interactive tool that allows users to easily input, analyze, and visualize data without requiring complex coding or technical expertise. It plays a significant role in enhancing efficiency, accuracy, and accessibility in engineering studies by providing a clear and organized platform for data handling and result interpretation. In this study, a specialized GUI was developed for the direct calculation of compressive strength (C.S) of plastic-based mortars (PMMs) by inputting values for key variables, including ordinary Portland cement (OPC), sand (Sd), plastic waste (PW), marble powder (Ma-P), silica fume (Si-F), and glass powder (Gl-P), all in kg/m3 units, as can be seen in Figure 20. The GUI was designed to streamline the calculation process: users can enter any combination of these input variables, and the system instantly computes the compressive strength, ensuring quick and accurate results. This intuitive interface eliminates manual calculations and allows researchers to explore various material combinations efficiently, enabling the optimization of PMMs for improved performance. Overall, the GUI serves as a key tool in such studies, facilitating advanced research by simplifying complex computations and promoting broader adoption of sustainable construction practices.

Figure 20.
GUI for compressive strength calculation of plastic-based mortars.
4. Discussions
Ordinary Portland cement (OPC), the primary binding agent in concrete, has a considerable environmental footprint, contributing significantly to biodiversity loss and the rise in anthropogenic carbon emissions [81,82]. Therefore, in order to reduce its carbon dioxide emissions, the OPC industry must find ecologically better alternatives to OPC. There is a great chance to improve the material’s qualities by using plastic and other waste materials as cement substitutes in mortar and concrete. By reusing materials in a constructive way, this method not only makes mortar and concrete work better, but it also helps keep the environment cleaner. This study strove to improve human understanding of PMMs applications by using ML and SHAP approaches. Its goal was to contribute to this improvement. For the purpose of estimating PMM’s C.S, this work employed SVM, ABR, and XGB ML methods. A comparative analysis of their accuracy levels allows us to choose the most effective predictor among the strategies. With an R2 value of 0.94, the XGB method proved to be more accurate than the SVM and ABR procedures. The R2 values of the SVM and BR techniques were significantly different, coming in at 0.87 and 0.91, respectively. The discrepancy between predicted and actual outcomes (errors) further demonstrates the superior accuracy of the XGB method. Error analysis showed that the XGB models exhibited a closer alignment between experimental and predicted results compared to the SVM and ABR models. Prior research has shown consistent results when comparing the XGB method’s accuracy against a variety of machine learning algorithms for determining a building material’s strength [69,83,84].
The precision of machine learning techniques was evaluated using both mathematical metrics and K-fold cross-validation. Models demonstrating lower RMSE, NSE, MAPE, R, and MAE values, alongside higher R2 scores, are considered more accurate. However, because these methods are sensitive to the data samples and input variables, identifying the optimal machine learning approach for domain-independent attribute prediction remains a complex challenge [69]. Ensemble ML approaches sometimes use a less effective learner to train and fine-tune sub-models on the dataset, resulting in better outcomes than individual ML models. These results indicate that, regarding accuracy, the XGB model outperforms both the SVM and BR models. In addition, the SHAP analysis was used to investigate how different raw materials affected the C.S of PMMs. The C.S of PMMs is positively correlated with the material’s input properties, which include Sd, OPC, and Si-F. The C.S of PMMs rises as the aforementioned variables’ contents do. Nevertheless, the SHAP investigation did show that, in relation to the input variables Gl-P and Ma-P, the C.S of PMMs is balanced. It follows that PMMs, when substituted for OPC-based materials, will, in theory, yield better construction materials with the same strength-wise performance. On top of that, it will aid in lowering the environmental problems connected to OPC production, such as waste in the environment and the control of the dwindling raw supplies utilized in OPC manufacture.
The present study utilized a dataset comprising 408 entries and six key input variables to predict C.S. Future work could enhance model accuracy and reliability by expanding the dataset with additional experimental data, which would strengthen the robustness and generalizability of predictions. While this study employed SVM, ABR, and XGB, future research could explore hybrid machine learning techniques such as Genetic Algorithm–Particle Swarm Optimization (GA-PSO) and Random Forest–artificial neural network (RF-ANN) to further improve predictive performance. Additionally, individual and ensemble methods, including Gene Expression Programming (GEP) and Model Expression Programming (MEP), show promising potential for refinement. Integrating these hybrid approaches may significantly enhance the predictive capabilities of ML models. Although post hoc interpretation tools like sensitivity analysis, LIME, and Partial Dependence Plots (PDP) were not applied in this study, they represent valuable strategies for increasing the interpretability of machine learning predictions and should be incorporated into future work. Furthermore, current ML-based research in concrete largely emphasizes mechanical properties, with limited attention given to other critical aspects such as microstructural characteristics, fatigue behavior, and long-term durability. To achieve a more holistic understanding of concrete performance, it is essential that future studies apply machine learning methods to investigate these underexplored domains.
5. Conclusions
This work aims to analyze and forecast the compressive strength (C.S) of plastic-based mortar mixes (PMMs) using machine learning approaches such as support vector machine (SVM), AdaBoost regressors (ABR), and extreme gradient boosting (XGB). The research used 408 sets of C.S data from PMM’s laboratory investigations to train, test, and validate the model. The key findings are as follows:
- The XGB method outperformed the ABR and SVM approaches in accurately estimating the C.S of PMMs (R2 = 0.940), while the other two methods achieved R2 values of 0.91 and 0.87, respectively.
- The average difference between the test and forecasted C.S (errors) for the SVM, ABR, and XGB techniques was 1.016 MPa, 0.772 MPa, and 0.592 MPa, respectively. Although the XGB method demonstrated superior accuracy in predicting PMM’s strength, the error levels validated the accuracy of the SVM and ABR models as presented.
- The effectiveness of the built models was confirmed by statistical and K-fold tests. Improved R2, fewer mistakes, and greater efficiency all point to ML models being accurate. For the C.S prediction, the SVM model had a root mean square error (MAPE) of 2.80%, the ABR model of 2.10%, and the XGB model of 1.60%. According to the MAPE values, the XGB model performed better in predicting the C.S of PMMs.
- The SHAP study found that the PMM’s strength was positively correlated with Sd, OPC, and Si-F, the three primary raw materials and factors. While PW had no effect throughout, Ma-P and Gl-P had a good effect on PMMs strength at the outset but a negative effect as their content increased.
- The created graphical user interface (GUI) is a crucial instrument for predicting the C.S of PMMs, providing a rapid, precise, and intuitive solution that enhances material optimization and encourages sustainable construction practices.
This study offers valuable insights into PMMs design through advanced prediction frameworks. These methods help scientists and engineers assess, optimize, and rationalize PMMs quantities in mixtures. Machine learning models enhance chemical mixture efficiency, promoting greener construction practices and reducing the environmental impact of traditional concrete production.
Author Contributions
Conceptualization, A.R. and A.H.A.; methodology, A.A.A.E.; software, A.A.A.E.; validation, A.R.; formal analysis, A.A.A.E. and A.H.A.; investigation, A.A.A.E. and A.H.A.; resources, M.A.; data curation, M.A. and A.H.A.; writing—original draft, A.R.; writing—review and editing, A.A.A.E., M.A. and A.H.A.; visualization, M.A.; supervision, A.R.; project administration, M.A.; funding acquisition, A.R. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-DDRSP2502).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author(s).
Conflicts of Interest
The authors declare no conflicts of interest.
Correction Statement
This article has been republished with a minor correction to the Funding statement. This change does not affect the scientific content of the article.
Abbreviations
| ABRs | AdaBoost regressors |
| C.S | Compressive strength |
| CBMs | Cement-based materials |
| Gl-P | Glass powder |
| GUI | Graphical user interface |
| Ma-P | Marble powder |
| ML | Machine learning |
| OPC | Ordinary Portland cement |
| PMMs | Plastic-based mortar mixes |
| PW | Plastic |
| R | Pearson correlation |
| R2 | Coefficient of determination |
| SCMs | Supplementary cementitious materials |
| Sd | Sand |
| SHAP | SHapley Additive exPlanations |
| Si-F | Silica fume |
| SVM | Support vector machines pot |
| XGB | Extreme gradient boosting |
Appendix A

Table A1.
Dataset used for modeling was sourced from [58]. (Zero (0) may refer unavailable value/data).
Table A1.
Dataset used for modeling was sourced from [58]. (Zero (0) may refer unavailable value/data).
| OPC (kg/m3) | Sd (kg/m3) | PW (kg/m3) | Si-F (kg/m3) | Ma-P (kg/m3) | Gl-P (kg/m3) | C.S (MPa) |
|---|---|---|---|---|---|---|
| 825 | 1240 | 0 | 0 | 0 | 0 | 49.29 |
| 825 | 1240 | 0 | 0 | 0 | 0 | 45.7 |
| 825 | 1240 | 0 | 0 | 0 | 0 | 47.2 |
| 825 | 1178 | 62 | 0 | 0 | 0 | 37.13 |
| 825 | 1178 | 62 | 0 | 0 | 0 | 38.2 |
| 825 | 1178 | 62 | 0 | 0 | 0 | 39.87 |
| 825 | 1116 | 124 | 0 | 0 | 0 | 35.38 |
| 825 | 1116 | 124 | 0 | 0 | 0 | 37.41 |
| 825 | 1116 | 124 | 0 | 0 | 0 | 38.01 |
| 825 | 1054 | 186 | 0 | 0 | 0 | 32.49 |
| 825 | 1054 | 186 | 0 | 0 | 0 | 38.37 |
| 825 | 1054 | 186 | 0 | 0 | 0 | 36.14 |
| 825 | 992 | 248 | 0 | 0 | 0 | 36.21 |
| 825 | 992 | 248 | 0 | 0 | 0 | 31.84 |
| 825 | 992 | 248 | 0 | 0 | 0 | 35.07 |
| 825 | 930 | 310 | 0 | 0 | 0 | 33.45 |
| 825 | 930 | 310 | 0 | 0 | 0 | 35.03 |
| 825 | 930 | 310 | 0 | 0 | 0 | 29.95 |
| 783.75 | 1178 | 62 | 41.25 | 0 | 0 | 44.32 |
| 783.75 | 1178 | 62 | 41.25 | 0 | 0 | 40.21 |
| 783.75 | 1178 | 62 | 41.25 | 0 | 0 | 42.02 |
| 742.5 | 1178 | 62 | 82.5 | 0 | 0 | 43.35 |
| 742.5 | 1178 | 62 | 82.5 | 0 | 0 | 46.53 |
| 742.5 | 1178 | 62 | 82.5 | 0 | 0 | 42.01 |
| 701.25 | 1178 | 62 | 123.75 | 0 | 0 | 42.91 |
| 701.25 | 1178 | 62 | 123.75 | 0 | 0 | 44.68 |
| 701.25 | 1178 | 62 | 123.75 | 0 | 0 | 47.52 |
| 660 | 1178 | 62 | 165 | 0 | 0 | 43.69 |
| 660 | 1178 | 62 | 165 | 0 | 0 | 46.39 |
| 660 | 1178 | 62 | 165 | 0 | 0 | 44.31 |
| 618.75 | 1178 | 62 | 206.25 | 0 | 0 | 46.05 |
| 618.75 | 1178 | 62 | 206.25 | 0 | 0 | 44.21 |
| 618.75 | 1178 | 62 | 206.25 | 0 | 0 | 41.64 |
| 783.75 | 1116 | 124 | 41.25 | 0 | 0 | 38.63 |
| 783.75 | 1116 | 124 | 41.25 | 0 | 0 | 35.48 |
| 783.75 | 1116 | 124 | 41.25 | 0 | 0 | 40.26 |
| 742.5 | 1116 | 124 | 82.5 | 0 | 0 | 42.17 |
| 742.5 | 1116 | 124 | 82.5 | 0 | 0 | 39.36 |
| 742.5 | 1116 | 124 | 82.5 | 0 | 0 | 36.75 |
| 701.25 | 1116 | 124 | 123.75 | 0 | 0 | 43.56 |
| 701.25 | 1116 | 124 | 123.75 | 0 | 0 | 38.83 |
| 701.25 | 1116 | 124 | 123.75 | 0 | 0 | 42.62 |
| 660 | 1116 | 124 | 165 | 0 | 0 | 38.54 |
| 660 | 1116 | 124 | 165 | 0 | 0 | 40.65 |
| 660 | 1116 | 124 | 165 | 0 | 0 | 41.79 |
| 618.75 | 1116 | 124 | 206.25 | 0 | 0 | 38.41 |
| 618.75 | 1116 | 124 | 206.25 | 0 | 0 | 39.79 |
| 618.75 | 1116 | 124 | 206.25 | 0 | 0 | 34.75 |
| 783.75 | 1054 | 186 | 41.25 | 0 | 0 | 38.46 |
| 783.75 | 1054 | 186 | 41.25 | 0 | 0 | 37.77 |
| 783.75 | 1054 | 186 | 41.25 | 0 | 0 | 34.76 |
| 742.5 | 1054 | 186 | 82.5 | 0 | 0 | 39.74 |
| 742.5 | 1054 | 186 | 82.5 | 0 | 0 | 37.18 |
| 742.5 | 1054 | 186 | 82.5 | 0 | 0 | 38.03 |
| 701.25 | 1054 | 186 | 123.75 | 0 | 0 | 39.77 |
| 701.25 | 1054 | 186 | 123.75 | 0 | 0 | 38.32 |
| 701.25 | 1054 | 186 | 123.75 | 0 | 0 | 42.2 |
| 660 | 1054 | 186 | 165 | 0 | 0 | 40.91 |
| 660 | 1054 | 186 | 165 | 0 | 0 | 36.23 |
| 660 | 1054 | 186 | 165 | 0 | 0 | 37.31 |
| 618.75 | 1054 | 186 | 206.25 | 0 | 0 | 36.42 |
| 618.75 | 1054 | 186 | 206.25 | 0 | 0 | 37.11 |
| 618.75 | 1054 | 186 | 206.25 | 0 | 0 | 35.13 |
| 783.75 | 992 | 248 | 41.25 | 0 | 0 | 36.45 |
| 783.75 | 992 | 248 | 41.25 | 0 | 0 | 36.68 |
| 783.75 | 992 | 248 | 41.25 | 0 | 0 | 34.14 |
| 742.5 | 992 | 248 | 82.5 | 0 | 0 | 38.96 |
| 742.5 | 992 | 248 | 82.5 | 0 | 0 | 37.42 |
| 742.5 | 992 | 248 | 82.5 | 0 | 0 | 35.15 |
| 701.25 | 992 | 248 | 123.75 | 0 | 0 | 38.5 |
| 701.25 | 992 | 248 | 123.75 | 0 | 0 | 37.61 |
| 701.25 | 992 | 248 | 123.75 | 0 | 0 | 40.94 |
| 660 | 992 | 248 | 165 | 0 | 0 | 32.87 |
| 660 | 992 | 248 | 165 | 0 | 0 | 36.29 |
| 660 | 992 | 248 | 165 | 0 | 0 | 37.48 |
| 618.75 | 992 | 248 | 206.25 | 0 | 0 | 34.23 |
| 618.75 | 992 | 248 | 206.25 | 0 | 0 | 35.85 |
| 618.75 | 992 | 248 | 206.25 | 0 | 0 | 33.12 |
| 783.75 | 930 | 310 | 41.25 | 0 | 0 | 33.62 |
| 783.75 | 930 | 310 | 41.25 | 0 | 0 | 35.53 |
| 783.75 | 930 | 310 | 41.25 | 0 | 0 | 33.2 |
| 742.5 | 930 | 310 | 82.5 | 0 | 0 | 33.81 |
| 742.5 | 930 | 310 | 82.5 | 0 | 0 | 35.39 |
| 742.5 | 930 | 310 | 82.5 | 0 | 0 | 38.2 |
| 701.25 | 930 | 310 | 123.75 | 0 | 0 | 39.31 |
| 701.25 | 930 | 310 | 123.75 | 0 | 0 | 36.78 |
| 701.25 | 930 | 310 | 123.75 | 0 | 0 | 35.88 |
| 660 | 930 | 310 | 165 | 0 | 0 | 32.47 |
| 660 | 930 | 310 | 165 | 0 | 0 | 34.49 |
| 660 | 930 | 310 | 165 | 0 | 0 | 31.98 |
| 618.75 | 930 | 310 | 206.25 | 0 | 0 | 33.12 |
| 618.75 | 930 | 310 | 206.25 | 0 | 0 | 31.25 |
| 618.75 | 930 | 310 | 206.25 | 0 | 0 | 29.65 |
| 783.75 | 1178 | 62 | 0 | 41.25 | 0 | 41.21 |
| 783.75 | 1178 | 62 | 0 | 41.25 | 0 | 40.09 |
| 783.75 | 1178 | 62 | 0 | 41.25 | 0 | 38.25 |
| 742.5 | 1178 | 62 | 0 | 82.5 | 0 | 39.58 |
| 742.5 | 1178 | 62 | 0 | 82.5 | 0 | 41.73 |
| 742.5 | 1178 | 62 | 0 | 82.5 | 0 | 42 |
| 701.25 | 1178 | 62 | 0 | 123.75 | 0 | 43.23 |
| 701.25 | 1178 | 62 | 0 | 123.75 | 0 | 44.1 |
| 701.25 | 1178 | 62 | 0 | 123.75 | 0 | 39.12 |
| 660 | 1178 | 62 | 0 | 165 | 0 | 42.62 |
| 660 | 1178 | 62 | 0 | 165 | 0 | 39.17 |
| 660 | 1178 | 62 | 0 | 165 | 0 | 38.43 |
| 618.75 | 1178 | 62 | 0 | 206.25 | 0 | 37.57 |
| 618.75 | 1178 | 62 | 0 | 206.25 | 0 | 39.17 |
| 618.75 | 1178 | 62 | 0 | 206.25 | 0 | 40.11 |
| 783.75 | 1116 | 124 | 0 | 41.25 | 0 | 38.28 |
| 783.75 | 1116 | 124 | 0 | 41.25 | 0 | 39.69 |
| 783.75 | 1116 | 124 | 0 | 41.25 | 0 | 35.82 |
| 742.5 | 1116 | 124 | 0 | 82.5 | 0 | 38.89 |
| 742.5 | 1116 | 124 | 0 | 82.5 | 0 | 37.38 |
| 742.5 | 1116 | 124 | 0 | 82.5 | 0 | 40.85 |
| 701.25 | 1116 | 124 | 0 | 123.75 | 0 | 41.15 |
| 701.25 | 1116 | 124 | 0 | 123.75 | 0 | 40.86 |
| 701.25 | 1116 | 124 | 0 | 123.75 | 0 | 38.77 |
| 660 | 1116 | 124 | 0 | 165 | 0 | 37.58 |
| 660 | 1116 | 124 | 0 | 165 | 0 | 39.54 |
| 660 | 1116 | 124 | 0 | 165 | 0 | 38.51 |
| 618.75 | 1116 | 124 | 0 | 206.25 | 0 | 37.72 |
| 618.75 | 1116 | 124 | 0 | 206.25 | 0 | 38.2 |
| 618.75 | 1116 | 124 | 0 | 206.25 | 0 | 35.16 |
| 783.75 | 1054 | 186 | 0 | 41.25 | 0 | 37.52 |
| 783.75 | 1054 | 186 | 0 | 41.25 | 0 | 36.24 |
| 783.75 | 1054 | 186 | 0 | 41.25 | 0 | 34.25 |
| 742.5 | 1054 | 186 | 0 | 82.5 | 0 | 36.75 |
| 742.5 | 1054 | 186 | 0 | 82.5 | 0 | 35.78 |
| 742.5 | 1054 | 186 | 0 | 82.5 | 0 | 38.23 |
| 701.25 | 1054 | 186 | 0 | 123.75 | 0 | 38.79 |
| 701.25 | 1054 | 186 | 0 | 123.75 | 0 | 39.33 |
| 701.25 | 1054 | 186 | 0 | 123.75 | 0 | 36.19 |
| 660 | 1054 | 186 | 0 | 165 | 0 | 35.65 |
| 660 | 1054 | 186 | 0 | 165 | 0 | 34.9 |
| 660 | 1054 | 186 | 0 | 165 | 0 | 37.3 |
| 618.75 | 1054 | 186 | 0 | 206.25 | 0 | 33.79 |
| 618.75 | 1054 | 186 | 0 | 206.25 | 0 | 34.46 |
| 618.75 | 1054 | 186 | 0 | 206.25 | 0 | 37.35 |
| 783.75 | 992 | 248 | 0 | 41.25 | 0 | 37.02 |
| 783.75 | 992 | 248 | 0 | 41.25 | 0 | 34.72 |
| 783.75 | 992 | 248 | 0 | 41.25 | 0 | 34.25 |
| 742.5 | 992 | 248 | 0 | 82.5 | 0 | 34.29 |
| 742.5 | 992 | 248 | 0 | 82.5 | 0 | 36.26 |
| 742.5 | 992 | 248 | 0 | 82.5 | 0 | 37.8 |
| 701.25 | 992 | 248 | 0 | 123.75 | 0 | 37.61 |
| 701.25 | 992 | 248 | 0 | 123.75 | 0 | 38.34 |
| 701.25 | 992 | 248 | 0 | 123.75 | 0 | 35.12 |
| 660 | 992 | 248 | 0 | 165 | 0 | 37.92 |
| 660 | 992 | 248 | 0 | 165 | 0 | 34.86 |
| 660 | 992 | 248 | 0 | 165 | 0 | 33.14 |
| 618.75 | 992 | 248 | 0 | 206.25 | 0 | 34.83 |
| 618.75 | 992 | 248 | 0 | 206.25 | 0 | 35.4 |
| 618.75 | 992 | 248 | 0 | 206.25 | 0 | 32.49 |
| 783.75 | 930 | 310 | 0 | 41.25 | 0 | 35.62 |
| 783.75 | 930 | 310 | 0 | 41.25 | 0 | 33.32 |
| 783.75 | 930 | 310 | 0 | 41.25 | 0 | 31.4 |
| 742.5 | 930 | 310 | 0 | 82.5 | 0 | 35.07 |
| 742.5 | 930 | 310 | 0 | 82.5 | 0 | 32 |
| 742.5 | 930 | 310 | 0 | 82.5 | 0 | 36.14 |
| 701.25 | 930 | 310 | 0 | 123.75 | 0 | 37.67 |
| 701.25 | 930 | 310 | 0 | 123.75 | 0 | 34.47 |
| 701.25 | 930 | 310 | 0 | 123.75 | 0 | 33.78 |
| 660 | 930 | 310 | 0 | 165 | 0 | 28.56 |
| 660 | 930 | 310 | 0 | 165 | 0 | 32.69 |
| 660 | 930 | 310 | 0 | 165 | 0 | 32.08 |
| 618.75 | 930 | 310 | 0 | 206.25 | 0 | 31.66 |
| 618.75 | 930 | 310 | 0 | 206.25 | 0 | 29.42 |
| 618.75 | 930 | 310 | 0 | 206.25 | 0 | 34.91 |
| 783.75 | 1178 | 62 | 0 | 0 | 41.25 | 39.6 |
| 783.75 | 1178 | 62 | 0 | 0 | 41.25 | 42.23 |
| 783.75 | 1178 | 62 | 0 | 0 | 41.25 | 40.68 |
| 742.5 | 1178 | 62 | 0 | 0 | 82.5 | 42.89 |
| 742.5 | 1178 | 62 | 0 | 0 | 82.5 | 44.05 |
| 742.5 | 1178 | 62 | 0 | 0 | 82.5 | 41.2 |
| 701.25 | 1178 | 62 | 0 | 0 | 123.75 | 43.54 |
| 701.25 | 1178 | 62 | 0 | 0 | 123.75 | 41.42 |
| 701.25 | 1178 | 62 | 0 | 0 | 123.75 | 39.61 |
| 660 | 1178 | 62 | 0 | 0 | 165 | 38.91 |
| 660 | 1178 | 62 | 0 | 0 | 165 | 39.87 |
| 660 | 1178 | 62 | 0 | 0 | 165 | 41.73 |
| 618.75 | 1178 | 62 | 0 | 0 | 206.25 | 37 |
| 618.75 | 1178 | 62 | 0 | 0 | 206.25 | 41.78 |
| 618.75 | 1178 | 62 | 0 | 0 | 206.25 | 37.54 |
| 783.75 | 1116 | 124 | 0 | 0 | 41.25 | 40.15 |
| 783.75 | 1116 | 124 | 0 | 0 | 41.25 | 38.48 |
| 783.75 | 1116 | 124 | 0 | 0 | 41.25 | 36.14 |
| 742.5 | 1116 | 124 | 0 | 0 | 82.5 | 41.29 |
| 742.5 | 1116 | 124 | 0 | 0 | 82.5 | 42.53 |
| 742.5 | 1116 | 124 | 0 | 0 | 82.5 | 38.81 |
| 701.25 | 1116 | 124 | 0 | 0 | 123.75 | 40.39 |
| 701.25 | 1116 | 124 | 0 | 0 | 123.75 | 39.62 |
| 701.25 | 1116 | 124 | 0 | 0 | 123.75 | 38.29 |
| 660 | 1116 | 124 | 0 | 0 | 165 | 35.48 |
| 660 | 1116 | 124 | 0 | 0 | 165 | 37.73 |
| 660 | 1116 | 124 | 0 | 0 | 165 | 38.42 |
| 618.75 | 1116 | 124 | 0 | 0 | 206.25 | 34.91 |
| 618.75 | 1116 | 124 | 0 | 0 | 206.25 | 35.87 |
| 618.75 | 1116 | 124 | 0 | 0 | 206.25 | 38.98 |
| 783.75 | 1054 | 186 | 0 | 0 | 41.25 | 37.45 |
| 783.75 | 1054 | 186 | 0 | 0 | 41.25 | 38.92 |
| 783.75 | 1054 | 186 | 0 | 0 | 41.25 | 35.26 |
| 742.5 | 1054 | 186 | 0 | 0 | 82.5 | 36.74 |
| 742.5 | 1054 | 186 | 0 | 0 | 82.5 | 37.68 |
| 742.5 | 1054 | 186 | 0 | 0 | 82.5 | 41.26 |
| 701.25 | 1054 | 186 | 0 | 0 | 123.75 | 37.67 |
| 701.25 | 1054 | 186 | 0 | 0 | 123.75 | 35.38 |
| 701.25 | 1054 | 186 | 0 | 0 | 123.75 | 38.45 |
| 660 | 1054 | 186 | 0 | 0 | 165 | 35.34 |
| 660 | 1054 | 186 | 0 | 0 | 165 | 36.28 |
| 660 | 1054 | 186 | 0 | 0 | 165 | 38.83 |
| 618.75 | 1054 | 186 | 0 | 0 | 206.25 | 37.2 |
| 618.75 | 1054 | 186 | 0 | 0 | 206.25 | 35.21 |
| 618.75 | 1054 | 186 | 0 | 0 | 206.25 | 33.88 |
| 783.75 | 992 | 248 | 0 | 0 | 41.25 | 34.69 |
| 783.75 | 992 | 248 | 0 | 0 | 41.25 | 35.74 |
| 783.75 | 992 | 248 | 0 | 0 | 41.25 | 37.27 |
| 742.5 | 992 | 248 | 0 | 0 | 82.5 | 39.6 |
| 742.5 | 992 | 248 | 0 | 0 | 82.5 | 36.64 |
| 742.5 | 992 | 248 | 0 | 0 | 82.5 | 35.82 |
| 701.25 | 992 | 248 | 0 | 0 | 123.75 | 35.78 |
| 701.25 | 992 | 248 | 0 | 0 | 123.75 | 35.58 |
| 701.25 | 992 | 248 | 0 | 0 | 123.75 | 38.6 |
| 660 | 992 | 248 | 0 | 0 | 165 | 34.79 |
| 660 | 992 | 248 | 0 | 0 | 165 | 35.64 |
| 660 | 992 | 248 | 0 | 0 | 165 | 37.08 |
| 618.75 | 992 | 248 | 0 | 0 | 206.25 | 33.57 |
| 618.75 | 992 | 248 | 0 | 0 | 206.25 | 35 |
| 618.75 | 992 | 248 | 0 | 0 | 206.25 | 34.73 |
| 783.75 | 930 | 310 | 0 | 0 | 41.25 | 35.82 |
| 783.75 | 930 | 310 | 0 | 0 | 41.25 | 32.28 |
| 783.75 | 930 | 310 | 0 | 0 | 41.25 | 33.83 |
| 742.5 | 930 | 310 | 0 | 0 | 82.5 | 33.68 |
| 742.5 | 930 | 310 | 0 | 0 | 82.5 | 35.63 |
| 742.5 | 930 | 310 | 0 | 0 | 82.5 | 36.93 |
| 701.25 | 930 | 310 | 0 | 0 | 123.75 | 36.69 |
| 701.25 | 930 | 310 | 0 | 0 | 123.75 | 34.06 |
| 701.25 | 930 | 310 | 0 | 0 | 123.75 | 32.21 |
| 660 | 930 | 310 | 0 | 0 | 165 | 31.32 |
| 660 | 930 | 310 | 0 | 0 | 165 | 33.4 |
| 660 | 930 | 310 | 0 | 0 | 165 | 35.38 |
| 618.75 | 930 | 310 | 0 | 0 | 206.25 | 31.41 |
| 618.75 | 930 | 310 | 0 | 0 | 206.25 | 32.84 |
| 618.75 | 930 | 310 | 0 | 0 | 206.25 | 34.24 |
| 742.5 | 1178 | 62 | 41.25 | 41.25 | 0 | 42.95 |
| 742.5 | 1178 | 62 | 41.25 | 41.25 | 0 | 40.36 |
| 742.5 | 1178 | 62 | 41.25 | 41.25 | 0 | 40.22 |
| 660 | 1178 | 62 | 82.5 | 82.5 | 0 | 41 |
| 660 | 1178 | 62 | 82.5 | 82.5 | 0 | 44.17 |
| 660 | 1178 | 62 | 82.5 | 82.5 | 0 | 43.7 |
| 577.5 | 1178 | 62 | 123.75 | 123.75 | 0 | 41.37 |
| 577.5 | 1178 | 62 | 123.75 | 123.75 | 0 | 39.26 |
| 577.5 | 1178 | 62 | 123.75 | 123.75 | 0 | 37.32 |
| 742.5 | 1116 | 124 | 41.25 | 41.25 | 0 | 36.08 |
| 742.5 | 1116 | 124 | 41.25 | 41.25 | 0 | 36.75 |
| 742.5 | 1116 | 124 | 41.25 | 41.25 | 0 | 38.54 |
| 660 | 1116 | 124 | 82.5 | 82.5 | 0 | 40.08 |
| 660 | 1116 | 124 | 82.5 | 82.5 | 0 | 41 |
| 660 | 1116 | 124 | 82.5 | 82.5 | 0 | 38.72 |
| 577.5 | 1116 | 124 | 123.75 | 123.75 | 0 | 35.71 |
| 577.5 | 1116 | 124 | 123.75 | 123.75 | 0 | 37.54 |
| 577.5 | 1116 | 124 | 123.75 | 123.75 | 0 | 39.63 |
| 742.5 | 1054 | 186 | 41.25 | 41.25 | 0 | 36.09 |
| 742.5 | 1054 | 186 | 41.25 | 41.25 | 0 | 38.82 |
| 742.5 | 1054 | 186 | 41.25 | 41.25 | 0 | 34.5 |
| 660 | 1054 | 186 | 82.5 | 82.5 | 0 | 36.92 |
| 660 | 1054 | 186 | 82.5 | 82.5 | 0 | 37.04 |
| 660 | 1054 | 186 | 82.5 | 82.5 | 0 | 40.2 |
| 577.5 | 1054 | 186 | 123.75 | 123.75 | 0 | 37.54 |
| 577.5 | 1054 | 186 | 123.75 | 123.75 | 0 | 36.01 |
| 577.5 | 1054 | 186 | 123.75 | 123.75 | 0 | 33.58 |
| 742.5 | 992 | 248 | 41.25 | 41.25 | 0 | 33.71 |
| 742.5 | 992 | 248 | 41.25 | 41.25 | 0 | 34.17 |
| 742.5 | 992 | 248 | 41.25 | 41.25 | 0 | 36.94 |
| 660 | 992 | 248 | 82.5 | 82.5 | 0 | 37.2 |
| 660 | 992 | 248 | 82.5 | 82.5 | 0 | 34.44 |
| 660 | 992 | 248 | 82.5 | 82.5 | 0 | 36.1 |
| 577.5 | 992 | 248 | 123.75 | 123.75 | 0 | 31.83 |
| 577.5 | 992 | 248 | 123.75 | 123.75 | 0 | 32.66 |
| 577.5 | 992 | 248 | 123.75 | 123.75 | 0 | 34.91 |
| 742.5 | 930 | 310 | 41.25 | 41.25 | 0 | 32.85 |
| 742.5 | 930 | 310 | 41.25 | 41.25 | 0 | 30.87 |
| 742.5 | 930 | 310 | 41.25 | 41.25 | 0 | 35.6 |
| 660 | 930 | 310 | 82.5 | 82.5 | 0 | 33.88 |
| 660 | 930 | 310 | 82.5 | 82.5 | 0 | 35.93 |
| 660 | 930 | 310 | 82.5 | 82.5 | 0 | 32.65 |
| 577.5 | 930 | 310 | 123.75 | 123.75 | 0 | 30.12 |
| 577.5 | 930 | 310 | 123.75 | 123.75 | 0 | 33.65 |
| 577.5 | 930 | 310 | 123.75 | 123.75 | 0 | 32.84 |
| 742.5 | 1178 | 62 | 0 | 41.25 | 41.25 | 42.62 |
| 742.5 | 1178 | 62 | 0 | 41.25 | 41.25 | 42.04 |
| 742.5 | 1178 | 62 | 0 | 41.25 | 41.25 | 39.7 |
| 660 | 1178 | 62 | 0 | 82.5 | 82.5 | 44.72 |
| 660 | 1178 | 62 | 0 | 82.5 | 82.5 | 42.24 |
| 660 | 1178 | 62 | 0 | 82.5 | 82.5 | 40.58 |
| 577.5 | 1178 | 62 | 0 | 123.75 | 123.75 | 38.38 |
| 577.5 | 1178 | 62 | 0 | 123.75 | 123.75 | 40.91 |
| 577.5 | 1178 | 62 | 0 | 123.75 | 123.75 | 41.5 |
| 742.5 | 1116 | 124 | 0 | 41.25 | 41.25 | 40.72 |
| 742.5 | 1116 | 124 | 0 | 41.25 | 41.25 | 41.1 |
| 742.5 | 1116 | 124 | 0 | 41.25 | 41.25 | 37.63 |
| 660 | 1116 | 124 | 0 | 82.5 | 82.5 | 39.75 |
| 660 | 1116 | 124 | 0 | 82.5 | 82.5 | 39.86 |
| 660 | 1116 | 124 | 0 | 82.5 | 82.5 | 42.63 |
| 577.5 | 1116 | 124 | 0 | 123.75 | 123.75 | 39.72 |
| 577.5 | 1116 | 124 | 0 | 123.75 | 123.75 | 36.78 |
| 577.5 | 1116 | 124 | 0 | 123.75 | 123.75 | 37.3 |
| 742.5 | 1054 | 186 | 0 | 41.25 | 41.25 | 36.37 |
| 742.5 | 1054 | 186 | 0 | 41.25 | 41.25 | 38.09 |
| 742.5 | 1054 | 186 | 0 | 41.25 | 41.25 | 35.24 |
| 660 | 1054 | 186 | 0 | 82.5 | 82.5 | 40.19 |
| 660 | 1054 | 186 | 0 | 82.5 | 82.5 | 38.01 |
| 660 | 1054 | 186 | 0 | 82.5 | 82.5 | 37.42 |
| 577.5 | 1054 | 186 | 0 | 123.75 | 123.75 | 34.79 |
| 577.5 | 1054 | 186 | 0 | 123.75 | 123.75 | 35.51 |
| 577.5 | 1054 | 186 | 0 | 123.75 | 123.75 | 38.67 |
| 742.5 | 992 | 248 | 0 | 41.25 | 41.25 | 36.58 |
| 742.5 | 992 | 248 | 0 | 41.25 | 41.25 | 35.91 |
| 742.5 | 992 | 248 | 0 | 41.25 | 41.25 | 33.08 |
| 660 | 992 | 248 | 0 | 82.5 | 82.5 | 34.51 |
| 660 | 992 | 248 | 0 | 82.5 | 82.5 | 36.45 |
| 660 | 992 | 248 | 0 | 82.5 | 82.5 | 38.1 |
| 577.5 | 992 | 248 | 0 | 123.75 | 123.75 | 33.52 |
| 577.5 | 992 | 248 | 0 | 123.75 | 123.75 | 34.18 |
| 577.5 | 992 | 248 | 0 | 123.75 | 123.75 | 34.61 |
| 742.5 | 930 | 310 | 0 | 41.25 | 41.25 | 32 |
| 742.5 | 930 | 310 | 0 | 41.25 | 41.25 | 32.87 |
| 742.5 | 930 | 310 | 0 | 41.25 | 41.25 | 35.21 |
| 660 | 930 | 310 | 0 | 82.5 | 82.5 | 35.45 |
| 660 | 930 | 310 | 0 | 82.5 | 82.5 | 35.73 |
| 660 | 930 | 310 | 0 | 82.5 | 82.5 | 32.28 |
| 577.5 | 930 | 310 | 0 | 123.75 | 123.75 | 34.42 |
| 577.5 | 930 | 310 | 0 | 123.75 | 123.75 | 32.67 |
| 577.5 | 930 | 310 | 0 | 123.75 | 123.75 | 29.7 |
| 742.5 | 1178 | 62 | 41.25 | 0 | 41.25 | 41 |
| 742.5 | 1178 | 62 | 41.25 | 0 | 41.25 | 43.5 |
| 742.5 | 1178 | 62 | 41.25 | 0 | 41.25 | 39.64 |
| 660 | 1178 | 62 | 82.5 | 0 | 82.5 | 42.04 |
| 660 | 1178 | 62 | 82.5 | 0 | 82.5 | 42.5 |
| 660 | 1178 | 62 | 82.5 | 0 | 82.5 | 46.64 |
| 577.5 | 1178 | 62 | 123.75 | 0 | 123.75 | 40.37 |
| 577.5 | 1178 | 62 | 123.75 | 0 | 123.75 | 40.18 |
| 577.5 | 1178 | 62 | 123.75 | 0 | 123.75 | 38.14 |
| 742.5 | 1116 | 124 | 41.25 | 0 | 41.25 | 37.92 |
| 742.5 | 1116 | 124 | 41.25 | 0 | 41.25 | 38.61 |
| 742.5 | 1116 | 124 | 41.25 | 0 | 41.25 | 41.22 |
| 660 | 1116 | 124 | 82.5 | 0 | 82.5 | 39.41 |
| 660 | 1116 | 124 | 82.5 | 0 | 82.5 | 42.01 |
| 660 | 1116 | 124 | 82.5 | 0 | 82.5 | 43.93 |
| 577.5 | 1116 | 124 | 123.75 | 0 | 123.75 | 37.23 |
| 577.5 | 1116 | 124 | 123.75 | 0 | 123.75 | 39.41 |
| 577.5 | 1116 | 124 | 123.75 | 0 | 123.75 | 35.28 |
| 742.5 | 1054 | 186 | 41.25 | 0 | 41.25 | 35.41 |
| 742.5 | 1054 | 186 | 41.25 | 0 | 41.25 | 36.05 |
| 742.5 | 1054 | 186 | 41.25 | 0 | 41.25 | 38.68 |
| 660 | 1054 | 186 | 82.5 | 0 | 82.5 | 40.89 |
| 660 | 1054 | 186 | 82.5 | 0 | 82.5 | 40.31 |
| 660 | 1054 | 186 | 82.5 | 0 | 82.5 | 37.15 |
| 577.5 | 1054 | 186 | 123.75 | 0 | 123.75 | 35.76 |
| 577.5 | 1054 | 186 | 123.75 | 0 | 123.75 | 33.97 |
| 577.5 | 1054 | 186 | 123.75 | 0 | 123.75 | 37.23 |
| 742.5 | 992 | 248 | 41.25 | 0 | 41.25 | 35.48 |
| 742.5 | 992 | 248 | 41.25 | 0 | 41.25 | 37.17 |
| 742.5 | 992 | 248 | 41.25 | 0 | 41.25 | 33.66 |
| 660 | 992 | 248 | 82.5 | 0 | 82.5 | 37.09 |
| 660 | 992 | 248 | 82.5 | 0 | 82.5 | 38.83 |
| 660 | 992 | 248 | 82.5 | 0 | 82.5 | 37.19 |
| 577.5 | 992 | 248 | 123.75 | 0 | 123.75 | 32.4 |
| 577.5 | 992 | 248 | 123.75 | 0 | 123.75 | 33.69 |
| 577.5 | 992 | 248 | 123.75 | 0 | 123.75 | 35.53 |
| 742.5 | 930 | 310 | 41.25 | 0 | 41.25 | 34.91 |
| 742.5 | 930 | 310 | 41.25 | 0 | 41.25 | 33.25 |
| 742.5 | 930 | 310 | 41.25 | 0 | 41.25 | 32.96 |
| 660 | 930 | 310 | 82.5 | 0 | 82.5 | 33.34 |
| 660 | 930 | 310 | 82.5 | 0 | 82.5 | 33.47 |
| 660 | 930 | 310 | 82.5 | 0 | 82.5 | 36.91 |
| 577.5 | 930 | 310 | 123.75 | 0 | 123.75 | 33.97 |
| 577.5 | 930 | 310 | 123.75 | 0 | 123.75 | 31.08 |
| 577.5 | 930 | 310 | 123.75 | 0 | 123.75 | 31.64 |
| 701.25 | 1178 | 62 | 41.25 | 41.25 | 41.25 | 44 |
| 701.25 | 1178 | 62 | 41.25 | 41.25 | 41.25 | 44.66 |
| 701.25 | 1178 | 62 | 41.25 | 41.25 | 41.25 | 40.94 |
| 577.5 | 1178 | 62 | 82.5 | 82.5 | 82.5 | 39.43 |
| 577.5 | 1178 | 62 | 82.5 | 82.5 | 82.5 | 40.33 |
| 577.5 | 1178 | 62 | 82.5 | 82.5 | 82.5 | 41.75 |
| 701.25 | 1116 | 124 | 41.25 | 41.25 | 41.25 | 42 |
| 701.25 | 1116 | 124 | 41.25 | 41.25 | 41.25 | 39.29 |
| 701.25 | 1116 | 124 | 41.25 | 41.25 | 41.25 | 40.84 |
| 577.5 | 1116 | 124 | 82.5 | 82.5 | 82.5 | 37.09 |
| 577.5 | 1116 | 124 | 82.5 | 82.5 | 82.5 | 38.24 |
| 577.5 | 1116 | 124 | 82.5 | 82.5 | 82.5 | 40.08 |
| 701.25 | 1024 | 186 | 41.25 | 41.25 | 41.25 | 37.74 |
| 701.25 | 1024 | 186 | 41.25 | 41.25 | 41.25 | 36.91 |
| 701.25 | 1024 | 186 | 41.25 | 41.25 | 41.25 | 40.38 |
| 577.5 | 1024 | 186 | 82.5 | 82.5 | 82.5 | 36.03 |
| 577.5 | 1024 | 186 | 82.5 | 82.5 | 82.5 | 34.66 |
| 577.5 | 1024 | 186 | 82.5 | 82.5 | 82.5 | 38.48 |
| 701.25 | 992 | 248 | 41.25 | 41.25 | 41.25 | 35 |
| 701.25 | 992 | 248 | 41.25 | 41.25 | 41.25 | 34.82 |
| 701.25 | 992 | 248 | 41.25 | 41.25 | 41.25 | 38.12 |
| 577.5 | 992 | 248 | 82.5 | 82.5 | 82.5 | 36.39 |
| 577.5 | 992 | 248 | 82.5 | 82.5 | 82.5 | 34.73 |
| 577.5 | 992 | 248 | 82.5 | 82.5 | 82.5 | 32.16 |
| 701.25 | 920 | 310 | 41.25 | 41.25 | 41.25 | 32.24 |
| 701.25 | 920 | 310 | 41.25 | 41.25 | 41.25 | 32.05 |
| 701.25 | 920 | 310 | 41.25 | 41.25 | 41.25 | 35.23 |
| 577.5 | 920 | 310 | 82.5 | 82.5 | 82.5 | 32.59 |
| 577.5 | 920 | 310 | 82.5 | 82.5 | 82.5 | 32.64 |
| 577.5 | 920 | 310 | 82.5 | 82.5 | 82.5 | 29.71 |
References
- Kang, S.; Zhao, Y.; Wang, W.; Zhang, T.; Chen, T.; Yi, H.; Rao, F.; Song, S. Removal of methylene blue from water with montmorillonite nanosheets/chitosan hydrogels as adsorbent. Appl. Surf. Sci. 2018, 448, 203–211. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, Y.; Bai, H.; Zhang, T.; Ibarra-Galvan, V.; Song, S. Methylene blue removal from water using the hydrogel beads of poly (vinyl alcohol)-sodium alginate-chitosan-montmorillonite. Carbohydr. Polym. 2018, 198, 518–528. [Google Scholar] [CrossRef] [PubMed]
- Alharthai, M.; Onyelowe, K.C.; Ali, T.; Qureshi, M.Z.; Rezzoug, A.; Deifalla, A.; Alharthi, K. Enhancing concrete strength and durability through incorporation of rice husk ash and high recycled aggregate. Case Stud. Constr. Mater. 2025, 22, e04152. [Google Scholar] [CrossRef]
- Li, X.; Ling, T.-C.; Mo, K.H. Functions and impacts of plastic/rubber wastes as eco-friendly aggregate in concrete—A review. Constr. Build. Mater. 2020, 240, 117869. [Google Scholar] [CrossRef]
- Ismail, Z.Z.; Al-Hashmi, E.A. Use of waste plastic in concrete mixture as aggregate replacement. Waste Manag. 2008, 28, 2041–2047. [Google Scholar] [CrossRef]
- Tafheem, Z.; Rakib, R.I.; Esharuhullah, M.D.; Alam, S.M.R.; Islam, M.M. Experimental investigation on the properties of concrete containing post-consumer plastic waste as coarse aggregate replacement. J. Mater. Eng. Struct. 2018, 5, 23–31. [Google Scholar]
- Thorneycroft, J.; Orr, J.; Savoikar, P.; Ball, R.J. Performance of structural concrete with recycled plastic waste as a partial replacement for sand. Constr. Build. Mater. 2018, 161, 63–69. [Google Scholar] [CrossRef]
- Saxena, R.; Siddique, S.; Gupta, T.; Sharma, R.K.; Chaudhary, S. Impact resistance and energy absorption capacity of concrete containing plastic waste. Constr. Build. Mater. 2018, 176, 415–421. [Google Scholar] [CrossRef]
- Asif, U.; Javed, M.F.; Alyami, M.; Hammad, A.W.A. Performance evaluation of concrete made with plastic waste using multi-expression programming. Mater. Today Commun. 2024, 39, 108789. [Google Scholar] [CrossRef]
- Asif, U.; Javed, M.F.; Alsekait, D.M.; Aslam, F.; Elminaam, D.S.A. Data-driven evolutionary programming for evaluating the mechanical properties of concrete containing plastic waste. Case Stud. Constr. Mater. 2024, 21, e03763. [Google Scholar] [CrossRef]
- Mehta, A.; Ashish, D.K. Silica fume and waste glass in cement concrete production: A review. J. Build. Eng. 2020, 29, 100888. [Google Scholar] [CrossRef]
- Khodabakhshian, A.; Ghalehnovi, M.; De Brito, J.; Shamsabadi, E.A. Durability performance of structural concrete containing silica fume and marble industry waste powder. J. Clean. Prod. 2018, 170, 42–60. [Google Scholar] [CrossRef]
- Barham, W.S.; Albiss, B.; Latayfeh, O. Influence of magnetic field treated water on the compressive strength and bond strength of concrete containing silica fume. J. Build. Eng. 2021, 33, 101544. [Google Scholar] [CrossRef]
- Ashish, D.K. Concrete made with waste marble powder and supplementary cementitious material for sustainable development. J. Clean. Prod. 2019, 211, 716–729. [Google Scholar] [CrossRef]
- Khan, M.; McNally, C. A holistic review on the contribution of civil engineers for driving sustainable concrete construction in the built environment. Dev. Built Environ. 2023, 16, 100273. [Google Scholar] [CrossRef]
- Shanmugasundaram, N.; Praveenkumar, S. Influence of supplementary cementitious materials, curing conditions and mixing ratios on fresh and mechanical properties of engineered cementitious composites—A review. Constr. Build. Mater. 2021, 309, 125038. [Google Scholar] [CrossRef]
- Gupta, S.; Chaudhary, S. State of the art review on supplementary cementitious materials in India–I: An overview of legal perspective, governing organizations, and development patterns. J. Clean. Prod. 2020, 261, 121203. [Google Scholar] [CrossRef]
- Sandanayake, M.; Bouras, Y.; Haigh, R.; Vrcelj, Z. Current sustainable trends of using waste materials in concrete—A decade review. Sustainability 2020, 12, 9622. [Google Scholar] [CrossRef]
- Singh, G.V.P.B.; Subramaniam, K.V.L. Production and characterization of low-energy Portland composite cement from post-industrial waste. J. Clean. Prod. 2019, 239, 118024. [Google Scholar] [CrossRef]
- Khan, M.; Rehman, A.; Ali, M. Efficiency of silica-fume content in plain and natural fiber reinforced concrete for concrete road. Constr. Build. Mater. 2020, 244, 118382. [Google Scholar] [CrossRef]
- Khan, M.; Cao, M.; Hussain, A.; Chu, S.H. Effect of silica-fume content on performance of CaCO3 whisker and basalt fiber at matrix interface in cement-based composites. Constr. Build. Mater. 2021, 300, 124046. [Google Scholar] [CrossRef]
- Bouchelil, L.; Jafar, S.B.S.; Khanzadeh Moradllo, M. Evaluating the performance of internally cured limestone calcined clay concrete mixtures. J. Sustain. Cem.-Based Mater. 2025, 14, 198–208. [Google Scholar] [CrossRef]
- Lou, Y.; Khan, K.; Amin, M.N.; Ahmad, W.; Deifalla, A.F.; Ahmad, A. Performance characteristics of cementitious composites modified with silica fume: A systematic review. Case Stud. Constr. Mater. 2023, 18, e01753. [Google Scholar] [CrossRef]
- Khan, K.; Ahmad, W.; Amin, M.N.; Rafiq, M.I.; Arab, A.M.A.; Alabdullah, I.A.; Alabduljabbar, H.; Mohamed, A. Evaluating the effectiveness of waste glass powder for the compressive strength improvement of cement mortar using experimental and machine learning methods. Heliyon 2023, 9, e16288. [Google Scholar] [CrossRef]
- Ashish, D.K. Feasibility of waste marble powder in concrete as partial substitution of cement and sand amalgam for sustainable growth. J. Build. Eng. 2018, 15, 236–242. [Google Scholar] [CrossRef]
- Siddique, R. Utilization of silica fume in concrete: Review of hardened properties. Resour. Conserv. Recycl. 2011, 55, 923–932. [Google Scholar] [CrossRef]
- Sun, M.; Bennett, T.; Visintin, P. Plastic and early-age shrinkage of ultra-high performance concrete (UHPC): Experimental study of the effect of water to binder ratios, silica fume dosages under controlled curing conditions. Case Stud. Constr. Mater. 2022, 16, e00948. [Google Scholar] [CrossRef]
- Nochaiya, T.; Suriwong, T.; Julphunthong, P. Acidic corrosion-abrasion resistance of concrete containing fly ash and silica fume for use as concrete floors in pig farm. Case Stud. Constr. Mater. 2022, 16, e01010. [Google Scholar] [CrossRef]
- Mokhtari, S.; Madhkhan, M. The performance effect of PEG-silica fume as shape-stabilized phase change materials on mechanical and thermal properties of lightweight concrete panels. Case Stud. Constr. Mater. 2022, 17, e01298. [Google Scholar] [CrossRef]
- Sarıdemir, M. Effect of silica fume and ground pumice on compressive strength and modulus of elasticity of high strength concrete. Constr. Build. Mater. 2013, 49, 484–489. [Google Scholar] [CrossRef]
- Qin, D.; Hu, Y.; Li, X. Waste Glass Utilization in Cement-Based Materials for Sustainable Construction: A Review. Crystals 2021, 11, 710. [Google Scholar] [CrossRef]
- Meena, A.; Singh, R. Comparative Study of Waste Glass Powder as Pozzolanic Material in Concrete. Ph.D. Thesis, 2012. Available online: https://www.academia.edu/ (accessed on 5 May 2024).
- Mohajerani, A.; Vajna, J.; Cheung, T.H.H.; Kurmus, H.; Arulrajah, A.; Horpibulsuk, S. Practical recycling applications of crushed waste glass in construction materials: A review. Constr. Build. Mater. 2017, 156, 443–467. [Google Scholar] [CrossRef]
- Aliabdo, A.A.; Abd Elmoaty, M.; Aboshama, A.Y. Utilization of waste glass powder in the production of cement and concrete. Constr. Build. Mater. 2016, 124, 866–877. [Google Scholar] [CrossRef]
- Prakash, B.; Saravanan, T.J.; Kabeer, K.I.S.A.; Bisht, K. Exploring the potential of waste marble powder as a sustainable substitute to cement in cement-based composites: A review. Constr. Build. Mater. 2023, 401, 132887. [Google Scholar] [CrossRef]
- Yuan, X.; Tian, Y.; Ahmad, W.; Ahmad, A.; Usanova, K.I.; Mohamed, A.M.; Khallaf, R. Machine Learning Prediction Models to Evaluate the Strength of Recycled Aggregate Concrete. Materials 2022, 15, 2823. [Google Scholar] [CrossRef] [PubMed]
- Ali, T.; Onyelowe, K.C.; Mahmood, M.S.; Qureshi, M.Z.; Kahla, N.B.; Rezzoug, A.; Deifalla, A. Advanced and hybrid machine learning techniques for predicting compressive strength in palm oil fuel ash-modified concrete with SHAP analysis. Sci. Rep. 2025, 15, 4997. [Google Scholar] [CrossRef] [PubMed]
- Chang, Q.; Zhao, C.; AlAteah, A.H.; Alinsaif, S.; Sufian, M.; Ahmad, A. AI-powered optimization of engineered cementitious composites properties and CO2 emissions for sustainable construction. Case Stud. Constr. Mater. 2025, 22, e04405. [Google Scholar] [CrossRef]
- Singh, N.; Kumar, P.; Goyal, P. Reviewing the behaviour of high volume fly ash based self compacting concrete. J. Build. Eng. 2019, 26, 100882. [Google Scholar] [CrossRef]
- Althoey, F. Compressive strength reduction of cement pastes exposed to sodium chloride solutions: Secondary ettringite formation. Constr. Build. Mater. 2021, 299, 123965. [Google Scholar] [CrossRef]
- Awoyera, P.O. Nonlinear finite element analysis of steel fibre-reinforced concrete beam under static loading. J. Eng. Sci. Technol. 2016, 11, 1669–1677. [Google Scholar]
- Huang, J.; Zhang, J.; Li, X.; Qiao, Y.; Zhang, R.; Kumar, G.S. Investigating the effects of ensemble and weight optimization approaches on neural networks’ performance to estimate the dynamic modulus of asphalt concrete. Road Mater. Pavement Des. 2023, 24, 1939–1959. [Google Scholar] [CrossRef]
- Ahmad, W.; Veeraghantla, V.S.S.C.S.; Byrne, A. Advancing Sustainable Concrete Using Biochar: Experimental and Modelling Study for Mechanical Strength Evaluation. Sustainability 2025, 17, 2516. [Google Scholar] [CrossRef]
- Amin, M.N.; Ahmad, W.; Khan, K.; Al-Hashem, M.N.; Deifalla, A.F.; Ahmad, A. Testing and modeling methods to experiment the flexural performance of cement mortar modified with eggshell powder. Case Stud. Constr. Mater. 2023, 18, e01759. [Google Scholar] [CrossRef]
- Emad, W.; Mohammed, A.S.; Kurda, R.; Ghafor, K.; Cavaleri, L.; Qaidi, S.M.A.; Hassan, A.M.T.; Asteris, P.G. Prediction of concrete materials compressive strength using surrogate models. In Structures; Elsevier: Amsterdam, The Netherlands, 2022; pp. 1243–1267. [Google Scholar]
- Asteris, P.G.; Roussis, P.C.; Douvika, M.G. Feed-forward neural network prediction of the mechanical properties of sandcrete materials. Sensors 2017, 17, 1344. [Google Scholar] [CrossRef]
- Arif, M.; Jan, F.; Rezzoug, A.; Afridi, M.A.; Luqman, M.; Khan, W.A.; Kujawa, M.; Alabduljabbar, H.; Khan, M. Data-driven models for predicting compressive strength of 3D-printed fiber-reinforced concrete using interpretable machine learning algorithms. Case Stud. Constr. Mater. 2024, 21, e03935. [Google Scholar] [CrossRef]
- Javed, M.F.; Amin, M.N.; Shah, M.I.; Khan, K.; Iftikhar, B.; Farooq, F.; Aslam, F.; Alyousef, R.; Alabduljabbar, H. Applications of gene expression programming and regression techniques for estimating compressive strength of bagasse ash based concrete. Crystals 2020, 10, 737. [Google Scholar] [CrossRef]
- Marani, A.; Jamali, A.; Nehdi, M.L. Predicting ultra-high-performance concrete compressive strength using tabular generative adversarial networks. Materials 2020, 13, 4757. [Google Scholar] [CrossRef]
- Marani, A.; Nehdi, M.L. Machine learning prediction of compressive strength for phase change materials integrated cementitious composites. Constr. Build. Mater. 2020, 265, 120286. [Google Scholar] [CrossRef]
- Nunez, I.; Marani, A.; Nehdi, M.L. Mixture optimization of recycled aggregate concrete using hybrid machine learning model. Materials 2020, 13, 4331. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, Y.; Aslani, F.; Ma, G.; Nener, B. A hybrid intelligent system for designing optimal proportions of recycled aggregate concrete. J. Clean. Prod. 2020, 273, 122922. [Google Scholar] [CrossRef]
- Zhang, J.; Li, D.; Wang, Y. Toward intelligent construction: Prediction of mechanical properties of manufactured-sand concrete using tree-based models. J. Clean. Prod. 2020, 258, 120665. [Google Scholar] [CrossRef]
- Wahab, S.; Salami, B.A.; Danish, H.; Nisar, S.; AlAteah, A.H.; Alsubeai, A. A hybrid machine learning approach for predicting fiber-reinforced polymer-concrete interface bond strength. Eng. Appl. Artif. Intell. 2025, 148, 110458. [Google Scholar] [CrossRef]
- Rajasekar, A.; Arunachalam, K.; Kottaisamy, M. Assessment of strength and durability characteristics of copper slag incorporated ultra high strength concrete. J. Clean. Prod. 2019, 208, 402–414. [Google Scholar] [CrossRef]
- Naseri, H.; Jahanbakhsh, H.; Hosseini, P.; Nejad, F.M. Designing sustainable concrete mixture by developing a new machine learning technique. J. Clean. Prod. 2020, 258, 120578. [Google Scholar] [CrossRef]
- Young, B.A.; Hall, A.; Pilon, L.; Gupta, P.; Sant, G. Can the compressive strength of concrete be estimated from knowledge of the mixture proportions?: New insights from statistical analysis and machine learning methods. Cem. Concr. Res. 2019, 115, 379–388. [Google Scholar] [CrossRef]
- Yun, M.; Li, X.; Amin, M.N.; Khan, Z.; Al-Naghi, A.A.A.; Latifee, E.R.; Nazar, S. Experimenting the effectiveness of waste materials in improving the compressive strength of plastic-based mortar. Case Stud. Constr. Mater. 2024, 21, e03543. [Google Scholar] [CrossRef]
- Iqbal, M.F.; Liu, Q.-f.; Azim, I.; Zhu, X.; Yang, J.; Javed, M.F.; Rauf, M. Prediction of mechanical properties of green concrete incorporating waste foundry sand based on gene expression programming. J. Hazard. Mater. 2020, 384, 121322. [Google Scholar] [CrossRef]
- Egidi, G.; Edwards, M.; Cividino, S.; Gambella, F.; Salvati, L. Exploring non-linear relationships among redundant variables through non-parametric principal component analysis: An empirical analysis with land-use data. Reg. Stat. 2021, 11, 25–41. [Google Scholar] [CrossRef]
- Lee, B.C.; Brooks, D.M. Accurate and efficient regression modeling for microarchitectural performance and power prediction. ACM SIGOPS Oper. Syst. Rev. 2006, 40, 185–194. [Google Scholar] [CrossRef]
- Wang, D.; Peng, J.; Yu, Q.; Chen, Y.; Yu, H. Support Vector Machine Algorithm for Automatically Identifying Depositional Microfacies Using Well Logs. Sustainability 2019, 11, 1919. [Google Scholar] [CrossRef]
- Suthaharan, S. Support vector machine. In Machine Learning Models and Algorithms for Big Data Classification: Thinking with Examples for Effective Learning; Springer: Boston, MA, USA, 2016; pp. 207–235. [Google Scholar]
- Ribeiro, M.H.D.M.; dos Santos Coelho, L. Ensemble approach based on bagging, boosting and stacking for short-term prediction in agribusiness time series. Appl. Soft Comput. 2020, 86, 105837. [Google Scholar] [CrossRef]
- Ahmad, A.; Ahmad, W.; Chaiyasarn, K.; Ostrowski, K.A.; Aslam, F.; Zajdel, P.; Joyklad, P. Prediction of Geopolymer Concrete Compressive Strength Using Novel Machine Learning Algorithms. Polymers 2021, 13, 3389. [Google Scholar] [CrossRef] [PubMed]
- Yeh, I.C. Prediction of strength of fly ash and slag concrete by the use of artificial neural networks. J. Chin. Inst. Civ. Hydraul. Eng. 2003, 15, 659–663. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Amjad, M.; Ahmad, I.; Ahmad, M.; Wróblewski, P.; Kamiński, P.; Amjad, U. Prediction of pile bearing capacity using XGBoost algorithm: Modeling and performance evaluation. Appl. Sci. 2022, 12, 2126. [Google Scholar] [CrossRef]
- Farooq, F.; Ahmed, W.; Akbar, A.; Aslam, F.; Alyousef, R. Predictive modeling for sustainable high-performance concrete from industrial wastes: A comparison and optimization of models using ensemble learners. J. Clean. Prod. 2021, 292, 126032. [Google Scholar] [CrossRef]
- Asif, U.; Javed, M.F.; Abuhussain, M.; Ali, M.; Khan, W.A.; Mohamed, A. Predicting the mechanical properties of plastic concrete: An optimization method by using genetic programming and ensemble learners. Case Stud. Constr. Mater. 2024, 20, e03135. [Google Scholar] [CrossRef]
- Ahmad, A.; Chaiyasarn, K.; Farooq, F.; Ahmad, W.; Suparp, S.; Aslam, F. Compressive Strength Prediction via Gene Expression Programming (GEP) and Artificial Neural Network (ANN) for Concrete Containing RCA. Buildings 2021, 11, 324. [Google Scholar] [CrossRef]
- Alade, I.O.; Bagudu, A.; Oyehan, T.A.; Abd Rahman, M.A.; Saleh, T.A.; Olatunji, S.O. Estimating the refractive index of oxygenated and deoxygenated hemoglobin using genetic algorithm–support vector regression model. Comput. Methods Programs Biomed. 2018, 163, 135–142. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, R.; Wu, C.; Goh, A.T.C.; Lacasse, S.; Liu, Z.; Liu, H. State-of-the-art review of soft computing applications in underground excavations. Geosci. Front. 2020, 11, 1095–1106. [Google Scholar] [CrossRef]
- Alavi, A.H.; Gandomi, A.H.; Nejad, H.C.; Mollahasani, A.; Rashed, A. Design equations for prediction of pressuremeter soil deformation moduli utilizing expression programming systems. Neural Comput. Appl. 2013, 23, 1771–1786. [Google Scholar] [CrossRef]
- Kisi, O.; Shiri, J.; Tombul, M. Modeling rainfall-runoff process using soft computing techniques. Comput. Geosci. 2013, 51, 108–117. [Google Scholar] [CrossRef]
- Alade, I.O.; Abd Rahman, M.A.; Saleh, T.A. Modeling and prediction of the specific heat capacity of Al2O3/water nanofluids using hybrid genetic algorithm/support vector regression model. Nano-Struct. Nano-Objects 2019, 17, 103–111. [Google Scholar] [CrossRef]
- Shahin, M.A. Use of evolutionary computing for modelling some complex problems in geotechnical engineering. Geomech. Geoeng. 2015, 10, 109–125. [Google Scholar] [CrossRef]
- Band, S.S.; Heggy, E.; Bateni, S.M.; Karami, H.; Rabiee, M.; Samadianfard, S.; Chau, K.-W.; Mosavi, A. Groundwater level prediction in arid areas using wavelet analysis and Gaussian process regression. Eng. Appl. Comput. Fluid Mech. 2021, 15, 1147–1158. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Lyu, Z.; Yu, Y.; Samali, B.; Rashidi, M.; Mohammadi, M.; Nguyen, T.N.; Nguyen, A. Back-propagation neural network optimized by K-fold cross-validation for prediction of torsional strength of reinforced Concrete beam. Materials 2022, 15, 1477. [Google Scholar] [CrossRef]
- Naqi, A.; Jang, J.G. Recent progress in green cement technology utilizing low-carbon emission fuels and raw materials: A review. Sustainability 2019, 11, 537. [Google Scholar] [CrossRef]
- Valente, M.; Sambucci, M.; Chougan, M.; Ghaffar, S.H. Reducing the emission of climate-altering substances in cementitious materials: A comparison between alkali-activated materials and Portland cement-based composites incorporating recycled tire rubber. J. Clean. Prod. 2022, 333, 130013. [Google Scholar] [CrossRef]
- Khan, K.; Ahmad, W.; Amin, M.N.; Ahmad, A.; Nazar, S.; Al-Faiad, M.A. Assessment of artificial intelligence strategies to estimate the strength of geopolymer composites and influence of input parameters. Polymers 2022, 14, 2509. [Google Scholar] [CrossRef]
- Alyami, M.; Ullah, I.; AlAteah, A.H.; Alsubeai, A.; Alahmari, T.S.; Farooq, F.; Alabduljabbar, H. Machine learning models for predicting the compressive strength of cement-based mortar materials: Hyper tuning and optimization. Structures 2025, 71, 107931. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).