Influence of Fast Freeze-Thaw Cycles on the Behavior of Segmental Bridge Shear Key Joints Using Nonlinear Finite Element Analysis
Abstract
1. Introduction
2. Nonlinear Finite Element Analysis (NLFEA)
2.1. The CDP Parameters Values
2.1.1. The Compression Behavior of Concrete
2.1.2. The Tensile Behavior of Concrete Material
2.2. Steel Reinforcement
2.3. ABAQUS Model Setup and Subroutines
2.3.1. Finite Element Type
2.3.2. Finite Meshing (Discretization)
2.3.3. Key Contact Relationship
2.3.4. Boundary Conditions and Applied Load
2.3.5. The Freezing-Thawing Effect
2.3.6. The Investigated Parameters
2.3.7. ABAQUS Model Validation
3. New Theoretical Formula for Predicting Shear Key Joint Strength
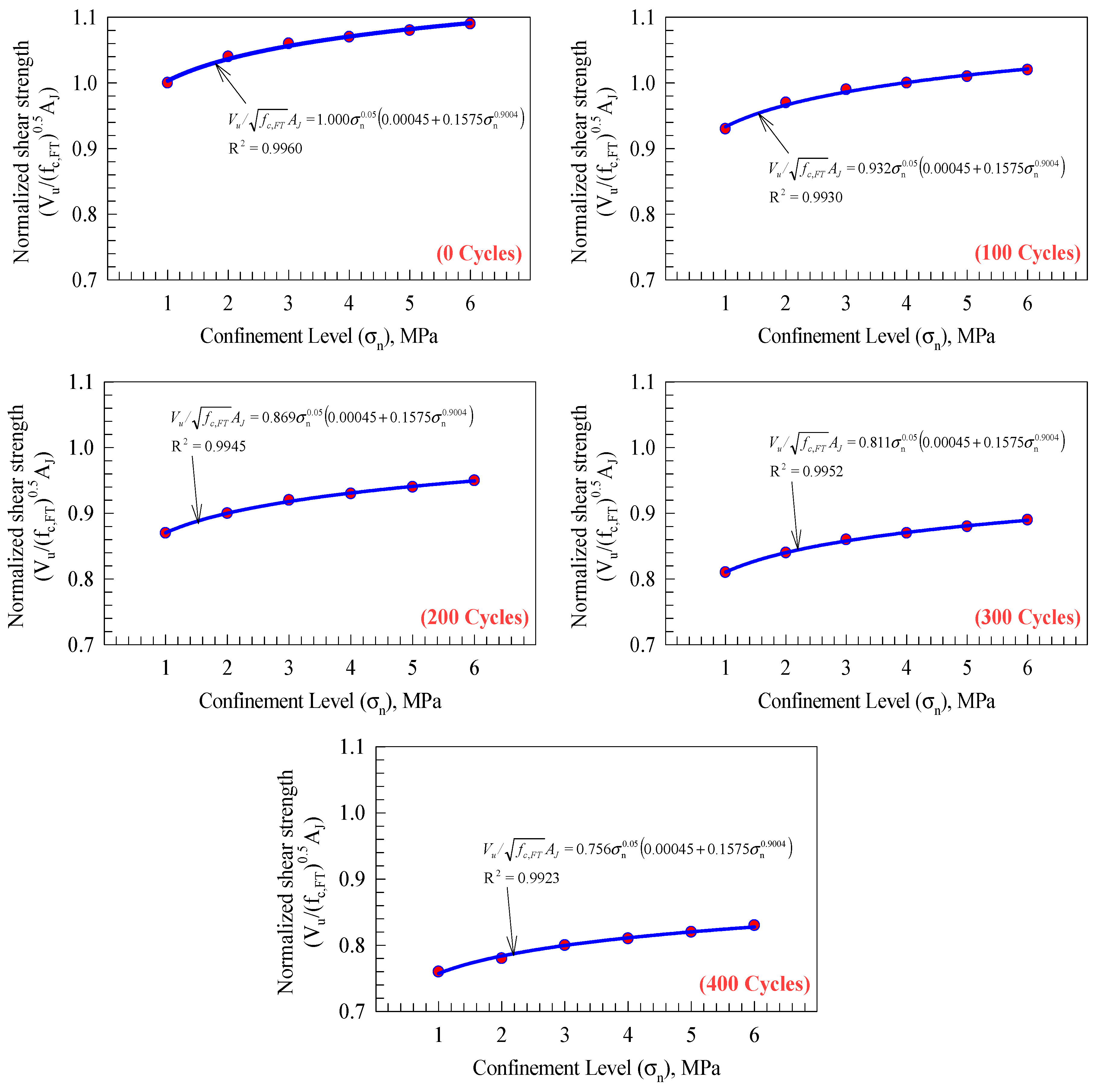
3.1. Results Comparison Against Numerical Data and Theoretical Formulas

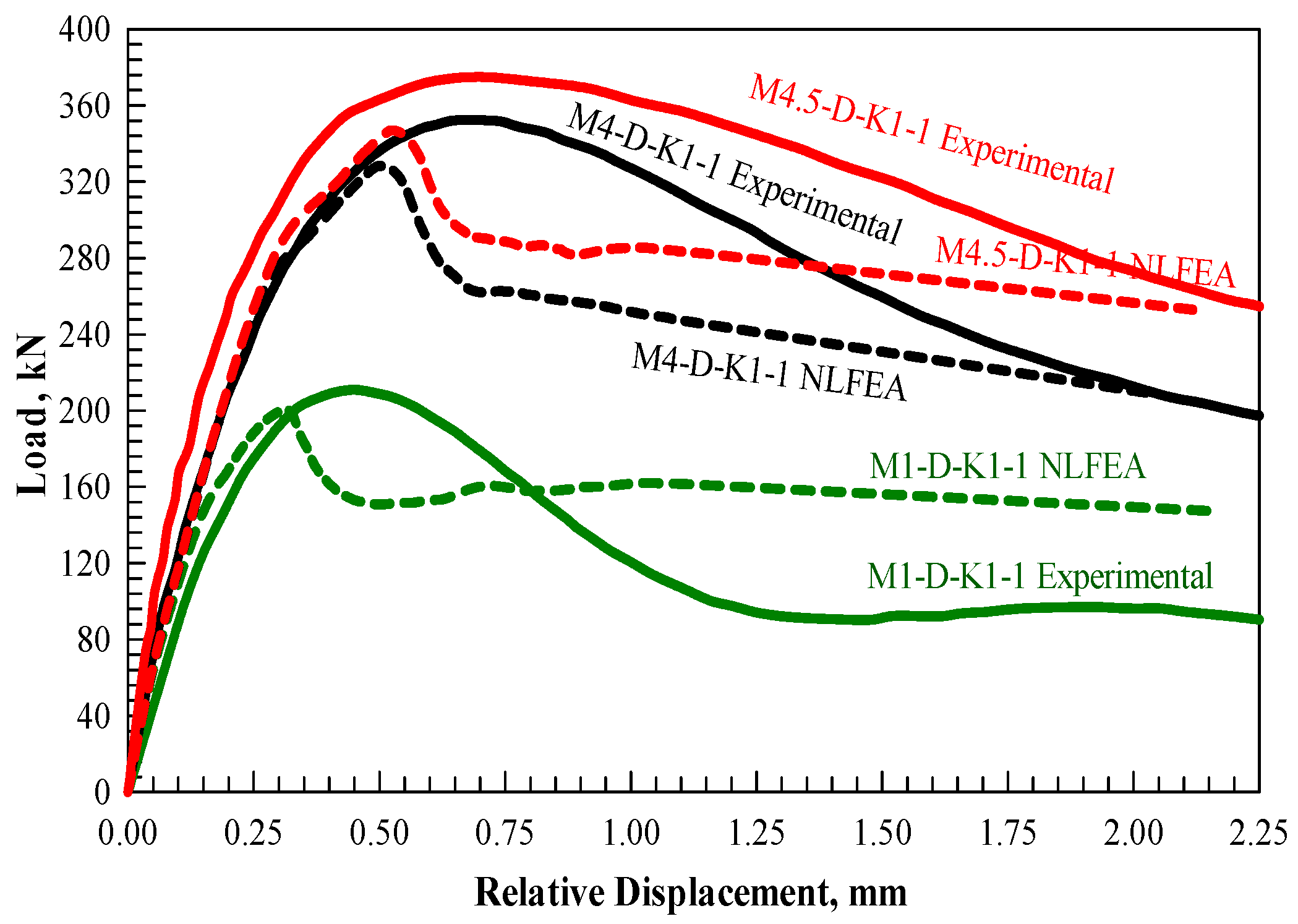
3.2. Results Comparison Against Experimental Data
4. NLFEA Results and Discussion
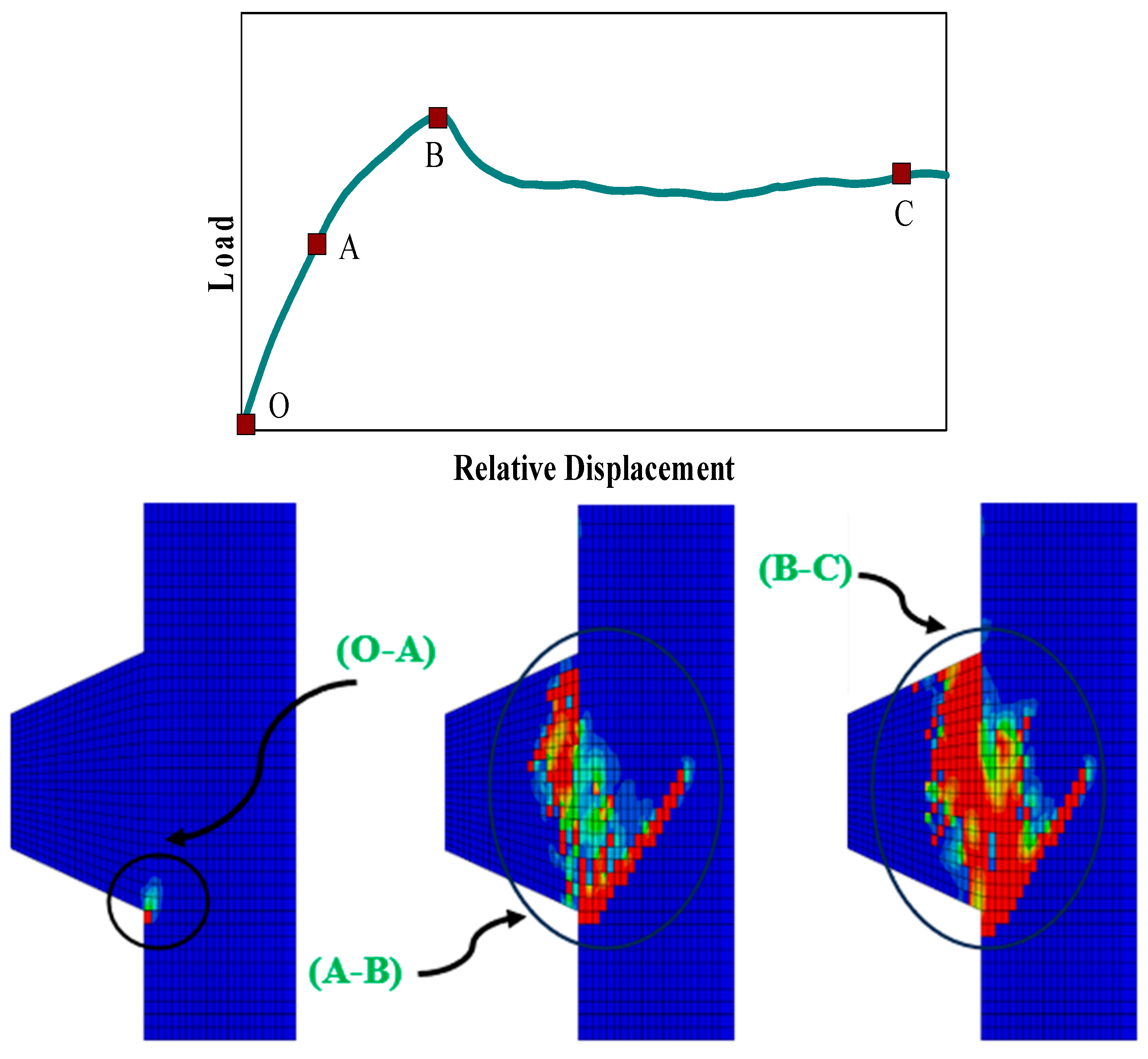
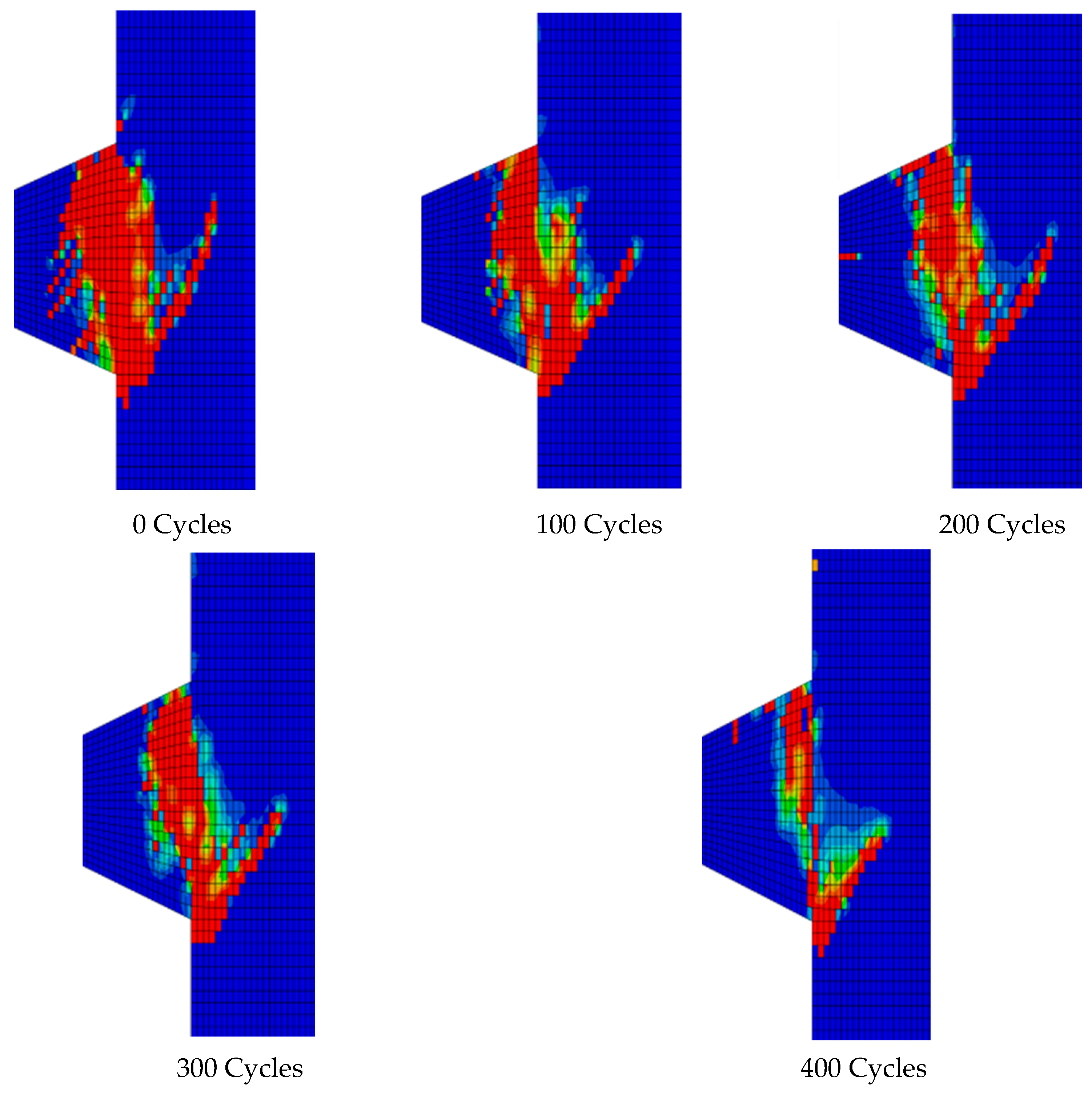
4.1. NLFEA Behavior and Concrete Damage
4.2. Crack Patterns
4.3. Cracking Propagation Process
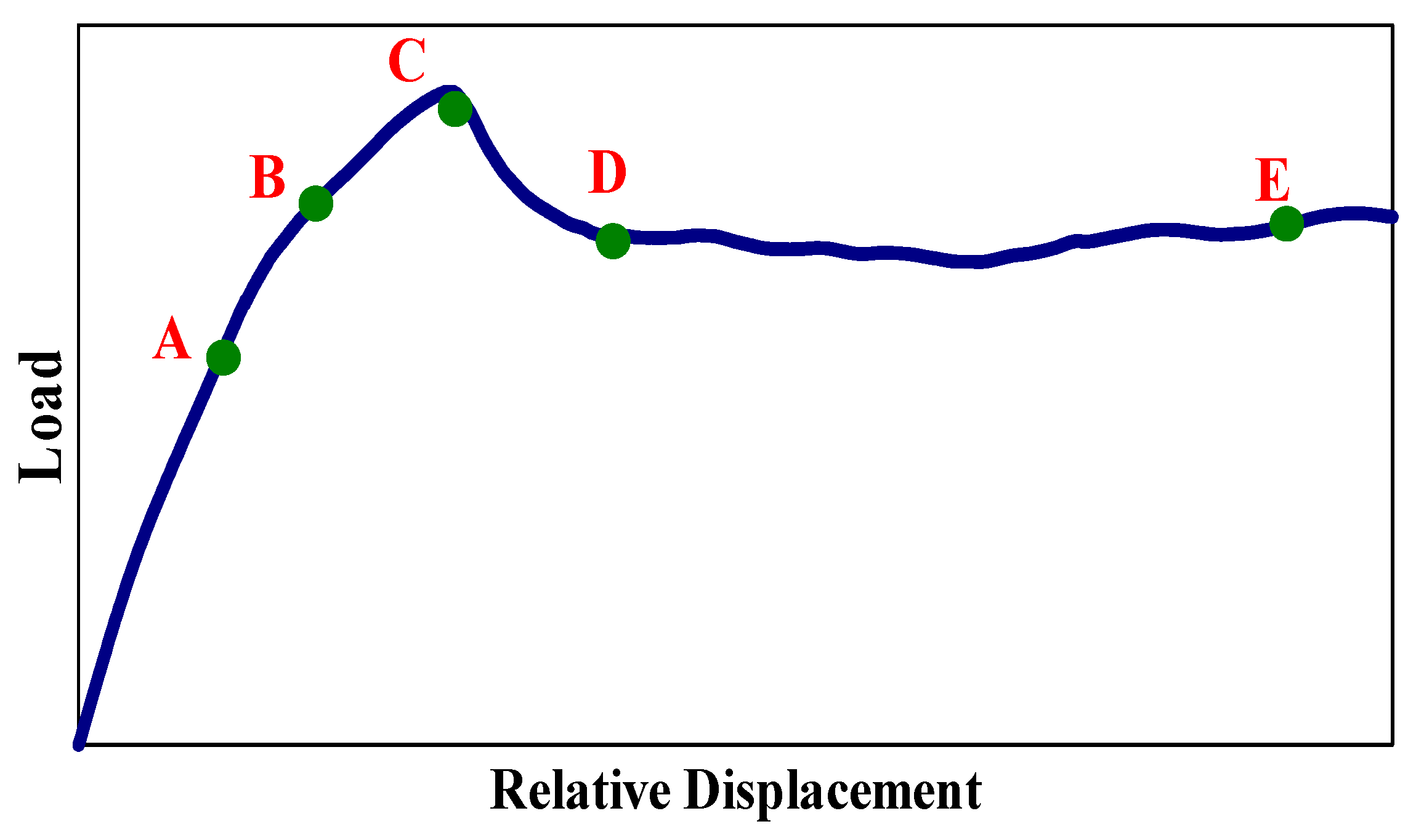
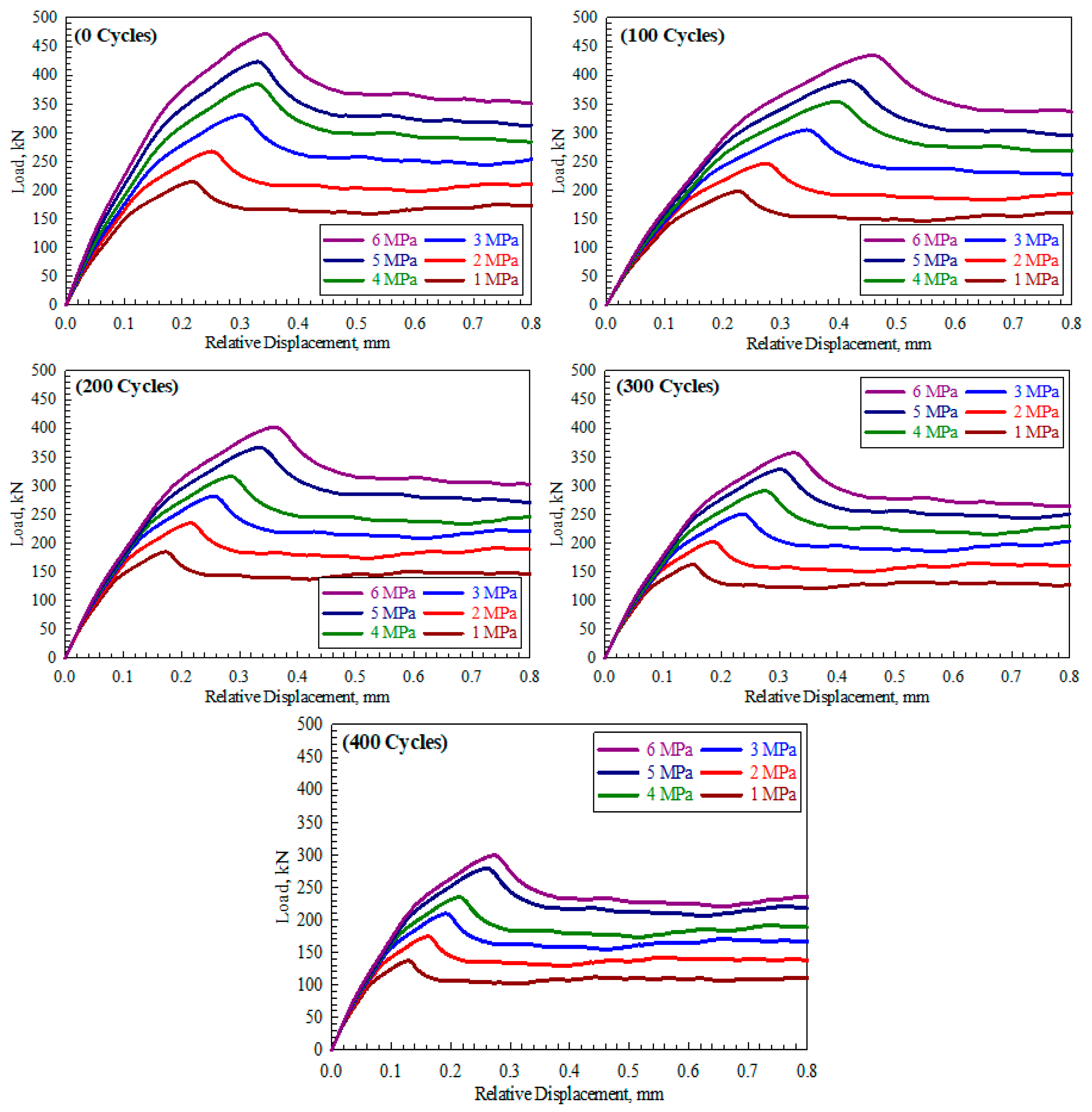
4.4. Load-Displacement Curves
4.5. Ultimate Shear Capacity and Corresponding Deflection Ratios
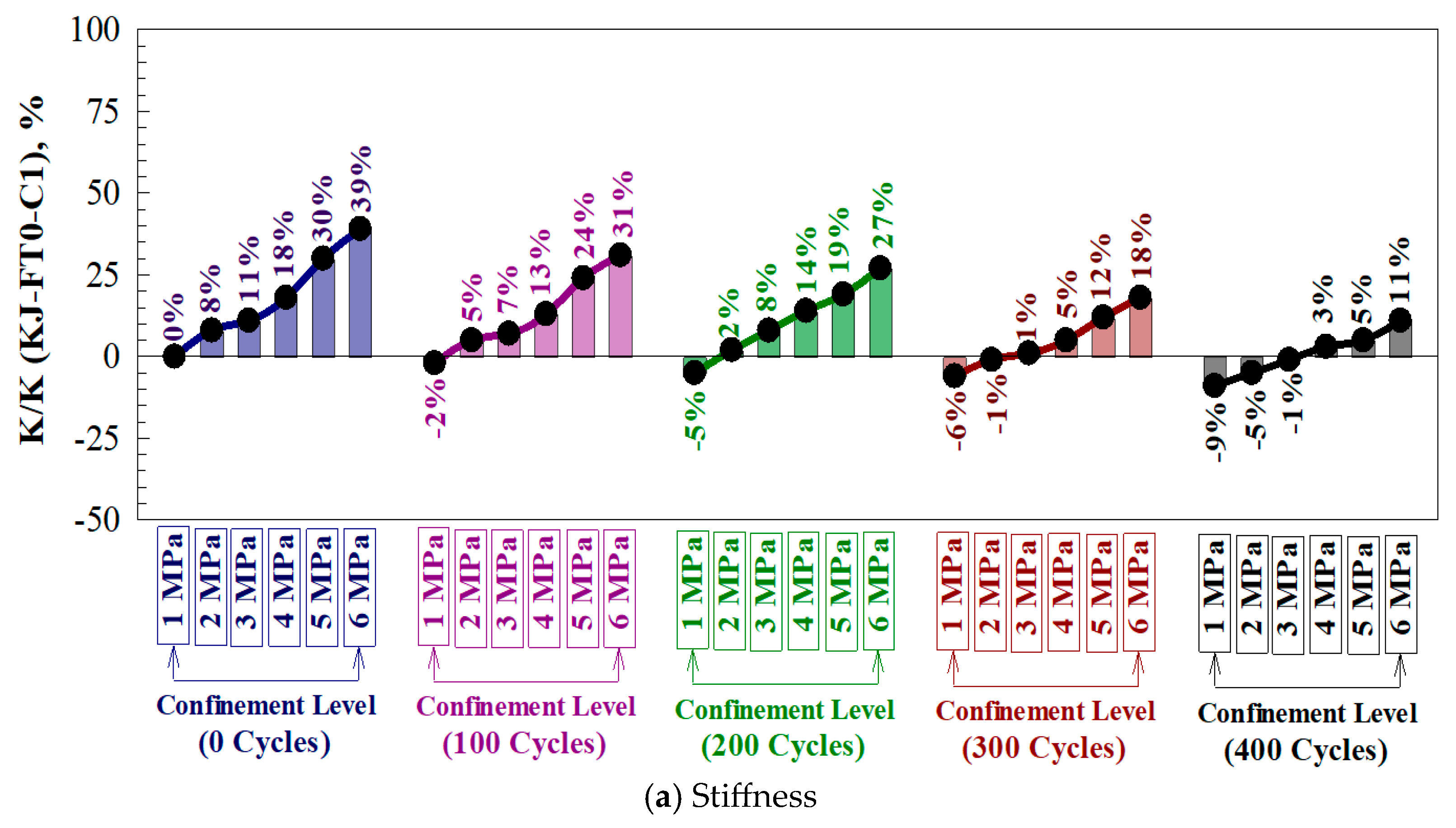
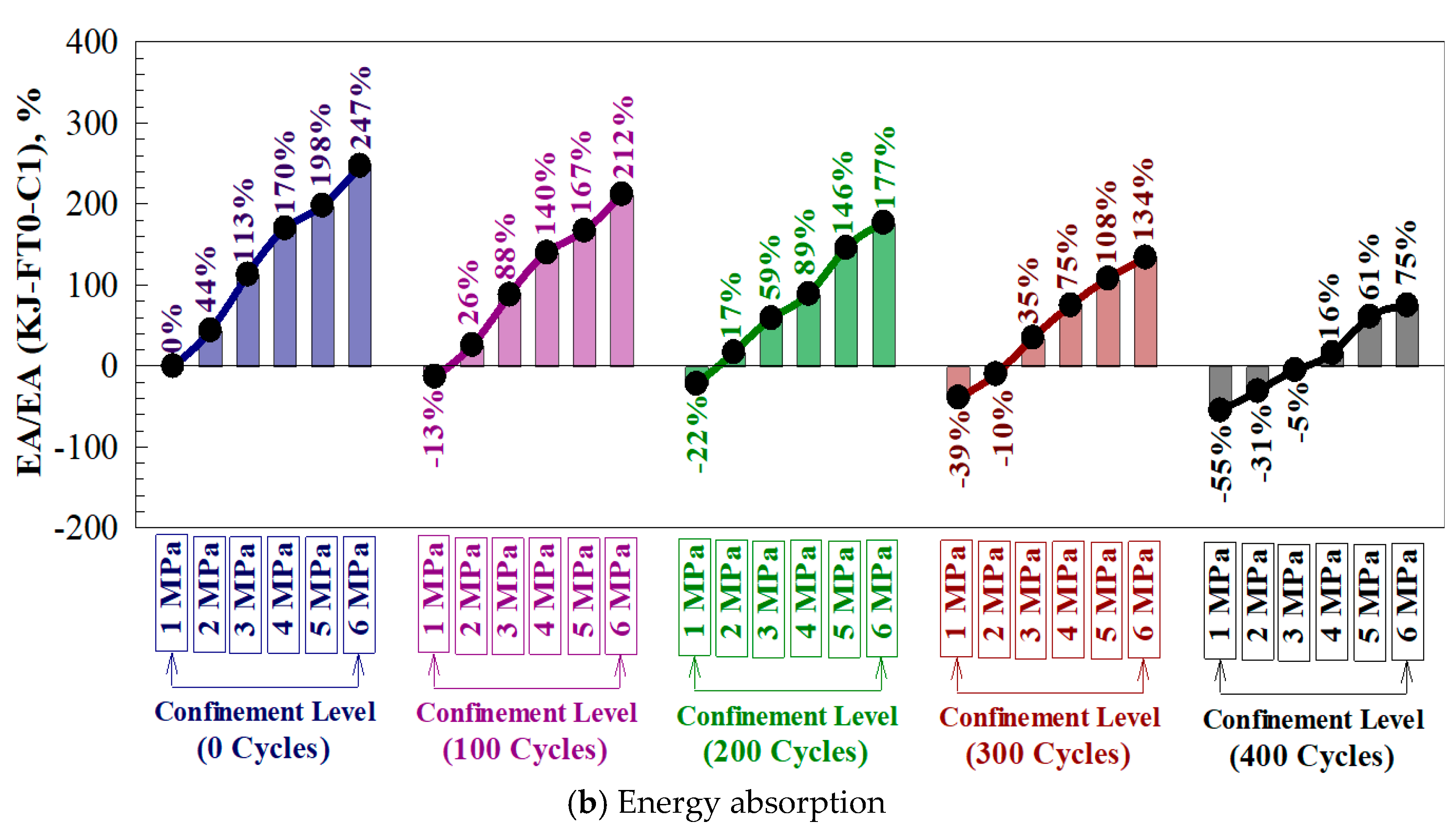
4.6. Stiffness and Energy Absorption Ratios
5. Conclusions
- Two main shear transfer mechanisms contribute to the shear capacity of a single dried key joint: key bearing and friction. The observed failure is associated with a 45-degree inclination crack, shearing-off, concrete crushing, and joint slippage.
- The propagated cracks are significantly affected by the amount of lateral confinement provided, where cracks are shortened and narrowed at high confinement levels until they become invisibly propagated.
- Exposing the shear keys to 100, 200, 300, and 400 freeze and thaw cycles reduces the ultimate shear capacity by 8, 15, 24, and 36%, respectively, compared to 4, 9, 14, and 25% for the ultimate deflection, 6, 11, and 14% for the stiffness, and 11, 22, 34, and 42% for the energy absorption.
- Providing a confinement level of 2, 3, 4, 5, and 6 MPa improves the overall behavior, where increasing percentages of 25, 53, 76, 99, and 119% and 18, 39, 52, 61, and 67% were recorded for the ultimate load and ultimate deflection, compared to 6, 10, 16, 23, and 31% and 47, 113, 167, 219, and 263% for the stiffness and energy absorption.
- A new expression was proposed for predicting single-shear key capacity, where good predictions were recorded with an average standard deviation value of less than 4% in the conservative direction.
- The results of this study are subject to some limitations regarding the concrete material grade, where it applies to normal concrete strength only and it is not valid for high and ultra-high grades due to their different behavior.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pan, R.; Yang, P.; Shi, X.; Zhang, T. Effects of freeze–thaw cycles on the shear stress induced on the cemented sand–structure interface. Constr. Build. Mater. 2023, 371, 130671. [Google Scholar] [CrossRef]
- Wang, W.; Li, J.; Chen, P.; Zhou, C.; Wang, Z. Effects of Freeze-Thaw Cycles on Interfacial Shear Transfer Characteristics in Section Steel Reinforced Concrete Composite Structures with Stud Connectors. Eng. Struct. 2024, 307, 117948. [Google Scholar] [CrossRef]
- Al-Rousan, R.Z.; Alnemrawi, B.a.R. Impact of column axial load level of the seismic behavior of concrete-filled UHPC tubular column-to-footing connections reinforced with different spiral stirrup spacing. Results Eng. 2025, 26, 104952. [Google Scholar] [CrossRef]
- Yun, Y.; Wu, Y.-F. Durability of CFRP–concrete joints under freeze–thaw cycling. Cold Reg. Sci. Technol. 2011, 65, 401–412. [Google Scholar] [CrossRef]
- Özgan, E.; Serin, S. Investigation of certain engineering characteristics of asphalt concrete exposed to freeze–thaw cycles. Cold Reg. Sci. Technol. 2013, 85, 131–136. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, X.; Yu, S.; Guan, J. Effect of Cyclic Soil Freezing and Thawing on the Lateral Load Response of Bridge Pile Foundations. Buildings 2024, 14, 2540. [Google Scholar] [CrossRef]
- Dong, L.; Liu, J.; Wang, K.; Tian, S.; Su, Y. The Longitudinal Push-Out Effect and Differential Settlement Control Measures of the Transition Section of Road and Bridge Induced by Freeze–Thaw Inducing. Sustainability 2024, 16, 9972. [Google Scholar] [CrossRef]
- Zou, Y.; Xu, D. Mechanical Characteristics of Steel Shear Keyed Joints in the Construction and Finished States. Adv. Civ. Eng. 2021, 2021, 7252122. [Google Scholar] [CrossRef]
- Wang, X.; Li, L.; Mu, W.; Yang, T.; Du, Y.; Lu, J. Damage characteristics and mechanisms of shear strength at the interface between fiber-reinforced concrete and rock under freeze-thaw cycles. J. Build. Eng. 2024, 98, 111191. [Google Scholar] [CrossRef]
- Xiao, L.; Wei, X.; Kang, Z.; Zhang, J.; Zhan, G. Numerical Studies on the Performance Degradation of Headed Stud Shear Connectors in Composite Structures Under Freeze–Thaw Cycles. Int. J. Civ. Eng. 2024, 22, 639–653. [Google Scholar] [CrossRef]
- Al-Rousan, R.Z.; Alnemrawi, B.a.R. The extent of high-temperatures on the interfacial shear strength of CFRP-strengthened shear keys: NLFEA and theoretical calculation. Comput. Concr. 2025, 35, 441. [Google Scholar] [CrossRef]
- Gerges, N.N.; Issa, C.A.; Fawaz, S. The effect of construction joints on the flexural bending capacity of singly reinforced beams. Case Stud. Constr. Mater. 2016, 5, 112–123. [Google Scholar] [CrossRef]
- Zou, Y.; Xu, D. Experimental study on shear behavior of joints in precast concrete segmental bridges. Structures 2022, 39, 323–336. [Google Scholar] [CrossRef]
- Ahmed, G.H.; Aziz, O.Q. Shear behavior of dry and epoxied joints in precast concrete segmental box girder bridges under direct shear loading. Eng. Struct. 2019, 182, 89–100. [Google Scholar] [CrossRef]
- AASHTO. Guide Specifications for Design and Construction of Segmental Concrete Bridges 2024; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2024. [Google Scholar]
- Mohamad, M.E.; Ibrahim, I.S.; Abdullah, R.; Abd Rahman, A.B.; Kueh, A.B.H.; Usman, J. Friction and cohesion coefficients of composite concrete-to-concrete bond. Cem. Concr. Compos. 2015, 56, 1–14. [Google Scholar] [CrossRef]
- Buyukozturk, O.; Bakhoum, M.M.; Beattie, S.M. Shear Behavior of Joints in Precast Concrete Segmental Bridges. J. Struct. Eng. 1990, 116, 3380–3401. [Google Scholar] [CrossRef]
- Ahmed, G.H.; Aziz, O.Q. Shear strength of joints in precast posttensioned segmental bridges during 1959–2019, review and analysis. Structures 2019, 20, 527–542. [Google Scholar] [CrossRef]
- Ahmed, G.H.; Aziz, O.Q. Stresses, deformations and damages of various joints in precast concrete segmental box girder bridges subjected to direct shear loading. Eng. Struct. 2020, 206, 110151. [Google Scholar] [CrossRef]
- Turmo, J.; Ramos, G.; Aparicio, A. Towards a model of dry shear keyed joints: Modelling of panel tests. Comput. Concr. 2012, 10, 469–487. [Google Scholar] [CrossRef]
- Li, G.; Yang, D.; Lei, Y. Combined Shear and Bending Behavior of Joints in Precast Concrete Segmental Beams with External Tendons. J. Bridge Eng. 2013, 18, 1042–1052. [Google Scholar] [CrossRef]
- Algorafi, M.A.; Ali, A.A.A.; Othman, I.; Jaafar, M.S.; Anwar, M.P. Experimental study of externally prestressed segmental beam under torsion. Eng. Struct. 2010, 32, 3528–3538. [Google Scholar] [CrossRef]
- Zhou, X.; Mickleborough, N.; Li, Z. Shear Strength of Joints in Precast Concrete Segmental Bridges. ACI Struct. J. 2005, 102, 3–11. [Google Scholar] [CrossRef]
- Rombach, G. Precast segmental box girder bridges with external prestressing-design and construction. Segmental Bridges INSA Rennes 2002, 19, 1–15. [Google Scholar]
- EC2. Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings; British Standard Institution: London, UK, 2004. [Google Scholar]
- Alcalde, M.; Cifuentes, H.; Medina, F. Influence of the number of keys on the shear strength of post-tensioned dry joints. Mater. Construcción 2013, 63, 297–307. [Google Scholar] [CrossRef]
- del Pozo Vindel, F.J. Información sobre ATEP (Asociación Técnica Española del Pretensado), GEHO (Grupo Español del Hormigón), FIP (Federación Internacional del Pretensado) y CEB (Comité Eurointernacional del Hormigón). Hormigón Y Acero 1996, 202, 9–12. [Google Scholar]
- Kim, T.-H.; Kim, Y.-J.; Jin, B.-M.; Shin, H.-M. Numerical study on the joints between precast post-tensioned segments. Int. J. Concr. Struct. Mater. 2007, 19, 3–9. [Google Scholar] [CrossRef]
- Liu, T.; Wang, Z.; Guo, J.; Wang, J. Shear Strength of Dry Joints in Precast UHPC Segmental Bridges: Experimental and Theoretical Research. J. Bridge Eng. 2019, 24, 04018100. [Google Scholar] [CrossRef]
- Turmo, J.; Ramos, G.; Aparicio, A.C. Shear strength of dry joints of concrete panels with and without steel fibres: Application to precast segmental bridges. Eng. Struct. 2006, 28, 23–33. [Google Scholar] [CrossRef]
- ABAQUS Dassault Systemes Simulia Corp. P (2024) ABAQUS Analysis User’s Guide (6.24), 14th ed.; ABAQUS Dassault Systemes Simulia Corp.: Providence, RI, USA, 2024. [Google Scholar]
- Al-Rousan, R.Z.; Alnemrawi, B.a.R. Interaction diagram of rectangular RC columns confined with CFRP composite under biaxial bending. Structures 2025, 75, 108833. [Google Scholar] [CrossRef]
- Al-Rousan, R.Z.; Alnemrawi, B.a.R. Empirical and precise finite element modelling of bond-slip contact behavior between heat-damaged concrete and anchored CFRP composites with groove. Eng. Struct. 2025, 332, 120042. [Google Scholar] [CrossRef]
- Kmiecik, P.; KamiŃSki, M. Modelling of reinforced concrete structures and composite structures with concrete strength degradation taken into consideration. Arch. Civ. Mech. Eng. 2011, 11, 623–636. [Google Scholar] [CrossRef]
- Jiang, H.; Chen, L.; Ma, Z.J.; Feng, W. Shear Behavior of Dry Joints with Castellated Keys in Precast Concrete Segmental Bridges. J. Bridge Eng. 2015, 20, 04014062. [Google Scholar] [CrossRef]
- Shamass, R.; Zhou, X.; Alfano, G. Finite-Element Analysis of Shear-Off Failure of Keyed Dry Joints in Precast Concrete Segmental Bridges. J. Bridge Eng. 2015, 20, 04014084. [Google Scholar] [CrossRef]
- Wai, C.; Rivai, A.; Bapokutty, O. Modelling Optimization Involving Different Types of Elements in Finite Element Analysis. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2013; Volume 1, p. 012036. [Google Scholar] [CrossRef]
- Hou, W.; Peng, M.; Jin, B.; Tao, Y.; Guo, W.; Zhou, L. Influencing Factors and Shear Capacity Formula of Single-Keyed Dry Joints in Segmental Precast Bridges under Direct Shear Loading. Appl. Sci. 2020, 10, 6304. [Google Scholar] [CrossRef]
- Garg, A.K.; Abolmaali, A. Finite-Element Modeling and Analysis of Reinforced Concrete Box Culverts. J. Transp. Eng. 2009, 135, 121–128. [Google Scholar] [CrossRef]
- Shang, H.-s.; Cao, W.-q.; Wang, B. Effect of Fast Freeze-Thaw Cycles on Mechanical Properties of Ordinary-Air-Entrained Concrete. Sci. World J. 2014, 2014, 923032. [Google Scholar] [CrossRef] [PubMed]
- Kaneko, Y.; Connor, J.J.; Triantafillou, T.C.; Leung, C.K. Fracture Mechanics Approach for Failure of Concrete Shear Key. I: Theory. J. Eng. Mech. 1993, 119, 681–700. [Google Scholar] [CrossRef]
- Jiang, H.; Li, Y.; Liu, A.; Ma, Z.J.; Chen, L.; Chen, Y. Shear Behavior of Precast Concrete Segmental Beams with External Tendons. J. Bridge Eng. 2018, 23, 04018049. [Google Scholar] [CrossRef]
- Yang, I.-H.; Kim, K.-C.; Kim, Y.-J. Shear Strength of Dry Joints in Precast Concrete Modules. In Proceedings of the Thirteenth East Asia-Pacific Conference on Structural Engineering and Construction (EASEC-13), Sapporo, Japan, 11–13 September 2013; pp. 1–5. [Google Scholar]
- Bažant, Z.P.; Pfeiffer, P.A. Shear fracture tests of concrete. Mater. Struct. 1986, 19, 111–121. [Google Scholar] [CrossRef]

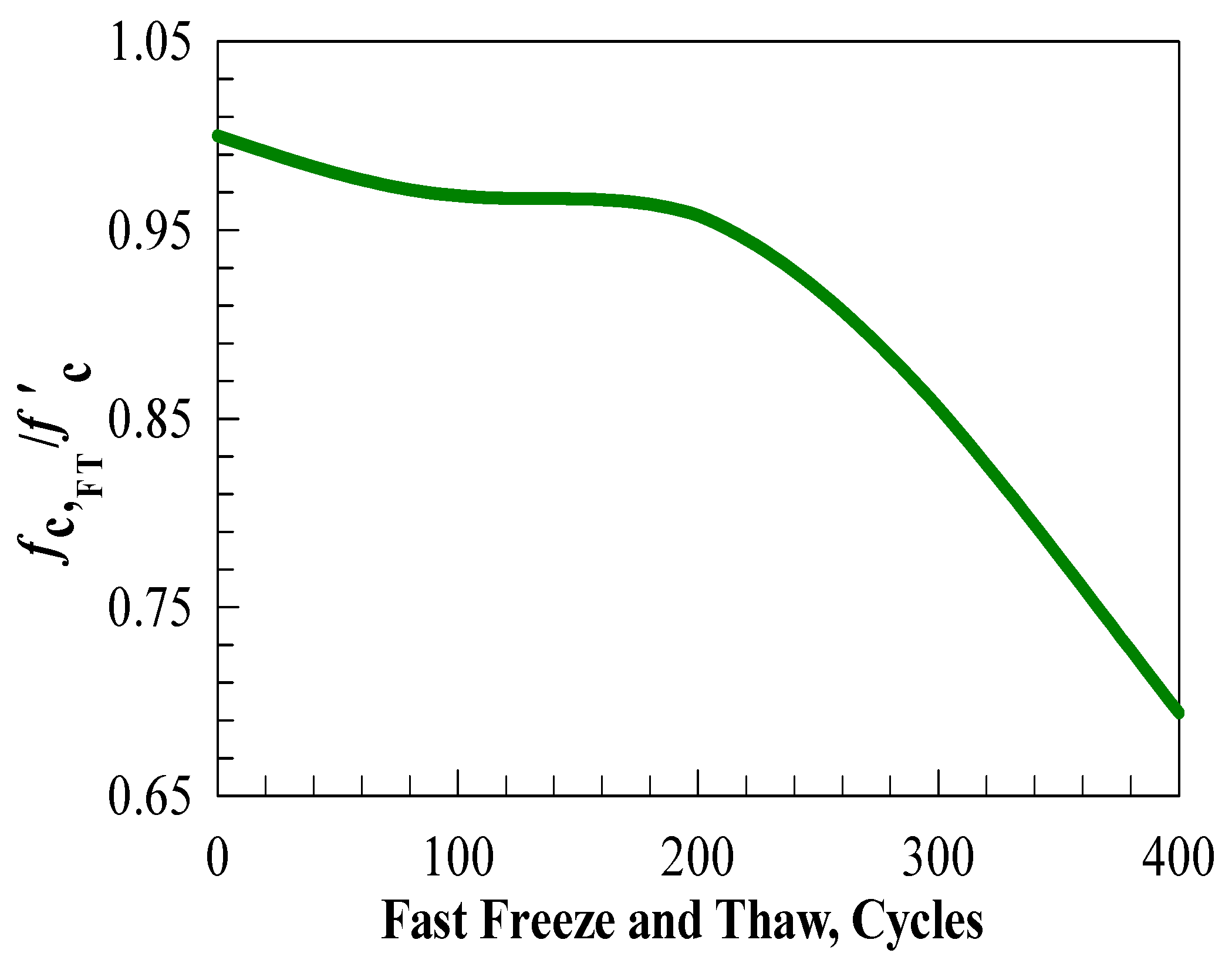



| Keyed Joint Designation | Fast Freeze-Thaw Cycles [40] | Level of Confinement, MPa | , MPa [40] |
|---|---|---|---|
| KJ-FT0-C1 | 0 | 1 | 50.0 |
| KJ-FT0-C2 | 2 | 50.0 | |
| KJ-FT0-C3 | 3 | 50.0 | |
| KJ-FT0-C4 | 4 | 50.0 | |
| KJ-FT0-C5 | 5 | 50.0 | |
| KJ-FT0-C6 | 6 | 50.0 | |
| KJ-FT100-C1 | 100 | 1 | 48.4 |
| KJ-FT100-C2 | 2 | 48.4 | |
| KJ-FT100-C3 | 3 | 48.4 | |
| KJ-FT100-C4 | 4 | 48.4 | |
| KJ-FT100-C5 | 5 | 48.4 | |
| KJ-FT100-C6 | 6 | 48.4 | |
| KJ-FT200-C1 | 200 | 1 | 47.9 |
| KJ-FT200-C2 | 2 | 47.9 | |
| KJ-FT200-C3 | 3 | 47.9 | |
| KJ-FT200-C4 | 4 | 47.9 | |
| KJ-FT200-C5 | 5 | 47.9 | |
| KJ-FT200-C6 | 6 | 47.9 | |
| KJ-FT300-C1 | 300 | 1 | 42.8 |
| KJ-FT300-C2 | 2 | 42.8 | |
| KJ-FT300-C3 | 3 | 42.8 | |
| KJ-FT300-C4 | 4 | 42.8 | |
| KJ-FT300-C5 | 5 | 42.8 | |
| KJ-FT300-C6 | 6 | 42.8 | |
| KJ-FT400-C1 | 400 | 1 | 34.7 |
| KJ-FT400-C2 | 2 | 34.7 | |
| KJ-FT400-C3 | 3 | 34.7 | |
| KJ-FT400-C4 | 4 | 34.7 | |
| KJ-FT400-C5 | 5 | 34.7 | |
| KJ-FT400-C6 | 6 | 34.7 |
| Criteria | New Model | Buyukozturk | AASHTO | Rombach | Turmo | ATEP |
|---|---|---|---|---|---|---|
| R2 | 0.964 | 0.945 | 0.955 | 0.894 | 0.952 | 0.946 |
| RMSE | 34.850 | 94.844 | 30.757 | 86.900 | 118.370 | 25.265 |
| Ref. | Specimen Designation | , (MPa) | , (MPa) | (AJ) (mm2) | Experimental | New Model | AASHTO | ||
|---|---|---|---|---|---|---|---|---|---|
(kN) | (kN) | (kN) | |||||||
| [31] | S60-H10-P1 | 64 | 1.0 | 17,000 | 76 | 87 | 14 | 71 | 7 |
| S60-H10-P2 | 64 | 2.0 | 17,000 | 105 | 106 | 1 | 88 | 16 | |
| S60-H10-P3 | 64 | 3.0 | 17,000 | 131 | 125 | 5 | 105 | 20 | |
| S70-H10-P1 | 64 | 1.0 | 17,000 | 86 | 87 | 1 | 71 | 17 | |
| S70-H10-P2 | 64 | 2.0 | 17,000 | 108 | 106 | 2 | 88 | 19 | |
| S70-H10-P3 | 64 | 3.0 | 17,000 | 135 | 125 | 7 | 105 | 22 | |
| S70-H20-P1 | 64 | 1.0 | 17,000 | 87 | 87 | 0 | 71 | 18 | |
| S70-H20-P3 | 64 | 3.0 | 17,000 | 112 | 125 | 12 | 105 | 6 | |
| [43] | K1-01 | 42 | 1.0 | 20,000 | 90 | 83 | 8 | 97 | 8 |
| K1-02 | 42 | 2.0 | 20,000 | 114 | 101 | 11 | 126 | 11 | |
| K1-03 | 41 | 1.0 | 20,000 | 91 | 82 | 10 | 89 | 2 | |
| K1-04 | 41 | 1.0 | 20,000 | 95 | 82 | 14 | 108 | 14 | |
| 0.79 | 0.46 | ||||||||
| RMSE | 8.7 | 16.3 | |||||||
| Model Designation | , mm | , kN | , kN/mm | , kN.mm | , MPa | , kN | ||
|---|---|---|---|---|---|---|---|---|
| KJ-FT0-C1 | 0.2175 | 214.8 | 1880 | 110 | 4.30 | 0.61 | 214.8 | 1.000 |
| KJ-FT0-C2 | 0.2511 | 267.5 | 2028 | 159 | 5.35 | 0.76 | 272.4 | 1.018 |
| KJ-FT0-C3 | 0.3006 | 330.6 | 2094 | 235 | 6.61 | 0.94 | 326.4 | 0.987 |
| KJ-FT0-C4 | 0.3286 | 384.3 | 2226 | 298 | 7.69 | 1.09 | 378.6 | 0.985 |
| KJ-FT0-C5 | 0.3294 | 423.2 | 2446 | 329 | 8.46 | 1.20 | 429.7 | 1.015 |
| KJ-FT0-C6 | 0.3436 | 471.7 | 2614 | 383 | 9.43 | 1.33 | 479.9 | 1.017 |
| KJ-FT100-C1 | 0.2052 | 198.1 | 1837 | 96 | 3.96 | 0.56 | 197.1 | 0.995 |
| KJ-FT100-C2 | 0.2386 | 246.6 | 1968 | 139 | 4.93 | 0.70 | 249.9 | 1.013 |
| KJ-FT100-C3 | 0.2876 | 304.8 | 2018 | 207 | 6.10 | 0.86 | 299.4 | 0.982 |
| KJ-FT100-C4 | 0.3164 | 354.3 | 2132 | 265 | 7.09 | 1.00 | 347.3 | 0.980 |
| KJ-FT100-C5 | 0.3192 | 390.2 | 2327 | 294 | 7.80 | 1.10 | 394.2 | 1.010 |
| KJ-FT100-C6 | 0.3350 | 435.0 | 2472 | 344 | 8.70 | 1.23 | 440.3 | 1.012 |
| KJ-FT200-C1 | 0.1963 | 184.8 | 1792 | 86 | 3.70 | 0.52 | 182.8 | 0.989 |
| KJ-FT200-C2 | 0.2335 | 234.8 | 1914 | 129 | 4.70 | 0.66 | 231.8 | 0.987 |
| KJ-FT200-C3 | 0.2632 | 281.7 | 2038 | 175 | 5.63 | 0.80 | 277.7 | 0.986 |
| KJ-FT200-C4 | 0.2797 | 316.0 | 2151 | 209 | 6.32 | 0.89 | 322.1 | 1.019 |
| KJ-FT200-C5 | 0.3133 | 366.7 | 2228 | 271 | 7.33 | 1.04 | 365.6 | 0.997 |
| KJ-FT200-C6 | 0.3216 | 402.2 | 2381 | 305 | 8.04 | 1.14 | 408.3 | 1.015 |
| KJ-FT300-C1 | 0.1753 | 162.7 | 1767 | 67 | 3.25 | 0.46 | 161.1 | 0.990 |
| KJ-FT300-C2 | 0.2067 | 202.6 | 1866 | 99 | 4.05 | 0.57 | 204.3 | 1.008 |
| KJ-FT300-C3 | 0.2526 | 250.4 | 1888 | 149 | 5.01 | 0.71 | 244.8 | 0.977 |
| KJ-FT300-C4 | 0.2815 | 291.1 | 1968 | 193 | 5.82 | 0.82 | 283.9 | 0.975 |
| KJ-FT300-C5 | 0.2963 | 328.5 | 2111 | 230 | 6.57 | 0.93 | 322.2 | 0.981 |
| KJ-FT300-C6 | 0.3058 | 357.3 | 2224 | 258 | 7.15 | 1.01 | 359.9 | 1.007 |
| KJ-FT400-C1 | 0.1529 | 137.4 | 1711 | 50 | 2.75 | 0.39 | 135.3 | 0.984 |
| KJ-FT400-C2 | 0.1853 | 174.6 | 1794 | 76 | 3.49 | 0.49 | 171.5 | 0.982 |
| KJ-FT400-C3 | 0.2127 | 209.5 | 1876 | 105 | 4.19 | 0.59 | 205.5 | 0.981 |
| KJ-FT400-C4 | 0.2300 | 235.0 | 1945 | 128 | 4.70 | 0.66 | 238.4 | 1.014 |
| KJ-FT400-C5 | 0.2699 | 279.5 | 1972 | 178 | 5.59 | 0.79 | 270.5 | 0.968 |
| KJ-FT400-C6 | 0.2735 | 299.1 | 2082 | 193 | 5.98 | 0.85 | 302.2 | 1.010 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alnemrawi, B.R.; Al-Rousan, R. Influence of Fast Freeze-Thaw Cycles on the Behavior of Segmental Bridge Shear Key Joints Using Nonlinear Finite Element Analysis. Buildings 2025, 15, 1892. https://doi.org/10.3390/buildings15111892
Alnemrawi BR, Al-Rousan R. Influence of Fast Freeze-Thaw Cycles on the Behavior of Segmental Bridge Shear Key Joints Using Nonlinear Finite Element Analysis. Buildings. 2025; 15(11):1892. https://doi.org/10.3390/buildings15111892
Chicago/Turabian StyleAlnemrawi, Bara’a R., and Rajai Al-Rousan. 2025. "Influence of Fast Freeze-Thaw Cycles on the Behavior of Segmental Bridge Shear Key Joints Using Nonlinear Finite Element Analysis" Buildings 15, no. 11: 1892. https://doi.org/10.3390/buildings15111892
APA StyleAlnemrawi, B. R., & Al-Rousan, R. (2025). Influence of Fast Freeze-Thaw Cycles on the Behavior of Segmental Bridge Shear Key Joints Using Nonlinear Finite Element Analysis. Buildings, 15(11), 1892. https://doi.org/10.3390/buildings15111892







