Dynamic Damage Characteristics of Red Sandstone: An Investigation of Experiments and Numerical Simulations
Abstract
1. Introduction
2. Experimental Materials and Methods
2.1. Engineering Background
2.2. Specimen Preparation
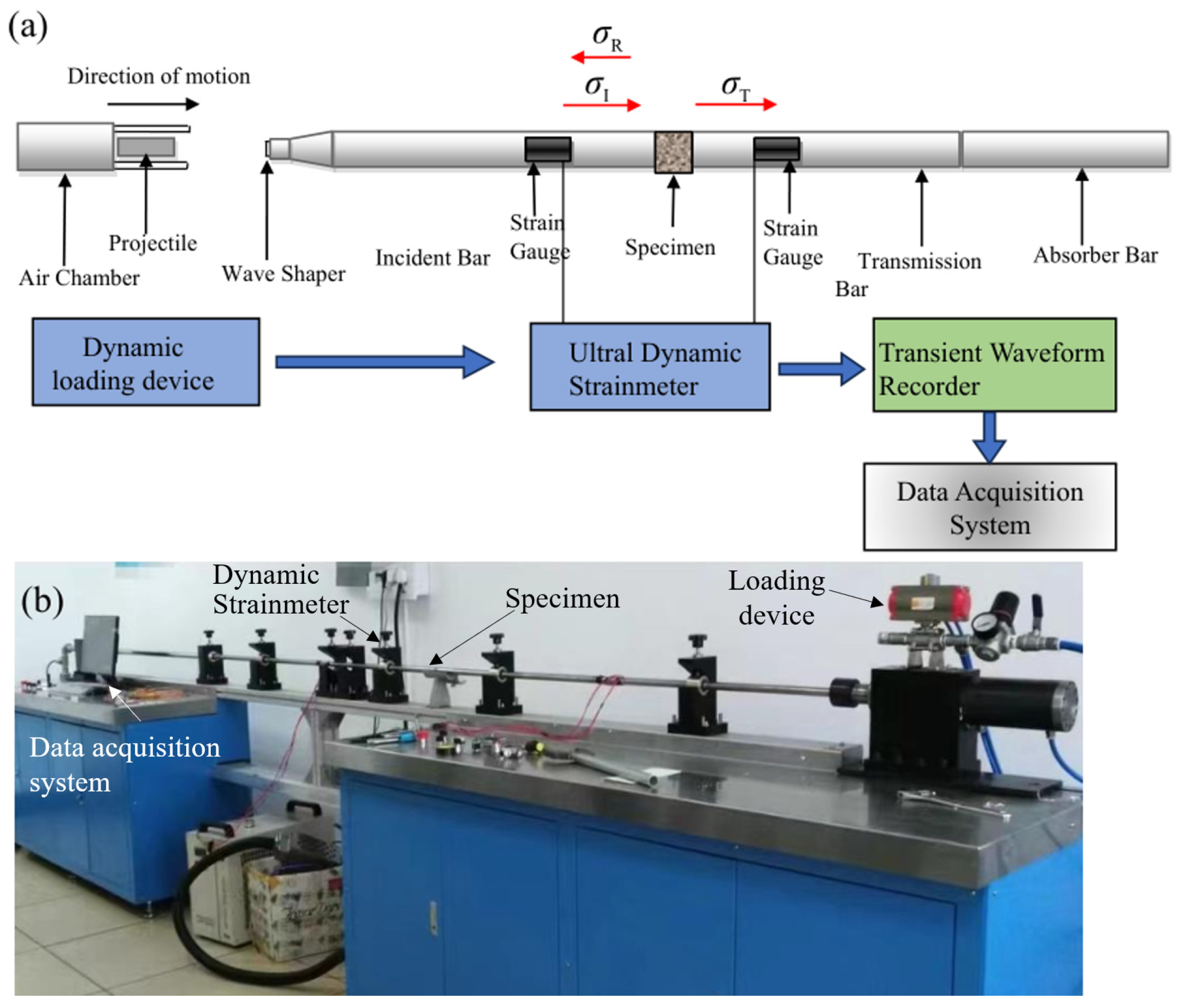
2.3. Testing Program
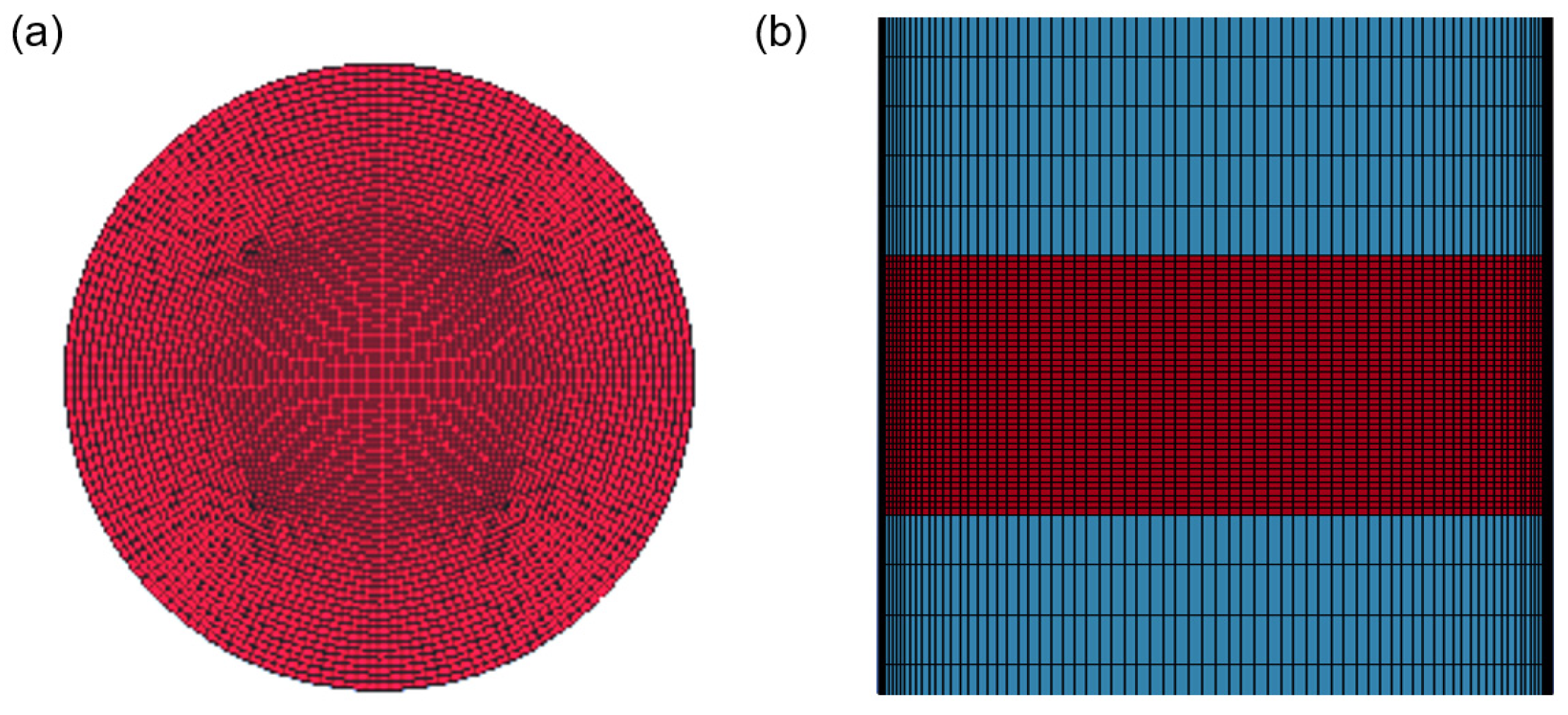
2.4. Numerical Modelling and Analysis
3. Results
3.1. Test Conditions
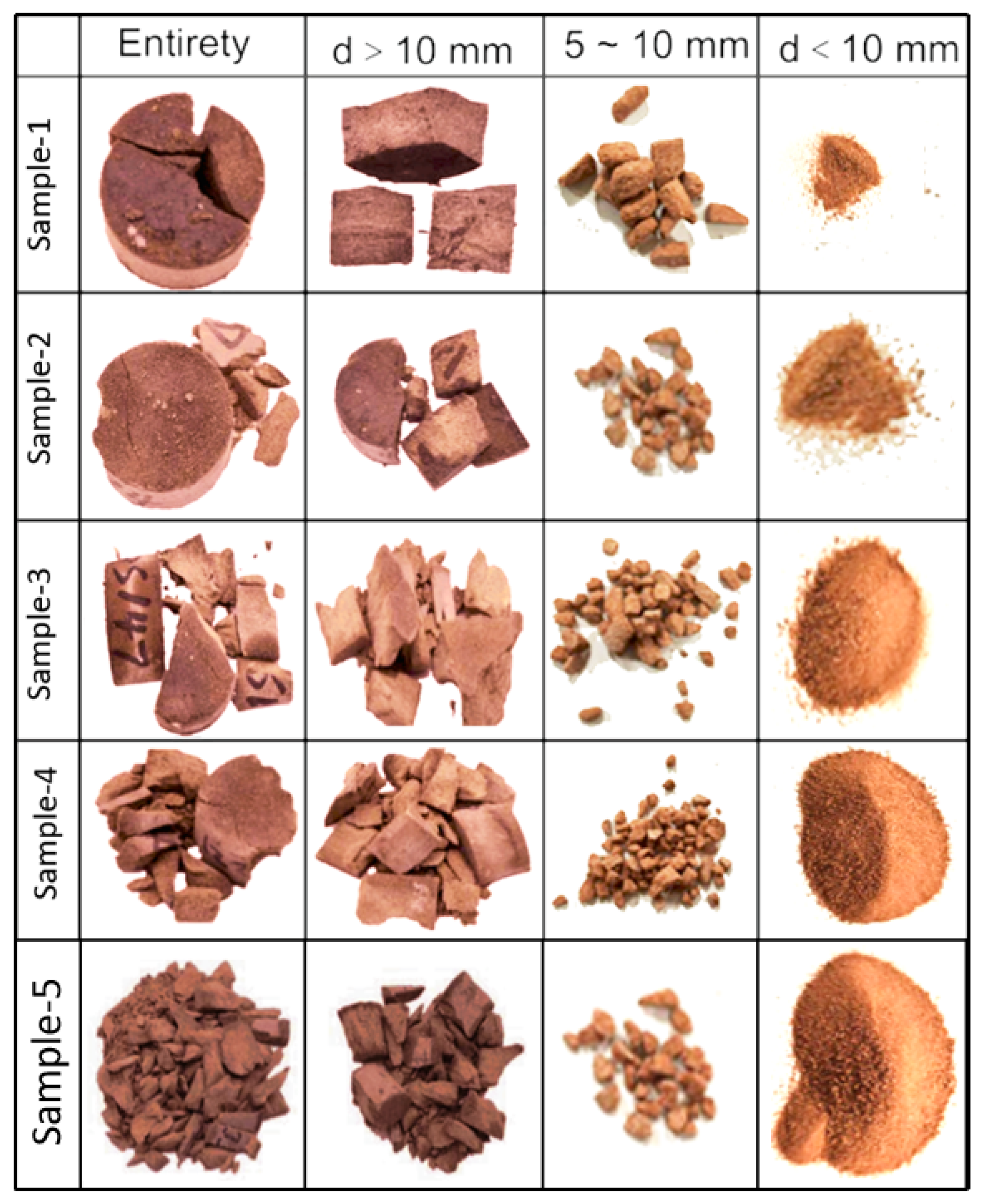
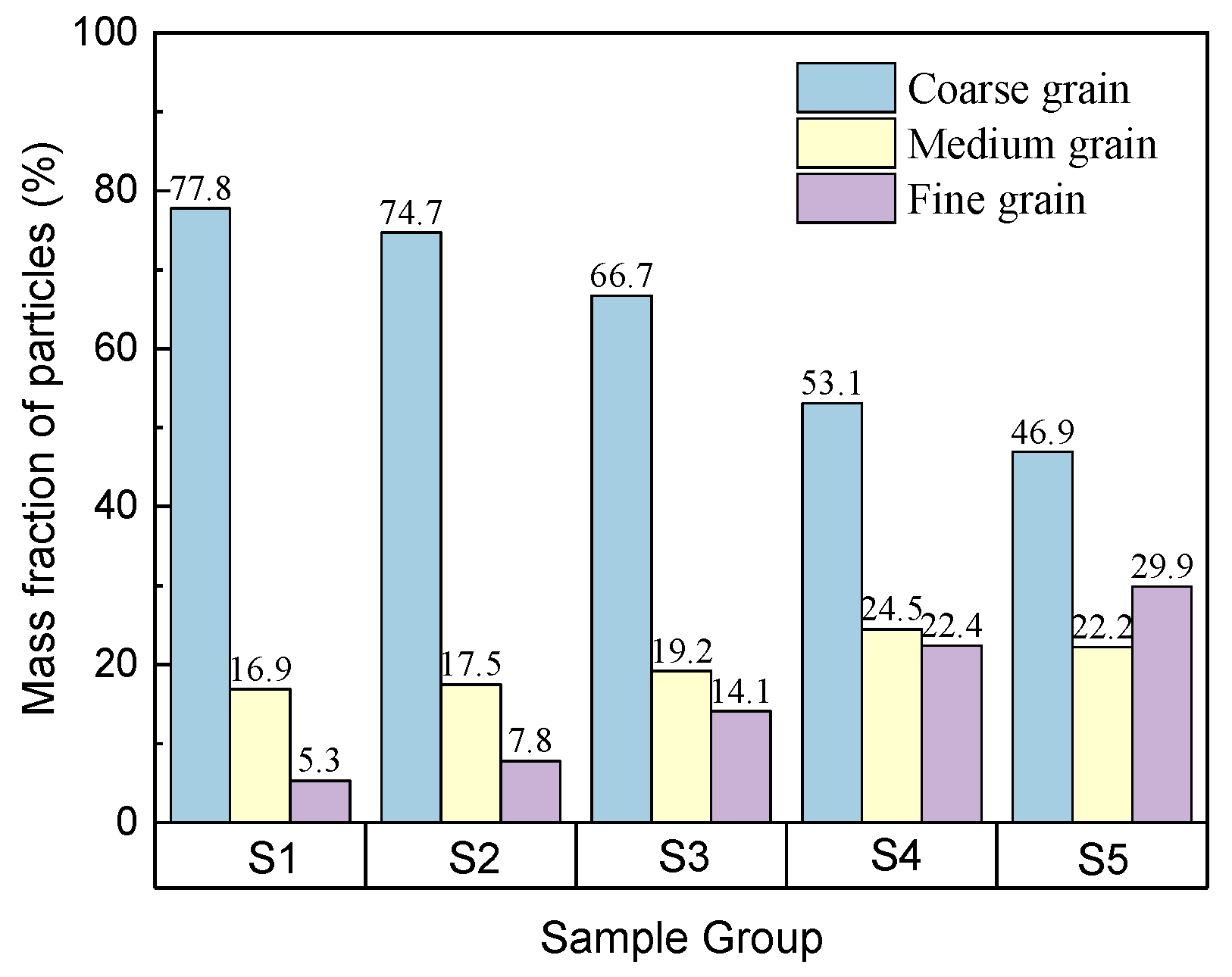
3.2. Fracture Morphology of Red Sandstone
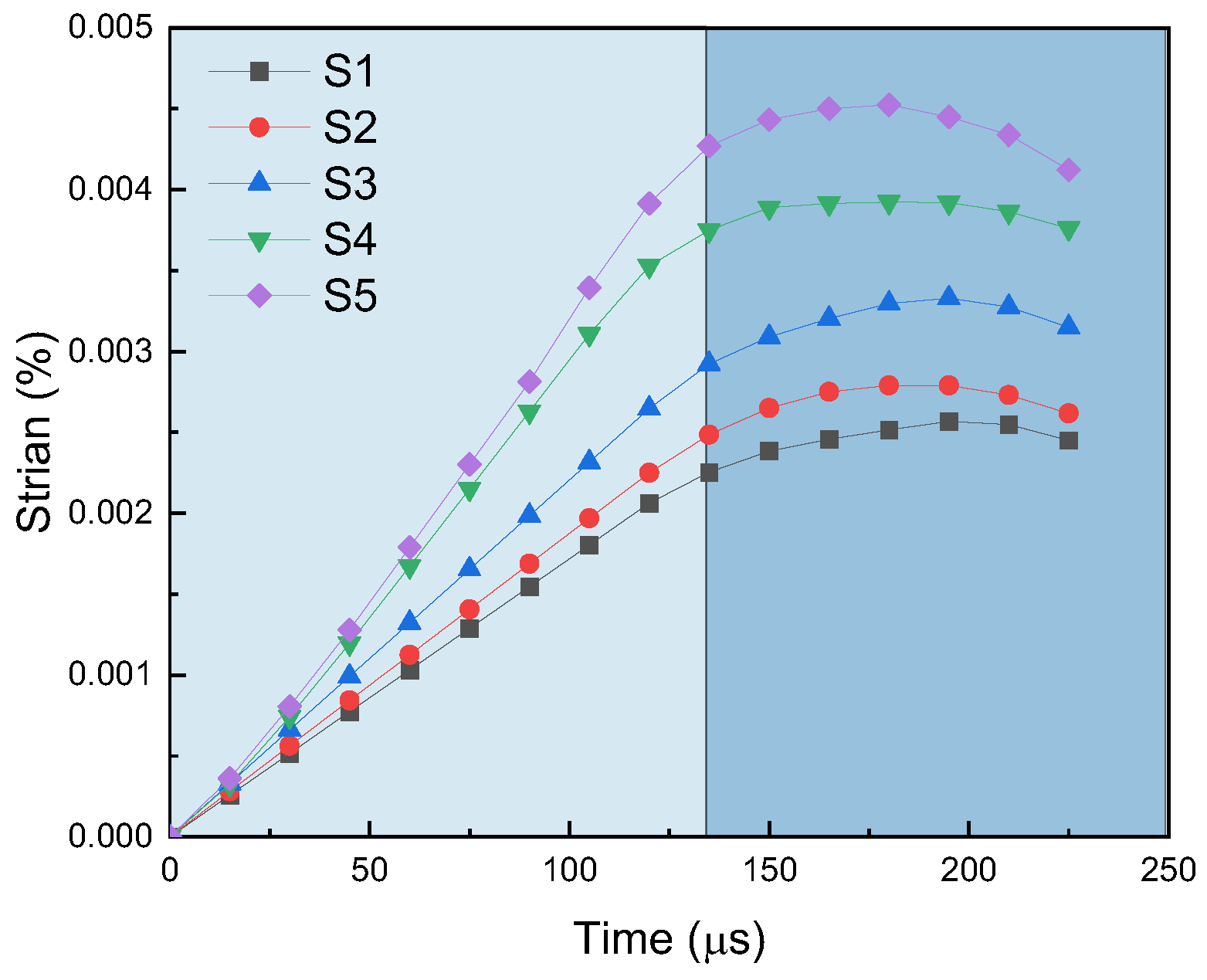
3.3. Stress-Strain Curves
4. Simulation Analysis
5. Discussion
5.1. Comparison of Simulated and Tested Results on Stress-Strain Relationship
5.2. Comparison of Simulated and Tested Results on Failure Modes
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mangano, G.; Alves, T.M.; Zecchin, M.; Civile, D.; Critelli, S. The Rossano-San Nicola Fault Zone evolution impacts the burial and maturation histories of the Crotone Basin, Calabrian Arc, Italy. Pet. Geosci. 2023, 29, 2022–2085. [Google Scholar] [CrossRef]
- Sadisun, I.A.; Bandono; Shimada, H.; Ichinose, M.; Matsui, K. Physical disintegration characterization of mudrocks subjected to slaking exposure and immersion tests. Indones. J. Geosci. 2010, 5, 219–255. [Google Scholar]
- Walske, M.L.; McWilliam, H.; Doherty, J.; Fourie, A. Influence of curing temperature and stress conditions on mechanical properties of cementing paste backfill. Can. Geotech. J. 2016, 53, 148–161. [Google Scholar] [CrossRef]
- Liu, J.; Xu, Q.; Wang, S.; Siva Subramanian, S.; Wang, L.; Qi, X. Formation and chemo-mechanical characteristics of weak clay interlayers between alternative mudstone and sandstone sequence of gently inclined landslides in Nanjiang, SW China. Bull. Eng. Geol. Environ. 2020, 79, 4701–4715. [Google Scholar] [CrossRef]
- Njeru, R.M.; Sofyan, A.; Halisch, M.; Kóbor, B.; Szanyi, J. Optimizing Micro-CT Resolution for Geothermal Reservoir Characterization in the Pannonian Basin. Energies 2024, 17, 3081. [Google Scholar] [CrossRef]
- Gelencsér, O.; Árvai, C.; Mika, L.T.; Breitner, D.; LeClair, D.; Szabó, C.; Falus, G.; Szabó-Krausz, Z. Effect of hydrogen on calcite reactivity in sandstone reservoirs: Experimental results compared to geochemical modeling predictions. J. Energy Storage 2023, 61, 106737. [Google Scholar] [CrossRef]
- Munoz, H.; Taheri, A.; Chanda, E. Rock Drilling Performance Evaluation by an Energy Dissipation Based Rock Brittleness Index. Rock Mech. Rock Eng. 2016, 49, 3343–3355. [Google Scholar] [CrossRef]
- Michal, K.; Pawel, B.; Jerzy, M. Determination and validation of Karagozian-Case Concrete constitutive model parameters for numerical modeling of dolomite rock. Int. J. Rock Mech. Min. Sci. 2020, 129, 512–522. [Google Scholar]
- Kong, L.W.; Zeng, Z.X.; Bai, W.; Wang, M. Engineering geological properties of weathered swelling mudstones and their effectson the landslides occurrence in the Yanji section of the Jilin-Hunchun high-speed railway. Bull. Eng. Geol. Environ. 2018, 77, 1491–1503. [Google Scholar] [CrossRef]
- Chloe, A. Micro-macro mechanics of damage and healing in rocks. Open Geomech. 2020, 25, 251–257. [Google Scholar]
- Alves, M.; Karagiozova, D.; Micheli, G.B.; Calle, M.A.G. Limiting the influence of friction on the split Hopkinson pressure bar tests by using a ring specimen. Int. J. Impact. Eng. 2012, 49, 130–141. [Google Scholar] [CrossRef]
- Che, W.; Li, L.; Chen, Z.; Liang, D.; Guo, Y. Impact Resistance of Rubberized Alkali-Activated Concrete Incorporating Recycled Aggregate and Recycled Steel Fiber. Buildings 2024, 14, 322. [Google Scholar] [CrossRef]
- Gao, H.; An, R.; Zhang, X.; Wang, G.; Liu, X.; Xu, Y. Dynamic evolution of desiccation cracks and their relationship with the hydraulic properties of expansive soil. Int. J. Geomech. 2024, 24, 04023299. [Google Scholar] [CrossRef]
- Yao, Y.; Zhao, F.; Li, J.; Liu, J.; Liu, Z.; Wang, Y.; Zhuang, R.; Liu, L.; Zhao, Y.; Xu, Z. SHPB Experiment and MPM Simulation on Dynamic Properties of Unsaturated Clay UnderImpact Loading. Appl. Sci. 2025, 15, 3123. [Google Scholar] [CrossRef]
- Qi, C.Z.; Wang, M.Y.; Bai, J.P.; Wei, X.K.; Wang, H.S. Investigation into size and strain rate effects on the strength of rock-like materials. Int. J. Rock Mech. Min. Sci. 2016, 86, 132–140. [Google Scholar] [CrossRef]
- Hartley, R.S.; Cloete, T.J.; Nurick, G.N. An experimental assessment of friction effects in the split Hopkinson pressure bar using the ring compression test. Int. J. Impact. Eng. 2007, 34, 1705–1728. [Google Scholar] [CrossRef]
- Maassen, S.F.; Niekamp, R.; Bergmann, J.A.; Pöhl, F.; Schröder, J.; Wiederkehr, P. Modeling of the Split-Hopkinson-Pressure-Bar experiment with the explicit material point method. Comput. Part. Mech. 2022, 9, 153–166. [Google Scholar] [CrossRef]
- Zhu, W.C.; Bai, Y.; Li, X.B.; Niu, L.L. Numerical simulation on rock failure under combined static and dynamic loading during SHPB tests. Int. J. Impact. Eng. 2012, 49, 142–157. [Google Scholar] [CrossRef]
- Mahabadi, O.K.; Cottrell, B.E.; Grasselli, G. An Example of Realistic Modelling of Rock Dynamics Problems: FEM/DEM Simulation of Dynamic Brazilian Test on Barre Granite. Rock. Mech. Rock. Eng. 2010, 43, 707–716. [Google Scholar] [CrossRef]
- Flores-Johnson, E.A.; Li, Q.M. Structural Effects on Compressive Strength Enhancement of Concrete-like Materials in a Split Hopkinson Pressure Bar Test. Int. J. Impact. Eng. 2017, 109, 408–418. [Google Scholar] [CrossRef]
- Jankowiak, T.; Rusinek, A.; Voyiadjis, G.Z. Modeling and Design of SHPB to Characterize Brittle Materials under Compression for High Strain Rates. Materials 2020, 13, 2191. [Google Scholar] [CrossRef] [PubMed]
- Yao, W.; Xia, K.W.; Zhang, T. Dynamic fracture test of Laurentian granite subjected to hydrostatic pressure. Exp. Mech. 2019, 59, 245–250. [Google Scholar] [CrossRef]
- Wang, C.L.; Zhou, B.K.; Li, C.F.; Cao, C.; Sui, Q.R.; Zao, G.M.; Yu, W.J.; Chen, Z.; Wang, Y.; Liu, B.; et al. Experimental investigation on the spatio-temporal-energy evolution pattern of limestone fracture using acoustic emission monitoring. J. Appl. Geophys. 2022, 206, 104787. [Google Scholar] [CrossRef]
- Gong, F.Q.; Li, X.B.; Rao, Q.H.; Liu, X. Reference method for determining sample size in SHPB tests of rock materials. J. Vib. Shock 2013, 32, 24–28. [Google Scholar]
- Xu, D.S.; Zhang, Z.J.; Qin, Y.; Yang, Y. Effect of particle size on the failure behavior of cemented coral sand under impact loading. Soil Dyn. Earthq. Eng. 2021, 149, 106884. [Google Scholar] [CrossRef]
- Prabhu, S.; Qiu, T. Simulation of Split Hopkinson Pressure Bar Tests on Sands Using the Discrete-Element Method. Int. J. Geomech. 2022, 22, 06021036. [Google Scholar] [CrossRef]
- Rotariu, A.-N.; Trana, E.; Matache, L. Young’s Modulus Calculus Using Split Hopkinson Bar Tests on Long and Thin Material Samples. Materials 2022, 15, 3058. [Google Scholar] [CrossRef] [PubMed]
- Khosravani, M.R. Inverse characterization of UHPC material based on Hopkinson bar test. Appl. Eng. Sci. 2021, 6, 100043. [Google Scholar] [CrossRef]
- Merle, R.; Zhao, H. On the errors associated with the use of large diameter SHPB, correction for radially non-uniform distribution of stress and particle velocity in SHPB testing. Int. J. Impact Eng. 2006, 32, 1964–1980. [Google Scholar] [CrossRef]
- Tian, H.; Kempka, T.; Yu, S.; Ziegler, M. Mechanical properties of sandstones exposed to high temperature. Rock. Mech. Rock. Eng. 2016, 49, 321–327. [Google Scholar] [CrossRef]
- Fang, F.; Chen, S.J.; Wang, Y.J.; Huang, W.P.; Han, Z.Y. Cracking mechanism and strength criteria evaluation of granite affected by intermediate principal stresses subjected to unloading stress state. Int. J. Rock Mech. Min. Sci. 2021, 143, 104783. [Google Scholar] [CrossRef]
- Gavrus, A.; Bucur, F.; Rotariu, A.; Cananau, S. Mechanical behavior analysis of metallic materials using a Finite Element modeling of the SHPB test, a numerical calibration of the bar’s elastic strains and an inverse analysis method. Int. J. Mater. Form. 2014, 8, 567–579. [Google Scholar] [CrossRef]







| Parameter | Dry Density (g/cm) | Saturation Degree (%) | Cohesion (MPa) | Internal Friction Angle (%) | Elastic Modulus (GPa) | Permeability (m/s) |
|---|---|---|---|---|---|---|
| Value | 2.37 | 23.5 | 6.42 | 39.51 | 5.43 | 1.52 × 10−7 |
| COV | 6.2 | 13.5 | 8.8 | 6.7 | 11.2 | 9.3 |
| Specimen | Diameter (mm) | Thickness (mm) | Impact Load/MPa | Velocity (m·s−1) | Peak Stress/MPa | Strain Rate/s−1 | Degree of Fragmentation |
|---|---|---|---|---|---|---|---|
| S1 | 49.93 | 25.08 | 0.5 | 4.65 | 39.81 | 30.22 | Minor cracking |
| S2 | 50.02 | 24.93 | 0.5 | 4.92 | 43.65 | 32.53 | Minor cracking |
| S3 | 49.96 | 25.02 | 0.6 | 6.12 | 53.22 | 75.25 | Severe cracking |
| S4 | 50.07 | 25.11 | 0.7 | 8.00 | 89.30 | 94.24 | Severe fragmentation |
| S5 | 50.05 | 25.13 | 0.8 | 9.27 | 122.14 | 113.7 | Pulverization |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, Y.; Su, Y.; Han, R.; Li, C.; An, R. Dynamic Damage Characteristics of Red Sandstone: An Investigation of Experiments and Numerical Simulations. Buildings 2025, 15, 1845. https://doi.org/10.3390/buildings15111845
Qian Y, Su Y, Han R, Li C, An R. Dynamic Damage Characteristics of Red Sandstone: An Investigation of Experiments and Numerical Simulations. Buildings. 2025; 15(11):1845. https://doi.org/10.3390/buildings15111845
Chicago/Turabian StyleQian, Yelin, Ying Su, Ruicai Han, Changchun Li, and Ran An. 2025. "Dynamic Damage Characteristics of Red Sandstone: An Investigation of Experiments and Numerical Simulations" Buildings 15, no. 11: 1845. https://doi.org/10.3390/buildings15111845
APA StyleQian, Y., Su, Y., Han, R., Li, C., & An, R. (2025). Dynamic Damage Characteristics of Red Sandstone: An Investigation of Experiments and Numerical Simulations. Buildings, 15(11), 1845. https://doi.org/10.3390/buildings15111845






