Research on the Longitudinal Deformation of Segments Induced by Pipe-Jacking Tunneling over Existing Shield Tunnels
Abstract
1. Introduction
2. On-Site Monitoring and Analysis of Shield Tunnel Deformation
2.1. Overview of the Project and Configuration of Monitoring Points
2.2. Analysis of Displacement Monitoring Data for Existing Shield Tunnel Structures
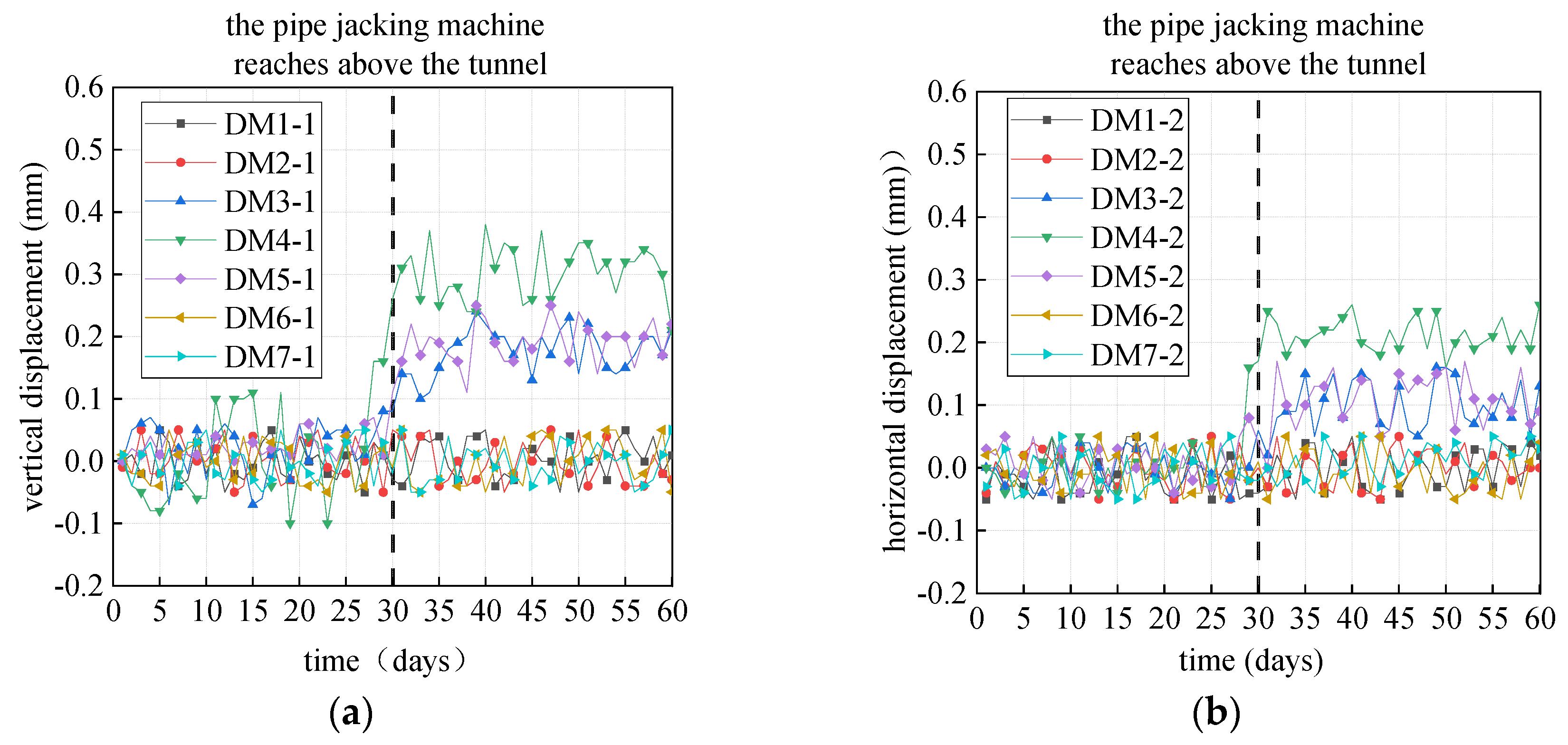
2.2.1. Analysis of Cumulative Deformation
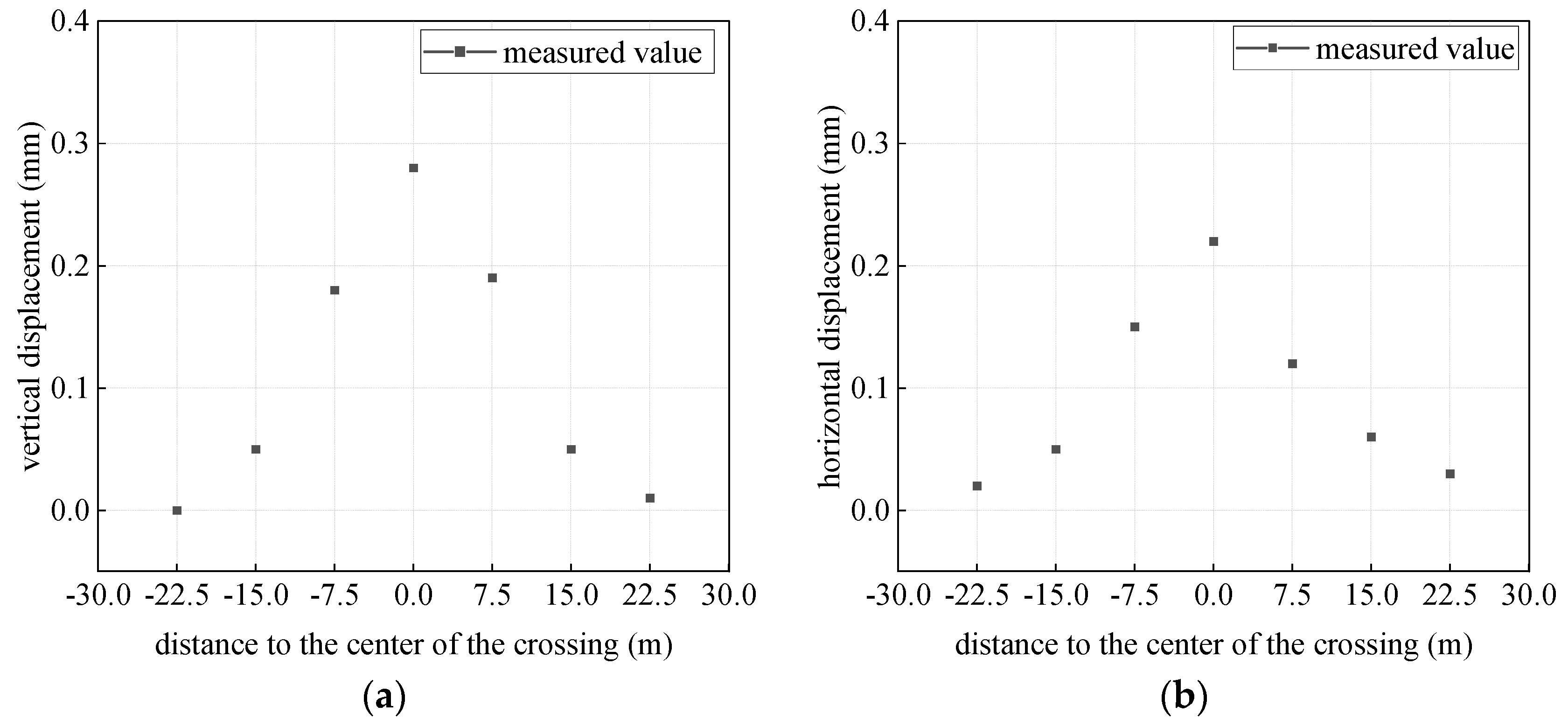
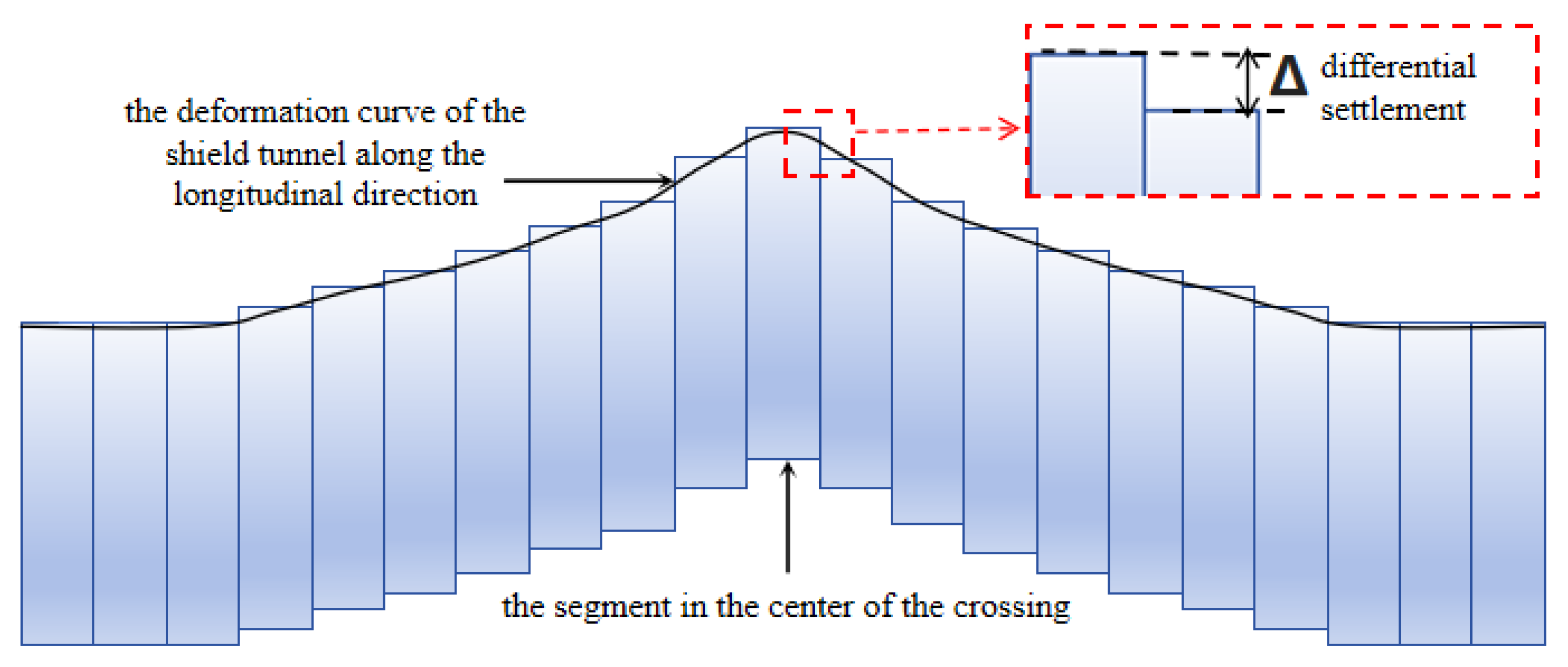
2.2.2. Analysis of Longitudinal Deformation
3. Numerical Model
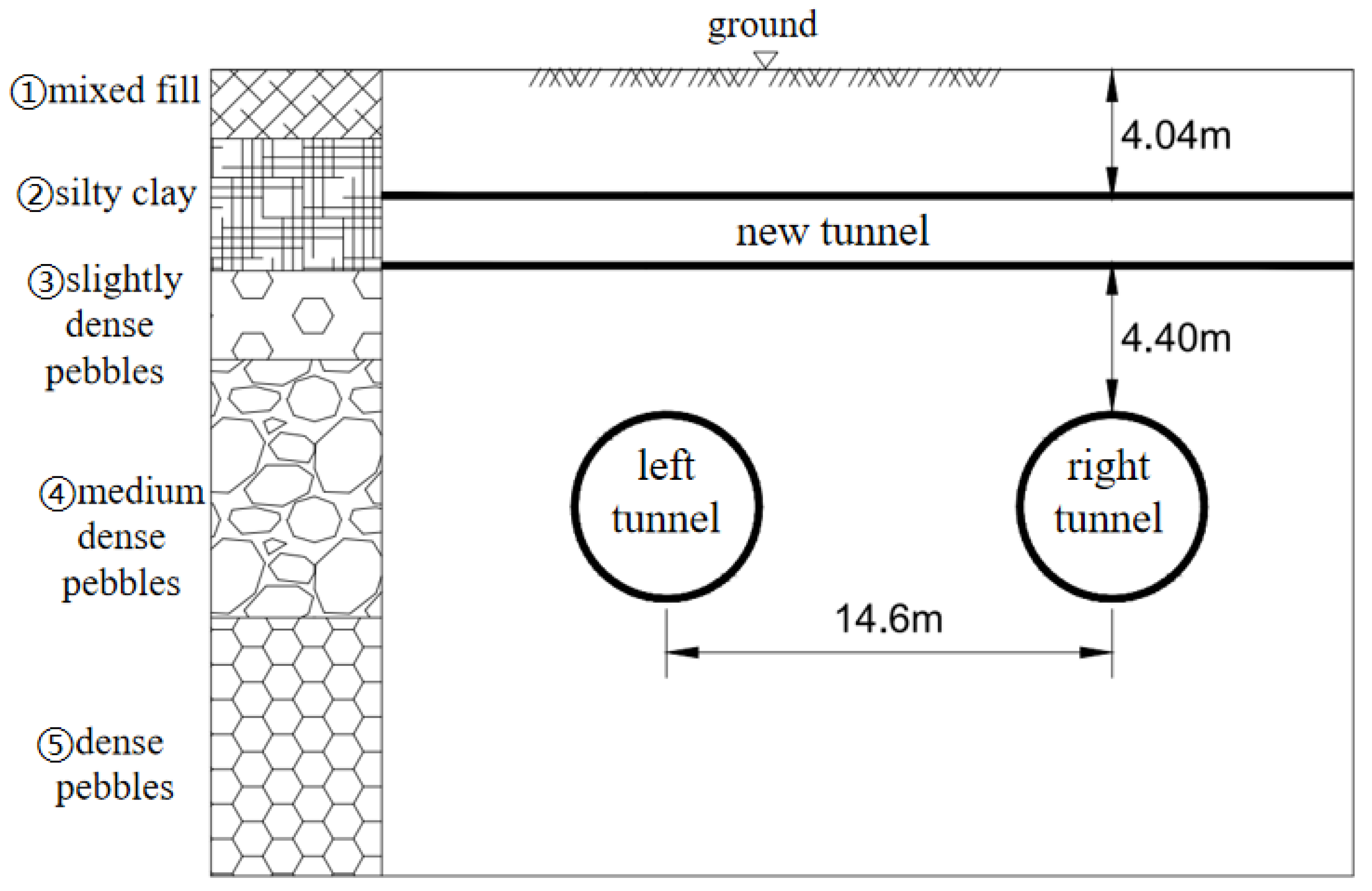
3.1. Establishment of Numerical Model
3.2. Assumptions of Numerical Model
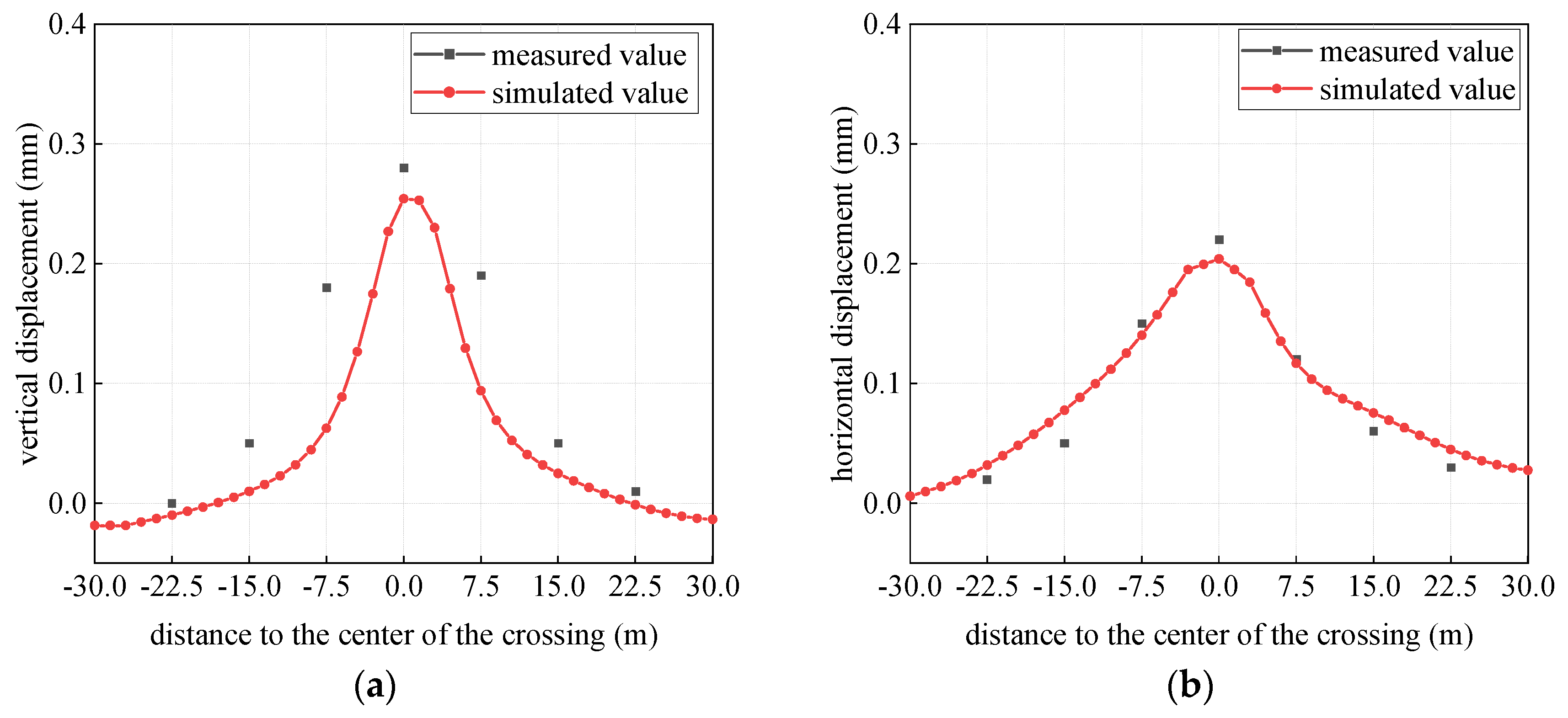
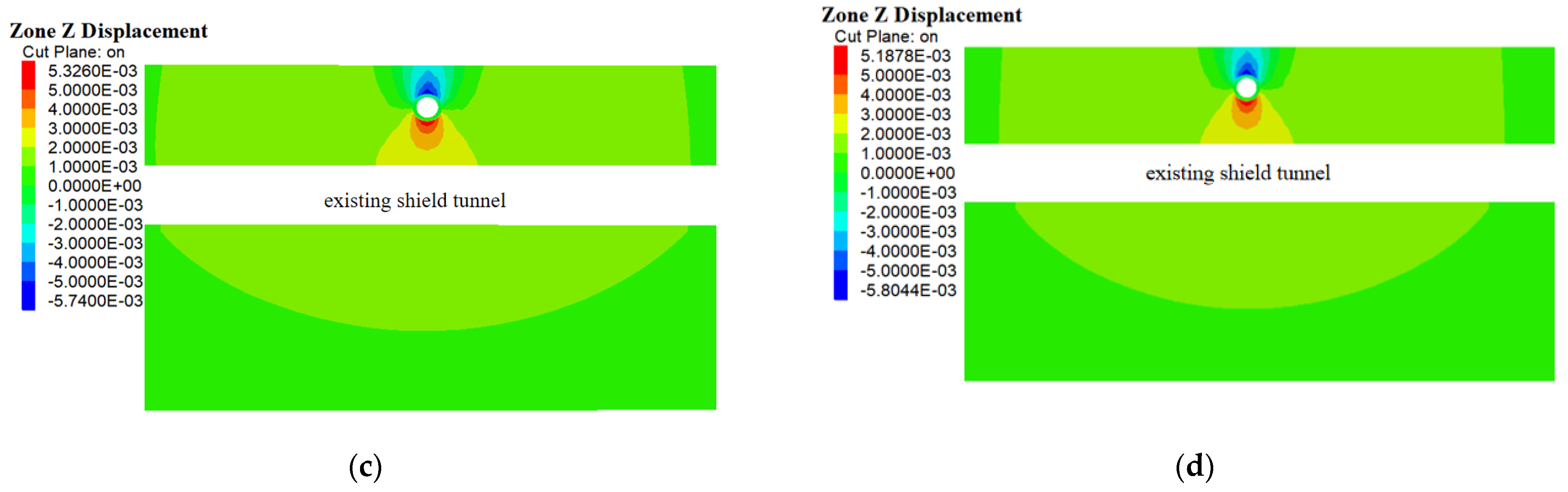
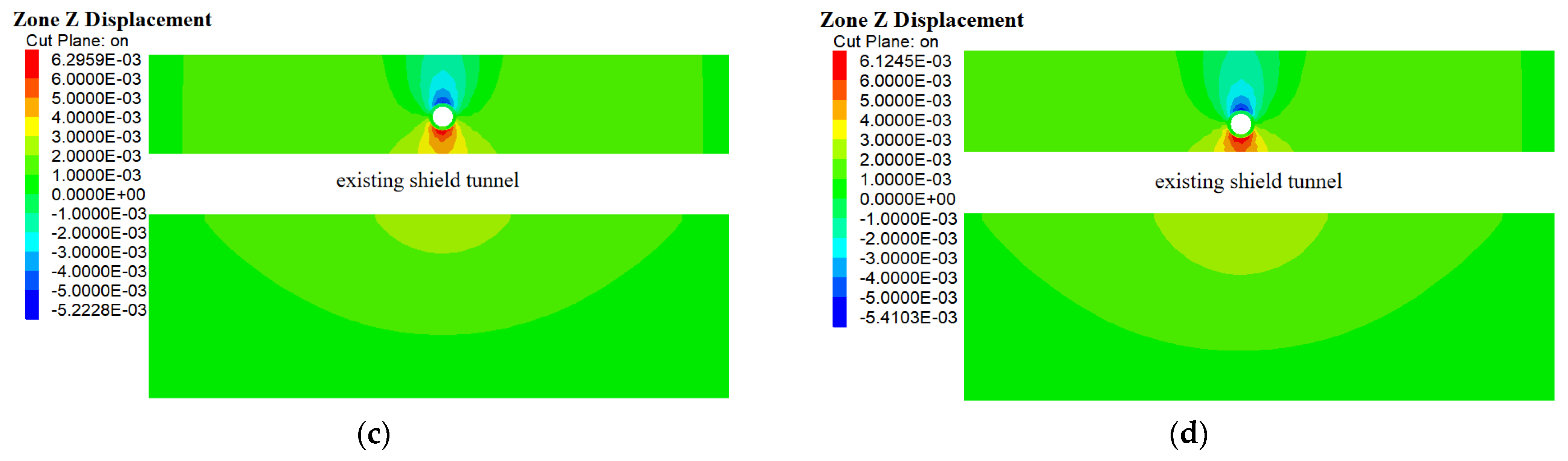
3.3. Validation of Numerical Model
4. Results and Discussion
4.1. Different Geological Conditions of the Shield Tunnel
4.1.1. Longitudinal Deformation of Shield Segments
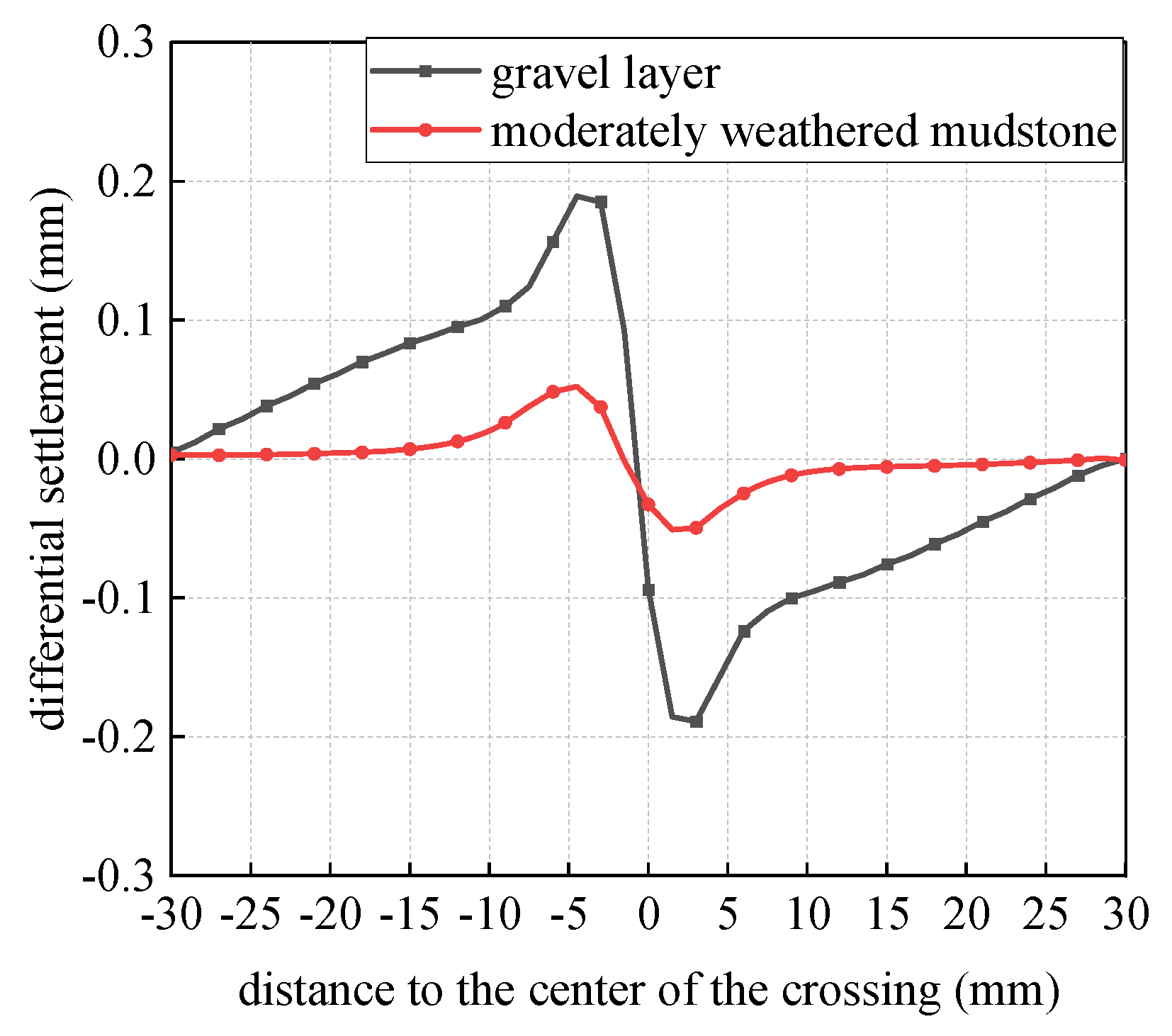
4.1.2. Differential Settlement of Shield Segments
4.2. Different Angles Between Pipes and Shield Tunnels
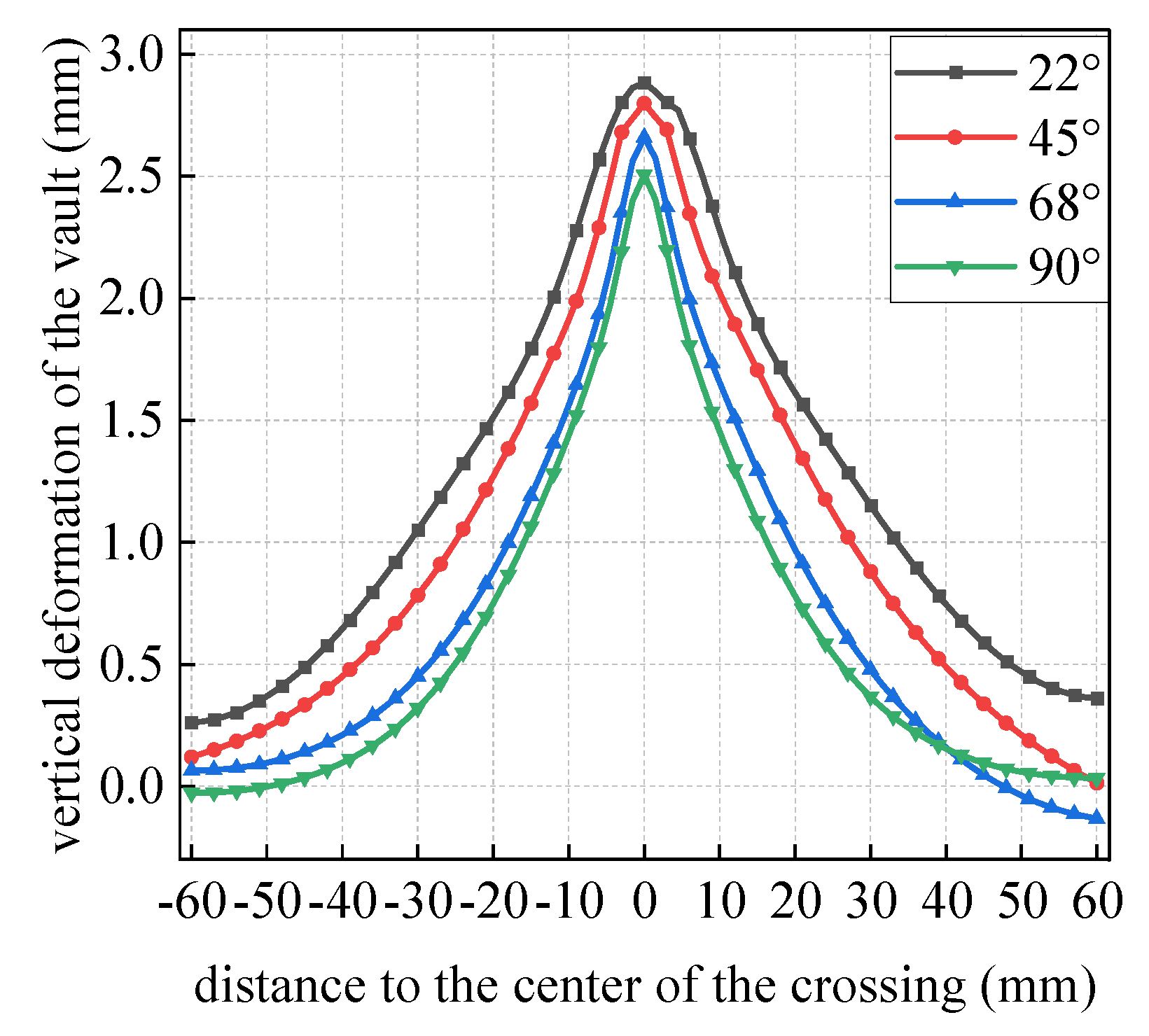
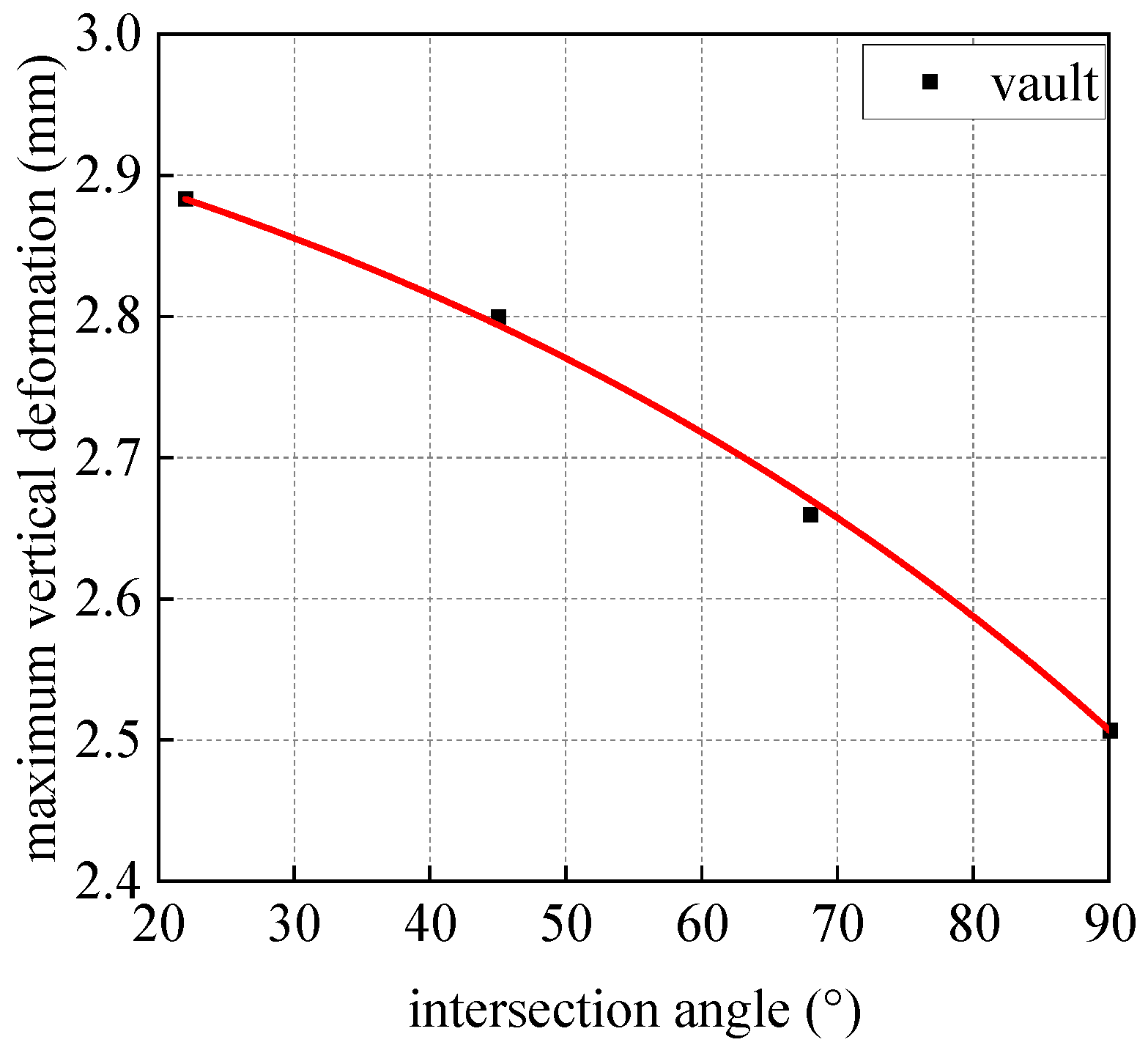
4.2.1. Longitudinal Deformation of Shield Segments
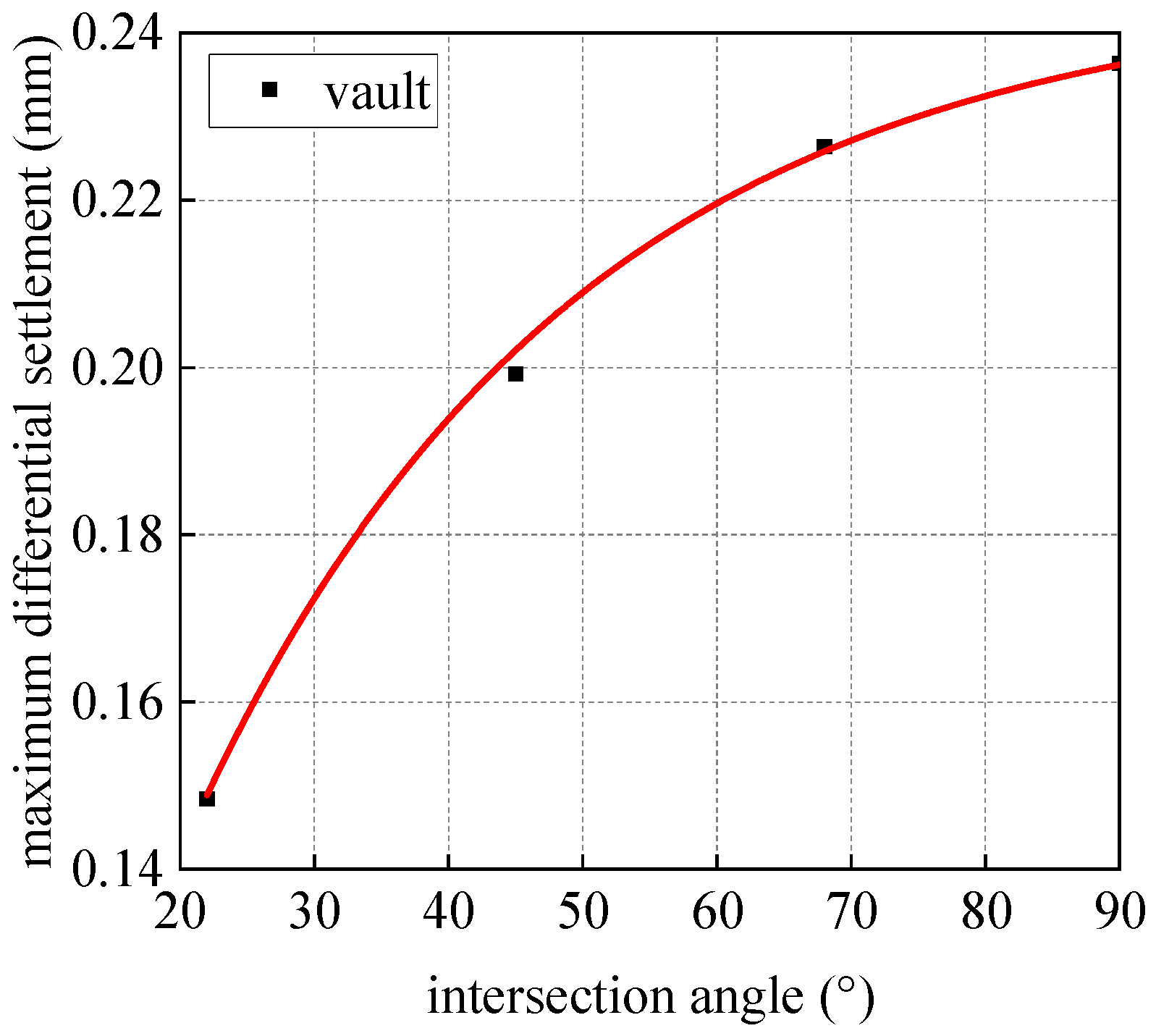
4.2.2. Differential Settlement of Shield Segments
4.3. Different Vertical Clearances Between Pipes and Shield Tunnels
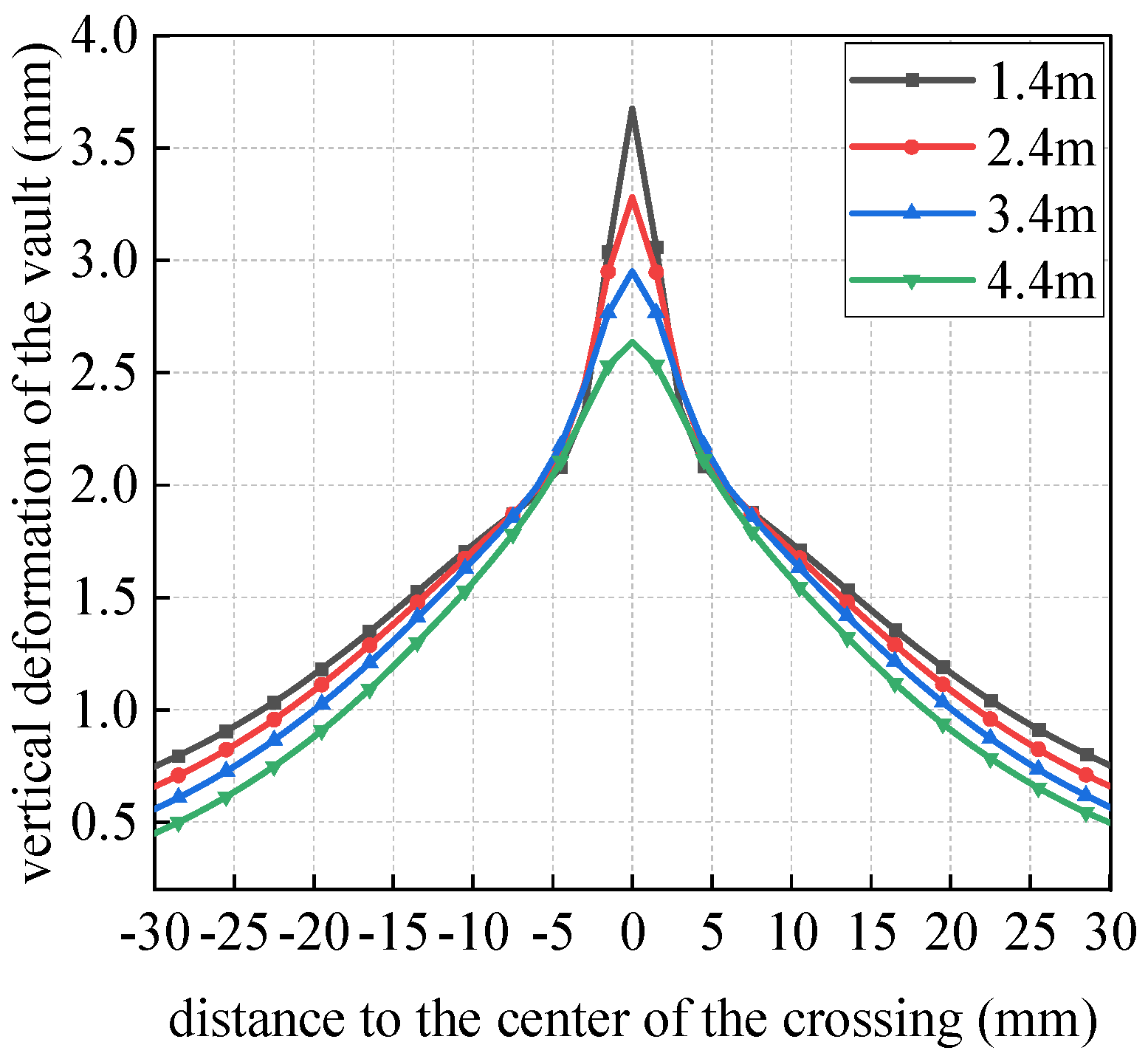
4.3.1. Longitudinal Deformation of Shield Segments
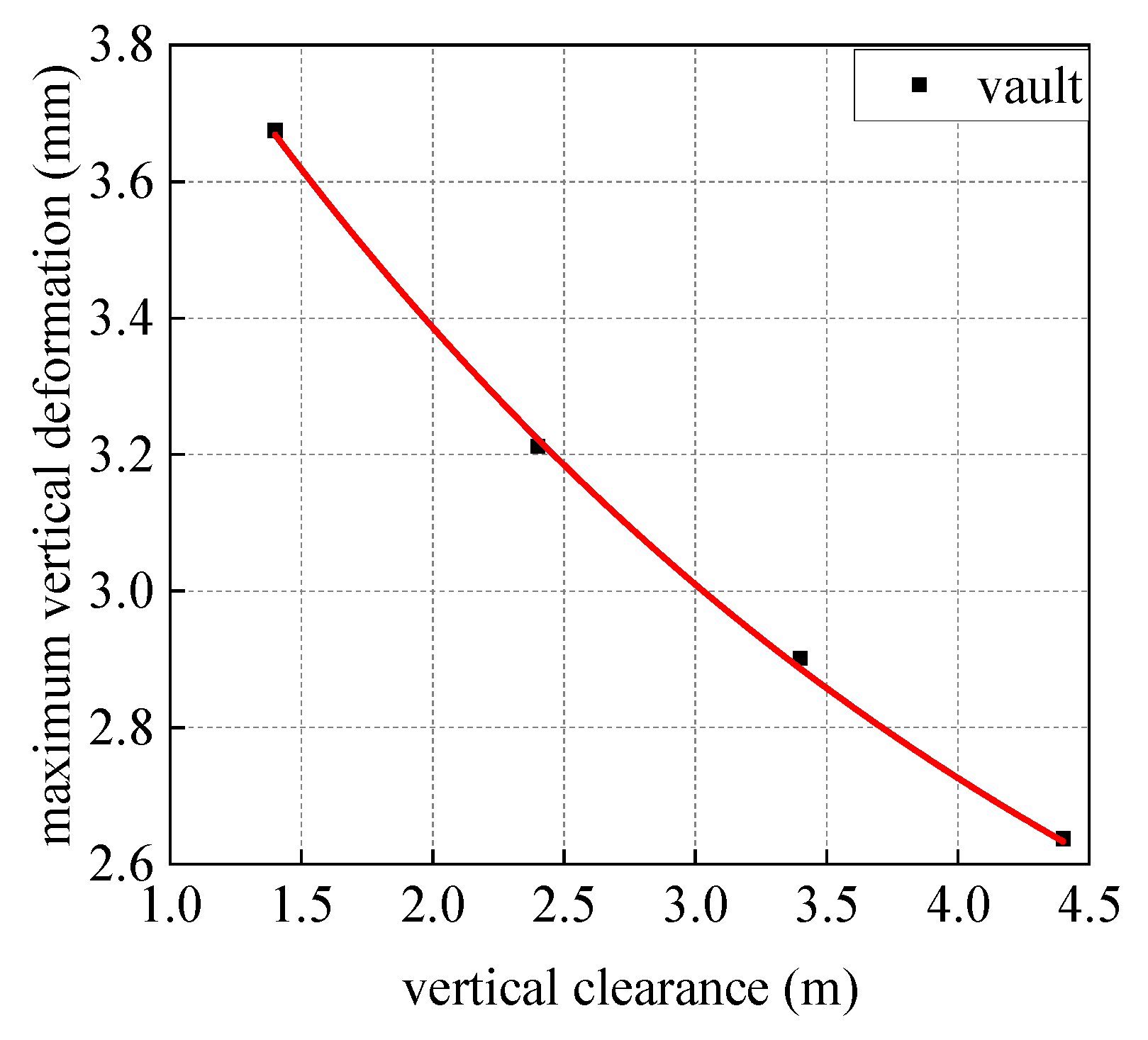
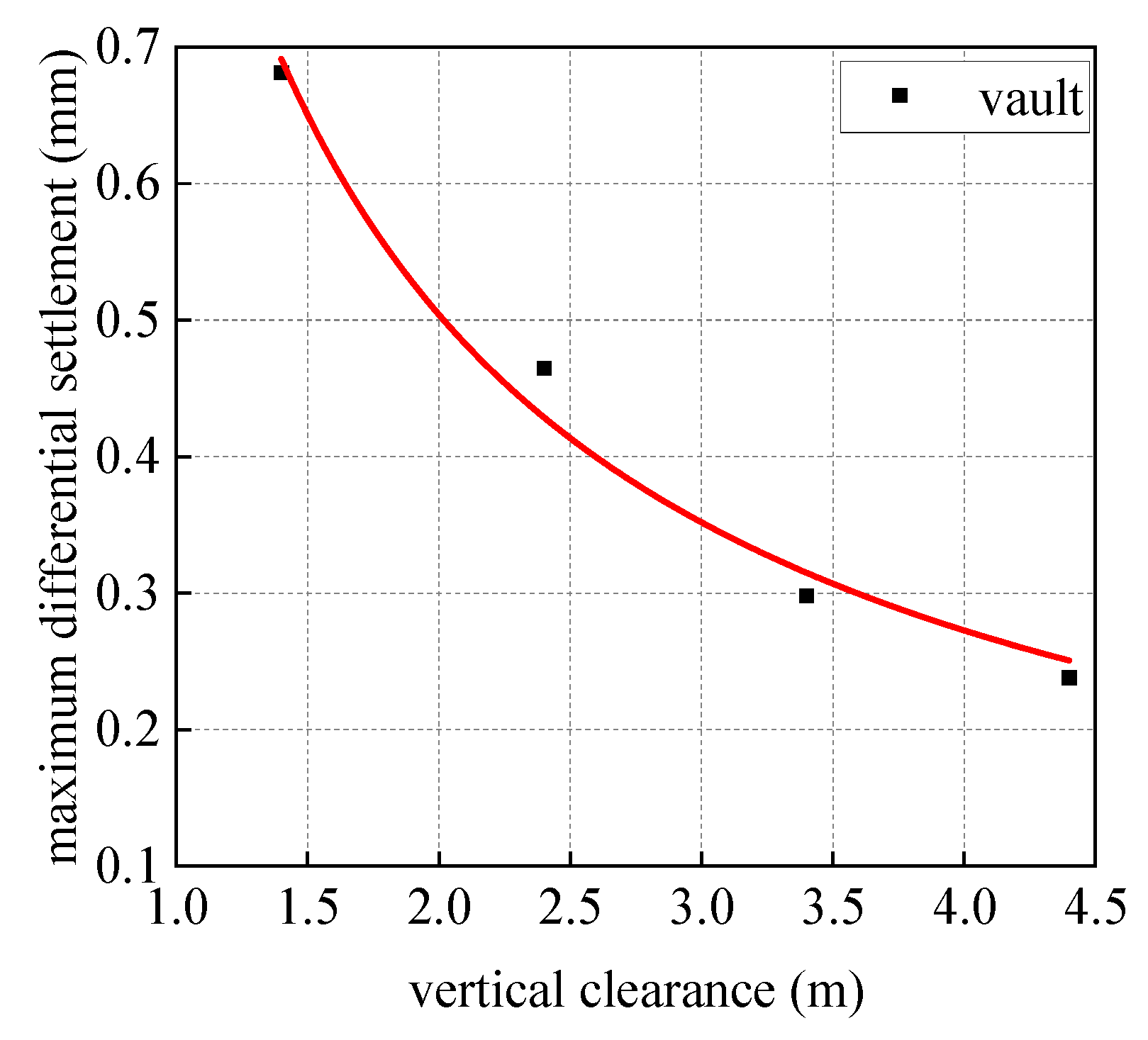
4.3.2. Differential Settlement of Shield Segments
5. Conclusions
- (1)
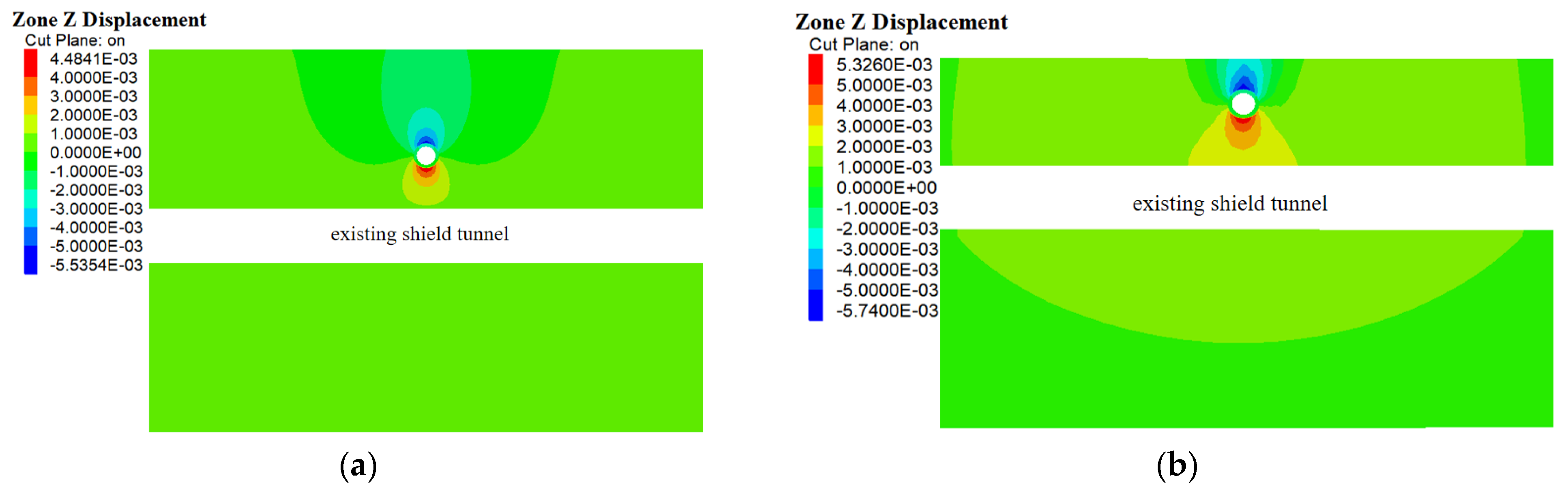
- The disruption of the existing shield tunnel primarily takes place following the passage of the pipe through the shield tunnel. The most significant disturbance is observed at the tunnel cross-section located directly beneath the newly constructed segment of the jacking pipe. The existing shield tunnel exhibits both “V”-shaped vertical deformation and horizontal deformation.
- (2)
- Maintaining a consistent clearance and angle in relation to the jacking pipe, the longitudinal deformation recorded in the shield tunnel in the gravel layer is significantly more pronounced than that in the moderately weathered mudstone layer. The peak vertical deformation at the vault reaches 2.67 mm, which is approximately tenfold greater than the deformation noted in the shield tunnel situated in the moderately weathered mudstone layer. Therefore, it is essential to prioritize the protection of shield tunnels located in soils with a low deformation modulus and low cohesion. In practical engineering contexts, methods such as grouting can be utilized to improve the stability of the interlayer soil, thereby reducing disturbances to the existing shield tunnels.
- (3)
- As the angle between the pipe and the shield tunnel increases, there is a significant reduction in the vertical deformation of the shield tunnel; however, the differential settlement between the segments tends to increase. Specifically, when the angle is raised from 45° to 68°, the maximum vertical deformation at the vault is notably reduced by 4.97%. In contrast, the increase in the maximum differential settlement between the segments is relatively modest, at 13.66%. To mitigate the effects of longitudinal deformation of the segments and differential settlement between them, it is advisable in practical engineering applications to intersect shield tunnels at angles ranging from 45° to 68°. Therefore, it is essential to carefully consider the placement of both the launch shaft and the receiving shaft in accordance with site limitations.
- (4)
- As the vertical clearance between the pipe and the shield tunnel decreases, both the longitudinal settlement of the tunnel structure and the differential deformation of the pipe segments exhibit a parabolic escalation. In particular, when the separation between the pipe and the shield tunnel is reduced from 2.4 m (which corresponds to one pipe diameter) to 1.4 m, there is a notable increase in the maximum vertical deformation at the vault and the differential settlement among the pipe segments, with increases of 14.40% and 46.6%, respectively. Therefore, in the domain of practical engineering, it is advisable to maintain a clearance greater than one pipe diameter during the construction of the pipe over the subway shield tunnel. It is feasible to enhance the clearances by proactively modifying the pipe jacking correction system, contingent upon compliance with site-specific constraints.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Deng, Z.; Liang, N.; Liu, X.; De La Fuente, A.; Lin, P.; Peng, H. Analysis and Application of Friction Calculation Model for Long-clearance Rock Pipe Jacking Engineering. Tunn. Undergr. Space Technol. 2021, 115, 104063. [Google Scholar] [CrossRef]
- Lehmann, G.; Käsling, H.; Cambier, A.; Praetorius, S.; Thuro, K. Performance Analysis of Utility Tunneling Data: A Case Study of Pipe Jacking in Hard Rock in Brittany, France. Tunn. Undergr. Space Technol. 2022, 127, 104574. [Google Scholar] [CrossRef]
- Li, Y.; Liu, G.; Liu, J.; Huang, J.; Tian, F.; Liu, F. Case Study on the Large Diameter Pipe Jacking for Utility Tunnel. Staveb. Obz. Civ. Eng. J. 2023, 32, 70–82. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, Y.; Ariaratnam, S.T.; Ma, B.; Zeng, C.; Liu, K. Field Monitoring and Analysis of Soil Deformation of Curved Steel Pipe Jacking in Gongbei Tunnel. Tunn. Undergr. Space Technol. 2023, 138, 105153. [Google Scholar] [CrossRef]
- Qi, Z.; Liu, J.; Gong, K. The Impact of Pipe Jacking Method Entrance and Exit Construction on the Surrounding Environment. IOP Conf. Ser. Earth Environ. Sci 2021, 634, 12103. [Google Scholar] [CrossRef]
- Li, Z.; Weng, X.; Cui, Y. Study on the Influence of Pipe Jacking Construction on Existing Subway Tunnels. Environ. Earth Sci. 2024, 83, 651. [Google Scholar] [CrossRef]
- Liu, W.; Wu, Y.; Zhao, H.; Xu, X.; Miao, L. Deformations of Subway Tunnels Induced by the Overcrossing Jacked Box Tunnels. Symmetry 2021, 13, 1800. [Google Scholar] [CrossRef]
- Xu, X.; Tong, L.; Li, Z.; Liu, X.; Hu, Q.; Yao, H.; Li, J. Influence of Extreme Shallow Jacked Box Tunnelling on Underlying Metro Tunnels: A Case Study. Undergr. Space 2023, 12, 234–250. [Google Scholar] [CrossRef]
- He, Q. Analysis of Influence Due to Pipe Jacking Traversing Subway Tunnel. Ind. Constr. 2011, 41, 821–823, 857. [Google Scholar] [CrossRef]
- Liu, X.; Wang, L.; Zhou, X.; Wang, J.; Zhong, Z.; Liu, P.; Xiong, F.; He, C. E-M Calculation Model and Its Application of Calculating Deformation in a New Tunnel Orthogonally Undercrossing an Existing Tunnel. Tunn. Undergr. Space Technol. 2022, 123, 104418. [Google Scholar] [CrossRef]
- Ren, D.-J.; Xu, Y.-S.; Shen, J.S.; Zhou, A.; Arulrajah, A. Prediction of Ground Deformation during Pipe-Jacking Considering Multiple Factors. Appl. Sci. 2018, 8, 1051. [Google Scholar] [CrossRef]
- Zhang, X.; Li, L.; Xu, Y.; Meng, Y. Mathematical Modelling for Strata Deformation Caused by Rectangular Pipe Jacking Construction in Composite Layered Ground. Appl. Math. Model. 2024, 136, 115649. [Google Scholar] [CrossRef]
- Chen-jie, L.; Bo, L.; Cong-an, L.; Zhi-peng, W. Centrifuge Model Test of the Influence of Tunnel Excavation with Different Spacings on Existing Tunnels. IOP Conf. Ser. Earth Environ. Sci 2024, 1333, 12032. [Google Scholar] [CrossRef]
- Fang, Q.; Liu, X.; Zeng, K.; Zhang, X.; Zhou, M.; Du, J. Centrifuge Modelling of Tunnelling below Existing Twin Tunnels with Different Types of Support. Undergr. Space 2022, 7, 1125–1138. [Google Scholar] [CrossRef]
- Guo, H.; Zhang, G.; Mao, X.; Zan, J. A Novel Simplified Physical Model Testing Method for Ground Settlement Induced by Shield Tunnel Excavation. Buildings 2025, 15, 710. [Google Scholar] [CrossRef]
- Tang, J.; Xu, J.; Zhou, D.; Huang, D.; Zeng, K.; Li, Y.; Chen, Z. Ground Surface Deformation Caused by Pipe Jacking Construction in a Soft Soil Area: An Experiment-Based Study. Buildings 2023, 13, 1628. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Z.; Yang, Y.; Jiang, Y.; Xu, X.; Hu, Q. Deformation Characteristics of Existing Tunnels Induced by Above-Crossing Quasi-Rectangular Shield Tunnel. Transp. Geotech. 2024, 45, 101227. [Google Scholar] [CrossRef]
- Shao, G.; Yang, N.; Han, J. Study on the Deformation Induced by Vertical Two-Layer Large Diameter Pipe-Jacking in the Soil-Rock Composite Stratum. Appl. Sci. 2022, 12, 12780. [Google Scholar] [CrossRef]
- Yang, X.; Liu, Y.; Yang, C. Research on the Slurry for Long-clearance Large-diameter Pipe Jacking in Expansive Soil. Adv. Civ. Eng. 2018, 2018, 9040471. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, X.; Luo, F.; Shi, T.; Xu, T.; Zhang, P. Field Test and Numerical Simulation Study on Pipe Sticking of Pipe Jacking in Composite Stratum. Buildings 2024, 14, 3992. [Google Scholar] [CrossRef]
- Xie, C.; Qu, Y.; Lu, H.; Song, S. Study on Deformation of New Tunnels Overcrossing Existing Tunnels underneath Operating Railways. Buildings 2024, 14, 2420. [Google Scholar] [CrossRef]
- Ye, P.; Lan, B.; Zhang, P.; Zeng, C.; Xu, T.; Xu, Y.; Wu, R. Numerical Simulation Study on Evolution Process of Carrying-Soil Effect of Rectangular Pipe Jacking. Buildings 2024, 14, 3057. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, J.; Li, C.; Liu, Y.; Tian, L.; He, Y.; Zhang, Q. Deformation and Reinforcement of the Existing Tunnel Affected by New Shield Tunnel Construction with Small Clearance. Buildings 2025, 15, 265. [Google Scholar] [CrossRef]
- Wei, G.; Yang, B.; Zhang, X.; Wu, H. Research on Longitudinal Deformation of Existing Shield Tunnel Caused by Shield Tunneling. Chin. J. Undergr. Space Eng. 2020, 16, 1754–1762, 1808. [Google Scholar]
- Yu, D.; Li, Z.; Liang, R. Coupling Analysis of Longitudinal Deformation of Shield Tunnel Caused by Overcrossing Tunneling in Layered Soils. Tunn. Constr. 2023, 43, 804–815. [Google Scholar]
- Xu, Y.; Du, Y. Analysis of Longitudinal Deformation of Existing Tunnel Caused by Overpassing of New Shield Tunneling Based on Timoshenko-Pasternak Model. Technol. Highw. Transp. 2024, 40, 29–42. [Google Scholar]
- Zhang, B.; Xie, J.; Huang, X. Three Dimensional Numerical Analysis of the Interaction Mechanism between Shield Tunneling and Existing Double Track Tunnels. J. China Foreign Highw. 2023, 43, 247–252. [Google Scholar] [CrossRef]
- LI, Y.; Chen, S.; Zhou, Z. Study on Reasonable Clear clearance for a Shield Tunnel’s Excavation Closely Adjacent to a Shallowly-Buried Rectangular Tunnel. Railw. Stand. Des. 2014, 58, 80–83. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, X.; Gou, M.; Cui, G. Method of Three-Dimensional Simulation for Shield Tunneling Process and Study of Adjacent Partition of Overlapped Segment. Rock Soil Mech. 2012, 33, 273–279. [Google Scholar] [CrossRef]
- Wen, S.; Zhang, M.; Zhou, Y.; Sheng, G. Reasonable Vertide Net clearance of Urban Rail Transit Double-Track Overlapping Shield Tunnels. Urban Mass Tranbit 2023, 26, 68–72. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, H.; Hu, Y.; Liu, R.; Tan, Q.; Xie, N.; Ye, W. Deformation Control of Shield Short-clearance Crossing Existing Tunnels in Silt Reclamation Stratum. J. Railw. Eng. Soc. 2024, 41, 87–91. [Google Scholar]
- Jiang, Z.; Zhang, B.; Liu, S.; Wang, H.; Liu, Y. Influence of Large-Section Rectangular Pipe Jacking on Deformation of Existing Subway Tunnels. J. Eng. Geol. 2022, 30, 1703–1712. [Google Scholar]
- Ying, H.; Yao, Y.; Wang, K.; Zhang, C. Observed Environment Response Caused by Construction of Double-Line Parallel Pipe Jacking Crossing over Metro Shield Tunnels1. J. Shanghaijiaotong Univ. 2023, 57, 1639–1647. [Google Scholar] [CrossRef]
- He, H.; Wang, S.; Shen, W.; Zhang, W. The Influence of Pipe-Jacking Tunneling on Deformation of Existing Tunnels in Soft Soils and the Effectiveness of Protection Measures. Transp. Geotech. 2023, 42, 101061. [Google Scholar] [CrossRef]
- Xiao, D.; Zhang, S.; Hu, Z.; Yu, Y.; Yan, X. Research on the Influence of Construction of Large-section Rectangular Pipe Jacking on Adjacent Obliquely Intersected Existing Tunnel. Mod. Tunn. Technol. 2022, 59, 411–447. [Google Scholar] [CrossRef]
- Wang, Y. Analysis of influencing factors for subway construction in special soil layers based on FLAC3D. J. Liaoning Tech. Univ. (Nat. Sci.) 2024, 14, 179–186. [Google Scholar]

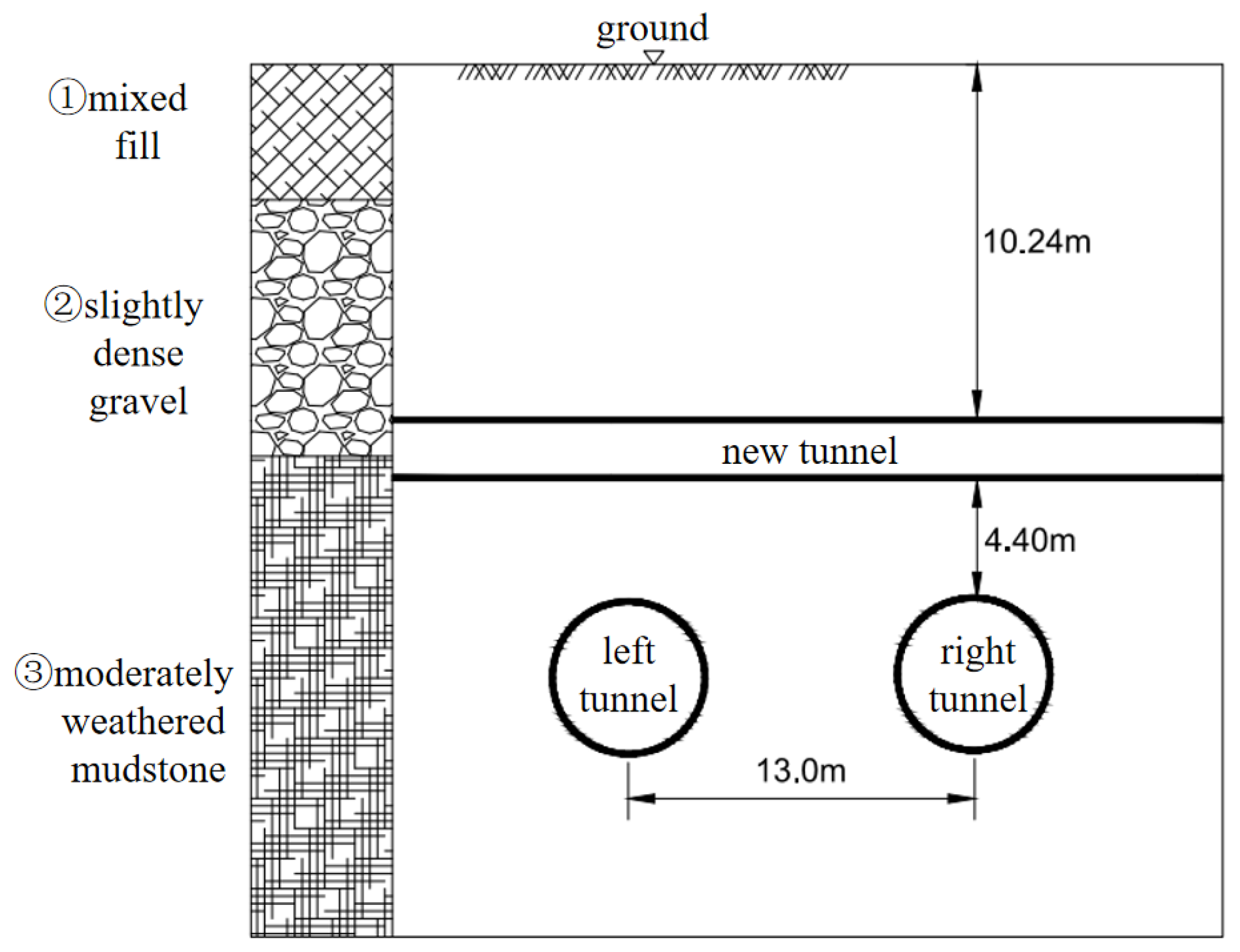


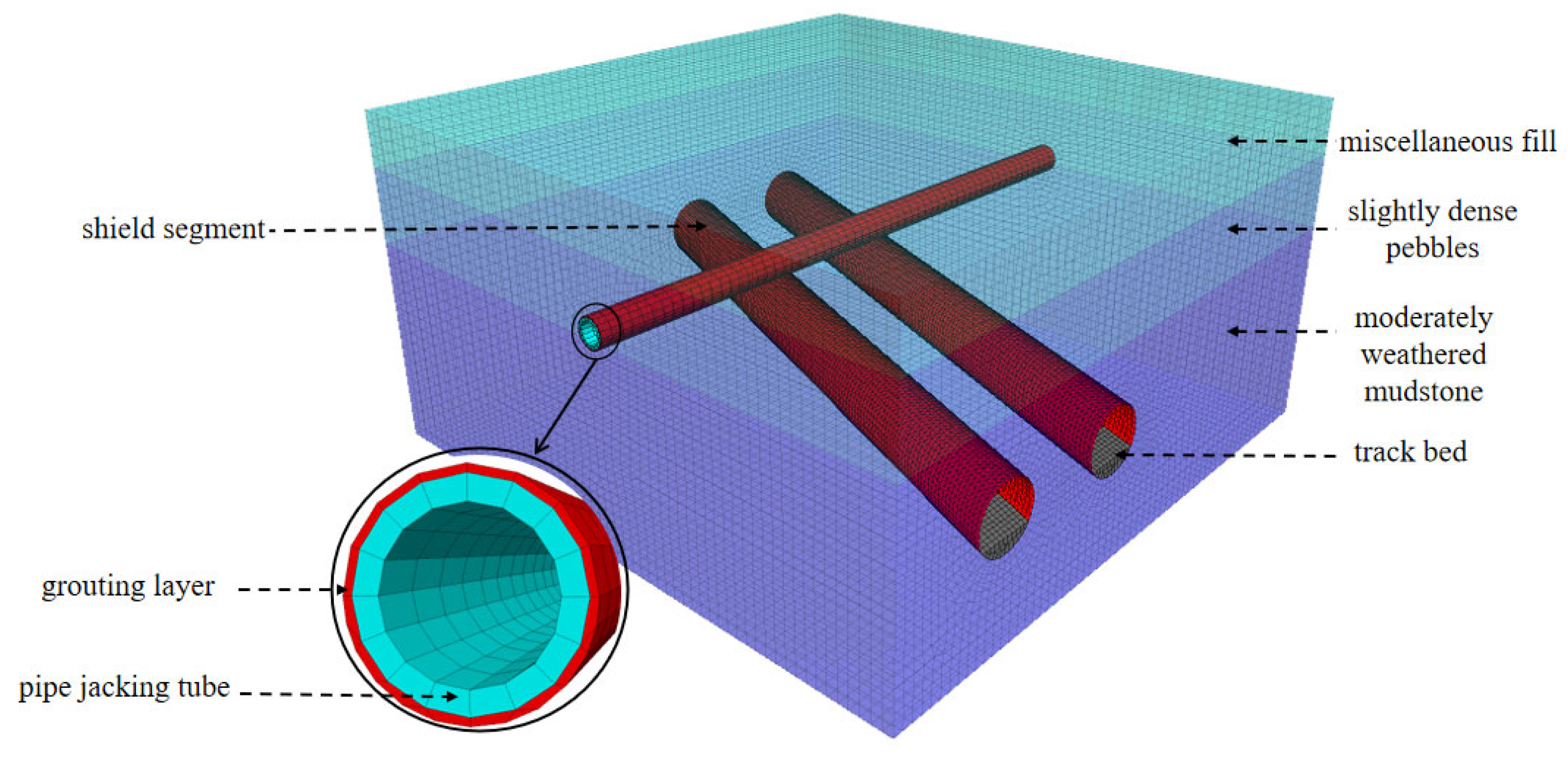






| Materials | Unit Weight (kN/m3) | Young’s Modulus (MPa) | Poisson’s Ratio (μ) | Friction (°) | Cohesion (kPa) | Thickness (m) |
|---|---|---|---|---|---|---|
| miscellaneous fill | 17.5 | 10 | 0.30 | 10 | 8.0 | 4.6 |
| slightly dense pebbles | 21.0 | 22 | 0.28 | 31 | 0 | 7.1 |
| moderately weathered mudstone | 23.5 | 140 | 0.25 | 35 | 200 | 28.3 |
| pipes | 26.48 | 35,500 | 0.2 | - | - | 0.2 |
| grouting layer | 18.0 | 10 | - | - | - | - |
| shield segments | 26.48 | 35,500 | 0.2 | - | - | 0.3 |
| track bed | 20.00 | 480 | 0.25 | - |
| Soil Layer | Unit Weight (kN/m3) | Young’s Modulus (MPa) | Poisson’s Ratio (μ) | Friction (°) | Cohesion (kPa) | Thickness (m) |
|---|---|---|---|---|---|---|
| miscellaneous fill | 17.5 | 10 | 0.30 | 10 | 8.0 | 2.17 |
| silty clay | 19.5 | 8.5 | 0.30 | 18 | 25.0 | 4.91 |
| slightly dense pebbles | 21.0 | 18 | 0.28 | 35 | 0 | 2.8 |
| medium dense pebbles | 22.0 | 28 | 0.25 | 40 | 0 | 8.14 |
| dense pebbles | 23.0 | 54 | 0.22 | 45 | 0 | 13.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, L.; Zhe, Q.; Liu, W.; Fang, Y.; Wang, F. Research on the Longitudinal Deformation of Segments Induced by Pipe-Jacking Tunneling over Existing Shield Tunnels. Buildings 2025, 15, 1394. https://doi.org/10.3390/buildings15091394
Luo L, Zhe Q, Liu W, Fang Y, Wang F. Research on the Longitudinal Deformation of Segments Induced by Pipe-Jacking Tunneling over Existing Shield Tunnels. Buildings. 2025; 15(9):1394. https://doi.org/10.3390/buildings15091394
Chicago/Turabian StyleLuo, Li, Qiuyi Zhe, Weihua Liu, Yabiao Fang, and Feng Wang. 2025. "Research on the Longitudinal Deformation of Segments Induced by Pipe-Jacking Tunneling over Existing Shield Tunnels" Buildings 15, no. 9: 1394. https://doi.org/10.3390/buildings15091394
APA StyleLuo, L., Zhe, Q., Liu, W., Fang, Y., & Wang, F. (2025). Research on the Longitudinal Deformation of Segments Induced by Pipe-Jacking Tunneling over Existing Shield Tunnels. Buildings, 15(9), 1394. https://doi.org/10.3390/buildings15091394




