Time-Dependent Bearing Capacity of Jacked Piles in Soft Soil Based on Non-Darcy Seepage

Abstract

Non-Darcy seepage can more accurately quantify the bearing capacity of jacked piles during the bearing and reconsolidation processes. This paper is divided into three parts. Firstly, it theoretically analyzes the pore water pressure distribution in the soil around the pile through differential treatment of the equation. Secondly, it simulates the pile sinking process and the reconsolidation process of the soil around the pile after sinking by ABAQUS, and then a parameter analysis is conducted. Finally, a time analysis of the pile bearing capacity is conducted. The results show that the dissipation rate of excess pore water pressure (EPWP) and the consolidation rate of the pile side will be underestimated at the initial stage of consolidation if the influence of non-Darcy seepage is ignored, while the opposite is true in the later stage. The strength and effective stress of the soil are greatly improved in the early stage of consolidation, and the bearing capacity of the static pressure pile is also significantly enhanced. In the later stage of consolidation, as the excess pore pressure of the soil around the pile slowly dissipates, the bearing capacity of the static pressure pile also increases steadily. This paper studies the dissipation of EPWP to make the design of pile foundation bearing capacity more rational and to improve the economic benefits.

1. Introduction

The bearing capacity of a pile increases over time in the later stage of pile sinking as the soil mass reconsolidates. This phenomenon, known as the time-effect of jacked pile bearing capacity, was first noticed in the early 20th century and still remains a popular research topic. Due to the differences in soil properties, scholars have different research findings on the internal mechanisms of this time-effect. There are three methods used in most studies, including theoretical analysis, numerical simulation, and experimental investigation.

Theoretical analysis is widely used for the time-dependent bearing capacity of jacked piles. Cao et al. [1] developed a mechanical model for undrained cavity expansion in modified Cam-clay, which elucidated the influence of the over-consolidation ratio on pore water pressure due to cavity expansion. Wang et al. [2] established a formula for the ultimate side-friction resistance of piles with the spherical cavity expansion theory and determined the ultimate bearing capacity of a single pile. Chen and Abousleiman [3] derived the distribution of pore water pressure by equations for radial, tangential, and vertical effective stresses in the plastic zone. Grevtsev and Fedorovski [4] proposed a formula for the ultimate expansion pressure of circular/spherical cavity expansion based on the M-C criterion. Li et al. [5] assessed the dissipation of excess pore water pressure (EPWP) and the increase in effective stress around piles through radial consolidation theory. Cheng et al. [6] modified the circular cavity expansion equation using large-strain plasticity theory and derived an expression for EPWP. Zhou et al. [7] utilized an improved circular cavity expansion theory to derive the relationship between soil strength and stress state and found excellent agreement between measured and predicted values. Zhong et al. [8] proposed a method for calculating the overall deformation of excavation support structures and demonstrated that the method can better predict the deformation of piles by combining numerical simulation and field tests.

Some scholars have used finite-element analysis to study the initial stress and displacement fields during pile jacking, aiming to accurately simulate the actual pile sinking process. Basu et al. [9] developed a quantitative formula for the side-frictional resistance of statically pressed piles. Murad et al. [10] applied vertical deformation at the pile top to activate pile–soil interface friction and incorporated a time-dependent reduction parameter (β) to account for thixotropic effects. Shao et al. [11] utilized ABAQUS to analyze soil displacement during pile sinking in soft foundations and soft clays. Sabetamal et al. [12] used the modified Cambridge model to simulate pile sinking and analyze the effects of pile sinking rate on excess pore pressure, pile sinking resistance, and frictional forces. Dou et al. [13] developed a three-dimensional numerical model considering pore water effects to simulate pile sinking and proposed a formula for the distribution of excess static pore water pressure. Karlsson et al. [14] combined the strain-path method with an effective stress-based soft-soil constitutive model in a multi-term numerical framework. Su et al. [15] simulated pile sinking in silica sand and established a functional relationship between soil relative density and pile length-to-diameter ratio.

Experimental methods are also useful for this question. Zuo et al. [16] derived a functional relationship between the ultimate bearing capacity and the dormancy time by using 10 PHC pipe piles. Ng et al. [17] discovered that the rate of pile foundation consolidation development has a logarithmic relationship with pore water pressure dissipation. Attar and Fakharian [18] developed a regional pile foundation time-effect formula to provide a basis for optimizing regional pile foundation design. Elkasabgy and El Naggar [19] revealed soil disturbance during pile installation significantly affects pile failure by axial compression tests. Afshin and Rayhani [20] found that pile side resistance increases after pile driving is completed in clay. Wang et al. [21] obtained variation laws for pile tip and side resistance through a series of indoor model tests on static pressure piles in clay. Wang et al. [22] studied the effects of pile strength and design parameters on composite foundation bearing capacity through tests and simulations, finding that pile end stress increases with pile length and diameter.

In conclusion, research on the internal mechanisms of pile-bearing capacity growth in soft-soil foundations and the dissipation of EPWP in the surrounding soils under non-Darcy seepage is still limited. It is crucial to study the dissipation laws of excess static pore water pressure caused by pile driving in highly sensitive soft soils and the time-dependent behavior of the bearing capacity of statically pressed piles due to the unique engineering characteristics of soft-soil foundations. This paper is divided into three parts. Firstly, the consolidation degree on the pile is derived through theoretical analysis. Secondly, a numerical model is used to analyze the changes in soil displacement, stress, and pore pressure during pile driving and the reconsolidation process. Finally, the time-dependent behavior of the pile foundation bearing capacity is analyzed by theoretical methods.

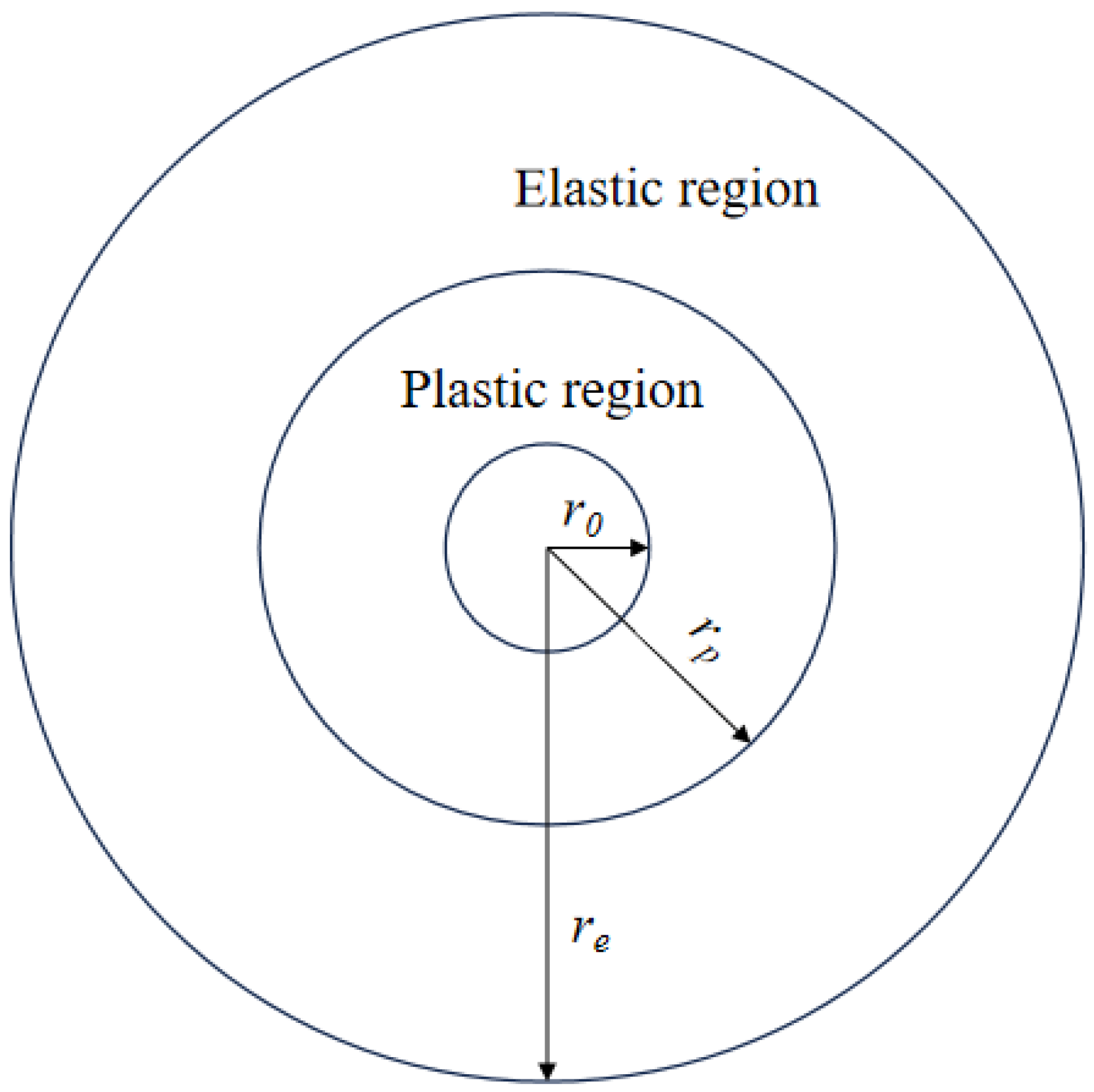
2. Theoretical Analysis

The excess pore pressure dissipation is used to quantify the consolidation of pile-surrounding soils which can be calculated by the finite difference method under non-Darcy seepage conditions.

2.1. Consolidation Governing Equation

The influence radius of the plastic zone is determined by the cavity expansion theory, and the boundary conditions are derived from the dissipation characteristics of EPWP in the pile–soil system. And then, an exponential seepage equation formulates the radial consolidation equation.

2.1.1. Fundamental Assumption

Some fundamental assumptions are as follows: (1) isotropic fully saturated soil; (2) incompressible soil matrix and pore water with compression solely from drainage; (3) purely radial seepage; (4) permeability governed by exponential seepage law.

2.1.2. Consolidation Governing Equations

By employing the Slepicka’s exponential seepage equation [23], the velocity of pore water in soil units is as in Equation (1).

$$v=-k{\left({\displaystyle \frac{1}{{\gamma }_w}}{\displaystyle \frac{\partial u}{\partial r}}\right)}^m$$

(1)

where r is the distance between the soil around the pile and the pile center; u is the EPWP; i is the hydraulic gradient; v is the seepage velocity; k is the non-Darcy permeability coefficient; m is the non-Darcy flow index (1 ≤ m ≤ 2.38) [24] dependent on hydraulic gradient magnitude; and γ_w is the weight of water.

Under Darcy seepage conditions, the radial consolidation equation governing the pile-surrounding soil is established using axisymmetric plane strain modeling [25] in Equation (2).

$${\displaystyle \frac{\partial u}{\partial t}}={\displaystyle \frac{K_r}{m_v{\gamma }_w}}\left({\displaystyle \frac{{\partial }^{2}u}{\partial r^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial u}{\partial r}}\right)$$

(2)

where m_v is coefficient of volume compressibility, which is defined as in Equation (3).

m_v = a/(1 + e₁)

(3)

where e₁ and a denote the initial void ratio and the average coefficient of compressibility.

By substituting Equation (1) into Equation (2), the radial consolidation governing equation for the pile-surrounding soil under exponential-form seepage conditions is derived as in Equation (4).

$${\displaystyle \frac{\partial u}{\partial t}}={\displaystyle \frac{m{K}_r}{m_v{\gamma }_w}}{\left({\displaystyle \frac{1}{{\gamma }_w}}{\displaystyle \frac{\partial u}{\partial r}}\right)}^{m-1}\left[{\displaystyle \frac{{\partial }^{2}u}{\partial r^2}}+{\displaystyle \frac{1}{mr}}{\displaystyle \frac{\partial u}{\partial r}}\right]$$

(4)

2.1.3. Initial EPWP

The soil surrounding the pile can be divided into plastic and elastic zones based on the disturbance intensity according to the cavity expansion theory, as shown in Figure 1.

Zhao et al. [26] established the plastic zone radius through cavity expansion theory-based analysis of excess pore pressure characteristics (magnitude, distribution, and influence zone) in the soil surrounding a single pile after installation, expressed as in Equation (5).

$${\displaystyle \frac{r_p}{r_0}}=\sqrt{{\displaystyle \frac{E}{2\left(1+\mu \right)C_u}}}$$

(5)

where E is the elastic modulus of the soil; μ is the Poisson’s ratio of the soil; r₀ is the pile radius; r_p is the radius of the plastic zone; and C_u is the undrained shear strength of the soil.

It is found that the distribution range of EPWP in the soil around the static pressure pile is generally about 20 r₀, and the radius of the plastic zone is about 1/10~1/5 of the radius of the affected zone through the analysis of the actual pile foundation engineering data. In this research, the radius of the pile r₀ = 0.25 m, so the radius of the elastic zone r_e and the radius of the plastic zone r_p are as in Equations (6) and (7).

r_e = 20 r₀ = 5 m

(6)

r_p = 1/5 r_e = 1 m

(7)

2.1.4. Solution Constraints

The elastic zone boundary is the drainage interface from which EPWP dissipates outward from the pile, and the pile–soil contact is an undrained interface for the impermeable pile, as shown in Figure 2.

Therefore, the initial and boundary conditions governing post-installation reconsolidation of the pile soils are defined as in Equations (8) and (9).

(1)

Initial condition

$$u\left(r,0\right)=u_r$$

(8)

(2)

Boundary conditions

$$\left\{\begin{array}{l}u\left(r_e,t\right)=0\hfill \\ {\displaystyle \frac{\partial u\left(r_0,t\right)}{\partial t}}=0\hfill \end{array}\right.\hspace{1em}\hspace{1em}t >0$$

(9)

2.2. Finite Difference Solution of the Consolidation Control Equation

The formulas in Section 2.1 are solved using the finite difference method. This allows for quantitative determination of the spatiotemporal evolution characteristics of EPWP around the pile.

2.2.1. Non-Dimensionalization

To solve the soil consolidation equation around the pile numerically, the following variables are defined in Equations (10)–(13).

$$U={\displaystyle \frac{u}{u_{r0}}}$$

(10)

$$R={\displaystyle \frac{r}{r_e}}$$

(11)

$$T={\displaystyle \frac{K_{r}t}{m_v{\gamma }_w{r_e}^2}}={\displaystyle \frac{C_{h}t}{{r_e}^2}}$$

(12)

$$u_e={\displaystyle \frac{u_{r0}}{{\gamma }_w{r}_e}}$$

(13)

where u_r0 represents the EPWP at the pile–soil interface, corresponding to the maximum EPWP.

Using the dimensionless variables defined by Equations (10)–(13), Equation (4) can be rewritten in its non-dimensional form as in Equation (14).

$${\displaystyle \frac{\partial U}{\partial T}}=m{\left(u_e{\displaystyle \frac{\partial U}{\partial R}}\right)}^{m-1}\left[{\displaystyle \frac{{\partial }^{2}U}{\partial R^2}}+{\displaystyle \frac{1}{mR}}{\displaystyle \frac{\partial U}{\partial R}}\right]$$

(14)

The corresponding solution conditions become in Equations (15) and (16).

(1)

Initial condition

$$U\left(R,0\right)=u_r/u_{r0}\hspace{1em}\hspace{1em}{r}_0/r_e\le R\le 1$$

(15)

(2)

Boundary conditions

$$\left\{\begin{array}{c}U\left(1,T\right)=0\\ {\displaystyle \frac{\partial U\left(r_0/r_e,T\right)}{\partial R}}=0\end{array}\right.\hspace{1em}\hspace{1em}T=0$$

(16)

2.2.2. Finite Difference Solution

The Crank–Nicolson scheme is used for its the numerical stability. Discretize the soil mass around the pile into n thin layers from the pile side to the elastic zone boundary. Then, discretize the time. Here, i and j are the space and time nodes, respectively, where i = 0, 1, 2, …, n (0 represents the elastic zone boundary); j = 0, 1, 2, …, N (0 represents the initial time). Denote the space step length as ∆R and the time step length as ∆T. According to the Crank–Nicolson difference scheme, Equation (14) can be discretized under a very small time-step length as in Equation (17). The parameters can be expressed by Equations (18)–(21).

$$\begin{array}{l}2U_i^j=2U_i^{j-1}+m\lambda {\left(u_e{\displaystyle \frac{U_{i+1}^{j-1}-U_{i-1}^{j-1}}{2\Delta R}}\right)}^{m-1}\\ \times \left[\left({\Psi }_i^{j-1}-{\Psi }_{i-1}^{j-1}+{\Psi }_i^j-{\Psi }_{i-1}^j\right)+\alpha \left({\Phi }_i^{j-1}+{\Phi }_i^j\right)\right]\end{array}$$

(17)

$$\lambda ={\displaystyle \frac{\Delta T}{\Delta R^2}}$$

(18)

$$\alpha ={\displaystyle \frac{\Delta R}{2m\left(1-i·\Delta R\right)}}$$

(19)

$${\Psi }_i^j=U_{i+1}^j-U_i^j$$

(20)

$${\Phi }_i^j=U_{i+1}^j-U_{i-1}^j$$

(21)

where $U_i^j$ denotes the non-dimensionless value of EPWP at time j at node i.

Equation (17) shows that, on undrained surfaces, the EPWP does not dissipate as time passes. This presents difficulties for numerical solutions such as the difference method. Nevertheless, Darcy’s law is used on undrained surfaces for its effectiveness.

To simplify programming, the difference equations are temporally discretized using a backward difference scheme and, along with solution conditions, are expressed in matrix form, as in Equation (22). The parameters can be expressed by Equations (23)–(29).

$${\left\{\begin{array}{ccccccc}{A}_{11}& A_{12}& & & & & \\ & A_{21}& A_{22}& A_{23}& & & \\ & & A_{32}& A_{33}& A_{34}& & \\ & & & \cdots & & & \\ & & & & A_{\left(n-1\right)\left(n-2\right)}& A_{\left(n-1\right)\left(n-1\right)}& A_{\left(n-1\right)n}\\ & & & & & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}2\lambda \hspace{1em}-2\left(1+\lambda \right)& \end{array}\right\}}^{j-1}{\left\{\begin{array}{c}\begin{array}{c}{U}_1\\ U_2\\ U_3\end{array}\\ \begin{array}{c}\dots \\ U_{n-1}\\ U_n\end{array}\end{array}\right\}}^j={\left\{\begin{array}{c}\begin{array}{c}{B}_1\\ B_2\\ B_3\end{array}\\ \begin{array}{c}\dots \\ B_{n-1}\\ B_n\end{array}\end{array}\right\}}^{j-1}$$

(22)

where j = 0, 1, 2, …, N;

$$A_{nn}=-2\left(1+\lambda \right)$$

(23)

$$A_{n\left(n-1\right)}=2\lambda$$

(24)

$$A_{ii}=-2\left[1+m\lambda {\left(u_e{\displaystyle \frac{U_{i+1}^{j-1}-U_{i-1}^{j-1}}{2\Delta R}}\right)}^{m-1}\right]$$

(25)

$$A_{i\left(i-1\right)}=m\lambda {\left(u_e{\displaystyle \frac{U_{i+1}^{j-1}-U_{i-1}^{j-1}}{2\Delta R}}\right)}^{m-1}\left(1-\alpha \right)$$

(26)

$$A_{i\left(i+1\right)}=m\lambda {\left(u_{\mathrm{e}}{\displaystyle \frac{U_{i+1}^{j-1}-U_{i-1}^{j-1}}{2\Delta R}}\right)}^{m-1}\left(1+\alpha \right)$$

(27)

$$\begin{gathered} B_i=2\left[1+m\lambda {\left(u_e{\displaystyle \frac{U_{i+1}^{j-1}-U_{i-1}^{j-1}}{2\Delta R}}\right)}^{m-1}\right]U_i^{j-1} \\ -m\lambda {\left(u_e{\displaystyle \frac{U_{i+1}^{j-1}-U_{i-1}^{j-1}}{2\Delta R}}\right)}^{m-1}\left(1-\alpha \right)U_{i-1}^{j-1}-m\lambda {\left(u_e{\displaystyle \frac{U_{i+1}^{j-1}-U_{i-1}^{j-1}}{2\Delta R}}\right)}^{m-1}\left(1+\alpha \right)U_{i+1}^{j-1} \end{gathered}$$

(28)

$$B_i=2\left(\lambda -1\right)U_n^{j-1}-2\lambda U_{n-1}^{j-1}$$

(29)

Equation (22) is linear with respect to its unknowns. This allows the use of the chasing method to find solutions based on the initial EPWP. For linear equations, the Crank–Nicolson scheme is unconditionally convergent. However, trial calculations are required in nonlinear cases. The results indicate that convergence occurs when the time step is reduced by two orders of magnitude compared to the space step.

2.3. Calculate the Pile Consolidation Degree

Solve consolidation degree on the pile side using excess static pore water pressure data, as in Equation (30):

$$U_r=1-U_n$$

(30)

where U_n is the dimensionless value of the EPWP at pile side node n, which is used to represent the consolidation rate on the pile side; the consolidation degree U_r on the pile side reflects the dissipation rate of the EPWP at the pile–soil interface. Also, it represents the magnitude of the frictional resistance at the pile–soil interface.

3. Numerical Simulation

ABAQUS software was utilized to simulate the pile driving process and the subsequent soil reconsolidation, aiming to verify the rationality of the radial consolidation equation for the soil around piles.

3.1. Numerical Model

Some fundamental assumptions are as follows: (1) the soil is fully consolidated under self-weight; (2) the soil is saturated; (3) the pile is modeled as a discrete rigid body with RAX2 elements; (4) the permeability coefficient remains constant during consolidation.

3.1.1. Basic Information of the Model

This section creates pile sinking models through the selection of constitutive models, pile–soil interfaces, loading methods, EPWP parameters, and initial stress balance.

The displacement penetration method is used to simulate pile installation, and the practical stress approach takes into account EPWP dissipation and its influence on soil displacement effects and the evolution of time-dependent bearing capacity. Other information considerations are as follows:

• Determine the soil constitutive model

The modified Cam-clay model can effectively integrate elastic–plastic behavior and soil structure characteristics, which enables the accurate simulation of soil responses under various stress–strain conditions. It has practical advantages such as minimal parameter requirements and high computational efficiency. Adopting ABAQUS, the modified Cam-clay model is coupled with poro-elastic theory to simulate soil deformation and pore pressure dissipation during consolidation.

2.

Set up pile–soil contact

The model enforces surface-to-surface contact. A rigid pile penetrates deformable soil. Unilateral constraints are enforced to prevent soil intrusion while allowing controlled pile penetration.

The contact model utilizes hard normal contact and tangential penalty friction governed by Coulomb’s law. Friction coefficients define pile–soil interface resistance.

3.

Boundary conditions

The soil model has free top, fixed bottom, and horizontally constrained appropriate boundaries. The left boundary is governed by pile–soil contact. A 10 m downward displacement drives pile penetration, and then the pile is fixed for subsequent analysis stages.

4.

Initial in situ stress equilibrium

The balance of initial in situ stress can enhance simulation accuracy. It does this by replicating field conditions and influencing soil responses, such as pile bearing capacity and lateral soil pressure, during driving. When this step is performed before pile installation, it can reduce system imbalance, which improves numerical stability and convergence, so ensuring reliable results.

This study established soil body forces and self-weight stress fields based on practical stress principles by ABAQUS’s built-in automatic in situ stress equilibrium method. The results in Figure 3 show that the vertical stress grows linearly with depth with a unit weight of 10 kN/m³ and a depth of 20 m. The theoretical bottom stress is 200 kPa, while the simulated bottom stress is 198.8 kPa, with an error of 0.6%. The maximum displacement magnitudes of 10⁻¹⁶ confirm an effective equilibrium which is far less than the 10⁻⁶.

3.1.2. Modeling Steps

A 2D axisymmetric model (10 × 20 m) was established for pile installation and soil consolidation analysis; the modeling steps are as follows:

(1)

Soil modeling. CAX4P elements, which are four-node x axisymmetric pore pressure elements with structured meshing.

(2)

Pile configuration. A discrete rigid body (r = 0.25 m) using two-node axisymmetric elements, 10 m penetration via displacement boundary.

(3)

Geometry optimization. A 60° tapered pile tip with arc transition.

(4)

Constraint solution. A frictionless rigid pipe with 1 mm diameter along the central axis to prevent soil displacement crossover.

Figure 4 and

Table 1. Soil parameters.

Effective Unit Weight $\mathit{\gamma }\mathbf{\prime }$ (kN∙m−3)	Consolidation Parameter $\mathit{\lambda }$	Spring-Back Parameters $\mathit{\kappa }$	Poisson Ratio $\mathit{\upsilon }$	Destructive Parameter $\mathsf{{\rm M}}$	Permeability Coefficient k (m/s)	NCL Calculates the Intercept e*
10	0.15	0.05	0.3	1	$1\times {10}^{-7}$	1.1

show the model details and material parameters, respectively, with tension-free soil–pile interaction.

3.2. Results and Discussion

This section analyzes the pile driving process and post-installation consolidation results and discusses the impacts of the parameters on soil displacement and reconsolidation around piles.

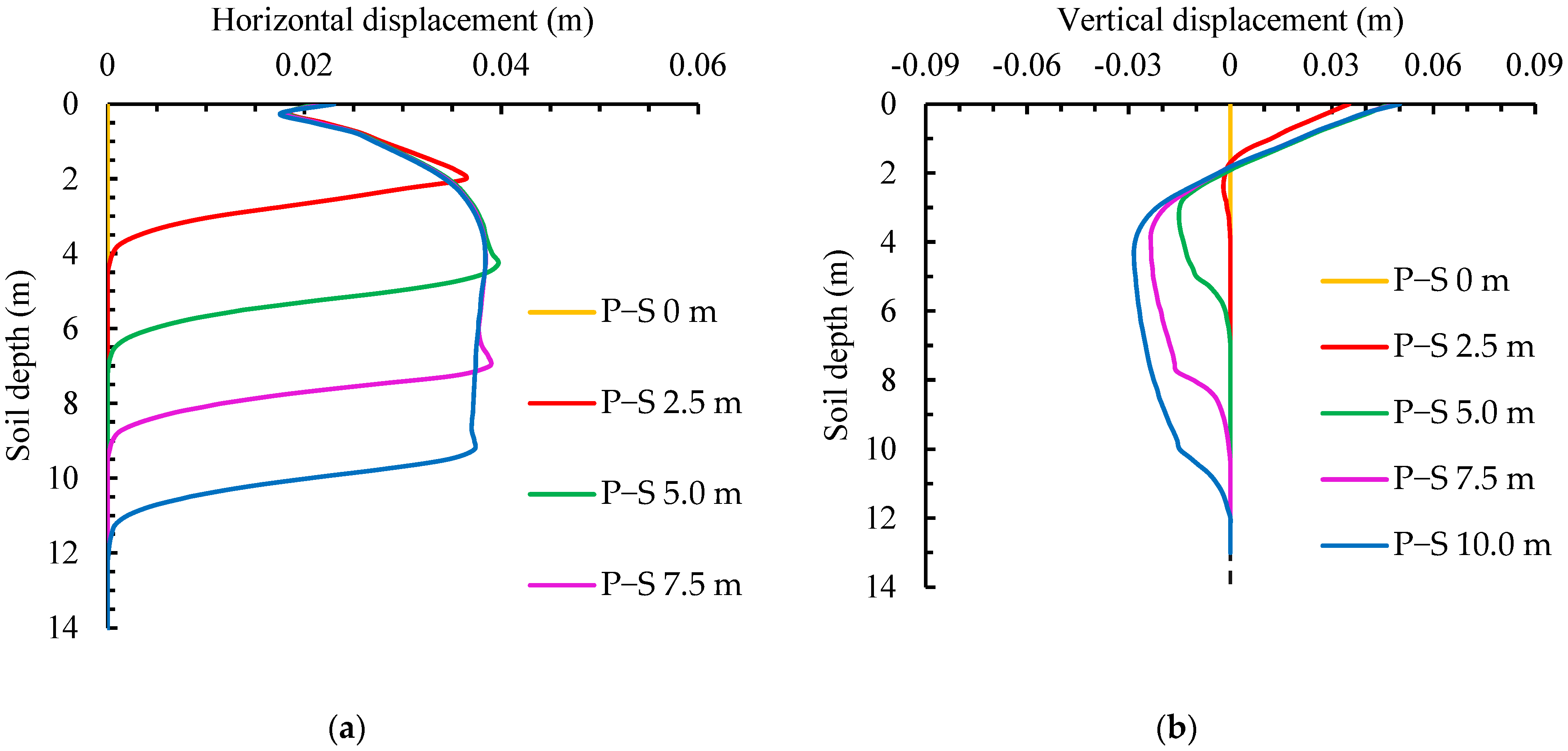
3.2.1. Pile Sinking Process

This subsection analyses pile-induced soil displacement, stress field evolution, and pore water pressure redistribution.

• Displacement

(1)

Pile installation

Figure 5 shows the ground soil displacement during pile driving. Radial displacement decreases logarithmically with distance from the pile side (Figure 5a), consistent with theoretical analysis. Near the pile side, vertical displacement shows settlement due to drag force, while soil at one pile diameter distance exhibits a maximum heave of 0.1–0.15 m (Figure 5b). Heave increases with pile penetration up to 5 m but stabilizes thereafter, indicating diminishing soil displacement effect beyond 5 m, in line with Shao et al. [11]. At distances greater than two pile diameters from the pile side, the vertical displacement of the surface soil is minimal. Significant radial and vertical displacements occur near the pile (less than 2 D) but do not increase significantly with further pile penetration, while the distance far from the pile shows no substantial displacement.

Figure 6 shows soil displacement at 3 R from the pile center during pile driving. In Figure 6a, significant radial deformation occurs at the surface during static pile pressing, with a maximum of 40 mm. Radial displacement increases with pile penetration, peaking 0.5–1.5 m above the pile tip and decreasing rapidly below it. In Figure 6b, upward heave occurs at 2 m depth, reaching 60 mm, while settlement occurs below 2 m, with a maximum of 30 mm. The maximum settlement position stabilizes at 3–4 m depth after 10 m penetration. Vertical displacement at the pile tip increases suddenly then decreases rapidly, approaching 0 at the pile base. The radial displacement increasing then decreasing and vertical displacement showing heave in shallow soil and settlement in deep soil, both varying along the pile shaft during pile driving.

Combined, Figure 5 and Figure 6 show that the radial deformation of the soil increases with proximity to the pile and with greater pile penetration depth during pile driving.

(2)

After pile installation

Figure 7 shows the radial distribution of soil displacement at different depths after pile driving. The soil around the pile experiences outward displacement, which decays logarithmically with radial distance. The radial deformation varies with depth, being smaller near the surface. Near the pile tip, radial displacement is initially 0, then increases and decreases, due to the transition from cylindrical to spherical expansion. The surface soil within 0.07 m of the pile heaves between 0.07 and 1.5 m. The vertical displacement within the pile body increases with depth, while outside the pile body, it decreases logarithmically with distance from the pile side. Significant displacement occurs near the pile tip, decreasing exponentially with distance.

Figure 8 shows soil displacement after pile driving under different distances from the pile center (3 R, 6 R, 9 R). In Figure 8a, significant radial displacement occurs at the surface due to soil compression during pile driving. The radial displacement drops sharply within 0.5 m of the surface, then increases and stabilizes at 4 m depth, reaching a maximum value near the pile tip and decreasing to zero within 1–2 m below the pile tip. In Figure 8b, upward heave occurs within 2 m of the surface, decreasing with distance from the pile center. Below 2 m, settlement occurs, with vertical displacement increasing in the 2–4 m range, then decreasing within the pile body and reducing to zero within 1–2 m below the pile tip. The analysis shows that the influence of pile driving on soil displacement decreases with distance from the pile and is minimal at the pile tip.

Combined, Figure 7 and Figure 8 show that the soil near the pile side is susceptible to disturbance during pile driving, generating a significant soil displacement effect that attenuates with increasing distance from the pile center.

2.

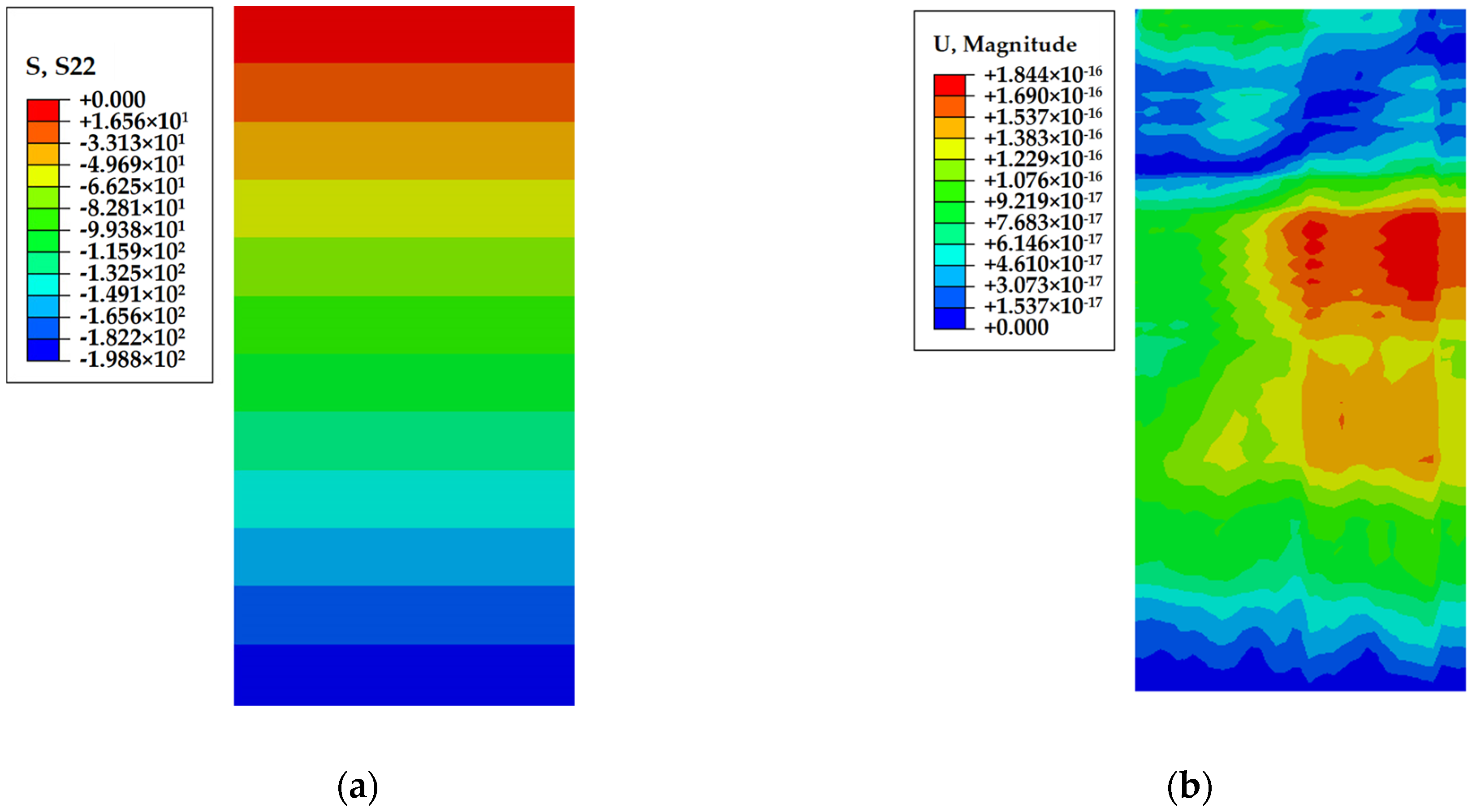
Stress

(1)

Stress during pile driving

Figure 9 shows the variation of soil stress at a distance of 3 R from the pile center during pile driving. Both the radial and vertical stresses in the soil around the pile increase gradually with pile penetration and reach their maximum values within ±0.5 m of the pile tip. After the pile tip passes, the stresses can even drop below their initial values due to soil disturbance and strength reduction.

(2)

Stress post-pile driving

Figure 10 shows the distribution of radial stress and vertical stress in the soil according to the pile core (3 R, 6 R, 9 R) after pile driving. Both radial and vertical stresses increase with soil depth, show a sudden increase at the pile tip, and then decrease sharply, due to the initial in situ stress field. The radial stress increment is greater than the vertical stress increment within the pile body. Both stresses reach their maximum at the pile side, then decay logarithmically and stabilize at 6 D. At the pile tip, soil stress near the pile side is similar to that at 5 m distance, increases sharply near the pile side, reaches a maximum at 1 m (2 D), and then decays logarithmically, due to the pile tip and lack of pile tip resistance consideration.

3.

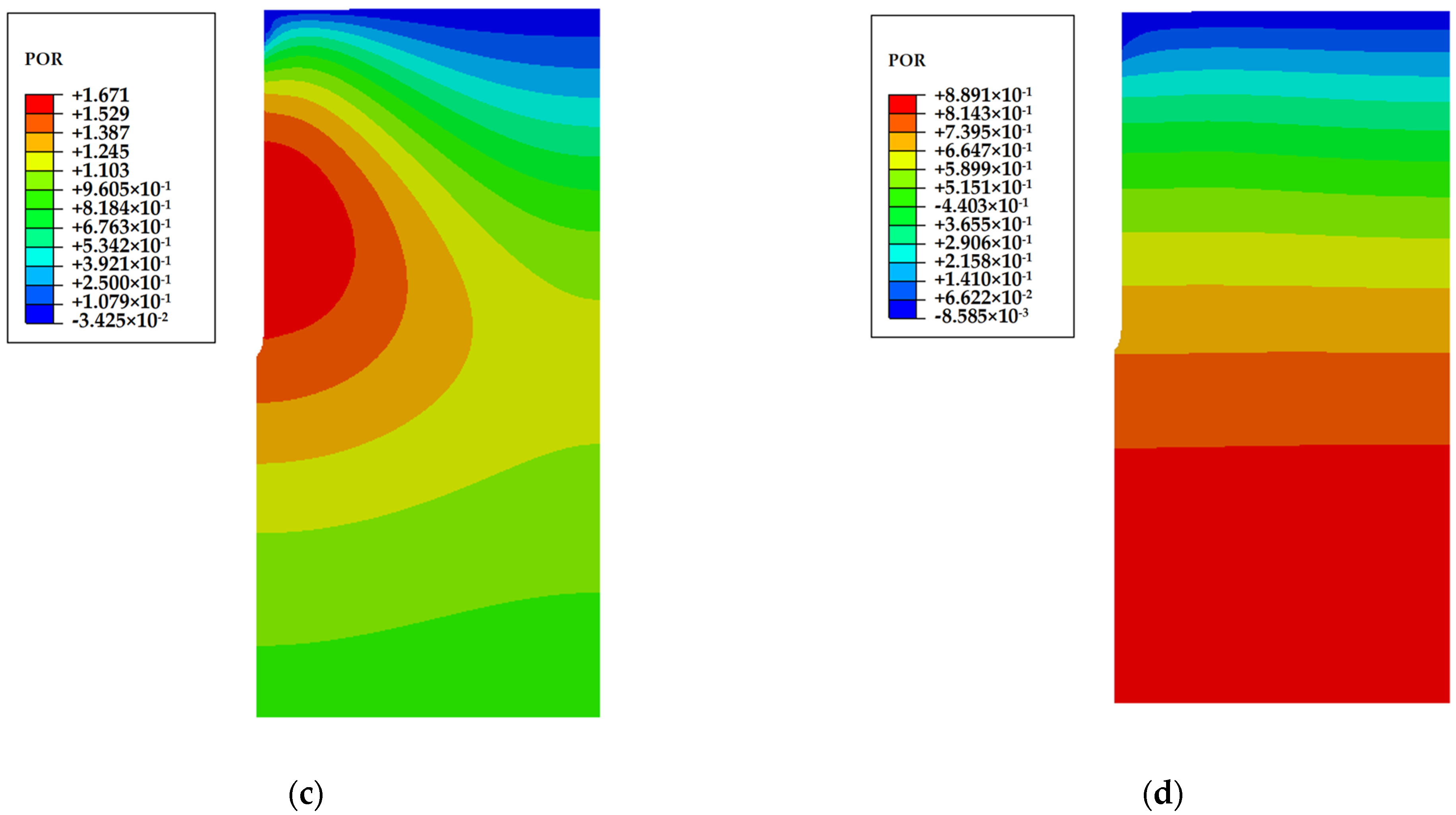
Pore pressure of soil

(1)

EPWP variation during pile driving

Figure 11 shows the EPWP variation at 3 R from the pile center during pile driving. The EPWP increases along the pile shaft and peaks within ±0.5 m of the pile tip. It rises with pile penetration but drops sharply as the pile continues to penetrate.

The distribution of EPWP during pile driving, as shown in Figure 12, also reveals the phenomenon. Negative pore pressure appears in the soil at the pile tip due to deformation from static pile pressing.

(2)

Soil EPWP field post-pile driving

Figure 13 shows the radial and vertical distribution of EPWP in the soil after pile driving. Figure 13a indicates that the maximum EPWP is at the pile–soil interface. It decays nonlinearly in the radial direction, mainly within 2 D from the pile side, and stabilizes beyond this range. Within the pile body, EPWP increases with soil depth. Figure 13b shows that the EPWP increases linearly with depth (3 R, 6 R, 9 R) after pile driving, surges near the pile tip, and then drops sharply, dissipating completely around 4 m (8 D) below the pile tip. This is due to the concentration and diffusion of EPWP during pile driving. The EPWP is zero at the soil surface because it is a drainage boundary, with shorter drainage paths leading to faster EPWP dissipation.

Combined, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 show that, during pile driving, soil displacement within the pile body initially increases and then decreases. The radial stress variation in the surrounding soil is consistent with the radial displacement. EPWP increases along the pile body and peaks at the pile tip, growing with pile penetration but dropping sharply as the pile advances further. After pile driving, EPWP increases linearly with depth, surges near the pile tip, and then drops sharply.

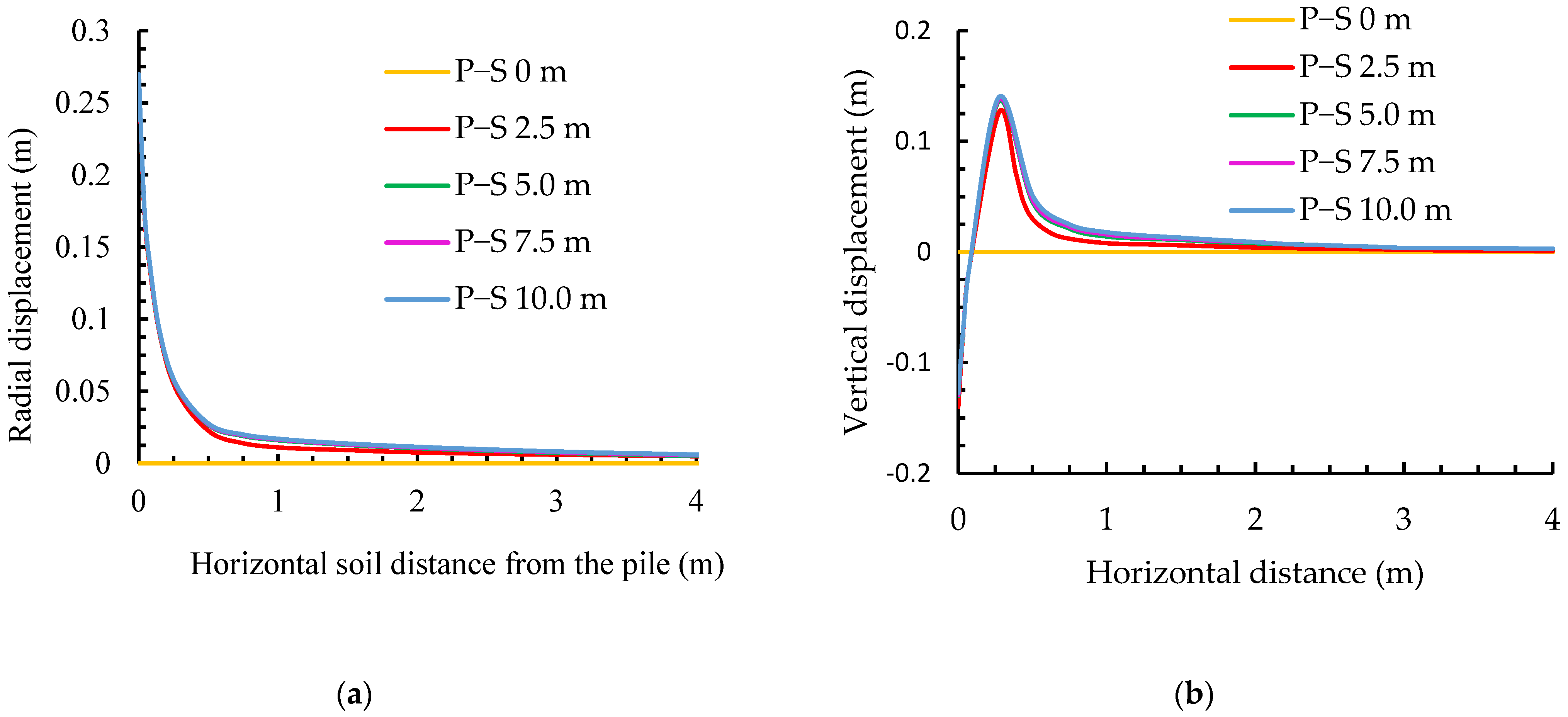
3.2.2. Soil Reconsolidation Around Piles

This subsection discusses the dissipation of EPWP and stress changes in the soil around the pile after different consolidation times.

• EPWP dissipation

Figure 14 presents the variation of EPWP in the soil around the pile over a 20-day consolidation period. Immediately upon the completion of pile driving, the soil around the pile is squeezed. This squeezing leads to high EPWP near the pile. Meanwhile, due to soil compaction and drainage, negative pore water pressure occurs at the pile bottom. After 2.5 days, the EPWP near the ground surface dissipates rapidly because of the short drainage paths. After 5 days, the EPWP decreases, with some still remaining at the pile bottom. After 20 days, the EPWP correlates with the soil depth and is nearly dissipated, which indicates the completion of soil consolidation.

The analysis of EPWP dissipation was conducted at a depth of 5 m, where the soil displacement effect during pile driving was most pronounced. As depicted in Figure 15a, prior to consolidation, a significant EPWP was observed within a certain range of soil adjacent to the pile side. The pressure was highest at the pile side and decreased logarithmically with increasing distance. After 2.5 days, the EPWP dissipates rapidly, leaving only 15% remaining. After 5 days, it is mostly below 2 kPa and is nearly dissipated. After 20 days, it has almost completely dissipated, with the consolidation reaching nearly 100%. The initial EPWP far from the pile side is nearly zero. As the consolidation progresses, the EPWP near the pile side dissipates outward while experiencing a slight increase.

Figure 15b shows how the EPWP in soil 3 R away from the pile center varies with different consolidation times. In the range of the pile body, this pressure has a positive correlation with soil depth. After the end of pile driving, it reaches a peak near the pile tip and then drops rapidly. As the consolidation time increases, the peak gradually moves upward. The reason is that the soil surface serves as a drainage boundary, which enables the EPWP to dissipate upward and slightly raise the pore pressure in the upper soil.

2.

Soil Stress Changes

Figure 16 illustrates the variation of soil stress at 5 m depth with different consolidation times. As the consolidation progresses, the EPWP dissipates. Consequently, the radial stress near the pile side increases substantially, while the vertical stress adjacent to the pile perimeter decreases. In contrast, in the area around the pile, due to soil compaction from pile driving, the vertical stress increases slightly. With the passage of time and the continuation of consolidation, the soil around the pile gradually stabilizes, resulting in a more uniform distribution of both radial and vertical stresses and ultimately reaching a relatively stable state.

Figure 17 shows the stress variations in soil at a distance of 3 R from the pile center during different consolidation durations. It can be seen from the figure that the vertical radial stress along the vertical axis increases significantly. At the end of pile driving, due to the displacement caused by the pile body, the vertical stress instantaneously forms a high stress zone. As time goes by, the vertical stress gradually decreases with a relatively small amplitude and finally stabilizes, reaching an equilibrium state. This is consistent with Hajduk’s [25] findings on the dissipation of excess static pore water pressure in the soil around the pile.

3.2.3. Impact of Various Parameters on Soil Squeezing

This subsection discusses how different parameters affect soil squeezing, focusing on pile diameter and pile–soil interface friction.

• Pile diameter

Figure 18 shows the displacement fields at the normalized radial distances of 3 R (solid line) and 6 R (dashed line) for three different pile diameters (R = 0.2 m, 0.25 m, 0.3 m). The radial displacement has diameter-dependent amplification. At 3 R, there are incremental increases of 13.2% (D = 0.4→0.5 m) and 16.3% (D = 0.5→0.6 m), which shows nonlinear proportionality; the vertical displacement components have spatial decay characteristics. Both the surface heave and subsurface settlement become more intense as D increases. However, their magnitudes decrease exponentially with the radial distance from the pile periphery, which is in line with the cylindrical cavity expansion theory.

2.

Friction Coefficient

Figure 19 shows the correlation between soil displacement and pile–soil interface friction coefficients. The solid line represents the distance from the pile 3 R, and the dotted line represents 6 R. The analysis results are as follows: An increase in the friction coefficient leads to a slight increase in the radial displacement of the soil around the pile. At a radial distance of 3 R from the pile end, when the friction coefficient increases from 0.1 to 0.2, the radial displacement increases by about 2.7%; when it increases from 0.2 to 0.3, the radial displacement increases by about 2.9%. The influence of the friction coefficient on vertical displacement is more significant than that on radial displacement. At 3 R, when the friction coefficient increases from 0.1 to 0.2, the maximum vertical displacement increases by approximately 28.7%; when it increases from 0.2 to 0.3, the maximum vertical displacement increases by about 13.0%. This phenomenon can be attributed to the fact that, as the friction coefficient increases, the pile exerts a greater drag force on the soil, thus causing a more significant vertical displacement. But this influence gradually weakens as the distance from the pile center increases.

3.2.4. Impact of Soil Parameters on the Reconsolidation Process

As Section 3.2.2 and the research of scholars such as Hajduk [25] indicate, the gradient of EPWP dissipation mainly changes in the radial direction during the consolidation phase. Therefore, this section focuses on examining the radial dissipation of EPWP in the soil surrounding the pile at a depth of 5 m under different soil parameter conditions.

• Permeability coefficient

Figure 20 shows the variation of EPWP in soil at a 5 m depth with different permeability coefficients (1 × 10⁻⁷, 1 × 10⁻⁸, 1 × 10⁻⁹). Soils with higher permeability coefficients enable water to diffuse and drain more quickly, which reduces the EPWP. Higher permeability coefficients result in a faster dissipation of EPWP as the consolidation time rises. After 2.5 days, the EPWP for a permeability coefficient of 1 × 10⁻⁷ is almost dissipated. After 20 days, most of the EPWP for 1 × 10⁻⁸ has dissipated, while, for 1 × 10⁻⁹, some EPWP still remains above 5 kPa. In the later stages of consolidation, there is a negative correlation between the permeability coefficient and the residual EPWP.

2.

Poisson’s ratio

Figure 21 shows the variation of EPWP in soil at a depth of 5 m for different Poisson’s ratios (0.25, 0.30, 0.35). A higher Poisson’s ratio leads to lower EPWP generated by the soil squeezing effect. The Poisson’s ratio has a significant impact on EPWP in the plastic zone near the pile side, while its effects are negligible beyond four pile diameters. EPWP decreases as the Poisson’s ratio increases after 2.5 and 5 days of consolidation, and the dissipation rates are similar. After 20 days, the residual EPWP levels off, which indicates that lower Poisson’s ratios lead to faster dissipation at this stage.

4. Analysis of the Timeliness of Piles’ Bearing Capacity

Pile bearing capacity theories can be classified into the α-method and β-method [27] The β-method is based on the effective stress principle. The β-method is considered suitable for analysis, as the numerical simulation in this study uses the effective stress principle.

(1)

Ultimate frictional resistance in Equation (31).

$$f_s=\mu {\sigma }_h^{\prime }$$

(31)

where ${\sigma }_h^{\prime }$ represents the horizontal effective earth pressure at the pile side; $\mu$ denotes the friction coefficient between the pile and soil. By applying the relationship between vertical and horizontal earth pressures, the formula can be rewritten as in Equation (32):

$$f_s=\mu K_0{\sigma }_v^{\prime }$$

(32)

where $K_0$ presents the coefficient of horizontal earth pressure. The calculation formula for normally consolidated soil is given as in Equation (33):

$$K_0=1-\sin {\phi }^{\prime }$$

(33)

where ${\phi }^{\prime }$ is the effective friction angle of soil.

$$K_0=(1-\sin {\phi }^{\prime })OC{R}^{0.5}$$

(34)

where OCR is the over-consolidation ratio in Equation (34).

(2)

Ultimate end resistance in Equation (35)

$$f_b={(c^{\prime })}_b{N}_c+{({\sigma }_v^{\prime })}_b{N}_q$$

(35)

In the formula, ${(c^{\prime })}_b$ represents the effective cohesion of the soil at the pile tip; ${({\sigma }_v^{\prime })}_b$ denotes the vertical effective stress of the soil at the pile end; $N_c$ and $N_q$ are the bearing capacity coefficients in Equations (36) and (37). These coefficients can be calculated using the formula proposed by Janbu [28]:

$$N_q={(\tan \phi \prime +\sqrt{1+{\tan }^2\phi \prime })}^2\exp (2\eta \tan \phi \prime )$$

(36)

$$N_c=(N_q-1)\cot \phi \prime$$

(37)

where η signifies the angle that governs the failure surface characteristics at the pile tip. As depicted in Figure 22, it ranges from $0.33 \pi$ for clay to $0.58 \pi$ for dense sand.

The dissipation rate of EPWP is relatively rapid, and nearly complete dissipation occurs within the first 5 days, and then the rate slows down (see in Section 3.2.2). According to the β-method, the consolidation of the soil around the pile can significantly enhance soil strength and effective stress in the early consolidation stage, which greatly increases the bearing capacity of the jacked pile. In the later consolidation stage, the bearing capacity of the jacked pile continues to increase steadily as the EPWP in the soil around the pile gradually dissipates. This reflects the timeliness law of the bearing capacity of the jacked pile.

5. Conclusions

This paper theoretically analyzes the reconsolidation process of soil surrounding static pressure piles after they are driven into soft-soil foundations based on the cavity expansion theory. Then, numerical simulation analysis is carried out by using the ABAQUS software to clarify the timeliness of the bearing capacity of static pressure piles more clearly. This analysis mainly focuses on the soil squeezing effect during pile driving, the reconsolidation process of the surrounding soil, and the influence of relevant parameters. The following conclusions are drawn:

(1)

A radial consolidation equation for soil around statically pressed piles in soft-soil foundations based on non-Darcy seepage was established by incorporating the Slepicka exponential seepage equation. Subsequently, the EPWP in the soil surrounding the piles was solved using the Crank–Nicolson difference method.

(2)

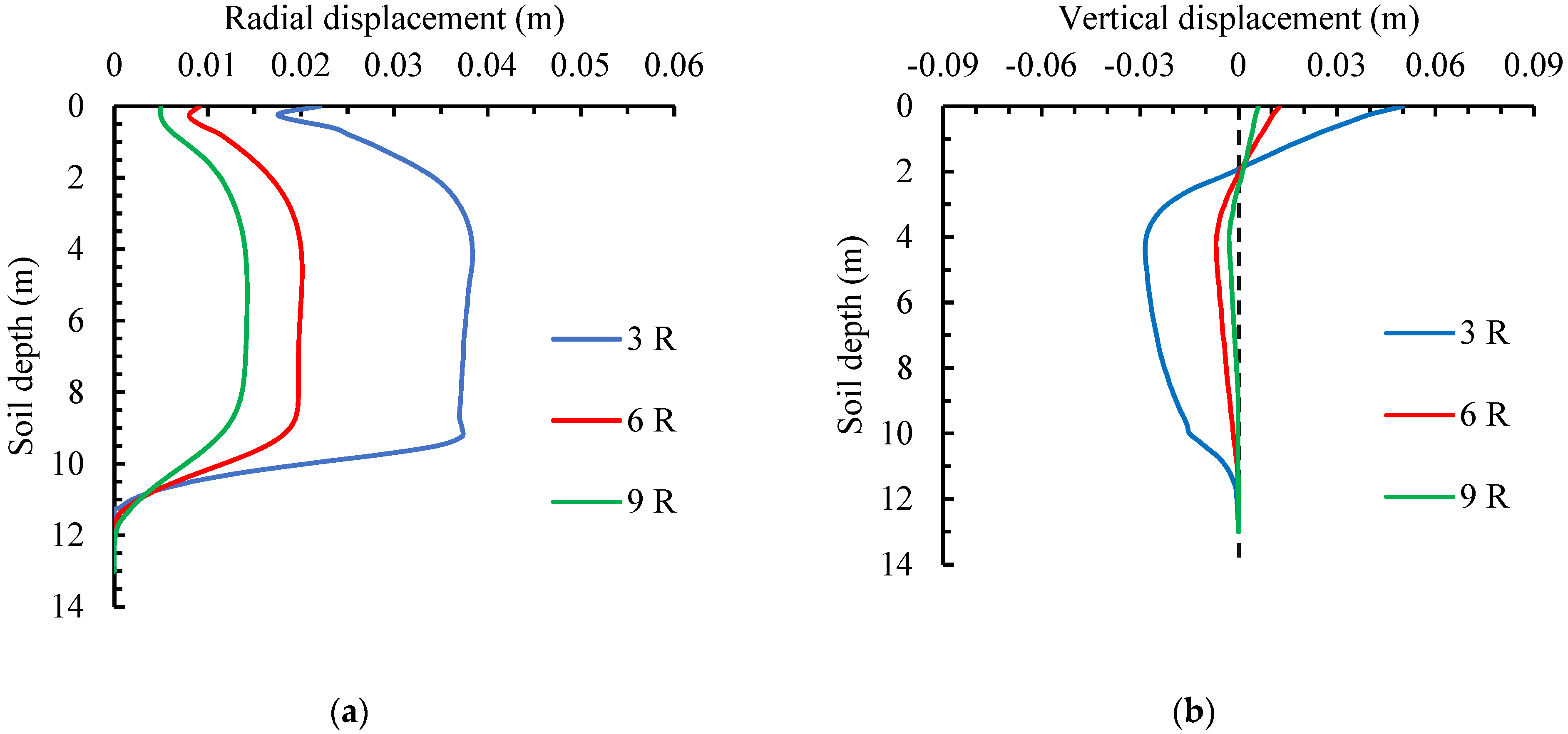
The radial displacement of the soil decreases logarithmically as the radial distance increases. The vertical displacement drops rapidly in the range of 2 m underground. Then, it first increases and finally stabilizes with depth, reaching its peak near the pile tip. Both the radial and vertical stresses decreased with the increase in radial distance and rise with the increase in depth, attaining their maximum values at the pile tip. EPWP decays logarithmically in the radial direction, increases linearly within the pile body along the vertical direction, and spikes sharply at the pile tip.

(3)

In the early consolidation stage, the soil around the pile consolidates, which significantly enhances the soil strength and effective stress. As a result, the bearing capacity of the statically pressed piles is greatly increased. In the later stage (5 days after consolidation), with the gradual dissipation of EPWP in the surrounding soil, the bearing capacity of the piles continues to increase steadily. Therefore, in practical projects, when designing pile foundations, the timeliness of the pile foundation bearing capacity should be fully considered.

The three-dimensional modeling will be used to study the timeliness of pile bearing capacity and for further exploring the distribution and dissipation patterns of excess pore water pressure generated by the soil-squeezing effect of pile groups for better practical applicability.