Performance Analysis of Control Valves for Supply–Demand Balance Regulation in Heating Stations
Abstract
1. Introduction
- This study takes the ideal flow characteristics and working flow characteristics of the control valve as the theoretical starting point, systematically analyses the dual-constraint mechanism of the minimum control impedance and maximum control impedance of the control valve on the response characteristics and control accuracy of the control valve and further explores the action laws of the two key parameters on the comprehensive performance of the control valve.
- According to the fluctuation conditions of the secondary network water supply temperature and the bypass flow rate when the dead zone is 1% under different setting situations of control valve parameters, the optimal parameter configurations of the bypass control valve and the heat exchange control valve are obtained.
2. Thermal Storage Bypass Configuration Scheme
3. Supply–Demand Balance Regulation and Decoupling Control in Heat Stations
3.1. Calculation of Control Valve Flow Rate
3.2. Calculation of Control Valve Impedance
3.3. The Calculation of the Theoretical Opening of the Heat Exchange Control Valve
3.4. The Calculation of the Theoretical Opening of the Bypass Control Valve
4. Regulation Accuracy of Control Valve
4.1. Control Valve Dead Zone
4.2. The Calculation of the Theoretical Opening of the Bypass Control Valve
4.3. Accuracy of Bypass Control Valve
4.4. Research Process
5. Case Analysis
5.1. Calculation of Supply–Demand Balance Regulation in Heat Stations
5.2. Working Process and Precision Analysis of Heat Exchange Control Valves
5.2.1. Impact of Minimum Control Impedance
5.2.2. Impact of Maximum Control Impedance
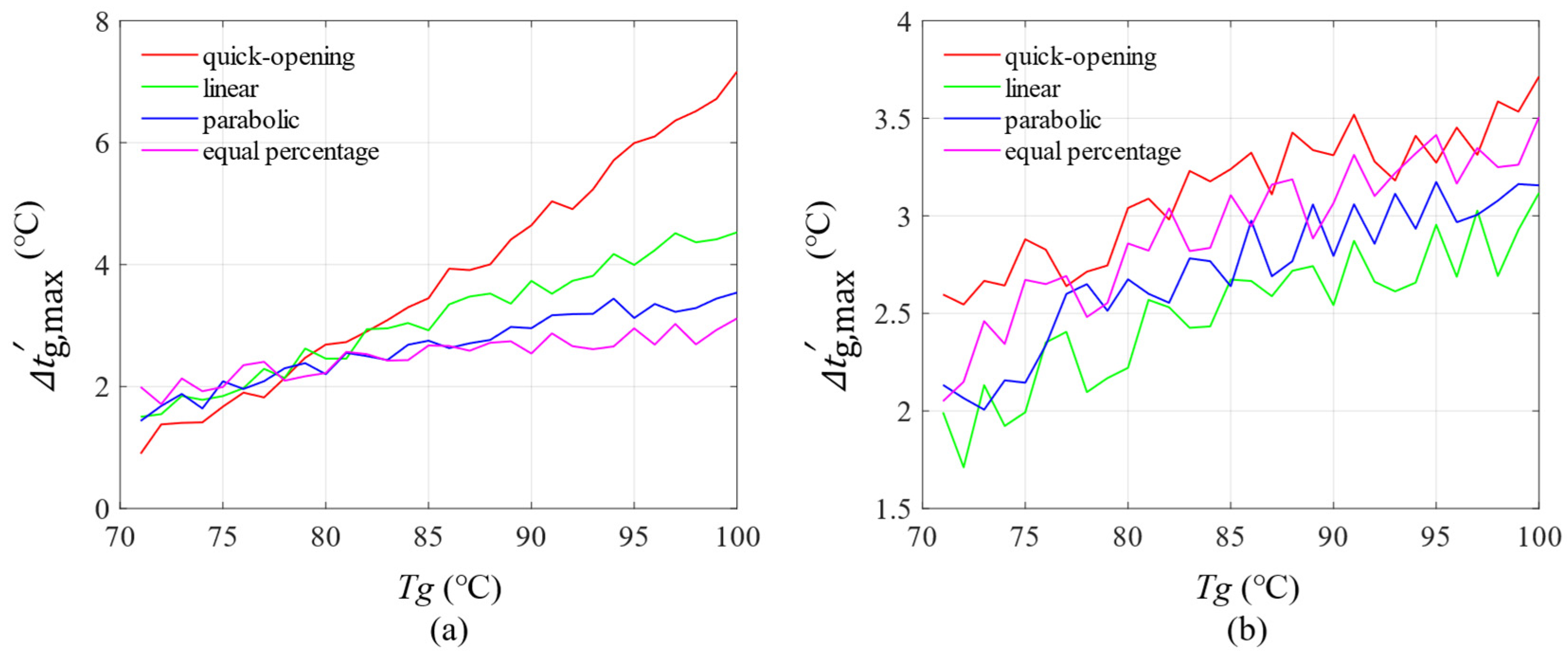
5.2.3. Comparison of Optimal Parameters of Different Control Valves
5.3. Working Process and Precision Analysis of Bypass Control Valve
5.3.1. Impact of Minimum Control Impedance
5.3.2. Impact of Maximum Control Impedance
5.3.3. Comparison of Optimal Parameters of Different Control Valves
6. Optimization Verification Based on the Real Heating Network
6.1. Basic Situation of the Heating System
6.2. Methods
6.3. Engineering Data Analysis
7. Conclusions
- (1)
- The influence of the maximum and minimum control impedance of the valve.
- (2)
- Selection of valve types.
- (3)
- Practical significance and prospects.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations and Nomenclatures
| symbol | significance represented |
| BTS | bypass thermal storage |
| LMTD | logarithmic mean temperature difference |
| Tg,ref | reference supply water temperature of the primary network, K |
| Th,ref | reference return water temperature of the primary temperature, K |
| tg,ref | reference supply water temperature of the secondary network, K |
| th,ref | reference return water temperature of secondary network, K |
| cp | constant-pressure specific heat of heat medium, J/(kg · K) |
| Z | characteristic curve exponent |
| β | proportion of bypass control valve cost in the total cost of bypass branch |
| Tg,Th | design supply and return water temperatures of the primary network, K |
| Sv | valve authority |
| tg,th | design supply and return water temperatures of the secondary network, K |
| B | empirical parameters to characterize the convective heat transfer intensity of radiators |
| Sh | equivalent impedance of plate heat exchange in the secondary network, Pa·s2/m6 |
| symbol | significance represented |
| PHE | plate heat exchange |
| PLC | Programmable Logic Controller |
| Sp | impedance distribution of the secondary side bypass regulation valves of the heat substation, Pa·s2/m6 |
| LMTDref | reference LMTD of PHE, K |
| LMTD* | LMTD of PHE after throttling regulation, K |
| KDt | relative opening of heat exchange control valve |
| KDp | relative opening of bypass control valve |
| tg′ | secondary side supply temperature corresponding to the actual valve opening |
| R | rangeability |
| Sp,min | minimum impedance of bypass regulation on the secondary side of the heat substation, Pa·s2/m6 |
| Sp,max | maximum impedance of bypass regulation on the secondary side of the heat substation, Pa·s2/m6 |
| St,min | minimum impedance of heat-exchange regulation on the secondary side of the heat substation, Pa·s2/m6 |
| St,max | maximum impedance of heat-exchange regulation on the secondary side of the heat substation, Pa·s2/m6 |
| St | impedance of the secondary side heat exchange regulation of the heat substation, Pa·s2/m6 |
References
- Ma, G.; Liu, M.; Wang, Z.; Zhao, Y.; Wang, C.; Yan, J. Energy saving and flexibility analysis of combined heat and power systems integrating heat-power decoupling technologies in renewable energy accommodation. Energy Convers. Manag. 2024, 310, 118487. [Google Scholar] [CrossRef]
- Pokhrel, S.; Amiri, L.; Poncet, S.; Sasmito, A.P.; Ghoreishi-Madiseh, S.A. Renewable heating solutions for buildings; a techno-economic comparative study of sewage heat recovery and Solar Borehole Thermal Energy Storage System. Energy Build. 2022, 259, 111892. [Google Scholar] [CrossRef]
- Nuytten, T.; Claessens, B.; Paredis, K.; Van Bael, J.; Six, D. Flexibility of a combined heat and power system with thermal energy storage for district heating. Appl. Energy 2013, 104, 583–591. [Google Scholar] [CrossRef]
- Mitterrutzner, B.; Callegher, C.Z.; Fraboni, R.; Wilczynski, E.; Pezzutto, S. Review of heating and cooling technologies for buildings: A techno-economic case study of eleven European countries. Energy 2023, 284, 129252. [Google Scholar] [CrossRef]
- Leśko, M.; Bujalski, W. Modeling of district heating networks for the purpose of operational optimization with thermal energy storage. Arch. Thermodyn. 2017, 38, 139–163. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, S.; Wang, J.; Zhang, T.; Ma, Z.; Jiang, S. Key district heating technologies for building energy flexibility: A review. Renew. Sustain. Energy Rev. 2023, 189, 114017. [Google Scholar] [CrossRef]
- Wang, J.; Pan, B.; Rong, L.; Sun, C.; Qi, C. Topology reconstruction of the district heating network for maximizing comprehensive benefits of thermal storage. Energy 2024, 313, 134065. [Google Scholar] [CrossRef]
- Kuosa, M.; Kiviranta, P.; Sarvelainen, H.; Tuliniemi, E.; Korpela, T.; Tallinen, K.; Koponen, H.-K. Optimisation of district heating production by utilising the storage capacity of a district heating network on the basis of weather forecasts. Results Eng. 2022, 13, 100318. [Google Scholar] [CrossRef]
- Hao, J.; Zheng, P.; Li, Y.; Zhang, Z.; Zhang, J.; Yang, J.; Yue, Y.; Li, X. Study on the operational feasibility domain of combined heat and power generation system based on compressed carbon dioxide energy storage. Energy 2023, 291, 130122. [Google Scholar] [CrossRef]
- Zhang, Y.; Johansson, P.; Kalagasidis, A.S. Applicability of thermal energy storage in future low-temperature district heating systems—Case study using multi-scenario analysis. Energy Convers. Manag. 2021, 244, 114518. [Google Scholar] [CrossRef]
- Hassan, M.A.; Serra, S.; Sochard, S.; Viot, H.; Marias, F.; Reneaume, J.-M. Optimal scheduling of energy storage in district heating networks using nonlinear programming. Energy Convers. Manag. 2023, 295, 117652. [Google Scholar] [CrossRef]
- Yang, Z.; Zhou, Y.; Zhang, J.; Lin, X.; Du-Ikonen, L.; Zhong, W.; Zhang, H.; Huang, L.; Liu, B.; Xia, G. Bi-level optimal configuration of renewable electricity based heating in substations of district heating systems. J. Build. Eng. 2024, 95, 110285. [Google Scholar] [CrossRef]
- Knudsen, B.R.; Rohde, D.; Kauko, H. Thermal energy storage sizing for industrial waste-heat utilization in district heating: A model predictive control approach. Energy 2021, 234, 121200. [Google Scholar] [CrossRef]
- Yu, L.; Sun, Y.; Xu, Z.; Shen, C.; Yue, D.; Jiang, T.; Guan, X. Multi-agent deep reinforcement learning for hvac control in commercial buildings. IEEE Trans. Smart Grid 2020, 12, 407–419. [Google Scholar] [CrossRef]
- Zheng, X.; Shi, Z.; Wang, Y.; Zhang, H.; Tang, Z. Digital twin modeling for district heating network based on hydraulic resistance identification and heat load prediction. Energy 2023, 288, 129726. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, Z.; Zhao, J.; Zheng, J.; Guan, Z. Optimizing for clean-heating improvements in a district energy system with high penetration of wind power. Energy 2019, 175, 1085–1099. [Google Scholar] [CrossRef]
- Zhang, Z.; Fedorovich, K.S. Optimal operation of multi-integrated energy system based on multi-level Nash multi-stage robust. Appl. Energy 2024, 358, 122557. [Google Scholar] [CrossRef]
- Zotică, C.; Pérez-Piñeiro, D.; Skogestad, S. Supervisory control design for balancing supply and demand in a district heating system with thermal energy storage. Comput. Chem. Eng. 2021, 149, 107306. [Google Scholar] [CrossRef]
- Xu, X.; Wang, Y.; Fang, L.; Wang, Z.; Li, Y. Numerical study on cavity-vortex evolution in cavitation flow in nuclear control valves with different openings and structural parameters. Ann. Nucl. Energy 2024, 211, 110880. [Google Scholar] [CrossRef]
- Bünning, F.; Warrington, J.; Heer, P.; Smith, R.S.; Lygeros, J. Robust MPC with data-driven demand forecasting for frequency regulation with heat pumps. Control. Eng. Pract. 2022, 122, 105101. [Google Scholar] [CrossRef]
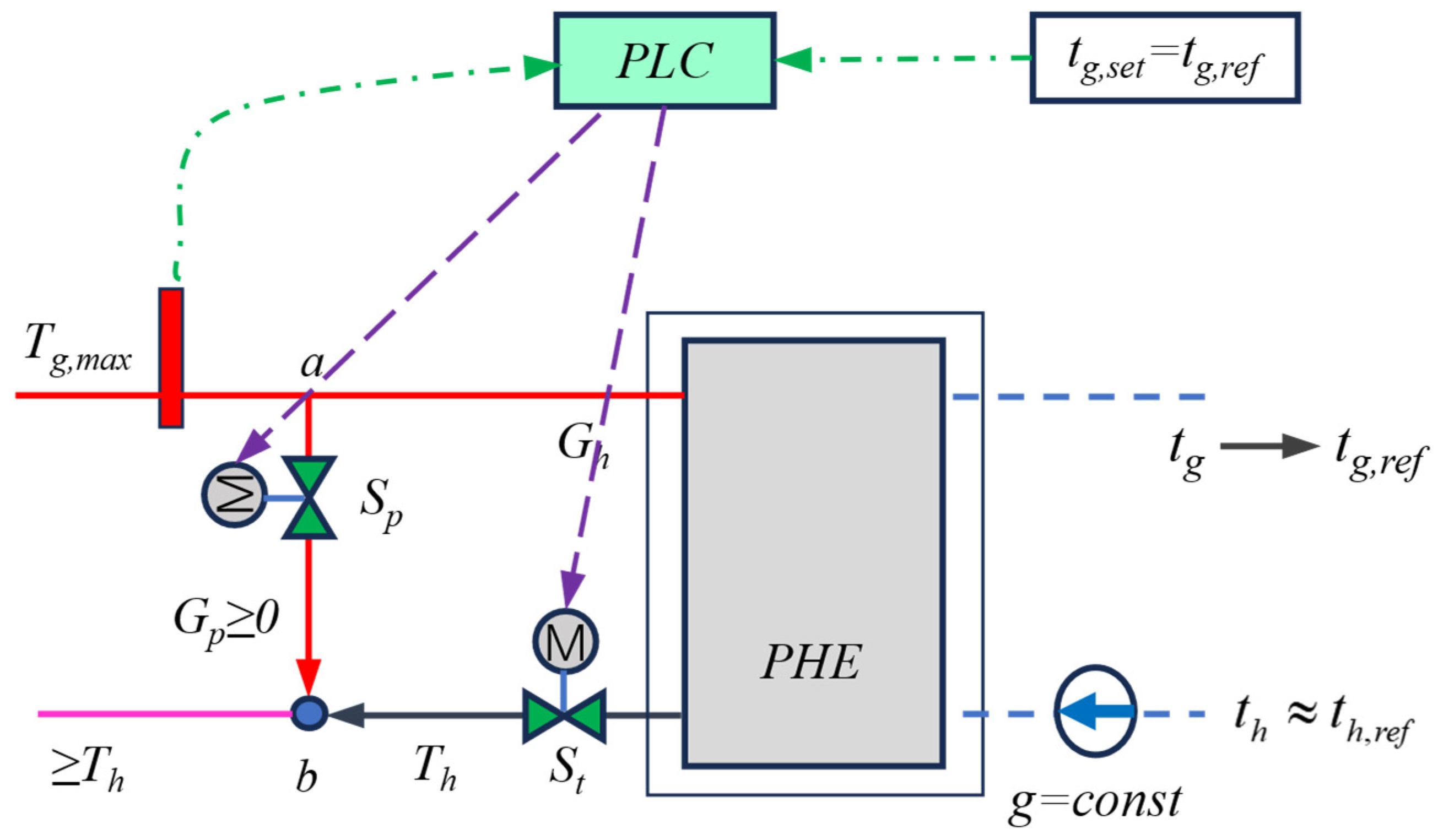

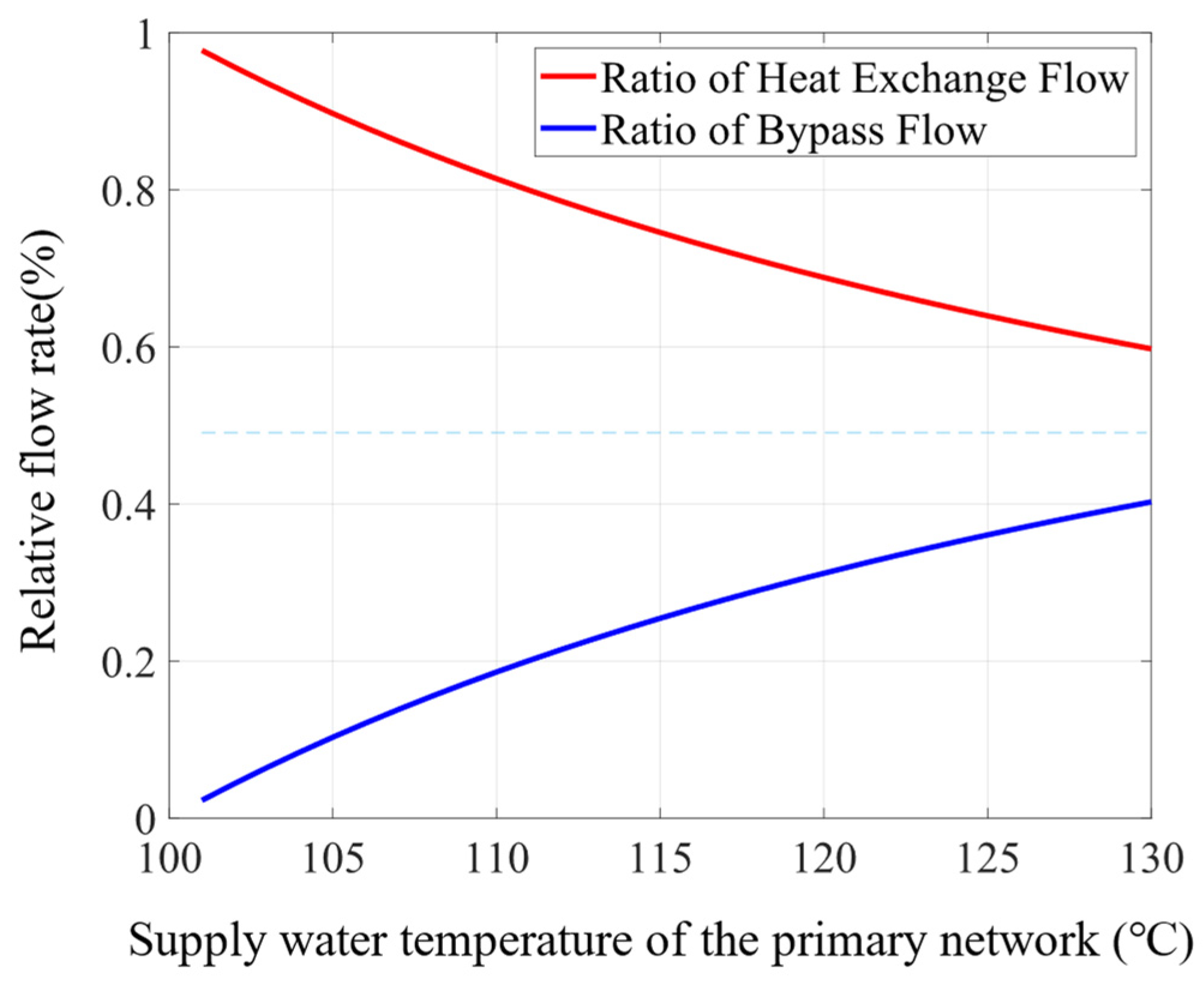
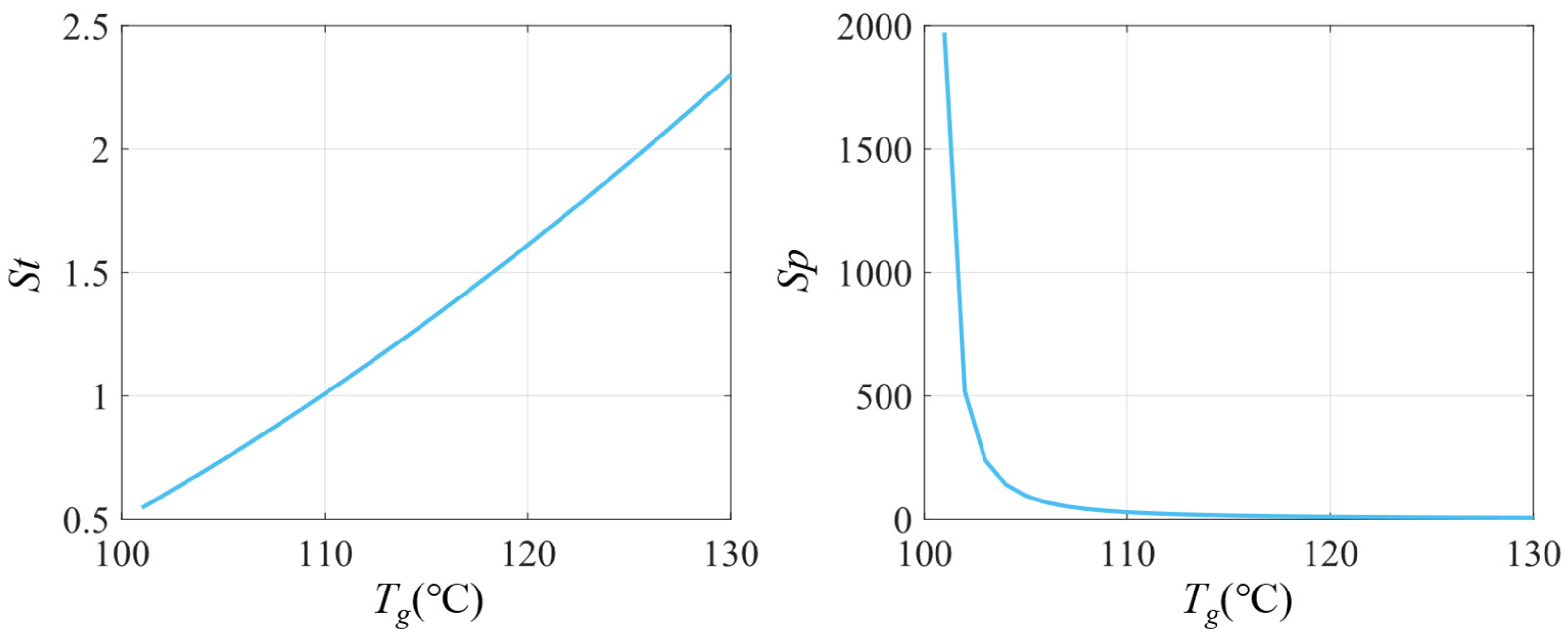
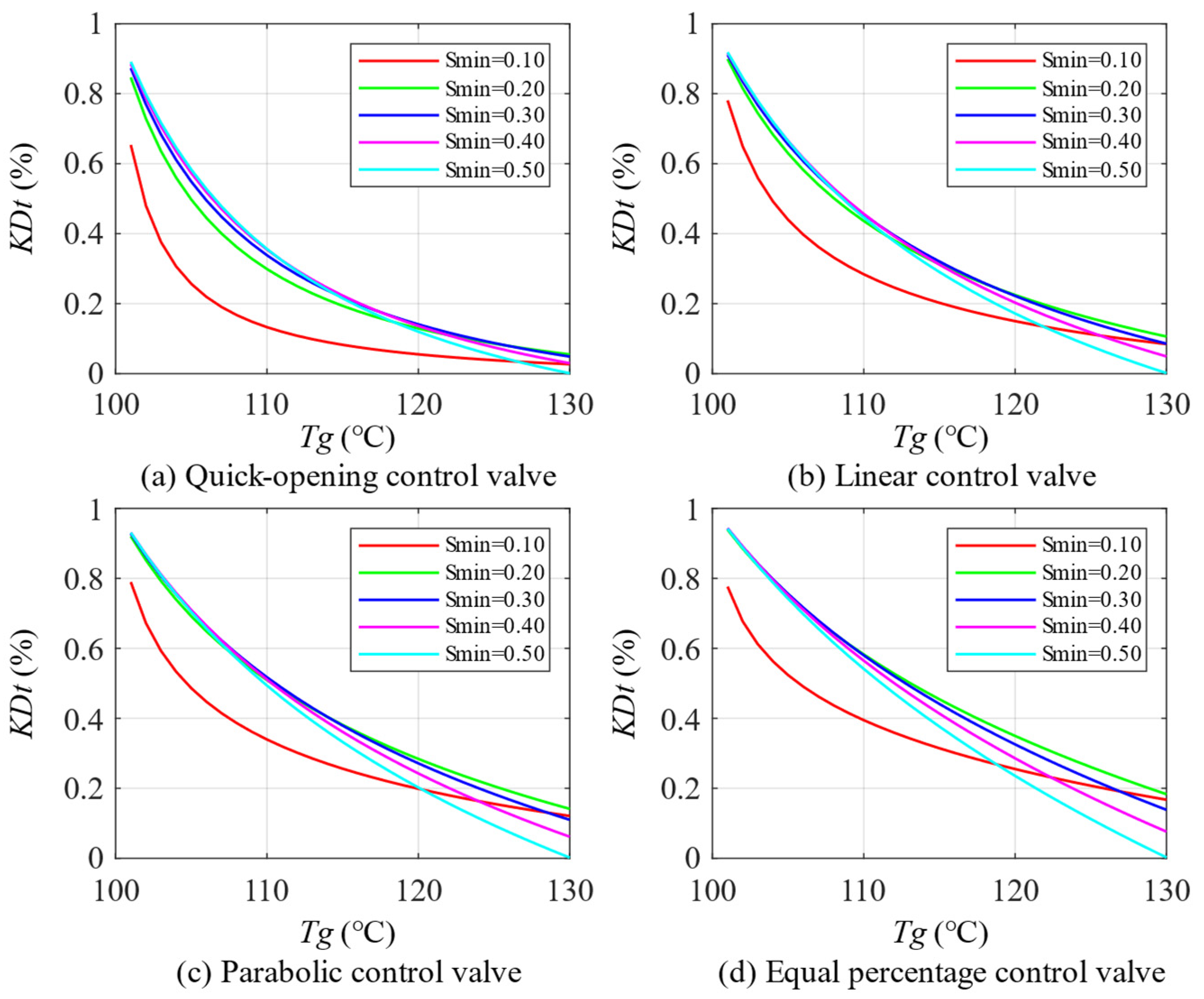

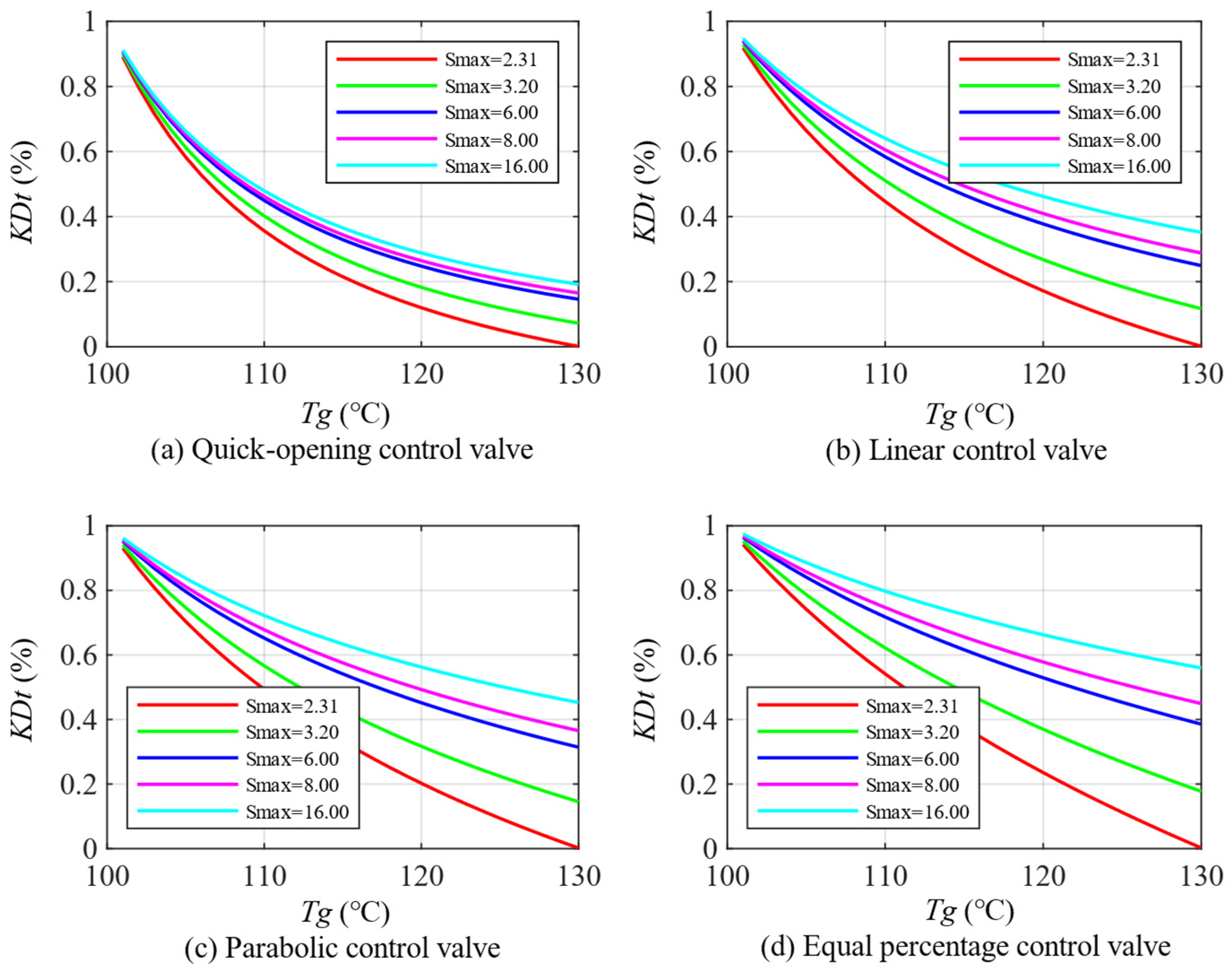
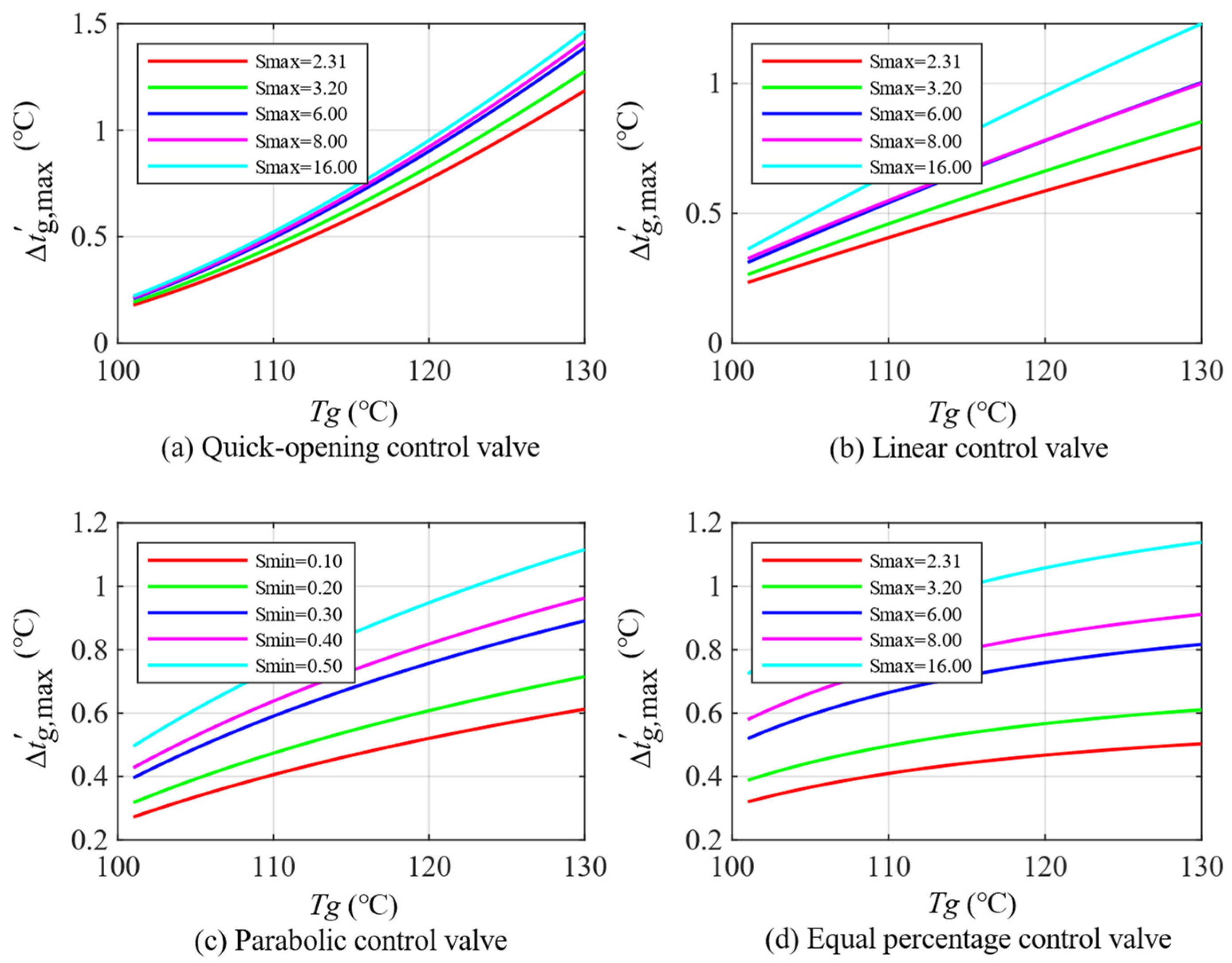
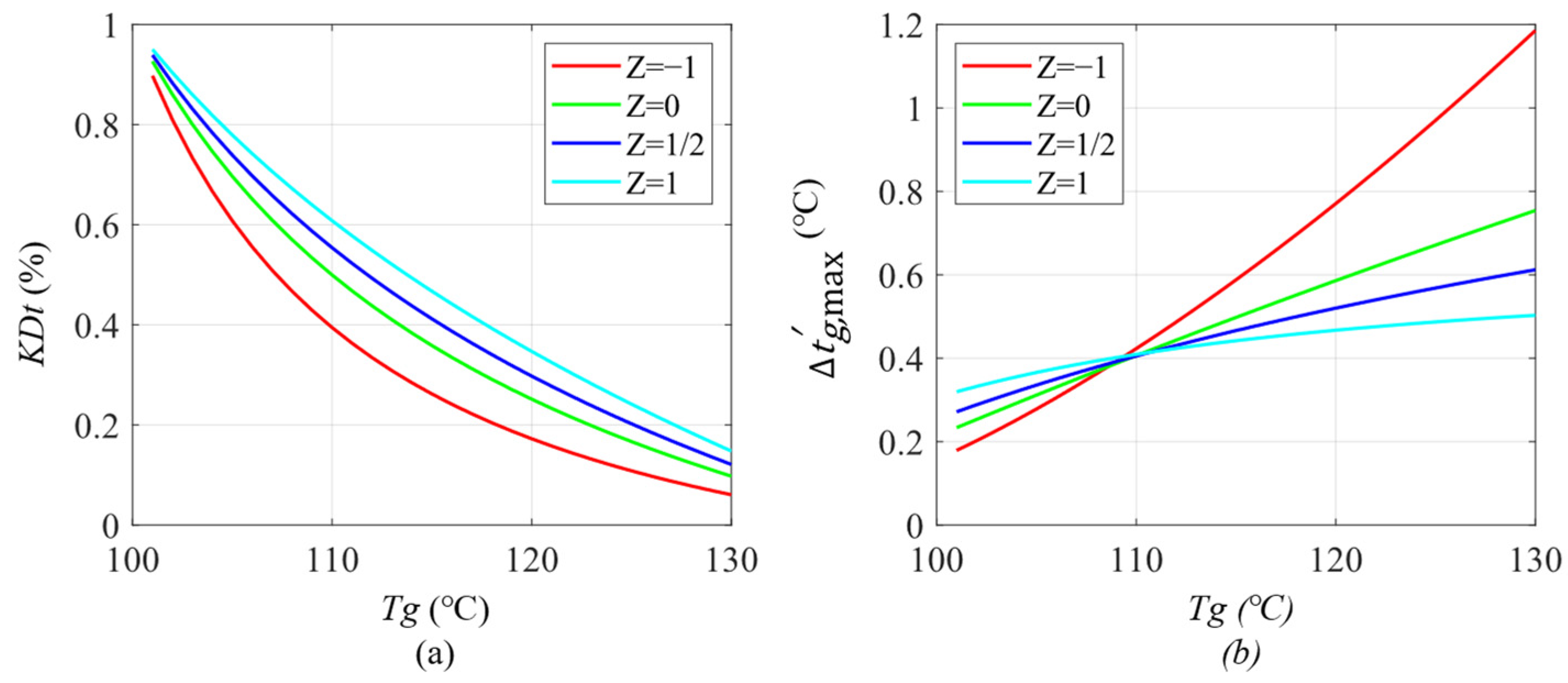
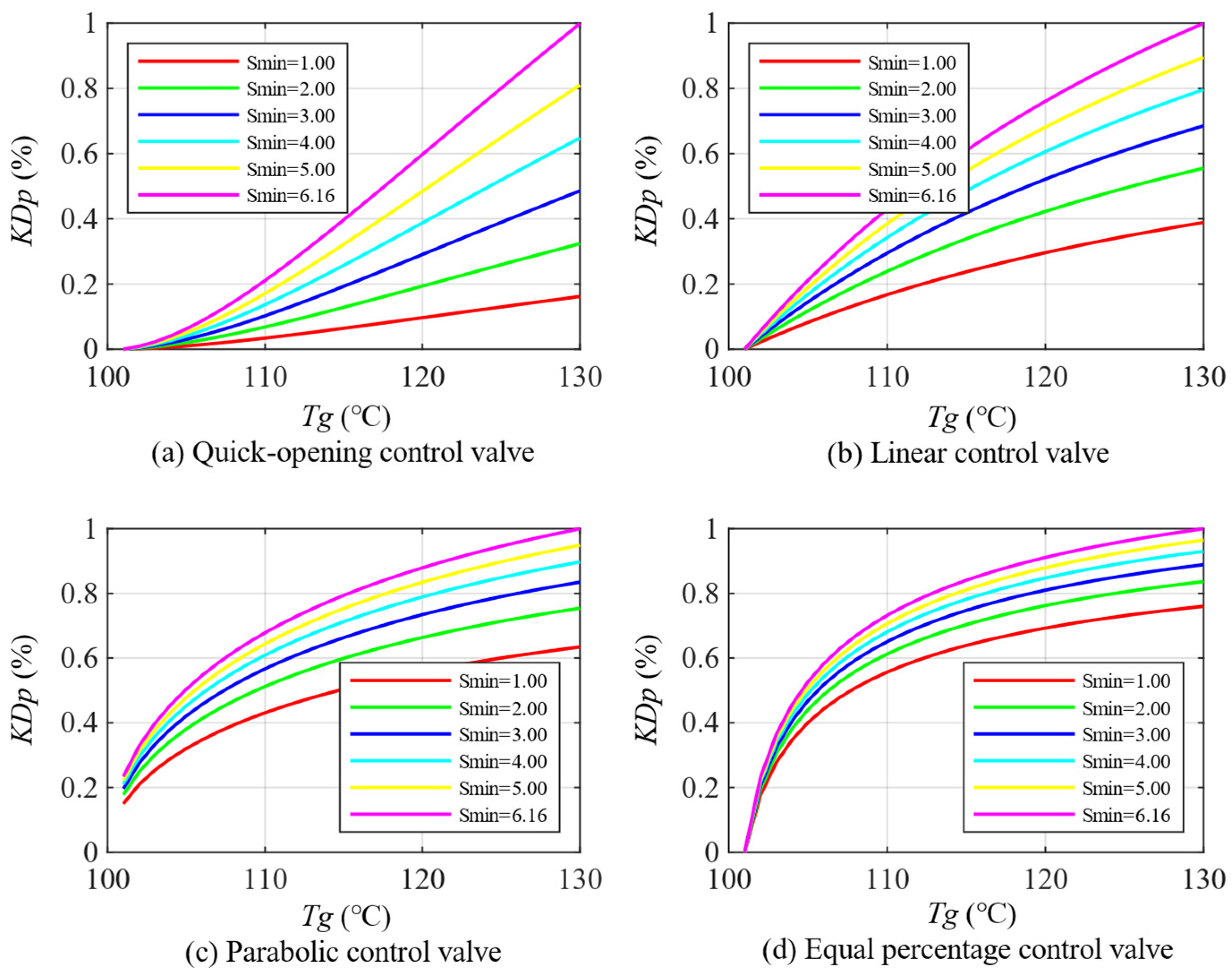
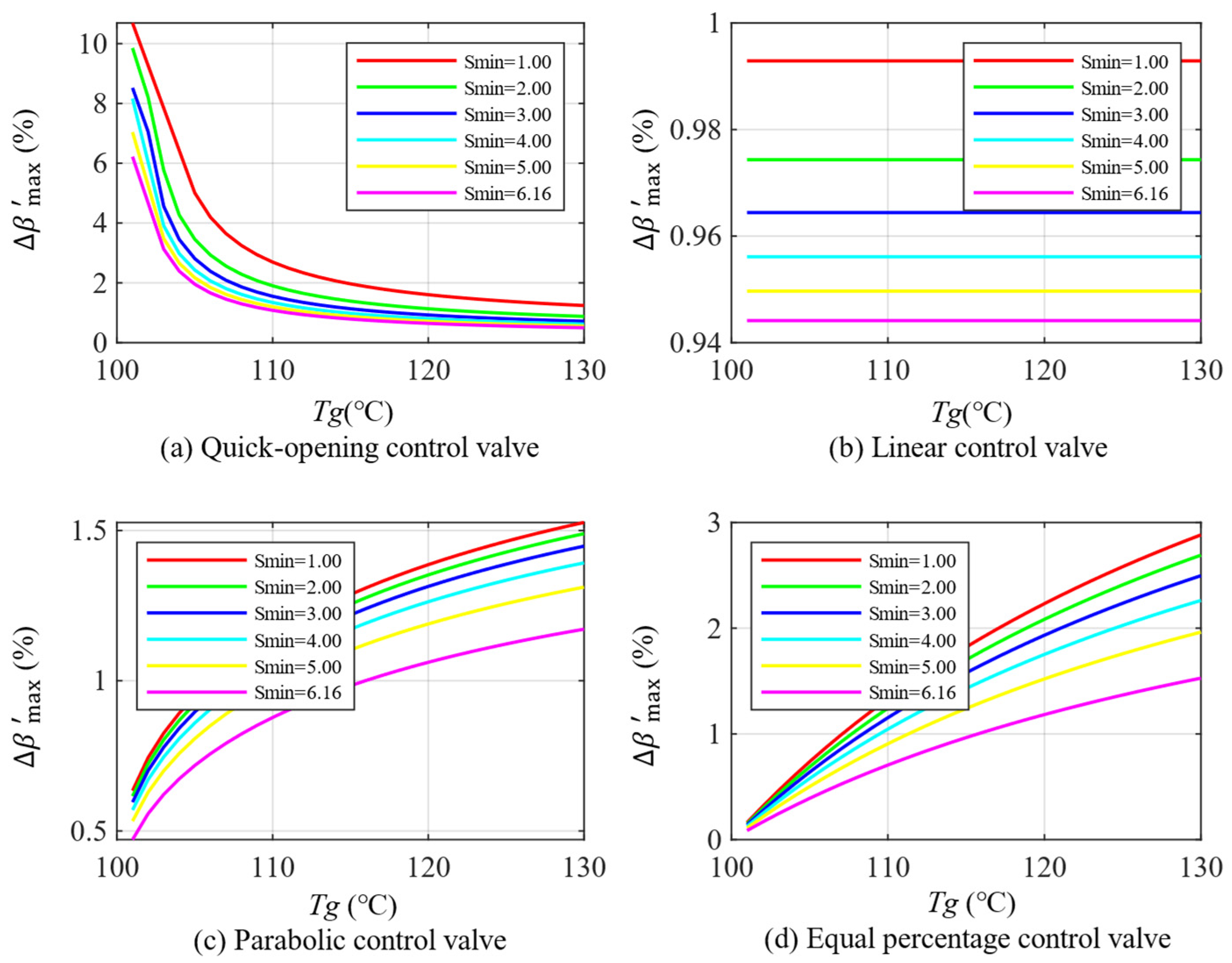
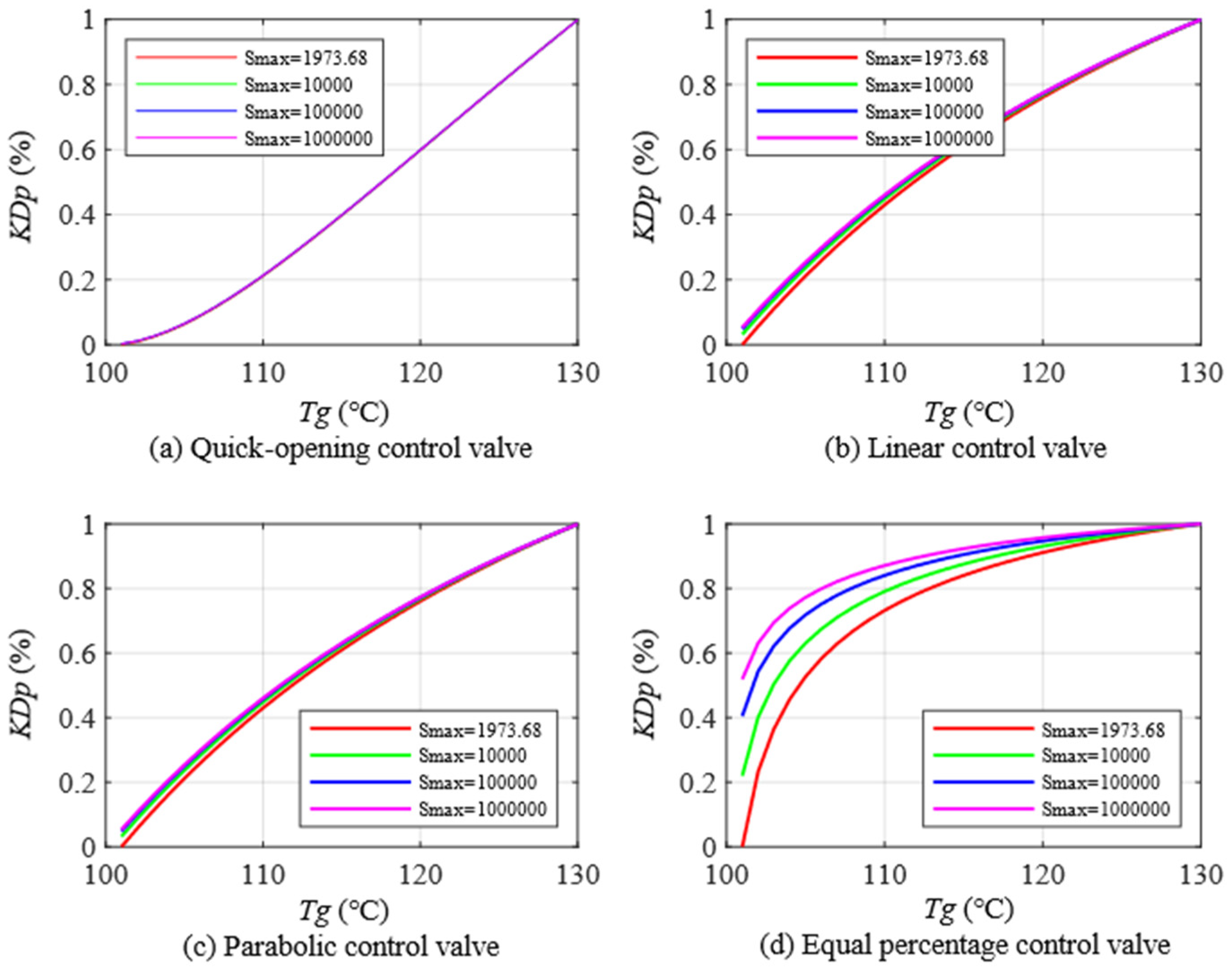
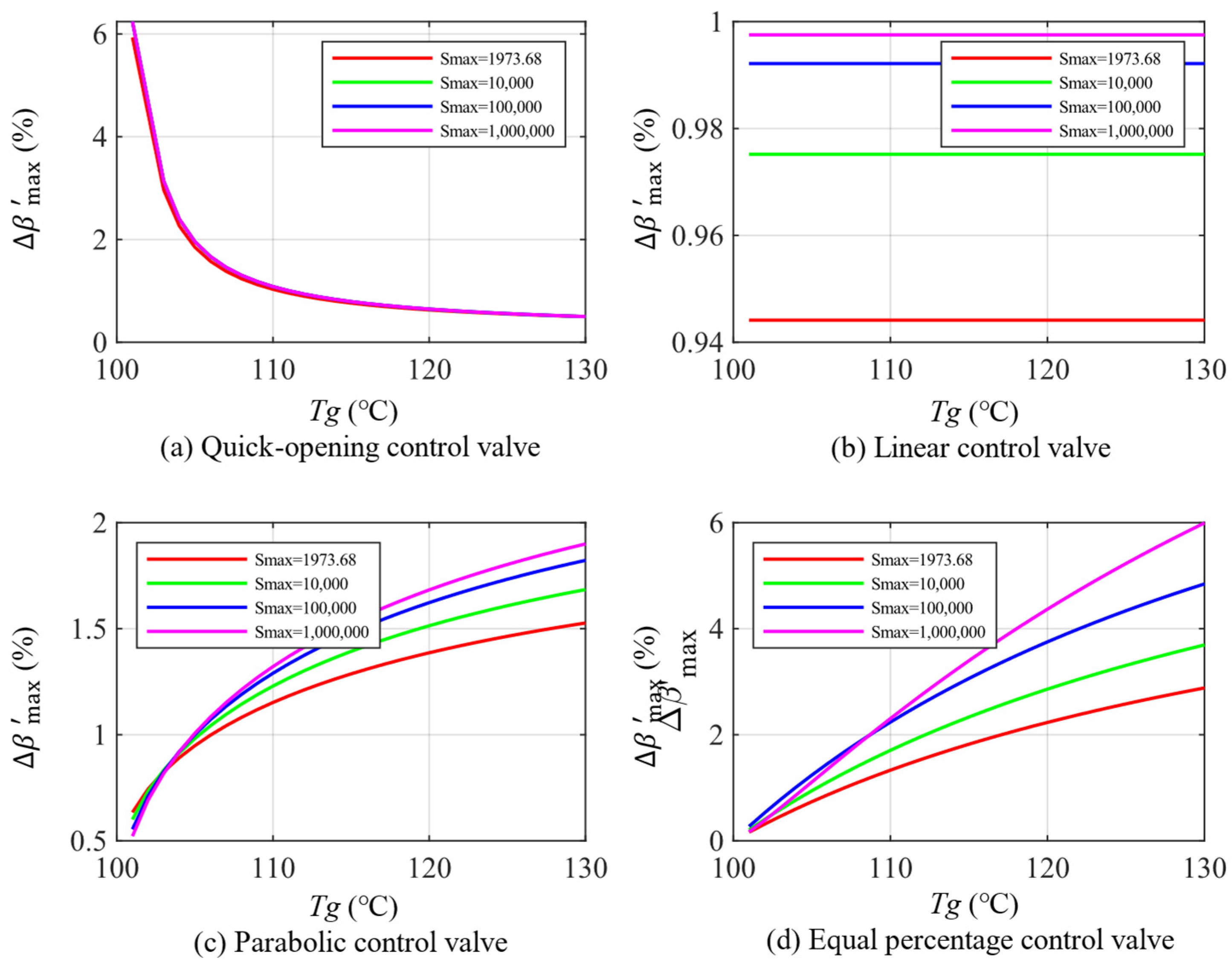
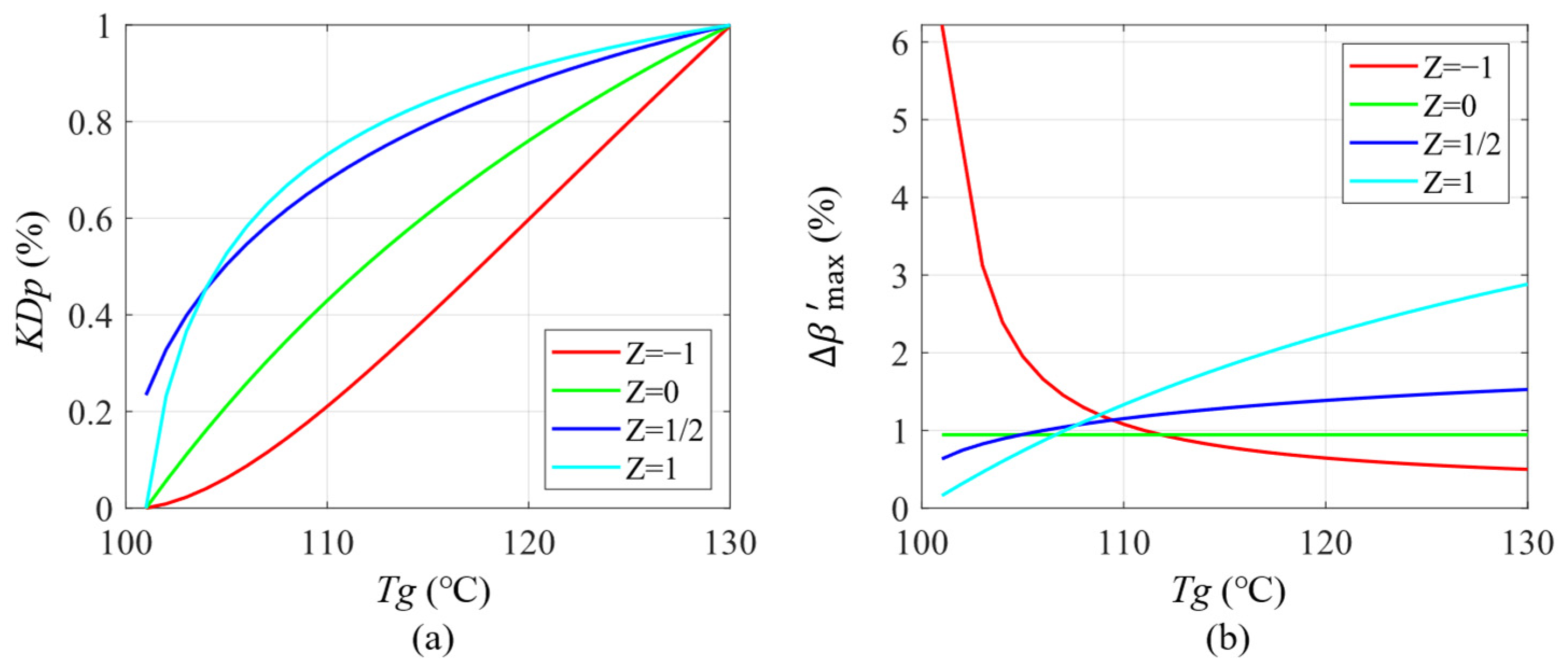
| Impedance Range | Minimum Controllable Impedance Range | Maximum Controllable Impedance Range |
|---|---|---|
| 0.55~2.31 | 0~0.55 | 2.31~+∞ |
| Types of Control Valves | Water Supply Temperature of the Primary Network (°C) | Average Value | |||||
|---|---|---|---|---|---|---|---|
| 105 | 110 | 115 | 120 | 125 | 130 | ||
| Quick-opening | 0.2782 | 0.4230 | 0.5879 | 0.7708 | 0.9704 | 1.1857 | 0.7027 |
| Linear control | 0.3116 | 0.4064 | 0.4978 | 0.5861 | 0.6713 | 0.7541 | 0.5379 |
| Parabolic control | 0.3356 | 0.4054 | 0.4663 | 0.5201 | 0.5683 | 0.6121 | 0.4846 |
| Equal percentage | 0.3659 | 0.4093 | 0.4420 | 0.4672 | 0.4870 | 0.5029 | 0.4457 |
| Impedance Range | Minimum Controllable Impedance Range | Maximum Controllable Impedance Range |
|---|---|---|
| 66.16~1973.68 | 0~6.16 | 1973.68~+∞ |
| Types of Control Valves | Water Supply Temperature of the Primary Network (°C) | Average Value | |||||
|---|---|---|---|---|---|---|---|
| 105 | 110 | 115 | 120 | 125 | 130 | ||
| Quick opening | 1.9527 | 1.0800 | 0.7895 | 0.6442 | 0.5570 | 0.4988 | 0.92 |
| Linear control | 0.9441 | 0.9441 | 0.9441 | 0.9441 | 0.9441 | 0.9441 | 0.94 |
| Parabolic control | 0.9486 | 1.1522 | 1.2869 | 1.3864 | 1.4641 | 1.5268 | 1.29 |
| Equal percentage | 0.7369 | 1.3315 | 1.8214 | 2.2321 | 2.5815 | 2.8826 | 1.93 |
| Group | Heat Station | Heat Exchange Control Valve | Bypass Control Valve | Group | Heat Station | Heat Exchange Control Valve | Bypass Control Valve |
|---|---|---|---|---|---|---|---|
| 1 | Lixiang1 | Quick-opening | Quick-opening | 9 | Ximao | Parabolic | Quick-opening |
| 2 | Lixang2 | Quick-opening | Linear | 10 | Zhangheng | Parabolic | Linear |
| 3 | Ningxin | Quick-opening | Parabolic | 11 | Tetao | Parabolic | Parabolic |
| 4 | Fuyuan | Quick-opening | Equal percentage | 12 | Gongye | Parabolic | Equal percentage |
| 5 | Tianxiu | Linear | Quick-opening | 13 | Zhonghang | Equal percentage | Quick-opening |
| 6 | Jingyang | Linear | Linear | 14 | Guangming | Equal percentage | Linear |
| 7 | Yijing | Linear | Parabolic | 15 | Feicui | Equal percentage | Parabolic |
| 8 | Fugui | Linear | Equal percentage | 16 | Qiantun | Equal percentage | Equal percentage |
| Heat station | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Average value | 4.0 | 3.8 | 4.0 | 3.9 | 3.2 | 3.1 | 3.3 | 3.3 |
| Heat station | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Average value | 2.9 | 2.7 | 3.0 | 3.1 | 3.1 | 2.5 | 2.7 | 2.9 |
| Group | Heat Station | Heat Exchange Control Valve | Bypass Control Valve | Group | Heat Station | Heat Exchange Control Valve | Bypass Control Valve |
|---|---|---|---|---|---|---|---|
| 2 | Lixang2 | Quick-opening | Linear | 13 | Zhonghang | Equal percentage | Quick-opening |
| 6 | Jingyang | Linear | Linear | 14 | Guangming | Equal percentage | Linear |
| 10 | Zhangheng | Parabolic | Linear | 15 | Feicui | Equal percentage | Parabolic |
| 10 | Zhangheng | Parabolic | Linear | 16 | Qiantun | Equal percentage | Equal percentage |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, P.; Yin, J.; Wang, J. Performance Analysis of Control Valves for Supply–Demand Balance Regulation in Heating Stations. Buildings 2025, 15, 1624. https://doi.org/10.3390/buildings15101624
Zhao P, Yin J, Wang J. Performance Analysis of Control Valves for Supply–Demand Balance Regulation in Heating Stations. Buildings. 2025; 15(10):1624. https://doi.org/10.3390/buildings15101624
Chicago/Turabian StyleZhao, Pengpeng, Jiaxiang Yin, and Jinda Wang. 2025. "Performance Analysis of Control Valves for Supply–Demand Balance Regulation in Heating Stations" Buildings 15, no. 10: 1624. https://doi.org/10.3390/buildings15101624
APA StyleZhao, P., Yin, J., & Wang, J. (2025). Performance Analysis of Control Valves for Supply–Demand Balance Regulation in Heating Stations. Buildings, 15(10), 1624. https://doi.org/10.3390/buildings15101624






