Modeling the Strain-Range Dependent Cyclic Hardening of SS304 and 08Ch18N10T Stainless Steel with a Memory Surface
Abstract
1. Introduction
2. New Constitutive Model
2.1. Yield Surface and Flow Rule
2.2. Virtual Back-Stress
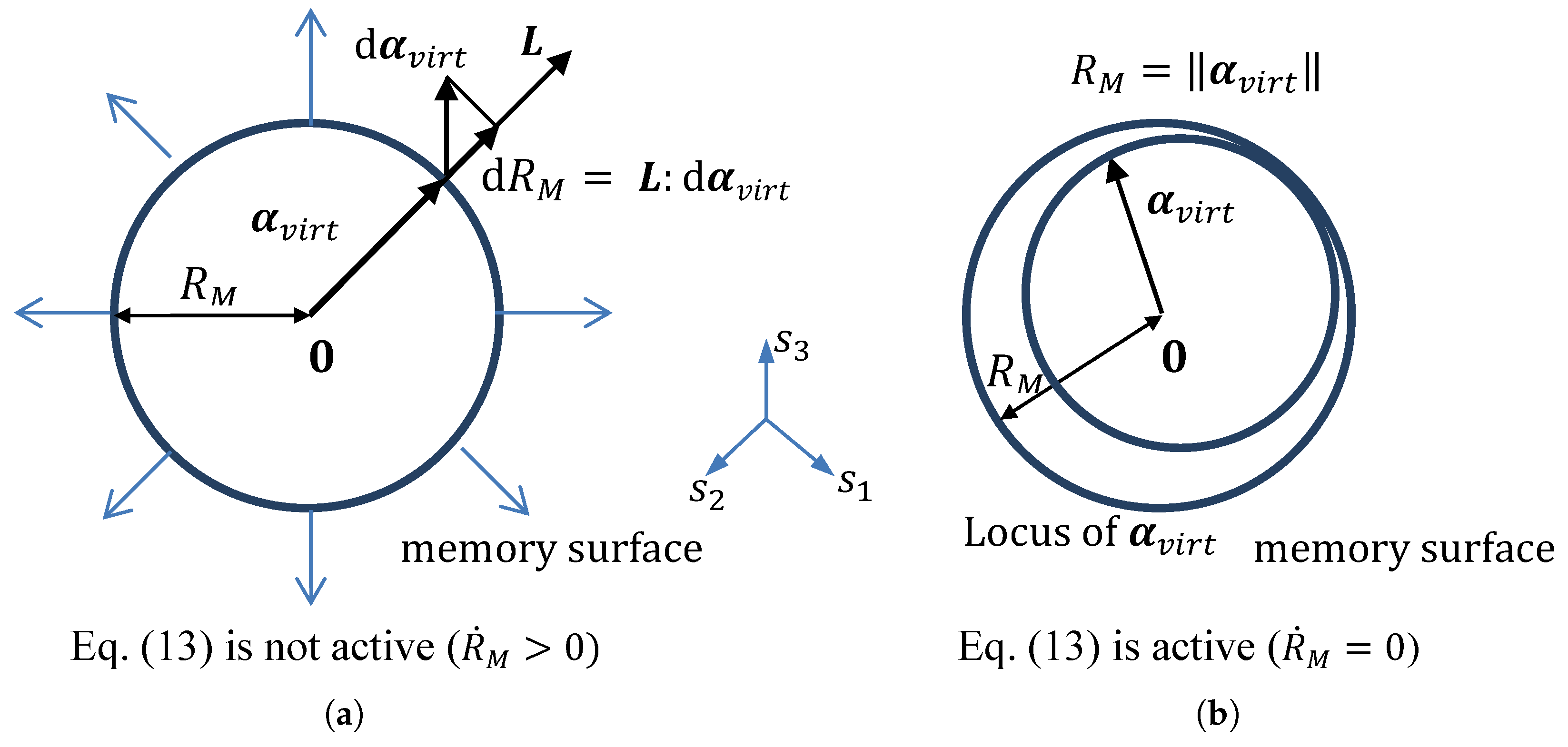
2.3. Memory Surface
2.4. Kinematic Hardening Rule
2.5. Isotropic Hardening Rule
3. Identification of Material Parameters and Model Verification on SS304 Data
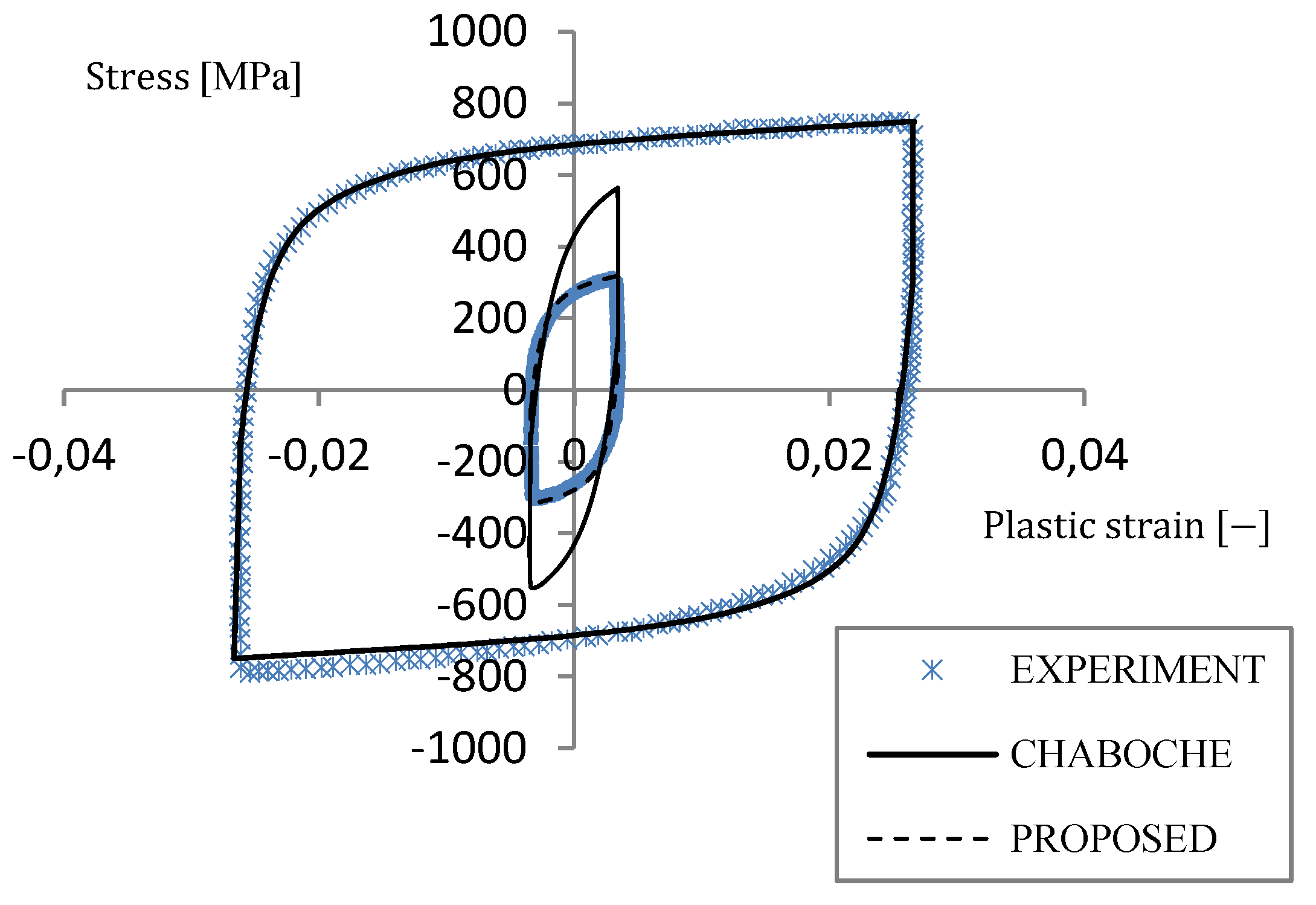
3.1. Uniaxial Large Hysteresis Loop
3.2. Static Strain Curve
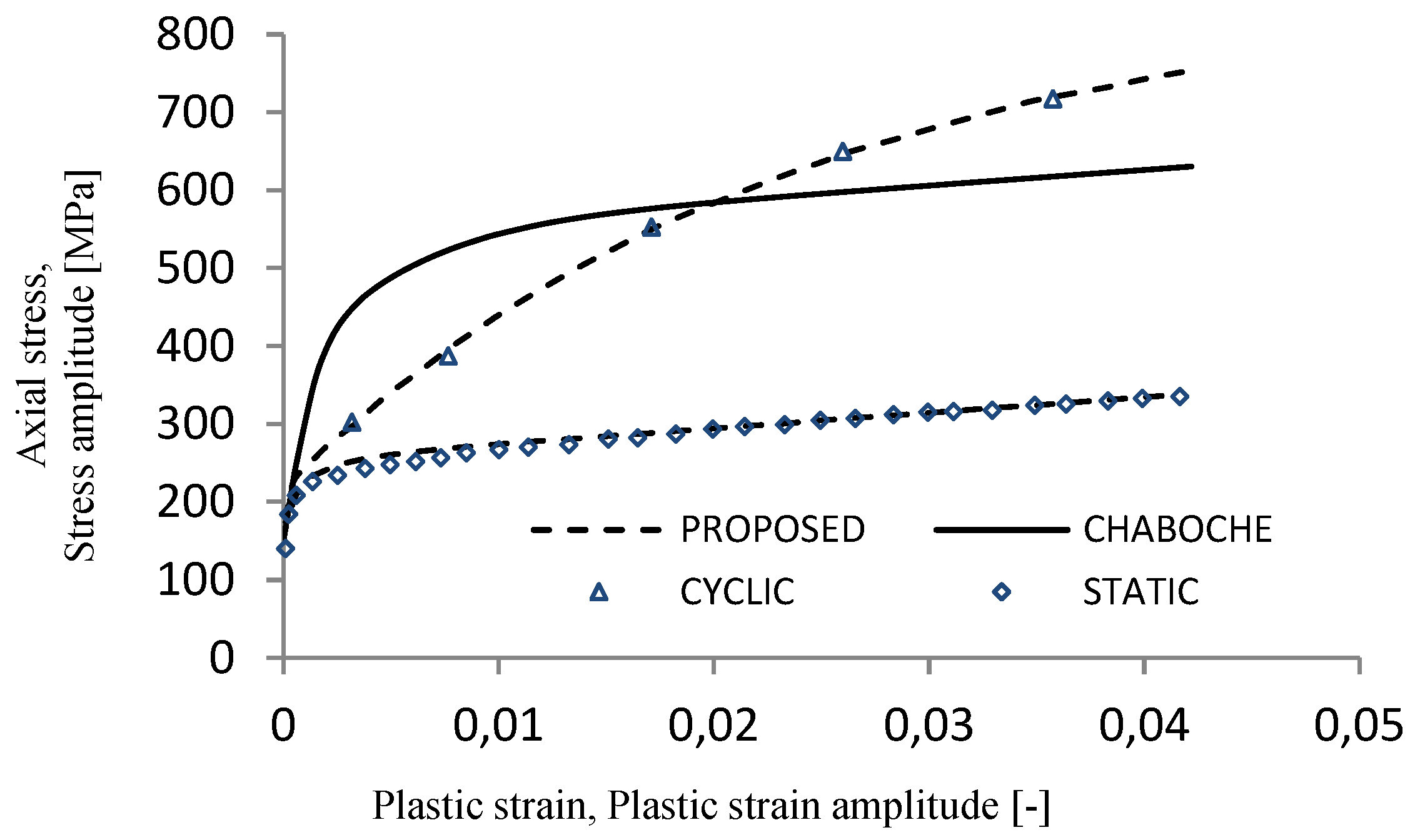
3.3. Cyclic Stress–Strain Curve
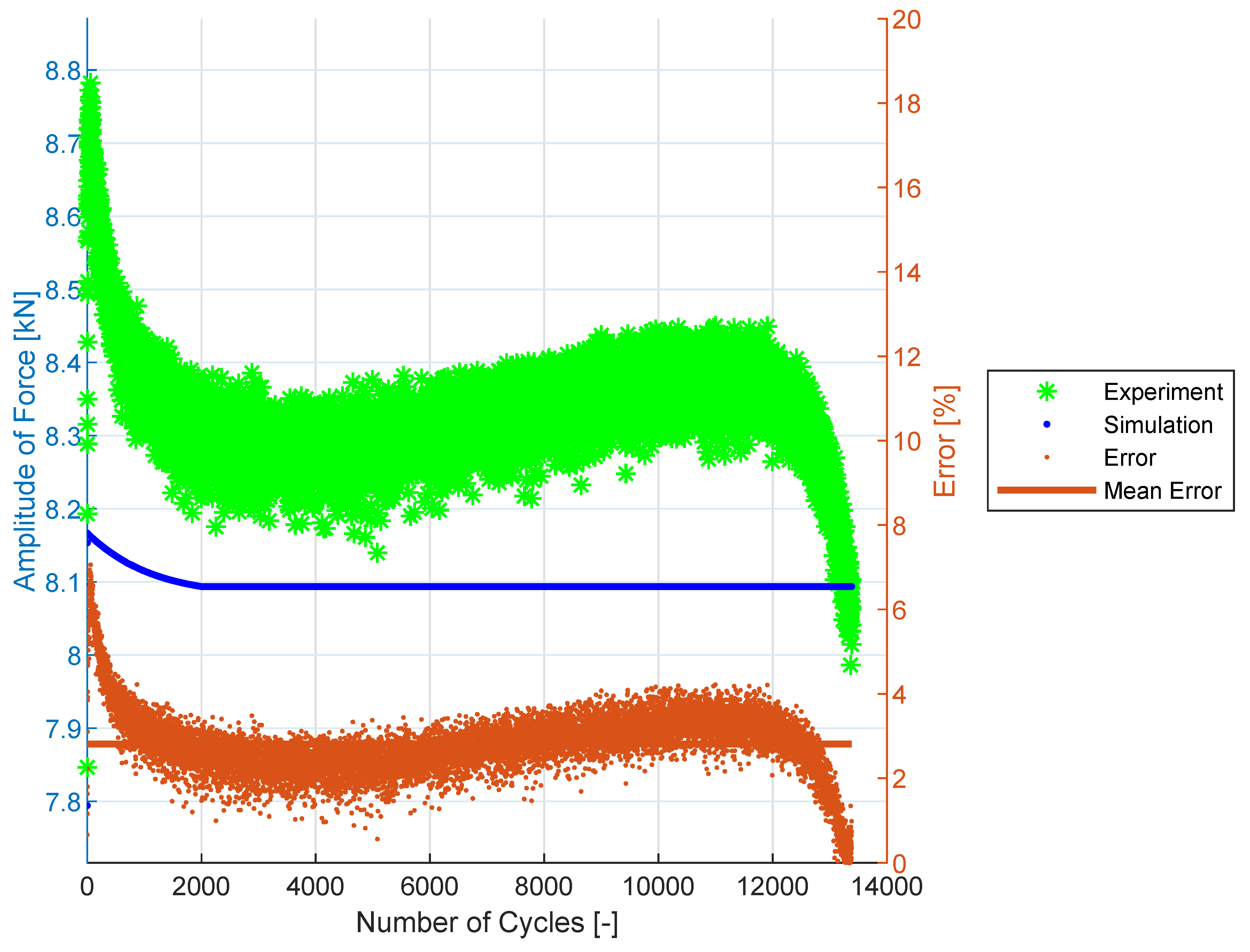
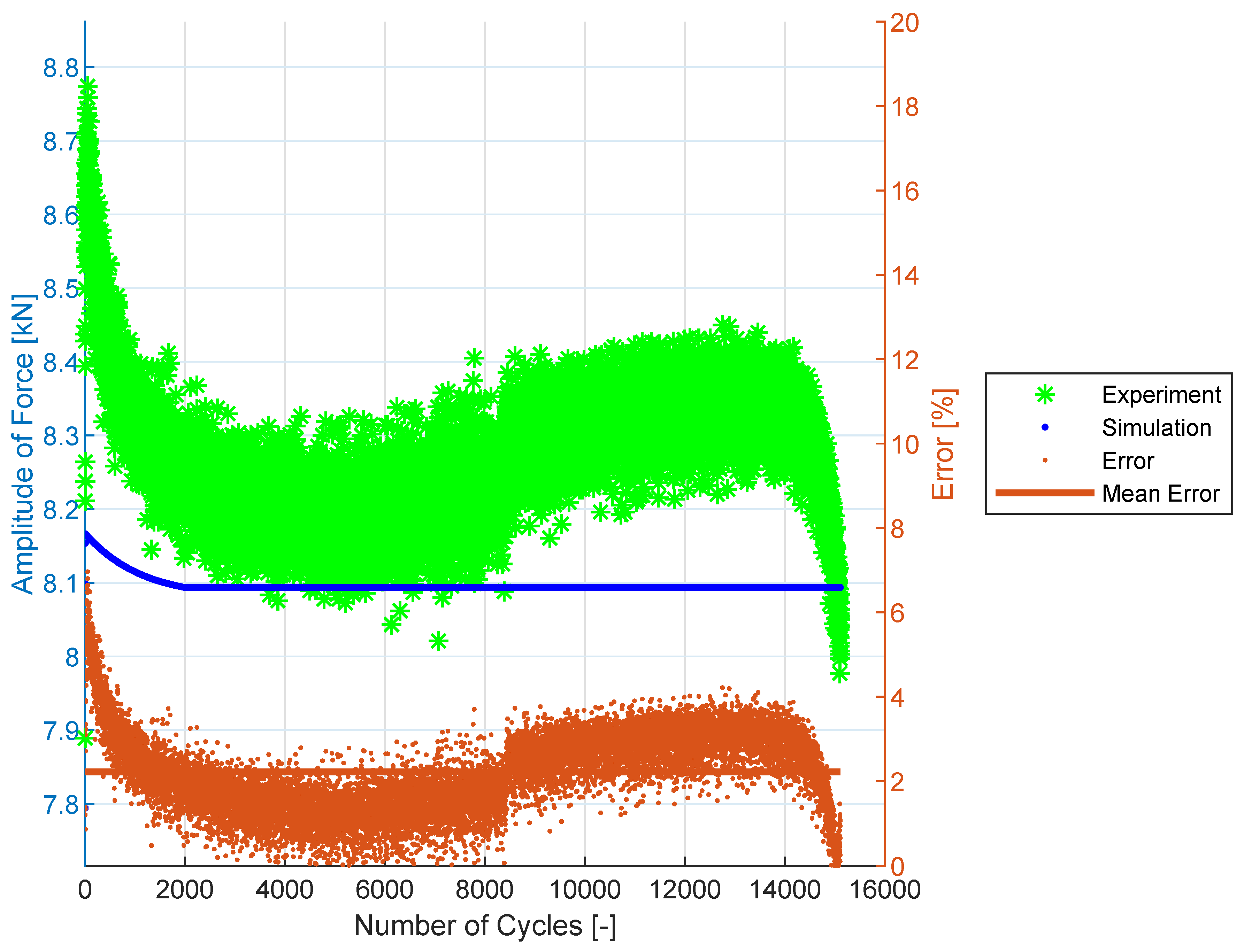
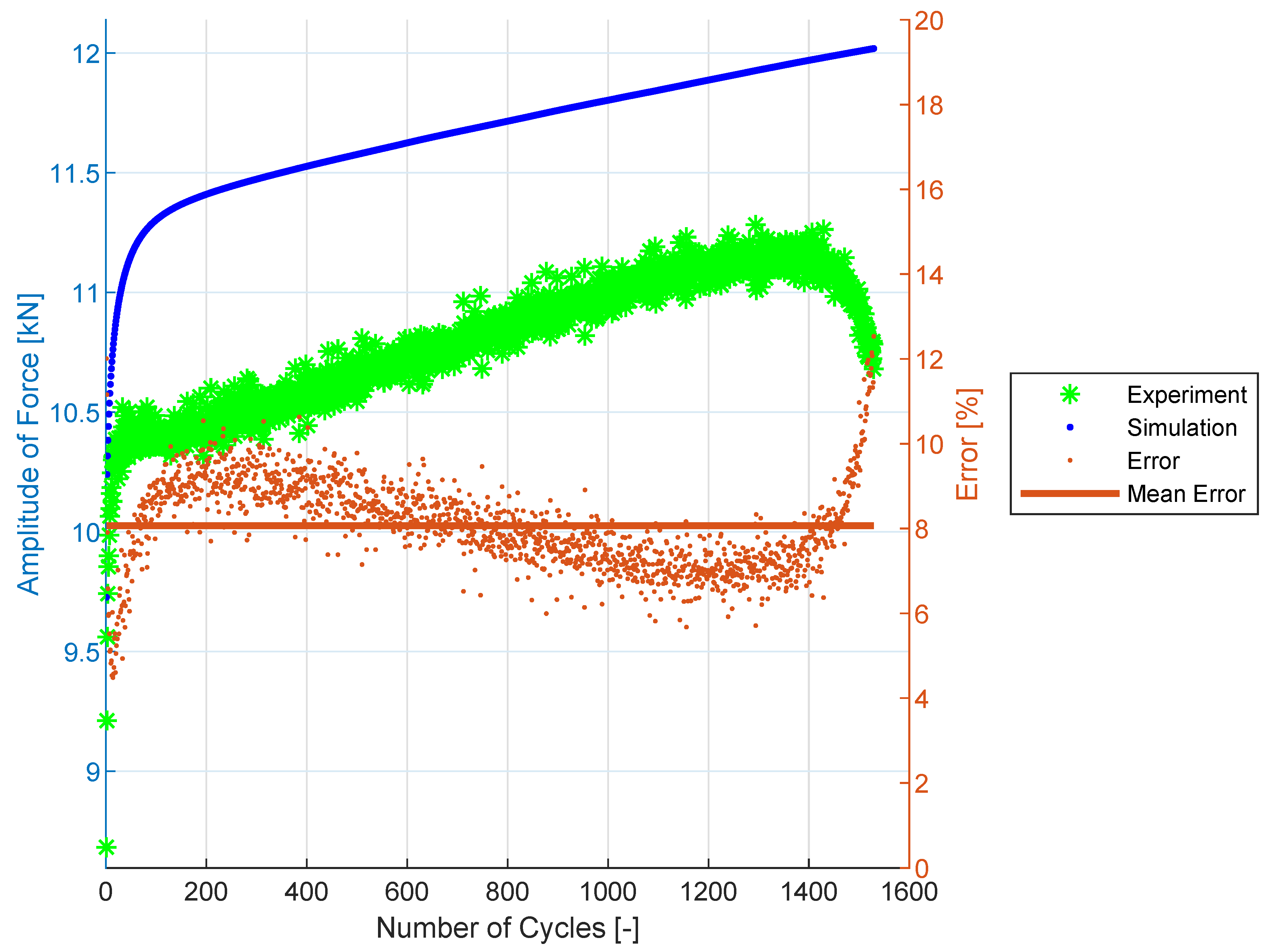
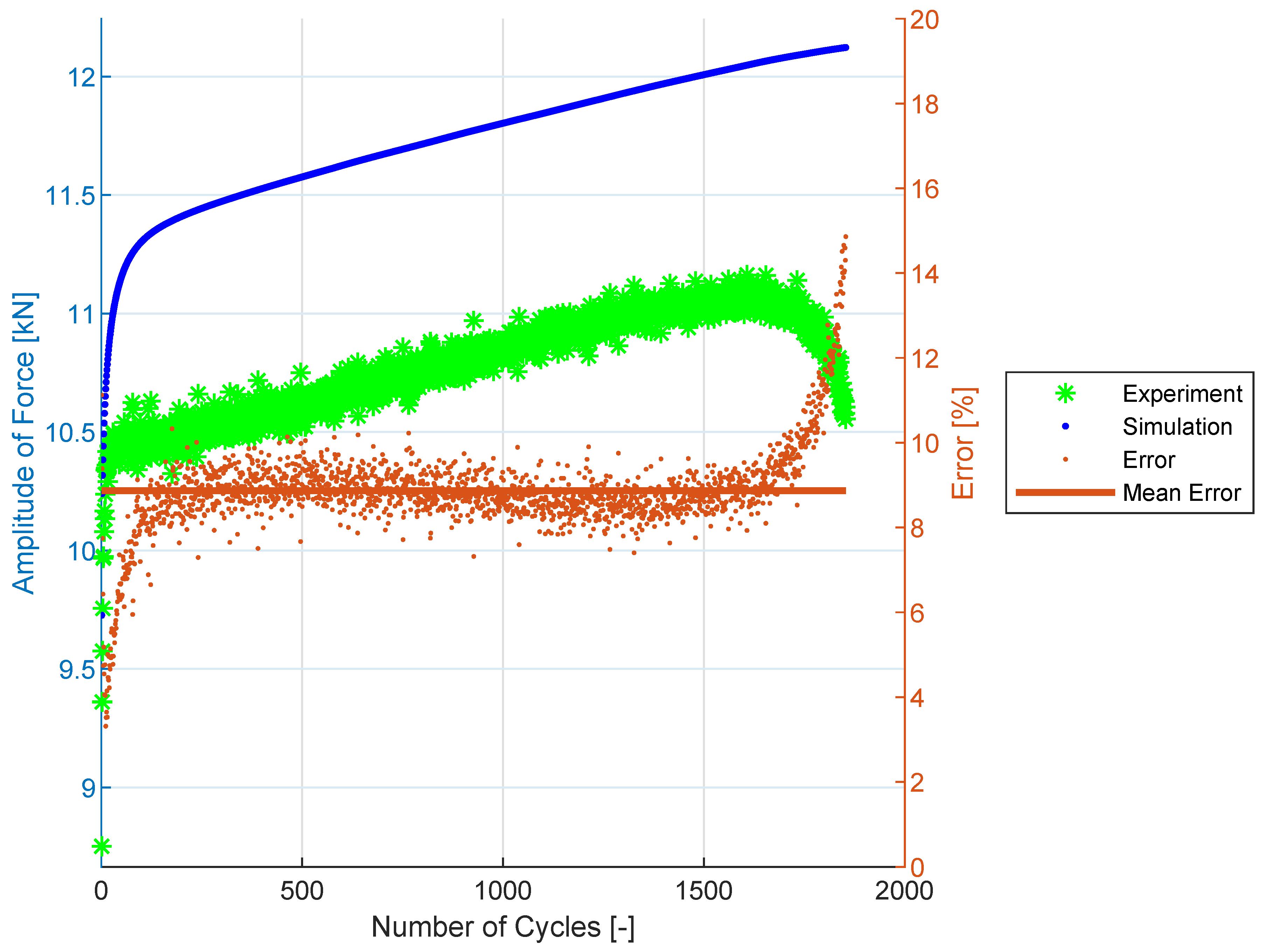
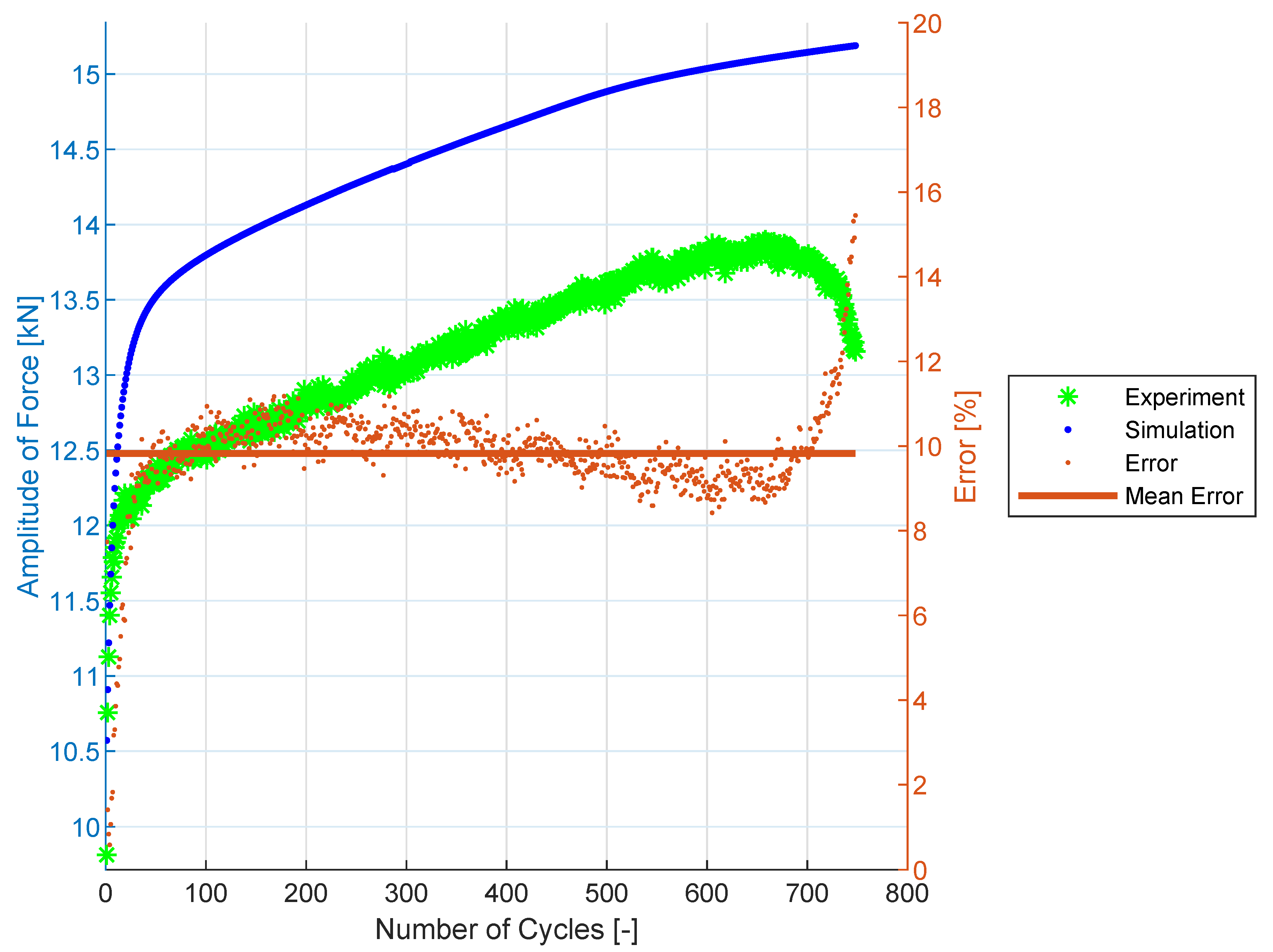
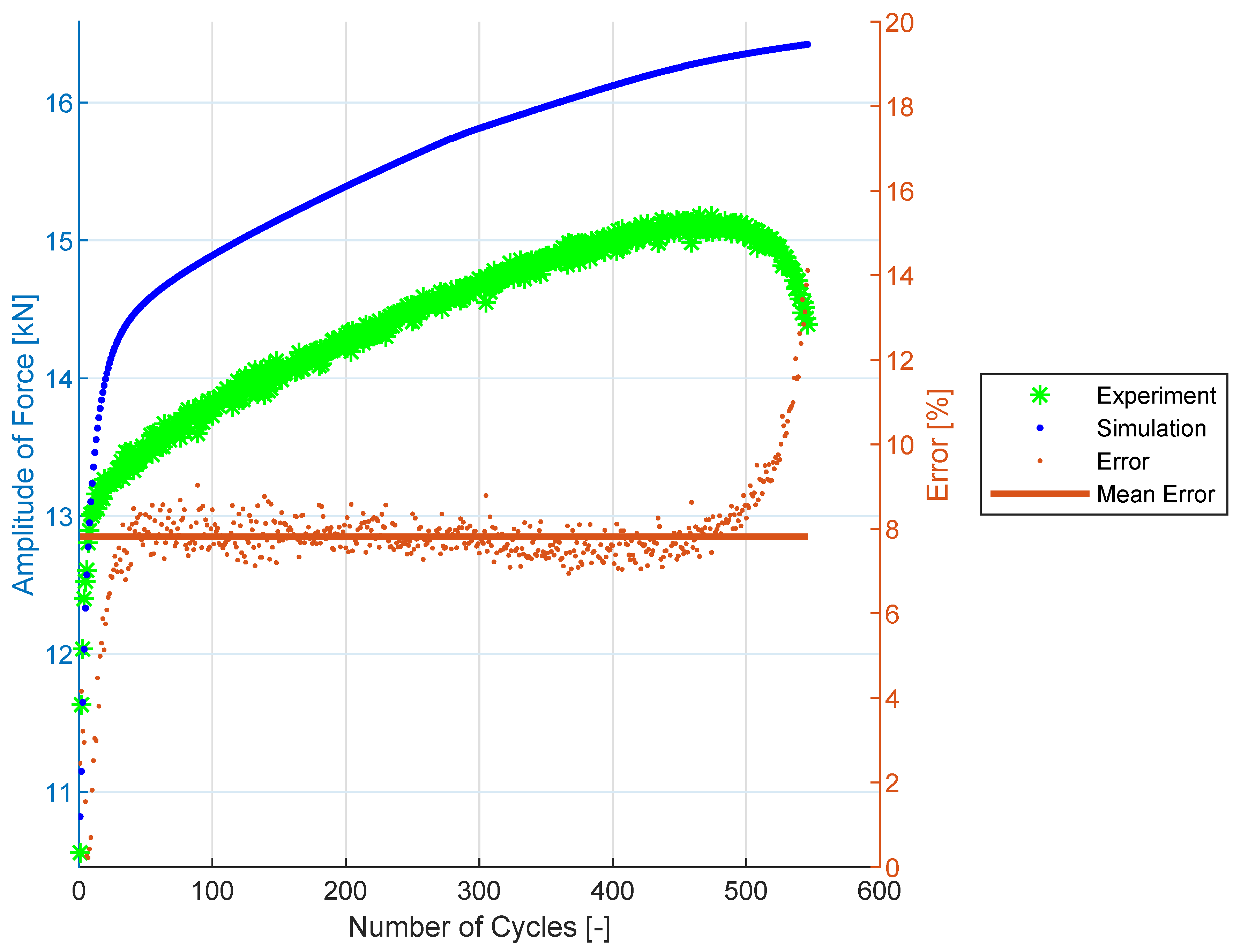
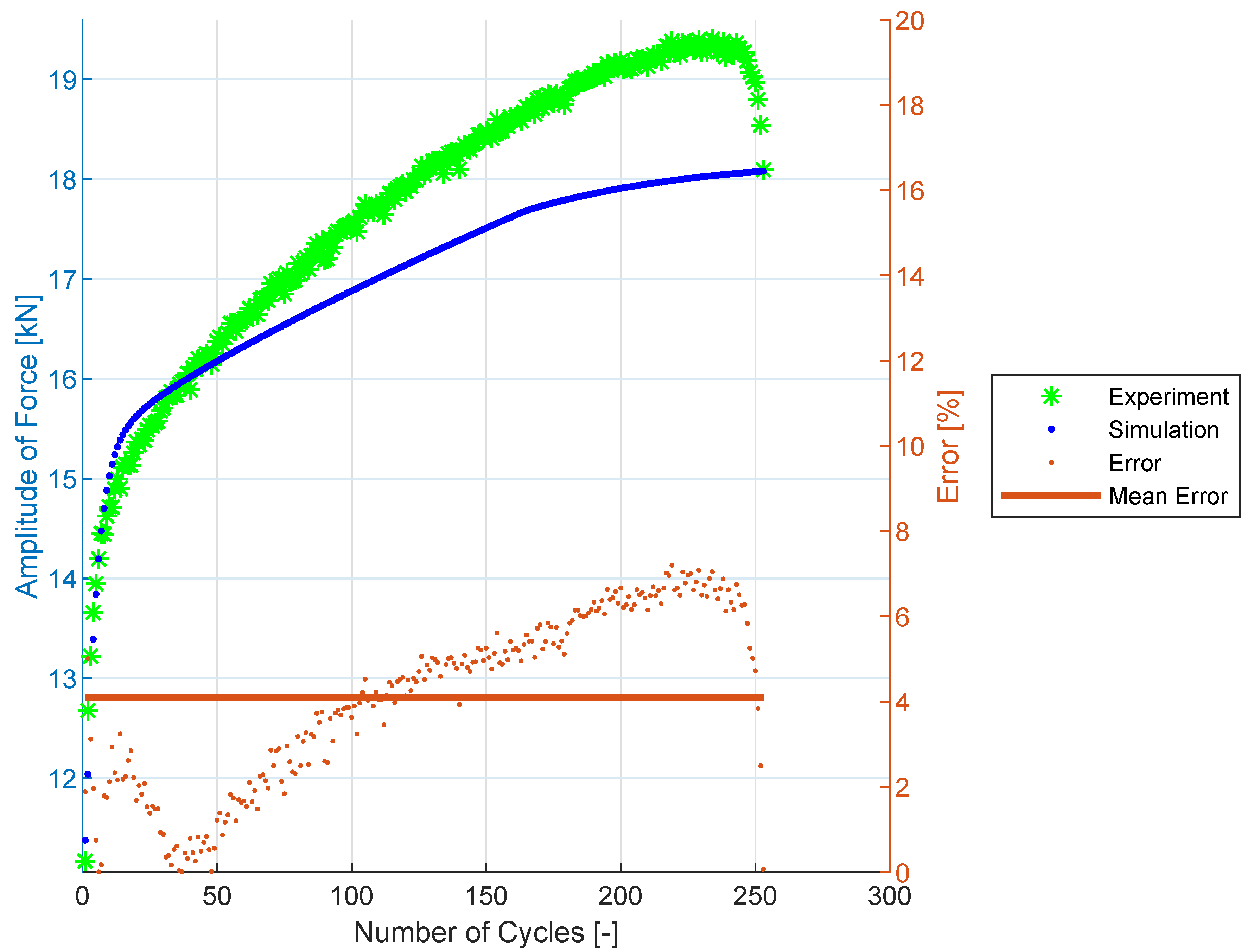
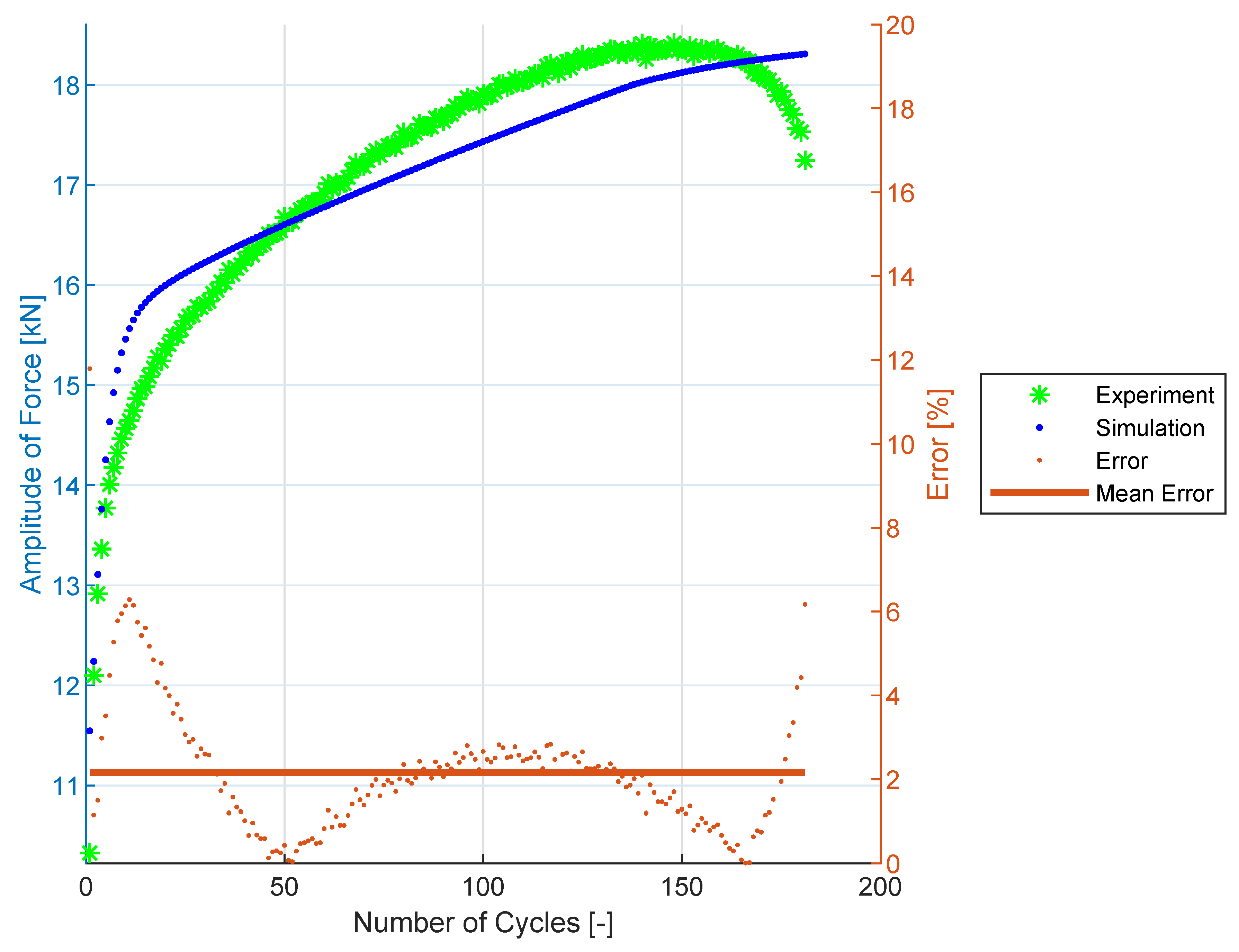
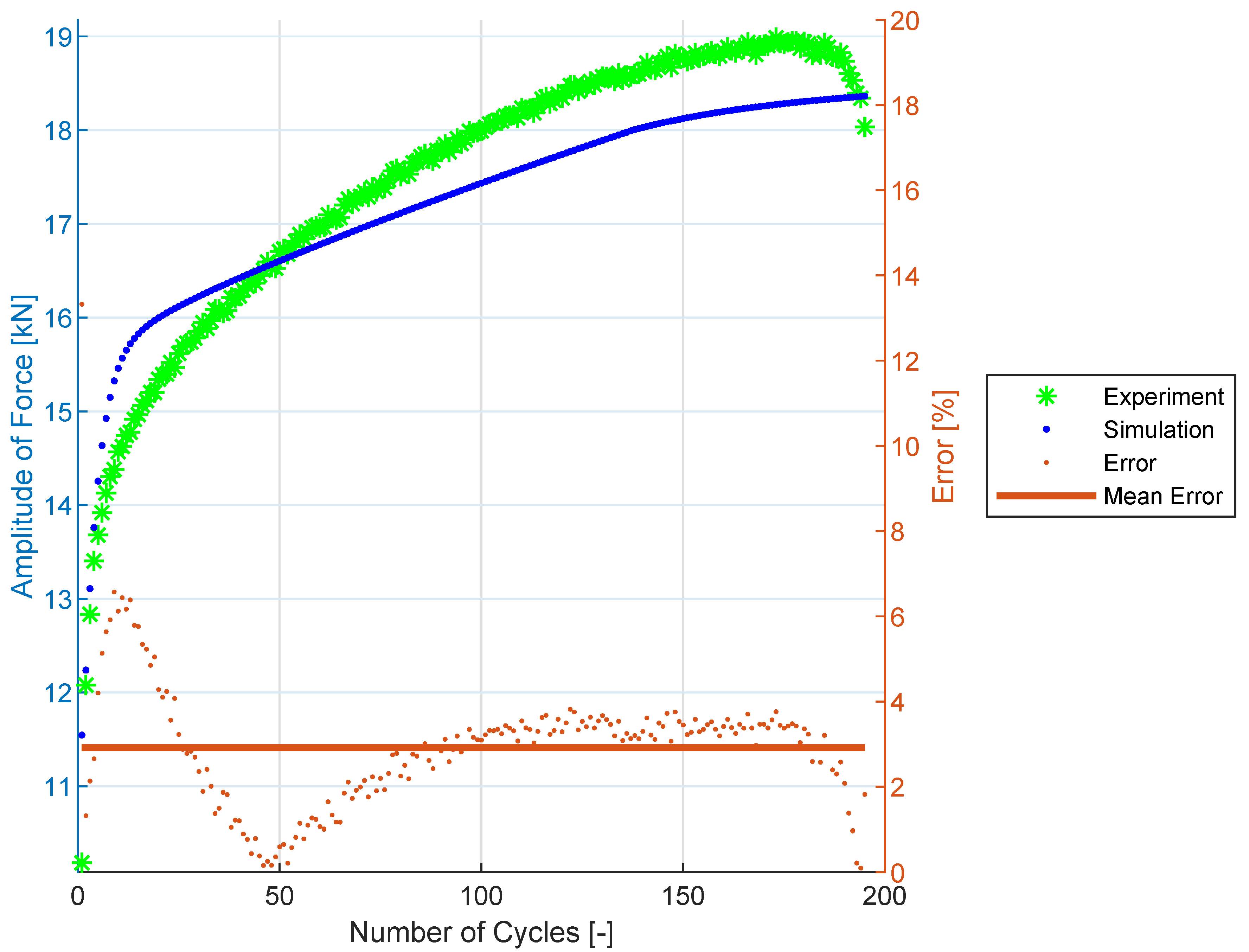
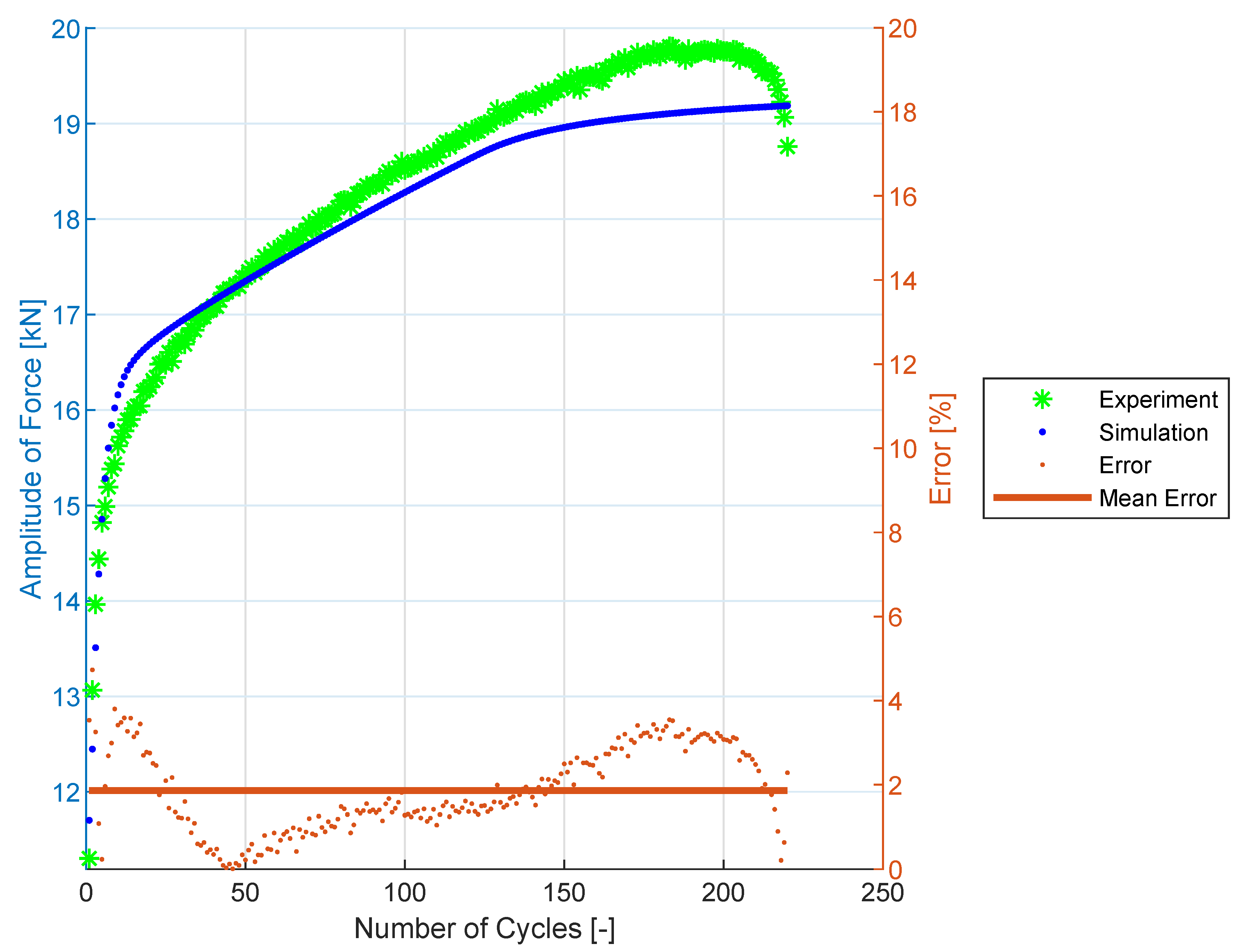
3.4. Cyclic Hardening Curves
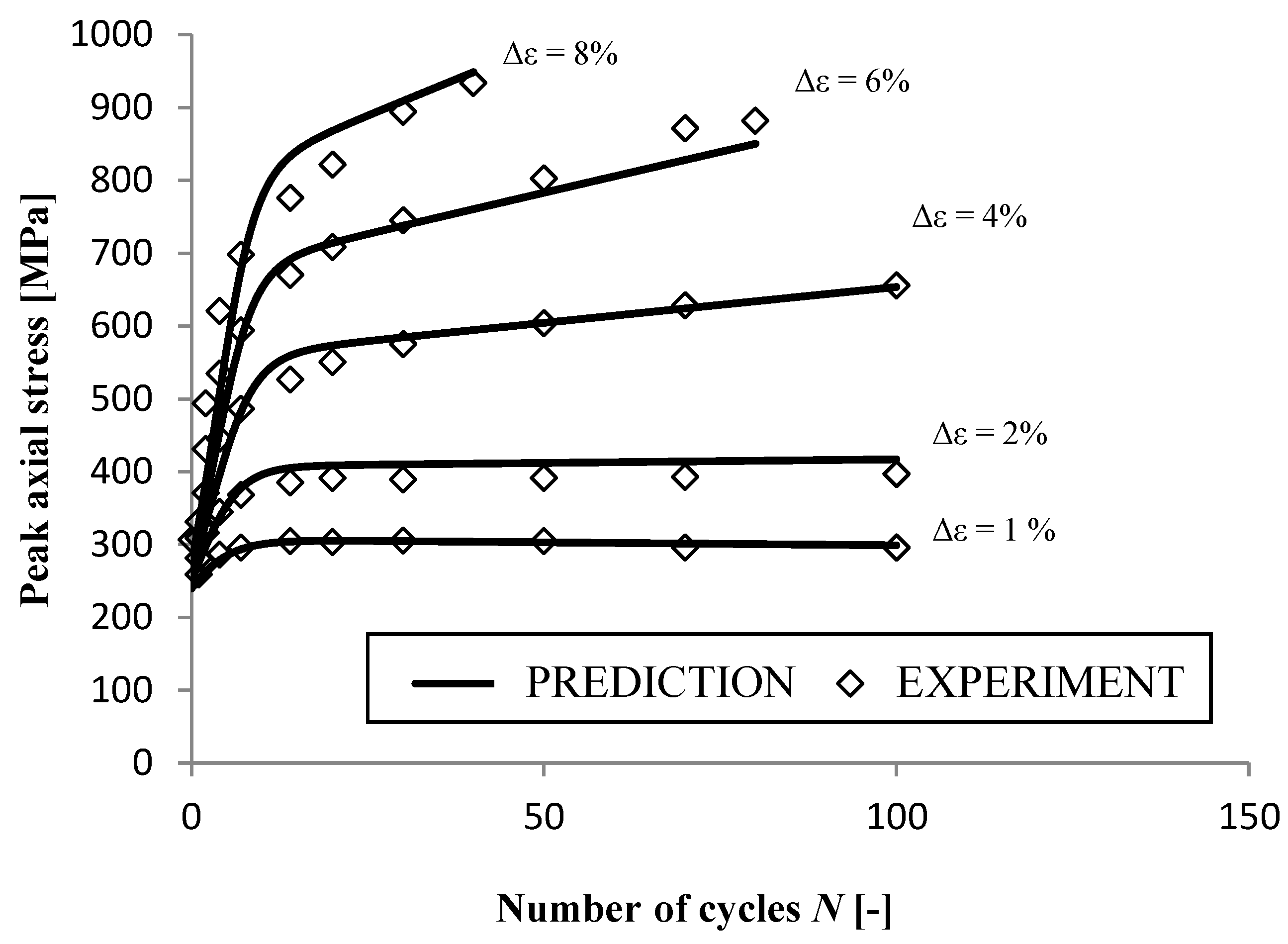
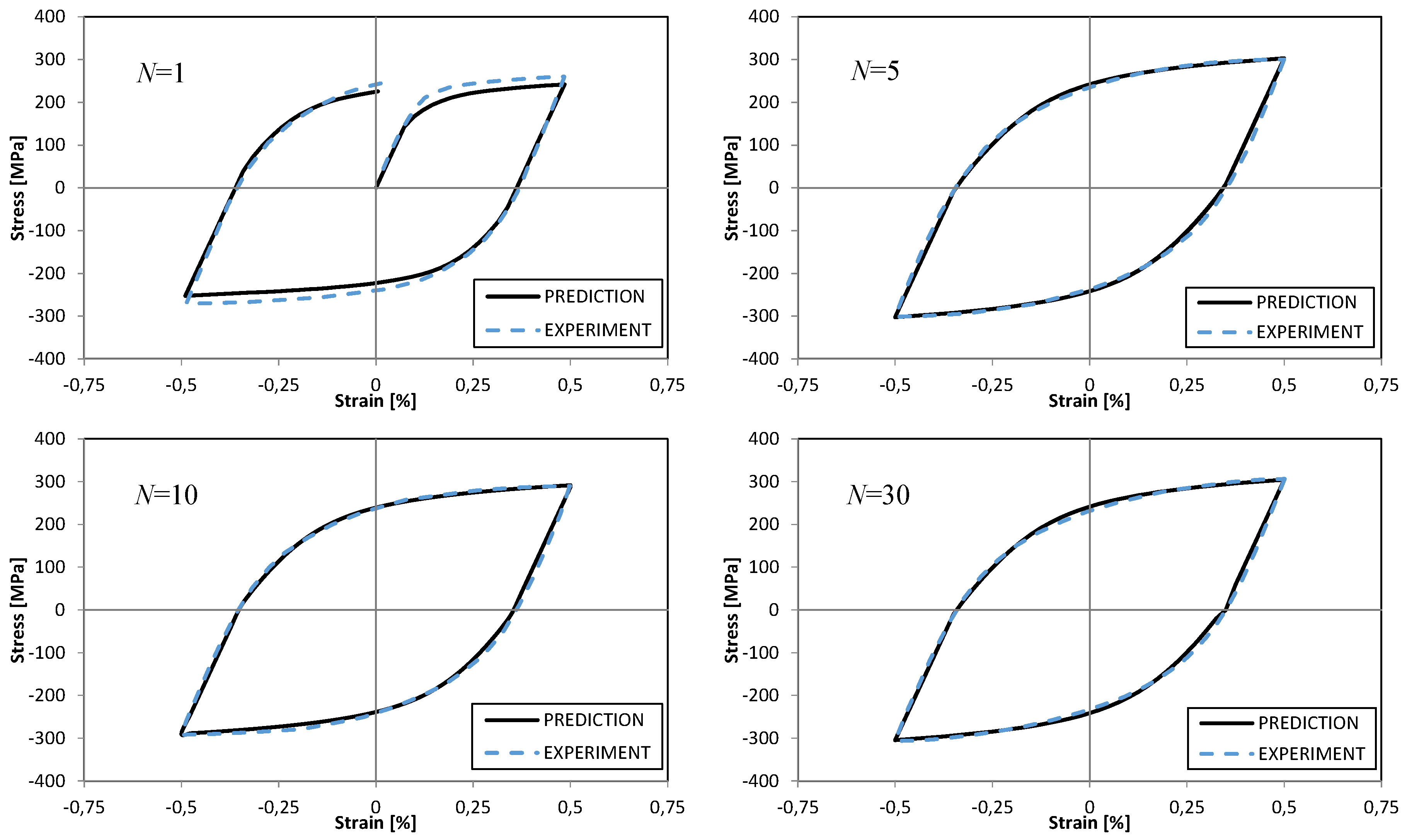
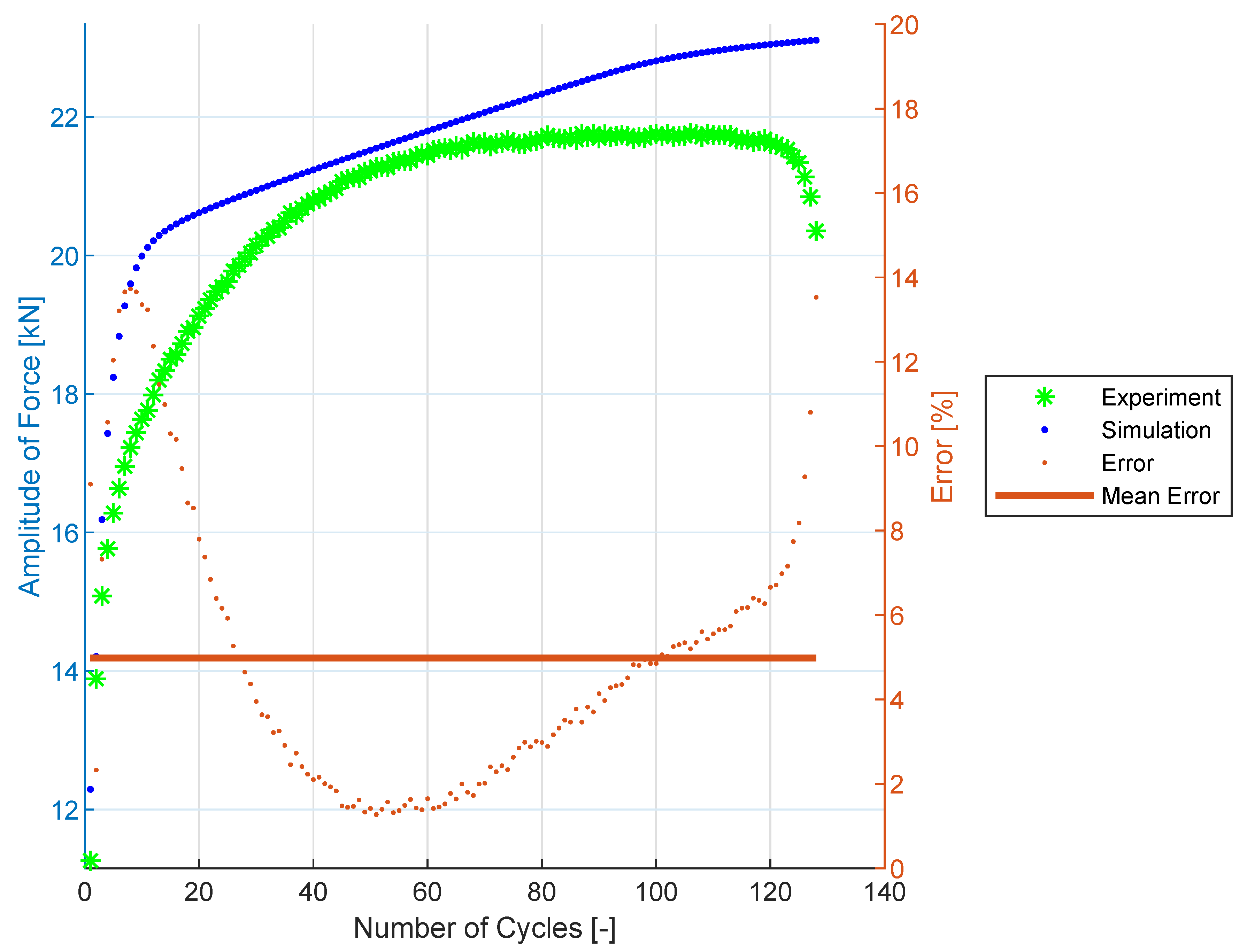
3.5. Prediction Results for SS304
4. Application to Uniaxial Cyclic Tests of 08Ch18N10T Stainless Steel
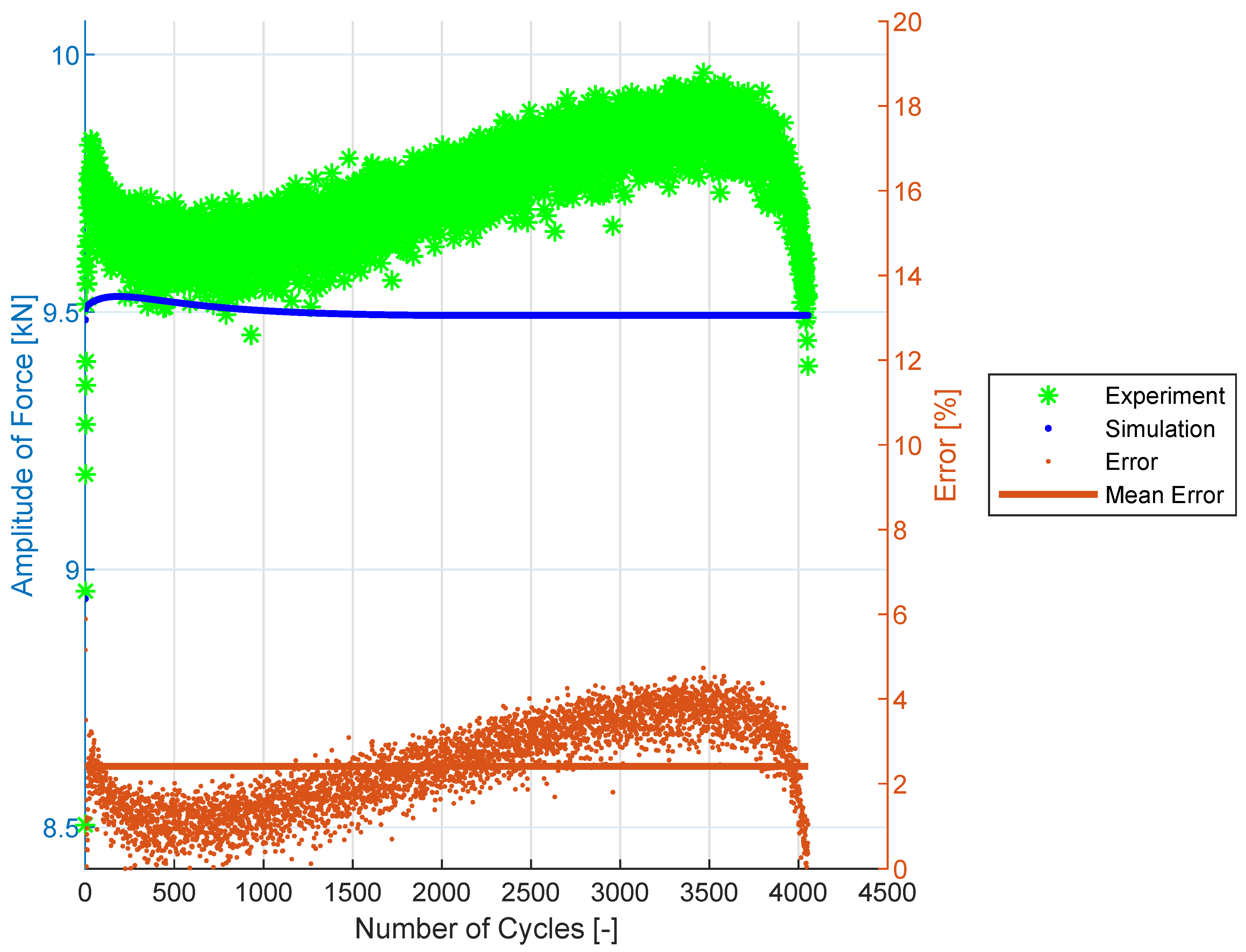
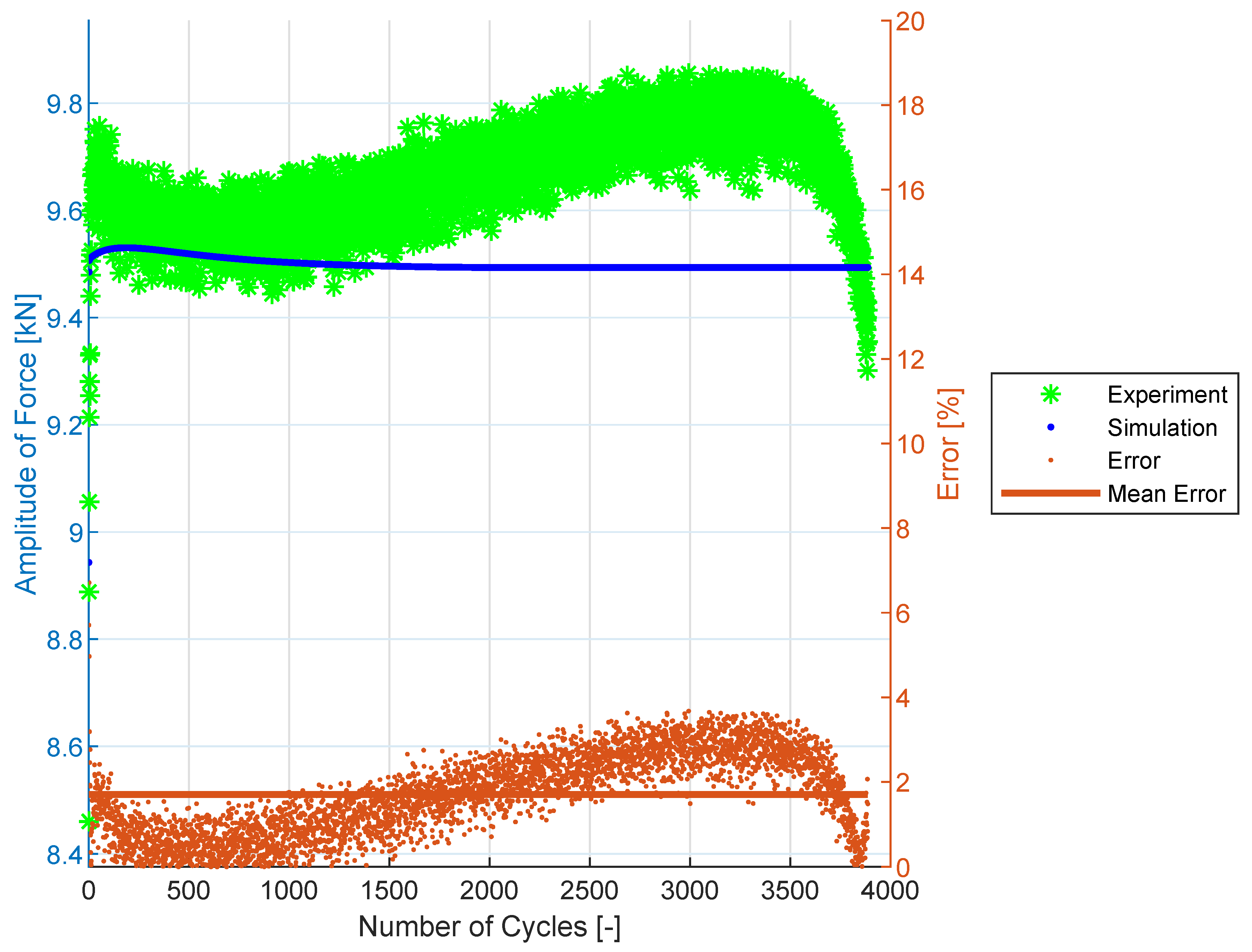
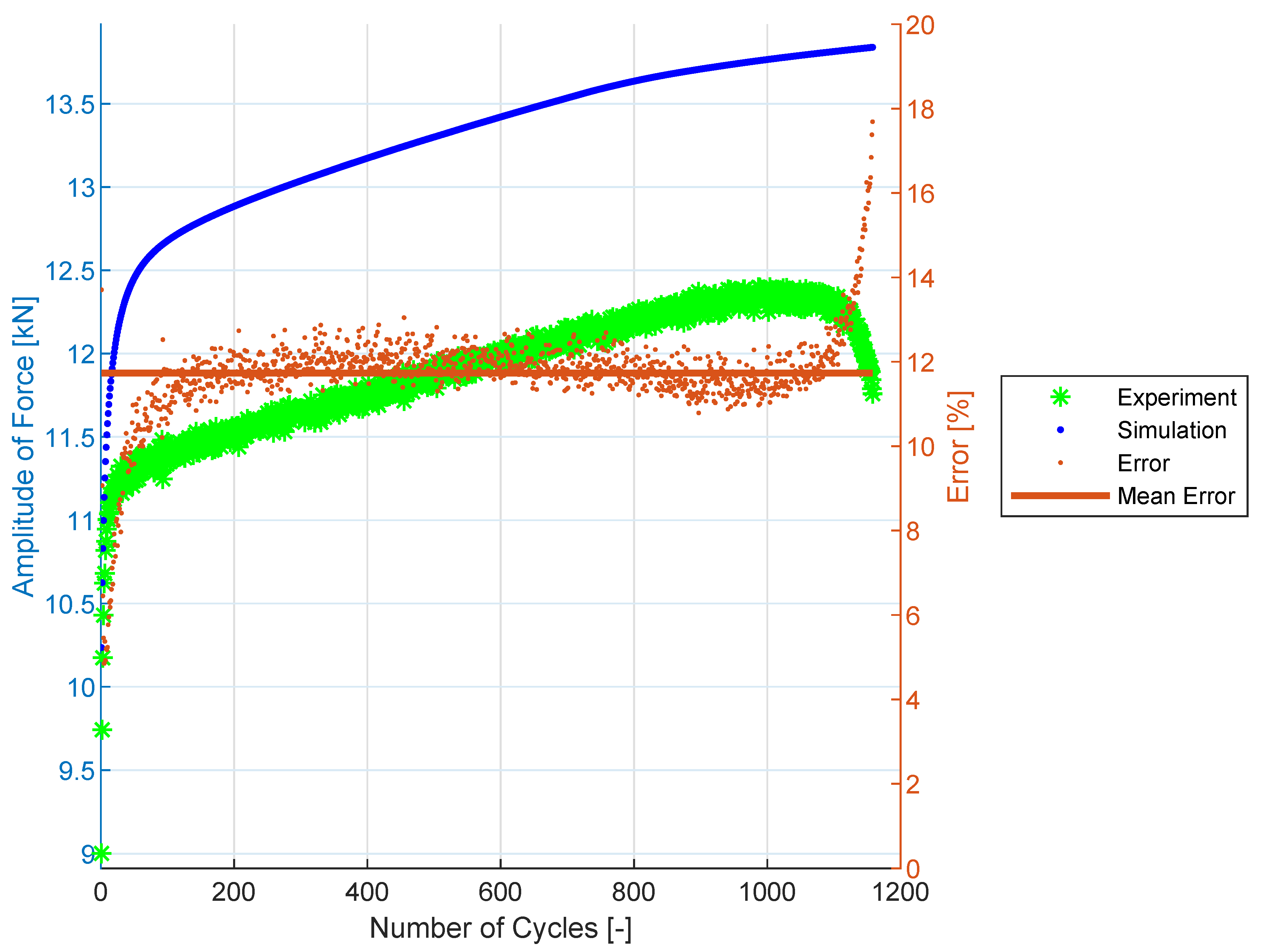
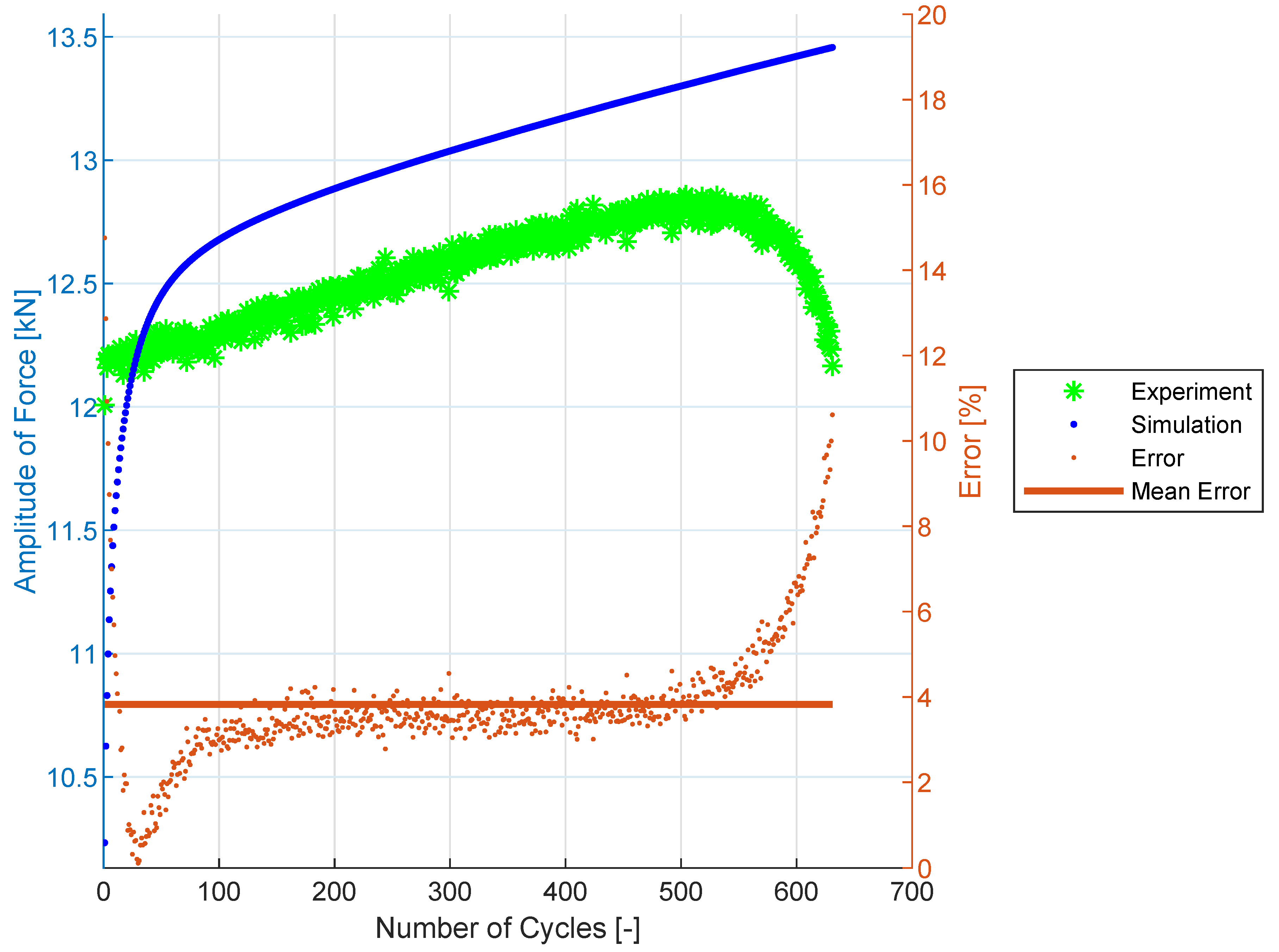
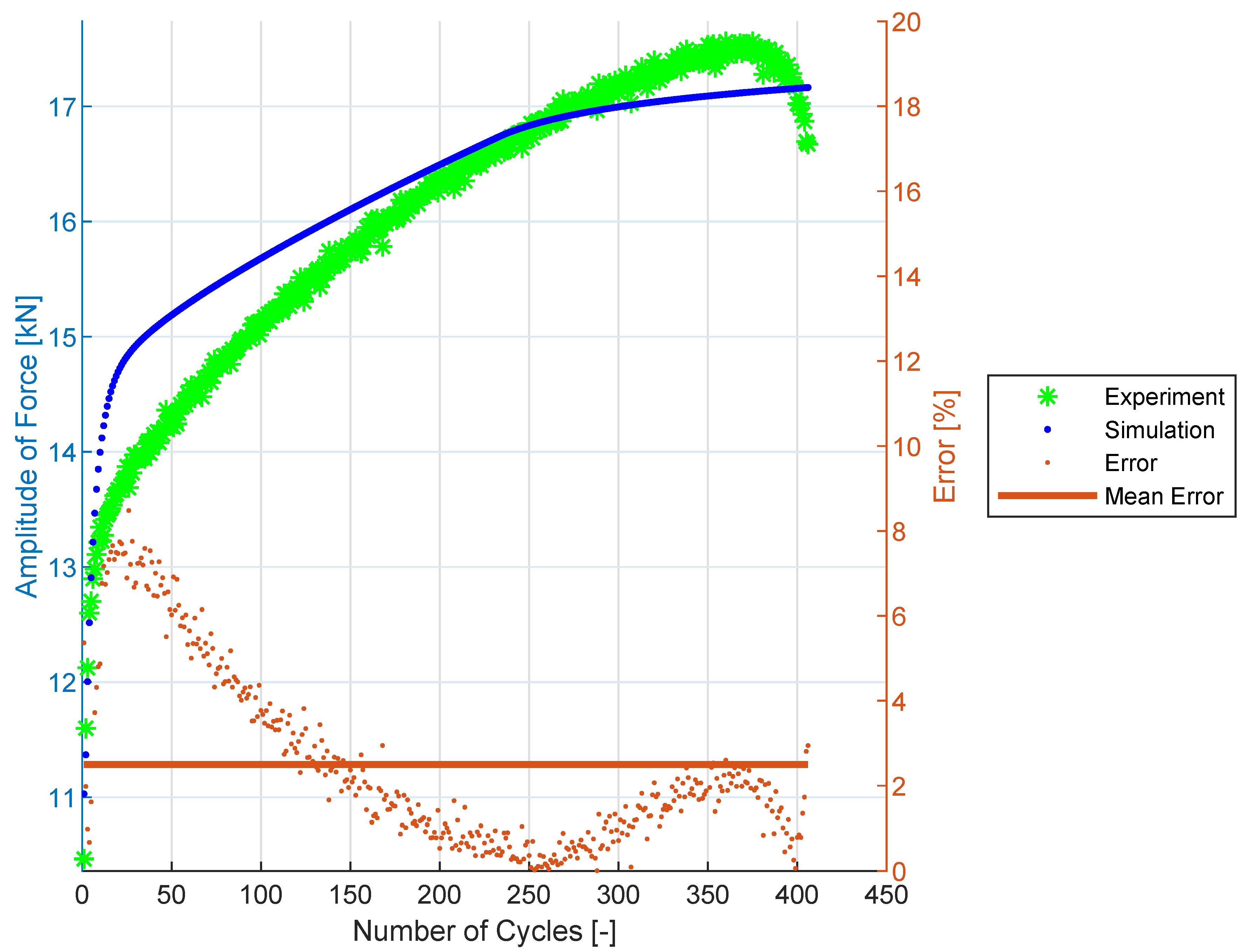
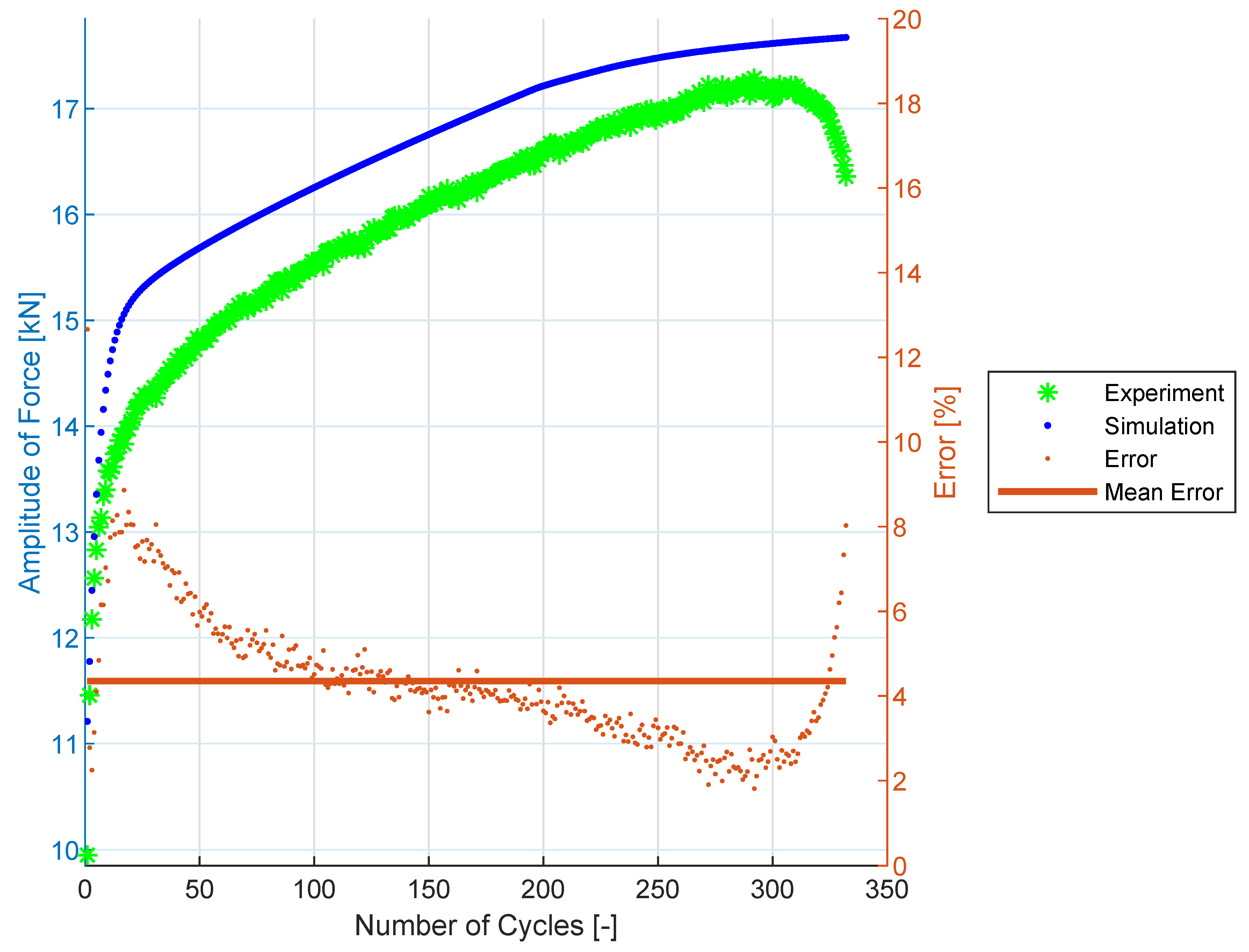
4.1. Identification of the Material Parameters for 08Ch18N10T Stainless Steel
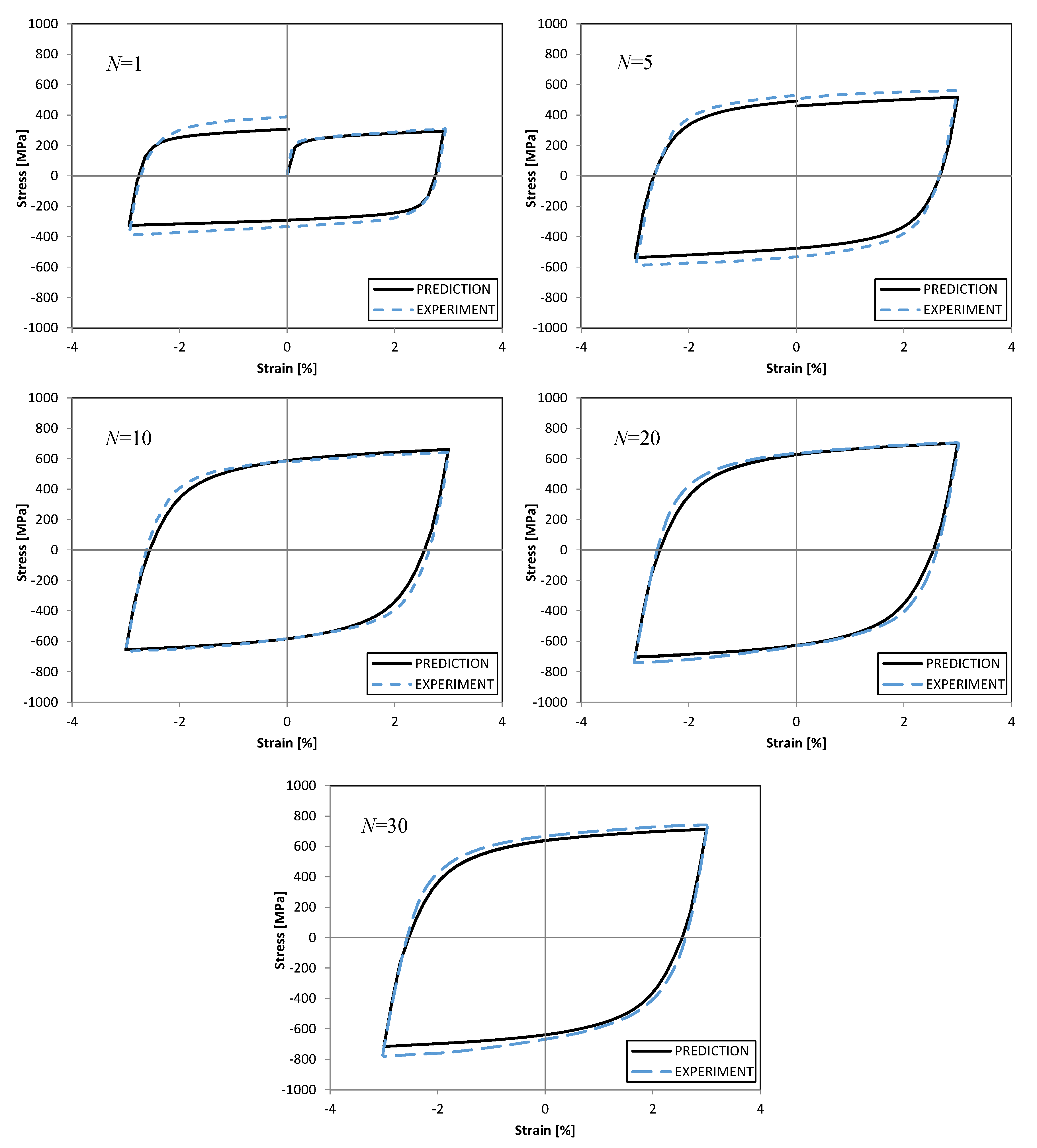
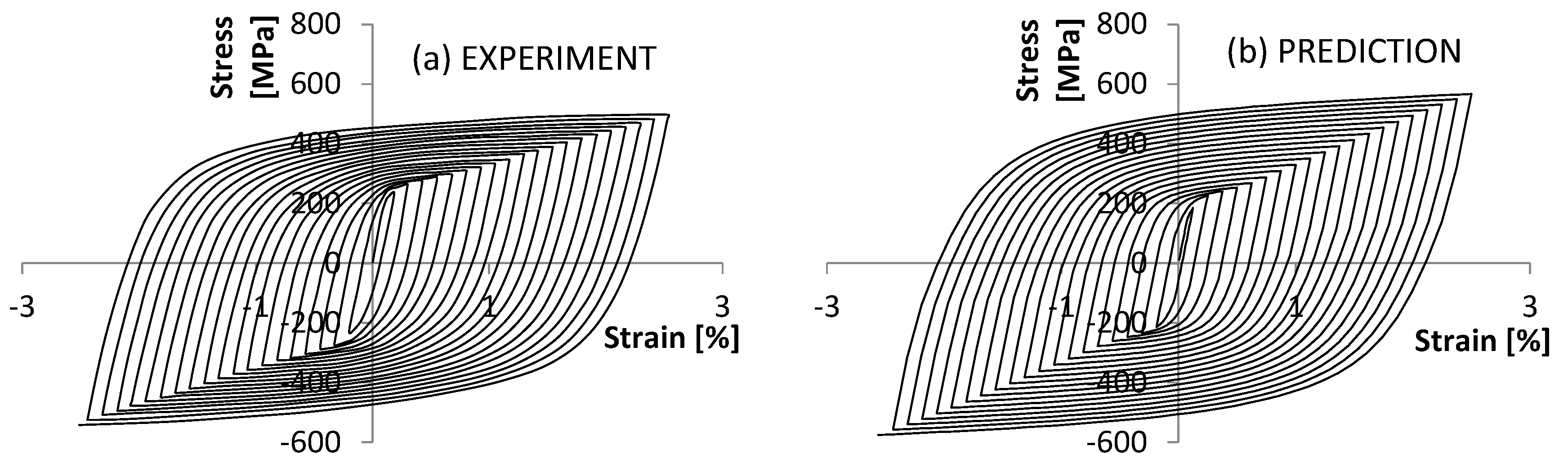
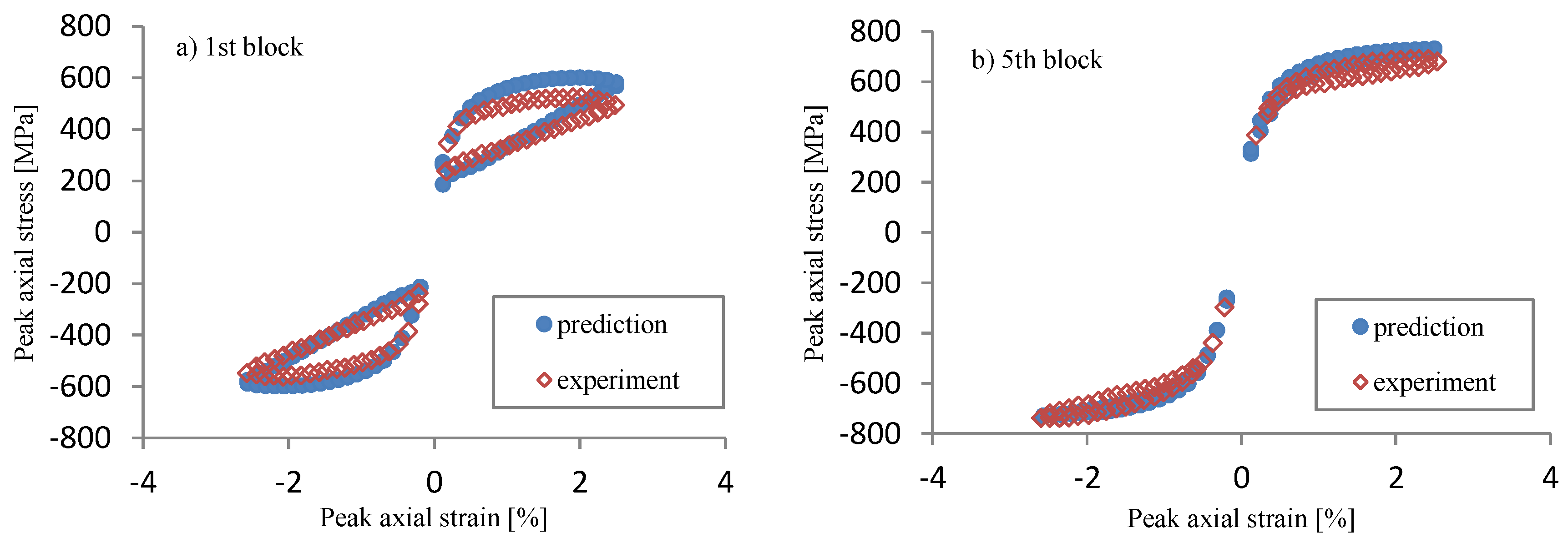
4.2. Uniaxial Prediction for 08Ch18N10T Stainless Steel
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| IDF | identification specimen series |
| NPP | nuclear power plant |
| SHL | selected hysteresis loop |
| SHLs | selected hysteresis loops |
References
- Halama, R.; Sedlák, J.; Šofer, M. Phenomenological Modelling of Cyclic Plasticity. In Numerical Modelling; Miidla, P., Ed.; IntechOpen: London, UK, 2012; pp. 329–354. Available online: http://www.intechopen.com/books/numerical-modelling/phenomenological-modelling-of-cyclic-plasticity (accessed on 23 March 2012).
- Kopas, P.; Saga, M.; Baniari, V.; Vasko, M.; Handrik, M. A plastic strain and stress analysis of bending and torsion fatigue specimens in the low-cycle fatigue region using the finite element methods. Procedia Eng. 2017, 177, 526–531. [Google Scholar] [CrossRef]
- Chen, X.; Chen, X.; Yu, D.; Gao, B. Recent progresses in experimental investigation and finite element analysis of ratcheting in pressurized piping. Int. J. Press. Vessel. Pip. 2013, 101, 113–142. [Google Scholar] [CrossRef]
- Armstrong, P.J.; Frederick, C.O. A Mathematical Representation of the Multiaxial Bauschinger Effect. Mater. High Temp. 2007, 24, 1–26. [Google Scholar]
- Chaboche, J.L.; Van Dang, K.; Cordier, G. Modelization of the Strain Memory Effect on the Cyclic Hardening of 316 Stainless Steel. In Proceedings of the 5th International Conference on Structural Mechanics in Reactor Technology, Berlin, Germany, 13–17 August 1979; pp. 1–10. [Google Scholar]
- Ohno, N.; Wang, J.D. Kinematic Hardening Rules with Critical State of Dynamic Recovery. Part I: Formulation and Basic Features for Ratchetting Behavior. Int. J. Plast. 1993, 9, 375–390. [Google Scholar] [CrossRef]
- Abdel-Karim, M.; Ohno, N. Kinematic hardening model suitable for ratchetting with steady-state. Int. J. Plast. 2000, 16, 225–240. [Google Scholar] [CrossRef]
- Halama, R.; Fusek, M.; Šofer, M.; Poruba, Z.; Matušek, P.; Fajkoš, R. Ratcheting Behavior of Class C Wheel Steel and Its Prediction by Modified AbdelKarim-Ohno Model. In Proceedings of the 10th International Conference on Contact Mechanics CM2015, Colorado Springs, CO, USA, 30 August–3 September 2015. [Google Scholar]
- Feigenbaum, H.P.; Dafalias, Y.F. Directional distortional hardening in metal plasticity within thermodynamics. Int. J. Solids Struct. 2007, 44, 7526–7542. [Google Scholar] [CrossRef]
- Parma, S.; Plešek, J.; Marek, R.; Hrubý, Z.; Feigenbaum, H.P.; Dafalias, Y.F. Calibration of a simple directional distortional hardening model for metal plasticity. Int. J. Solids Struct. 2018, 143, 113–124. [Google Scholar] [CrossRef]
- Sung, S.J.; Liu, L.W.; Hong, H.K.; Wu, H.C. Evolution of yield surface in the 2D and 3D stress spaces. Int. J. Solids Struct. 2011, 48, 1054–1069. [Google Scholar] [CrossRef]
- Ohno, N. A constitutive model of cyclic plasticity with a nonhardening strain region. J. Appl. Mech. 1982, 49, 721–727. [Google Scholar] [CrossRef]
- Jiang, Y.; Sehitoglu, H. Modeling of cyclic ratchetting plasticity, part I: Development of constitutive relations. J. Appl. Mech. 1996, 63, 720–725. [Google Scholar] [CrossRef]
- Halama, R.; Fojtík, F.; Markopoulos, A. Memorization and Other Transient Effects of ST52 Steel and Its FE Description. Appl. Mech. Mater. 2013, 486, 48–53. [Google Scholar] [CrossRef]
- Kang, G.Z.; Ohno, N.; Nebu, A. Constitutive modeling of strain-range dependent cyclic hardening. Int. J. Plast. 2003, 19, 1801–1819. [Google Scholar] [CrossRef]
- Schäfer, B.J.; Song, X.; Sonnweber-Ribic, P.; Hassan, H.; Hartmaier, A. Micromechanical Modelling of the Cyclic Deformation Behavior of Martensitic SAE 4150—A Comparison of Different Kinematic Hardening Models. Metals 2019, 9, 368. [Google Scholar] [CrossRef]
- Moeini, G.; Ramazani, A.; Myslicki, S.; Sundararaghavan, V.; Könke, C. Low Cycle Fatigue Behaviour of DP Steels: Micromechanical Modelling vs. Validation. Metals 2017, 7, 265. [Google Scholar] [CrossRef]
- Msolli, S. Thermoelastoviscoplastic modeling of RAFM steel JLF-1 using tensile and low cycle fatigue experiments. J. Nucl. Mater. 2014, 451, 336–345. [Google Scholar] [CrossRef]
- Ji, S.; Liu, C.; Li, Y.; Shi, S.; Chen, X. Effect of torsional pre-strain on low cycle fatigue performance of 304 stainless steel. Mater. Sci. Eng. 2019, 746, 50–57. [Google Scholar] [CrossRef]
- Kang, G.; Li, Y.; Gao, Q. Non-proportionally multiaxial ratcheting of cyclic hardening materials at elevated temperatures: Experiments and simulations. Mech. Mater. 2005, 37, 1101–1118. [Google Scholar] [CrossRef]
- Kang, G.; Gao, Q.; Yang, X. A visco–plastic constitutive model incorporated with cyclic hardening for uniaxial/multiaxial ratcheting of SS304 stainless steel at room temperature. Mech. Mater. 2002, 34, 521–531. [Google Scholar] [CrossRef]
- Halama, R.; Markopoulos, A.; Jančo, R.; Bartecký, M. Implementation of MAKOC Cyclic Plasticity Model with Memory. Adv. Eng. Softw. 2018, 113, 34–46. [Google Scholar] [CrossRef]
- Chaboche, J.L.; Lemaitre, J. Mechanics of Solid Materials; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Bari, S.; Hassan, T. Anatomy of Coupled Constitutive Models for Ratcheting Simulations. Int. J. Plast. 2000, 16, 381–409. [Google Scholar] [CrossRef]
- Fumfera, J.; Halama, R.; Kuželka, J.; Španiel, M. Strain-Range Dependent Cyclic Plasticity Material Model Calibration for the 08Ch18N10T Steel. In Proceedings of the 33rd conference with international participation on Computational Mechanics 2017, Špičák, Czech Republic, 6–8 November 2017. [Google Scholar]
- ASTM Standard E606-92, 1998, Standard Practise for Strain-Controlled Fatigue Testing; ASTM International: West Conshohocken, PA, USA, 1998.
- Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature; ISO 6892-1:2016; International Organization for Standardization: Geneva, Switzerland, 2016.
- Halama, R.; Bartecka, J.; Gal, P. FE Prediction and Extrapolation of Multiaxial Ratcheting for R7T Steel. Key Eng. Mater. 2019, 810, 76–81. [Google Scholar] [CrossRef]
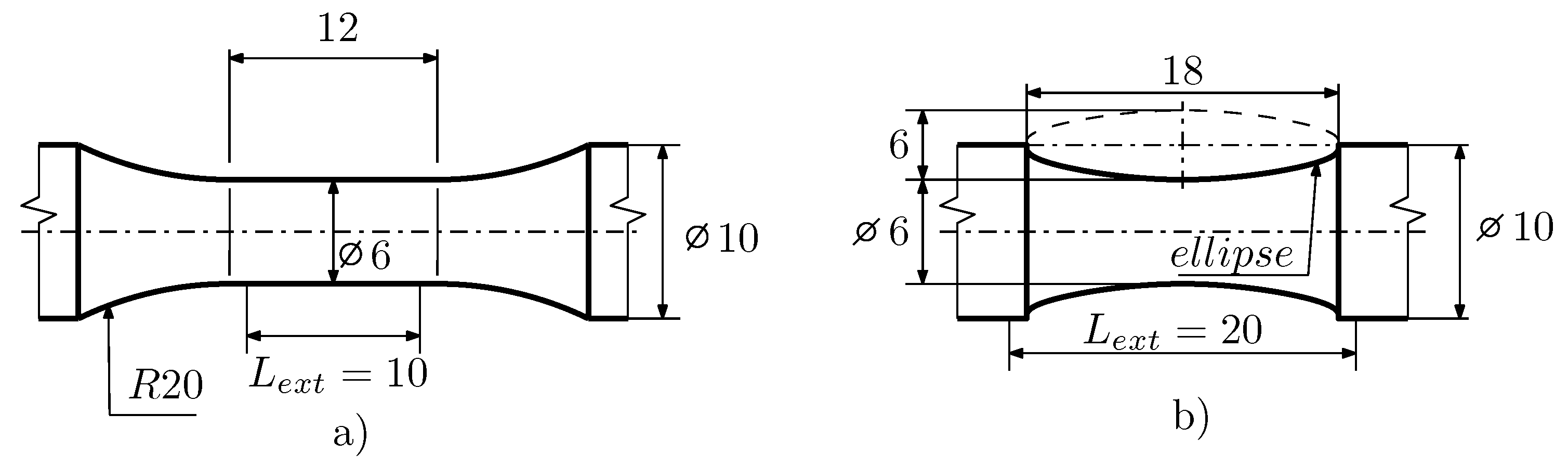
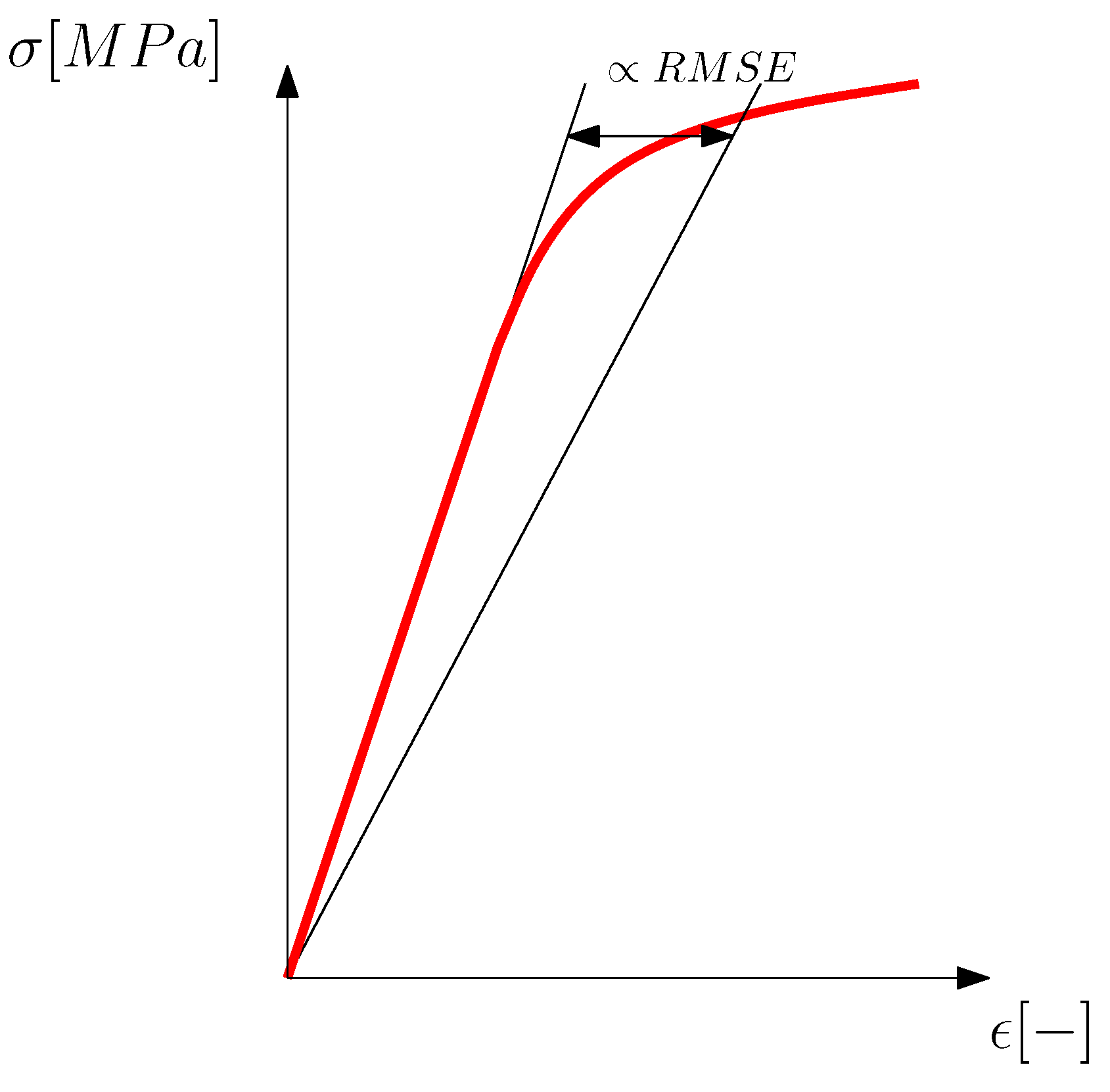
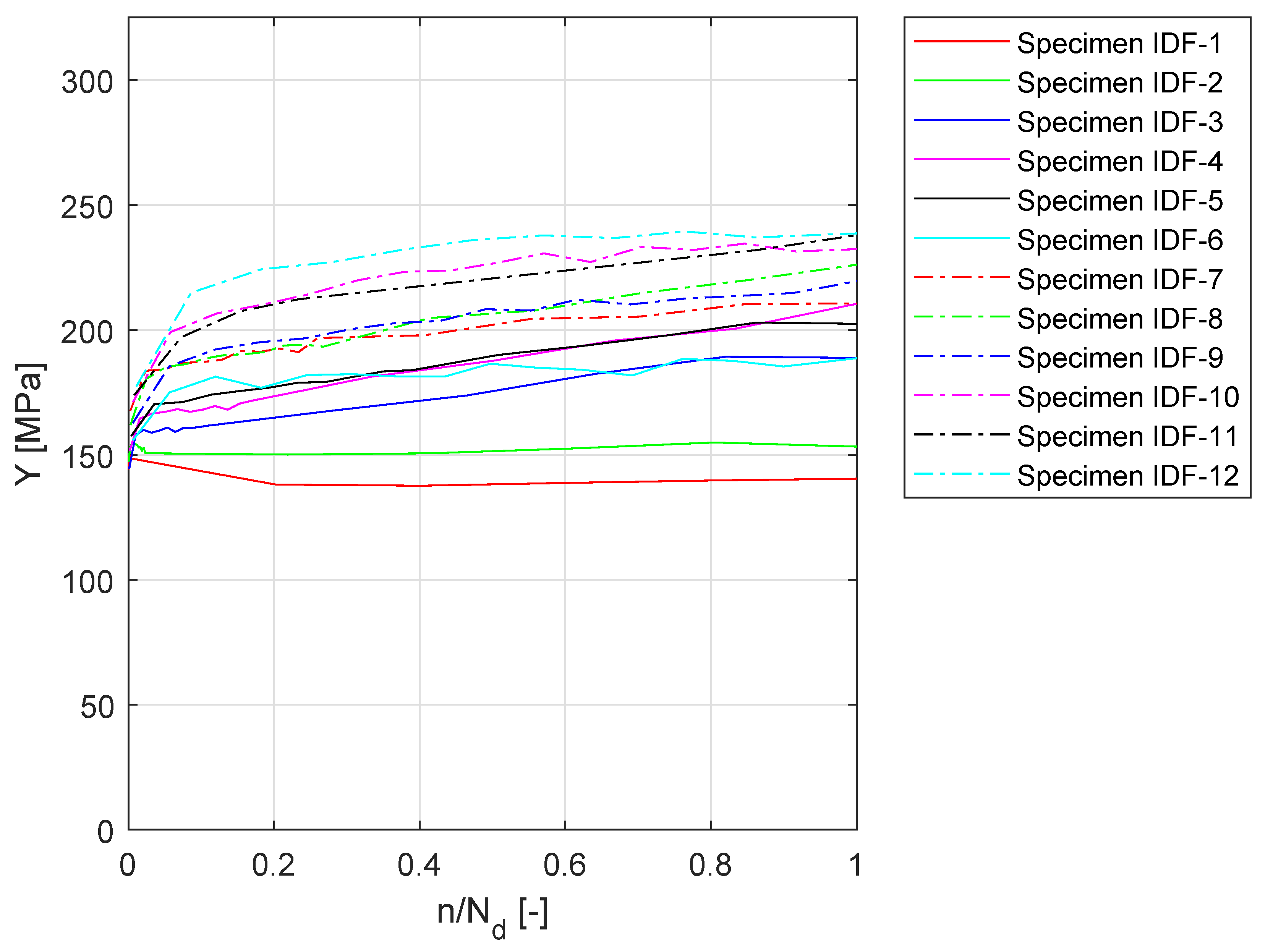
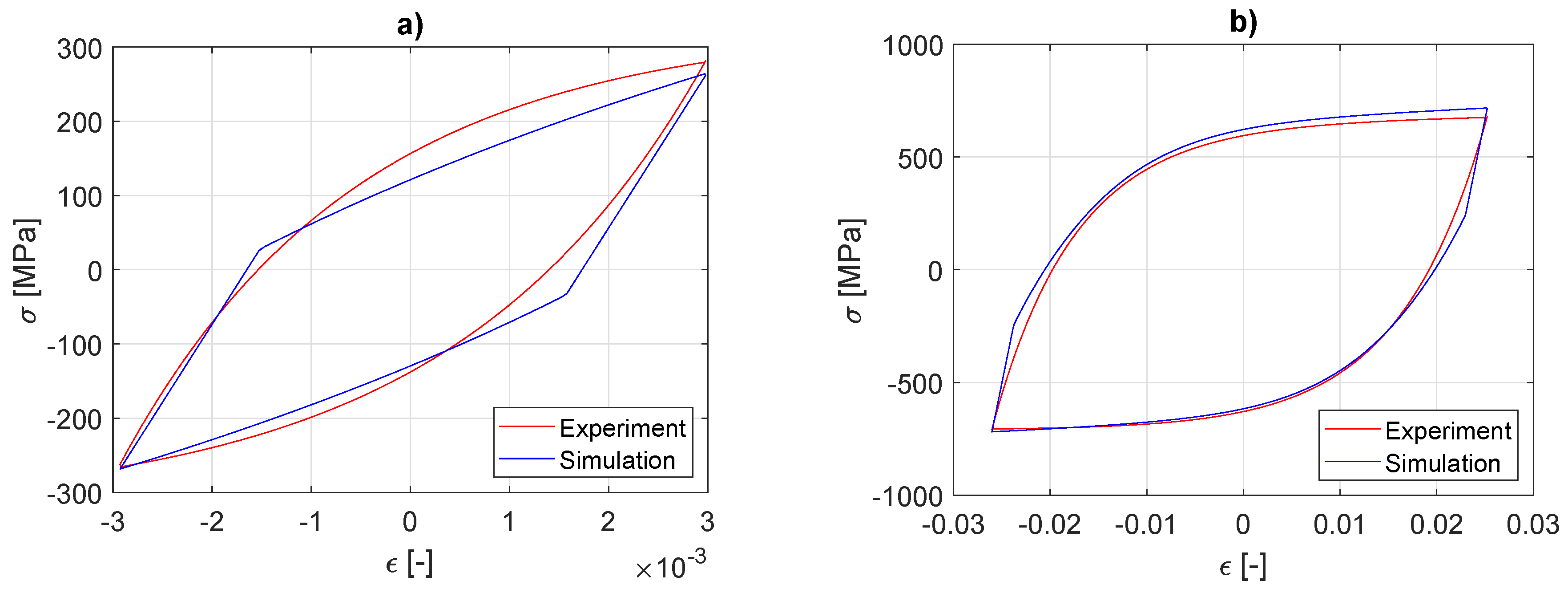
| [MPa] | |||||
| 196,000 | 0.3 | 150 | 150,000 | 622 | 19,827 |
| 128 | 2000 | 10 | 0 | ||
| 0.032 | −3.6 | 0.000915 | −0.5 | 60.7 | 305 |
| 0 | 6.424 | 344 | 4.5 |
| [MPa] | |||||
| 210,000 | 0.3 | 150 | 63,400 | 148.6 | 10,000 |
| 911.4 | 2000 | 0 | |||
| 3.801 | 225.4 | ||||
| 0 | −4.197 | 130.5 | 2.318 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Halama, R.; Fumfera, J.; Gál, P.; Kumar, T.; Markopoulos, A. Modeling the Strain-Range Dependent Cyclic Hardening of SS304 and 08Ch18N10T Stainless Steel with a Memory Surface. Metals 2019, 9, 832. https://doi.org/10.3390/met9080832
Halama R, Fumfera J, Gál P, Kumar T, Markopoulos A. Modeling the Strain-Range Dependent Cyclic Hardening of SS304 and 08Ch18N10T Stainless Steel with a Memory Surface. Metals. 2019; 9(8):832. https://doi.org/10.3390/met9080832
Chicago/Turabian StyleHalama, Radim, Jaromír Fumfera, Petr Gál, Tadbhagya Kumar, and Alexandros Markopoulos. 2019. "Modeling the Strain-Range Dependent Cyclic Hardening of SS304 and 08Ch18N10T Stainless Steel with a Memory Surface" Metals 9, no. 8: 832. https://doi.org/10.3390/met9080832
APA StyleHalama, R., Fumfera, J., Gál, P., Kumar, T., & Markopoulos, A. (2019). Modeling the Strain-Range Dependent Cyclic Hardening of SS304 and 08Ch18N10T Stainless Steel with a Memory Surface. Metals, 9(8), 832. https://doi.org/10.3390/met9080832






