Identification of Relationships between Heat Treatment and Fatigue Crack Growth of αβ Titanium Alloys
Abstract
:1. Introduction
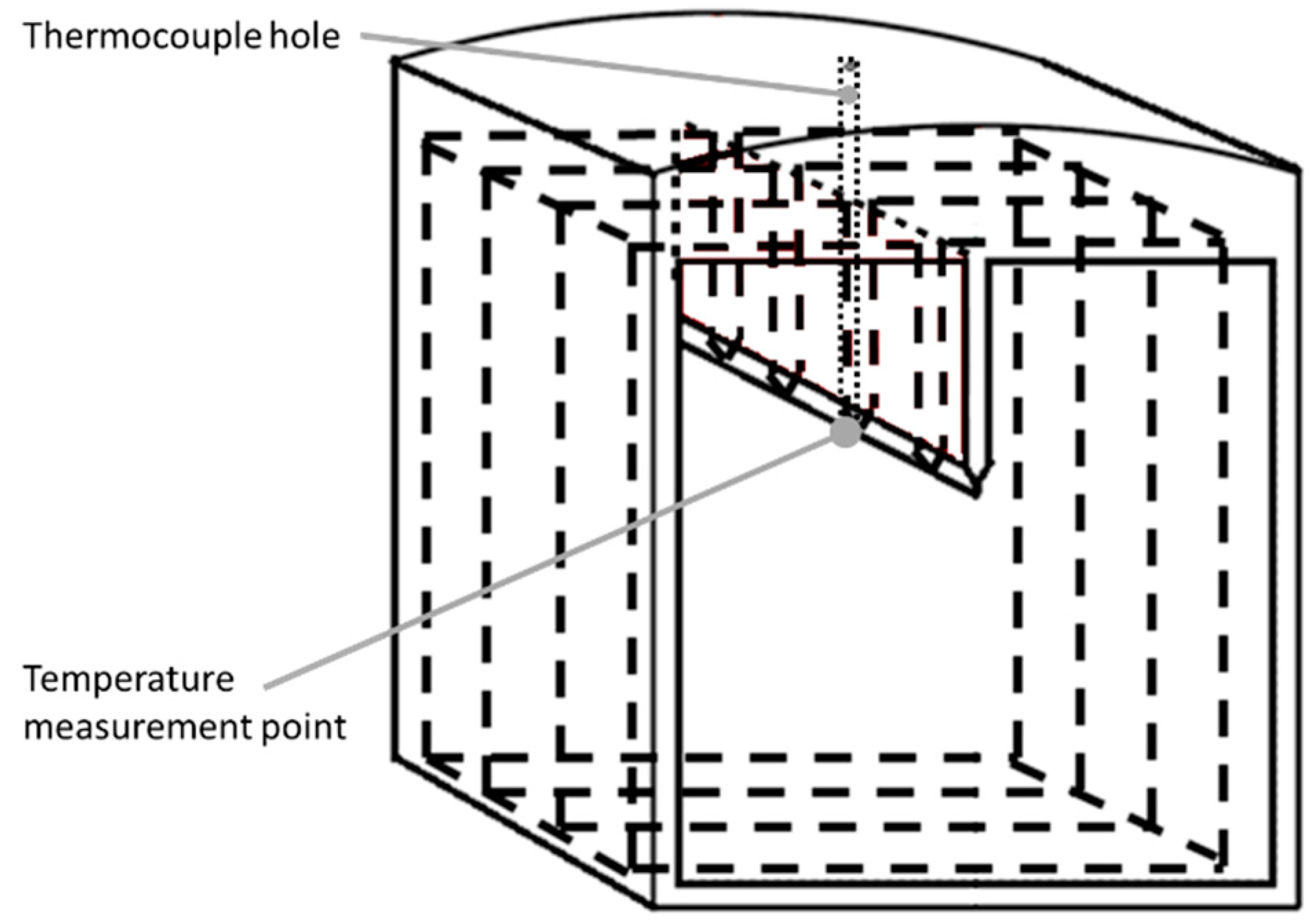
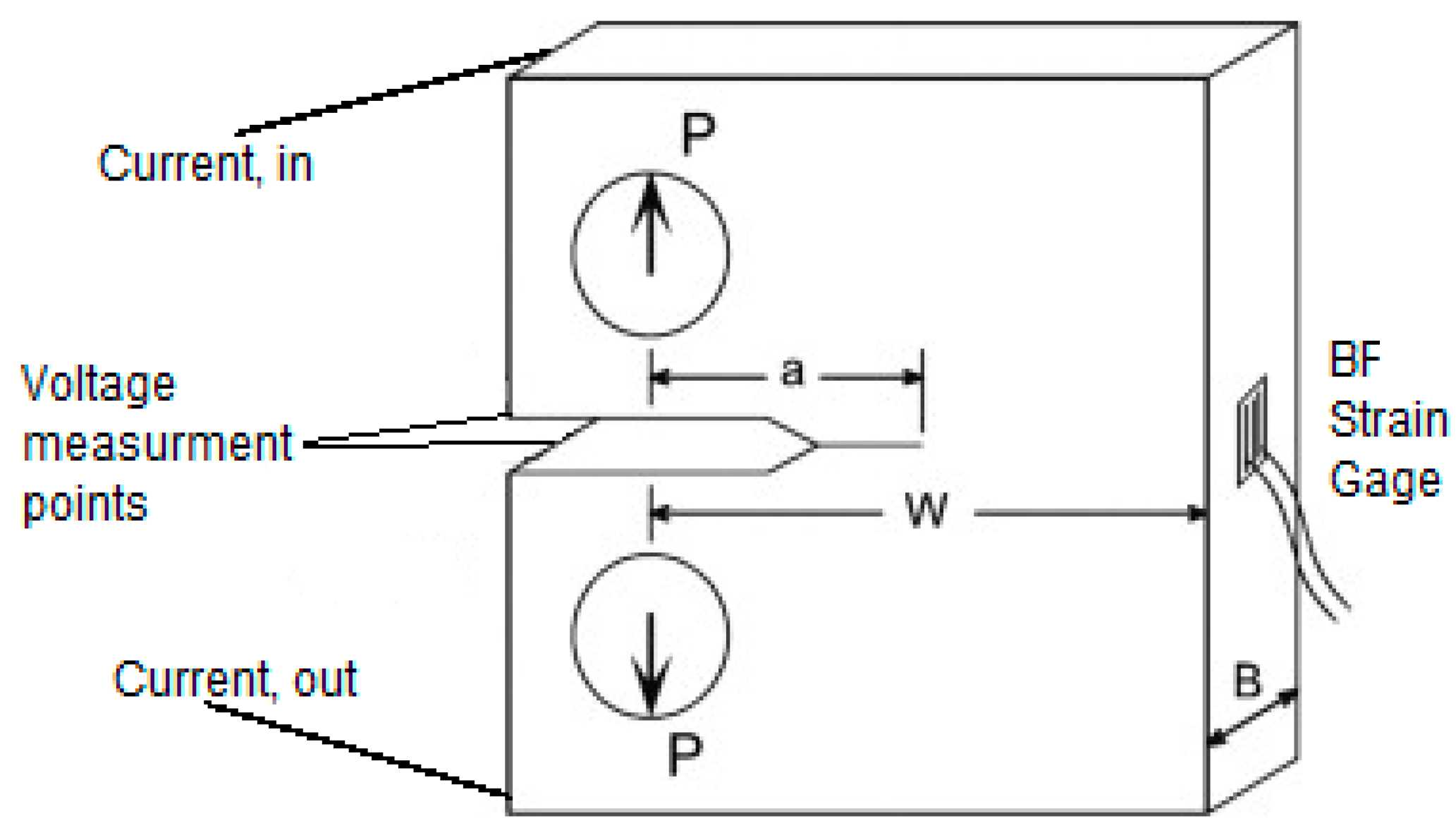
2. Materials and Methods
3. Microstructure Generation
4. Results
5. Conclusions
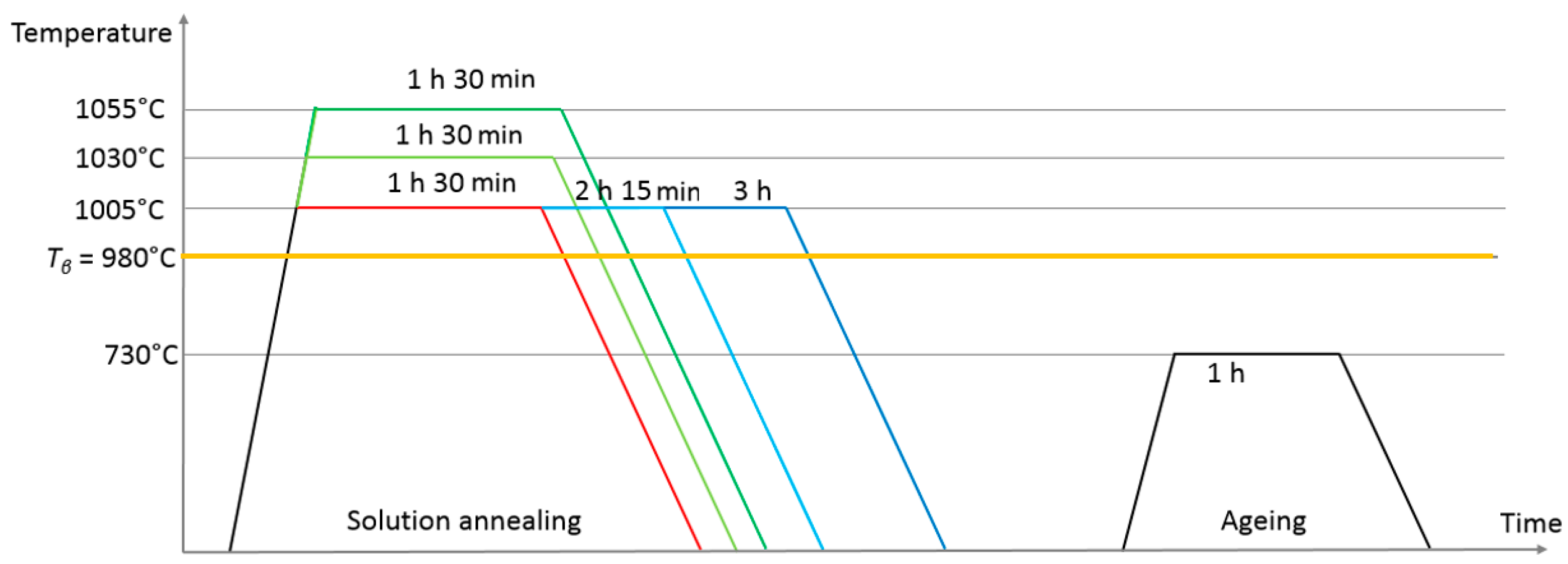
- The duration and the temperature above the beta transus of the solution-annealing step have an impact on the resultant microstructure. The main impact identified is the ex-β grain coarsening, with a limited impact on lamellar colony size, whereas no impact was evidenced on lamellae size. The increase in temperature from Tβ + 25 to Tβ + 75 or duration from 1 h 30 min to 3 h resulted in an increase in ex-β grain growth of about 30–40%.
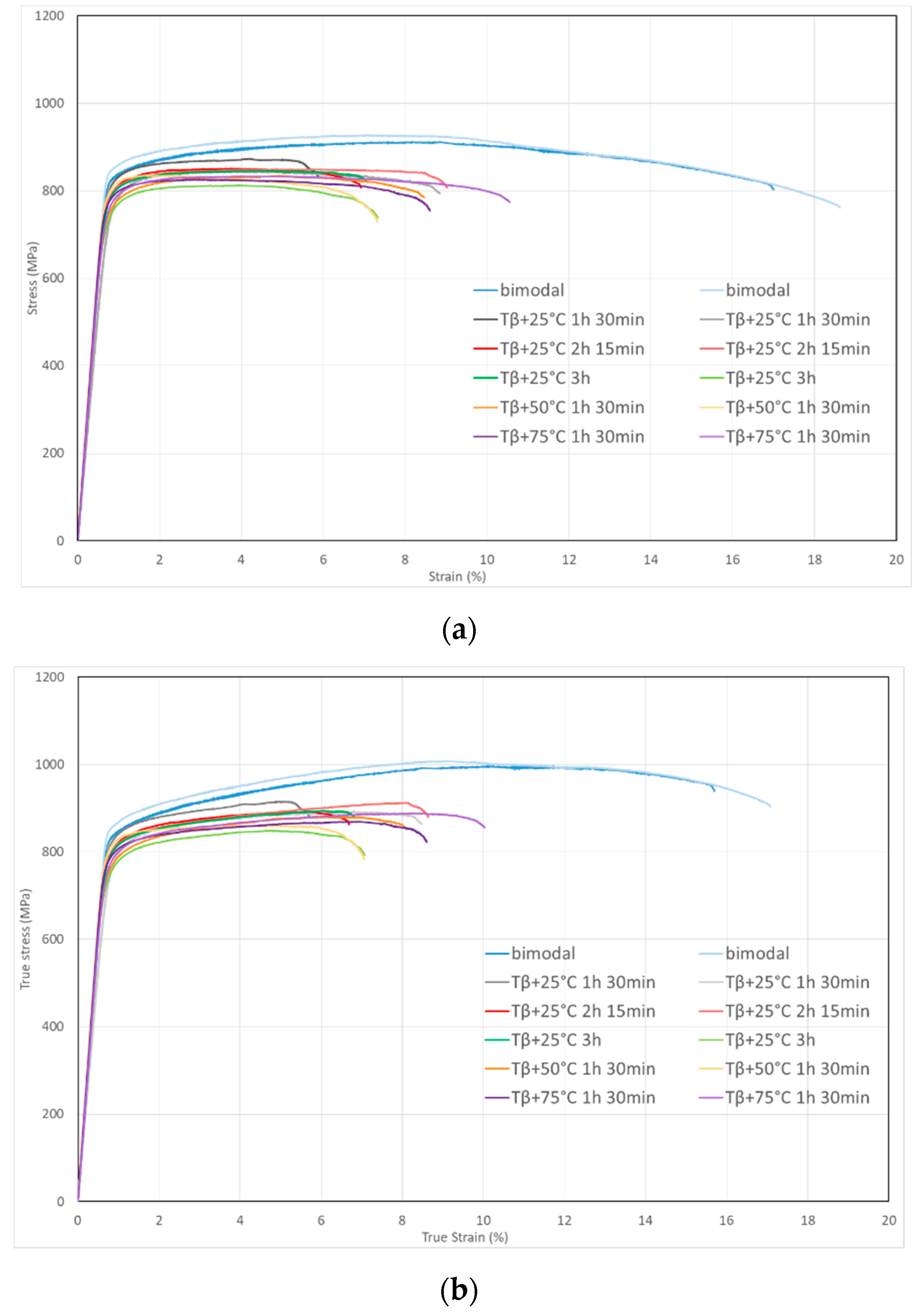
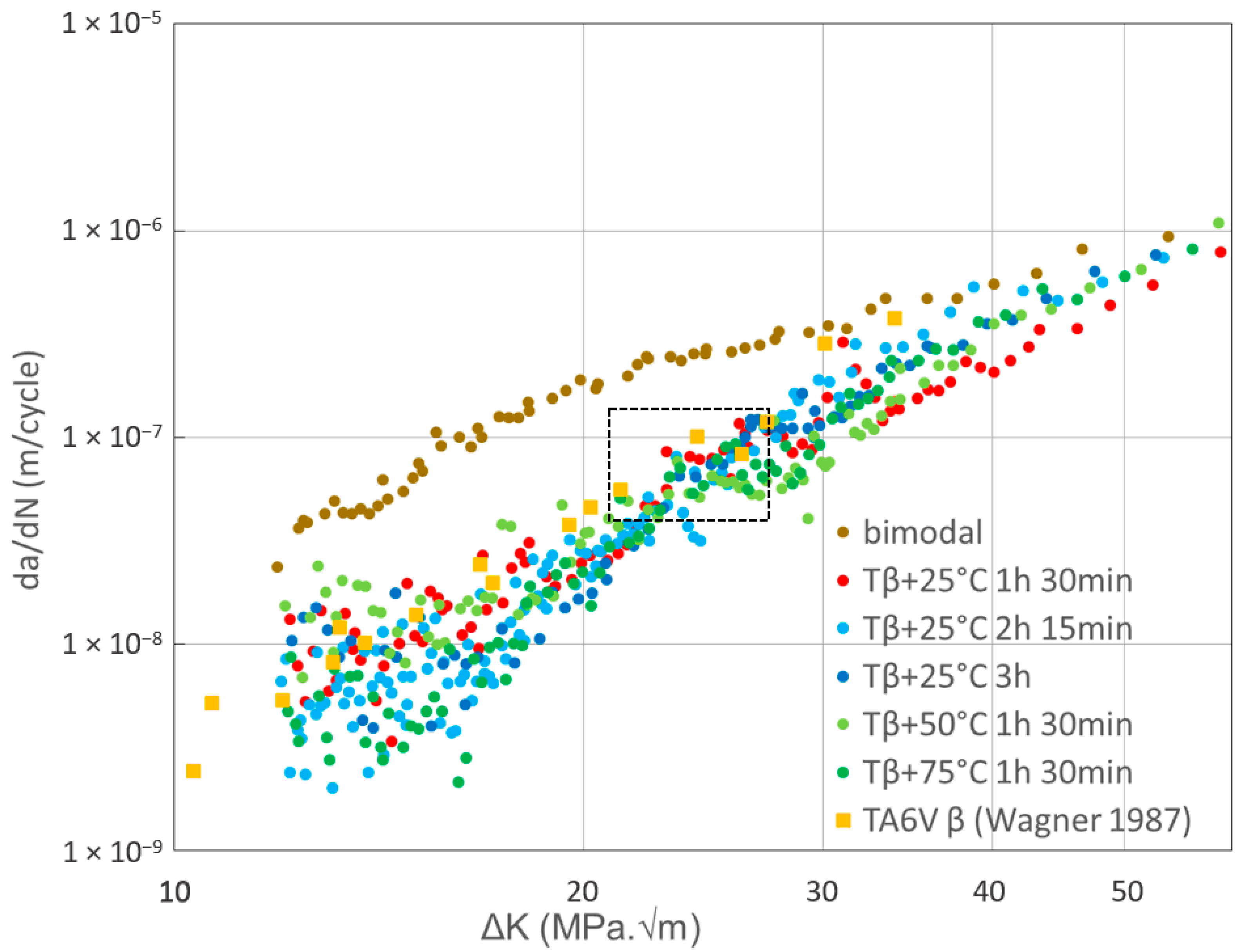
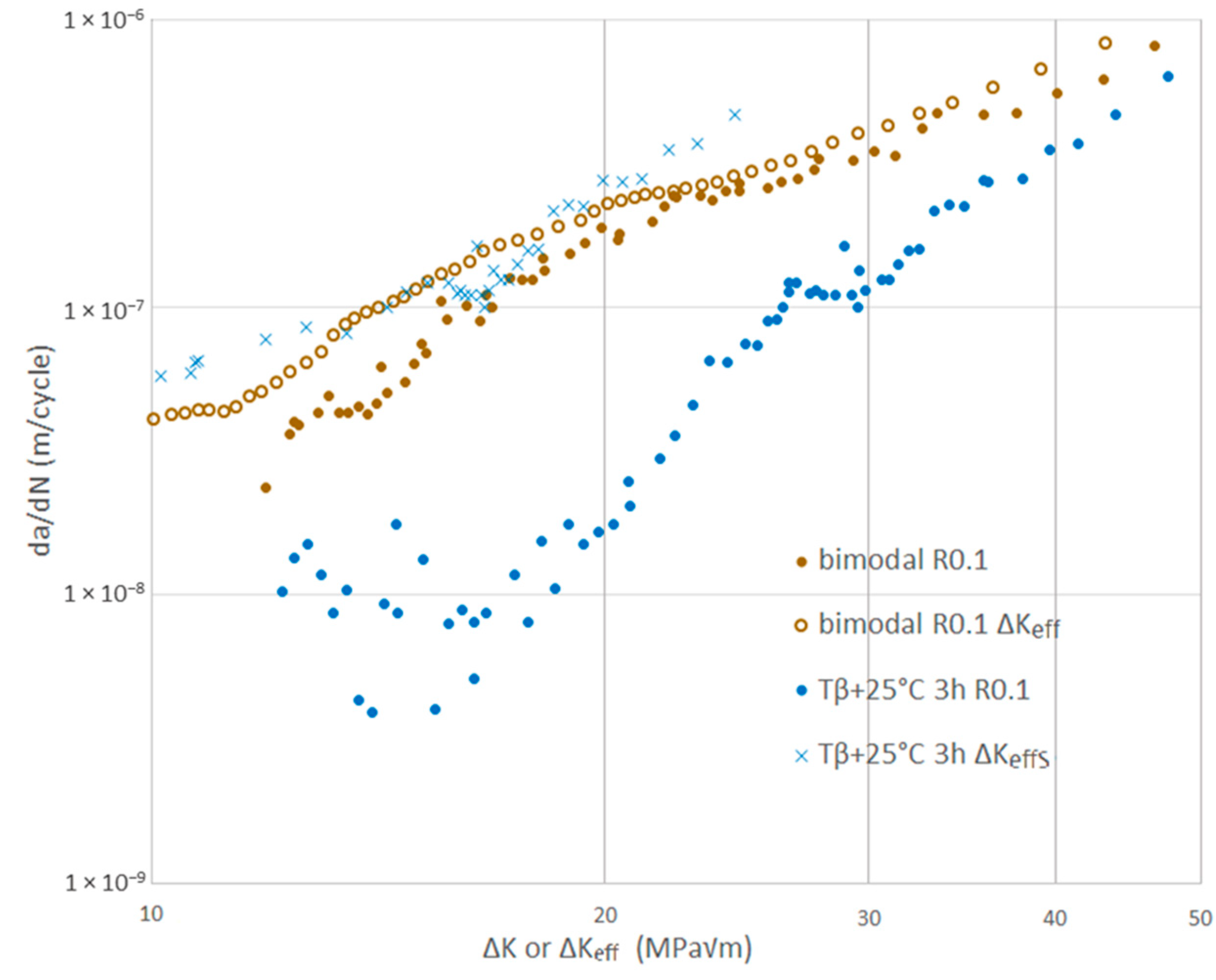
- As previously seen for standard Ti-6Al-4V, the Ti-6Al-4V ELI lamellar microstructures generated by β heat treatments presented superior fatigue crack propagation properties as compared to the bimodal microstructure, especially for ΔK < ΔKT. However the difference in prior β grain size had no influence on the resistance of lamellar microstructures.
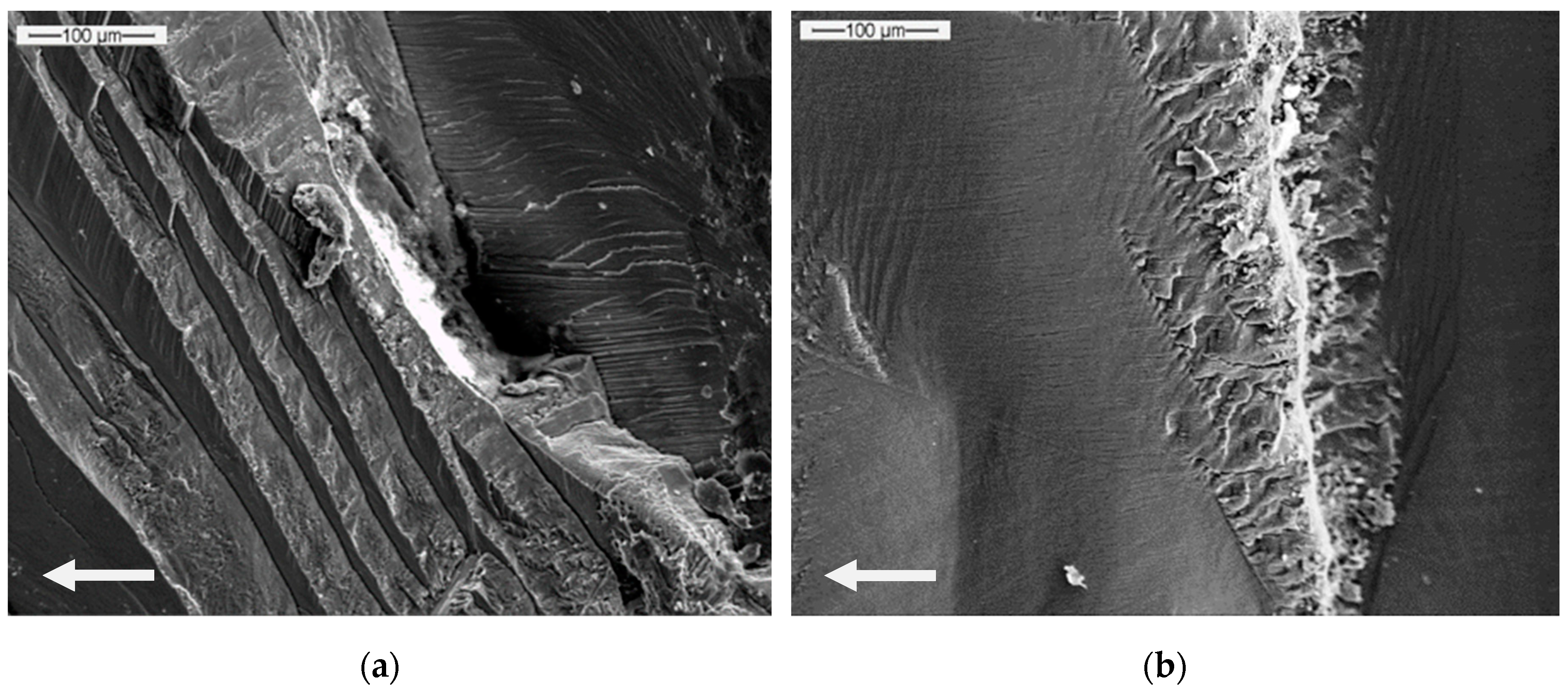
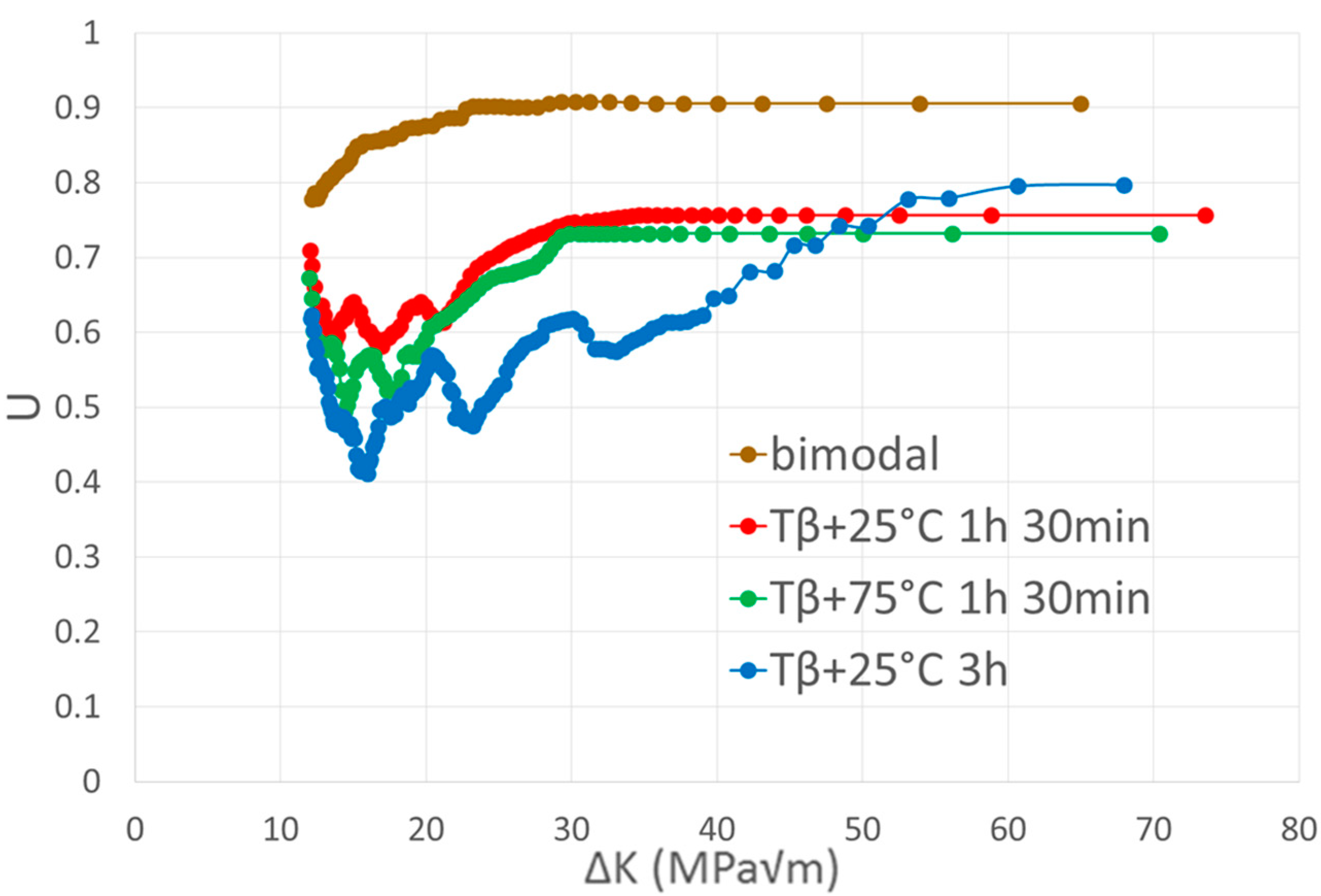
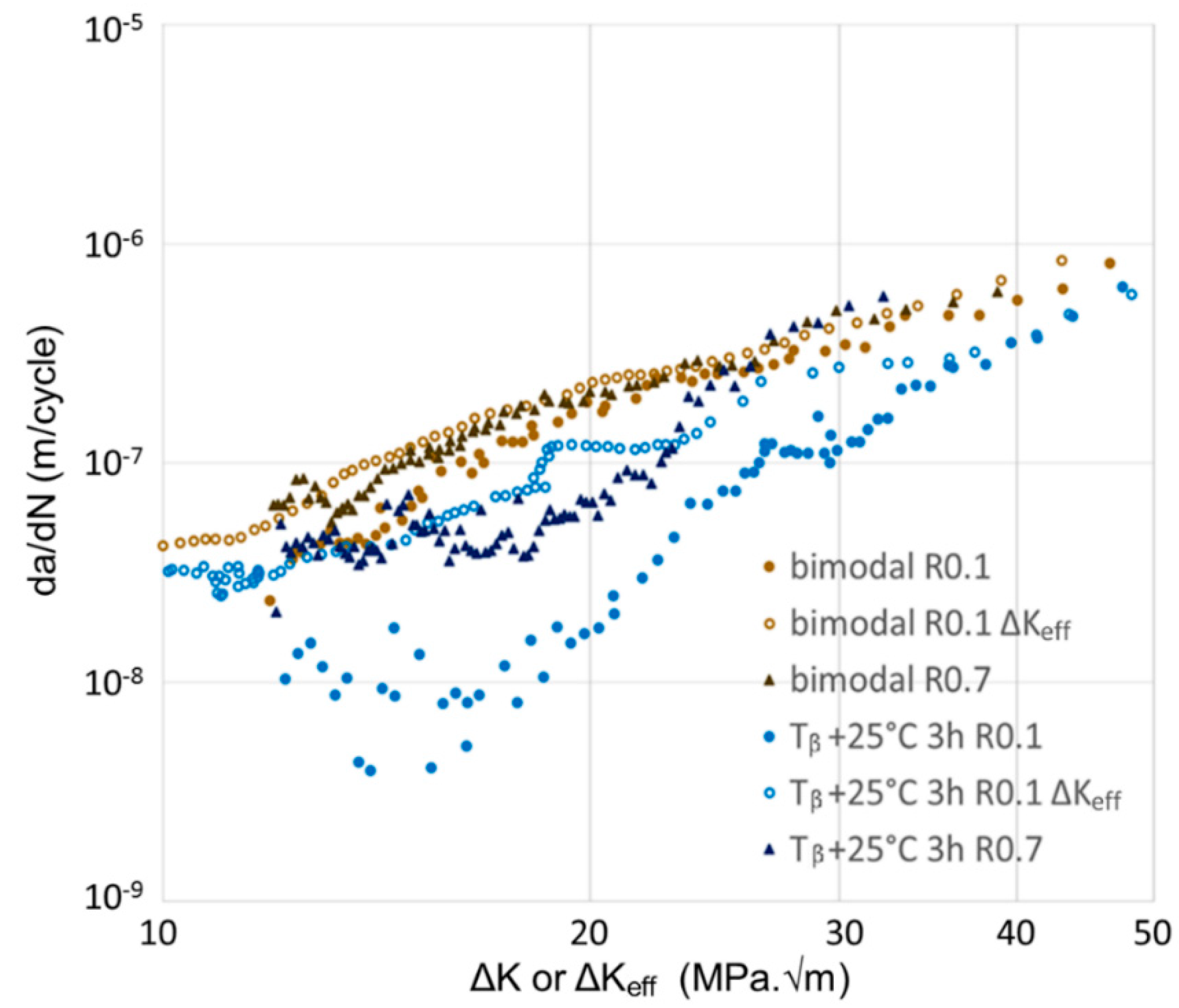
- The differences in fatigue crack propagation properties between lamellar and bimodal microstructures can be partially accounted for by crack closure effects. The roughness of crack surfaces can explain the remaining difference by generating mixed mode I and mode II propagation. Using both crack closure correction and the Suresh model for mixed mode propagation, the difference between the two microstructure can be fully explained.
- Two characteristic fatigue crack propagation regimes with a transition point were observed on lamellar microstructures for R = 0.1 and for R = 0.7. The cracks tended to grow along crystallographic planes before the transition, generating the high fracture surface roughness and a lot of secondary cracks, while microstructure had less effect after transition with crack without important deflections. The ΔKT value at the transition was the same at R = 0.1 and R = 0.7, confirming that the transition was mainly controlled by cyclic plasticity.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nalla, R.K.; Ritchie, R.O.; Boyce, B.L.; Campbell, J.P.; Peters, J.O. Influence of microstructure on high-cycle fatigue of Ti-6Al-4V: Bimodal vs. lamellar structures. Metall. Mater. Trans. A 2002, 33, 899–918. [Google Scholar] [CrossRef]
- Irving, P.E.; Beevers, C.J. Microstructural influences on fatigue crack growth in Ti-6Al-4V, Mater. Sci. Eng. 1974, 14, 229–238. [Google Scholar]
- Hadj Sassi, B.; Lehr, P. Ténacité et résistance à la propagation des fissures de fatigue de l’alliage de titane TA6V. J. Less-Common Met. 1997, 56, 157–165. [Google Scholar] [CrossRef]
- Laziou, J. Influence de la structure sur les propriétés mécaniques, la ténacité et la tenue à la fatigue de l’alliage de titane TA6V. J. Less-Common Met. 1976, 46, 129–249. [Google Scholar] [CrossRef]
- Krüger, L.; Grundmann, N.; Trubitz, P. Influence of Microstructure and Stress Ratio on Fatigue Crack Growth in a Ti-6-22-22-S alloy. Mater. Today Proc. 2015, 2, S205–S211. [Google Scholar]
- Walker, K.; Wang, C.H.; Newman, J.C., Jr. Fatigue Crack Closure due to Surface Roughness and Plastic Deformation. Adv. Mater. Res. 2014, 891–892, 319–324. [Google Scholar]
- Eylon, D. Faceted fracture in beta annealed titanium alloys, Metall. Trans. A. 1979, 10, 311–317. [Google Scholar]
- Qiu, J.; Feng, X.; Ma, Y.; Lei, J.; Liu, Y.; Huang, A.; Rugg, D.; Yang, R. Fatigue crack growth behavior of beta-annealed Ti–6Al–2Sn–4Zr–xMo (x = 2, 4 and 6) alloys: Influence of microstructure and stress ratio. Int. J. Fatigue 2016, 83, 150–160. [Google Scholar] [CrossRef]
- Yoder, G.R.; Cooley, L.A.; Crooker, T.W. Quantitative analysis of microstructural effects on fatigue crack growth in widmanstätten Ti-6A1-4V and Ti-8Al-1Mo-1V, Eng. Fract. Mech. 1979, 11, 805–816. [Google Scholar] [CrossRef]
- Kikukawa, M.; Jono, M.; Mikami, S. Fatigue Crack Propagation and Crack Closure Behavior under Stationary and Varying Loadings (Test Results of Aluminum Alloy). J. Soc. Mater. Sci. Jpn. 1982, 31, 483–487. [Google Scholar] [CrossRef]
- Elber, W. Fatigue crack closure under cyclic tension. Eng. Fract. Mech. 1970, 2, 37–45. [Google Scholar]
- ASTM International. ASTM E112-12 Standard Test Methods for Determining Average Grain Size; ASTM International: West Conshohocken, PA, USA, 2013. [Google Scholar]
- Wagner, L.; Lutjering, G. Microstructural Influence on Propagation Behavior of Short Cracks in an (alpha + beta) Titanium Alloy. Z. Metallkd. 1987, 78, 369–375. [Google Scholar]
- Yoder, G.R.; Cooley, L.A.; Crooker, T.W. Fatigue Crack Propagation Resistance of Beta-Annealed Ti-6Al-4V Alloys of differing interstitial oxygen contents. Metall. Trans. A 1978, 9A, 1413–1420. [Google Scholar] [CrossRef]
- Wanhill, R.; Barter, S. Fatigue of Beta Processed and Beta Heat-treated Titanium Alloys; Springer: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Wanhill, R. Material-based failure analysis of a helicopter rotor hub; ASM International: Geauga County, OH, USA, 2003. [Google Scholar]
- Wanhill, R.J.H.; Galatolo, R.; Looije, C.E.W. Fractographic and microstructural analysis of fatigue crack growth in a Ti-6A1-4V fan disc forging. Int. J. Fatigue 1989, 17, 407–416. [Google Scholar] [CrossRef]
- Suresh, S. Crack deflection: Implications for the growth of long and short fatigue cracks. Metall. Trans. A 1983, 14, 2375–2385. [Google Scholar] [CrossRef]





| Aluminum | Vanadium | Carbon | Iron | Oxygen | Nitrogen | Hydrogen | Titanium |
|---|---|---|---|---|---|---|---|
| 6.24 | 3.97 | 0.015 | 0.16 | 0.12 | 0.002 | <0.003 | Balance |
| Heat Treatment (Duration/Temperature) | Ex-β Grain Size (µm) | Lamellar Colony Size (µm) | Lamellae Width (µm) | |||
|---|---|---|---|---|---|---|
| Value | Standard Deviation | Value | Standard Deviation | Value | Standard Deviation | |
| Tβ + 25 °C 1 h 30 min | 1283 | 108 | 461 | 292 | 1.25 | 0.28 |
| Tβ + 25 °C 2 h 15 min | 1615 | 58 | 466 | 294 | 1.24 | 0.32 |
| Tβ + 25 °C 3 h | 1686 | 101 | 425 | 225 | 1.46 | 0.42 |
| Tβ + 50 °C 1 h 30 min | 1614 | 99 | 508 | 239 | 1.22 | 0.36 |
| Tβ + 75 °C 1 h 30 min | 1764 | 215 | 436 | 283 | 1.35 | 0.43 |
| Heat Treatment (Duration/Temperature) | E (GPa) | Rp 0.2 (MPa) | Rm (MPa) | A% | ||||
|---|---|---|---|---|---|---|---|---|
| Value | Standard Deviation | Value | Standard Deviation | Value | Standard Deviation | Value | Standard Deviation | |
| As received (bimodal) | 121 | 3 | 848 | 11 | 1001 | 5.5 | 15.6 | 0.75 |
| Tβ + 25 °C 1 h 30 min | 114 | 9 | 803 | 23 | 904 | 11.5 | 6.5 | 1.35 |
| Tβ + 25 °C 2 h 15 min | 125 | 1.5 | 803 | 1.5 | 902 | 10.5 | 7.4 | 1.15 |
| Tβ + 25 °C 3 h | 123 | 0 | 776 | 24 | 871 | 23 | 6.4 | 0.1 |
| Tβ + 50 °C 1 h 30 min | 124 | 3.5 | 790 | 24 | 869 | 10 | 7.0 | 0.45 |
| Tβ + 75 °C 1 h 30 min | 124 | 1.5 | 786 | 4.5 | 878 | 10 | 8.8 | 0.65 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Renon, V.; Henaff, G.; Larignon, C.; Perusin, S.; Villechaise, P. Identification of Relationships between Heat Treatment and Fatigue Crack Growth of αβ Titanium Alloys. Metals 2019, 9, 512. https://doi.org/10.3390/met9050512
Renon V, Henaff G, Larignon C, Perusin S, Villechaise P. Identification of Relationships between Heat Treatment and Fatigue Crack Growth of αβ Titanium Alloys. Metals. 2019; 9(5):512. https://doi.org/10.3390/met9050512
Chicago/Turabian StyleRenon, Vincent, Gilbert Henaff, Céline Larignon, Simon Perusin, and Patrick Villechaise. 2019. "Identification of Relationships between Heat Treatment and Fatigue Crack Growth of αβ Titanium Alloys" Metals 9, no. 5: 512. https://doi.org/10.3390/met9050512
APA StyleRenon, V., Henaff, G., Larignon, C., Perusin, S., & Villechaise, P. (2019). Identification of Relationships between Heat Treatment and Fatigue Crack Growth of αβ Titanium Alloys. Metals, 9(5), 512. https://doi.org/10.3390/met9050512







