Tribo-Dynamics and Fretting Behavior of Connecting Rod Big-End Bearings in Internal Combustion Engines
Abstract
1. Introduction
2. Mixed Lubrication Model
2.1. Average Reynolds Equation
2.2. Asperity Contact
2.3. FEM Solving Method
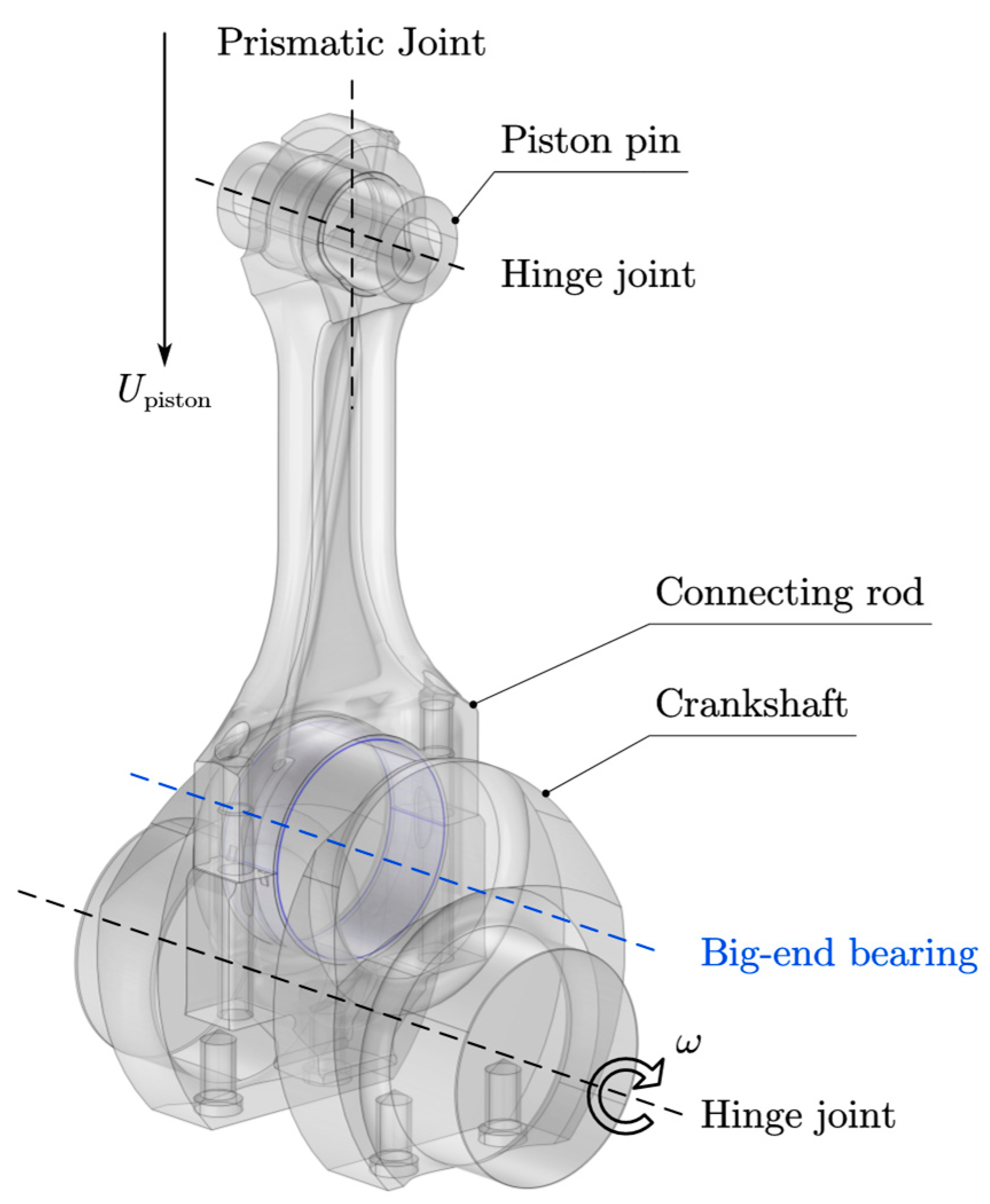
3. Multi-Body Dynamics Model
3.1. System Kinematic Equations
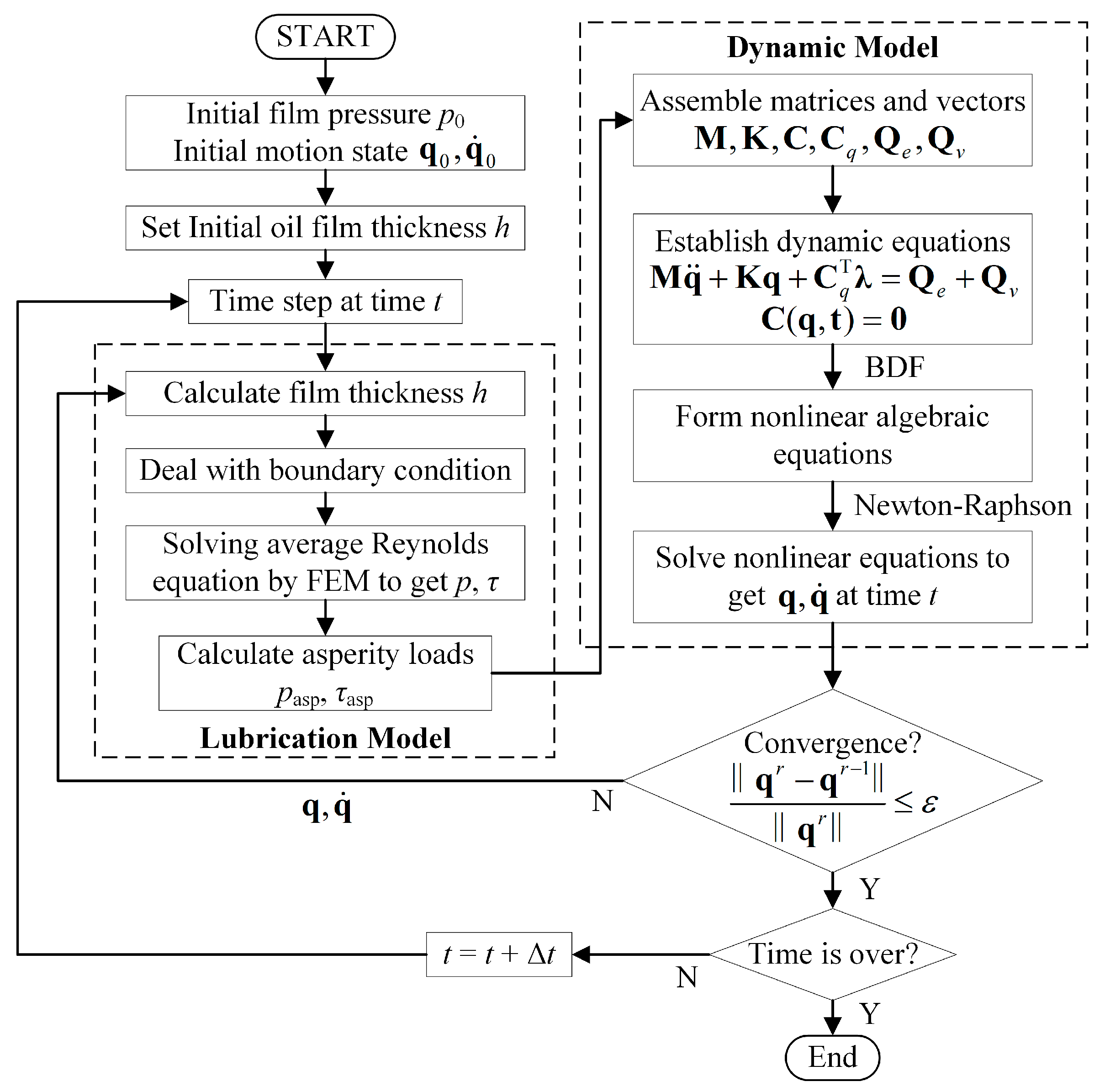
3.2. Coupled Solving Algorithm
- 1.
- Initial assembly configuration defines the generalized coordinate vector q0.
- 2.
- Spatial positions of the bearing bush and crankpin, derived from q, determine the spatial film thickness distribution over the lubrication domain.
- 3.
- The averaged Reynolds equation is solved via the finite element method, yielding:
- (a)
- Hydrodynamic pressure;
- (b)
- Fluid shear traction;
- (c)
- Asperity contact pressure;
- (d)
- Asperity friction traction.
- 4.
- These tractions are integrated into generalized force vector Q input to the multi-body system.
| Parameters | Descriptions | Values |
|---|---|---|
| D | Bore of cylinder | 280 (mm) |
| S | Stroke | 330 (mm) |
| Lrod | Length of connecting rod | 660 (mm) |
| R | Crank radius | 165 (mm) |
| n | Rotation speed | 1000 (rpm) |
| ρpin | Equivalent density of piston pin | 28,850 (kg/m3) |
| ρrod | Density of connecting rod | 7850 (kg/m3) |
| νrod | Poisson’s ratio of connecting rod | 0.3 (-) |
| Erod | Elastic modulus of connecting rod | 212 (GPa) |
| ρbush | Density of big-end bearing bush | 8900 (kg/m3) |
| νbush | Poisson’s ratio of big-end bearing bush | 0.3 (-) |
| Ebush | Elastic modulus of big-end bearing bush | 211 (GPa) |
| ρcrank | Density of crankshaft | 7850 (kg/m3) |
| νcrank | Poisson’s ratio of crankshaft | 0.3 (-) |
| Ecrank | Elastic modulus of crankshaft | 210 (GPa) |
| Parameters | Descriptions | Values |
|---|---|---|
| c | Nominal clearance of big-end bearing | 120 (μm) |
| σ | Composite roughness of big-end bearing | 1.2 (μm) |
| ρoil | Density of lubricating oil | 860 (kg/m3) |
| μ | Viscosity of lubricating oil | 0.039 (Pa·s) |
| μb | Boundary coefficient of friction | 0.09 (-) [25] |
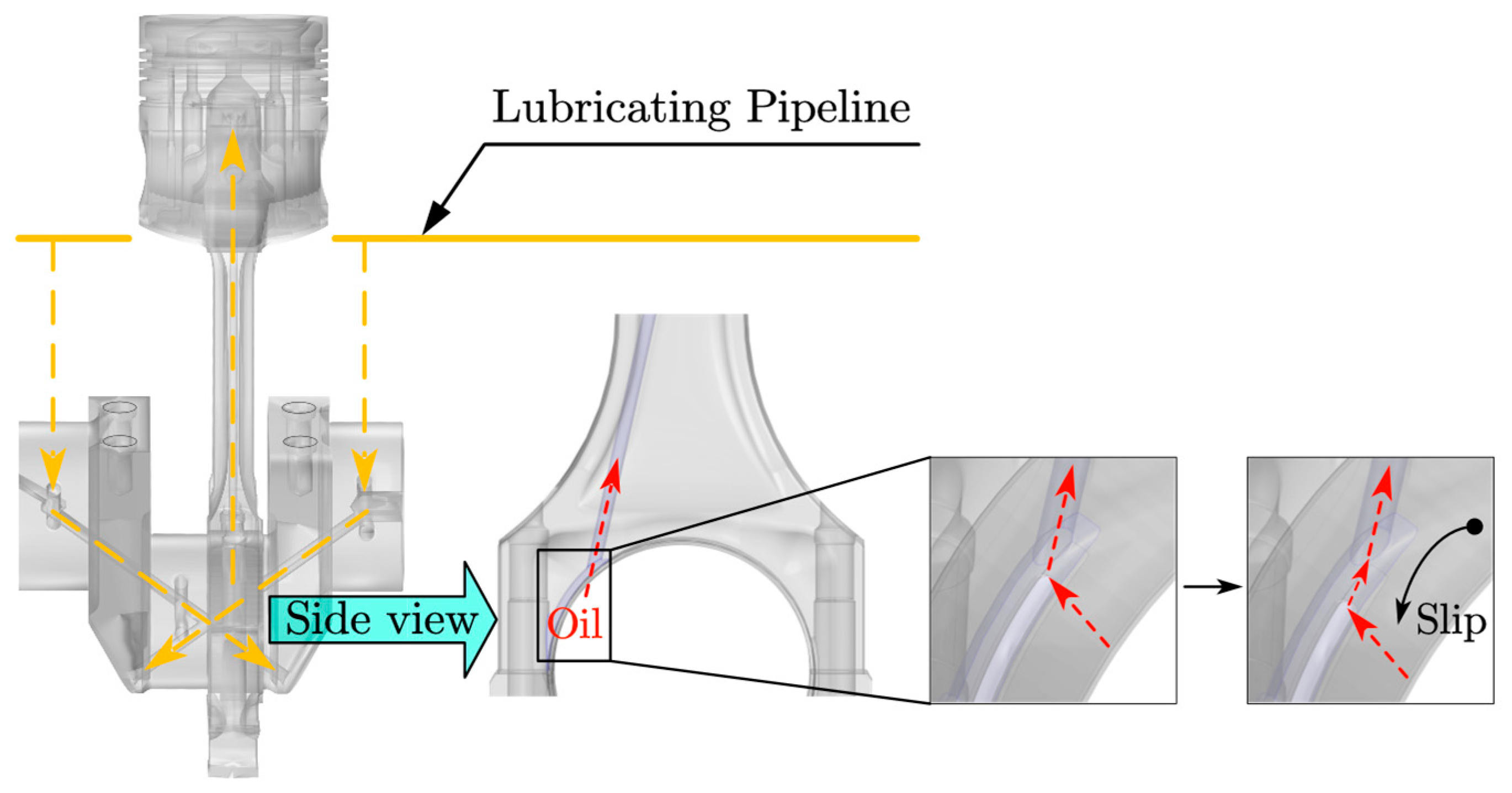
4. Fretting Wear Model
- ▪
- Lubricated Interface (Bushing-Inner/Crankshaft Journal): Governed by a fluid–structure interaction (FSI) model (Section 2 and Section 3), resolving transient mixed lubrication behavior via the Average Reynolds equation and asperity contact (Greenwood and Tripp model). This interface assumes fully flooded hydrodynamic conditions.
- ▪
- Fretting Interface (Bushing-Back/Big-End Bore): Modeled as a dry, solid–solid micro-motion regime (Section 4), where fretting wear is quantified using the Archard equation. Critically, no fluid film or flooding conditions are assumed at this press-fit interface.
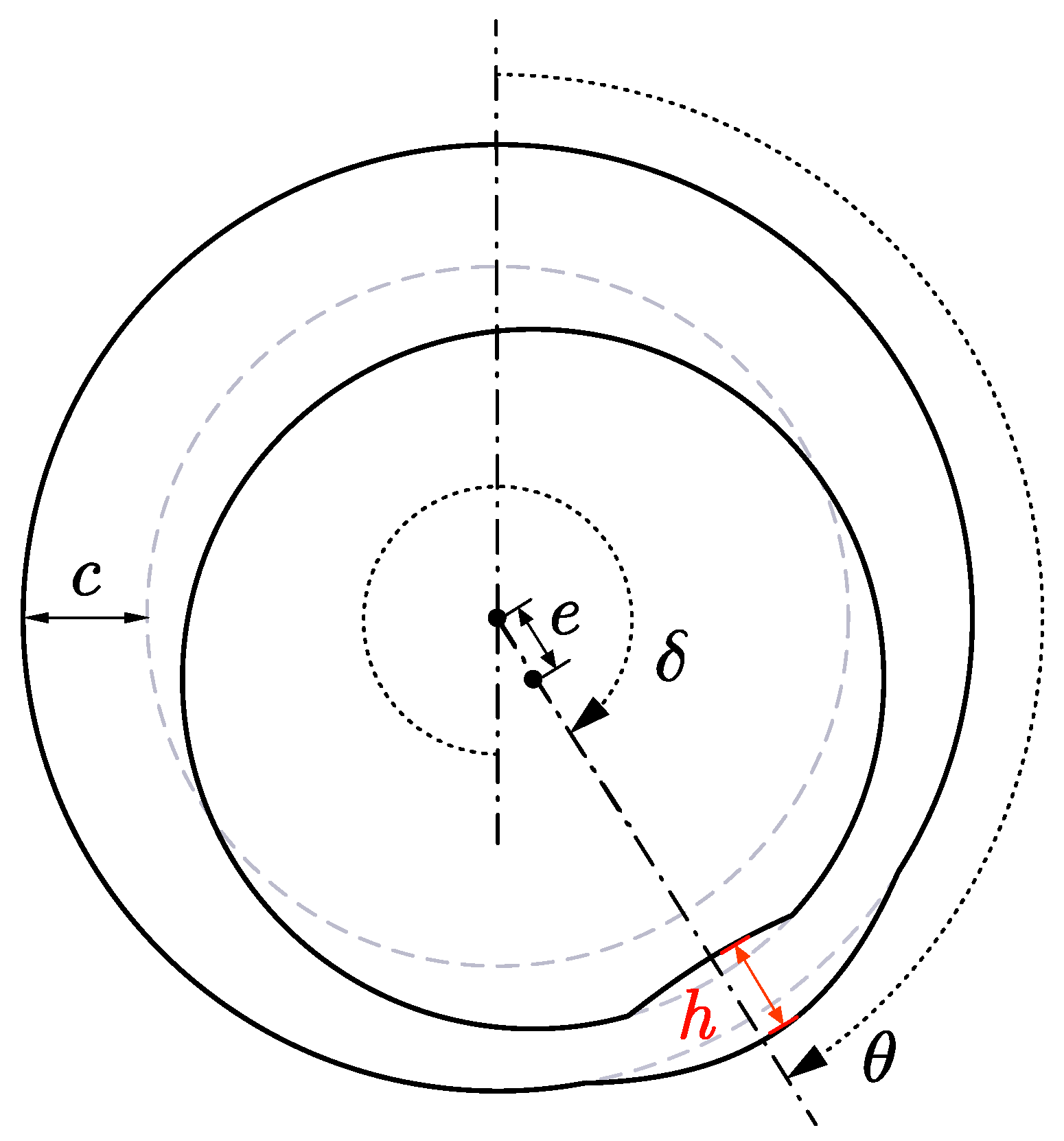
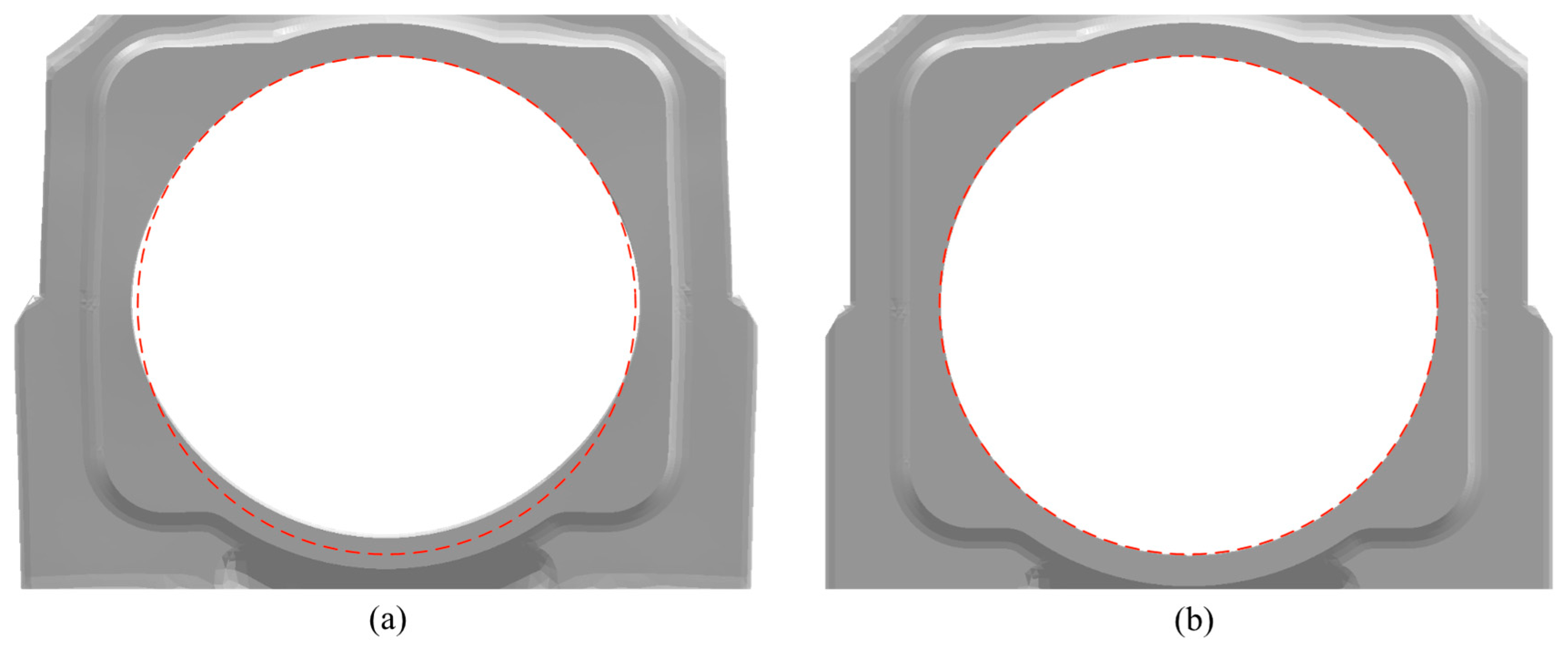
4.1. Connecting Rod Boring Process
- Apply bolt preload to assemble the connecting rod body and cap, inducing non-cylindrical deformation in the big-end bore.
- Extract nodal displacement results of the big-end bore in this deformed configuration.
- Apply reverse deformation to the nodal coordinates of the big-end bore in the reference configuration based on the extracted displacements.
- Verify cylindrical integrity: upon reapplication of identical bolt preload, the compensated bore recovers its nominal cylindrical form.
4.2. Calculation Methods for Fretting Wear
- Boring process simulation (incorporating geometric compensation);
- Application of bolt preload (461 kN nominal/decayed);
- Imposition of bearing bush interference fit (0.264 mm nominal/degraded);
- Solution of 26 characteristic crankshaft angle positions (critical loading instants);
- Quantification of fretting slip distance and wear depth.
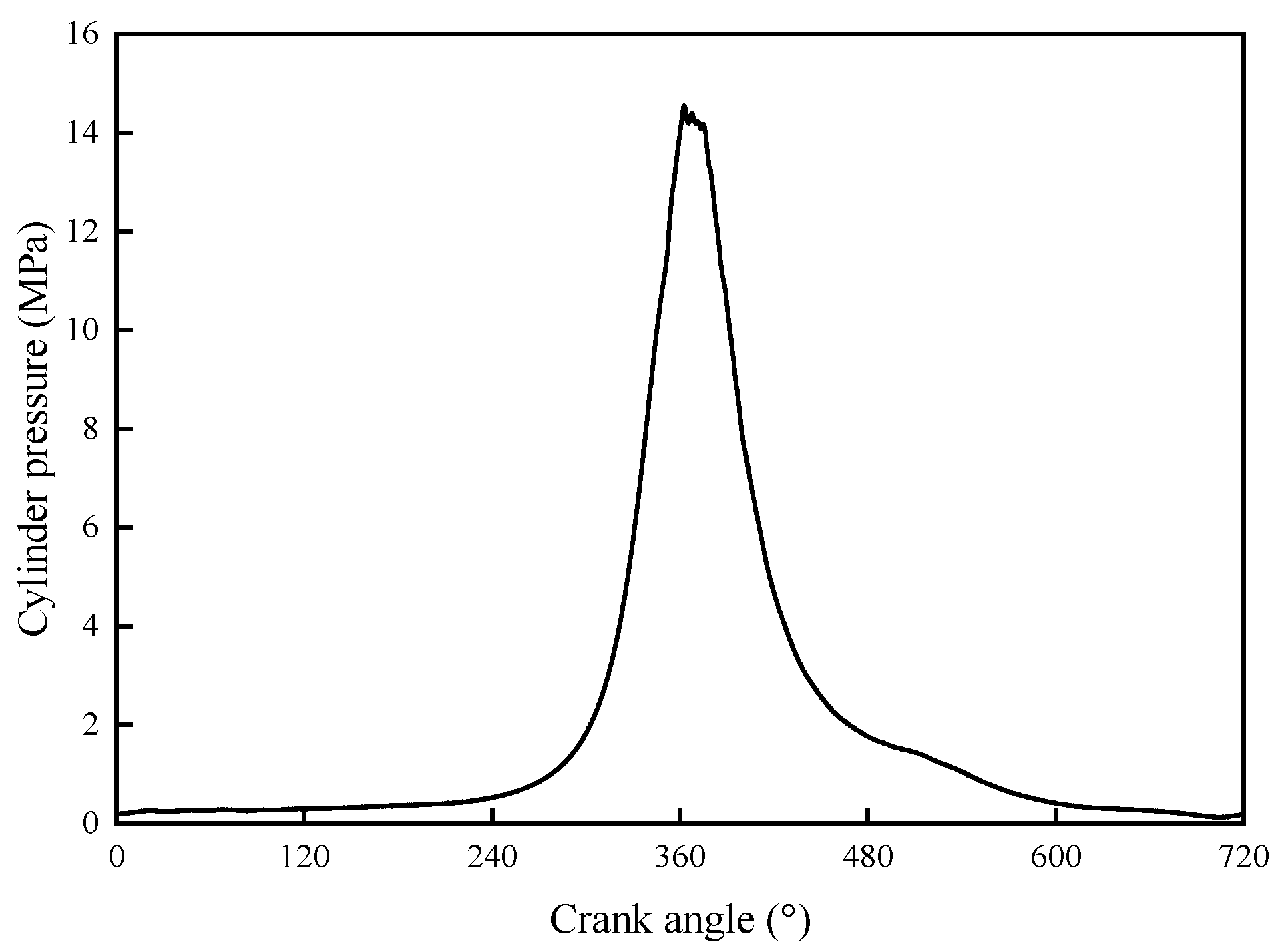
5. Results and Discussion
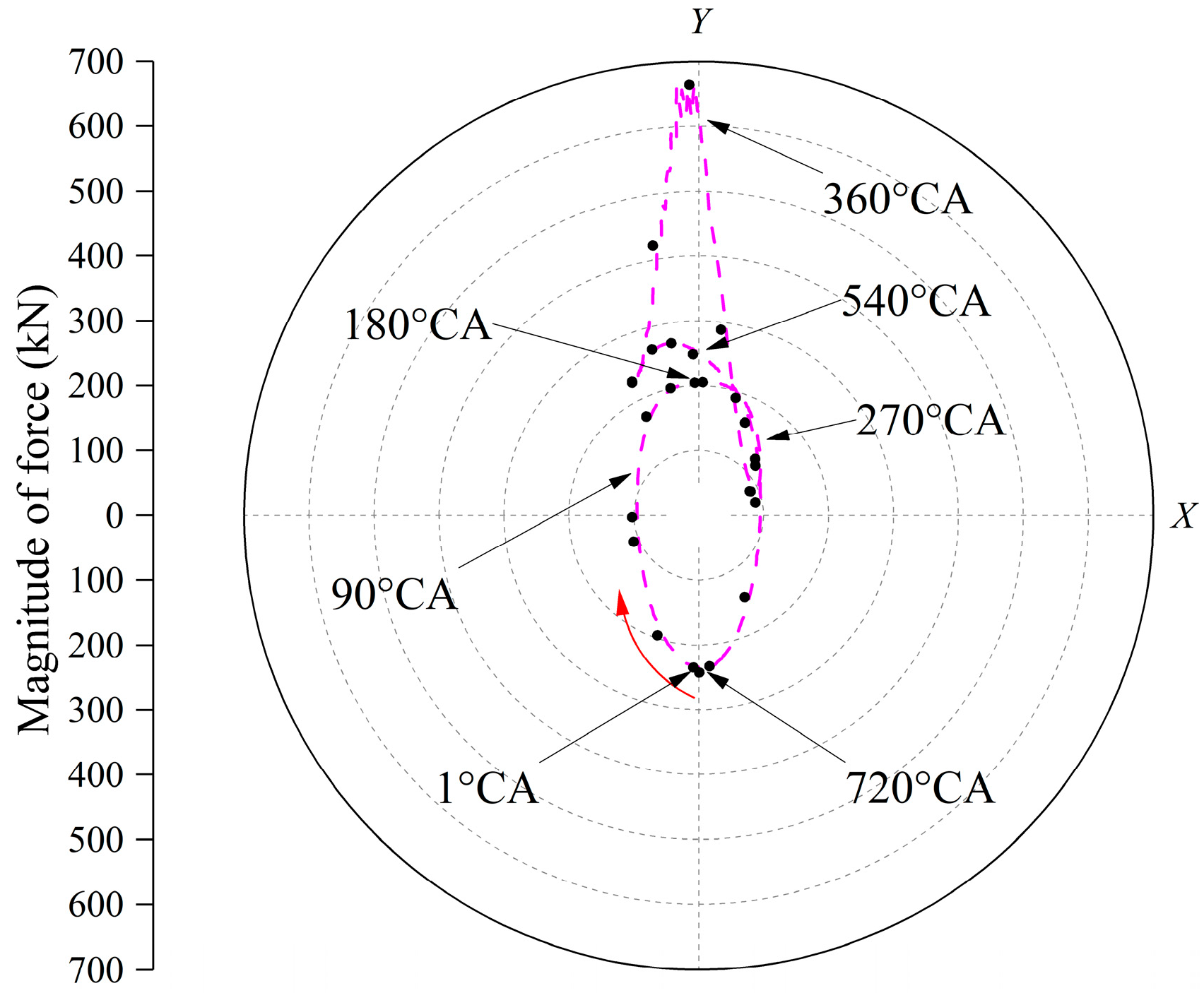
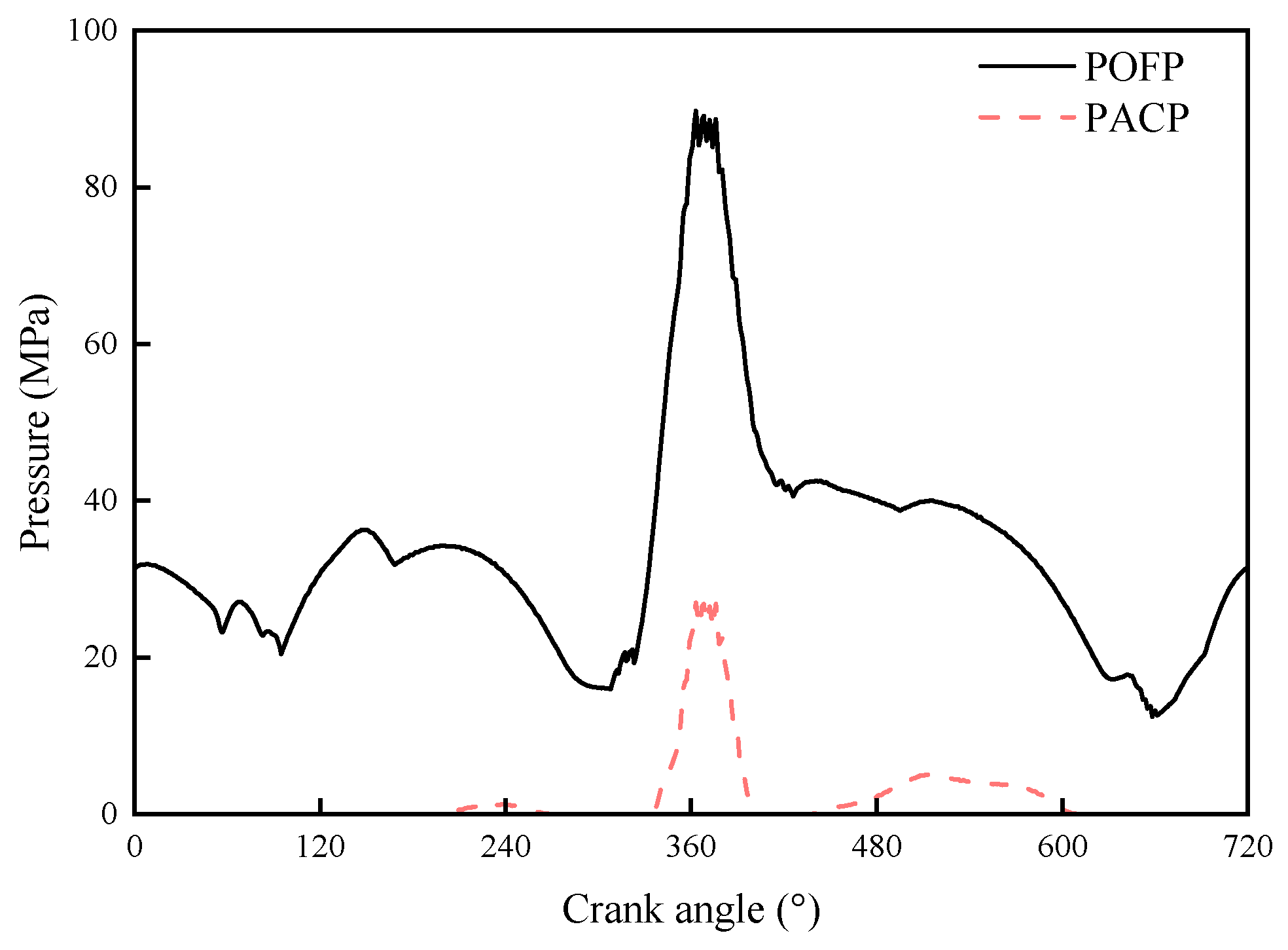
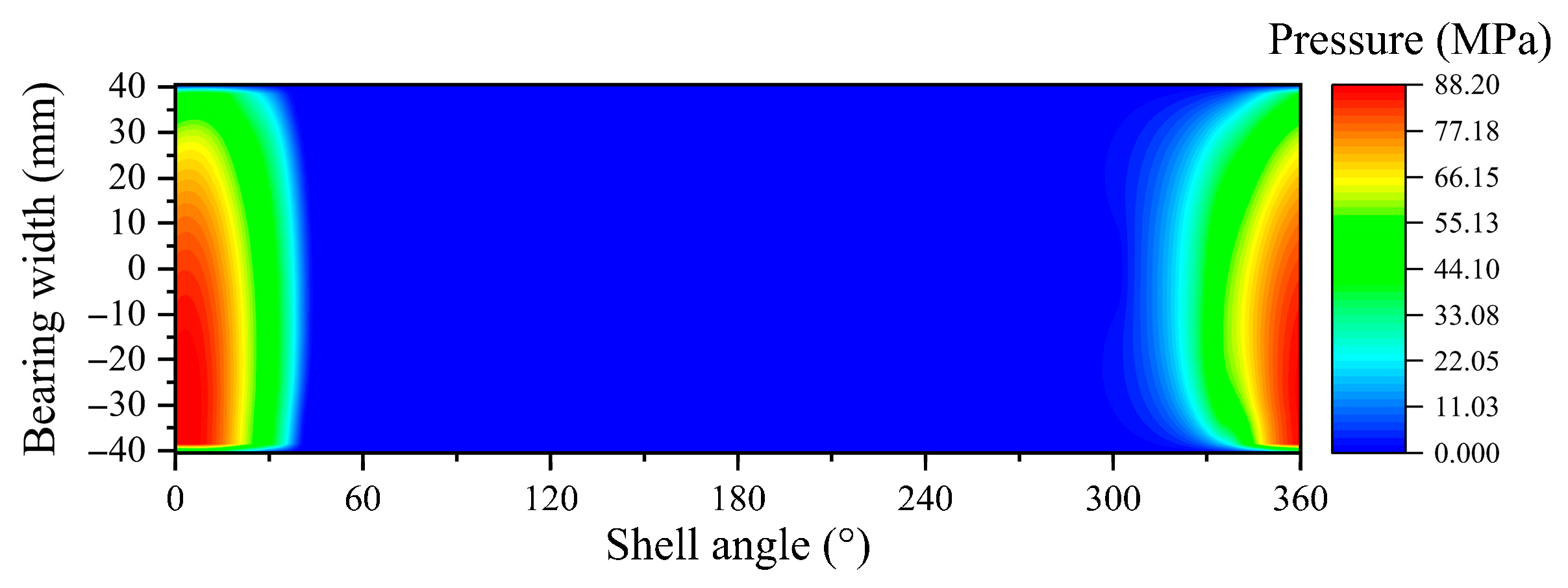
5.1. Tribo-Dynamic Results
5.2. Fretting Slip Results
5.3. Fretting Wear Results
5.4. Analysis of Reasons for Failure
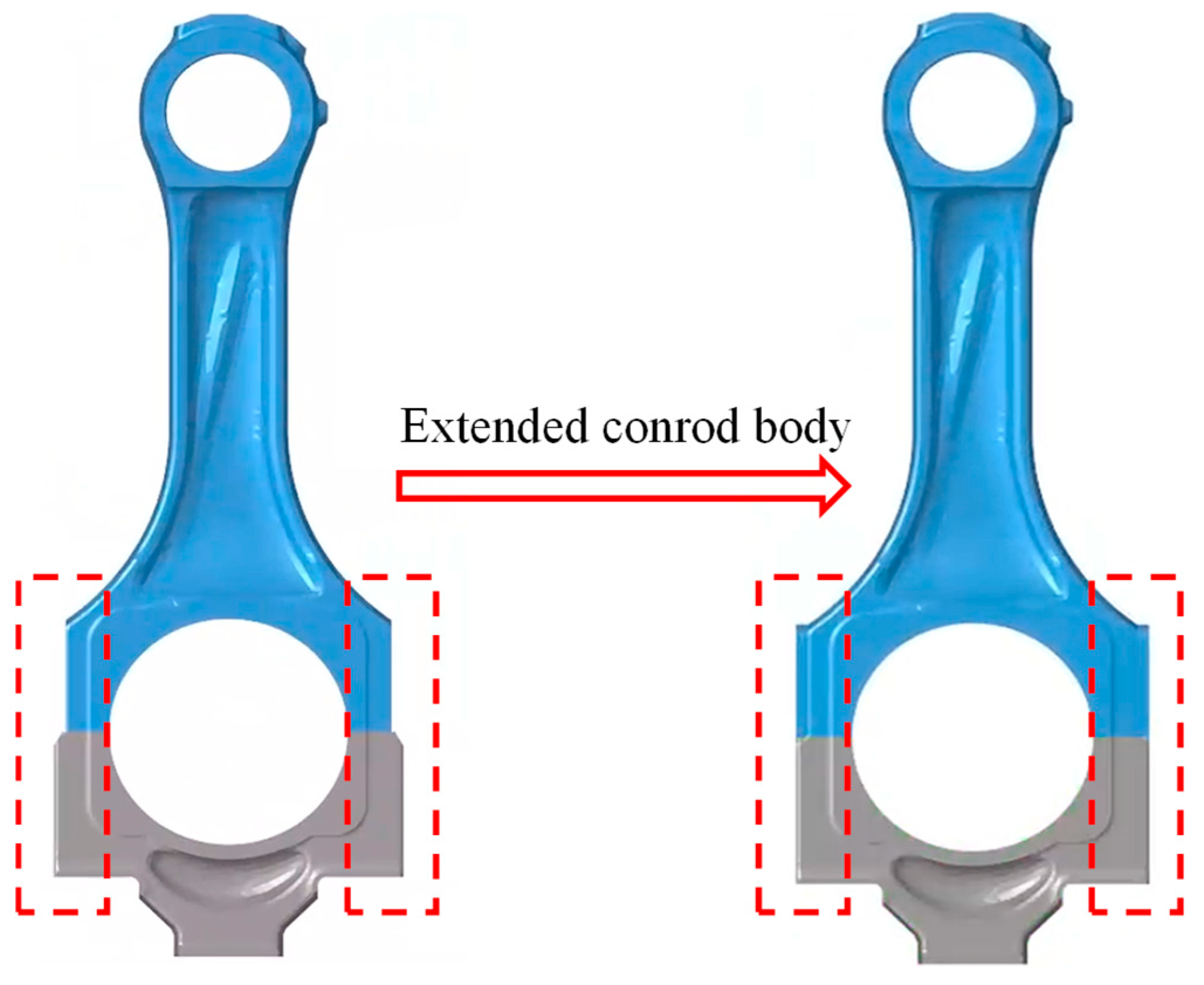
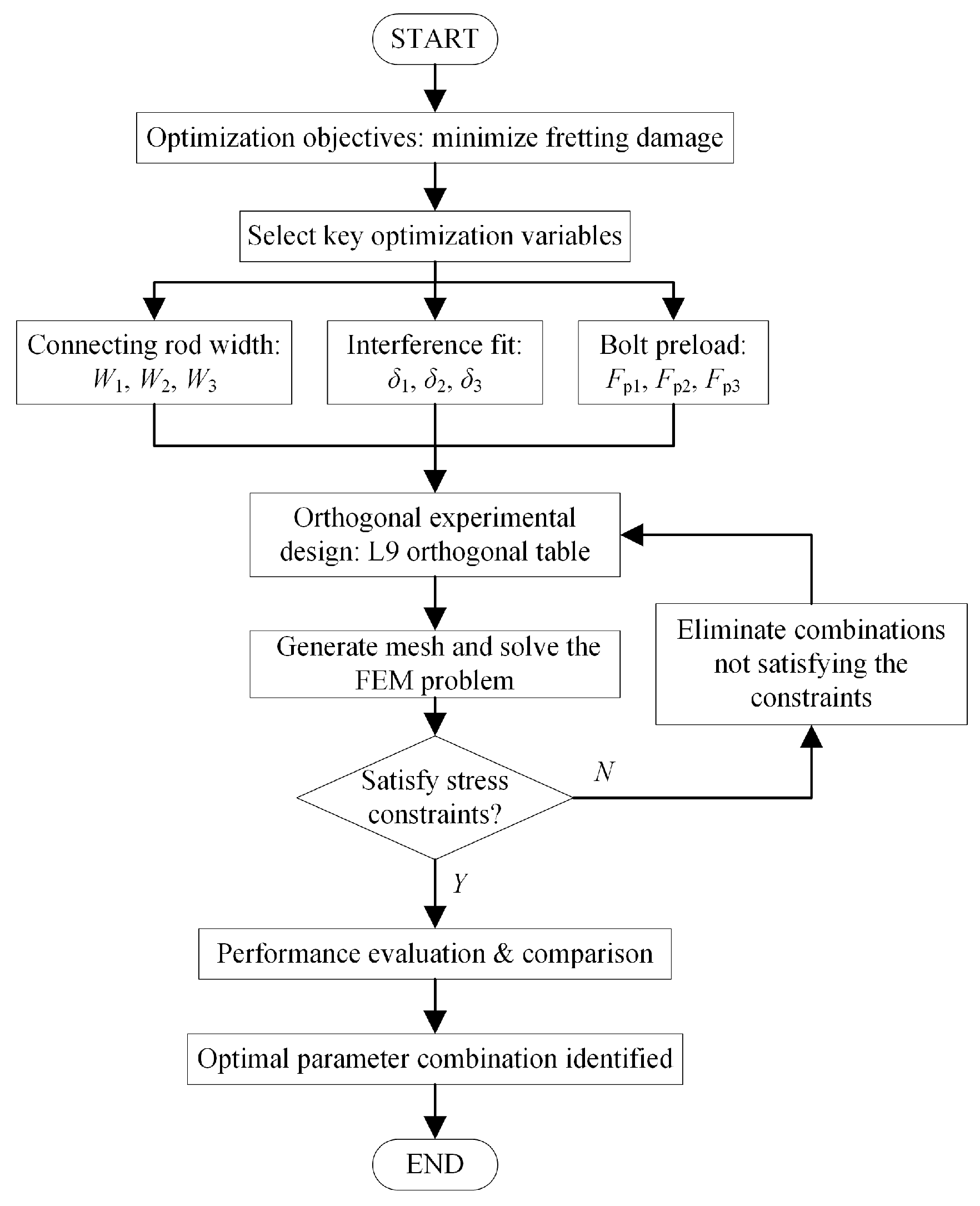
5.5. Optimization Scheme
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Anenberg, S.C.; Miller, J.; Minjares, R.; Du, L.; Henze, D.K.; Lacey, F.; Malley, C.S.; Emberson, L.; Franco, V.; Klimont, Z.; et al. Impacts and Mitigation of Excess Diesel-Related NOx Emissions in 11 Major Vehicle Markets. Nature 2017, 545, 467–471. [Google Scholar] [CrossRef]
- Waterhouse, R.B. Fretting Wear. Wear 1984, 100, 107–118. [Google Scholar] [CrossRef]
- Badding, B.; Bhalerao, M.; Dowell, J.P.; Gambheera, R.; Sundaram, S. A Method to Predict Fretting in Diesel Engine Connecting Rod Bearing Bores. In Proceedings of the ASME 2004 Internal Combustion Engine Division Fall Technical Conference, Long Beach, CA, USA, 24–27 October 2004; ASMEDC: Long Beach, CA, USA, 2004; pp. 607–616. [Google Scholar]
- Chen, J.; Randall, R.B. Intelligent Diagnosis of Bearing Knock Faults in Internal Combustion Engines Using Vibration Simulation. Mech. Mach. Theory 2016, 104, 161–176. [Google Scholar] [CrossRef]
- Carden, P.; Pisani, C.; Andersson, J.; Field, I.; Lainé, E.; Bansal, J.; Devine, M. The Effect of Low Viscosity Oil on the Wear, Friction and Fuel Consumption of a Heavy Duty Truck Engine. SAE Int. J. Fuels Lubr. 2013, 6, 311–319. [Google Scholar] [CrossRef]
- Dou, Q.; Luo, H.; Song, Y.; Zhang, Z.; Zhang, J. Failure Analysis of Diesel Engine Connecting Rod Big-End Bearing Wear Considering Coupled Clearance Lubrication Joints. Eng. Fail. Anal. 2025, 169, 109136. [Google Scholar] [CrossRef]
- Merritt, D.; Zhu, G. The Prediction of Connecting Rod Fretting and Fretting Initiated Fatigue Fracture; SAE Technical Paper 2004-1-3015; SAE International: Warrendale, PA, USA, 2004. [Google Scholar]
- Wang, B.; Wang, D.; Lei, J.; Deng, X.; Liu, Y.; Yang, H. Study on Low-Cycle Fatigue Life of Diesel Engine Piston Considering Oil Cooling Gallery Structure. Appl. Therm. Eng. 2025, 264, 125382. [Google Scholar] [CrossRef]
- Peng, W.; Jizu, L.; Minli, B.; Yuyan, W.; Chengzhi, H.; Liang, Z. Numerical Simulation on the Flow and Heat Transfer Process of Nanofluids inside a Piston Cooling Gallery. Numer. Heat Transf. Part Appl. 2014, 65, 378–400. [Google Scholar] [CrossRef]
- Razavykia, A.; Delprete, C.; Baldissera, P. Numerical Study of Power Loss and Lubrication of Connecting Rod Big-End. Lubricants 2019, 7, 47. [Google Scholar] [CrossRef]
- Zhao, B.; Zhou, K.; Xie, Y.-B. A New Numerical Method for Planar Multibody System with Mixed Lubricated Revolute Joint. Int. J. Mech. Sci. 2016, 113, 105–119. [Google Scholar] [CrossRef]
- Moon, S.M.; Cho, Y.J.; Kim, T.W. Evaluation of Lubrication Performance of Crank Pin Bearing in a Marine Diesel Engine. Friction 2018, 6, 464–471. [Google Scholar] [CrossRef]
- Bukovnik, S.; Dörr, N.; Čaika, V.; Bartz, W.J.; Loibnegger, B. Analysis of Diverse Simulation Models for Combustion Engine Journal Bearings and the Influence of Oil Condition. Tribol. Int. 2006, 39, 820–826. [Google Scholar] [CrossRef]
- Zhu, J.; Zhu, H.; Fan, S.; Xue, L.; Li, Y. A Study on the Influence of Oil Film Lubrication to the Strength of Engine Connecting Rod Components. Eng. Fail. Anal. 2016, 63, 94–105. [Google Scholar] [CrossRef]
- Profito, F.J.; Zachariadis, D.C.; Dini, D. Partitioned Fluid-Structure Interaction Techniques Applied to the Mixed-Elastohydrodynamic Solution of Dynamically Loaded Connecting-Rod Big-End Bearings. Tribol. Int. 2019, 140, 105767. [Google Scholar] [CrossRef]
- Ma, M.-T.; Loibnegger, B. Simulation of EHD Lubrication of Common-Pin Conrod Big End Bearings in High Speed IC Engines. In Proceedings of the World Tribology Congress III, Volume 2, Washington, DC, USA, 12–16 September 2005; ASMEDC: Washington, DC, USA, 2005; pp. 547–548. [Google Scholar]
- Ma, M.-T.; Loibnegger, B.; Herster, P. Advanced Elastohydrodynamic Analysis of Journal Bearings in IC Engines With a Multi-Body System Approach. In Proceedings of the ASME 2006 Internal Combustion Engine Division Spring Technical Conference (ICES2006), Aachen, Germany, 8–10 May 2006; ASMEDC: Aachen, Germany, 2006; pp. 709–717. [Google Scholar]
- Son, J.H.; Ahn, S.C.; Bae, J.G.; Ha, M.Y. Fretting Damage Prediction of Connecting Rod of Marine Diesel Engine. J. Mech. Sci. Technol. 2011, 25, 441–447. [Google Scholar] [CrossRef]
- Mäntylä, A.; Göös, J.; Leppänen, A.; Frondelius, T. Large Bore Engine Connecting Rod Fretting Analysis. Raken. Mek. 2017, 50, 239–243. [Google Scholar] [CrossRef]
- Chao, J. Fretting-Fatigue Induced Failure of a Connecting Rod. Eng. Fail. Anal. 2019, 96, 186–201. [Google Scholar] [CrossRef]
- Renso, F.; Barbieri, S.G.; Mangeruga, V.; Giacopini, M. Finite Element Analysis of the Influence of the Assembly Parameters on the Fretting Phenomena at the Bearing/Big End Interface in High-Performance Connecting Rods. Lubricants 2023, 11, 375. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. Application of Average Flow Model to Lubrication between Rough Sliding Surfaces. J. Lubr. Technol. 1979, 101, 220–229. [Google Scholar] [CrossRef]
- Wu, C.; Zheng, L. An Average Reynolds Equation for Partial Film Lubrication With a Contact Factor. J. Tribol. 1989, 111, 188–191. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Tripp, J.H. The Contact of Two Nominally Flat Rough Surfaces. Proc. Inst. Mech. Eng. 1970, 185, 625–633. [Google Scholar] [CrossRef]
- Gao, L.; Liu, S.; Cui, Y.; Zhang, M.; Xu, Z.; Meng, X. A New Coupled Multi-Physics Modeling Method for Flexible PRCL Conjunctions. Int. J. Mech. Sci. 2025, 287, 109956. [Google Scholar] [CrossRef]
- Archard, J.F. Contact and Rubbing of Flat Surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]




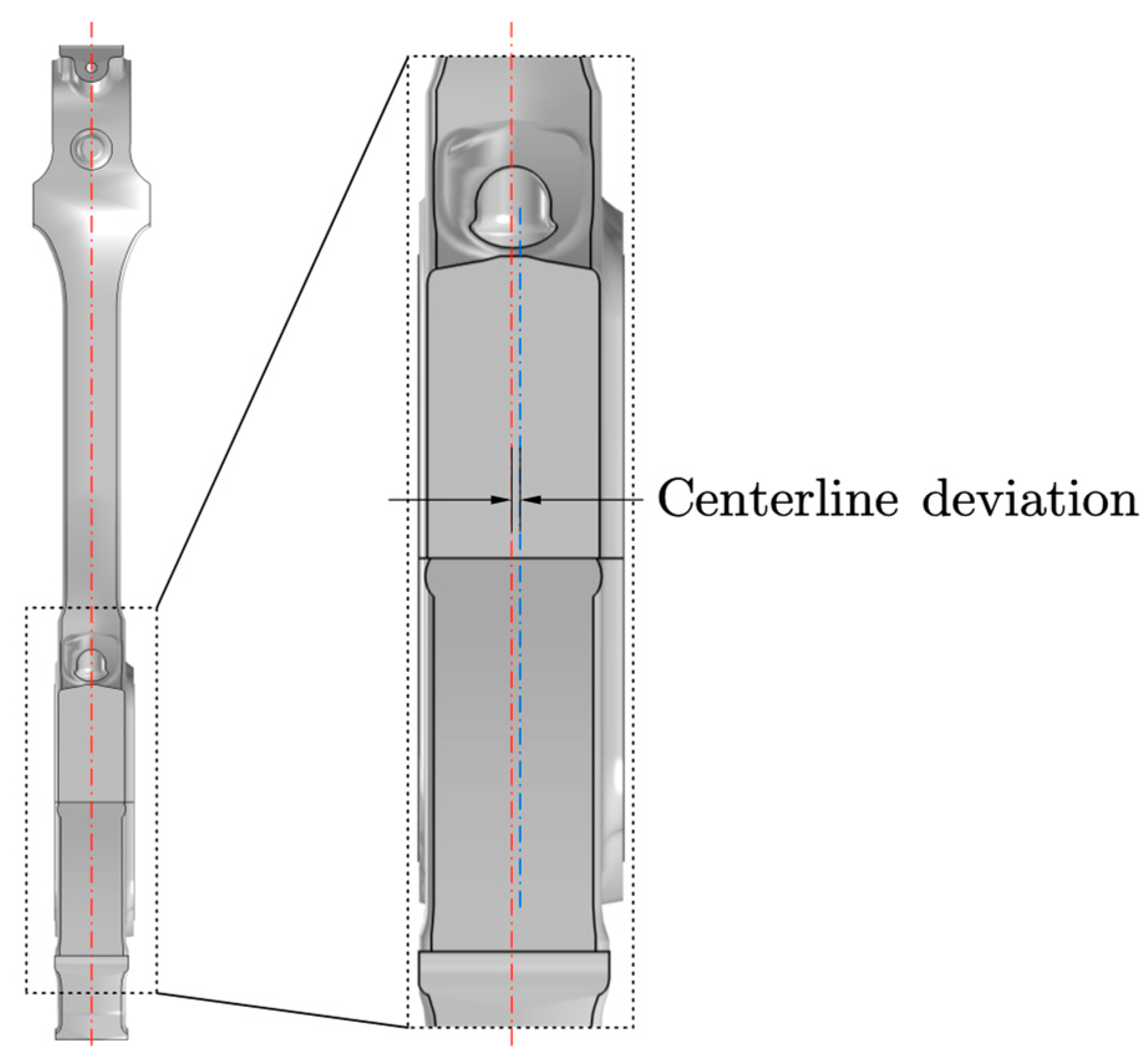
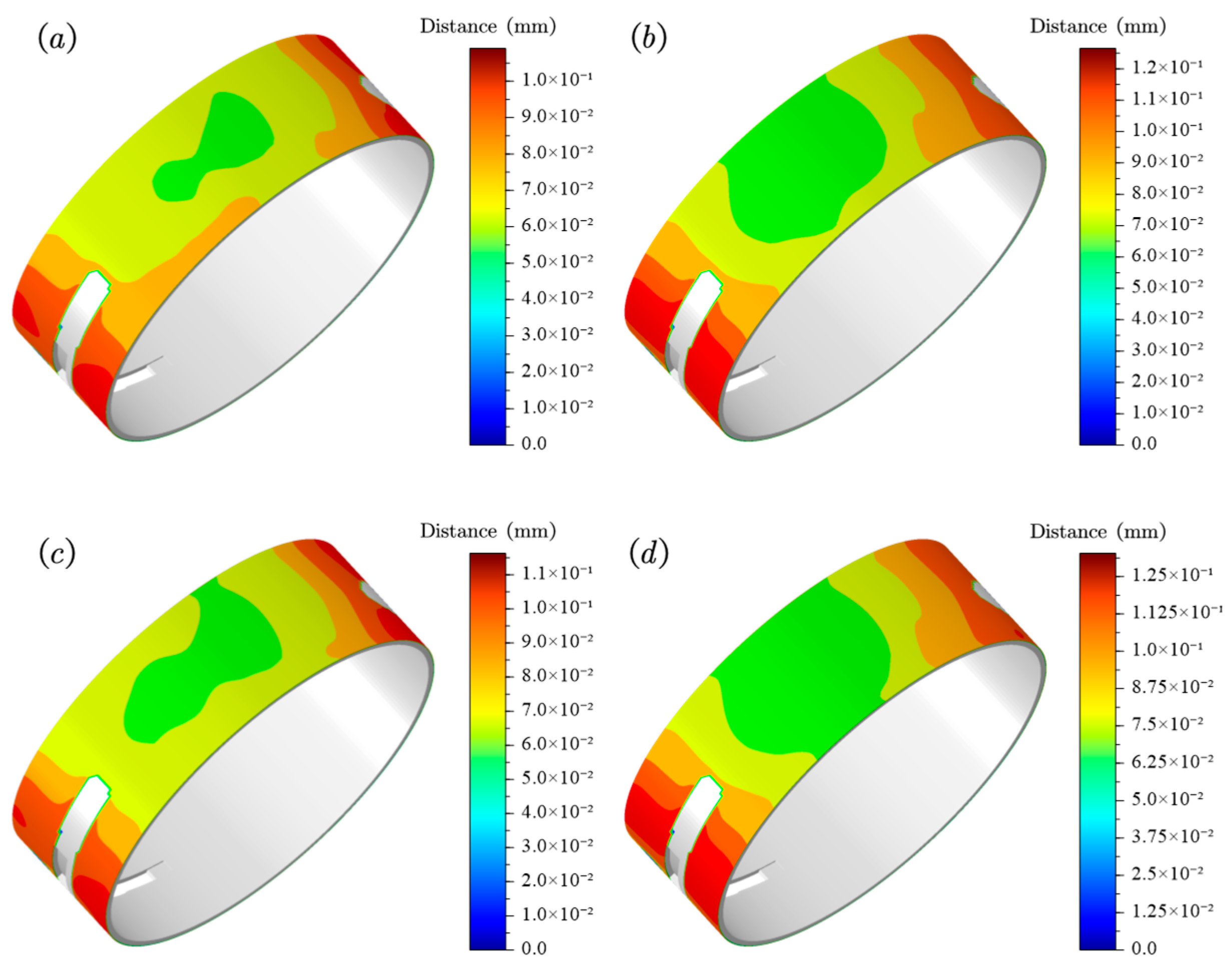
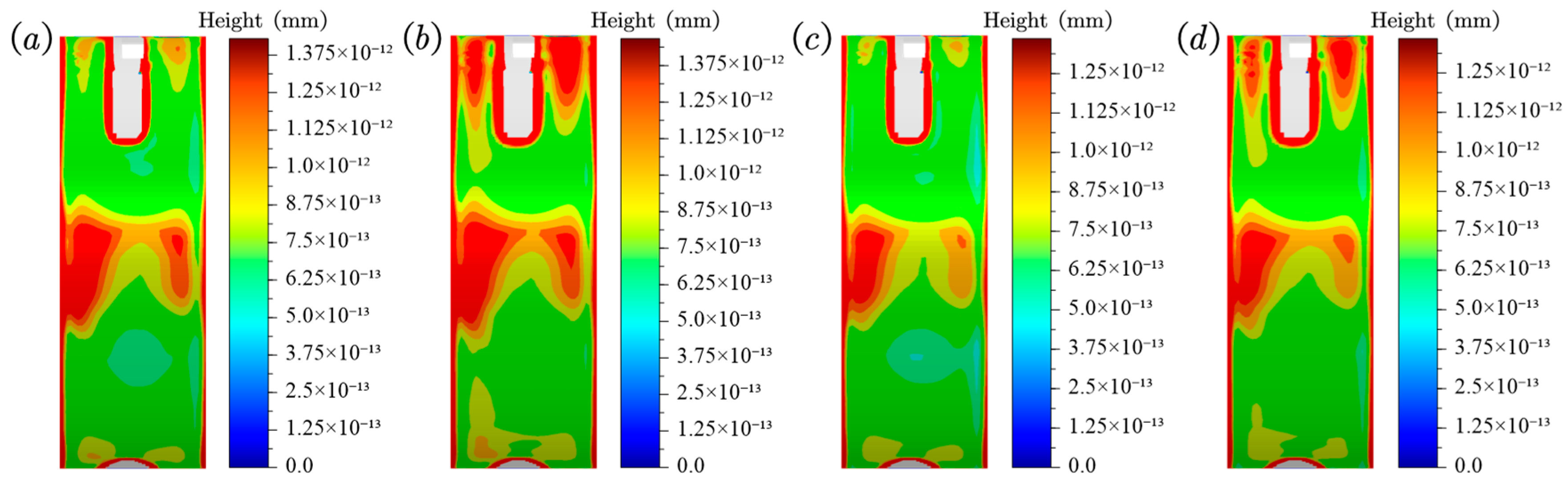


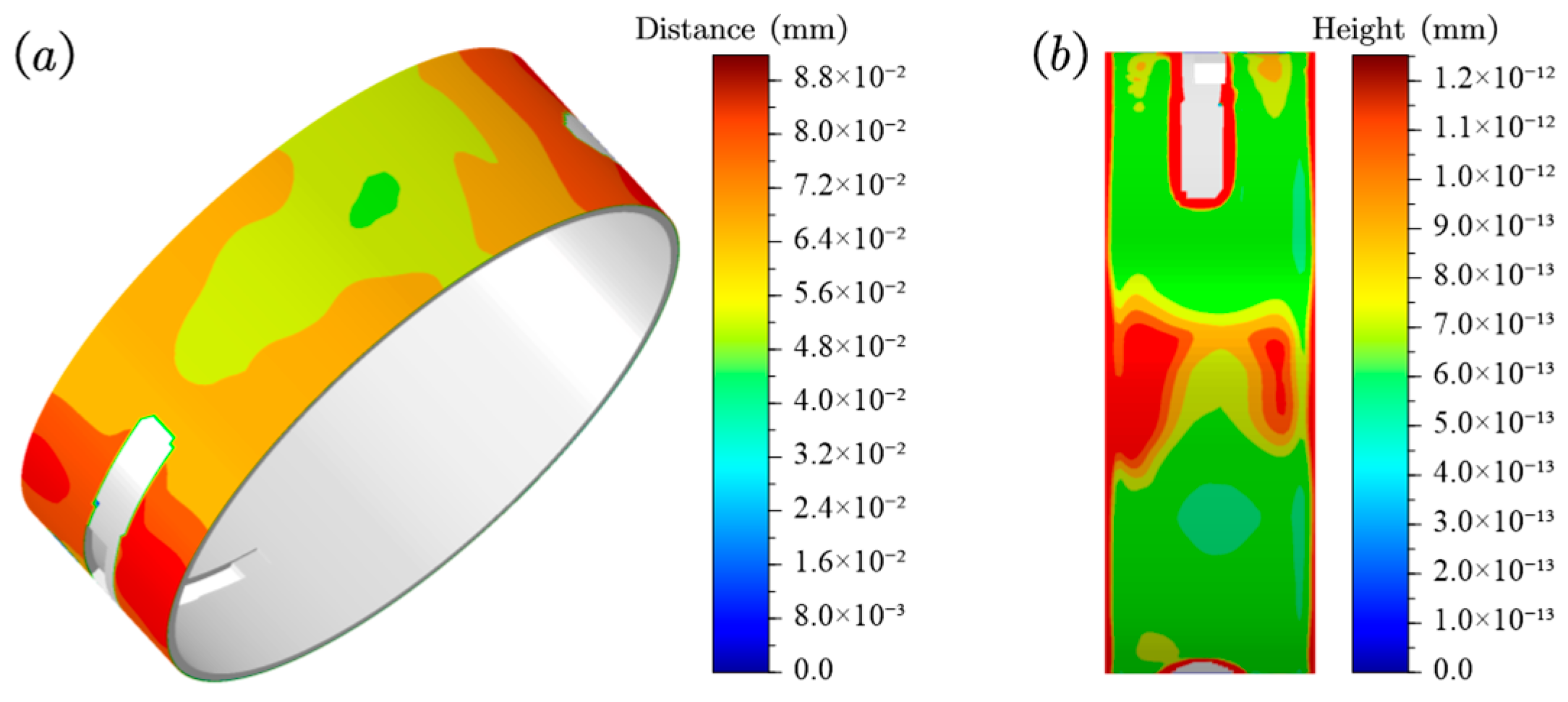
| Parameters | Descriptions | Unit | Values |
|---|---|---|---|
| δ | Bearing diametral interference amount | mm | 0.310 |
| 0.264 | |||
| Fp | Connecting rod bolt preload | kN | 510 |
| 461 | |||
| kg | Global wear coefficient | mm2/N | 4.637 × 10−12 |
| Bolt Preload (kN) | Interference Fit (mm) | Values (mm) |
|---|---|---|
| 550 | 0.31 | 0.109 |
| 550 | 0.264 | 0.1163 |
| 461 | 0.31 | 0.1265 |
| 461 | 0.264 | 0.1328 |
| Bolt Preload (kN) | Interference Fit (mm) | Values (mm) |
|---|---|---|
| 550 | 0.31 | 1.430 × 10−12 |
| 550 | 0.264 | 1.361 × 10−12 |
| 461 | 0.31 | 1.467 × 10−12 |
| 461 | 0.264 | 1.359 × 10−12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Che, Y.; Zhang, M.; Chen, Q.; Ren, H.; Li, N.; Liu, S.; Cui, Y. Tribo-Dynamics and Fretting Behavior of Connecting Rod Big-End Bearings in Internal Combustion Engines. Lubricants 2025, 13, 376. https://doi.org/10.3390/lubricants13090376
Che Y, Zhang M, Chen Q, Ren H, Li N, Liu S, Cui Y. Tribo-Dynamics and Fretting Behavior of Connecting Rod Big-End Bearings in Internal Combustion Engines. Lubricants. 2025; 13(9):376. https://doi.org/10.3390/lubricants13090376
Chicago/Turabian StyleChe, Yinhui, Meng Zhang, Qiang Chen, Hebin Ren, Nan Li, Shuo Liu, and Yi Cui. 2025. "Tribo-Dynamics and Fretting Behavior of Connecting Rod Big-End Bearings in Internal Combustion Engines" Lubricants 13, no. 9: 376. https://doi.org/10.3390/lubricants13090376
APA StyleChe, Y., Zhang, M., Chen, Q., Ren, H., Li, N., Liu, S., & Cui, Y. (2025). Tribo-Dynamics and Fretting Behavior of Connecting Rod Big-End Bearings in Internal Combustion Engines. Lubricants, 13(9), 376. https://doi.org/10.3390/lubricants13090376






