Abstract
Approaches to solving viscoelastic problems have received extensive attention in recent decades as viscoelastic materials have been widely applied in various fields. An overview of relevant modelling approaches is provided in the paper. The review starts with a brief introduction of some basic terminologies and theories that are commonly used to describe the contact behaviour of viscoelastic materials. By building up the complexity of contact problems, including dry contact, lubricated contact, thermoviscoelastic contact and non-linear viscoelastic contact, tentative analytical solutions are first introduced as essential milestones. Afterwards, a series of numerical models for the various types of contact problems with and without surface roughness are presented and discussed. Examples, in which computational tools were employed to assist the analysis of viscoelastic components in different fields, are given as case studies to demonstrate that a comprehensive numerical framework is currently being developed to address complex viscoelastic contact problems that are prevalent in real life.
1. Introduction
Viscoelastic materials such as polymers have been extensively applied in many fields owing to their combined advantages, including low friction and weight, slight rubbing noise, inexpensive cost, dimensional stability, biocompatibility and capacity to sustain load in the long run. As a result, viscoelastic contact problems are prevailing, for example, the optimization of mouthfeel for chocolate in the food industry [1], the contact between human skins and scalpels in the biomedical industry [2], the tire-road contact in the automotive engineering industry [3] and the movement of basaltic lavas under high temperature in the geothermal field [4]. When designing and analyzing the engineering or natural products related to viscoelastic materials, the corresponding interfacial mechanics system must be understood, particularly where the roles played by the viscoelastic deformation, viscoelastic lubrication condition, energy dissipation and frictional temperature need to be considered. Taking a knee replacement made of polymers as an example, its long-term service life is determined by the time-dependent response of the prosthesis under different loading and lubrication conditions affected by human activities [5]. More efficient product designs based on the enhanced understanding of relevant viscoelastic contact problems can have prominent impacts in terms of energy savings and quality of life improvement. Currently, the increasingly strict efficiency requirements and demands to minimize material use, as well as environmental impact, have been driving the development of analytical tools for viscoelastic materials.
Great efforts have been made in the mathematical analysis and numerical simulations of viscoelastic contact problems in the past decades [6,7]. Due to the structural complexity and strong time-varying constitutive laws governing the behaviour of viscoelastic materials, a closed-form mathematical solution to viscoelastic contact problems can hardly be developed within the framework of classical contact mechanics. Although a series of analytical solutions based on the proposed assumptions have been developed [7,8], they are subject to many limitations, including the simplified contact geometries, monotonic loading history and ideal rheological behaviour of viscoelastic materials (usually characterised by merely one relaxation time). Considering the existence of surface roughness and complicated interaction between contacting bodies in practical contact problems, it seems tougher to find the time-varying solution to viscoelastic contact problems solely on the basis of existing analytical theories. The numerical model presents itself as a suitable alternative tool in this dilemma. Various simulation tools have been advanced to assist the analysis of the products made from viscoelastic materials by predicting the time-dependent contact response in different contact systems [6]. Through applying different enrichment techniques, where the enrichment fields from the solutions to adhesive contact (e.g., [9,10]), thermal-elastic contact problems (e.g., [7]), etc. are superimposed to basic viscoelastic models, more generalized numerical tools are currently being built up to tackle the complicated viscoelastic problems that are commonly encountered in our daily life.
To date, the extraordinary interest in the modelling of viscoelastic contact problems has been witnessed by hundreds of papers published on the topic. This review paper is intended to provide a systematic overview of these modelling attempts in a way where the complexity of contacting problems is built up. It is structured as follows: some basic terminology and theories of viscoelasticity are described briefly in Section 2. The modelling approaches to dry contact modelling (under non-lubricated and isothermal conditions) of linear viscoelastic materials are introduced in Section 3, where the indentation, frictionless or frictional sliding and rolling, rough surface contact and adhesive contact problems are included. The review on the modelling of the lubricated contact of viscoelastic materials (viscoelastic-hydrodynamic lubrication (VEHL)) is given in Section 4, while Section 5 and Section 6 provide a brief review of the modelling of temperature effects and material nonlinearity in viscoelastic contact problems, respectively. Section 7 provides some examples of numerical studies, where various numerical tools were applied to analyse viscoelastic contact problems in different fields. In Section 8, the existing knowledge gaps in viscoelastic modelling are summarised, which remain to be addressed in the future for a more accurate understanding of tribological systems that involve viscoelastic materials.
2. Linear and Non-Linear Viscoelastic Materials
In this section, some basic terminology and relationships used to describe the contact behaviour of viscoelastic materials are introduced. It also presents a brief review of some fundamental physical laws, including the theory of linear viscoelasticity and the Boltzmann superposition principle. The contents of this section are mainly a summary of materials from several mechanics books, including [11,12,13,14,15,16,17,18].
2.1. Characteristics of Viscoelastic Materials
Materials deform under an applied load. The behaviour of an ideal elastic solid follows the law of Hooke, which indicates that there is a linear relationship between stress and strain. Ideal elastic solids deform instantaneously when a load is applied and recover completely when it is unloaded. In comparison, an ideal viscous Newtonian fluid has no definite shape and will deform irreversibly and gradually under the action of external forces, exhibiting a linear relationship between the stress and strain rates. The materials exhibiting the behaviour of both elastic and viscous properties, as shown in Figure 1a, are the so-called viscoelastic materials. Among them, those that exhibit a linear relationship between stress and strain at any instant are known as linear viscoelastic materials. As illustrated in Figure 1b, the strain of a linear viscoelastic material is proportional to the stress for any specific time point (e.g., strain under is three times that under ). In contrast, materials that exhibit time- and stress-dependent characteristics and thus hardly follow the linear relation are named non-linear viscoelastic materials. It is of note that the linear response of a viscoelastic material is not its inherent property because the limit of linearity is determined by the experienced strain. For example, concrete and steel under small deformation can be assumed to exhibit linear viscoelastic behaviour, where infinitesimal strain theory can be applied. However, when it comes to elastomers and some biological soft tissues that experience large deformations, finite strain theory needs to be employed to characterise their non-linear contact response. Generally, the performance of viscoelastic materials is influenced by four parameters: load, strain, temperature and time. During the investigation of viscoelastic materials, two of the parameters are usually set to be constant to investigate the relation between the other two parameters. Three characteristic phenomena are widely found for viscoelastic materials: creep, stress relaxation and hysteresis.
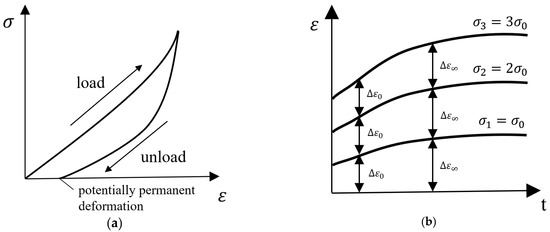
Figure 1.
(a) Stress-strain curve of viscoelastic materials and (b) Strain-time curve of linear viscoelastic materials with varying stress.
To explain them briefly, creep is the phenomenon where the strain continues increasing with time, as shown in Figure 2. Under a constant load, the instantaneous elastic strain first appears. It is followed by an ever-increasing strain over time, known as creep strain. The creep strain normally would increase with an ever-decreasing strain rate, which eventually leads to a constant-strain steady state. When the surface is unloaded, the elastic recovery is experienced immediately, which is followed by anelastic recovery. A permanent strain might be experienced arising from viscosity. The creep performance of viscoelastic materials reveals their dimensional stability and their capacity to sustain the load in the long run.
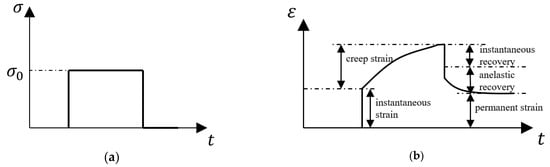
Figure 2.
Input and output in a creep test for viscoelastic materials: (a) load input and (b) response of strain with time.
As to stress relaxation, it is the phenomenon where the internal stress of viscoelastic materials continues decreasing with time under a constant temperature and strain, as shown in Figure 3. Physically, stress relaxation results from the re-arrangement of the viscoelastic material on the molecular or micro-scale.
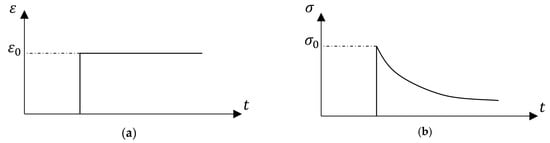
Figure 3.
Input and output in a stress relaxation test for viscoelastic materials: (a) strain input and (b) response of stress with time.
Hysteresis is the lag of the strain () change to the stress () change under a certain temperature and cyclic stress. A typical hysteresis phenomenon is illustrated in Figure 4. To explain it briefly, under the sinusoidal stress (solid line) expressed as:
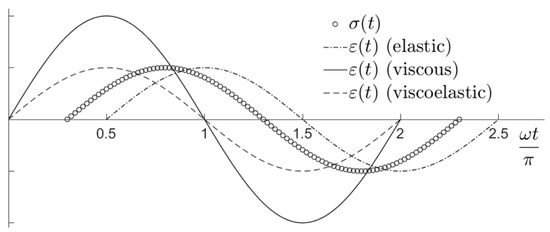
Figure 4.
The strain response to sinusoidal stress (solid line) of different materials: elastic (dash line), viscous (dash-dot line) and viscoelastic (scatter).
The response of an ideal elastic material as shown in Figure 4 (dash line) should be a corresponding sinusoidal strain expressed as:
which implies that the work done by the external force in the period of loading is stored in the form of elastic energy and then released completely to return the material to its initial state. In other words, there is no energy loss during this process.
The response of an ideal viscous material (dash-dot line in Figure 4) is represented as follows:
The phase difference of radians indicates that the energy derived from the external force is completely transformed into heat.
As viscoelasticity incorporates aspects of both solid behaviour (elastic) and fluid behaviour (viscous), the response of a viscoelastic material (scatter in Figure 4) is indicated by the following equation:
where is the phase difference between the stress and strain, ranging from to radians. This demonstrates that part of the energy is lost in every cycle of deformation (stress). As shown in Figure 1, the region under the unloading curve is smaller than that under the loading curve in the hysteresis loop. The loss of energy caused by the hysteresis can be determined by the difference between the two regions (the area enclosed by the two curves).
2.2. Constitutive Law and Relevant Rheological Models
The theory of small-strain linear viscoelasticity plays an essential role in the modelling of viscoelastic materials. Although this material model framework was derived based on linear elasticity with linear viscoelasticity, it can always function as a useful starting point, even in instances that require more elaborate treatment (e.g., non-linear viscoelastic contact problems). Following the theory of linear viscoelasticity, for materials exhibiting the linear relation, the response of stress to successive strain is cumulative and vice versa. Two time-varying material properties, namely creep compliance () and relaxation modulus (), are always used to characterise the constitutive law of linear viscoelastic materials. As the name implies, creep compliance reveals the creep phenomenon of viscoelastic materials. Physically, the property describes the response of viscoelastic strain to a unit stress change. In contrast, the relaxation modulus reveals the stress relaxation phenomenon. Physically, it describes the viscoelastic stress response to a unit change in strain. These two properties play an essential role when analysing the transient contact response of viscoelastic materials.
To mathematically describe the contact behaviour of linear viscoelastic materials, the Boltzmann superposition principle is commonly applied, where the response to successful excitations can be the sum of the response generated by applying each excitation individually. To determine stress at time under the action of a certain strain that is applied at the time before , it can be expressed based on the definition of the relaxation modulus:
where is the Heaviside step function.
Identically, stress at the same time under the action of a strain that is applied at another time in advance of can be determined as followed:
Following the analogous way, the response of the strain to a sequence of strain increments, which are arbitrary but can be considered as a continuous distribution, can be determined:
The response of strain to stress can be obtained by a similar derivation by switching the input and output:
Different from the case where the compliance and elastic modulus are reciprocal of each other in ideal elastic contact, the relationship between the creep compliance and relaxation modulus of linear viscoelastic materials in the time domain is expressed in the following form:
There exists the following essential mathematical relationship between these two material properties in the Laplace transform domain:
where hat ‘-’ denotes Laplace functional transformation and is a complex number frequency parameter in the Laplace transform domain .
To characterize the time-dependent material property of linear viscoelastic materials, rheological models, which are established with linear springs (representing perfectly elastic solid as the stress is proportional to the strain) and dashpots (representing ideal Newtonian fluid as the stress is proportional to the rate of strain), are built. If the spring and dashpot are arranged in series, as presented in Figure 5a, such a rheological model is called the Maxwell model. A Kelvin–Voigt model is established when the two elements are arranged in parallel, as illustrated in Figure 5b. According to theoretical analysis [13], a Maxwell model can appropriately demonstrate the stress relaxation phenomenon of linear viscoelastic materials. However, it fails to account for their creep and recovery characteristics. In contrast, the Kelvin–Voigt model behaves in the opposite way. Moreover, it does not exhibit any instantaneous elastic response. A detailed description of these two models can be found in the work of Popov [13]. Since these two-element models can only provide qualitative descriptions, through coupling several numbers of Maxwell or Kelvin–Voigt units, more sophisticated models, such as the Maxwell–Wiechert model, as shown in Figure 5c, are commonly employed to characterize real-life viscoelastic materials with more than one relaxation time. The number of elements required in a generalized Wiechert model depends on the naturally occurring spectrum of relaxation times of materials. The relaxation time is usually denoted by and determined by parameters of the rheological models in the following way:
where denotes the viscosity of the -th dashpot and denotes the modulus of the -th spring.
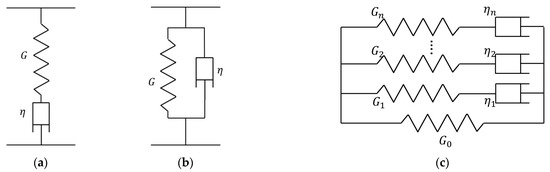
Figure 5.
Rheological models describing the behaviour of linear viscoelastic materials: (a) Maxwell model, (b) Kelvin-Voigt model and (c) Maxwell–Wiechert model.
By using the Maxwell–Wiechert model, the relaxation modulus of any linear viscoelastic material can be characterised by fitting the experimental data from standard relaxation tests to the following equation (Prony series):
Notably, the spectrum of relaxation times of linear viscoelastic materials could be characterized by introducing as many exponential terms as required to obtain the desired accuracy of curve fitting. Once the relaxation modulus function is available, the corresponding creep compliance function can be easily determined by applying its mathematical relationship in the Laplace domain (Equation (10)). A typical example can be found in the work of Chen et al. [8]. By fitting a two-term Prony series to the relaxation curve from the standard relaxation test by Kumar and Narasimhan [19], the relaxation modulus and creep compliance functions of a thermoplastic polymer known as polymethyl methacrylate (PMMA) were determined. When a Maxwell–Wiechert model only contains one relaxation time, such a three-element model is known as the Zener model or standard linear solid (SLS) model. SLS models are frequently employed in numerical studies about viscoelastic contact problems owing to their capacity to capture the creep, as well as stress relaxation, phenomena.
The way to correctly reproduce the viscoelastic response of a half-space with the available rheological models can be found in the work of Bugnicourt et al. [20,21]. They argued that the Maxwell–Wiechert model (known as the generalized Zener model in their study) should be used for rubber to capture its contact behaviour over a range of frequencies. It is also of note that the choice of models should be expressed by a function of the wavelength at small scales.
With the rheological models presented above, the complex modulus of viscoelastic materials can be determined by applying the Fourier transform to the discrete form of the creep function with respect to the time variable :
where hat ‘~’ denotes Fourier functional transformation and is the time-related frequency. The viscoelastic complex modulus is commonly employed when it comes to the steady-state contact analysis of viscoelastic materials.
The nonlinear viscoelastic response is usually encountered when a viscoelastic surface experiences large deformation or the material exhibits specific creep and relaxation functions, which are not only dependent on time, but also on the experienced stress or strain. Compared with literature regarding linear viscoelastic response, relatively limited work sheds light on the characterization of non-linear viscoelastic behaviours, as the Boltzmann superposition principle is unable to describe the creep and relaxation phenomena. Without the aim of providing an exhausting literature review on this topic here, credit for the development of a generalized constitutive equation for nonlinear viscoelastic materials can be given to the contributors Green [22], Rivlin [23], Spencer [24], Pipkin and Rogers [25], who adopted multiple integral representations by using multivariable relaxation functions as kernels, and Leaderman [26], Brueeller [27,28] and Schapery [29], who used single integral representation based on the nonlinearization of stress and strain measurements.
3. Dry Contact Modelling of Viscoelastic Materials
The review of the methods to simulate viscoelastic contact problems starts with dry contact problems, where lubricants are not involved, temperature effects are neglected and the material behaviour is assumed to be linear viscoelastic. The indentation problem, which tends to be the simplest among contact problems, is discussed first. Afterwards, the numerical solutions to tangential contact problems, including the quasi-static partial slip contact (e.g., Figure 6a) and dynamic sliding and rolling contact problems (e.g., Figure 6b), are presented. Apart from the simplified single-asperity contact problems, models that simulate multi-asperity problems, which closely resemble real-life contact problems, are discussed. Effects of surface roughness on the viscoelastic contact solutions are highlighted in special. The models investigating the effects of surface adhesion on viscoelastic contact are also presented in this section.
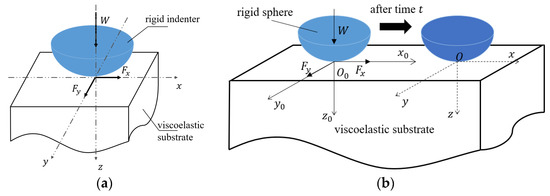
Figure 6.
Typical geometries of dry viscoelastic contact problems: (a) quasi-static contact and (b) dynamic sliding contact.
3.1. Indentation
By applying the Laplace transform to reduce viscoelastic problems to elastic ones, the problem of the time-dependent constitutive laws of viscoelastic materials was found avoidable mathematically by Lee [30]. The application of this convenient approach was later extended by Radok [31] to establish the independence of the Laplace method from the elastic problem. Based on the assumption that the contact area increases monotonically with time without surface adhesion (pressure ), solutions to spherical indentation problems of linear viscoelastic materials were developed by Lee and Radok [32]. An essential concept, known as the ‘elastic-viscoelastic correspondence principle’ later, which was proposed by Alfrey [33] and generalized by Tsien [34], was first implemented in the analysis of Lee and Radok [30,31,32]. Instead of deducing solutions from scratch, small-strain, linearly viscoelastic contact problems can be solved by manipulating the well-established theory of elastic contact via the elastic-viscoelastic correspondence principle (e.g., replacing the elastic compliance with the viscoelastic creep compliance in the Hertzian solution). Owing to this advantage, the principle has now become the foundation for many analytical and numerical models of viscoelastic contact problems recently developed. A detailed description of the principle can be found in the mechanics book by Christensen [18]. Limitations of the tentative analytical approach by Lee and Radok [32], including the ideal contact geometry and the monotony of contact radius, were later partially released by different researchers. Among them, Hunter [35] and Graham [36] obtained solutions to a similar problem in the case of a monotonically increasing contact radius, or when the radius attains a single maximum value. Yang [37] improved the viscoelastic contact solution by taking arbitrary quadratic contact geometry into account. The limitation regarding the monotony of contact radius was overcome by Ting [38,39], who proposed a viscoelastic solution with further increased generality by describing contact radii with arbitrary functions of time and multiple connected contact regions.
The contact between a viscoelastic material and a pyramidal or spherical indenter under a triangle or trapezoidal loading history was investigated by Oyen [40], both experimentally and mathematically. Based on the solution of Ting [38], a theoretical model solving the contact problem between an axisymmetric indenter and a viscoelastic half-space was proposed by Greenwood [41]. For the contact problem where the whole indenter surface is in contact with the viscoelastic half-space, a theoretical solution was proposed by Fu [42], who related the indentation load to the penetration depth. By applying the correspondence principle, Yakovenko and Goryacheva [43] developed the analytical solution to periodic contact problems of multiple identical spherical indenters against a viscoelastic half-space, where the mutual influence of indenters was investigated. Recently, based on the solution of Lee and Radok [32], the cyclic repetitive indentation problem of a rigid sphere against a viscoelastic half-space and the involved viscoelastic dissipation were investigated by Papangelo and Ciavarella [44]. Apart from these half-space contacts, Argatov and Mishuris developed analytical solutions to elliptical [45], rebound spherical [46] and cylindrical [47] indentation contact problems between thin compressible and incompressible layers of arbitrary viscoelastic materials. However, these solutions are only applicable to the indentation problem with an arbitrary monotonic loading. Using the Hankel transform, a more general solution to indentation problems for a viscoelastic layer on an elastic half-space was developed by Chen et al. [48].
As mentioned before, the application of these partially or fully analytical solutions is still limited, considering the existence of the surface roughness, arbitrary loading history and complicated rheological behaviour of viscoelastic materials (usually more than one relaxation time) in practical contact problems. The mathematical complexity of these solutions, which are frequently encountered during applications, also discourages their practical usage. Based on the matrix inversion method (MIM), the indentation problem of a rigid body with an arbitrary shape against a viscoelastic half-space was solved by Kalker [49], who later adopted an alternative scheme named the two-scale iterative method (TIM) to improve the computational efficiency of the Boundary Element Method (BEM)-based model [50]. By making use of the elastic-viscoelastic correspondence principle, the displacement response of viscoelastic solids under any arbitrary distribution of surface tractions was derived by Chen et al. [8], based on the Boussinesq integral for elastic surfaces [51]. A robust model for solving the point contact problem between a rigid indenter and a homogeneous viscoelastic half-space was then developed by Chen using the Fast Fourier Transform (FFT)-based BEM model (also known as the semi-analytical method (SAM) in some literature), where the technique named the discrete convolution fast Fourier transform (DC-FFT) [52] was implemented. Although it was initially developed to simulate the non-conformal and normal contact of polymer-based materials characterised by a wide spectrum of relaxation times and complicated surface topographies, the model was later extended to investigate more complicated contact problems by different researchers. Among them, Koumi et al. [53] investigated the effects of inhomogeneities in viscoelastic indentation problems, where isotropic or anisotropic elastic inhomogeneity of any orientation is embedded into a viscoelastic half-space. They reported that the effects of the inhomogeneity, such as the decline of the normal and shear stresses at the interface between the elastic inhomogeneity and viscoelastic matrix, become more significant with time. A similar model for the indentation problem of viscoelastic composite materials was developed by Liu et al. [54], who focused on the effects of the location of the inhomogeneity, in relation to the indenter and its volume fraction, on the modulus of the composite material. Based on the model of Chen [8], the line contact configuration in viscoelastic indentation problems was simulated by Spinu [55].
Recently, the indentation problem for a viscoelastic half-space was revisited by Zhao et al. [56], who used the derivative of the creep compliance function instead of the pressure to determine the surface deformation in the formulation of surface deformation caused by contact tractions. They claimed that the new equation allows more efficient computation, while providing valid solutions simultaneously. A more complicated indentation problem, where anisotropic viscoelastic solids are involved, was simulated by Nguyen and Hwu [57,58] using BEM-based models based on the correspondence principle and time-stepping method. In addition to the BEM, by making use of the discrete element method (DEM), a normal contact model for viscoelastic particles was developed by Olsson and Jelagin [59]. However, their model can only provide approximate solutions when the contacting viscoelastic surfaces are unloaded, as it is based on the analytical solution of Lee and Radok [8,35].
It is of note that two different shapes of pressure distribution, including the Hertzian-type contact pressure (e.g., Figure 7a [60]) and pressure with spikes on the contacting edges (e.g., Figure 7b [60]), were reported extensively for the spherical indention problem of viscoelastic bodies [8,32,56]. To explain such a phenomenon, a numerical study was recently conducted by Wang et al. [60] using a SAM-based model. The effect of the material parameter (e.g., the ratio of retardation time to relaxation time) in an SLS model on the shape of pressure distribution was reported in their work. Another argument was proposed by Koumi et al. [61], who argued that the shape of contact pressure is determined by the contact configuration. According to them, a Hertzian-type pressure distribution will be obtained for a viscoelastic sphere indenting a rigid plane. The pressure spikes will only be obtained for a rigid sphere indenting a viscoelastic half-space.
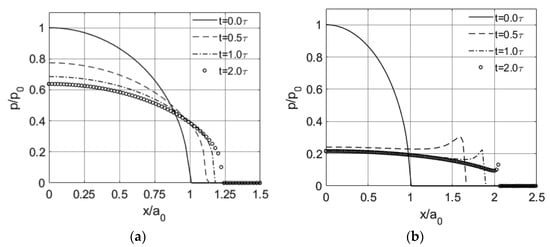
Figure 7.
Different shapes of pressure profiles for spherical indentation problems of viscoelastic bodies (modified from the work of Wang et al. [60]): (a) Hertzian-type pressure and (b) pressure profile with spikes on the contacting edges. and here represent the Hertz solution of contact radius and peak pressure, respectively, using the instantaneous modulus of the viscoelastic material.
3.2. Frictionless or Frictional Sliding/Rolling Contact
Relative motion between contacting surfaces, including sliding and rolling, is commonly encountered in practice, such as the type-road contact. Concerning the analysis of relative motion between viscoelastic surfaces, Hunter [62] first studied the two-dimensional (2D) frictionless rolling of a rigid cylinder over a viscoelastic half-space. At a low or medium speed, the pressure distribution in viscoelastic rolling contact was found to be significantly different from that in elastic contact, where an asymmetric pressure profile can be observed exhibiting a spike at the leading edge in the moving direction. This, consequently, leads to asymmetric surface formation. By extending the solution to a similar problem [63], the line contact problem between two viscoelastic cylinders with different radii and mechanical responses was analyzed by Morland [64]. The steady-state analysis of Hunter [62] was later extended by Panek and Kaller [65] to three-dimensional (3D) problems by adopting an approximation on the basis of elastic line integral theory. Apart from these plane strain problems, Aleksandrov et al. [66] simulated the frictionless contact between a smooth sphere sliding on a viscoelastic half-space. The application of these approaches is limited to ideal viscoelastic materials characterized by one relaxation time. Based on the assumption that the viscoelastic material stiffens when the rolling speed increases (e.g., higher frequency), while the pressure distribution remains of a Hertzian type, a novel analytical theory was proposed by Persson [67] to solve the rolling contact of a rigid cylinder or a sphere over a flat viscoelastic substrate. The rolling friction coefficient can be estimated reasonably by the theory of Persson [67]. However, the information on pressure distribution, especially its non-Hertzian profile in a force-driven problem, is not available within the framework of this theory.
The Finite Element Method (FEM) was frequently employed in early attempts [68,69,70,71,72,73] to simulate viscoelastic rolling and sliding contact problems based on Lagrangian formulations. However, the computational complexity, which is related to the extremely fine mesh of both the interface and bulk requested to capture the extremely irregular contact geometries of rough bodies in real life, impedes the further application of FEM-based models. Regarding the models developed based on the alternative method (e.g., BEM), Carbone and Putignano [74] developed a model to generate steady-state solutions to sliding or rolling contact problems, where the involved viscoelastic material can either exist in the form of a half-space [75] or a layer [76,77,78] by adjusting the thickness of the contacting body in their novel equation. The viscoelasticity was found to induce shrinkage of the contact area when the sliding speed increases [74]. The effects of the surface layer in sliding contact of viscoelastic materials were investigated by Torskaya and Stepanov [79], where the material combinations, including a viscoelastic layer bonded with a rigid half-space and a viscoelastic half-space covered by a rigid layer, were simulated. For the combination of a viscoelastic layer on a rigid substrate, it was found that the hysteretic losses increase with the layer, while the opposite effect was obtained for the combination of a rigid layer on a viscoelastic substrate. They also investigated the internal stress states for the sliding contact problem between a viscoelastic half-space and a smooth indenter [80].
Based on a novel formulation of the surface deformation, the frictionless sliding and rolling contact was efficiently simulated by Zhao et al. [56]. Regarding the transient viscoelastic analysis, the frictionless rolling contact of a rigid smooth indenter against a flat viscoelastic half-space was simulated by Koumi et al. [61], where the material inhomogeneity was considered. Based on Green’s function molecular dynamics (GFMD), Dokum and Nicola [81] developed a model to provide transient, as well as steady-state, solutions to frictionless indentation and rolling contact problems of a rigid cylinder against a viscoelastic half-plane. Recently, Wallace et al. [82] proposed a model that provides transient analysis of frictionless rolling and sliding viscoelastic problems, in which the involved viscoelastic layer and substrate can exhibit distinct properties. Meanwhile, the effects of imperfect bonding between layer and substrate on the transient, as well as steady-state, frictionless viscoelastic sliding contact problems were recently investigated by Zhang et al. [83]. They reported that the subsurface stresses become lower when the contact is subjected to an imperfect bonding interface.
It is of note that there exist different friction laws in the theory of contact mechanics. The word ‘frictionless’ in the above contact analysis means that no explicit friction at the interface between the solids (e.g., Coulomb friction) was taken into account. Therefore, tangential contact problems (e.g., tangential shear stresses due to Coulomb friction) were not investigated because the surface can be in the sliding state without any input in the tangential direction. However, the friction derived from the viscoelastic loss, which is quantified as the product of the apparent friction coefficient and normal load in the literature, was always considered. In the presence of dry contact friction, surfaces might experience the partial slip state before the frictional sliding motion when the input lateral loads shown in Figure 6b are not sufficient to induce gross sliding (e.g., shear tractions are lower than the local static friction). To briefly explain the two concepts, gross sliding is a dynamic process, in which the contacting bodies continuously move relative to each other over time. In contrast, the partial slip contact is a quasi-static process, where there is no actual global relative sliding between surfaces. In this case, the contacting area is separated into the stick region, in which no relative motion occurs, and the slip region, in which local relative movement does happen. The typical evolution of the stick and slip regions with increasing tangential load in a spherical viscoelastic partial slip problem is illustrated in Figure 8 [60], where a creep phenomenon is experienced in the normal direction. Based on SAM, the conformal partial slip contact between a rigid pin and a viscoelastic plate was simulated by Dayalan and Sundaram [84], where fretting contact analysis was provided. A FEM-based model was developed by Bonari and Paggi [85] to investigate the periodic partial slip contact between a sinusoidal indenter and a viscoelastic layer with finite thickness. Similarly, a study of the effects of viscoelasticity on the partial slip solutions of a spherical contact problem, where the coupling effects between pressure and shear tractions arising from the material discrepancy were taken into account, was recently conducted by Wang et al. [60] using a BEM-based model. An abrupt transition from partial slip to gross sliding, caused by the unstable and time-varying property of viscoelastic materials under fully-coupled conditions, was found in their study. By using the time-stepping method, the stick-slip solutions to the contact of anisotropic viscoelastic solids were proposed by Nguyen and Hwu [86]. Regarding the dry contact friction in sliding or rolling contact, it was analyzed by Goriacheva [87] in a cylindrical rolling problem. However, the pressure solution was not affected by the dry contact friction (shear traction), as the two contacting viscoelastic bodies were assumed to exhibit the same mechanical properties (thus no mutual effects between contact tractions) in the study. Later, the Goodman approximation [88], which neglects the effect of shear tractions on normal pressure, but considers that of pressure on shear tractions, was adopted by Goryacheva and Sadeghi [89] to analyse the role of Coulomb friction in the cylindrical rolling or sliding problem of an elastic substrate covered by a viscoelastic layer. Excluding the partial slip period, the frictional sliding of a sphere against a viscoelastic half-space was simulated by Goryacheva et al. [90], where the effects of dry friction on sliding solutions were investigated [91]. Their results showed that the existence of shear stress (Coulomb friction) could increase the peak pressure and shift the contacting region in the direction of the sliding motion. In addition to the half-space contact, Goryacheva and Miftakhova [92] analysed the effect of viscoelastic layers in the frictional rolling contact. The range of the relative slippage, which occurs in frictional rolling contact, was found to be significantly affected by the viscoelastic layer.
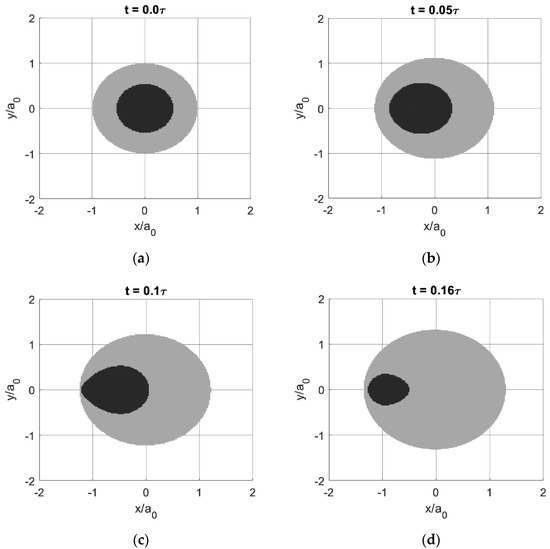
Figure 8.
Evolution of the stick (dark) and slip (grey) regions with increasing tangential input for a viscoelastic material (reproduced from the work of Wang et al. [60]): (a) , (b) , (c) and (d) .
Beyond the unidirectional sliding or rolling contact, there are several numerical attempts to simulate reciprocating contacts. A BEM-based model was recently developed by Putignano and Carbone and Dini [93,94,95] to investigate the oscillating contact between a sinusoidal indenter and a viscoelastic half-space. In the meantime, a novel boundary element methodology was developed by Santeramo et al. [96] to simulate conformal contact problems of viscoelastic materials. Although the study only investigated the frictionless and steady-state contact of 2D circular surfaces, it filled in the gap about viscoelastic circular contact solutions for conformal geometries based on BEM.
3.3. Viscoelastic Rough Contact
The above modelling work focuses mainly on single-asperity contact problems. However, it is known that surfaces encountered in real life are usually irregular, showing complicated topography, and many of interest often exhibit a self-affine fractal feature [97,98]. The power-law relation that holds in a limited wavevector region () (illustrated in Figure 9) for the power spectral density of a typical fractal rough surface can be expressed with the following equation [97,98,99]:
where is the Hurst exponent linked to the fractal dimension and , and are known as the smallest possible wavevector, short-distance roll-off wavevector and long-distance cut-off wavevector, respectively. The fractal dimension can be determined by the slope of the plot for the part where , as shown in Figure 9. The smallest possible wavevector, , can be determined from the lateral size of the rough surface (, and it can be related to the long-distance cut-off wavevector with the number of scales ().
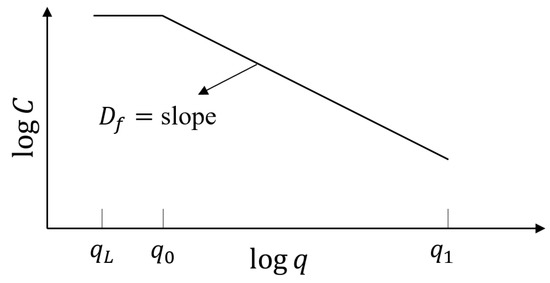
Figure 9.
The PSD of a typical fractal rough surface that is self-affine for .
The requirement to resolve interactions between surface asperities exacerbates the complexity of viscoelastic contact problems. The solution of the real contact area for a viscoelastic solid squeezed into a fractal rough surface was proposed by Persson et al. [100] using a contact-mechanics-based theory [101]. Based on his theory of contact mechanics and rubber friction [101], the sliding contact of viscoelastic surfaces with anisotropic surface roughness was analyzed by Carbone et al. [102] and Afferrante et al. [103]. The contribution of the fractal roughness to the rubber friction was analyzed by Scaraggi and Persson [101,104]. Their theories were later applied by Scaraggi and Comingio [105], who developed a model underpinned by a Fourier-based residual molecular dynamics formulation to investigate the rough contact of viscoelastic-graded materials. The role of small-scale wavelengths, which is related to the largest roughness frequency , on rubber friction was highlighted in their study. The sliding contact between a rigid sinusoid against a viscoelastic half-space was solved by Menga et al. [75] analytically, where the role of viscoelastic interaction between asperities in periodic contact (e.g., viscoelastic stiffening and periodicity of contact) was investigated. The analytical solution to indentation problems of nominally flat viscoelastic surfaces was proposed by Papangelo and Ciavarella [106] by extending the contact theories of Persson [101] using the elastic-viscoelastic correspondence principle. The solution was then employed to analyze the viscoelastic bulk dissipation under a full cycle of harmonic loading and unloading. According to their numerical study [106], the maximum energy dissipation can be achieved when the loading period is close to the relaxation time of the viscoelastic materials, and it can be increased by increasing the mean normal pressure and the ratio of retardation time to the relaxation time of the material.
By using an adaptive nonuniform mesh to address the huge computational complexity [107], Carbone and Putignano conducted a numerical study to simulate the sliding contact of rough viscoelastic materials in different forms (half-space [108] and layer [76,78]) based on their BEM-based model [74]. The roughness power spectrum cut-off, which indicates the number of scales of rough surfaces , was found by Putignano [109] to have significant effects on the viscoelastic friction, such that the friction tends to increase with the number of scales. The anisotropy in terms of contact areas and displacement distribution was confirmed to be caused by the viscoelasticity in rough contact, according to their later numerical investigation [110]. In the presence of Coulomb friction, the sliding contact of viscoelastic thin layers on a rigid substrate was simulated by Menga et al. [111], where the coupling effects between the normal and tangential tractions on the enhanced viscoelastic friction and energy dissipation were highlighted. The transient frictionless contact of an incompressible viscoelastic semi-infinite body rolling on a rough rigid surface was analyzed by Bugnicourt et al. [21] numerically. The apparent friction coefficient derived from dissipative losses inside the viscoelastic bulk in tyre-road contact was evaluated in their study. A numerical study was conducted by Liu et al. [54] to study the effect of microstructure and surface roughness on the indentation creep of viscoelastic composite materials using a SAM-based model. It was found that although the modulus of the composite materials increases with the surface roughness, the indentation creep is barely influenced by the surface roughness. Recently, a new BEM-based model was developed by Putignano and Carbone [112] to simulate the one-dimensional indentation problem between a rigid rough surface and a viscoelastic half-plane. The effects of surface roughness parameters, including the root mean square roughness, root mean square slope and Hurst exponent, on the viscoelastic dissipation were revealed in the indentation problem. The root mean square roughness was found to play a leading role, which suggests that it is sufficient to estimate the viscoelastic dissipation by a simple measure of this roughness parameter. By using a BEM-based model to simulate the configuration of a rigid finite-size rough punch against a viscoelastic rough surface, the peculiar role played by surface roughness in viscoelastic reciprocating contact solutions was investigated by Putignano and Carbone [95].
3.4. Viscoelastic-Adhesive Contact
A common limitation among the models presented above is the neglecting of adhesive force. Practically, such interaction force always exists between two contacting bodies. It decreases appreciably with the increasing distance between the surfaces. Although the adhesive force is usually relatively weak, it plays a significant role as long as one of the following conditions fits [13]:
- (1)
- The contacting surface is extremely smooth;
- (2)
- One of the contacting components is much softer or compliant;
- (3)
- The surface contact is considered on a micro-scale.
The adhesive force in contact mechanics can be explained by the Lennard-Jones potential [13,113,114], which is a model used conventionally to describe simple interactions between two particles (atoms). The model describes the inter-atomic Van der Waals forces while neglecting the electrostatic and capillary force, the effects of which on adhesion can be found in the work of Israelachvili [114]. Based on physics, when the distance between the electrically neutral atoms is less than or larger than the size of the atoms (), the mutual interaction between them occurs under the influence of the Van der Waals forces. As illustrated in Figure 10a, when the distance between two neutral atoms is over the equilibrium distance (), the adhesive (attractive) force starts to perform. However, once the two atoms are moving close to each other (smaller than the equilibrium distance), repulsive force tends to be generated [13,113,114].
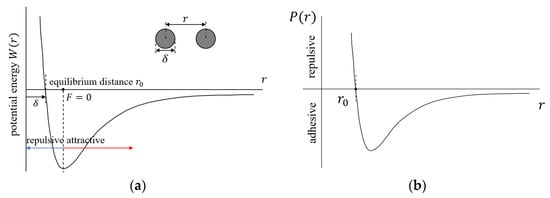
Figure 10.
(a) Lennard-Jones potential representation, here represents the equilbrium distance where the surface force is zero, and here represents the size of the interacting particles (atoms) and (b) Force ()-separation () for the parallel surface representation of the Lennard-Jones potential.
It is of note that the Lennard-Jones potential is limited in the reflection of interatomic potential in reality. Without the aim of giving an exhaustive discussion on this topic in this review paper, readers can refer to the latest work by Muser et al. [115] for a detailed description of interatomic potentials, where different functional forms for potentials (e.g., the Buckingham potential and Axilrod–Teller–Muto potential) and potential classes (e.g., two-body potentials and multi-body potentials) were introduced from a physical perspective.
Given that the maximum adhesive force has a fundamental limit, as shown in Figure 10b, the effects of the adhesion on contact are often neglected in contact analysis. It would not highly affect the modelling result when the contact pressure induced by the load applied to the surface is significantly higher than the maximum adhesive force. Hence, it is a common practice to ignore the adhesion when it comes to the contact problems of metallic materials, where the effect of adhesion is usually insignificant. However, since viscoelastic materials usually have low contact compliance and exhibit the soft feature corresponding to the second condition shown above, they would have considerable deformation when having contact with hard materials. This would induce a relatively large contact area, thus narrowing the gap between the contact pressure and the adhesive force. As a result, the reliability of the simulation results derived from the viscoelastic contact models discussed above can be undermined due to the neglect of adhesion.
The development of the contact model integrating adhesion and viscoelasticity is still in its early stage, where the available solutions are usually developed by applying an enrichment technique, in which the enrichment fields from adhesive contact solutions (such as the Johnson–Kendall–Roberts (JKR) theory [9] and Derjaguin–Muller–Toporov (DMT) theory [10]) are superimposed on the ordinary elastic and viscoelastic problem solutions. Both the JKR and DMT models studied the adhesive contact between a smooth sphere and a flat body, but with different assumptions and methods, which leads to different results. It was suggested by Tabor [116] that both solutions are correct depending on the contact type, which could be characterised by the Tabor parameter expressed as:
where represents the Tabor parameter; and are the combined radius and composite modulus of contacting surfaces, respectively; and is the work of adhesion. The JKR model was found to be valid only for the contact problem with a Tabor parameter (), while the DMT model is applicable for the Tabor parameter (). A more common summary of the two models states that the JKR model is effective for solving larger and more compliant contact problems, while the DMT model is suitable for handling stiffer and smaller contact problems. Notably, neither of the two models can provide a comprehensive understanding of the adhesion in contact mechanics, although they could offer a decent approximate solution for a certain range of contact problems.
Classical theories of fracture mechanics also played an essential role in the early studies of viscoelastic-adhesive contact [117,118,119]. An attempt was conducted by Hui et al. [120], where the JKR model and theory of viscoelastic fracture mechanics were implemented to simulate the viscoelastic-adhesive contact of spheres. By integrating the solution of Ting [38] and the restricted self-consistent adhesive model by Tabor [116], Haiat et al. [121] developed a solution to the adhesive contact problems of viscoelastic spheres. A FEM-based model was developed by Lin and Hui [122] to simulate the spherical contact, where the adhesion was accounted for by the Dugdale–Barenblatt model [123,124]. Based on the JKR model, an analytical solution to the adhesive contact of elastomer was proposed by Barthel and Fretigny [125]. The role played by viscoelasticity in the effective adhesion energy was quantified as a function of the contact edge velocity in the approximate analytical expressions. Yu et al. [126] developed a model for the contact of viscoelastic materials with the adhesive interaction, where the viscoelastic aspect of the model is based on the model of Chen [8] for the indentation contact of viscoelastic materials, while the adhesive aspect of the model is based on the theory of fracture mechanics by Schapery [127] and the theories of JKR [9], DMT [10] and Maugis [128]. By using the Maugis–Dugdale model [128] to characterise the dependence of the adhesive force on the gap between surfaces, a model was developed by Goryacheva and Makhovskaya [129] to investigate the adhesion effect in the sliding contact of a spherical indenter [130] or a periodic surface [131] against a viscoelastic substrate.
A fully deterministic model for the normal contact of viscoelastic-adhesive contact was recently developed by Afferrante and Violano [132] using FEM. Inspired by the Derjaguin approximation [133], the adhesive interaction between surfaces was characterised by non-linear springs following Lennard-Jones traction-gap law in their model. The pull-off load in smooth and adhesive viscoelastic contact problems was analysed by Afferrante and Violano [132], and they reported that the viscous dissipation is confined to the contact edges when short-ranged adhesion is considered. Together with the study of Afferrante and Violano [132], Muser and Persson [134] conducted a numerical work that supported the model of Persson and Brener [135], which was developed based on viscoelastic crack propagation. In their simulation of the adhesive contact between a rigid cylinder and a viscoelastic half-space, a maximum in the work of adhesion was found at intermediate pull-off velocities. Additionally, they reported that realistic dissipation can hardly be achieved without correct short-range adhesion. The interplay between adhesion and viscoelasticity in steady sliding contact was studied by Carbone et al. [136] numerically. Compared with the adhesiveless viscoelastic contact, the curve of hysteretic friction and sliding velocity is significantly changed, presenting a more pronounced friction peak. By simulating the viscoelastic adhesive contact between a sphere and a 2D nano-wavy surface, Yang et al. [137] reported that the effects of viscoelasticity can be neglected when the approach speed is high. However, viscoelasticity would bring significant change under low approaching speed, such as the increases of the maximum contact area and the pull-off load, when compared with the elastic case. Furthermore, the pull-off force was found to change monotonically with the increasing wavy parameter, while the maximum contact area responds in a nonmonotonically way. The effects of viscoelasticity on the adhesive hysteresis was investigated in the latest numerical work of Perez-Rafols et al. [138]. Apart from the finding that the viscoelasticity results in an increased effective work of adhesion due to the stiffening of contact, they argued that the contributions of surface roughness and viscoelasticity to the hysteresis in soft adhesive contacts are linearly additive in the region where viscoelasticity is confined to the edges of the wavy contact. This novel opinion remains up to further investigations, as they considered a single wavelength roughness instead of a realistic rough surface.
4. Lubricated Contact of Viscoelastic Bodies
As lubricants are frequently applied in practice for the control of friction and wear, appropriate lubrication analysis plays a vital role, as it can not only evaluate the lubrication regimes, but also helps to determine the design and manufacturing parameters of components working in a lubricated environment.
Regarding the effect of viscoelasticity on the lubrication performance, it was reported by Yoo [139] and Kaneko et al. [140] that the solution, in which the viscoelastic effect is accounted for in the squeeze film lubrication model, can be significantly different from that under the elastohydrodynamic lubrication (EHL) environment. Compared with the elastic counterpart, the film thickness, as well as the bearing volume, in the viscoelastic cases exhibit lower values [139]. By using an iterative Newton–Raphson scheme, Elsharkawy [141] proposed a numerical solution to the line contact lubrication problem of viscoelastic half-space. Similar contact problems were also analysed by Hooke and Huang [142], Scaraggi et al. [143] and Pandey et al. [144]. All of them reported remarkably different results in terms of the asymmetric pressure profiles and shrunk film thickness at the flow outlet when compared with the classical EHL regimeresponse, which is derived from viscoelasticity. Apart from EHL, by studying the lubricating performance of a smooth cylinder sliding against a randomly rough, nominally flat viscoelastic solid, Scaraggi et al. [143] reported that the minimum (average) film separation does not monotonically increase with the sliding velocity from the boundary lubrication regimeto the ordinary EHL regime. A Stribeck curve, which exhibits different structures when compared with that of elastic solids, was reported in their study. They argued that the common procedure to attain a Stribeck curve for elastic solids (e.g., using different fluid viscosities and plotting the friction coefficient as a function of the product of the kinetic viscosity and sliding speed) can be invalid for viscoelastic solids [143].
The newly defined viscoelasto-hydrodynamic lubrication (VEHL) has now been recognized as a peculiar regime that needs to be carefully considered when viscoelastic materials come into lubricated contact. A point contact lubrication model was developed by Putignano and Dini [145], where the effects of coupling between the fluid flow and the solid hysteretic response were considered. According to their simulation results, the friction in the VEHL system was found to be affected by the viscous loss, as well as the viscoelastic hysteresis. The numerical approach was later generalized by Putignano [146] to take into account different contact configurations and to investigate the effects of viscoelasticity in each case. The latest work of Putignano and Campanale [147] extended the study of VEHL contact to non-steady-state conditions, where a strong coupling between the time-dependent features of the fluid-dynamics problems and the viscoelastic relaxation of the material was found. A point VEHL contact model was recently developed by Zhao et al. [148]. A novel equation for determining the viscoelastic deformation was employed in their model to release the computational burden. A more complicated VEHL contact situation, in which layered materials with imperfect layer-substrate bonding are involved, was recently simulated by He et al. [149] using SAM. Meanwhile, Li et al. [150] developed a model to investigate the VEHL contact of viscoelastic materials containing arbitrary inhomogeneities.
It is of note that the role of viscoelasticity in the contact mechanics of lubricated solids has not been investigated theoretically and numerically to the same extent as for dry contact. To date, the role of surface roughness was barely investigated, as the fluid film was fully formed in VEHL. However, when it comes to boundary lubrication or mixed lubrication, the effects of surface roughness can be significant on the lubricating performance, which is worthwhile to investigate in future numerical studies.
5. Thermoviscoelastic (TVE) Contact
Due to the time and temperature dependency, the properties of viscoelastic materials, including creep compliance and relaxation modulus, can be characterised as a function of temperature, as well as time. However, the numerical studies discussed above were conducted with the assumption of isothermal conditions to simplify the contact problems. The viscoelastic contact problem, in which the mutual influences of material properties and temperature rise are involved, has attracted the attention of several studies in the last few decades. Persson [151] analysed the sliding contact of a rubber indenter against a rigid rough substrate, where the effects of the flash temperature derived from friction were taken into account. As highlighted in their later numerical analysis [152,153], the temperature rise due to relative motion during the contact of surfaces is of essential concern when viscoelastic materials are applied to a high-speed working environment. In addition to friction-induced heating, the heating derived from energy dissipation due to hysteresis, which tends to be unavoidable in the contact of viscoelastic materials, was considered in the formulation of Persson [151].
The development of the numerical model for thermoviscoelastic contact problems is still in its early period. By using an approximated approach to adapt the viscoelastic modulus to thermal effects in their BEM-based model [74], Putignano et al. [154] provided qualitative solutions to thermos-viscoelastic rolling contact problems at high speeds. By extending the SAM-based VEHL model [149], He et al. [155] developed a thermal-viscoelasto-hydrodynamic lubrication model (TVEHL) model to simulate the contact behaviour of an elastic sphere against a viscoelastic half-space, where the temperature dependency of the surface displacement was determined using the frequency-temperature superposition [156,157]. The thermos-viscoelastic contact of layered materials was simulated by Zhang et al. [158], where the fully coupled velocity-frequency-temperature relationships were taken into account. The contact configurations, including rubber coating against elastic substrate and elastic layer against rubber substrate, were investigated in their study. To date, the effects of surface roughness in thermoviscoelastic contact were barely reported in the numerical studies based on these models, which is worthwhile to investigate in the future.
6. Non-Linear Viscoelastic Contact
Although the models based on linear viscoelastic theory provide great knowledge of the contact behaviour of viscoelastic materials, the simulation results are still an ideal abstraction of some real material behaviours to some degree. The nonlinearity of viscoelastic materials tends to be the biggest bottleneck problem for researchers. Efforts have been made in developing a suitable rheological (mathematical) model to characterise the nonlinear viscoelastic behaviour [159,160,161]. Thus far, a few models based on finite element analysis have been raised. By using the single-integral creep model with stress-dependent properties of Schapery [29], Henriksen [162] and Roy and Reddy [163] developed their own incremental iterative algorithms to solve the contact problems of nonlinear viscoelastic bodies. The work of Henriksen [162] was then extended by Lai and Bakker [164], who included the nonlinear effects derived from temperature and physical ageing in the constitutive model. By decoupling the deviatoric and volumetric response and subdividing the strain vector into instantaneous and hereditary parts, a finite element formulation was developed by Haj-Ali and Muliana [165] to model the nonlinear viscoelastic behaviour of isotropic materials. By characterising the material nonlinearity with the strain-softening function and employing updated Lagrangian formulations, another formulation was developed by Shen et al. [166] to analyse the three-dimensional contact of nonlinear viscoelastic problems with large deformations.
Apart from these early attempts, Mahmoud et al. [167] recently developed a FEM-based model to simulate two-dimensional quasistatic frictionless contact problems, where nonlinear viscoelastic behaviour and large deformations were taken into account. The model was later extended to simulate the quasistatic frictional contact [168] and steady-state frictional rolling contact [169] of non-linear viscoelastic solids. As the modelling of nonlinear viscoelastic contact is still in its early stage, the role played by surface roughness was barely investigated in the numerical studies, which needs to be investigated in the future.
7. Case Studies
The numerical tools discussed above can be readily extended to practical applications by specifying the contact input used in real life, including load, material properties, relative motion, surface geometry, lubricating conditions and operating temperature. Of course, additional expertise may be required for effective numerical analysis in specialized disciplines. In this section, numerical studies based on various viscoelastic models in different fields, including the contact of ultra-high molecular weight polyethylene (UHMWPE) hip replacement in the biomedical field, contact of polydimethylsiloxane (PDMS) surface in the nanotechnology field and contact of rocks in the geological field, are presented and discussed to demonstrate how numerical models can help analyse and improve the design of various components in different contact systems.
7.1. Lubrication Analysis of UHMWPE Hip Replacements
In the biomedical industry, total hip replacement (THP) is a medical treatment that is usually implemented when the hip joint is worn or damaged to such a serious extent that personal mobility is significantly reduced and the patient experiences pain from the hip even when resting. Due to the existence of synovial fluid in human bodies, hip prostheses may work under different types of lubrication regimes, depending on human activities. Based on the linear elastic theory, the squeeze-film lubrication problem for hip replacements, including an acetabular cup made of UHMWPE and a femoral head made of metal or ceramic materials, has been investigated numerically by several researchers [170,171,172]. The reported viscoelasticity of UHMWPE [173] undermines the reliability of these numerical studies. The essential role played by the viscoelasticity of UHMWPE in the lubrication performance of hip prostheses was reported by Lu et al. [174] using a SAM-based transient lubrication model. By establishing the ball-in-socket lubrication model of the hip joint and specifying the contact inputs, including load and angular velocity during the gait cycle, the viscoelasticity of the UHMWPE cup was found to have significant effects on the pressure profile, such as lower peak pressure, despite barely influencing the lubricating film thickness. Recently, with the developed transient viscoelastic squeeze-film lubrication model, Lu et al. [175] furthered the study on the viscoelastic effects of UHMWPE on the squeeze-film lubrication action of artificial hip replacements. Although the central film thickness increased, the minimum film thickness was found to be decreased by the viscoelasticity, which leads to early direct contact. Moreover, the viscoelastic lubricating performance was found to be enhanced by decreasing the relaxation time and mechanical loss factor of the material. The enhanced lubrication analysis helps to develop appropriate methods to ensure the long-term successful functioning of artificial joints by reducing wear. The parametric analysis in these numerical studies, including the relaxation time and the ratio of the storage and the loss modulus of the UHMWPE cup, provides essential guidance for the future design of UHMWPE hip implants. The contact performance of a hip replacement, such as the pressure and lubrication film thickness, can be manipulated by tuning these material parameters.
7.2. Viscoelastic-Adhesive Contact Analysis of PDMS in Nanotechnology
In terms of the nanotechnology field, the triboelectric nanogenerator (TENG) is an evolving mechanical energy harvesting technology, which can be applied to collect mechanical energy from the surrounding environment and convert it into electrical energy for powering small devices based on the principles of contact charging and electrostatic induction [176]. A typical viscoelastic material known as PDMS is frequently applied. Micro- or nano-size textures are commonly fabricated on the PDMS surface in order to enhance the electrical performance of TENG, on which occasion the role of Van der Waals interaction becomes dominant. By assuming that PDMS behaves as a linear elastic material, adhesive contact models were developed by Jin et al. [177] and Yang et al. [178] to investigate the contact of the textured film with the metal electrode. Recently, a viscoelastic-adhesive model was developed by Wang et al. [179] to investigate the effects of viscoelasticity and texture sizes on the contact and electrical behaviour of TENG. By specifying the contact inputs of TENG that work in a repeated contact-separation mode, the simulation results from the model were found to be closer to the experimental results when compared with those from an elastic-adhesive model. The effects of surface adhesion (e.g., the increase of the pull-off force with the loading cycle) and viscoelasticity (e.g., a larger contact area ratio and higher electrical outputs, including open circuit voltage, short circuit current, transferred charge and load voltage) were reported in their numerical study. Under the application of a higher load, those with a smaller pitch and a larger width were found to produce higher electrical performance among the tested pyramid textures. These simulation results can serve as a useful reference when designing the viscoelastic surface texture of TENG in the future.
Apart from TENG, PDMS is also widely applied in micro-transfer printing, which is an advanced technology that makes use of surface adhesion to integrate functional devices by transferring pre-fabricated micro- or nano-elements from the growth substrate to the receiver substrate through a viscoelastic stamp [180]. A FEM-based viscoelastic-adhesive model was recently developed by Jiang et al. [181] to investigate the adhesive contact between a PDMS stamp and a spherical transferred element, where the Lennard-Jones surface force law was applied to simulate Van der Waals forces. After specifying a loading-dwelling-unloading history, which is usually employed during the process of micro-transfer printing, a parametric study, including the effects of unloading velocity, preload and the thermodynamic work of adhesion on the pull-off force (e.g., adhesion strength), was conducted. These numerical results revealing relations between these parameters and the pull-off force provide a theoretical reference to control strategies of adhesive force between the viscoelastic stamp and the transferred element in the transfer printing process, which determines the capability of the sophisticated technique.
7.3. Failure and Instability Analysis of Viscoelastic Rocks
Applications of viscoelastic models can also be found in the geological field. Considering that rocks exhibit a pronounced time-dependent mechanical behaviour (e.g., the deformation and failure of rocks evolve gradually over time instead of occurring instantaneously), which is supported by evidence from several field studies [182,183,184], the rheology of rocks has become one of the essential topics in geomechanics. Recently, within the framework of irreversible thermodynamics, a finite-strain viscoelastic-damage model was developed by Cheng et al. [185] using FEM to investigate the long-term strength and time-dependent failure and instability of rocks. Within the model, the heterogeneity of materials was considered on the mesoscale, and a continuum damage constitutive relationship was employed to characterize the material damage process. In addition to the time-dependent property, the buckling instability mechanism of rocks was taken into account during modelling. After calibration with experimental results from creep and stress relaxation tests, the model was used to simulate the collapse of rock slab. It was found that the collapse of rock slabs is caused by the interaction effect between the buckling instability mechanism and the time-dependent failure mechanism. The numerical analysis from the model shall provide meaningful guidance in terms of engineering design, safe construction and disaster prevention or mitigation where rocks are involved.
8. Conclusions and Future Research
Numerical research over the last six decades has brought forward numerous fundamental insights into the contact analysis of viscoelastic bodies. The implications for enhanced comprehension of the mechanical and tribological behaviour of viscoelastic materials under different operating conditions are profound by providing us with a better view of how full use can be made of these time-dependent materials in a more scientific way. Through applying efficient modelling techniques, along with the comprehensive theories that mathematically describe the contact response of viscoelastic materials under dry, lubricated or non-isothermal environments, various numerical tools have been developed to simulate the corresponding contact problems. The contact analysis derived from these models shall benefit all walks of life, given the ubiquitous viscoelasticity problems to be addressed. Although a comprehensive numerical framework is being built up owing to the considerable efforts dedicated by the model developers shown in this review paper, the following knowledge gaps remain to be filled in for the further development of an ideal panacea that can tackle intractable viscoelastic contact problems in practice:
- (1)
- As discussed in Section 3.2, the simulation of sliding or rolling contact was commonly assumed to be frictionless. The reason behind such practice is relevant to the intrinsic property of some specific polymers. It is known that elastomers are incompressible. For the problem of an incompressible half-space sliding on a rigid surface, there exists no coupling between the normal pressure and shear tractions. As the normal and tangential contact problems are independent of each other, the simplest way to simulate the sliding or rolling contact problems of viscoelastic materials is to neglect shear tractions in the lateral direction, together with their related coupling effects affecting the pressure profile, and to quantify the friction force exclusively derived from the viscoelastic losses. However, the case where uncoupled conditions can be applied is not ubiquitous. When addressing the common material combination for engineering products, such as the knee or hip prosthesis (usually a hard metal against a soft and compressible polymer), the inclusion of the coupling effect seems inevitable. A fully coupled model, which provides information on both normal and tangential fields in frictional viscoelastic sliding contact problems, is worth studying for fine precision engineering applications. To date, there is no exhaustive numerical analysis in terms of the effects of the coupled partial slip period on the later sliding contact solutions, which is worthwhile to investigate.
- (2)
- As mentioned in Section 3.4, the development of viscoelastic-adhesive contact models is still in the early stage, as the developed models can only solve indentation problems. Since the additional adhesive force makes it difficult to obtain closed-form contact solutions based on energy approaches, and extremely careful consideration of energy terms is required, the surface adhesion in coupled normal and tangential contact of viscoelastic surfaces seems to be a knowledge gap.
- (3)
- Few BEM-based models simulating the nonlinear viscoelastic model were reported, as BEM-based algorithms are limited by the assumptions of linear viscoelasticity. However, the extension of BEM-based models to contact problems, where nonlinear interface constitutive response is involved, may be possible by applying specific computational techniques or approximation approaches. Considering the higher computational efficiency of BEM compared to FEM, it is worthwhile to develop a general BEM-based nonlinear viscoelastic model.
- (4)
- Although the effect of surface roughness on the dry contact of linear viscoelastic materials was investigated and reported in several numerical studies, as mentioned in Section 3.3, it was barely included when it comes to the modelling of lubricated contact, thermoviscoelastic contact and nonlinear viscoelastic contact. The synergy of the surface roughness and other variables can be essential, which needs to be analyzed in future modelling work.
Author Contributions
D.W.: Study conception and design, literature collection, formal analysis and writing. G.d.B.: Writing—Review & Editing, supervision and formal analysis. A.N.: Supervision. A.G.: Study conception and design, formal analysis, writing—review & editing and supervision. All authors have read and agreed to the published version of the manuscript.
Funding
The authors are thankful to the school of mechanical engineering at the University of Leeds for supporting this study by funding the PhD studentship of Dongze Wang. This work is supported by the Engineering and Physical Sciences Research Council (grant no. EP/T024542/1) as part of ‘STOP fibrous microplastic pollution from textiles by elucidating fibre damage and manufacturing novel textiles’ standard research.
Conflicts of Interest
All authors declare no conflict of interest.
Nomenclature
| 2D | two-dimensional |
| 3D | three-dimensional |
| BEM | boundary Element Method |
| DC-FFT | discrete convolution fast Fourier transform |
| DEM | discrete element method |
| DMT | Derjaguin–Muller–Toporov |
| EHL | elastohydrodynamic lubrication |
| FEM | Finite Element Method |
| FFT | Fast Fourier Transform |
| GFMD | Green’s function molecular dynamics |
| JKR | Johnson–Kendall–Roberts |
| MIM | matrix inversion method |
| PDMS | polydimethylsiloxane |
| PMMA | polymethyl methacrylate |
| SLS | standard linear solid |
| SAM | semi-analytical method |
| TENG | triboelectric nanogenerator |
| THP | total hip replacement |
| TIM | two-scale iterative method |
| TVE | thermoviscoelastic |
| TVEHL | thermal-viscoelasto-hydrodynamic lubrication |
| UHMWPE | ultra-high molecular weight polyethylene |
| VEHL | viscoelastic-hydrodynamic lubrication |
| Hertz solution of contact radius using the instantaneous modulus | |
| power spectral density of a fractal rough surface | |
| fractal dimension | |
| composite modulus of contacting surfaces | |
| complex modulus of material | |
| modulus of spring in rheological model | |
| Hurst exponent | |
| Heaviside step function | |
| lateral size of rough surface | |
| number of scales when describing fractal rough surface | |
| Hertz solution of peak pressure using the instantaneous modulus | |
| wavevector | |
| short-distance roll-off wavevector | |
| long-distance cut-off wavevector | |
| smallest possible wavevector | |
| distance between two interacting particles (bodies) | |
| combined radius of contacting bodies | |
| equilibrium distance | |
| complex number frequency parameter in the Laplace transform domain | |
| time | |
| potential energy | |
| work of adhesion | |
| size of the interacting particles | |
| strain | |
| viscosity of dashpot in rheological model | |
| Tabor parameter | |
| stress | |
| relaxation time | |
| function of creep compliance | |
| function of relaxation modulus | |
| frequency |
References
- Kiumarsi, M.; Rafe, A.; Yeganehzad, S. Effect of Different Bulk Sweeteners on the Dynamic Oscillatory and Shear Rheology of Chocolate. Appl. Rheol. 2017, 27, 11–19. [Google Scholar] [CrossRef]
- Cheng, Q.Q.; Liu, P.X.; Lai, P.H.; Ni Zou, Y. An Interactive Meshless Cutting Model for Nonlinear Viscoelastic Soft Tissue in Surgical Simulators. IEEE Access 2017, 5, 16359–16371. [Google Scholar] [CrossRef]
- Persson, B. Rubber friction and tire dynamics. J. Phys. Condens. Matter 2010, 23, 015003. [Google Scholar] [CrossRef]
- James, M.; Bagdassarov, N.; Müller, K.; Pinkerton, H. Viscoelastic behaviour of basaltic lavas. J. Volcanol. Geotherm. Res. 2004, 132, 99–113. [Google Scholar] [CrossRef]
- Cowie, R.M.; Briscoe, A.; Fisher, J.; Jennings, L.M. Wear and Friction of UHMWPE-on-PEEK OPTIMATM. J. Mech. Behav. Biomed. Mater. 2018, 89, 65–71. [Google Scholar] [CrossRef] [PubMed]
- Vakis, A.; Yastrebov, V.; Scheibert, J.; Nicola, L.; Dini, D.; Minfray, C.; Almqvist, A.; Paggi, M.; Lee, S.; Limbert, G.; et al. Modeling and simulation in tribology across scales: An overview. Tribol. Int. 2018, 125, 169–199. [Google Scholar] [CrossRef]
- Banks, H.T.; Hu, S.; Kenz, Z.R. A Brief Review of Elasticity and Viscoelasticity for Solids. Adv. Appl. Math. Mech. 2011, 3, 1–51. [Google Scholar] [CrossRef]
- Chen, W.W.; Wang, Q.J.; Huan, Z.; Luo, X. Semi-Analytical Viscoelastic Contact Modeling of Polymer-Based Materials. J. Tribol. 2011, 133, 041404. [Google Scholar] [CrossRef]
- Johnson, K.L.; Kendall, K.; Roberts, A.D. Surface energy and the contact of elastic solids. Proc. R. Soc. Lond. A 1971, 324, 301–313. [Google Scholar]
- Derjaguin, B.; Muller, V.; Toporov, Y. Effect of contact deformations on the adhesion of particles. J. Colloid Interface Sci. 1975, 53, 314–326. [Google Scholar] [CrossRef]
- Bergström, J. Linear Viscoelasticity. In Mechanics of Solid Polymers: Theory and Computational Modelling; Bergström, J., Ed.; William Andrew Publishing: San Diego, CA, USA, 2015. [Google Scholar] [CrossRef]
- Marques, S.P.C.; Creus, G.J. Computational Viscoelasticity; Springer: Berlin, Germany, 2012. [Google Scholar]
- Popov, V. Contact Mechanics and Friction-Physical Principles and Applications; Springer: Berlin, Germany, 2010. [Google Scholar]
- Popov, V.L.; Heß, M.; Willert, E. Handbook of Contact Mechanics; Springer: Berlin, Germany, 2019. [Google Scholar]
- Phan-Thien, N.; Mai-Duy, N. Understanding Viscoelasticity: An Introduction to Rheology; Springer: Berlin, Germany, 2017. [Google Scholar]
- Papanicolaou, G.; Zaoutsos, S. Viscoelastic constitutive modeling of creep and stress relaxation in polymers and polymer matrix composites. In Creep and Fatigue in Polymer Matrix Composites; Guedes, R.M., Ed.; Woodhead Publishing: Cambridge, UK, 2019. [Google Scholar] [CrossRef]
- Kelly, P. Solid Mechanics Part I: An Introduction to Solid Mechanics; Solid Mechanics Lecture Notes; University of Auckland: Auckland, New Zealand, 2019. [Google Scholar]
- Christensen, R.M. Theory of Viscoelasticity; Academic Press: London, UK, 1982. [Google Scholar]
- Kumar, M.; Narasimhan, R. Analysis of spherical indentation of linear viscoelastic materials. Curr. Sci. 2004, 87, 1088–1095. [Google Scholar]
- Bugnicourt, R. Simulation of the Contact between a Rough Surface and a Viscoelastic Material with Friction; Université de Lyon: Lyon, France, 2017. [Google Scholar]
- Bugnicourt, R.; Sainsot, P.; Lesaffre, N.; Lubrecht, A. Transient frictionless contact of a rough rigid surface on a viscoelastic half-space. Tribol. Int. 2017, 113, 279–285. [Google Scholar] [CrossRef]
- Green, A.E.; Rivlin, R.S. The mechanics of non-linear materials with memory, Part III. Arch. Ration. Mech. Anal. 1959, 4, 387–404. [Google Scholar] [CrossRef]
- Green, A.E.; Rivlin, R.S. The mechanics of non-linear materials with memory, Part I. Arch. Ration. Mech. Anal. 1957, 1, 1–21. [Google Scholar] [CrossRef]
- Green, A.E.; Rivlin, R.S.; Spencer, A.J.M. The mechanics of non-linear materials with memory, Part II. Arch. Ration. Mech. Anal. 1959, 3, 82–90. [Google Scholar] [CrossRef]
- Pipkin, A.; Rogers, T. A non-linear integral representation for viscoelastic behaviour. J. Mech. Phys. Solids 1968, 16, 59–72. [Google Scholar] [CrossRef]
- Leaderman, H. Elastic and Creep Properties of Filamentous Materials and Other High Polymers; Massachusetts Institute of Technology: Cambridge, MA, USA, 1941. [Google Scholar]
- Brueller, O.S. On the nonlinear characterization of the long term behavior of polymeric materials. Polym. Eng. Sci. 1987, 27, 144–148. [Google Scholar] [CrossRef]
- Brueller, O.S. Predicting the behavior of nonlinear viscoelastic materials under spring loading. Polym. Eng. Sci. 1993, 33, 97–99. [Google Scholar] [CrossRef]
- Schapery, R.A. On the characterization of nonlinear viscoelastic materials. Polym. Eng. Sci. 1969, 9, 295–310. [Google Scholar] [CrossRef]
- Lee, E.H. Stress analysis in visco-elastic bodies. Q. Appl. Math. 1955, 13, 183–190. [Google Scholar] [CrossRef]
- Radok, J.R.M. Visco-elastic stress analysis. Q. Appl. Math. 1957, 15, 198–202. [Google Scholar] [CrossRef]
- Lee, E.H.; Radok, J.R.M. The Contact Problem for Viscoelastic Bodies. J. Appl. Mech. 1960, 27, 438–444. [Google Scholar] [CrossRef]
- Alfrey, T. Non-homogeneous stresses in visco-elastic media. Q. Appl. Math. 1944, 2, 113–119. [Google Scholar] [CrossRef]
- Tsien, H.S. A generalization of Alfrey’s theorem for visco-elastic media. Q. Appl. Math. 1950, 8, 104–106. [Google Scholar] [CrossRef][Green Version]
- Hunter, S. The Hertz problem for a rigid spherical indenter and a viscoelastic half-space. J. Mech. Phys. Solids 1960, 8, 219–234. [Google Scholar] [CrossRef]
- Graham, G. The contact problem in the linear theory of viscoelasticity when the time dependent contact area has any number of maxima and minima. Int. J. Eng. Sci. 1967, 5, 495–514. [Google Scholar] [CrossRef]
- Yang, W.H. The Contact Problem for Viscoelastic Bodies. J. Appl. Mech. 1966, 33, 395–401. [Google Scholar] [CrossRef]
- Ting, T.C.T. The Contact Stresses Between a Rigid Indenter and a Viscoelastic Half-Space. J. Appl. Mech. 1966, 33, 845–854. [Google Scholar] [CrossRef]
- Ting, T.C.T. Contact Problems in the Linear Theory of Viscoelasticity. J. Appl. Mech. 1968, 35, 248–254. [Google Scholar] [CrossRef]
- Oyen, M.L. Analytical techniques for indentation of viscoelastic materials. Philos. Mag. 2006, 86, 5625–5641. [Google Scholar] [CrossRef]
- Greenwood, J. Contact between an axisymmetric indenter and a viscoelastic half-space. Int. J. Mech. Sci. 2010, 52, 829–835. [Google Scholar] [CrossRef]
- Fu, G. Theoretical study of complete contact indentations of viscoelastic materials. J. Mater. Sci. 2004, 39, 2877–2878. [Google Scholar] [CrossRef]
- Yakovenko, A.; Goryacheva, I. The periodic contact problem for spherical indenters and viscoelastic half-space. Tribol. Int. 2021, 161, 107078. [Google Scholar] [CrossRef]
- Papangelo, A.; Ciavarella, M. Viscoelastic dissipation in repeated normal indentation of an Hertzian profile. Int. J. Solids Struct. 2022, 236–237, 111362. [Google Scholar] [CrossRef]
- Argatov, I.; Mishuris, G. Frictionless elliptical contact of thin viscoelastic layers bonded to rigid substrates. Appl. Math. Model. 2011, 35, 3201–3212. [Google Scholar] [CrossRef]
- Argatov, I. An analytical solution of the rebound indentation problem for an isotropic linear viscoelastic layer loaded with a spherical punch. Acta Mech. 2012, 223, 1441–1453. [Google Scholar] [CrossRef]
- Argatov, I.; Mishuris, G. An analytical solution for a linear viscoelastic layer loaded with a cylindrical punch: Evaluation of the rebound indentation test with application for assessing viability of articular cartilage. Mech. Res. Commun. 2011, 38, 565–568. [Google Scholar] [CrossRef]
- Chen, Y.-H.; Jia, Y.; Yang, F.; Huang, C.-C.; Lee, S. Boussinesq problem of a Burgers viscoelastic layer on an elastic substrate. Mech. Mater. 2015, 87, 27–39. [Google Scholar] [CrossRef]
- Kozhevnikov, I.; Cesbron, J.; Duhamel, D.; Yin, H.; Anfosso-Lédée, F. A new algorithm for computing the indentation of a rigid body of arbitrary shape on a viscoelastic half-space. Int. J. Mech. Sci. 2008, 50, 1194–1202. [Google Scholar] [CrossRef][Green Version]
- Kozhevnikov, I.; Duhamel, D.; Yin, H.; Feng, Z.-Q. A new algorithm for solving the multi-indentation problem of rigid bodies of arbitrary shapes on a viscoelastic half-space. Int. J. Mech. Sci. 2010, 52, 399–409. [Google Scholar] [CrossRef]
- Boussinesq, J. Applications des Potentiels à l’étude de l’équilibre et Mouvement des Solides Elastiques; Gauthier–Villard: Paris, France, 1885. [Google Scholar]
- Liu, S.; Wang, Q.; Liu, G. A versatile method of discrete convolution and FFT (DC-FFT) for contact analyses. Wear 2000, 243, 101–111. [Google Scholar] [CrossRef]
- Koumi, K.E.; Nelias, D.; Chaise, T.; Duval, A. Modeling of the contact between a rigid indenter and a heterogeneous viscoelastic material. Mech. Mater. 2014, 77, 28–42. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, W.; Zhao, Z.; Zhang, H. The effect of meso-structure and surface topography on the indentation variability of viscoelastic composite materials. Compos. Struct. 2019, 220, 81–92. [Google Scholar] [CrossRef]
- Spinu, S. Viscoelastic Contact Modelling: Application to the Finite Length Line Contact. Tribol. Ind. 2018, 40, 538–551. [Google Scholar] [CrossRef]
- Zhao, Y.; Morales-Espejel, G.; Venner, C. Aspects of modeling and numerical simulation of dry point contacts between viscoelastic solids. Tribol. Int. 2021, 165, 107245. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Hwu, C. Boundary element method for contact between multiple rigid punches and anisotropic viscoelastic foundation. Eng. Anal. Bound. Elements 2020, 118, 295–305. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Hwu, C. Indentation by multiple rigid punches on two-dimensional anisotropic elastic or viscoelastic solids. Int. J. Mech. Sci. 2020, 178, 105595. [Google Scholar] [CrossRef]
- Olsson, E.; Jelagin, D. A contact model for the normal force between viscoelastic particles in discrete element simulations. Powder Technol. 2019, 342, 985–991. [Google Scholar] [CrossRef]
- Wang, D.; de Boer, G.; Ghanbarzadeh, A. A Numerical Model for Investigating the Effect of Viscoelasticity on the Partial Slip Solution. Materials 2022, 15, 5182. [Google Scholar] [CrossRef]
- Koumi, K.E.; Chaise, T.; Nelias, D. Rolling contact of a rigid sphere/sliding of a spherical indenter upon a viscoelastic half-space containing an ellipsoidal inhomogeneity. J. Mech. Phys. Solids 2015, 80, 1–25. [Google Scholar] [CrossRef]
- Hunter, S.C. The Rolling Contact of a Rigid Cylinder With a Viscoelastic Half Space. J. Appl. Mech. 1961, 28, 611–617. [Google Scholar] [CrossRef]
- Morland, L.W. Exact solutions for rolling contact between viscoelastic cylinders. Q. J. Mech. Appl. Math. 1967, 20, 73–106. [Google Scholar] [CrossRef]
- Morland, L.W. Rolling contact between dissimilar viscoelastic cylinders. Q. Appl. Math. 1968, 25, 363–376. [Google Scholar] [CrossRef]
- Panek, C.; Kalker, J.J. Three-dimensional Contact of a Rigid Roller Traversing a Viscoelastic Half Space. IMA J. Appl. Math. 1980, 26, 299–313. [Google Scholar] [CrossRef]
- Aleksandrov, V.M.; Goryacheva, I.G.; Torskaya, E.V. Sliding contact of a smooth indenter and a viscoelastic half-space (3D problem). Dokl. Phys. 2010, 55, 77–80. [Google Scholar] [CrossRef]
- Persson, B.N.J. Rolling friction for hard cylinder and sphere on viscoelastic solid. Eur. Phys. J. E 2010, 33, 327–333. [Google Scholar] [CrossRef]
- Padovan, J.; Paramadilok, O. Transient and steady state viscoelastic rolling contact. Comput. Struct. 1985, 20, 545–553. [Google Scholar] [CrossRef]
- Padovan, J.; Kazempour, A.; Tabaddor, F.; Brockman, B. Alternative formulations of rolling contact problems. Finite Elem. Anal. Des. 1992, 11, 275–284. [Google Scholar] [CrossRef]
- Le Tallec, P.; Rahler, C. Numerical models of steady rolling for non-linear viscoelastic structures in finite deformations. Int. J. Numer. Methods Eng. 1994, 37, 1159–1186. [Google Scholar] [CrossRef]
- Nackenhorst, U. The ALE-formulation of bodies in rolling contact: Theoretical foundations and finite element approach. Comput. Methods Appl. Mech. Eng. 2004, 193, 4299–4322. [Google Scholar] [CrossRef]
- Padovan, J. Finite element analysis of steady and transiently moving/rolling nonlinear viscoelastic structure—I. Theory. Comput. Struct. 1987, 27, 249–257. [Google Scholar] [CrossRef]
- Nasdala, L.; Kaliske, M.; Becker, A.; Rothert, H. An efficient viscoelastic formulation for steady-state rolling structures. Comput. Mech. 1998, 22, 395–403. [Google Scholar] [CrossRef]
- Carbone, G.; Putignano, C. A novel methodology to predict sliding and rolling friction of viscoelastic materials: Theory and experiments. J. Mech. Phys. Solids 2013, 61, 1822–1834. [Google Scholar] [CrossRef]
- Menga, N.; Putignano, C.; Carbone, G.; Demelio, G.P. The sliding contact of a rigid wavy surface with a viscoelastic half-space. Proc. R. Soc. A:Math. Phys. Eng. Sci. 2014, 470, 20140392. [Google Scholar] [CrossRef]
- Putignano, C.; Carbone, G.; Dini, D. Mechanics of rough contacts in elastic and viscoelastic thin layers. Int. J. Solids Struct. 2015, 69–70, 507–517. [Google Scholar] [CrossRef]
- Menga, N.; Afferrante, L.; Carbone, G. Effect of thickness and boundary conditions on the behavior of viscoelastic layers in sliding contact with wavy profiles. J. Mech. Phys. Solids 2016, 95, 517–529. [Google Scholar] [CrossRef]
- Menga, N.; Afferrante, L.; Demelio, G.; Carbone, G. Rough contact of sliding viscoelastic layers: Numerical calculations and theoretical predictions. Tribol. Int. 2018, 122, 67–75. [Google Scholar] [CrossRef]
- Torskaya, E.V.; Stepanov, F.I. Effect of Surface Layers in Sliding Contact of Viscoelastic Solids (3-D Model of Material). Front. Mech. Eng. 2019, 5, 26. [Google Scholar] [CrossRef]
- Stepanov, F.I.; Torskaya, E.V. Study of stress state of viscoelastic half-space in sliding contact with smooth indenter. J. Frict. Wear 2016, 37, 101–106. [Google Scholar] [CrossRef]
- van Dokkum, J.S.; Nicola, L. Green’s function molecular dynamics including viscoelasticity. Model. Simul. Mater. Sci. Eng. 2019, 27, 075006. [Google Scholar] [CrossRef]
- Wallace, E.R.; Chaise, T.; Nelias, D. Three-dimensional rolling/sliding contact on a viscoelastic layered half-space. J. Mech. Phys. Solids 2020, 143, 104067. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Q.J.; He, T. Transient and steady-state viscoelastic contact responses of layer-substrate systems with interfacial imperfections. J. Mech. Phys. Solids 2020, 145, 104170. [Google Scholar] [CrossRef]
- Dayalan, S.K.; Sundaram, N.K. Partial slip contact of a rigid pin and a linear viscoelastic plate. Int. J. Solids Struct. 2016, 100, 319–331. [Google Scholar] [CrossRef]
- Bonari, J.; Paggi, M. Viscoelastic Effects during Tangential Contact Analyzed by a Novel Finite Element Approach with Embedded Interface Profiles. Lubricants 2020, 8, 107. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Hwu, C. Time-stepping method for frictional contact of anisotropic viscoelastic solids. Int. J. Mech. Sci. 2020, 184, 105836. [Google Scholar] [CrossRef]
- Goriacheva, I. Contact problem of rolling of a viscoelastic cylinder on a base of the same material. J. Appl. Math. Mech. 1973, 37, 877–885. [Google Scholar] [CrossRef]
- Goodman, L.E. Contact Stress Analysis of Normally Loaded Rough Spheres. J. Appl. Mech. 1962, 29, 515–522. [Google Scholar] [CrossRef]
- Goryacheva, I.; Sadeghi, F. Contact characteristics of a rolling/sliding cylinder and a viscoelastic layer bonded to an elastic substrate. Wear 1995, 184, 125–132. [Google Scholar] [CrossRef]
- Goryacheva, I.; Stepanov, F.; Torskaya, E. Sliding of a smooth indentor over a viscoelastic half-space when there is friction. J. Appl. Math. Mech. 2015, 79, 596–603. [Google Scholar] [CrossRef]
- Goryacheva, I.; Stepanov, F.; Torskaya, E. Effect of Friction in Sliding Contact of a Sphere Over a Viscoelastic Half-Space. In Mathematical Modeling and Optimization of Complex Structures; Neittaanmäki, P., Repin, S., Tuovinen, T., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 93–103. [Google Scholar]
- Goryacheva, I.; Miftakhova, A. Modelling of the viscoelastic layer effect in rolling contact. Wear 2019, 430–431, 256–262. [Google Scholar] [CrossRef]
- Putignano, C.; Carbone, G. Viscoelastic Damping in alternate reciprocating contacts. Sci. Rep. 2017, 7, 8333. [Google Scholar] [CrossRef]
- Putignano, C.; Carbone, G.; Dini, D. Theory of reciprocating contact for viscoelastic solids. Phys. Rev. E 2016, 93, 043003. [Google Scholar] [CrossRef] [PubMed]
- Putignano, C.; Carbone, G. Viscoelastic reciprocating contacts in presence of finite rough interfaces: A numerical investigation. J. Mech. Phys. Solids 2018, 114, 185–193. [Google Scholar] [CrossRef]
- Santeramo, M.; Putignano, C.; Vorlaufer, G.; Krenn, S.; Carbone, G. Viscoelastic steady-state rolling contacts: A generalized boundary element formulation for conformal and non-conformal geometries. J. Mech. Phys. Solids 2023, 171, 105129. [Google Scholar] [CrossRef]
- Persson, B. Contact mechanics for randomly rough surfaces. Surf. Sci. Rep. 2006, 61, 201–227. [Google Scholar] [CrossRef]
- Persson, B.; Albohr, O.; Tartaglino, U.; Volokitin, A.; Tosatti, E. On the nature of surface roughness with application to contact mechanics, sealing, rubber friction and adhesion. J. Phys. Condens. Matter 2004, 17, R1–R62. [Google Scholar] [CrossRef]
- Jacobs, T.D.B.; Junge, T.; Pastewka, L. Quantitative characterization of surface topography using spectral analysis. Surf. Topogr. Metrol. Prop. 2017, 5, 013001. [Google Scholar] [CrossRef]
- Persson, B.N.J.; Albohr, O.; Creton, C.; Peveri, V. Contact area between a viscoelastic solid and a hard, randomly rough, substrate. J. Chem. Phys. 2004, 120, 8779–8793. [Google Scholar] [CrossRef]
- Persson, B.N.J. Theory of rubber friction and contact mechanics. J. Chem. Phys. 2001, 115, 3840–3861. [Google Scholar] [CrossRef]
- Carbone, G.; Lorenz, B.; Persson, B.; Wohlers, A. Contact mechanics and rubber friction for randomly rough surfaces with anisotropic statistical properties. Eur. Phys. J. E 2009, 29, 275–284. [Google Scholar] [CrossRef]
- Afferrante, L.; Putignano, C.; Menga, N.; Carbone, G. Friction in rough contacts of linear viscoelastic surfaces with anisotropic statistical properties. Eur. Phys. J. E 2019, 42, 80. [Google Scholar] [CrossRef] [PubMed]
- Scaraggi, M.; Persson, B.N.J. Friction and universal contact area law for randomly rough viscoelastic contacts. J. Phys. Condens. Matter 2015, 27, 105102. [Google Scholar] [CrossRef] [PubMed]
- Scaraggi, M.; Comingio, D. Rough contact mechanics for viscoelastic graded materials: The role of small-scale wavelengths on rubber friction. Int. J. Solids Struct. 2017, 125, 276–296. [Google Scholar] [CrossRef]
- Papangelo, A.; Ciavarella, M. Viscoelastic normal indentation of nominally flat randomly rough contacts. Int. J. Mech. Sci. 2021, 211, 106783. [Google Scholar] [CrossRef]
- Putignano, C.; Afferrante, L.; Carbone, G.; Demelio, G. The influence of the statistical properties of self-affine surfaces in elastic contacts: A numerical investigation. J. Mech. Phys. Solids 2012, 60, 973–982. [Google Scholar] [CrossRef]
- Carbone, G.; Putignano, C. Rough viscoelastic sliding contact: Theory and experiments. Phys. Rev. E 2014, 89, 032408. [Google Scholar] [CrossRef]
- Putignano, C. Viscoelastic rough contact mechanics: A multiscale investigation. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 230, 1374–1381. [Google Scholar] [CrossRef]
- Putignano, C.; Menga, N.; Afferrante, L.; Carbone, G. Viscoelasticity induces anisotropy in contacts of rough solids. J. Mech. Phys. Solids 2019, 129, 147–159. [Google Scholar] [CrossRef]
- Menga, N.; Carbone, G.; Dini, D. Exploring the effect of geometric coupling on friction and energy dissipation in rough contacts of elastic and viscoelastic coatings. J. Mech. Phys. Solids 2020, 148, 104273. [Google Scholar] [CrossRef]
- Putignano, C.; Carbone, G. On the Role of Roughness in the Indentation of Viscoelastic Solids. Tribol. Lett. 2022, 70, 117. [Google Scholar] [CrossRef]
- Medina, S.; Dini, D. A numerical model for the deterministic analysis of adhesive rough contacts down to the nano-scale. Int. J. Solids Struct. 2014, 51, 2620–2632. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces: Revised, 3rd ed.; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Müser, M.H.; Sukhomlinov, S.V.; Pastewka, L. Interatomic potentials: Achievements and challenges. Adv. Phys. X 2023, 8, 2093129. [Google Scholar] [CrossRef]
- Tabor, D. Surface forces and surface interactions. J. Colloid Interface Sci. 1977, 58, 2–13. [Google Scholar] [CrossRef]
- Maugis, D.; Barquins, M. Fracture Mechanics and Adherence of Viscoelastic Solids. In Adhesion and Adsorption of Polymers; Lee, L.-H., Ed.; Springer: Boston, MA, USA, 1980; pp. 203–277. [Google Scholar]
- Greenwood, J.A.; Johnson, K.L. The mechanics of adhesion of viscoelastic solids. Philos. Mag. A 1981, 43, 697–711. [Google Scholar] [CrossRef]
- Muller, V. On the theory of pull-off of a viscoelastic sphere from a flat surface. J. Adhes. Sci. Technol. 1999, 13, 999–1016. [Google Scholar] [CrossRef]
- Hui, C.-Y.; Baney, J.M.; Kramer, E.J. Contact Mechanics and Adhesion of Viscoelastic Spheres. Langmuir 1998, 14, 6570–6578. [Google Scholar] [CrossRef]
- Haiat, G.; Huy, M.P.; Barthel, E. The adhesive contact of viscoelastic spheres. J. Mech. Phys. Solids 2003, 51, 69–99. [Google Scholar] [CrossRef]
- Lin, Y.-Y.; Hui, C.Y. Mechanics of contact and adhesion between viscoelastic spheres: An analysis of hysteresis during loading and unloading. J. Polym. Sci. Part B Polym. Phys. 2002, 40, 772–793. [Google Scholar] [CrossRef]
- Dugdale, D.S. Yielding of steel sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Barenblatt, G.I. The Mathematical Theory of Equilibrium Cracks in Brittle Fracture. In Advances in Applied Mechanics; Dryden, H.L., von Kármán, T., Kuerti, G., van den Dungen, F.H., Howarth, L., Eds.; Elsevier: Cambridge, MA, USA, 1962; Volume 7, pp. 55–129. [Google Scholar]
- Bärthel, E.; Frétigny, C. Adhesive contact of elastomers: Effective adhesion energy and creep function. J. Phys. D Appl. Phys. 2009, 42, 195302. [Google Scholar] [CrossRef]
- Yu, H.; Li, Z.; Wang, Q.J. Viscoelastic-adhesive contact modeling: Application to the characterization of the viscoelastic behavior of materials. Mech. Mater. 2013, 60, 55–65. [Google Scholar] [CrossRef]
- Schapery, R.A. On the mechanics of crack closing and bonding in linear viscoelastic media. Int. J. Fract. 1989, 39, 163–189. [Google Scholar] [CrossRef]
- Maugis, D. Adhesion of spheres: The JKR-DMT transition using a dugdale model. J. Colloid Interface Sci. 1992, 150, 243–269. [Google Scholar] [CrossRef]
- Goryacheva, I.; Makhovskaya, Y. Adhesion effect in sliding of a periodic surface and an individual indenter upon a viscoelastic base. J. Strain Anal. Eng. Des. 2016, 51, 286–293. [Google Scholar] [CrossRef]
- Goryacheva, I.G.; Gubenko, M.M.; Makhovskaya, Y.Y. Sliding of a spherical indenter on a viscoelastic foundation with the forces of molecular attraction taken into account. J. Appl. Mech. Tech. Phys. 2014, 55, 81–88. [Google Scholar] [CrossRef]
- Goryacheva, I.G.; Makhovskaya, Y.Y. Sliding of a wavy indentor on a viscoelastic layer surface in the case of adhesion. Mech. Solids 2015, 50, 439–450. [Google Scholar] [CrossRef]
- Afferrante, L.; Violano, G. On the effective surface energy in viscoelastic Hertzian contacts. J. Mech. Phys. Solids 2021, 158, 104669. [Google Scholar] [CrossRef]
- Derjaguin, V.B. Theorie des Anhaftens kleiner Teilchen. Prog. Surf. Sci. 1992, 40, 6–15. [Google Scholar] [CrossRef]
- Müser, M.H.; Persson, B.N.J. Crack and pull-off dynamics of adhesive, viscoelastic solids. EPL Europhys. Lett. 2022, 137, 36004. [Google Scholar] [CrossRef]
- Persson, B.N.J.; Brener, E.A. Crack propagation in viscoelastic solids. Phys. Rev. E 2005, 71, 036123. [Google Scholar] [CrossRef]
- Carbone, G.; Mandriota, C.; Menga, N. Theory of viscoelastic adhesion and friction. Extreme Mech. Lett. 2022, 56, 101877. [Google Scholar] [CrossRef]
- Yang, W.; Wang, X.; Chen, P.; Qiao, X. Viscoelastic adhesive contact between a sphere and a two-dimensional nano-wavy surface. Appl. Surf. Sci. 2022, 586, 152828. [Google Scholar] [CrossRef]
- Pérez-Ràfols, F.; Van Dokkum, J.S.; Nicola, L. On the interplay between roughness and viscoelasticity in adhesive hysteresis. J. Mech. Phys. Solids 2023, 170, 105079. [Google Scholar] [CrossRef]
- Yoo, H.S. Some Effects of Viscoelastic Matrix on the Squeeze Films. ASLE Trans. 1987, 30, 403–408. [Google Scholar] [CrossRef]
- Kaneko, S.; Tanaka, T.; Abe, S.; Ishikawa, T. A Study on Squeeze Films Between Porous Rubber Surface and Rigid Surface: Analysis Based on the Viscoelastic Continuum Model. J. Tribol. 2004, 126, 719–727. [Google Scholar] [CrossRef]
- Elsharkawy, A.A. Visco-elastohydrodynamic lubrication of line contacts. Wear 1996, 199, 45–53. [Google Scholar] [CrossRef]
- Hooke, C.J.; Huang, P. Elastohydrodynamic lubrication of soft viscoelastic materials in line contact. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 1997, 211, 185–194. [Google Scholar] [CrossRef]
- Scaraggi, M.; Persson, B. Theory of viscoelastic lubrication. Tribol. Int. 2014, 72, 118–130. [Google Scholar] [CrossRef]
- Pandey, A.; Karpitschka, S.; Venner, C.H.; Snoeijer, J.H. Lubrication of soft viscoelastic solids. J. Fluid Mech. 2016, 799, 433–447. [Google Scholar] [CrossRef][Green Version]
- Putignano, C.; Dini, D. Soft Matter Lubrication: Does Solid Viscoelasticity Matter? ACS Appl. Mater. Interfaces 2017, 9, 42287–42295. [Google Scholar] [CrossRef]
- Putignano, C. Soft lubrication: A generalized numerical methodology. J. Mech. Phys. Solids 2019, 134, 103748. [Google Scholar] [CrossRef]
- Putignano, C.; Campanale, A. Squeeze lubrication between soft solids: A numerical study. Tribol. Int. 2022, 176, 107824. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, H.; Morales-Espejel, G.; Venner, C. Effects of solid viscoelasticity on elastohydrodynamic lubrication of point contacts. Tribol. Int. 2022, 171, 107562. [Google Scholar] [CrossRef]
- He, T.; Wang, Q.J.; Zhang, X.; Liu, Y.; Li, Z.; Kim, H.J.; Pack, S. Visco-elastohydrodynamic lubrication of layered materials with imperfect layer-substrate interfaces. Int. J. Mech. Sci. 2020, 189, 105993. [Google Scholar] [CrossRef]
- Li, D.; Zhu, C.; Wang, A.; He, T. Modelling visco-elastohydrodynamic lubrication of polymer-based composites. Tribol. Int. 2022, 174, 107716. [Google Scholar] [CrossRef]
- Persson, B. Rubber friction: Role of the flash temperature. J. Phys. Condens. Matter 2006, 18, 7789–7823. [Google Scholar] [CrossRef]
- Persson, B.N.J. Role of Frictional Heating in Rubber Friction. Tribol. Lett. 2014, 56, 77–92. [Google Scholar] [CrossRef]
- Fortunato, G.; Ciaravola, V.; Furno, A.; Lorenz, B.; Persson, B.N.J. General theory of frictional heating with application to rubber friction. J. Phys. Condens. Matter 2015, 27, 175008. [Google Scholar] [CrossRef]
- Putignano, C.; Le Rouzic, J.; Reddyhoff, T.; Carbone, G.; Dini, D. A theoretical and experimental study of viscoelastic rolling contacts incorporating thermal effects. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2014, 228, 1112–1121. [Google Scholar] [CrossRef]
- He, T.; Wang, Q.J.; Zhang, X.; Liu, Y.; Li, Z.; Kim, H.J.; Pack, S. Modeling thermal-visco-elastohydrodynamic lubrication (TVEHL) interfaces of polymer-based materials. Tribol. Int. 2021, 154, 106691. [Google Scholar] [CrossRef]
- Zhang, X.; Gan, R.Z. Dynamic Properties of Human Tympanic Membrane Based on Frequency-Temperature Superposition. Ann. Biomed. Eng. 2013, 41, 205–214. [Google Scholar] [CrossRef] [PubMed]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The Temperature Dependence of Relaxation Mechanisms in Amorphous Polymers and Other Glass-forming Liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Q.J.; He, T.; Liu, Y.; Li, Z.; Kim, H.J.; Pack, S. Fully coupled thermo-viscoelastic (TVE) contact modeling of layered materials considering frictional and viscoelastic heating. Tribol. Int. 2022, 170, 107506. [Google Scholar] [CrossRef]
- Corr, D.T.; Starr, M.J.; Vanderby, R.; Best, T.M. A Nonlinear Generalized Maxwell Fluid Model for Viscoelastic Materials. J. Appl. Mech. 2001, 68, 787–790. [Google Scholar] [CrossRef]
- Zhang, W.; Capilnasiu, A.; Nordsletten, D. Comparative Analysis of Nonlinear Viscoelastic Models Across Common Biomechanical Experiments. J. Elast. 2021, 145, 117–152. [Google Scholar] [CrossRef]
- Balbi, V.; Shearer, T.; Parnell, W.J. A modified formulation of quasi-linear viscoelasticity for transversely isotropic materials under finite deformation. Proc. R. Soc. A Math. Phys. Eng. Sci. 2018, 474, 20180231. [Google Scholar] [CrossRef]
- Henriksen, M. Nonlinear viscoelastic stress analysis—A finite element approach. Comput. Struct. 1984, 18, 133–139. [Google Scholar] [CrossRef]
- Roy, S.; Reddy, J. A finite element analysis of adhesively bonded composite joints with moisture diffusion and delayed failure. Comput. Struct. 1988, 29, 1011–1031. [Google Scholar] [CrossRef]
- Lai, J.; Bakker, A. 3-D schapery representation for non-linear viscoelasticity and finite element implementation. Comput. Mech. 1996, 18, 182–191. [Google Scholar] [CrossRef]
- Haj-Ali, R.M.; Muliana, A.H. Numerical finite element formulation of the Schapery non-linear viscoelastic material model. Int. J. Numer. Methods Eng. 2004, 59, 25–45. [Google Scholar] [CrossRef]
- Shen, Y.; Hasebe, N.; Lee, L. The finite element method of three-dimensional nonlinear viscoelastic large deformation problems. Comput. Struct. 1995, 55, 659–666. [Google Scholar] [CrossRef]
- Mahmoud, F.; El-Shafei, A.; Abdelrahman, A.; Attia, M. Modeling of nonlinear viscoelastic contact problems with large deformations. Appl. Math. Model. 2013, 37, 6730–6745. [Google Scholar] [CrossRef]
- Mahmoud, F.; El-Shafei, A.; Attia, M.; Rahman, A.A. Analysis of quasistatic frictional contact problems in nonlinear viscoelasticity with large deformations. Int. J. Mech. Sci. 2013, 66, 109–119. [Google Scholar] [CrossRef]
- Abdelrahman, A.A.; El-Shafei, A.G.; Mahmoud, F.F. Analysis of steady-state frictional rolling contact problems in Schapery–nonlinear viscoelasticity. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2019, 233, 911–926. [Google Scholar] [CrossRef]
- Mabuchi, K.; Sasada, T. Numerical analysis of elastohydrodynamic squeeze film lubrication of total hip prostheses. Wear 1990, 140, 1–16. [Google Scholar] [CrossRef]
- Wang, C.-T.; Wang, Y.-L.; Chen, Q.-L.; Yang, M.-R. Calculation of Elastohydrodynamic Lubrication Film Thickness for Hip Prostheses During Normal Walking. Tribol. Trans. 1990, 33, 239–245. [Google Scholar] [CrossRef]
- Jagatia, M.; Jalali-Vahid, D.; Jin, Z.M. Elastohydrodynamic lubrication analysis of ultra-high molecular weight polyethylene hip joint replacements under squeeze-film motion. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2001, 215, 141–151. [Google Scholar] [CrossRef]
- Deng, M.; Uhrich, K. Viscoelastic Behaviors of Ultrahigh Molecular Weight Polyethylene under Three-Point Bending and Indentation Loading. J. Biomater. Appl. 2010, 24, 713–732. [Google Scholar] [CrossRef]
- Lu, X.; Meng, Q.; Wang, J.; Jin, Z. Transient viscoelastic lubrication analyses of UHMWPE hip replacements. Tribol. Int. 2018, 128, 271–278. [Google Scholar] [CrossRef]
- Lu, X.; Meng, Q.; Jin, Z. Effects of UHMWPE viscoelasticity on the squeeze-film lubrication of hip replacements. Biosurf. Biotribol. 2021, 7, 60–69. [Google Scholar] [CrossRef]
- Wu, C.; Wang, A.; Ding, W.; Guo, H.; Wang, Z.L. Triboelectric Nanogenerator: A Foundation of the Energy for the New Era. Adv. Energy Mater. 2018, 9, 1802906. [Google Scholar] [CrossRef]
- Jin, C.; Kia, D.S.; Jones, M.; Towfighian, S. On the contact behavior of micro-/nano-structured interface used in vertical-contact-mode triboelectric nanogenerators. Nano Energy 2016, 27, 68–77. [Google Scholar] [CrossRef]
- Yang, W.; Wang, X.; Li, H.; Wu, J.; Hu, Y. Comprehensive contact analysis for vertical-contact-mode triboelectric nanogenerators with micro-/nano-textured surfaces. Nano Energy 2018, 51, 241–249. [Google Scholar] [CrossRef]
- Wang, C.; Wang, X.; Hu, Y.; Li, L.; Li, Z.; Wu, H.; Zhao, Z. Investigation on the adhesive contact and electrical performance for triboelectric nanogenerator considering polymer viscoelasticity. Nano Res. 2021, 14, 4625–4633. [Google Scholar] [CrossRef]
- Zhou, H.; Qin, W.; Yu, Q.; Cheng, H.; Yu, X.; Wu, H. Transfer Printing and its Applications in Flexible Electronic Devices. Nanomaterials 2019, 9, 283. [Google Scholar] [CrossRef]
- Jiang, L.; Wu, M.; Yu, Q.; Shan, Y.; Zhang, Y. Investigations on the Adhesive Contact Behaviors between a Viscoelastic Stamp and a Transferred Element in Microtransfer Printing. Coatings 2021, 11, 1201. [Google Scholar] [CrossRef]
- Wang, M.; Li, H.-B.; Han, J.-Q.; Xiao, X.-H.; Zhou, J.-W. Large deformation evolution and failure mechanism analysis of the multi-freeface surrounding rock mass in the Baihetan underground powerhouse. Eng. Fail. Anal. 2019, 100, 214–226. [Google Scholar] [CrossRef]
- Ma, T.; Tang, C.; Tang, L.; Zhang, W.; Wang, L. Rockburst characteristics and microseismic monitoring of deep-buried tunnels for Jinping II Hydropower Station. Tunn. Undergr. Space Technol. 2015, 49, 345–368. [Google Scholar] [CrossRef]
- Sun, T.; Wang, K.; Iinuma, T.; Hino, R.; He, J.; Fujimoto, H.; Kido, M.; Osada, Y.; Miura, S.; Ohta, Y.; et al. Prevalence of viscoelastic relaxation after the 2011 Tohoku-oki earthquake. Nature 2014, 514, 84–87. [Google Scholar] [CrossRef]
- Cheng, X.; Tang, C.; Zhuang, D. A finite-strain viscoelastic-damage numerical model for time-dependent failure and instability of rocks. Comput. Geotech. 2022, 143, 104596. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).