Full and Hybrid Multiscale Lubrication Modeling
Abstract
1. Introduction
2. Materials and Methods
2.1. Model Equations
- is the streamline length of an element;
- , is the Peclet number of an element;
- .
- is the subdomain where is not null;
- ;
- .
2.2. Tested Cavitation Algorithms
2.2.1. Elrod’s Algorithm, the Reference
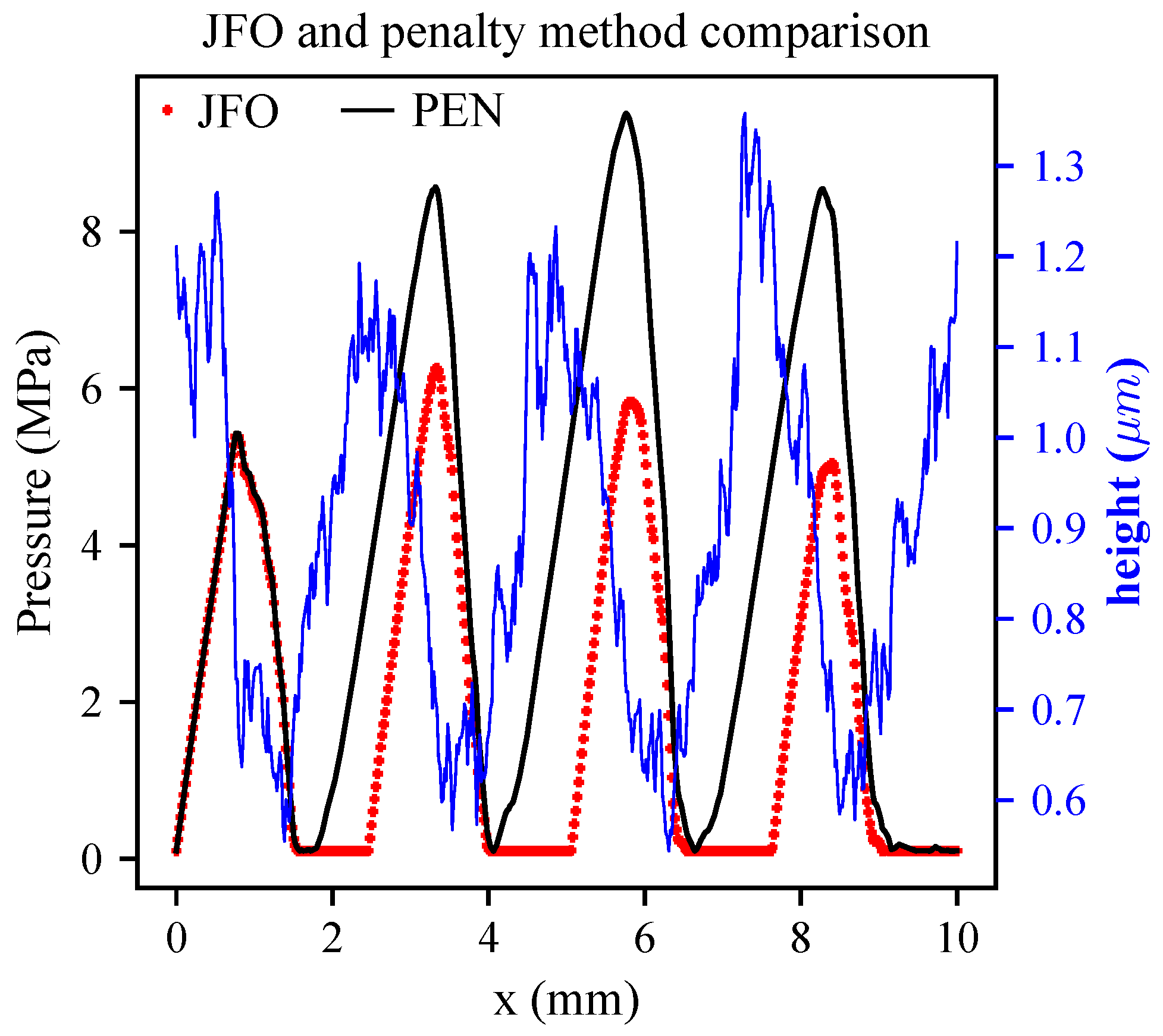
2.2.2. The Penalty Method
2.2.3. The Lubricant General Model
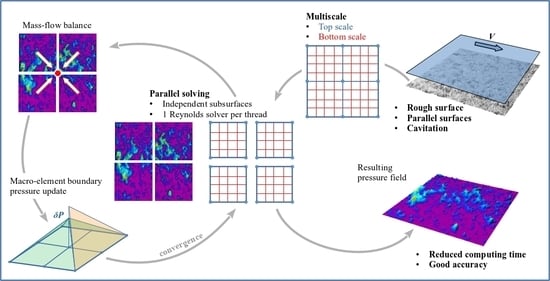
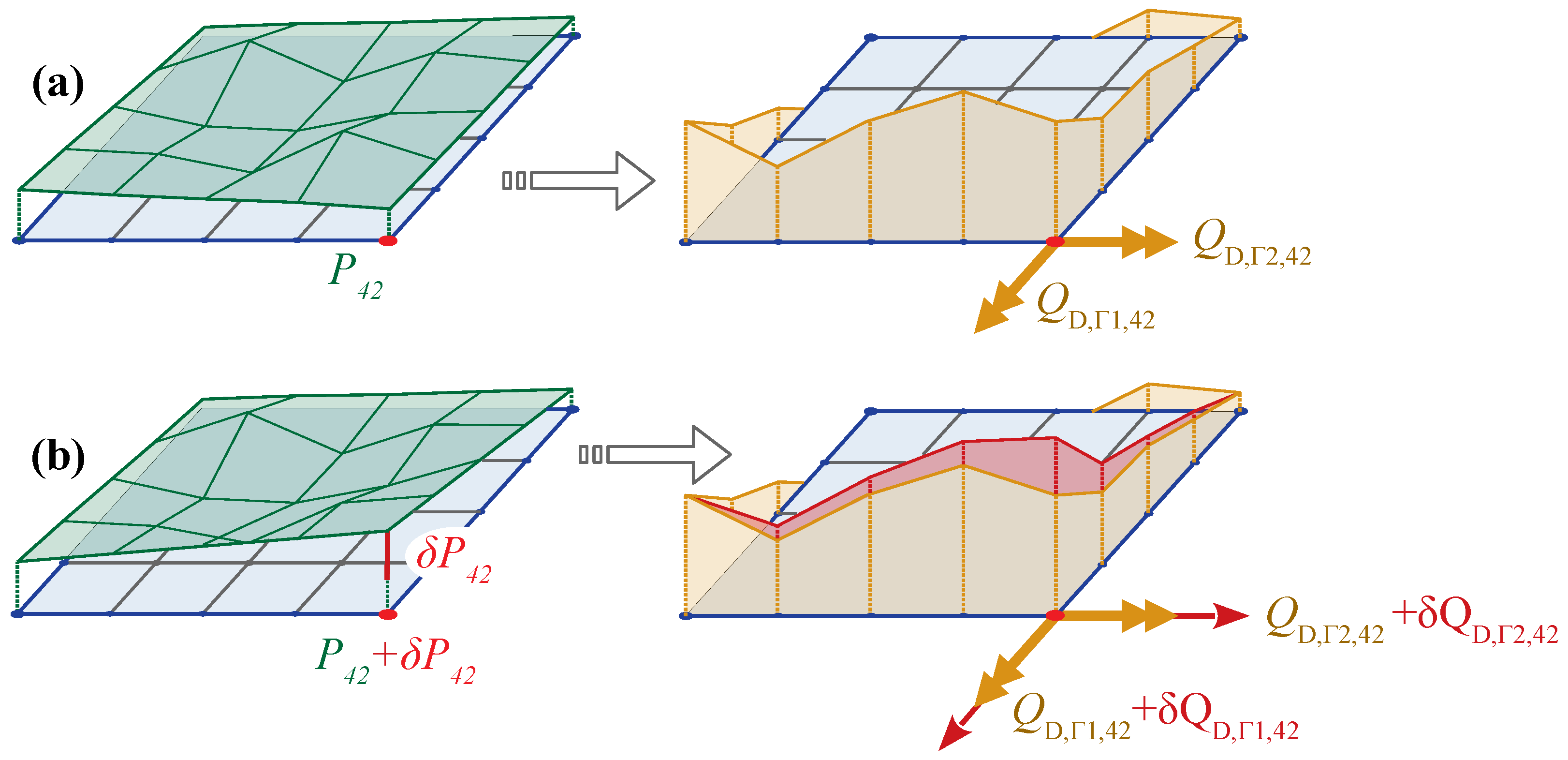
2.3. The Multiscale Approach
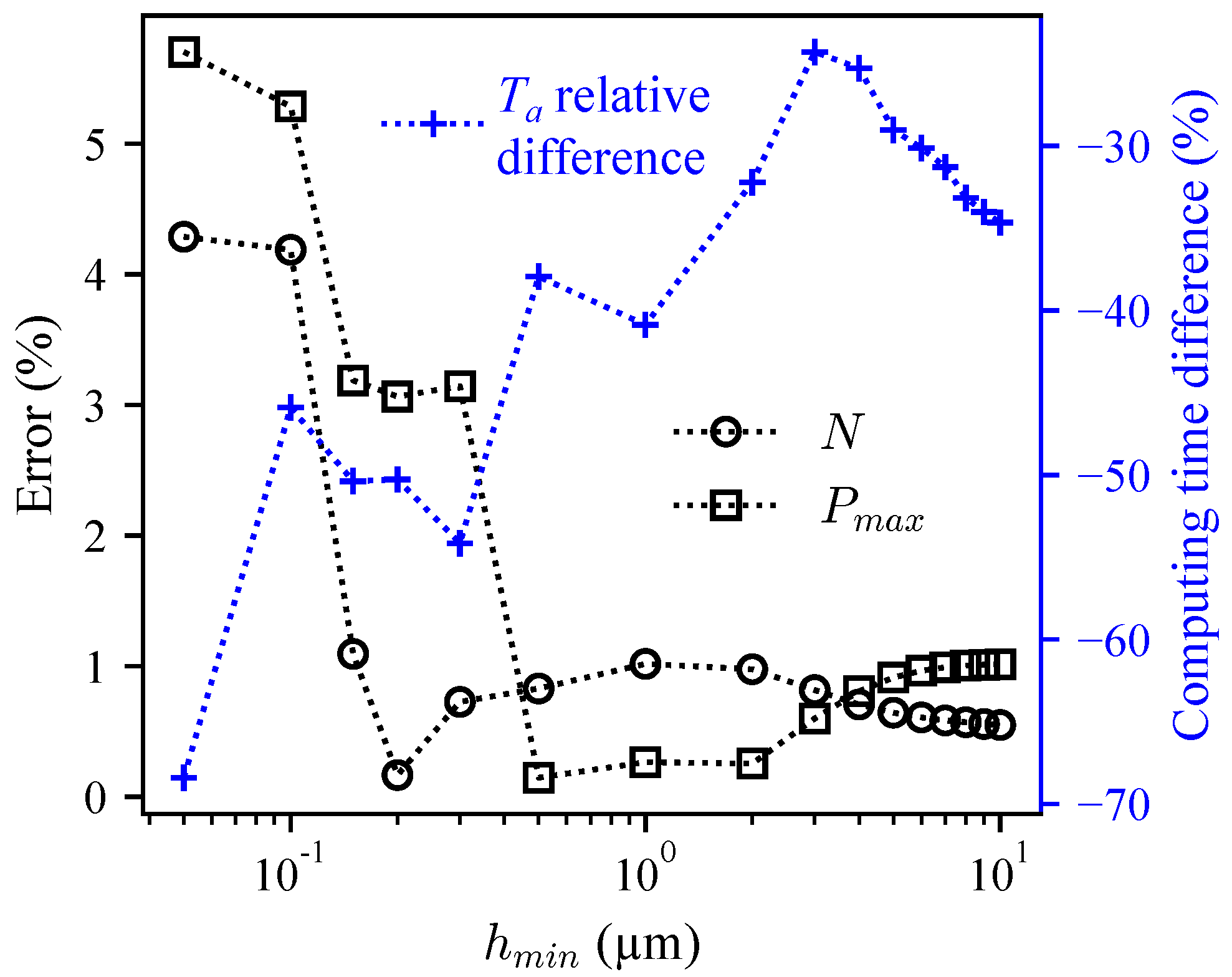
3. Results and Discussion
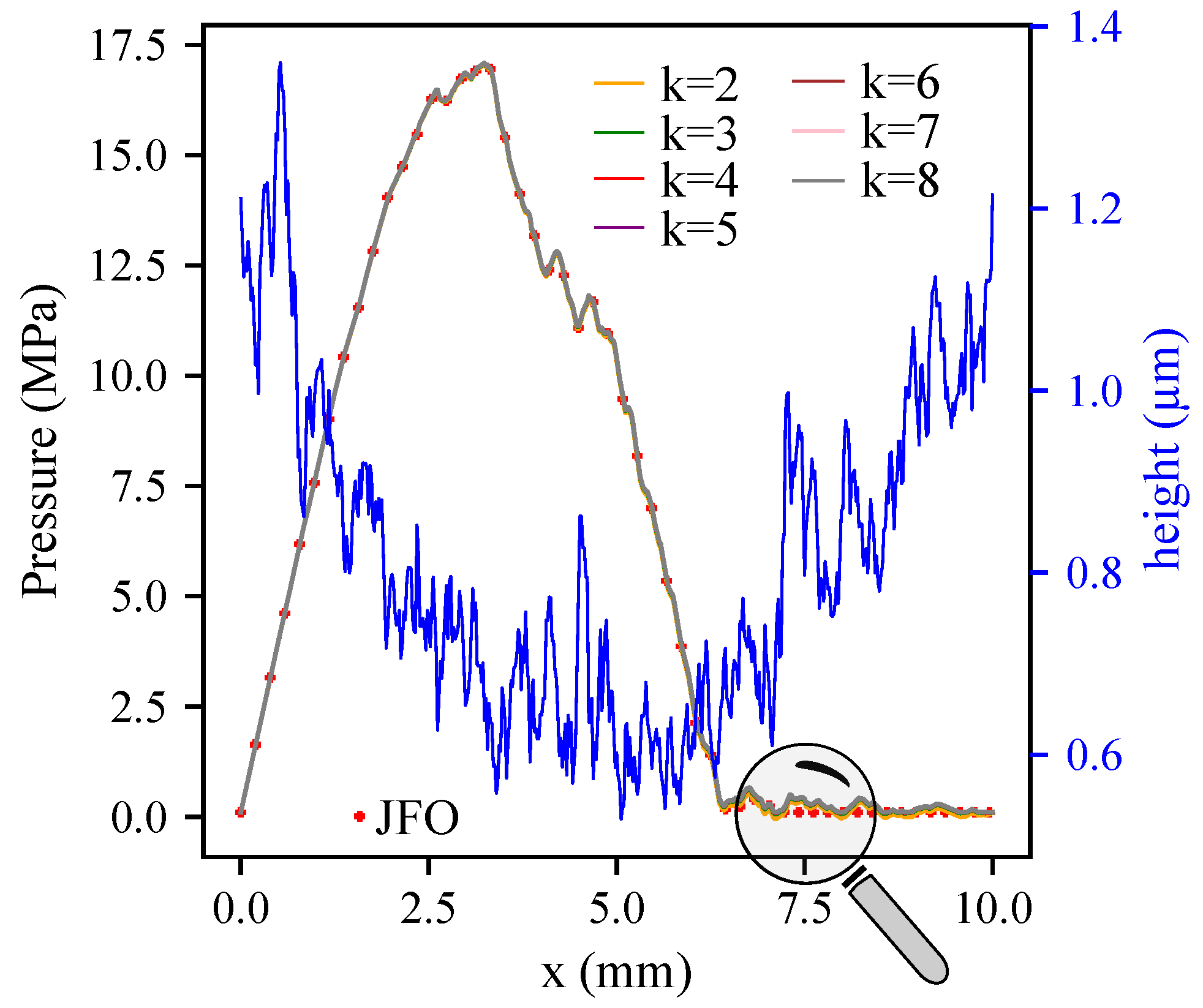
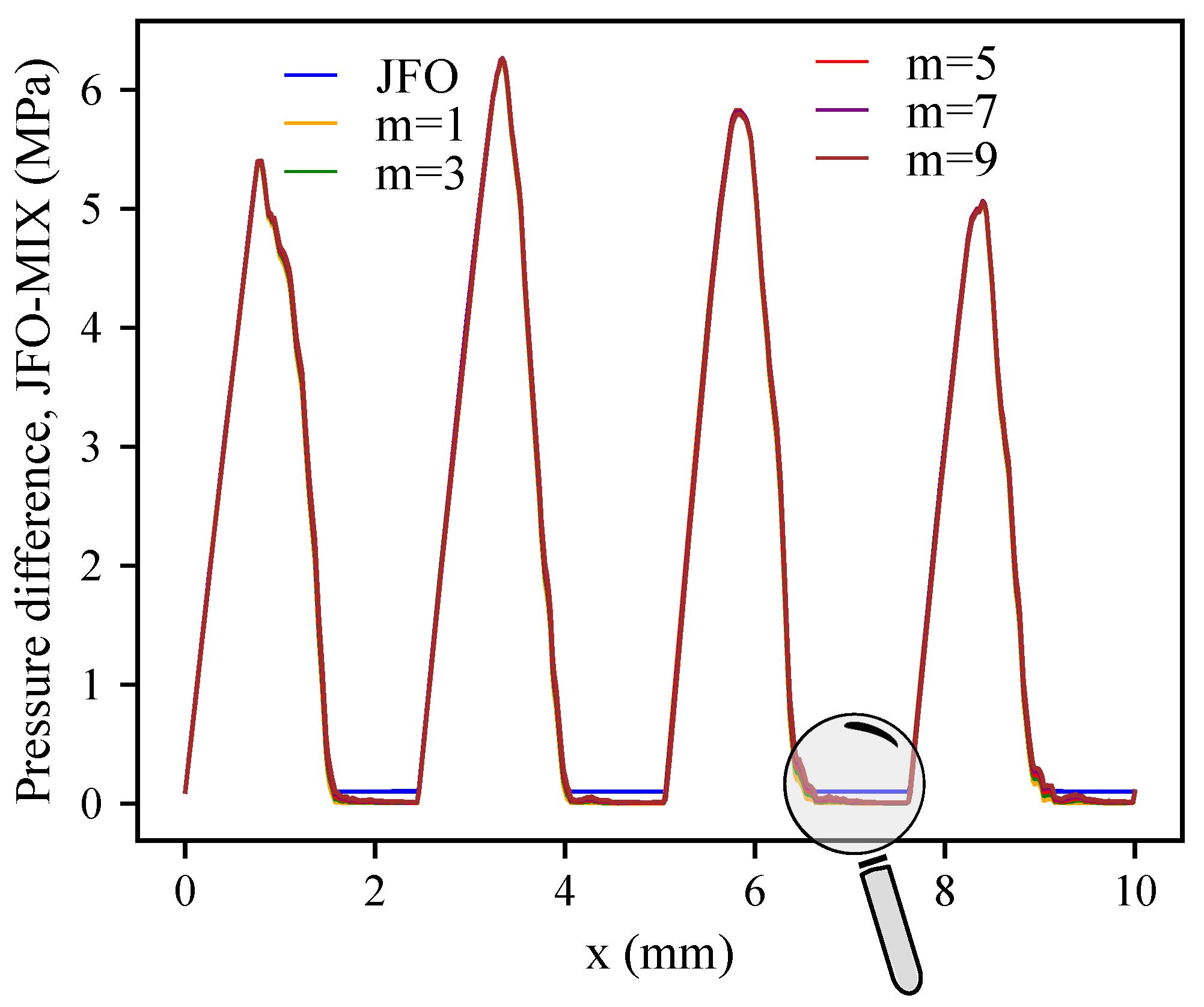
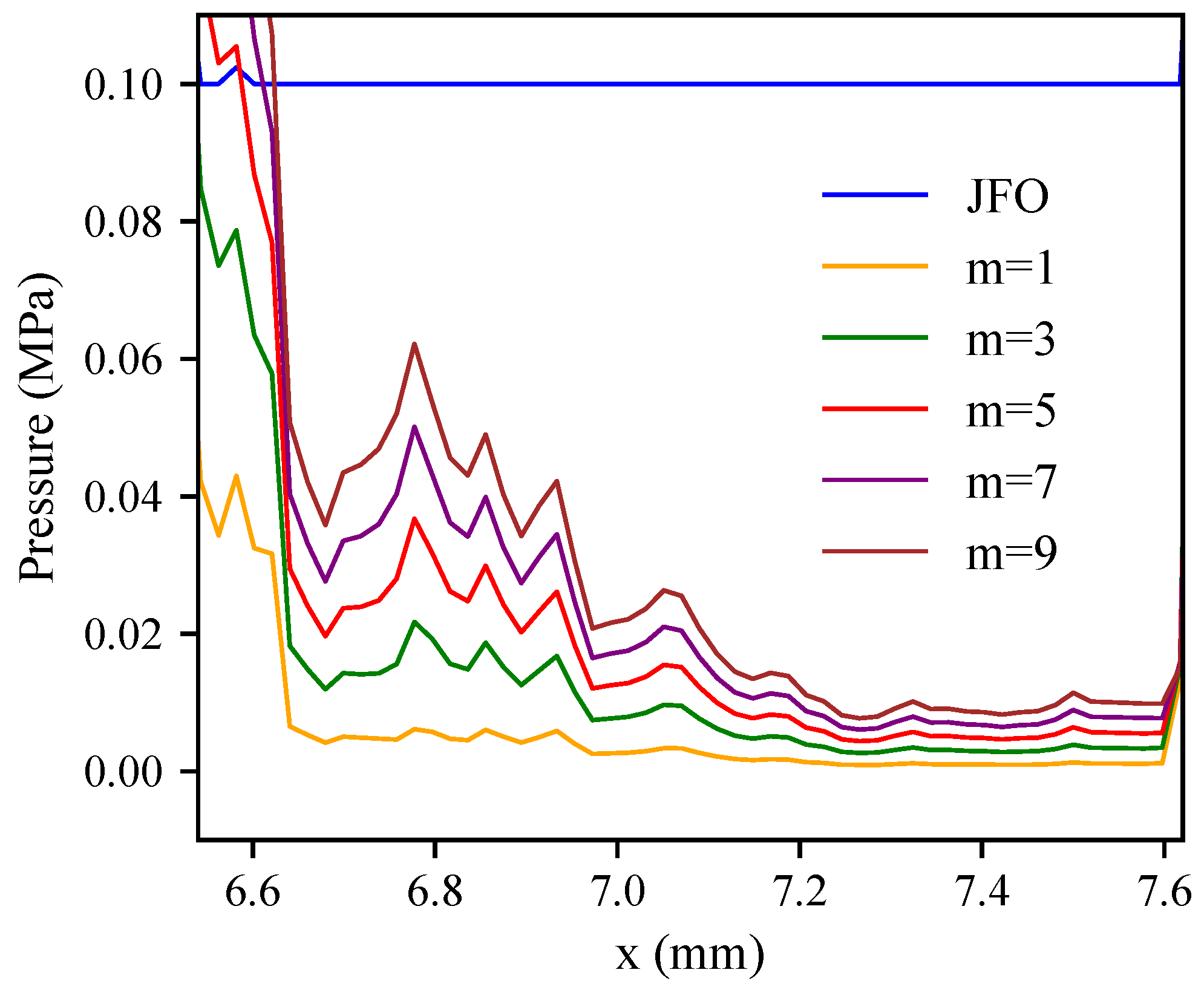
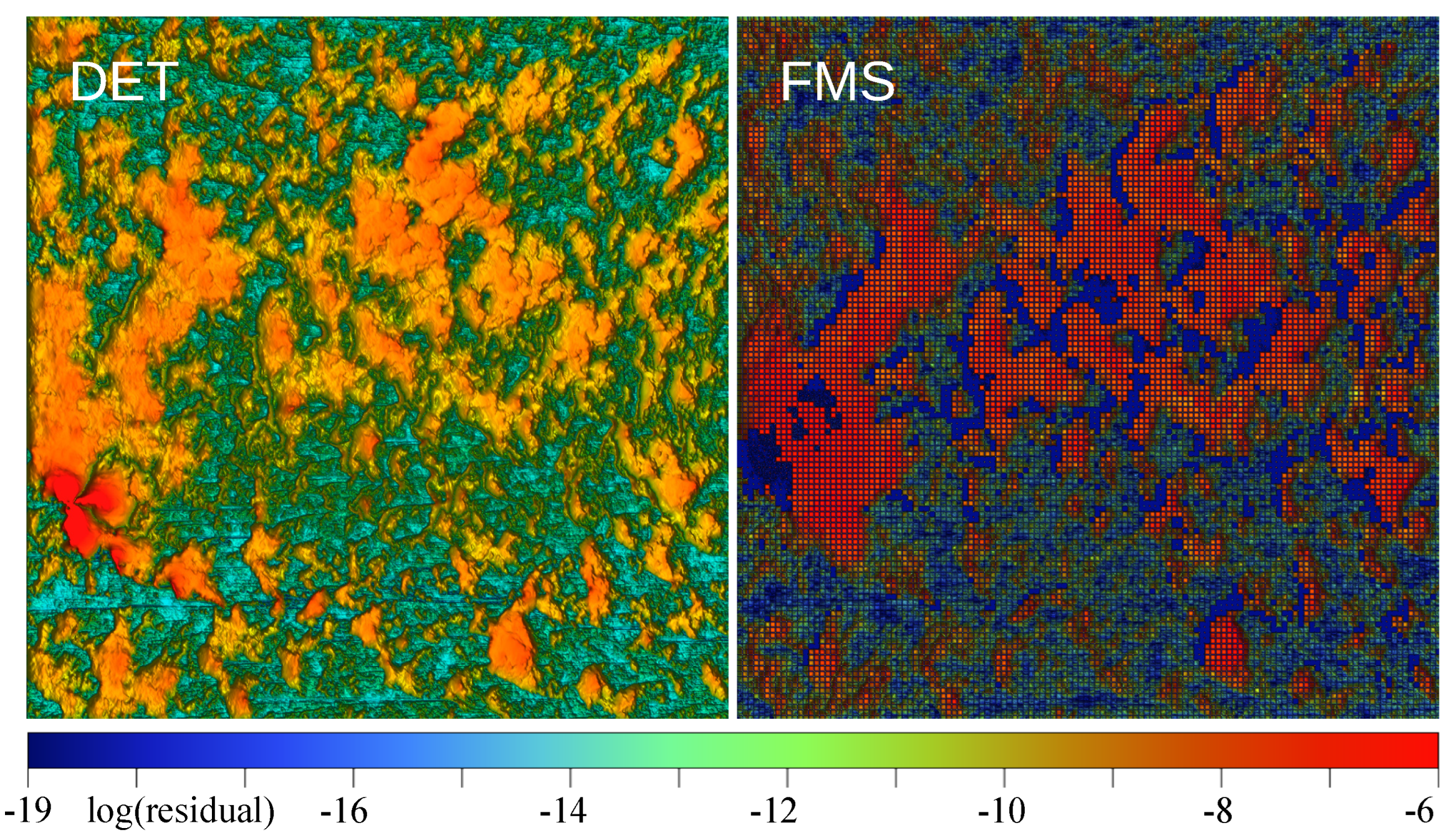
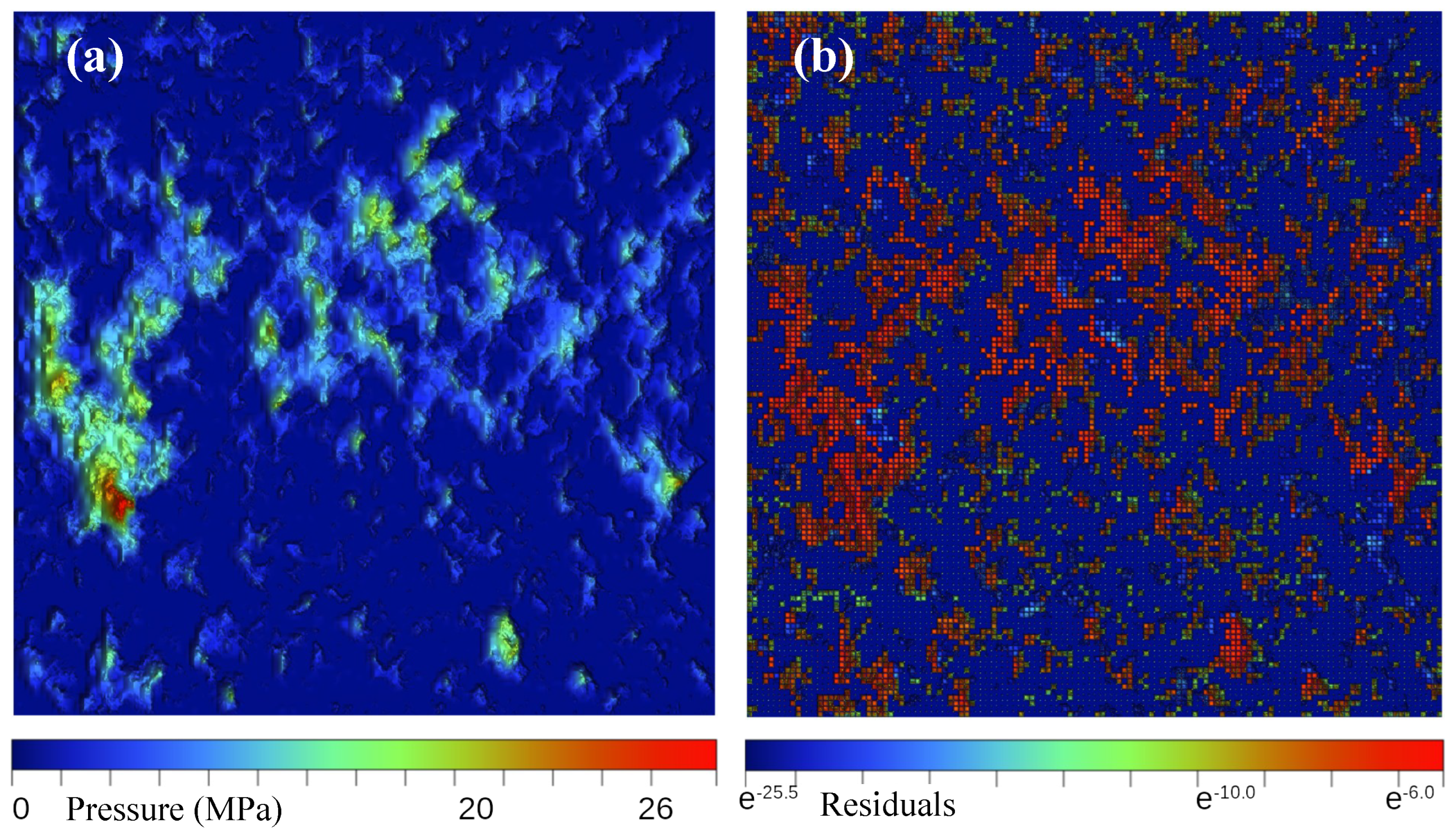
3.1. Deterministic Case
3.2. FMS, Full Multiscale
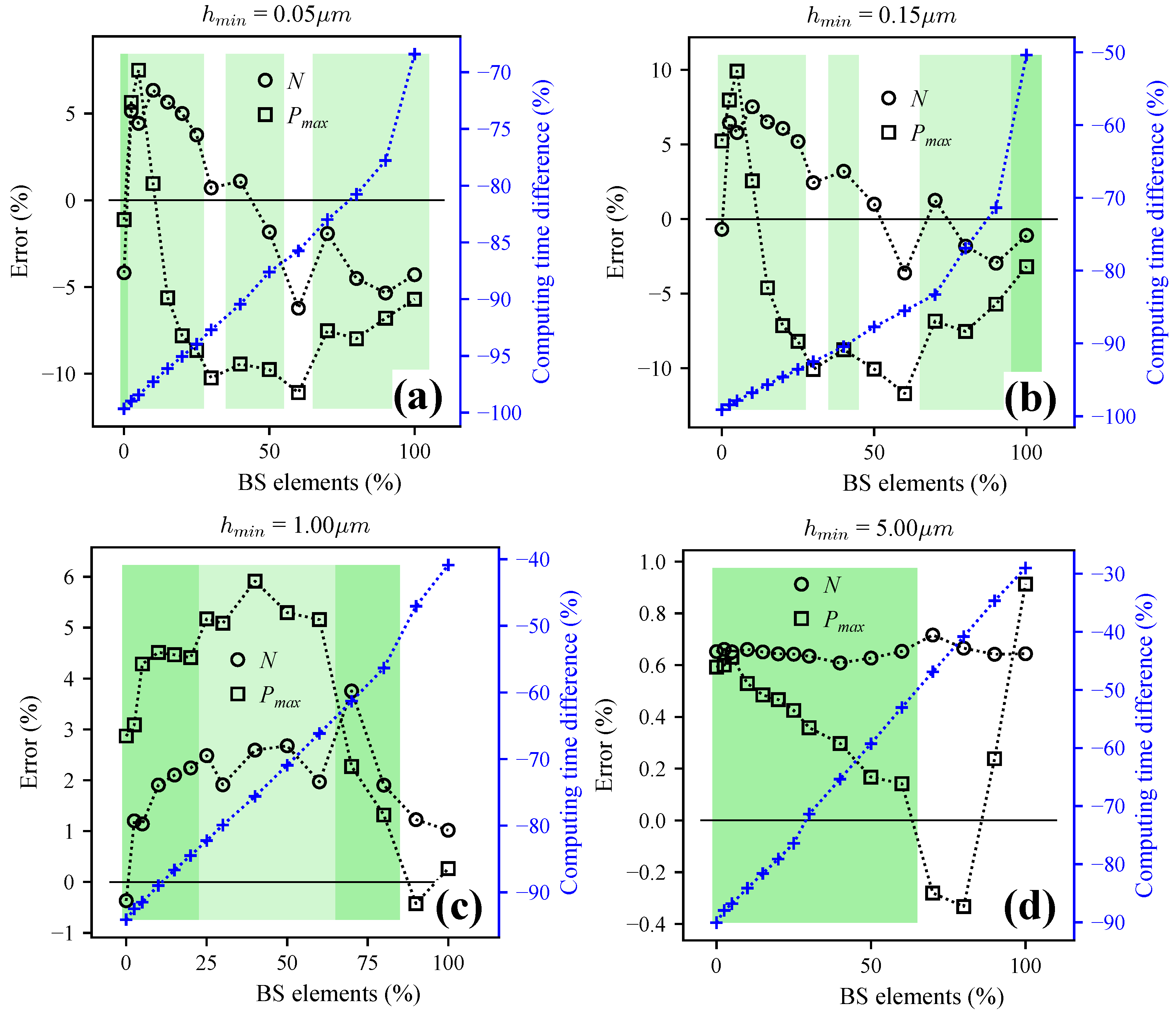
3.3. Beyond FMS: Hybrid Multiscale (HMS)
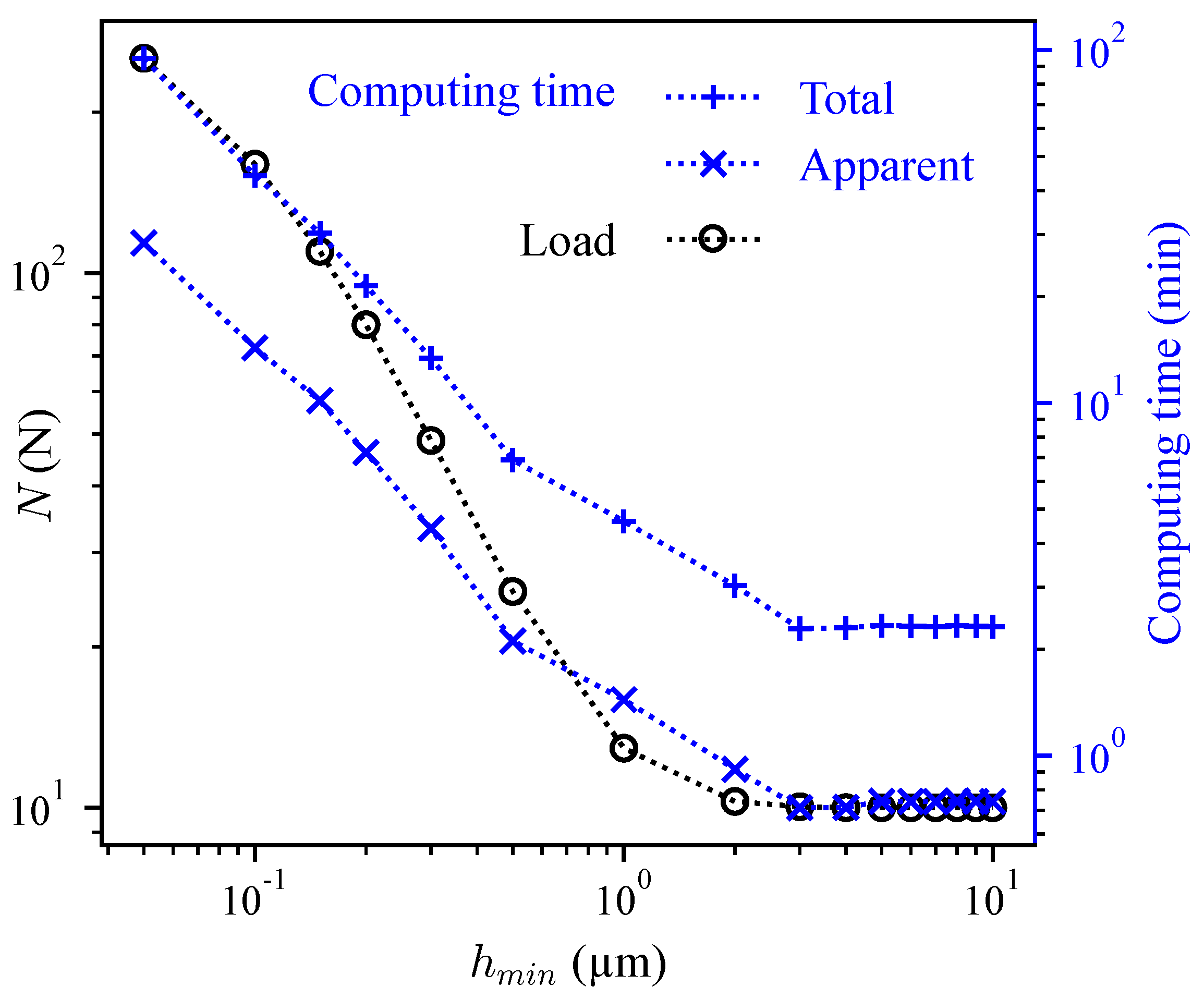
3.4. Mesh Size Reduction
4. Conclusions
- 1.
- Shorter wavelengths— and mm;
- 2.
- Rough texturized surfaces—square dimples being modeled with simple FEM macro-elements, and rough contacting parts discretized with BS elements;
- 3.
- As many threads as there are macro-elements—which leads to a GPU implementation of the numerical code.
- 1.
- The TS element boundaries are updated once the whole TS element batch is processed. However, some TS elements converge slowly—mainly because of a local narrow slider gap. Therefore, a new criterion has to be set up to locally guarantee the best compromise accuracy/iteration number.
- 2.
- The TS element boundary update must be monitored because important changes in the TS pressure field affect the four other connected macro-elements—in particular, oscillations are undesirable.
- 3.
- The heights of the element boundaries are the result of the domain division, and this can lead to rough relief for some of them, with convergence problems. In a future work, a sensitivity analysis will study the effect of numerically smoothed boundaries on the slider lubrication. We are confident that the results will not change much and that the Reynolds equation will be solved faster on TS elements.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BS | Bottom Scale |
| FEM | Finite Element Method |
| FMS | Full Multiscale |
| HMS | Hybrid Multiscale |
| LGM | Lubricant General Model |
| MIX | MIXture, same as GLM |
| TS | Top Scale; TS element = a macro-element. |
Nomenclature
| Reynolds equation | |
| e | finite element |
| h | film thickness |
| p | pressure |
| streamline length of an element e | |
| N | slider normal load |
| shape and weighting function at node i | |
| cavitation pressure | |
| Reynolds equation residual at node i | |
| slider speed vector | |
| element right-hand side | |
| element elementary matrix | |
| pressure increment at node j | |
| fluid dynamic viscosity | |
| lubricated contact domain | |
| fluid density | |
| Penalty method | |
| arbitrary chosen coefficient for the penalty method | |
| penalty coefficient, | |
| Elrod algorithm | |
| fluid volume fraction | |
| General model | |
| p | partial pressure |
| the specific gas constant; for dry air | |
| liquid concentration of a species a | |
| Henry’s constant of a species a | |
| atmospheric pressure, | |
| mass fraction | |
| Multiscale | |
| film thickness threshold | |
| n | , total number of BS nodes |
| number of bottom-scale (BS) elements of a TS element, along x or y | |
| number of top-scale (TS) elements, or macro-elements, along x or y | |
| BS | Bottom scale |
| P | TS pressure |
| Q | TS nodal mass flow |
| TS | Top scale |
| subdivided macro-element FEM right-hand side | |
| subdivided macro-element FEM system matrix | |
References
- Wu, S.R. A Penalty Formulation and Numerical Approximation of the Reynolds-Hertz Problem of Elastohydrodynamic Lubrication. Int. J. Eng. Sci. 1986, 24, 1001–1013. [Google Scholar] [CrossRef]
- Elrod, H.G.; Adams, M.L. A Computer Program for Cavitation and Starvation Problems. In Proceedings of the 1st Leeds—Lyon Symposium on Tribology, Leeds, UK, September 1974; Mechanical Engineering Publications Ltd.: Leeds, UK, 1974. [Google Scholar]
- Elrod, H.G. A Cavitation Algorithm. J. Lubr. Technol. 1981, 103, 350–354. [Google Scholar] [CrossRef]
- Braun, M.J.; Hannon, W.M. Cavitation Formation and Modelling for Fluid Film Bearings: A Review. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 839–863. [Google Scholar] [CrossRef]
- Bai, L.; Yan, J.; Zeng, Z.; Ma, Y. Cavitation in Thin Liquid Layer: A Review. Ultrason. Sonochemistry 2020, 66, 105092. [Google Scholar] [CrossRef]
- Belova, V.; Krasowska, M.; Wang, D.; Ralston, J.; Shchukin, D.G.; Möhwald, H. Influence of Adsorbed Gas at Liquid/Solid Interfaces on Heterogeneous Cavitation. Chem. Sci. 2012, 4, 248–256. [Google Scholar] [CrossRef]
- Li, X.S.; Song, Y.; Hao, Z.R.; Gu, C.W. Cavitation Mechanism of Oil-Film Bearing and Development of a New Gaseous Cavitation Model Based on Air Solubility. J. Tribol. 2012, 134, 031701. [Google Scholar] [CrossRef]
- Song, Y.; Gu, C.W. Development and Validation of a Three-Dimensional Computational Fluid Dynamics Analysis for Journal Bearings Considering Cavitation and Conjugate Heat Transfer. J. Eng. Gas Turbines Power 2015, 137, 122502. [Google Scholar] [CrossRef]
- Hao, Z.R.; Gu, C.w. Numerical Modeling for Gaseous Cavitation of Oil Film and Non-Equilibrium Dissolution Effects in Thrust Bearings. Tribol. Int. 2014, 78, 14–26. [Google Scholar] [CrossRef]
- Ding, A.; Ren, X.; Li, X.; Gu, C. A New Gaseous Cavitation Model in a Tilting-Pad Journal Bearing. Sci. Prog. 2021, 104, 00368504211029431. [Google Scholar] [CrossRef]
- Ransegnola, T.; Sadeghi, F.; Vacca, A. An Efficient Cavitation Model for Compressible Fluid Film Bearings. Tribol. Trans. 2021, 64, 434–453. [Google Scholar] [CrossRef]
- Magaletti, F.; Gallo, M.; Casciola, C.M. Water Cavitation from Ambient to High Temperatures. Sci. Rep. 2021, 11, 20801. [Google Scholar] [CrossRef]
- Brunetière, N. A General Model for Liquid and Gas Lubrication, Including Cavitation. J. Tribol. 2018, 140, 021702. [Google Scholar] [CrossRef]
- Grützmacher, P.G.; Profito, F.J.; Rosenkranz, A. Multi-Scale Surface Texturing in Tribology—Current Knowledge and Future Perspectives. Lubricants 2019, 7, 95. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. An Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication. J. Lubr. Technol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. Application of Average Flow Model to Lubrication Between Rough Sliding Surfaces. J. Lubr. Technol. 1979, 101, 220–229. [Google Scholar] [CrossRef]
- Harp, S.R.; Salant, R.F. An Average Flow Model of Rough Surface Lubrication with Inter-Asperity Cavitation. J. Tribol. 2000, 123, 134–143. [Google Scholar] [CrossRef]
- Elrod, H.G. A General Theory for Laminar Lubrication with Reynolds Roughness. J. Lubr. Technol. 1979, 101, 8–14. [Google Scholar] [CrossRef]
- Bayada, G.; Faure, J.B. A Double Scale Analysis Approach of the Reynolds Roughness Comments and Application to the Journal Bearing. J. Tribol. 1989, 111, 323–330. [Google Scholar] [CrossRef]
- Bayada, G.; Martin, S.; Vázquez, C. An Average Flow Model of the Reynolds Roughness Including a Mass-Flow Preserving Cavitation Model. J. Tribol. 2005, 127, 793–802. [Google Scholar] [CrossRef]
- de Boer, G.N.; Gao, L.; Hewson, R.W.; Thompson, H.M.; Raske, N.; Toropov, V.V. A Multiscale Method for Optimising Surface Topography in Elastohydrodynamic Lubrication (EHL) Using Metamodels. Struct. Multidiscip. Optim. 2016, 54, 483–497. [Google Scholar] [CrossRef]
- de Boer, G.N.; Gao, L.; Hewson, R.W.; Thompson, H.M. Heterogeneous Multiscale Methods for Modelling Surface Topography in Elastohydrodynamic Lubrication Line Contacts. Tribol. Int. 2017, 113, 262–278. [Google Scholar] [CrossRef]
- de Boer, G.; Almqvist, A. On the Two-Scale Modelling of Elastohydrodynamic Lubrication in Tilted-Pad Bearings. Lubricants 2018, 6, 78. [Google Scholar] [CrossRef]
- Han, Y.; Meng, Q.; de Boer, G. Two-Scale Homogenization of Hydrodynamic Lubrication in a Mechanical Seal with Isotropic Roughness Based on the Elrod Cavitation Algorithm. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2022, 236, 359–385. [Google Scholar] [CrossRef]
- Rom, M.; König, F.; Müller, S.; Jacobs, G. Why Homogenization Should Be the Averaging Method of Choice in Hydrodynamic Lubrication. Appl. Eng. Sci. 2021, 7, 100055. [Google Scholar] [CrossRef]
- Sen, O.T.; Akalin, O. A Multiscale Cylinder Bore Honing Pattern Lubrication Model for Improved Engine Friction. SAE Int. J. Fuels Lubr. 2019, 12, 155–166. [Google Scholar] [CrossRef]
- König, F.; Rosenkranz, A.; Grützmacher, P.G.; Mücklich, F.; Jacobs, G. Effect of Single- and Multi-Scale Surface Patterns on the Frictional Performance of Journal Bearings—A Numerical Study. Tribol. Int. 2020, 143, 106041. [Google Scholar] [CrossRef]
- Shisode, M.; Hazrati, J.; Mishra, T.; de Rooij, M.; van den Boogaard, T. Mixed Lubrication Friction Model Including Surface Texture Effects for Sheet Metal Forming. J. Mater. Process. Technol. 2021, 291, 117035. [Google Scholar] [CrossRef]
- Annadi, R.R.; Ismail, S. Tribological Performance of Textured Parallel Sliding Contact under Mixed Lubrication Condition by Considering Mass Conservation Condition and Couple-Stress Parameter. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 235, 410–422. [Google Scholar] [CrossRef]
- Annadi, R.R.; Syed, I. Tribological Study of Multi-Scale Textured Parallel Sliding Contacts by Considering a Mixed Lubrication Regime and Mass Conservation Condition. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2022, 236, 807–822. [Google Scholar] [CrossRef]
- Lebeck, A.O. Parallel Sliding Load Support in the Mixed Friction Regime. Part 1—The Experimental Data. J. Tribol. 1987, 109, 189–195. [Google Scholar] [CrossRef]
- Lebeck, A.O. Parallel Sliding Load Support in the Mixed Friction Regime. Part 2—Evaluation of the Mechanisms. J. Tribol. 1987, 109, 196–205. [Google Scholar] [CrossRef]
- Nyemeck, A.P.; Brunetière, N.; Tournerie, B. A Multiscale Approach to the Mixed Lubrication Regime: Application to Mechanical Seals. Tribol. Lett. 2012, 47, 417–429. [Google Scholar] [CrossRef]
- Brunetière, N.; Francisco, A. Lubrication Mechanisms Between Parallel Rough Surfaces. Tribol. Lett. 2019, 67, 116. [Google Scholar] [CrossRef]
- Brunetiere, N.; Wang, Q.J. Large-Scale Simulation of Fluid Flows for Lubrication of Rough Surfaces. J. Tribol. 2014, 136, 011701. [Google Scholar] [CrossRef]
- Pei, S.; Ma, S.; Xu, H.; Wang, F.; Zhang, Y. A Multiscale Method of Modeling Surface Texture in Hydrodynamic Regime. Tribol. Int. 2011, 44, 1810–1818. [Google Scholar] [CrossRef]
- Pei, S.; Xu, H.; Shi, F. A Deterministic Multiscale Computation Method for Rough Surface Lubrication. Tribol. Int. 2016, 94, 502–508. [Google Scholar] [CrossRef]
- Brunetière, N.; Francisco, A. Multiscale Modeling Applied to the Hydrodynamic Lubrication of Rough Surfaces for Computation Time Reduction. Lubricants 2018, 6, 83. [Google Scholar] [CrossRef]
- Wikipedia. Henry’s Law. 2020. Available online: https://en.wikipedia.org/wiki/Henry’s_law (accessed on 26 October 2022).
- Sander, R. Compilation of Henry’s Law Constants (Version 4.0) for Water as Solvent. Atmos. Chem. Phys. 2015, 15, 4399–4981. [Google Scholar] [CrossRef]
- Grando, F.P.; Priest, M.; Prata, A.T. A Two-Phase Flow Approach to Cavitation Modelling in Journal Bearings. Tribol. Lett. 2006, 21, 233. [Google Scholar] [CrossRef]
- Amestoy, P.R.; Duff, I.S.; L’Excellent, J.Y.; Koster, J. A Fully Asynchronous Multifrontal Solver Using Distributed Dynamic Scheduling. SIAM J. Matrix Anal. Appl. 2001, 23, 15–41. [Google Scholar] [CrossRef]
- Amestoy, P.R.; Buttari, A.; L’Excellent, J.Y.; Mary, T. Performance and Scalability of the Block Low-Rank Multifrontal Factorization on Multicore Architectures. ACM Trans. Math. Softw. 2019, 45, 1–26. [Google Scholar] [CrossRef]

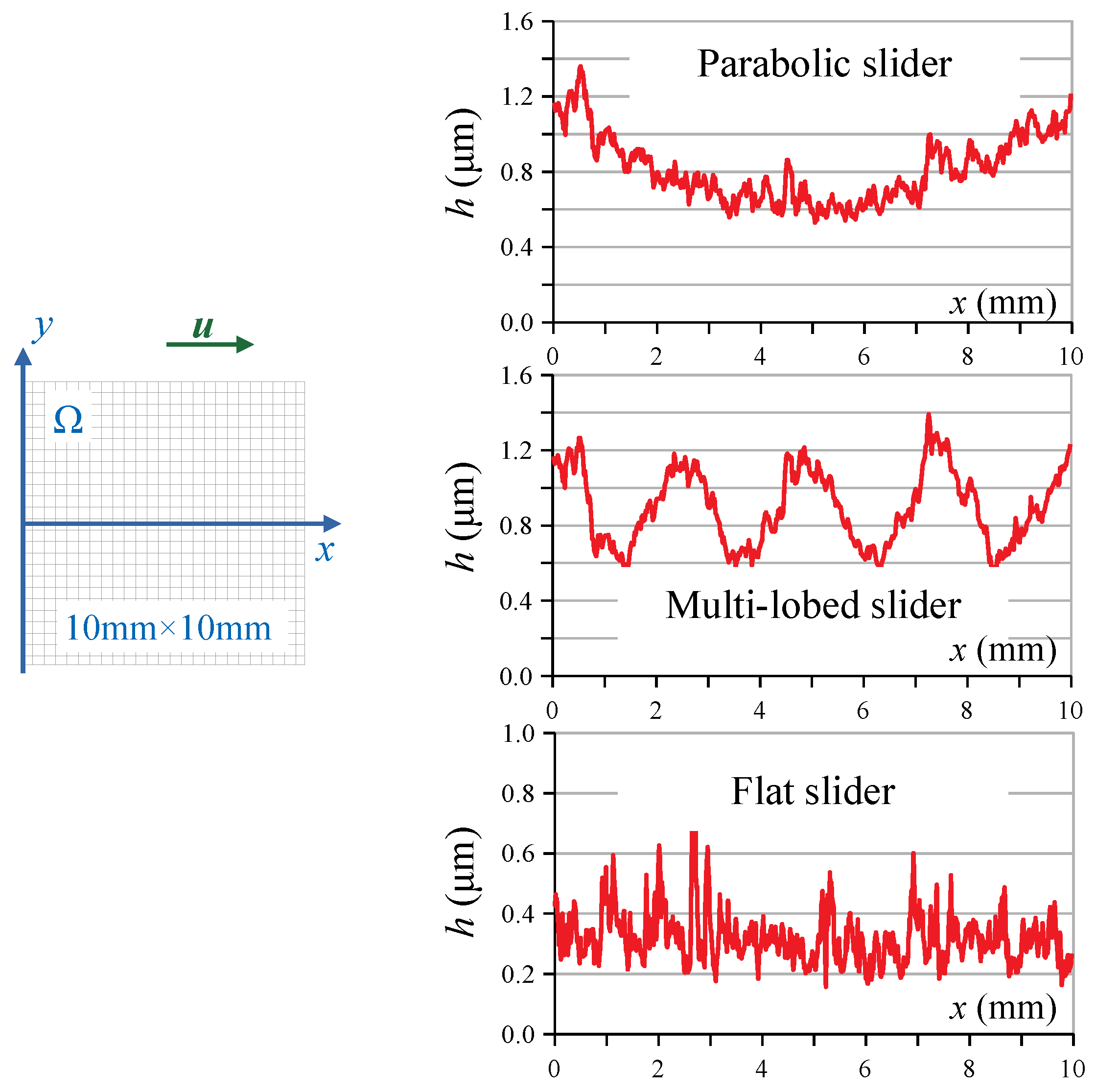






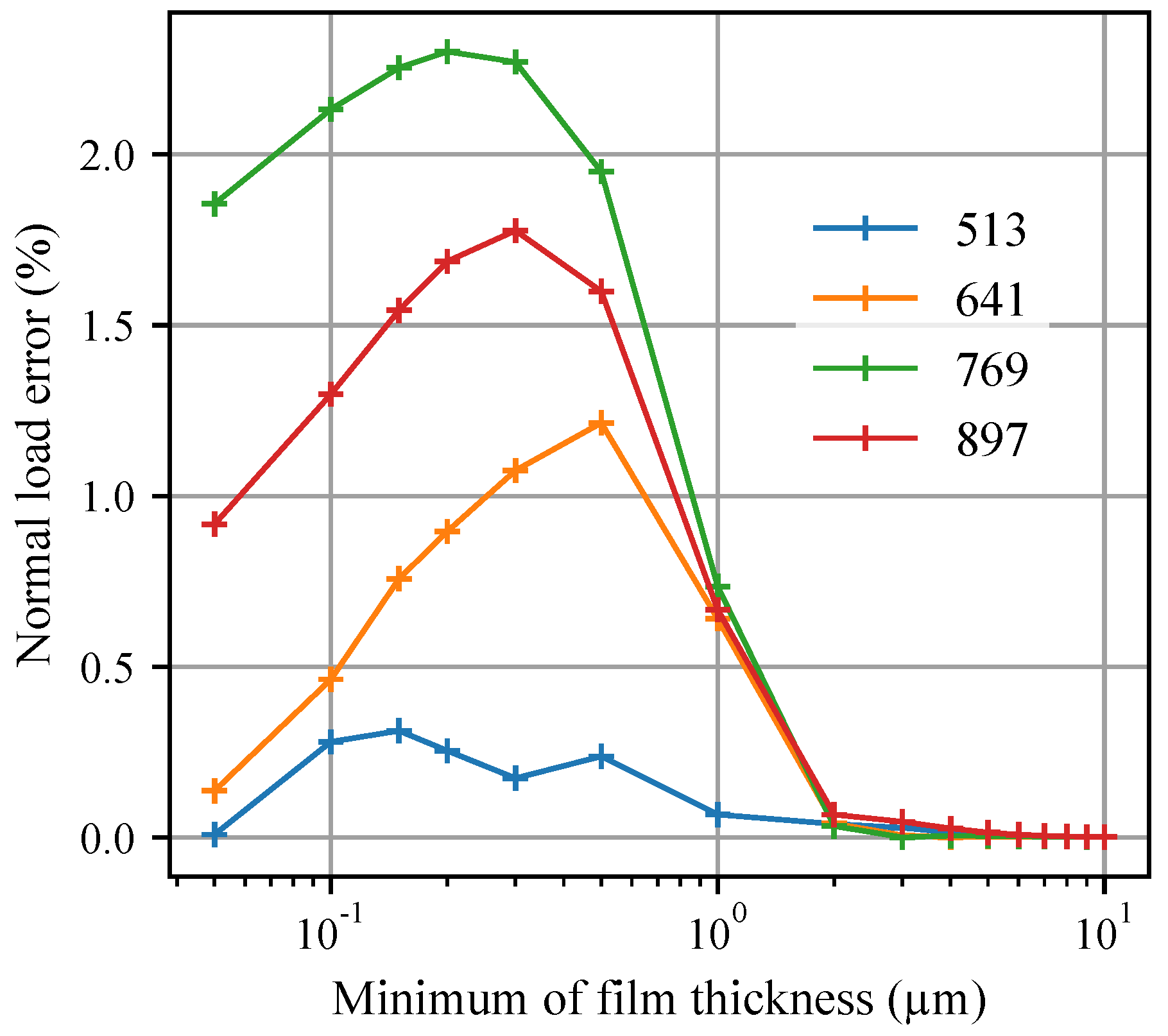

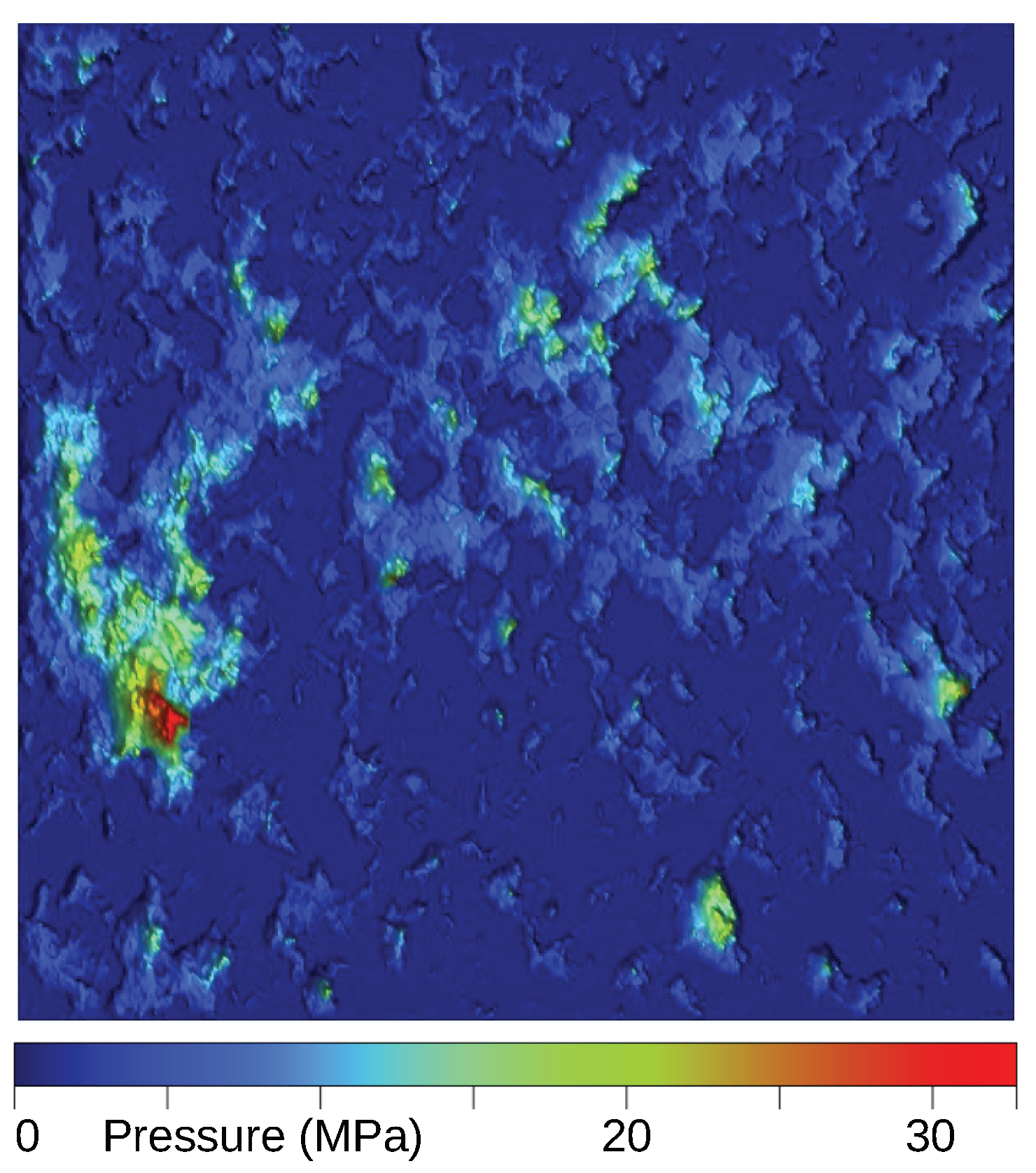
| Parameter | Value |
|---|---|
| Minimum of the film thickness | to |
| Fluid type | mixture (liquid and gas) |
| Top-scale mesh, elements | |
| Bottom-scale meshes, elements | |
| Sliding speed along x | |
| Fluid viscosity | |
| Fluid density | |
| Ambient pressure |
| Parameter | Value |
|---|---|
| Surface type | numerically generated |
| Numerical size points (nodes) | |
| Physical size, | 1 × 1 |
| RMS roughness, | 0.1 |
| Roughness skewness, | −1.4 |
| Roughness kurtosis, | 6.3 |
| Autocorrelation length, | 124 |
| Ratio of domain length to correlation length , | 80.4 |
| JFO | ||||||||
| 33 | 29 | 34 | 39 | 43 | 47 | 52 | 63 | |
| cpu (s) | 317.7 | 266.7 | 309.5 | 361.9 | 402.2 | 434.7 | 606.3 | 614.1 |
| Load (N) | 480.7 | 481.7 | 486.2 | 487.3 | 487.5 | 487.5 | 487.6 | 487.6 |
| JFO | ||||||
| 22 | 19 | 17 | 16 | 18 | 22 | |
| cpu (s) | 231.9 | 181.4 | 161.6 | 152.2 | 171.1 | 226.8 |
| Load (N) | 127.9 | 125.7 | 127.1 | 127.8 | 128.0 | 127.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Francisco, A.; Brunetière, N. Full and Hybrid Multiscale Lubrication Modeling. Lubricants 2022, 10, 329. https://doi.org/10.3390/lubricants10120329
Francisco A, Brunetière N. Full and Hybrid Multiscale Lubrication Modeling. Lubricants. 2022; 10(12):329. https://doi.org/10.3390/lubricants10120329
Chicago/Turabian StyleFrancisco, Arthur, and Noël Brunetière. 2022. "Full and Hybrid Multiscale Lubrication Modeling" Lubricants 10, no. 12: 329. https://doi.org/10.3390/lubricants10120329
APA StyleFrancisco, A., & Brunetière, N. (2022). Full and Hybrid Multiscale Lubrication Modeling. Lubricants, 10(12), 329. https://doi.org/10.3390/lubricants10120329