Abstract
Monitoring the thermal state of windings of electrical machines is a backbone for protection from unacceptable overheating. A large number of different methods and systems aim to solve this problem. This article discusses the main known methods of thermal protection of electric motors and provides their comparative analysis. This paper shows that the most promising methods are those based on control of the current active resistance of the stator winding, as its value uniquely depends on temperature. It is demonstrated that the known methods have a number of disadvantages. A new phase method for thermal protection of AC motors is proposed. The method is based on the fact that a temperature-induced change in the active and reactive components of the winding impedance causes a corresponding change in the angle between the vectors of phase voltages and currents. This allows for thermal protection by controlling the change in this angle. This article provides tabular analytical substantiation of the proposed method, which is based on the direct measurements of voltage and current and the subsequent algorithmic calculation of physical values functionally related to the sought angle. The authors develop a structural block diagram of a device that implements the proposed thermal protection method. All relevant experimental studies were carried out. In this case, a small-sized electronic thermometer with a remote digital temperature sensor connected to the USB port of a personal computer was used as a temperature meter. The results obtained confirm the functional capability and efficiency of the proposed technical solution.
1. Introduction
As known, the overwhelming majority of modern electric actuators are based on alternating current electric motors (EM), most often asynchronous motors (AM). According to statistics, EM failures are caused mainly by thermal destruction of the stator insulation due to overload, by increases in ambient temperature, by violation of cooling conditions, etc. This is because heating of the insulation leads to a change in its physical state: with rising temperature, the dielectric becomes less solid and more susceptible to mechanical damage. In addition, heat exposure dries out the insulation, which leads to cracks and chipping of the insulating layer and, accordingly, to electrical breakdown. At the same time, thermal overload can also cause mechanical stress in AM windings, which may lead to fatigue and deterioration of their characteristics over time [1].
Obviously, the failure of almost any electric motor leads to electric actuator malfunction as a whole. Consequently, all electric drive motors must be equipped with thermal protection devices capable of effective and reliable monitoring of the current temperature of their windings and able to integrate into the electric drive automatic control system.
2. Overview of the Most Common Thermal Protection Systems
In general, any thermal protection system functionally contains two main units:
- a monitoring unit, for which its output signal informs about the current temperature of the winding, and
- an executive unit, which processes the signal received from the monitoring unit and uses its own input (about the maximum permissible heating limit) to disconnect the electric motor from the power supply in the case of unacceptable overheating and/or to provide relevant signaling.
Structurally, during hardware implementation of the thermal protection system, these two functional units can be combined into a single block.
Practical implementation of the executive unit is easy: in general, it contains electromechanical and logical blocks. Here, the electromechanical block can be made, for example, in the form of a relay protection unit based on electromechanical or electronic relays and starters [2,3].
Obviously, the key problems in creating a thermal protection system lie in the implementation of the monitoring unit, as its reliability and accuracy provide the correctness and functional reliability of the entire EM thermal protection system as a whole. Therefore, in this article, the authors focus on this particular main unit of the thermal protection system.
The monitoring unit of the thermal protection system can be based either on direct measurement of the temperature or on its indirect determination, executed by monitoring certain physical quantities that determine the heating of the winding. Accordingly, the design approaches, which are currently used for this unit in practice when building thermal protection systems, can be divided into several groups:
- indirect methods, by the magnitude of the stator current;
- methods based on the use of built-in thermal sensors;
- methods based on the use of a thermal model of the machine;
- methods based on assessment of the electrical parameters of the machine;
- hybrid methods based on combined use of the listed methods.
Indirect methods of thermal protection based on monitoring the stator current are widely used in practice as overcurrent protection [4,5]. Obviously, when implementing such methods, there is no direct measurement of the heating temperature of the stator windings; therefore, protection will not work in the case of significant overheating, for example, with a prolonged start of the motor under load. In addition, this protection method cannot take into account the changes in ambient temperature or the cooling and heat-transfer conditions. The same points apply to AM thermal protection too.
The simplest thermal protection methods are based on direct temperature measurement using temperature sensors built into the machine’s windings. Usually, these are placed in the protruding end coils of the stator winding, one for each phase on the side opposite the fan. However, this approach is rarely used in electric drives due to a number of significant drawbacks, the main one being the need to install temperature sensors at the manufacturing stage (for small machines, this becomes extremely difficult and expensive). Another significant disadvantage is the local nature of temperature sensor readings. Additionally, significant thermal inertia of insulation present between the sensor and the winding makes prompt deactivation of the machine when the heating of the winding spikes up impossible. Thus, methods based on the use of built-in temperature sensors do not provide credible and reliable thermal protection of an electric machine, especially in nonstationary and emergency modes of operation.
In thermal protection design, one of the methods for determining the temperature of the winding is to use a thermal model of an electric motor (TMEM). This allows for an algorithmic calculation of the temperatures for various parts of an electric motor based on real-time monitoring of the current via the design parameters of the machine [6,7]. The accuracy of the temperature calculation depends on the TMEM structure and complexity—the former increases with more accurate monitoring of all of the thermal connections of the machine. However, this requires detailed knowledge of all internal thermal parameters as well as a very precise description of the heating-cooling processes of the machine, which complicates implementation of real-time temperature calculation. Therefore, in practice, reduced-order TMEMs are used. For example, in [8], the authors proposed a simplified AM thermal model with a transfer function instead of a concentrated thermal model, in order to reduce the TMEM order. The proposed thermal model requires a significantly smaller number of thermal parameters for accurate modelling of the thermal behavior of an AC machine while maintaining an acceptable accuracy and reliability of heating control for its winding, which is generally sufficient for thermal protection tasks on a machine operated under specified operating conditions. However, installation of simplified TMEMs in the motor prohibit accurate assessment of stator winding temperatures with due consideration of current cooling conditions, which is crucial for the AMs used, for example, in unheated premises or outside. In [9], a hybrid thermal model was presented to account for differences in thermal operating conditions for different motors of the same rating and the same cooling system. That paper showed the possibility to use theoretical analysis and mathematical modelling for thermal control of the motor in dynamic cooling conditions. The authors proposed an online parameter-tuning algorithm that adapts the hybrid thermal model to changing thermal operating conditions of the motor. This provides complete overload protection.
The introduction of TMEMs for real-time thermal protection of AC machines is very difficult as there is no accurate information about the actual operating or cooling conditions of the machine, while the experimental or mathematical determination of the thermal model parameters is highly complex (for AC machines already in operation, this information is practically inaccessible). Thus, the widespread use of TMEM thermal protection systems has little production prospects.
As shown by the analysis of the professional literature, one of the most promising recent methods of thermal control and protection is based on assessment of the electrical parameters of the machine, first of all, on the control of the RC active resistance of the stator winding, as its value is uniquely determined by its temperature. This provides direct use of the winding itself as a temperature sensor and determines its average temperature T by using the magnitude of the change in RC due to heating of the winding, according to the following equation:
where is the operating resistance, is the initial winding resistance at known temperature , and is the temperature coefficient of electrical resistance (which depends on the winding material).
Therefore, we consider the methods of thermal protection based on monitoring the stator winding resistance in greater detail. The easiest way to determine the RC value is by the “voltmeter–ammeter” method, by applying a constant voltage to the winding:
where and are the voltage drop and current of the stator winding.
At the same time, it is quite obvious that, to provide thermal protection, the RC value must be controlled directly during AM operation. For this, it is necessary to introduce a small instrumental direct current (DC) into the operating AC circuit. In principle, this can be done by using an additional external DC source. This source can be connected either in series in the stator winding circuit using a custom circuit [10] or connected between the neutral of the motor windings and the neutral of the supply network [11]. However, the reviewed systems for introducing the instrumental DC can be effectively used when measuring the winding temperature without disconnecting the AM from the power supply, for example, during tests in lab conditions [12]. These methods are not economically viable for thermal protection tasks. The reviewed systems for introducing the instrumental DC via an additional external DC source can be effectively used when measuring the winding temperature without disconnecting the AM from the power supply, for example, during tests in lab conditions [12]. These methods are not economically viable for thermal protection tasks.
The possibility of forming DC from the operating AC was proposed in [13], and the use of this method in a thermal control system is described in [14] and shown in Figure 1.
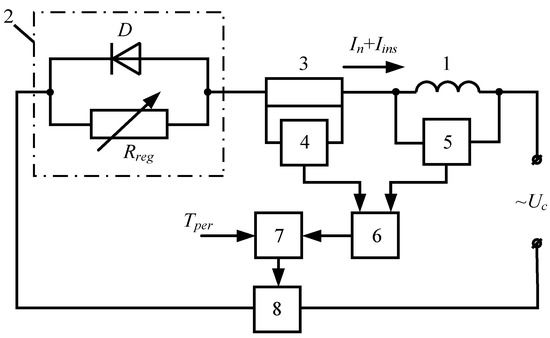
Figure 1.
A schematic block diagram of a thermal protection device generating an instrumental current from the operating AC: 1, thermal sensor; 2, DC input block; 3, measuring shunt; 4, block for measuring the value of the instrumental DC ; 5, block for measuring the value of voltage drop on the temperature sensor caused by the current ; 6, computing block; 7, threshold switch; and 8, executive unit.
It is evident that, due to the inequality of resistances for different half-waves of the supply voltage, the circuit will include a direct current , the value of which can be adjusted by changing the resistance of the resistor .
Block 6 calculates the current temperature of the winding on the basis of Equations (1) and (2), and if it exceeds the temperature permissible under operating conditions, then the threshold element generates an output signal fed to the executive unit 8, which disconnects the winding from the power circuit . The main difficulty in practical implementation of this solution is the need to eliminate the influence of the operating current on the measuring circuits.
A large number of research works have been devoted to the formation of a instrumental DC directly from the operating AC. For example, the authors of [15,16] present an overview of the relevant modern methods of thermal protection for AC motors with linear starting, soft starting, and inverter power supply. These active methods of thermal protection usually control the average stator temperature by evaluating the stator resistance via stator’s voltage and current values and use various methods to generate the instrumental DC voltage. We consider the main ones.
The work in [17,18,19] show that the input of DC signals can be achieved by replacing diode D (see Figure 1) with an insulated-gate MOSFET (metal–oxide–semiconductor field-effect transistor). The equivalent resistance of the DC input circuit is changed by controlling MOSFET switching when the current flows in different directions. The actual applied DC voltage can be controlled by adjusting the resistance R in the signal input circuit.
Control of the resistance value of the AM stator winding, which is connected to the mains via a soft-starter, is described in [20,21,22,23]. The instrumental DC is introduced by changing the delay angle of the soft-starter thyristors. The level of the input DC signal is controlled by the value of the delay angle. The soft-starter gate control signal causes a short delay in a half cycle for one phase of the machine. The DC components are then obtained from Fourier analysis of current and voltage. Using the value of the DC signals, it is then possible to calculate the resistance and temperature of the stator winding. To obtain the exact temperature of the stator winding, the authors propose to process the obtained values via a special program, together with other parameters.
The thermal protection of inverter-powered motors is described in [24,25,26]. In an open-loop motor drive, instrumental DC voltage is periodically injected into the motor by varying the spatial vector pulse-width modulation (PWM). For injection of the metering signal, the authors propose a modified PWM space vector circuit, which allows automatic input of DC components in addition to the original power voltage signals, changing the position of the switches of power electronics.
However, it should be noted that using arbitrary routines to inject the additional instrumental DC into the stator winding has a certain impact on the EM indicators. In particular, this includes torque ripple and negative torque caused by the DC component [17]. Therefore, it is required to split the DC components from phase currents and voltages. The relevant methodology is presented in [27,28]. In addition, DC presence changes the heating conditions of the machine. To reduce the additional heat generation from the instrumental DC in the electric motor, it is possible, for example, to inject these signals intermittently (for soft-starter circuits). The breaks can last for about 3–5 min, depending on the type of motor and its operating conditions. To do this, after each supply of a DC signal and, accordingly, the procedure for controlling the heating of the winding, a “clean” operating AC voltage is fed to the winding. In this case, the AM thermal protection remains practically unchanged due to the thermal inertia of the machine. However, all these procedures lead to a higher complexity of the devices for AM thermal protection.
3. Statement of the Research Problem
As shown above, the known methods based on measuring the change in the value of active resistance of the stator winding due to heating cannot provide accurate control of the winding temperature without disturbing normal operation of the machine. Obviously, the optimal method of thermal protection is a method that does not require injection of an additional instrumental DC. One of the possible ways to solve this problem is described in [29], where the authors offer a method of operational temperature control based on measuring the resistance of the EM AC windings in EM operating mode by splitting the corresponding components from the phase voltages and currents using synchronous detectors [30]. To control the value of the active resistance of the winding, two independent “asymmetric” measuring channels are used for measuring the active components of the current and voltage of the winding and for subsequent calculation of its resistance. To control the current, a current sensor in the form of a measuring shunt 1 with a benchmark active resistance is introduced into the winding circuit 2 (Figure 2).
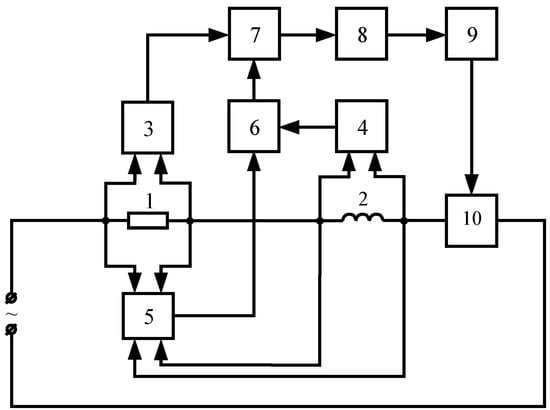
Figure 2.
A schematic block diagram of a thermal protection device with the procedure for extracting DC components from alternating phased voltages and currents: 1, measuring shunt; 2, winding–stator temperature sensor; 3, 4, and 5, the first, second, and third recording blocks; 6 and 7, primary and secondary computing blocks; 8, block for recording the winding 2 temperature; 9, comparison block; and 10, executive unit.
The recording blocks 3 and 4 are presented as amplitude detectors, and the third recording block (block 5) is presented as a phase detector. The first computing block 6 is an analogue signal multiplier, and the second computing block 7 is an analogue divider of two signals. The registering block 3 generates as an output an electrical signal proportional to the amplitude value of the current in the circuit. Block 5 generates an electrical signal proportional to . Block 6 multiplies electrical signals fed from blocks 5 and 4; this results in an output electrical signal, which is proportional to the amplitude value of the active component of the voltage drop on the resistance of the winding 2. Block 7 runs an analogue calculation of the current value of the winding 2 resistance and, thus taking into account Equation (1), runs algorithmic determination of its temperature. Block 9 runs a comparison procedure for this temperature value against the permissible heating value and, if necessary, sends a signal to the executive unit 10.
However, the presence of the shunt 1 (connected in series to the power circuit of the winding 2) has a number of disadvantages, the main one being power loss in the shunt, which leads to its heating as well as the presence of a galvanic connection with the operating circuit.
Thus, it can be seen that the problem of EM thermal protection has not been fully resolved and that new principles for constructing protection systems with zero impact on normal operation should be developed.
4. Study Results
In the thermal control systems considered above, active resistance of the winding was used as a physical value characterizing its heating, since the numerical value of active resistance uniquely determines the temperature of the winding in accordance with Equation (1). However, the need to control the value of active resistance of the winding requires, in line with Equation (2), the measurement of the drops in voltage and current of the stator winding, which, in turn, needs either an injection of the instrumental DC or the use of a measuring shunt with the subsequent algorithmic separation of relevant parameters from and . This greatly complicates practical implementation of this approach to temperature control, resulting in a violation of the EM operation mode and, therefore, reduced reliability of the entire system as a whole. In order to eliminate these disadvantages, a new approach to the construction of operational temperature control systems is proposed, designed to provide thermal protection of the EM. This approach is based on the methods of graphic interpretation and analytical generalization of posterior information about functional relationships between measured data in the form of corresponding phase relations.
The proposed method is based on indirect monitoring of the thermal state of the EM stator winding, using the results of direct measurements and the subsequent algorithmic calculation of a physical value functionally related to the desired number, namely, the phase difference between the vectors and , which depends on the values of the active and reactive components of the impedance of the EM stator winding, as its numerical values depend on heating of this winding. To summarize, we can state that the proposed control method is actually based on the following property of the phase difference between the vectors and : .
In a systemic way, we consider the substantiation of the essence of the proposed new method of thermal control for measuring the components of full impedance of the EM stator winding and the particular features of the device, which are used for its implementation.
The circuit for EM connection to the power mains can be represented in the form of an unbranched circuit of sinusoidal current (Figure 3).
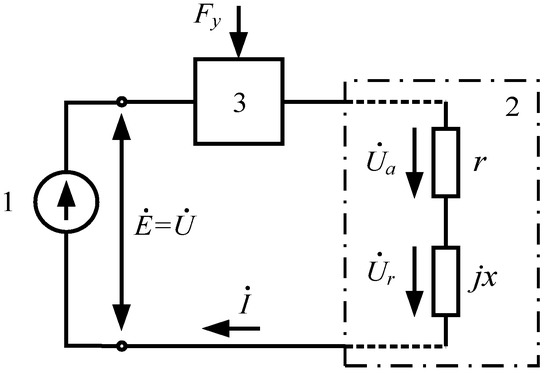
Figure 3.
General block diagram of EM activation: 1, mains voltage supply; 2, EM stator winding; 3, controlled switching device; and , control signal, connecting or disconnecting the EM to the mains.
By measuring the supply voltage of the EM stator winding (SW) and the current in the circuit of this winding, it is possible to determine the impedance of the EM SW using the following equation:
where and are the complex effective values of voltage and current in the winding circuit, is the angle between vector and the real axis on the complex plane, is the angle between vector and the real axis on the complex plane, is the angle (phase difference) between vectors and , is the active components of the EM SW impedance, is the reactive components of the EM SW impedance, is the cyclic frequency EM SW power supply voltage, is the EM SW inductance, is the magnetic permeability of the EM stator material, and is a set of design parameters of the SW and the EM stator itself.
To analyze the features of the physical processes occurring in the electrical circuit under consideration, we construct the corresponding vector voltage diagram on the complex plane (Figure 4).
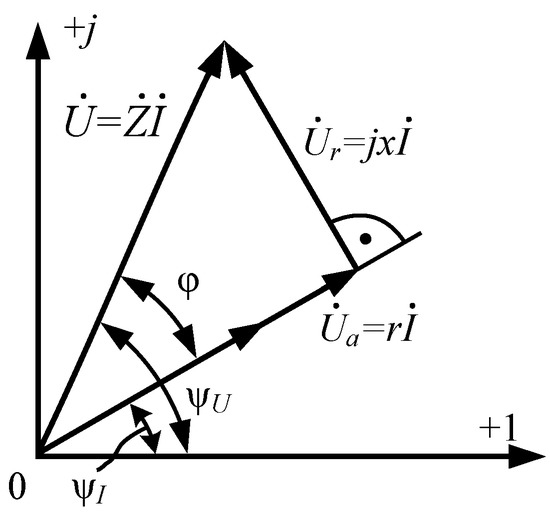
Figure 4.
Voltages, a vector diagram.
In accordance with (3) and Figure 3, we can write the following circuit equation:
where is the voltage on the EM SW internal active resistance and is the voltage across the EM SW internal reactive resistance.
We combine the current vector of the electric circuit with the real coordinate axis on the complex plane (Figure 5).
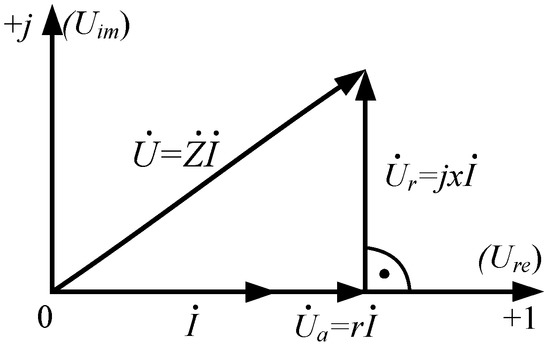
Figure 5.
Voltages, a transformed vector diagram.
From the analysis of Equation (4) and Figure 3, it follows that, when the current vector is combined with the real coordinate axis of the complex plane, the mains voltage vector can be conditionally split with respect to the current phase into the in-phase (real) and quadrature (imaginary) components:
Moreover, and .
Notably, the specific resistance of the SW material is a function of temperature and, in the linear approximation, is determined by a dependence of the following form:
where and is the specific resistivity and temperature coefficient of specific resistivity, referring to the beginning of the temperature range , and is the specific resistivity at temperature .
In turn, it is known that, for ferromagnets, which are a material for the magnetic conductive elements of electric motors, an increase in temperature (up to the Curie temperature (TC) under operating conditions) means a relatively smooth decrease in magnetic permeability.
Heating a ferromagnet leads to a gradual thermal disorientation of the spin magnetic moments and a decrease in the magnetization. Above a certain temperature TC, when the thermal motion energy becomes comparable to the exchange interaction energy, the thermal motion completely destroys the magnetic order (disintegration of the domain structure), transferring the ferromagnet into a paramagnetic state. Therefore, increasing the temperature (up to the Curie temperature point) results in a smooth decrease in the magnetic permeability of a ferromagnet.
The thermal instability of inductance with a ferromagnetic core is primarily due to the dependence of a core’s magnetic permeability coefficient on temperature μ(T).
For the temperature coefficient of inductance, which describes the winding inductance/temperature dependence, we can write:
where and is the current and nominal inductance values, respectively, referring to the lower limit of the temperature range , and is the current temperature value.
Considering that .
Equation (7) is easily transformed to the following form:
where and are, respectively, the current and nominal values of the magnetic permeability of the ferromagnet material referring to the lower limit of the temperature range and is the temperature coefficient of magnetic permeability.
Then, taking into account the existing trend of change in (αμ < 0) as per (8), for the coefficient of magnetic permeability, it would be valid to state that
In fact, in the case under consideration, the magnetic permeability is characterized by the temperature coefficient of the magnetic permeability. In this case, in a certain temperature range, the magnetic permeability can be conventionally considered a linear function.
Since SW reactance is determined by the equation x = ωL, it is obvious that the following functional dependence takes place:
Importantly, Equations (6) and (9) imply the presence of multidirectional trends in the changes of and when these parameters are affected by temperature fluctuations.
In accordance with Equation (5) and the above remarks, it can be concluded that any change in the active or reactive components of the EM SW impedance with a change in the EM SW temperature will cause a corresponding change in the angle between vectors and on the complex plane.
In other words, between the angle and EM SW temperature , there is an explicit functional dependence determined by the relationship between and :
When the temperature changes, the end of the vector moves on the complex plane along a circle of radius centered at point 0, occupying a position corresponding to the ratio . Moreover, the presence of temperature-induced multidirectional trends in the changes of and provides, in accordance with (11), significant changes in .
From Equations (5) and (11), it is evident that, to solve the problem, i.e., to control the EM SW temperature, it is enough to register the state of the phase difference between vectors and . Using the synchronization of signal processing via the phase of the current in an unbranched circuit, it is possible to use the equipment to register the effective values of the quadrature and in-phase supply voltage components and, therefore, to obtain the current value of in order to provide EM thermal protection. In fact, we are talking about the possibility of implementing a new phase control method for EM SW temperature.
To implement the considered method for controlling the EM SW temperature, the authors propose an appropriate design of the structural block diagram of the EM thermal protection device (Figure 6). Consider the particular operating features of the proposed EM thermal protection device.
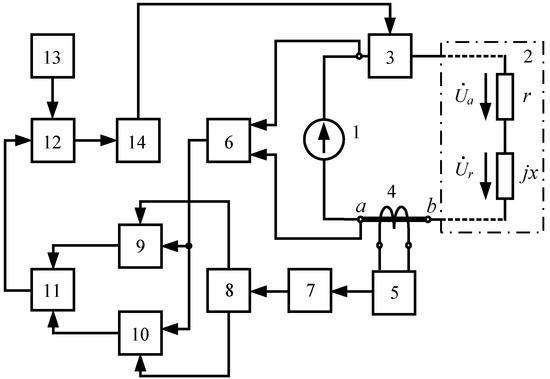
Figure 6.
Block diagram of EM thermal protection device: 1, power supply of the EM stator winding (SW); 2, EM SW used as a temperature sensor; 3, EM SW switching device; 4, instrument current transformer (ICT); 5, current-to-voltage converter; 6, recorder attenuator; 7, phase shifter; 8, quadrature reference voltage generator; 9 and 10, synchronous detectors, respectively, of the in-phase and quadrature components of the EM SW power supply voltage; 11, ratiometric converter with digital output; 12, digital comparator; 13, block for setting the level of comparison; and 14, control signal generator.
The original unbranched sinusoidal current circuit includes an electric current sensor, the ICT, which houses the instrumentation bus that closes the electric circuit through the corresponding contact connectors a and b.
When activating on the supply voltage 3, sinusoidal supply voltage with the corresponding vector voltage value , an electric current arises in a closed electrical circuit, with the corresponding vector current value .
The ICT metering winding registers the current , which, through block 5, is converted into voltage
where is the ICT transformation ratio and is the dimensional factor.
By means of phase shifter 7, the initial diagram of voltage vectors (Figure 4) is transformed into operating diagram voltage vectors (Figure 5) whereas the phase error of the previous transformations of the recorded signal is corrected. Subsequently, block 8 uses the corrected input signal to form the corresponding quadrature reference voltages for synchronous detectors:
- —co-phased reference voltage;
- —quadrature reference voltage,
where is the phase of the reference voltages, synchronized with phase of the electric circuit current.
For the transformed coordinates of the complex plane, we can write the following:
In fact, synchronous detectors 9 and 10 are coherent converters that multiply the input information signal with the input reference voltage, with subsequent low-pass filtering of the obtained signal.
In accordance with (13), block 6 scales the supply mains voltage to the level of which is then fed to the information inputs of the synchronous detectors 9 and 10, where it is transformed, as required, into the following corresponding signals at the output of the synchronous detectors 9 and 10:
where and are, respectively, in-phase and quadrature components of the supply voltage; and are the conversion factors of the synchronous detector 9 and synchronous detector 10, respectively; and KM is the scaling factor for block 6.
Block 11 converts input signals and by a computational procedure in accordance with the following equation:
Block 11 additionally carries out an analogue-to-digital conversion of :
where is the analogue-to-digital operator; is the discrete time function; is the signal sampling rate; and .
From block 11, the output digital signal is fed to block 12, which compares with a given reference value , issued by block 13.
Based on the results of the comparison operation, block 12 generates a binary signal of a logic level 0 or 1, based on the following conditions:
Subsequently, the signal is fed to the input of block 14, which, depending on the state of the signal , generates the necessary control signal for the switching device 3.
In a critical situation, when the level of the block 12 output signal , i.e., the EM overheating temperature exceeds the permissible value , block 3 disconnects the EM SW from the power supply source, thereby preventing an emergency situation on the operating electrical equipment.
5. Experimental Proof of the Designed Device
The experiments were carried out using two identical asynchronous electric motors (EM) of the 4A63V4 type with 0.37 kW power rating. In this case, the readings of one EM (base EM) were taken as a benchmark for assessing the precision of the results obtained on the second EM (tested EM). Both electric motors were connected for 380 V AC main supplies. All measuring procedures were carried out at no-load operation in the S1 mode with a steady thermal condition.
For the experimental studies, the authors designed a specialized test bench, shown in the structural block diagram (Figure 7). A general view of the test bench is shown in Figure 8.
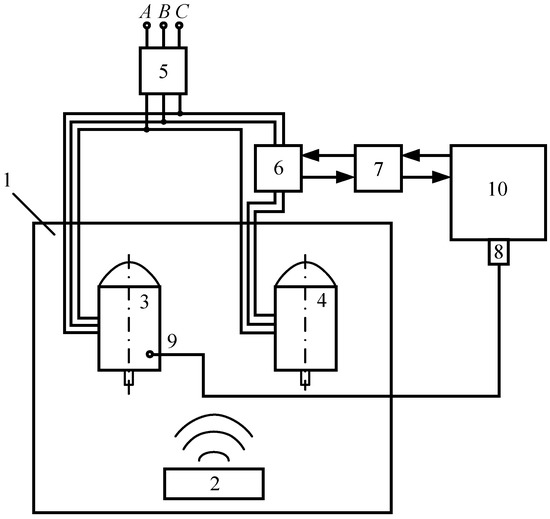
Figure 7.
Test bench, a block diagram: 1, test chamber; 2, adjustable air heater; 3, base EM; 4, tested EM; 5, power switch: 6, EM thermal protection device, which implements a new phase control method for EM SW temperature; 7, data collection system E502 manufactured by “LKard” (Moscow, Russian Federation), 8, miniature electronic thermometer (MET) with a remote digital temperature sensor 9; and 10, personal computer (PC).

Figure 8.
General view of the test bench: 1, test chamber; 2, adjustable air heater; 3, base EM; 4, tested EM; 5, power switch; 6, EM thermal protection device, which implements a new phase control method for EM SW temperature; 7, data collection system E502 manufactured by “LKard” (Moscow, Russian Federation), 8, miniature electronic thermometer (MET) with a remote digital temperature sensor 9; and 10, personal computer (PC).
By adjusting the heater 2, various temperature environments were set in the test chamber 1 with EMs 3 and 4 in it; the temperature of their SW was measured by means of the miniature electronic thermometer (MET) and the EM thermal protection device 6, respectively. The data obtained from the results of these measurements were recorded by PC 10 with the corresponding hardware/software interface and compared with each other, followed by a final analysis of the results of the experimental studies.
A miniature electronic thermometer (MET) 8 with a remote digital temperature sensor 9, specially designed for this purpose and connected to the USB port of a personal computer (PC), was used as the temperature meter. The specific feature of this MET is that its operation is controlled by a microcontroller (MC) PIC18F14K50 with a built-in USB module and a sensitive thermoelement (a digital sensor (DS) LM75AD) connected to the MC via a 5 m shielded twisted pair cable (Z = 90 Ohm). The MET also provides visible indication of its operating mode control via a corresponding LED.
To provide normal functioning of the MET, the respective software driver was installed in the computer OS, creating a virtual COM port with a specific operating mode: eight non-parity information bits and one stop bit as well as automatic determination of the information flow rate.
By default, the MC was polled every 5 s, and in the “computer demand” mode, information was entered no more than once a second. To compensate for systematic error, the program provides the option to enter and change the necessary correction that adjusts (increases or decreases) the MET readings with a step of 0.1 °C. The contact method was used to measure the temperature of the protruding SW end coils of the base EM through a special DS attached thereon.
During operation, the MET showed fairly high accuracy parameters: the measurement error within the entire operating temperature range of 10 + 125 °C did not exceed 1 °C.
Data Collection System E502 manufactured by “LKard” provided correct joint operation of the PC and the EM thermal protection device; E502 is a universal 16-bit I/O module for up to 32 analogue and 17 digital signals to a personal computer via USB 2.0 (high-speed) interfaces and 100 Mbit Ethernet with up to 2 MHz conversion frequency and the option of real-time digital processing.
In fact, the PC through the Data Collection System 7 ran a sweeping scanning of the measurement result by block 6 of phase ϕ between parameters and by forming a sequential enumeration of possible values in this phase. In the case, the measurement result of block 6 matched the present digital phase value set by the PC; this value was recorded and used to determine temperature in accordance with the calibration curve .
The values of all the necessary coefficients and the choice of the calibration curve were determined at the stage of preliminary calibration of the measuring channels of the EM thermal protection device and placed in the PC memory for subsequent use in the process of experimental research.
The direct measurement was used as a reference measurement method; this provided temperature control with at least 0.5% accuracy. This reference method uses the known calibration curve of the temperature sensor (a particular thermistor and a standard measuring transducer (MET) with normalized parameters). The reference method used is one of the most accurate methods for measuring temperature in the specific conditions under consideration and is the one with a simple technical implementation.
The experimental research methodology was as follows: every 40 min, the heater was switched on, increasing the chamber temperature by 20 °C; subsequently, the SW temperature of the corresponding electric motors was measured (the results are presented in Figure 9).
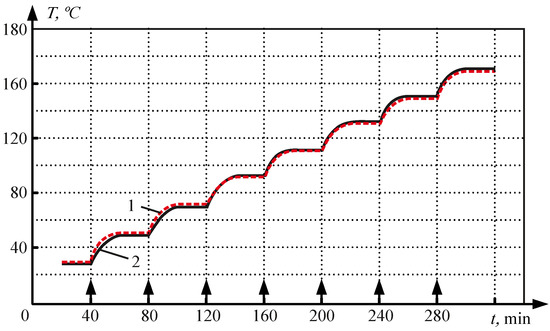
Figure 9.
The results of measuring the temperature of the stator windings of the base (1) and tested (2) electric motors.
It should be noted that, on average, the EM SW temperature reached a steady-state value within ≈20 min after turning on the heater. Therefore, multiple temperature measurements were carried out during each step of the heater temperature change, including during the steady-state temperature regime of the electric motor. For each subsequent time interval of the experiment, the processes of changing the temperature and measuring the SW steady-state temperature values of the corresponding electric motors were cyclically reproduced.
In Figure 9, on the abscissa axis, the vertical arrows indicate the moments of changing the operating mode of the heater. The diagram shown in the figure shows a fairly high coincidence rate between the results of SW temperature measurement by the direct method using the MET and the indirect phase method using the EM thermal protection device.
The results from determining the temperature measurement error by the phase method in relation to the indirect method are presented in Figure 10. The results from determining the measurement error are presented in the form of temperature growth diagrams, which is traditional for the electrical engineering. This is because the EM temperature depends not only on the load but also on the temperature of the ambient (cooling) medium. Therefore, for electric motors, it is not the absolute temperature of the winding but the excess winding temperature T over ambient temperature that is normalized:
where and are the factual and base temperature values.
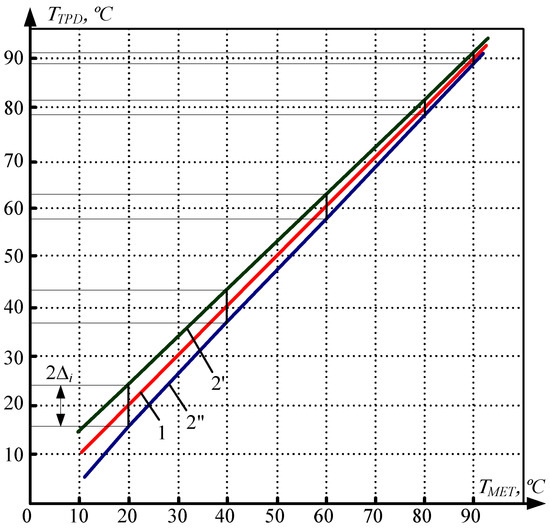
Figure 10.
The results from determining the temperature measurement error by the phase method: TTPD is the EM SW overtemperature recorded by the EM thermal protection device; TMET is the overtemperature measured with a miniature electronic thermometer MET; 1, a diagram corresponding to the ideal case when the accuracy parameters of the indirect phase measurement method by means of the EM thermal protection device fully correspond to the accuracy parameters of the direct measurement method by means of MET; 2′ and 2″, diagrams of maximum deviations of the SW temperature of the test EM, reflecting the results of multiple measurements of the test EM by the thermal protection device; and 2Δi, range spread of SW overtemperature in the test EM as measured by the EM thermal protection device.
The value was taken as the base temperature (it is specified in the regulatory documentation to be the standard temperature of the cooling medium).
Figure 10 shows that the measurement accuracy increases in the zone of operating SW overtemperatures. Since it is exactly where the EM thermal protection should take place, it can be concluded that, in spite of its relatively simple technical implementation, the proposed control method provides a sufficiently high triggering accuracy.
Notably, Figure 10 actually represents the final generalization of graphical interpretation of the results of the corresponding processing of multiple measurements, with due consideration of the particular features of methodology used for the experimental research.
6. Conclusions
An analysis of the graphical interpretation of the results of experimental studies shows that the proposed new phase method for controlling the EM SW temperature is technically feasible and provides quite an acceptable precision in measuring the EM SW temperature in the required range of variation (5 ÷ 3% in the range 10 ÷ 125 °C).
In conclusion, it should be noted that the proposed thermal protection method is valid not only for EM but also for the protection of any other AC electrical equipment, for example, generators, transformers, reactors, electromagnets, and so on.
Author Contributions
Conceptualization, I.V.B. (Igor V. Bochkarev) and I.V.B. (Ivan V. Bryakin); methodology, V.R.K.; software, K.V.L. and A.R.S.; validation, I.V.B. (Igor V. Bochkarev) and V.R.K.; formal analysis, A.R.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Silwal, B.; Sergeant, P. Thermally induced mechanical stress in the stator windings of electrical machines. Energies 2018, 11, 2113. [Google Scholar] [CrossRef]
- Hewitson, L.; Brown, M.; Balakrishnan, R. Practical Power Systems Protection; Elsevier Ltd.: Newnes, Australia, 2005; 288p. [Google Scholar]
- Paithankar, Y.G.; Bhide, S.R. Fundamentals of Power System Protection; Prentice-Hall of India Pvt. Ltd.: New Delhi, India, 2004; 301p. [Google Scholar]
- McCleer, P.J. The Theory and Practice of Overcurrent Protection; Mechanical Products: Lombard, IL, USA, 1987; 233p. [Google Scholar]
- Choong-Koo, C. Improving motor protection using thermal model. Trans. Korean Inst. Electr. Eng. 2015, 64, 473–479. [Google Scholar] [CrossRef][Green Version]
- Zhi, G. Sensorless Stator Winding Temperature Estimation for Induction Machines; Georgia Institute of Technology: Atlanta, GA, USA, 2006; 204p. [Google Scholar]
- Kylander, G. Thermal Modelling of Small Cage Induction Motors; Chalmers University of Technology: Gothenburg, Sweden, 1995; 113p. [Google Scholar]
- Zhi, G.; Habetler, T.G.; Harley, R.A. An online adaptive stator winding temperature estimator based on a hybrid thermal model for induction machines. In Proceedings of the IEEE International Conference on Electric Machines and Drives, San Antonio, TX, USA, 15 May 2005; pp. 754–761. [Google Scholar] [CrossRef]
- Zhang, P.; Du, Y.; Habetler, T.G. A transfer function-based thermal model reduction study for induction machine thermal overload protective relays. IEEE Trans. Ind. Appl. 2009, 46, 1919–1926. [Google Scholar] [CrossRef]
- Bochkarev, I.V.; Ashmarin, A.V. A Device for Measuring the Temperature of the Winding of an Alternating Current Electric Machine under Load. SU Patent No. 1108337, G01K7/16, G01R27/08, 15 August 1984. [Google Scholar]
- Bochkarev, I.V. Measuring the winding temperature of AC machines under load. Russ. Electr. Eng. 1999, 70, 28–32. [Google Scholar]
- Albla, A.A.H.; Brkovic, B.M.; Ječmenica, M.M.; Lazarevic, Z.M. Online temperature monitoring of a grid connected induction motor. Int. J. Electr. Power Energy Syst. 2017, 93, 276–282. [Google Scholar] [CrossRef]
- Bochkarev, I.V.; Ashmarin, A.V. Device for Measuring the Temperature of the Winding of an Electric Machine. SU Patent No. 998873, G01K 7/16, 23 February 1983. [Google Scholar]
- Bochkarev, I.V.; Ashmarin, A.V. A Device for Thermal Protection of an Electric Machine. SU Patent No. 1187234, H02H5/04, H02H7/08, 23 October 1985. [Google Scholar]
- Zhang, P.; Lu, B.; Habetler, T.G. Active stator winding thermal protection for AC motors. In Proceedings of the Annual Pulp and Paper Industry Technical Conference, Birmingham, AL, USA, 21–26 June 2009; pp. 11–19. [Google Scholar] [CrossRef]
- Zhang, P. Active Thermal Protection for Induction Motors Fed by Motor Control Devices; Georgia Institute of Technology: Atlanta, GA, USA, 2010; 202p. [Google Scholar]
- Lee, S.B.; Habetler, T.G. An on-line stator winding resistance estimation technique for temperature monitoring of line-connected induction machines. IEEE Trans. Ind. Appl. 2003, 39, 685–694. [Google Scholar] [CrossRef]
- Sabaghi, M.; Feshki Farahani, H.; Hafezi, H.R.; Kiani, P.; Jalilian, A. Stator winding resistance estimation for temperature monitoring of induction motor under unbalance supplying by DC injection method. In Proceedings of the 42nd International Universities Power Engineering Conference, Brighton, UK, 4–6 September 2007; pp. 217–222. [Google Scholar] [CrossRef]
- Sabaghi, M.; Farahani, H.F. Monitoring of induction motor temperature under unbalanced supplying by stator resistance estimation. Indian J. Sci. Technol. 2012, 5, 2354–2359. [Google Scholar] [CrossRef]
- Enany, T.A.; Wahba, W.I.; Hassan, M.A. Remote and sensorless stator winding temperature estimation method for thermal protection for induction motor. Int. J. Syst. Dyn. Appl. 2014, 3, 53–72. [Google Scholar] [CrossRef][Green Version]
- Zhang, P.; Lu, B.; Habetler, T.G. a remote and sensorless stator winding resistance estimation method for thermal protection of soft-starter-connected induction machines. IEEE Trans. Ind. Electron. 2008, 55, 3611–3618. [Google Scholar] [CrossRef]
- Zhang, P.; Du, Y.; Lu, B.; Habetler, T.G. A DC signal injection-based thermal protection scheme for soft-starter-connected induction motors. IEEE Trans. Ind. Appl. 2009, 45, 1351–1358. [Google Scholar] [CrossRef]
- Enany, T.A.; Hassan, M.; Othman, E.S. Induction motor temperature monitoring via signal injection enhanced with adaptive neuro-fuzzy inference system. Int. Inf. Eng. Technol. Assoc. 2017, 91–109. [Google Scholar] [CrossRef]
- Zhang, P.; Lu, B.; Habetler, T.G. An active stator temperature estimation technique for thermal protection of inverter-fed induction motors with considerations of impaired cooling detection. Proceedings of IEEE International Electric Machines and Drives Conference, Miami, FL, USA, 3–6 May 2009. [Google Scholar] [CrossRef]
- Matic, P.R.; Gecic, M.A.; Lekić, Đ.; Marcetic, D.P. Thermal protection of vector-controlled IM drive based on DC current injection. IEEE Trans. Ind. Electron. 2015, 62, 2082–2089. [Google Scholar] [CrossRef]
- Tshimanga, T.P.; Bezabih, E.; Iyer, V.R.; Zhang, S.; He, L.; Harley, R.G. Stator temperature estimation of open-loop controlled induction machines via active DC voltage injection. In Proceedings of the North American Power Symposium (NAPS), Charlotte, NC, USA, 4–6 October 2015. [Google Scholar] [CrossRef]
- Baneira, F.; Asiminoaei, L.; Doval-Gandoy, J.; Delpino, H.A.M.; Yepes, A.G.G.; Godbersen, J. Estimation method of stator winding resistance for induction motor drives based on DC-signal injection suitable for low inertia. IEEE Trans. Power Electron. 2019, 34, 5646–5654. [Google Scholar] [CrossRef]
- Yoo, J.; Lee, J.H.; Sul, S.K.; Baloch, N.A. Stator resistance estimation using DC injection with reduced torque ripple in induction motor sensorless drives. IEEE Trans. Ind. Appl. 2020, 3744–3754. [Google Scholar] [CrossRef]
- Bryakin, I.V.; Bochkarev, I.V.; Bagiyev, H.G.; Kelebaev, K.K. Electric AC machines temperature control and overheating protection using leakage currents to evaluate the induction motor insulation condition. Bull. South Ural State Univ. Ser. Power Eng. 2019, 19, 75–84. [Google Scholar] [CrossRef]
- Brykin, I.V.; Bochkarev, I.V. Method for Measuring Impedance Components and Device for its Implementation. RF Patent No. 2691624, G01R 27/02, 17 July 2019. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).