A Review of Artificial Intelligence-Driven Active Vibration and Noise Control
Abstract
1. Introduction
2. Overview of AI-AVNC
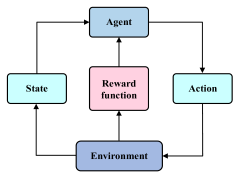
2.1. The Physical Mechanism of Vibration and Noise
2.2. System Architecture of AVNC
2.3. The Development History of Traditional AVNC Technology
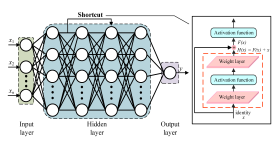
2.4. The Development History of AI-AVNC Technology
3. Technical Path Classification of AI-AVNC
3.1. AI-Based Input Shaping Parameter Optimization
3.1.1. IS Theory
3.1.2. Artificial Intelligence Method
3.2. AI-Based System Identification and Modeling
3.2.1. AI-Based Secondary Path Modeling
3.2.2. AI-Based Structural Dynamics Modeling
3.2.3. AI-Based Incentive Disturbance Source Modeling
| AI-Based Secondary Path Modeling | |
|---|---|
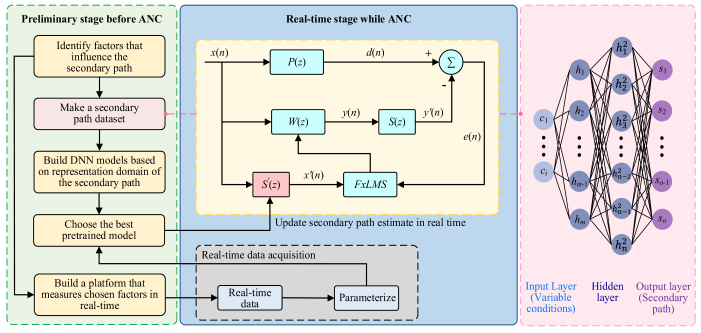 | |
| (a) Block diagram of FxLMS algorithm with DL-based, real-time secondary path estimate updates. | |
| It first builds a secondary-path dataset offline and pretrains a DNN (steps shown in the left figure). At runtime, real operating conditions are used to update the secondary-path estimate online, and the updated estimate then drives FxLMS to achieve real-time adaptive noise cancellation. This method typically assesses performance using ERLE, with the time taken to reach the target ERLE serving as an indicator of convergence speed. Robustness is evaluated based on performance degradation under conditions such as sensor position changes, secondary path gain or delay drift [128,129,130,131]. | |
| AI-Based Structural Dynamics Modeling | |
 | 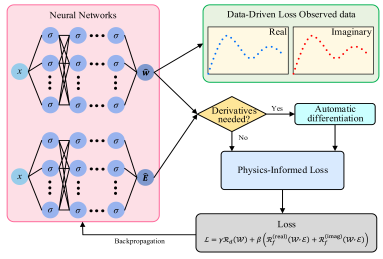 |
| (b) Block diagram of dynamic inverse control based on NARX neural network | (c) Block diagram of a PINN framework for structural identification |
| The NARX neural network incorporates time delays and feedback, thereby enhancing its memory of historical data. In the figure, NNI means neural network identifier, NNC means neural network controller. Set their structures similar. The online single data weight updating method is used to identify the dynamic inverse model of the control object. At the same time, the weight matrix of the neural network is transferred to the inverse model controller NNC. Based on this method, the identifier can dynamically identify the system parameters and improve the accuracy. This method is usually evaluated for accuracy by the RMSE of displacement or acceleration prediction, for convergence speed by the number of samples or time required for the weights to enter the steady state, and for robustness by the rate of increase of RMSE under different excitation spectra, amplitude variations, and measurement signal-to-noise ratios [132]. | The neural network takes the spatial position x as input and outputs the estimated displacement and the complex elastic modulus. Observed data define a data-driven loss; when higher-order derivatives are needed, they are obtained via automatic differentiation. This is then combined with a physics-based loss derived from the structural mechanics equations to form a weighted total loss. Finally, the total loss is minimized by backpropagation, simultaneously identifying the parameters and reconstructing the displacement. This method typically assesses accuracy by the RMSE of displacement or acceleration prediction, measures convergence speed by the number of iterations or time required for the physical loss to drop to a set threshold, and evaluates robustness by the growth of RMSE and physical residuals under scenarios such as boundary condition changes, load variations, or sparse training samples [135]. |
| AI-Based Incentive Disturbance Source Modeling | |
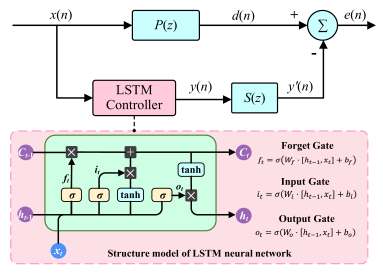 | 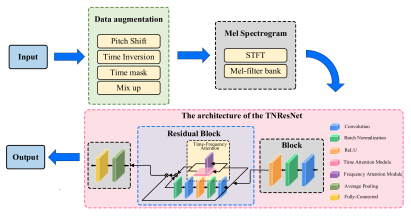 |
| (d) Block diagram of deep neural network filters with LSTM | (e) Block diagram of road terrain recognition based on TNResNet |
| LSTM is a type of recurrent neural network designed for managing long sequence data, consisting of three gates that regulate the flow of information: the forget gate, the input gate, and the output gate. The ANC controller based on LSTM layers is suitable for predicting reference noise and generating control signals to minimize residual noise. This method typically assesses performance using MSE and ERLE, measures convergence speed by the time required for the system to reach the target performance from startup, and evaluates robustness by the ability to maintain performance under conditions such as changes in noise spectrum characteristics, secondary path drift, or data frame loss [140]. | It begins with data augmentation techniques, followed by converting the data into Mel spectrograms that are input into the TNResNet model for feature extraction through the network’s convolutional layers. Residual blocks are used to improve training efficiency, and a time-frequency attention module focuses on relevant features. The final output is the classification of different terrain categories based on the extracted features. This method is typically evaluated in terms of Top-1 accuracy for performance, end-to-end inference time for convergence speed, and the ability to maintain recognition accuracy under various conditions such as different signal-to-noise ratios and changes in sensor installation positions for robustness [142]. |
3.3. AI-Based Controller Parameter Optimization
3.3.1. AI-Based Linear Feedback Controller
3.3.2. AI-Based Adaptive Controller
3.3.3. AI-Based Robust Controller
3.3.4. AI-Based Model Predictive Controller
3.4. AI-Based Controller Modeling
3.5. Evaluation Metrics
3.6. Section Summary
4. Typical Engineering Application Scenarios
4.1. New Energy Vehicle Sector
4.2. Aerospace Sector
| Application | Characteristics & Specific AI-AVNC |
|---|---|
 (a) NEVs | Interior road noise: Tires-Road excitation transmitted into the vehicle interior through the suspension or body; wide frequency band, strong time variation. Methods: DNN for real-time secondary-path update [130]; STFNet-headrest ANC to predict ear-side reference and cancel in-cabin noise [195]; CNN-SVR hybrid prediction improving mid-/low-frequency control [196]. |
| Vibration and noise in electric drive systems: Radial electromagnetic force waves (REFW) and sideband harmonics induce narrowband “whine” and couple with structure/gear meshing. Methods: ANN-based high-fidelity stator model for NVH improvement [198]; BPNN sensorless IPMSM control reducing current harmonics or torque ripple [199]; MAC-DDPG suppressing synchronous vibration of a flexible rotor without prior dynamics [200]. | |
| Suspension and seat vibration: Road conditions and load variability, multiple constraints. Methods: PPO for semi-active suspension [88]; DRL for active suspension improving ride comfort and generalization [204]; DDPG for optimal active suspension control [205]. | |
 (b) Aerospace | Aviation: Pneumatic noise and structural vibration coupling, strong time variation; Equal emphasis on cabin local sound pressure and overall aircraft vibration. Methods: RL for helicopter trailing-edge flap control with delay compensation and disturbance rejection [206]; NN-GA for sensor/actuator co-placement [207]; FLNN-based ANC reducing seat-headrest sound pressure in a tilt-rotor aircraft with low compute cost [208]. |
| Space: Lightweight flexible structures with large uncertainty; Vacuum and thermoelastic conditions induce parameter drift. Methods: Actor-Critic NN with improved prescribed-performance function for microgravity isolation under uncertainties [209]; Hybrid lumped and distributed parameter modeling and NN control [211]; DL-NMPC for precise vibration suppression of a flexible satellite antenna at low SNR [168]. | |
 (c) High-precision manufacturing | High-precision manufacturing: Nano-scale accuracy and millisecond-level responsiveness; Hysteresis/friction/structural resonances and machining chatter Methods: SAC (soft actor-critic) driving bonded piezo actuators to suppress chatter in peripheral milling of large flexible plates [212]; NN-SORC (NN-based switched output regulation controller) compensating hysteresis and reducing residual vibration on high-speed nanopositioning stages [213]. |
4.3. High-Precision Equipment Manufacturing Sector
5. Technical Challenges and Future Development Trends
5.1. Technical Challenges
5.2. Future Development Trends
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Scheidler, J.J. A review of noise and vibration control technologies for rotorcraft transmissions. In Proceedings of the INTER-NOISE and NOISE-CON Congress and Conference Proceedings, Hamburg, Germany, 21–24 August 2016; Volume 253, pp. 2986–2997. [Google Scholar]
- Zhang, Y.; Zhao, Z.; Li, X.; Xue, Z.; Jin, M.; Deng, B. Near-infrared-based measurement method of mass flow rate in grain vibration feeding system. Agriculture 2024, 14, 1476. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Y.; Li, M.; Liu, Y.; Huang, Y. Dynamics analysis and wear prediction of rigid-flexible coupling deployable solar array system with clearance joints considering solid lubrication. Mech. Syst. Signal Process. 2022, 162, 108059. [Google Scholar] [CrossRef]
- Kusano, T.; Shige, K.; Inoue, T.; Oba, Y.; Takeda, N.; Terashima, O.; Yamada, S. Active Noise Control for Noise Generated by Electric Vehicle HVAC Systems Using Virtual Sensing. Int. J. Automot. Eng. 2025, 16, 27–32. [Google Scholar] [CrossRef] [PubMed]
- Tao, Y.; Ge, C.; Feng, H.; Xue, H.; Yao, M.; Tang, H.; Liao, Z.; Chen, P. A novel approach for adaptively separating and extracting compound fault features of the in-wheel motor bearing. ISA Trans. 2025, 159, 337–351. [Google Scholar] [CrossRef]
- Zhu, J.; Ouyang, X.; Jiang, Z.; Xu, Y.; Xue, H.; Yue, H.; Feng, H. In-Wheel Motor Fault Diagnosis Method Based on Two-Stream 2DCNNs with DCBA Module. Sensors 2025, 25, 4617. [Google Scholar] [CrossRef]
- Feng, H.; Tao, Y.; Feng, J.; Zhang, Y.; Xue, H.; Wang, T.; Xu, X.; Chen, P. Fault-tolerant collaborative control of four-wheel-drive electric vehicle for one or more in-wheel motors’ faults. Sensors 2025, 25, 1540. [Google Scholar] [CrossRef]
- Chamble, P.; Bharath, M.R.; Lokesha, K.; Ezhil Singh, S.C. Machine tool vibration on dimensional accuracy and surface roughness during milling operation of Al6082 with indexable carbide inserts. J. Appl. Res. Technol. 2020, 18, 69–76. [Google Scholar] [CrossRef]
- Yuan, W.; Cheung, C.F. Characterization of surface topography variation in the ultra-precision tool servo-based diamond cutting of 3d microstructured surfaces. Micromachines 2021, 12, 1448. [Google Scholar] [CrossRef] [PubMed]
- Grigoruță, C.; Grigoruță, L.-C.; Simon, I.; Chitariu, D.-F.; Eduțanu, F.-D.; Horodincă, M. Considerations on the Accuracy and Precision of Machine Tools: A Review; Gheorghe Asachi Technical University of Iasi: Iasi, Romania, 2025. [Google Scholar]
- Pan, X.; Zhang, X.; Jiang, Z.; Bin, G. Real-time intelligent diagnosis of co-frequency vibration faults in rotating machinery based on lightweight-convolutional neural networks. Chin. J. Mech. Eng. 2024, 37, 41. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, H.; Wang, N.; Zhang, S.; Luo, Z.; Xuan, X.; Liu, M.; Chen, X.; Li, X.; Xue, L.; et al. Effects of air pollution and noise exposure on occupational hearing loss in oil workers: A prospective cohort study. BMC Public Health 2025, 25, 1–21. [Google Scholar] [CrossRef]
- Qian, P.; Lu, T.; Shen, C.; Chen, S. Influence of vibration on the grain flow sensor during the harvest and the difference elimination method. Int. J. Agric. Biol. Eng. 2021, 14, 149–162. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, Z.; Zhang, Z.; Song, Z.; Liu, Y.; Li, Y.; Xu, L. Durable testing and analysis of a cleaning sieve based on vibration and strain signals. Agriculture 2023, 13, 2232. [Google Scholar] [CrossRef]
- Wang, X.; Hong, T.; Fang, W.; Chen, X. Optimized design for vibration reduction in a residual film recovery machine frame based on modal analysis. Agriculture 2024, 14, 543. [Google Scholar] [CrossRef]
- Chun-Sheng, S.; Xue-Chun, X.; Bo-Yuan, C.; Gang, D.U. An Active Vibration Control Method Based on NARX Neural Network. Noise Vib. Control 2024, 44, 1. [Google Scholar]
- Lopes, P.A.C.; Piedade, M.S. The behavior of the modified FX-LMS algorithm with secondary path modeling errors. IEEE Signal Process. Lett. 2004, 11, 148–151. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, H.; Xu, N.; Zhong, J.; Wang, Z.; Yao, W.; Jiang, Y.; Laima, S. A data-driven model for predictive modeling of vortex-induced vibrations of a long-span bridge. Appl. Sci. 2024, 14, 2233. [Google Scholar] [CrossRef]
- Zhou, X.; Sun, J.; Tian, Y.; Lu, B.; Hang, Y.; Chen, Q. Hyperspectral technique combined with deep learning algorithm for detection of compound heavy metals in lettuce. Food Chem. 2020, 321, 126503. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Zhu, W.; Steibel, J.; Siegford, J.; Han, J.; Norton, T. Classification of drinking and drinker-playing in pigs by a video-based deep learning method. Biosyst. Eng. 2020, 196, 1–14. [Google Scholar] [CrossRef]
- Tian, Y.; Sun, J.; Zhou, X.; Yao, K.; Tang, N. Detection of soluble solid content in apples based on hyperspectral technology combined with deep learning algorithm. J. Food Process. Preserv. 2022, 46, e16414. [Google Scholar] [CrossRef]
- Tao, K.; Wang, A.; Shen, Y.; Lu, Z.; Peng, F.; Wei, X. Peach flower density detection based on an improved CNN incorporating attention mechanism and multi-scale feature fusion. Horticulturae 2022, 8, 904. [Google Scholar] [CrossRef]
- Li, H.; Luo, X.; Haruna, S.A.; Zareef, M.; Chen, Q.; Ding, Z.; Yan, Y. Au-Ag OHCs-based SERS sensor coupled with deep learning CNN algorithm to quantify thiram and pymetrozine in tea. Food Chem. 2023, 428, 136798. [Google Scholar] [CrossRef]
- Guo, Z.; Zou, Y.; Sun, C.; Jayan, H.; Jiang, S.; El-Seedi, H.R.; Zou, X. Nondestructive determination of edible quality and watercore degree of apples by portable Vis/NIR transmittance system combined with CARS-CNN. J. Food Meas. Charact. 2024, 18, 4058–4073. [Google Scholar] [CrossRef]
- Zhang, T.; Zhou, J.; Liu, W.; Yue, R.; Shi, J.; Zhou, C.; Hu, J. SN-CNN: A Lightweight and Accurate Line Extraction Algorithm for Seedling Navigation in Ridge-Planted Vegetables. Agriculture 2024, 14, 1446. [Google Scholar] [CrossRef]
- Wang, Y.; Li, T.; Chen, T.; Zhang, X.; Taha, M.F.; Yang, N.; Mao, H.; Shi, Q. Cucumber downy mildew disease prediction using a CNN-LSTM approach. Agriculture 2024, 14, 1155. [Google Scholar] [CrossRef]
- Heller, N.; Anderson, D.; Baker, M.; Juffer, B.; Papanikolopoulos, N. Convolutional neural networks for aircraft noise monitoring. arXiv 2018, arXiv:1806.04779. [Google Scholar] [CrossRef]
- Cabrera-Ponce, A.A.; Martinez-Carranza, J.; Rascon, C. Detection of nearby UAVs using CNN and Spectrograms. In Proceedings of the International Micro Air Vehicle Conference and Competition (IMAV) (Madrid), Madrid, Spain, 30 September–4 October 2019; p. 29. [Google Scholar]
- Wang, C.; Cui, X.; Zhao, S.; Zhou, X.; Song, Y.; Wang, Y.; Guo, K. Enhancing vehicle ride comfort through deep reinforcement learning with expert-guided soft-hard constraints and system characteristic considerations. Adv. Eng. Inform. 2024, 59, 102328. [Google Scholar] [CrossRef]
- Dridi, I.; Hamza, A.; Ben Yahia, N. A new approach to controlling an active suspension system based on reinforcement learning. Adv. Mech. Eng. 2023, 15. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, C.; Zhao, S.; Guo, K. Research on deep reinforcement learning control algorithm for active suspension considering uncertain time delay. Sensors 2023, 23, 7827. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Z.; Li, Y.; Guan, Z.; Tang, X. Research on following suction and discharging motion control method of vacuum-vibration precision seeding manipulator. Appl. Eng. Agric. 2022, 38, 873–883. [Google Scholar] [CrossRef]
- Liao, C.; Chen, J.; Geng, F.; Tang, X. Airflow basin structure numerical optimisation analysis and suction nozzle characteristics experimental study of vacuum-vibration tray precision seeder. J. Agric. Eng. 2022, 53. [Google Scholar] [CrossRef]
- Lu, L.; Yin, K.-L.; de Lamare, R.C.; Zheng, Z.; Yu, Y.; Yang, X.; Chen, B. Active noise control techniques for nonlinear systems. arXiv 2021, arXiv:2110.09672. [Google Scholar] [CrossRef]
- El Ouni, M.H.; Abdeddaim, M.; Elias, S.; Kahla, N.B. Review of vibration control strategies of high-rise buildings. Sensors 2022, 22, 8581. [Google Scholar] [CrossRef]
- Cunha, B.Z.; Droz, C.; Zine, A.-M.; Foulard., S.; Ichchou, M. A review of machine learning methods applied to structural dynamics and vibroacoustic. Mech. Syst. Signal Process. 2023, 200, 110535. [Google Scholar] [CrossRef]
- Liu, Y.; Lei, Z. Review of advances in active impulsive noise control with focus on adaptive algorithms. Appl. Sci. 2024, 14, 1218. [Google Scholar] [CrossRef]
- Liu, R.; Liu, Q.; Wang, Y.; Yu, W.; Cheng, G. Neural network-based ANC algorithms: A review. J. Vibroengineering 2025. [Google Scholar] [CrossRef]
- Ibraheem, A.A.; Ghazaly, N.M.; Abd el-Jaber, G. Review of rotor balancing techniques. Am. J. Ind. Eng. 2019, 6, 19. [Google Scholar]
- Åkerblom, M. Gear Noise and Vibration: A Literature Survey; TRITA-MMK 2001:11; KTH Royal Institute of Technology: Stockholm, Sweden, 2001; 25p, Available online: https://www.diva-portal.org/smash/get/diva2:139878/FULLTEXT01.p (accessed on 1 October 2025).
- Fu, Z.F.; He, J. Modal Analysis; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Lin, H.; Xu, P.; Sun, L.; Bi, X.; Zhao, J.; Cai, J. Identification of eggshell crack using multiple vibration sensors and correlative information analysis. J. Food Process Eng. 2018, 41, e12894. [Google Scholar] [CrossRef]
- Xi, T.; Li, C.; Qiu, W.; Wang, H.; Lv, X.; Han, C.; Ahmad, F. Droplet deposition behavior on a pear leaf surface under wind-induced vibration. Appl. Eng. Agric. 2020, 36, 913–926. [Google Scholar] [CrossRef]
- Blevins, R.D. Flow-Induced Vibration; Academic Press: New York, NY, USA, 1977. [Google Scholar]
- Auld, B.A. Acoustic Fields and Waves in Solids; Ripol Klassik: Moscow, Russia, 1973. [Google Scholar]
- Faheem, M.; Liu, J.; Chang, G.; Abbas, I.; Xie, B.; Shan, Z.; Yang, K. Experimental research on grape cluster vibration signals during transportation and placing for harvest and post-harvest handling. Agriculture 2021, 11, 902. [Google Scholar] [CrossRef]
- Rao, S.S. Vibration of Continuous Systems; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Faheem, M.; Liu, J.; Chang, G.; Ahmad, I.; Peng, Y. Hanging force analysis for realizing low vibration of grape clusters during speedy robotic post-harvest handling. Int. J. Agric. Biol. Eng. 2021, 14, 62–71. [Google Scholar] [CrossRef]
- Putra, A.; Thompson, D.J. Radiation efficiency of unbaffled and perforated plates near a rigid reflecting surface. J. Sound Vib. 2011, 330, 5443–5459. [Google Scholar] [CrossRef]
- Gao, Y.; Yang, Y.; Fu, S.; Feng, K.; Han, X.; Hu, Y.; Zhu, Q.; Wei, X. Analysis of vibration characteristics of tractor–rotary cultivator combination based on time domain and frequency domain. Agriculture 2024, 14, 1139. [Google Scholar] [CrossRef]
- Gao, Y.; Yang, Y.; Hu, Y.; Han, X.; Feng, K.; Li, P.; Wei, X.; Zhai, C. Study on Operating Vibration Characteristics of Different No-Tillage Planter Row Units in Wheat Stubble Fields. Agriculture 2024, 14, 1878. [Google Scholar] [CrossRef]
- Gao, Y.; Hu, Y.; Yang, Y.; Feng, K.; Han, X.; Li, P.; Zhu, Y.; Song, Q. Optimization of operating parameters for straw returning machine based on vibration characteristic analysis. Agronomy 2024, 14, 2388. [Google Scholar] [CrossRef]
- Xu, B.; Liu, J.; Jin, Y.; Yang, K.; Zhao, S.; Peng, Y. Vibration–Collision Coupling Modeling in Grape Clusters for Non-Damage Harvesting Operations. Agriculture 2025, 15, 154. [Google Scholar] [CrossRef]
- Santos Fernandes, L.; Housman, J.A.; Stich, G.-D.; Duensing, J. Fan Noise Predictions of the NASA Source Diagnostic Test Using Unsteady Simulations with LAVA Part II–Tonal and Broadband Noise Assessment. In Proceedings of the 30th AIAA/CEAS Aeroacoustics Conference, Rome, Italy, 4–7 June 2024; p. 3228. [Google Scholar] [CrossRef]
- Qian, K.; Hou, Z.; Liang, J.; Liu, R.; Sun, D. Interior sound quality prediction of pure electric vehicles based on transfer path synthesis. Appl. Sci. 2021, 11, 4385. [Google Scholar] [CrossRef]
- Ji, K.; Li, Y.; Liu, Y.; Yu, Z.; Cheng, J. Vibration signal extraction and analysis of combine harvester based on low-pass filter-eemd combination. Eng. Agrícola 2024, 44, e20240006. [Google Scholar] [CrossRef]
- Bortolotti, P.; Branlard, E.; Platt, A.; Moriarty, P.; Sucameli, C.; Bottasso, C.L. Aeroacoustics Noise Model of OpenFAST; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2020. [Google Scholar] [CrossRef]
- Nelson, P.A.; Elliott, S.J. Active Control of Sound; Academic Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Shi, D.; Gan, W.-S.; Lam, B.; Wen, S. Feedforward selective fixed-filter active noise control: Algorithm and implementation. IEEE/ACM Trans. Audio Speech Lang. Process. 2020, 28, 1479–1492. [Google Scholar] [CrossRef]
- Akhtar, M.T.; Tufail, M.; Abe, M.; Kawamata, M. Acoustic feedback neutralization in active noise control systems. IEICE Electron. Express 2007, 4, 221–226. [Google Scholar] [CrossRef]
- Elliott, S.J.; Nelson, P.A. Active noise control. IEEE Signal Process. Mag. 2002, 10, 12–35. [Google Scholar] [CrossRef]
- Martins, N.C.; Dahleh, M.A. Feedback control in the presence of noisy channels:“Bode-like” fundamental limitations of performance. IEEE Trans. Autom. Control 2008, 53, 1604–1615. [Google Scholar] [CrossRef]
- Streeter, A.D.; Ray, L.R.; Collier, R.D. Hybrid feedforward-feedback active noise control. Proc. Am. Control. Conf. IEEE 2004, 3, 2876–2881. [Google Scholar] [CrossRef]
- Ma, Y.; Xiao, Y.; Ma, L.; Khorasani, K. A robust feedforward hybrid active noise control system with online secondary-path modelling. IET Signal Process. 2023, 17, e12183. [Google Scholar] [CrossRef]
- Bai, T.; Kijimoto, S.; Ishikawa, S.; Koba, Y. A new feedforward hybrid active noise control system using an adaptive notch filter bank and its application to fan noise. Appl. Acoust. 2025, 231, 110492. [Google Scholar] [CrossRef]
- Rayleigh, J.W.S.B. The Theory of Sound; Macmillan: New York, NY, USA, 1896. [Google Scholar]
- Leug, P. Process of Silencing Sound Oscillations. U.S. Patent 2,043,416, 9 June 1936. [Google Scholar]
- Fogel, L.J. Apparatus for Improving Intelligence under High Ambient Noise Levels. U.S. Patent 2,966,549, 27 December 1960. [Google Scholar]
- Casali, J.; Robinson, G.; Urquhart, R. Evaluation of an Improved Active Noise Reduction Microphone Using Speech Intelligibility and Performance-Based Testing; Virginia Polytechnic Institute and State University: Blacksburg, VI, USA, 2010. [Google Scholar]
- Conover, W.B. Fighting noise with noise. Noise Control. 1956, 2, 78–92. [Google Scholar] [CrossRef]
- Widrow, B.; Glover, J.R.; McCool, J.M.; Kaunitz, J.; Williams, C.S.; Hearn, R.H.; Zeidler, J.R.; Dong, J.E.; Goodlin, R.C. Adaptive noise cancelling: Principles and applications. Proc. IEEE 1975, 63, 1692–1716. [Google Scholar] [CrossRef]
- Karnopp, D.; Crosby, M.J.; Harwood, R.A. Vibration control using semi-active force generators. J. Eng. Ind. 1974, 96, 619–626. [Google Scholar] [CrossRef]
- Morgan, D.R. An analysis of multiple correlation cancellation loops with a filter in the auxiliary path. IEEE Trans. Accoustics Speech Signal Process. 1987, 36, 145–152. [Google Scholar] [CrossRef]
- Singer, N.C.; Seering, W.P. Preshaping command inputs to reduce system vibration. J. Dyn. Syst. Meas. Control. 1990, 112, 76–82. [Google Scholar] [CrossRef]
- Hagood, N.W.; Von Flotow, A. Damping of structural vibrations with piezoelectric materials and passive electrical networks. J. Sound Vib. 1991, 146, 243–268. [Google Scholar] [CrossRef]
- Preumont, A. Vibration Control of Active Structures: An Introduction; Springer Netherlands: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Kajikawa, Y.; Gan, W.S.; Kuo, S.M. Recent advances on active noise control: Open issues and innovative applications. APSIPA Trans. Signal Inf. Process. 2012, 1, e3. [Google Scholar] [CrossRef]
- Snyder, S.D.; Tanaka, N. Active control of vibration using a neural network. IEEE Trans. Neural Netw. 1995, 6, 819–828. [Google Scholar] [CrossRef]
- Bouchard, M.; Paillard, B.; Le Dinh, C.T. Improved training of neural networks for the nonlinear active control of sound and vibration. IEEE Trans. Neural Netw. 1999, 10, 391–401. [Google Scholar] [CrossRef] [PubMed]
- Bosse, A.; Lim, T.W.; Shelley, S. Modal filters and neural networks for adaptive vibration control. J. Vib. Control 2000, 6, 631–648. [Google Scholar] [CrossRef]
- Jha, R.; Rower, J. Experimental investigation of active vibration control using neural networks and piezoelectric actuators. Smart Mater. Struct. 2001, 11, 115. [Google Scholar] [CrossRef]
- Zhang, Q.Z.; Gan, W.S.; Zhou, Y. Adaptive recurrent fuzzy neural networks for active noise control. J. Sound Vib. 2006, 296, 935–948. [Google Scholar] [CrossRef]
- Chen, K.T.; Chou, C.H.; Chang, S.H.; Liu, Y.H. Intelligent active vibration control in an isolation platform. Appl. Acoust. 2008, 69, 1063–1084. [Google Scholar] [CrossRef]
- Xie, J.; Li, T.; Yang, Y.; Jin, W. Learning features from high speed train vibration signals with deep belief networks. In Proceedings of the 2014 International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 2205–2210. [Google Scholar] [CrossRef]
- Huang, H.B.; Huang, X.R.; Li, R.X.; Lim, T.C.; Ding, W.P. Sound quality prediction of vehicle interior noise using deep belief networks. Appl. Acoust. 2016, 113, 149–161. [Google Scholar] [CrossRef]
- Liu, J.; Yang, X. Learning to see the vibration: A neural network for vibration frequency prediction. Sensors 2018, 18, 2530. [Google Scholar] [CrossRef]
- Febvre, M.; Rodriguez, J.; Chesne, S.; Collet, M. Artificial intelligence for active vibration control optimization on smart structures. Smart Materials, Adaptive Structures and Intelligent Systems. Am. Soc. Mech. Eng. 2023, 857523, V001T04A001. [Google Scholar] [CrossRef]
- Han, S.Y.; Liang, T. Reinforcement-learning-based vibration control for a vehicle semi-active suspension system via the PPO approach. Appl. Sci. 2022, 12, 3078. [Google Scholar] [CrossRef]
- Chen, H.; Yu, Y.; Li, P. Transformer-based denoising of mechanical vibration signals. arXiv 2023, arXiv:2308.02166. [Google Scholar] [CrossRef]
- Zhang, Y.A.; Ma, F.; Abhayapala, T.D.; Samarasinghe, P.N.; Bastine, A. An active noise control system based on soundfield interpolation using a physics-informed neural network. In Proceedings of the ICASSP 2024—2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 506–510. [Google Scholar] [CrossRef]
- Tollardo, A.; Cadini, F.; Giglio, M.; Lomazzi, L. DeepF-fNet: A physics-informed neural network for vibration isolation optimization. arXiv 2024, arXiv:2412.21132. [Google Scholar] [CrossRef]
- Bai, L.; Li, M.; Lian, S.; Chen, K.; Lu, J. WaveNet-Volterra Neural Networks for Active Noise Control: A Fully Causal Approach. arXiv 2025, arXiv:2504.04450. [Google Scholar] [CrossRef]
- Engelberg, S. Input shaping: A tutorial introduction [lecture notes]. IEEE Control Syst. Mag. 2021, 41, 45–51. [Google Scholar] [CrossRef]
- Liu, D.X.; Zhang, J.C.; Li, Y.; Fang, J.J. Research on adaptive input shaping control of fruits and vegetable harvesting robot arm. Control Theory Appl. 2022, 39, 1043–1050. [Google Scholar]
- Pham, M.-N.; Hazel, B.; Hamelin, P.; Liu, Z. Vibration control of flexible joint robots using a discrete-time two-stage controller based on time-varying input shaping and delay compensation. J. Dyn. Syst. Meas. Control. 2021, 143, 101001. [Google Scholar] [CrossRef]
- Njåstad, E.B.; Tysse, G.O.; Egeland, O. Residual vibration control for robotic 3D scanning with application to inspection of marine propellers. Model. Identif. Control. A Nor. Res. Bull. 2021, 42, 83–98. [Google Scholar] [CrossRef]
- Singhose, W. Command shaping for flexible systems: A review of the first 50 years. Int. J. Precis. Eng. Manuf. 2009, 10, 153–168. [Google Scholar] [CrossRef]
- Singh, T.; Singhose, W. Input shaping/time delay control of maneuvering flexible structures. In Proceedings of the 2002 American Control Conference (IEEE Cat. No. CH37301), Anchorage, AK, USA, 8–10 May 2002; IEEE: Piscataway, NJ, USA, 2002; Volume 3, pp. 1717–1731. [Google Scholar] [CrossRef]
- Stein, A.; Singh, T. Input shaped control of a gantry crane with inertial payload. In Proceedings of the 2022 American Control Conference (ACC), Atlanta, GA, USA, 8–10 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 4127–4132. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, T.; Song, A.; Zhang, Y. An input shaping based active vibration control and adaptive RBF impedance control for suppressing the myospasm in upper-limb rehabilitation. Appl. Soft Comput. 2020, 95, 106380. [Google Scholar] [CrossRef]
- Vu, M.; Newman, D.; Vaughan, J. Designing input shapers using reinforcement learning. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 228–233. [Google Scholar] [CrossRef]
- El-Sharkawy, M.; Li, J.; Kamal, N.; Mahmoud, E.; Omara, A.E.-D.; Du, D. Assessing and predicting soil quality in heavy metal-contaminated soils: Statistical and ANN-based techniques. J. Soil Sci. Plant Nutr. 2023, 23, 6510–6526. [Google Scholar] [CrossRef]
- Zhao, S.; Jiao, T.; Adade, S.Y.-S.S.; Wang, Z.; Wu, X.; Li, H.; Chen, Q. Based on vis-NIR combined with ANN for on-line detection of bacterial concentration during kombucha fermentation. Food Biosci. 2024, 60, 104346. [Google Scholar] [CrossRef]
- Ramli, L.; Mohamed, Z.; Jaafar, H.I. A neural network-based input shaping for swing suppression of an overhead crane under payload hoisting and mass variations. Mech. Syst. Signal Process. 2018, 107, 484–501. [Google Scholar] [CrossRef]
- Zhang, T.; Kang, Z.; Zou, Y.; Liao, C. Deep neural network input shaper for residual vibration suppression. J. S. China Univ. Technol. (Nat. Sci. Ed.) 2021, 49, 103–112. [Google Scholar]
- Ur Rehman, S.F.; Mohamed, Z.; Husain, A.R.; Jaafar, H.I.; Shaheed, M.H.; Abbasi, M.A. Input shaping with an adaptive scheme for swing control of an underactuated tower crane under payload hoisting and mass variations. Mech. Syst. Signal Process. 2022, 175, 109106. [Google Scholar] [CrossRef]
- Ramli, L.; Mohamed, Z.; Efe, M.; Lazim, I.M.; Jaafar, H.I. Efficient swing control of an overhead crane with simultaneous payload hoisting and external disturbances. Mech. Syst. Signal Process. 2020, 135, 106326. [Google Scholar] [CrossRef]
- Yang, W.; Li, S.; Luo, X. Robust input shaping vibration control via extended Kalman filter-incorporated residual neural network. arXiv 2024, arXiv:2408.12126. [Google Scholar] [CrossRef]
- Li, T.; Xiao, T. Physics-Informed Neural Network-Based Input Shaping for Vibration Suppression of Flexible Single-Link Robots. Actuators 2025, 14, 14. [Google Scholar] [CrossRef]
- Xu, J.; Cao, J.; Zhang, Y. Vibration suppression of picking device with improved input shaping algorithm. J. Northeast For. Univ. 2020, 48, 79–84. [Google Scholar]
- Gulde, R.; Tuscher, M.; Csiszar, A.; Riedel, O.; Verl, A. Reinforcement learning approach to vibration compensation for dynamic feed drive systems. In Proceedings of the 2019 Second International Conference on Artificial Intelligence for Industries (AI4I), Laguna Hills, CA, USA, 25–27 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 26–29. [Google Scholar] [CrossRef]
- Zhang, T.; Chu, H.; Zou, Y.; Liu, T. A deep reinforcement learning-based optimization method for vibration suppression of articulated robots. Eng. Optim. 2023, 55, 1189–1206. [Google Scholar] [CrossRef]
- Mohammed, A.; Altuwais, H.; Alghanim, K. An optimized shaped command of overhead crane nonlinear system for rest-to-rest maneuver. J. Eng. Res. 2023, 11, 548–554. [Google Scholar] [CrossRef]
- Alam, M.S.; Tokhi, M.O. Designing feedforward command shapers with multi-objective genetic optimisation for vibration control of a single-link flexible manipulator. Eng. Appl. Artif. Intell. 2008, 21, 229–246. [Google Scholar] [CrossRef]
- Maghsoudi, M.J.; Mohamed, Z.; Sudin, S.; Buyamin, S.; Jaafar, H.I.; Ahmad, S.M. An improved input shaping design for an efficient sway control of a nonlinear 3D overhead crane with friction. Mech. Syst. Signal Process. 2017, 92, 364–378. [Google Scholar] [CrossRef]
- Tang, W.; Ma, R.; Wang, W.; Gao, H. Optimization-based input-shaping swing control of overhead cranes. Appl. Sci. 2023, 13, 9637. [Google Scholar] [CrossRef]
- Mohammed, A.; Alghanim, K.; Andani, M.T. An optimized non-linear input shaper for payload oscillation suppression of crane point-to-point maneuvers. Int. J. Dyn. Control 2019, 7, 567–576. [Google Scholar] [CrossRef]
- Xu, B.; Wang, R.; Peng, B.; Alqurashi, F.A.; Salama, M. Automatic parameter selection ZVD shaping algorithm for crane vibration suppression based on particle swarm optimisation. Appl. Math. Nonlinear Sci. 2022, 7, 73–82. [Google Scholar] [CrossRef]
- Fu, W.; Tao, Y.; Han, X.; Hu, J.; Zhang, J.; Li, S.; Pei, W. Improved THEI input shaper for the vibration suppression of flexible systems under variable loads. J. Vib. Shock 2024, 43, 113–120. [Google Scholar]
- Lu, L.; Yin, K.L.; de Lamare, R.C.; Zheng, Z.; Yu, Y.; Yang, X.; Chen, B. A survey on active noise control in the past decade—Part I: Linear systems. Signal Process. 2021, 183, 108039. [Google Scholar] [CrossRef]
- Moon, S.P.; Chang, T.G. The derivation of the stability bound of the feedback ANC system that has an error in the estimated secondary path model. Appl. Sci. 2018, 8, 210. [Google Scholar] [CrossRef]
- Akhtar, M.T. Narrowband feedback active noise control systems with secondary path modeling using gain-controlled additive random noise. Digit. Signal Process. 2021, 111, 102976. [Google Scholar] [CrossRef]
- Guo, R.; Wei, X.K.; Gao, J. Extended filtered-x-least-mean-squares algorithm for an active control engine mount based on acceleration error signal. Adv. Mech. Eng. 2017, 9, 1687814017724350. [Google Scholar] [CrossRef]
- Park, U.; Kang, Y.J. Operational transfer path analysis based on neural network. J. Sound Vib. 2024, 579, 118364. [Google Scholar] [CrossRef]
- Liang, R.; Liu, W.; Fu, Y.; Ma, M. Physics-informed deep learning for structural dynamics under moving load. Int. J. Mech. Sci. 2024, 284, 109766. [Google Scholar] [CrossRef]
- Mostafavi, A.; Cha, Y.J. Deep learning-based active noise control on construction sites. Autom. Constr. 2023, 151, 104885. [Google Scholar] [CrossRef]
- Martinez, Y.; Rojas, L.; Peña, A.; Valenzuela, M.; Garcia, J. Physics-Informed Neural Networks for the Structural Analysis and Monitoring of Railway Bridges: A Systematic Review. Mathematics 2025, 13, 1571. [Google Scholar] [CrossRef]
- Im, S.; Kim, S.; Woo, S.; Jang, I.; Han, T.; Hwang, U.; Ohm, W.-S.; Lee, M. Deep learning-assisted active noise control in a time-varying environment. J. Mech. Sci. Technol. 2023, 37, 1189–1196. [Google Scholar] [CrossRef]
- Cha, Y.J.; Mostafavi, A.; Benipal, S.S. DNoiseNet: Deep learning-based feedback active noise control in various noisy environments. Eng. Appl. Artif. Intell. 2023, 121, 105971. [Google Scholar] [CrossRef]
- Oh, J.Y.; Jung, H.W.; Lee, M.H.; Lee, K.H.; Kang, Y.J. Enhancing active noise control of road noise using deep neural network to update secondary path estimate in real time. Mech. Syst. Signal Process. 2024, 206, 110940. [Google Scholar] [CrossRef]
- Cheng, C.; Liu, Z.; Chen, W.; Li, X.; Liao, W.; Lu, C. A multi-channel active noise control system using deep learning-based method to estimate secondary path and normalized-clustered control strategy for vehicle interior engine noise. Appl. Acoust. 2025, 228, 110263. [Google Scholar] [CrossRef]
- Song, H.; Shan, X.; Zhang, L.; Wang, G.; Fan, J. Research on identification and active vibration control of cantilever structure based on NARX neural network. Mech. Syst. Signal Process. 2022, 171, 108872. [Google Scholar] [CrossRef]
- Liu, T.; Meidani, H. Physics-informed neural networks for system identification of structural systems with a multiphysics damping model. J. Eng. Mech. 2023, 149, 04023079. [Google Scholar] [CrossRef]
- Lai, Z.; Mylonas, C.; Nagarajaiah, S.; Chatzi, E. Structural identification with physics-informed neural ordinary differential equations. J. Sound Vib. 2021, 508, 116196. [Google Scholar] [CrossRef]
- Teloli, R.d.O.; Tittarelli, R.; Bigot, M.; Coelho, L.; Ramasso, E.; Le Moal, P.; Ouisse, M. A physics-informed neural networks framework for model parameter identification of beam-like structures. Mech. Syst. Signal Process. 2025, 224, 112189. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Z.; Li, L.; Hao, H.; Chen, W.; Shao, Y. Machine learning prediction of structural dynamic responses using graph neural networks. Comput. Struct. 2023, 289, 107188. [Google Scholar] [CrossRef]
- Pang, J.; Li, Y.; Ji, J.; Xu, L. Vibration excitation identification and control of the cutter of a combine harvester using triaxial accelerometers and partial coherence sorting. Biosyst. Eng. 2019, 185, 25–34. [Google Scholar] [CrossRef]
- Chen, S.; Zhou, Y.; Tang, Z.; Lu, S. Modal vibration response of rice combine harvester frame under multi-source excitation. Biosyst. Eng. 2020, 194, 177–195. [Google Scholar] [CrossRef]
- Ding, Z.; Tang, Z.; Zhang, B.; Ding, Z. Vibration response of metal plate and shell structure under multi-source excitation with welding and bolt connection. Agriculture 2024, 14, 816. [Google Scholar] [CrossRef]
- Kwon, S.; Kim, B.S.; Park, J. Active Noise Reduction with Filtered Least-Mean-Square Algorithm Improved by Long Short-Term Memory Models for Radiation Noise of Diesel Engine. Appl. Sci. 2022, 12, 10248. [Google Scholar] [CrossRef]
- Nunekpeku, X.; Zhang, W.; Gao, J.; Adade, S.Y.S.S.; Li, H.; Chen, Q. Gel strength prediction in ultrasonicated chicken mince: Fusing near-infrared and Raman spectroscopy coupled with deep learning LSTM algorithm. Food Control 2025, 168, 110916. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, D.; Yuan, Y.; Lei, Z.; Ding, B.; Bo, L. Road terrain recognition based on tire noise for autonomous vehicle. Sci. Rep. 2024, 14, 30913. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, C.; Bridgelall, R.; Sun, M. Road profile reconstruction using connected vehicle responses and wavelet analysis. J. Terramechanics 2018, 80, 21–30. [Google Scholar] [CrossRef]
- Redonnet, S.; Bose, T.; Seth, A.; Li, L.K. Airfoil self-noise prediction using deep neural networks. Eng. Anal. Bound. Elem. 2024, 159, 180–191. [Google Scholar] [CrossRef]
- Ma, Q.; Wu, Y.; Shoukat, M.U.; Yan, Y.; Wang, J.; Yang, L.; Yan, F.; Yan, L. Deep reinforcement learning-based wind disturbance rejection control strategy for uav. Drones 2024, 8, 632. [Google Scholar] [CrossRef]
- Beijen, M.A.; Heertjes, M.F.; Butler, H.; Steinbuch, M. H∞ feedback and feedforward controller design for active vibration isolators. IFAC-Pap. 2017, 50, 13384–13389. [Google Scholar] [CrossRef]
- Zhang, S.; Schmidt, R.; Qin, X. Active vibration control of piezoelectric bonded smart structures using PID algorithm. Chin. J. Aeronaut. 2015, 28, 305–313. [Google Scholar] [CrossRef]
- Vasques, C.M.A.; Rodrigues, J.D. Active vibration control of smart piezoelectric beams: Comparison of classical and optimal feedback control strategies. Comput. Struct. 2006, 84, 1402–1414. [Google Scholar] [CrossRef]
- Awada, A.; Younes, R.; Ilinca, A. Optimized active control of a smart cantilever beam using genetic algorithm. Designs 2022, 6, 36. [Google Scholar] [CrossRef]
- Febvre, M.; Rodriguez, J.; Chesne, S.; Collet, M. Deep reinforcement learning for tuning active vibration control on a smart piezoelectric beam. J. Intell. Mater. Syst. Struct. 2024, 35, 1149–1165. [Google Scholar] [CrossRef]
- Song, X.; Li, H.; Chen, C.; Xia, H.; Zhang, Z.; Tang, P. Design and experimental testing of a control system for a solid-fertilizer-dissolving device based on fuzzy PID. Agriculture 2022, 12, 1382. [Google Scholar] [CrossRef]
- Ziegler, J.G.; Nichols, N.B. Optimum settings for automatic controllers. Trans. Am. Soc. Mech. Eng. 1942, 64, 759–765. [Google Scholar] [CrossRef]
- Kalman, R.E. Contributions to the theory of optimal control. Bol. Soc. Mat. Mex. 1960, 5, 102–119. [Google Scholar]
- Yatim, H.; Darus, I.Z.M. Self-tuning active vibration controller using particle swarm optimization for flexible manipulator system. WSEAS Trans. Syst. Control 2014, 9, 55–66. [Google Scholar]
- Huang, Z.; Cheng, Y.; Wang, X.; Wu, N. Active Vibration Control and Parameter Optimization of Genetic Algorithm for Partially Damped Composites Beams. Biomimetics 2024, 9, 584. [Google Scholar] [CrossRef]
- Syafiqah Shaari, A.N.; Hadi, M.S.; Abdul Wahab, A.M.; Ab Talib, M.H.; Yatim, H.M.; Mat Darus, I.Z.; Tokhi, M.O. Intelligent proportional-integral-derivate controller using metaheuristic approach via crow search algorithm for vibration suppression of flexible plate structure. J. Low Freq. Noise Vib. Act. Control. 2024, 43, 560–574. [Google Scholar] [CrossRef]
- Silva, T.M.; Balasubramanian, P.; Franchini, G.; Buabdulla, A.; Amabili, M. Experiment-in-the-Loop system for fast and effective tuning of active vibration controllers. Int. J. Mech. Sci. 2024, 284, 109753. [Google Scholar] [CrossRef]
- Lakhani, A.I.; Chowdhury, M.A.; Lu, Q. Stability-preserving automatic tuning of PID control with reinforcement learning. arXiv 2021, arXiv:2112.15187. [Google Scholar] [CrossRef]
- Nguyen, T.T.T.; Zhang, F.; Na, J.; Nguyen, L.T.; Li, G.; Ahmed, A.A.M. A Variable Step-Size FxLMS Algorithm for Nonlinear Feedforward Active Noise Control. Sensors 2025, 25, 2569. [Google Scholar] [CrossRef]
- Le Thai, N.; Wu, X.; Na, J.; Guo, Y.; Tin, N.T.; Le, P.X. Adaptive variable step-size neural controller for nonlinear feedback active noise control systems. Appl. Acoust. 2017, 116, 337–347. [Google Scholar] [CrossRef]
- Zorić, N.D.; Simonović, A.M.; Mitrović, Z.S.; Stupar, S.N.; Obradović, A.M.; Lukić, N.S. Free vibration control of smart composite beams using particle swarm optimized self-tuning fuzzy logic controller. J. Sound Vib. 2014, 333, 5244–5268. [Google Scholar] [CrossRef]
- Jafarzadeh, O.; Mousavi Ghasemi, S.A.; Zahrai, S.M.; Mohammadzadeh, A.; Vafaei Poursorkhabi, R. Online adaptive neurochaotic fuzzy controller design to reduce the seismic response of buildings equipped with active tuned mass damper system. Int. J. Intell. Syst. 2023, 2023, 8460498. [Google Scholar] [CrossRef]
- Wang, A.; Feng, X.; Liu, H.; Yao, M. Design of sliding mode controller for servo feed system based on generalized extended state observer with reinforcement learning. Sci. Rep. 2024, 14, 24976. [Google Scholar] [CrossRef] [PubMed]
- Mu, X.; Huang, R.; Zou, Q.; Hu, H. Machine learning-based active flutter suppression for a flexible flying-wing aircraft. J. Sound Vib. 2022, 529, 116916. [Google Scholar] [CrossRef]
- Sun, J.; Zhao, K. Adaptive neural network sliding mode control for active suspension systems with electrohydraulic actuator dynamics. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420941986. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhu, B. Multi-objective optimization of active suspension predictive control based on improved PSO algorithm. J. Vibroengineering 2019, 21, 1388–1404. [Google Scholar] [CrossRef]
- Ogawa, H.; Takahashi, Y. Echo state network based model predictive control for active vibration control of hybrid electric vehicle powertrains. Appl. Sci. 2021, 11, 6621. [Google Scholar] [CrossRef]
- Kalaycioglu, S.; Ding, D. NMPC and Deep Learning-Based Vibration Control of Satellite Beam Antenna Dynamics Using PZT Actuators and Sensors. arXiv 2024, arXiv:2412.16805. [Google Scholar] [CrossRef]
- Schöning, J.; Pfisterer, H.J. Safe and trustful AI for closed-loop control systems. Electronics 2023, 12, 3489. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, D.L. Deep MCANC: A deep learning approach to multi-channel active noise control. Neural Netw. 2023, 158, 318–327. [Google Scholar] [CrossRef]
- Luo, Z.; Shi, D.; Shen, X.; Ji, J.; Gan, W.-S. Deep generative fixed-filter active noise control. In Proceedings of the ICASSP 2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Ouyang, Q.; Fan, Z.; Chang, H.; Shoaib, M.; Chen, Q. Analyzing TVB-N in snakehead by Bayesian-optimized 1D-CNN using molecular vibrational spectroscopic techniques: Near-infrared and Raman spectroscopy. Food Chem. 2025, 464, 141701. [Google Scholar] [CrossRef] [PubMed]
- Ryu, S.; Lim, J.; Lee, Y.S. Narrowband Active Noise Control with DDPG Based on Reinforcement Learning. Int. J. Automot. Technol. 2024, 25, 1389–1397. [Google Scholar] [CrossRef]
- Nguyen, T.T.T.; Na, J.; Wang, X. Neuro-Fuzzy Network-Based Nonlinear Hybrid Active Noise Control Systems. Entropy 2025, 27, 138. [Google Scholar] [CrossRef] [PubMed]
- Miao, X.; Yang, L.; Ouyang, H. Artificial-neural-network-based optimal Smoother design for oscillation suppression control of underactuated overhead cranes with distributed mass beams. Mech. Syst. Signal Process. 2023, 200, 110497. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Q.; Zhang, T.; Zou, Y. Vibration suppression of ball-screw drive system based on flexible dynamics model. Eng. Appl. Artif. Intell. 2023, 117, 105506. [Google Scholar] [CrossRef]
- Ghorbani, H.; Alipour, K.; Tarvirdizadeh, B.; Hadi, A. Comparison of various input shaping methods in rest-to-rest motion of the end-effecter of a rigid-flexible robotic system with large deformations capability. Mech. Syst. Signal Process. 2019, 118, 584–602. [Google Scholar] [CrossRef]
- Jallouli-Khlif, R.; Maalej, B.; Melchior, P.; Derbel, N. Control of prosthetic hand based on input shaping combined to fractional PI controller. In Proceedings of the 2021 9th International Conference on Systems and Control (ICSC), Caen, France, 24–26 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 449–454. [Google Scholar]
- Cutler, R.; Saabas, A.; Pärnamaa, T.; Purin, M.; Indenbom, E.; Ristea, N.-C.; Gužvin, J.; Gamper, H.; Braun, S.; Aichner, R. ICASSP 2023 acoustic echo cancellation challenge. IEEE Open J. Signal Process. 2024, 5, 675–685. [Google Scholar] [CrossRef]
- Fernandez, J.; Kahn, J.; Na, C.; Bisk, Y.; Strubell, E. The framework tax: Disparities between inference efficiency in nlp research and deployment. arXiv 2023, arXiv:2302.06117. [Google Scholar] [CrossRef]
- Yang, W.; Li, S.; Luo, X. Data driven vibration control: A review. IEEE/CAA J. Autom. Sin. 2024, 11, 1898–1917. [Google Scholar] [CrossRef]
- He, T.; Su, W. Co-design of active vibration control and optimal sensor and actuator placement for a flexible wing using reinforcement learning. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2023, 237, 2240–2251. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, A.; Lv, Z.; Gao, Z. Nondestructive measurement of kiwifruit firmness, soluble solid content (SSC), titratable acidity (TA), and sensory quality by vibration spectrum. Food Sci. Nutr. 2020, 8, 1058–1066. [Google Scholar] [CrossRef]
- Liu, J.; Yuan, Y.; Gao, Y.; Tang, S.; Li, Z. Virtual model of grip-and-cut picking for simulation of vibration and falling of grape clusters. Trans. ASABE 2019, 62, 603–614. [Google Scholar] [CrossRef]
- Tahir, H.E.; Xiaobo, Z.; Jianbo, X.; Mahunu, G.K.; Jiyong, S.; Xu, J.-L.; Sun, D.-W. Recent progress in rapid analyses of vitamins, phenolic, and volatile compounds in foods using vibrational spectroscopy combined with chemometrics: A review. Food Anal. Methods 2019, 12, 2361–2382. [Google Scholar] [CrossRef]
- Qiu, Z.; Yang, Y.; Zhang, X. Reinforcement learning vibration control of a multi-flexible beam coupling system. Aerosp. Sci. Technol. 2022, 129, 107801. [Google Scholar] [CrossRef]
- Xie, S.; Ren, J. Recurrent-neural-network-based predictive control of piezo actuators for trajectory tracking. IEEE/ASME Trans. Mechatron. 2019, 24, 2885–2896. [Google Scholar] [CrossRef]
- Oh, C.S.; Kang, J.; Kim, J.K. Active Noise Control with Head Tracking System. SAE Tech. Pap. 2025. [Google Scholar] [CrossRef]
- Hua, X.; Thomas, A.; Shultis, K. Recent progress in battery electric vehicle noise, vibration, and harshness. Sci. Prog. 2021, 104, 00368504211005224. [Google Scholar] [CrossRef]
- Xu, L.; Chai, X.; Gao, Z.; Li, Y.; Wang, Y. Experimental study on driver seat vibration characteristics of crawler-type combine harvester. Int. J. Agric. Biol. Eng. 2019, 12, 90–97. [Google Scholar] [CrossRef]
- Forssén, J.; Hoffmann, A.; Kropp, W. Auralization model for the perceptual evaluation of tyre–road noise. Appl. Acoust. 2018, 132, 232–240. [Google Scholar] [CrossRef]
- Yang, H.; Shi, W.; Xu, M.; Yang, X.; Yang, D.; Xin, L. Analysis and control of gearbox whine of a heavy commercial vehicle based on planet phasing theory and bench test. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2025, 239, 214–233. [Google Scholar] [CrossRef]
- Dai, D.; Chen, D.; Wang, S.; Li, S.; Mao, X.; Zhang, B.; Wang, Z.; Ma, Z. Compilation and Extrapolation of Load Spectrum of Tractor Ground Vibration Load Based on CEEMDAN-POT Model. Agriculture 2023, 13, 125. [Google Scholar] [CrossRef]
- Wang, B.; Que, K.; Tang, Z.; Sun, M.; Lian, Y.; Wang, H. Multivariate Structural Vibration Coupling Response of the Self-Propelled Straw Pickup Baler Under Time-Varying Loads. Agriculture 2024, 14, 1960. [Google Scholar] [CrossRef]
- Liang, Z.; Wang, H.; Yang, Y.; Zhang, W.; Abhayapala, T.D. Active Road Noise Control Based on Data-Driven Predictions of Passenger Ear Noise Signal. In Proceedings of the 2024 18th International Workshop on Acoustic Signal Enhancement (IWAENC), Aalborg, Denmark, 9–12 September 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 424–428. [Google Scholar] [CrossRef]
- Jia, X.; Zhou, L.; Huang, H.; Pang, J.; Yang, L. Improving Electric Vehicle Structural-Borne Noise Based on Convolutional Neural Network-Support Vector Regression. Electronics 2023, 13, 113. [Google Scholar] [CrossRef]
- Lou, X.; Zhang, S.; Chen, X.; Gao, Y.; Ji, W. Improvement and application of electromagnetic vibration and noise suppression method for electric vehicle motor. Heliyon 2023, 9, e20900. [Google Scholar] [CrossRef]
- Rao, B.R.; Gautam, G.S.J.; He, S. High-Fidelity NVH Model Development for Electric Motors Using Deep Learning and Machine Learning Algorithms. SAE Tech. Pap. 2025. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Z.; Sun, X.; Gao, C.; Liu, X.; Guo, Y. Back propagation neural network-based torque ripple reduction strategy for high frequency square-wave voltage injection-based interior permanent magnet synchronous motor sensorless control. IET Electr. Power Appl. 2023, 17, 195–205. [Google Scholar] [CrossRef]
- Ahmed, M.H.; AboHussien, A.; El-Shafei, A.; Darwish, A.M.; Abdel-Gawad, A.H. Active control of flexible rotors using deep reinforcement learning with application of multi-actor-critic deep deterministic policy gradient. Eng. Appl. Artif. Intell. 2023, 124, 106593. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, L.; Wang, R.; Xu, X.; Shen, Y.; Liu, Y. Modeling and test on height adjustment system of electrically-controlled air suspension for agricultural vehicles. Int. J. Agric. Biol. Eng. 2016, 9, 40–47. [Google Scholar] [CrossRef]
- Cui, L.; Mao, H.; Xue, X.; Ding, S.; Qiao, B. Optimized design and test for a pendulum suspension of the crop spray boom in dynamic conditions based on a six DOF motion simulator. Int. J. Agric. Biol. Eng. 2018, 11, 76–85. [Google Scholar] [CrossRef]
- Cui, L.; Xue, X.; Le, F.; Mao, H.; Ding, S. Design and experiment of electro hydraulic active suspension for controlling the rolling motion of spray boom. Int. J. Agric. Biol. Eng. 2019, 12, 72–81. [Google Scholar] [CrossRef]
- Wang, C.; Cui, X.; Zhao, S.; Zhou, X.; Song, Y.; Wang, Y.; Guo, K. A deep reinforcement learning-based active suspension control algorithm considering deterministic experience tracing for autonomous vehicle. Appl. Soft Comput. 2024, 153, 111259. [Google Scholar] [CrossRef]
- Nhu, A.N.; Le, N.-A.; Li, S.; Truong, T.D. Physics-guided reinforcement learning system for realistic vehicle active suspension control. In Proceedings of the 2023 International Conference on Machine Learning and Applications (ICMLA), Jacksonville, FL, USA, 15–17 December 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 422–429. [Google Scholar] [CrossRef]
- Yu, C.; Qun, Z.; Jinna, L.I. Data-driven active vibration control for helicopter with trailing-edge flaps using adaptive dynamic programming. Chin. J. Aeronaut. 2024, 37, 151–166. [Google Scholar] [CrossRef]
- Yuan, Y.; Lu, Y.; Sun, J.; Wang, C. Research on the optimal selection method of sensors/actuators in active structural acoustic control for helicopter based on machine learning. Measurement 2025, 245, 116631. [Google Scholar] [CrossRef]
- Mylonas, D.; Erspamer, A.; Yiakopoulos, C.; Antoniadis, I. A virtual sensing active noise control system based on a functional link neural network for an aircraft seat headrest. J. Vib. Eng. Technol. 2024, 12, 3857–3872. [Google Scholar] [CrossRef]
- Wang, A.; Wang, S.; Xia, H.; Ma, G.; Zhang, L.; Liu, W. Adaptive neural control of microgravity active vibration isolation system subject to output constraint and unexpected disturbance. Acta Astronaut. 2023, 213, 168–176. [Google Scholar] [CrossRef]
- Fu, Y. Neural network–based active control of a rigid–flexible spacecraft with bounded input. J. Vib. Control 2024, 30, 1117–1132. [Google Scholar] [CrossRef]
- Li, Y.; Xu, L.; Gao, Z.; Lu, E.; Li, Y. Effect of vibration on rapeseed header loss and optimization of header frame. Am. Soc. Agric. Biol. Eng. 2021, 64, 1247–1258. [Google Scholar] [CrossRef]
- Nasiri, K.; Moradi, H. Chatter suppression in nonlinear milling of a flexible plate-workpiece with attached piezoelectric actuators: Comparison of soft-actor-critic-based controller vs optimized type-2 fuzzy controller. Mech. Syst. Signal Process. 2025, 224, 112198. [Google Scholar] [CrossRef]
- Sun, H.; Xing, N.; Zou, J.; Rong, Y.; Shi, Y.; Ding, H.; Zhang, H.-T. Neural Network-Based Switching Output Regulation Control for High-Speed Nano-Positioning Stages. Engineering 2025, in press. [Google Scholar] [CrossRef]
- Zhang, H.; Pandey, A. Low-latency active noise control using attentive recurrent network. IEEE/ACM Trans. Audio Speech Lang. Process. 2023, 31, 1114–1123. [Google Scholar] [CrossRef] [PubMed]
- Shen, D. A Study on Active Suspension System with Reinforcement Learning; University of Technology Sydney: Sydney, Australia, 2022. [Google Scholar]
- Wang, W.; Zhang, Y.; Gao, J.; Jiang, Y.; Yang, Y.; Zheng, Z.; Zou, W.; Li, J.; Zhang, C.; Cao, W. GOPS: A general optimal control problem solver for autonomous driving and industrial control applications. Commun. Transp. Res. 2023, 3, 100096. [Google Scholar] [CrossRef]
- Gleave, A.; Dennis, M.; Wild, C.; Kant, N.; Levine, S.; Russell, S. Adversarial policies: Attacking deep reinforcement learning. arXiv 2019, arXiv:1905.10615. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, H.; Xiao, C.; Li, B.; Liu, M.; Boning, D.; Hsieh, C.-J. Robust deep reinforcement learning against adversarial perturbations on state observations. Adv. Neural Inf. Process. Syst. 2020, 33, 21024–21037. [Google Scholar]
- Zhang, H.; Wang, D.L. Deep ANC: A deep learning approach to active noise control. Neural Netw. 2021, 141, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Lau, M.A.; Pao, L.Y. Input shaping and time-optimal control of flexible structures. Automatica 2003, 39, 893–900. [Google Scholar] [CrossRef]
- Kuo, S.M.; Morgan, D.R. Active noise control: A tutorial review. Proc. IEEE 2002, 87, 943–973. [Google Scholar] [CrossRef]
- Moslemi, A.; Briskina, A.; Dang, Z.; Li, J. A survey on knowledge distillation: Recent advancements. Mach. Learn. Appl. 2024, 18, 100605. [Google Scholar] [CrossRef]
- Weng, O. Neural network quantization for efficient inference: A survey. arXiv 2021, arXiv:2112.06126. [Google Scholar] [CrossRef]
- Ngo, D.; Park, H.C.; Kang, B. Edge Intelligence: A Review of Deep Neural Network Inference in Resource-Limited Environments. Electronics 2025, 14, 2495. [Google Scholar] [CrossRef]
- Garcıa, J.; Fernández, F. A comprehensive survey on safe reinforcement learning. J. Mach. Learn. Res. 2015, 16, 1437–1480. [Google Scholar]
- Guo, C.; Pleiss, G.; Sun, Y.; Weinberger, K.Q. On calibration of modern neural networks. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 1321–1330. [Google Scholar]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Linardatos, P.; Papastefanopoulos, V.; Kotsiantis, S. Explainable ai: A review of machine learning interpretability methods. Entropy 2020, 23, 18. [Google Scholar] [CrossRef]
- Ali, S.; Abuhmed, T.; El-Sappagh, S.; Muhammad, K.; Alonso-Moral, J.M.; Confalonieri, R.; Guidotti, R.; Del Ser, J.; Díaz-Rodríguez, N.; Herrera, F. Explainable Artificial Intelligence (XAI): What we know and what is left to attain Trustworthy Artificial Intelligence. Inf. Fusion 2023, 99, 101805. [Google Scholar] [CrossRef]
- Yang, L.; Dai, H.; Shi, Z.; Hsieh, C.-J.; Tedrake, R.; Zhang, H. Lyapunov-stable neural control for state and output feedback: A novel formulation for efficient synthesis and verification. arXiv 2024. [Google Scholar] [CrossRef]
- Richards, S.M.; Berkenkamp, F.; Krause, A. The lyapunov neural network: Adaptive stability certification for safe learning of dynamical systems. In Proceedings of the Conference on Robot Learning, PMLR, Beijing, China, 29–31 October 2018; pp. 466–476. [Google Scholar]
- Abdar, M.; Pourpanah, F.; Hussain, S.; Rezazadegan, D.; Liu, L.; Ghavamzadeh, M.; Fieguth, P.; Cao, X.; Khosravi, A.; Acharya, U.R. A review of uncertainty quantification in deep learning: Techniques, applications and challenges. Inf. Fusion 2021, 76, 243–297. [Google Scholar] [CrossRef]
- Lin, Y.; Zhang, Q.; Gao, B.; Tang, J.; Yao, P.; Li, C.; Huang, S.; Liu, Z.; Zhou, Y.; Liu, Y. Uncertainty quantification via a memristor Bayesian deep neural network for risk-sensitive reinforcement learning. Nat. Mach. Intell. 2023, 5, 714–723. [Google Scholar] [CrossRef]
- Boscariol, P.; Richiedei, D.; Tamellin, I. Residual vibration suppression in uncertain systems: A robust structural modification approach to trajectory planning. Robot. Comput.-Integr. Manuf. 2022, 74, 102282. [Google Scholar] [CrossRef]
- Billings, S.A.; Guo, Y.; Guo, L.; Wei, H. Identification of nonlinear systems with non-persistent excitation using an iterative forward orthogonal least squares regression algorithm. Int. J. Model. Identif. Control. 2015, 23, 1–7. [Google Scholar] [CrossRef]
- De Persis, C.; Tesi, P. On persistency of excitation and formulas for data-driven control. In Proceedings of the 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, 11–13 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 873–878. [Google Scholar] [CrossRef]
- Dulac-Arnold, G.; Levine, N.; Mankowitz, D.J.; Li, J.; Paduraru, C.; Gowal, S.; Hester, T. Challenges of real-world reinforcement learning: Definitions, benchmarks and analysis. Mach. Learn. 2021, 110, 2419–2468. [Google Scholar] [CrossRef]
- Fujimoto, T.; Suetterlein, J.; Chatterjee, S.; Ganguly, A. Assessing the impact of distribution shift on reinforcement learning performance. arXiv 2024, arXiv:2402.03590. [Google Scholar] [CrossRef]
- Xia, B.; Kong, Y.; Chang, Y.; Yuan, B.; Li, Z.; Wang, X.; Liang, B. Deer: A delay-resilient framework for reinforcement learning with variable delays. arXiv 2024, arXiv:2406.03102. [Google Scholar] [CrossRef]
- Arjovsky, M.; Bottou, L.; Gulrajani, I.; Lopez-Paz, D. Invariant risk minimization. arXiv 2019, arXiv:1907.02893. [Google Scholar] [CrossRef]
- Liu, H.; Kamarthi, H.; Kong, L.; Zhao, Z.; Zhang, C.; Prakash, B.A. Time-series forecasting for out-of-distribution generalization using invariant learning. arXiv 2024, arXiv:2406.09130. [Google Scholar] [CrossRef]
- Kamath, P.; Tangella, A.; Sutherland, D.; Srebro, N. Does invariant risk minimization capture invariance? In Proceedings of the International Conference on Artificial Intelligence and Statistics, PMLR, Virtual, 13–15 April 2021; pp. 4069–4077. [Google Scholar]
- Gu, S.; Yang, L.; Du, Y.; Chen, G.; Walter, F.; Wang, J.; Knoll, A. A review of safe reinforcement learning: Methods, theories and applications. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 11216–11235. [Google Scholar] [CrossRef]
- Guerrier, M.; Fouad, H.; Beltrame, G. Learning control barrier functions and their application in reinforcement learning: A survey. arXiv 2024, arXiv:2404.16879. [Google Scholar] [CrossRef]
- Ye, J.; Yu, Y.; Zhang, W.; Wang, L.; Li, J.; Tsung, F. A survey of time series foundation models: Generalizing time series representation with large language model. arXiv 2024, arXiv:2405.02358. [Google Scholar] [CrossRef]
- Hu, E.J.; Shen, Y.; Wallis, P.; Allen-Zhu, Z.; Li, Y.; Wang, S.; Wang, L.; Chen, W. Lora: Low-rank adaptation of large language models. ICLR 2022, 1, 3. [Google Scholar]
- Wang, D.; Shelhamer, E.; Liu, S.; Olshausen, B.; Darrell, T. Tent: Fully test-time adaptation by entropy minimization. arXiv 2020, arXiv:2006.10726. [Google Scholar] [CrossRef]
- Kuhn, D.; Shafiee, S.; Wiesemann, W. Distributionally robust optimization. Acta Numer. 2025, 34, 579–804. [Google Scholar] [CrossRef]
- Söyleyici, C.; Ünver, H.Ö. A Physics-Informed Deep Neural Network based beam vibration framework for simulation and parameter identification. Eng. Appl. Artif. Intell. 2025, 141, 109804. [Google Scholar] [CrossRef]
- Antoniadis, A.; Gaucher, S.; Goude, Y. Hierarchical transfer learning with applications to electricity load forecasting. Int. J. Forecast. 2024, 40, 641–660. [Google Scholar] [CrossRef]


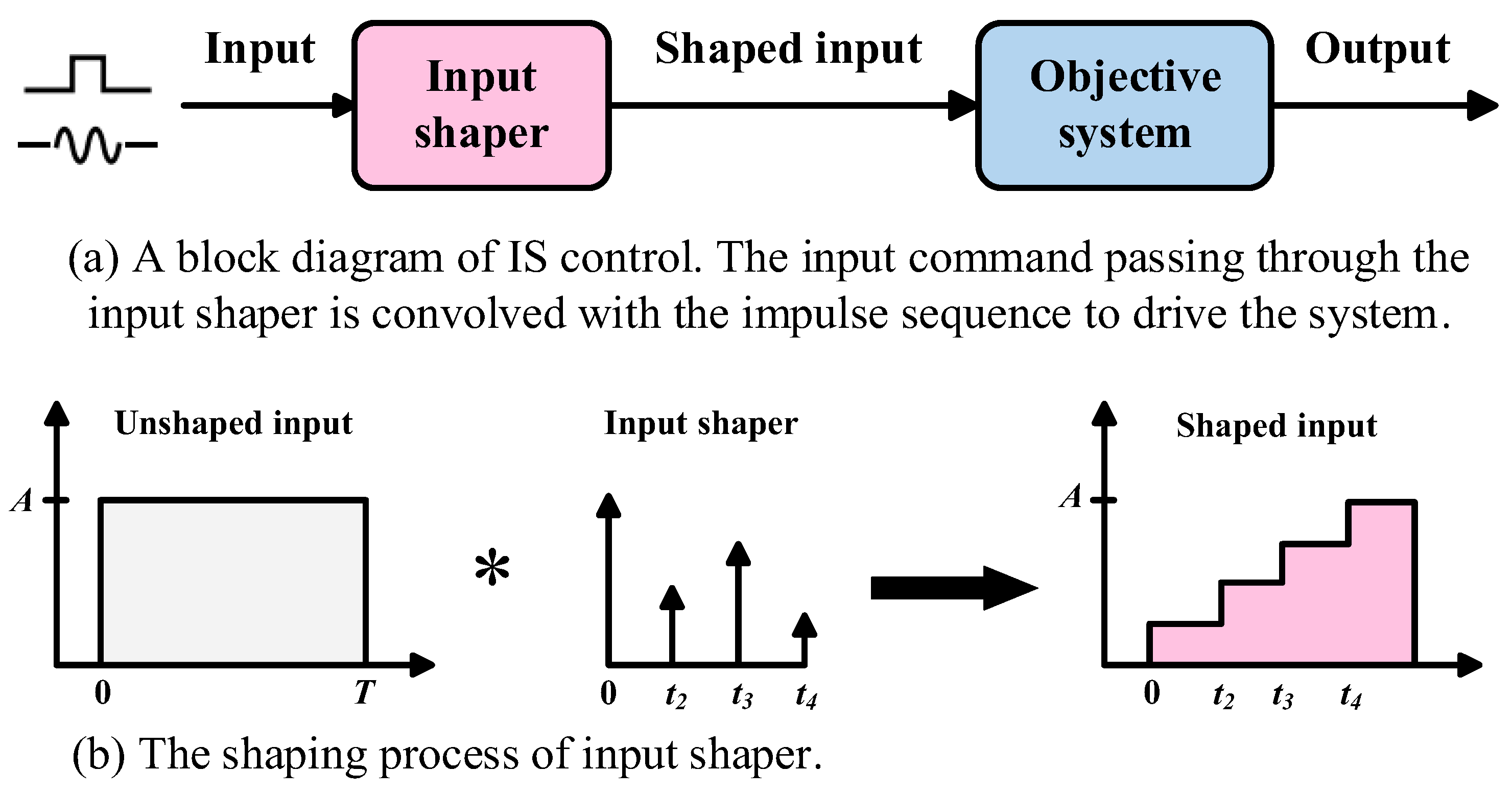
| Feedforward Control System | Feedback Control System | Hybrid Control System | |
|---|---|---|---|
| Structure | 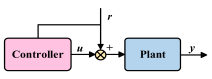 | 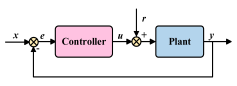 | 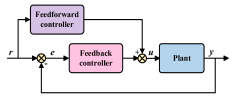 |
| Advantages | It can respond in advance before interference affects the system, improving control efficiency; it works well under periodic or predictable noise. | No reference signal is required, and the system structure is simple; it has strong adaptability to changes in system parameters and external interference. | Combining the advantages of feedforward and feedback, it has good control performance, strong adaptability, and robustness. |
| Disadvantages | Highly dependent on reference signals and system model quality; poor control effectiveness against sudden or non-periodic interference. | High gain can easily cause system instability, especially in the high frequency domain, where control failure is likely to occur; control effectiveness is limited for high frequency interference. | The system structure is complex, which can easily cause coupling interference; hardware requirements are high, and the deployment and optimization process is cumbersome. |
| Technical Paths | Classification | Methods |
|---|---|---|
| Input shaping parameter optimization | Neural network-based methods | ANN-UMZV (Ramli et~al., 2018), NN-ZVD (Ur Rehman et~al., 2022), NNUMZV (Ramli et~al., 2020), ResNN-ZVD (Yang et~al., 2024), PINN-IS (Li and Xiao, 2025) |
| Reinforcement learning-based methods | RL-SI (Xu et~al., 2020), RL-IS (Gulde et al., 2019), DRL-IS (Zhang et al., 2023) | |
| Metaheuristics-based methods | GA-IS (Mohammed et~al., 2019), PSO-ZVD (Xu et~al., 2022), ACO-THEI (Fu et~al., 2024) | |
| System identification and modeling | Secondary path modeling | DNN (Im et al., 2023, Oh et al., 2024, Cheng et al., 2025), DNoiseNet (Cha et al., 2023) |
| Structural dynamics modeling | NARX (Song et al., 2022), PIDynNet (Liu and Meidani 2023), Neural ODE (Lai et al., 2021), PINN (Teloli et al., 2025), GNN (Li et al., 2023) | |
| Incentive Perturbation Source Modeling | LSTM (Kwon et al., 2022), TNResNet (Yang et al., 2024), NARX (Zhang et al., 2018), DNN (Redonnet et al., 2024), DDPG (Ma et al., 2024) | |
| Adaptive optimization of controller parameters | Linear feedback controller | PSO-PID (Yatim and Darus 2014, Silva et al., 2024), GA-LQR (Huang et al., 2024), CS-PID (Syafiqah et al., 2024), RL-PID (Lakhani et al., 2021) |
| Adaptive controller | ANFN-LMS (Nguyen et al., 2025), ANN-FxLMS (Le et al., 2017), PSO-FLC (Zorić et al., 2014), ACNF (Jafarzadeh et al., 2023) | |
| Robust controller | GESO-SMC (Wang et al., 2024), RL-AFS (Mu et al., 2022), RBFNN-SMC (Sun and Zhao 2020) | |
| Model Predictive Controller | MPSO-MPC (Zhao and Zhu 2019), ESN-MPC (Ogawa and Takahashi 2021), NARX-NMPC (Kalaycioglu and Ding 2024) | |
| Controller modeling | DL/GF/DRL/ANFN controller | Deep MCANC (Zhang and Wang 2023), GFANC (Luo et al., 2023), DRL-ANC (Ryu et al., 2024), ANFN-HANC (Nguyen et al., 2025) |
| Neural Network | ||
|---|---|---|
 |  |  |
| (a) ANN | (b) ResNet | (c) PINN |
| It uses the residual oscillation response characteristics of the system, such as displacement and acceleration spectrum, as input and leverages the powerful nonlinear mapping capabilities of neural networks to directly learn the complex relationship between vibration characteristics and optimal shaper parameters, such as damping ratio and natural frequency, replacing the traditional parameter tuning process that relies on precise mathematical models. | It utilizes a cross-layer jump connection structure to effectively capture multi-scale features in vibration signals. Through a deep network, it extracts the coupling relationship between high-frequency oscillations and low-frequency modes, directly mapping residual vibration responses to optimal shaping parameters. Compared to ordinary neural networks, its deep architecture avoids the gradient vanishing problem, significantly improving the parameter prediction accuracy of nonlinear systems (such as robotic arms with variable joint friction) under wide-band disturbances. | It embeds the control equations of the vibration system as a regularization term in the loss function, forcing the network to follow the laws of physical conservation during training. By jointly optimizing the network weights and the residuals of the vibration differential equations, it directly outputs the optimal shaping parameters that satisfy the energy constraints, achieving high-precision generalization with a small number of samples. |
| Reinforcement Learning | ||
 | 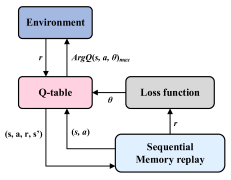 | 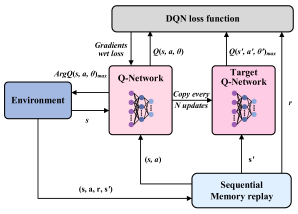 |
| (d) RL | (e) Q-table learning | (f) Deep Q-Network(DQN) |
| It models the vibration system as a Markov decision process (MDP): real-time vibration spectrum as the state, shaping parameters as actions, and negative residual vibration energy as rewards. Through continuous interaction between the intelligent agent and the environment, it autonomously learns the optimal control strategy. | It discretizes the vibration system into finite states, quantizes the shaping parameters into discrete actions, and allows the agent to select actions at each time step according to a certain strategy. Based on the reward signals returned by the environment, the agent updates the values of the corresponding state-action pairs in the Q-table, gradually learning the optimal strategy. | It uses deep neural networks to fit Q-value functions, breaking through the limitations of traditional Q-table learning, which requires the state-action space to be discrete. It can directly process high-dimensional continuous vibration spectrum features. Parameters are obtained through empirical replay and target network mechanisms, enabling efficient learning of optimal strategies under time-varying operating conditions from complex state spaces. |
| Heuristic Algorithm | ||
 | 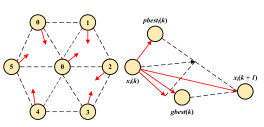 | 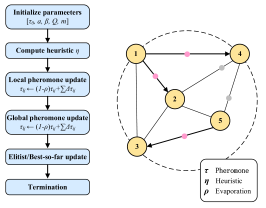 |
| (g) GA | (h) PSO | (i) ACO |
| It encodes the parameters of the shaper into chromosome genes and iteratively evolves the population through selection, crossover, and mutation operations. It then performs a global search for the optimal solution using residual vibration energy as the fitness function. | It considers the optimization problem as an objective function, and represents the solutions as particles which are randomly initialized as a swarm. Besides, each particle has its own velocity and position, and iteratively searches for the optimal solution by interacting with other particles in the swarm. | It views optimization as path finding by multiple randomly initialized ants on a solution-space graph; ants transition probabilistically based on pheromone trails and heuristic cues and apply evaporation and reinforcement updates. Leveraging pheromone-driven stigmergic cooperation, the colony iteratively converges to a optimal solution. |
| Control Algorithm | Expression | Variable Description |
|---|---|---|
| PID | Continuous: Discrete: | Kp, Ki, Kd: P/I/D gains, Ts: sampling period, e: error |
| LMS | Filter output: Error: Update: | W[k]: adaptive weights, d[k]: measurement, e: error, μ: step size |
| Fuzzy control (Sugeno) | Rule activation: Defuzzification: | μAij: membership functions, wi: rule firing strength, ai, ci: consequent params |
| LQR | System: Cost: Optimal law: CARE: | x: state, u: control, A, B: system matrices, Q, R: weights, P: Riccati solution, K: LQR gain |
| H∞ | Disturbed plant: perf. Output: Goal: Sufficient condition: | w: disturbance, E: disturbance matrix, z: performance output, Q, R: weights, γ: bound, K: feedback gain |
| Sliding-Mode Control (SMC) | Sliding surface: Control: Reaching law: | e: tracking error, s: sliding variable, Λ: surface params, ueq: equivalent control, Ks: switching gain, ϕ: boundary layer, η: reaching rate |
| Model Predictive Control (MPC) | Prediction model: | xk, uk, yk: state, control, output, A, B, C: discrete model matrix |
| AI-Based Linear Feedback Controller | |
|---|---|
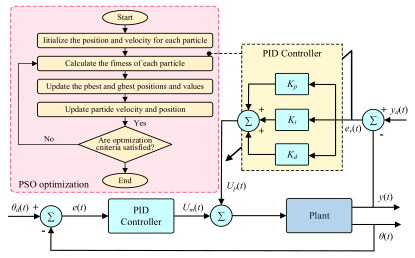 (a) Block diagram of PSO-PID control structure |  (b) Block diagram of RL-PID control structure |
| It encodes PID parameters (Kp, Ki, Kd) as the positions of individuals in a particle swarm and iteratively searches for the optimal solution through group collaboration. Using system performance indicators (such as ISE and ITAE) as the fitness function, particles dynamically update their positions based on individual and group optimal experiences, ultimately outputting the globally optimal PID parameter combination. | It parameterizes the PID gain vector as the continuous action of the DPG agent and iteratively updates it in a closed-loop environment in a state-action-reward cycle; the reward is composed of trajectory-based performance metrics, which are used to measure the tuning quality and drive policy improvement. To ensure safety, a supervisor monitors the running reward at each step. Once the degradation exceeds the threshold set by a conservative baseline PID, it reverts to the baseline controller. |
| AI-BasedAdaptiveController | |
 | 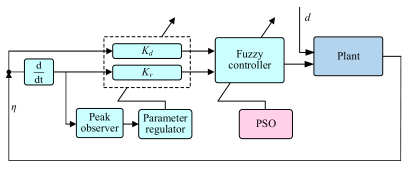 |
| (c) Block diagram of Adaptive neural network feedback ANC system | (d) Block diagram of PSO-FLC control structure |
| It replaces the linear FIR controller with a neural network, uses LMS to update the neural network weights, and introduces a variable step size strategy to make the learning rate adapt online according to the error energy. During the large error stage, the learning rate is increased to accelerate convergence, and during the small error stage, the step size is reduced to suppress instability. | It encodes the shape parameters of membership functions (such as the vertex position of trigonometric functions and the mean and variance of Gaussian functions) as particle swarm positions. Through iterative optimization using swarm intelligence, the fitness function is defined as the control system performance index, and the antecedent or consequent membership functions of fuzzy rules are dynamically adjusted. |
| AI-BasedRobustController | |
 |  |
| (e) Block diagram of DCDDPG-GESO Control Method | (f) Block diagram of RBFNN-SMC Control Method |
| It models GESO gain tuning as continuous action RL: using position and velocity errors as states, the actor outputs key gains online; rewards are constructed based on observation errors, with dual critics taking min-Q to suppress overestimation, and experience replay and soft updates to stabilize training; after convergence, the agent can adaptively adjust gains according to operating conditions. | It uses RBFNN to approximate the unknown nonlinearity and time-varying uncertainty of the actuator online, and derives the weight self-tuning law and saturation convergence law based on Lyapunov to suppress vibration. This ensures that the sliding surface converges and the force tracking error is bounded. |
| AI-BasedModelPredictiveController | |
 | 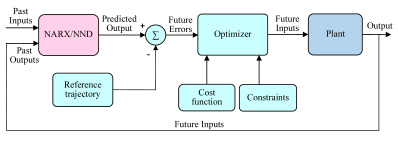 |
| (g) Block diagram of ESN-MPC Control Method | (h) Block diagram of NMPC-NARX Control Method |
| It uses ESN to predict time-varying disturbances such as engine torque in multiple steps ahead of each sampling cycle, and writes the prediction sequence directly into the output prediction and cost function of MPC to form a constrained QP for online solution of the optimal control sequence. | NMPC solves for the optimal PZT actuation with constraints in the rolling time domain; NARX learns the nonlinearity of the object using historical or online data and corrects prediction errors online. Working together, the two enable the system to converge faster and provide more robust vibration suppression performance even under model uncertainty and external disturbances. |
| Deep MCANC | GFANC |
|---|---|
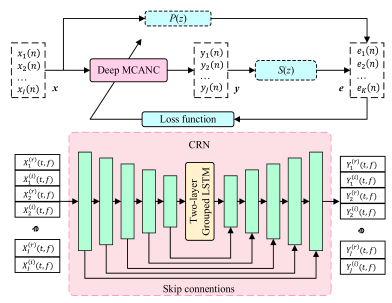 |  |
| (a) Block diagram of CRN based deep MCANC system | (b) Block diagram of GFANC Method |
| It uses a hybrid structure of convolutional and recurrent layers to generate multiple noise control signals end-to-end: the convolutional layer extracts local spectral and phase clues of the reference signal in the short-time frequency domain, while the recurrent layer models long-term dependencies and operational evolution across frames. The two layers work together to perform complex spectrum mapping, directly outputting the real and imaginary control signals for multiple speakers to maintain cross-channel coherence. | It uses a lightweight 1D-CNN to extract features from the original noisy frame, assigns binary weights to the stator filter, and performs an inner product to synthesize the control filter, thereby bypassing online optimization and cumbersome tuning. This framework does not rely on error feedback adaptation and requires only minimal prior knowledge to achieve fast response and high noise reduction for multiple types of non-stationary noise. |
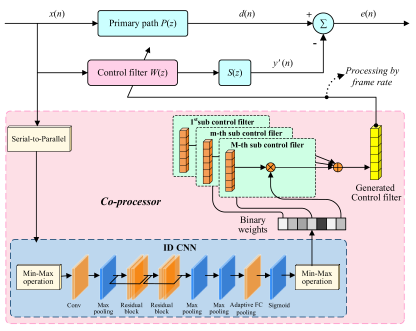
| DRL-ANC | ANFN-HANC |
 | 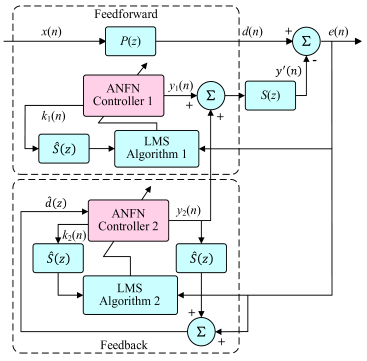 |
| (c) Block diagram of DRL-ANC Method | (d) Block diagram of ANFN-HANC system |
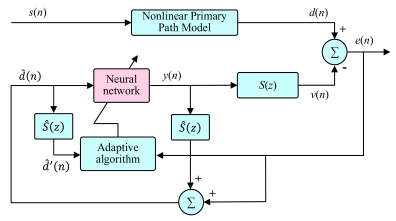
| DRL-ANC allows the intelligent agent to act directly as a controller: it removes the secondary path mathematical model and uses the actor-critic structure of DDPG to learn control laws from data through interaction with the physical environment. It uses the main noise frequency as the state, outputs two-parameter control filter coefficients as actions from the strategy end-to-end, and multiplies them by the sine and cosine bases to generate anti-noise. It uses error energy as the reward to drive strategy updates, thereby maintaining robust control. | In hybrid ANC, two adaptive neuro-fuzzy networks directly replace traditional linear controllers. Control laws are learned online from data and error signals rather than relying on precise models. The output layer of ANFN adjusts weights online under FxLMS to minimize residuals, and Lyapunov conditions are used to provide a learning gain range to ensure closed-loop stability. |
| Evaluation Metrics | Equation & Description |
|---|---|
| δi | The absolute error ratio [104]. |
| PA | The prediction accuracy [104]. |
| R2 | The coefficient of determination [175]. |
| RMSE | The root mean square error [176]. |
| MSE | The maximum transient swing [112]. |
| RAE | The relative absolute errors [164]. |
| Transient response time | The time required for the system to reach steady state from disturbance [177]. |
| Settling time | The time required for the system to reach and maintain within a given error band in its state after disturbance [178]. |
| ERLE | The echo return loss enhancement [179] |
| Te2e | The end-to-end latency (Zhang and Pandey 2023) |
| MTS | The maximum transient swing [112]. |
| Robustness | Robustness is used to evaluate the ability of controllers to resist external interference such as uncertainty, disturbance, and noise [177]. |
| FLOPs | The total number of floating-point operations (addition, subtraction, multiplication, and division) required to execute the algorithm [180]. |
| Params | The total number of parameters (e.g., weights and biases) that need to be trained in the model [180]. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Z.; Xue, H.; Yue, H.; Bao, X.; Zhu, J.; Wang, X.; Zhang, L. A Review of Artificial Intelligence-Driven Active Vibration and Noise Control. Machines 2025, 13, 946. https://doi.org/10.3390/machines13100946
Jiang Z, Xue H, Yue H, Bao X, Zhu J, Wang X, Zhang L. A Review of Artificial Intelligence-Driven Active Vibration and Noise Control. Machines. 2025; 13(10):946. https://doi.org/10.3390/machines13100946
Chicago/Turabian StyleJiang, Zongkang, Hongtao Xue, Huiyu Yue, Xiaoyi Bao, Junwei Zhu, Xuan Wang, and Liang Zhang. 2025. "A Review of Artificial Intelligence-Driven Active Vibration and Noise Control" Machines 13, no. 10: 946. https://doi.org/10.3390/machines13100946
APA StyleJiang, Z., Xue, H., Yue, H., Bao, X., Zhu, J., Wang, X., & Zhang, L. (2025). A Review of Artificial Intelligence-Driven Active Vibration and Noise Control. Machines, 13(10), 946. https://doi.org/10.3390/machines13100946






