Performance Analysis of Nonlinear Stiffness Suspension Based on Multi-Objective Optimization

Abstract

This study optimizes vehicle suspension dynamics by introducing a controllable degree of nonlinearity, characterized by a parameter ε, into the spring element of Inerter-Spring-Damper (ISD) systems. Quarter-vehicle models for parallel and series ISD configurations are established, and a multi-objective genetic algorithm optimizes the parameters under random road excitation to minimize body acceleration (BA), suspension working space (SWS), and dynamic tire load (DTL). Results demonstrate that optimizing ε brings advantages: compared to a conventional passive suspension, the optimized parallel ISD suspension reduces BA, SWS, and DTL by 7.98%, 8.57%, and 1.69%, respectively, with the BA reduction notably improving from 5.94% (achieved by the linear ISD with ε = 0) to 7.98%. Similarly, the optimized series ISD achieves reductions of 2.53%, 7.62%, and 6.42% in BA, SWS, and DTL, showing a more balanced enhancement over its linear counterpart. The analysis reveals how ε distinctly influences the performance trade-offs, validating that strategically tuning the spring nonlinearity degree, in synergy with the inerter and damper, provides an effective method for superior suspension performance customization.

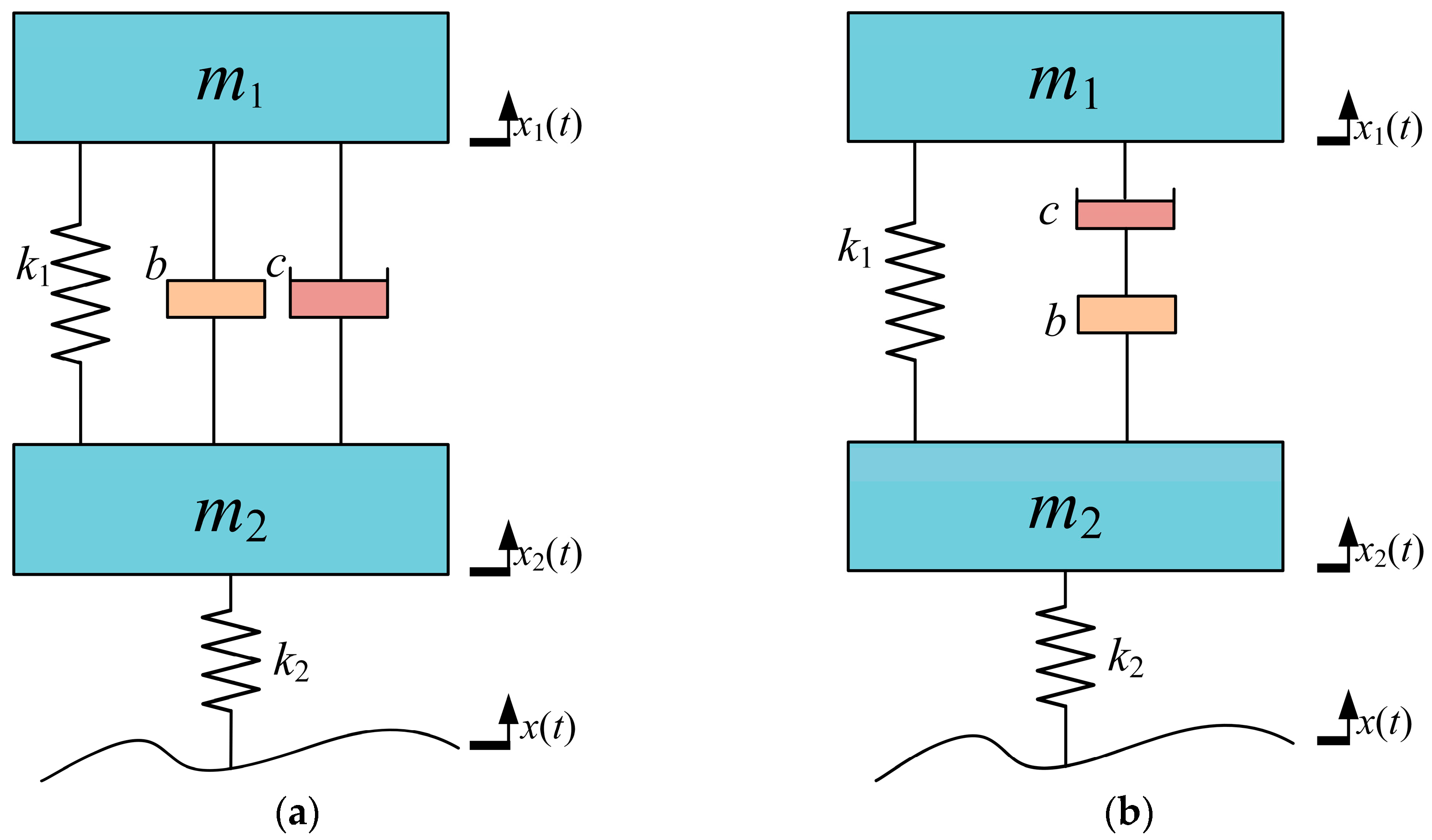
1. Introduction

The suspension system is a critical component that connects the vehicle body to the wheels, and its performance directly determines ride comfort, handling stability, and driving safety. The pursuit of superior suspension performance has driven innovations across various vehicle types. For mainstream vehicle suspension systems, the limitations of traditional passive suspensions [1] with fixed parameters have spurred the development of semi-active [2] and active [3] suspensions. Despite their enhanced performance, issues such as high costs and energy consumption persist. Smith introduced the inerter, a new element for vibration isolation [4]. Due to the tremendous success of the inerter in Formula 1 racing, new mechanical vibration isolation networks composed of ISDs have been widely applied in the field of mechanical vibration isolation. Generally, inertial elements have been successfully applied across various interdisciplinary domains, including automotive engineering [5,6,7,8], civil engineering [9,10], aerospace engineering [11], and ocean engineering [12].

In the structural design of ISD suspensions, Du et al. adopted an analytical method to enumerate 21 types of ISD suspension structures, selected 9 typical ISD suspension structures, and obtained 5 ISD suspension structures with good vibration reduction performance and simple structure through simulation [13]. Shen et al. proposed a positive real synthesis design method for ISD suspensions based on fractional order, taking the biquadratic transfer function as the research object to design the equivalent network structure of fractional order components [14]. Control strategy design includes sliding mode control [15,16,17,18], fuzzy control [19,20,21,22], etc., and these methods have been widely applied in suspension systems. Shen et al. proposed a fractional-order sliding mode control to adjust the output force through ISD suspension, which shows excellent vibration suppression performance [23]. Jin et al. proposed a semi-active ISD suspension control strategy based on improved fuzzy neural network PID control, which improves the ride comfort and handling stability of vehicles [24]. Zhang et al. proposed a model-free adaptive control based on genetic algorithm, which effectively improves the vehicle dynamic performance [25]. The functional scope of ISD suspensions is also expanding beyond mere vibration isolation, for instance, through integration with energy-harvesting technologies, revealing intrinsic trade-offs between ride comfort and energy-harvesting efficiency across different ISD structures [26].

However, despite these significant and promising advancements across methodological, functional, and control dimensions, a critical and ubiquitous physical characteristic remains largely unexplored within the ISD framework: the intrinsic nonlinearity of the suspension spring itself. Current research has considered the nonlinear characteristics of springs. Zhu et al. studied the nonlinear dynamic characteristics of a vehicle semi-active suspension system with SMA spring, developed the nonlinear dynamic model based on hysteretic nonlinear theory, and analyzed the stability and bifurcation characteristics of the suspension system [27]. Huang et al. proposed adaptive control designs for vehicle active suspension systems with unknown nonlinear dynamics (e.g., nonlinear spring and piece-wise linear damper dynamics), using an augmented neural network to compensate for the unknown nonlinearities and a novel adaptive law to estimate both NN weights and uncertain model parameters, improving control performance and simplifying parameter tuning [28]. Lauß et al. proposed a parameter identification approach formulated as an optimization task to quantify the nonlinear spring and damper characteristics of motorcycle suspension modifications, using efficient gradient computation with the adjoint variable approach and cubic splines to minimize the deviation between simulation and measurement [29]. Zhao et al. analyzed the performance of suspensions with nonlinear springs, and the results show that the variation in nonlinear springs has a significant impact on suspension performance [30]. Current research primarily focuses on structural design and linear spring analysis, neglecting the nonlinearity of suspension springs. Considering the hypothesis that the interaction between nonlinear springs, inerters, and dampers might lead to unprecedented changes in vehicle dynamic performance, it seems necessary to reveal the underlying correlations.

This paper aims to analyze the dynamic performance of ISD suspensions with both linear and nonlinear suspension springs and to explore the influence of spring nonlinearity on suspension dynamic performance. The structure of the paper is organized as follows.

In Section 2, a quarter-vehicle model of a four-element ISD suspension considering nonlinear springs is established. Section 3 details the multi-objective optimization under random road input conditions using a genetic algorithm. Section 4 presents a simulation analysis of the dynamic performance of the proposed vehicle ISD suspension. Section 5 discusses the influence of spring nonlinearity on body acceleration, suspension dynamic deflection, and tire dynamic load. Finally, conclusions are drawn.

2. Model Formulation of Suspension Systems

2.1. Parallel Linear ISD Suspension Model

The quarter-vehicle model effectively illustrates the relative motion between the sprung mass and unsprung mass. Vehicle suspension systems employing inerter, spring, and damper elements exhibit diverse configurations. This study first examines a passive ISD suspension with a three-element parallel configuration comprising the suspension spring, inerter, and damper. Figure 1a shows the model of a 1/4 parallel linear vehicle ISD system.

In Figure 1, m₁ is sprung mass, m₂ is unsprung mass, k₁ is suspension stiffness coefficient, c is damping coefficient, b is inertance coefficient, and k₂ is tire stiffness. x₁, x₂, and x are vertical displacements of the sprung mass, unsprung mass, and road input, respectively.

Figure 1a shows the model of a 1/4 passive parallel vehicle suspension system. Traditional suspensions employ linear springs with constant stiffness. The force displacement relationship of a constant-stiffness spring is given by the following equation:

$$F_s=kx$$

(1)

where F_s is spring force, k is spring stiffness, and x is spring displacement.

Combining Equation (1) and applying Newton’s second law of motion, the governing differential equations of motion for the parallel suspension 2-DOF quarter-vehicle model are derived as follows:

$$\left\{\begin{array}{l}{m}_1{\ddot{x}}_1+k_1\left(x_1-x_2\right)+c\left({\dot{x}}_1-{\dot{x}}_2\right)+b\left({\ddot{x}}_1-{\ddot{x}}_2\right)=0\hfill \\ m_2{\ddot{x}}_2-k_1\left(x_1-x_2\right)-c\left({\dot{x}}_1-{\dot{x}}_2\right)-b\left({\ddot{x}}_1-{\ddot{x}}_2\right)+k_2\left(x_2-x\right)=0\hfill \end{array}\right.$$

(2)

2.2. Series Linear ISD Suspension Model

The passive ISD suspension configuration with the inerter and damper arranged in series, while the suspension spring is connected in parallel with the damper, is studied. Figure 1b shows the model of the 1/4 series linear vehicle ISD system.

The Laplace transform of its dynamic equation is as follows:

$$\left\{\begin{array}{l}{m}_1{s}^2{X}_1+k_1\left(X_1-X_2\right)+sT\left(s\right)\left(X_1-X_2\right)=0\\ m_2{s}^2{X}_2+k_2\left(X_2-X\right)-k_1\left(X_1-X_2\right)-sT\left(s\right)\left(X_1-X_2\right)=0\end{array}\right.$$

(3)

where X₁, X₂, and X are the Laplace transform forms of x₁, x₂, and x, respectively.

The expression of the velocity-type impedance T(s) is as follows:

$$T\left(s\right)={\displaystyle \frac{bsc}{bs+c}}$$

(4)

2.3. Suspension Model Considering Spring Nonlinearity

In practical suspension systems, springs often exhibit nonlinear force displacement characteristics, especially under large deformations. This nonlinear stiffness is a critical factor influencing ride comfort and handling stability. To quantitatively analyze this effect, a parametric model is introduced where the spring force is defined by a variable stiffness relationship characterized by a nonlinearity parameter ε. The force displacement relationship can be expressed as follows [31]:

$$F_s=kx+\epsilon k_3{x}^3$$

(5)

where ε is a small parameter ranging over (0, 1), representing the degree of spring nonlinearity. When ε = 0, the spring is linear. k denotes the linear stiffness (unit: N/m), and k₃ represents the cubic stiffness coefficient (unit: N·m⁻³), which characterizes the intensity of the cubic nonlinearity.

Consequently, for the nonlinear parallel suspension quarter-vehicle model,

$$\left\{\begin{array}{l}{m}_1{\ddot{x}}_1+k_1\left(x_1-x_2\right)+\epsilon k_3{\left(x_1-x_2\right)}^3+c\left({\dot{x}}_1-{\dot{x}}_2\right)+b\left({\ddot{x}}_1-{\ddot{x}}_2\right)=0\hfill \\ m_2{\ddot{x}}_2-k_1\left(x_1-x_2\right)-\epsilon k_3{\left(x_1-x_2\right)}^3-c\left({\dot{x}}_1-{\dot{x}}_2\right)-b\left({\ddot{x}}_1-{\ddot{x}}_2\right)+k_2\left(x_2-x\right)=0\hfill \end{array}\right.$$

(6)

For the nonlinear series suspension quarter-vehicle model,

$$\left\{\begin{array}{l}{m}_1{s}^2{X}_1+k_1\left(X_1-X_2\right)+\epsilon k_3{\left(X_1-X_2\right)}^3+sT\left(s\right)\left(X_1-X_2\right)=0\hfill \\ m_2{s}^2{X}_2+k_2\left(X_2-X\right)-k_1\left(X_1-X_2\right)-\epsilon k_3{\left(X_1-X_2\right)}^3-sT\left(s\right)\left(X_1-X_2\right)=0\hfill \end{array}\right.$$

(7)

3. Optimization of Suspension Parameters

3.1. Multi-Objective Optimization for Linear Springs Using Genetic Algorithm

According to the fitting expression for road surface power spectral density specified in GB/T 7031-2005 [32] ‘Mechanical Vibration—Road Surface Profiles—Reporting of Measured Data’, this study employs a first-order filtered band-limited white noise method to establish the random road excitation model:

$$\dot{q}\left(t\right)=-2\pi f_{0}q\left(t\right)+2\pi \sqrt{G\left(n_0\right)v}w\left(t\right)$$

(8)

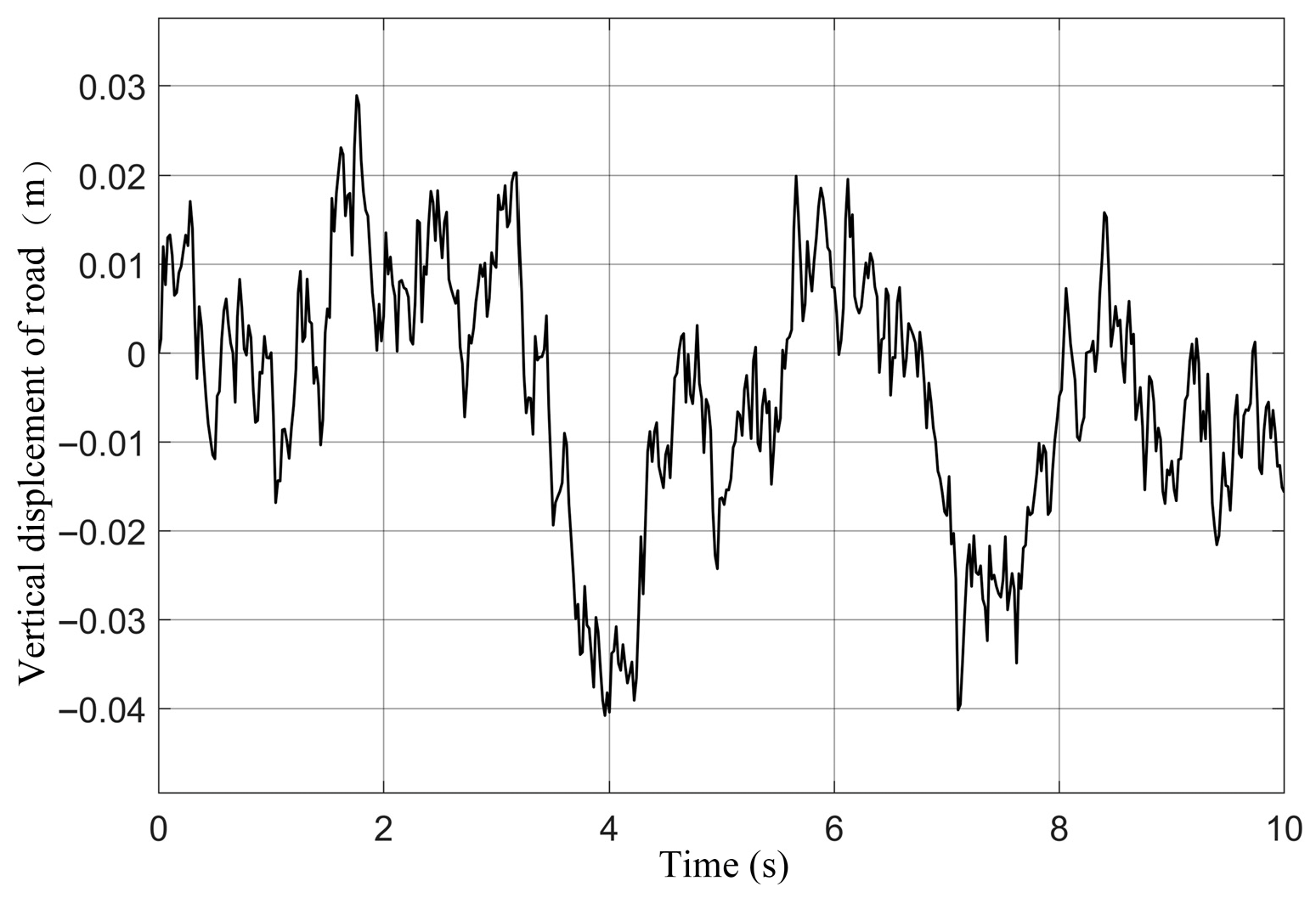
where f₀ is lower cutoff frequency, q(t) is random road excitation signal, and G(n₀) is road roughness coefficient. For the simulated Class C road: G(n₀) = 2.56 × 10⁻⁵ m³·cycle⁻¹, and v is vehicle speed (simulation value: 20 m/s). w(t) is gaussian white noise signal with zero mean. Figure 2 shows the road input displacement.

Model parameters are selected from a passenger vehicle.

Table 1. Parameters of the passive suspension model.

Description	Parameters	Value
Sprung mass	m1	320 kg
Unsprung mass	m2	45 kg
Stiffness of tire	k2	190,000 N·m−1
Cutoff Frequency	f0	0.01 Hz
Vehicle Speed	v	20 m·s−1
Road roughness coefficient	G(n0)	2.56 × 10−5 m3·cycle−1

presents relevant parameters of the vehicle’s passive suspension model [33].

Under Class C random road input at 20 m/s, the RMS values for the conventional passive suspension are as follows: BA_pass is 1.1868 m·s⁻², SWS_pass is 0.0105 m, DTL_pass is 888 N.

The suspension stiffness k₁, inertance coefficient b, and damping coefficient c of the suspension are selected as optimization variables, with respective ranges of (0–30,000) N m⁻¹, (0–300) kg, and (0–3000) N s m⁻¹. Optimization is performed separately for parallel and series suspension configurations. But the parameters for the multi-objective genetic algorithm are same: population size = 60, crossover probability = 0.8, mutation probability = 0.2, and number of iterations = 20.

To enhance vehicle ride comfort (meeting vibration isolation requirements) while reducing the probability of wheel lift-off and suspension bottoming-out, the optimization objectives are defined as BA, SWS, and DTL.

Variable boundary conditions are listed in

Table 2. Parameter settings for the variable boundary conditions.

	Optimized Parameters	lbi	ubi
Linear ISD	Suspension Spring Stiffness k1/(N·m−1)	0	30,000
	Inertance b/(kg)	0	300
	Suspension Damping Coefficient c/(N·s·m−1)	0	3000
Nonlinear ISD	Suspension Spring Stiffness k1/(N·m−1)	0	30,000
	Inertance b/(kg)	0	300
	Suspension Damping Coefficient c/(N·s·m−1)	0	3000
	ε	0	1
	Cubic Stiffness Coefficient k3/(N·m−3)	0	300

. The objective functions are formulated as follows:

$$\begin{array}{l}\left\{\begin{array}{l}{J}_1={\omega }_1{\displaystyle \frac{B{A}_{-}RMS}{B{A}_{pass}}}+{\omega }_2{\displaystyle \frac{SW{S}_{-}RMS}{SW{S}_{pass}}}\\ J_2={\displaystyle \frac{DT{L}_{-}RMS}{DT{L}_{pass}}}\end{array}\right.\\ \left\{\begin{array}{c}l{b}_1\le b\le u{b}_1\\ l{b}_2\le c\le u{b}_2\\ l{b}_3\le k_1\le u{b}_3\end{array}\right.\end{array}$$

(9)

where J₁ is comprehensive evaluation index for ride comfort and smoothness. J₂ is wheel grounding capability, critically impacting vehicle driving stability. BA_RMS, SWS_RMS, DTL_RMS, are RMS values of the suspension. A penalty-augmented composite objective is constructed as follows:

$$J={\omega }_1{J}_1+{\omega }_2{J}_2+punishment$$

(10)

In Equation (10), the penalty rule is defined as follows: if any RMS value (BA, SWS, DTL) of the optimized suspension is worse than the conventional passive counterpart, a penalty term p = 100 is applied.

Weight coefficients w₁ and w₂ are set to 0.6 and 0.4, respectively, prioritizing passenger-oriented comfort in this study.

3.2. Multi-Objective Optimization for Nonlinear Springs Using Genetic Algorithm

For the nonlinear spring ISD suspension, four variables are designated as optimization parameters: k₁, b, c, and ε, k₃. The optimization range for ε is (0–1), while the lower bounds lb_i and upper bounds ub_i for k₁, b, k₃, and c remain identical to Equation (11). Variable boundary conditions are listed in Table 2. Optimization is performed separately for both parallel suspension configuration and series suspension configuration. The objective functions remain identical to those defined in Section 3.1. The optimization, however, is conducted over the augmented set of design variables, which incorporates the nonlinearity parameter ε bounded in the interval (0, 1):

$$\left\{\begin{array}{c}\begin{array}{c}l{b}_1\le b\le u{b}_1\\ l{b}_2\le c\le u{b}_2\\ l{b}_3\le k_1\le u{b}_3\end{array}\\ \begin{array}{l}l{b}_4\le \epsilon \le u{b}_4\\ l{b}_5\le k_3\le u{b}_5\end{array}\end{array}\right.$$

(11)

4. Performance Analysis

4.1. Optimized Parameters

To demonstrate the dynamic performance of the optimized ISD suspension under random road excitation, simulations are conducted on a Class C road at 20 m/s.

Table 3. Optimized parameters for the linear and nonlinear ISD suspension configurations.

	Optimal Parameters	Values (Parallel)	Values (Series)
Linear ISD	Suspension Spring Stiffness k1/(N·m−1)	13,005	17,706
	Inertance b/(kg)	2.75	298.64
	Suspension Damping Coefficient c/(N·s·m−1)	1240	1297
Nonlinear ISD	Suspension Spring Stiffness k1/(N·m−1)	11,592	18,965
	Inertance b/(kg)	1.01	270.27
	Suspension Damping Coefficient c/(N·s·m−1)	1204	1351
	ε	0.18	0.07
	Cubic Stiffness Coefficient k3/(N·m−3)	81	26

lists the optimal parameters for each configuration.

4.2. Optimized RMS Values

The RMS values of BA, SWS, and DTL for the parallel suspension comparing passive, linear-optimized, and nonlinear-optimized cases are shown in

Table 4. Dynamic performance indices comparison for the parallel ISD suspension.

Name	Conventional Suspension	Parallel Linear ISD	Decrease	Nonlinear Parallel ISD	Decrease
RMS of body acceleration (m·s−2)	1.1868	1.1163	5.94%	1.0921	7.98%
RMS of suspension working space (m)	0.0105	0.0094	10.48%	0.0096	8.57%
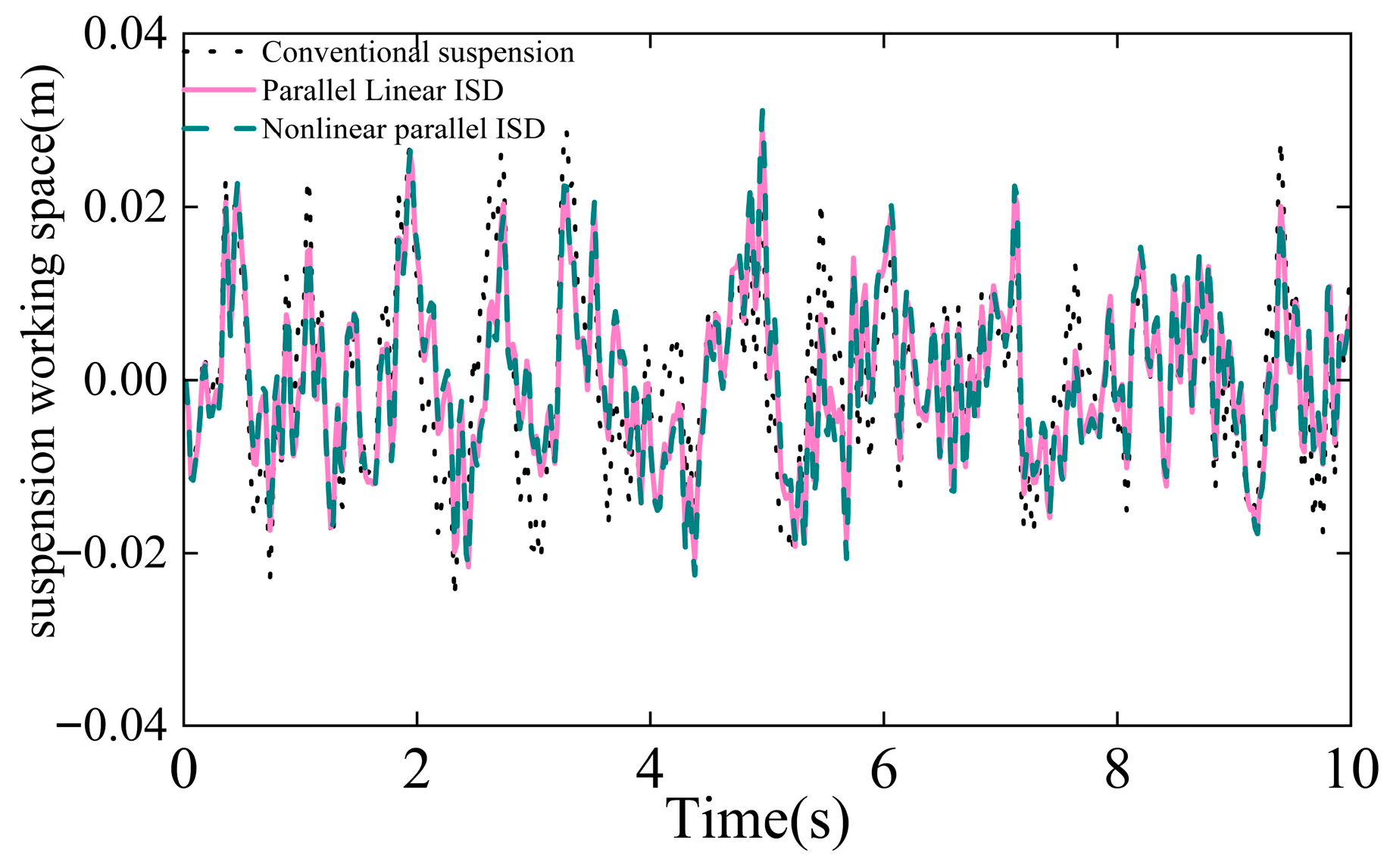
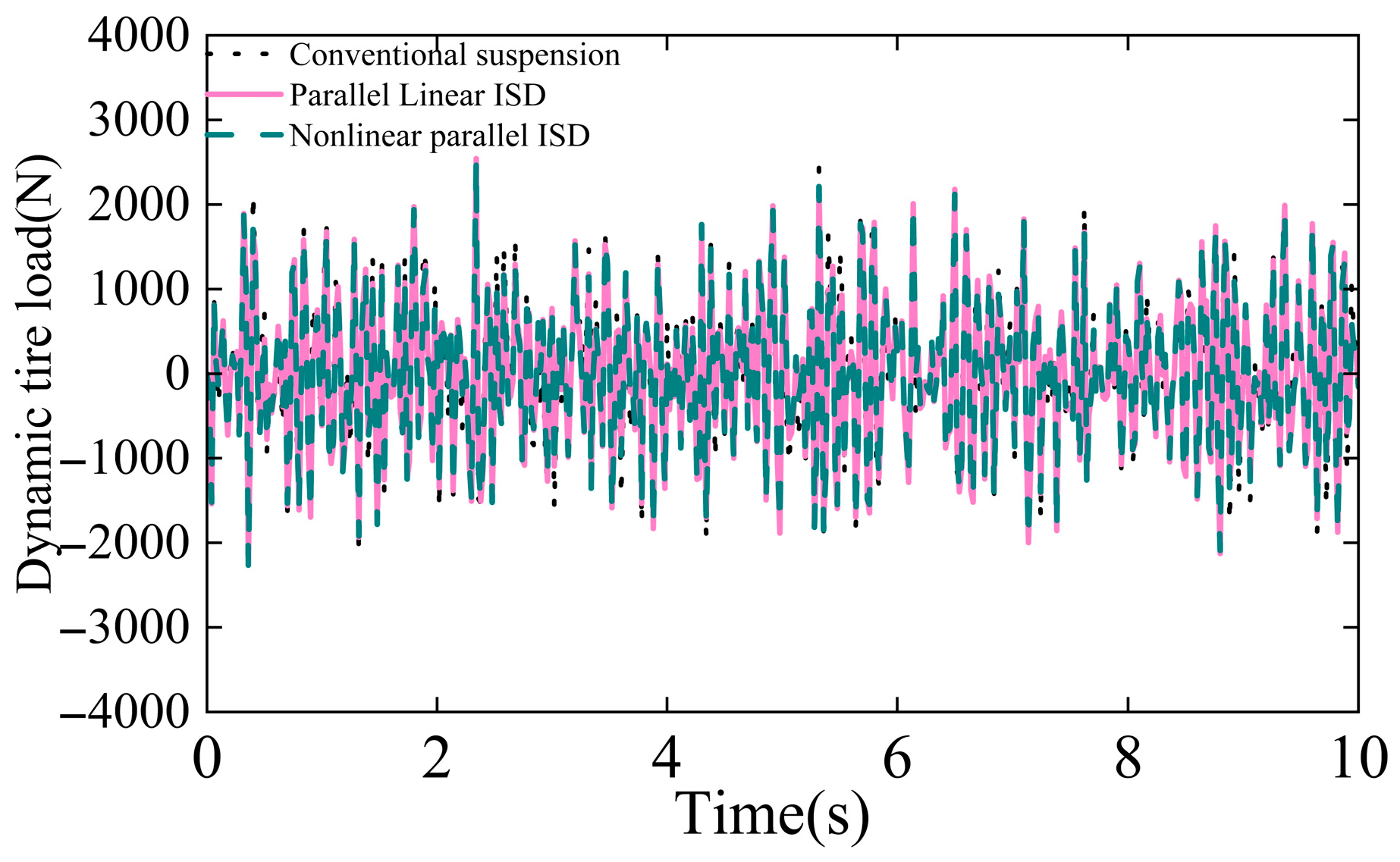
RMS of dynamic tire load (N)	888	880	0.9%	873	1.69%

. This paper reuses the optimized parameters to perform time-domain simulations. Results of the parallel suspension are presented in Figure 3, Figure 4 and Figure 5. Similarly, RMS values for the series suspension comparing passive, linear-optimized, and nonlinear-optimized cases are summarized in

Table 5. Dynamic performance indices comparison for the series ISD suspension.

Name	Conventional Suspension	Series Linear ISD	Decrease	Nonlinear Series ISD	Decrease
RMS of body acceleration (m·s−2)	1.1868	1.1360	4.28%	1.1568	2.53%
RMS of suspension working space (m)	0.0105	0.0098	6.67%	0.0097	7.62%
RMS of dynamic tire load (N)	888	842	5.18%	831	6.42%

. Results of the series suspension are presented in Figure 6, Figure 7 and Figure 8.

Name	Conventional Suspension	Series Linear ISD	Decrease	Nonlinear Series ISD	Decrease
RMS of body acceleration (m·s−2)	1.1868	1.1360	4.28%	1.1568	2.53%
RMS of suspension working space (m)	0.0105	0.0098	6.67%	0.0097	7.62%
RMS of dynamic tire load (N)	888	842	5.18%	831	6.42%

Compared to the conventional passive suspension, all dynamic performance indices exhibit significant reductions. For the parallel suspension with linear springs, RMS values of BA, SWS, and DTL decrease by 5.94%, 10.48%, and 0.9%, respectively. With nonlinear springs, these indices decrease by 7.98%, 8.57%, and 1.69%, respectively. For the series suspension with linear springs, RMS values of BA, SWS, and DTL decrease by 4.28%, 6.67%, and 5.18%, respectively. With nonlinear springs, these indices decrease by 2.53%, 7.62%, and 6.42%, respectively. For the series suspension, the optimal ε = 0.07, although the BA shows a slight increase (1.1568 m·s⁻²) compared to the linear ISD suspension (1.1360 m·s⁻²); this represents a deliberate trade-off to achieve more substantial reductions in SWS and DTL.

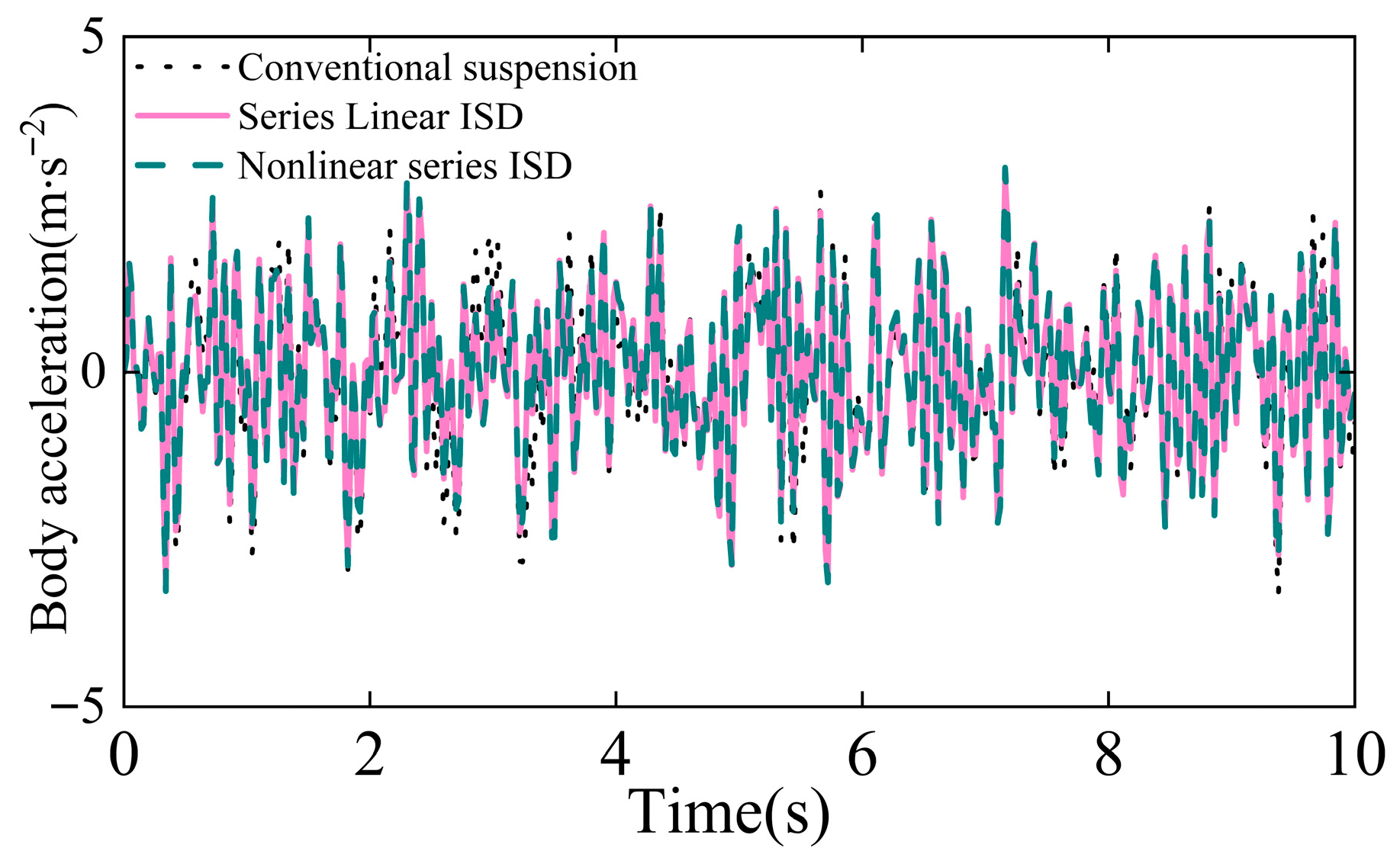
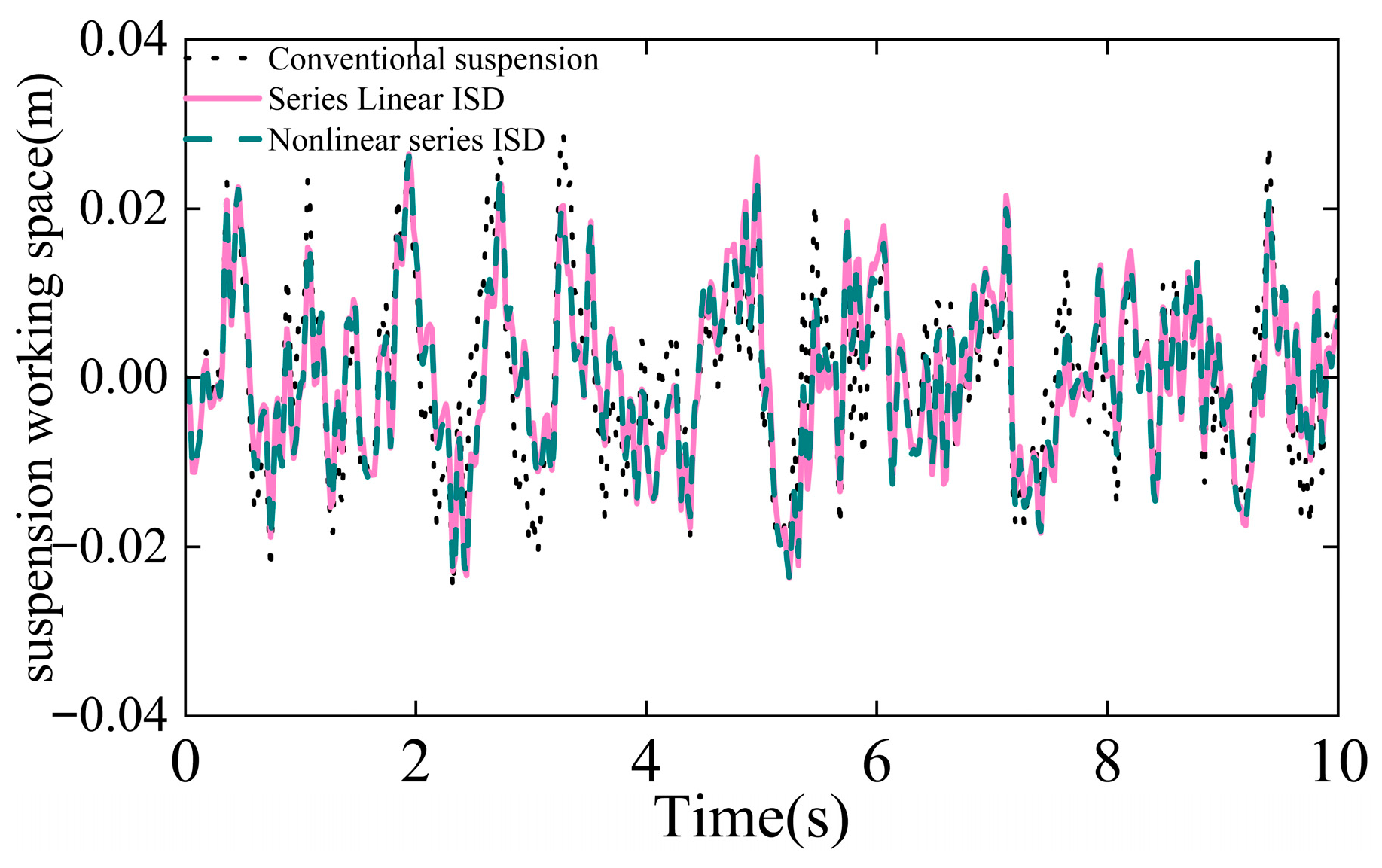
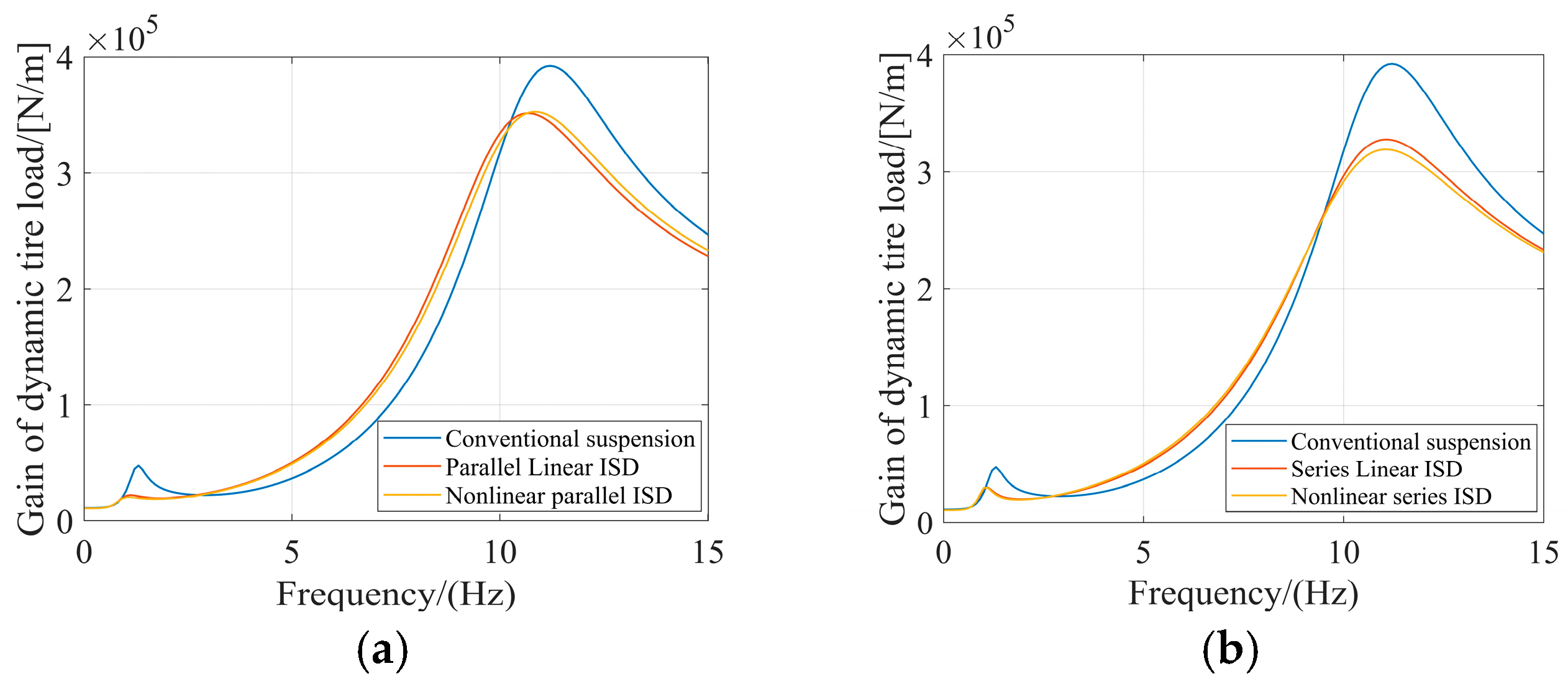
The time-domain responses visually corroborate these improvements. Figure 3 and Figure 6 show that both linear and nonlinear ISD suspensions effectively attenuate body acceleration compared to the passive baseline. Figure 4 and Figure 7 demonstrate improved control over suspension working space, with the nonlinear parallel ISD exhibiting the smallest deflection. Furthermore, Figure 5 and Figure 8 confirm enhanced dynamic tire load management, particularly for the nonlinear parallel ISD configuration.

4.3. Simulation in the Frequency Domain

To further evaluate the vibration isolation performance under periodic excitations, frequency-domain simulations were conducted using sinusoidal inputs. Figure 9, Figure 10 and Figure 11 compare the frequency responses of BA, SWS, and DTL for the conventional passive suspension, linear ISD suspension (ε = 0), and nonlinear ISD suspension with optimized ε.

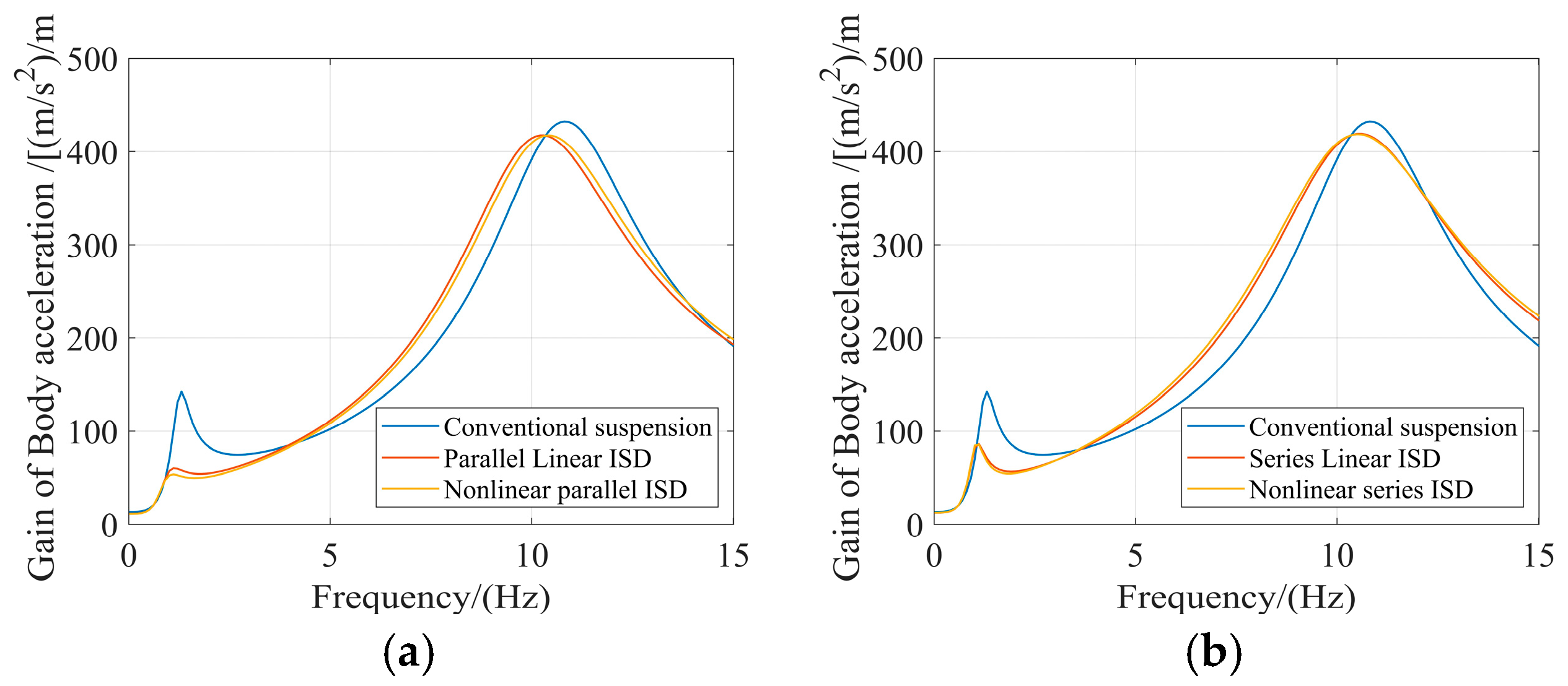
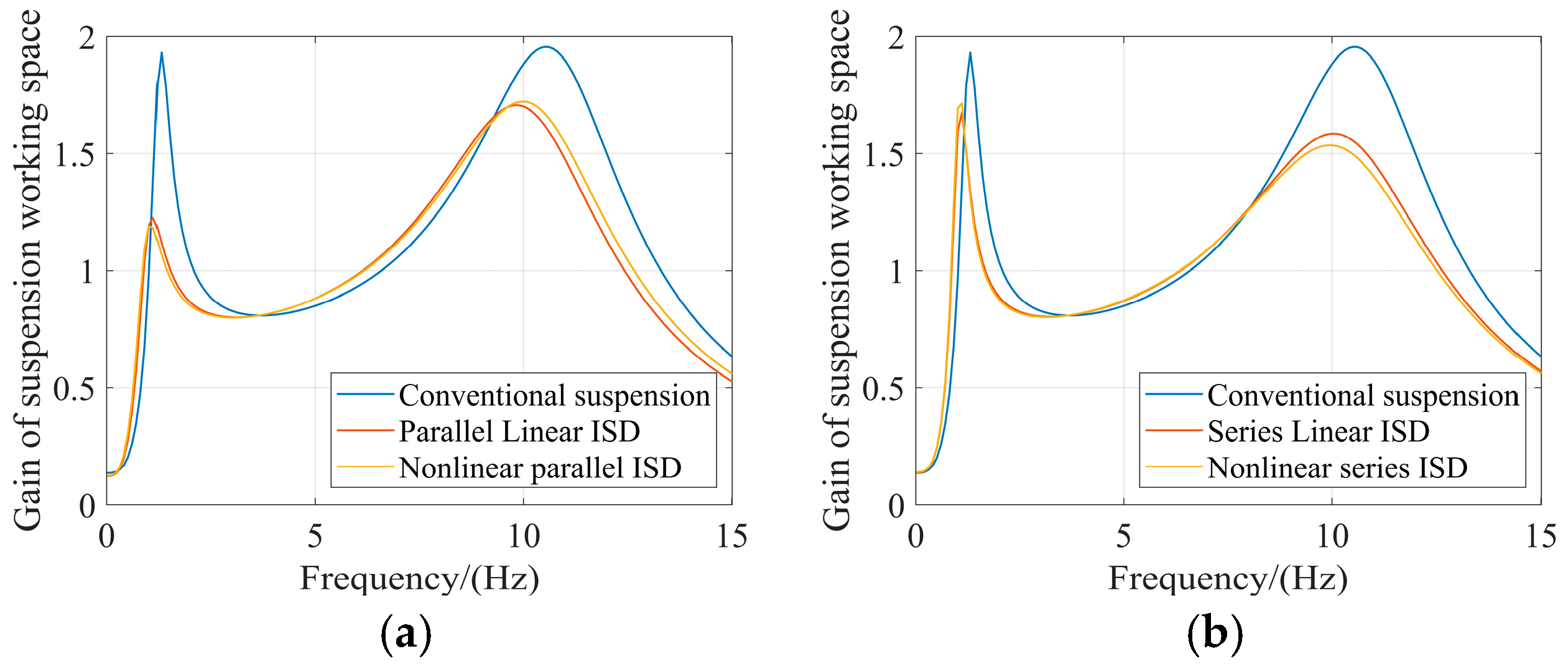
The conventional passive suspension exhibits pronounced resonance peaks across the evaluated frequency spectrum. In contrast, the incorporation of the inerter in both linear ISD configurations demonstrates a clear advantage in resonance control, effectively suppressing these critical resonance peaks compared to the passive baseline.

The introduction of optimized spring nonlinearity further enhances performance in specific configurations. For the parallel ISD suspension, the nonlinear design provides additional resonance suppression at identified critical frequencies. The nonlinear parallel ISD achieves improved control of BA at resonance frequencies of 1.11 Hz and 10.31 Hz, demonstrates better SWS performance at 1.11 Hz and 10.01 Hz, and shows the most substantial improvement in DTL control at 1.11 Hz and 10.91 Hz, significantly enhancing wheel ground contact stability.

For the series configuration, the nonlinear ISD suspension exhibits resonance frequencies at 1.11 Hz and 10.51 Hz for BA, 1.11 Hz and 10.01 Hz for SWS, and 1.01 Hz and 11.01 Hz for DTL. However, the performance improvement compared to the linear series ISD is minimal, with response curves showing considerable overlap at these resonance frequencies. This indicates that the linear series design already provides effective vibration isolation without requiring additional nonlinearity.

In summary, while both linear ISD configurations provide significant resonance suppression advantages over the conventional passive suspension, the benefits of spring nonlinearity are configuration-dependent. The parallel ISD suspension achieves meaningful performance gains through optimized nonlinearity, particularly in DTL control, whereas the series ISD configuration obtains sufficient performance from the linear design alone.

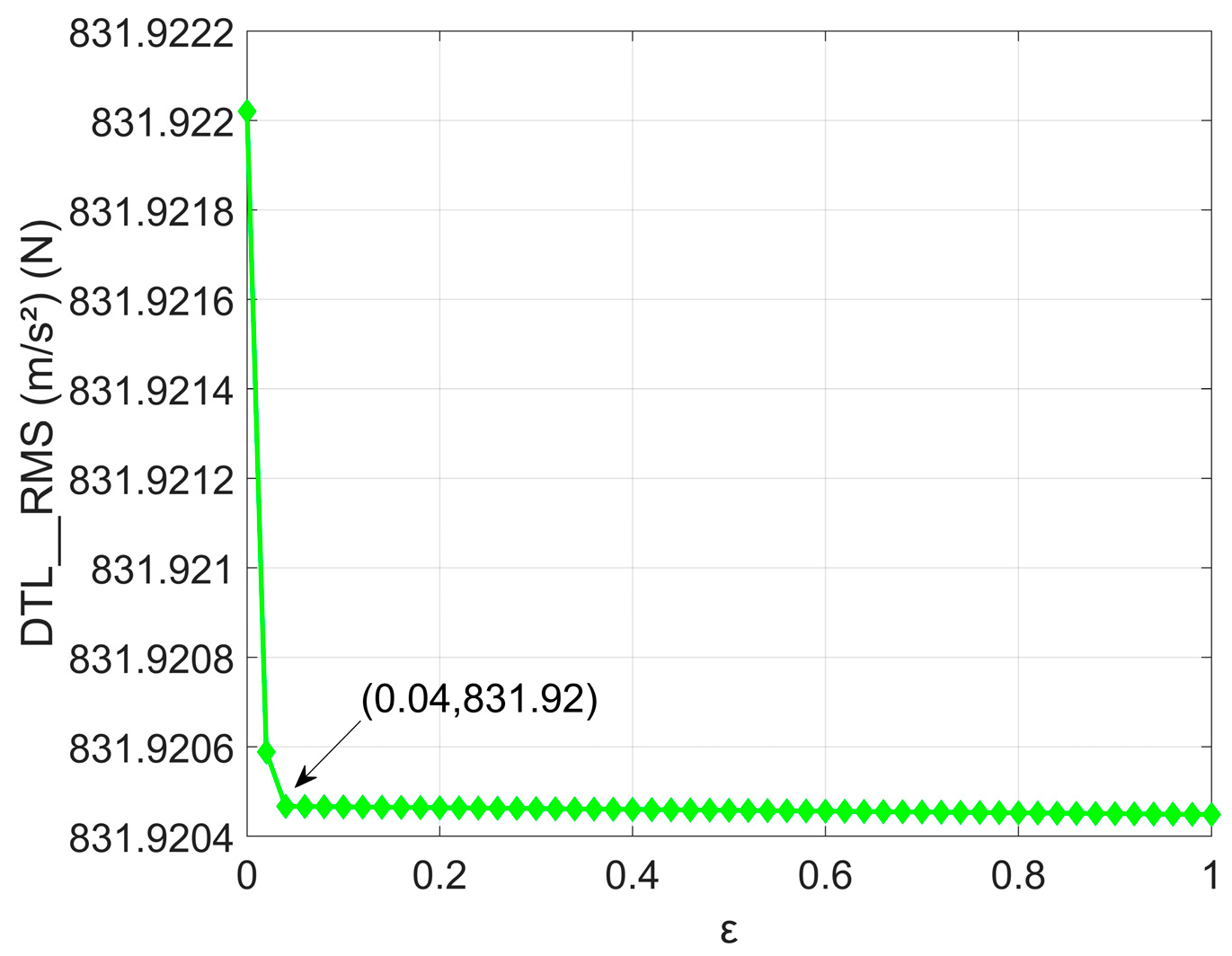
5. Analysis of Nonlinearity Degree Influence

To systematically investigate the influence of spring nonlinearity on suspension dynamic performance, the parameter ε was varied within the range of (0, 1) while maintaining other optimized parameters as constant. The RMS values of BA, SWS, and DTL were analyzed as functions of ε for both parallel and series ISD configurations, with the results presented in Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17.

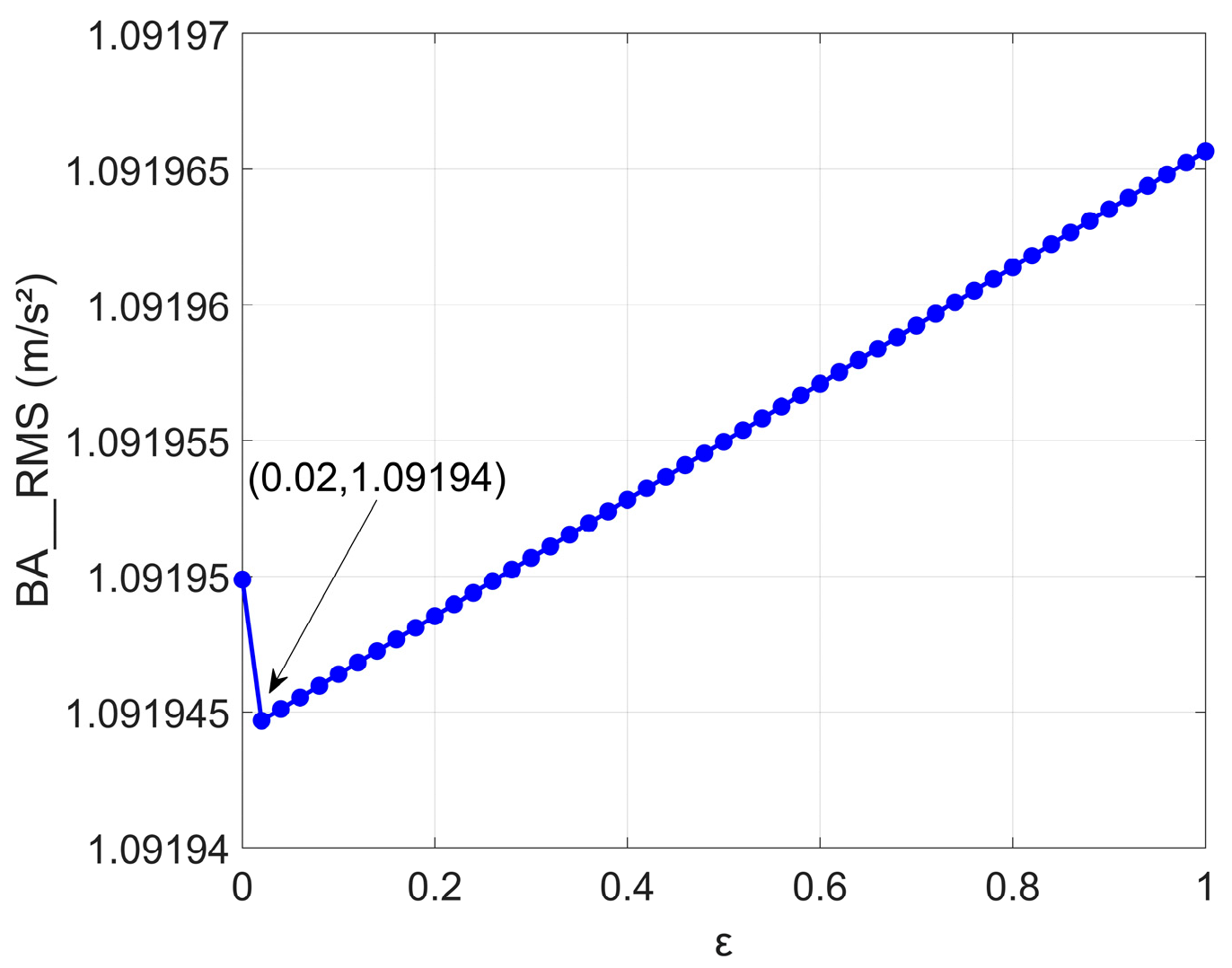
For the parallel ISD suspension, distinct correlations between each performance metric and ε are observed. The RMS of BA (Figure 12) exhibits a positive correlation with parameter ε, indicating a gradual deterioration in ride comfort as nonlinearity intensifies. Conversely, the RMS of SWS (Figure 14) and DTL (Figure 16) demonstrate a clear negative correlation with ε. This trend signifies that increasing the nonlinearity degree progressively improves the suspension’s ability to limit dynamic deflection and enhances tire ground contact stability. The opposing trends establish a fundamental performance trade-off in the parallel configuration.

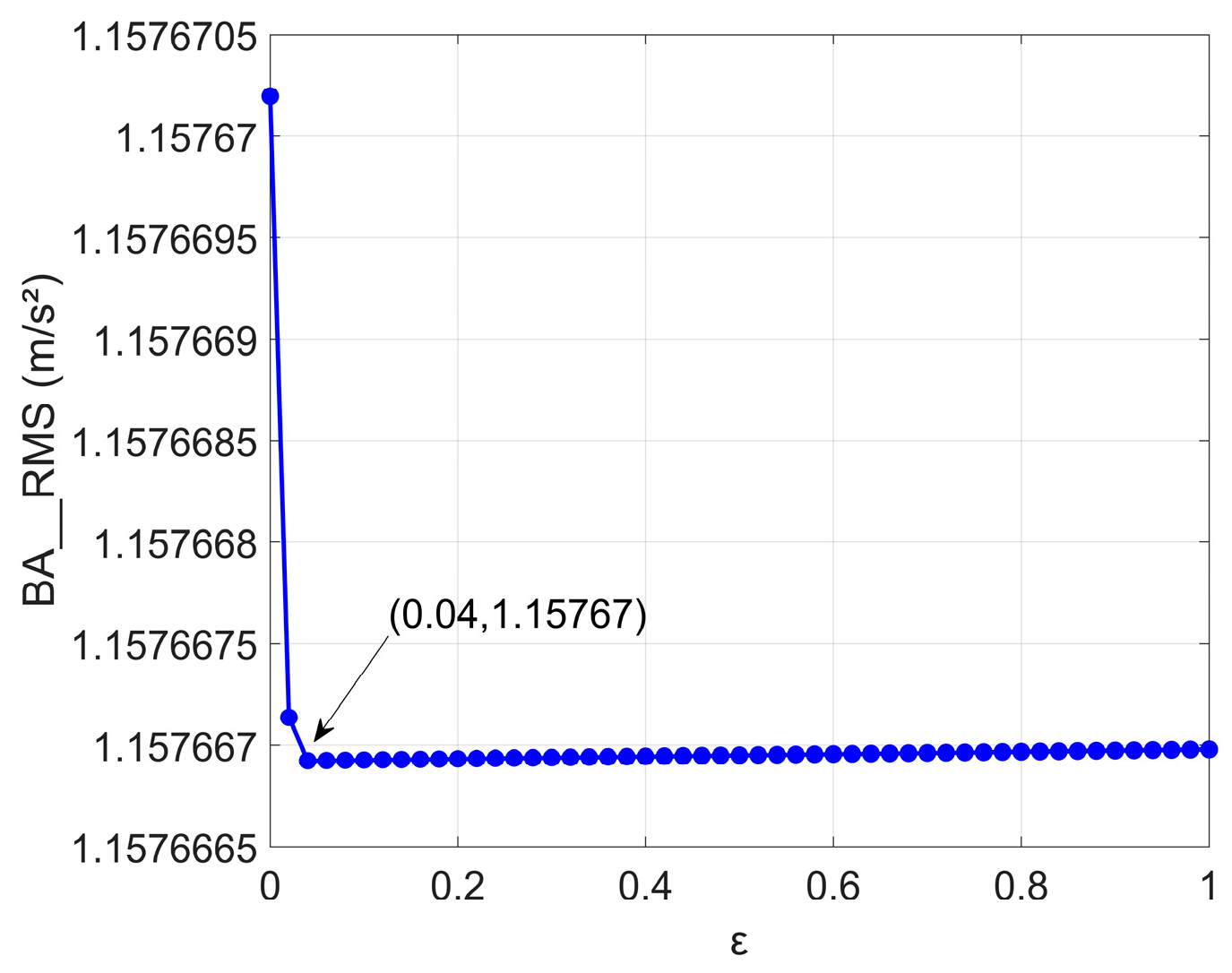
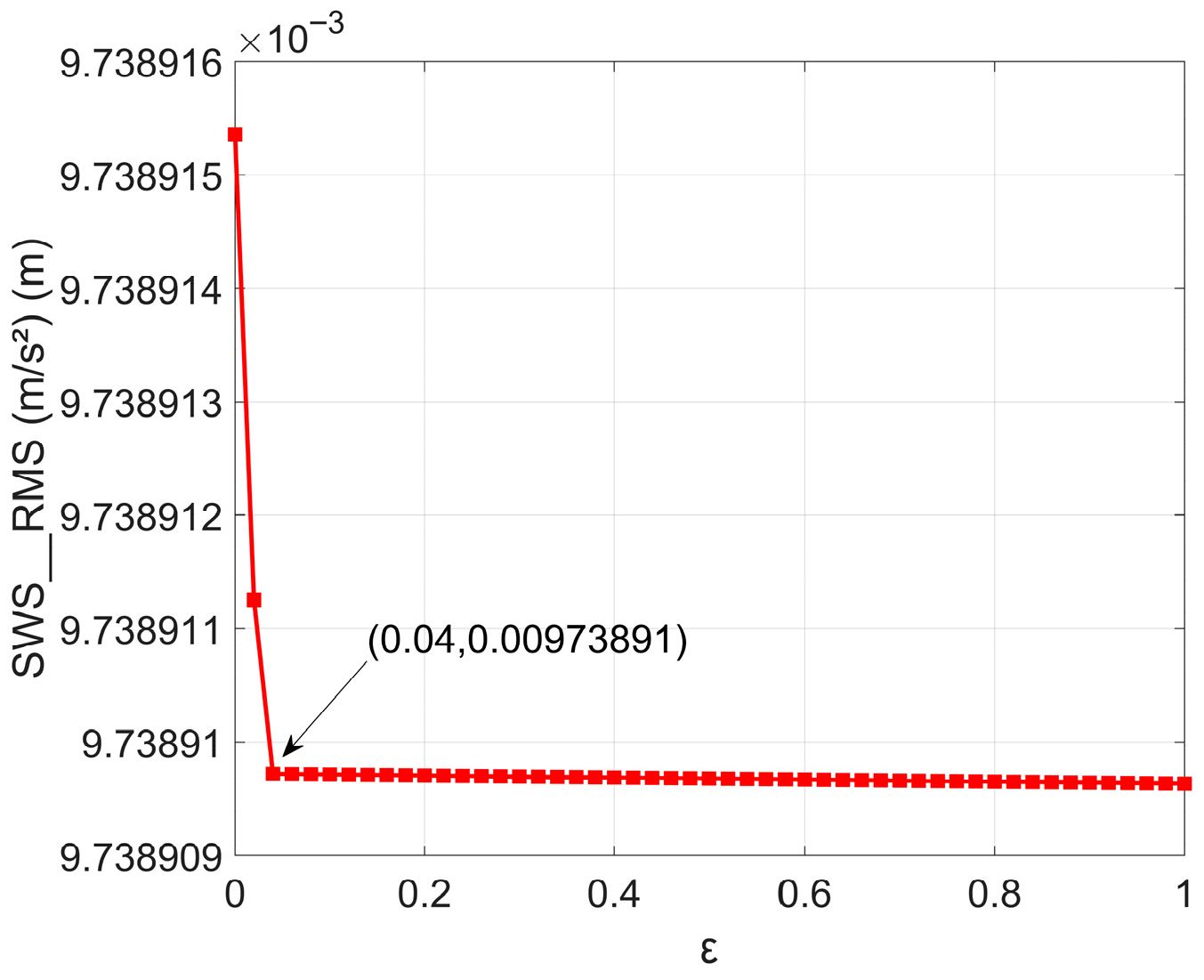
For the series ISD suspension, the influence of ε reveals more complex and non-monotonic behavior. As shown in Figure 13, BA initially decreases within a specific ε range, suggesting improved ride comfort, but subsequently increases as ε continues to rise. The SWS (Figure 15) and DTL (Figure 17) responses also exhibit optimal zones where performance improvements are achieved. However, beyond these optimal ranges, the benefits diminish or reverse, indicating that excessive nonlinearity can compromise performance balance in the series configuration.

Vehicle suspension design necessitates the simultaneous minimization of BA, SWS, and DTL to comprehensively enhance ride comfort and handling stability. The ε-sensitivity analysis conducted in this study provides crucial insights for suspension optimization. It reveals that the parallel and series ISD configurations respond fundamentally differently to changes in spring nonlinearity. Consequently, strategic tuning of ε, tailored to the specific suspension architecture, is imperative for achieving optimized performance trade-offs in practical suspension design applications.

6. Conclusions

This study optimized vehicle suspension dynamics by introducing a controllable degree of spring nonlinearity into ISD systems. Quarter-vehicle models for parallel and series configurations were established, and a multi-objective genetic algorithm was employed to optimize the parameters, including the nonlinearity coefficient ε, under random road excitation. The primary goal was to minimize BA, SWS, and DTL, with performance evaluated through comprehensive time-domain and frequency-domain analyses.

For the parallel configuration, the nonlinear ISD achieved a 7.98% BA reduction over the conventional suspension and a 2.04% BA reduction over the linear ISD, along with a 1.69% DTL reduction and a 0.79% DTL reduction over the linear ISD. For the series configuration, the nonlinear ISD achieved a 7.62% SWS reduction over the conventional suspension and a 0.95% SWS reduction over the linear ISD, along with a 6.42% DTL reduction and a 1.24% DTL reduction over the linear ISD.

Future work will focus on the experimental validation of these findings, extension to full-vehicle models, and the integration of advanced control strategies to fully exploit this potential.