Abstract
Trajectory prediction is a critical component of autonomous driving decision-making systems, directly impacting driving safety and traffic efficiency. Despite advancements, existing reviews exhibit limitations in timeliness, classification frameworks, and challenge analysis. This paper systematically reviews multi-agent trajectory prediction technologies, focusing on generating future position sequences from historical trajectories, high-precision maps, and scene context. We propose a multi-dimensional classification framework integrating input representation, output forms, method paradigms, and interaction modeling. The review comprehensively compares conventional methods and deep learning architectures, including diffusion models and large language models. We further analyze five core challenges: complex interactions, rule and map dependence, long-term prediction errors, extreme-scene generalization, and real-time constraints. Finally, interdisciplinary solutions are prospectively explored.
1. Introduction
The rapid development of autonomous driving technology has raised higher requirements for the accuracy and robustness of trajectory prediction. As the core component of the autonomous driving decision-making system, trajectory prediction directly determines driving safety and traffic efficiency [1]. In complex dynamic traffic environments, vehicles need to predict the future movement trajectories of surrounding traffic participants (such as vehicles and pedestrians) in real time to avoid collision risks and plan the optimal path [2,3,4]. However, the randomness of traffic participant behavior, the complexity of multi-agent interaction, and the uncertainty of environmental perception pose significant challenges to high-precision trajectory prediction.
Although there are existing reviews covering traditional methods and deep learning models, the following deficiencies still exist: (1) lagging in timeliness: lacking systematic analysis of frontier technologies such as diffusion models and large language models (LLMs); (2) single classification framework: not unified in the classification dimensions based on interaction modeling, output modalities, and uncertainty handling; (3) insufficient analysis of challenges: no in-depth exploration of key challenges such as cumulative long-term prediction errors and generalization in rare scenarios. This paper focuses on the multi-agent trajectory prediction problem and aims to systematically review the key technologies for generating future position sequences based on historical trajectories, high-precision maps, and scene context. This paper focuses on the following issues:
- Modeling of input elements: how dynamic information, static information, and scene context can be collaboratively represented;
- Evolution of output form: from single-modal deterministic trajectories to multi-modal probabilized trajectories;
- Innovation of method paradigms: the efficacy boundaries of traditional methods and deep learning methods;
- Completeness of evaluation system: the adaptability of dataset characteristics and multi-dimensional evaluation indicators.
Therefore, we propose a multi-dimensional classification framework, integrating traditional methods and deep learning models; deeply analyze the mechanisms of five major challenges (complex interaction, rule dependence, long-term prediction error, extreme scene generalization, real-time constraints); and prospectively explore interdisciplinary integration directions such as embodied intelligence and vehicle-road collaboration. The main contributions of this paper are as follows:
- Proposing a multi-dimensional classification framework, organizing the evolution of trajectory prediction technology from four dimensions: input representation, output form, method paradigm, and interaction modeling;
- Systematically comparing the advantages and limitations of traditional methods and deep learning models, covering the latest progress of diffusion models, Transformer architectures, and generative methods;
- Deeply analyzing the current five major challenges (complex interaction, rule dependence, long-term prediction error, extreme scene generalization, real-time constraints), providing directional guidance for future research.
This paper is organized as follows. Section 2 establishes the trajectory prediction problem formulation and classification framework. Section 3 reviews conventional methods: physics models, maneuver-based approaches, and probabilistic graphical models. Section 4 analyzes deep learning methods categorized by architecture: RNNs, CNNs, GNNs, Transformers, and generative models, detailing feature encoding/fusion. Section 5 evaluates datasets and metrics. Section 6 discusses multi-task applications and core challenges with solutions. Section 7 concludes and proposes future directions including end-to-end frameworks and causal reasoning systems.
2. Key Problems and Method Classification
2.1. Core Input Element
The precision of trajectory prediction relies significantly on the quality and nature of input data, which encompass dynamic information, static information, and scene context. Collectively, these elements offer a thorough depiction of the traffic setting for the trajectory prediction algorithm.
2.1.1. Dynamic Information
Dynamic information primarily comprises historical trajectory data of the host vehicle and surrounding traffic participants, encompassing their position, velocity, acceleration, and heading angle. This data characterizes the immediate movement status of traffic participants and serves as the foundation for trajectory prediction, particularly crucial in short-term trajectory prediction, as it directly indicates the instantaneous movement tendencies of traffic participants [5,6,7]. The collection of dynamic information typically relies on the vehicle’s sensors and V2X communication technology [8].
2.1.2. Static Information
Static information in the traffic environment includes lane lines, curbs, traffic signs, traffic lights, drivable areas, and intersection structures. This data serves as a constant representation of the traffic surroundings and forms the foundational backdrop for trajectory prediction. Typically acquired from high-precision maps and on-board sensors, static information aids vehicles in comprehending traffic regulations and road layout. It holds significant relevance in long-range trajectory forecasting and route mapping by furnishing a comprehensive overview of the traffic landscape [9].
2.1.3. Scenario Context
Enabling vehicles to comprehend the attributes and possible hazards of the present situation, scene context encompasses factors such as traffic regulations, lighting conditions, weather, and the type of scene. This data is typically acquired through sensor data and algorithms that are aware of the environment [10,11,12,13]. Across various scene categories, the utilization of scene context information can assist vehicles in adapting prediction strategies and enhancing the precision of predictions.
2.2. Output Representation
2.2.1. Trajectory Representation
Trajectory representation in autonomous driving trajectory prediction involves converting the movement path of a vehicle or traffic participant into a format that can be analyzed. The selection of a trajectory representation method significantly impacts both the construction of prediction models and the comprehensibility of prediction outcomes [14]. Typical trajectory representation approaches comprise discrete point sequences, parametric curves, and grid occupancy.
- Discrete Point Sequence
A discrete point sequence depicts a trajectory through a series of discrete points in time, providing a direct representation of the trajectory’s temporal evolution. In the context of autonomous driving, a discrete point sequence serves as an intuitive method to capture the vehicle’s position at each time point, with each point encapsulating positional coordinates along with potential speed, acceleration, and related data [15]. Each individual point corresponds to the positional data at a specific time step, denoted as t. This can be mathematically formulated as:
where denotes the pedestrian position at time step and is the total time step of the trajectory.
- 2.
- Parametric Curve
A parametric curve is defined by one or more parameters that determine the coordinates of points along the curve [16]. Examples of parametric curves commonly used include polynomials and spline curves.
The polynomial curve follows a fundamental structure:
where represents the time variable and denotes the polynomial coefficient.
For instance, Buhet et al. [17] introduce a probabilistic prediction approach utilizing polynomial trajectories. This method represents the vehicle trajectory as a polynomial function and forecasts the future trajectory distribution through a probabilistic model, effectively addressing trajectory uncertainty and diversity.
A spline curve, commonly employed for interpolation and fitting, is a smooth curve determined by a series of control points. The B-spline curve is currently the most prevalent type utilized. For instance, Cao et al. [18] illustrates the creation of a trajectory from predetermined waypoints, delineating the path’s form through the node vectors and control polygons of the B-spline. Furthermore, a real-time path planning strategy leveraging the B-spline curve is introduced in [19], enabling swift generation of obstacle-avoidance paths in dynamic environments.
- 3.
- Grid Occupation
The concept of grid occupancy involves partitioning space into grids and projecting the likelihood of each grid being occupied in the future. Schreiber et al. [20] proposed a new encoder–decoder framework, which utilizes convolutional long short-term memory networks to predict future trajectory patterns based on the grid occupancy mapping. Additionally, Zeng et al. [21] proposed an end-to-end interpretable neural motion planner, which employes a grid occupancy graph to delineate various potential trajectories.
2.2.2. Unimodal Prediction and Multimodal Prediction
The unimodal prediction method involves predicting the most likely trajectory for each target. A physical model-based single-modal prediction method utilizes kinematic and dynamic properties to determine a singular, probable future trajectory by considering the vehicle’s position, velocity, and yaw rate [22]. Conversely, a machine learning-based unimodal prediction method extracts key feature information from vehicle lane change trajectory data using SVM’s nonlinear learning and pattern recognition capabilities. This method models the vehicle’s actual lane change process and calculates the probability distribution of behavior parameters that represent changing motion characteristics [23].
The multimodal prediction approach can produce multiple plausible trajectories while accounting for the uncertainty in the target’s intention [24]. By incorporating probabilistic models or deep learning techniques, this approach can assign a probability to each trajectory, reflecting its likelihood. This method integrates historical target trajectories, environmental data, and potential driving intentions to create a probability distribution model using recurrent neural networks and mixed density network output functions, enabling the generation of diverse trajectories and their associated probabilities [25]. Another multi-modal trajectory prediction technique, employing deep learning and adversarial training of generator and discriminator, generates multiple feasible trajectories, capturing the uncertainty in vehicle behavior [26]. Table 1 conducts a comparative analysis of unimodal and multimodal trajectory prediction methods, summarizing their applicable scenarios, main advantages, disadvantages, and representative methods.

Table 1.
Comparison of unimodal prediction and multimodal prediction.
2.2.3. Uncertainty Quantification
Accurately quantifying uncertainty is crucial for ensuring the reliability and robustness of trajectory predictions, especially given the intricate nature of traffic environments and sensor data noise. Decision support systems rely heavily on precise uncertainty quantification methods such as probability distributions, confidence intervals, and generative model sampling to enhance the accuracy of prediction outcomes [27,28].
Common probability distributions comprise the Gaussian distribution and the mixture Gaussian distribution. Yoon et al. [29] employed Gaussian process regression to derive the probability distribution of behavioral parameters that depict lane change motion characteristics, thereby offering a probability estimate for trajectory prediction. Mao et al. [30] introduced a random trajectory prediction approach grounded on the jump diffusion model, and characterized the uncertainty of trajectory prediction through the Gaussian mixture distribution. This technique adeptly addresses multi-modal and uncertainty challenges.
The confidence interval is a statistical tool used to quantitatively and intuitively measure the uncertainty of trajectory predictions. It not only reflects the reliability of the prediction results but can also be applied to tasks such as path planning and collision detection. The confidence interval based on the Gaussian distribution provides the uncertainty range of the predicted values, which is helpful for evaluating the prediction stability of the model, while the confidence interval based on non-parametric methods can determine its coverage range through Monte Carlo simulation based on a large number of pseudo-experiments, thereby improving the accuracy of the estimation [31,32].
Uncertainty quantification combined with generative model sampling allows for a more comprehensive treatment of uncertainty in trajectory prediction. Li et al. [33] employed uncertainty quantification methods to estimate the uncertainty range of trajectory prediction, and then sampled the model within this range to generate trajectory samples that conform to the uncertainty.
2.3. Classification of Trajectory Prediction Methods
2.3.1. Based on Method Paradigm
Predictions based on the method paradigm can be mainly classified into traditional methods and those based on deep learning.
Traditional trajectory prediction methods typically rely on physical models, kinematic models, or rule-based models [34,35]. The advantages of these methods are interpretability and computational efficiency, but they may not be flexible enough to deal with complex traffic scenarios and nonlinear behaviors.
Trajectory prediction methods based on deep learning can automatically extract features and make predictions by learning patterns and relationships in data. Deep learning models, such as recurrent neural networks (RNN), long-short term memory networks (LSTM), and Transformer architectures, have been widely used for trajectory prediction tasks. These methods perform well in dealing with complex traffic scenarios and nonlinear behavior, but often require large amounts of data and calculations [36]. Figure 1 shows the percentage of articles using traditional and deep learning for trajectory prediction. The proportions are derived from our analysis of over 100 relevant studies from 2014 to 2024.
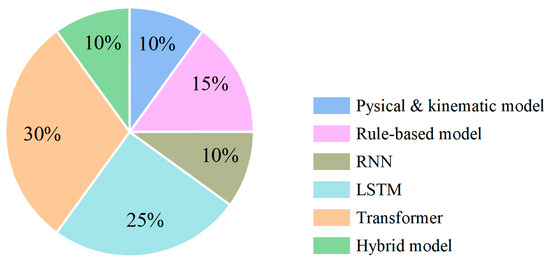
Figure 1.
The proportion of prediction methods based on method.
2.3.2. Based on Interaction Modeling
Interaction among traffic participants is one of the key factors affecting the prediction accuracy in autonomous driving trajectory prediction. Interaction modeling methods can be divided into three categories according to whether they explicitly represent and process these interactions: interaction modeling, implicit interaction modeling, and explicit interaction modeling. Figure 2 shows the proportion of articles that use these three types of interactions for trajectory prediction.
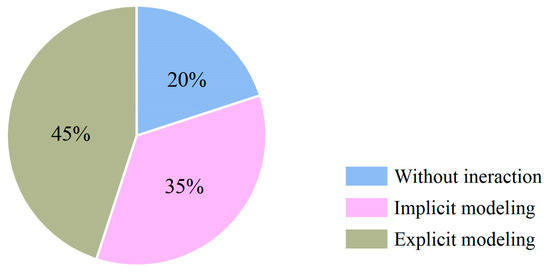
Figure 2.
The proportion of prediction methods based on interaction modeling.
Methods that do not consider interaction treat each traffic participant as an independent individual, regardless of its interaction with other traffic participants, and are usually applied in low-density traffic scenarios, but in high-density traffic scenarios, interactions between vehicles are complex and frequent, and methods that do not consider interaction may lead to reduced prediction accuracy [29].
Implicit interaction modeling methods consider the interaction between traffic participants by means of shared feature extraction or joint training, and are often applied to medium density traffic scenes. Implicit interaction modeling methods can improve prediction accuracy through learned implicit relationships while maintaining high computational efficiency. Xin et al. [37] used LSTM to encode the historical trajectory data of vehicles and predict their future trajectories. They proved that this method is capable of implicitly capturing the interaction relationships among vehicles and is suitable for medium-density traffic scenarios. However, in complex traffic scenarios, implicit modeling may fail to capture complex interaction relationships, resulting in insufficient prediction accuracy.
Explicit interaction modeling method improves prediction accuracy by explicitly expressing the interaction between traffic participants. Explicit modeling can significantly improve prediction accuracy and is applicable to scenarios that require high-precision predictions. Zhao et al. [38] proposed a trajectory prediction method based on Graph Neural Network (GNN), which can explicitly simulate the interactions between vehicles. This method performs well in complex traffic scenarios and is suitable for high-density traffic situations. However, explicit modeling usually requires more computing resources and may not be suitable for scenarios with high real-time requirements.
3. Conventional Trajectory Prediction Methods
Conventional trajectory prediction methods each have their own focuses. Figure 3 illustrates several conventional methods and their application in addressing the trajectory prediction task for Autonomous Vehicles (AVs). Analysis of the papers indicates that in this review, 38% of the papers focus on Physics Model-Driven Approaches, 27% of the papers concern Maneuver-Based Methods, 22% of the papers concentrate on PGM-Based Approaches, and the remaining 13% are centered on Gaussian Process regression.
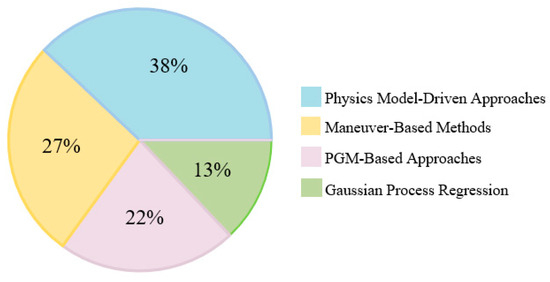
Figure 3.
Participation of research articles in trajectory prediction task using conventional approaches.
Conventional methods for trajectory prediction form the foundation of the autonomous driving trajectory prediction field. Centered around mathematical models and statistical patterns, these methods estimate the future motion of traffic participants through explicit physical principles or probabilistic reasoning. Although they have limitations in complex interactive scenarios, these methods remain relevant in specific scenarios due to their interpretability and efficiency. A summary of these models, including representative models, strengths and weaknesses, and applicable scenarios, is presented in Table 2.

Table 2.
Summary of research on cumulative errors and behavioral uncertainty issues.
3.1. Physics Model-Driven Methods
Physics model-driven approaches are grounded in principles of classical mechanics and kinematics [66,67]. Physics-model-driven methods predict trajectories by constructing mathematical equations of vehicle motion based on classical mechanics and kinematic principles. The core idea is to treat vehicle motion as a process that can be described by physical laws. These methods do not rely on large amounts of data; instead, they capture the dynamic characteristics of vehicles through preset motion models and achieve high accuracy within a short time range.
3.1.1. Constant Velocity/Acceleration Models
The Constant Velocity (CV) model assumes a vehicle maintains its current speed throughout the prediction horizon, calculating future positions solely based on its present location and velocity. The Constant Acceleration (CA) model further incorporates acceleration effects, making it suitable for scenarios involving vehicle acceleration or deceleration. In practical applications, these models are often combined with Kalman filtering to address uncertainties from sensor noise. For instance, Zhang et al. [39] proposed a method based on Vehicle-to-Vehicle (V2V) communication and Kalman filtering, enabling ego vehicles to predict trajectories of remote vehicles and achieve obstacle avoidance. Lefkopoulos et al. [40] introduced an Interacting Multiple Model Kalman Filter (IMM-KF), which enhances the accuracy of physics-based trajectory predictions by integrating interaction-related parameters.
3.1.2. Bicycle Model
The bicycle model simplifies vehicles into a “bicycle” structure, characterizing motion through front-wheel steering angles and longitudinal velocity. It comprises two variants: Kinematic model: Ignores dynamic factors like tire forces, considering only geometric constraints. Suitable for low-speed scenarios. Dynamic model: Incorporates parameters such as tire forces and vehicle mass, better capturing motion characteristics during high-speed or limit-handling conditions. In trajectory prediction, bicycle models often integrate with filtering techniques to address motion disturbances. As noted in [46], some studies combine this model with a Monte Carlo approach—randomly sampling input variables to simulate state distributions and generate potential future trajectories.
3.1.3. Advantages and Limitations
Physics-based model-driven approaches offer distinct advantages: their principles are simple, based on explicit kinematic or dynamic laws, requiring no complex training process. With high computational efficiency, they fulfill real-time requirements. Their strong physical interpretability ensures predictions align with human intuition about vehicle motion, facilitating verification and calibration. For instance, physics models demonstrate stable performance in short-term predictions (typically ≤ 1 s), providing reliable trajectory references for safety assessment [41].
However, physics-based model-driven approaches exhibit significant limitations. Its core assumption is that the movement of vehicles follows fixed physical laws (as emphasized in [42]), which prevents them from capturing the interactions between vehicles and the changes in the drivers’ intentions. Furthermore, as the prediction horizons extends, the model errors will gradually accumulate, resulting in a significant decline in the accuracy of long-term predictions.
3.2. Maneuver-Based Methods
Maneuver-based approaches abstract vehicle behavior into discrete “maneuver actions” such as lane changes, car-following, turns, etc., generating future trajectories by recognizing current maneuver types.
3.2.1. Maneuver Recognition and Classification
Maneuver recognition serves as the prerequisite for maneuver-based methods, determining a vehicle’s current behavior by analyzing historical trajectory features. Common maneuver types include longitudinal maneuvers and lateral maneuvers, with combined maneuvers such as intersection turns and U-turns observed in complex scenarios. Houenou et al. [49] identified lane-change maneuvers and integrated them with the Constant Yaw Rate and Acceleration (CYRA) model for trajectory prediction. Tran and Firl [50] leveraged Monte Carlo Simulation (MCS) to forecast multimodal trajectories and employed Gaussian Process Regression to learn behavioral patterns at intersections.
3.2.2. Maneuver Library-Based Trajectory Generation
Trajectory generation based on maneuver libraries involves predefining typical trajectory models for various maneuvers to form a “maneuver library.” Upon identifying a vehicle’s maneuver type, the corresponding model is retrieved from this library to generate future trajectories by combining it with the current kinematic state. Wissing et al. [51] proposed an interaction-aware trajectory prediction method that simulates interactive behaviors using MCS, integrating the Intelligent Driver Model (IDM) and lane-change models to generate distributions of potential future positions for target vehicles. Similarly, Okamoto et al. [52] utilized identified maneuvers in their maneuver-based framework to generate future trajectories through Monte Carlo methods.
3.2.3. Advantages and Limitations
The primary strength of maneuver-based methods lies in their explicit behavioral intent representation, where prediction results directly correlate with a vehicle’s driving objectives. This enables Autonomous Driving Systems (ADS) to intuitively comprehend surrounding vehicles’ behavioral purposes, providing actionable input for decision-making and planning.
While effective in intent interpretation, maneuver-based methods face three core limitations, as discussed in [53]: (1) Maneuver library is unable to comprehensively cover all possible actions, especially in edge scenarios such as emergency avoidance, which can lead to prediction failures. (2) Inherent classification ambiguity exists as real-world driving often involves transitional states overlapping multiple maneuver categories. (3) Its interactive modeling capability is relatively weak, and it neglects dynamic interaction relationships between vehicles.
3.3. PGM-Based Methods
Probabilistic Graphical Model (PGM)-based methods leverage graphical structures to represent conditional dependencies among variables, employing probabilistic inference to handle trajectory prediction uncertainties, thereby proving effective in complex operational environments with multi-factorial interactions.
3.3.1. Hidden Markov Model
The Hidden Markov Model (HMM) conceptualizes trajectory generation as a stochastic process governed by latent states (satisfying the Markov property) and observable states, characterizing motion patterns through initial state probabilities, transition probabilities, and emission probabilities [54]. For instance, Qiao et al. [56] employs HMM with adaptive parameter selection to simulate real-time scenarios, enhancing dynamic adaptability in trajectory prediction. Concurrently, Deng et al. [57] integrate HMM with fuzzy logic to forecast driver maneuvers, ensuring prediction reliability through multiple initial-value iterations.
3.3.2. Dynamic Bayesian Network
The Dynamic Bayesian Network (DBN) extends HMM by incorporating a temporal dimension to model time-evolving dependencies among variables, specifically targeting multi-vehicle interaction scenarios. This framework represents variables—including vehicle states, road structures, and interaction relationships—as nodes interconnected via directed edges to encode dependencies, subsequently enabling trajectory prediction through probabilistic inference. Gindele et al. [59] leverage DBN to model multi-vehicle maneuvers using inputs of all vehicles’ states, interactions, and road structures. He et al. [60] employ it to recognize car-following and lane-changing behaviors while predicting trajectories.
3.3.3. Advantages and Limitations
The core strength of probabilistic graphical model-based approaches lies in their inherent ability to naturally accommodate uncertainties in trajectory prediction, representing potential future trajectories through probability distributions that support risk assessment for autonomous driving systems. For instance, both HMM and DBN output trajectory probability distributions—rather than single deterministic results—thereby enhancing robustness against sensor noise and environmental dynamics [58,68]. Furthermore, these models integrate multi-source information and outperform physics-based models in complex operational scenarios.
Probabilistic graphical model-based approaches exhibit notable constraints: (1) The complexity of their structure requires manual specification of the dependencies between variables, which demands profound domain expertise. (2) Precise reasoning necessitates a thorough traversal of the entire state space, which often forces the use of approximate algorithms, thereby reducing the accuracy of predictions. (3) In high-dimensional continuous state spaces, scalability issues arise. As the number of variables increases, computational efficiency and stability will sharply decline.
3.4. Gaussian Process Regression
Gaussian Process Regression (GPR), a non-parametric Bayesian approach, treats trajectories as samples drawn from a Gaussian process, leveraging kernel functions to characterize similarities between data points for future trajectory prediction. Its core mechanism estimates the mean and covariance functions of the Gaussian process from historical trajectories, ultimately outputting future paths in the form of probabilistic distributions.
3.4.1. Principles and Applications in Trajectory Prediction
Gaussian Process Regression fundamentally operates by assuming all trajectory samples follow a multivariate Gaussian distribution, predicting unobserved future trajectories through estimation of distribution parameters from observed data. In trajectory prediction applications, it processes historical vehicle position sequences as input and outputs probabilistic distributions of future locations. For instance, Laugier et al. [64] first assessed possible vehicle behaviors via HMM before deploying GPR to predict corresponding trajectories. Guo et al. [65] integrated GPR with Dirichlet processes (DP) to construct motion models that extract latent movement patterns.
3.4.2. Advantages and Limitations
Gaussian Process Regression offers the distinctive advantage of naturally outputting uncertainty estimates for trajectories, directly yielding probabilistic distributions of future positions without additional processing. Furthermore, as a non-parametric model, GPR requires no predefined functional forms for trajectories, flexibly fitting complex nonlinear motion patterns while outperforming parametric counterparts in small-sample scenarios.
The main limitation of Gaussian process regression lies in its high computational complexity, which results in a significant decrease in efficiency when dealing with large datasets and makes it difficult to meet real-time requirements. Moreover, Gaussian process regression performs poorly in handling multi-vehicle interaction scenarios because predicting the joint trajectory will significantly increase the number of variables, thereby causing excessively high computational and storage costs for the covariance matrix.
4. Deep Learning-Based Trajectory Prediction Methods
Compared to conventional approaches, deep learning models move away from a heavy reliance on explicit rules and prior models [69,70,71]. They leverage their deep network structures and powerful nonlinear fitting capabilities to automatically learn spatio-temporal dependencies and interaction patterns directly from vast amounts of real-world data [72]. This fundamental shift has led to breakthroughs in prediction accuracy and robustness, significantly enhancing the models’ ability to handle extreme scenarios.
This chapter presents a systematic review of deep learning-based trajectory prediction methods, following the general framework illustrated in Figure 4. The review begins with the foundational technique of feature encoding. Subsequently, it follows the evolutionary trajectory of network architectures, delving into how RNN process temporal data, Convolutional Neural Networks (CNN) extract spatial features, GNN model structured relationships, and Transformers capture global dependencies. Finally, to address the inherent uncertainty of forecasting, the chapter focuses on generative models—including GAN, CVAE, and Diffusion Models—and analyzes their role in multimodal prediction.
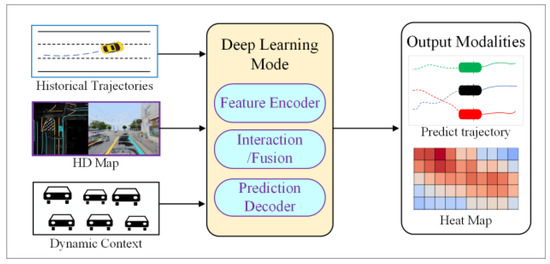
Figure 4.
Framework of deep learning trajectory prediction method. The input is multi-source information, and the output is multimodal trajectory, accompanied by attention distribution map.
4.1. Feature Encoding
The primary task in deep learning trajectory prediction is to convert raw, multi-modal inputs—like historical trajectories, HD maps, and the movement of other agents—into dense features a neural network can process. The quality of this encoding is foundational and sets the performance limit for the entire model. The raw input data is typically heterogeneous, primarily including: the historical trajectory of the target agent itself, the surrounding static high-definition (HD) map, and the dynamics of other traffic participants in the environment.
4.1.1. Historical Trajectory Encoding
The historical trajectory, typically represented as a sequence of the agent’s states over the past timesteps, serves as the foundation for understanding its motion patterns and intent. Each state usually contains position , and may also include information such as velocity , acceleration , and heading angle θ. The first step for a deep learning model is to use an Encoder to compress this variable-length, temporally ordered sequence into a fixed-dimensional feature vector h. This vector h should encapsulate all information from the trajectory valuable for future prediction, such as current motion trends and critical past behaviors. The following are several mainstream trajectory encoding techniques.
One-Dimensional Convolutional Neural Networks (1D CNN): This method treats a trajectory as a one-dimensional signal, processing it by sliding a convolutional kernel along the time steps to identify local motion patterns [73,74,75]. Gilles et al. [76] uses a 1D CNN layer as a parallel local pattern detector to extract short-term motion features, such as acceleration or turns, providing dynamic information for subsequent modeling. A more advanced version is the Temporal Convolutional Network (TCN), which captures longer-range temporal dependencies with high parallel efficiency. Azadani and Boukerche [77] use a TCN encoder on historical trajectories to extract spatio-temporal features and create a compact latent representation. Wang et al. [78] leverage a TCN to replace traditional RNNs for temporal modeling. By stacking layers with causal convolutions and dilated convolutions, their model efficiently captures long-term temporal dependencies.
The most natural and classic approach for processing sequential data is the RNN and its advanced variants—LSTM and Gated Recurrent Unit (GRU)—which are essential tools for handling temporal dynamics [79,80]. Within the basic Sequence-to-Sequence (Seq2Seq) framework, Zyner et al. [81] utilized an RNN to encode the vehicle’s historical data, compressing the historical trajectory into a context vector rich in dynamic information. As research progressed, the RNN encoder became the backbone of more complex generative models, such as Generative Adversarial Networks (GAN) [82] and Conditional Variational Autoencoders (CVAE) [83]. Its task is to map the historical trajectory into a latent space to achieve multi-modal prediction. Even in cutting-edge GNN methods, the RNN remains a critical component. It is commonly utilized to pre-encode the temporal dynamics of each node (agent), furnishing the graph convolution operations with node features that are rich in historical context.
4.1.2. Map Information Encoding
Unlike models relying solely on trajectory history, advanced autonomous systems must deeply understand their static surroundings. High-Definition (HD) maps offer powerful prior knowledge of road topology, traffic rules, and geometric constraints, which is critical for generating safe, compliant, and plausible trajectories. To use this information, deep learning models employ specialized encoders to transform static map features into numerical representations. This geographic information is generally categorized and encoded as either rasterized or vectorized maps.
CNN-based Rasterized Map Encoding. The most intuitive approach involves rasterizing vectorized map data into a multi-channel Bird’s-Eye View (BEV) image centered on the ego-vehicle. As in [84], a multi-channel image is created where each channel represents a specific semantic element. In this format, each channel corresponds to a specific semantic element, such as lane lines or drivable areas. This BEV image is then processed by a standard 2D CNN to extract rich spatial context features.
PointNet-based Vectorized Map Encoding. To overcome information loss associated with rasterization, researchers operate directly on vectorized map data by treating elements like lane centerlines as an unordered point cloud. Bojarski et al. [85] utilizes a shared MLP and a symmetric function to process the unordered set of points from forward-looking road imagery to aid in decision-making, thereby ensuring permutation invariance to the order of the points. Despite their strength in geometry, these models were designed for unordered sets and thus cannot capture the connectivity between points.
Graph Neural Networks offer a state-of-the-art framework for map encoding that models both geometric and topological structures. This method explicitly constructs a graph from the scene, where nodes represent meaningful map units and edges encode their topological relationships. The GNN then iteratively propagates information between nodes via a message-passing mechanism, allowing each node’s feature representation to incorporate data from its surroundings and the broader network structure for a deep understanding of the environment. As exemplified by [86], this approach has proven to be highly effective at capturing the relationships between agents and the map, as well as the indirect relationships between agents established through the map.
4.1.3. Context Information Fusion
For effective trajectory prediction, it is crucial to analyze both an agent’s historical trajectory (dynamic information) and the scene map (static information). Efficiently fusing these modalities is a critical step for high-performance models [87,88]. We will introduce the mainstream fusion strategies, categorized as basic static methods and the more advanced attention-based dynamic methods that represent the current standard.
Concatenation and MLP. Basic static fusion methods were applied in early models due to their simplicity and computational efficiency. In research by Chandra et al. [89], features from trajectories and maps were extracted by separate encoders, concatenated into a single vector, and then processed by an MLP to learn nonlinear associations. The main limitation of this static approach is its inability to dynamically prioritize information based on context. Furthermore, flattening structured data into a single vector can lead to the loss of important geometric and topological relationships.
Dynamic Fusion Methods. To overcome these limitations, state-of-the-art models now widely employ dynamic fusion mechanisms based on Cross-Attention [8,90,91]. This is a specific form of attention mechanism where the ‘Query’ vectors originate from one modality (e.g., the dynamic agent’s state), while the ‘Key’ and ‘Value’ vectors are derived from another modality (e.g., the static map features or other agents’ states). This allows the model to dynamically and selectively retrieve relevant information from the environment context for each agent, much like how a person focuses on specific landmarks or vehicles when making a driving decision. This approach mimics selective human attention by using an agent’s state as a “Query” to dynamically probe “Key-Value” pairs derived from the environmental context. Zhou et al. [92] has demonstrated that this approach enables selective and explicit interaction between agents and the map, as well as between agents themselves.
4.2. RNN-Based Methods
As the earliest deep learning architectures successfully applied to sequence modeling, RNN and their variants, especially LSTM and GRU, naturally became the primary tools for solving the trajectory prediction problem. The chain-like structure and internal gating mechanisms of RNN allow them to naturally and effectively learn and remember both long-term and short-term dependencies in time-series data [93,94]. This aligns perfectly with the inherent temporal evolution of trajectory data.
To systematically organize these research findings and clearly present the technological evolution, the comprehensive comparison is presented in Table 3. We can observe that RNN-based prediction methods have evolved from basic models that handle a single agent and output a deterministic trajectory to advanced frameworks capable of handling multi-modal uncertainty and ultimately modeling complex social interactions.

Table 3.
Summary of RNN-based trajectory prediction methods.
4.2.1. The Basic Seq2Seq Framework
The Seq2Seq model is the foundational application paradigm for RNNs in trajectory prediction. This framework utilizes an Encoder and a Decoder, typically built from LSTM or GRUs. The Encoder’s primary function is to compress an entire historical state sequence into a single, information-dense context vector. This fixed-dimensional vector serves as a holistic summary of the agent’s past motion, acting as the informational bridge connecting the observed past to the predicted future. The Seq2Seq framework’s effectiveness was initially demonstrated by research from Zyner et al. [95] on single-agent vehicle prediction. The inherent drawback of this basic framework was its determinism—the inability to generate multiple potential future trajectories. Later efforts aimed to overcome this by extending the framework to support multi-modality, such as the work by Sriram et al. [100], which proposed forecasting for all agents in the scene simultaneously instead of one by one.
4.2.2. Social Pooling
While the basic and probabilistic Seq2Seq frameworks can handle the temporal dynamics and uncertainty of a single agent, their common and more critical limitation is their lack of interaction awareness. They treat each traffic participant as an independent entity, completely ignoring the fact that in dense traffic environments, the mutual influence between individuals is a key factor in determining future behavior.
To address this challenge, Alahi et al. [96] pioneered Social-LSTM, which employed the “Social Pooling” mechanism. This mechanism operates by first defining a spatial grid around each agent. The hidden states of all agents whose current positions fall into the same grid cell are aggregated (e.g., pooled together using a max or average operation). This creates a social tensor that encodes the collective state of an agent’s local neighborhood. This tensor is then concatenated with the agent’s own hidden state and used for the next prediction step. This integrated social interactions into an RNN framework for the first time, enabling each agent to “perceive” its surroundings when predicting its future path, resulting in more realistic, collision-free trajectories. The core concept introduced by Social-LSTM laid the groundwork for the field of interaction-aware prediction, with subsequent works by Xue et al. [97], Xu et al. [98], and others replacing simple pooling with more sophisticated attention mechanisms or GNN.
4.2.3. Advantages and Limitations
RNN and their variants offer powerful temporal modeling capabilities, making them a flexible and scalable backbone for trajectory prediction. Their encoder–decoder architecture allows for the seamless integration of components for multi-modality and social interactions. Despite these strengths, RNN have inherent limitations. Even with LSTM and GRU mitigating the classic vanishing/exploding gradient problem, an information bottleneck can still arise with very long historical sequences. Furthermore, they are often inadequate at modeling spatial relationships.
4.3. CNN-Based Methods
While RNN excel at modeling temporal dependencies, they often struggle to capture the rich spatial context of the traffic scene. In contrast to the temporal focus of RNN, CNN offers a powerful alternative for understanding the spatial context of trajectory prediction. Leveraging their proven ability to extract hierarchical spatial features, CNN-based methods rasterize the complex traffic scene into one or more image-like grids. Standard convolutional operations are then applied to automatically learn and extract the spatio-temporal patterns essential for prediction [101,102,103,104]. A typical framework for this approach is depicted in Figure 5, with key works summarized in Table 4.
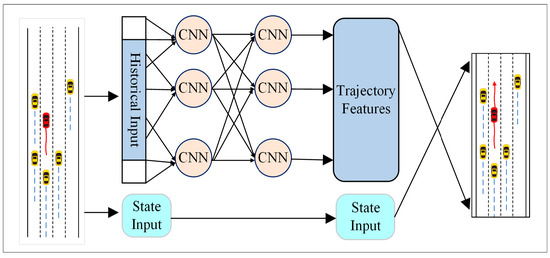
Figure 5.
CNN model trajectory prediction framework.

Table 4.
Summary of reviewed DL-based Models relying on CNNs.
4.3.1. Prediction Based on Rasterized Scenes
A prevalent paradigm in trajectory prediction utilizes CNN with BEV representation. This approach encodes static and dynamic information into a multi-channel BEV image centered on the ego-vehicle. This image is then processed by a CNN backbone for feature extraction. Cui et al. [105] pioneered this end-to-end multi-modal method by systematically rasterizing complex traffic scenes into a BEV representation for direct input into a deep CNN. The effectiveness of this paradigm was validated by CoverNet, which demonstrated that scene rasterization allows a CNN to implicitly model agent interactions, leading to more plausible and compliant trajectory predictions.
4.3.2. Variant Architectures
While CNNs excel at spatial modeling, they lack inherent capabilities for explicitly modeling time series data. To overcome this limitation, hybrid architectures combining CNNs with RNNs have been proposed for more effective spatio-temporal fusion [108,109,110,111]. In this framework, the CNN serves as a spatial feature extractor, processing a BEV scene image at each timestep to produce a feature vector. This sequence of vectors is then fed into an RNN (such as LSTM or GRU), which models the temporal dynamics. TraPHic [89] exemplifies this CNN-LSTM approach, explicitly modeling spatio-temporal interactions among agents at intersections to achieve state-of-the-art results. Conversely, Deo et al. [99] proposed an alternative flow: first, an LSTM encodes each agent’s temporal dynamics, then Social Pooling aggregates these hidden states into a spatial tensor, which a CNN subsequently processes to learn high-level spatial correlations.
With advancing research, CNN applications have moved beyond 2D image processing. While 2D CNN excel at static spatial features, they cannot directly model the temporal dimension. The CNN-TP framework by Nikhil et al. [106] utilizes stacked convolutional layers to process all timesteps in parallel, efficiently modeling spatio-temporal trajectory dependencies with a lightweight and real-time structure. The work of Chaabane et al. [107] represents a leap toward modeling higher-dimensional spatio-temporal sequences. Its key innovation lies in redesigning the model’s fundamental units to simultaneously capture spatial and temporal correlations within a unified module, rather than simply stacking CNNs and RNNs.
4.3.3. Advantages and Limitations
The widespread adoption of CNNs in trajectory prediction is due to their significant advantages, particularly their highly parallelizable nature. Unlike the sequential processing of RNNs, CNNs’ convolutional operations can fully leverage modern GPU capabilities, leading to faster inference, a critical requirement for real-time autonomous driving applications. However, a fundamental limitation of CNN methods that rely on BEV images is the information loss from rasterization. The process of converting precise, continuous vectorized data—such as map details and agent coordinates—into a discrete, fixed-resolution grid inevitably discards geometric details and reduces accuracy.
4.4. GNN-Based Methods
Despite their effectiveness, CNN-based methods that rely on rasterization suffer from information loss and difficulties in modeling the explicit topological structure of roads and interactions. GNN offers a powerful alternative by natively operating on vectorized data, allowing them to explicitly model the relationships between agents and map elements as a graph. Therefore, GNNs are particularly effective for modeling the complex interactions between agents and the environment in traffic scenes, as illustrated in Figure 6 and summarized in Table 5.
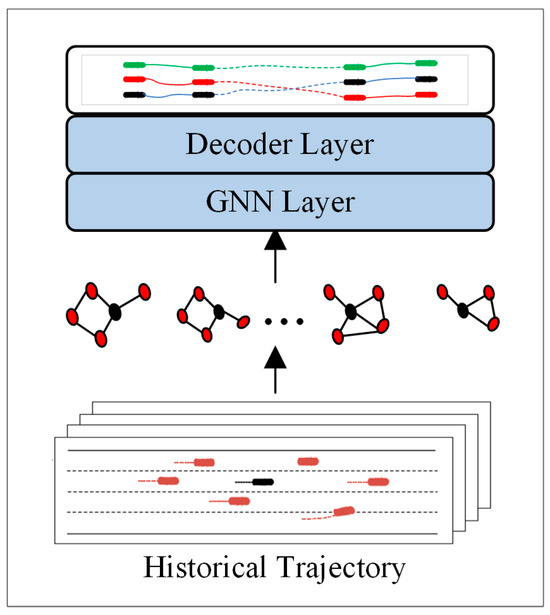
Figure 6.
GNN model trajectory prediction framework. The scene is first represented as a graph where nodes denote agents and map elements, and edges represent their relationships.

Table 5.
Summary of GNN based trajectory prediction methods.
4.4.1. Graph Representation
To apply a GNN, the traffic scene must be abstracted into a relational graph. This involves defining dynamic agents and static elements as nodes, and their complex relationships as edges. Typically, nodes represent agents like vehicles and map features like lane centerlines. This creates an “irregular graph” where edges signify distinct relationships: social interactions between agents, environmental constraints linking agents to the map, and the road network’s topology connecting map nodes. This process transforms the unstructured scene into a structured, relational network with embedded prior knowledge, enabling efficient GNN processing.
4.4.2. Mainstream Architectures
After the scene graph is constructed, the mainstream GNN architectures learn the relationships between nodes through their core message-passing mechanism. Graph Convolutional Network (GCN) and Graph Attention Networks (GAT) are two key architectures, and the main difference between them lies in how to aggregate information from neighboring nodes.
GCN is a foundational graph learning architecture that updates node representations by aggregating features from their neighbors. In trajectory prediction, the pioneering works GRIP++ [112] applied GCNs to explicitly model spatio-temporal interactions. Traffic participants are treated as nodes with edges defined by spatio-temporal proximity, allowing GCN layers to propagate interaction information. Furthermore, SCALE-Net [113] employed an Edge-enhanced GCN (EGCN) to demonstrate the architecture’s scalability and effectiveness with a varying number of agents.
GAT is a significant advancement over the GCN. It incorporates an attention mechanism, enabling the model to dynamically assign different importance weights to neighboring nodes based on the current context, rather than treating them all equally. LaneGCN [114] is a prime example of applying GAT, where it specifically constructs a lane graph from vectorized HD maps and uses GAT to learn the interaction strength between an agent and different lane lines, thereby achieving highly accurate, context-aware trajectory prediction. Similarly, in VectorNet [115], GAT is also used to aggregate information from different subgraphs to form a comprehensive understanding of the entire scene. RAGAT [116] utilizes two stacked GATs to model these distinct social forces separately, and combines them with vehicle state and free-space information for prediction.
4.4.3. Variant and Hybrid Architectures
While basic GCN and GAT architectures provide powerful tools for capturing interactions in a single spatial snapshot, the spatio-temporal and multi-modal nature of trajectory prediction necessitates more advanced models. Purely spatial modeling cannot capture dynamic evolution, and deterministic outputs fail to account for behavioral diversity. Consequently, the research frontier has shifted to complex GNN variants and hybrid architectures. Trajectron++ [117] is a prime example, constructing a scene as a heterogeneous spatio-temporal graph. It integrates GNNs and LSTMs for spatio-temporal encoding, which then conditions a CVAE to achieve precise multi-modal prediction. This “GNN encoder + RNN temporal modeling” paradigm became a state-of-the-art approach. S2TNet [118] follows a similar structure but substitutes the RNN with a Transformer, making it theoretically more effective than RNNs at capturing long-term and non-continuous dynamic patterns.
To model group behaviors beyond pairwise relationships, research has explored Hypergraph Networks. As shown in Figure 7, a standard graph edge connects only two nodes, representing a pairwise interaction. Real-world scenarios, however, often involve higher-order interactions, like multiple vehicles at an intersection. A hypergraph generalizes this concept by allowing a ‘hyperedge’ to connect any number of nodes. This provides a flexible and natural way to represent higher-order group interactions, such as the collective behavior of multiple vehicles negotiating a busy intersection or a crowd of pedestrians. For instance, Wen et al. [119] use clustering to identify agent groups and construct a hyperedge for each. A hypergraph network then learns the complex dynamics both within and between these groups, it offers a promising framework for understanding complex collective behaviors.
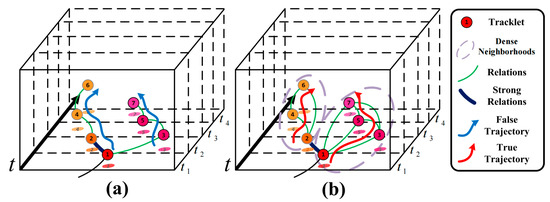
Figure 7.
(a) Standard graph. (b) Undirected hierarchical relation hypergraph. [119].
4.4.4. Advantages and Limitations
The core strengths of GNNs are their explicit relational modeling and native support for non-Euclidean data. This allows them to effectively integrate agent interactions and road topology into a deep learning framework, enhancing prediction plausibility and accuracy. In dense scenes, the resulting large graphs lead to high computational complexity from message passing, which can compromise the real-time performance required for on-board systems. Furthermore, GNNs are primarily powerful “spatial snapshot” processors and are not complete spatio-temporal solutions on their own. They typically rely on external modules like RNNs or Transformers for temporal modeling, making their handling of time indirect and separate.
4.5. Transformer-Based Methods
GNN are powerful for relational reasoning but often require additional modules (e.g., RNN) for temporal modeling and can be computationally intensive for large graphs. The Transformer architecture, with its self-attention mechanism, provides a unified and highly parallelizable framework for capturing both long-range temporal dependencies and complex spatial interactions globally. Transformer architecture has introduced a third paradigm to trajectory prediction, enabling a shift towards global modeling [120,121,122]. As illustrated in Figure 8, this allows the model to directly and simultaneously compute the association strength between any element in a sequence and all other elements, overcoming the limitations of previous architectures.
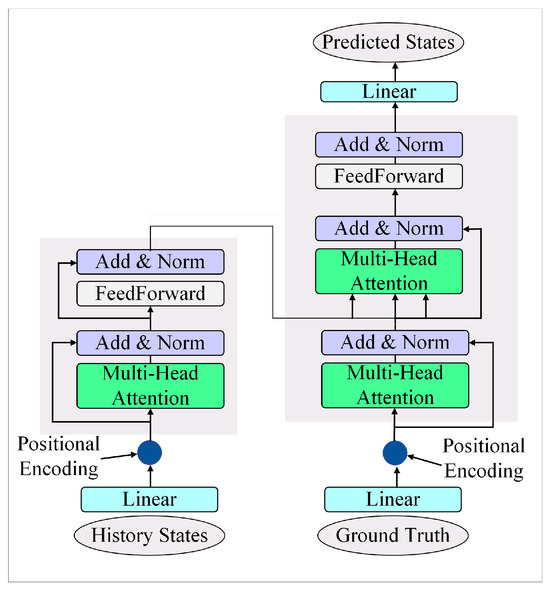
Figure 8.
Illustration of Transformer for trajectory prediction. The attention mechanism allows the model to globally contextualize all elements in the scene.
4.5.1. Self-Attention and Global Modeling
The core of Transformer-based trajectory prediction is the Self-Attention mechanism. This mechanism treats all historical trajectory and scene context information as a single set of tokens, enabling the direct and parallel computation of associations between all elements [123,124,125]. This unified process captures both long-range temporal dependencies and complex spatial interactions. To counteract the inherent permutation-invariance of self-attention, Positional Encoding is introduced to provide temporal context. This is further enhanced by Multi-Head Attention, which allows the model to learn diverse dependency relationships in parallel across different representational subspaces.
4.5.2. Representative Architectures
The power of the self-attention mechanism has catalyzed a series of advanced Transformer-based prediction models. Pioneering work by Giuliari et al. [126] employed a standard encoder–decoder Transformer to process trajectory sequences, proving that self-attention alone, without recurrent structures, could effectively capture temporal dependencies and generate plausible predictions. SceneTransformer [127] takes a holistic view, treating all dynamic and static scene elements as an unordered set of “tokens” and using a single powerful Transformer to learn all interactions end-to-end. AgentFormer [128] offers a more granular approach to social dynamics. Its core innovation is an attention mechanism that distinguishes and simultaneously models individual temporal dynamics (intra-agent attention) and multi-agent social interactions (inter-agent attention), resulting in high-quality, socially compliant predictions.
While the aforementioned models have achieved significant success in accuracy and expressiveness, they also highlight the standard Transformer’s inherent high computational complexity in large-scale scenes. To address the quadratic complexity bottleneck of the self-attention mechanism, HiVT [129] proposed a hierarchical solution. It first uses a lightweight local module to efficiently process each agent’s interaction with its immediate environment, such as its current lane. Subsequently, it employs a global attention module to capture more critical, long-range dependencies between agents. Achaji et al. [130] designed a Factorized Spatio-Temporal Attention module. This module uses separate, lightweight attention layers to efficiently process spatial interactions between agents and their own temporal dynamics independently, before fusing this information.
4.5.3. Advantages and Limitations
The Transformer architecture, while a leading methodology in trajectory prediction, presents a trade-off between its revolutionary performance and inherent challenges. Its primary advantage is superior global dependency modeling; the self-attention mechanism overcomes the limitations of RNN and CNN by capturing long-range spatiotemporal dependencies in a single computational step. This capability is critical for understanding global scene layouts and long-term driving intentions. Additionally, its highly parallelizable nature aligns perfectly with modern hardware, providing superior training efficiency and scalability over RNN. However, these strengths are accompanied by significant challenges. As a model with weak inductive bias, the Transformer requires massive and diverse training data, and its ability to generalize to out-of-distribution, long-tail scenarios is a concern.
4.6. Generative Model-Based Methods
While the aforementioned discriminative models predict a deterministic output, they often fail to capture the inherent multi-modality and uncertainty of future trajectories. To fundamentally address this, researchers have turned to generative models. Generative models address this core limitation by learning the underlying probability distribution of future motions, enabling the prediction of multiple plausible outcomes. The objective of these models is not to predict a single correct answer but to learn and fit the underlying probability distribution of the training data. This provides the autonomous driving system with a complete, probabilistic, and multi-faceted view of the future. The three most prominent generative models in trajectory prediction are GAN, CVAE, and Diffusion Models, with representative works summarized in Table 6.

Table 6.
Summary of reviewed DL-based models reloading on Generative Model Methods.
4.6.1. Generative Adversarial Networks
GAN learns data distributions through a sophisticated “two-player zero-sum game” framework. In trajectory prediction, the Generator creates synthetic future trajectories from historical and scene context, while the Discriminator learns to distinguish these fakes from real data. This adversarial process compels the Generator to master the complex dynamics and constraints of real trajectories, enabling it to produce highly realistic and diverse multi-modal outputs.
The pioneering work, Social-GAN [131], first applied this framework to interaction-aware pedestrian prediction. It combined LSTM-based encoders with a Social Pooling mechanism, demonstrating the potential of GANs to generate socially compliant trajectories. Subsequent research has built upon this foundation; for instance, SoPhie [132] introduced an attention mechanism for more refined constraint modeling, while MATF-GAN [133] tackled more complex vehicle interactions through multi-agent tensor fusion, further enhancing the model’s expressive power.
4.6.2. Conditional Variational Autoencoder
CVAE provides a stable, probabilistic alternative to adversarial training for generating diverse future trajectories. Instead of the competitive framework of GAN, a CVAE learns a low-dimensional, structured latent space designed to capture unobservable factors like intent or goals that drive behavioral diversity. Its classic encoder–decoder architecture functions by first having the encoder map historical trajectories to a probability distribution, typically a Gaussian, in the latent space. The decoder then samples from this latent space. This sampled latent vector, combined with the encoded historical information, is used to generate a specific future trajectory. By repeatedly sampling from this latent space, a CVAE can produce a variety of distinct, conditioned future paths.
DESIRE [134] is a classic application of the CVAE framework. It uses CVAE to generate multiple initial trajectory hypotheses and introduces a sophisticated scoring module to select the final prediction. The highly influential Trajectron++ [117] seamlessly combines CVAE with an advanced GNN encoder. It leverages the GNN to capture complex spatio-temporal interactions and then conditions the CVAE on this rich contextual information to model the uncertainty of future trajectories in the latent space.
4.6.3. Diffusion Models
Diffusion Models represent the latest and most powerful wave in generative modeling [137], their success in fields like image generation having inspired their application to trajectory prediction. The model’s principle involves two stages: a fixed Forward Process and a learnable Reverse Process. In the forward process, Gaussian noise is iteratively added to real trajectory data until it becomes pure noise. The reverse process involves training a denoising network, typically a Transformer, to reverse these steps. For inference, the model begins with pure noise and repeatedly applies the learned denoising network to generate a new, high-quality future trajectory.
Due to their iterative generation process and powerful modeling capabilities, diffusion models generally outperform GAN and CVAE in terms of the quality and diversity of the generated trajectories. MotionDiffuser [135] utilizes a Transformer-based denoiser to capture complex spatio-temporal dependencies and introduces various guidance mechanisms to ensure the physical plausibility and goal-orientation of the generated trajectories. Yuan et al. [136] directly embed kinematic or dynamic models into the iterative denoising process of the diffusion model. This approach fundamentally eliminates physical artifacts and ensures the dynamic feasibility of every generated trajectory.
4.6.4. Advantages and Limitations
The primary advantage of generative models is their inherent ability to model the multi-modal uncertainty of trajectory prediction, producing a probabilistic view of the future that is crucial for safe downstream planning. However, this expressive power comes with specific challenges for each paradigm: GAN can generate sharp, realistic trajectories, but their adversarial training is notoriously unstable, prone to mode collapse and divergence, and requires careful tuning. CVAE offer stable training and a robust probabilistic framework, but their outputs can be overly smooth. Diffusion Models typically produce the highest quality and most diverse samples, but their iterative denoising process results in very slow inference speeds. Furthermore, objectively assessing the quality of a predicted distribution, rather than a single trajectory’s error, remains an open research problem.
5. Evaluation
5.1. Datasets
To assess the accuracy of an autonomous driving trajectory prediction model, the predicted trajectory is typically compared to the real trajectory. The trajectory data comes from multiple public datasets collected by sensors such as LiDAR, cameras, radar, etc. In recent years, modern benchmark datasets have made significant progress in the field of autonomous driving trajectory prediction, overcoming the limitations of earlier datasets in environmental and traffic participant categories, such as NGSIM-180 and highD datasets that capture vehicle motion on highways using drones and surveillance cameras, focusing primarily on a single type of traffic participant whose possible actions include turning left, turning right, and keeping straight.
As AI model complexity increases, more image data is needed to achieve efficient generalization [138,139,140]. The vehicle-centric dataset and the pedestrian/hybrid centric dataset not only contain camera and lidar data, but also provide high-precision (HD) maps for capturing the topology of the road. Compared to earlier datasets, these datasets cover more categories, record mileage data for own vehicles, cover multiple cities, different weather and lighting conditions (including rain and night), and provide labels for other traffic participants such as traffic lights and road rules.
Vehicle-centric datasets focus on vehicle trajectory prediction. These datasets usually contain rich vehicle motion information and are suitable for studying vehicle interactions and vehicle relationships with road environments [141,142]. Pedestrian/mix-centric datasets focus not only on vehicle trajectories, but also on pedestrian trajectories and interactions with other traffic participants [96]. These datasets are of great significance for studying trajectory prediction in multimodal traffic environment. Table 7 provides detailed information about the commonly used datasets in the existing research.

Table 7.
Commonly used datasets.
5.2. Evaluation Index
The evaluation index of trajectory prediction of automatic driving is the key to measuring the performance of the model. These indexes evaluate the accuracy, reliability, efficiency and practicability of the model from different angles. According to the characteristics of trajectory prediction task, the evaluation indicators are divided into modal, multimodal, probability/uncertainty, cross-correlation and computational efficiency indicators.
- Monomodal
ADE is the average Euclidean distance between the predicted trajectory and the true trajectory at each time step and measures the average error of the model over the entire prediction time range. This can be mathematically formulated as:
FDE is the Euclidean distance between the final position of the predicted trajectory and the final position of the true trajectory, focusing on the accuracy of the model at the predicted endpoint. This can be mathematically formulated as:
- 2.
- Multimoding
minADE is the ADE that selects the trajectory with the smallest error from the true trajectory among the k predicted trajectories generated by the model, and measures the average error of the best trajectory of the model in multimodal prediction. This can be mathematically formulated as:
minFDE is the FDE that selects the trajectory with the smallest error from the true trajectory from the k predicted trajectories generated by the model, focusing on the endpoint error of the best trajectory of the model in multimodal prediction. This can be mathematically formulated as:
Miss Rate measures the proportion of k predicted trajectories generated by the model that differ from the true trajectory by more than a certain threshold. This can be mathematically formulated as:
Overlap Rate measures the degree of overlap between multiple prediction trajectories generated by the model and is used to assess the diversity of the model in multimodal prediction. This can be mathematically formulated as:
- 3.
- Probability/uncertainty index
NLL measures how well the model-predicted trajectory distribution matches the true trajectory, with a lower NLL indicating that the model-predicted distribution is closer to the true distribution. This can be mathematically formulated as:
The Brier Score measures the difference between the probability of the model prediction and the true result, with a lower Brier Score indicating that the probability of the model prediction is more accurate. This can be mathematically formulated as:
ECE measures how well the model predicts probability, with lower ECE indicating more reliable model predictions.
AURC measures the risk coverage ability of a model at different confidence thresholds, with a higher AURC indicating that the model covers the true trajectory better at high confidence.
6. Challenges and Outlook
6.1. Challenges
- Complex Interactions Among Traffic Participants
Self-driving vehicles and other vehicles on the road will have behaviors such as following, overtaking, lane change and merging, forming vehicle-vehicle interaction. In the multi-vehicle interaction scene, the dynamic information such as relative position, velocity and acceleration between vehicles changes constantly, and the interaction relationship between vehicles is complex. For example, in the intersection, highway ramp junction and other scenes, vehicles need to consider multiple directions at the same time, predicting the intention and trajectory of other vehicles is difficult. The dynamic nature of traffic environment makes the interaction between vehicles full of uncertainty. For example, sudden lane changes, acceleration or deceleration are difficult to predict accurately in advance. Pedestrians may cross the road without a clear signal, or change direction at an intersection. These behaviors form vehicle-pedestrian interactions and increase the difficulty of trajectory prediction.
- 2.
- Strong Reliance on Traffic Rules and High-Precision Maps
Traffic rules set clear boundaries and priorities for the trajectory planning of autonomous vehicles, but traffic rules are not static, and the rule differences in different regions and scenarios increase the complexity of trajectory prediction. Autonomous driving systems need to understand the semantics of traffic rules, which requires a combination of computer vision technology and natural language processing technology to ensure that rule information is accurately integrated into the trajectory prediction model.
High-precision maps provide detailed lane information, traffic location, road slope, curvature and other data, which are crucial for accurate trajectory prediction. At the same time, high-precision maps need to be updated in real time to reflect dynamic changes such as road construction and accidents, so the fusion of high-precision maps and vehicle perception systems is the key to trajectory prediction.
- 3.
- Cumulative Error and Behavioral Uncertainty in Long-Term Prediction
Automatic driving needs to predict the trajectories of surrounding vehicles and pedestrians in the future. Many prediction models are based on simplified traffic flow assumptions. In long-term prediction, deviations from these assumptions and actual situations will gradually accumulate. The intentions and interaction behaviors of traffic participants have multimodal characteristics. Traditional deterministic prediction is difficult to cover all possible scenarios and accurately capture future states, resulting in error accumulation. At the same time, the uncertainty of driving behavior will be further amplified in long-term prediction, resulting in deviation of prediction results. In complex traffic scenes, the interaction behavior of vehicles is more complex, which increases the uncertainty of behavior.
- 4.
- Generalization Ability for Corner Cases
Although many autonomous driving trajectory prediction models have made some progress in common scenarios, their generalization ability still faces many challenges in rare scenarios. Rare scenarios are those that occur less frequently in real driving but may have a significant impact on driving safety, such as road ponding in extreme weather conditions, abnormal stops caused by sudden vehicle failures, and the appearance of non-standard traffic signs or gestures.
Existing models tend to learn common patterns in training data and lack sufficient capture power for rare scenarios. In order to improve the generalization ability of the model in rare scenarios, the researchers collected a large amount of rich and diverse driving data to enable the model to learn various possible scene features and patterns, thus improving the adaptability to rare scenarios. However, collecting data covering all possible rare scenarios is unrealistic because actual driving scenarios have extremely high complexity and uncertainty. There is also the use of techniques such as GAN to generate rare scene data, which helps the model learn the characteristics and distribution of rare scenes and improve its prediction ability in these scenarios, but the quality and authenticity of the generated data is still a problem to be solved.
- 5.
- Real-Time Requirements and Computational Efficiency
Real-time performance and computational efficiency are the key factors to ensure vehicle safety and efficiency in automatic driving trajectory prediction. Real-time means that the trajectory prediction model can complete the prediction of the future trajectory of the surrounding traffic participants in a very short time, and computational efficiency refers to the ability of the model to complete the calculation task quickly and efficiently under the limited hardware resources. However, there is a contradiction between the real-time requirement of trajectory prediction and the limitation of computational resources. On the one hand, trajectory prediction must be completed in a very short time to ensure vehicle safety and driving efficiency; on the other hand, there is a significant conflict between the computational complexity of high-precision models and limited hardware resources.
6.2. Future Research Directions
The future research directions are proposed to directly address the core challenges outlined in Section 6.1. The mapping between these challenges and directions is summarized in Table 8, which provides a structured overview of the proposed solutions. Each direction is then elaborated in detail below, with discussions on specific technical pathways and current limitations.

Table 8.
Mapping between Challenges and Future Research Directions.
- Interactive Game Theory and Embodied Intelligence
Current interaction modeling mostly relies on data-driven implicit learning (such as GNN), lacking explicit descriptions of game decisions. In the future, it is necessary to combine multi-agent reinforcement learning (MARL) with cognitive theory to construct interpretable interaction models. For example, a hierarchical game-theoretic framework can be designed: the upper level utilizes inverse reinforcement learning (IRL) or Bayesian inference to reason about the intentions and rewards of other vehicles; the lower level then employs multi-agent reinforcement learning (MARL) or model predictive control (MPC) to optimize collaborative and competitive strategies in real-time [143]. This creates a closed loop of “perception-intention reasoning-decision-prediction”.
Additionally, embodied intelligence (Embodied AI) can be introduced, where the predictive model is not just a passive observer but is integrated with a vehicle dynamics model and perception simulator. This allows the model to understand the physical constraints and consequences of actions through interaction and simulation, leading to more physically plausible and causal predictions.
The primary application of this direction is in the development of more transparent and trustworthy autonomous vehicles (AVs), particularly in unstructured and complex scenarios. This can significantly reduce ambiguous situations and improve traffic flow efficiency and safety in urban environments.
- 2.
- Reduction and Dynamic Fusion of High-Precision Maps
To reduce reliance on static high-precision maps, real-time map construction technology needs to be developed. By integrating vehicle sensors and Vehicle-to-Everything (V2X) communication, the road topology can be dynamically updated. Vehicles and roadside units (RSUs) can share their locally perceived BEV map snippets or detected objects with each other [144]. By fusing these distributed perceptions, a vehicle can obtain a collective field view that extends far beyond its own sensor range. Crowdsourced mapping can aggregate and update map changes detected by fleets of vehicles into a cloud-based dynamic map service, enabling continuous, automated map updates. Furthermore, a no map prediction paradigm should be further developed. Using the visual-language model (VLM), the semantic of traffic rules can be parsed, and rule embedding vectors can be generated to replace the traditional map input.
The practical value of significantly reducing reliance on expensive and hard-to-maintain high-definition maps is huge. AVs could operate seamlessly in suburban, rural, or newly constructed areas where HD maps are unavailable. The real-time map building and V2X fusion allow AVs to adapt immediately without waiting for map updates, thus enhancing the robustness and geographical scalability of autonomous driving services.
- 3.
- Closed-Loop Error Correction for Long-Term Prediction
To address the issue of error accumulation, a neural-symbolic hybrid system can be constructed in conjunction with the World Models to simulate the dynamic evolution of traffic scenarios. For example, The NEST model [145] combines Small-world Networks with Hypergraphs and introduces neuromodulators, aiming to efficiently and accurately capture the intricate relationships among traffic participants, and is particularly suitable for high-density urban environments. Moreover, a closed-loop prediction framework can be established, where the prediction results are fed back to the planning module, and the trajectory deviations are corrected through online re-planning.
This capability is crucial for high-speed planning and safety assurance on highways and in complex urban corridors. By continuously correcting predictions against a simulated reality, the vehicle can anticipate and avoid potential “edge cases” before they become critical. For example, when a predicted trajectory of a nearby vehicle increasingly conflicts with the ego vehicle’s plan over a 5 s horizon, the system can proactively initiate a smooth and early lane change or deceleration, moving from reactive collision avoidance to proactive risk mitigation, thereby greatly enhancing passenger comfort and safety.
- 4.
- Causal Reasoning and Simulation Migration
To enhance the generalization ability in long-tail scenarios, causal intervention models can be employed. Beyond correlation, we need to model the causal effect of scene changes on agent behavior. Techniques such as counterfactual analysis and causal generative models can be used to generate ‘what-if’ trajectory samples This helps the model learn the true causal mechanisms behind behaviors rather than just statistical associations.
Furthermore, advanced generative models (such as Diffusion Models) can be utilized to synthesize high-fidelity, diverse rare scene data. The key is to achieve unsupervised domain adaptation or sim-to-real transfer. This can be performed by training the generative model on a mixture of real and simulated data, using techniques like domain adversarial training to minimize the distribution gap between synthetic and real-world data. This creates a virtuous cycle where the model improves by learning from its own generated challenging scenarios.
The most direct application is in drastically improving the performance and safety of AVs in rare but critical “corner cases”. By training on causally generated synthetic data, the AV system can obtain more robust and generalized performance. This reduces the need for driving billions of miles to collect rare events naturally, accelerating the validation process and bringing safer autonomous vehicles to market faster.
- 5.
- Lightweight Architecture and Hardware Co-Design
The contradiction between real-time requirements and computational complexity necessitates a system-level approach. Algorithmic innovations are crucial and mainly includes the following three aspects.
Model Compression & Quantization: Techniques like knowledge distillation can be used to train small, efficient ‘student’ models from large, accurate ‘teacher’ models. Post-training quantization can reduce the precision of network weights and activations, reduce memory footprint and accelerate inference on supported hardware. Dynamic Inference: A hierarchical prediction system can be implemented where simple scenarios trigger efficient physical models or tiny neural networks, while complex scenarios switch to more computationally intensive deep learning models. Hardware Co-design: Designing dedicated AI accelerators is key. This involves software-hardware co-optimization, where the neural network architecture is designed in tandem with the hardware architecture. For example, optimizing the memory access patterns and computational parallelism of the self-attention mechanism to fit the specific computed fabric of an FPGA can yield significant latency and power efficiency gains.
This direction is fundamental to making advanced AI models feasible for mass production vehicles, where cost, power consumption, and computational resources are severely constrained. Deploying a lightweight prediction model on an efficient FPGA enables real-time decision-making on low-power, automotive-grade hardware. This translates directly to more affordable and energy-efficient autonomous driving systems for consumer vehicles.
7. Conclusions
This comprehensive review has systematically analyzed the evolution of trajectory prediction methods for autonomous driving, spanning from conventional physics-based models to cutting-edge deep learning architectures. We established a novel multidimensional classification framework integrating sensing paradigms, interaction modeling, and output characteristics, while critically evaluating performance across benchmark datasets using standardized metrics. The in-depth examination of five core challenges—including interaction complexity under dense scenarios, HD map dependency, and long-term uncertainty propagation—reveals fundamental limitations in current methods. By proposing cross-disciplinary solutions such as embodied cognition-enhanced prediction and V2X-coordinated frameworks, this survey not only consolidates the state-of-the-art but also provides a structured roadmap for developing robust, safety-compliant prediction systems essential for L4/L5 autonomy.
Author Contributions
Conceptualization, M.X.; methodology, M.X.; investigation, Z.L.; resources, S.L. and B.W.; writing—original draft preparation, Z.L., S.L., B.W. and M.X.; writing—review and editing, M.X.; funding acquisition, M.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the China Postdoctoral Science Foundation, grant number 2024M761190.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bharilya, V.; Kumar, N. Machine learning for autonomous vehicle’s trajectory prediction: A comprehensive survey, challenges, and future research directions. Veh. Commun. 2024, 46, 100733. [Google Scholar] [CrossRef]
- Madjid, N.A.; Ahmad, A.; Mebrahtu, M.; Babaa, Y.; Nasser, A.; Malik, S.; Hassan, B.; Werghi, N.; Dias, J.; Khonji, M. Trajectory prediction for autonomous driving: Progress, limitations, and future directions. arXiv 2025, arXiv:2503.03262. [Google Scholar] [CrossRef]
- Zhang, S.; Bai, R.; He, R.; Meng, Z.; Chang, Y.; Zhi, Y.; Sun, N. Research on vehicle trajectory prediction methods in urban main road scenarios. IEEE Trans. Intell. Transp. Syst. 2024, 25, 16392–16408. [Google Scholar] [CrossRef]
- Chen, T.; Xu, L.; Ahn, H.S.; Lu, E.; Liu, Y.; Xu, R. Evaluation of headland turning types of adjacent parallel paths for combine harvesters. Biosyst. Eng. 2023, 233, 93–113. [Google Scholar] [CrossRef]
- Jiang, J.; Yan, K.; Xia, X.; Yang, B. A survey of deep learning-based pedestrian trajectory prediction: Challenges and solutions. Sensors 2025, 25, 957. [Google Scholar] [CrossRef]
- Chen, C.; Cao, G.-Q.; Zhang, J.-L.; Hu, J.-P. Dynamic monitoring of harvester working progress based on traveling trajectory and header status. Eng. Agrícola 2023, 43, e20220196. [Google Scholar] [CrossRef]
- Li, J.; Wu, Z.; Li, M.; Shang, Z. Dynamic measurement method for steering wheel angle of autonomous agricultural vehicles. Agric. Basel 2024, 14, 1602. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, B.; Shen, C.; Liu, H.; Huang, J.; Tian, K.; Tang, Z. Review of the field environmental sensing methods based on multi-sensor information fusion technology. Int. J. Agric. Biol. Eng. 2024, 17, 1–13. [Google Scholar]
- Liu, W.; Hu, J.-P.; Liu, J.-X.; Yue, R.-C.; Zhang, T.-F.; Yao, M.-J.; Li, J. Method for the navigation line recognition of the ridge without crops via machine vision. Int. J. Agric. Biol. Eng. 2024, 17, 230–239. [Google Scholar] [CrossRef]
- Lu, Y.F.; Li, X.P.; Xue, Q.F. Vehicle trajectory prediction model for unknown domain scenarios. CAAI Trans. Intell. Syst. 2024, 19, 1238–1247. [Google Scholar]
- Ahmed, S.; Qiu, B.; Ahmad, F.; Kong, C.W.; Xin, H. A state-of-the-art analysis of obstacle avoidance methods from the perspective of an agricultural sprayer UAV’s operation scenario. Agronomy 2021, 11, 1069. [Google Scholar] [CrossRef]
- Chauhdary, J.N.; Li, H.; Akbar, N.; Javaid, M.; Rizwan, M.; Akhlaq, M. Evaluating corn production under different plant spacings through integrated modeling approach and simulating its future response under climate change scenarios. Agric. Water Manag. 2024, 293, 108691. [Google Scholar] [CrossRef]
- Jing, L.; Yu, R.; Chen, X.; Zhao, Z.L.; Sheng, S.W.; Graber, C.; Chen, Q.; Li, Q.R.; Wu, S.X.; Deng, H.; et al. STT: Stateful tracking with transformers for autonomous driving. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; IEEE: Piscataway, NJ, USA; pp. 4442–4449. [Google Scholar]
- Lu, E.; Ma, Z.; Li, Y.; Xu, L.; Tang, Z. Adaptive backstepping control of tracked robot running trajectory based on real-time slip parameter estimation. Int. J. Agric. Biol. Eng. 2020, 13, 178–187. [Google Scholar] [CrossRef]
- Mo, X.; Liu, H.; Huang, Z.; Li, X.; Lv, C. Map-adaptive multimodal trajectory prediction via intention-aware unimodal trajectory predictors. IEEE Trans. Intell. Transp. Syst. 2023, 25, 5651–5663. [Google Scholar] [CrossRef]
- Lu, E.; Xue, J.; Chen, T.; Jiang, S. Robust trajectory tracking control of an autonomous tractor-trailer considering model parameter uncertainties and disturbances. Agriculture 2023, 13, 869. [Google Scholar] [CrossRef]
- Buhet, T.; Wirbel, E.; Bursuc, A.; Perrotton, X. Plop: Probabilistic polynomial objects trajectory prediction for autonomous driving. IEEE Trans. Intell. Transp. Syst. 2021, 22, 2823–2834. [Google Scholar]
- Cao, H.; Zoldy, M. Implementing B-spline path planning method based on roundabout geometry elements. IEEE Access 2022, 10, 81434–81446. [Google Scholar] [CrossRef]
- Johnson, A.; Smith, B. Real-time path planning for obstacle avoidance in intelligent driving sightseeing cars using spatial perception. IEEE Trans. Intelli. Veh. 2023, 8, 567–580. [Google Scholar]
- Schreiber, M.; Hoermann, S.; Dietmayer, K. Long-term occupancy grid prediction using recurrent neural networks. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 9299–9304. [Google Scholar]
- Zeng, W.; Luo, W.; Suo, S.; Sadat, A.; Yang, B.; Casas, S.; Urtasun, R. End-to-end interpretable neural motion planner. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Liu, H.; Yan, S.; Shen, Y.; Li, C.; Zhang, Y.; Hussain, F. Model Predictive Control System Based on Direct Yaw Moment Control for 4WID Self-Steering Agriculture Vehicle. Int. J. Agric. Biol. Eng. 2021, 14, 175–181. [Google Scholar] [CrossRef]
- Feng, Y.Y.; Yan, X.L. Support vector machine based lane changing behavior recognition and lateral trajectory prediction. Comp. Intell. Neurosci. 2022, 2022, 36362333. [Google Scholar] [CrossRef]
- Han, L.; Mao, H.; Kumi, F.; Hu, J. Development of a multi-task robotic transplanting workcell for greenhouse seedlings. Appl. Eng. Agric. 2018, 34, 335–342. [Google Scholar] [CrossRef]
- Sun, S.; Zhao, C.; Sun, Z.; Chen, Y.V.; Chen, M. SplatFlow: Self-supervised dynamic gaussian splatting in neural motion flow field for autonomous driving. In Proceedings of the Computer Vision and Pattern Recognition Conference (CVPR), Nashville TN, USA, 11–15 June 2025; pp. 27487–27496. [Google Scholar]
- Xing, Z.; Zhang, X.; Hu, Y.; Jiang, B.; He, T.; Zhang, Q.; Long, X.X.; Wei, Y. Goalflow: Goal-driven flow matching for multimodal trajectories generation in end-to-end autonomous driving. In Proceedings of the Computer Vision and Pattern Recognition Conference (CVPR), Nashville TN, USA, 11–15 June 2025; pp. 1602–1611. [Google Scholar]
- Luo, L.; Liu, X.; Ma, S.; Li, L.; You, T. Quantification of zearalenone in mildewing cereal crops using an innovative photoelectrochemical aptamer sensing strategy based on ZnO-NGQDs composites. Food Chem. 2020, 322, 126778. [Google Scholar] [CrossRef] [PubMed]
- Shen, G.; Cao, Y.; Yin, X.; Dong, F.; Xu, J.; Shi, J.; Lee, Y.W. Rapid and nondestructive quantification of deoxynivalenol in individual wheat kernels using near-infrared hyperspectral imaging and chemometrics. Food Control 2022, 131, 108420. [Google Scholar] [CrossRef]
- Yoon, Y.; Kim, C.; Lee, J.; Yi, K. Interaction-aware probabilistic trajectory prediction of cut-in vehicles using Gaussian process for proactive control of autonomous vehicles. IEEE Access 2021, 9, 63440–63455. [Google Scholar] [CrossRef]
- Mao, W.; Xu, C.; Zhu, Q.; Chen, S.; Wang, Y. Leapfrog diffusion model for stochastic trajectory prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023. [Google Scholar]
- Choi, J.; Kim, B.; Kim, H. Trajectory generation for autonomous vehicles using generative adversarial imitation learning. IEEE Trans. Intell. Transp. Syst. 2020, 21, 4684–4695. [Google Scholar]
- Hu, D.; Sun, T.; Yao, L.; Yang, Z.; Wang, A.; Ying, Y. Monte Carlo: A flexible and accurate technique for modeling light transport in food and agricultural products. Trends Food Sci. Techn. 2020, 102, 280–290. [Google Scholar] [CrossRef]
- Li, G.P.; Li, Z.R.; Knoop, V.L.; van Lint, H. Unravelling uncertainty in trajectory prediction using a non-parametric approach. Transp. Res. Part C Emerg. Technol. 2024, 163, 104659. [Google Scholar] [CrossRef]
- Yang, H.B.; Wang, Z.Y.; Xu, M.; Yang, D.P.; Zhao, Z.F. Improved deep transfer learning and transmission error based method for gearbox fault diagnosis with limited test samples. Mech. Syst. Sig. Process. 2025, 230, 112593. [Google Scholar] [CrossRef]
- Zhang, W.; Luo, Z.; Wang, A.; Gu, X.; Lv, Z. Kinetic models applied to quality change and shelf life prediction of kiwifruits. LWT 2021, 138, 110610. [Google Scholar] [CrossRef]
- Soni, D.; Kumar, N. Machine learning techniques in emerging cloud computing integrated paradigms: A survey and taxonomy. J. Netw. Comput. Appl. 2022, 205, 103419. [Google Scholar] [CrossRef]
- Xin, L.; Wang, P.; Chan, C.Y.; Chen, J.; Li, S.E.; Cheng, B. Intention-aware long horizon trajectory prediction of surrounding vehicles using dual LSTM networks. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 1441–1446. [Google Scholar]
- Zhao, S.E.; Su, T.B.; Zhao, D.Y. Interactive Vehicle Driving Intention Recognition and Trajectory Prediction Based on Graph Neural Network. Automob. Technol. 2023, 7, 24–30. [Google Scholar]
- Zhang, R.; Cao, L.; Bao, S.; Tan, J. A method for connected vehicle trajectory prediction and collision warning algorithm based on v2v communication. Int. J. Crash Worthiness 2017, 22, 15–25. [Google Scholar] [CrossRef]
- Lefkopoulos, V.; Menner, M.; Domahidi, A.; Zeilinger, M.N. Interaction-aware motion prediction for autonomous driving: A multiple model Kalman filtering scheme. IEEE Robot. Autom. Lett. 2020, 6, 80–87. [Google Scholar] [CrossRef]
- Brännström, M.; Coelingh, E.; Sjöberg, J. Model-based threat assessment for avoiding arbitrary vehicle collisions. IEEE Trans. Intell. Transp. Syst. 2010, 11, 658–669. [Google Scholar] [CrossRef]
- Lytrivis, P.; Thomaidis, G.; Amditis, A. Cooperative path prediction in vehicular environments. In Proceedings of the 2008 11th International IEEE Conference on Intelligent Transportation Systems, Beijing, China, 12–15 October 2008; IEEE: Piscataway, NJ, USA; pp. 803–808. [Google Scholar]
- Lin, C.F.; Ulsoy, A.G.; LeBlanc, D.J. Vehicle dynamics and external disturbance estimation for vehicle path prediction. IEEE Trans. Control Syst. Technol. 2000, 8, 508–518. [Google Scholar]
- Barth, A.; Franke, U. Where will the oncoming vehicle be the next second? In Proceedings of the 2008 IEEE Intelligent Vehicles Symposium, Eindhoven, The Netherlands, 4–6 June 2008; IEEE: Piscataway, NJ, USA; pp. 1068–1073. [Google Scholar]
- Batz, T.; Watson, K.; Beyerer, J. Recognition of dangerous situations within a cooperative group of vehicles. In Proceedings of the 2009 IEEE Intelligent Vehicles Symposium, Xi’an, China, 3–5 June 2009; IEEE: Piscataway, NJ, USA; pp. 907–912. [Google Scholar]
- Ammoun, S.; Nashashibi, F. Real time trajectory prediction for collision risk estimation between vehicles. In Proceedings of the 2009 IEEE 5th International Conference on Intelligent Computer Communication and Processing (ICCP), Cluj-Napoca, Romania, 27–29 August 2009; IEEE: Piscataway, NJ, USA; pp. 417–422. [Google Scholar]
- Schubert, R.; Richter, E.; Wanielik, G. Comparison and evaluation of advanced motion models for vehicle tracking. In Proceedings of the 2008 11th International Conference on Information Fusion, Cologne, Germany, 30 June–3 July 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1–6. [Google Scholar]
- Polychronopoulos, A.; Tsogas, M.; Amditis, A.J.; Andreone, L. Sensor fusion for predicting vehicles’ path for collision avoidance systems. IEEE Trans. Intell. Transp. Syst. 2007, 8, 549–562. [Google Scholar] [CrossRef]
- Houenou, A.; Bonnifait, P.; Cherfaoui, V.; Yao, W. Vehicle trajectory prediction based on motion model and maneuver recognition. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; IEEE: Piscataway, NJ, USA; pp. 4363–4369. [Google Scholar]
- Tran, Q.; Firl, J. Online maneuver recognition and multimodal trajectory prediction for intersection assistance using non-parametric regression. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium, Dearborn, MI, USA, 8–11 June 2014; IEEE: Piscataway, NJ, USA; pp. 918–923. [Google Scholar]
- Wissing, C.; Nattermann, T.; Glander, K.H.; Bertram, T. Interaction-aware long-term driving situation prediction. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; IEEE: Piscataway, NJ, USA; pp. 137–143. [Google Scholar]
- Okamoto, K.; Berntorp, K.; Di Cairano, S. Driver intention-based vehicle threat assessment using random forests and particle filtering. IFAC Pap. OnLine 2017, 50, 13860–13865. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.; Zuo, Z.; Li, Z.; Wang, L.; Luo, X. Trajectory planning and safety assessment of autonomous vehicles based on motion prediction and model predictive control. IEEE Trans. Veh. Technol. 2019, 68, 8546–8556. [Google Scholar] [CrossRef]
- Wang, B.; Deng, J.; Jiang, H. Markov transition field combined with convolutional neural network improved the predictive performance of near-infrared spectroscopy models for determination of aflatoxin B1 in maize. Foods 2022, 11, 2210. [Google Scholar] [CrossRef]
- Albeaik, S.; Bayen, A.; Chiri, M.T.; Gong, X.; Hayat, A.; Kardous, N.; Keimer, A.; McQuade, S.T.; Piccoli, B.; You, Y. Limitations and improvements of the intelligent driver model (IDM). SIAM J. Appl. Dyn. Syst. 2022, 21, 1862–1892. [Google Scholar] [CrossRef]
- Qiao, S.; Shen, D.; Wang, X.; Han, N.; Zhu, W. A self-adaptive parameter selection trajectory prediction approach via hidden Markov models. IEEE Trans. Intell. Transp.Syst. 2014, 16, 284–296. [Google Scholar] [CrossRef]
- Deng, Q.; Söffker, D. Improved driving behaviors prediction based on fuzzy logic-hidden Markov model (FL-HMM). In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; IEEE: Piscataway, NJ, USA; pp. 2003–2008. [Google Scholar]
- Wang, Y.; Wang, C.; Zhao, W.; Xu, C. Decision-making and planning method for autonomous vehicles based on motivation and risk assessment. IEEE Trans. Veh. Technol. 2021, 70, 107–120. [Google Scholar] [CrossRef]
- Gindele, T.; Brechtel, S.; Dillmann, R. Learning driver behavior models from traffic observations for decision making and planning. IEEE Intell. Transp. Syst. Mag. 2015, 7, 69–79. [Google Scholar] [CrossRef]
- He, G.; Li, X.; Lv, Y.; Gao, B.; Chen, H. Probabilistic intention prediction and trajectory generation based on dynamic Bayesian networks. In Proceedings of the 2019 Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019; IEEE: Piscataway, NJ, USA; pp. 2646–2651. [Google Scholar]
- Murphy, K.P. Dynamic Bayesian Networks: Representation, Inference and Learning. Ph.D. Thesis, University of California, Berkeley, CA, USA, 2002. [Google Scholar]
- Schreier, M.; Willert, V.; Adamy, J. An integrated approach to maneuver-based trajectory prediction and criticality assessment in arbitrary road environments. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2751–2766. [Google Scholar] [CrossRef]
- Li, J.; Dai, B.; Li, X.; Xu, X.; Liu, D. A dynamic Bayesian network for vehicle maneuver prediction in highway driving scenarios: Framework and verification. Electronics 2019, 8, 40. [Google Scholar] [CrossRef]
- Laugier, C.; Paromtchik, I.E.; Perrollaz, M.; Yong, M.; Yoder, J.-D.; Tay, C.; Mekhnacha, K.; Nègre, A. Probabilistic analysis of dynamic scenes and collision risks assessment to improve driving safety. IEEE Intell. Transp. Syst. Mag. 2011, 3, 4–19. [Google Scholar] [CrossRef]
- Guo, Y.; Kalidindi, V.V.; Arief, M.; Wang, W.; Zhu, J.; Peng, H.; Zhao, D. Modeling multi-vehicle interaction scenarios using Gaussian random field. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; IEEE: Piscataway, NJ, USA; pp. 3974–3980. [Google Scholar]
- Dabbour, M.; He, R.; Mintah, B.; Tang, Y.; Ma, H. Ultrasound assisted enzymolysis of sunflower meal protein: Kinetics and thermodynamics modeling. J. Food Proc. Eng. 2018, 41, e12865. [Google Scholar] [CrossRef]
- Sun, J.; Shi, J.; Mu, Y.; Zhou, S.; Chen, Z.; Xu, B. Subcritical butane extraction of oil and minor bioactive components from soybean germ: Determination of migration patterns and a kinetic model. J. Food Proc. Eng. 2018, 41, e12697. [Google Scholar] [CrossRef]
- Ouyang, Q.; Fan, Z.; Chang, H.; Shoaib, M.; Chen, Q. Analyzing TVB-N in snakehead by Bayesian-optimized 1D-CNN using molecular vibrational spectroscopic techniques: Near-infrared and Raman spectroscopy. Food Chem. 2025, 464, 141701. [Google Scholar] [CrossRef]
- Zhou, X.; Sun, J.; Tian, Y.; Lu, B.; Hang, Y.; Chen, Q. Hyperspectral technique combined with deep learning algorithm for detection of compound heavy metals in lettuce. Food Chem. 2020, 321, 126503. [Google Scholar] [CrossRef]
- Chen, C.; Zhu, W.; Steibel, J.; Siegford, J.; Han, J.; Norton, T. Classification of drinking and drinker-playing in pigs by a video-based deep learning method. Biosyst. Eng. 2020, 196, 1–14. [Google Scholar] [CrossRef]
- Zhou, X.; Zhao, C.; Sun, J.; Cao, Y.; Yao, K.; Xu, M. A deep learning method for predicting lead content in oilseed rape leaves using fluorescence hyperspectral imaging. Food Chem. 2023, 409, 135251. [Google Scholar] [CrossRef]
- Wang, J.; Gao, Z.; Zhang, Y.; Zhou, J.; Wu, J.; Li, P. Real-time detection and location of potted flowers based on a ZED camera and a YOLO V4-tiny deep learning algorithm. Horticulturae 2021, 8, 21. [Google Scholar] [CrossRef]
- Li, H.; Luo, X.; Haruna, S.A.; Zareef, M.; Chen, Q.; Ding, Z.; Yan, Y. Au-Ag OHCs-based SERS sensor coupled with deep learning CNN algorithm to quantify thiram and pymetrozine in tea. Food Chem. 2023, 428, 136798. [Google Scholar] [CrossRef]
- Cheng, J.; Sun, J.; Yao, K.; Xu, M.; Dai, C. Multi-task convolutional neural network for simultaneous monitoring of lipid and protein oxidative damage in frozen-thawed pork using hyperspectral imaging. Meat Sci. 2023, 201, 109196. [Google Scholar]
- Cheng, J.; Sun, J.; Yao, K.; Dai, C. Generalized and hetero two-dimensional correlation analysis of hyperspectral imaging combined with three-dimensional convolutional neural network for evaluating lipid oxidation in pork. Food Control 2023, 153, 109940. [Google Scholar]
- Gilles, T.; Sabatini, S.; Tsishkou, D.V.; Stanciulescu, B.; Moutarde, F. Home: Heatmap output for future motion estimation. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; pp. 500–507. [Google Scholar]
- Azadani, M.N.; Boukerche, A. A novel multimodal vehicle path prediction method based on temporal convolutional networks. IEEE Trans. Intell. Transp. Syst. 2022, 23, 25384–25395. [Google Scholar] [CrossRef]
- Wang, C.; Cai, S.; Tan, G.S.H. Graphtcn: Spatio-temporal interaction modeling for human trajectory prediction. In Proceedings of the 2021 IEEE Winter Conference on Applications of Computer Vision (WACV), Vancouver, BC, Canada, 17–24 June 2020; pp. 3449–3458. [Google Scholar]
- Chen, X.; Hassan, M.M.; Yu, J.; Zhu, A.; Han, Z.; He, P.; Ouyang, Q. Time series prediction of insect pests in tea gardens. J. Sci. Food Agric. 2024, 104, 5614–5624. [Google Scholar]
- Nunekpeku, X.; Zhang, W.; Gao, J.; Adade, S.Y.S.S.; Li, H.; Chen, Q. Gel strength prediction in ultrasonicated chicken mince: Fusing near-infrared and Raman spectroscopy coupled with deep learning LSTM algorithm. Food Control 2025, 168, 110916. [Google Scholar]
- Zyner, A.; Worrall, S.; Nebot, E. A recurrent neural network solution for predicting driver intention at unsignalized intersections. IEEE Robot. Auto. Lett. 2018, 3, 1759–1764. [Google Scholar] [CrossRef]
- Roy, D.; Ishizaka, T.; Mohan, C.K.; Fukuda, A. Vehicle trajectory prediction at intersections using interaction based generative adversarial networks. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; IEEE: Piscataway, NJ, USA; pp. 2318–2323. [Google Scholar]
- Cho, K.; Ha, T.; Lee, G.; Oh, S. Deep predictive autonomous driving using multi-agent joint trajectory prediction and traffic rules. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; IEEE: Piscataway, NJ, USA; pp. 2076–2081. [Google Scholar]
- Zhang, Z. Resnet-based model for autonomous vehicles trajectory prediction. In Proceedings of the 2021 IEEE International Conference on Consumer Electronics and Computer Engineering (ICCECE), Guangzhou, China, 15–17 January 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 565–568. [Google Scholar]
- Bojarski, M.; Yeres, P.; Choromanska, A.; Choromanski, K.; Firner, B.; Jackel, L.; Muller, U. Explaining how a deep neural network trained with end-to-end learning steers a car. arXiv 2017, arXiv:1704.07911. [Google Scholar]
- Jeong, H.; Shin, J.; Rameau, F.; Kum, D. Multi-modal place recognition via vectorized HD maps and images fusion for autonomous driving. IEEE Robot. Autom. Let. 2024, 9, 4710–4717. [Google Scholar] [CrossRef]
- Huang, X.Y.; Pan, S.H.; Sun, Z.Y.; Ye, W.T.; Aheto, J.H. Evaluating quality of tomato during storage using fusion information of computer vision and electronic nose. J. Food Proc. Eng. 2018, 41, e12832. [Google Scholar] [CrossRef]
- Zhou, X.; Sun, J.; Tian, Y.; Wu, X.; Dai, C.; Li, B. Spectral classification of lettuce cadmium stress based on information fusion and VISSA-GOA-SVM algorithm. J. Food Proc. Eng. 2019, 42, e13085. [Google Scholar] [CrossRef]
- Chandra, R.; Bhattacharya, U.; Bera, A.; Manocha, D. Traphic: Trajectory prediction in dense and heterogeneous traffic using weighted interactions. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 8483–8492. [Google Scholar]
- Xu, S.; Xu, X.; Zhu, Q.; Meng, Y.; Yang, G.; Feng, H.; Yang, M.; Zhu, Q.; Xue, H.; Wang, B. Monitoring leaf nitrogen content in rice based on information fusion of multi-sensor imagery from UAV. Precis. agric. 2023, 24, 2327–2349. [Google Scholar]
- Tao, K.; Wang, A.; Shen, Y.; Lu, Z.; Peng, F.; Wei, X. Peach flower density detection based on an improved CNN incorporating attention mechanism and multi-scale feature fusion. Horticulturae 2022, 8, 904. [Google Scholar] [CrossRef]
- Zhou, Z.; Wang, J.; Li, Y.H.; Huang, Y.K. Query-centric trajectory prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 17863–17873. [Google Scholar]
- Chen, J.; Lian, Y.; Zou, R.; Zhang, S.; Ning, X.; Han, M. Real-time grain breakage sensing for rice combine harvesters using machine vision technology. Int. J. Agric. Biol. Eng. 2020, 13, 194–199. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, J.; Wang, J.; Cai, L.; Jin, Y.; Zhao, S.; Xie, B. Realtime picking point decision algorithm of trellis grape for high-speed robotic cut-and-catch harvesting. Agronomy 2023, 13, 1618. [Google Scholar] [CrossRef]
- Zyner, A.; Worrall, S.; Ward, J.; Nebot, E. Long short-term memory for driver intent prediction. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; IEEE: Piscataway, NJ, USA; pp. 1484–1489. [Google Scholar]
- Alahi, A.; Goel, K.; Ramanathan, V.; Robicquet, A.; Savarese, S. Social LSTM: Human Trajectory Prediction in Crowded Spaces. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; Volume 9, pp. 961–971. [Google Scholar]
- Xue, H.; Huynh, D.Q.; Reynolds, M. Pedestrian trajectory prediction using a social pyramid. In Proceedings of the Pacific Rim International Conference on Artificial Intelligence; Springer International Publishing: Cham, Switzerland, 2019; pp. 439–453. [Google Scholar]
- Xu, Y.; Piao, Z.; Gao, S. Encoding crowd interaction with deep neural network for pedestrian trajectory prediction. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 5275–5284. [Google Scholar]
- Deo, N.; Rangesh, A.; Trivedi, M.M. How would surround vehicles move? A unified framework for maneuver classification and motion prediction. IEEE Trans. Intell. Veh. 2018, 3, 129–140. [Google Scholar] [CrossRef]
- Sriram, N.N.; Liu, B.; Pittaluga, F.; Chandraker, M. Smart: Simultaneous multi-agent recurrent trajectory prediction. In Proceedings of the European Conference on Computer Vision; Springer International Publishing: Cham, Switzerland, 2020; pp. 463–479. [Google Scholar]
- Zhang, T.; Zhou, J.; Liu, W.; Yue, R.; Shi, J.; Zhou, C.; Hu, J. SN-CNN: A lightweight and accurate line extraction algorithm for seedling navigation in ridge-planted vegetables. Agric. Basel 2024, 14, 1446. [Google Scholar] [CrossRef]
- Pan, Y.; Jin, H.; Gao, J.; Rauf, H.T. Identification of buffalo breeds using self-activated-based improved convolutional neural networks. Agriculture 2022, 12, 1386. [Google Scholar] [CrossRef]
- Guo, Z.; Zou, Y.; Sun, C.; Jayan, H.; Jiang, S.; El-Seedi, H.R.; Zou, X. Nondestructive determination of edible quality and watercore degree of apples by portable Vis/NIR transmittance system combined with CARS-CNN. J. Food Meas. Charact. 2024, 18, 4058–4073. [Google Scholar] [CrossRef]
- Huang, Y.; Pan, Y.; Liu, C.; Zhou, L.; Tang, L.; Wei, H.; Tang, Y. Rapid and non-destructive geographical origin identification of Chuanxiong slices using near-infrared spectroscopy and convolutional neural networks. Agriculture 2024, 14, 1281. [Google Scholar] [CrossRef]
- Cui, H.; Radosavljevic, V.; Chou, F.C.; Lin, T.-H.; Nguyen, T.; Huang, T.-K.; Schneider, J.; Djuric, N. Multimodal trajectory predictions for autonomous driving using deep convolutional networks. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; IEEE: Piscataway, NJ, USA; pp. 2090–2096. [Google Scholar]
- Nikhil, N.; Morris, B.T. Convolutional neural network for trajectory prediction. In Proceedings of the European Conference on Computer Vision (ECCV) Workshops; Springer International Publishing: Cham, Switzerland, 2019; pp. 186–196. [Google Scholar]
- Chaabane, M.; Trabelsi, A.; Blanchard, N.; Beveridge, R. Looking ahead: Anticipating pedestrians crossing with future frames prediction. In Proceedings of the 2020 IEEE Winter Conference on Applications of Computer Vision (WACV), Snowmass Village, CO, USA, 1–5 March 2020; IEEE Computer Society: Los Alamitos, CA, USA, 2020; pp. 2286–2295. [Google Scholar]
- Lian, J.; Luo, Y.; Wang, X.; Li, L.; Guo, G.; Ren, W.; Zhang, T. Dual-STGAT: Dual spatio-temporal graph attention networks with feature fusion for pedestrian crossing intention prediction. IEEE Trans. Intell. Transp. Syst. 2025, 26, 5396–5410. [Google Scholar] [CrossRef]
- Wang, Y.; Li, T.; Chen, T.; Zhang, X.; Taha, M.F.; Yang, N.; Shi, Q. Cucumber downy mildew disease prediction using a CNN-LSTM approach. Agriculture 2024, 14, 1155. [Google Scholar] [CrossRef]
- Qiu, D.; Guo, T.; Yu, S.; Liu, W.; Li, L.; Sun, Z.; Hu, D. Classification of apple color and deformity using machine vision combined with CNN. Agriculture 2024, 14, 978. [Google Scholar] [CrossRef]
- Lin, H.; Pan, T.; Li, Y.; Chen, S.; Li, G. Development of analytical method associating near-infrared spectroscopy with one-dimensional convolution neural network: A case study. J. Food Meas. Charac. 2021, 15, 2963–2973. [Google Scholar] [CrossRef]
- Li, X.; Ying, X.; Chuah, M.C. Grip++: Enhanced graph-based interaction-aware trajectory prediction for autonomous driving. arXiv 2019, arXiv:1907.07792. [Google Scholar]
- Jeon, H.; Choi, J.; Kum, D. Scale-net: Scalable vehicle trajectory prediction network under random number of interacting vehicles via edge-enhanced graph convolutional neural network. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October–24 January 2021; IEEE: Piscataway, NJ, USA, 2020; pp. 2095–2102. [Google Scholar]
- Liang, M.; Yang, B.; Hu, R.; Chen, Y.; Liao, R.; Feng, S.; Urtasun, R. Learning lane graph representations for motion forecasting. In Proceedings of the European Conference on Computer Vision; Springer International Publishing: Cham, Switzerland, 2020; pp. 541–556. [Google Scholar]
- Gao, J.; Sun, C.; Zhao, H.; Shen, Y.; Anguelov, D.; Li, C.; Schmid, C. Vectornet: Encoding HD maps and agent dynamics from vectorized representation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 11525–11533. [Google Scholar]
- Ding, Z.; Yao, Z.; Zhao, H. RA-GAT: Repulsion and attraction graph attention for trajectory prediction. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; IEEE: Piscataway, NJ, USA; pp. 734–741. [Google Scholar]
- Salzmann, T.; Ivanovic, B.; Chakravarty, P.; Pavone, M. Trajectron++: Dynamically-feasible trajectory forecasting with heterogeneous data. arXiv 2021, arXiv:2001.03093v5. [Google Scholar]
- Chen, W.; Wang, F.; Sun, H. S2TNet: Spatio-temporal transformer networks for trajectory prediction in autonomous driving. In Proceedings of the 13th Asian Conference on Machine Learning, Virtual, 17–19 November 2021; Volume 157, pp. 454–469. [Google Scholar]
- Wen, L.; Li, W.; Yan, J.; Lei, Z.; Yi, D.; Li, S.Z. Multiple Target Tracking Based on Undirected Hierarchical Relation Hypergraph. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 1282–1289. [Google Scholar]
- Zhu, W.; Sun, J.; Wang, S.; Shen, J.; Yang, K.; Zhou, X. Identifying field crop diseases using transformer-embedded convolutional neural network. Agriculture 2022, 12, 1083. [Google Scholar] [CrossRef]
- Ji, W.; Zhai, K.; Xu, B.; Wu, J. Green apple detection method based on multidimensional feature extraction network model and transformer module. J. Food Protec. 2025, 88, 100397. [Google Scholar] [CrossRef]
- Ji, W.; Wang, J.; Xu, B.; Zhang, T. Apple grading based on multi-dimensional view processing and deep learning. Foods 2023, 12, 2117. [Google Scholar] [CrossRef]
- Zuo, X.; Chu, J.; Shen, J.; Sun, J. Multi-granularity feature aggregation with self-attention and spatial reasoning for fine-grained crop disease classification. Agriculture 2022, 12, 1499. [Google Scholar] [CrossRef]
- Zhao, S.; Peng, Y.; Liu, J.; Wu, S. Tomato leaf disease diagnosis based on improved convolution neural network by attention module. Agriculture 2021, 11, 651. [Google Scholar] [CrossRef]
- You, J.; Li, D.; Wang, Z.; Chen, Q.; Ouyang, Q. Prediction and visualization of moisture content in Tencha drying processes by computer vision and deep learning. J. Sci. Food Agric. 2024, 104, 5486–5494. [Google Scholar] [CrossRef]
- Giuliari, F.; Hasan, I.; Cristani, M.; Galasso, F. Transformer networks for trajectory forecasting. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 10335–10342. [Google Scholar]
- Ngiam, J.; Caine, B.; Vasudevan, V.; Zhang, Z.; Chiang, H.T.L.; Ling, J.; Roelofs, R.; Bewley, A.; Liu, C.X.; Venugopal, A.; et al. Scene transformer: A unified multi-task model for behavior prediction and planning. arXiv 2021, arXiv:2106.08417. [Google Scholar]
- Yuan, Y.; Weng, X.; Ou, Y.; Kitani, K. Agentformer: Agent-aware transformers for socio-temporal multi-agent forecasting. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), 10–17 October 2021; pp. 9793–9803. [Google Scholar]
- Zhou, Z.; Ye, L.; Wang, J.; Wu, K.; Lu, K.J. Hivt: Hierarchical vector transformer for multi-agent motion prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 8823–8833. [Google Scholar]
- Achaji, L.; Barry, T.; Fouqueray, T.; Moreau, J.; Aioun, F.; Charpillet, F. Pretr: Spatio-temporal non-autoregressive trajectory prediction transformer. In Proceedings of the IEEE 25th International Conference on Intelligent Transportation Systems (ITSC), Macau, China, 8–12 October 2022; pp. 2457–2464. [Google Scholar]
- Gupta, A.; Johnson, J.; Fei-Fei, L.; Savarese, S.; Alahi, A. Social Gan: Socially acceptable trajectories with generative adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 2255–2264. [Google Scholar]
- Sadeghian, A.; Kosaraju, V.; Sadeghian, A.; Hirose, N.; Rezatofighi, H.; Savarese, S. Sophie: An attentive gan for predicting paths compliant to social and physical constraints. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 1349–1358. [Google Scholar]
- Zhao, T.; Xu, Y.; Monfort, M.; Choi, W.; Baker, C.; Zhao, Y.; Wu, Y.N. Multi-agent tensor fusion for contextual trajectory prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 12126–12134. [Google Scholar]
- Lee, N.; Choi, W.; Vernaza, P.; Choy, C.B.; Torr, P.H.; Chandraker, M. Desire: Distant future prediction in dynamic scenes with interacting agents. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 336–345. [Google Scholar]
- Jiang, C.M.; Cornman, A.; Park, C.; Sapp, B.; Zhou, Y.; Anguelov, D. MotionDiffuser: Controllable multi-agent motion prediction using diffusion. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, Canada, 18–22 June 2023; IEEE Computer Society: Los Alamitos, CA, USA, 2023; pp. 9644–9653. [Google Scholar]
- Yuan, Y.; Song, J.; Iqbal, U.; Vahdat, A.; Kautz, J. Physdiff: Physics-guided human motion diffusion model. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 4–6 October 2023; pp. 16010–16021. [Google Scholar]
- Li, W.; Shi, Y.; Huang, X.; Li, Z.; Zhang, X.; Zou, X.; Shi, J. Study on the diffusion and optimization of sucrose in gaido seak based on finite element analysis and hyperspectral imaging technology. Foods 2024, 13, 249. [Google Scholar] [CrossRef]
- Aheto, J.H.; Huang, X.; Tian, X.; Ren, Y.; Bonah, E.; Alenyorege, E.A. Combination of spectra and image information of hyperspectral imaging data for fast prediction of lipid oxidation attributes in pork meat. J. Food Proc. Eng. 2019, 42, e13225. [Google Scholar] [CrossRef]
- Awais, M.; Li, W.; Hussain, S.; Cheema, M.J.M.; Li, W. Comparative evaluation of land surface temperature images from unmanned aerial vehicle and satellite observation for agricultural areas using in situ data. Agriculture 2022, 12, 184. [Google Scholar] [CrossRef]
- Zhu, W.; Li, J.; Li, L.; Wang, A.; Wei, X.; Mao, H. Nondestructive diagnostics of soluble sugar, total nitrogen and their ratio of tomato leaves in greenhouse by polarized spectra–hyperspectral data fusion. Int. J. Agr. Biol. Eng. 2020, 13, 189–197. [Google Scholar] [CrossRef]
- Caesar, H.; Bankiti, V.; Lang, A.H.; Vora, S.; Liong, V.E.; Xu, Q.; Krishnan, A.; Pan, Y.; Baldan, G.; Beijbom, O. nuScenes: A multimodal dataset for autonomous driving. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; IEEE Computer Society: Los Alamitos, CA, USA, 2020; pp. 11618–11628. [Google Scholar]
- Chang, M.F.; Lambert, J.; Sangkloy, P.; Singh, J.; Bak, S.; Hartnett, A.; Wang, D.; Carr, P.; Lucey, S.; Ramanan, D.; et al. Argoverse: 3D Tracking and forecasting with rich maps. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–17 June 2019; pp. 8748–8757. [Google Scholar]
- Zhang, B.; Li, J.; Song, N.; Zhang, L. Perception in Plan: Coupled perception and planning for end-to-end autonomous driving. arXiv 2025, arXiv:2508.11488. [Google Scholar]
- Guo, E.; An, P.; Yang, Y.; Liu, Q.; Liu, A.A. FSF-Net: Enhance 4D occupancy forecasting with coarse BEV scene flow for autonomous driving. Pattern Recognit. 2025, 112372. [Google Scholar] [CrossRef]
- Wang, C.; Liao, H.; Wang, B.; Guan, Y.; Rao, B.; Pu, Z.; Cui, Z.; Xu, C.-Z.; Li, Z. Nest: A neuromodulated small-world hypergraph trajectory prediction model for autonomous driving. In Proceedings of the AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 25 February–4 March 2025; Volume 39, pp. 808–816. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).