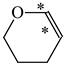
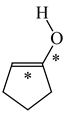
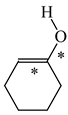
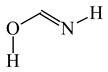
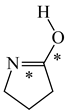
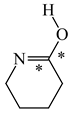
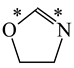
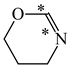
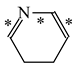
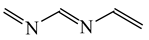
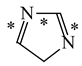
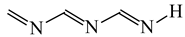
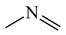Abstract
The HOMA (Harmonic Oscillator Model of Aromaticity) index, reformulated in 1993, has been very often applied to describe π-electron delocalization for mono- and polycyclic π-electron systems. However, different measures of π-electron delocalization were employed for the CC, CX, and XY bonds, and this index seems to be inappropriate for compounds containing heteroatoms. In order to describe properly various resonance effects (σ-π hyperconjugation, n-π conjugation, π-π conjugation, and aromaticity) possible for heteroatomic π-electron systems, some modifications, based on the original HOMA idea, were proposed and tested for simple DFT structures containing C, N, and O atoms. An abbreviation HOMED was used for the modified index.
1. Introduction
The geometries of molecules, as well as their energetic and magnetic properties, provide principal information about electron distribution, particularly that related to π-electron delocalization. To describe quantitatively the π-electron delocalization in various mono- and polynuclear aromatic compounds and to define their aromatic nature, numerous theories have been formulated and various numerical descriptors of aromaticity, classified as geometric, energetic, and magnetic indices, were proposed in the 20th century [1,2,3,4,6,5,7,8,9,10,11,12,13,14,15,16]. Some of these indices were also applied to describe the structure and to explain the reactivity of other neutral, ionic, and radical species, in which π-electrons of double bond(s) are conjugated with π-electrons of other double bond(s), with σ-electrons of single bond(s), with electrons of lone pair(s), with unpaired electron(s), or just with vacant p-orbital(s) [13,17,18,19].
The geometry-based HOMA (Harmonic Oscillator Model of Aromaticity) index was defined more than 30 years ago to describe quantitatively π-electron delocalization in homo- and heteroaromatic systems [20,21,22,23]. In 1993, the HOMA index was reformulated [24] taking the Jug and Koester concept of resonance coordinate into account [25]. The reformulated HOMA (rHOMA) index has been applied to various cyclic and acyclic conjugated systems [13]. However, its application to compounds containing heteroatoms has led to some unexpected results [13,16,18,26,27,28,29,30]. For example, the rHOMA values are close to zero, or even, they are negative for furan and its derivatives, whereas they are close to unity for pyrrole, benzene, benzenoid hydrocarbons and their nitrogen derivatives [13,16]. According to the general physicochemical and chemical knowledge of heteroaromatic systems, the HOMA values should be close to unity. The negative rHOMA values have been also observed for some tautomeric π-electron systems [18,26,27,28,29,30]. All these discrepancies encouraged us to re-examine the geometry-based HOMA index.
To clarify the discrepancies of the reformulated HOMA index and to explain the necessity of its modification, we returned to the original HOMA idea. We reviewed the principal changes proposed for the reformulated HOMA index, which led to the unexpected values for π-electron systems containing heteroatoms. Based on the original HOMA idea, some modifications are formulated for the geometry-based index. To distinguish the HOMA index, reserved for aromatic systems, an abbreviation HOMED (Harmonic Oscillator Model of Electron Delocalization) was proposed for the modified index [31]. The HOMED index was defined in this way that it could measure any type of resonance effect possible for π-electron systems such as σ-π hyperconjugation, n-π conjugation, π-π conjugation, and also aromaticity.
Due to different experimental and computational errors, the CC, CX, and XY bond lengths for the same molecules may differ when going from one method to another one. In some cases (e.g., tautomeric systems), experimental determinations may be difficult or even impossible. For these reasons, we chose the quantum-chemical methods to estimate the bond lengths for all compound considered in this paper, for the reference molecules as well as for different π-electron delocalized acyclic and cyclic compounds containing the C, N, and/or O atoms. The use of the same level of theory for the reference molecules and for π-electron heteroatomic systems has this advantage that computational errors may cancel out in the procedure of the HOMED estimation. We confirmed this cancellation for simple molecules using various quantum-chemical methods and various basis sets. In this paper, we chose the DFT (Density Functional Theory) method [32] with the Becke three-parameter hybrid exchange functional and the non-local correlation functional of Lee, Yang and Parr (B3LYP) [33,34]. For B3LYP calculations, the 6-311+G(d,p) basis set with the diffuse and polarization functions was applied [4,35]. The DFT method has been very often used in the literature to study the geometry of π-electron systems in which various phenomena, such as protobranching, hyperconjugation, conjugation, aromaticity, tautomerism, proton-transfer, and/or hydrogen bonding, may take place [10,11,36,37,38,39,40]. We analyzed π-electron delocalization for simple σ-π hyperconjugated, n-π conjugated, π-π conjugated, and aromatic compounds including those displaying prototropic tautomerism.
2. Results and Discussion
2.1. Original HOMA Index (oHOMA)
The principal idea of the geometry-based index, proposed in 1972 by Kruszewski and Krygowski, was based on the harmonic oscillator model of aromaticity [20,21]. In order to describe deviation of the bond lengths from its optimal value, the HOMA index was defined according to equation (1). We use here an abbreviation oHOMA for the original index to distinguish it from that reformulated in 1993. In equation (1), n is the number of bonds taken into account, Ro is the appropriate optimum bond length, and Ri is the real bond length. A factor of 98.89 is the normalization constant for the CC bond, and fulfils the following conditions: oHOMA = 0 for the Kekul? structure of benzene, and oHOMA = 1 for benzene. The same normalization factor (98.89) was applied for the CX bonds in heterocycles containing the odd and even number of bonds [22,23]. The Ro bond length was calculated according to equation (2) using the harmonic oscillator method of optimization. In equation (2), Rs and Rd are the reference single and double bond lengths, and ω is the ratio of stretching force constants for pure double and pure single bonds. The ω ratio close to 2 was taken for the CC and CX bonds [13,16,20,21,22,23,24,41].
oHOMA = 1 − 98.89/n⋅Σ(Ro − Ri)2
Ro = (Rs + ω⋅Rd)/(1 + ω)
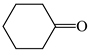
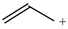
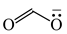
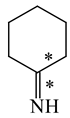
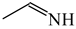
The C−C single bond in ethane, the C−N single bond in methylamine, and the C−O single bond in methanol were proposed for the reference Rs bonds [20,21,22,23]. In some cases, the Rs value for propane was also considered [22]. The C=C double bond in ethene, the C=N double bond in methylimine, and the C=O bond in formaldehyde were proposed for the reference Rd bonds [20,21,22,23]. For all reference molecules, weak electron delocalization (e.g., hyperconjugation in ethane, methylamine and methanol [40,42,43,44,45]) takes place, and thus, the reference CC and CX bonds could be treated as almost pure single and pure double bonds. The oHOMA values estimated for simple heteroaromatic compounds are close to unity [22,23].
Parametrization, i.e., oHOMA = 1 for fully aromatic systems and oHOMA = 0 for fully non-aromatic systems, is a fundamental concept of the HOMA index. According to this concept, benzene with equal CC bond lengths (Ro = 1.397 Å) was taken as a model for fully aromatic system. On the other hand, the Kekulé structure of benzene with alternating C−C single and C=C double bond lengths, equal to those for the reference molecules, ethane (Rs = 1.524 Å) and ethene (Rd = 1.334 Å), respectively, was proposed for fully non-aromatic system. For such hypothetical (restricted) 1,3,5-cyclohexatriene structure, the C−C and C=C bonds were considered as almost pure single and almost pure double bonds, and consequently, it was assumed that solely weak electron delocalization may be expected.
However, the assumption that 1,3,5-cyclohexatriene is a fully non-aromatic system may be considered as false. In the literature, numerous quantum-chemical data have been reported from which completely different conclusions have been derived. For example, in 1994 Kutzelnigg and coworkers [46], using the IGLO (Individual Gauge for Localized Orbitals) method, found only little reduction of aromaticity when benzene was deformed to a 1,3,5-cyclohexatriene geometry. Two planar structures with all angles equal to 120° were considered for cyclohexatriene, one structure with alternating single and double bond lengths equal to 1.501 and 1.336 Å, and the other one with the C−C and C=C bond lengths equal to 1.479 and 1.323 Å, respectively. In both cases, the C−C single bonds are remarkably shorter than that for ethane (1.524 Å) indicating some electron delocalization in the system. The IGLO calculations of the magnetic susceptibility tensors, as well as of the 1H and 13C shielding tensors, showed only little reduction of magnetic aromaticity when proceeding from benzene to the hypothetical structures of cyclohexatriene. This phenomenon was confirmed recently by Corminboeuf and coworkers [47], who combined the BLW (Block-Localized Wave-function) scheme with the IGLO method and applied to benzene and cyclohexatriene. The BLW-IGLO study showed that deformation of benzene to a cyclohexatriene geometry with the C−C (1.527 Å) and C=C (1.330 Å) bond lengths close to those for ethane and ethene decreases moderately magnetic and energetic parameters of aromaticity. This was explained by the π overlap and cyclic delocalization which only is diminished modestly by bond lengths alternation. Fully non-aromatic system can be found by the BLW-IGLO method when the π-π conjugation is eliminated by blocking all three π orbitals. Blocking only a single π bond also disables the π ring current completely. This phenomenon cannot be detected by variations of geometrical parameters.
2.2. Reformulated HOMA Index (rHOMA)
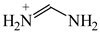
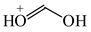
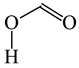
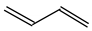
To distinguish the π-electron delocalization, and to study the inter- and intramolecular interactions such as H-bonds and internal (substituent) effects in strongly conjugated aromatic systems, Krygowski reformulated the HOMA index in 1993, and proposed equation (3), where n, Ro and Ri have the same meaning as in equation (1) [24]. Following the Jug and Koester concept of resonance coordinate [25], some new reference molecules were proposed. For example, 1,3-butadiene and formic acid were used for the CC and CO bonds, respectively. π-Electrons are moderately delocalized in these molecules by π-π conjugation in 1,3-butadiene, CH2=CH−CH=CH2 ↔ −:CH2−CH=CH−CH2+ ↔ +CH2−CH=CH−CH2:−, and by n-π conjugation in formic acid, :OH−CH=O ↔ +OH=CH−O:− [41]. However, for the CN bonds the same reference molecules of slight electron delocalization, methylamine and methylimine, were employed for rHOMA, similarly as for oHOMA. For other CX and XY bonds, compounds of different electron delocalization were used. This reformulation involved a necessity of use of the normalization α constant for each type of bond. The α constants, calculated from equation (4), have been applied for the systems containing the odd and even number of bonds, for cyclic and acyclic compounds, for the whole molecules and also for their fragments [13,16,18,24,28,29,30].
rHOMA = 1 − α/n⋅Σ(Ro − Ri)2
α = 2⋅{(Ro − Rs)2 + (Ro − Rd)2}−1
Consequently to the use of different measures of π-electron delocalization for the CC, CX, and XY bonds in the reformulated HOMA index, the α(CC), α(CX), and α(XY) constants are not the same. They vary from 57.21 (NO) through 93.52 (CN), 94.09 (CS), 118.91 (CP), 130.33 (NN), 157.38 (CO) to 257.7 (CC) [13,16,24]. Hence, it is not wonder that application of the reformulated HOMA index to heteroatomic systems has led to unexpected results [13,16,18,26,27,28,29,30]. For example, the rHOMA value is close to zero for furan (0.298), whereas it is close to unity for pyrrole (0.876) [16]. When the CH groups are replaced in the ring by the N-aza groups, surprisingly, the rHOMA values increase (to 0.332, 0.527, and 0.586 for 3-aza-, 2-aza-, and 2,3,5-triazafuran, and to 0.908, 0.926, and 0.960 for 3-aza, 2-aza, and 2,3,5-triazapyrrole, respectively [16]). The variations of the rHOMA index are only numerical and have nothing common with real π-electron delocalization in heteroaromatic systems. They result mainly from the use of different measures of π-electron delocalization for the CC, CN, and CO bonds, i.e., from the use of already delocalized reference molecule for the CC bonds (1,3-butadiene, oHOMA = 0.687, rHOMA = 0.202), from the use of already delocalized reference molecule for the CO bonds (formic acid, oHOMA = 0.437, rHOMA = 0), and also from the use of slightly delocalized reference molecules for the CN bonds (methylamine and methylimine).
In the case of tautomeric systems containing sp3 hybridized atoms, some unexpected results have been also observed for the rHOMA index [18,26,27,28,29,30]. For example, σ-π hyperconjugation may take place for the keto and imine tautomers {>C(−H)−C(=X)− ↔ >C(H+)=C(−X:−)−, X = O and NH}, whereas n-π conjugation is possible for the enol and enamine forms {>C=C(−HX:)− ↔ >−:C−C(=HX+)−} [48]. Both resonance effects (with separation of charge) are considerably weaker than π-π and n-π conjugations occurring in heteroaromatic compounds. In many cases, they are also weaker than those for the reference molecules (1,3-butadiene and formic acid). Generally, for tautomeric π-electron systems the geometry-based indices should be lower than unity but larger than zero. However, in many cases the negative rHOMA values have been found [18,26,27,28,29,30]. These results cannot be considered as lack of π-electron delocalization. They are solely a consequence of the use of the new reference molecules with different π-electron delocalization for the CC and CX bonds in the rHOMA procedure.
2.3. HOMED Index
Taking the discrepancies of the reformulated HOMA index into account, a necessity of modification of the geometry-based index has been signaled three years ago [31]. It has been found that equation (5), which is similar to that (3) proposed for rHOMA, can be applied for the modified index. For the system containing the even number of bonds (2i), i.e., the same number of single (i) and double (i) bonds, the normalization α constant can be calculated from equation (4) proposed for the rHOMA index. However, equation (4) cannot be used for the systems with the odd number of bonds (2i + 1). For such systems, the α constant can be calculated from equation (6) or (7). Equation (6) corresponds to the systems possessing (i + 1) single bonds and (i) double bonds, and equation (7) refers to the system having (i) single bonds and (i + 1) double bonds.
HOMED = 1 − α/n⋅Σ(Ro − Ri)2
α = (2i + 1)⋅{(i + 1)⋅(Ro − Rs)2 + i⋅(Ro − Rd)2}−1
α = (2i + 1)⋅{i⋅(Ro − Rs)2 + (i + 1)⋅(Ro − Rd)2}−1
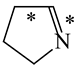
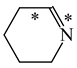
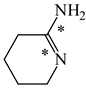
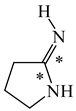
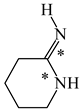
In order to properly describe π-electron delocalization in cyclic and acyclic heteroatomic systems, we considered single and double CC, CX, and XY bond lengths in various simple molecules which could be employed as the reference molecules in the modified geometry-based index. We found that in the HOMED procedure, the simplest acyclic saturated molecules such as ethane, methylamine, and methanol can be used for the reference single C−C, C−N, and C−O bond lengths, and the simplest acyclic unsaturated molecules such as ethene, methylimine, and formaldehyde can be applied for the reference double C=C, C=N, and C=O bond lengths, similarly as it was proposed for the original HOMA index [20,21,22,23]. At the B3LYP/6-311+G(d,p) level, the single CC and CX bond lengths for ethane, methylamine, and methanol are very close to those for cyclic six-membered compounds, cyclohexane, piperidine, and tetrahydropyran, respectively (Table 1). Except cyclopentane, they are also close to those for cyclic five-membered compounds, pyrrolidine and tetrahydrofuran. For cyclopentane, the envelope conformation involves the non-equivalent CC bond lengths.

Table 1.
Single CC, CN, and CO bond lengths (Rs in Å) calculated at the B3LYP/6-311+G(d,p) level for simple acyclic and cyclic compounds.
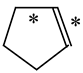
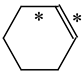
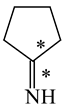
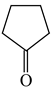
In the case of unsaturated compounds, the simplest acyclic molecules are less delocalized than the five- and six-membered ones. Due to σ-π hyperconjugation possible for cyclopentene, cyclohexene, 1-pyrroline, cyclopentylimine, 3,4,5,6-tetrahydropyridine, cyclohexylimine, cyclopentanone, and cyclohexanone, their C=C and C=X bonds are slightly longer than those for ethene, methylimine, and formaldehyde (Table 2). The C=O bonds for charged cyclic O-derivatives are even longer. The resonance conjugation possible for these derivatives and occurring with transfer of the positive charge from the O to H atom {>C(−H)−C=O+− ↔ >C(H+)=C−O−} is stronger than that in the corresponding carbonyl derivatives where separation of the charge takes place {>C(−H)−C=O ↔ >C(H+)=C−O:−}.

Table 2.
Double CC, CN, and CO bond lengths (Rd in Å) calculated at the B3LYP/6-311+G(d,p) level for simple acyclic and cyclic compounds.
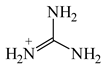
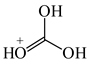
For the optimum (Ro) bond lengths, we considered various molecules, for which the equalization of the CC, CX, and XY bonds takes place. Since the CC, CN, and CO bond lengths (Table 3) depend on the geometry of the system and on the charge (0, +1, +2, −1, or −2), we selected the simplest aromatic six-membered molecules, benzene and s-triazine, for the optimum CC and CN bond length, respectively. In the case of the CO bond, to our knowledge, there is no neutral, symmetric, and aromatic molecule with complete delocalization of π-electrons. Therefore, the CO bond length in the branching Y-conjugated molecule-protonated carbonic acid, (HO)3C+, was selected for Ro. Note that analogs Y-conjugated guanidinium cation, (H2N)3C+, possesses the CN bond length (1.335 Å) very close to that of s-triazine (1.334 Å). Table 4 summarizes the Rs, Rd, and Ro values selected for the HOMED procedure. The normalization α constants calculated according to equations (4), (6), and (7) for even (2i) and odd (2i + 1) number of bonds are given in Table 5.

Table 3.
Optimum CC, CN, and CO bond lengths (Ro in Å) calculated at the B3LYP/6-311+G(d,p) level for simple acyclic and cyclic compounds.

Table 4.
Reference bond lengths (Rs, Rd, and Ro in Å) employed in the HOMED procedure.

Table 5.
Normalization α constants for even (2i) and odd (2i + 1 = 3, 5, 7) number of bonds employed in the HOMED procedure.
From a mathematical point of view, the procedure of the HOMED index is the same as that of the reformulated and original HOMA index [20,21,22,23,24,31]. Solely the reference Rs, Rd, and Ro bond lengths and the normalization α constants are different. The HOMED index describes the same phenomenon – shortening of the single bond and lengthening of the double bond due to π-electron delocalization in the system. The choice of the simplest compounds for the reference molecules gives the possibilities to measure the strength of any type of resonance conjugation, weak σ-π hyperconjugation, medium n-π and π-π conjugation, and strong aromaticity in any type of π-electron heteroatomic system.
2.4. Non-aromatic π-electron Systems
For acyclic π-electron systems of general formulae H3C−Y=X and HZ−Y=X, one part of the atoms (C or other atom in Z group) occurs in the sp3 state of hybridization and the other ones (atoms in X and Y groups) in the sp2 state of hybridization. Two types of resonance conjugation are possible: σ-π hyperconjugation (8) and n-π conjugation (9), respectively [48]. For acyclic polyenes and their N or O analogs of general formula Y=B−A=X, each atom in A, B, Y and X group has the sp2 state of hybridization, and π-π conjugation (10) takes place. For all these conjugated π-electron systems, various resonance structures with separation of charge can be written. According to the general rules of writing resonance contributors, the structures with separation of charge are less important in the resonance hybrid than those without separation of charge. Since the resonance structures are non-equivalent, acyclic π-electron systems are usually less delocalized than aromatic ones for which the complete delocalization is possible.
H−CH2−Y=X ↔ H+ CH2=Y−X:−
:ZH−Y=X ↔ +ZH=Y−X:− ↔ :ZH−Y+−X:−
Y=B−A=X ↔ −:Y−B=A−X+ ↔ +Y−B=A−X:− ↔ −:Y−B+−A=X ↔ Y=B−A+−X:−
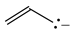
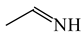
To test the geometry-based HOMED index for hyperconjugated acyclic π-electron systems, we chose the simplest triad molecules of general formula H3C−CH=X such as propene (X = CH2), E-acetaldimine (X = NH), and acetaldehyde (X = O). For one of them (propene), various basis sets [35] and the DFT method [32] with the B3LYP functional [33,34] were considered (Table 6). Calculations were also performed for the reference molecules (ethane, ethene, and benzene) at the same levels of theory. For comparison, the MP2 (second-order Möller-Plesset) perturbation [49,50] with two basis sets, 6-31G(d) and 6-311++G(d,p), were applied. At each level of theory, the α constant values were calculated according to equation (4). Although the bond lengths and the α constant values vary when proceeding from one level of theory to the other one, the HOMED values for propene, estimated according to equation (5), are close to 0.33 at the DFT levels. They are only slightly larger than those estimated at the MP2 levels (0.32). This indicates that computational errors for the bond lengths almost cancel out in the HOMED procedure, and that the DFT results are not very different from those calculated at the MP2 levels. Calculations performed at the HF/6-31G(d) and HF/6-311++G(d,p) levels [35] lead to lower HOMED indices for propene (0.265 and 0.270, respectively) than those at the DFT and MP2 levels. Use of the polarization and diffuse functions has no important effect on the estimated HOMED values. It should be noted here that involvement of the H atoms in σ-π hyperconjugation does not require application of the diffuse function on these atoms, because in fact, the protons (not H atoms) are engaged in hyperconjugation. Hence, the bond lengths for the reference molecules as well as for propene, calculated with the use of the 6-31+G(d,p), 6-311+G(d,p), and 6-311+G(3df,2p) basis sets are almost the same as those calculated with use of the diffuse function on the H atoms, i.e., the 6-31++G(d,p), 6-311++G(d,p), and 6-311++G(3df,2p) basis sets. Differences in the calculated bond lengths are not larger than 0.0002 Å.

Table 6.
Comparison of the bond lengths for the reference molecules (Rs for ethane, Rd for ethene, and Ro for benzene, all in Å), the normalization α constants, and the HOMED indices for propene calculated at various DFT, MP2, and HF levels.
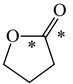
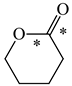
Since the DFT(B3LYP)/6-311+G(d,p) level has been very often used in the literature to study the geometry of π-electron systems [10,11,36,37,38,39], we chose this level of theory for the HOMED estimation of all heteroatomic π-electron systems considered in this paper. Table 7 summarizes the HOMED indices for the DFT structures of the simplest triad molecules. The HOMED values were estimated using equation (5), and parameters from Table 4 and Table 5 for normal chain acyclic compounds with even number of bonds. σ-π Hyperconjugation is also possible for simple cyclic π-electron systems containing the −CH2−CH=X− fragments (X = CH or N). For comparison, we applied the HOMED procedure to various fragments of five- and six-membered derivatives. For the HOMED estimation, the DFT computed C−C and C=X bond lengths (marked with asterisks), equation (5), and parameters from Table 4 and Table 5 were taken. All HOMED values, except that for cyclopentanone, are positive. They are not larger than 0.35. For cyclopentanone, the HOMED index has the negative value (−0.029). This is a consequence of slightly longer C−C bond length for cyclopentanone (marked with asterisks) than for the reference molecule (ethane). Longer C−C bond lengths are also for the envelope conformation of cyclopentane (Table 1). The rHOMA indices calculated for the same DFT structures are also given in Table 7. Almost all of them have strongly negative values (−1.9−0.1) contrary to the HOMED indices which are close to zero (0.0−0.3). The variation of the rHOMA indices is only numerical. It is a consequence of the use of different measures of π-electron delocalization for the CC, CN, and CO bonds.

Table 7.
HOMED indices for σ-π hyperconjugated systems (rHOMA indices given in italic).
Solely the HOMED indices can give direct information about π-electron delocalization. Being not very different from zero, they confirm that σ-π hyperconjugated structures and fragments are weakly delocalized. The σ-bonded substituents (CH3 and CH2) act as weak electron donors to the completely planar π-bonded Y=X moiety. This resonance effect dictates the product formation of numerous reactions in organic chemistry. Many substitution, addition, and condensation reactions can be understood and explained taking the σ-π hyperconjugation effect into account [48,51]. Recently, it has been also suggested that hyperconjugation is responsible for the structure of σ-bonded organic compounds such as alkanes, alcohols, and amines [40,42,43,44,45]. The conformational preferences seem to be favored by this special type of resonance, not by steric repulsion.
Many organic compounds such as enamines, enols, carboxylic acids, esters, amides, amidines, etc. are commonly known to be stabilized by electron delocalization [48]. They are particular cases of n-π conjugated heteroallylic systems which are isoconjugated to the allyl anion. Their structures can be described by a hybrid of at least three resonance contributors (9). The conjugation between π-electrons of the Y=X double bond and n-electrons of the lone pair of Z has been often considered to explain the mechanisms of various organic reactions catalyzed by acids. It has been also used to analyze particular physicochemical properties such as hindered rotation, favored site of protonation, acid-base properties, etc. [48,51]. Generally, the resonance model predicts that the electron delocalization in such systems is directly linked with the electronegativity of the double bonded atom (more electronegative atom, greater delocalization). However, theoretical studies and discussions on the origin of these properties questioned the resonance model [52,53]. The resonance stabilization seems to not be the most important factor in leading to the increased hindered rotation, acidity, basicity, etc. Mó et al. [54] suggested that the rotational barrier is not a good measure of the ‘pure’ n-π conjugation.
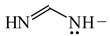
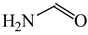
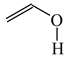
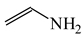
To study quantitatively π-electron delocalization for heteroallyl systems and to test the HOMED index, we chose the simplest triad molecules of general formula HY−CH=X such as vinylamine (X = CH2 and Y = NH), formamidine (X, Y = NH), formamide (X = O and Y = NH), vinyl alcohol (X = CH2 and Y = O), formamidic acid (X = NH and Y = O) and formic acid (X, Y = O). The HOMED values estimated for the DFT structures according to equation (5) and parameters given in Table 4 and Table 5 for normal chain acyclic systems with even number of bonds are summarized in Table 8. Generally, n-π conjugated heteroallyl systems are moderately delocalized. The HOMED values are larger than those for the corresponding σ-π hyperconjugated systems. They are between 0.4 and 0.8. The same trend is found for the n-π conjugated fragments (marked with asterisks) in cyclic systems, for which the estimated HOMED indices are also given in Table 8. The variation of the HOMED indices is in good agreement with general knowledge of π-electron systems. Quite a different situation takes place for the rHOMA indices. They vary from −0.3 to 0.8. They are negative or close to zero for O-sp3 derivatives, whereas they are positive for N-derivatives. This variation results solely from the use of different measures of π-electron delocalization for the CC, CN, and CO bonds. It has nothing common with intrinsic π-electron delocalization.

Table 8.
HOMED indices for n-π conjugated heteroallyl systems (rHOMA indices given in italic).
For polyenes and their heteroanalogs, double bonds are separated by one single bond, and π-π conjugation takes place. This conjugation has been often considered to explain particular product formation in various addition reactions [48,51]. The structure of polyenes can be described by a hybrid of different resonance contributors (10). To study quantitatively π-electron delocalization in π-π conjugated polyenes and their heteroanalogs, and to test the HOMED index, we chose the simplest acyclic molecules with two double bonds of general formula H2C=Y−CH=X (X = CH2, NH or O, and Y = CH or N). We selected also trans-1,3,5-hexatriene and its mono-, di-, and tri-N analogs. For comparison, we studied the polyene fragments (marked with asterisks) included in five- and six-membered cycles. The HOMED values estimated for the DFT structures according to equation (5) and parameters given in Table 4 and Table 5 are summarized in Table 9. Generally, π-π conjugated compounds and fragments are moderately delocalized similarly as n-π conjugated heteroallyl systems. The HOMED values are between 0.4 and 0.8. This variation describes properly π-electron delocalization contrary to the variation of the rHOMA indices. They vary from 0 to 0.6. They are close to zero for hydrocarbons and its O-derivatives, whereas they are larger than 0.2 for N-derivatives. This difference is only numerical. It is a consequence of the use of the new reference molecules with different π-electron delocalization.

Table 9.
HOMED indices for π-π conjugated systems (rHOMA indices given in italic).
Some simple acyclic molecules of general formula H2C=CH−X−CH=CH2 and HX−HC=CH−CH=Y (X = NH or O, and Y = CH2, NH or O) can model π-electron delocalization in five-membered heteroaromatic systems such as pyrrole and furan. π-Electrons in H2C=CH−X−CH=CH2 are delocalized by mixed double n-π conjugation (11). π-Electrons in HX−HC=CH−CH=Y are delocalized by mixed n-π and π-π conjugations (12). For both types of derivatives, the structures with separation of charge occur in the resonance hybrids. Thus, the resonance structures are non-equivalent. The HOMED indices (Table 10) estimated for the DFT structures according to equation (5) and parameters given in Table 4 and Table 5 are not very different from those found for simple n-π and π-π conjugated compounds (Table 8 and Table 9). This indicates that n-π conjugation included to the π-π conjugated system has not important effect on π-electron delocalization for the whole acyclic π-electron system. All compounds are moderately delocalized. The HOMED indices are between 0.5 and 0.8 contrary to the rHOMA indices which vary from −0.3 to 0.6. They are negative or close to zero for O-derivatives, whereas they are larger than 0.4 for N-derivatives. The variation of the rHOMA values does not describe properly π-electron delocalization.
H2C=CH−X:−CH=CH2 ↔ −:H2C−CH=X+−CH=CH2 ↔ H2C=CH−X+=CH−CH2:−
:XH−HC=CH−CH=Y ↔ +XH=HC−CH:−−CH=Y ↔ +XH=HC−CH=CH−Y:− ↔ ↔ :XH−HC+−CH=CH−Y:−

Table 10.
HOMED indices for mix-conjugated (n-π and π-π) acyclic systems–models for pyrrole and furan (rHOMA indices given in italic).
2.5. Aromatic Systems
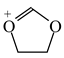
It is well known that resonance conjugations which take place for heteroaromatics are not the same. They depend on the geometry of the system and/or on the type of heteroatom(s) present in the ring [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. In the case of five-membered compounds such as pyrrole, furan, and their derivatives, mixed n-π and π-π conjugations are possible. These conjugations lead to non-equivalent resonance structures (13), one without separation of charge (13a) and the others with separation of charge (13b–13e). Consequently, the complete delocalization of π-electrons is not possible. In the case of six-membered compounds such as pyridine and its derivatives, resonance π-π conjugation (14) leads to equivalent resonance structures without separation of charge (14a and 14b). Similarly as for benzene, π-electrons are completely delocalized. Quite a different situation takes place for the pyranyl ion and its derivatives (15). Since the positive charge may be placed at different atoms (C, N, or O), the resonance structures (15a–15e) are non-equivalent. Thus, π-electrons are less delocalized than those for benzene and its N-derivatives.
Following the resonance effects, the HOMED indices (Table 11) calculated for the DFT structures of pyrrole and furan are larger than those for acyclic mix-conjugated systems (Table 10), and they are lower than those for six-membered heteroaromatics such as pyridine and the pyranyl ion, respectively. The HOMED index for the pyranyl ion is also lower than that for pyridine. A replacement of the CH group by the N-aza atom in five-membered rings seems to reduce the HOMED index in higher degree for O- than N-derivatives. For six-membered rings, presence of the additional N-aza atom in azines does not destroy the complete π-electron delocalization in the system. For six-membered O-derivatives, the HOMED index strongly depends on the position of the N-aza atom. It decreases for 3- and 3,5-positions where the N atom may be near the C+ atom (15c and 15e), and increases for 4-position where the N atom may take the positive charge (15d). Similarly as for acyclic π-electron systems, the rHOMA values do not describe properly π-electron delocalization in heteroaromatics. The rHOMA indices are close to zero for furan and its N-aza derivative. They are larger than 0.6 for pyrrole, imidazole, and the pyranyl ions, and almost equal to unity for azines. The rHOMA indices do not follow the resonance effects.
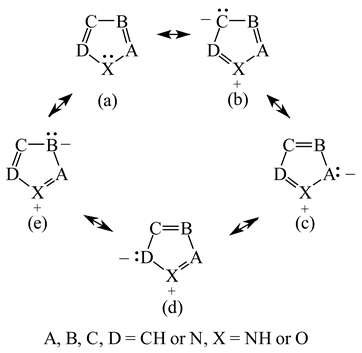
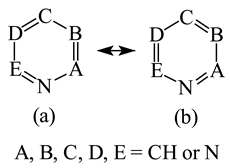
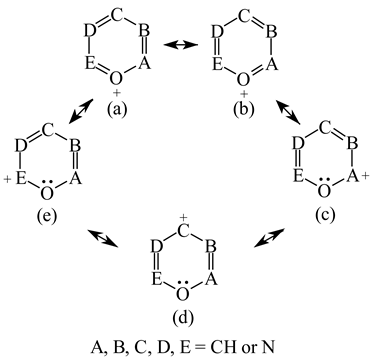




Table 11.
HOMED indices for simple heteroaromatic systems (rHOMA indices given in italic).
Pyrones are particular cases of heterocyclic compounds. They are less delocalized (Table 12) than the pyranyl ion (Table 11). For α- (16) and γ-pyrone (17), mixed n-π conjugations are possible similarly as for furan. Moreover, the exo-carbonyl group may be conjugated with the endo-C=C or C=N groups or with the endo-O atom. Due to charge separation in the resonance structures (16b–16d and 17b–17d), the mixed conjugations lead to lower HOMED indices for α- (0.618) and γ-pyrone (0.666) than for the pyranyl ion (0.926). Presence of the N-aza groups reduces the HOMED values. The rHOMA indices are negative or close to zero. They do not follow the resonance and N-aza effects.
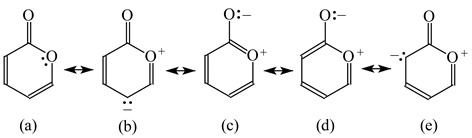
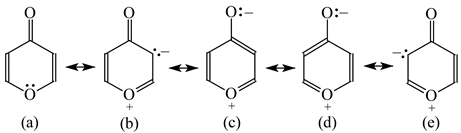



Table 12.
HOMED indices for pyrones (rHOMA indices given in italic).
2.6. Tautomeric Systems
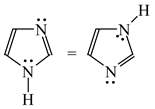
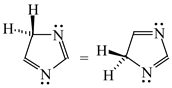
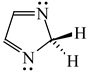
Intramolecular proton-transfer in tautomeric systems includes always the migration of π-electrons [18,55,56,57,58]. In many cases, π-electron delocalization (e.g., aromaticity) dictates the tautomeric preferences. For example, the NH tautomers of pyrrole and imidazole (Scheme 1), strongly stabilized in the ring by mixed n-π and π-π conjugation, are favored in the tautomeric mixture [55]. Their HOMED indices (Table 13) are close to 0.9. When the C atoms take the moving proton in pyrrole and imidazole, they loss the sp2 state of hybridization and the rare CH tautomers become non-aromatic. They are considerably less delocalized than the NH tautomers due to weaker mixed σ-π and π-π conjugation. The HOMED indices estimated for the whole five-membered CH forms (five bonds) are between 0.3 and 0.5. Similar difference in π-electron delocalization is found for the simplest enamine and imine tautomers given also in Table 13. The σ-π hyperconjugated imine forms are less delocalized and have lower HOMED indices than the n-π conjugated enamine forms. Principal difference takes place for the relative energies. The enamine forms have larger G values. Although the enamine forms are more delocalized, they are not favored in the tautomeric mixtures. The stability of functionalities (imine groups) seems to determine the tautomeric preferences in non-aromatic systems. An application of the rHOMA procedure leads to similar general conclusion. However, the rHOMA indices do not describe properly the resonance effects because different measures of π-electron delocalization were used for the reference CC, CN, and CO bonds. The rHOMA values are negative for the imine forms and positive for the enamine forms.
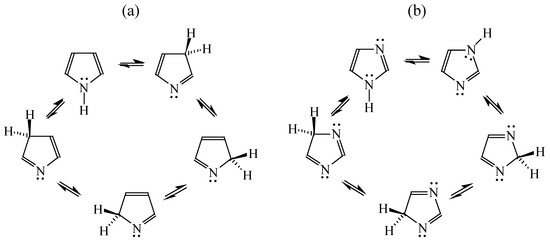
Scheme 1.
Tautomeric equilibria for azoles. (a) pyrrole; (b) imidazole.

Table 13.
Relative energies (ΔG in kcal mol−1) and HOMED indices for simple imine-enamine tautomers and for azoles (rHOMA indices given in italic).
In the case of simple six-membered rings with one exo-OH or NH2 group (Scheme 2), aromaticity seems to be also the principal factor that dictates the tautomeric preferences (Table 14). For phenol, the hydroxy tautomer is favored [55,57]. This form is well delocalized due to cross n-π conjugation of the exo-OH group with the π-π conjugated phenyl ring. The HOMED index is close to 0.9 for the whole tautomeric system including the exo-OH group (seven bonds). The same is true for aniline. The well delocalized amine tautomer is favored. In this form, the exo-NH2 group is cross n-π conjugated with the π-π conjugated phenyl ring. The HOMED index is close to 0.9 for the whole tautomeric system including the exo-NH2 group (seven bonds). When the C atoms take the moving proton in phenol and aniline, they lose the sp2 state of hybridization. The rare CH tautomers are non-aromatic (HOMED close to 0.5). They are considerably less delocalized than phenol and aniline due to weaker mixed conjugation (σ-π and π-π).
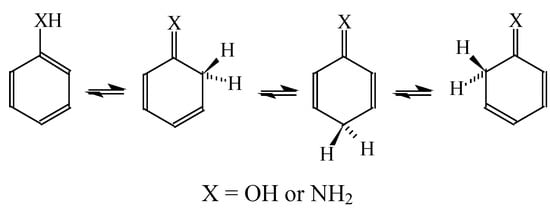
Scheme 2.
Tautomeric equilibria for six-membered ring with one exo group.

Table 14.
Relative energies (ΔG in kcal mol−1) and HOMED indices for simple keto-enol and imine-enamine tautomers, and for phenol and aniline (rHOMA indices given in italic).
The N-aza atoms at 2,4- and 2,6-positions in the ring are able to change the tautomeric preferences when going from phenol and aniline to pyrimidine nucleobases (uracil, thymine, and cytosine), which prefer the amide forms [59,60,61]. Moreover, stability of functional groups (the amide functions) seems to dictate the tautomeric preferences in nucleobases. Aromaticity plays a secondary role. π-Electron delocalization is also less important factor in acyclic keto-enol and imine-enamine tautomeric systems for which less delocalized keto and imine forms are favored in the tautomeric mixtures (Table 14). Although the rHOMA indices follow this general trend, their values have no physicochemical sense, because different measures of π-electron delocalization were used for the reference CC, CN, and CO bonds. The rHOMA values are negative for the keto and imine forms, and positive for phenol, aniline, and for the other imine forms. For the non-aromatic enol forms, the rHOMA values are negative.
3. Computational Details
Geometries of all compounds were fully optimized without symmetry constrains using the DFT(B3LYP) method and the 6-311+G(d,p) basis set [4,32,33,34,35]. Other basis sets such as 6-31G(d), 6-31G(d,p), 6-31+G(d,p), 6-31++G(d,p), 6-311++G(d,p), 6-311+G(3df,2p), 6-311++G(3df,2p), cc-pVTZ, and aug-cc-pVTZ were additionally applied for geometry optimization of ethane, ethene, benzene, and propene. The MP2 [49,50] and HF [35] methods with the 6-31G(d) and 6-311++G(d,p) basis sets were also tested for selected compounds. For all minima (with real frequencies), the CC and CX bond lengths and the Gibbs (free) energies (G at 298.15 K) were calculated. For calculations, the Gaussian 03 program [62] was used.
4. Conclusions
Use of the simplest reference molecules of similar π-electron delocalization in the HOMED procedure gives the possibilities to describe properly any type of π-electron delocalization in non-aromatic as well as in aromatic systems. Moreover, use of the same quantum-chemical method for the reference molecules and for π-electron systems diminishes computational errors. The HOMED index follows well the resonance conjugations. For weak σ-π hyperconjugated systems or fragments the HOMED indices are not larger than 0.4. For medium n-π and π-π conjugated non-aromatic systems and fragments, the HOMED indices are between 0.4 and 0.8. For strongly conjugated aromatic systems, the HOMED indices are close to unity. This order of the HOMED indices is in good agreement with the BLW-based data order for energy evaluation of σ-π hyperconjugation (6.3 kcal mol−1 for propene), π-π conjugation (12.7 kcal mol−1 for butadiene) and aromaticity (ASE 25.7 and RE 65.4 kcal mol−1 for benzene) [39,40,63].
The choice of the reference molecules with different π-electron delocalization for the reformulated HOMA index is the principal reason leading to serious discrepancies for the rHOMA values. For compounds containing various heteroatoms, the rHOMA indices have no physicochemical sense. They are negative or close to zero for many delocalized O-derivatives, whereas they are positive or close to unity for many delocalized N-derivatives. The rHOMA indices do not describe well the intrinsic π-electron delocalization. Solely for homoaromatic or heteroaromatic systems with the same type of the CC, CX, or XX bonds and containing the even number of bonds, the rHOMA procedure can be applied. For strongly delocalized heteroaromatics with different CC and CX bonds, the reference molecules of similar geometry and of similar π-electron delocalization should be employed in the HOMA procedure.
Acknowledgments
We thank the Guest Editor of special issue: Aromaticity and Molecular Symmetry for valuable comments and suggestions.
References and Notes
- Streiwieser, A. Molecular Orbital Theory for Organic Chemists; Wiley: New York, NY, USA, 1961. [Google Scholar]
- Dewar, M.J.S. The Molecular Orbital Theory of Organic Chemistry; McGraw-Hill: New York, NY, USA, 1969. [Google Scholar]
- Hess, B.A., Jr.; Schaad, L.J. Hueckel Molecular Orbital π-Resonance Energies. Heterocycles Containing Divalent Sulfur. J. Am. Chem. Soc. 1973, 95, 3907–3912. [Google Scholar] [CrossRef]
- Hehre, W.J.; Radom, L.; Schleyer, P.v.R.; Pople, J.A. Ab initio Molecular Theory; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Bird, C.W. A New Aromaticity Index and Its Application to Five-Membered Ring Heterocycles. Tetrahedron 1985, 41, 1409–1414. [Google Scholar] [CrossRef]
- Bird, C.W. The Application of a New Aromaticity Index to Six-Membered Ring Heterocycles. Tetrahedron 1986, 42, 89–92. [Google Scholar] [CrossRef]
- Katritzky, A.R.; Barczyński, P.; Musumurra, G.; Pisano, D.; Szafran, M. Aromaticity as a Quantitative Concept. 1. A Statistical Demonstration of the Orthogonality of ‘Classical’ and ‘Magnetic’ Aromaticity in Five- and Six-Membered Heterocycles. J. Am. Chem. Soc. 1989, 11, 7–15. [Google Scholar] [CrossRef]
- Minkin, V.I.; Glukhovtsev, M.N.; Simkin, B.Y. Aromaticity and Antiaromaticity. Electronic and Structural Aspects; Wiley: New York, NY, USA, 1994. [Google Scholar]
- Schleyer, P.v.R.; Maerker, C.; Dransfield, A.; Jiao, H.; van Eikema Hommes, N.J.R. Nucleus-Independent Chemical Shifts: A Simple and EfficientAromaticity Probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef] [PubMed]
- Schleyer, P.v.R.; Jiao, H. What is Aromaticity? Pure Appl. Chem. 1996, 68, 209–218. [Google Scholar] [CrossRef]
- Chen, Z.; Wannere, C.S.; Corminboeuf, C.; Puchta, R.; Schleyer, P.v.R. Nucleus-Independent Chemical Shifts (NICS) as Aromaticity Criterion. Chem. Rev. 2005, 105, 3842–3888. [Google Scholar] [CrossRef] [PubMed]
- Katritzky, A.R.; Jug, K.; Oniciu, D.C. Quantitative Measures of Aromaticity for Mono-, Bi-, and Tricyclic Penta- and Hexaatomic Heteroaromatic Ring Systems and Their Interrelations. Chem. Rev. 2001, 101, 1421–1450. [Google Scholar] [CrossRef] [PubMed]
- Krygowski, T.M.; Cyrański, M.K. Structural Aspects of Aromaticity. Chem. Rev. 2001, 101, 1385–1419, and references cited therein. [Google Scholar] [CrossRef]
- Randić, M. Aromaticity of Polycyclic Conjugated Hydrocarbons. Chem. Rev. 2003, 103, 3449–3606. [Google Scholar] [CrossRef]
- Balaban, A.T.; Oniciu, D.C.; Katritzky, A.R. Aromaticity as a Cornestone of Heterocyclic Chemistry. Chem. Rev. 2004, 104, 2777–2812. [Google Scholar] [CrossRef] [PubMed]
- Cyrański, M.K. Energetic Aspects of Cyclic Pi-Electron Delocalization: Evaluation of the Methods of Estimating Aromatic Stabilization Energies. Chem. Rev. 2005, 105, 3773–3811, and references cited therein. [Google Scholar] [CrossRef] [PubMed]
- Krygowski, T.M.; Stępień, B.T. Sigma- and Pi-Electron Delocalization: Focus on Substituent Effects. Chem. Rev. 2005, 105, 3482–3512, and references cited therein. [Google Scholar] [CrossRef] [PubMed]
- Raczyńska, E.D.; Kosińska, W.; Ośmiałowski, B.; Gawinecki, R. Tautomeric Equilibria in Relation to Pi-Electron Delocalization. Chem. Rev. 2005, 105, 3561–3612, and references cited therein. [Google Scholar] [CrossRef] [PubMed]
- Poater, J.; Duran, M.; Sola, M.; Silvi, B. Theoretical Evaluation of Electron Delocalization in Aromatic Molecules by Means of Atoms in Molecules (AIM) and Electron Localization Function (ELF) Topological Approaches. Chem. Rev. 2005, 105, 3911–3947. [Google Scholar] [CrossRef] [PubMed]
- Kruszewski, J.; Krygowski, T.M. Harmonic Oscillator Approach to the Definition of Aromaticity. Bull. Acad. Pol. Sci. Chim. 1972, 20, 907–915. [Google Scholar]
- Kruszewski, J.; Krygowski, T.M. Definition of Aromaticity Basing on the Harmonic Oscillator Model. Tetrahedron Lett. 1972, 3839–3842. [Google Scholar] [CrossRef]
- Krygowski, T.M.; Kruszewski, J. Bond Reactivity Index (BRI) in Terms of Simple Harmonic Oscillator Theory. Bull. Acad. Pol. Sci. Chim. 1973, 21, 409–412. [Google Scholar]
- Krygowski, T.M.; Kruszewski, J. Aromaticity of Thiophene, Pyrrole and Furan in Terms of Aromaticity Indices and Hammett ρ Constants. Bull. Acad. Pol. Sci. Chim. 1974, 22, 871–876. [Google Scholar]
- Krygowski, T.M. Crystallographic Studies of Inter- and Intramolecular Interactions Reflected in Aromatic Character of π-Electron Systems. J. Chem. Inform. Comput. Sci. 1993, 33, 70–78. [Google Scholar] [CrossRef]
- Jug, K.; Koester, A. Influence of σ and π Electrons on Aromaticity. J. Am. Chem. Soc. 1990, 112, 6772–6777. [Google Scholar] [CrossRef]
- Raczyńska, E.D. On n-π Electron Distribution in Simple Keto-Enol Tautomeric Systems: H3C−C(R)=OH2C=C(R)−OH and RH2CCH=ORHC=CH−OH. Pol. J. Chem. 2005, 79, 749–758. [Google Scholar]
- Raczyńska, E.D.; Ośmiałowski, B.; Gawinecki, R. Tautomeric Equilibria (1,5-Proton Shift) in Simple Heteroconjugated Systems HX−A=B−C=YX=A−B=C−YH in Relation to π Electron Delocalization. Pol. J. Chem. 2005, 79, 1093–1097. [Google Scholar]
- Raczyńska, E.D. On n-π Electron Distribution in Simple Acyclic Tetrad and Pentad Tautomeric Systems. Pol. J. Chem. 2005, 79, 1003–1013. [Google Scholar]
- Raczyńska, E.D.; Krygowski, T.M.; Zachara, J.E.; Ośmiałowski, B.; Gawinecki, R. Tautomeric Equilibria, H-Bonding and π-Electron Delocalization in o-Nitrosophenol. A B3LYP/6-311+G(2df,2p) Study. J. Phys. Org. Chem. 2005, 18, 892–897. [Google Scholar] [CrossRef]
- Osmialowski, B.; Raczyńska, E.D.; Krygowski, T.M. Tautomeric Equilibria and Pi Electron Delocalization for Some Monohydroxyarenes–Quantum Chemical Studies. J. Org. Chem. 2006, 71, 3727–3736. [Google Scholar] [CrossRef] [PubMed]
- Raczyńska, E.D.; Krygowski, T.M.; Duczmal, K.; Hallmann, M. On Geometry-Based HOMED (A Measure of Hyperconjugation, n-π, and π-π Conjugation) and HOMA Index (A Measure of Aromaticity). In Proceedings of the XVIII International Conference on Physical Organic Chemistry, Warsaw, Poland, 20–25 August 2006; p. 31. [Google Scholar]
- Parr, R.G.; Yang, W. Density Functional Theory of Atoms and Molecules; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. 1988, B37, 785–789. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional Exchange-energy Approximation with Correct Asymptotic Behavior. Phys. Rev. 1988, A38, 3098–3100. [Google Scholar] [CrossRef]
- Jensen, F. Introduction to Computational Chemistry; John Wiley & Sons: New York, NY, USA, 1999. [Google Scholar]
- Cyrański, M.K.; Gilski, M.; Jaskólski, M.; Krygowski, T.M. On the Aromatic Character of the Heterocyclic Bases of DNA and RNA. J. Org. Chem. 2003, 68, 8607–8613. [Google Scholar] [CrossRef]
- Böhm, S.; Fiedler, P.; Exner, O. Analysis of the Ortho Effect. Acidity of 2-Substituted Benzoic Acids. New. J. Chem. 2004, 28, 67–74. [Google Scholar] [CrossRef]
- Fiedler, P.; Böhm, S.; Kulhánek, J.; Exner, O. Acidity of Ortho-Substituted Benzoic Acids: An Infrared and Theoretical Study of the Intramolecular Hydrogen Bonds. Org. Biomol. Chem. 2006, 4, 2003–2011. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.L.; Wannere, C.S.; Mo, Y.; Schleyer, P.v.R.; Bunz, U.H.F. 4n π Electron but Stable: N,N-Dihydrodiazapentacenes. J. Org. Chem. 2009, 74, 4343–4349. [Google Scholar] [CrossRef] [PubMed]
- Wodrich, M.D.; Wannere, C.S.; Mo, Y.; Jarowski, P.D.; Houk, K.N.; Schleyer, P.v.R. The Concept of Protobranching and Its Many Paradigm Shifting Implications for Energy Evaluations. Chem. Eur. J. 2007, 13, 7731–7744. [Google Scholar] [CrossRef] [PubMed]
- Madura, I.D.; Krygowski, T.M.; Cyrański, M.K. Structural Aspects of the Aromaticity of Cyclic π-Electron Systems with BN Bonds. Tetrahedron 1998, 54, 14913–14918. [Google Scholar] [CrossRef]
- Weinhold, F. Chemistry: A New Twist on Molecular Shape. Nature 2001, 411, 539–541. [Google Scholar] [CrossRef]
- Pophristic, V.; Goodman, L. Hyperconjugation not Steric Repulsion Leads to the Staggered Structure of Ethane. Nature 2001, 411, 565–568. [Google Scholar] [CrossRef] [PubMed]
- Pophristic, V.; Goodman, L. Origin of Staggered Conformational Preference in Methanol. J. Phys. Chem. A 2002, 106, 1642–1646. [Google Scholar] [CrossRef]
- Mó, Y.R.; Wu, W.; Song, L.C.; Lin, M.H.; Zhang, Q.; Gao, J.L. The Magnitude of Hyperconjugation in Ethane: A Perspective from Ab initio Valence Bond Theory. Angew. Chem. Int. Ed. 2004, 43, 1986–1990. [Google Scholar] [CrossRef]
- Fleischer, U.; Kutzelnigg, W.; Lazzeretti, P.; Mühlenkamp, V. IGLO Study of Benzene and Some of Ist Isomers and Related Molecules. Search for Evidence of the Ring Current Model. J. Am. Chem. Soc. 1994, 116, 5298–5306. [Google Scholar] [CrossRef]
- Steinmann, S.N.; Jana, D.F.; Wu, J.I.C.; Schleyer, P.v.R.; Mo, Y. Corminboeuf C. Direct Assessment of Electron Delocalization Using NMR Chemical Shifts. Angew. Chem. Int. Ed. 2009, 48, 9828–9833. [Google Scholar] [CrossRef]
- Carey, F.A.; Sundberg, R.J. Advanced Organic Chemistry, 3rd ed.; Plenum Press: New York, NY, USA, 1993. [Google Scholar]
- Möller, C.; Plesset, M.S. Note on an Approximation Treatment for Many-electron Systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef]
- Pople, J.A.; Brinkley, J.S.; Seeger, R. Theoretical Models Incorporating Electron Correlation. Int. J. Quantum. Chem. 1976, 10, 1–19. [Google Scholar] [CrossRef]
- March, J. Advanced Organic Chemistry, Reaction, Mechanism and Structure, 4th ed.; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Prasad, B.V.; Grover, G.; Uppal, P.; Kaur, D. N-Inversion and C–N Rotational Barriers in HX=CH–NH2 (X = N, P, As) Compounds: An Ab initio Study. Theochem-J. Mol. Struct. 1999, 458, 227–237. [Google Scholar] [CrossRef]
- Burk, P.; Schleyer, P.v.R. Why Are Carboxylic Acids Stronger Acids than Alcohols? The Electrostatic Theory of Siggel-Thomas Revisites. Theochem-J. Mol. Struct. 2000, 505, 161–167. [Google Scholar] [CrossRef]
- Mó, Y.; Schleyer, P.v.R.; Wu, W.; Menghai, L.; Zhang, Q.; Gao, J. Importance of Electrostatic Delocalization on the C−N Bond Rotation in HCX(NH2) (X = O, NH, CH2, S, and Se). J. Phys. Chem. A 2003, 107, 10011–10018. [Google Scholar] [CrossRef]
- Elguero, J.; Marzin, C.; Katritzky, A.R.; Linda, P. Advances in Heterocyclic Chemistry, Supplement 1; Katritzky, A.R., Boulton, A.J., Eds.; Academic Press: New York, NY, USA, 1976. [Google Scholar]
- Rappoport, Z. (Ed.) The Chemistry of Enols; Wiley: Chichester, UK, 1990. [Google Scholar]
- Rappoport, Z. (Ed.) The Chemistry of Phenols; John Wiley & Sons: Chichester, UK, 2003. [Google Scholar]
- Pozharskii, A.F.; Soldatenkov, A.T.; Katritzky, A.R. Heterocycles in Life and Society; Wiley: New York, NY, USA, 1997. [Google Scholar]
- Raczyńska, E.D.; Zientara, K.; Kolczyńska, K.; Stępniewski, T.M. Change of Tautomeric Equilibria, Intramolecular Interactions and π-Electron Delocalization when Going from Phenol to Uracil. Theochem-J. Mol. Struct. 2009, 894, 103–111. [Google Scholar] [CrossRef]
- Raczyńska, E.D.; Kolczyńska, K.; Stępniewski, T.M. Influence of N-Aza Group(s), Intramolecular Interactions and Ionization on Tautomeric Equilibria for Cytosine. In Proceedings of the 42nd IUPAC Congress, Chemistry Solution, Glasgow, UK, 2–7 August 2009. P202_021. [Google Scholar]
- Raczyńska, E.D.; Zientara, K.; Stępniewski, T.M.; Kolczyńska, K. Stability, Polarity, Intramole-cular Interactions and π-Electron Delocalization for all Eighteen Tautomers Rotamers of Uracil. DFT Studies in the Gas Phase. Collect. Czech. Chem. Commun. 2009, 74, 57–72. [Google Scholar] [CrossRef]
- Firsch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A., Jr.; Vreven, T.; Kudin, K.N.; Burant, J.C.; Millam, J.M.; Iyengar, S.S.; Tomasi, J.; Barone, V.; Mennucci, B.; Cossi, M.; Scalmani, G.; Rega, N.; Petersson, R.; Nakatsuji, H.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Klene, M.; Li, X.; Knox, J.E.; Hratchian, H.P.; Cross, J.B.; Bakken, V.; Adamo, C.; Jaramillo, R.; Gomperts, R.; Stratmann, R.E.; Yazyev, O.; Austin, A.J.; Cammi, R.; Pomelli, C.; Ochterski, J.W.; Ayala, P.Y.; Morokuma, K.; Voth, G.A.; Salvador, P.; Dannenberg, J.J.; Zakrzewski, V.G.; Dapprich, S.; Daniels, A.D.; Strain, M.C.; Farkas, O.; Malick, D.K.; Rabuck, A.D.; Raghavachari, K.; Foresman, J.B.; Oritz, J.V.; Cui, Q.; Baboul, A.G.; Clifford, S.; Cioslowski, J.; Stefanov, B.B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Martin, R.L.; Fox, D.J.; Keith, T.; Al-Laham, M.A.; Peng, C.Y.; Nanayakkara, A.; Challacombe, M.; Gill, P.M.W.; Johnson, B.; Chen, W.; Wong, M.W.; Gonzalez, C.; Pople, J.A. Gaussian-03, Revision E.01; Gaussian, Inc.: Wallingford, CT, USA, 2004. [Google Scholar]
- Mo, Y.; Schleyer, P.v.R. An Energetic Measure of Aromaticity and Antiaromaticity Based on the Pauling-Wheland Resonance Energies. Chem. Eur. J. 2006, 12, 2009–2020. [Google Scholar] [CrossRef] [PubMed]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an Open Access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).