On the Importance of Clar Structures of Polybenzenoid Hydrocarbons as Revealed by the π-Contribution to the Electron Localization Function
Abstract
:1. Introduction
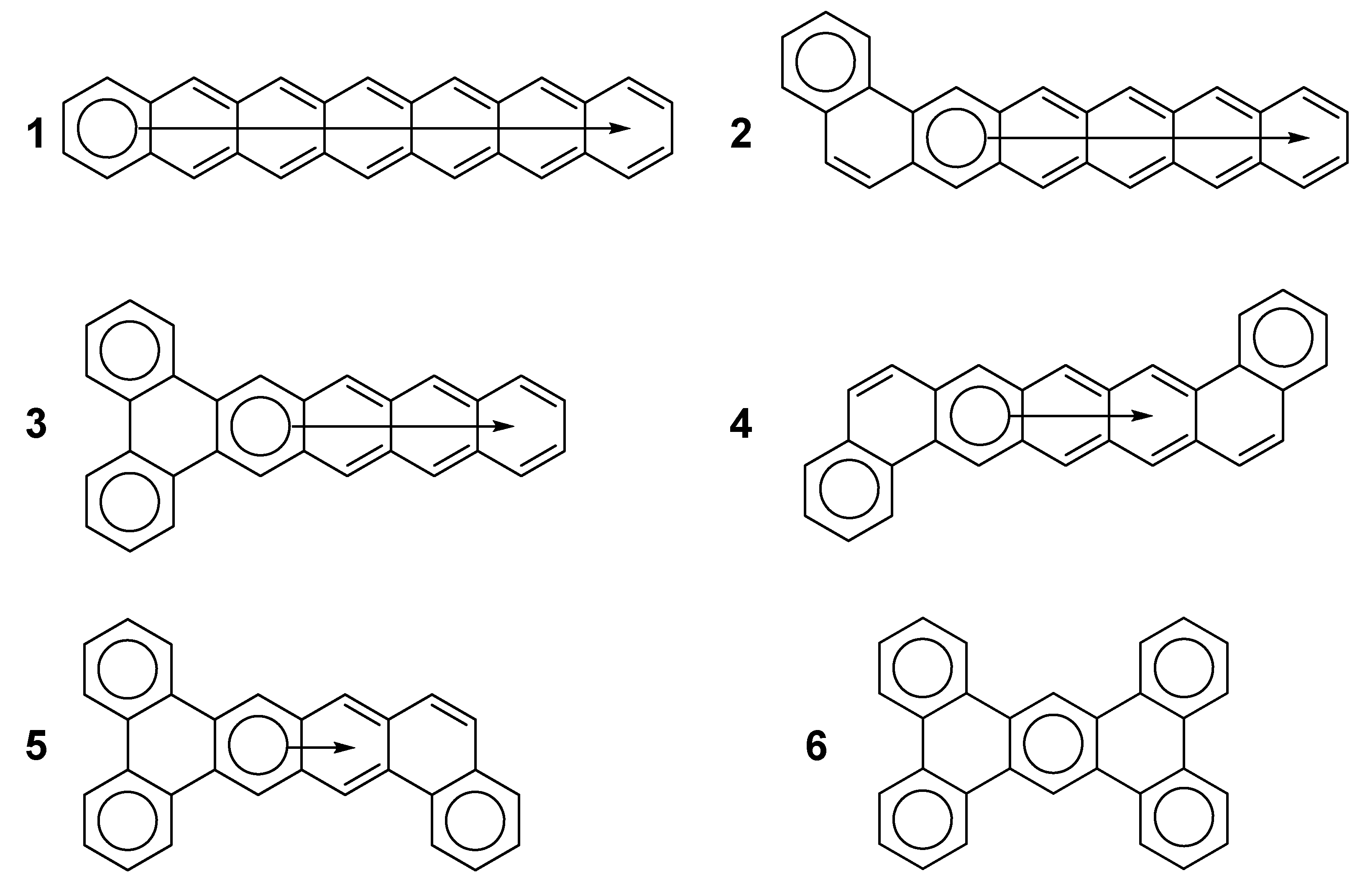
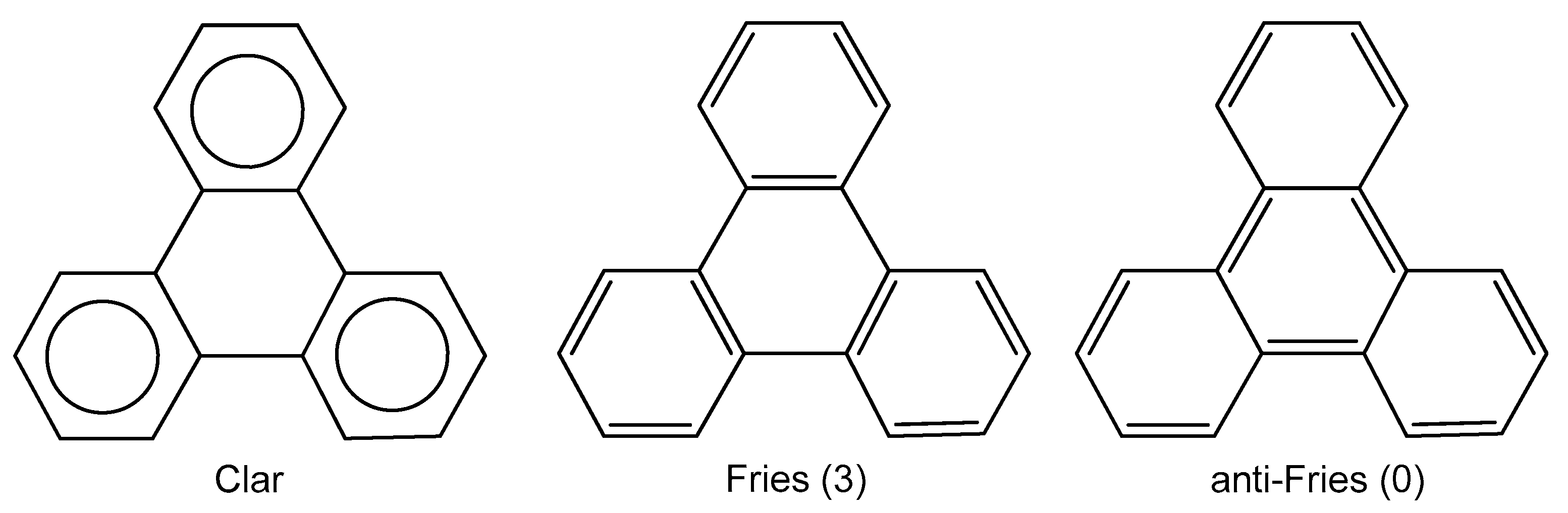
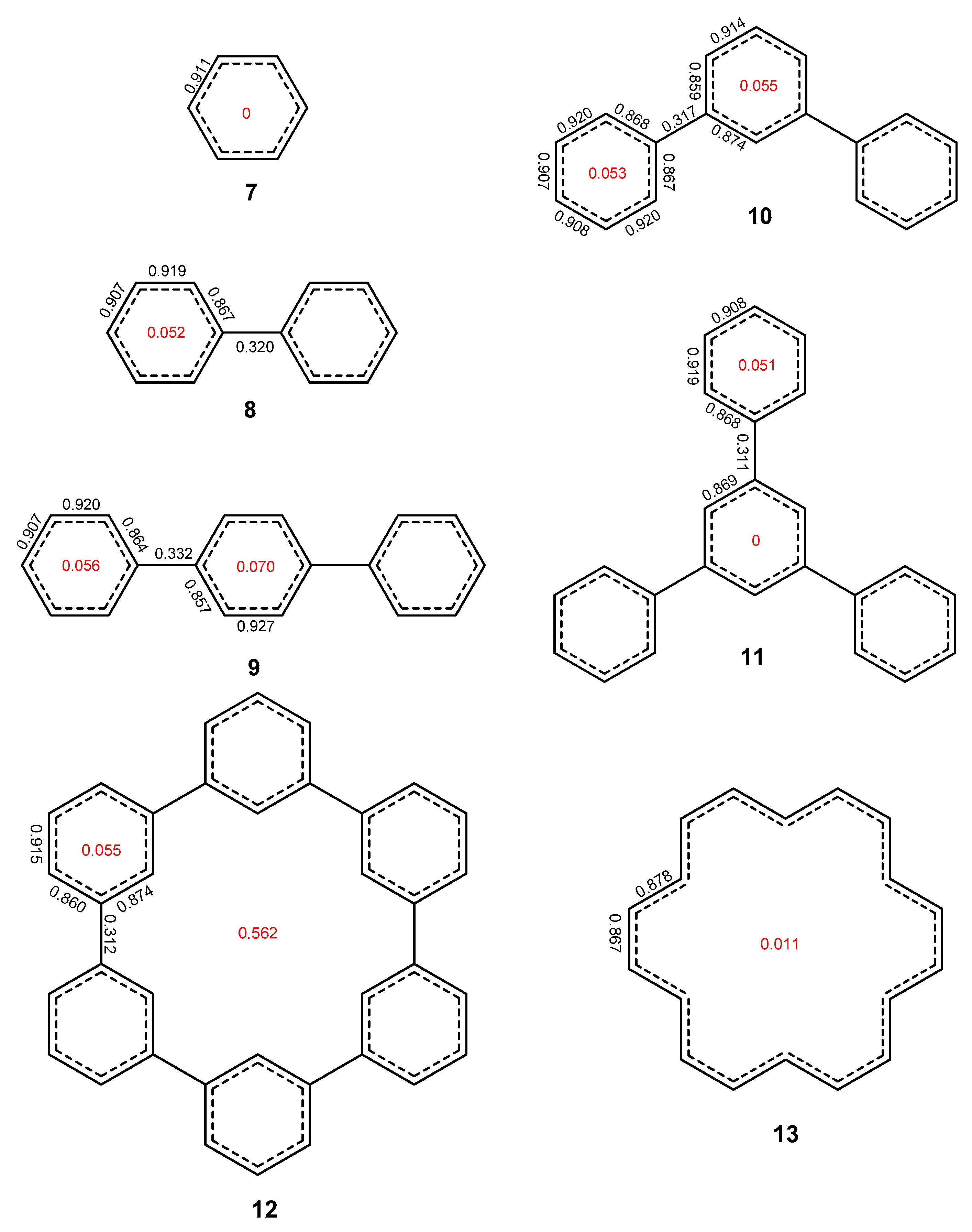
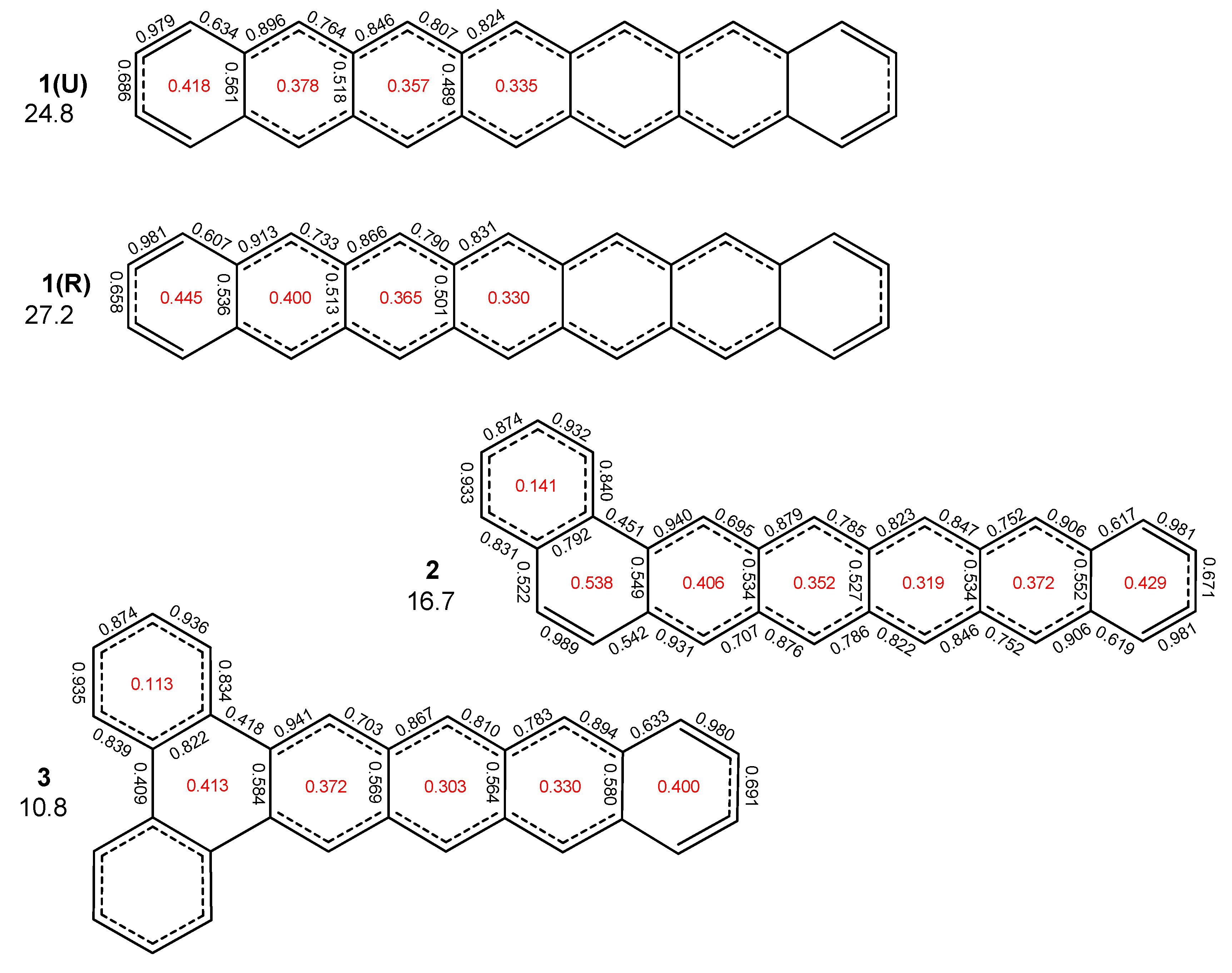
2. Results and Discussion
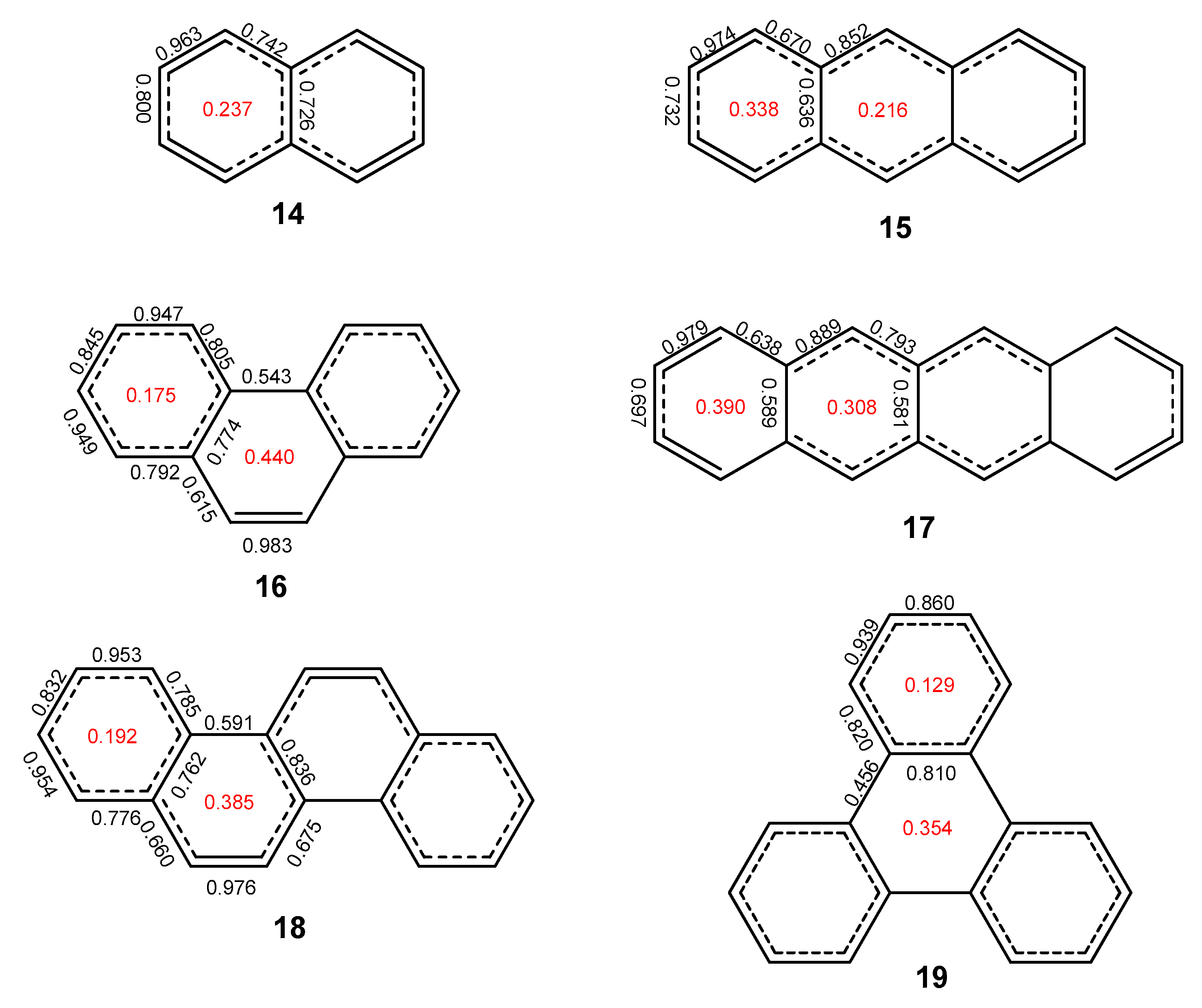
2.1. Oligophenyls
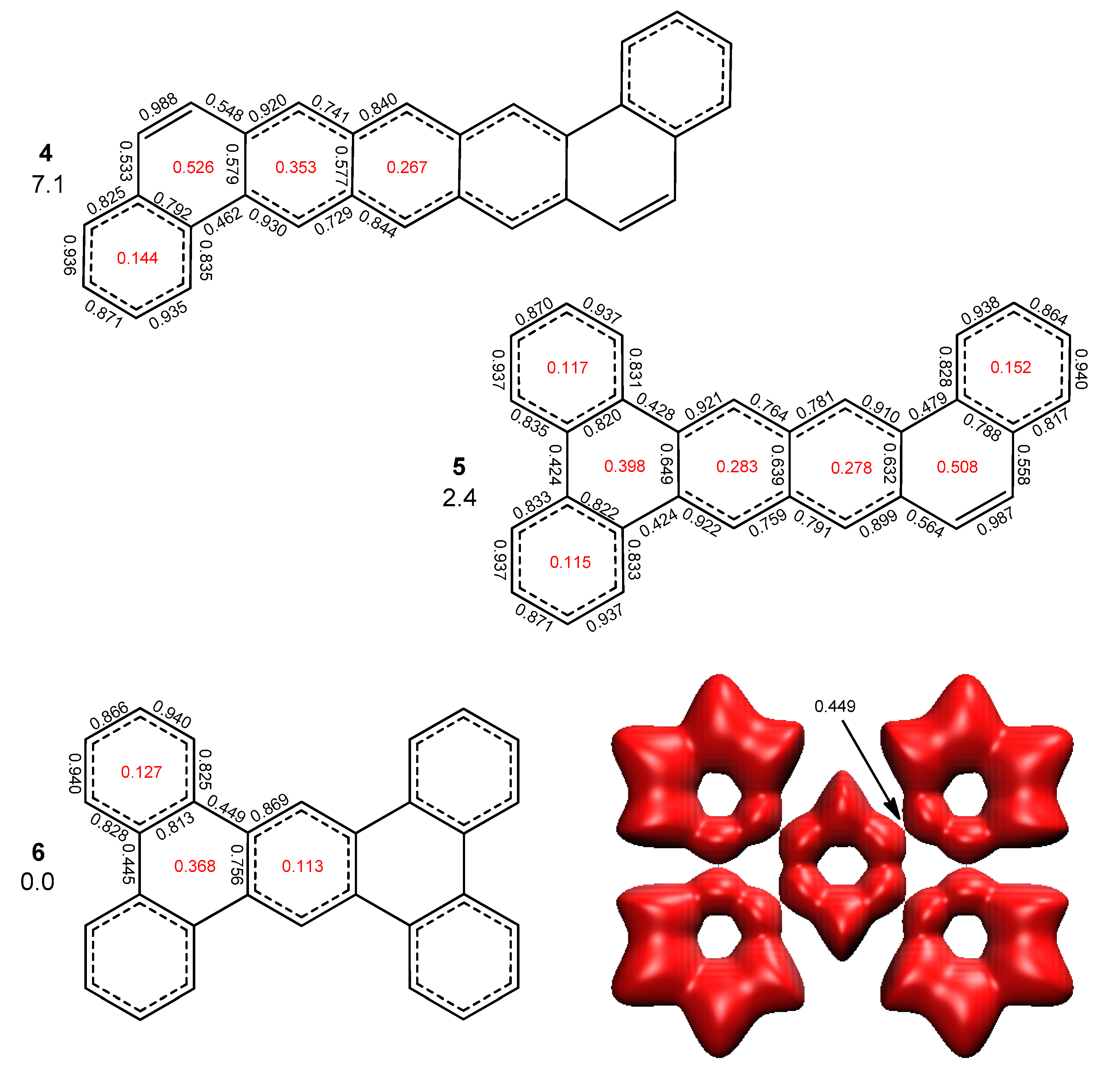
2.2. Heptabenzenoids
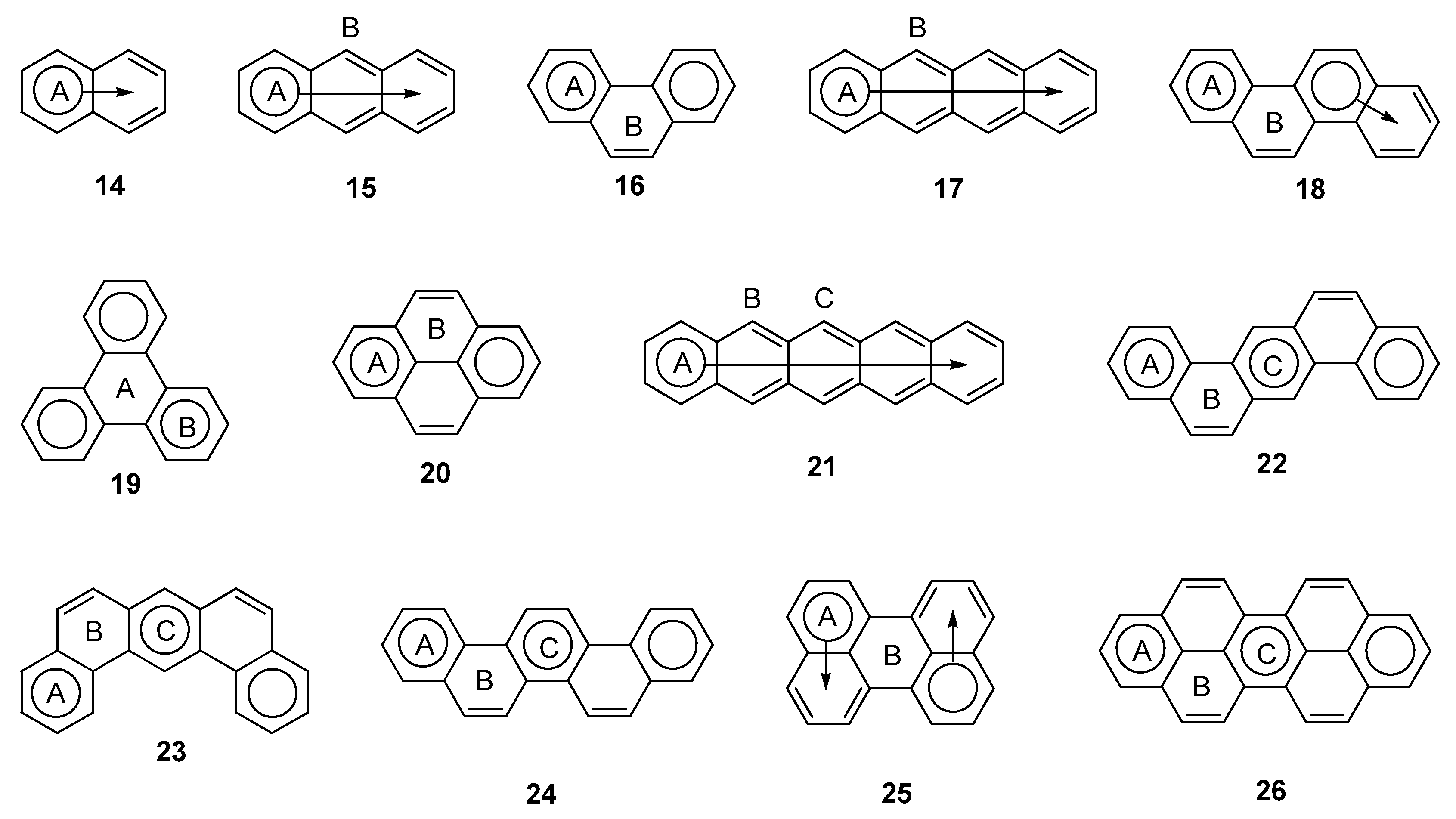
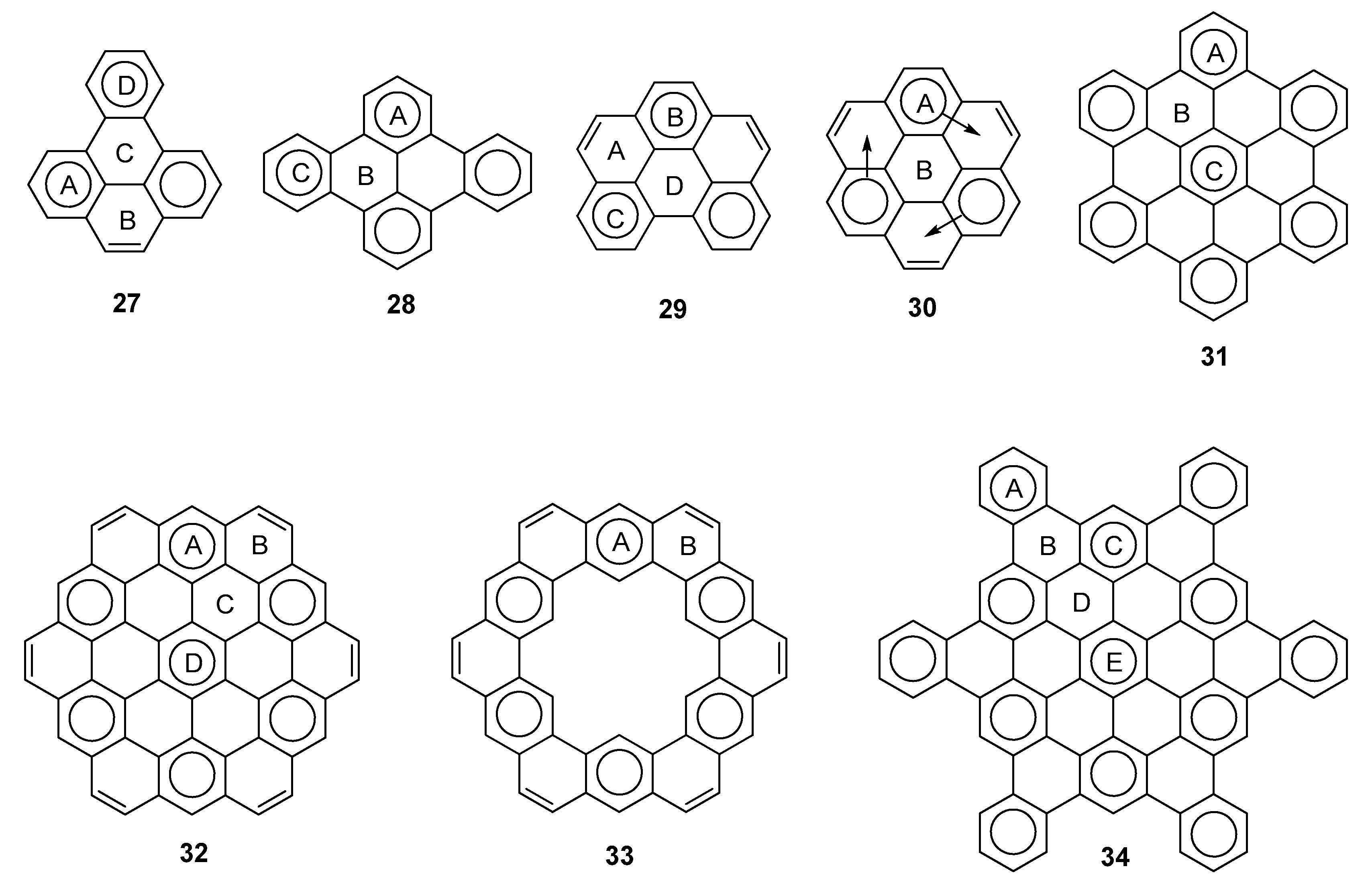
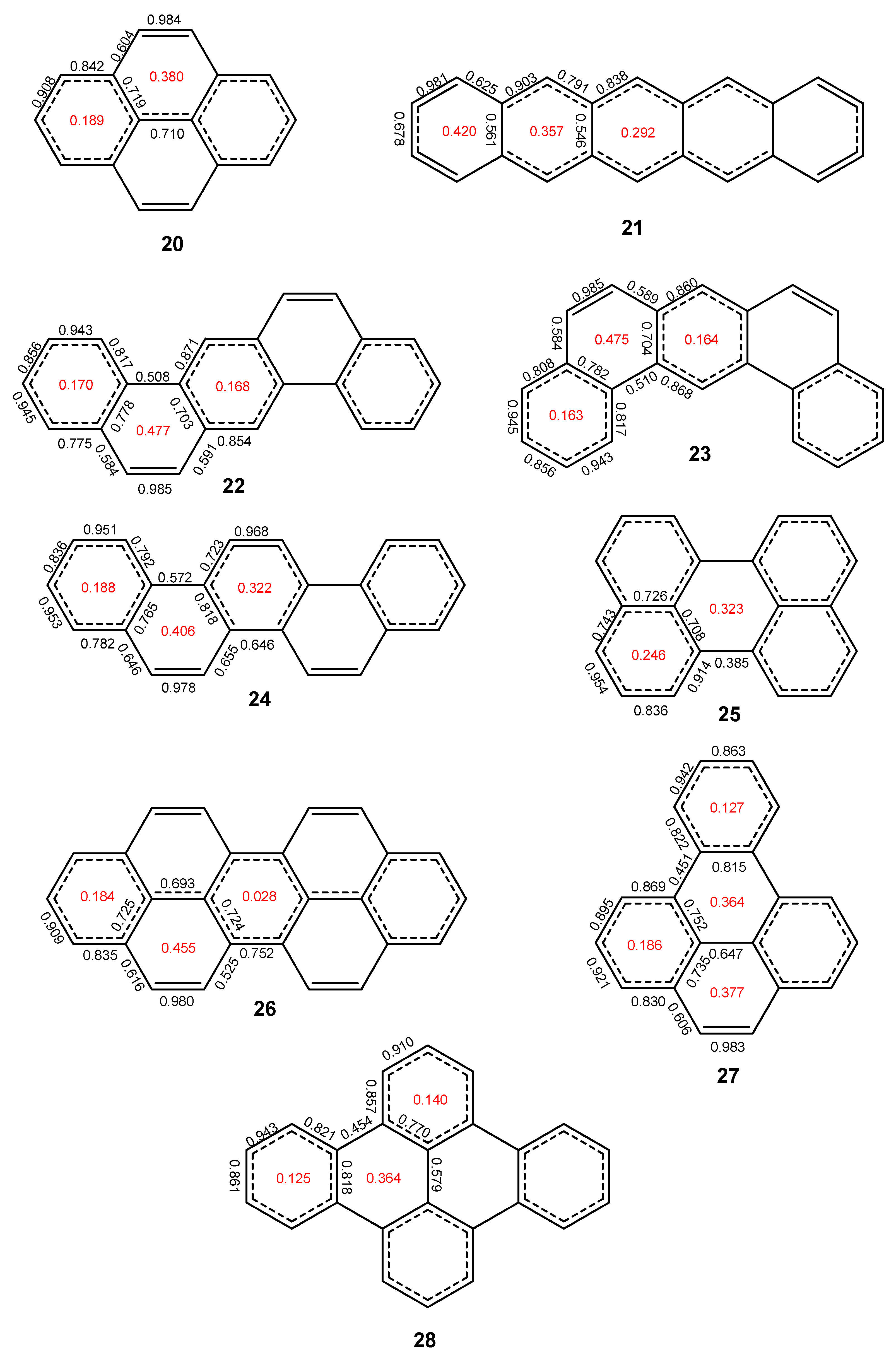
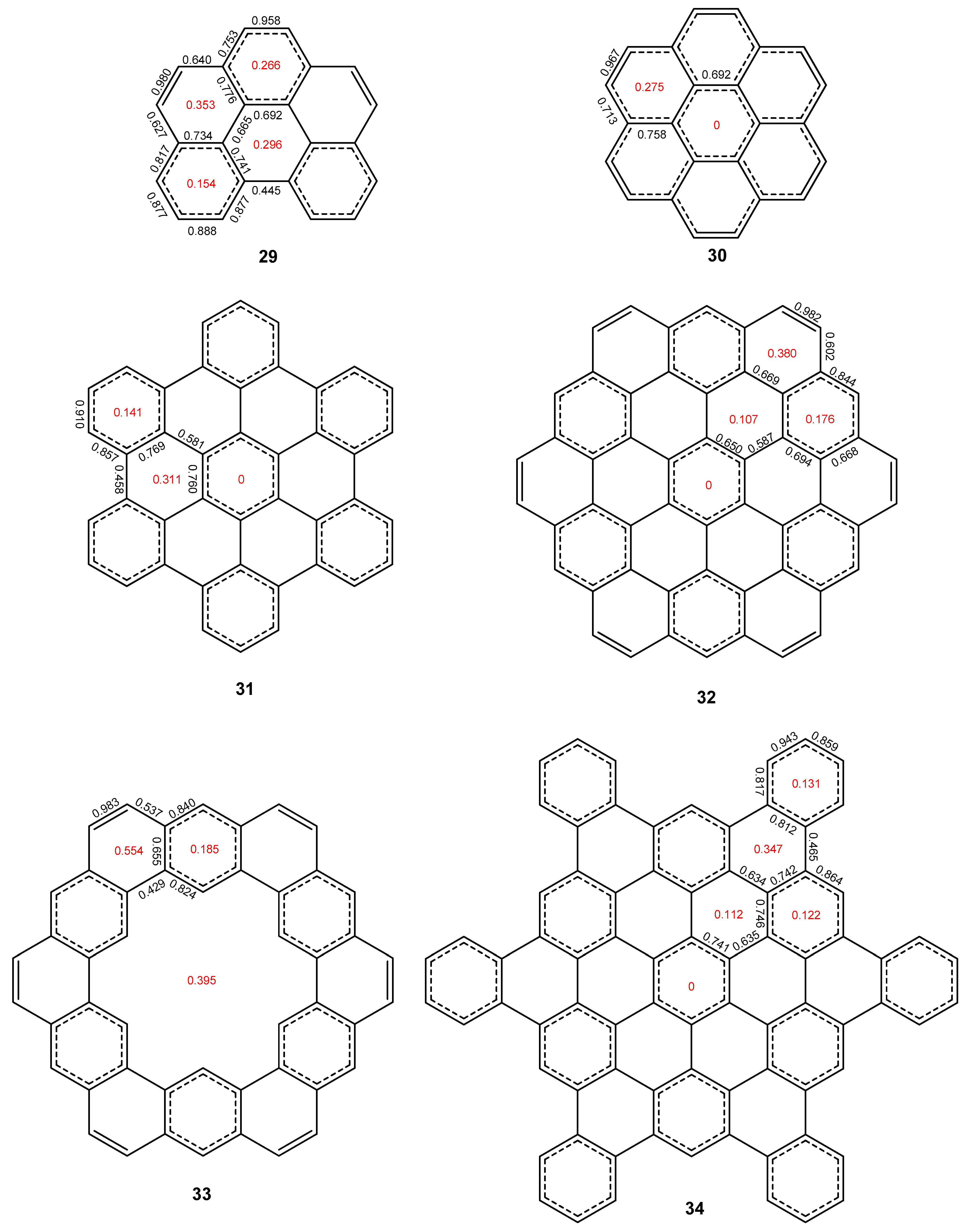
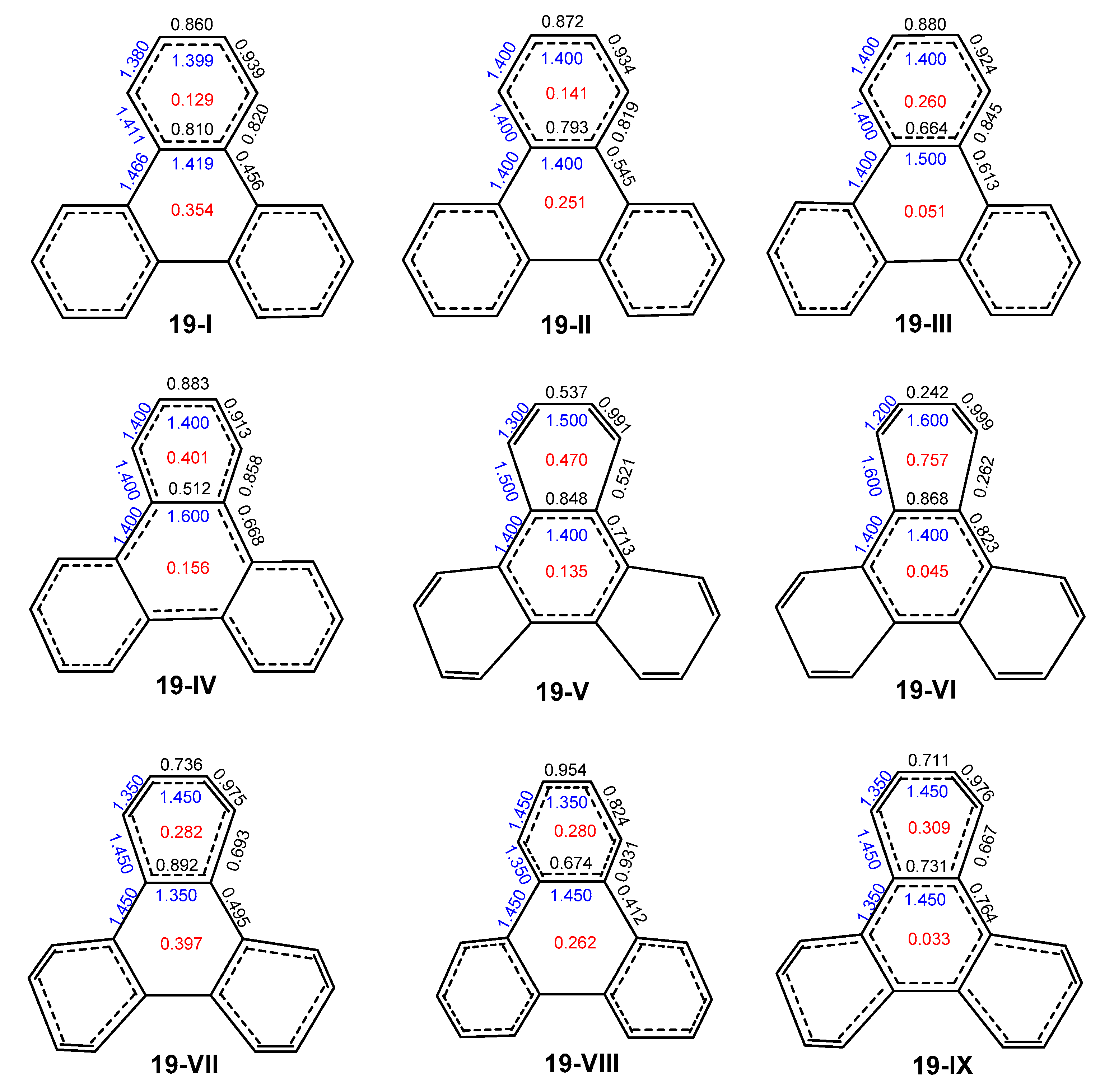
2.3. Other Polybenzenoid Hydrocarbons
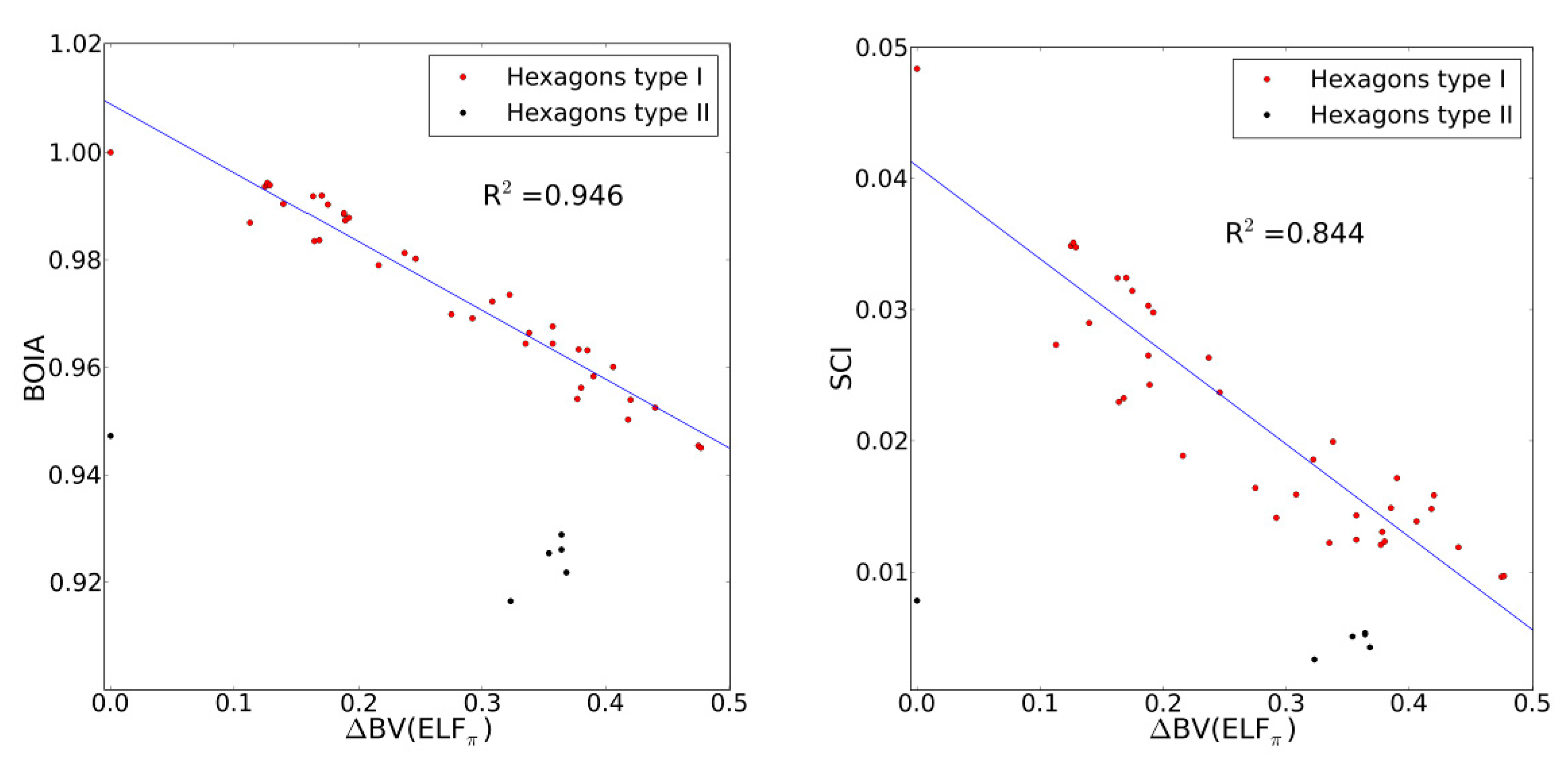
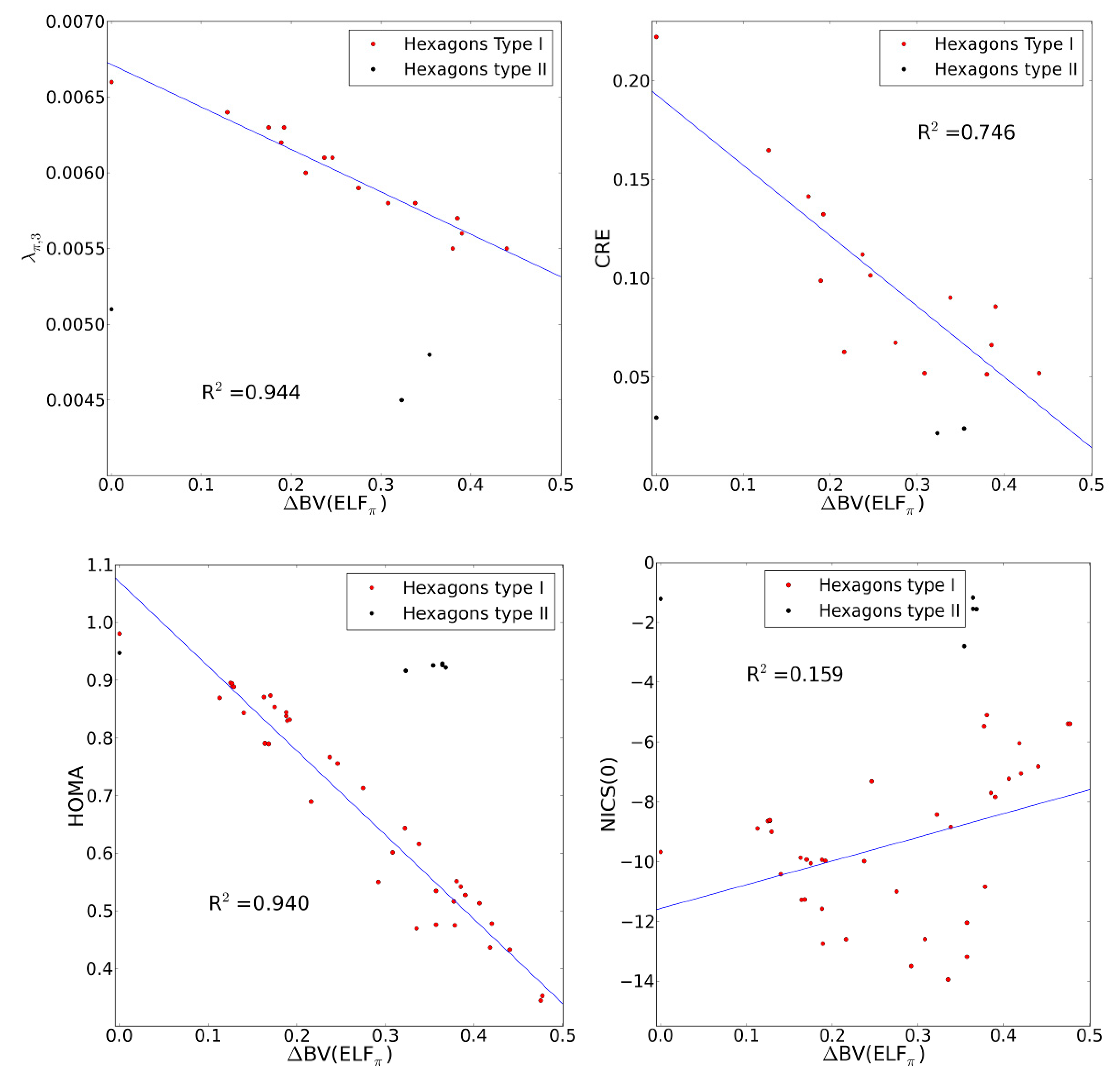
2.4. Comparison with Previous Aromaticity Indices
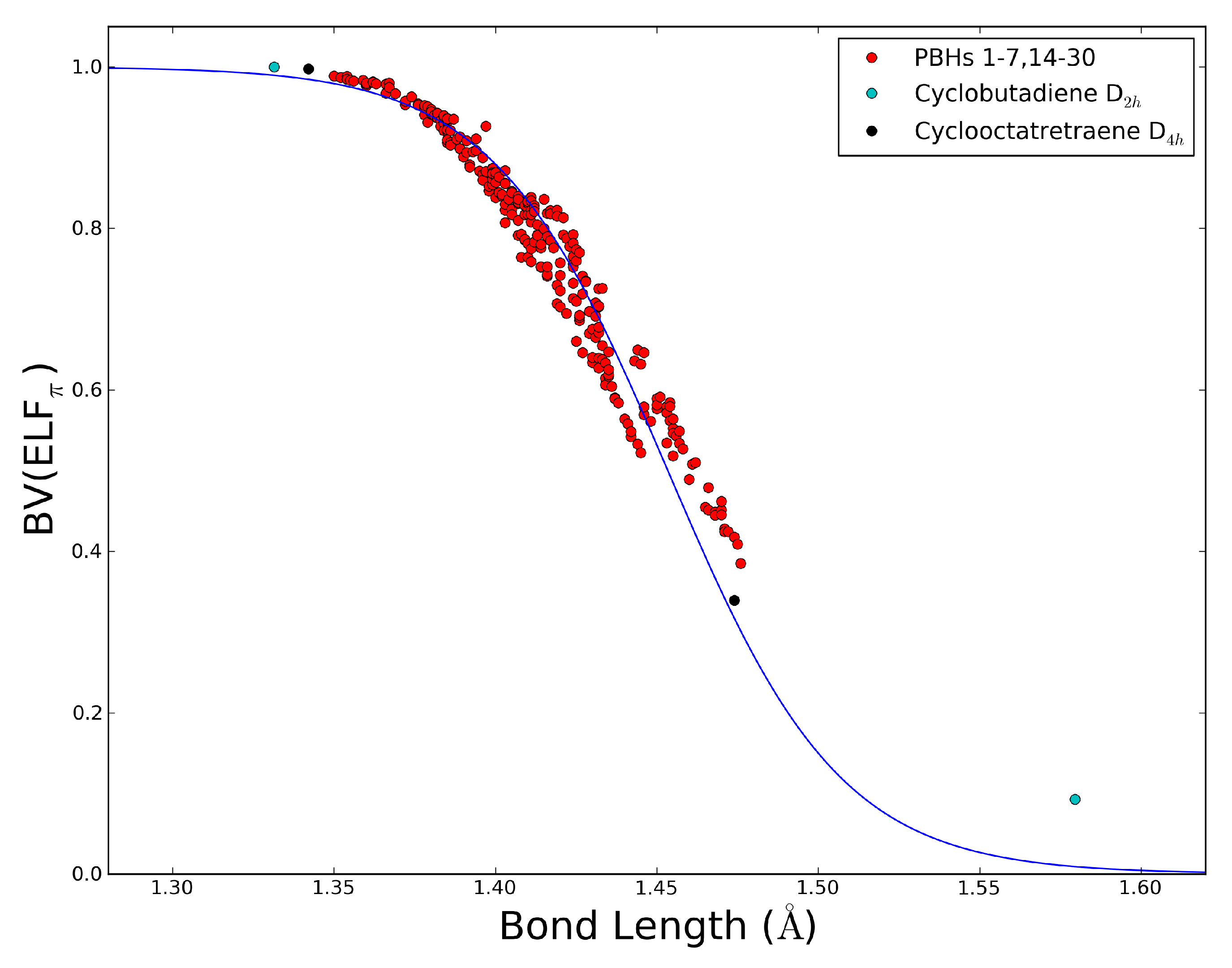
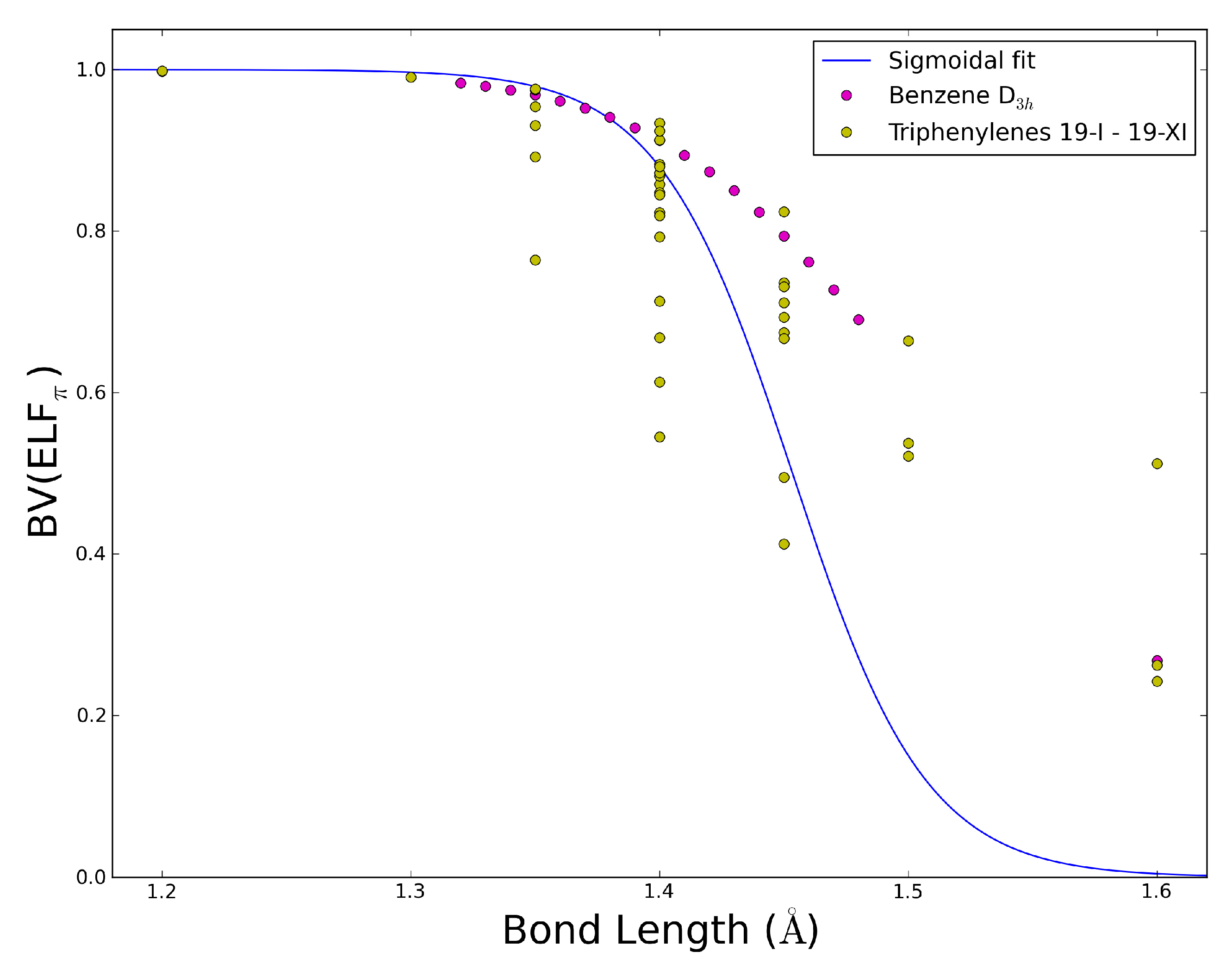
2.5. The ELFπ Bifurcation Values and CC Bond Lengths
3. Computational Methods
4. Conclusions
Acknowledgements
References and Notes
- Dimitrakopoulos, C.D.; Malenfant, P.R.L. Organic Thin Film Transistors for Large Area Electronics. Adv. Mater. 2002, 14, 99–117. [Google Scholar] [CrossRef]
- Bao, Z.; Locklin, J. Organic Field-Effect Transistors; CRC Press: Boca Raton, Fl, USA, 2007. [Google Scholar]
- Asadi, K.; Wu, Y.; Gholamrezaie, F.; Rudolf, P.; Blom, P.W.M. Single-Layer Pentacene Field-Effect Transistors Using Electrodes Modified with Self-Assembled Monolayers. Adv. Mater. 2009, 21, 4109–4114. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Tung, V.C.; Allen, M.J.; Yang, Y.; Kaner, R.B. High-Throughput Solution Processing of Large-Scale Graphene. Nature Nanotech. 2009, 4, 25–29. [Google Scholar] [CrossRef]
- Kechedzhi, K.; Horsell, D.W.; Tikhonenko, F.V.; Savchenko, A.K.; Gorbachev, R.V.; Lerner, I.V.; Fal’ko, V.I. Quantum Transport Thermometry for Electrons in Graphene. Phys. Rev. Lett. 2009, 102, 066801. [Google Scholar] [CrossRef]
- Elias, D.C.; Nair, R.R.; Mohiuddin, T.M.G.; Morozov, S.V.; Blake, P.; Halsall, M.P.; Ferrari, A.C.; Boukhvalov, D.W.; Katsnelson, M.I.; Geim, A.K.; Novoselov, K.S. Control of Graphene’s Properties by Reversible Hydrogenation: Evidence for Graphane. Science 2009, 323, 610–613. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K.; Novoselov, K.S. The Rise of Graphene. Nature Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Radovic, L.R.; Bockrath, B. On the Chemical Nature of Graphene Edges: Origin of Stability and Potential for Magnetism in Carbon Materials. J. Am. Chem. Soc. 2005, 127, 5917–5927. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-Dimensional Gas of Massless Dirac Fermions in Graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef]
- Zhang, Y.; Tan, J.W.; Stormer, H.L.; Kim, P. Experimental Observation of the Quantum Hall Effect and Berry’s Phase in Graphene. Nature 2005, 438, 201–204. [Google Scholar] [CrossRef]
- Zheng, Y.S.; Ando, T. Hall Conductivity of a Two-Dimensional Graphite System. Phys. Rev. B. 2002, 65, 245420. [Google Scholar] [CrossRef]
- Gusynin, V.P.; Sharapov, S.G. Unconventional Integer Quantum Hall Effect in Graphene. Phys. Rev. Lett. 2005, 95, 146801. [Google Scholar] [CrossRef] [PubMed]
- Peres, N.M.R.; Guinea, F.; Neto, A.H.C. Electronic Properties of Two-Dimensional Carbon. Ann. Phys. 2006, 321, 1559–1567. [Google Scholar] [CrossRef]
- Clar, E.; Kelly, W. Aromatic Hydrocarbons. 67. Heptaphene and 2,3,8,9-Dibenzopicene. J. Am. Chem. Soc. 1954, 76, 3502–3504. [Google Scholar]
- Clar, E.; McCallum, A. The Significance of Benzenoid Rings for the Stability of Aromatic Hydrocarbons. Tetrahedron 1960, 10, 171–174. [Google Scholar] [CrossRef]
- Clar, E. Polycyclic Hydrocarbons; AP: London, UK, 1964. [Google Scholar]
- Clar, E. The Aromatic Sextet; Wiley: New York, NY, USA, 1972. [Google Scholar]
- See e.g., the two comprehensive review collections edited by Schleyer, P. v. R. in Chem. Rev. 2001, 101, number 5 on the topic of Aromaticity, and Chem. Rev. 2005, 105, number 10 on the topic of Delocalization—Pi and Sigma, as well as the present special issue of Symmetry on the topic of Aromaticity and Molecular Symmetry, Guest Editor: P. v. R. Schleyer.
- Feixas, F.; Matito, E.; Poater, J.; Solà, M. On the Performance of Some Aromaticity Indices: A Critical Assessment Using a Test Set. J. Comput. Chem. 2008, 29, 1543–1554. [Google Scholar] [CrossRef] [PubMed]
- Solà, M.; Feixas, F.; Jiménez-Halla, J.O.C.; Matito, E.; Poater, J. A Critical Assessment of the Performance of Magnetic and Electronic Indices of Aromaticity. Symmetry 2010, 2, 1156–1179. [Google Scholar] [CrossRef]
- Becke, A.D.; Edgecombe, K.E. A Simple Measure of Electron Localization in Atomic and Molecular Systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Santos, J.C.; Tiznado, W.; Contreras, R.; Fuentealba, P. Sigma-Pi Separation of the Electron Localization Function and Aromaticity. J. Chem. Phys. 2004, 120, 1670–1673. [Google Scholar] [CrossRef]
- Santos, J.C.; Andres, J.; Aizman, A.; Fuentealba, P. An Aromaticity Scale Based on the Topological Analysis of the Electron Localization Function Including σ and π Contributions. J. Chem. Theory Comput. 2005, 1, 83–86. [Google Scholar] [CrossRef]
- Malrieu, J.P.; Lepetit, C.; Gicquel, M.; Heully, J.-L.; Fowler, P.W.; Chauvin, R. Evaluating the Cyclic π-Electron Delocalization Energy through a Double Cut of Conjugated Rings. New J. Chem. 2007, 31, 1918–1927. [Google Scholar] [CrossRef]
- Villaume, S.; Fogarty, H.A.; Ottosson, H. Triplet-State Aromaticity of 4nπ-Electron Monocycles: Analysis of Bifurcation in the π-Contribution to the Electron Localization Function. Chem. Phys. Chem. 2008, 9, 257–264. [Google Scholar] [CrossRef] [PubMed]
- Villaume, S.; Ottosson, H. Aromaticity Changes along the Lowest-Triplet-State Path for C=C Bond Rotation of Annulenyl-Substituted Olefins Probed by the Electron Localization Function. J. Phys. Chem. A 2009, 113, 12304–12310. [Google Scholar] [CrossRef] [PubMed]
- In reference 24 we found a connection between the CC bond lengths and the BV(ELFπ)’s of annulenes at their equilibrium geometries, and the BV(ELFπ)’s of 0.65 and 0.96 approximately correspond to CC bond lengths of 1.43 and 1.38 Å, respectively.
- Mandado, M.; Gonzalez-Moa, M.J.; Mosquera, R.A. Chemical Graph Theory and n-Center Electron Delocalization Indices: A Study of Polycyclic Aromatic Hydrocarbons. J. Comput. Chem. 2007, 28, 1625–1633. [Google Scholar] [CrossRef]
- Balaban, A.T.; Pompe, M.; Randic, M. π-Electron Partitions, Signatures, and Clar Structures of Selected Benzenoid Hydrocarbons. J. Phys. Chem. A 2008, 112, 4148–4157. [Google Scholar] [CrossRef] [PubMed]
- Balaban, A.T.; Randic, M. Correlations between Various Ways of Accounting for the Distribution of π-Electrons in Benzenoids. New J. Chem. 2008, 32, 1071–1078. [Google Scholar] [CrossRef]
- Misra, A.; Klein, D.J.; Morikawa, T. Clar Theory for Molecular Benzenoids. J. Phys. Chem. A 2009, 113, 1151–1158. [Google Scholar] [CrossRef] [PubMed]
- Howard, S.T.; Krygowski, T.M. Benzenoid Hydrocarbon Aromaticity in Terms of Charge Density Descriptors. Can. J. Chem. 1997, 75, 1174–1181. [Google Scholar] [CrossRef]
- Portella, G.; Poater, J.; Sola, M. Assessment of Clar’s Aromatic π-Sextet Rule by Means of PDI, NICS and HOMA Indicators of Local Aromaticity. J. Phys. Org. Chem. 2005, 18, 785–791. [Google Scholar] [CrossRef]
- Poater, J.; Fradera, X.; Duran, M.; Sola, M. The Delocalization Index as an Electronic Aromaticity Criterion: Application to a Series of Planar Polycyclic Aromatic Hydrocarbons. Chem. Eur. J. 2003, 9, 400–406. [Google Scholar] [CrossRef]
- Matta, C.F.; Hernández-Trujillo, J. Bonding in Polycyclic Aromatic Hydrocarbon in Terms of the Electron Density and of Electron Delocalization. J. Phys. Chem. A. 2003, 107, 7496–7504. [Google Scholar] [CrossRef]
- Bultinck, P.; Ponec, R.; van Damme, S. Multicenter Bond Indices as a New Measure of Aromaticity in Polycyclic Aromatic Hydrocarbons. J. Phys. Org. Chem. 2005, 18, 706–718. [Google Scholar] [CrossRef]
- Mandado, M.; Bultinck, P.; González-Moa, M.J.; Mosquera, R.A. Multicenter Delocalization Indices vs. Properties of the Electron Density at Ring Critical Points: A Study of Polycyclic Aromatic Hydrocarbons. Chem. Phys. Lett. 2006, 433, 5–9. [Google Scholar] [CrossRef]
- Palusiak, M.; Krygowski, T.M. Application of AIM Parameters at Ring Critical Points for Estimation of π-Electron Delocalization in Six-Membered Aromatic and Quasi-Aromatic Rings. Chem. Eur. J. 2007, 13, 7996–8006. [Google Scholar] [CrossRef] [PubMed]
- Mohajeri, A.; Ashrafi, A. Aromaticity in Terms of Ring Critical Point Properties. Chem. Phys. Lett. 2008, 458, 378–383. [Google Scholar] [CrossRef]
- Ebrahimi, A.A.; Ghiasi, R.; Foroutan-Nejad, C. Topological Characteristics of the Ring Critical Points and the Aromaticity of Groups IIIA to VIA Hetero-Benzenes. J. Mol. Struct. THEOCHEM 2010, 941, 47–52. [Google Scholar] [CrossRef]
- Anusooya, Y.; Chakrabarti, A.; Pati, S.K.; Ramasesha, S. Ring Currents in Condensed Ring Systems. Int. J. Quant. Chem. 1998, 70, 503–513. [Google Scholar] [CrossRef]
- Aihara, J. π-Electron Currents Induced in Polycyclic Benzenoid Hydrocarbons and Their Relationship to Clar Structures. J. Phys. Chem. A 2003, 107, 11553–11557. [Google Scholar] [CrossRef]
- Aihara, J.; Kanno, H. Local Aromaticities in Large Polyacene Molecules. J. Phys. Chem. A 2005, 109, 3717–3721. [Google Scholar] [CrossRef]
- Aihara, J. Circuit Resonance Energy: A Key Quantity That Links Energetic and Magnetic Criteria of Aromaticity. J. Phys. Chem. A 2006, 128, 2873–2879. [Google Scholar] [CrossRef]
- Bultinck, P.; Fias, S.; Ponec, R. Local Aromaticity in Polycyclic Aromatic Hydrocarbons. Electron Delocalization versus Magnetic Indices. Chem. Eur. J. 2006, 12, 8813–8818. [Google Scholar] [CrossRef]
- Fias, S.; Fowler, P.W.; Delgado, J.L.; Hahn, U.; Bultinck, P. Correlation of Delocalization Indices and Current-Density Maps in Polycyclic Aromatic Hydrocarbons. Chem. Eur. J. 2008, 14, 3093–3099. [Google Scholar] [CrossRef] [PubMed]
- Mandado, M. Determinaton of London Susceptibilities and Ring Current Intensities using Conjugated Circuits. J. Chem. Theory Comput. 2009, 5, 2694–2701. [Google Scholar] [CrossRef] [PubMed]
- Schleyer, P.v.R.; Maerker, C.; Dransfeld, A.; Jiao, H.; von Eikema Hommes, N.J.R. Nucleus-Independent Chemical Shifts (NICS): A Simple and Efficient Aromaticity Probe. J. Am Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef] [PubMed]
- Schleyer, P.v.R.; Jiao, H.; van Eikema Hommes, N.J.R.; Malkin, V.G.; Malkina, O. An Evaluation of Aromaticity of Inorganic Rings: Refined Evidence from Magnetic Properties. J. Am. Chem. Soc. 1997, 119, 12669–12670. [Google Scholar] [CrossRef]
- Moran, D.; Stahl, F.; Bettinger, H.F.; Schaefer, H.F., III; Schleyer, P.v.R. Towards Graphite: Magnetic Properties of Large Polybenzenoid Hydrocarbons. J. Am. Chem. Soc. 2003, 125, 6746–6752. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Wannere, C.S.; Corminboeuf, C.; Puchta, R.; Schleyer, P.v.R. Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion. Chem. Rev. 2005, 105, 3842–3888. [Google Scholar] [CrossRef] [PubMed]
- Schleyer, P.v.R.; Manoharan, M.; Jiao, H.; Stahl, F. The Acenes: Is There a Relationship between Aromatic Stabilization and Reactivity? Org. Lett. 2001, 3, 3643–3646. [Google Scholar] [CrossRef]
- Fallah-Bagher-Shaidaei, H.; Wannere, C.S.; Corminboeuf, C.; Puchta, R.; Schleyer, P.v.R. Which NICS Aromaticity Index for Planar π Rings is Best? Org. Lett. 2006, 8, 863–866. [Google Scholar] [CrossRef]
- Krygowski, T.M. Crystallographic Studies of Inter- and Intramolecular Interactions Reflected in Aromatic Character of π-electron Systems. J. Chem. Inf. Comput. Sci. 1993, 33, 70–78. [Google Scholar] [CrossRef]
- Krygowski, T.M.; Cyrański, M.K. Structural Aspects of Aromaticity. Chem. Rev. 2001, 101, 1385–1419. [Google Scholar] [CrossRef]
- Maksić, Z.B.; Barić, D.; Müller, T. Clar’s Sextet Rule Is a Consequence of the σ-Electron Framework. J. Phys. Chem. A 2006, 110, 10135–10147. [Google Scholar] [CrossRef] [PubMed]
- Shaik, S.; Shurki, A.; Danovich, D.; Hiberty, P.C. A Different Story of π-Delocalization—the Distortivity of π-Electrons and Its Chemical Manifestation. Chem. Rev. 2001, 101, 1501–1539. [Google Scholar] [CrossRef] [PubMed]
- Hiberty, P.C.; Shaik, S. The Distortive Tendencies of π Electronic Systems, Their Relationship to Isoelectronic σ Bonded Analogs, and Observables: A Description Free of Classical Paradoxes. Phys. Chem. Chem. Phys. 2004, 6, 224–231. [Google Scholar] [CrossRef]
- Hiberty, P.C.; Shaik, S. Some Answers to Frequently Asked Questions About the Distortive Tendencies of π-Electronic System. Theor. Chem. Acc. 2005, 114, 169–181. [Google Scholar] [CrossRef]
- Angeli, C.; Malrieu, J.-P. Aromaticity: An ab Initio Evaluation of the Properly Cyclic Delocalization Energy and the π-Delocalization Energy Distortivity of Benzene. J. Phys. Chem. A 2008, 112, 11481–11486. [Google Scholar] [CrossRef]
- Malrieu, J.-P.; Gicquel, M.; Fowler, P.W.; Lepetit, C.; Heully, J.-L.; Chauvin, R. Direct Evaluation of Cyclic Contributions to the π Energy of Conjugated Hydrocarbons From Strongly Localized Zero-Order Pictures. J. Phys. Chem. A 2008, 112, 13203–13214. [Google Scholar] [CrossRef] [PubMed]
- Frank, N.L.; Baldridge, K.K.; Siegel, J.S. Synthesis and Characterization of Trisbicyclo[2.2.1]-hexabenzene, A Highly Strained Bicycloannelated Benzene. J. Am. Chem. Soc. 1995, 117, 2102–2103. [Google Scholar] [CrossRef]
- Fowler, P.W.; Havenith, R.W.A.; Jenneskens, L.W.; Soncini, A.; Steiner, E. Survival and Extinction of Delocalized Ring Currents in Clamped Benzenes. Chem. Commun. 2001, 2386–2387. [Google Scholar] [CrossRef]
- Soncini, A.; Havenith, R.W.A.; Fowler, P.W.; Jenneskens, L.W.; Steiner, E. Control of Diatropic π Ring Current in Strained Benzenes: Effects of Annelation with Cyclopropa, Cyclobuta, and Cyclobutadieno Clamping Groups. J. Org. Chem. 2002, 67, 4753–4758. [Google Scholar] [CrossRef]
- Stanger, A. The Different Aromatic Characters of Some Localized Benzene Derivatives. J. Phys. Chem. A 2008, 112, 12849–12854. [Google Scholar] [CrossRef]
- Aihara, J.; Ishida, T. Unusually High Aromaticity and Diatropicity of Bond-Alternate Benzene. J. Phys. Chem. A 2010, 114, 1093–1097. [Google Scholar] [CrossRef] [PubMed]
- Steinmann, S.N.; Jana, D.F.; Wu, J.I.-C.; Schleyer, P.v.R.; Mo, Y.; Corminboeuf, C. Direct Assessment of Electron Delocalization Using NMR Chemical Shifts. Angew. Chem. Int. Ed. 2009, 48, 9828–9833. [Google Scholar] [CrossRef] [PubMed]
- Wannere, C.S.; Sattelmeyer, K.W.; Schaefer, H.F.; Schleyer, P.v.R. Aromaticity: The Alternating CC Bond Length Structures of [14]-, [18]-, and [22]Annulene. Angew. Chem. Int. Ed. 2004, 43, 4200–4206. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Bendikov, M.; Duong, H.M.; Starkey, K.; Houk, K.N.; Carter, E.A.; Wudl, F. Oligoacenes: Theoretical Prediction of Open-Shell Singlet Diradical Ground States. J. Am. Chem. Soc. 2004, 126, 7416–7417. [Google Scholar] [CrossRef]
- Hajgató, B.; Szieberth, D.; Geerlings, P.; De Proft, F.; Deleuze, M.S. A Benchmark Theoretical Study of the Electronic Ground State and of the Singlet-Triplet Split of Benzene and Linear Acenes. J. Chem. Phys. 2009, 131, 224321. [Google Scholar] [CrossRef] [PubMed]
- Brock, C.P.; Dunitz, J.D. Temperature Dependence of Thermal Motion in Crystalline Naphthalene. Acta. Crystallogr. 1982, B38, 2218–2228. [Google Scholar] [CrossRef]
- Bultinck, P.; Rafat, M.; Ponec, R.; Van Gheluwe, B.; Carbó-Dorca, R.; Popelier, P. Electron Delocalization and Aromaticity in Linear Polyacenes: Atoms in Molecules Multicenter Delocalization Index. J. Phys. Chem. A 2006, 110, 7642–7648, and references therein. [Google Scholar] [CrossRef]
- Poater, J.; Bofill, J.M.; Alemany, P.; Solà, M. Local Aromaticity of the Lowest-Lying Singlet States of [n]Acenes (n = 6-9). J. Phys. Chem. A 2005, 109, 10629–10632. [Google Scholar] [CrossRef]
- Poater, J.; Visser, R.; Sola, M.; Bickelhaupt, F.M. Polycyclic Benzenoids: Why Kinked is More Stable than Straight. J. Org. Chem. 2007, 72, 1134–1142. [Google Scholar] [CrossRef]
- Matta, C.F.; Hernandez-Trujillo, J.; Tang, T.-H.; Bader, R.F.W. Hydrogen-Hydrogen Bonding: A Stabilizing Interaction in Molecules and Crystals. Chem. Eur. J. 2003, 9, 1940–1951. [Google Scholar] [CrossRef]
- Wu, J.I.; Dobrowolski, M.A.; Cyrański, M.K.; Merner, B.L.; Bodwell, G.J.; Mo, Y.; Schleyer, P.v.R. On the Aromatic Stabilization of the 4N π Electron Pyrene. Mol. Phys. 2009, 107, 1177–1186. [Google Scholar] [CrossRef]
- Aihara, J. The Origin of Counter-Rotating Rim and Hub Currents in Coronene. Chem. Phys. Lett. 2004, 393, 7–11. [Google Scholar] [CrossRef]
- Ciesielski, A.; Cyrański, M.K.; Krygowski, T.M.; Fowler, P.W.; Lillington, M. Super-Delocalized Valence Isomer of Coronene. J. Org. Chem. 2006, 71, 6840–6845. [Google Scholar] [CrossRef] [PubMed]
- Staab, H.A.; Diederich, F. Benzenoid versus Annulenoid Aromaticity: Synthesis and Properties of Kekulene. Angew. Chem. Int. Ed. Engl. 1978, 17, 372–374. [Google Scholar]
- Aihara, J. Is Superaromaticity a Fact or an Artifact? The Kekulene Problem. J. Am. Chem. Soc. 1992, 114, 865–868. [Google Scholar] [CrossRef]
- Jiao, H.; Schleyer, P.v.R. Is Kekulene Really Superaromatic? Angew. Chem. Int. Ed. Engl. 1996, 35, 2383–2386. [Google Scholar] [CrossRef]
- Steiner, E.; Fowler, P.W.; Jenneskens, L.W.; Acocella, A. Visualisation of Counter-Rotating Ring Currents in Kekulene. Chem. Commun. 2001, 659–660. [Google Scholar] [CrossRef]
- Bultinck, P.; Ponec, R.; Van Damme, S. Multicenter Bond Indices as a New Measure of Aromaticity in Polycyclic Aromatic Hydrocarbons. J. Phys. Org. Chem. 2005, 18, 706–718. [Google Scholar] [CrossRef]
- Bultinck, P. Critical Analysis of the Local Aromaticity Concept in Polyaromatic Hydrocarbons. Faraday Trans. 2007, 135, 347–365. [Google Scholar] [CrossRef]
- Fias, S.; van Damme, S.; Bultinck, P. Multidimensionality of Delocalization Indices and Nucleus Independent Chemical Shifts in Polycyclic Aromatic Hydrocarbons. J. Comput. Chem. 2008, 29, 358–366. [Google Scholar] [CrossRef] [PubMed]
- Ponec, R.; Fias, S.; van Damme, S.; Bultinck, P.; Gutman, I.; Stanković, S. The Close Relation between Cyclic Delocalization, Energy Effects of Cycles and Aromaticity. Collect. Czech. Chem. Commun. 2009, 74, 147–166. [Google Scholar] [CrossRef]
- Aihara, J.-i.; Oe, S. Graph-Theoretical Re-interpretation of NICS Values for Polycyclic Aromatic Hydrocarbons: Naphthalene and Azulene. Bull. Chem. Soc. Jpn 2003, 76, 1363–1364. [Google Scholar] [CrossRef]
- Stanger, A. Nucleus-Independent Chemical Shifts (NICS): Distance Dependence and Revised Criteria for Aromaticity and Antiaromaticity. J. Org. Chem. 2006, 71, 883–893. [Google Scholar] [CrossRef] [PubMed]
- The dependence of BV(ELFπ) on the CC bond lengths (RCC) is fitted using the function 1/(1 + exp(a(RCC - b))) with the best parameters a and b as 37.2357 and 1.4534. Upon rearrangement to BV(ELFπ)’ = ln((1/BV(ELFπ)) − 1) = a(RCC − b) a linear regression can be performed giving an r2 of 0.946.
- Baird, N.C. Quantum Organic Photochemistry. II. Resonance and Aromaticity in the Lowest 3ππ* State of Cyclic Hydrocarbons. J. Am. Chem. Soc. 1972, 94, 4941–4948. [Google Scholar] [CrossRef]
- Aihara, J. Aromaticity-Based Theory of Pericyclic Reactions. Bull. Chem. Soc. Jpn 1978, 51, 1788–1792. [Google Scholar] [CrossRef]
- Jug, K.; Malar, E.J.P. Geometry of Triplets and Dianions of Aromatic and Antiaromatic Systems. J. Mol. Struct. (THEOCHEM) 1987, 153, 221–226. [Google Scholar] [CrossRef]
- Gogonea, V.; Schleyer, P.v.R.; Schreiner, P.R. Consequences of Triplet Aromaticity in 4nπ-Electron Annulenes: Calculation of Magnetic Shieldings for Open-Shell Species. Angew. Chem. Int. Ed. 1998, 37, 1945–1948. [Google Scholar] [CrossRef]
- Karadakov, P.B. Aromaticity and Antiaromaticity in the Low-Lying Electronic States of Cyclooctatetraene. J. Phys. Chem. A 2008, 112, 12707–12713. [Google Scholar] [CrossRef] [PubMed]
- Nishinaga, T.; Ohmae, T.; Iyoda, M. Recent Studies on the Aromaticity and Antiaromaticity of Planar Cyclooctatetraene. Symmetry 2010, 2, 76–97. [Google Scholar] [CrossRef]
- Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J. A Self-Consistent Molecular Orbital Methods. XX. A Basis Set for Correlated Wave Functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A.; Vreven, T., Jr.; Kudin, K.N.; Burant, J.C.; Millam, J.M.; Iyengar, S.S.; Tomasi, J.; Barone, V.; Mennucci, B.; Cossi, M.; Scalmani, G.; Rega, N.; Petersson, G.A.; Nakatsuji, H.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Klene, M.; Li, X.; Knox, J.E.; Hratchian, H.P.; Cross, J.B.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R.E.; Yazyev, O.; Austin, A.J.; Cammi, R.; Pomelli, C.; Ochterski, J.W.; Ayala, P.Y.; Morokuma, K.; Voth, G.A.; Salvador, P.; Dannenberg, J.J.; Zakrzewski, V.G.; Dapprich, S.; Daniels, A.D.; Strain, M.C.; Farkas, O.; Malick, D.K.; Rabuck, A.D.; Raghavachari, K.; Foresman, J.B.; Ortiz, J.V.; Cui, Q.; Baboul, A.G.; Clifford, S.; Cioslowski, J.; Stefanov, B.B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Martin, R.L.; Fox, D.J.; Keith, T.; Al-Laham, M.A.; Peng, C.Y.; Nanayakkara, A.; Challacombe, M.; Gill, P.M.W.; Johnson, B.; Chen, W.; Wong, M.W.; Gonzalez, C.; Pople, J.A. Gaussian 03, revision C02, Gaussian, Inc.: Pittsburgh, PA, USA, 2004.
- Kohout, M. Program DGrid, version 4.3, Max-Planck Institut f r Chemische Physik fester Stoffe: Dresden, Germany, 2008.
- Humphrey, W.; Dalke, A.; Schutten, K. VMD—Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhu, J.; Dahlstrand, C.; Smith, J.R.; Villaume, S.; Ottosson, H. On the Importance of Clar Structures of Polybenzenoid Hydrocarbons as Revealed by the π-Contribution to the Electron Localization Function. Symmetry 2010, 2, 1653-1682. https://doi.org/10.3390/sym2031653
Zhu J, Dahlstrand C, Smith JR, Villaume S, Ottosson H. On the Importance of Clar Structures of Polybenzenoid Hydrocarbons as Revealed by the π-Contribution to the Electron Localization Function. Symmetry. 2010; 2(3):1653-1682. https://doi.org/10.3390/sym2031653
Chicago/Turabian StyleZhu, Jun, Christian Dahlstrand, Joshua R. Smith, Sébastien Villaume, and Henrik Ottosson. 2010. "On the Importance of Clar Structures of Polybenzenoid Hydrocarbons as Revealed by the π-Contribution to the Electron Localization Function" Symmetry 2, no. 3: 1653-1682. https://doi.org/10.3390/sym2031653
APA StyleZhu, J., Dahlstrand, C., Smith, J. R., Villaume, S., & Ottosson, H. (2010). On the Importance of Clar Structures of Polybenzenoid Hydrocarbons as Revealed by the π-Contribution to the Electron Localization Function. Symmetry, 2(3), 1653-1682. https://doi.org/10.3390/sym2031653



