How to Find the Fries Structures for Benzenoid Hydrocarbons
Abstract
:1. Introduction
2. Method and Applications
3. Conclusions
Acknowledgements
References and Notes
- Garratt, P.J. Aromaticity; Wiley Inc.: New York, NY, USA, 1986. [Google Scholar]
- Lloyd, D. The Chemistry of Conjugated Cyclic Compounds: To Be or Not to Be like Benzene; J. Wiley: New York, NY, USA, 1990. [Google Scholar]
- Minkin, V.I.; Glukhovtsev, M.N.; Simkin, B.Y. Aromaticity and Antiaromaticity; J. Wiley: New York, NY, USA, 1994. [Google Scholar]
- Hopf, H. Classics in Hydrocarbon Chemistry: Syntheses, Concepts, Perspectives; Wiley – VCH: Weinheim, Germany, 2000. [Google Scholar]
- Pascal, R.A., Jr. Twisted Acenes. Chem. Rev. 2006, 106, 4809–4819. [Google Scholar] [CrossRef] [PubMed]
- Schleyer, P.v.R. Special Issue of the Journal Devoted to Aromaticity. Chem. Rev. 2001, 101, 1115–1566. [Google Scholar] [CrossRef] [PubMed]
- Lazzeretti, P.; Corminboeuf, C.; Heine, T.; Seifert, G.; Schleyer, P.v.R.; Weber, J.; De Proft, F.; Geerlings, P.; Hiberty, P.C.; Shaik, S.; Rassat, A.; Soncini, A.; Fowler, P.W.; Jenneskens, L.W.; Havenith, R.W.A.; Engelberts, J.J.; Fowler, P.W.; Steiner, E.; van Lenthe, J.; Poater, J.; Garcia-Cruz, I.; Illas, F.; Solà, M.; Diudea, M.V.; Taylor, R.; Steiner, E.; Fowler, P.W.; Steiner, E.; Shetty, S.; Kanhere, D.; Pal, S.; Krygowski, T.M.; Cyrański, M.K. Lectures at the European Science Foundation Workshop: New Perspectives on Aromaticity, Exeter, UK, 5–9 July, 2003. Phys. Chem. Chem. Phys. 2005, 6, 217–339. [Google Scholar] [CrossRef]
- Schleyer, P.v.R. Special Issue of the Journal Devoted to Delocalization Sigma and Pi. Chem. Rev. 2005, 105, 3433–3948. [Google Scholar] [CrossRef]
- Randić, M. Aromaticity of Polycyclic Conjugated Hydrocarbons. Chem. Rev. 2003, 103, 3449–3605. [Google Scholar] [CrossRef]
- Clar, E. Polycyclic Hydrocarbons; Academic Press: London, UK, 1964; Volume 1–2. [Google Scholar]
- Clar, E. The aromatic Sextet; Wiley: New York, NY, USA, 1972. [Google Scholar]
- Poater, J.; Solà, M.; Duran, M.; Fradera, X. The Calculation of Electron Localization and Delocalization Indices at the Hartree-Fock, Density Functional and Post-Hartree-Fock Levels of Theory. Theor. Chem. Acc. 2002, 107, 362–371. [Google Scholar] [CrossRef]
- Poater, J.; Fradera, X.; Duran, M.; Solà, M. The Delocalization Index as an Electronic Aromaticity Criterion: Application to a Series of Planar Polycyclic Aromatic Hydrocarbons. Chem. Eur. J. 2003, 9, 400–406. [Google Scholar] [CrossRef]
- Portella, G.; Poater, J.; Solà, M. Assessment of Clar’ s Aromatic π-Sextet Rule by Means of PDI, NICS and HOMA Indicators of Local Aromaticity. J. Phys. Org. Chem. 2005, 18, 785–791. [Google Scholar] [CrossRef]
- Faglioni, F.; Ligabue, A.; Pelloni, S.; Soncini, A.; Viglione, R.G.; Ferraro, M.B.; Zanasi, R.; Lazzaretti, P. Why Downfield Proton Chemical Shifts Are Not Reliable Aromaticity Indicators? Org. Lett. 2005, 7, 3457–3460. [Google Scholar] [CrossRef]
- Maksić, Z.B.; Barić, D.; Muller, T. Clar’s Sextet Rule Is a Consequence of the σ-Electron Framework. J. Phys. Chem. 2006, 110, 10135–10147. [Google Scholar] [CrossRef]
- Bultinck, P.; Ponec, R.; Gallegos, A.; Fias, S.; Van Damme, S.; Carbó-Dorca, R. Generalized Polansky Index as an Aromaticity Measure in Polycyclic Aromatic Hydrocarbons. Croat. Chem. Acta 2006, 79, 363–371. [Google Scholar]
- Bultinck, P. Critical Analysis of the Local Aromaticity Concept in Polyaromatic Hydrocarbons. Farad. Disc. 2007, 135, 347–365. [Google Scholar] [CrossRef]
- Alonso, M.; Herradon, B. Neural Networks as a Tool to Classify Compounds According to Aromaticity Criteria. Chem. Eur. J. 2007, 13, 3913–3923. [Google Scholar] [CrossRef] [PubMed]
- Fias, S.; van Damme, S.; Bultinck, P. Multidimensionality of Delocalization Indices and Nucleus Independent Chemical Shifts in Polycyclic Aromatic Hydrocarbons. J. Comput. Chem. 2008, 29, 358–366. [Google Scholar] [CrossRef] [PubMed]
- Fias, S.; Fowler, P.W.; Delgado, J.L.; Hahn, U.; Bultinck, P. Correlation of Delocalization Indices and Current-Density Maps in Polycyclic Aromatic Hydrocarbons. Chem. Eur. J. 2008, 14, 3093–3099. [Google Scholar] [CrossRef] [PubMed]
- Balaban, A.T.; Schleyer, P.v.R.; Rzepa, H.S. Crocker, Not Armit and Robinson, Begat the Six Aromatic Electrons. Chem. Rev. 2005, 105, 3436–3447. [Google Scholar] [CrossRef]
- Balaban, A.T.; Klein, D.J. Claromatic Carbon Nanostructures. J. Phys. Chem. C 2009, 113, 19123–19133. [Google Scholar] [CrossRef]
- Fries, K. Über bicyclische Verbindungen und ihren Vergleich mit dem Naphtalin. Justus Liebigs Ann. Chem. 1927, 454, 121–324. [Google Scholar] [CrossRef]
- Graovac, A.; Gutman, I.; Randic, M.; Trinajstic, N. Kekule index for valence bond structures of conjugated polycyclic systems. J. Am. Chem. Soc. 1973, 95, 6267–6273. [Google Scholar] [CrossRef]
- Krygowski, T.M.; Cyrański, M.K. Structural Aspects of Aromaticity. Chem. Rev. 2001, 101, 1385–1419. [Google Scholar] [CrossRef]
- Schleyer, P.v.R.; Maerker, C.; Dransfeld, A.; Jiao, H.J.; Hommes, N.J.R.V. Nucleus-independent chemical shifts: A simple and efficient aromaticity probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Wannere, C.S.; Corminboeuf, C.; Puchta, R.; Schleyer, P.v.R. Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion. Chem. Rev. 2005, 105, 3842–3888. [Google Scholar] [CrossRef] [PubMed]
- Ciesielski, A.; Krygowski, T.M.; Cyrański, M.K.; Dobrowolski, M.A.; Aihara, J.-I. Graphtopological approach to magnetic properties of benzenoid hydrocarbons. Phys. Chem. Chem. Phys. 2009, 11, 11447–11445. [Google Scholar] [CrossRef] [PubMed]
- Trinajstić, N. Chemical Graph Theory, 2nd ed.; CRC press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Horn, R.A.; Johnson, C.R.; Johnson, C.R. Topics in Matrix Analysis; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
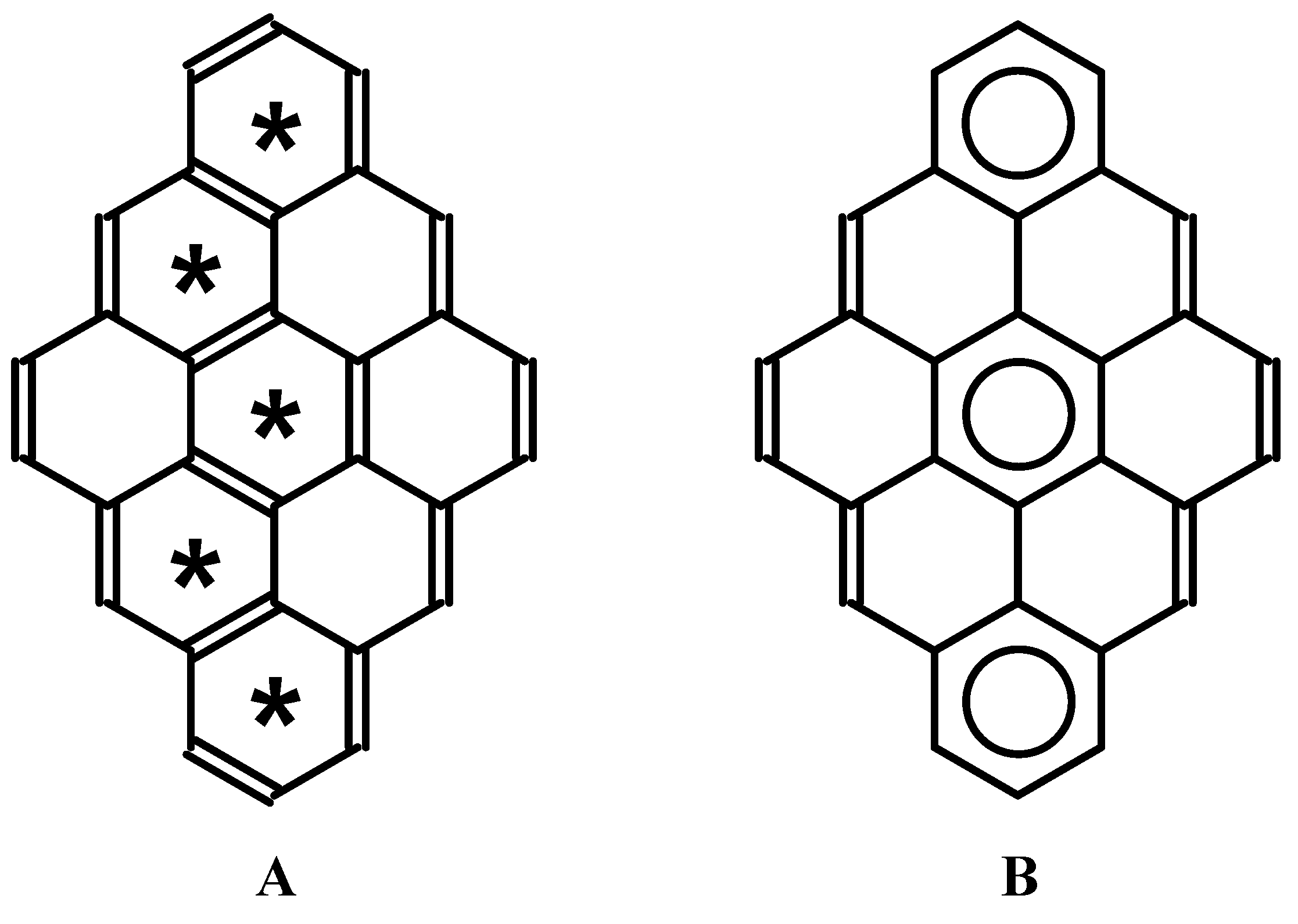
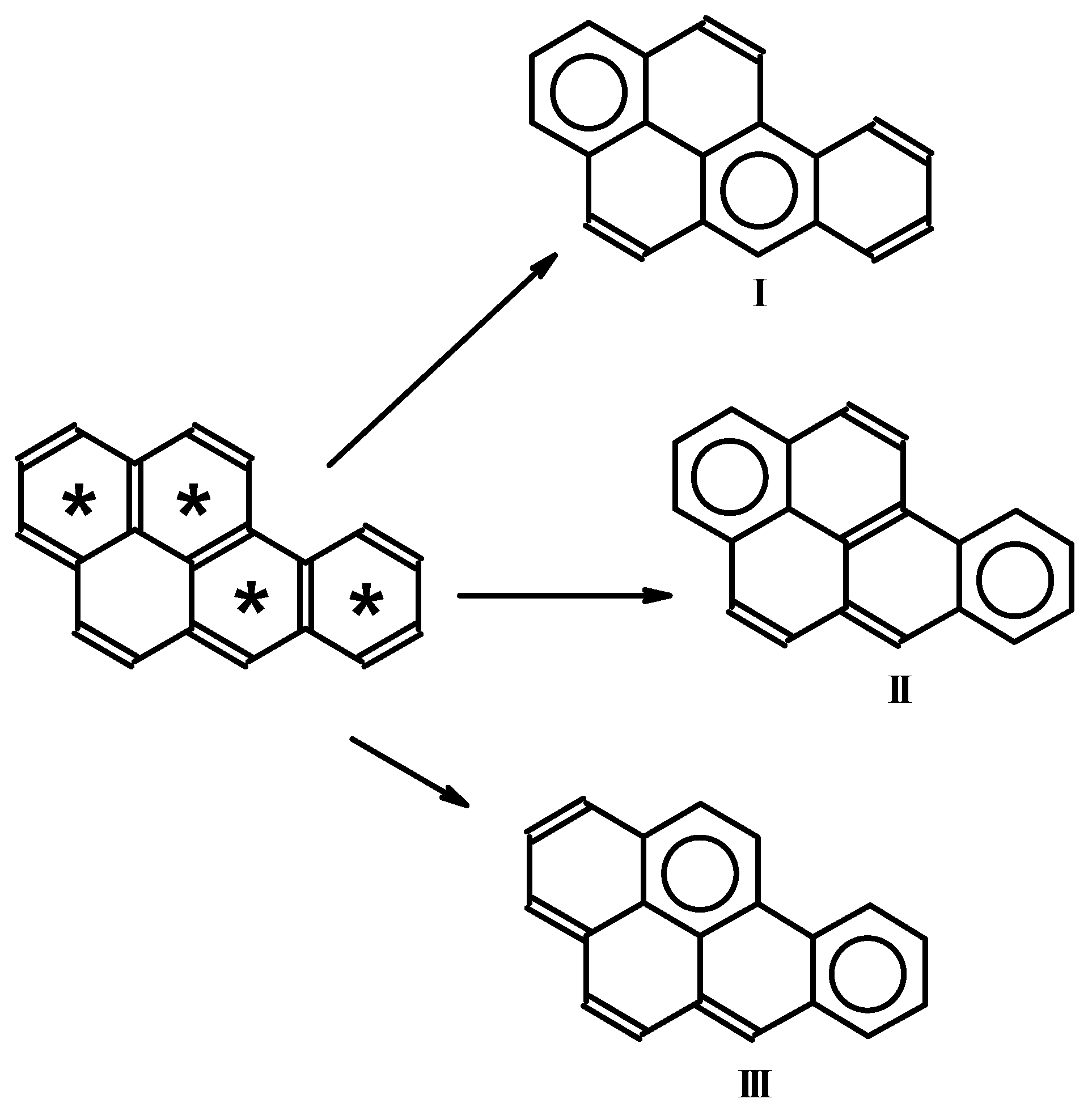
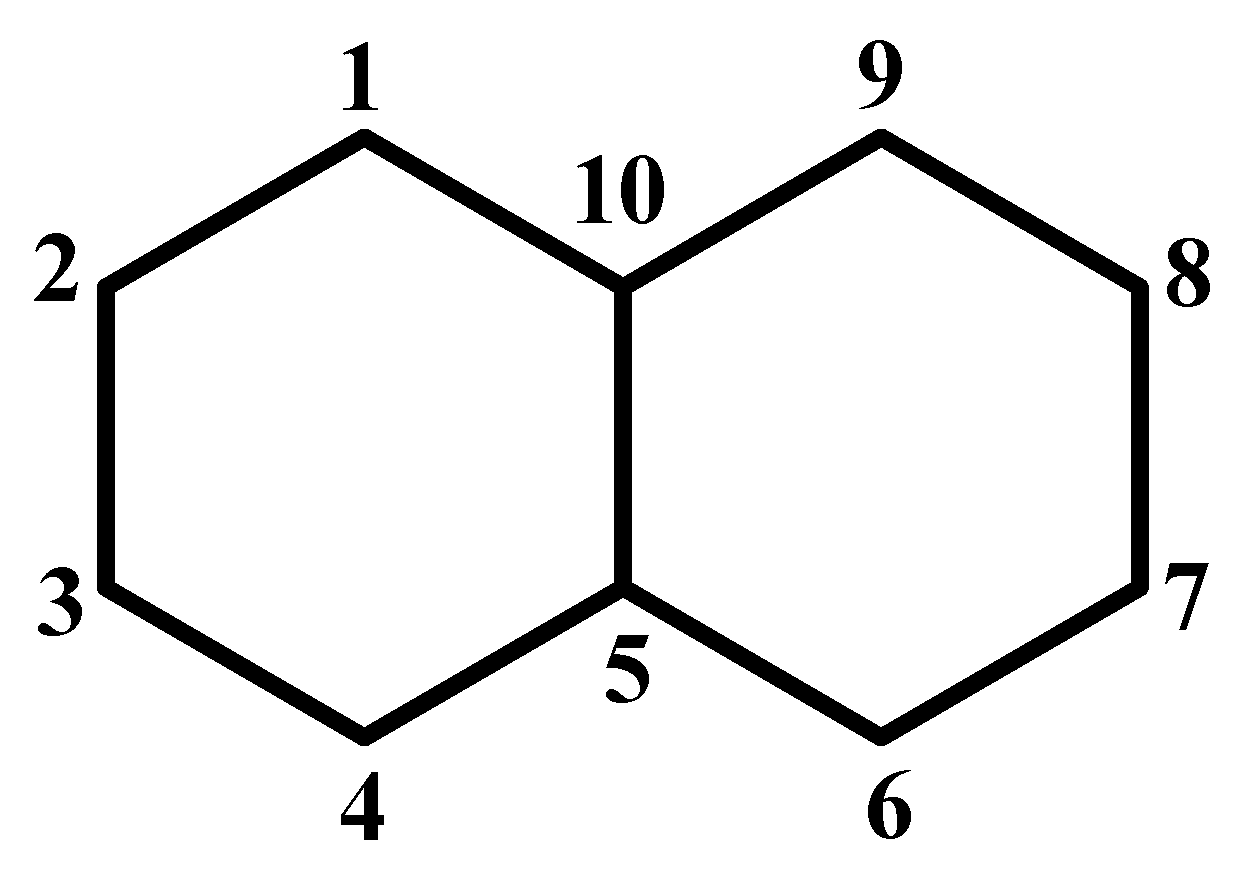
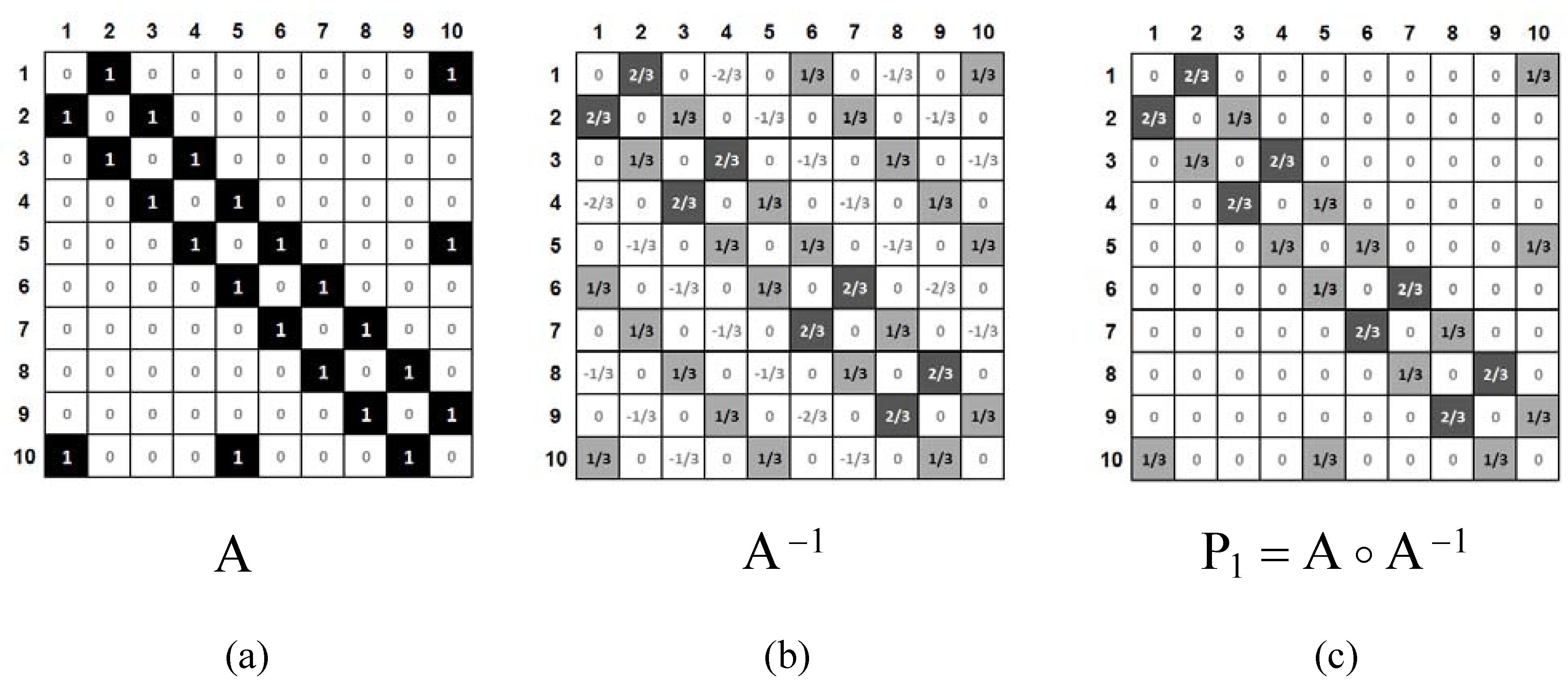
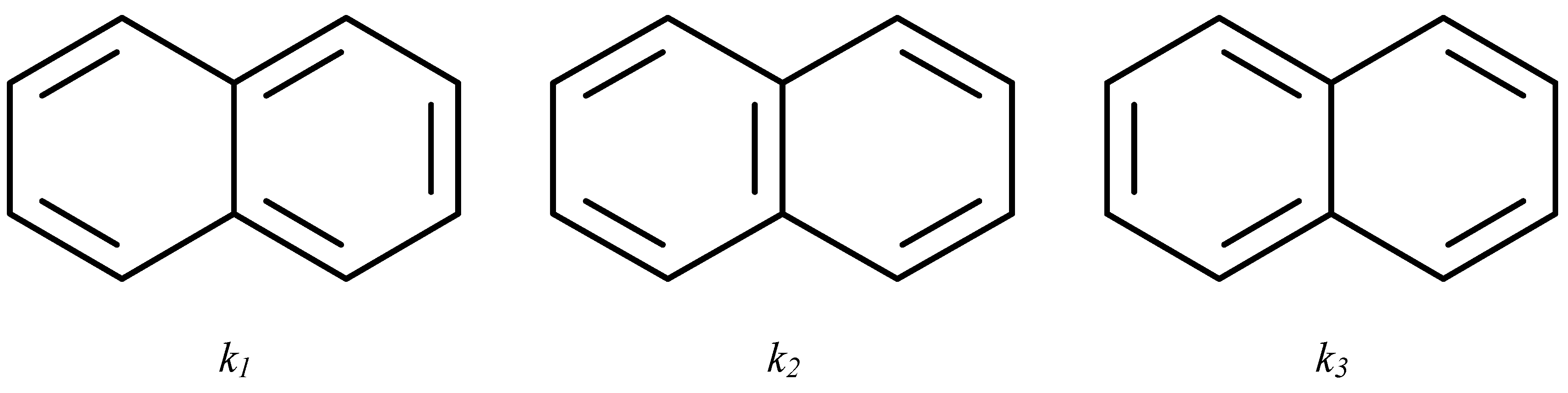
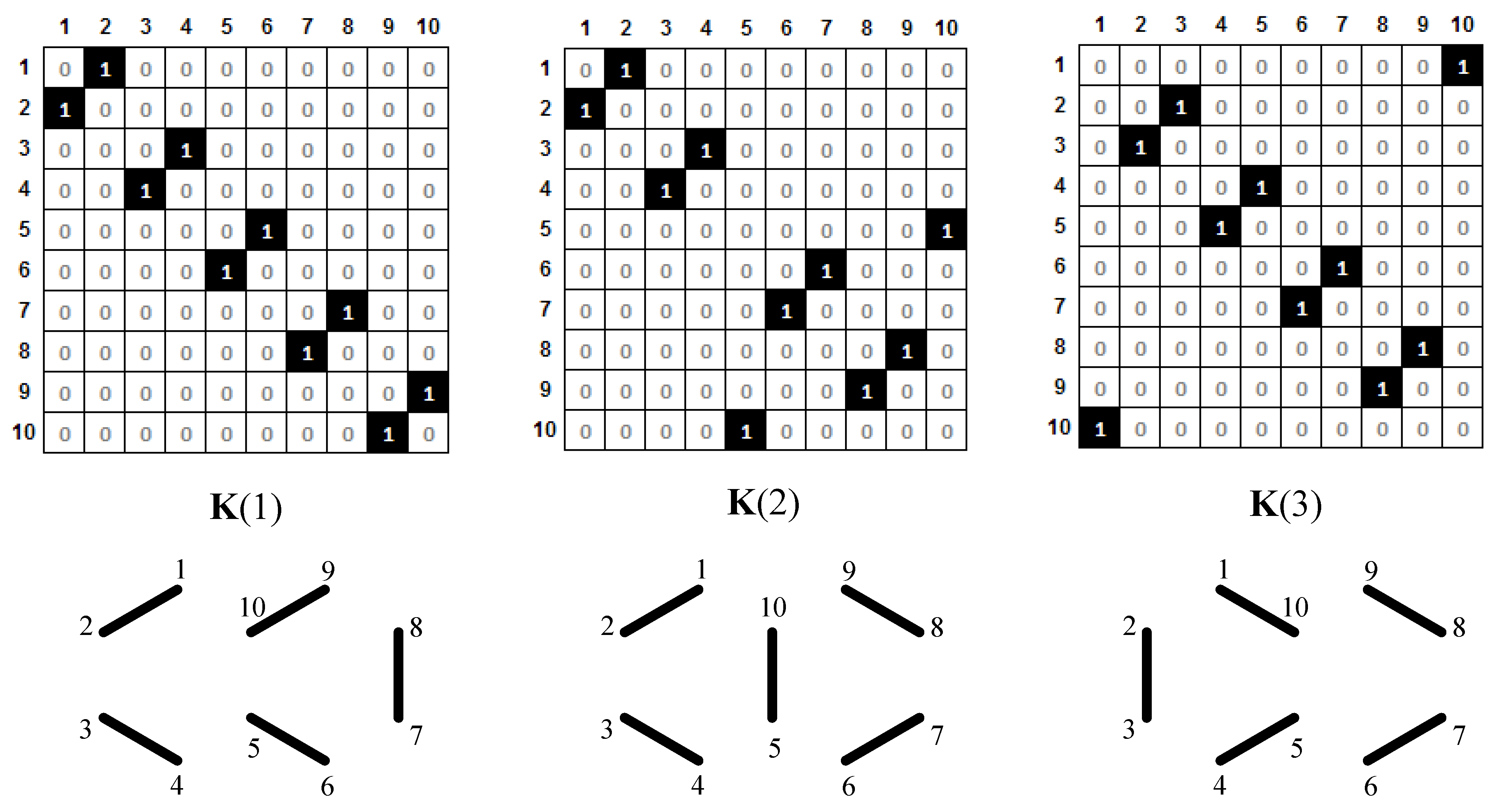

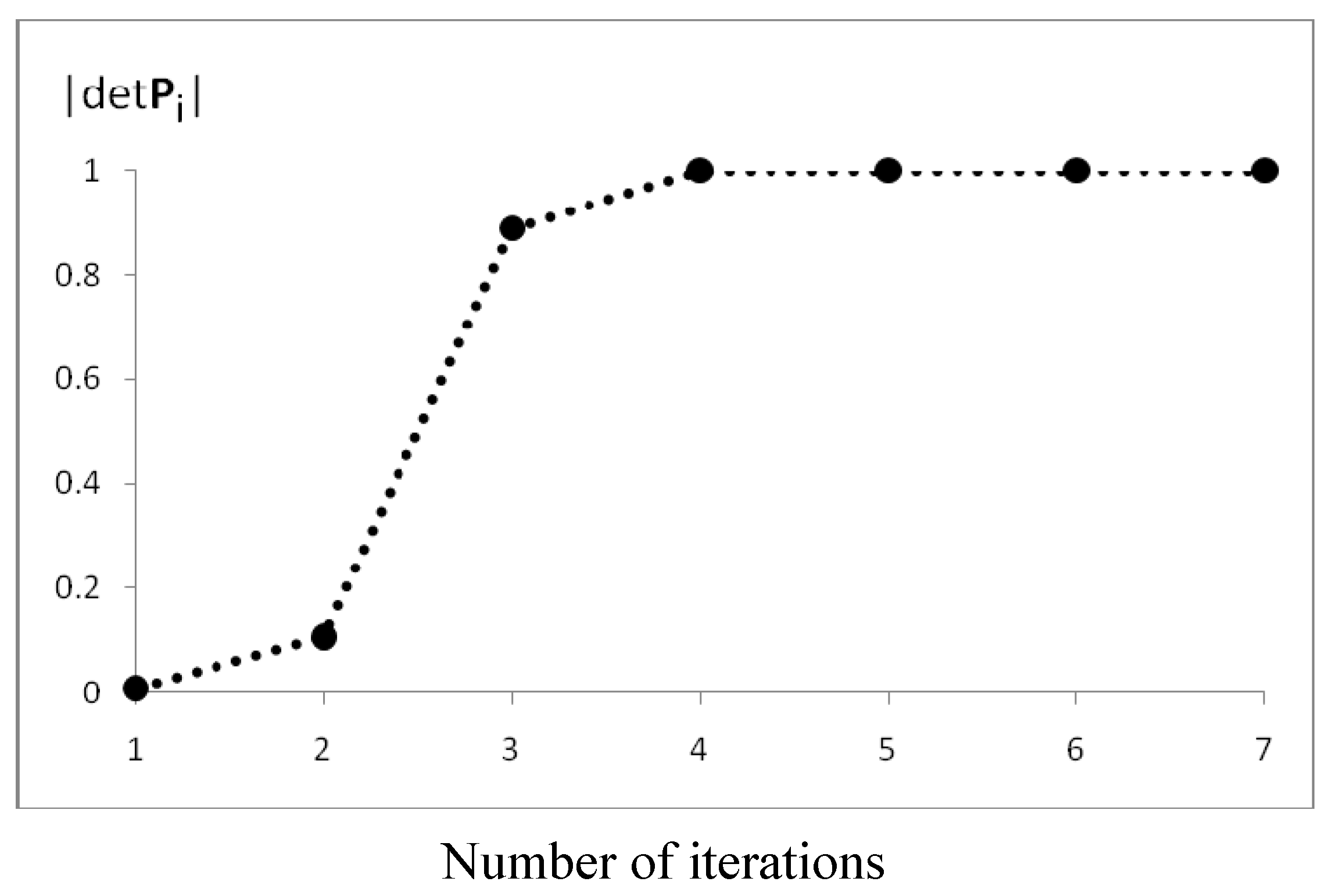

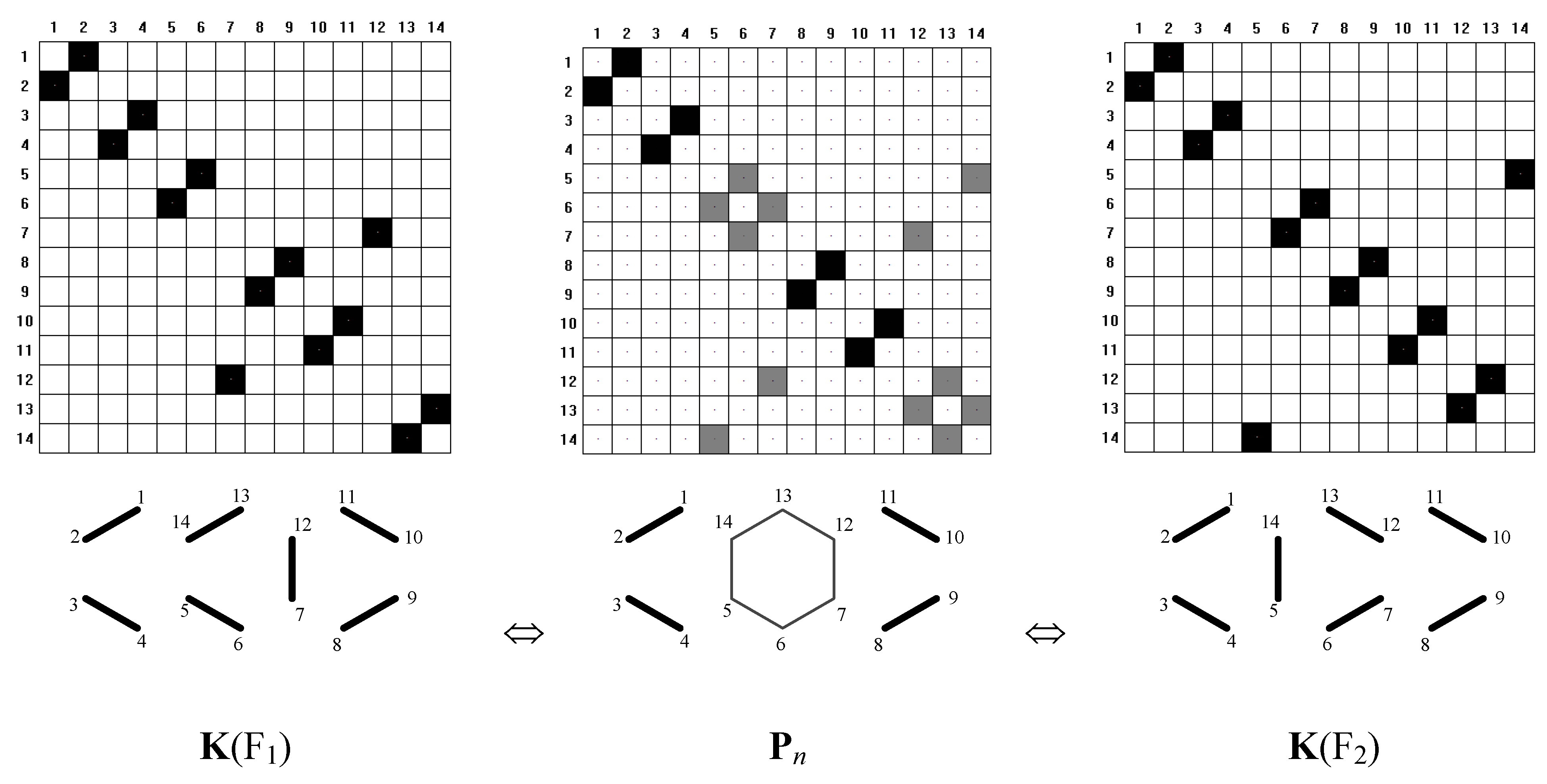
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an Open Access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ciesielski, A.; Krygowski, T.M.; Cyrański, M.K. How to Find the Fries Structures for Benzenoid Hydrocarbons. Symmetry 2010, 2, 1390-1400. https://doi.org/10.3390/sym2031390
Ciesielski A, Krygowski TM, Cyrański MK. How to Find the Fries Structures for Benzenoid Hydrocarbons. Symmetry. 2010; 2(3):1390-1400. https://doi.org/10.3390/sym2031390
Chicago/Turabian StyleCiesielski, Arkadiusz, Tadeusz M. Krygowski, and Michał K. Cyrański. 2010. "How to Find the Fries Structures for Benzenoid Hydrocarbons" Symmetry 2, no. 3: 1390-1400. https://doi.org/10.3390/sym2031390
APA StyleCiesielski, A., Krygowski, T. M., & Cyrański, M. K. (2010). How to Find the Fries Structures for Benzenoid Hydrocarbons. Symmetry, 2(3), 1390-1400. https://doi.org/10.3390/sym2031390



