Behind the Looking-Glass: A Review on Human Symmetry Perception

Abstract

The human visual system is highly proficient in extracting bilateral symmetry from visual input. This paper reviews empirical and theoretical work on human symmetry perception with a focus on recent issues such as its neural underpinnings. Symmetry detection is shown to be a versatile, ongoing visual process that interacts with other visual processes. Evidence seems to converge towards the idea that symmetry detection is subserved by a preprocessing stage involving spatial filters followed by information integration across the visual field in higher-tier cortical areas.

Contents

1	Introduction	1511
	1.1 Motivation. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	1511
	1.2 The Symmetry of Nature. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	1511
	1.3 The Nature of Symmetry. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	1513
2	The Role of Symmetry Processing in Perceptual Organization	1514
	2.1 Object Formation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	1514
	2.2 Automatic Processing. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	1516
	2.3 Conclusion. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	1516
3	The Relationship between Symmetry Processing and Cognition	1517
	3.1 Attention and Awareness. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	1517
	3.2 Cuing, Expectancy and Voluntary Control. . . . . . . . . . . . . . . . . . . . . . . . . . .	1519
4	Functional Characteristics	1519
	4.1 Modus Operandi. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	1519
	4.2 Temporal Efficiency and Noise-Resistance. . . . . . . . . . . . . . . . . . . . . . . . . . .	1521
	4.3 Orientation and Location of the Symmetry Axis. . . . . . . . . . . . . . . . . . . . . . .	1521
	4.4 Information Integration and Scale Invariance. . . . . . . . . . . . . . . . . . . . . . . . .	1522
	4.5 Multiple Symmetry. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	1523
	4.6 Symmetry versus Antisymmetry. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	1524
	4.7 Symmetry Detection in Complex Biological Stimuli. . . . . . . . . . . . . . . . . . . .	1526
	4.8 Recovery of 3D Structure from Symmetry. . . . . . . . . . . . . . . . . . . . . . . . . . . .	1526
5	Neural Implementation	1527
6	Models of Symmetry Processing	1528
	6.1 Representational Models. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	1529
	6.2 Process Models. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	1530
	6.3 Spatial Filtering Models. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	1532
	6.4 Artificial Neural Network Models. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	1534
	6.5 Neural Models. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	1535
7	Discussion and Conclusions	1535

1. Introduction

1.1. Motivation

Research into mirror-symmetry research has a long tradition, with the first psychophysical studies conducted as early as 1886 by Mach [1]. The literature contains a number of excellent overviews of human symmetry perception research [2,3,4,5,6]. Comprehensive reviews date back to the 1990s, however, and since then, advances have been made on all fronts of human symmetry research. To give just a few examples, recent experiments addressed the role of spatial filters, specialized mechanisms for facial symmetry processing have been identified, and the interaction between symmetry processing and other visual processes such as depth and motion processing was investigated. Furthermore, a handful of neuroimaging studies provided first insights about how and where symmetry detection is implemented in the human brain. The purpose of the present review paper is to give a critical and comprehensive documentation of the status quo in symmetry research.

1.2. The Symmetry of Nature

Before expanding on the cognitive mechanisms underlying human mirror-symmetry perception, it seems intuitive to start from the level that is most relevant to humans: the world we perceive. Symmetry pervades nature at all scales that have been subject to human investigation, whether the microcosm of string theory and the structure of crystals, or the gigantic architecture of galaxies. Not surprisingly, then, the concept of symmetry can be encountered in scientific disciplines as diverse as social sciences, mathematics, physics, chemistry, and even philosophy of science (e.g., [7]). The exact definition, however, varies considerably with the area of application. Many of the symmetries in nature are beyond the reach of our visual system [8,9]. Some can be visualized with appropriate magnification (e.g., microscopes and telescopes), while others are even hard to imagine.

With respect to the environment accessible to our visual system, there is an abundance of both natural and artificial bilateral symmetries (Figure 1). For such a symmetric object, there is at least one symmetry axis (or symmetry plane in 3D) that splits the object into two identical but mirror-inverted halves. Animal species predominantly belong to the group of bilateria, that is, bilaterally symmetric animals; furthermore, flowers often feature multiple symmetry axes (Figure 1a). Not only bodily symmetry, also visual sensitivity to symmetry is encountered throughout the animal kingdom. For instance, pigeons [10], bees [11,12], and dolphins [13] have been shown to be sensitive to symmetry. There have been attempts to attribute sensitivity to symmetry to evolutionary pressure. In humans, symmetry has been associated with genetic quality, developmental stability and judgments of physical attractiveness [14,15,16,17]. At least regarding facial attractiveness, however, symmetry does not appear to be the only relevant factor, because symmetric faces are judged as more attractive than less symmetric faces even if symmetry cues are removed by showing only one half of the face [18]. This suggests the involvement of other factors, such as cheek-bone prominence, that are positively correlated with the degree of symmetry. Consequently, whether or not sensitivity to symmetry evolved due to evolutionary pressure is still a matter of debate. For a more extensive treatment of symmetry in the animal world and the role of natural selection, refer to [3].

As illustrated in Figure 1b, there is also a striking preponderance of symmetries in the artificial environment [8]. First, for a part, this can be attributed to human anatomy, because a symmetric body can often interact more efficiently with another object if the counterpart is also symmetric (e.g., a chair or a bicycle). Second, symmetric objects are usually well-balanced and therefore may be more stable than asymmetric objects. For instance, the Maya pyramid depicted in Figure 1b has its point of mass exactly in the center. Third, the use of symmetric objects may also involve affordance. Affordance is a term used in ergonomics which implies that visual features of objects can prompt motor actions. An object that is invariant under a symmetry operation ‘signals’ that it may be used in the same way after an action is performed, that is, it affords the same actions. For instance, a rotary knob will appear the same under rotations, indicating that it allows for the same actions to be performed after it has been used (see [19] for a detailed discussion of this interesting topic). Fourth, the use of symmetry goes beyond mere functionality. This is witnessed by the fact that symmetry is omnipresent in art, craft, and architecture, where symmetrical compositions are sometimes used by virtue of the fact that they are aesthetically pleasing to the observer [20,21,22,23]. Aesthetic preference is not restricted to the manufacturing of single objects, since even symmetric arrangements of multiple objects seem to evoke a sense of beauty (see Figure 1b). For a more detailed overview of symmetry in culture, refer to [8].

1.3. The Nature of Symmetry

In geometry, the term symmetry refers to a family of isometries, that is, geometric invariance operations in 2D or 3D Euclidean space that preserve an object’s structure. These isometries consist of reflection symmetry (aka mirror symmetry or bilateral symmetry), rotational symmetry, translational symmetry (aka repetition), and of combinations of these three basic operations. Although the human visual system is sensitive to all of these symmetries, bilateral symmetry is probably the single most salient symmetry [24], the most investigated, and the most relevant to humans and other vertebrates [3]. The rest of this paper focuses on bilateral symmetry, for which the shorthand ‘symmetry’ will be adopted.

Phenomenologically, a striking characteristic of symmetry is that it seems to impose structure when viewed by an observer. As Figure 2a–c illustrates intuitively, a meaningless pattern appears as a whole, or Gestalt, if it features symmetry. However, the ease with which our visual system seems to extract symmetry from a stimulus belies the complexity of this task. The following sections address the functional characteristics and neural underpinnings of symmetry perception that have been uncovered by empirical research. Subsequently, I expand on the numerous models about symmetry perception.

2. The Role of Symmetry Processing in Perceptual Organization

The tenet of this paper, and an idea expressed before (e.g., [2,5,25,26]), is that symmetry processing is an automatic visual process that forms an integral part of perceptual organization. In other words, symmetry detection is a visual process that is constantly applied to any visual input and it affects the way we perceive our visual environment. This will be substantiated next. To start, note that it is true that symmetric objects yield a symmetric projection on the retina only if viewed head-on. However, the degradation of 2D symmetry induced by perspective is gradual and systematic [27,28,29,30]. For instance, as Figure 2d,e illustrates, the lines connecting symmetric elements are not parallel any more under perspective distortion, but adjacent lines are still approximately parallel. The fact that symmetry detection is fairly robust to perturbations of symmetry indicates that symmetry might be recovered from objects rotated in depth.

To qualify as an integral part of perceptual organization, symmetry processing has to comply to two requirements. First, symmetry has to be part of object formation, that is, it has to be involved in grouping and segmentation of the visual input and it should affect the visual interpretation of a stimulus. Second, symmetry processing should be automatic rather than mediated by a conscious cognitive effort. These points will be addressed one by one.

2.1. Object Formation

A number of different studies suggests that symmetry processing is directly involved in the grouping and segmentation of visual input. For instance, symmetry was shown to affect figure-ground segregation, one of the principal operations during object formation. In stimuli with ambiguous figure-ground arrangements, participants tend to perceive symmetric shapes as figure and asymmetric shapes as ground [32,33]. A recent study corroborated the involvement of symmetry in grouping by co-alignment [34]. The authors used a stimulus consisting of Gabor elements, some of which joined together to form the outline of a shape. Psychophysical thresholds for the detection of shape were measured by varying the degree of alignment of the Gabor elements. Thresholds were significantly lower when the shape was symmetric than when it was asymmetric. A powerful demonstration that symmetry is involved in the perceptual formation of objects was given by [31]. The study started from the well-known phenomenon of structure-from-motion (SFM), which implies that 3D volumetric structure can be perceived when dots move sinusoidally [35,36]. 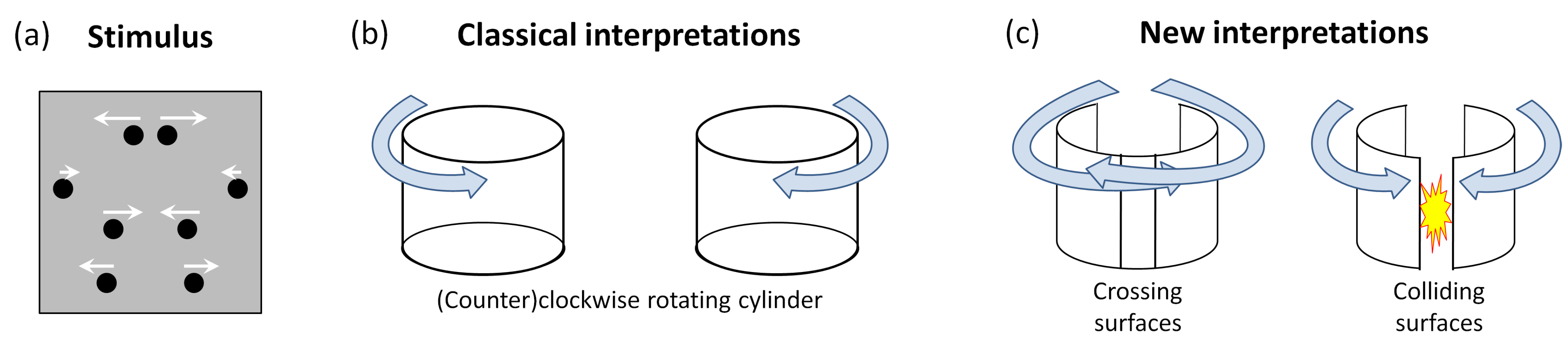The usual percept is a 3D rotating cylinder (Figure 3b). However, if the moving dot pattern is 2D symmetric (as sketched in Figure 3a), novel interpretations can be perceived. Now it is also possible to see two disjunct surfaces moving in opposite directions (Figure 3c). This suggests that symmetry is directly involved in the definition of the perceived object.

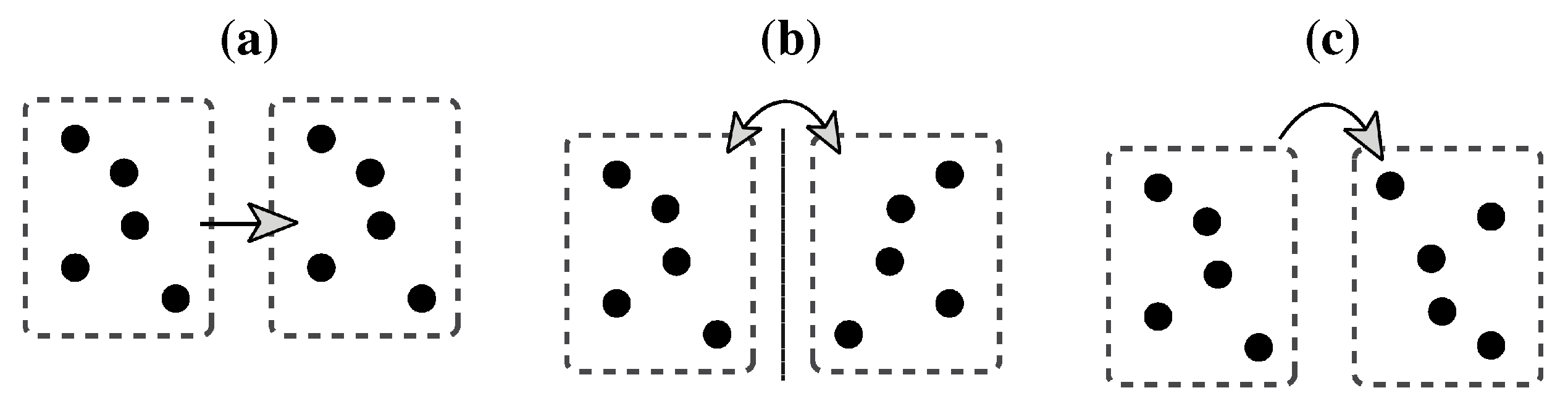
Furthermore, evidence converges towards the view that symmetry serves as a one-object cue, that is, it signifies the presence of a single object. As discussed above and shown in Figure 1, in our natural environment symmetry indeed characterizes single objects. Moreover, there is evidence that this fact is appreciated by our visual system. First, it is more difficult to perceptually split chromatically uniform surfaces when they are symmetric than when they are asymmetric, suggesting that symmetry serves as perceptual “glue” [37]. Second, there have been manifold reports that symmetry processing is affected by the number of perceived objects and depth planes in a display. For instance, symmetry in dot patterns is easier to detect when the two elements of each symmetry pair are in the same depth plane than when they are spread across two different depth planes [38]. Correspondingly, symmetric contours are easier to detect when they belong to the same object than when they belong to two different objects [39,40,41]. This effect cannot be ascribed to attentional effects alone (two objects require divided attention), because the opposite result was found for repetition, that is, the detection of repetition is easier in two objects than in one object.

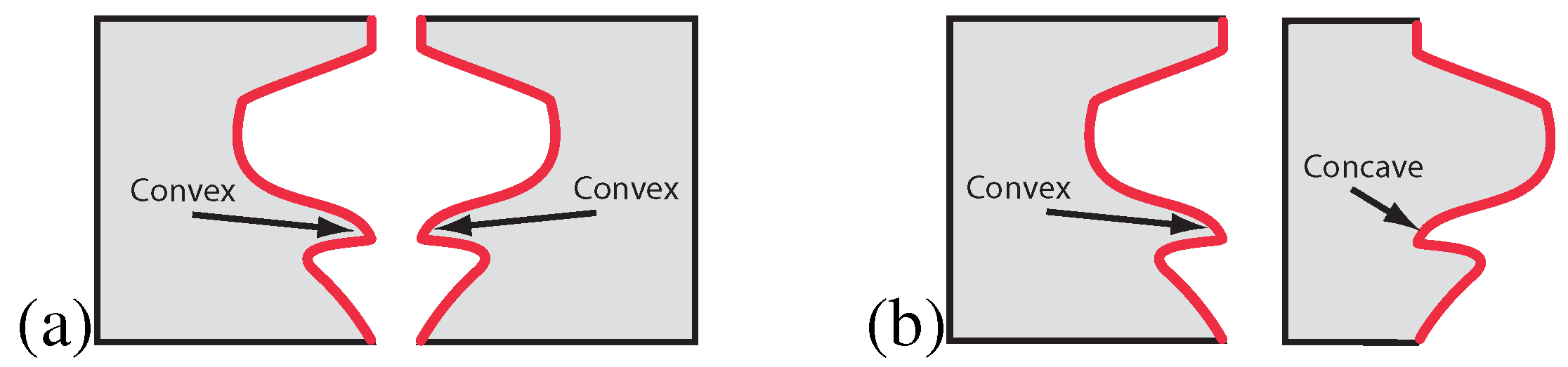
The latter suggests that symmetry not only affects the way we perceive objects. Objects also affect the way we perceive symmetry. The importance of the object level is corroborated by the fact that symmetry detection is more sensitive to convexities than to concavities, irrespective of which is closer to the symmetry axis [42]. Note that this does not torpedo the role of symmetry processing in perceptual organization. Although perception has to start from the retinal image, there is ample evidence that object-level properties can override image-level properties [43,44,45]. Or, as put in [38], the “perceptual organization process is not a uni-directional bottom-up process from images to objects but is a highly complex and combinatorial process which, for a given image, seems to search for the best-fitting object”.

2.2. Automatic Processing

The fact that symmetry processing is involved in object formation does not necessarily imply that its detection is automatic, that is, not relying on cognitive control. For instance, in the SFM study reported above [31], participants were to a certain extent able to voluntarily choose whether they perceived the symmetry-based interpretation or the motion-based interpretation. However, there is some evidence that symmetry detection is automatic.

First, symmetry detection is fast and noise-resistant [27,46,47], suggesting that it is supported by early visual mechanisms. Second, crucially, symmetry was shown to affect performance when it is not relevant for the task. In a task where participants had to judge whether or not the facing contours of two objects are symmetric, the outer task-irrelevant contours facilitated performance when they were also symmetric [26,40,48]. Third, as said above, symmetry can determine figure-ground segregation. In [32], figure-ground segregation was investigated in a patient who suffered from hemispatial neglect; following right-hemisphere damage, the patient was unable to deploy attention to the left half of the visual field, although he was not blind on that side. In stimuli with an ambiguous figure-ground organization, he perceived the symmetric parts of the stimulus as figure (just as healthy observers do), although he did not display conscious experience of the symmetry. Fourth, visual search is facilitated when the spatial arrangement of the distracters is symmetric compared to random [49]. Fifth, saliency models based on local symmetry (symmetry applying to only a part of the stimulus) in complex natural images are better in predicting human eye movements than conventional models based on contrast [50]. This indicates that the local symmetry is detected before an eye movement is made to the symmetric object, showing that overt attention is not necessary for symmetry detection.

2.3. Conclusion

The foregoing discussion suggests that symmetry detection is an automatic process that is involved in the perceptual formation of objects. A few caveats apply to this conclusion.

Symmetry might not rank with other visual features such as motion, color, or binocular disparity. Leaving context effects aside, the latter features are ‘atomic’ in the sense that they refer to properties of single stimulus elements. Symmetry, however, is given by spatial relationships between multiple stimulus elements. At least some of these other features seem to dominate over symmetry. For instance, the organization imposed by binocular disparity cues seems to dominate symmetry once disparity cues are fully computed [38,51,52,53]. In line with this, discrimination thresholds for two depth planes are not affected by whether or not the two planes together would form a symmetry [54]. In other words, symmetry does not perceptually fuse nearby depth planes although one might expect so from its role as a one-object cue. When multiple principles of grouping are involved, symmetry seems to be able to prevail mainly in ambiguous situations such as ambiguous figure-ground organization [32,33] or ambiguous structure-from-motion [31].

Furthermore, conscious experience of symmetry seems be attenuated in complex, pseudo-naturalistic patterns when they also involve regularities other than symmetry [55]. However, the fact that one is not consciously aware of a symmetry does not preclude that it is not computed at some level in the visual system. In this respect, it seems expedient to address the role of attention and awareness in symmetry processing, as done in the next section.

3. The Relationship between Symmetry Processing and Cognition

Until the 1990’s, the prevailing view was that symmetry detection and other kinds of grouping processes are pre-attentive, that is, encapsulated from attention and other higher cognitive processes. This view was falsified. Higher cognitive processes pervade all levels of cortical visual processing. Moreover, there is an ongoing discussion whether cognition might even be a necessary prerequisite for grouping to occur. With respect to symmetry processing, this issue was treated rather stepmotherly. Therefore, empirical evidence regarding the symmetry-cognition link is rather thin.

3.1. Attention and Awareness

It is now clear that attention is a multi-level selection process that can modulate brain activity in areas as early as the lateral geniculate nucleus [56,57]. This particular finding does not imply that grouping does not occur without attention but initial psychophysical studies suggested that grouping is indeed dependent on attention. To be clear, grouping processes were believed to be automatic, but only within the visual area targeted by attention. Proponents of this hypothesis usually invoke on the inattention paradigm. In this paradigm, the target stimulus relevant to the participant’s task is embedded in some task-irrelevant context. In a particular inattention trial, elements in the visual context should perceptually organize to a figure according to some law of grouping (e.g., proximity or color), and after the trial participants are asked whether or not they saw the corresponding organization. The often observed failure of participants to report having perceived the figure, coined inattention blindness, was taken as evidence that grouping does not occur without attention. For instance, using the inattention paradigm, it was suggested that neither texture segmentation nor grouping by lightness or proximity occurs under conditions of inattention [58].

Opponents of this hypothesis pointed out that, in inattention studies, the concept of inattention blindness is actually mixed up with inattention amnesia [59,60,61]. In other words, because this paradigm requires an overt response by the participant after the trial, the participant needs some awareness (i.e., conscious experience) of the figure during the trial so that the perception of the figure is stored in memory. Consequently, the failure to report can be related to memory failure (information was not encoded or cannot be retrieved) or, more generally speaking, to a lack of awareness. This leads to the question whether grouping can occur in the absence of awareness and, moreover, in the absence of both awareness and attention.

The answer to the first question seems to be yes. Spatial attention and awareness can be disentangled using the binocular suppression paradigm. In this paradigm, information in an attended region presented to one eye is masked by high-contrast elements presented to the other eye. Consequently, only the suppressors are consciously perceived. When the suppressors are removed, the suppressed elements appear within a few seconds. It was shown that, after removal of the suppressors, two suppressed elements tend to perceptually appear together more often when they share a common feature (color or orientation) than when they do not, suggesting that they were grouped outside of awareness [62].

There is also some evidence that neither awareness nor attention are necessary for grouping to occur. Rather than relying on explicit memory recall after the trial (such as in the inattention paradigm), some studies investigated implicit grouping effects during the trial [59,60,61]. For instance, the task of the participants was to judge which of two simultaneously presented lines is longer. The stimuli were surrounded by randomly distributed dots. On the inattention trial, these dots formed arrowheads that pointed inwards or outwards, thereby creating the Müller-Lyer illusion. Effects on line judgments were found although participants reported not having perceived the grouping. This supports the idea that there is a dissociation between awareness and subconscious grouping.

With respect to symmetry processing, there are only few instructive studies. In a brainimaging study, Sasaki et al. found that symmetry-specific brain activity persisted even when participants engaged in a task in which the symmetry was irrelevant [63]. This study is discussed in more detail in Section 5 Olivers and van der Helm used a search task in which there were one to four targets that were presented off the fixation point [64]. Participants’ task was to decide as quickly as possible whether or not any of the targets was symmetric. The authors found an effect of set size, that is, reaction times increased with the number of targets, and took this as evidence that symmetry is not computed in parallel across the visual field. There are a few difficulties with this study, however. First, it suffers from the same shortcoming as the standard inattention paradigm: it requires an overt response by the participant. Perhaps grouping by symmetry as such does not require awareness, but overtly reporting so surely does. Second, there was a possible confound. When there was only one target, the whole display was globally symmetric per definition. With increasing number of targets, global symmetry deteriorated, which might have lead to an increase in reaction times if participants used global symmetry as a cue. In line with this interpretation, [65] showed that global symmetry is generally more salient than local symmetries.

Another study on the symmetry-awareness link was the abovementioned case-study on a neglect patient [32]. Without displaying a conscious experience of the symmetry, he tended to perceive symmetric parts of the stimulus as figure. It is difficult to extrapolate from a clinical single-case study, and it is also difficult to tell in how far results on other grouping principles transfer to symmetry. Evidence seems to favor the view that neither attention nor awareness are necessary for grouping to occur, but this issue is not fully resolved. Both attention and awareness need to be addressed more thoroughly in symmetry research, possibly by means of indirect methods to rule out possible confounds by attention and awareness.

3.2. Cuing, Expectancy and Voluntary Control

A number of studies indicate that symmetry processing is affected by cuing, expectancy and voluntary control, possibly via means of focused attention. First, it was demonstrated that knowledge affects symmetry processing [66,67]. When the orientation of the symmetry axis varies across trials but is cued prior to each trial, a valid cue leads to an increase and an invalid cue leads to a decrease of the detection rate, relative to a neutral cue. Second, task parameters changing the expectancy of the participant affect performance. In particular, the salience of vertical symmetry was drastically reduced when the majority of the trials featured oblique or near-oblique symmetry axes, which indicates the involvement of voluntary shifts of attention [68]. Third, in structure-from-motion stimuli made of symmetric dot patterns (see Figure 3), participants can, at least partly, voluntarily control whether the percept they see is based on grouping by motion or based on grouping by symmetry [31].

4. Functional Characteristics

Experiments on symmetry detection relate to a number different subtopics, such as its spatial and temporal properties and the interaction with other visual cues. Since these lines of research developed largely in parallel, they will be discussed one by one.

4.1. Modus Operandi

Above, it was argued that symmetry processing does not strictly apply to the retinal image. Rather, it is also affected by properties of the perceptual objects themselves. This section extends this discussion to the role of 3D depth information. In 3D, the image level refers to the 2D retinal projection of a 3D object and the object level refers to the 3D object itself.

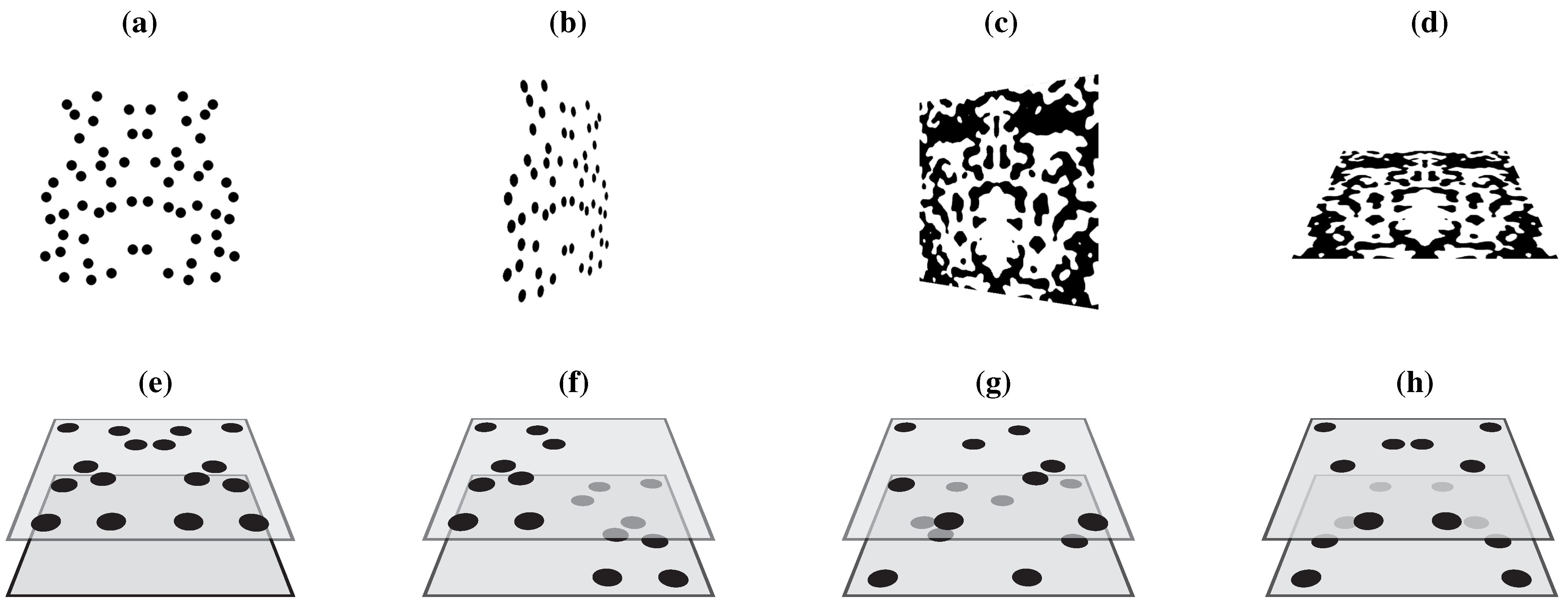
Compelling support for retinal processing of symmetry stems from van der Vloed et al. [30], who reported that symmetry detection is feasible for various veridical views of planar symmetries slanted in depth, but that there is a deterioration of detection performance that is well-predicted from the deterioration of symmetry in the retinal image. Sample stimuli are given in Figure 4a–d. Essentially, symmetry detection was not obstructed by perspective when a frontoparallel symmetry was rotated about the horizontal midline (x-axis) but it was severely obstructed following rotations about the vertical midline (y-axis). This is in accordance with the fact that retinal symmetry stays intact after rotations about the x-axis but not after rotations about the y-axis. In contrast, other studies reported that symmetry processing is preceded by depth perception. For instance, symmetry can be both perceptually destroyed and constructed by means of binocular depth information [51,52]. Additional evidence that symmetry is processed after binocular fusion stems from a study by Wenderoth who showed that two monocular symmetries cannot be perceived when they are not symmetric after binocular fusion, but binocular symmetry can be perceived even when there is no symmetry at a monocular level [69].

To appreciate the difference between these studies, note that linear perspective was used in [30], which is a figural depth cue. Depth from figural cues has to be inferred from the stimulus, that is, it needs a certain amount of preprocessing of the retinal image. In contrast, binocular disparity (the difference between the projections in the left eye and the right eye) is an ocular cue. This information is more directly available and disparity-sensitive visual neurons are found as early as V1. In other words, a possible view reconciling the above results could be that symmetry processing is preceded by the computation of ocular depth cues and followed by the computation of figural depth cues.

A more nuanced view on symmetry and depth processing was given by Treder and van der Helm [38]. As shown in Figure 4, a planar symmetry was disrupted in a number of different ways. Crucially, presentation time was also varied from 200–1000 ms in steps of 200 ms. For a short presentation time (200 ms), performance on the different stimulus manipulations was in line with the properties of the retinal projection. For long presentation times (800–1000 ms), however, the pattern of results was in accordance with the positions of the elements in stereoscopic space. Consequently, the authors concluded that symmetry perception can change from a retinotopic (i.e., image-level) frame of reference to a stereoscopic (i.e., object-level) frame of reference. In other words, symmetry processing can precede the processing of stereo cues, but stereo information can dominate symmetry processing if stereo cues have been fully processed, with presentation time being the critical parameter.

4.2. Temporal Efficiency and Noise-Resistance

A number of studies demonstrated that symmetry detection is feasible under presentation times of 100 ms and less [5,24,47,70]. Furthermore, it is remarkably noise-resistant, with the salience (i.e., detectability) of symmetry degrading gracefully with the amount of noise, whether interspersed random dots, spatial or phase jitter, or geometric transformations (e.g., [9,46,71,72]). At the same time, small deviations from perfect symmetry are easily picked up [46]. This combination of robustness and sensitivity to perturbations suggests that the amount of symmetry is rather accurately represented in the visual system. This idea was corroborated by Csatho et al. [73], who suggested that the salience of symmetry is a linear function of the noise proportion. Recently, this view was refined by van der Helm, who argued that symmetry detection deviates from Weber-Fechner law [74]. The magnitude of the deviation depends on regularity-to-noise ratio. In particular, it was demonstrated that symmetry detection is disproportionally sensitive to changes in regularity-to-noise ratio in the mid-range of noise proportions (i.e., around 50% noise).

4.3. Orientation and Location of the Symmetry Axis

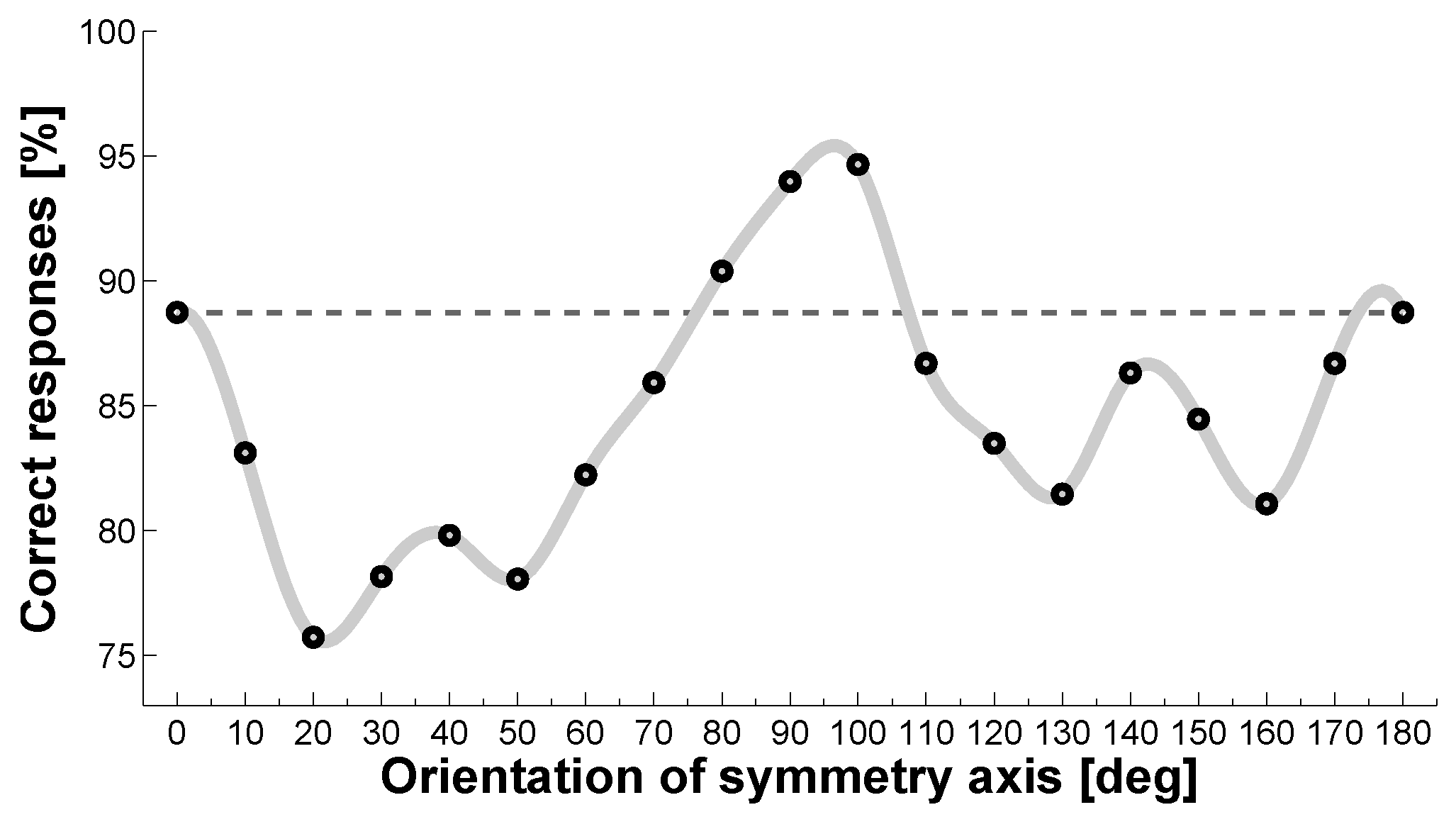
Symmetry processing is anisotropic with regard to the orientation of the symmetry axis. This was first noted by Mach [1] and since then has been confirmed in further experiments [76,77]. Despite some incongruity across different studies, the general picture seems to be that there is a gradient of sensitivities to different axis orientations, with orientations close to the vertical being most salient, followed by horizontal, then left/right oblique, and finally all other axis orientations [46,75] (see Figure 5). Even infants as young as 4 months process vertical symmetry more efficiently than other orientations [78]. Importantly, these effects are probably not due to a vertical default frame of reference or due to the application of cognitive strategies, because cuing of the symmetry axis does not obliterate these anisotropies [66].

Also the location of the symmetry axis in the visual field is relevant. Although foveation of the symmetry axis is not a prerequisite for symmetry detection, detectability drops considerably with axis eccentricity [79]. Symmetry detectability can be equated across eccentricities if stimuli are scaled with a factor F = 1 + E/E${}_2$, where E is eccentricity and E${}_2$, lying in the range of 0.88° to 1.38°, is the eccentricity at which stimulus size is doubled [80].

4.4. Information Integration and Scale Invariance

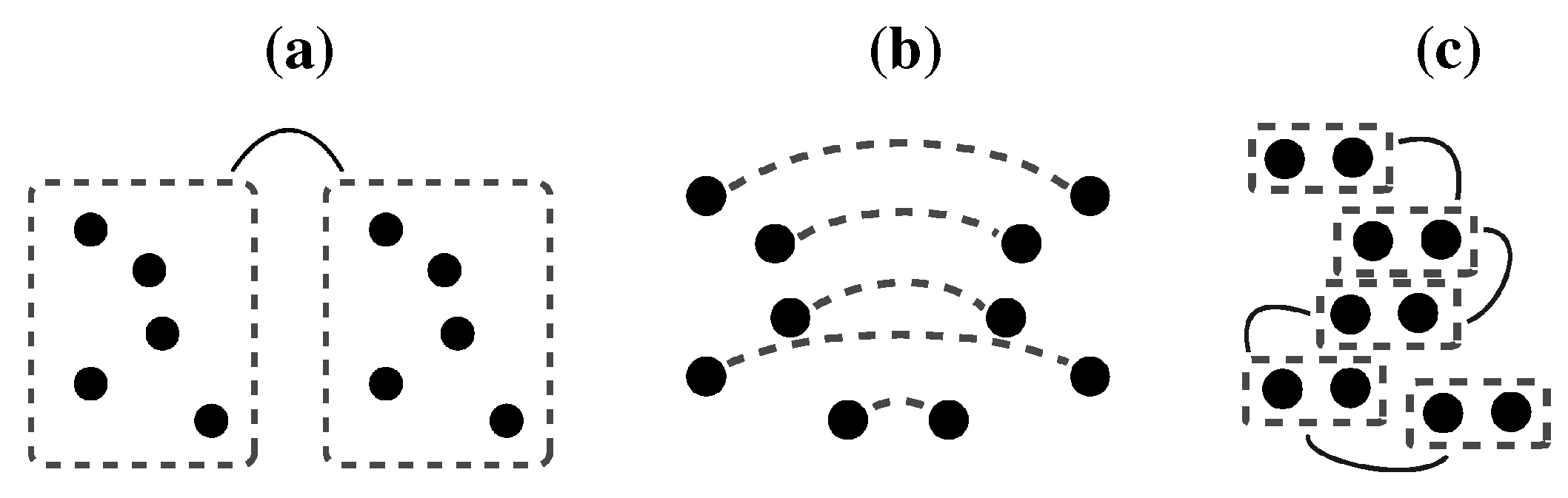
The detectability of symmetry is affected by the number of elements constituting the stimulus. Initially, performance increases with the number of elements and then saturates at a modest number [81]. This suggests that only a limited amount of symmetry information is integrated during symmetry processing. 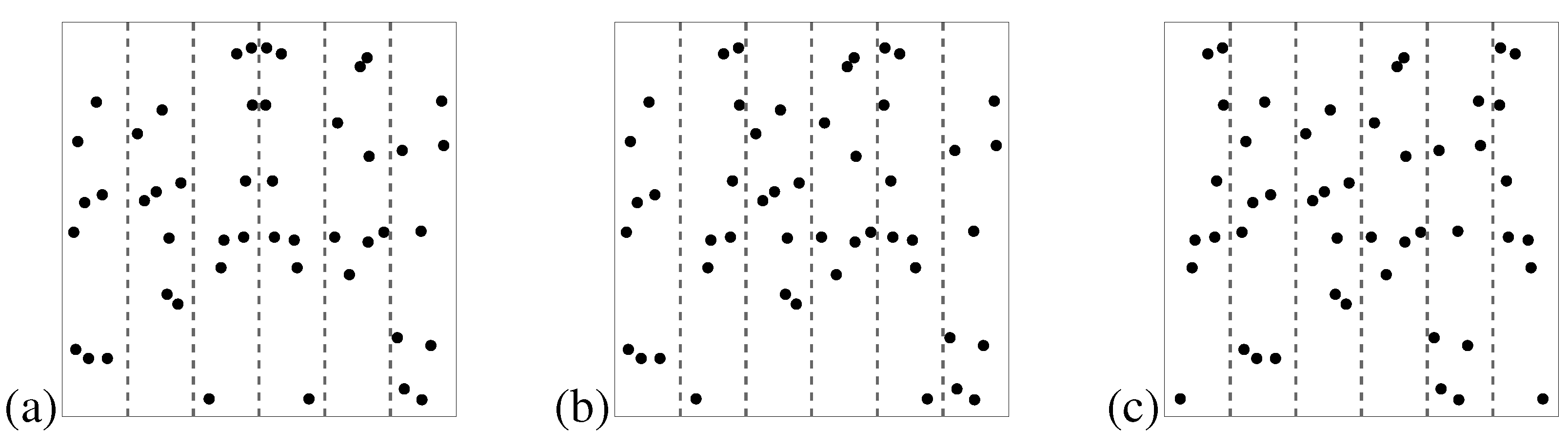Furthermore, the different parts of a stimulus do not weigh equally during symmetry detection [46]. A crucial role has been ascribed to the area about the symmetry axis. If a dot pattern is split into three pairs of vertical stripes (on either side of the symmetry axis) and symmetry is confined to one of the pairs, it is best perceived if the symmetry is located close to the axis (see Figure 6). This suggests that proximity to the symmetry axis is an important factor in symmetry detection. However, symmetry is also detected better when it is confined to the outermost stripes rather than when it is confined to the intermediate stripes. The latter effect is probably due to a symmetric ’subjective contour’ which arises when one connects the outermost dots by straight lines. Indeed, if one masks the pattern outline of dot stimuli by embedding them in surrounding random dots, the detectability of symmetry is reduced by a fixed amount for all axis orientations [82]. Similarly, if one introduces a gap between the two symmetry halves, symmetry detection deteriorates with increasing gap size [41]. However, if one compensates for the deterioration of symmetry processing by scaling up stimulus size proportionally with eccentricity, detection performance is fairly constant [83].

Information integration during symmetry processing was more rigorously investigated using dynamic random dot patterns [84]. Stimuli consisted of strips of symmetry surrounded by noise. By varying the width of the symmetric strips, the area of effective symmetry information uptake was shown to be limited to a 1.1° strip about the symmetry axis. Since the width of the strip was independent of stimulus size, it was considered to be spatially fixed. The latter conclusion was later disproved in a study using bandpass filtered Gaussian noise patterns [71]. Stimuli consisted of a central symmetric region embedded in noise of the same spatial frequency. Using phase jitter, the degree of symmetry was varied to obtain psychophysical thresholds. Furthermore, the size of the elliptical patch was varied along the x and y dimensions to find the maximum extent of the region wherein symmetry information is being processed. It was found that the region is elongated along the symmetry axis with an aspect ratio of approximately 2:1 and, furthermore, that it scales inversely with spatial frequency. In particular, the extent of the spatial region scales such that it encompasses a constant number of cycles.

This conclusion was somewhat refined in further research. It was shown that not only spatial-frequency content but also orientation content affects symmetry detection. Dakin and Hess used stimuli that were filtered for orientations either parallel to or perpendicular to the symmetry axis [85]. Detectability of symmetry was better when information perpendicular to the symmetry axis was preserved than when parallel information was preserved, suggesting that symmetry detection relies predominantly on information orthogonal to the symmetry axis. In another study testing more orientation bands, the symmetry integration region was shown to be flexible, with an aspect ratio varying from 20:1 to 2:1 as a function of orientation content [86]. A follow-up experiment addressed the question whether it is spatial frequency as such that is decisive to the extent of the symmetry integration region or rather one of the covarying factors numerosity (number of elements), element density (number of elements per unit area), or display size [87]. Interestingly, it was found that the symmetry integration regions scales with density only. In other words, the amount of information picked up from a stimulus is constant, showing that symmetry detection is scale invariant. In the kind of symmetry detection task used by the authors, information uptake was limited to about 18 elements.

4.5. Multiple Symmetry

There is consensus that the salience of symmetry generally increases with the number of symmetry axes [9,27,68,76,77]. Partly, this can be attributed to a probabilistic increase of chance in finding a symmetry axis. Furthermore, some researchers proposed that, in multiple symmetry, additional mechanisms come into play. In particular, it has been suggested that multiple symmetry gives rise to additional structural relationships, and that these relationships can be detected by the visual system, thereby enhancing symmetry detection [27,29,76]. A recent study cast doubt on this idea [88]. The authors found no evidence that so-called correlation rectangles [27,29] play a role in symmetry detection. However, they found that, in the absence of correlation rectangles, the angle between symmetry axes affects the salience of symmetry.

4.6. Symmetry versus Antisymmetry

It was recently argued that the term symmetry has been used as an umbrella term to also include structures the visual system is not sensitive to [48]. The term antisymmetry has been used to distinguish these structures from ordinary symmetry. Generally speaking, an antisymmetric stimulus may be conceived of as an ordinary symmetry wherein the elements of each symmetry pair have been assigned opposite values on a feature dimension other than position, for instance contour polarity in contour patterns (see [38,48] and Figure 7) or contrast polarity in dot patterns and checkerboard patterns (see [89,90,91] and Figure 8).

Using contour patterns, it was shown that symmetry (Figure 7a) is detected automatically while the detection of antisymmetry (Figure 7b) requires cognitive strategies involving selective attention [48]. This study is in accordance with earlier work using similar stimuli (e.g., [26,41,92,93]), but it is the first to honour the distinction between symmetry and antisymmetry in these stimuli.

For contrast polarity, results have been less consistent. While contrast polarity did not significantly affect symmetry detection in dot stimuli [91], detection of symmetry in checkerboard stimuli was significantly better than detection of antisymmetry [89]. To appreciate these results, one should note that, in sparse dot patterns, there are substantial variations in local dot density (i.e., the number of elements per unit area). Since density is distributed symmetrically, it betrays the presence of symmetry. In other words, symmetry or antisymmetry can always be discerned from random patterns based on the density distribution alone. Checkerboard patterns, in contrast, always have a uniform density, irrespective of whether they are (anti)symmetric or random. Here, (anti)symmetry is defined solely on the basis of contrast.

In line with the idea that dot density is the critical factor accounting for the difference between these studies, it was found that symmetry is detectable better than antisymmetry for high dot densities but not for low dot densities [87]. The effect on the density distribution of increasing dot density in antisymmetric and random patterns is illustrated in Figure 8; most importantly, the density distributions get less distinctive regarding (anti)symmetric and random stimuli, in line with the empirical results. More evidence stems from a study on visually-evoked potentials (VEPs). It was found that symmetric and antisymmetric patterns elicit similar VEPs at low densities. At high densities, the response to antisymmetry is attenuated while the response to symmetry is not.

4.7. Symmetry Detection in Complex Biological Stimuli

Usually, symmetry perception is construed as a general-purpose detection mechanism that applies to any visual input. Virtually all studies on symmetry perception make use of artificial, impoverished stimuli in order to not contaminate research results by uncontrolled stimulus factors. However, exploring more complex, biological stimuli might be an important step in order to further the comprehension of symmetry processing. First, symmetry detection in a highly impoverished environment does not necessarily transfer to a more complex setting. For instance, as stated above, the conscious perception of symmetry wanes in complex but abstract stimuli when other salient regularities are present [55]. However, there is also evidence that symmetry perception can be better in biological shapes than in dot patterns, indicating that biological shapes feature additional redundancies (e.g., texture) that can be picked up by the visual system [94]. Second, using naturalistic stimuli, one can assess whether there are higher-level symmetry detection processes tuned to particular kinds of stimuli. In fact, these seems to be the case for faces. Symmetry detection is better in normal faces than in inverted (turned upside-down) and contrast-reversed faces [95]. Moreover, if faces are tilted away from vertical in steps of 45°, detectability decreases monotonically from 0° to 135°. This is in line with the stimuli becoming less salient instances of faces with increasing orientation, but it is unlike the orientation tuning function established for dot patterns, where symmetry about the horizontal is usually better than symmetry about the diagonals (see Figure 5). More compelling evidence for the existence of specialized facial symmetry detection processes stems from a study on the effect of female menstrual cycles on symmetry detection. The ability to detect symmetry in male faces was better in the menses phase than in the luteal phase of the women’s cycle, which was attributed to systematic changes in the progesterone levels across the menstrual cycle. For dot patterns, the effect of menstrual phase was not significant and even had a trend in the opposite direction, suggesting a dissociation of the processes underlying the detection of symmetry in faces and in dot patterns [96].

4.8. Recovery of 3D Structure from Symmetry

Symmetry is a so-called non-accidental property. In other words, it is unlikely that a symmetric image results from a particular view of an asymmetric object. In the computer vision literature, image-symmetry has been appreciated as a powerful tool for more than 20 years. It has been used as a structural constraint to reduce the degrees of freedom in solving the inverse problem (i.e., recovery of 3D shape from a 2D view) for objects presented in slanted views, both under orthogonal projection, that is, affine transformations [97], and perspective projection [98]. Furthermore, it was shown that implementing a 3D symmetry constraint generally enhances the performance of reconstruction algorithms such as structure-from-motion algorithms [99]. Recently, a shape recovery model was introduced in which the constraint of symmetry makes the use of other depth cues superfluous [100].

Curiously, except for research on object representation and object recognition [101,102], empirical research in human symmetry perception treated this topic rather stepmotherly (but see [103], who suggested that symmetry aids human 3D perception by providing additional virtual views of an object). It is true that Wagemans et al. provided substantial work on skewed symmetry [5,27,28,29]. However, the experiments were aimed towards establishing the importance of certain higher-order structures in symmetry detection rather than its role in depth perception. Hence, the issue was closed by concluding that skewing seriously disrupts automatic processing of symmetry [28]. Moreover, the affine transformations that were used as stimuli are not veridical views for close-up objects. As reported above, van der Vloed et al. used veridical perspective views of symmetric stimuli but their research was aimed to investigate whether symmetry is detected from the retinal image or some form of transformed image normalized for perspective distortion [30].

This left open the question as to whether or not symmetry processing is directly involved in the computation of the orientation of objects in depth. To be more clear, perspective does not simply distort symmetry in a random way as noise would do. Rather, the virtual lines connecting symmetry pairs undergo lawful geometric transformations that could, in principle, be picked up by the visual system and serve as a depth cue (see Figure 2d,e). Recently, this issue came back into the focus of symmetry research. Using a depth-matching task for pairs of three-dimensional everyday objects viewed at different angles, it was found that participants used symmetry, among other cues, to determine object orientation [104]. Another study suggested that the convergence of virtual lines indeed plays a role in depth perception [105], but their stimuli were confounded. They used dot matrices which, in addition to symmetry, also featured repetition and good continuation. Consequently, at present, it is still unclear in how far symmetry contributes to depth perception, if at all.

5. Neural Implementation

While the functional properties of symmetry perception are, to a certain extent, well-articulated, its neural basis is still poorly understood. There is some evidence for the recruitment of binocular visual neurons during symmetry processing. Symmetry can be both defined and destroyed by binocular disparity [51,52]. In line with this, two random dot patterns presented to different eyes can be perceived as symmetric if their superposition yields a symmetry; vice versa, two monocular symmetries are perceived as random if their superposition does not yield a symmetry [69]. Another study argued that both V1 and extrastriate areas, and both monocular and binocular cells are involved in symmetry processing [106]. Using symmetric dot stimuli, the authors showed that symmetry axes elicit the same tilt-aftereffects as usually observed with oriented lines. Based on these results, they proposed that similar mechanisms might underlie the encoding of orientation and the encoding of symmetry. This accords with studies that demonstrate the simultaneous processing of symmetry at different spatial scales and for different orientation content, suggesting that simple cortical filters such as those found in V1 could subserve symmetry detection [71,86,87,107,108,109].

The neural foundations of symmetry processing were more directly assessed in neurofunctional studies employing electrophysiological and hemodynamic indices. In [110], participants engaged in a Landmark task wherein they had to judge whether or not the parts of a transected line are of equal length. It was shown that presence versus absence of symmetry is correlated to activity in right anterior cingulate gyrus, which is involved in the deployment of attention. However, no symmetry-specific activation was found in earlier cortical areas. For symmetric dot patterns, predominant symmetry-specific activity was found in dorsolateral occipital cortex, and none in earlier cortical areas either [111]. This picture was refined in a follow-up experiment, where a more widespread network including V3A, V4d/v, V7, and the lateral occipital complex (LOC) was identified [63]. The response of these areas was largely indifferent to changes in stimulus type (i.e., dot patterns and curved line patterns) and stimulus size. A control experiment revealed that these activations were partly modulated by attention, but symmetry-specific activity was found even when participants performed a probe-detection task to which the structure of the stimulus was not relevant. This is in line with the the idea that symmetry detection is an automatic mechanism that applies to any visual input. The authors also showed that the magnitude of activation in areas V3A, V4d/v, V7, and LOC was correlated with the perceptual salience of the percept. In other words, activation was higher for 4-fold symmetry than for 2-fold or 1-fold symmetry, higher for perfect than for noisy symmetry, and higher for vertical than for horizontal symmetry.

The picture sketched by the fMRI studies is complemented by electrophysiological studies on the temporal dynamics of symmetry processing. In line with the idea that primary visual areas do not contribute significantly to symmetry detection, symmetric stimuli were shown to modulate only later components of the event-related potential (ERP). For instance, in [112], participants were exposed to abstract geometric stimuli that were symmetric or non-symmetric and they had to judge either the beauty or the symmetry of the stimulus. In the symmetry judgment task, the ERP showed a late sustained negativity in the 500–1000 ms post-stimulus period for posterior electrode sites. A similar negativity was obtained in a precursor to that study [20]. In another study, participants viewed quick alternations (500 ms stimulus-to-stimulus time) of 2-fold symmetric and random dot patterns [113]. Again, a divergence of the ERPs in form of a sustained negativity for symmetric patterns was found. However, this time, ERPs diverged from about 200 ms post-stimulus, which is substantially earlier than in the previous study. Compatible results were reported in a study using symmetric checker stimuli [90].

Concluding, neurofunctional studies rather unequivocally pinpoint higher-tier visual areas as the locus of symmetry processing. One the one hand, this seems reasonable. Since symmetry is a global stimulus property, information needs to be integrated across large distances. Visual areas such as LOC, comprising neurons with large receptive fields, seem to form the adequate neural tissue for such global computations. On the other hand, there seems to be a discrepancy with parts of the psychophysical literature, which suggests that symmetry detection is critically supported by low-level filtering processes.

These seemingly contradictory views can possibly be reconciled if one takes into account the possibility that, as conjectured in [107], spatial filters involved in symmetry detection could be general-purpose filtering mechanisms recruited by many processes during perceptual organization. This indicates that one should not discount the role of early visual areas such as V1 prematurely, because EEG and fMRI analyses rely critically on differential activation (i.e., differences in activity elicited by symmetric stimuli versus control stimuli), so that they may be insensitive to a significant amount of preprocessing of symmetries that is performed in primary visual areas.

6. Models of Symmetry Processing

Over the years, numerous models of symmetry detection have been developed. Some are specialist, modeling a particular characteristic of symmetry perception, while others are more comprehensive (or at least they claim so). Since a short overview is necessarily incomplete, only those models with a relatively broad scope are considered. Furthermore, in an attempt to make the selection of models that are reviewed as representative as possible, different classes of models will be covered. Generally, one can distinguish five classes of symmetry detection models. Representational models of symmetry detection define the structures and relationships between stimulus parts underlying the perception of symmetry. Process models specify the operations to be carried out on raw visual input in order to enable the representation of symmetry. Neural models specify the neural architecture underlying the computation of symmetry. Finally, there are two classes of hybrid models that share characteristics with both process models and neural models. First, spatial filtering models, which draw upon spatial mechanisms reminiscent of the spatial filtering operations that are known to be carried out in visual cortex. So, in fact, spatial filtering models are process models, but processes are specified in a fashion that is suggested to be neurally plausible. Second, artificial neural network (ANN) models, in which functional units interact with each other via inhibitory or excitatory connections. These connections have weights that are usually adjusted in an initial training phase wherein the ANN “learns” to detect symmetry.

6.1. Representational Models

The most influential representational models on the perception of symmetry (and also other regularities) have been the transformational approach (TA) and the holographic approach (HA). In vision research, TA was promoted by Garner [114] and Palmer [115]. It conceives of symmetries as a number of geometric transformations including translation, rotation, and reflection. 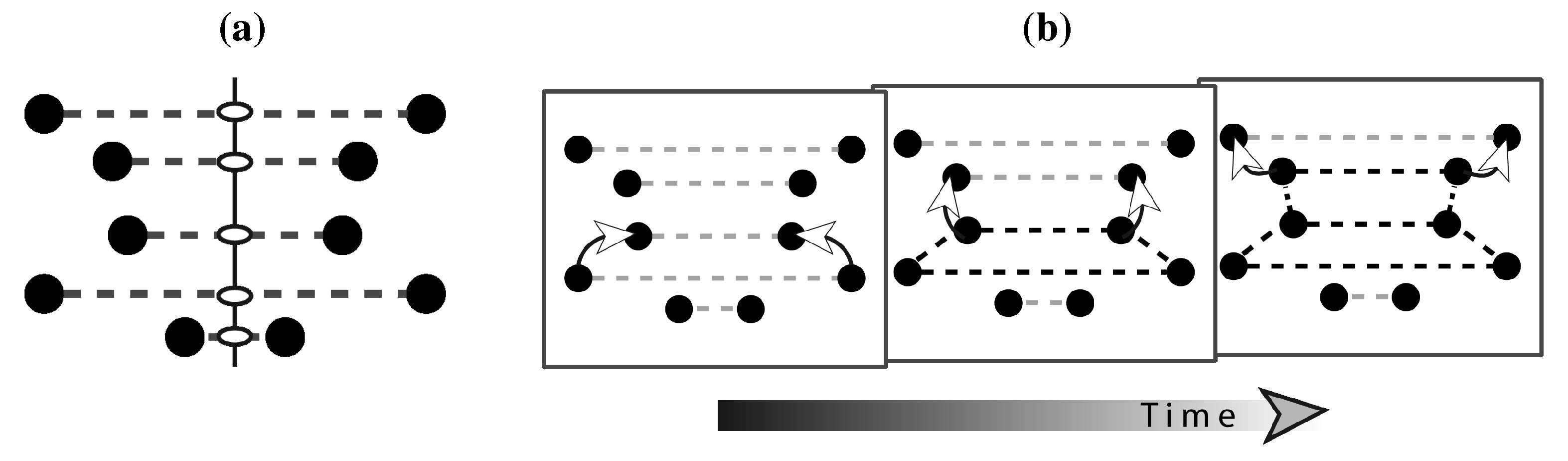Although TA was originally coined to describe 3D structures, it readily generalizes to 2D patterns, as illustrated in Figure 9. The TA owes its elegance to its mathematical roots, in which the formation of symmetry is broken down into a number of geometric operations. By this, TA provided a common framework encompassing the kinds of geometric relationships the human visual system seems to be sensitive to.

In contrast to TA’s invariance under motion, the rivaling holographic approach (HA) by van der Helm and Leeuwenberg postulates invariance under growth [2,25,116]. That is, in a regularity, each substructure should exhibit the same kind of regularity. This principle is known as holography and it can be exemplified by flowers, for instance, who preserve their symmetry when they grow. Based on mathematical analysis, HA proposes three kinds of regularities, repetition (which corresponds to TA’s translational symmetry), symmetry, and alternation (Figure 10). The latter regularity, alternation, gives rise to the class of Glass patterns to which the visual system has been shown to be sensitive to [117].

TA and HA differ mainly in the way they conceive of the structure of the regularities. HA gives symmetry a point structure rather than a block structure, as TA does. Furthermore, it makes quantitative predictions concerning the goodness (i.e., detectability) of a regularity. For instance, it predicts a graceful degradation of the goodness of symmetry with noise, which is supported by virtually all literature on symmetry detection [46,71,73]. A more detailed discussion on the commonalities and differences between TA and HA can be found in references [2,116,118].

6.2. Process Models

In contrast to representational models, which describe the static relationships between stimulus parts in symmetry and other regularities, process models address the dynamics of the mechanism extracting symmetry from visual input.

In his component processes model, Jenkins noted that, when symmetry pairs are connected by virtual lines, these lines are both of a uniform orientation and they are midpoint collinear [72]. This is illustrated in Figure 11a. Jenkins conjectured that the visual system is sensitive to these first-order structures and uses them as anchors for symmetry detection. His detection model comprises three component processes, one detecting the orientational uniformity of virtual lines, one fusing most salient point-pairs into a salient feature, and another estimating the symmetry in this feature.

Wagemans et al. pointed out that first-order structures are insufficient for an apprehension of symmetry detection [29]. In particular, using affine transformations, they showed that symmetry detection deteriorates in skewed symmetry even though orientational uniformity and midpoint collinearity are preserved. This led them to point out the importance of higher-order structures formed by joining symmetry pairs into so-called correlation quadrangles. They proposed that symmetry detection employs a bootstrapping process to form these higher-order structures by successively joining virtual lines, as illustrated in Figure 11b.

Two other process models bear on the remarkable resistance of symmetry detection to spatial jitter. Based on this observation, Barlow and Reeves concluded that the visual system does not perform a rigid point-to-point matching but rather operates within a certain tolerance area [46]. According to their model, the visual system mimics an operation that boils down to tiling the stimulus into a number of equisized rectangles corresponding to the size of this tolerance area, counting the number of elements within this area and comparing it to the number in the corresponding symmetry half. This is illustrated in Figure 12a.

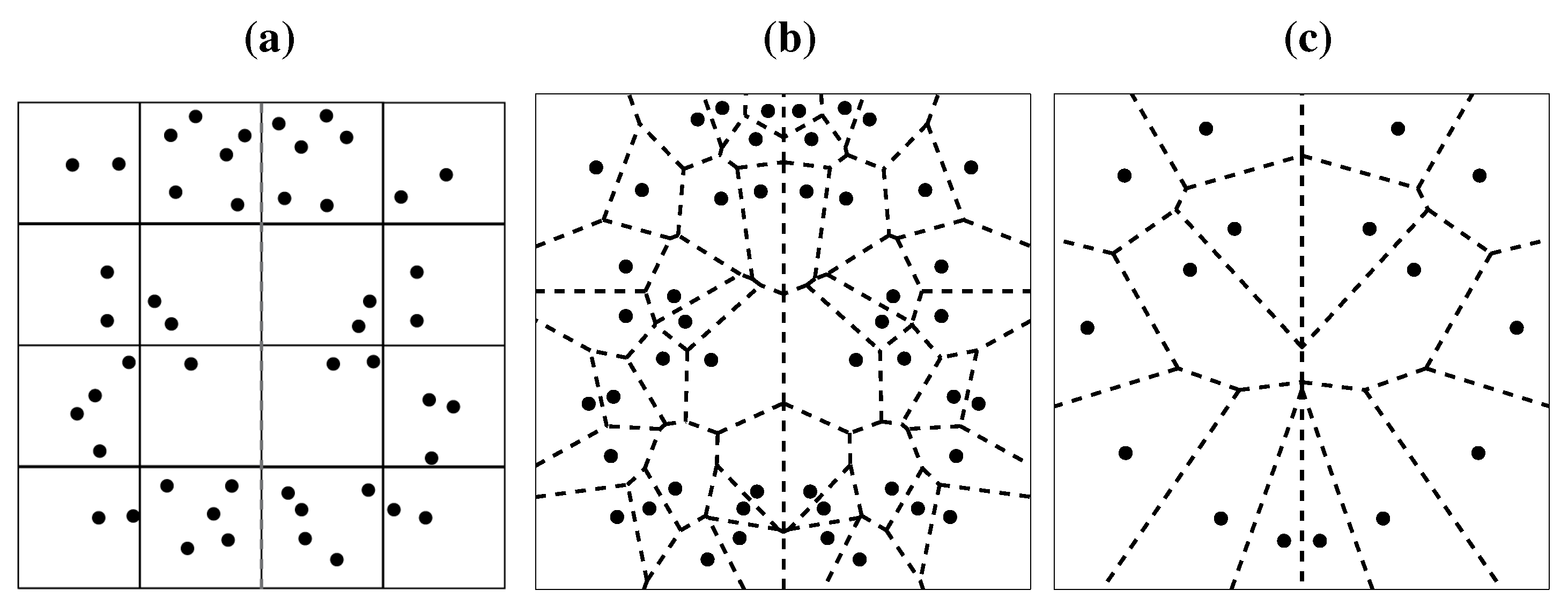
A recent model on symmetry detection, although based on a different rationale, constitutes in some respect a refinement of Barlow and Reeves’ account. Dry’s model utilizes Voronoi tesselation to render spatial relationships between the dots [119]. Each dot is placed in a cell of variable size, whereby the cell’s border circumscribes the area that is closest to the dot in the cell (Figure 12b). Similar to Barlow and Reeves’ account, symmetry detection is performed by superimposing one half of the pattern with the reflected Voronoi tesselation of the other half and then assessing the number of dots falling into each cell. In a perfect symmetry, there would be a perfect match. Interestingly, the Voronoi model explicitly predicts scale invariance (see Figure 12c), a property of symmetry perception that was verified earlier [87].

6.3. Spatial Filtering Models

The 90’s were the advent of spatial filtering models in symmetry detection. These models capitalize on the fact that the visual system is sensitive to the spatial frequency and the orientation content of the visual input [120,121,122,123]. Spatial filtering models recruit mechanisms sensitive to spatial frequency, orientation, and spatial phase.

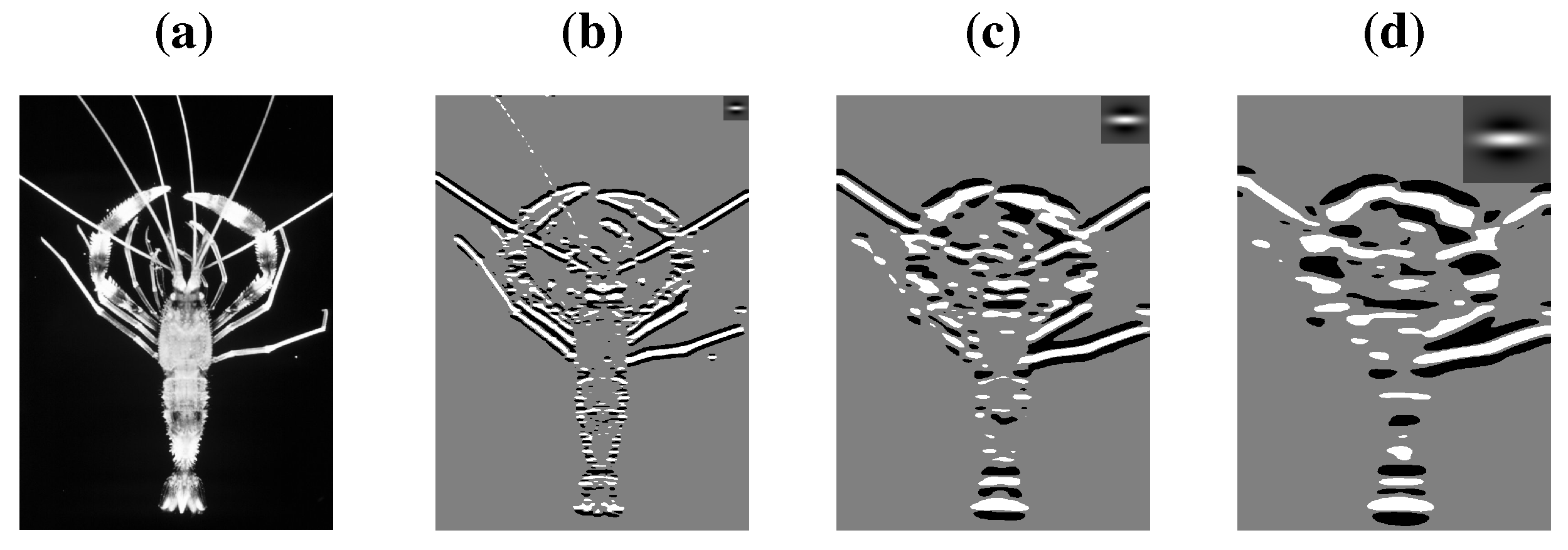
A two-stage model was introduced by Dakin and Watt [107]. In the filtering stage, the input image is convolved with an oriented filter responsive to particular spatial frequencies and then thresholded to a ternary image (Figure 13b–d), yielding a number of black and white blobs. In the second stage, a blob alignment procedure is applied that measures how well the centroids of the blob align about a putative symmetry axis. Upon visual inspection of the examples in Figure 13, blob alignment about the central vertical symmetry axis is obvious in only the lower half of the animal for rather coarse filters (Figure 13c,d).

More complex two-stage models were presented by Kovesi [124,125] and Osorio [126]. Both authors realized that, if an image is decomposed into its frequency components, phase information is instructive regarding the location of a local symmetry axis. In particular, three types of stimulus features, namely edges, lines, and symmetry axes, are characterized by phase congruency, as follows. Edges are defined by sharp luminance transitions, so that corresponding spatial harmonics can be characterized by sine waves in 0° or 180° phase. Lines feature luminance maxima or minima with spatial harmonics congruently in 90° (cosine) or 270° phase. Although there is no specific intensity change at symmetry axes, spatial harmonics are a mixture of 90° and 270° phase. To squeeze out symmetry information from an input image, both authors used quadrature-pair filters (two filters, one in sine phase and one in cosine phase) to obtain measures of symmetry and asymmetry. After this first filtering stage, signals were squared. Osorio separately added up energy from even-symmetric and odd-symmetric filters. Points were marked as lying on a symmetry axis when the sum obtained from the even-symmetric filters was at a maximum and the sum obtained from odd-symmetric filters was close to zero. Kovesi combined even- and odd-symmetric filter outputs by determining the absolute difference between the outputs for each spatial scale and then calculating a weighted mean normalized by the total energy. Note that these models compute only local symmetry. Information is not integrated across a larger area to find the global symmetry axis, as done by Dakin and Watt.

Global computation of the symmetry axis is achieved in a three-stage model presented in Gurnsey et al. [127]. In the first stage, the image is convolved with a Gaussian kernel to get a smoothed image. Then, a global differencing operation is performed, wherein the squared difference in luminance between symmetrically positioned pixels is calculated for each column in the image. In the third stage, the output of the differencing operation is convolved with a vertical filter to explicitly detect the symmetry axis. These stages are documented in Figure 14 for a sample stimulus.

A comprehensive spatial filtering model was recently introduced by Poirier and Wilson [128]. In contrast to the previous models, this model is sensitive to symmetry of the outline of a stimulus. It operates in five successive stages. First, the image is bandpass filtered for different orientations. Second, the object’s center is estimated by using higher-order filters that respond to the centers of concentric shapes. Third, shape curvature is recovered using combinations of filters arranged along a curved line. Fourth, object shape is represented as curvature signal strength as a function of the orientation around the center. Fifth, symmetry is extracted from the shape representation by comparing pairs of curvatures at opposite angular distances from a putative symmetry axis. The model provides a size invariant, object-centered quantification of the amount of shape symmetry. Although it was tailored to radial frequency patterns, the authors demonstrate that the model is also sensitive to facial symmetry and the virtual outline of dot patterns, making it applicable to a whole range of symmetric stimuli.

Note that this overview is not exhaustive. Other capable models have been proposed in the literature, such as a two-stage model by Rainville and Kingdom [87], which applies quadrature-pair filters first to luminances and then to filter output. The model is theoretically sound and it implements the complex process of density invariance.

6.4. Artificial Neural Network Models

Artificial neural network (ANN) models of symmetry detection is a strand of research in the computer vision community that developed largely in parallel with models in the cognitive science community, with relatively little cross-talk. One reason is that, in computer vision, ANN models serve as effective symmetry detectors rather than realistic models of human symmetry perception. Nevertheless, ANNs are excellent tools to simulate interactions between functional units as found in visual cortex, such as lateral inhibition. Consequently, there were attempts to design ANNs that give a biologically plausible account of symmetry perception.

For instance, Latimer, Joung, and Stevens showed that ANNs can mimick human anisotropy in the detection of symmetries of various absolute orientations, but their model was restricted in that it pertained to 6 × 6 pixels binary input images [129]. Fukushima and Kikuchi proposed a hierarchical multi-layer ANN which mimicks the functionality of early visual processes in lateral geniculate nucleus (LGN) and V1 [130]. First, the raw visual input passes a layer with on-center and off-center contrast sensitive units, resembling the functionality of retinal ganglion cells and LGN neurons. The outputs project to a layer comprising edge detectors, resembling simple cells in V1. The next layer is a blurred edge extraction layer similar to complex cells in V1. Finally, local symmetry is extracted by units pooling activity of units at opposite sides of a putative symmetry axis.

6.5. Neural Models

At present, there is no full-fledged neural model of symmetry detection. This is mostly due to the patchy knowledge we have about its neural underpinnings. Despite the lack of facts, there were some ideas about how symmetry processing might be implemented. In early approaches, the high salience of vertical symmetry spawned theories suggesting that symmetry processing is accounted for by the vertically symmetric architecture of the visual cortex [1,24]. Recently, a similar scheme was proposed, whereby the corpus callosum was speculated to establish long-range connections between cortical filters [131]. Both views can be regarded as obsolete, because virtually all experimental results militate against a rigid architecture involving interhemispheric point-to-point computations. In particular, as reviewed above, the fact that symmetry can be detected under various axis orientations, for different eccentricities, and the fact that the salience of symmetry increases when symmetry axes are added suggests a more flexible underlying substrate.

7. Discussion and Conclusions

We are not yet at the verge of understanding human symmetry perception, but significant progress has been made in over 100 years of symmetry research. Although its exact neural underpinnings are not known, the functional characteristics have been relatively well charted. I will first recap the key characteristics in an itemized form.

• symmetry detection is quick, sensitive to deviations from perfect symmetry, and robust to noise
• symmetry detection operates on 2D projections of (possibly 3D) objects, but disparity cues are incorporated when they have been processed
• symmetry detection operates automatically and it is involved in object formation
• symmetry detection is affected by higher-level cognition
• the salience of symmetry varies with the orientation of symmetry axis, with the most salient axes being, in order of salience, vertical, horizontal, left/right oblique axes
• generally, the salience of symmetry increases with the number of symmetry axes
• symmetry detection is most efficient when the symmetry axis is foveated, but performance can be equated across stimulus eccentricities by appropriate up-scaling with eccentricity
• the uptake of symmetry information is limited but it is scale invariant
• neurally, symmetry processing is supported by a widespread network of extrastriate visual areas, including V3A, V7, and LOC

There has been a proliferation of models of symmetry perception in the last two decades. The fact that none of them seems to be able to give a comprehensive account of symmetry perception bears witness to the intricacy and versatility of the process. Apart from not implementing all characteristics of symmetry perception, the Achilles’ heel of most models is their stimulus specificity. Many are tailored to a specific type of stimulus, such as dot stimuli, contour stimuli or dense noise. However, the failure to find a generic model of symmetry perception might also indicate that multiple processes contribute to it. For instance, human symmetry detection is both sensitive to the area close to the symmetry axis and to the pattern outline, despite their obviously different spatial properties.

With respect to outline symmetry, the model by Poirier and Wilson seems promising. It does not only recruit biologically plausible mechanisms but it is also applicable to a wide range of stimuli. Importantly, it is also in line with symmetry models at other levels of description. In particular, its quantification of the amount of symmetry largely agrees with van der Helm and Leeuwenberg’s holographic approach (see [128] for details).

With respect to central symmetry, no comparably mature model has emerged yet. Nevertheless, many spatial filtering and ANN models implicitly agree on a two-stage architecture. These accounts conceptualize an initial stage consisting of one or more filtering operations that serve as a kind of preprocessor. The second stage is a symmetry operator that extracts the amount of symmetry from the output of the preprocessing module. This symmetry operator can take very different forms, such as a global differencing operation [127], a blob-alignment measure [107], or a pairwise comparison of filter outputs [130].

Though speculative, such a two-stage architecture does not seem implausible given current knowledge about the neural implementation of symmetry detection. Symmetry is not detected in early visual areas, but these areas could perform a critical amount of preprocessing. The explicit detection of symmetry, which involves the integration of information across larger portions of the visual field, could then be subserved by neural structures such as LOC that are responsive to symmetry and whose neurons have large receptive fields.