A Lightweight Batch Authenticated Key Agreement Scheme Based on Fog Computing for VANETs
Abstract
1. Introduction
2. Related Works
3. Preliminaries
3.1. System Model
3.2. Security and Privacy Requirements
4. Proposed Scheme
4.1. Setup Phase
4.2. Registration Phase
4.2.1. Registration for Vehicles
4.2.2. Registration for Fog Node
4.3. Authentication and Key Agreement Phase
4.3.1. Vehicle Requests to Generate a Session Key
4.3.2. FN Aggregates the Request Data from Each Vehicle
- (1)
- Decision on Initiating the Aggregation Process
- (a)
- TCC congestion (): suspends the aggregation process and resumes only upon receiving a “congestion relief” signal from the TCC.
- (b)
- TCC busy (): immediately delays the aggregation process and continues collecting AKA requests until the maximum waiting time is reached.
- (c)
- TCC idle (): dynamically adjusts the window duration based on the vehicle density , with the following rules:
- High density (, where denotes the high-density threshold): If the number of accumulated AKA requests reaches , the aggregation process is immediately triggered, even if the dynamic window time has not expired. In this case, the window duration for the next batch is reset to the standard value .
- Low density (, where denotes the low-density threshold): If the dynamic window time expires and fewer than requests have been collected, the aggregation process is immediately initiated, and the window duration for the next batch is updated to , where is the minimum allowable window duration.
- Medium density (): The aggregation process is triggered immediately when either the timeout expires or the number of requests reaches . The window duration for the next batch remains unchanged.
- (2)
- Aggregation Process
| Algorithm 1 Aggregation |
|
4.3.3. TCC Authenticates and Processes the FN’s Requests
- It retrieves the i-th tuple from and obtains the real identity of by computing .
- It calculates the vehicle ’s certificate .
- It calculates , and verifies whether vehicle is revoked by checking if its real identity exists in the revocation list .
- –
- If it is not revoked, it indicates that the vehicle is legal, then calculates .
- –
- If it is revoked, it calculates , where the message authentication code of the illegal vehicle is removed from ; at the same time, the message of the illegal vehicle should be removed from .
- The TCC sets , and .
- Using the Lagrange interpolation formula, the TCC can obtain the equation of a straight line passing through points and . These straight lines corresponding to all legitimate vehicles pass through a common point , which can significantly reduce the computational and communication overheads.
- The TCC selects a random number for vehicle , such that , then substitutes into the straight line equation to compute the corresponding y coordinate, i.e., it evaluates . Therefore, in addition to the points and , the TCC has now obtained the third point on the straight line .
- The TCC obtains the verification message by computing .
| Algorithm 2 TCC Process |
|
4.3.4. FN Generates Session Keys
- The fog node sends the messages to the corresponding vehicles , respectively.
- It computes , and performs the following operations for each legal vehicle.
- –
- It substitutes into the straight line equation to obtain the y coordinate of the intersection point between the line and the Y-axis: . The line passes through points and , where point is set by fog node and point is set by the TCC.Note: It is unnecessary to first solve the explicit expression of the linear equation here.
- –
- It obtains the session key between the vehicle and the fog node by computing .
- –
- Fog node stores the session key .
| Algorithm 3 FN Generates session keys |
|
4.3.5. Vehicle Generates Session Key
- It sets , and computes .
- It substitutes into the linear equation to obtain the y coordinate of the intersection point between the line and the Y-axis: . The line passes through points and , where point is set by vehicle and point is set by the TCC.Note: For a specific vehicle , the three points , , and lie on the same straight line. Therefore, the line determined by any two of these points is identical, denoted as .
- It obtains the session key between the vehicle and the fog node by computing .
- Vehicle stores the session key .
5. Security Analysis
5.1. Informal Security Analysis
5.2. Formal Security Proof
5.2.1. Security Model
- : This query simulates the passive adversary to intercept messages exchanged among , , and .
- : The query models an active adversary sending message m to , , and . Upon receiving this query, these instances return corresponding response messages to .
- : When challenger receives this query from adversary , it randomly selects a bit ; if , sends the real session key of to ; if , sends a random key of the same length as the session key to the . If the session key of is undefined, or if a query has been made to or its partners, receives ⊥ as an invalid value.
5.2.2. Security Proof
6. Performance Evaluation
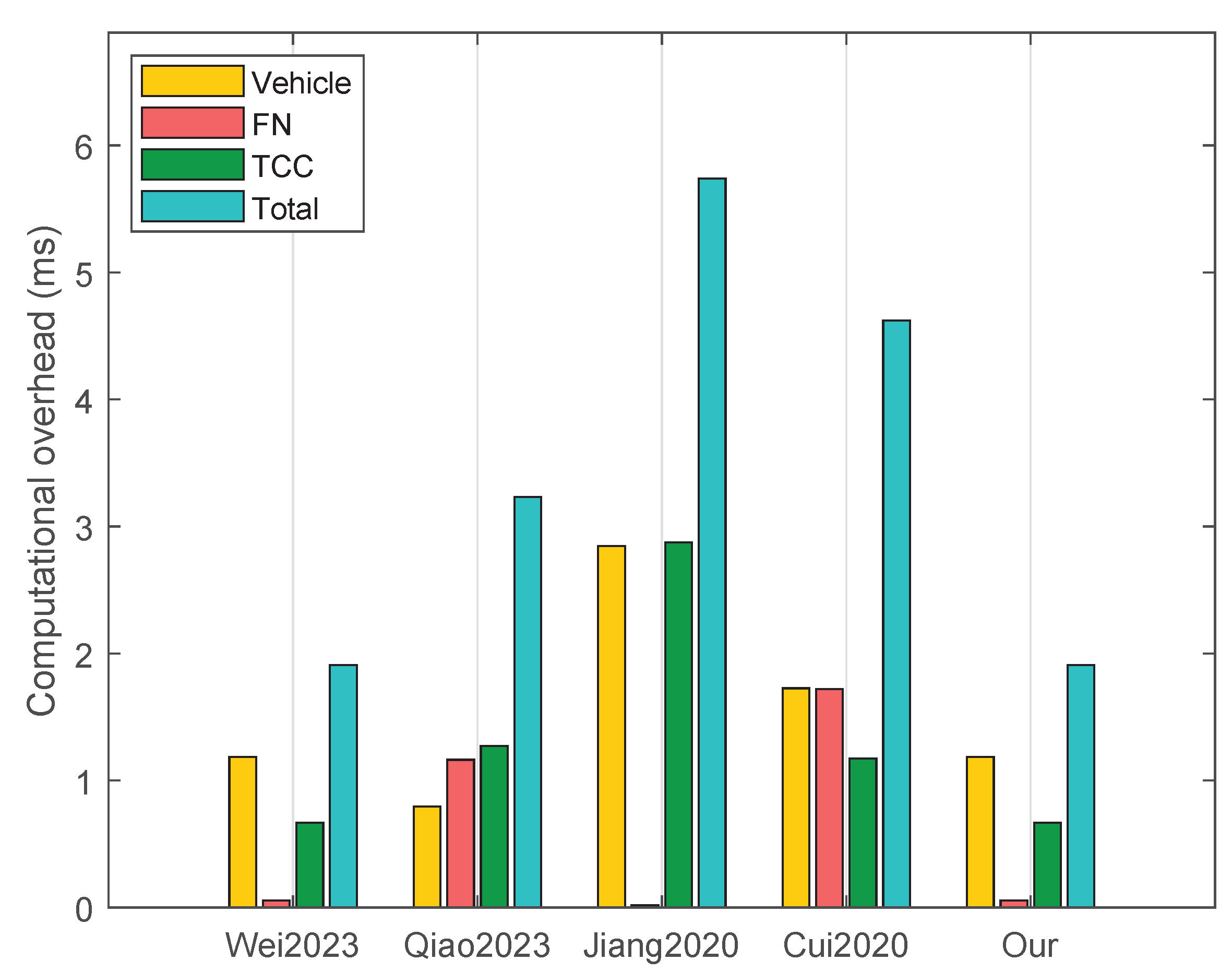
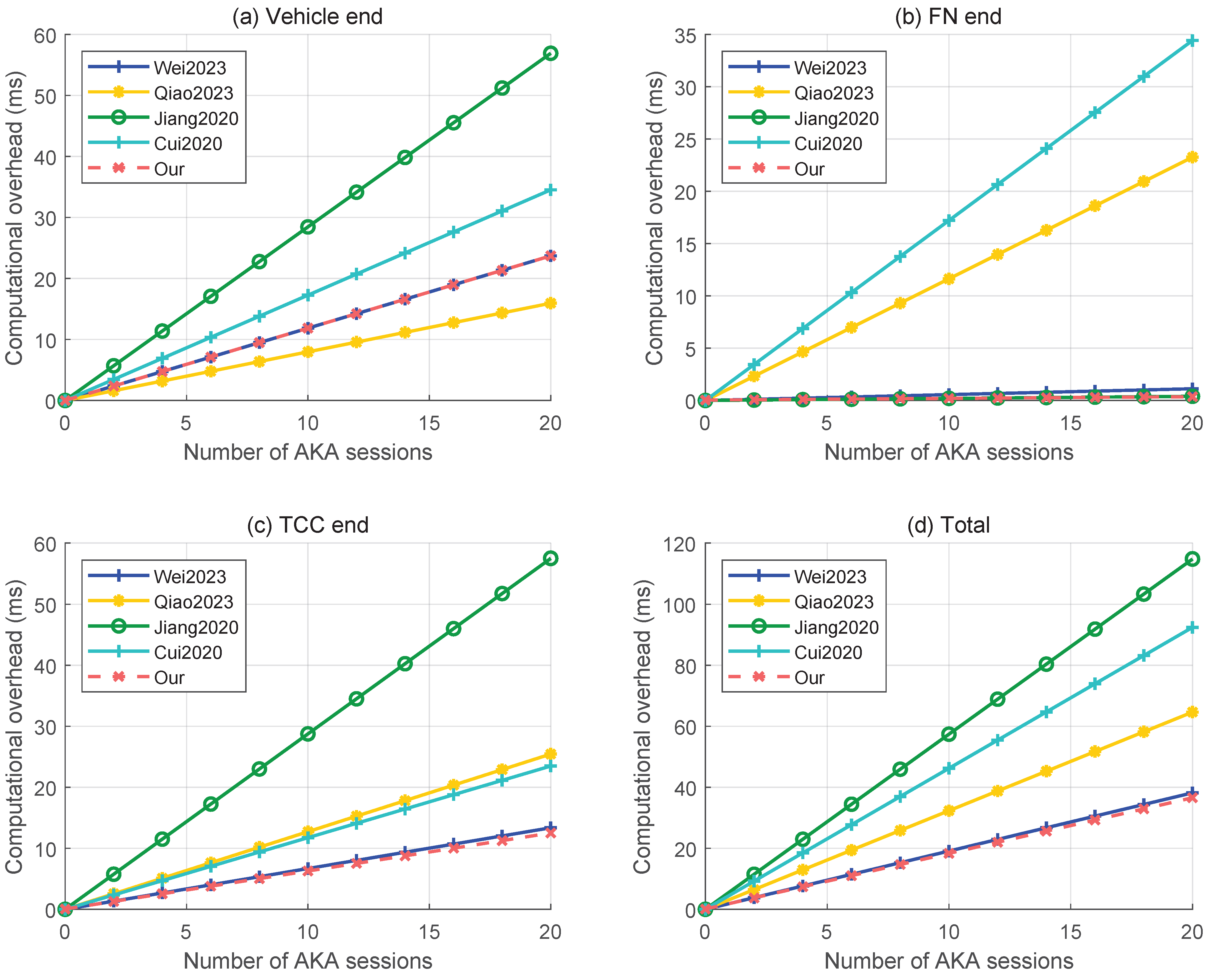
6.1. Computational Overhead Comparison
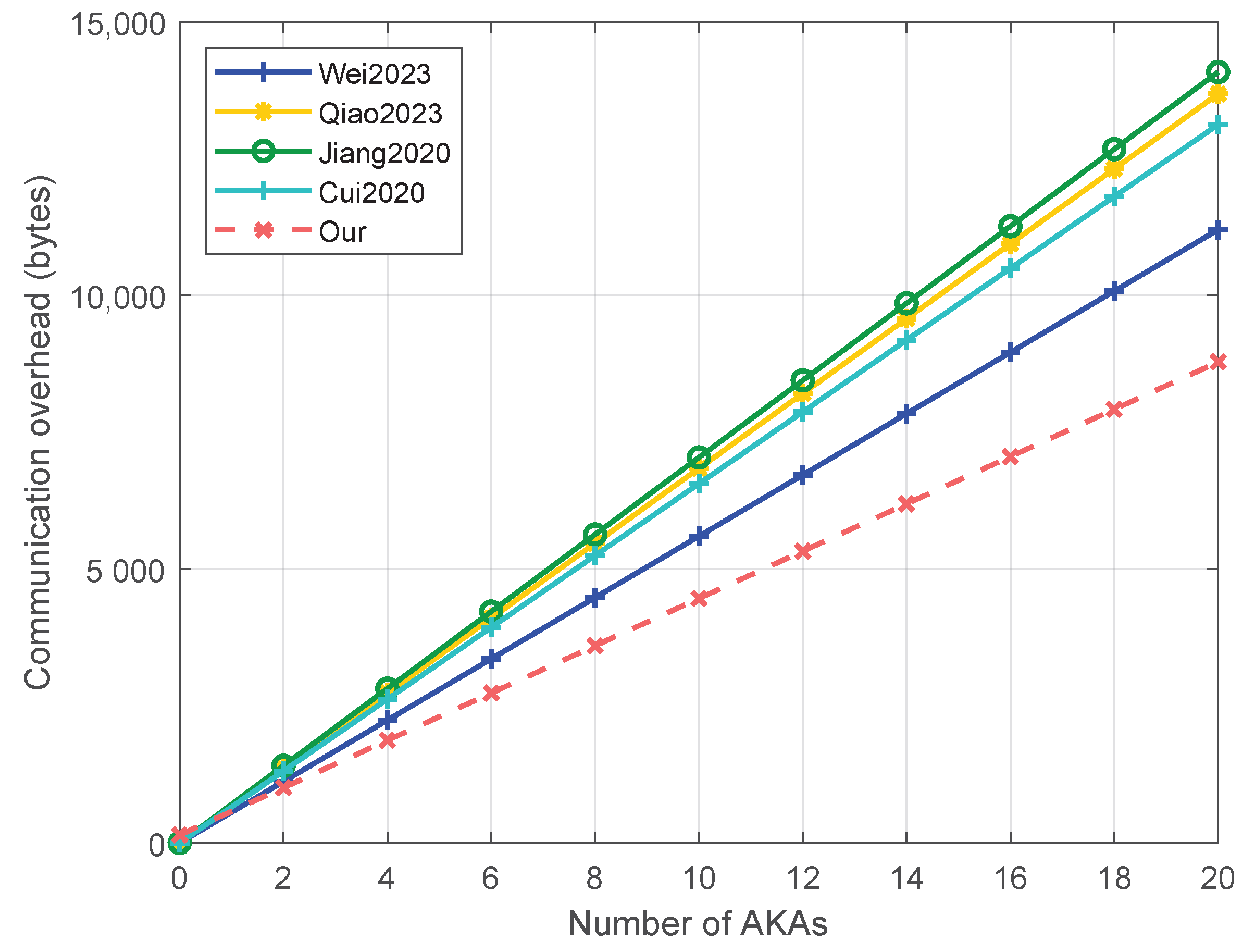
6.2. Communication Overhead Comparison
7. Conclusions and Remark
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Pseudo-Random Function (PRF)
Appendix A.2. Elliptic Curve Cryptography (ECC)
References
- Cao, J.; Feng, W.; Ge, N.; Lu, J. Delay Characterization of Mobile-Edge Computing for 6G Time-Sensitive Services. IEEE Internet Things J. 2021, 8, 3758–3773. [Google Scholar] [CrossRef]
- Cui, J.; Wei, L.; Zhong, H.; Zhang, J.; Xu, Y.; Liu, L. Edge Computing in VANETs-An Efficient and Privacy-Preserving Cooperative Downloading Scheme. IEEE J. Sel. Areas Commun. 2020, 38, 1191–1204. [Google Scholar] [CrossRef]
- Saleem, M.A.; Li, X.; Mahmood, K.; Shamshad, S.; Alenazi, M.J.F.; Das, A.K. A Cost-Efficient Anonymous Authenticated and Key Agreement Scheme for V2I-Based Vehicular Ad-Hoc Networks. IEEE Trans. Intell. Transp. Syst. 2024, 25, 12621–12630. [Google Scholar] [CrossRef]
- Lin, C.C.; Deng, D.J.; Yao, C.C. Resource Allocation in Vehicular Cloud Computing Systems with Heterogeneous Vehicles and Roadside Units. IEEE Internet Things J. 2018, 5, 3692–3700. [Google Scholar] [CrossRef]
- Awais, S.M.; Yucheng, W.; Mahmood, K.; Alenazi, M.J.F.; Bashir, A.K.; Das, A.K.; Lorenz, P. Provably Secure and Lightweight Authentication and Key Agreement Protocol for Fog-Based Vehicular Ad-Hoc Networks. IEEE Trans. Intell. Transp. Syst. 2024, 25, 21107–21116. [Google Scholar] [CrossRef]
- Bonomi, F.; Milito, R.; Zhu, J.; Addepalli, S. Fog Computing and Its Role in the Internet of Things. In Proceedings of the ACM SIGCOMM International Conference on Mobile Cloud Computing, Helsinki, Finland, 17 August 2012; pp. 13–16. [Google Scholar]
- Kenney, J.B. Dedicated Short-Range Communications (DSRC) Standards in the United States. Proc. IEEE 2011, 99, 1162–1182. [Google Scholar] [CrossRef]
- Jiang, D.; Delgrossi, L. IEEE 802.11p: Towards an International Standard for Wireless Access in Vehicular Environments. In In Proceedings of the VTC Spring 2008—IEEE Vehicular Technology Conference, Marina Bay, Singapore, 11–14 May 2008; pp. 2036–2040. [Google Scholar] [CrossRef]
- Islam, S.H.; Biswas, G.P. Design of Two-Party Authenticated Key Agreement Protocol Based on ECC and Self-Certified Public Keys. Wirel. Pers. Commun. 2015, 82, 2727–2750. [Google Scholar] [CrossRef]
- Dang, L.; Xu, J.; Cao, X.; Li, H.; Chen, J.; Zhang, Y.; Fu, X. Efficient identity-based authenticated key agreement protocol with provable security for vehicular ad hoc networks. Int. J. Distrib. Sens. Netw. 2018, 14, 155014771877254. [Google Scholar] [CrossRef]
- Deng, L.; Shao, J.; Hu, Z. Identity based two-party authenticated key agreement scheme for vehicular ad hoc networks. Peer-To-Peer Netw. Appl. 2021, 14, 2236–2247. [Google Scholar] [CrossRef]
- Xie, Q.; Wong, D.S.; Wang, G.; Tan, X.; Chen, K.; Fang, L. Provably Secure Dynamic ID-Based Anonymous Two-Factor Authenticated Key Exchange Protocol With Extended Security Model. IEEE Trans. Inf. Forensics Secur. 2017, 12, 1382–1392. [Google Scholar] [CrossRef]
- Li, X.; Yang, D.; Zeng, X.; Chen, B.; Zhang, Y. Comments on ‘Provably Secure Dynamic Id-Based Anonymous Two-Factor Authenticated Key Exchange Protocol With Extended Security Model’. IEEE Trans. Inf. Forensics Secur. 2019, 14, 3344–3345. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Chang, G. Efficient Privacy-Preserving Dual Authentication and Key Agreement Scheme for Secure V2V Communications in an IoV Paradigm. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2740–2749. [Google Scholar] [CrossRef]
- Lee, T.F.; Hsiao, C.H.; Hwang, S.H.; Lin, T.H. Enhanced smartcard-based password-authenticated key agreement using extended chaotic maps. PLoS ONE 2017, 12, e0181744. [Google Scholar] [CrossRef] [PubMed]
- Dua, A.; Kumar, N.; Das, A.K.; Susilo, W. Secure Message Communication Protocol Among Vehicles in Smart City. IEEE Trans. Veh. Technol. 2018, 67, 4359–4373. [Google Scholar] [CrossRef]
- Vijayakumar, P.; Azees, M.; Kozlov, S.A.; Rodrigues, J.J.P.C. An Anonymous Batch Authentication and Key Exchange Protocols for 6G Enabled VANETs. IEEE Trans. Intell. Transp. Syst. 2022, 23, 1630–1638. [Google Scholar] [CrossRef]
- Sun, Y.; Cao, J.; Ma, M.; Zhang, Y.; Li, H.; Niu, B. EAP-DDBA: Efficient Anonymity Proximity Device Discovery and Batch Authentication Mechanism for Massive D2D Communication Devices in 3GPP 5G HetNet. IEEE Trans. Dependable Secur. Comput. 2022, 19, 370–387. [Google Scholar] [CrossRef]
- Madanchi, M.; Abolhassani, B. Authentication and Key Agreement Based Binary Tree for D2D Group Communication. In Proceedings of the 2020 28th Iranian Conference on Electrical Engineering (ICEE), Tabriz, Iran, 4–6 August 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Wei, L.; Cui, J.; Zhong, H.; Bolodurina, I.; Liu, L. A Lightweight and Conditional Privacy-Preserving Authenticated Key Agreement Scheme With Multi-TA Model for Fog-Based VANETs. IEEE Trans. Dependable Secur. Comput. 2023, 20, 422–436. [Google Scholar] [CrossRef]
- Qiao, H.; Dong, X.; Jiang, Q.; Ma, S.; Liu, C.; Xi, N.; Shen, Y. Anonymous Lightweight Authenticated Key Agreement Protocol for Fog-Assisted Healthcare IoT System. IEEE Internet Things J. 2023, 10, 16715–16726. [Google Scholar] [CrossRef]
- Jiang, Q.; Zhang, N.; Ni, J.; Ma, J.; Ma, X.; Choo, K.K.R. Unified Biometric Privacy Preserving Three-Factor Authentication and Key Agreement for Cloud-Assisted Autonomous Vehicles. IEEE Trans. Veh. Technol. 2020, 69, 9390–9401. [Google Scholar] [CrossRef]
- Cui, J.; Zhang, X.; Zhong, H.; Zhang, J.; Liu, L. Extensible Conditional Privacy Protection Authentication Scheme for Secure Vehicular Networks in a Multi-Cloud Environment. IEEE Trans. Inf. Forensics Secur. 2020, 15, 1654–1667. [Google Scholar] [CrossRef]
- Wazid, M.; Bagga, P.; Das, A.K.; Shetty, S.; Rodrigues, J.J.P.C.; Park, Y. AKM-IoV: Authenticated Key Management Protocol in Fog Computing-Based Internet of Vehicles Deployment. IEEE Internet Things J. 2019, 6, 8804–8817. [Google Scholar] [CrossRef]
- Saleem, M.A.; Mahmood, K.; Kumari, S. Comments on “AKM-IoV: Authenticated Key Management Protocol in Fog Computing-Based Internet of Vehicles Deployment”. IEEE Internet Things J. 2020, 7, 4671–4675. [Google Scholar] [CrossRef]
- Ma, M.; He, D.; Wang, H.; Kumar, N.; Choo, K.K.R. An Efficient and Provably Secure Authenticated Key Agreement Protocol for Fog-Based Vehicular Ad-Hoc Networks. IEEE Internet Things J. 2019, 6, 8065–8075. [Google Scholar] [CrossRef]
- Cui, J.; Liu, X.; Zhong, H.; Zhang, J.; Wei, L.; Bolodurina, I.; He, D. A Practical and Provably Secure Authentication and Key Agreement Scheme for UAV-Assisted VANETs for Emergency Rescue. IEEE Trans. Netw. Sci. Eng. 2024, 11, 1454–1468. [Google Scholar] [CrossRef]
- Zhou, Y.; Cao, L.; Qiao, Z.; Xu, R.; Han, Y.; Xing, J.; Yang, B.; Xia, Z.; Zhang, M. A Novel Cloud-Assisted Authentication Key Agreement Protocol for VANET. IEEE Trans. Veh. Technol. 2024, 73, 13526–13541. [Google Scholar] [CrossRef]
- Abdalla, M.; Fouque, P.A.; Pointcheval, D. Password-Based Authenticated Key Exchange in the Three-Party Setting. In Public Key Cryptography—PKC 2005; Vaudenay, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 65–84. [Google Scholar]
- Liu, G.; Li, H.; Liang, Y.; Le, J.; Wang, N.; Mu, N.; Liu, Z.; Liu, Y.; Xiang, T. PSRAKA: Physically Secure and Robust Authenticated Key Agreement for VANETs. IEEE Trans. Veh. Technol. 2024, 74, 7953–7968. [Google Scholar] [CrossRef]
- Han, Y.; Guo, H.; Liu, J.; Ehui, B.B.; Wu, Y.; Li, S. An Enhanced Multifactor Authentication and Key Agreement Protocol in Industrial Internet of Things. IEEE Internet Things J. 2024, 11, 16243–16254. [Google Scholar] [CrossRef]
- Miracl Cryptographic SDK. 2019. Available online: https://github.com/miracl/MIRACL (accessed on 17 August 2025).
- Cui, J.; Wei, L.; Zhang, J.; Xu, Y.; Zhong, H. An Efficient Message-Authentication Scheme Based on Edge Computing for Vehicular Ad Hoc Networks. IEEE Trans. Intell. Transp. Syst. 2019, 20, 1621–1632. [Google Scholar] [CrossRef]

| Symbol | Definition |
|---|---|
| TCC | Traffic control center |
| RSU | Roadside unit |
| The f-th fog node | |
| The i-th vehicle | |
| Security parameter | |
| Cryptographic hash functions | |
| An additive elliptic curve group G with order q and generator P | |
| System master secret key/system public key | |
| Real identity/pseudonym of vehicle | |
| Real identity/pseudonym of | |
| The point selected by vehicle | |
| The point selected by | |
| The point that TCC selects for vehicle . | |
| Timestamps generated by | |
| Request message generated by vehicle | |
| Message authentication code of vehicle | |
| Aggregated data of all vehicles’ request messages | |
| Aggregated data of all vehicles’ | |
| Hash values | |
| The certificate of vehicle /fog node | |
| Random number/random point generated by vehicle | |
| XOR operation/concatenation of strings | |
| Maximum number of AKA requests processed in a single batch | |
| Maximum waiting time for request aggregation | |
| TCC status identifier | |
| Dynamic window time of | |
| Real-time vehicle density |
| Operation | Description | Time (ms) |
|---|---|---|
| Scale multiplication based on ECC | 0.562 | |
| Lagrange interpolation | 0.011 | |
| One-way hash | 0.005 | |
| AES-256 encryption/decryption | 0.016 | |
| Pseudo-random function | 0.015 | |
| Extended Chebyshev chaotic map | 0.381 |
| Scheme | Vehicle | FN | TCC | Total |
|---|---|---|---|---|
| [20] | = 1.185n | = 0.056n | = 0.668n | = 1.909n |
| [21] | = 0.797n | = 1.163n | = 1.272n | = 3.232n |
| [22] | = 2.845n | = 0.02n | = 2.875n | = 5.74n |
| [23] | = 1.726n | = 1.721n | = 1.174n | = 4.621n |
| Ours | = 1.185n | = 0.016n + 0.04 | = 0.623n + 0.045 | = 1.824n + 0.085 |
| Symbol | Description | Size (Byte) |
|---|---|---|
| The size of element in elliptic curve addition group | 64 | |
| The size of timestamp | 4 | |
| The size of real identity or pseudonym | 20 | |
| The size of message authentication code | 20 | |
| The size of element in | 32 | |
| The size of the output generated by extended Chebyshev polynomial | 32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Zhang, H.; Li, S.; Liu, J.; Chen, C. A Lightweight Batch Authenticated Key Agreement Scheme Based on Fog Computing for VANETs. Symmetry 2025, 17, 1350. https://doi.org/10.3390/sym17081350
Li L, Zhang H, Li S, Liu J, Chen C. A Lightweight Batch Authenticated Key Agreement Scheme Based on Fog Computing for VANETs. Symmetry. 2025; 17(8):1350. https://doi.org/10.3390/sym17081350
Chicago/Turabian StyleLi, Lihui, Huacheng Zhang, Song Li, Jianming Liu, and Chi Chen. 2025. "A Lightweight Batch Authenticated Key Agreement Scheme Based on Fog Computing for VANETs" Symmetry 17, no. 8: 1350. https://doi.org/10.3390/sym17081350
APA StyleLi, L., Zhang, H., Li, S., Liu, J., & Chen, C. (2025). A Lightweight Batch Authenticated Key Agreement Scheme Based on Fog Computing for VANETs. Symmetry, 17(8), 1350. https://doi.org/10.3390/sym17081350