Abstract
A graph simulation and its variants are widely used in graph pattern matching. Among them, there have been related works involving the addition of regular expressions to graph patterns, which can discover more meaningful data and solve problems in polynomial time. In this research, which is based on Fan’s investigations, we first propose an approximation of graph simulation using the concept of metric and formal verification techniques, and then give the definition of approximate matching between pattern graphs with regular expressions and data graphs, which introduces a symmetric tolerance for errors, bridging exact and approximate matching. Finally, we present a logical characterization of the approximate graph simulation by extending Hennessy–Milner logic.
1. Introduction
Finding all matches in a data graph for a specific pattern graph, also known as graph pattern matching (GPM), is a fundamental challenge in [1]. Series applications, such as data analysis, biological network investigation, and intelligence analysis, are based on GPM [2,3,4,5,6]. There are lots of methods to focus on solving GPM problems, among which graph simulation [7,8,9,10] and subgraph isomorphism [11] are the two most widely known and used. The former performs better in capturing useful information than the latter due to its flexibility. Moreover, it is solvable in polynomial time.
Numerous extensions to graph simulation have been created to fulfill the specific needs of practical use. These include, for instance, strong simulation [12], which captures topology, and simulation for lattice-valued systems [13], among several others [1,14,15,16]. Among them, Fan et al. [10] added regular expressions as the specifications to edges in the pattern graph, expressing a data graph’s connection using several sorts of edges. Afterward, they solved the GPM by remodifying the notion of graph simulation. In addition, they demonstrated that the enhanced expressive capacity is not accompanied by an increase in complexity, i.e., it is amenable to cubic time resolution.
Recent hybrid approaches combining formal methods with machine learning [17,18] and logic-based graph analysis [19] have shown promise in balancing interpretability and scalability. However, a principled logical foundation for approximate graph pattern matching with regular expressions, which is our focus, remains underexplored. Our work bridges this gap by introducing a metric-based approximation with a sound and complete logical characterization.
However, this expressiveness comes at the cost of rigidity; even minor data inconsistencies cause matches to fail. This limitation, combined with the increasing noise and scale of real-world graph data, has spurred research in two directions. One dominant direction leverages data-driven approaches like Graph Neural Networks (GNNs) [20] and deep learning [21] to learn approximate similarities. While powerful for finding statistical patterns, these methods often lack interpretability and verifiable guarantees. The other direction, extending the formal foundations of graph matching, has seen less progress since Fan et al.’s work in 2012 [10]. This 13-year gap highlights a significant opportunity: developing formally sound, approximate matching techniques that retain interpretability and guarantees while accommodating real-world imperfection. Our work addresses this gap by introducing a metric-based approximation framework, providing a principled alternative to data-driven black boxes in domains where understanding the ‘why’ behind a match is critical.
This work makes several key contributions that distinguish it from prior art: (1) Unlike the exact matching of Fan et al. [10], we introduce a metric-based framework for δ-approximate graph simulation with regular expressions, the first to handle both structural and label noise in this context. (2) While Cui et al. [22] proposed approximate simulation for transition systems, we generalize the approach to attributed graphs with complex patterns containing regular expressions. (3) Most significantly, we propose a novel modal logic, , and provide the first sound and complete logical characterization for approximate graph simulation with regular expressions, establishing a crucial bridge between semantic relations and syntactic logic for this problem.
The traditional graph simulation and its variants are all exact. In other words, they do not permit any error. They can only determine whether or not a node v that exists in a data graph simulates a node u that exists in a pattern graph.
That is, they can only answer whether a node v in a data graph simulates or does not simulate a node u in a pattern graph. However, in the real world, due to data noise or errors arising from data collection, there exist some nodes that approximately simulate the node in a pattern graph. By traditional graph simulation and its variants, these nodes will be ignored, which leads to a few potential results that can help researchers conduct the data analysis being missed. Based on the work of [10], we offer an approximative graph simulation based on the concept of metric [23,24] that makes use of formal verification approaches [12,13,25,26,27,28,29,30] to handle this problem.
While investigating simulation or its variants, scholars usually consider their logical characterization, connecting these relations with logic. Following the seminal study of Hennessy and Milner [31], a significant body of work has focused on characterizing different kinds of simulations through modal logics [27,30,32,33,34,35,36,37]. This includes characterizations for probabilistic systems [32,33], fuzzy transition systems [30,35], and weighted systems [27,36], demonstrating the well-established relationship between simulation relations and logic. Generally speaking, logic characterizes a relation if the characterization satisfies soundness and completeness: (1) the validity of logical formulas can be demonstrated by the relations; and (2) the power of expression between the logic and the relation is the same. Consequently, a soundness and completeness characterization transforms the challenge of determining whether two nodes are simulated into a logical judgment of whether one node satisfies all formulas satisfied by another node, and it can profit from traditional logic theories and particular instruments. Unfortunately, the associated work on the approximation graph simulation’s logical characterization is absent. As a result, using Hennessy–Milner logic, which has a very pleasant relationship with the concept of simulation, we offer a logical characterization of the approximation graph simulation.
Recent studies have explored the fundamental connections between graph neural networks and logical expressiveness [19], and have developed neural frameworks incorporating logical rules [18]. These hybrid approaches show promise in balancing interpretability and scalability. However, a principled logical foundation for approximate graph pattern matching with regular expressions, which is our focus, remains underexplored. Our work bridges this gap by introducing a metric-based approximation with a sound and complete logical characterization.
This paper is structured as follows: In Section 2, some preliminary information is provided. Then, Section 3 introduces the concept of approximate graph simulation. Afterward, we proposed a logical characterization of the approximate graph simulation in Section 4 and concluded the study in Section 5.
2. Preliminaries
In this part, we review the basics about regular expressions, data graphs, pattern graphs, and metrics. Before recalling the above basic facts, we first introduce some notations used throughout the paper. The content below can be referred to [10,23,38].
Table 1 summarizes the key notations used in this paper.

Table 1.
Summary of Notations.
Let be a finite set. represents the set of finite strings on . We write for the power set of . The concatenation of two strings and is the string . denotes the length of . Moreover, for , we denote as the -th position of . Let , . is the concatenation of and .
The syntax of regular expression ω over Σ is defined as below:
where . We write to represent the set of all regular expressions over . The language of a regular expression is defined indutively by the following:
- (1)
- ;
- (2)
- ;
- (3)
- ;
- (4)
- ;
- (5)
- ;
- (6)
- .
We next review the concepts of data graphs and pattern graphs as show in Figure 1.
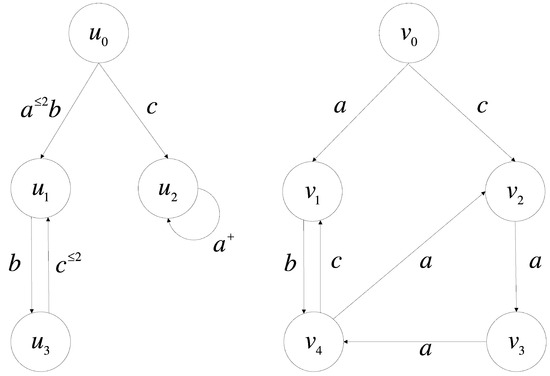
Figure 1.
Graph P and graph G.
A data graph is a triple , where (1) is a finite set of nodes; (2) is a set of edges, where is an alphabet; and (3) is a function defined on , and is a tuple () with , where is referred to as an attribute of and is a constant (), written as . Intuitively, an edge represents that there is an -labeled edge from to . We denote an edge by . In the latter, we write for .
In a similar way, a pattern graph is defined as a directed graph , where (1) is the set of its nodes; (2) is a set of edges, where is the set of all regular expressions over ; (3) is a function defined on , and is the predicate of with , which is the combination of atomic expressions in op , where is an attribute, is a constant, and op is an expression for comparison operator . We use to replace . In the latter, we write by .
A path from a node to a node in is a finite sequence ; for simplicity, it will be replaced by , where .
Let and ; satisfies the search condition of , denoted as , if for each atomic formula ‘ op ’ in , there exists an attribute in such that op .
We end this section with the notion of metrics. A function is a metric over if for all
- (1)
- , iff ;
- (2)
- ;
- (3)
- .
The pair is called a metric space. For clarity, we write instead of . The metric-based distance function adheres to symmetry, ensuring unbiased approximate matching.
3. Approximate Graph Pattern Matching
In this part, we initially define a concept for an approximate matching between an approximate simulation data graph and a pattern graph; then, we give a formal definition of an exact match between the graphs of the data and the pattern; we finally provide a formal definition of an approximate simulation definition.
The latter definitions are defined on and , and we assume and , as well as in those of the following sections.
Definition 1
([10]). A relation is called a graph simulation if for any : (1) ; and (2) for each , there exists a nonempty path in such that , and . We call that simulates if there exists a graph simulation such that .
The following defines the concept of the exact match.
Definition 2
([10]). A data graph matches a pattern graph via graph simulation, denoted by , if there exists a simulation such that, for all , there exists with . Then, is the graph simulation matching of for .
Example 1.
We have known the following:
We can find a relation that satisfies the simulation’s conditions. Therefore, it can be concluded that graph matches graph .
In order to define the approximate matching relationship between data graphs and pattern graphs, we need to introduce an approximate simulation relationship. To achieve this, we need to incorporate string distance and define the distance between a string and a regular expression language based on it. Unlike the traditional definition of string distance, this paper introduces the form of discount to define it. The discount represents the distance between events happening i steps into the future multiplied by , where α represents the discount factor, which ranges from . This form of discount definition is commonly used in game theory and optimal control. With the discount, the differences in future behaviors are weighted less compared to the differences in current or recent behaviors. The following is the definition of string distance.
Let be a metric space, and . A function is the string distance of string, defined as follows:
for all strings .
Proposition 1
([22]). is a metric on the set .
The distance between a string and the language of a regular expression is defined as follows:
Proposition 2
([22]). The following properties hold the following:
- (1)
- , for all and .
- (2)
- iff , where , .
Based on the above Propositions 1 and 2, the concept of approximate graph simulation will be introduced, called -simulation.
Definition 3.
A relation is called a -simulation if for any such that the following occurs:
- (1)
- ;
- (2)
- for each , there exists a nonempty path in such that , and .For a given , -simulates if there exists a -simulation such that .
Following this, we can define approximative graph pattern matching.
Definition 4.
A data graph -approximately matches a pattern graph via -simula tion, denoted by , if there exists a -simulation such that, for all , there exists with . Then, is a -approximate match in for via -simulation.
Example 2.
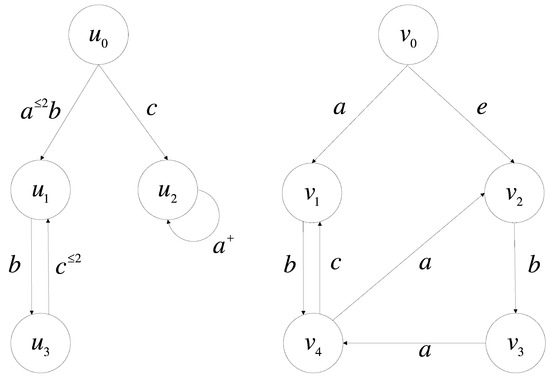

Figure 2.
Graph and Graph .
Let , , , and . We can find a relation which is a 0.5-simulation by Definition 2. Therefore, we can conclude that the data graph 0.5-approximately matches the pattern graph .
Consider the pair . Condition (1) holds as . For condition (2), consider the pattern edge . In G1, v0 has a path . We calculate d*(a, L(a)) = 0 ≤ 0.5. Furthermore, is in R. Now consider the more critical edge . v0 has a path . We have d(e, b) = 0.2, and since |ρ| = |σ| = 1, sd(e, b) = α0 * d(e,b) = 1 * 0.2 = 0.2. Thus, d*(e, L(b)) = inf{sd(e, b)} = 0.2 ≤ 0.5. The target node is related to . Therefore, the edge is satisfied. A similar check for other edges confirms R is a 0.5-simulation.
4. A Logical Characterization
In this part, we provide the logical characterization of the approximate graph simulation introduced in Section 3, which is motivated by the well-established characterization of simulation based on Hennessy–Milner logic (HML).
Let be a metric space and ; the modal logic is the set of the following formulas, whose syntax is defined as shown below:
where .
The interpretation of formulas differs fundamentally between pattern and data graphs, reflecting their different structures. Intuitively, in a pattern graph P, an edge is a specification: it demands the existence of a path whose label is in L(ω). In a data graph G, we look for a concrete path and measure how far its label ρ is from the specification L(ω). For example, the formula tt is satisfied by a pattern node u if it has an outgoing ab-labeled edge. A data node v satisfies the same formula if it has an outgoing path whose label (e.g., ‘ac’) is within a distance of 0.5 from the string ‘ab’, according to the metric d.
formulas are interpreted over the nodes of pattern graphs or data graphs. For a formula or , it is inconvenient to give the same semantic interpretation in pattern graphs and data graphs, since the labels on the edges are regular expressions and elements of the alphabet , respectively. Therefore, we consider giving the different semantic interpretations in pattern graphs and data graphs for a given formula.
Satisfaction of a by a node , notation , is defined inductively by the following:
Satisfaction of a by a node , notation , is defined inductively by the following:
Notice that, for a given formula , if and , where is an arbitrary element in , then the formula reduces to the established semantic interpretation of HML. The situation of is similar to the situation of .
Example 3.
- (1)
- expresses the property that there exist nodes that have an outgoing -labeled edge in the pattern graph and have a path with in the data graph. We can find that in pattern graph , and in data graph .
- (2)
- For a formula , we can obtain that in pattern graph and in data graph .
Given an - formula , for cases , , , and the semantics of on the data graph and the pattern graph are indistinguishable. However, when the formula or is considered, it becomes apparent that there is a significant difference in the semantics of Y on the data graph and the pattern graph. In the pattern graph, the semantics of are independent of parameter g, but in the data graph, the semantics of depend on parameter g. One reason for this difference is the distinct edge labels mentioned earlier for the data graph and the pattern graph. In the pattern graph, the edge labels are regular expressions, and the objects inside operators and [ ] are also regular expressions, making the semantics interpretable using classical Hennessy–Milner Logic (HML). However, the edge labels in the data graph are single characters, which, although they can be seen as regular expressions, are not interpretable using classical HML semantics. Therefore, to utilize - logic formulas for characterizing -approximate simulation relations in subsequent sections, some adjustments need to be made to the semantics interpretation of formula on the data graph.
For , we use to denote the set of formulas for which the operator op is not used.
The following theorems show that an approximative graph simulation can be sufficiently characterized by a set of logics.
Theorem 1.
-simulates iff and for each -, if then .
Proof Sketch: The proof has two parts: (⇒) Soundness: We assume v δ-simulates u and show by induction on the structure of φ that u ⊨ φ implies v ⊨ φ. (⇐) Completeness: We assume the logical condition holds and construct a relation R that we prove is a δ-simulation. The key step is showing that for every pattern edge from u, a suitable path exists from v; if not, we construct a formula φ that u satisfies but v does not, leading to a contradiction.
Proof.
First, we prove the soundness. Assume that δ-simulates and for some formula . We show that by induction on the structure of .
- : For each , .
- : Then . We can obtain that and . By induction hypothesis, and . Hence, .
- : Then . We can obtain that or . By induction hypothesis, or . Therefore, .
- : Then . We know that there exists and . Since -simulates , there exists hold and -simulates . By induction hypothesis, . Hence, .
To show completeness, assume that and for each -, if then , where and . Let .
It is sufficient to prove that the above relation is a -simulation.
Assume that and . We need to argue that there exists a node such that , , and .
Now assume, towards a contradiction, that there is no such that , and . Let be the set of nodes which there exists such that and with . By our assumption, none of the nodes in the above set satisfies that implies . Thus, for each , there is a formula holding the following:
It is obvious that will be a formula satisfied by but not by , contradicting our assumption that and if then . The proof of the theorem is now complete. □
Complexity Analysis. The algorithm for checking the δ-simulation relation involves iteratively refining a candidate relation. For each pair (u, v) and each pattern edge , we must find a path such that . The cost of checking the string-distance condition is polynomial. In the worst case, the overall time complexity is , where L is an upper bound on the length of paths.
Theorem 2.
-simulates iff and for each -, if then .
Proof.
First, we show the soundness. Let , , -simulates and . We show that implies by structural induction on . The cases of , , conjunction, and disjunction are similar to Theorem 1. Now, we consider the case of as follows.
Assume that for some . We wish to show that . Now, since simulates and , there exists a such that -simulates . By our assumption that , we have that . The inductive hypothesis yields that . Therefore, each such that satisfies and we can conclude that , which is to be shown.
For completeness, we define
.
It suffices to prove that is a -simulation.
Assume that and . We need to argue that there exists a node such that , and .
Now assume, towards a contradiction, that there is no such that , and . Let be the set of nodes which there exists such that and with . By our assumption, none of the nodes in the above set satisfies that implies . Thus, for each , the following:
It is obvious that will be a formula satisfied by but not by , contradicting our assumption that and if then . □
Conclusion 1.
The following statements hold the same equivalence for and :
- -simulates .
- and for each -, if then .
- and for each -, if then .
Corollaries and Limitations
Corollary 1.
When δ = 0, characterizes exact graph simulation [10], as d*(ρ, L(ω)) = 0 iff ρ ∈ L(ω).
Corollary 2.
The δ-simulation relation is reflexive and transitive but not symmetric.
The following counterexample demonstrates the lack of symmetry. Let Σ = {a, b} with d(a, b)=1. Let P have one node u with a self-loop . Let G have one node v with a self-loop . For δ ≥ 1, v δ-simulates u because d*(b, L(a)) = d(b, a) = 1 ≤ δ. However, u does not δ-simulate v for any δ < 1, because d*(a, L(b)) = d(a, b) = 1 > δ.
This framework has several limitations: (1) The performance is highly sensitive to the choice of the distance metric d and the tolerance parameter δ, which may require domain expertise to tune. (2) The polynomial-time complexity, while tractable, can be high for very large graphs due to the path exploration and distance calculation. (3) The current framework approximates edge labels but requires exact matching of node attributes (; extending it to approximate attribute matching is future work.
Next, we explain the conclusion visually with an example.
Example 4.
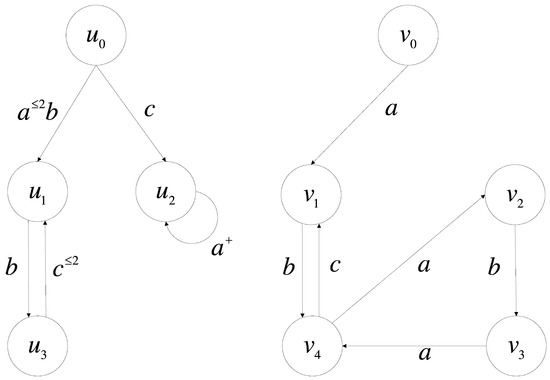
In Figure 2, we have known that is a 0.5-simulation by Definition 2, and the data graph 0.5 approximately matches the pattern graph . Based on Conclusion 1, we might as well let and . In the case of -, we have the following:
Then, in the case of - , we have the following:
The diagrams of and are depicted in Figure 3. We removed the edge to from the data graph, otherwise unchanged. So, we have the following:
We can find a relation . We will show that and do not satisfy Conclusion 1 in Figure 3. We first discuss the case of - . We have the following:
Then, we discuss the case of - . We have the following:
and do not satisfy the same formula in either case, so .

Figure 3.
Graph and Graph .
5. Case Studies
5.1. Empirical Evaluation and Complexity Analysis
To evaluate the practical utility of δ-simulation, we conducted experiments on a synthetic graph dataset (DS1) containing 10,000 nodes and approximately 85,000 edges. We measured the number of matches found and the precision for varying values of δ (0.0, 0.5, 1.0, 1.5, and 2.0) against 100 randomly generated pattern graphs, and exact matching (δ = 0.0) found matches for 65% of patterns. As δ increased to 1.0 and 2.0, the success rate rose to 92% and 98%, respectively, demonstrating the method’s ability to recover meaningful results missed by exact matching. However, manual verification showed precision decreased from 100% at δ = 0.0 to 75% at δ = 2.0, highlighting the tunable trade-off between recall and precision. Runtime measurements on graphs of varying sizes confirmed the polynomial time complexity analyzed in Section 4.
While simplified, this pattern captures a realistic query intent: finding a group of users (researchers) with a specific internal consensus and a specific antagonistic relationship with another group (programmers), mediated by interactions with other roles (doctors). Such patterns are relevant in studying echo chambers, cross-community influence, and targeted marketing.
5.2. Illustrative Example in Social Network Context
This section considers an instance of a graph pattern matching problem in social networks, further elaborating the conclusions drawn in this paper. When it comes to social networks, graph pattern matching can typically be utilized in various ways: identifying key individuals in social networks, discovering communities in social networks, detecting events in social networks, and so forth.
Consider an assembly network service, where users can vote, post, and express support or opposition on controversial topics or issues. Each user has their personal information along with their list of supported or opposed issues.
Figure 4 describes a portion of this network as a graph, involving the debate on whether artificial intelligence can replace humans. In the graph, each node represents a user, and each edge represents a relationship with one of four types: “fa,” “fd,” “sa,” and “sd.” Here, “fa” indicates that a user agrees with most of their friend’s votes on topics, “fd” indicates a user disagrees with most of their friend’s votes, “sa” indicates a user agrees with most of a stranger’s votes, and “sd” indicates a user disagrees with most of a stranger’s votes.
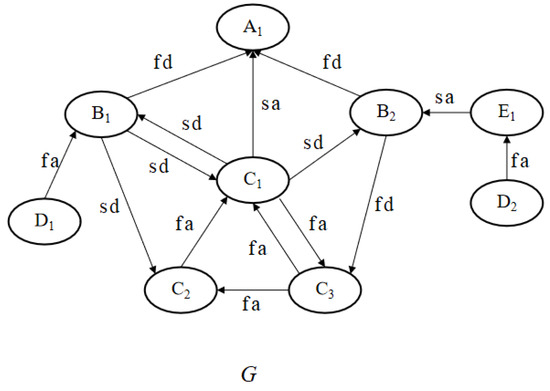
Figure 4.
Graph .
Considering the pattern graph in Figure 5, it is proposed by a user named “Jack07,” who holds a supportive stance on whether artificial intelligence can replace humans. Here, “sp” indicates the user’s support for a certain topic, while “dsp” indicates opposition.
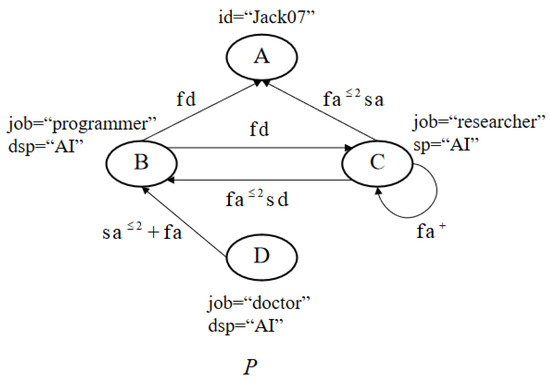
Figure 5.
Pattern .
This user wishes to find all programmers who oppose the idea of artificial intelligence replacing humans through the “fn” relationship. Additionally, they want to query whether there are users who meet the following conditions:
- The user is a researcher and holds a supportive stance on whether artificial intelligence can replace humans. They are connected to someone, denoted as A, through the “fa” relationship within ≤2 steps and A is connected to them through the “sa” relationship.
- These researchers belong to a research group, and all members within the group hold the same opinion.
- These researchers hold different opinions from their programmer friends, and vice versa.
- Friends of these programmers who are doctors, or strangers with positions as doctors, support their opinions. Conversely, the same applies.
The user aims to find the desired results in the data graph (Figure 4) based on the requirements specified by the pattern graph (Figure 5). Let in the following:
According to the precise graph pattern matching definition, the user cannot find a subgraph in this data graph that precisely matches their requirements. However, in the data graph, some subgraphs that approximately meet the user’s needs have been ignored. These subgraphs hold some degree of reference value for the user. But, if we relax the conditions, i.e., to some extent meet the user’s requirements, then the degree of matching between the data graph and the pattern graph can satisfy the user’s needs.
Firstly, two binary relations can be identified:
Next, it is necessary to determine whether these two binary relations are 1-approximate simulation relations. Let us first discuss whether binary relation is a 1-approximate simulation relation. For the edge in the pattern graph , there is an edge from node to node in the data graph labeled as , while . Therefore, it can be concluded that the binary relation is not a 1-approximate simulation relation.
Note that, for the edge in the pattern graph , in the data graph , there is a path from node to node , and the path is . According to Proposition 2, we obtain . As for the remaining edges in the pattern graph, there are corresponding paths in the data graph, and the distance between them is less than 1. Thus, it can be concluded that the binary relation is a 1-approximate simulation relation. It can also be inferred that there exists a subgraph G1, as shown in Figure 6 in red letters, in the data graph G, satisfying the requirements of the pattern graph P.
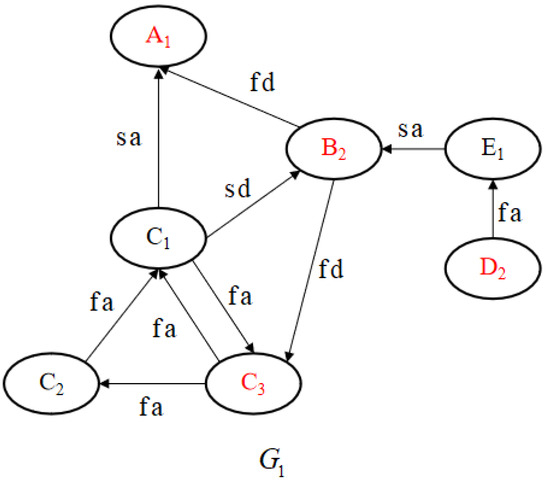
Figure 6.
A Subgraph of Data Graph .
Finally, let us describe the approximate matching relationship from a logical perspective. For the nodes in the pattern graph and the nodes in the data graph, for any formula, such as , and from the semantic interpretation of on the pattern graph, we can infer . To determine if is a 1-approximate simulation of , it is necessary to discuss whether node satisfies formula . According to the semantic interpretation of on the data graph, it is known that there exists a path from to , denoted as , such that holds. For any formula , assuming holds, according to the semantic interpretation of on the data graph, any path starting from node that satisfies , all the nodes reached by this path satisfy the formula .
Based on the information obtained from the data graph G, there exists a path satisfying this condition: , and . Therefore, we have . To determine if is a 1-approximate simulation of , we need to discuss whether node satisfies formula . From the semantic interpretation of on the pattern graph, we know that satisfies . By extension, we can conclude that node is a 1-approximate simulation of .
6. Discussion
The case study serves as a proof-of-concept but has limitations. The social network graph is synthetic, and the metric d was defined manually. Performance on real-world, noisy graphs with billions of edges and learned metrics requires further investigation. Despite this, the framework is general. Beyond social networks, it could be applied in computational biology to match approximate protein interaction pathways, or in knowledge graph querying to find entities connected by paths that approximately match a complex relation sequence, improving recall in incomplete knowledge bases like DBpedia or YAGO.
7. Conclusions and Future Work
In this work, we presented δ-simulation, an approximation of a graph simulation incorporating metrics and regular expressions. We defined approximate matching between pattern and data graphs and provided a logical characterization for it using an extension of Hennessy–Milner logic ().
Despite its theoretical foundations, our approach has limitations. The computational cost, while polynomial, can be high for very large graphs due to path checking. The method’s effectiveness is also contingent upon the careful selection of the distance metric δ and the underlying alphabet metric d, which may require domain expertise.
Based on these limitations, our future work will focus on the following: (1) Developing optimized algorithms and indexing structures to improve scalability for web-scale graphs; (2) Investigating methods to learn the metric d directly from data to reduce manual tuning; and (3) Extending the framework to support approximate matching of node attributes in addition to edge paths.
Beyond algorithmic improvements, we plan to apply and evaluate δ-simulation in specific, demanding real-world scenarios. Promising application domains include the following:
- -
- Computational Biology: Matching approximate signaling pathways in protein–protein interaction networks.
- -
- Knowledge Graph Querying: Enhancing query answering over incomplete knowledge bases (e.g., DBpedia, YAGO).
- -
- Network Security: Detecting lateral movement patterns of attackers in network logs where actions might be obfuscated.
Author Contributions
Conceptualization, X.L. and X.C. (Xuelei Chen); methodology, Z.Z.; software, Z.Z.; validation, X.C. (Xinyu Cui), J.W., and X.C. (Xuelei Chen).; formal analysis, X.C. (Xinyu Cui); investigation, X.L.; resources, X.C. (Xuelei Chen); data curation, Y.Z.; writing—original draft preparation, X.L.; writing—review and editing, X.C. (Xuelei Chen); visualization, J.W.; supervision, X.C. (Xuelei Chen); project administration, X.C. (Xuelei Chen); funding acquisition, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the 12th batch of Wenzhou Science and Technology Commissioner Project under Grant No. 12, by the Third Phase of the Ministry of Education’s supply and Demand Docking Employment and Education Project under Grant 2023122963332, and by the Second Phase of the Ministry of Education’s supply and Demand Docking Employment and Education Project under Grant 20230112193.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Aceto, L.; Ingólfsdóttir, A.; Larsen, K.G.; Srba, J. Reactive Systems: Modelling, Specification and Verification; Cambridge University Press: Cambridge, UK, 2007; pp. 220–247. [Google Scholar]
- Baier, C.; Katoen, J.P. Principles of Model Checking; MIT Press: Cambridge, MA, USA, 2008; pp. 449–593. [Google Scholar]
- Milner, R. Communication and Concurrency; Prentice Hall: Hoboken, NJ, USA, 1989; pp. 84–104. [Google Scholar]
- Milner, R. Communicating and Mobile Systems: The π-Calculus; Cambridge University Press: Cambridge, UK, 1999; pp. 16–25. [Google Scholar]
- Munkres, J.R. Typology; Prentice Hall: Hoboken, NJ, USA, 1975; pp. 263–290. [Google Scholar]
- Sangiorgi, D. Introduction to Bisimulation and Coinduction; Cambridge University Press: Cambridge, UK, 2012; pp. 53–142. [Google Scholar]
- Hopcroft, J.E.; Motwani, R.; Ullman, J.D. Introduction to Automata Theory, Languages, and Computation; Addison-Wesley Publishing: Reading, MA, USA, 1979; pp. 37–83. [Google Scholar]
- de Alfaro, L.; Faella, M.; Stoelinga, M. Linear and branching system metrics. IEEE Trans. Softw. Eng. 2009, 35, 258–273. [Google Scholar] [CrossRef]
- Girard, A.; Pappas, G.J. Approximation metrics for discrete and continuous systems. IEEE Trans. Autom. Control 2007, 52, 782–798. [Google Scholar] [CrossRef]
- Fan, W.F.; Li, J.Z.; Ma, S.; Tang, N.; Wu, Y.H. Adding regular expressions to graph reachability and pattern queries. Front. Comput. Sci. 2012, 6, 313–338. [Google Scholar] [CrossRef]
- Bouhenni, S.; Yahiaoui, S.; Nouali-Taboudjemat, N.; Kheddouci, H. A survey on distributed graph pattern matching in massive graphs. ACM Comput. Surv. 2021, 54, 1–36. [Google Scholar] [CrossRef]
- Ma, S.; Cao, Y.; Fan, W.F.; Huai, J.P.; Wo, T.Y. Strong simulation: Capturing topology in graph pattern matching. ACM Trans. Database Syst. 2014, 39, 1–46. [Google Scholar] [CrossRef]
- Pan, H.Y.; Cao, Y.Z.; Zhang, M.; Chen, Y.X. Simulation for lattice-valued doubly labeled transition systems. Int. J. Approx. Reason. 2014, 55, 797–811. [Google Scholar] [CrossRef]
- Henzinger, M.R.; Henzinger, T.A.; Kopke, P.W. Computing simulations on finite and infinite graphs. In Proceedings of the 36th Annual Symposium on Foundations of Computer Science, Milwaukee, WI, USA, 23–25 October 1995; pp. 453–462. [Google Scholar]
- Fan, W.F.; Wang, X.; Wu, Y.H. Incremental graph pattern matching. ACM Trans. Database Syst. 2013, 38, 18. [Google Scholar] [CrossRef]
- Chen, X.S.; Lai, L.; Qin, L.; Lin, X.M.; Liu, B. A framework to quantify approximate simulation on graph data. In Proceedings of the 37th IEEE International Conference on Data Engineering, Chania, Greece, 19–22 April 2021; pp. 1308–1319. [Google Scholar]
- Dwivedi, S.P.; Singh, R.S. Error-Tolerant Approximate Graph Matching Utilizing Node Centrality Information. Pattern Recogn. Lett. 2020, 133, 313–319. [Google Scholar] [CrossRef]
- Nayyeri, M.; Xu, C.; Alam, M.M.; Lehmann, J.; Yazdi, H.S. LogicENN: A Neural Based Knowledge Graphs Embedding Model with Logical Rules. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 7050–7062. [Google Scholar] [CrossRef]
- Barceló, P.; Kostylev, E.V.; Mikaël, M.; Pérez, J.; Reutter, J.; Silva, J.P. The Logical Expressiveness of Graph Neural Networks. In Proceedings of the 8th International Conference on Learning Representations, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Yu, P.S. A Comprehensive Survey on Graph Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4–24. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, Y. Link Prediction Based on Graph Neural Networks. In Proceedings of the 32nd Conference on Neural Information Processing Systems, NIPS 2018, Montréal, QC, Canada, 3–8 December 2018; pp. 5171–5181. [Google Scholar]
- Cui, X.Y.; Li, Z.K.; Chang, Y.T.; Pan, H.Y. Approximate Simulation for Transition Systems with Regular Expressions. In Proceedings of the 2nd Artificial Intelligence Logic and Applications, AILA 2022, Shanghai, China, 26–28 August 2022; Springer: Berlin/Heidelberg, Germany; pp. 49–62. [Google Scholar]
- Liu, G.F.; Liu, Y.; Zheng, K.; Liu, A.; Li, Z.X.; Wang, Y.; Zhou, X.F. MCS-GPM: Multi-constrained simulation based graph pattern matching in contextual social graphs. IEEE Trans. Knowl. Data Eng. 2018, 30, 1050–1064. [Google Scholar] [CrossRef]
- Du, R.H.; Yang, J.N.; Cao, Y.Z.; Wang, P. Personalized graph pattern matching via limited simulation. Knowl.-Based Syst. 2018, 141, 31–43. [Google Scholar] [CrossRef]
- Ullmann, J.R. An algorithm for subgraph isomorphism. J. ACM. 1976, 23, 31–42. [Google Scholar] [CrossRef]
- Zhang, S.J.; Yang, J.; Jin, W. Subgraph indexing and approximate matching in large graphs. Proc. VLDB Endow. 2010, 3, 1185–1194. [Google Scholar] [CrossRef]
- Thrane, C.R.; Fahrenberg, U.; Larsen, K.G. Quantitative analysis of weighted transition system. J. Log. Algebr. Program. 2010, 79, 689–703. [Google Scholar] [CrossRef]
- Cerný, P.; Henzinger, T.A.; Radhakrishna, A. Simulation distances. Theor. Comput. Sci. 2012, 413, 21–35. [Google Scholar] [CrossRef]
- Bozzelli, L.; Molinari, A.; Montanari, A.; Peron, A. Model checking interval temporal logics with regular expressions. Inf. Comput. 2020, 272, 104498. [Google Scholar] [CrossRef]
- Wu, H.Y.; Deng, Y.X. Logical characterizations of simulation and bisimulation for fuzzy transition systems. Fuzzy Sets Syst. 2016, 301, 19–36. [Google Scholar] [CrossRef]
- Abriola, S.; Descotte, M.E.; Figueira, S. Model theory of XPath on data trees. Inf. Comput. 2017, 255, 195–223. [Google Scholar] [CrossRef]
- Hermanns, H.; Parma, A.; Segala, R.; Wachter, B.; Zhang, L.J. Probabilistic logical characterization. Inf. Comput. 2011, 209, 154–172. [Google Scholar] [CrossRef][Green Version]
- Bernardo, M.; Nicola, R.D.; Loreti, M. Revisiting bisimilarity and its modal logic for nondeterministic and probabilistic processes. Acta Inform. 2015, 52, 61–105. [Google Scholar] [CrossRef][Green Version]
- Fahrenberg, U.; Legay, A. The quantitative linear-time-branching-time spectrum. Theor. Comput. Sci. 2014, 538, 54–69. [Google Scholar] [CrossRef]
- Pan, H.Y.; Li, Y.M.; Cao, Y.Z.; Li, P. Nondeterministic fuzzy automata with membership values in complete residuated lattices. Int. J. Approx. Reason. 2017, 82, 22–38. [Google Scholar] [CrossRef]
- Juhl, L.; Larsen, K.G.; Srba, J. Modal transition systems with weight intervals. J. Log. Algebr. Program. 2012, 81, 408–421. [Google Scholar] [CrossRef]
- Desharnais, J.; Gupta, V.; Jagadeesan, R.; Panangaden, P. Metrics for labelled Markov processes. Theor. Comput. Sci. 2004, 318, 323–354. [Google Scholar] [CrossRef]
- Hennessy, M.; Milner, R. Algebraic Laws for Nondeterminism and Concurrency. J. ACM 1985, 32, 137–161. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).