Parameter-Gain Accelerated ZNN Model for Solving Time-Variant Nonlinear Inequality-Equation Systems and Application on Tracking Symmetrical Trajectory

Abstract

Time-variant nonlinear problems have always been a kind of complex research object in the field of control. The accuracy and efficiency of settling time-variant nonlinear inequality-equation (NIE) systems are often affected by the nonlinearity degree of the systems, and there are currently no complete algorithms to settle the time-variant NIE systems effectively. To settle this class of complex systems effectively, time-variant NIE systems are first equivalently transformed into a time-variant equation by introducing a nonnegative variable. Then, through the idea of zeroing neural network (ZNN) and the role of time-variant parameter-gain functions, a parameter-gain accelerated ZNN (PGAZNN) model is proposed to solve time-variant NIE systems. Theoretically, the stability of the proposed PGAZNN model is proved by strict mathematical analysis. In addition, the PGAZNN model can achieve fixed-time convergence, and the upper-bound of convergence time is estimated. Finally, numerical simulation example and symmetry trajectory tracking are given to verify the validity and correctness of the proposed PGAZNN model.

1. Introduction

The analysis and solution of nonlinear systems is an important research branch of automation control theory [1,2,3,4]. Meanwhile, as nonlinear problems, nonlinear inequality systems and nonlinear equality equations have always been the focus of mathematicians and engineers [5,6,7]. In recent years, the theoretical research and practical application of nonlinear systems have been gradually strengthened and realized. In [8], Holger et al. analyzed the chaotic synchronization conditions of nonlinear systems under different states and proposed the consistency criterion of chaotic synchronization. In [9,10], the authors realized the control of nonlinear dynamic systems and an industrial redundant manipulator based on the mathematical model of nonlinear inequality and nonlinear equation, respectively. Therefore, the analysis and application of nonlinear systems influence the development and research of automation theory to a certain extent. It is worth noting that one of the most important characteristics of a nonlinear system is that it cannot be analyzed by the superposition principle, which determines the complexity of the research. Due to the difficulties in the mathematical processing of nonlinear systems, there is no general method available to deal with all types of nonlinear systems [11]. Taking $f\left(x\right(t),t)$ as an example, as a special kind of mathematical model of a time-variant nonlinear system, some scholars put forward a direct analysis method, that is, an analysis method based on the direct processing of the actual or simplified nonlinear differential equations of the system. This is also called the analytical method of Lyapunov fractional stability theory [12].

In recent years, due to the significant improvement in the computing capacity of computers and the parallel and distributed computing characteristics of neural solvers, neural networks have been developed into the most popular solution, analysis and application tool at the present stage [13,14,15,16,17]. The zeroing neural network (ZNN) [18,19,20], as a branch of the current popular recurrent neural network, is based on Lyapunov stability theory and is mainly used to solve and analyze the problems of time-variant systems. In recent years, scholars have continuously optimized and improved the network [21,22,23], and applied the solution and analysis of ZNN to different objects on this basis, such as the design and analysis of fuzzy neural network, the solution of time-variant quaternion matrix, the application of time-varying tensor and solving of time-variant plural Lyapunov equation [24,25,26,27], etc. At the same time, practical applications based on ZNNs are also achieved and implemented, such as system tracking control, robot manipulator application [28,29,30,31]. In [32,33], Xiao et al. designed a novel ZNN evolution formula, and on the basis of [18], the time-variant nonlinear inequality system and time-variant nonlinear equation were taken as the mathematical models for solving, thus promoting the study of ZNN in analyzing and solving the time-variant nonlinear systems. In addition, in [34], Zeng et al. analyzed and experimented with the convergence factors and different design parameters affecting the ZNN model. In [35], Cao et al. proposed the judgment criteria and design ideas of activation functions for the model to achieve finite time convergence and predefined time convergence, which undoubtedly greatly enriched the theoretical research on the ZNN.

From the perspective of mathematical analysis, the convergence effect of a model is undoubtedly influenced by the complexity of the system itself and the nonlinear structure of the system. However, on the other hand, the external disturbance and time-varying factors are also factors that cannot be ignored. In addition, some parameter setting of the model design also has a different impact on the model. For example, in [36,37], Yu et al. carried out different experimental analyses and comparisons of ZNN design parameters in the model, which referred to the parameters of activation functions and time-variant variables of functions, and resulted in different degrees affecting the convergence speed of the model. Therefore, when designing the ZNN model among different solution objects, some appropriate design parameters should be well studied and defined in order to improve the convergence performance. It is worth noting that appropriate design parameters can include new nonlinear activation functions (AFs), piecewise variable functions in [29,33].

By referring to the above literature and summarizing the design ideas, it can be found that a complex time-variant mathematical model can be studied and analyzed within the framework of Lyapunov stability theory, and a mature neural network method for solving time-variant problems can be used to model time-variant problems. To sum up, this paper attempts to mathematically model a class of nonlinear inequality-equation (NIE) systems and further convert it into a matrix-vector equation through an equivalent transformation. On this basis, a parameter-gain accelerated ZNN (PGAZNN) model is proposed to solve the transformed matrix equation. In addition, for the fixed and time-variant parameters in the PGAZNN model, this paper chooses to explore a function of time-variant parameter gain [37], which ensures the excellent convergence performance of the model. In terms of the selection of AFs, this paper studies a sign-bi-power activation function (SBP-AF) with an adjustable parameter, and several common monotone increasing odd functions are given as experimental comparison to ensure that the theoretical and experimental results are correct and corresponding.

Before concluding this section, it is necessary to state the main points of the following sections. In Section 2, the mathematical model and transformation process are introduced. In Section 3, the transformed mathematical model is constructed in detail by using the design idea of ZNN, and the PGAZNN model is derived. Section 4 focuses on the mathematical analysis of the PGAZNN model, including the stability and convergence analysis; in Section 5, two different simulation examples are given to show the consistency between the theoretical and experimental results, and the selection criteria of design parameters are pointed out. In Section 6, the conclusion of this paper is drawn. The main contributions of this paper are summarized as follows:

• For settling the time-variant NIE systems effectively, an equivalent transformation is explored, and the PGAZNN model is proposed, which is the main novelty of this paper.
• A time-variant parameter-gain function and a nonlinear SBP-AF are explored in the PGAZNN model. The stability and finite time convergence of the PGAZNN model are proved through rigorous mathematical analysis, and the upper bound of the convergence time is obtained.
• Simulation example verifies the effectiveness and superiority of the PGAZNN model after equivalent conversion in settling time-variant NIE systems. The practical application of Symmetrical trajectory tracking further confirms the superior performance of the PGAZNN model.

2. Problem Descriptions and Transformation

In this section, the descriptions of time-variant NIE systems and the equivalent transformation of the problem descriptions are given in detail.

2.1. Time-Variant NIE Systems

First, we consider a class of general time-variant NIE systems, and the formulation is expressed as follows:

$$\left\{\begin{array}{c}\mathit{f}\left(\mathit{x}\left(t\right),t\right)⩽\mathit{b}\left(t\right),\hfill \\ \mathit{h}\left(\mathit{x}\left(t\right),t\right)=\mathbf{0},\hfill \end{array}\right.$$

(1)

where $\mathit{f}(·)\in {\mathbb{R}}^m$, $\mathit{h}(·)\in {\mathbb{R}}^m$ denote continuous and differentiable nonlinear functions, $\mathit{b}\left(t\right)\in {\mathbb{R}}^m$ is a smooth nonlinear function and $\mathit{x}\left(t\right)\in {\mathbb{R}}^m$ and $t\in [0,+\infty ]$ are the dynamic unknown state solution and time variable, respectively. To guarantee the existence of the solution of time-variant NIE systems (1), the dynamic solution $\mathit{x}\left(t\right)$ is assumed to satisfy the inequality $\mathit{f}\left(\mathit{x}\right(t),t)⩽\mathit{b}\left(t\right)$ and equation $\mathit{h}\left(\mathit{x}\right(t),t)=0$ simultaneously.

2.2. Equivalent Transformation

In order to make time-variant NIE systems (1) have an equivalent transformation, a nonnegative vector $\mathit{v}{\left(t\right)}^{.2}$ is introduced into $\mathit{f}\left(\mathit{x}\right(t),t)$ (1), and the symbol ^.2 is a “superscript” that represents a square operator, where $\mathit{v}\left(t\right)$ is an unknown dynamic vector that needs to be solved. Let $\wedge \left(t\right)=\mathrm{diag}\{v_1\left(t\right),\dots ,v_m\left(t\right)\}$, where $\wedge \left(t\right)$ is a diagonal matrix, then $\mathit{v}{\left(t\right)}^{.2}=\wedge \left(t\right)\mathit{v}\left(t\right)$. The specific form is as follows:

$$\left\{\begin{array}{c}\mathit{f}\left(\mathit{x}\left(t\right),t\right)+\mathit{v}{\left(t\right)}^{.2}=\mathit{b}\left(t\right),\hfill \\ \mathit{h}\left(\mathit{x}\left(t\right),t\right)=\mathbf{0}.\hfill \end{array}\right.$$

(2)

It is obvious that the solution of time-variant Equation (2) is equivalent to time-variant NIE systems (1). Therefore, to obtain the unknown $\mathit{x}\left(t\right)$ and $\wedge \left(t\right)$, we will focus on the solution of time-variant Equation (2). In the following section, we introduce the ZNN algorithm to address time-variant Equation (2) in detail.

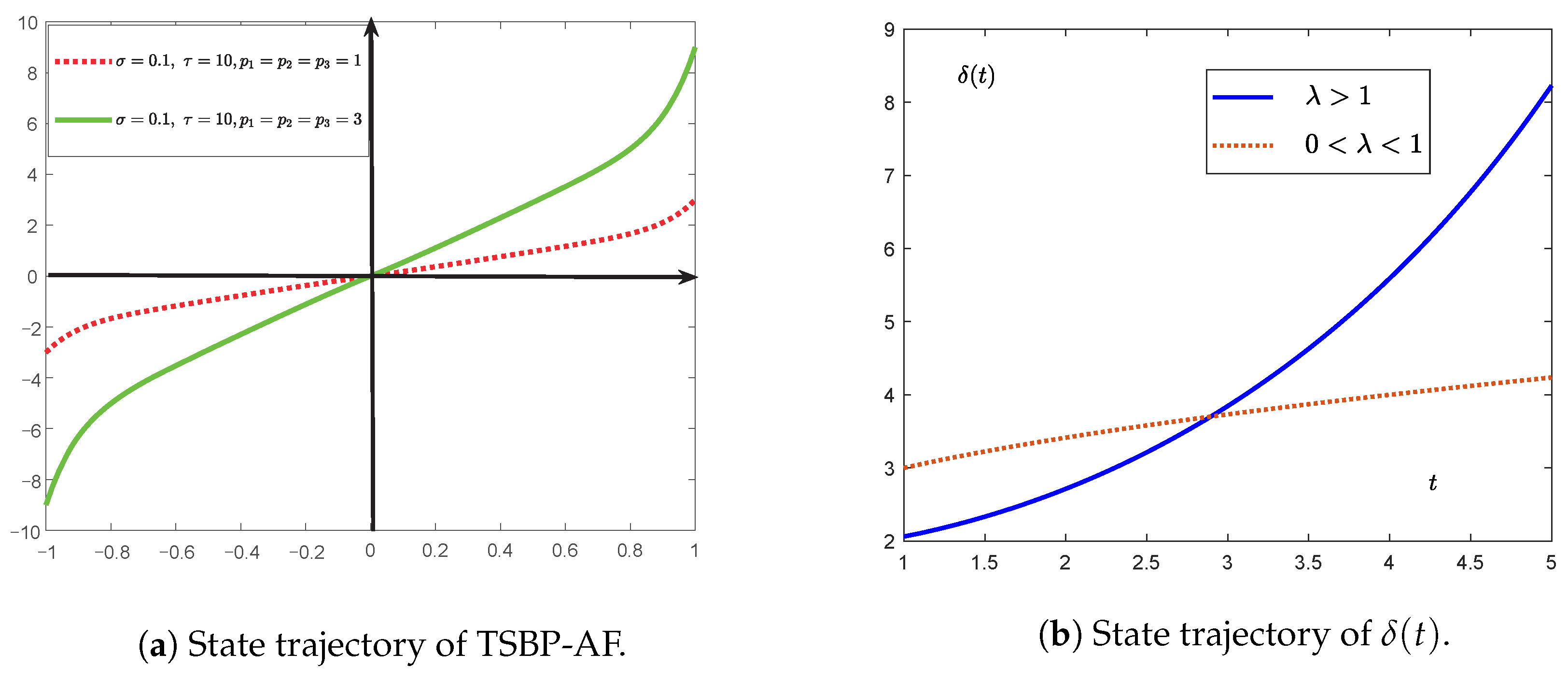
3. PGAZNN Model

In this section, in order to solve the equivalent conversion time-variant Equation (2), the process of the PGAZNN model is presented. Firstly, the concise design idea of the original ZNN model [18] is shown in the following three steps.

Step 1: Construct the error function according to the different problem formulations.

Step 2: Introduce the evolution formula to force the error function to equal zero.

Step 3: Combine the error function and the corresponding evolution formula to further deduce the ZNN models.

Inspired by the above modeling design ideas, we split the time-variant Equation (2) into two parts, that is, $\mathit{f}\left(\mathit{x}\right(t),t)$ and $\mathit{h}\left(\mathit{x}\right(t),t)$. Then they are, respectively, applied to deduce the ZNN model, and the specific processes are as follows:

For the part $\mathit{f}\left(\mathit{x}\right(t),t)$ of time-variant Equation (2), an error function is constructed:

$$R_1\left(t\right)=\mathit{f}\left(\mathit{x}\left(t\right),t\right)+\mathit{v}{\left(t\right)}^{.2}-\mathit{b}\left(t\right).$$

(3)

Then, introduce the ZNN evolution formula:

$${\dot{R}}_1\left(t\right)=-\mu \left(t\right)\Phi \left(R_1\left(t\right)\right),$$

(4)

where $\mu \left(t\right)$ denotes a nonnegative parameter-gain function, $\Phi (·)$ is a nonlinear activation function mapping. When $\Phi (·)$ is a monotonously increased and odd function, $R\left(t\right)$ was proved that would decrease to zero in previous literatures.

Next, combining Equations (3) and (4), we can obtain the following ZNN-f model:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial \mathit{f}}{\partial \mathit{x}}}\dot{\mathit{x}}\left(t\right)=& -2\wedge \left(t\right)\dot{\mathit{v}}\left(t\right)+\dot{\mathit{b}}\left(t\right)-{\displaystyle \frac{\partial \mathit{f}}{\partial t}}\hfill \\ \hfill & -\mu \left(t\right)\Phi (\mathit{f}(\mathit{x}\left(t\right),t)+\mathit{v}{\left(t\right)}^{.2}-\mathit{b}\left(t\right)).\hfill \end{array}$$

(5)

For the part $\mathit{h}\left(\mathit{x}\right(t),t)$ of time-variant Equation (2), applying a similar modeling idea, construct an error function $R_2\left(t\right)=\mathit{h}(\mathit{x}\left(t\right),t)$, where

$$R_2\left(t\right)={[h_1(x_1\left(t\right),t),h_2(x_2\left(t\right),t),\dots ,h_n(x_n\left(t\right),t)]}^{\mathrm{T}},$$

and the evolve formula ${\dot{R}}_2\left(t\right)=-\mu \left(t\right)\Phi \left(R_2\left(t\right)\right)$, one can obtain the following form of the ZNN-h model:

$$J(\mathit{x}\left(t\right),t)\dot{\mathit{x}}\left(t\right)=-\mu \Phi \left(\mathit{h}\left(\mathit{x}\right(t),t)\right)-{\displaystyle \frac{\partial \mathit{h}}{\partial t}},$$

(6)

where

$$\begin{array}{c}\hfill J(\mathit{x}\left(t\right),t)=\left[\begin{array}{cccc}{\displaystyle \frac{\partial h_1}{\partial x_1}}& {\displaystyle \frac{\partial h_1}{\partial x_2}}& \dots & {\displaystyle \frac{\partial h_1}{\partial x_n}}\\ {\displaystyle \frac{\partial h_2}{\partial x_1}}& {\displaystyle \frac{\partial h_2}{\partial x_2}}& \dots & {\displaystyle \frac{\partial h_2}{\partial x_n}}\\ ⋮& ⋮& \ddots & ⋮\\ {\displaystyle \frac{\partial h_n}{\partial x_1}}& {\displaystyle \frac{\partial h_n}{\partial x_2}}& \dots & {\displaystyle \frac{\partial h_n}{\partial x_n}}\end{array}\right],{\displaystyle \frac{\partial \mathit{h}}{\partial t}}=\left[\begin{array}{c}{\displaystyle \frac{\partial h_1}{\partial t}}\\ {\displaystyle \frac{\partial h_2}{\partial t}}\\ ⋮\\ {\displaystyle \frac{\partial h_n}{\partial t}}\end{array}\right].\end{array}$$

So far, we have obtained ZNN-f and ZNN-h models of the time-variant NIE systems (1) through the design idea of ZNN. In the next step, in order to simplify these two ZNN models to obtain a simple ZNN model, let

$$A\left(t\right)=\left[\begin{array}{cc}{\displaystyle \frac{\partial \mathit{f}}{\partial \mathit{x}}}& 2\wedge \left(t\right)\\ J\left(\mathit{x}\right(t),t)& \mathbf{0}\end{array}\right],\dot{S}\left(t\right)=\left[\begin{array}{c}\dot{\mathit{x}}\left(t\right)\\ \dot{\mathit{v}}\left(t\right)\end{array}\right],$$

$$Q\left(t\right)=\left[\begin{array}{c}\dot{\mathit{b}}\left(t\right)-{\displaystyle \frac{\partial \mathit{f}}{\partial t}}-\mu \left(t\right)\Phi (\mathit{f}(\mathit{x}\left(t\right),t)+\mathit{v}{\left(t\right)}^{.2}-\mathit{b}\left(t\right))\\ -\mu \Phi \left(\mathit{h}\left(\mathit{x}\right(t),t)\right)-{\displaystyle \frac{\partial \mathit{h}}{\partial t}}\end{array}\right],$$

which we call the novel combined ZNN model for solving the time-variant NIE systems (1). The specific form is as follows:

$$A\left(t\right)\dot{S}\left(t\right)=Q\left(t\right).$$

(7)

After a series of changes, settling time-variant NIE systems (1) have been transformed into settling matrix Equation (7). However, we know that the complexity of the system is uncontrollable. For this reason, we need to introduce some superior activation functions and parameter-gain function to make the ZNN model (7) more excellent, that is, to make the solution algorithm more efficient [22,26,36]. Next, we introduce several groups of common AFs and a time-variant parameter-gain function.

(1)

Linear AF:

$${\Phi }_1\left(e\right)=e.$$

(8)

(2)

Power type AF:

$${\Phi }_2\left(e\right)=e^x,x\ge 3.$$

(9)

(3)

Bipolar-sigmoid type AF:

$${\Phi }_3\left(e\right)={\displaystyle \frac{1+\exp (-x)}{1-\exp (-x)}}{\displaystyle \frac{1-\exp (-xe)}{1+\exp (-xe)}},x>2.$$

(10)

(4)

Power-sigmoid type AF:

$${\Phi }_4\left(e\right)={\displaystyle \frac{1+\exp (-x_2)}{1-\exp (-x_2)}}{\displaystyle \frac{1-\exp (-x_{2}e)}{1+\exp (-x_{2}e)}}+{\displaystyle \frac{1}{2}}{e}^{x_1},$$

(11)

where $x_2>2,x_1\ge 3$.

Compared with linearly activated ZNN (original ZNN), the above nonlinear activation functions can accelerate the convergence speed of ZNN, but cannot achieve finite-time convergence. In [34], a sign-bi-power activation function (SBP-AF) is designed to accelerate nonlinearly activated ZNN (NAZNN) to finite-time convergence, and its specific form is $\Phi \left(e\right)=0.5\left(\right|e{|}^{\sigma }+\left|e{|}^{{\displaystyle \frac{1}{\sigma }}}\right)\mathrm{sign}\left(e\right)$. In this work, curves of tunable SBP-AF (TSBP-AF) with different parameter values are demonstrated in Figure 1a.

$$\Psi \left(e\right)=p_1{\left|e\right|}^{\sigma }\mathrm{sign}\left(e\right)+p_2{\left|e\right|}^{\tau }\mathrm{sign}\left(e\right)+p_{3}e,$$

(12)

where $p_1>0,p_2>0,p_3>0$ are tunable design parameters, from Figure 1a, we can see that a larger value of the tunable design parameters prompts TSBP-AF to have a faster rate change. $0<\sigma <1,\tau >1$, $\mathrm{sign}(·)$ represents a symbolic function:

$$\mathrm{sign}\left(e\right)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if} e>0,\hfill \\ 0,\hfill & \mathrm{if} e=0,\hfill \\ -1,\hfill & \mathrm{if} e<0.\hfill \end{array}\right.$$

The practice of introducing a time-variant parameter-gain function into the ZNN model has been reflected in many literatures, such as [25,26,33,36,37]. The study of a ZNN model (7) with a time-variant parameter-gain function for settling the time-variant NIE systems (1), which is converted into matrix Equation (7), has not been explored. Therefore, we introduce a time-variant parameter-gain function to study the time-variant NIE systems (1) as follows:

$$\delta \left(t\right)=\left\{\begin{array}{cc}{\lambda }^{(k_1\mathrm{arccot}\left(\mathrm{t}\right)+k_{2}t)},\hfill & \lambda >1,\hfill \\ t^{\lambda }+{\displaystyle \frac{1}{\lambda }},\hfill & 0<\lambda ⩽1,\hfill \end{array}\right.$$

(13)

where $k_1,k_2>0$, and its change of state trajectory is shown in Figure 1b, the value of $\delta \left(t\right)$ will remain stable and gradually increase as time goes on.

Finally, substitute the tunable SBP-AF $\Psi (·)$ and the time-variant parameter-gain function $\delta \left(t\right)$ into the ZNN model (7), we can obtain the PGAZNN as follows:

$$\left[\begin{array}{cc}{\displaystyle \frac{\partial \mathit{f}}{\partial \mathit{x}}}& 2\wedge \left(t\right)\\ J\left(\mathit{x}\right(t),t)& \mathbf{0}\end{array}\right]\left[\begin{array}{c}\dot{\mathit{x}}\left(t\right)\\ \dot{\mathit{v}}\left(t\right)\end{array}\right]=\left[\begin{array}{c}\dot{\mathit{b}}\left(t\right)-{\displaystyle \frac{\partial \mathit{f}}{\partial t}}-\delta \left(t\right)\Psi (\mathit{f}(\mathit{x}\left(t\right),t)+\mathit{v}{\left(t\right)}^{.2}-\mathit{b}\left(t\right))\\ -\delta \Psi \left(\mathit{h}\left(\mathit{x}\right(t),t)\right)-{\displaystyle \frac{\partial \mathit{h}}{\partial t}}\end{array}\right]$$

(14)

Next, we conduct a detailed theoretical analysis of the proposed PGAZNN model (14).

4. Theoretical Testimony and Analysis

According to the above transformation and derivation results, the proposed PGAZNN model (14) is used to settle the time-variant NIE systems (1) in this paper. The stability proof and convergence analysis of the PGAZNN model are presented in detail in this section.

4.1. Stability Analysis

To facilitate the derivation of global stability, we first introduce the following two lemmas (Barbalat’s Lemma and its corollary).

Lemma 1 

([8]). If a scalar function f(t) is uniformly continuous for all $t\ge 0$, and the limit of its integral ${\lim }_{t\to \infty }{\int }_0^{t}f\left(\tau \right)d\tau$ exists and is finite, then ${\lim }_{t\to \infty }f\left(t\right)=0$.

Lemma 2 

([38]). If a scalar function $V(t,x)$ is lower-bounded, its time derivative $\dot{V}(t,x)$ is negative semi-definite and uniformly continuous in t, then ${\lim }_{t\to \infty }\dot{V}(t,x)=0$.

Theorem 1.

For a solvable time-variant system (1), the error function generated by the PGAZNN model (14) with activation function (12) is globally convergent to zero.

Proof of Theorem 1.

Considering ZNN-f (5) and ZNN-h (6) models, in view of their evolution formula ${\dot{R}}_{1,2}\left(t\right)=-\mu \dot{\Phi }\left(R_{1,2}\left(t\right)\right)$, we refer to the previous study [18,32], it is known that these two ZNN-f and ZNN-h models can converge stably, respectively. Therefore, we only need to consider the stability of the PGAZNN model (14) in this paper.

Without loss of generality, for the PGAZNN model (14), according to its evolution formula, we define a nonnegative Lyapunov function candidate $l_i\left(t\right)=r_i^2\left(t\right)/2⩾0$. The time derivative of the time-variant NIE systems (1) is calculated, and it is shown as follows:

$$\begin{array}{c}\hfill {\dot{l}}_i\left(t\right)=r_i\left(t\right){\dot{r}}_i\left(t\right)=-\delta \left(t\right)r_i\left(t\right)\varphi \left(r_i\left(t\right)\right),\end{array}$$

(15)

where $r_i\left(t\right)$ and $\varphi (·)$ denote the elements of $R\left(t\right)$ and $\Psi (·)$, respectively. As mentioned previously, TSBP-AF (12) is a monotonically increasing odd function, so the following equation holds:

$$\varphi \left(r_i\left(t\right)\right)\left\{\begin{array}{cc}>0,\hfill & r_i\left(t\right)>0;\hfill \\ =0,\hfill & r_i\left(t\right)=0;\hfill \\ <0,\hfill & r_i\left(t\right)<0,\hfill \end{array}\right.$$

and because $\delta \left(t\right)$ is a nonnegative parameter-gain function, it ensures that ${\dot{l}}_i\left(t\right)<0$ is valid for $l_i\left(t\right)\ne 0$ and ${\dot{l}}_i\left(t\right)=0$ only holds true for $l_i\left(t\right)=0$. According to Lemmas 1 and 2, $r_i\left(t\right)$ will converge to zero finally. That is, the state vector $\mathit{x}\left(t\right)$ of the PGAZNN model (14) globally converges to the time-variant theoretical solution when settling time-variant NIE systems (1).

The proof of Theorem 1 is complete. □

4.2. Convergence Analysis

Theorem 2.

From a stochastic initial error $r_i\left(0\right)$, when the proposed PGAZNN model (14) is applied to settle time-variant NIE systems (1), the finite-time convergence time $T_e$ of the model solution can be estimated as follows:

$$T_e⩽\left\{\begin{array}{c}{\displaystyle \frac{1}{k_2\ln \left(\lambda \right)}}\ln \left[{\displaystyle \frac{k_2\ln \left(\lambda \right)}{p_2\left(\tau -1\right)}}+{\displaystyle \frac{k_2\ln \left(\lambda \right)}{p_1\left(1-\sigma \right)}}+1\right],\lambda >1\hfill \\ {\left[{\displaystyle \frac{1+\lambda }{p_2\left(\tau -1\right)}}+{\displaystyle \frac{1+\lambda }{p_1\left(1-\sigma \right)}}\right]}^{{\displaystyle \frac{1}{1+\lambda }}},0<\lambda ⩽1\hfill \end{array}\right.,$$

(16)

where the definition of symbols $\lambda ,\tau ,\sigma ,p_1,p_2,k_2$ is the same as mentioned above.

Proof of Theorem 2.

For the PGAZNN model (14), in order to prove the above calculations, the following two cases are discussed.

Case 1: When $\lambda >1$, consider the following dynamic equation with element notation as follows:

$${\dot{r}}_i\left(t\right)=-\delta \left(t\right)\psi \left(r_i\left(t\right)\right).$$

Define a Lyapunov function candidate $l_i=\left|r_i\left(t\right)\right|$, and then calculate its derivative with respect to time t:

$$\begin{array}{cc}\hfill {\dot{l}}_i\left(t\right)& =\dot{r_i}\left(t\right)\mathrm{sign}\left(r_i\left(t\right)\right)\hfill \\ \hfill & =-\delta \left(t\right)r_i\left(t\right)\varphi \left(r_i\left(t\right)\right)\hfill \\ \hfill & =-{\lambda }^{(k_1\mathrm{arccot}\left(\mathrm{t}\right)+k_{2}t)}(p_1{r}_i^{\sigma }\left(t\right)+p_2{r}_i^{\tau }\left(t\right)+p_3{r}_i\left(t\right)).\hfill \end{array}$$

(17)

After scaling, the above equation can be transformed:

$${\dot{l}}_i\left(t\right)⩽-{\lambda }^{k_{2}t}(p_1{r}_i^{\sigma }\left(t\right)+p_2{r}_i^{\tau }\left(t\right)+p_3{r}_i\left(t\right)).$$

According to Theorem 1, $r_i\left(t\right)$ will globally converge to zero from a stochastic initial error $r_i\left(0\right)$. To meet the requirement of universality, it is divided into two situations according to the magnitude of $r_i\left(0\right)$, that is $r_i\left(0\right)>1$ and $0<r_i\left(0\right)⩽1$. In the first situation $|r_i\left(0\right)|>1$, the following inequality holds:

$${\dot{l}}_i\left(t\right)⩽-{\lambda }^{k_{2}t}{p}_2{r}_i^{\tau }\left(t\right).$$

Transform the above formula and integrate both sides of the inequality to obtain the following form

$${\int }_{l_i\left(0\right)}^{l_i\left(t_1\right)}{l}_i{\left(t\right)}^{-\tau \left(t\right)}\mathrm{d}{l}_i\left(t\right)⩽{\int }_0^{t_1}-p_2{\lambda }^{k_{2}t}\mathrm{d}t.$$

When time $t:0\to t_1$, $r_i\left(t\right):r_i\left(0\right)\to r_i\left(t_1\right)=1$, is elapsed that is $l_i\left(t_1\right)=1$, and we obtain the result:

$$\begin{array}{cc}\hfill t_1& ⩽{\displaystyle \frac{1}{k_2\ln \left(\lambda \right)}}\left[\ln (1+{\displaystyle \frac{k_2\ln \left(\lambda \right)(1-l_i^{1-\tau }\left(0\right))}{p_2(\tau -1)}})\right]\hfill \\ \hfill & ⩽{\displaystyle \frac{1}{k_2\ln \left(\lambda \right)}}\left[\ln (1+{\displaystyle \frac{k_2\ln \left(\lambda \right)}{p_2(\tau -1)}})\right].\hfill \end{array}$$

After the above time $t_1$, elapsed time $t:t_1\to t_1+t_2$, $r_i\left(t\right):r_i\left(t_1\right)\to r_i(t_1+t_2)=0$, that is $l_i(t_1+t_2)=0$, and $l_i\left(t\right)<1$ the following inequality holds

$${\dot{l}}_i\left(t\right)⩽-{\lambda }^{k_{2}t}{p}_1{r}_i^{\sigma }\left(t\right).$$

The same as the above calculation method, integrating from $t_1$ to $t_1+t_2$, $l_i\left(t_1\right)=1$ and $l_i(t_1+t_2)=0$, and we can obtain

$$t_2⩽{\displaystyle \frac{1}{k_2\ln \left(\lambda \right)}}\left[\ln (1+{\displaystyle \frac{k_2\ln \left(\lambda \right)}{p_2(1-\sigma )}})\right].$$

In a word, the upper bound of the convergence time when $\lambda >1$ is as follows:

$$T_c=t_1+t_2⩽{\displaystyle \frac{1}{k_2\ln \left(\lambda \right)}}\ln \left[{\displaystyle \frac{k_2\ln \left(\lambda \right)}{p_2\left(\tau -1\right)}}+{\displaystyle \frac{k_2\ln \left(\lambda \right)}{p_1\left(1-\sigma \right)}}+1\right].$$

Case 2: When $0<\lambda ⩽1$, consider ${\dot{r}}_i\left(t\right)=-\delta \left(t\right)\psi \left(r_i\left(t\right)\right)$, and then the following inequality holds

$$\begin{array}{cc}\hfill {\dot{l}}_i\left(t\right)& =\dot{r_i}\left(t\right)\mathrm{sign}\left(r_i\left(t\right)\right)\hfill \\ \hfill & =-\delta \left(t\right)r_i\left(t\right)\varphi \left(r_i\left(t\right)\right)\hfill \\ \hfill & =-(t^{\lambda }+{\displaystyle \frac{1}{\lambda }})(p_1{r}_i^{\sigma }\left(t\right)+p_2{r}_i^{\tau }\left(t\right)+p_3{r}_i\left(t\right))\hfill \\ \hfill & ⩽-t^{\lambda }(p_1{r}_i^{\sigma }\left(t\right)+p_2{r}_i^{\tau }\left(t\right)+p_3{r}_i\left(t\right)).\hfill \end{array}$$

It is still divided into two situations according to the magnitude of $r_i\left(0\right)$, that is $r_i\left(0\right)>1$ and $0<r_i\left(0\right)⩽1$. In the first situation, $|r_i\left(0\right)|>1$, the following inequality holds

$${\dot{l}}_i\left(t\right)⩽-t^{\lambda }{p}_2{r}_i^{\tau }\left(t\right).$$

Transform the above formula and integrate both sides of the inequality to obtain the following form:

$${\int }_{l_i\left(0\right)}^{l_i\left(t_1\right)}{l}_i{\left(t\right)}^{-\tau \left(t\right)}\mathrm{d}{l}_i\left(t\right)⩽{\int }_0^{t_1}-p_2{t}^{\lambda }\mathrm{d}t,$$

The same as Case 1, $l_i\left(t_1\right)=1$, and $t_1$ can be obtained:

$$\begin{array}{cc}\hfill t_1& ⩽{\left[{\displaystyle \frac{(1+\lambda )(1-l_i^{1-\tau }\left(0\right))}{p_2(\tau -1)}}\right]}^{{\displaystyle \frac{1}{1+\lambda }}}\hfill \\ \hfill & ⩽{\left[{\displaystyle \frac{1+\lambda }{p_2\left(\tau -1\right)}}\right]}^{{\displaystyle \frac{1}{1+\lambda }}}.\hfill \end{array}$$

After the above time $t_1$, the elapsed time $t:t_1\to t_1+t_2$, $r_i\left(t\right):r_i\left(t_1\right)\to r_i(t_1+t_2)=0$, that is $l_i(t_1+t_2)=0$, and $l_i\left(t\right)<1$, the following inequality holds:

$${\dot{l}}_i\left(t\right)⩽-t^{\lambda }{p}_1{r}_i^{\sigma }\left(t\right),$$

that is

$$l_i^{-\sigma }\mathrm{d}{l}_i\left(t\right)⩽-p_1{t}^{\lambda }\mathrm{d}t.$$

(18)

integrating from $t_1$ to $t_1+t_2$, $l_i\left(t_1\right)=1$ and $l_i(t_1+t_2)=0$, and we can obtain the following:

$$t_2⩽{\displaystyle \frac{1}{k_2\ln \left(\lambda \right)}}\left[\ln (1+{\displaystyle \frac{k_2\ln \left(\lambda \right)}{p_1(1-\sigma )}})\right],$$

so the upper bound of the convergence time when $0<\lambda ⩽1$ is

$$\begin{array}{cc}\hfill T_c& =t_1+t_2\hfill \\ \hfill & ⩽{[{\displaystyle \frac{(1+\lambda )(1-l_i^{1-\tau }\left(0\right))}{p_2(\tau -1)}}+{\displaystyle \frac{1+\lambda }{p_1(1-\sigma )}}]}^{{\displaystyle \frac{1}{1+\lambda }}}\hfill \\ \hfill & ⩽{[{\displaystyle \frac{1+\lambda }{p_2(\tau -1)}}+{\displaystyle \frac{1+\lambda }{p_1(1-\sigma )}}]}^{{\displaystyle \frac{1}{1+\lambda }}}.\hfill \end{array}$$

The proof of Theorem 2 is complete. □

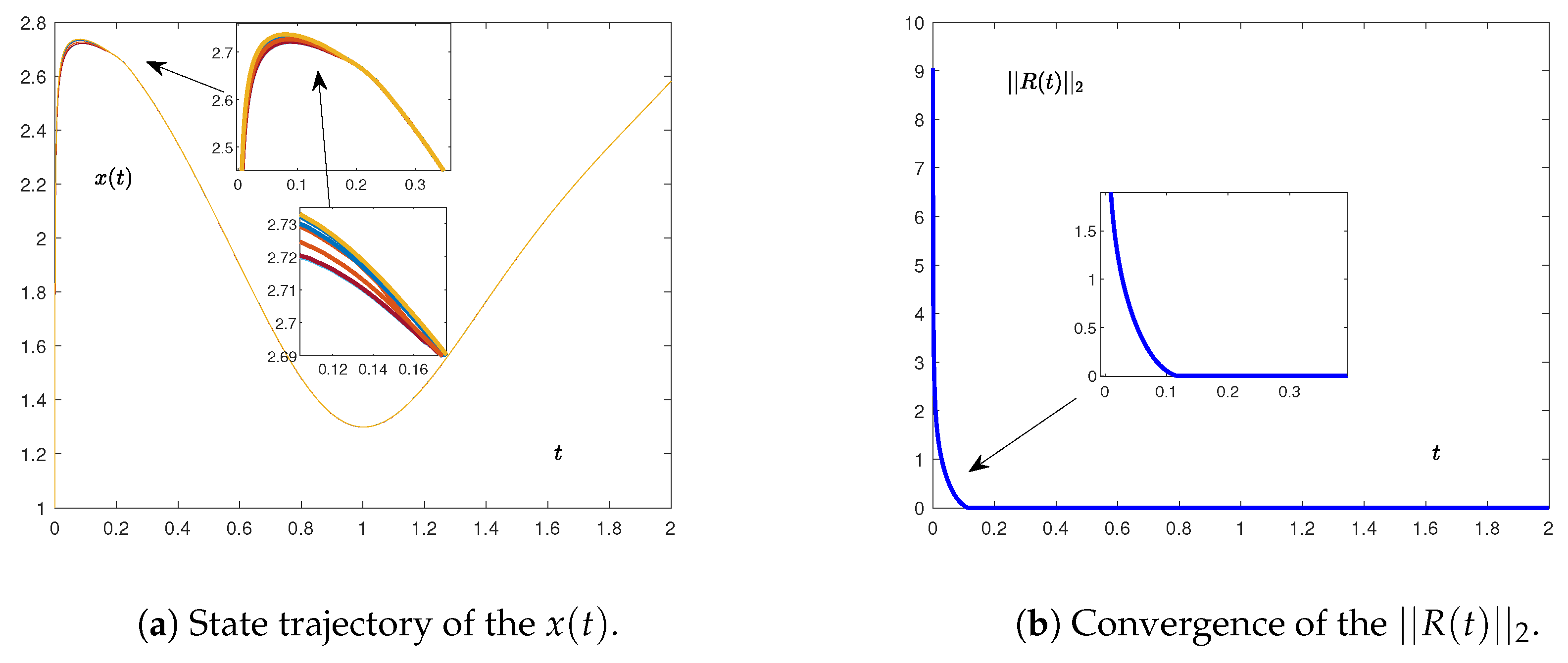
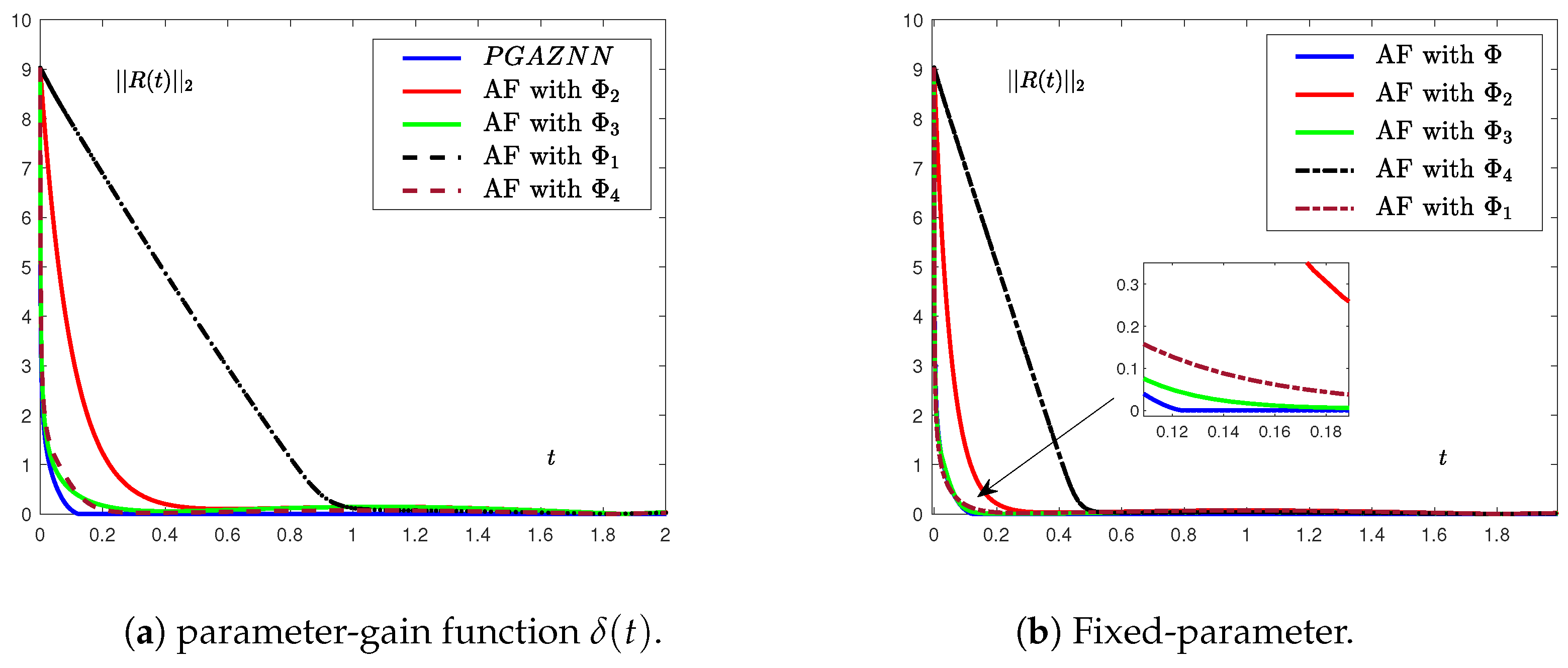
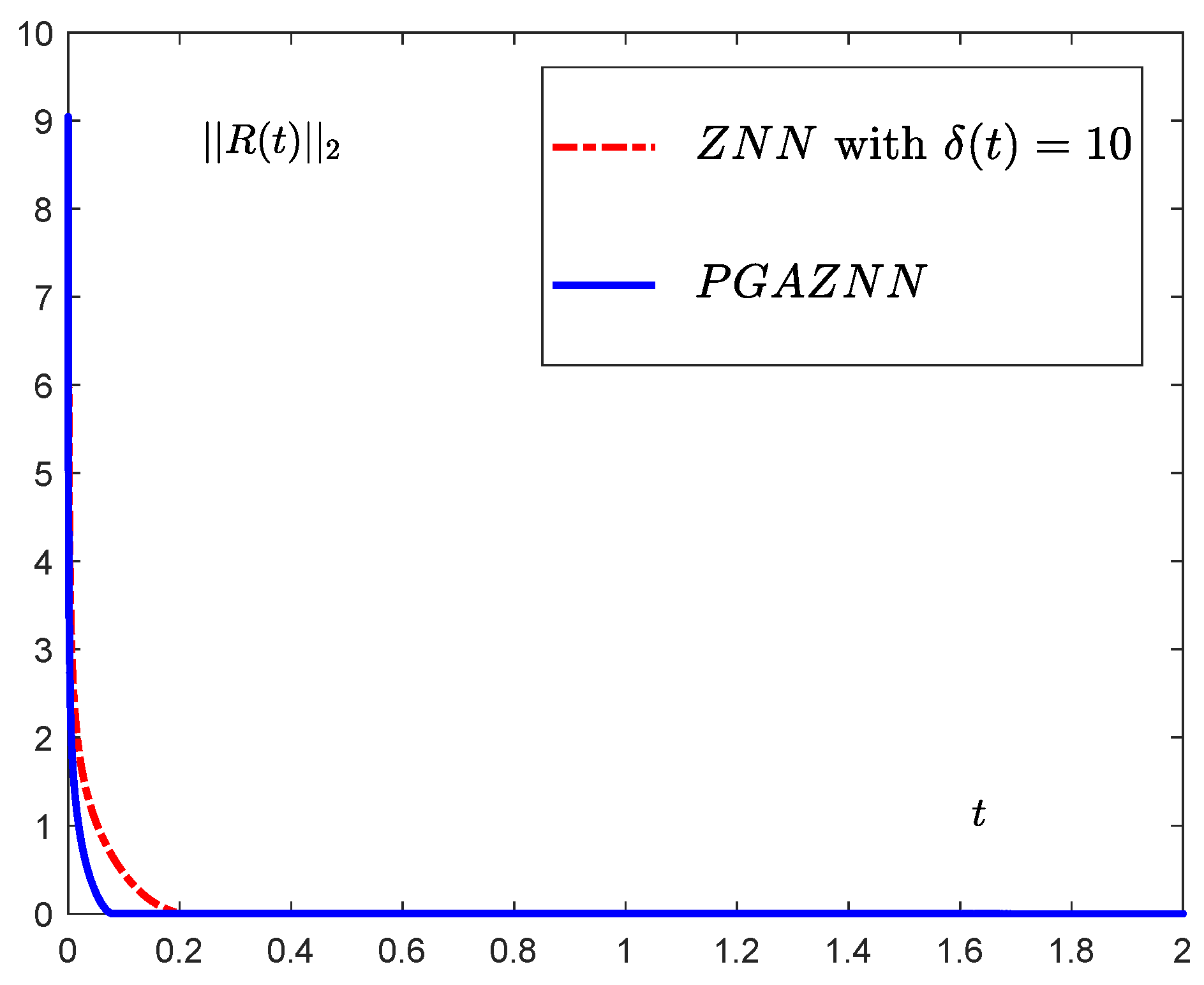
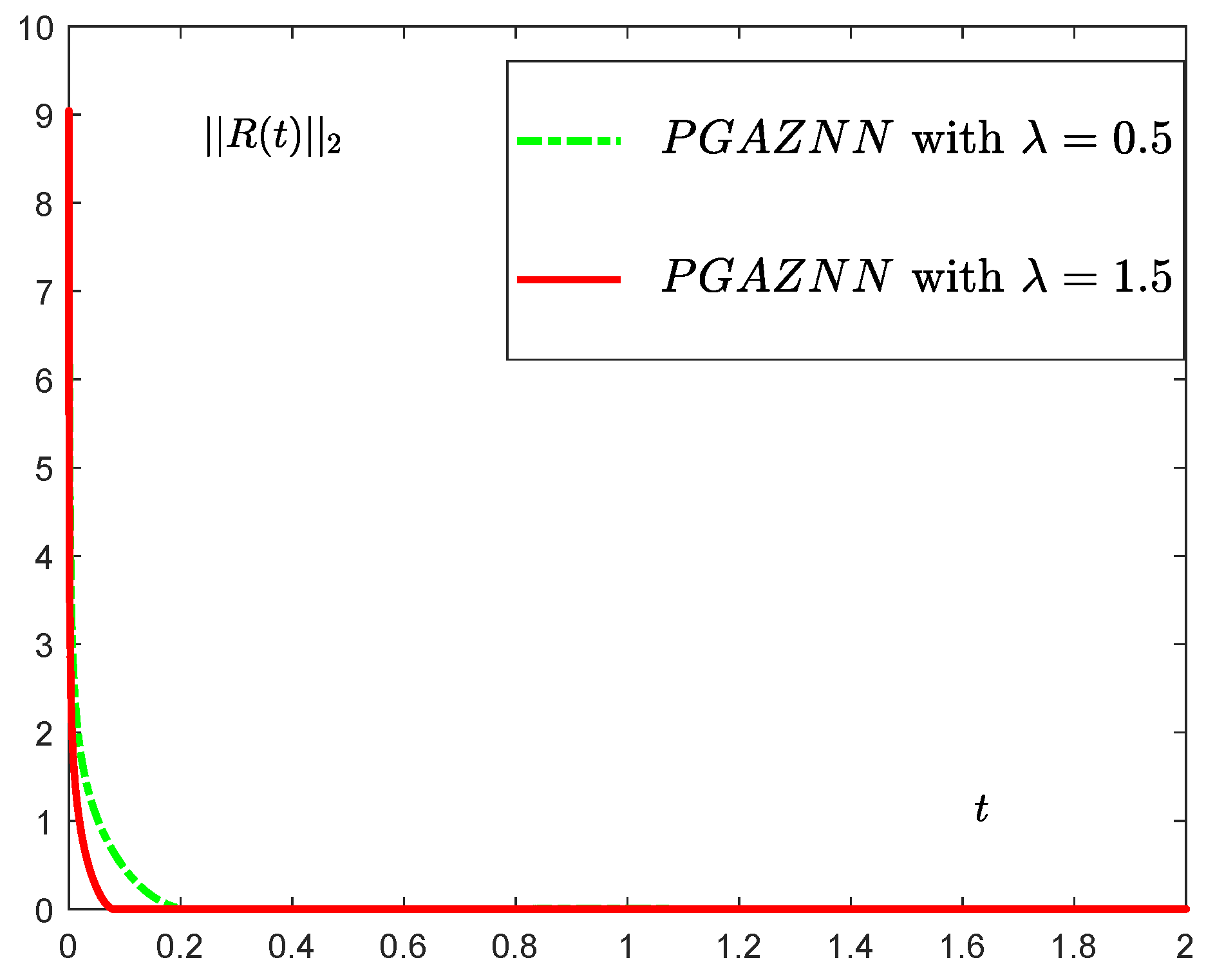
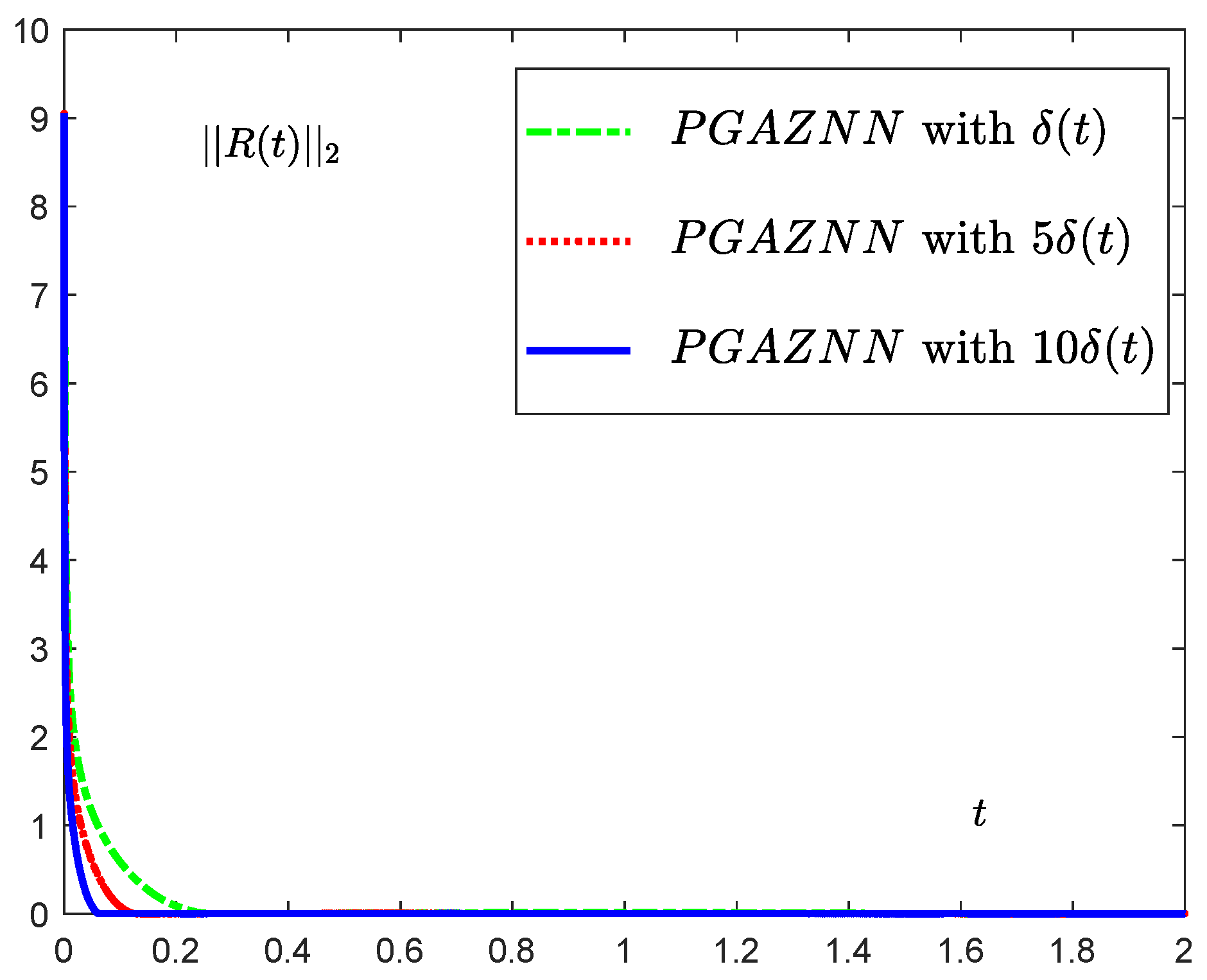
5. Numerical Simulation

This section presents a simulation example with different variables and appropriate initial conditions to verify the effectiveness and superiority of the PGAZNN model (14) in a time-varying NIE system (1). Furthermore, the superiority of the PGAZNN model is analyzed in the trajectory tracking application scenario.

5.1. Numerical Example

Firstly, consider the following time-variant NIE systems (1) as an example:

$$\left\{\begin{array}{c}{x}^2\left(t\right)-{\cos }^2\left(2t\right)-4\cos \left(2t\right)-4⩽\sin \left(t\right)+2t,\hfill \\ x^2\left(t\right)-{\sin }^2\left(2t\right)-2\sin \left(2t\right)-1=0.\hfill \end{array}\right.$$

(19)

The main goal of this paper is to explore the effect of the PGAZNN model on solving the time-variant NIE systems (19) under different parameters and initial conditions. Without loss of generality, the PGAZNN model (14) proposed in this paper needs to solve the time-variant NIE systems in a certain initial state.

Firstly, let the initial condition $\lambda =1.5,\sigma =0.3,\tau =3,p_{1,2,3}=k_{1,2,3}=1$, and the convergence accuracy be ${10}^{-3}$; the theoretical upper bound of the finite-time convergence time $T_c⩽{\displaystyle \frac{1}{k_2\ln \left(\lambda \right)}}\ln \left[{\displaystyle \frac{k_2\ln \left(\lambda \right)}{p_2\left(\tau -1\right)}}+{\displaystyle \frac{k_2\ln \left(\lambda \right)}{p_1\left(1-\sigma \right)}}+1\right]\approx 1.43$ s can be obtained. The abscissa unit of all figures in this paper is seconds, that is, $time/s$. In order to verify the effectiveness of the solution of PGAZNN model (14), Figure 2 shows the state trajectory of solving the time-variant NIE systems (19) under 10 randomly generated initial values $x\left(0\right)$ of size [0, 1], where Figure 2a is the trajectory variation in the $x\left(t\right)$, which shows the feasibility of the numerical solution generated by the PGAZNN model (14) when solving the time-variant NIE systems (19); Figure 2b presents the convergence of the error function ${\left|\right|R\left(t\right)\left|\right|}_2$ under any of the initial values $x\left(0\right)$, the finite-time convergence time $T_c\approx 0.116$ s <1.43 s which conforms to the argument result of Theorem 2. It is clear that the curves are a very effective solution to the time-variant NIE systems (19).

On the other hand, while ensuring the effectiveness of the PGAZNN model (14) in solving the time-variant NIE systems (1), it is also important to highlight the comparison of the PGAZNN model (14) proposed in this paper in terms of convergence time and speed. In Figure 3, the influences of different AFs and parameter gains on the convergence time are highlighted. Figure 3a shows the difference in the convergence time between the proposed PGAZNN model (14) and the ZNN model when using the AFs (${\Phi }_1(·)$, ${\Phi }_2(·)$, ${\Phi }_3(·)$, ${\Phi }_4(·)$), and it indicates that the PGAZNN model (14) has superior convergence performance. Figure 3b shows the comparison of the convergence of the error function when using a fixed parameter (the size is 10) instead of a parameter gain function $\delta \left(t\right)$. Combining with Figure 3a,b, it can be concluded that when the proposed PGAZNN model (14) solves the time-variant NIE systems (1), the PGAZNN model (14) has remarkable advantage in convergence speed. In addition, when using different AFs in ZNN models, there exists fluctuation in the error function $R\left(t\right)$, but the error in the PGAZNN model (14) can converge to zero. At the same time, by using the parameter-gain function $\delta \left(t\right)$, it accelerates the convergence of the error function to a certain extent, that is, it accelerates the convergence speed of the PGAZNN model (14) when solving the time-variant NIE systems (1).

The above description shows the effectiveness of the PGAZNN model (14) in solving the time-variant NIE systems (1) and the convergence advantage under different AFs. Next, in order to further explore the PGAZNN model (14) and clarify the influence of the parameters in the PGAZNN model on the convergence, we first consider the direct influence of the parameter-gain function $\delta \left(t\right)$ and the fixed parameter $\delta \left(t\right)=10$ on the convergence of the ZNN model. We take into account the time-variant NIE systems (19) solved under the same initial conditions as above, and the experimental results are shown in Figure 4. According to the analysis and estimation of Theorem 2, when the parameter-gain function $\delta \left(t\right)$ is applied, the convergence time of the error function norm of the corresponding PGAZNN model is faster, and when the fixed coefficient $\delta \left(t\right)=10$ is applied, the convergence time is slower than the former. It means that the difference between the two parameters involved in the ZNN model is because the parameter-gain function is gradually increasing with the change of time. Thus, its impact on the convergence speed of the ZNN model is greater than a fixed parameter, which does not change over time.

On the other hand, in Theorem 2, we can obtain a result of the convergence time of the PGAZNN model (14) under different values of $\lambda$ by calculation. Next, we use the experimental results to verify the correctness of Theorem 2. As shown in Figure 5, because $\lambda$ is divided into two cases, namely $\lambda =1.5$ and $\lambda =0.5$, when these two parameters are applied to the parameter-gain function $\delta \left(t\right)$, the corresponding convergence times of the error function norm of the PGAZNN model are shown differently, respectively, and the actual convergence time obtained in both cases is within the time estimated by Theorem 2. That is to say, the convergence time of the PGAZNN model (14) is within the upper bound of the convergence time calculated by Theorem 2, which is in line with our expectations and verifies the results in the theoretical analysis.

In addition, there has been a lot of literature on studying the convergence of design parameters to ZNN models, such as [29,33,36,37]. In this paper, one of the main influential factors is the parameter-gain function $\delta \left(t\right)$, so we set up some comparative experiments for parameter-gain functions with different coefficient sizes, and the experimental results are shown in Figure 6. When $\delta \left(t\right)=\delta \left(t\right),5\delta \left(t\right),10\delta \left(t\right)$, respectively, the convergence of the error function norm of the PGAZNN model is different. That is, the larger the coefficient of the parameter-gain function, the faster the convergence of the PGAZNN model (14). Therefore, the parameter of an appropriate size is an important indicator that affects the superiority of the ZNN model. On the other hand, in SBP-AF (12), three different parameters $p_1$, $p_2$, $p_3$ also affect the convergence speed of the ZNN model, which corresponds to the calculation result of different design parameters in Theorem 2.

5.2. Application

The aforementioned experimental results demonstrate the feasibility and superiority of the proposed PGAZNN model. Symmetrical trajectory tracking holds multiple significance in the fields of science, engineering and biology. Particularly in robot navigation and autonomous driving, symmetrical trajectories can optimize path planning, enhance the accuracy of motion control and improve energy efficiency. In this subsection, a three-dimensional symmetrical trajectory tracking device is employed to validate the effectiveness of the proposed PGAZNN model in practical application. As is well known, the position of the end effector is a vital control component, and the kinematical model of which can be represented as follows:

$$\Pi \left(t\right)=\mathbb{M}(\Sigma \left(t\right))\in {\mathbb{R}}^k,$$

where $\Pi \left(t\right)$ is the actual position of the end effector in three dimensions, which is controlled by $\mathbb{M}$, $\Sigma \left(t\right)={[{{\mathfrak{f}}_{\mathfrak{1}}}^T\left(t\right),{{\mathfrak{f}}_{\mathfrak{2}}}^T\left(t\right)]}^T\in {\mathbb{R}}^{l+2}$ is a function that includes the two angle vectors; ${\mathfrak{f}}_{\mathfrak{1}}^T\left(t\right)$ denotes the trajectory tracking device angle vector; ${\mathfrak{f}}_{\mathfrak{2}}^T\left(t\right)$ denotes the angle vector of the end effector. Then, the proposed PGAZNN model is embedded in a trajectory tracking device, and an improved kinetic equation can be obtained as

$$\Psi (\Sigma \left(t\right))\dot{\Sigma }\left(t\right)=\dot{\Pi }\left(t\right)-\delta \left(t\right)\mathbb{M}(\Pi \left(t\right)-\Sigma \left(t\right)).$$

The effect will be substantiated by controlling the device’s end effector to track a designated trajectory. In this simulation, a daisy trajectory can be tracked, To contrast the reliability, the original ZNN (OZNN) and NAZNN are introduced, and the parameters’ values in the dynamics control system are set the same as the numerical example; the corresponding results are displayed in Figure 7 and Figure 8. From Figure 7, we can see that the trajectory tracking device controlled by ZNN has a nice tracking effect; in contrast to OZNN and NAZNN, the PGAZNN further enhances the tracking capability of the ZNN. Figure 7d–f clearly shows that the convergence speed of the proposed PGAZNN is almost three times faster than that of OZNN. The specific convergence time is shown in

Table 1. The convergence time $T_c$ (in seconds) of GAZNN, GAZNN and OZNN without noise, and the convergence accuracy is ${\left|\right|R\left(t\right)\left|\right|}_2<{10}^{-4}$.

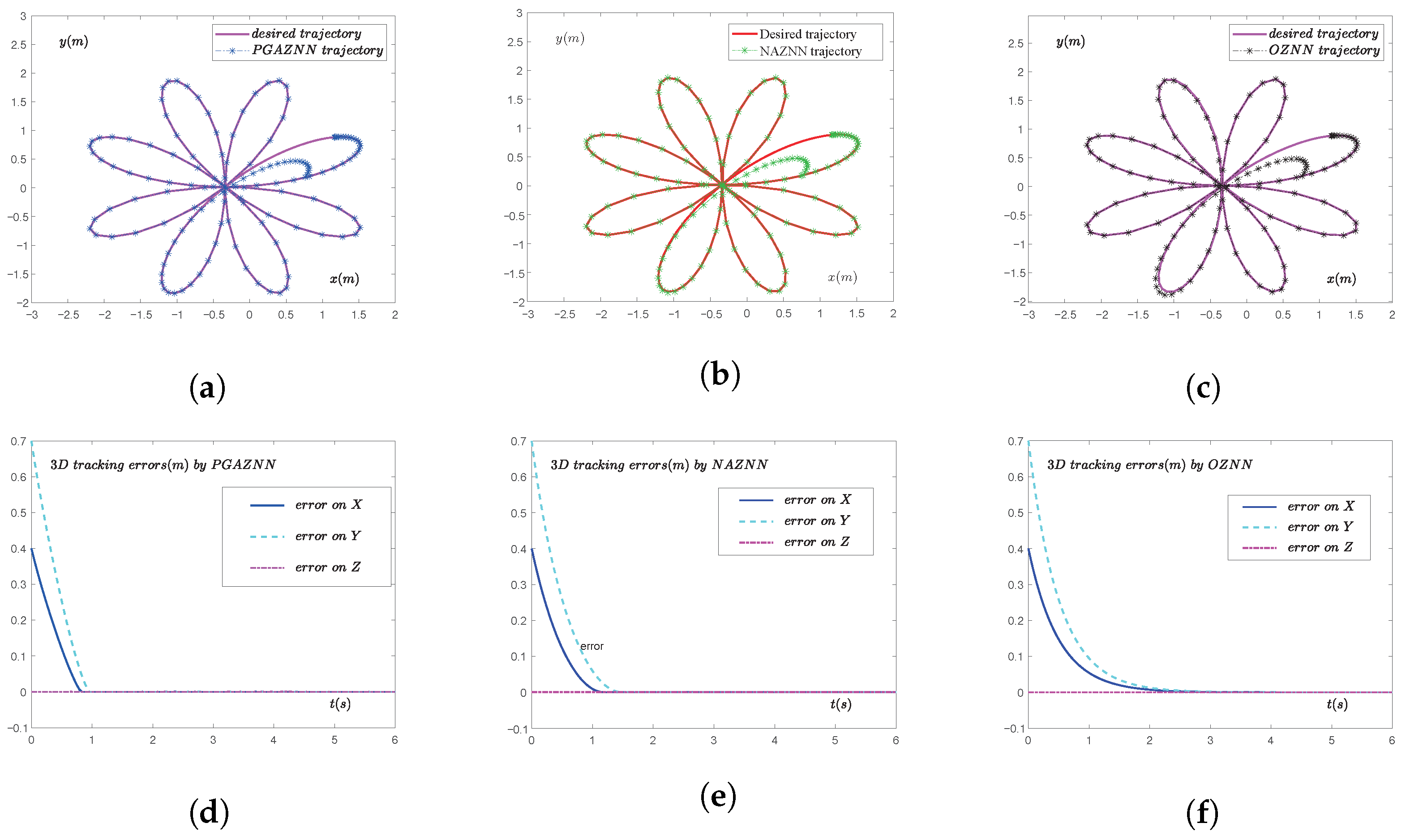
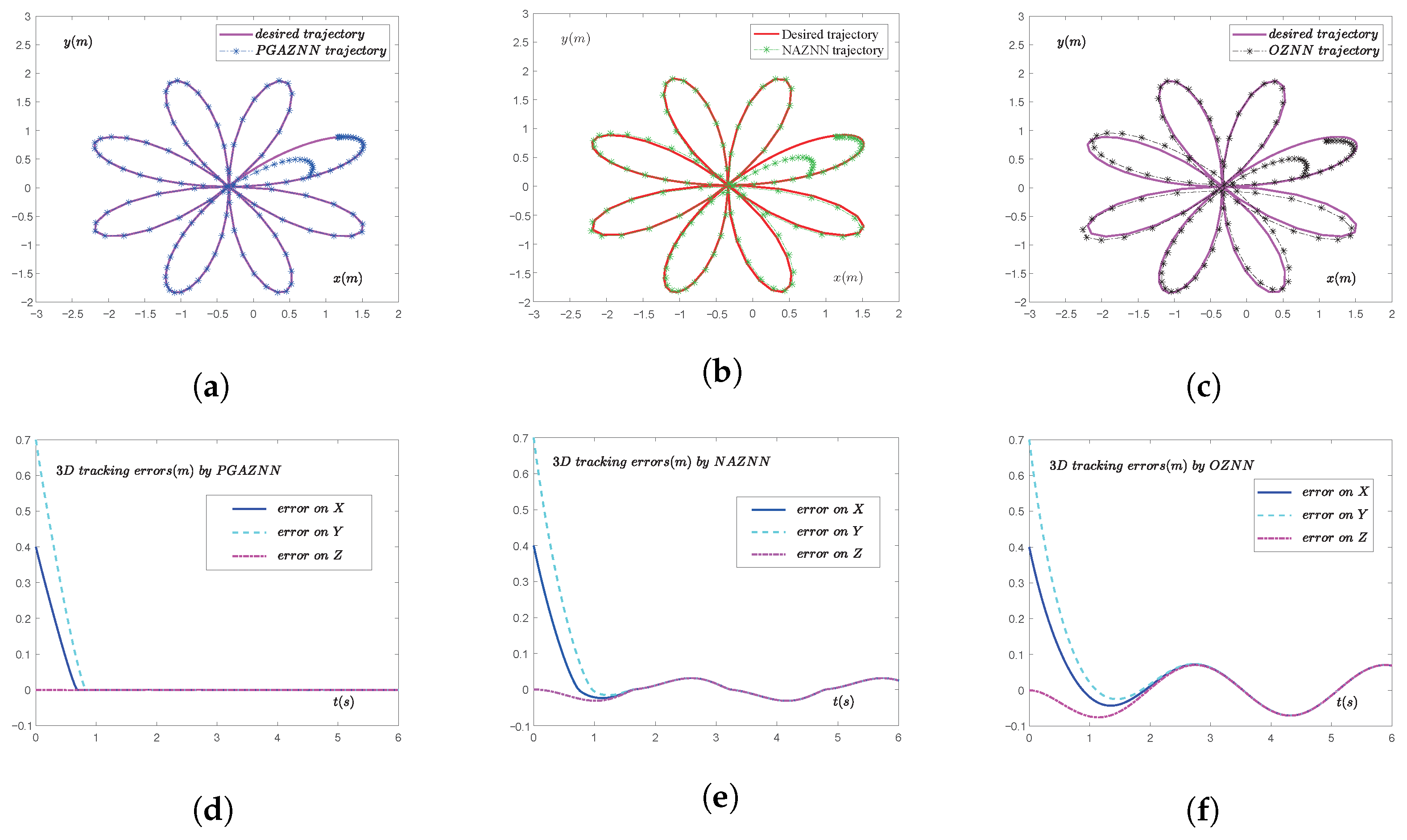
Model	GAZNN	NAZNN	OZNN
$T_c$	1.04	1.47	2.89

. As we know, interference is inevitable in the tracking process. Furthermore, in this application, the trajectory tracking device is set to run in a noisy environment (an additive bounded noise $0.2sin\left(2t\right)$ is set). The entire vertical view and the three-dimensional error of the trajectory tracking device controlled by the PGAZNN, NAZNN and OZNN are, respectively, depicted in Figure 8. From Figure 8a,d, we can see the tracking effect of PGAZNN is not disturbed by noise. Compared with Figure 7a,d, the accuracy is no different from that without noise interference. On the contrary, controlled by NAZNN or OZNN, noise largely defeats the accuracy. Obviously, the mobile manipulator controlled by PGAZNN can perfectly complete its tracking task in a disturbed environment. The robustness of the proposed PGAZNN is stronger than that of NAZNN and OZNN. From the above results, we can conclude that the PGAZNN further enhances the online processing capability of the ZNN.

6. Conclusions

In order to solve the time-variant NIE systems (1) with a concise algorithm, this paper proposes a method to convert the NIE systems (1) into a matrix equation solution. Inspired by the design of ZNN, according to the ZNN modeling process, this paper introduces the parameter-gain function, which is used to construct the PGAZNN model (14). In the theoretical analysis part, the stability and convergence of the PGAZNN model (14) are proved with rigorous and detailed mathematical analysis. In the experimental simulation part, this paper verifies the feasibility and superiority of the PGAZNN model for solving time-variant NIE systems (1) through a time-variant example and a practice application; all the experimental results also prove the correctness of the mathematical analysis of the theoretical part. In addition, for the PGAZNN model, comparative experiments about the influence of design parameters on convergence are carried out. With the continuous improvement of the ZNN model, the trends of the next research may focus on the robustness analysis of the ZNN model and the solution of more complex nonlinear systems.