Symmetry-Enhanced Locally Adaptive COA-ELM for Short-Term Load Forecasting
Abstract
1. Introduction
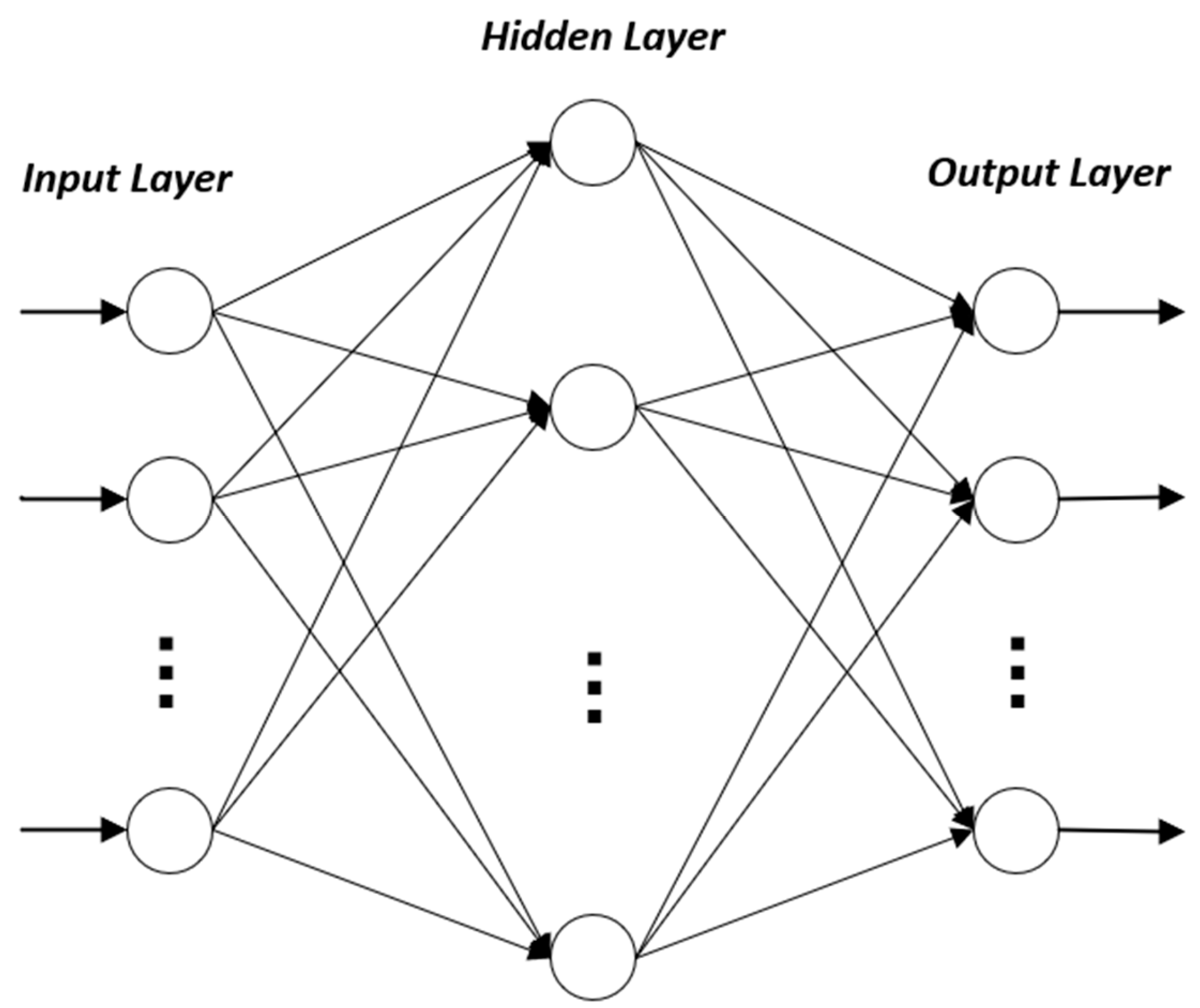
2. The ELM Model
3. Local Adaptive Parameter Adjustment COA
3.1. COA
3.2. Locally Adaptive Parameter Tuning for the COA
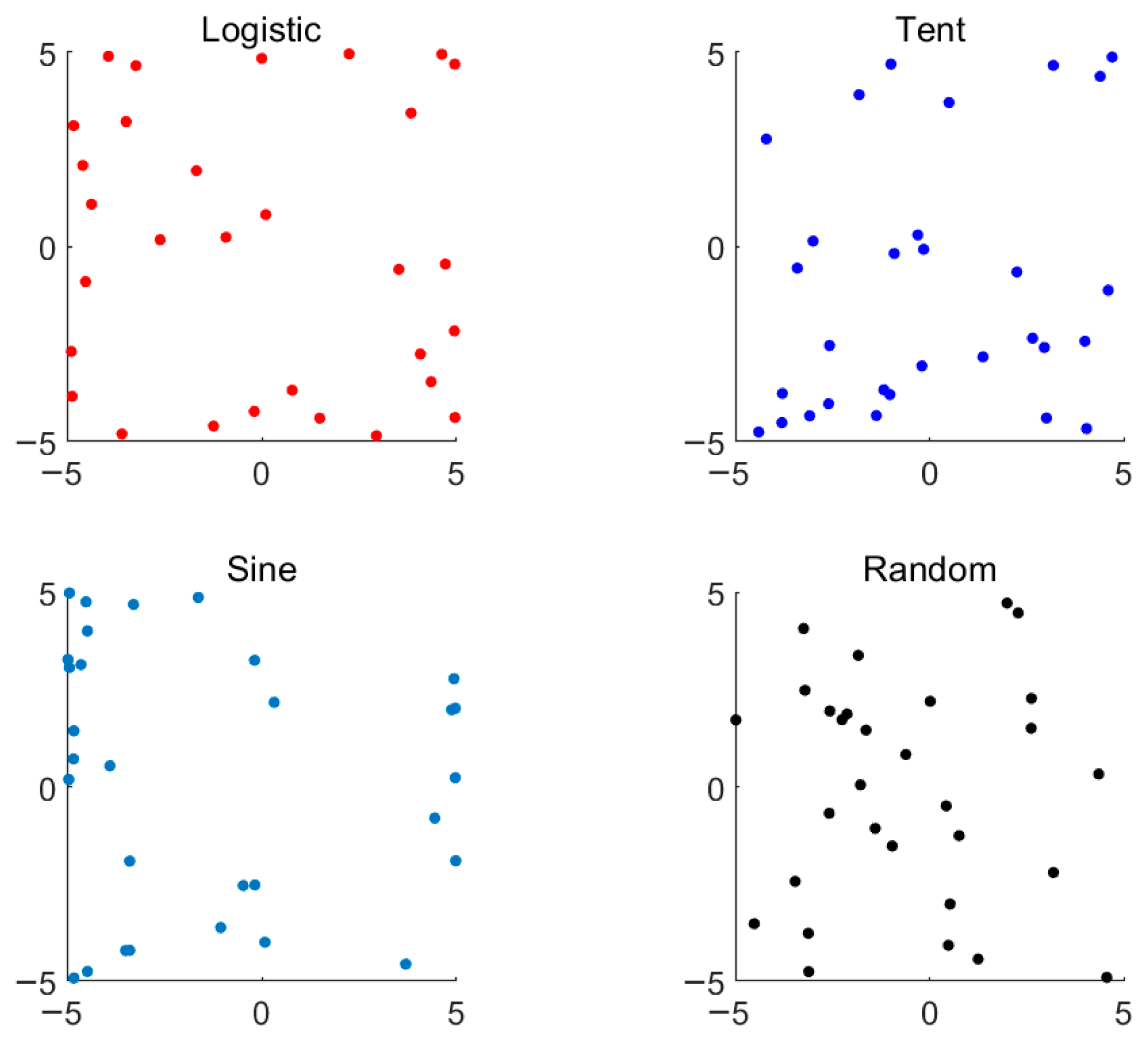
3.2.1. Logistic Chaotic Mapping Strategy
3.2.2. Local Precision Search Strategy
- Step 1: Initialize the best fitness value and the optimal position .
- Step 2: For each iteration i = 1, 2, 3,…, search_nb:
- Generate a candidate solution according to Equation (23).
- Apply boundary conditions to ensure stays within the search space, as shown in Equation (24).
- Calculate the fitness value of the candidate solution according to Equation (25).
- If , then update the best fitness value and the optimal position according to Equations (26) and (27).
- Step 3: Return the best fitness value and the optimal position .
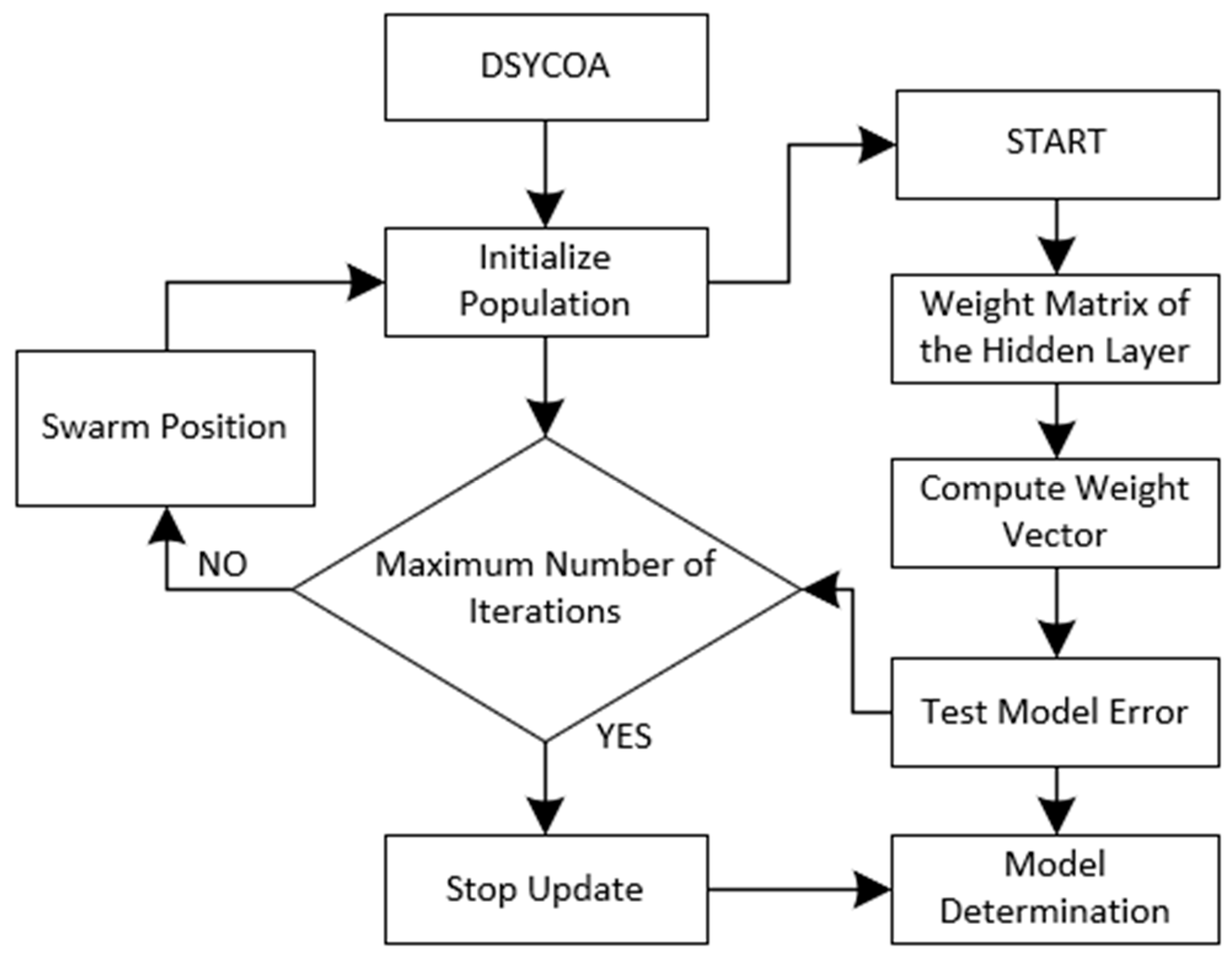
3.2.3. Dynamic Parameter Adjustment Strategies
| Algorithm 1: Pseudocode of DSYCOA |
| Input: N: Population size, MT: Maximum number of iterations, D: Dimension |
| Output: : Optimal solution’s objective function value : Optimal solution’s position |
| Algorithm Description: |
| 1: Initializing the population using Logistic chaotic mapping |
| 2: While t < 1/2MT |
| 3: Defining temperature Temp by Equation (10) |
| 4: If Temp >30 |
| 5: Define cave according to Equation (12) |
| 6: If r < 0.5 |
| 7: Crayfish conducts the summer resort stage by Equation (13) |
| 8: Else |
| 9: Crayfish compete for caves by Equation (14) |
| 10: End |
| 11: Else |
| 12: The food intake and food size F are obtained through Equations (17) and (18) |
| 13: If F > 2 |
| 14: Crayfish shreds food by Equation (19) |
| 15: Crayfish foraging according to Equation (20) |
| 16: Else |
| 17: Crayfish foraging according to Equation (21) |
| 18: End |
| 19: End |
| 20: Update fitness values |
| 21: t = t + 1 |
| 22: End |
| 23: While (t > 1/2MT)&&(t < MT) |
| 24: Repeat steps 3–18 |
| 25: If ( − )/ < search_ts |
| 26: Update search_nb according to Equation (28) |
| 27: Update search_ts according to Equation (29) |
| 28: Generate a candidate solution Equation (23) |
| 29: Ensure that according to Equation (24), the search remains within the search space |
| 30: Update the best fitness value and the best position according to Equations (26) and (27) |
| 31: t = t + 1 |
| 32: Else |
| 33: Update fitness values like step 20 |
| 34: t = t + 1 |
| 35: End |
| 36: End |
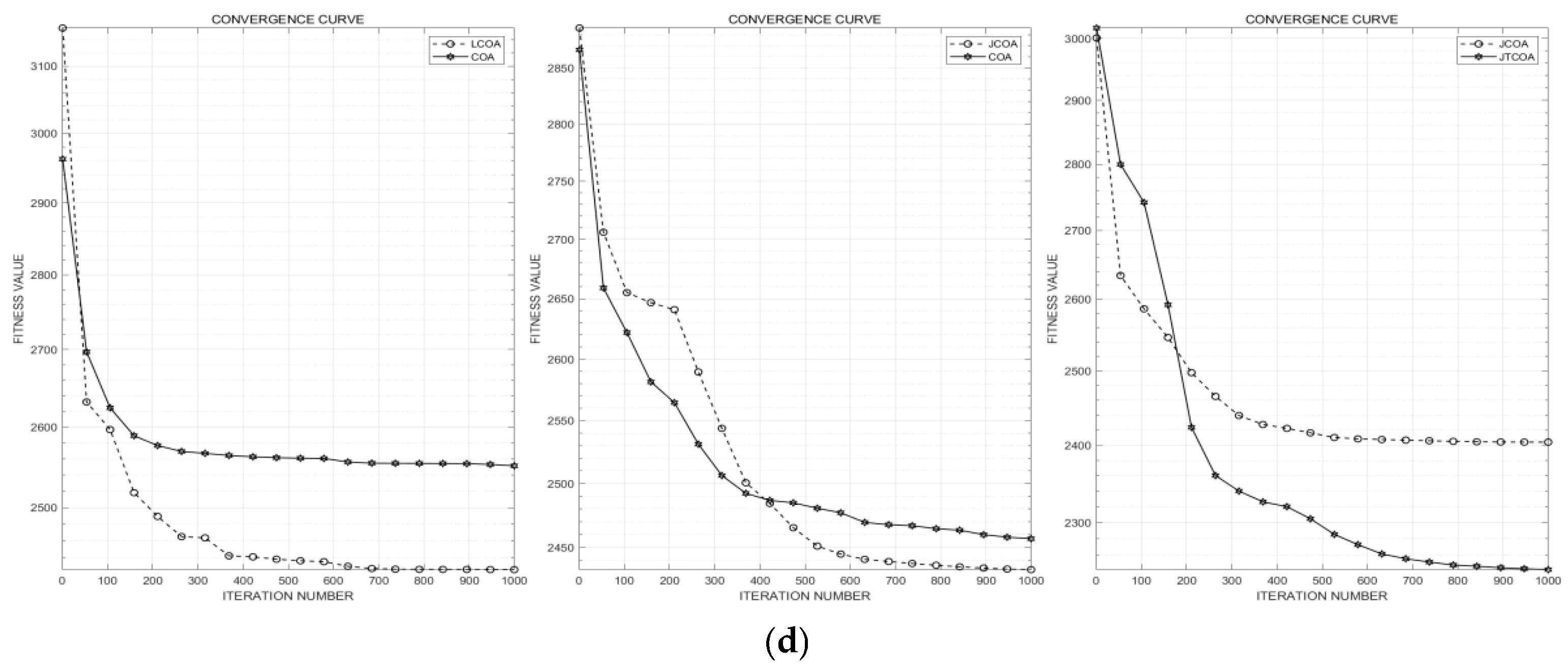
3.3. Performance Validation of the DSYCOA
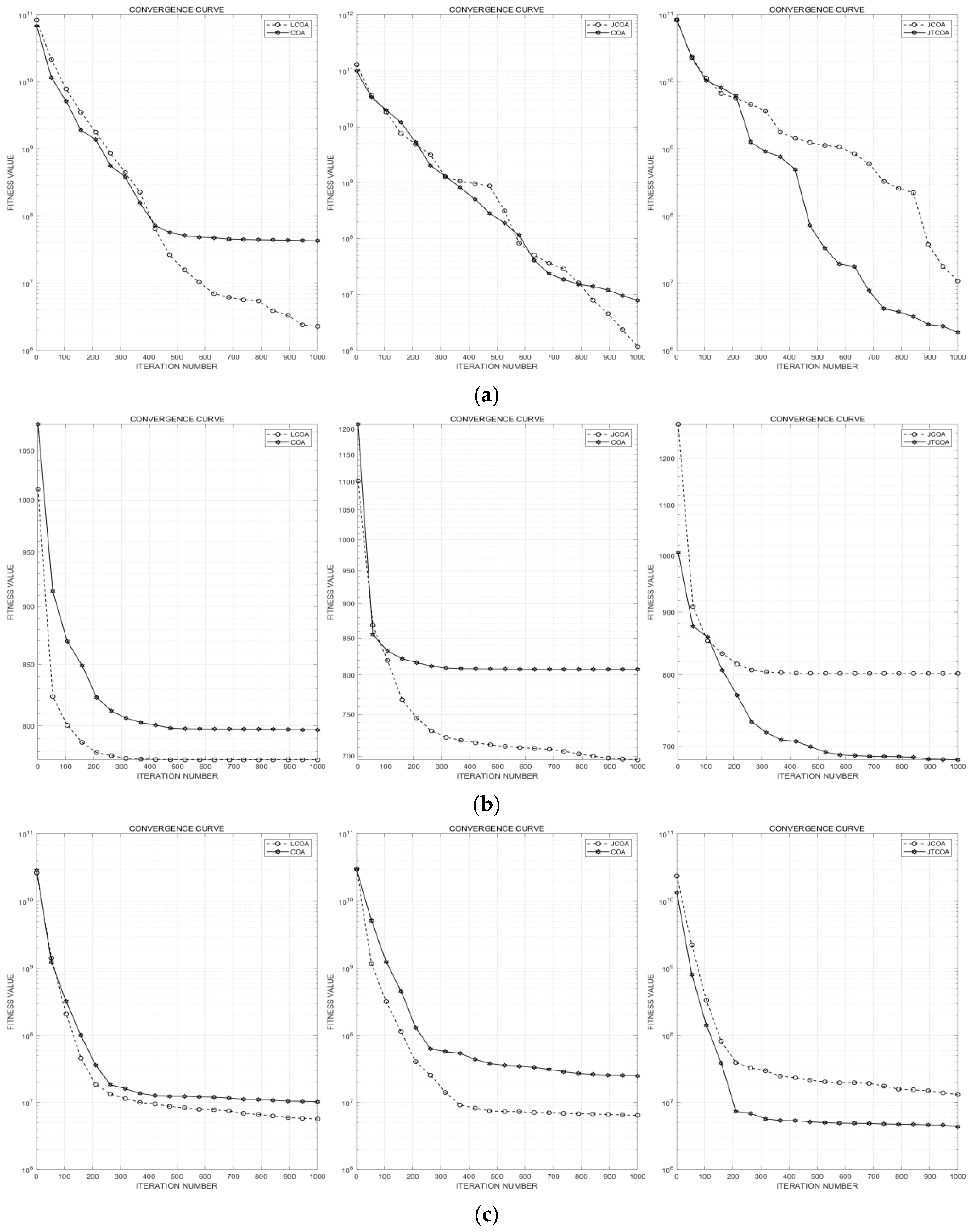
3.3.1. Analysis of the Effectiveness of Introduced Strategies
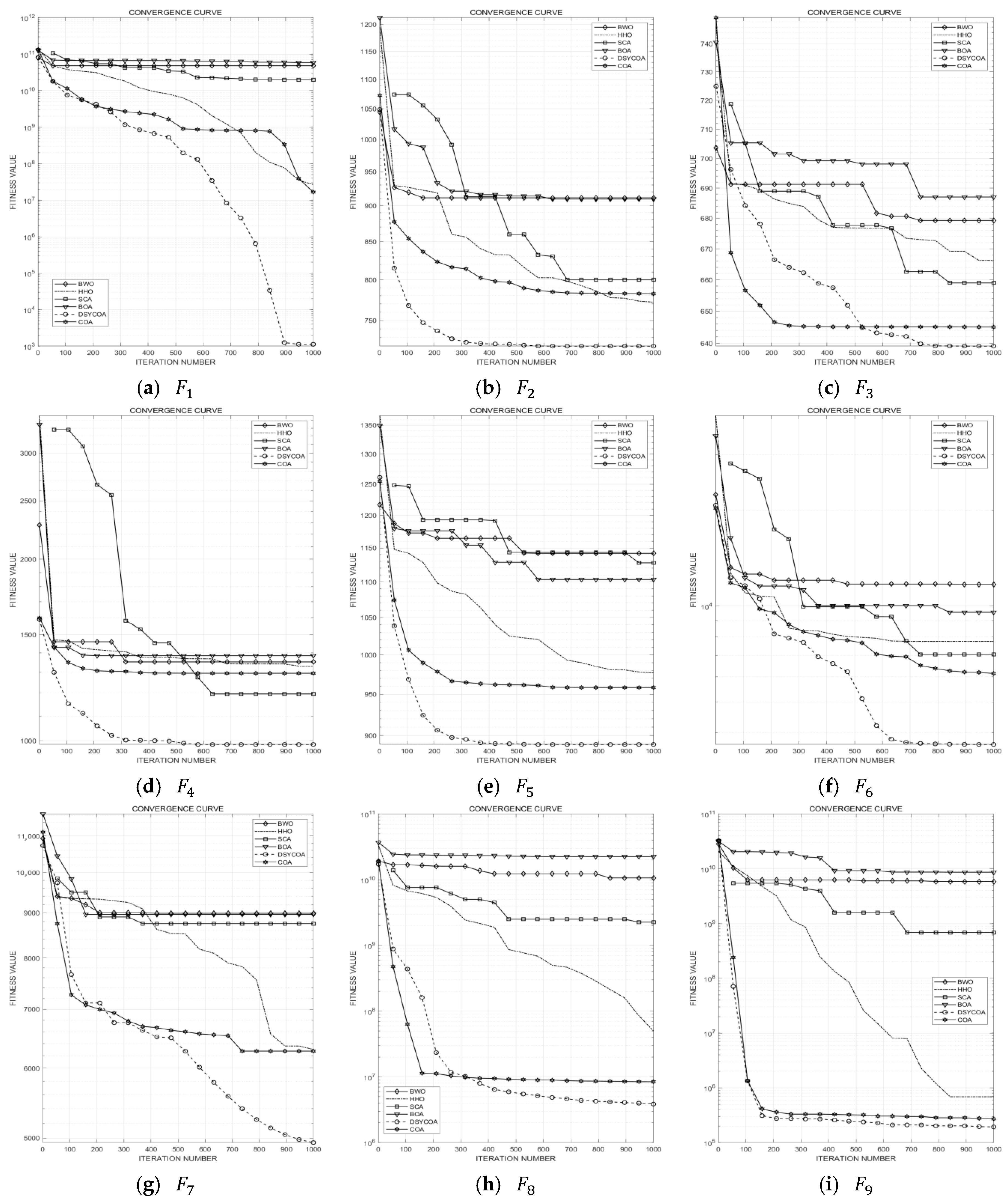
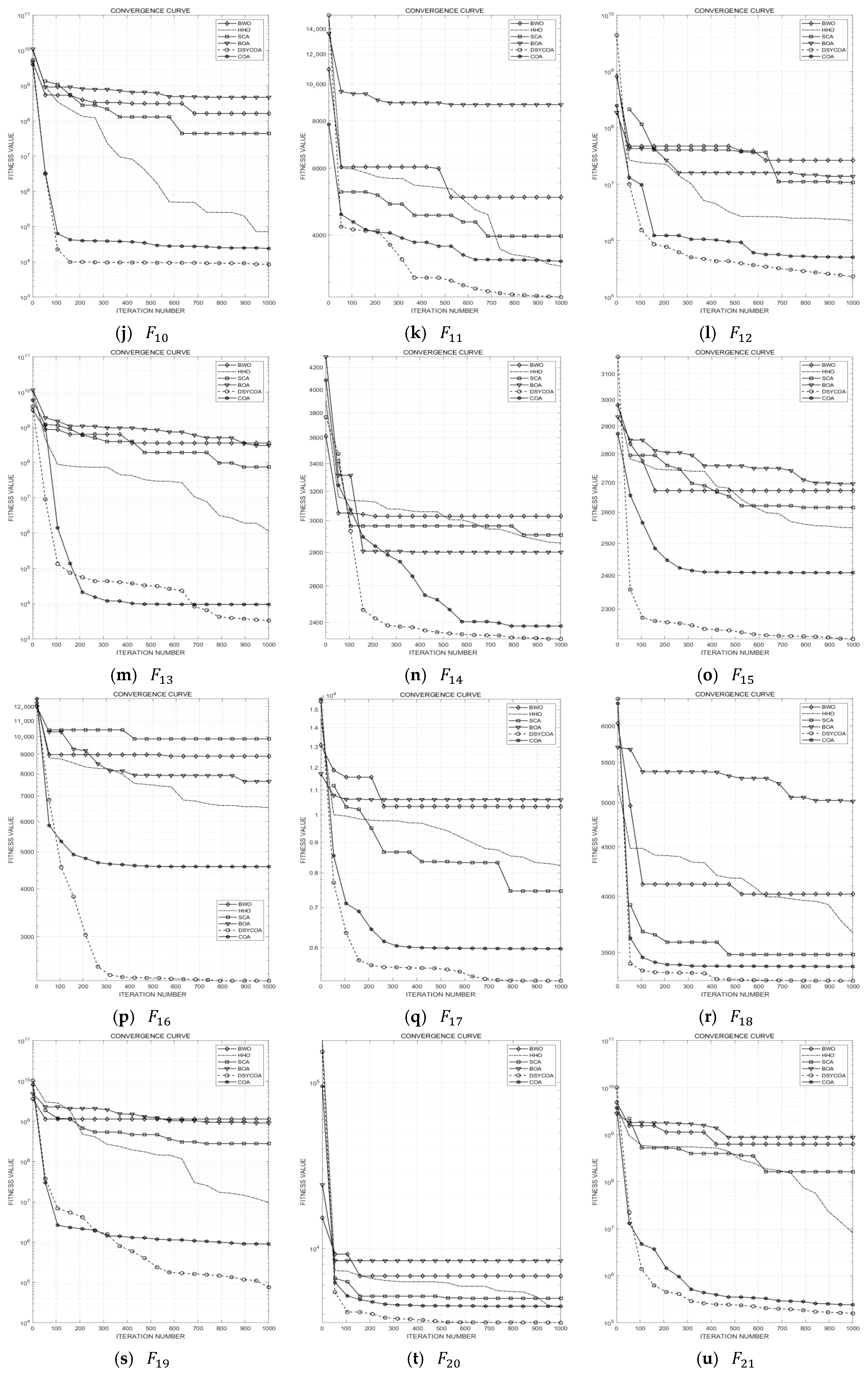
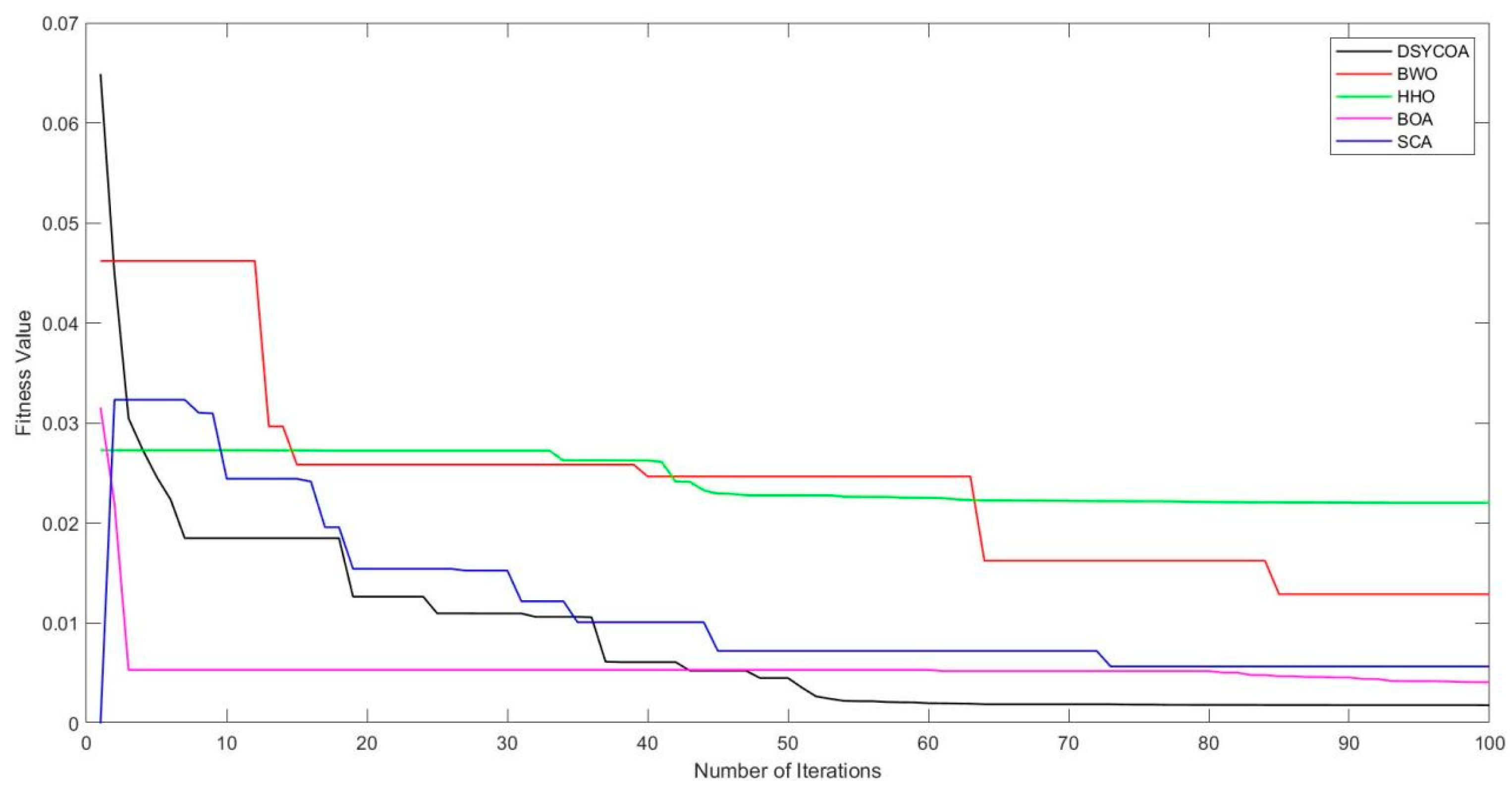
3.3.2. Comparison of DSYCOA with Other Algorithms
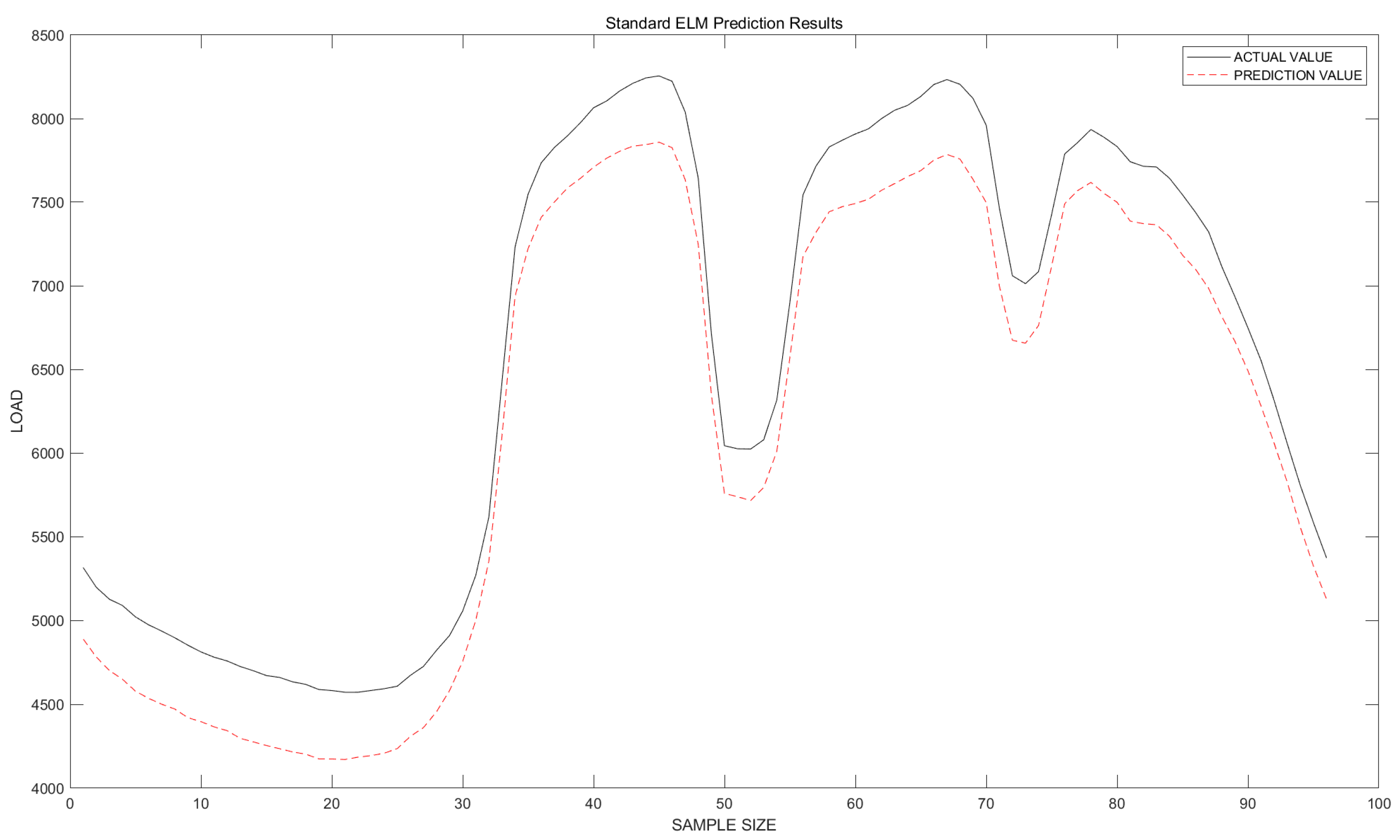
4. Simulation Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ELM | Extreme Learning Machine |
| DSYCOA | Symmetry-Enhanced Locally Adaptive COA |
| MAPE | Mean Absolute Percentage Error |
| MAE | Mean Absolute Error |
| RMSE | Root Mean Squared Error |
| COA | Crayfish Optimization Algorithm |
| SLFNs | Single-Hidden-Layer Feedforward Neural Networks |
| HHO | Harris Hawks Optimization |
| BWO | Black widow optimization algorithm |
| BOA | Butterfly Optimization Algorithm |
| SCA | Sine Cosine Algorithm |
| h_nb | Number of hidden-layer nodes |
| H(x) | Hidden-layer output matrix |
| Input weight vector of the i-th hidden node | |
| Bias of the i-th hidden node | |
| g(·) | Activation function (Sigmoid) |
| β | Output weight vector |
| H | Collective hidden-layer output matrix |
| C | Target output matrix |
| Moore–Penrose inverse of H | |
| M | Number of training samples |
| u | Input feature dimension |
| v | Output target dimension |
| N | Population size |
| D | Search-space dimension |
| ub, lb | Upper/lower bounds of the search space |
| r | Uniform random number in [0, 1] |
| Position vector of the i-th crayfish | |
| Temp | Simulated temperature in COA |
| q | Foraging quantity in COA |
| μ | Optimal temperature parameter |
| σ | Standard-deviation parameter |
| MT | Maximum iterations |
| t | Current iteration counter |
| Cave location | |
| Best solution position | |
| α | Control coefficient |
| m | Random crayfish index |
| Food-source location | |
| f(X)/fitness | Objective/fitness value |
| F | Food size in COA |
| R | Logistic-map parameter |
| Logistic-map initial value | |
| search_nb | Local-search iterations |
| search_ts | Local-search trigger threshold |
| search_nb_initial | Initial value of search_nb |
| ts_de_rate | Threshold decay rate |
| iter_in_rate | Iteration-increase rate |
| step_size | Local-search step size |
| C_X | Candidate solution vector |
| Q | Random perturbation vector |
| the current best fitness value |
References
- Lin, L.; Liu, J.; Huang, N.; Li, S.; Zhang, Y. Multiscale spatio-temporal feature fusion based non-intrusive appliance load monitoring for multiple industrial industries. Appl. Soft Comput. 2024, 167, 112445. [Google Scholar] [CrossRef]
- Jin, M.; Zhou, X.; Zhang, Z.M.; Tentzeris, M.M. Short-term power load forecasting using grey correlation contest modeling. Expert Syst. Appl. 2012, 39, 773–779. [Google Scholar] [CrossRef]
- Contreras, J.; Espinola, R.; Nogales, F.J.; Conejo, A. ARIMA models to predict next-day electricity prices. IEEE Trans. Power Syst. 2003, 18, 1014–1020. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Wu, F.; Cattani, C.; Song, W.; Zio, E. Fractional ARIMA with an improved cuckoo search optimization for the efficient Short-term power load forecasting. Alex. Eng. J. 2020, 59, 3111–3118. [Google Scholar] [CrossRef]
- Yuhong, W.; Jie, L. Improvement and application of GM (1, 1) model based on multivariable dynamic optimization. J. Syst. Eng. Electron. 2020, 31, 593–601. [Google Scholar] [CrossRef]
- Barman, M.; Choudhury, N.B.D. A similarity based hybrid GWO-SVM method of power system load forecasting for regional special event days in anomalous load situations in Assam, India. Sustain. Cities Soc. 2020, 61, 102311. [Google Scholar] [CrossRef]
- Dai, Y.; Zhao, P. A hybrid load forecasting model based on support vector machine with intelligent methods for feature selection and parameter optimization. Appl. Energy 2020, 279, 115332. [Google Scholar] [CrossRef]
- Luo, J.; Hong, T.; Gao, Z.; Fang, S.-C. A robust support vector regression model for electric load forecasting. Int. J. Forecast. 2023, 39, 1005–1020. [Google Scholar] [CrossRef]
- Khwaja, A.S.; Anpalagan, A.; Naeem, M.; Venkatesh, B. Joint bagged-boosted artificial neural networks: Using ensemble machine learning to improve short-term electricity load forecasting. Electr. Power Syst. Res. 2020, 179, 106080. [Google Scholar] [CrossRef]
- El Ouadi, J.; Malhene, N.; Benhadou, S.; Medromi, H. Towards a machine-learning based approach for splitting cities in freight logistics context: Benchmarks of clustering and prediction models. Comput. Ind. Eng. 2022, 166, 107975. [Google Scholar] [CrossRef]
- Fan, G.-F.; Zhang, L.-Z.; Yu, M.; Hong, W.-C.; Dong, S.-Q. Applications of random forest in multivariable response surface for short-term load forecasting. Int. J. Electr. Power Energy Syst. 2022, 139, 108073. [Google Scholar] [CrossRef]
- Yazici, I.; Beyca, O.F.; Delen, D. Deep-learning-based short-term electricity load forecasting: A real case application. Eng. Appl. Artif. Intell. 2022, 109, 104645. [Google Scholar] [CrossRef]
- Li, K.; Huang, W.; Hu, G.; Li, J. Ultra-short term power load forecasting based on CEEMDAN-SE and LSTM neural network. Energy Build. 2023, 279, 112666. [Google Scholar] [CrossRef]
- Mounir, N.; Ouadi, H.; Jrhilifa, I. Short-term electric load forecasting using an EMD-BI-LSTM approach for smart grid energy management system. Energy Build. 2023, 288, 113022. [Google Scholar] [CrossRef]
- Lin, J.; Ma, J.; Zhu, J.; Cui, Y. Short-term load forecasting based on LSTM networks considering attention mechanism. Int. J. Electr. Power Energy Syst. 2022, 137, 107818. [Google Scholar] [CrossRef]
- Singh, S.N.; Mohapatra, A. Data driven day-ahead electrical load forecasting through repeated wavelet transform assisted SVM model. Appl. Soft Comput. 2021, 111, 107730. [Google Scholar] [CrossRef]
- Yuqi, J.; An, A.; Lu, Z.; Ping, H.; Xiaomei, L. Short-term load forecasting based on temporal importance analysis and feature extraction. Electr. Power Syst. Res. 2025, 244, 111551. [Google Scholar] [CrossRef]
- Nie, Y.; Jiang, P.; Zhang, H. A novel hybrid model based on combined preprocessing method and advanced optimization algorithm for power load forecasting. Appl. Soft Comput. 2020, 97, 106809. [Google Scholar] [CrossRef]
- Zou, H.; Yang, Q.; Chen, J.; Chai, Y. Short-term power load forecasting based on phase space reconstruction and EMD-ELM. J. Electr. Eng. Technol. 2023, 18, 3349–3359. [Google Scholar] [CrossRef]
- Wang, J.; Niu, X.; Zhang, L.; Liu, Z.; Huang, X. A wind speed forecasting system for the construction of a smart grid with two-stage data processing based on improved ELM and deep learning strategies. Expert Syst. Appl. 2024, 241, 122487. [Google Scholar] [CrossRef]
- Loizidis, S.; Kyprianou, A.; Georghiou, G.E. Electricity market price forecasting using ELM and Bootstrap analysis: A case study of the German and Finnish Day-Ahead markets. Appl. Energy 2024, 363, 123058. [Google Scholar] [CrossRef]
- Wu, C.; Li, J.; Liu, W.; He, Y.; Nourmohammadi, S. Short-term electricity demand forecasting using a hybrid ANFIS–ELM network optimised by an improved parasitism–predation algorithm. Appl. Energy 2023, 345, 121316. [Google Scholar] [CrossRef]
- Rayi, V.K.; Mishra, S.P.; Naik, J.; Dash, P. Adaptive VMD based optimized deep learning mixed kernel ELM autoencoder for single and multistep wind power forecasting. Energy 2022, 244, 122585. [Google Scholar] [CrossRef]
- Li, C.; Zhou, J.; Tao, M.; Du, K.; Wang, S.; Armaghani, D.J.; Mohamad, E.T. Developing hybrid ELM-ALO, ELM-LSO and ELM-SOA models for predicting advance rate of TBM. Transp. Geotech. 2022, 36, 100819. [Google Scholar] [CrossRef]
- Ma, R.; Karimzadeh, M.; Ghabussi, A.; Zandi, Y.; Baharom, S.; Selmi, A.; Maureira-Carsalade, N. Assessment of composite beam performance using GWO–ELM metaheuristic algorithm. Eng. Comput. 2021, 38, 2083–2099. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Y.; Zhang, F.; Li, W.; Lv, S.; Jiang, M.; Jia, L. Accuracy-improved bearing fault diagnosis method based on AVMD theory and AWPSO-ELM model. Measurement 2021, 181, 109666. [Google Scholar] [CrossRef]
- Shariati, M.; Mafipour, M.S.; Ghahremani, B.; Azarhomayun, F.; Ahmadi, M.; Trung, N.T.; Shariati, A. A novel hybrid extreme learning machine–grey wolf optimizer (ELM-GWO) model to predict compressive strength of concrete with partial replacements for cement. Eng. Comput. 2022, 38, 757–779. [Google Scholar] [CrossRef]
- Ikram, R.M.A.; Dai, H.-L.; Chargari, M.M.; Al-Bahrani, M.; Mamlooki, M. Prediction of the FRP reinforced concrete beam shear capacity by using ELM-CRFOA. Measurement 2022, 205, 112230. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Hayyolalam, V.; Kazem, A.A.P. Black widow optimization algorithm: A novel meta-heuristic approach for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2020, 87, 103249. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. Butterfly optimization algorithm: A novel approach for global optimization. Soft Comput. 2019, 23, 715–734. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
| Type | No. | Description | |
|---|---|---|---|
| Unimodal functions | 1 | Shifted and Roatated Bent Cigar Function | 100 |
| Simple Multimodal functions | 2 | Shifted and Rotated Rastrigin’s Function | 500 |
| 3 | Shifted and Rotated Expanded Scaffer’s F6 Function | 600 | |
| 4 | Shifted and Rotated Lunacek Bi-Rastrigin Function | 700 | |
| 5 | Shifted and Rotated Non-Continuous Rastrigin’s Function | 800 | |
| 6 | Shifted and Rotated Levy Function | 900 | |
| 7 | Shifted and Rotated Schwefel’s Function | 1000 | |
| Hybrid functions | 8 | Hybrid Function 2 (N = 3) | 1200 |
| 9 | Hybrid Function 3 (N = 3) | 1300 | |
| 10 | Hybrid Function 5 (N = 4) | 1500 | |
| 11 | Hybrid Function 6 (N = 4) | 1600 | |
| 12 | Hybrid Function 6 (N = 5) | 1800 | |
| 13 | Hybrid Function 6 (N = 5) | 1900 | |
| 14 | Hybrid Function 6 (N = 6) | 2000 | |
| Composition Functions | 15 | Composition Function 1 (N = 3) | 2100 |
| 16 | Composition Function 2 (N = 3) | 2200 | |
| 17 | Composition Function 6 (N = 5) | 2600 | |
| 18 | Composition Function 7 (N = 6) | 2700 | |
| 19 | Composition Function 8 (N = 6) | 2800 | |
| 20 | Composition Function 9 (N = 3) | 2900 | |
| 21 | Composition Function 10 (N = 3) | 3000 |
| Function | Metric | COA | LCOA | JCOA | JTCOA |
|---|---|---|---|---|---|
| σ | 7.985 × 108 | 4.408 × 108 | 5.283 × 108 | 3.917 × 108 | |
| Mean | 5.014 × 108 | 3.084 × 108 | 4.816 × 108 | 3.396 × 108 | |
| σ | 5.552 × 101 | 5.184 × 101 | 4.346 × 101 | 5.006 × 100 | |
| Mean | 7.661 × 102 | 7.562 × 102 | 7.576 × 102 | 7.510 × 102 | |
| σ | 1.508 × 107 | 1.204 × 107 | 1.124 × 107 | 8.834 × 106 | |
| Mean | 1.754 × 107 | 1.252 × 107 | 1.449 × 107 | 8.830 × 106 | |
| σ | 7.343 × 101 | 4.769 × 101 | 4.597 × 101 | 4.076 × 101 | |
| Mean | 2.478 × 103 | 2.467 × 103 | 2.470 × 103 | 2.469 × 103 |
| Function | Metric | DSYCOA | COA | HHO | BOA | BWO | SCA |
|---|---|---|---|---|---|---|---|
| σ | 6.719 × 105 | 3.663 × 108 | 8.459 × 106 | 7.884 × 109 | 3.654 × 109 | 2.969 × 109 | |
| Mean | 2.028 × 105 | 1.291 × 108 | 3.004 × 107 | 5.244 × 1010 | 5.173 × 1010 | 1.767 × 1010 | |
| σ | 1.782 × 101 | 6.143 × 101 | 3.113 × 101 | 3.049 × 101 | 6.664 × 101 | 2.722 × 101 | |
| Mean | 7.427 × 102 | 7.497 × 102 | 7.523 × 102 | 9.208 × 102 | 9.192 × 102 | 8.211 × 102 | |
| σ | 1.396 × 101 | 1.458 × 101 | 6.549 × 100 | 5.566 × 100 | 4.743 × 100 | 7.081 × 100 | |
| Mean | 6.445 × 102 | 6.503 × 102 | 6.642 × 102 | 6.886 × 102 | 6.894 × 102 | 6.617 × 102 | |
| σ | 1.155 × 102 | 1.407 × 102 | 6.736 × 101 | 3.649 × 101 | 2.799 × 101 | 4.487 × 101 | |
| Mean | 1.200 × 103 | 1.210 × 103 | 1.283 × 103 | 1.402 × 103 | 1.392 × 103 | 1.209 × 103 | |
| σ | 1.743 × 101 | 2.815 × 101 | 2.907 × 101 | 1.975 × 101 | 2.872 × 101 | 2.152 × 101 | |
| Mean | 9.745 × 102 | 9.798 × 102 | 9.750 × 102 | 1.136 × 103 | 1.139 × 103 | 1.085 × 103 | |
| σ | 8.065 × 102 | 1.190 × 103 | 7.498 × 102 | 1.303 × 103 | 8.892 × 102 | 1.255 × 103 | |
| Mean | 4.553 × 103 | 6.621 × 103 | 8.318 × 103 | 1.101 × 104 | 1.115 × 104 | 7.367 × 103 | |
| σ | 2.687 × 102 | 9.920 × 102 | 6.927 × 102 | 3.045 × 102 | 4.117 × 102 | 6.017 × 102 | |
| Mean | 5.289 × 103 | 6.003 × 103 | 5.963 × 103 | 9.052 × 103 | 8.641 × 103 | 8.783 × 103 | |
| σ | 4.487 × 106 | 7.785 × 106 | 2.666 × 107 | 1.373 × 1010 | 1.012 × 1010 | 2.064 × 109 | |
| Mean | 8.271 × 104 | 9.300 × 104 | 2.748 × 105 | 5.762 × 109 | 1.776 × 109 | 5.015 × 108 | |
| σ | 1.320 × 105 | 1.415 × 105 | 6.633 × 105 | 1.058 × 1010 | 6.002 × 109 | 8.888 × 108 | |
| Mean | 1.251 × 104 | 1.906 × 104 | 4.831 × 104 | 5.165 × 108 | 1.247 × 108 | 3.334 × 107 | |
| σ | 1.429 × 104 | 2.145 × 104 | 8.350 × 104 | 6.255 × 108 | 2.406 × 108 | 3.353 × 107 | |
| Mean | 2.218 × 102 | 3.711 × 102 | 4.384 × 102 | 1.667 × 103 | 3.627 × 102 | 4.318 × 102 | |
| σ | 2.849 × 103 | 2.914 × 103 | 3.473 × 103 | 7.657 × 103 | 5.441 × 103 | 3.902 × 103 | |
| Mean | 1.132 × 106 | 3.624 × 106 | 4.566 × 106 | 5.211 × 107 | 2.032 × 107 | 6.360 × 106 | |
| σ | 9.135 × 105 | 2.296 × 106 | 2.800 × 106 | 4.847 × 107 | 3.724 × 107 | 1.055 × 107 | |
| Mean | 4.102 × 103 | 1.238 × 104 | 7.185 × 105 | 5.000 × 108 | 1.859 × 108 | 2.755 × 107 | |
| σ | 6.872 × 103 | 1.175 × 104 | 9.941 × 105 | 6.724 × 108 | 3.667 × 108 | 6.295 × 107 | |
| Mean | 1.181 × 102 | 2.081 × 102 | 2.212 × 102 | 1.491 × 102 | 1.816 × 102 | 1.591 × 102 | |
| σ | 2.543 × 103 | 2.642 × 103 | 2.804 × 103 | 3.030 × 103 | 2.989 × 103 | 2.859 × 103 | |
| Mean | 2.327 × 101 | 4.787 × 101 | 6.462 × 101 | 9.012 × 101 | 5.628 × 101 | 7.765 × 101 | |
| σ | 2.450 × 103 | 2.467 × 103 | 2.585 × 103 | 2.677 × 103 | 2.706 × 103 | 2.592 × 103 | |
| Mean | 1.395 × 103 | 2.301 × 103 | 1.701 × 103 | 2.292 × 103 | 6.606 × 102 | 2.293 × 103 | |
| σ | 4.030 × 103 | 3.815 × 103 | 7.029 × 103 | 6.821 × 103 | 8.458 × 103 | 9.046 × 103 | |
| Mean | 3.531 × 102 | 1.738 × 103 | 7.418 × 102 | 6.935 × 102 | 5.917 × 102 | 1.456 × 103 | |
| σ | 5.909 × 103 | 6.566 × 103 | 7.886 × 103 | 1.190 × 104 | 1.053 × 104 | 7.575 × 103 | |
| Mean | 3.929 × 101 | 5.142 × 101 | 1.945 × 102 | 3.325 × 102 | 1.277 × 102 | 6.391 × 101 | |
| σ | 3.275 × 103 | 3.286 × 103 | 3.529 × 103 | 4.234 × 103 | 3.968 × 103 | 3.514 × 103 | |
| Mean | 2.861 × 101 | 4.950 × 101 | 3.600 × 101 | 5.667 × 102 | 3.867 × 102 | 3.229 × 102 | |
| σ | 2.023 × 102 | 2.322 × 102 | 5.337 × 102 | 5.137 × 103 | 6.573 × 102 | 2.836 × 102 | |
| Mean | 4.090 × 103 | 4.110 × 103 | 4.721 × 103 | 1.203 × 104 | 6.926 × 103 | 5.121 × 103 | |
| σ | 1.887 × 105 | 2.973 × 105 | 3.029 × 106 | 1.138 × 109 | 4.077 × 108 | 6.423 × 107 | |
| Mean | 2.290 × 105 | 3.055 × 105 | 5.032 × 106 | 1.425 × 109 | 1.013 × 109 | 1.798 × 108 | |
| σ | 1.396 × 101 | 1.291 × 108 | 8.459 × 106 | 7.884 × 109 | 3.654 × 109 | 2.969 × 109 | |
| Mean | 6.143 × 102 | 6.445 × 102 | 3.004 × 107 | 5.244 × 1010 | 5.173 × 1010 | 1.767 × 1010 |
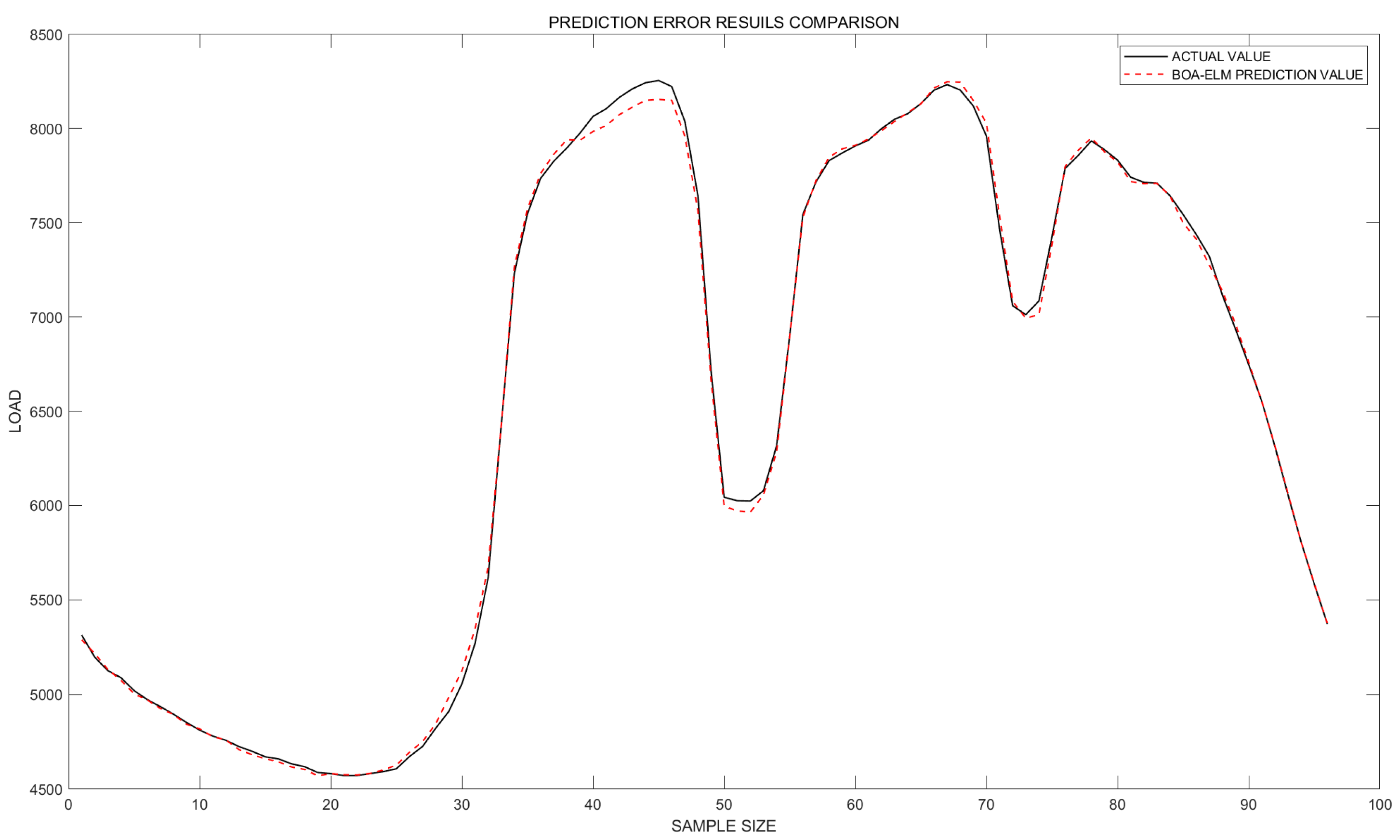
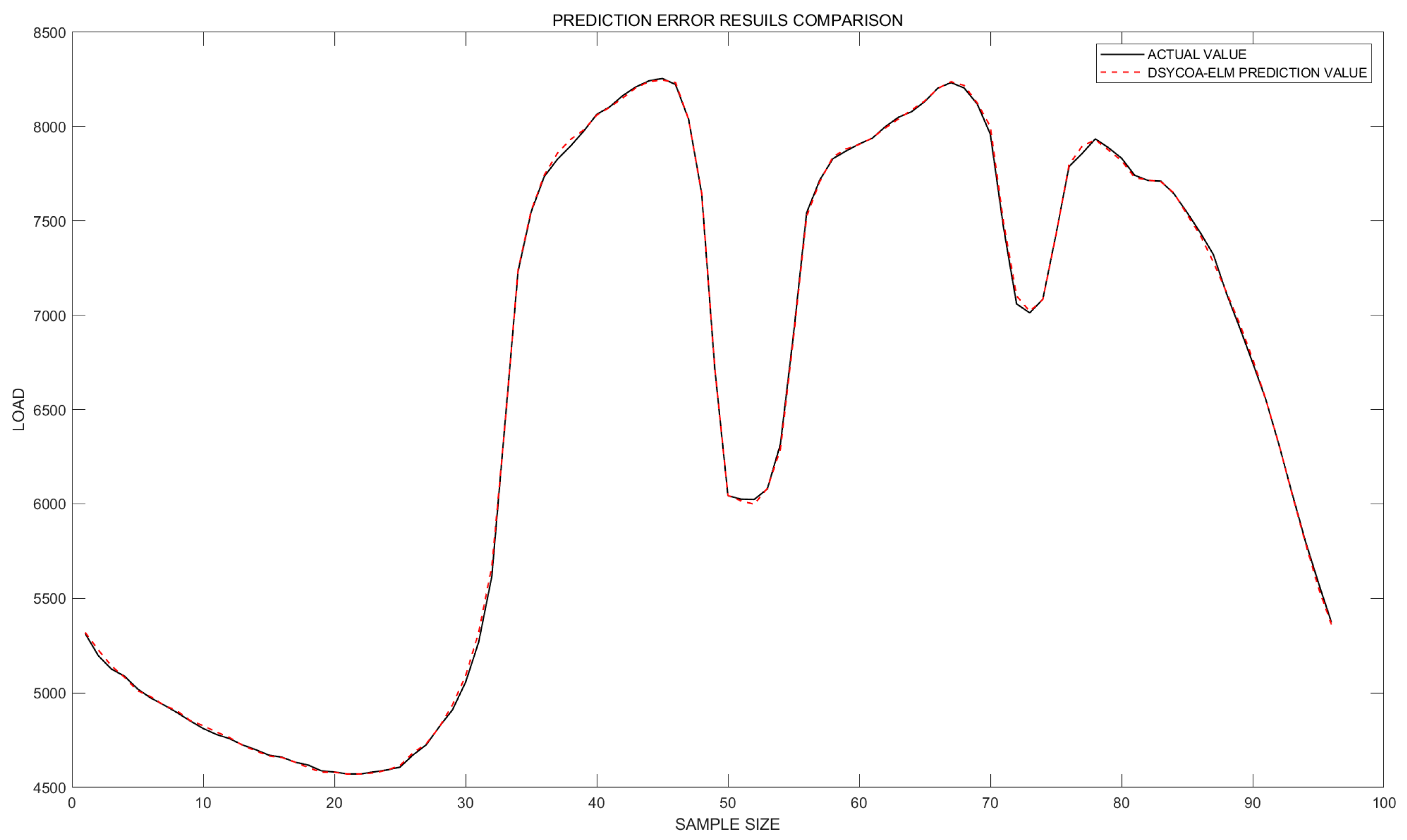
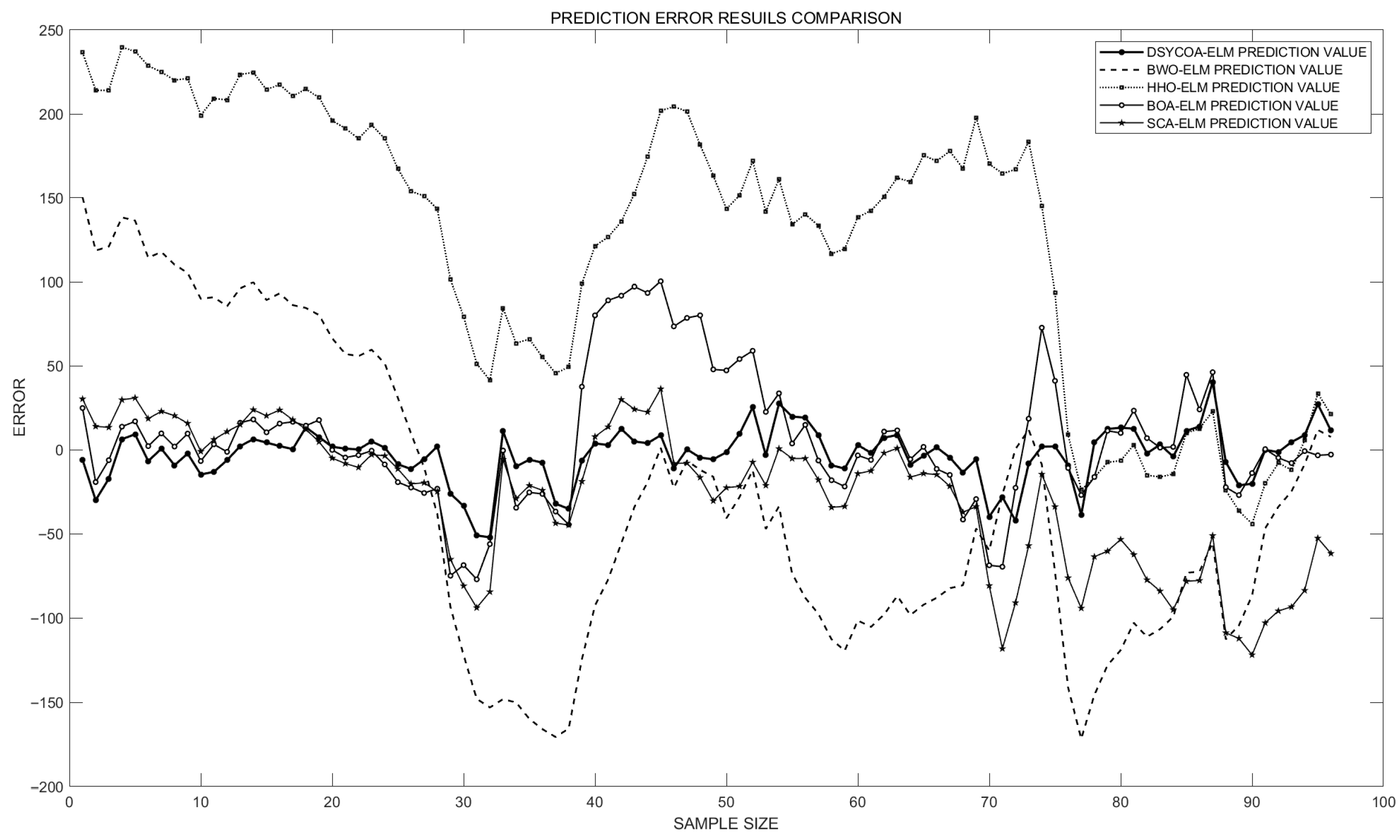
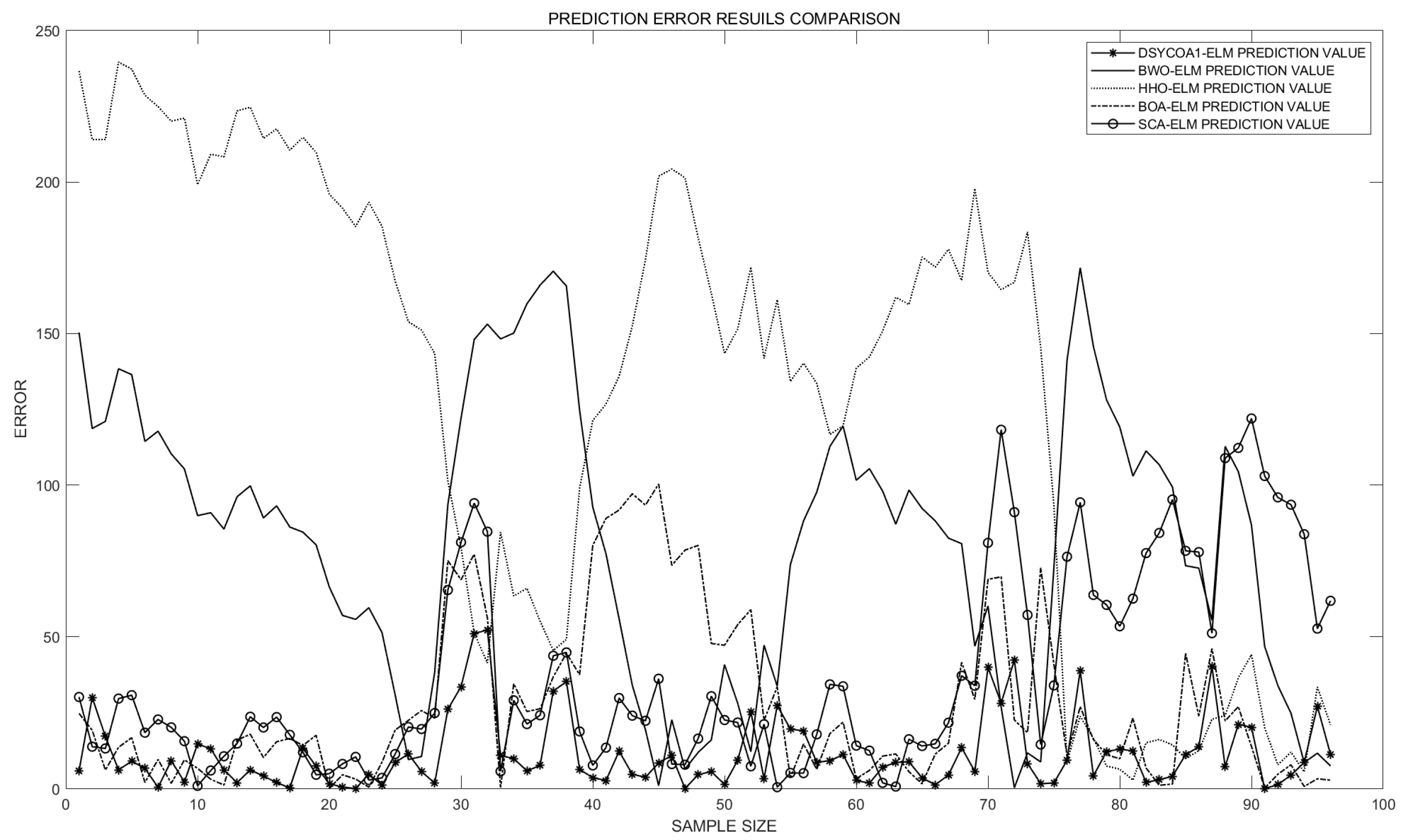
| Model | MAPE | MAE | RMSE | Rank | |
|---|---|---|---|---|---|
| ELM | 5.88% | 365.5229 | 370.554 | 0.99805 | 6 |
| DSYCOA-ELM | 0.18163% | 11.5356 | 16.4488 | 0.99986 | 1 |
| BWO-ELM | 1.2912% | 81.3237 | 93.4432 | 0.99825 | 4 |
| HHO-ELM | 2.2043% | 129.9936 | 150.1341 | 0.99703 | 5 |
| BOA-ELM | 0.41188% | 27.7587 | 38.7065 | 0.99925 | 2 |
| SCA-ELM | 0.56884% | 37.3977 | 49.5867 | 0.99919 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, S.; Sun, Z.; Sun, Z. Symmetry-Enhanced Locally Adaptive COA-ELM for Short-Term Load Forecasting. Symmetry 2025, 17, 1335. https://doi.org/10.3390/sym17081335
Dai S, Sun Z, Sun Z. Symmetry-Enhanced Locally Adaptive COA-ELM for Short-Term Load Forecasting. Symmetry. 2025; 17(8):1335. https://doi.org/10.3390/sym17081335
Chicago/Turabian StyleDai, Shiyu, Zhe Sun, and Zhixin Sun. 2025. "Symmetry-Enhanced Locally Adaptive COA-ELM for Short-Term Load Forecasting" Symmetry 17, no. 8: 1335. https://doi.org/10.3390/sym17081335
APA StyleDai, S., Sun, Z., & Sun, Z. (2025). Symmetry-Enhanced Locally Adaptive COA-ELM for Short-Term Load Forecasting. Symmetry, 17(8), 1335. https://doi.org/10.3390/sym17081335






