Abstract
The use of UAVs for logistics delivery has become a hot topic in current research, and how to plan a reasonable delivery route is the key to the problem. Therefore, this paper proposes a multi-environment logistics delivery route planning model that is based on UAVs, is characterized by a 3D environment model, and aims at the shortest delivery route with minimum flight undulation. In order to find the optimal route in various environments, a multi-strategy improved artificial lemming algorithm, which integrates the Cubic chaotic map initialization, double adaptive t-distribution perturbation, and population dynamic optimization, is proposed. The symmetric nature of the t-distribution ensures that the lemmings conduct extensive searches in both directions within the solution space, thus improving the convergence speed and preventing them from falling into local optimal solutions. Through data experiments and simulation analysis, the improved algorithm can be successfully applied to the 3D route planning model, and the route quality is superior.
1. Introduction
With the booming global economy and e-commerce, the logistics industry grapples with skyrocketing delivery demands [1]. Moreover, constrained by traffic congestion and high operating costs, traditional delivery methods struggle to keep pace with this escalating need. Against this backdrop, UAVs, with their unique advantages, have brought new solutions to the field of logistics delivery, as shown in Figure 1 [2]. One of the most significant advantages of UAVs is their ability to bypass traffic completely, which allows them to reach remote or congested areas with remarkable speed, slashing delivery times significantly [3]. By eliminating the need for human drivers and reducing reliance on ground vehicles, UAVs also help cut down on labor and vehicle expenses. Additionally, their precise point-to-point navigation systems ensure high delivery accuracy and enhance overall safety. Therefore, to give full play to the role of UAVs in logistics and delivery, route planning is crucial.

Figure 1.
Delivery via UAVs.
The problem of route planning for UAV logistics delivery is essentially a three-dimensional route planning problem. Currently, the mainstream solutions are mainly divided into two categories: traditional algorithms and swarm intelligence algorithms. Traditional algorithms mainly include the A* algorithm [4], the rapidly exploring random tree (RRT) algorithm [5], the artificial potential field (APF) method [6], etc. Although the implementation principles are relatively simple and easy to understand compared with two-dimensional space, the number of scalable nodes in three-dimensional space increases significantly. Traditional algorithms are faced with problems, such as a sharp increase in computational complexity, a larger consumption of system resources, and an excessively long solution time [7]. Especially in an environment with dense obstacles, the complex and changeable path selection further exacerbates the difficulty of applying traditional algorithms. In contrast, swarm intelligence algorithms, such as the particle swarm optimization (PSO) algorithm [8], the gray wolf optimizer (GWO) algorithm [9], the whale optimization algorithm (WOA) [10], the red-billed blue magpie optimizer (EBMO) algorithm [11], etc., have demonstrated unique advantages in handling such complex optimization problems. These algorithms can not only effectively deal with the challenge of a large number of nodes in the three-dimensional space, but they can also quickly converge to a better solution through information sharing and collaboration within the swarm, significantly improving the efficiency and accuracy of route planning. In addition, swarm intelligence algorithms have strong robustness and adaptability, and they can maintain good performance under different environmental conditions, which enhances the generalization ability of UAVs to perform delivery tasks in various environments.
Among swarm intelligence algorithms, the PSO algorithm has received extensive attention from scholars due to its simple structure and fast convergence speed. In order to address the deficiencies of the algorithm, such as its tendency to converge prematurely and become trapped in local optima, various strategies have been used in existing research to improve the PSO algorithm. For example, Yu et al. [12] used the simulated annealing algorithm to improve the update strategy of the global optimal solution in the PSO algorithm, forming a hybrid particle swarm optimization algorithm that integrates the simulated annealing algorithm and the dimensional learning strategy. This algorithm can plan higher-quality paths for UAVs in complex 3D environments. Liu et al. [13] proposed a novel particle swarm optimization based on the theory of random geometric graphs (RGG-PSO) and the divide-and-conquer idea, dynamically selecting the number of path nodes of the trajectory and, thus, balancing the search efficiency of the algorithm and the quality of the generated path. In addition, some emerging swarm intelligence algorithms are gradually emerging in the field of UAV route planning. For example, Liang et al. [14] proposed an improved lemur optimization algorithm (ILO). This algorithm combines the advantages of multiple algorithms and enhances its global exploration and local exploitation capabilities through some new strategies, and it has been successfully applied to generating UAV flight paths in mountainous environments. Shen et al. [15] designed a multi-strategy enhanced dung beetle optimizer (MDBO) for UAV 3D path planning. The performance of MDBO was verified in the simulation environment of an oil and gas plant, and it can better find safe and optimal paths in most cases.
However, existing research usually only conducts route planning for a single environment and fails to demonstrate its applicability in multiple environments. Moreover, when establishing the simulation environment, most of the research is constructed based on the grid method. The limitations of candidate points lead to paths that are not smooth enough and cannot reflect the actual flight situation. Therefore, the contributions of this paper are as follows:
- (1)
- A multi-environment UAV logistics delivery route planning model was constructed. This model is capable of simulating the logistics delivery environments in mountainous and urban areas.
- (2)
- In an urban environment, the environment is only rasterized in a two-dimensional space and the restriction that candidate points can only be at the grid centers is removed, allowing the UAV to select route points more freely and, thus, conforming it to the actual delivery environments.
- (3)
- Aiming at the problem that the artificial lemming algorithm (ALA) is prone to falling into local optimal solutions, three improvement strategies were applied to the original ALA algorithm, thus forming a new multi-strategy improved artificial lemming algorithm (MsIALA).
- (4)
- The improved algorithm was perfectly integrated with the proposed model, demonstrating the effectiveness and high efficiency of the algorithm and providing a certain reference for the 3D route planning of UAV logistics delivery.
The rest of this paper is structured as follows. In Section 2, the construction of a 3D route planning model constructed for multi-environment UAV logistics delivery is shown. In Section 3, in order to solve this model, the original ALA algorithm is shown to be improved to enhance its convergence speed and its ability to escape from local optimal solutions, and the effectiveness of the improved algorithm is verified. In Section 4, the new MsIALA algorithm is shown to be applied to the model proposed in Section 2, and its effectiveness is demonstrated from multiple aspects. Section 5 summarizes the research of this paper and makes some prospects.
2. Multi-Environment Logistics Delivery Route Planning Model Based on UAV
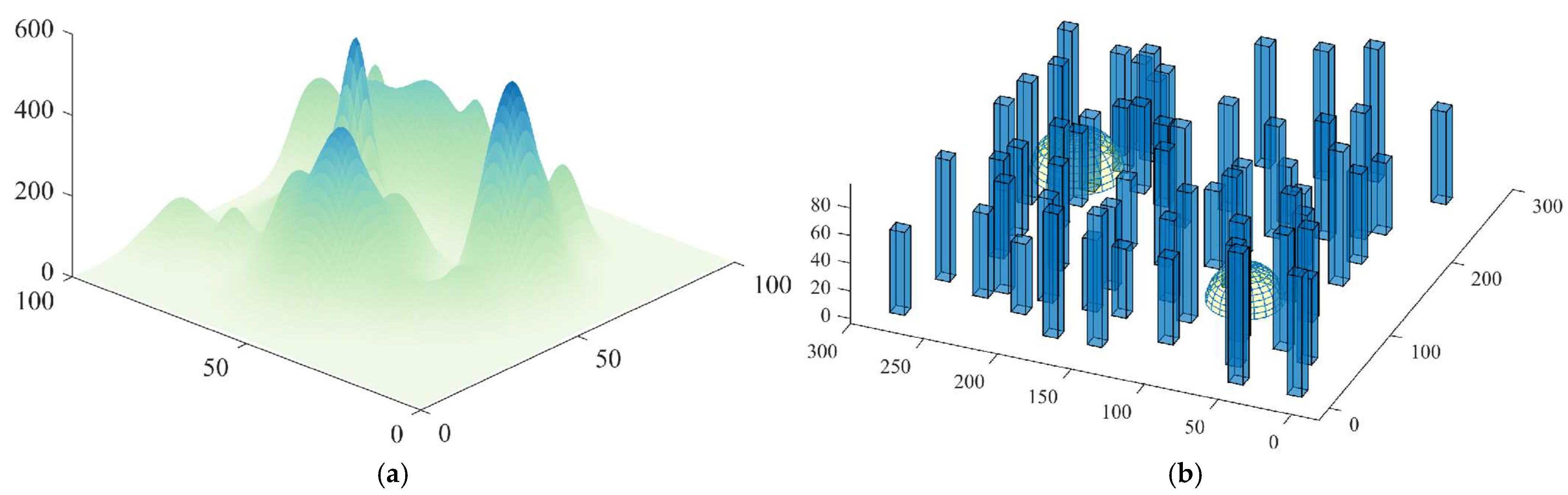
2.1. Environmental Model
- (a)
- Mountainous environments
To simulate the mountainous area delivery environment, some mountain peaks were randomly generated on the map using Equation (1) [16].
where n means the total number of mountain peaks; denotes the central coordinates of the -th mountain peak; is a parameter of the terrain and controls the height of that particular peak; and and , respectively, signify the attenuation magnitudes of the -th mountain peak along the x-axis and y-axis, which control the slope of the mountain.
- (b)
- Urban environments
Some cuboids are used to simulate urban environments. In addition, hemispheres are utilized to denote the no-fly zones within the city. Therefore, the urban environment model can be described as follows:
where , , ..., and represent the coordinates of the eight vertexes of each cuboid; and and are the central coordinates and the radius of the -th hemisphere, respectively.
Figure 2 shows the simulation environment model that was constructed in this paper.
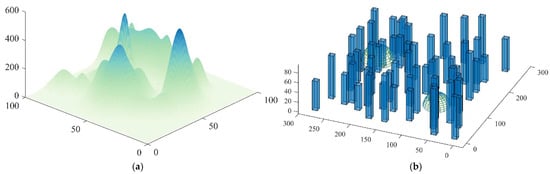
Figure 2.
Environmental model. (a) Mountainous environment. (b) Urban environment.
2.2. UAV Dynamics Model
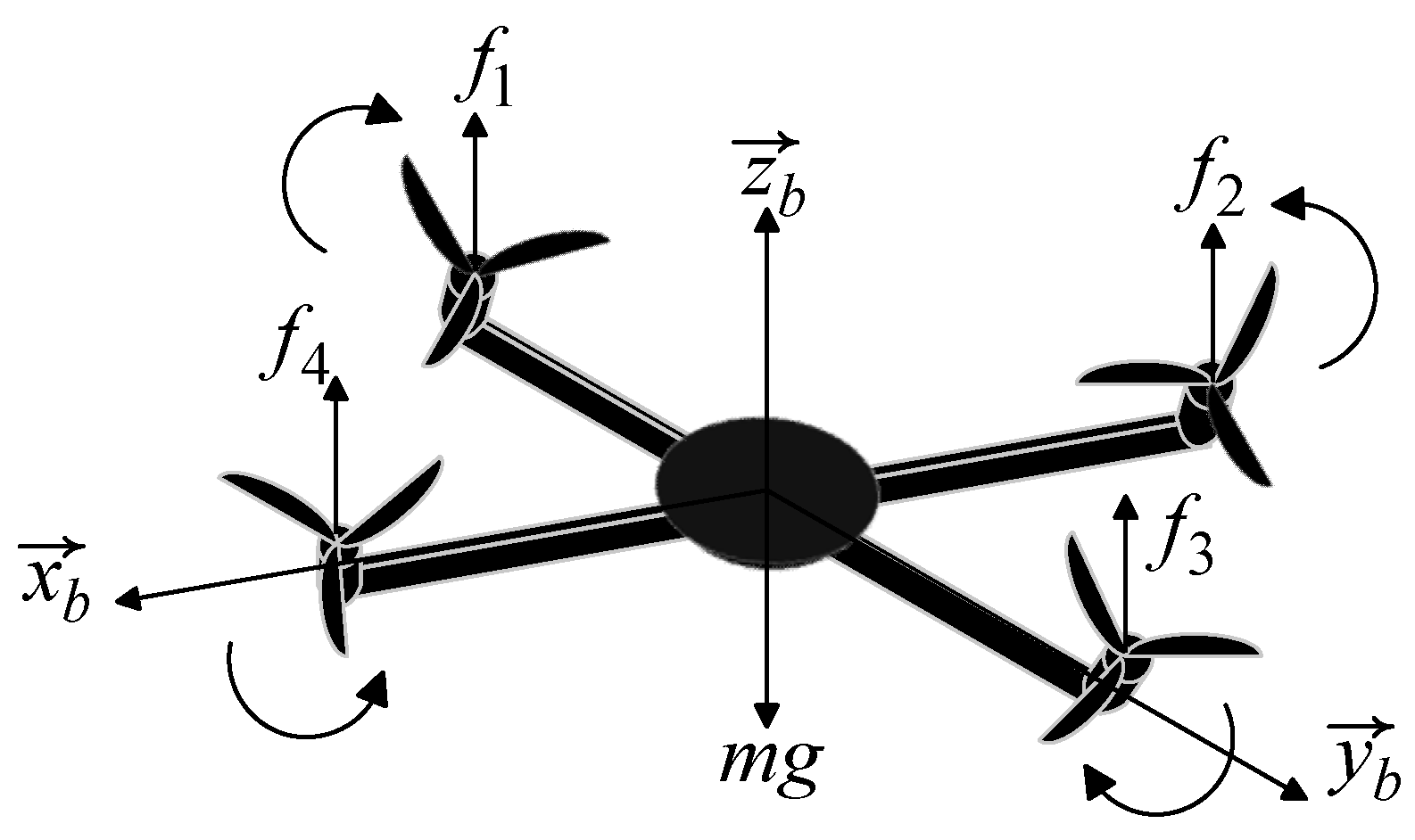
Quadrotor UAVs have been successfully applied in the logistics and distribution field. Their structure consists of a centrally symmetric X-shaped frame, four pairs of propellers, four independent motors, and various electronic components. The four motors are symmetrically fixed at the ends of the frame’s arms. A pair of motors that are symmetric about the geometric center rotate in the same direction to counteract the reaction torque generated by the propeller rotation during UAV hovering. By changing the rotational speeds of the four motors, the pitch, yaw, and other attitudes of the quadrotor UAV can be adjusted. The electronic components include sensors, such as accelerometers, magnetometers, gyroscopes, and global positioning systems, micro-control units, electronic speed controllers, etc., which are used for autonomous navigation, attitude estimation, and motor driving.
To construct the dynamics model of the UAV, the following assumptions were made:
Assumption 1.
The UAV is a rigid body, meaning its shape and size remain unchanged during motion, and the relative positions of internal points remain constant.
Assumption 2.
The geometric center of the UAV coincides with its center of gravity.
Assumption 3.
The UAV is only subject to gravity and the thrust generated by the propellers, with air resistance and gyroscopic effects ignored.
In this section, a dynamics model of the UAV will be established based on the Newton–Euler equations [17], and it is expressed by the following formulas:
where and are used to denote the velocity and rotation matrix attitude of the UAV in the earth-fixed coordinate system; characterizes the angular velocity of the UAV in the body-fixed frame; and symbolize the resultant thrust and torque generated by the UAV’s rotors, respectively; represents the mass of the UAV; is the gravitational constant; and represents the moment of inertia of the UAV.
For a more intuitive understanding of the model structure and the acting forces, Figure 3 presents a simplified dynamics model diagram of the UAV in a body-fixed coordinate system.
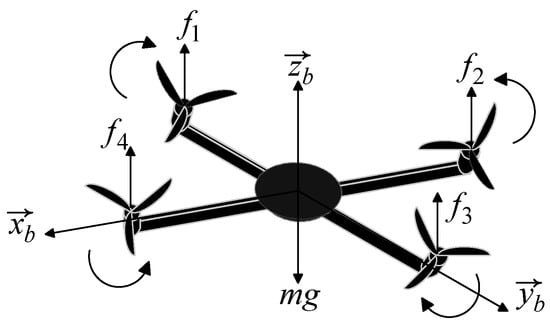
Figure 3.
Simplified diagram of the quadrotor UAV dynamics model.
2.3. Route Generation and Smoothing
2.3.1. Encoding and Decoding
When the number of control points to be solved is , the encoding of three-dimensional trajectory points into a solution vector of dimension is performed according to the following rules:
- (a)
- The x-coordinates of all points are sequentially placed in the first positions.
- (b)
- The y-coordinates are placed in the middle positions.
- (c)
- The z-coordinates occupy the last positions.
Mathematically, the encoded solution vector is structured as follows:
where each solution can be decoded into the coordinates of three-dimensional spatial points correspondingly. For the -th trajectory point (), its coordinates are determined by the following elements of the solution vector (Figure 4 shows an example of decoding process):

Figure 4.
Decoding process.
2.3.2. Cubic Spline Interpolation
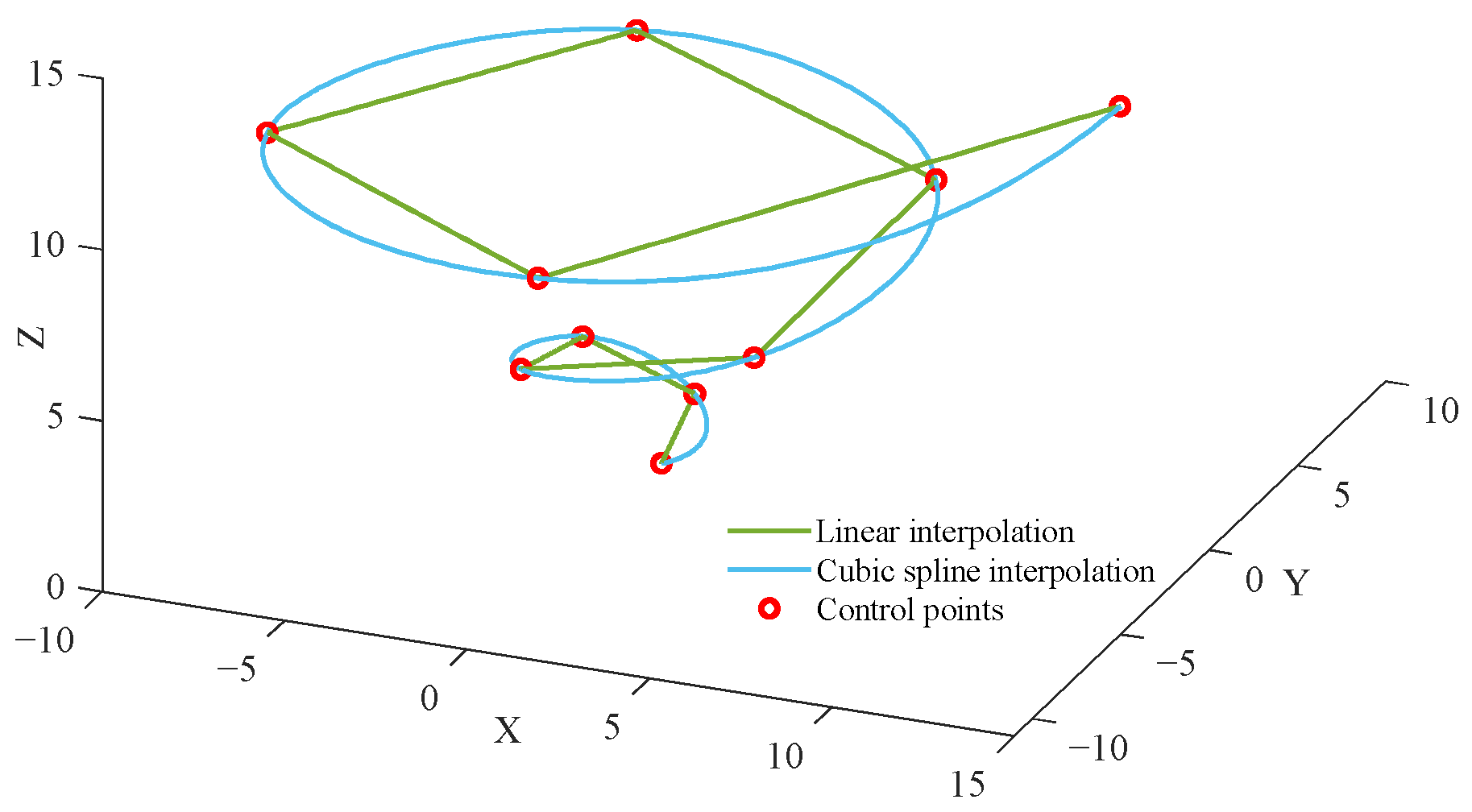
To make the generated route approximate the real flight trajectory of UAVs, cubic spline interpolation is used to smooth the route, and sudden changes in the velocity direction at inflection points are avoided.
Definition 1.
Let nodes be taken in the interval and let the function values at these nodes be given as
is called a cubic spline interpolation function if satisfies the following conditions:
- (a)
- ;
- (b)
- (c)
- On each sub-interval , is a cubic polynomial.
A cubic spline interpolation function can be expressed as a cubic polynomial on each sub-interval , where . Here, , , , and are undetermined coefficients; thus, has a total of undetermined coefficients. According to the definition, we can derive conditions. Therefore, two additional boundary conditions are required to solve for all the unknowns [18].
In the selection of boundary conditions, the default not-a-knot boundary condition of the spline function in MATLAB R2022a is employed. This boundary condition ensures the overall smoothness of the curve while maintaining the continuity of higher-order derivatives near the endpoints, thereby enabling a more natural and seamless transition of the curve at the endpoints. Figure 5 shows the routes generated by linear interpolation and cubic spline interpolation, respectively, and the latter better adheres to the kinematic laws of UAVs.
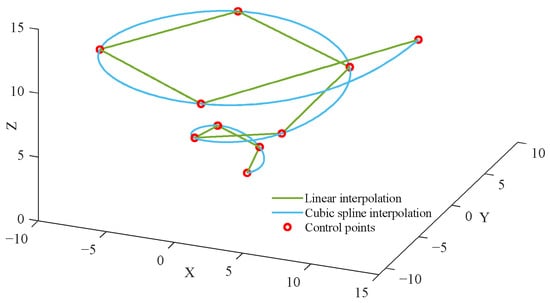
Figure 5.
Comparison of two interpolation methods.
After generating a smooth route in this way, high-density sampling is performed on the route to obtain a series of waypoints, which facilitates the operation of the model in Section 2.4.
2.4. UAV Logistics Delivery 3D Route Planning Model
Before introducing the UAV logistics delivery route planning model in this paper, some assumptions need to be put forward.
Assumption 4.
The drone departs from the starting point to perform one-to-one delivery.
Assumption 5.
The drone conducts deliveries in the mode of vertical takeoff, cruising along the planned route and vertical landing.
Assumption 6.
After completing the delivery task, the drone returns to the starting station via the original route, forming a reflexive symmetry characteristic based on the route structure.
2.4.1. Cost Function Design
- (a)
- Route length
To improve the delivery efficiency and reduce flight costs, it is expected that the length of the planned route can be minimized. Therefore, one of the cost functions is the length of the planned flight route, as shown in Equation (9):
where is the coordinates of the waypoints.
- (b)
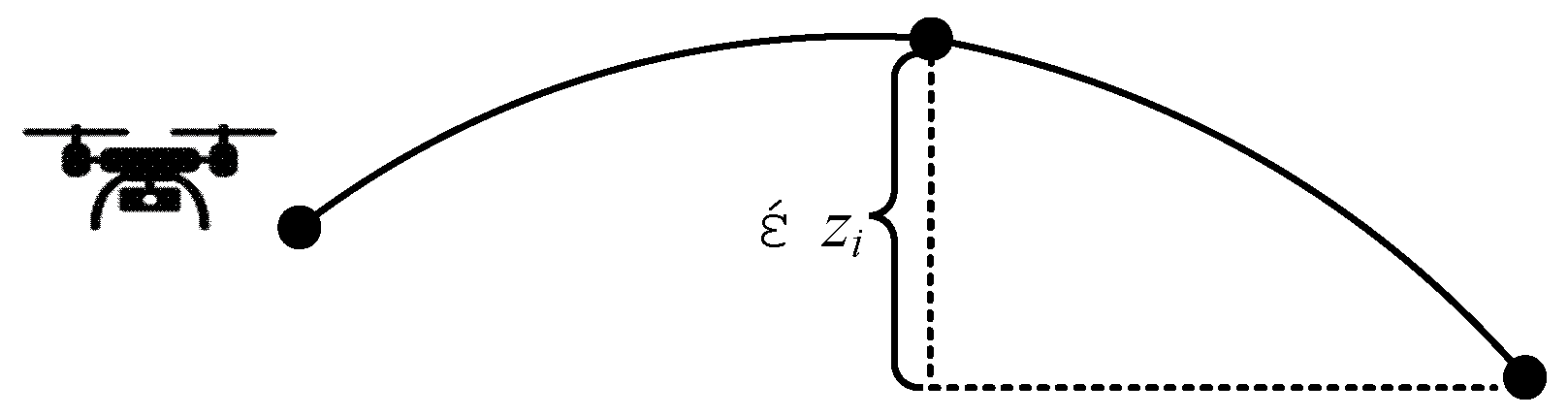
- Flight fluctuation
Frequent altitude changes will increase the power consumption of the drone, which is not conducive to reducing the delivery cost. As a result, the flight undulation cost is defined as shown in Equation (10):
where is the height difference between two nodes, as shown in Figure 6, and and are the heights of the start and the destination, respectively.
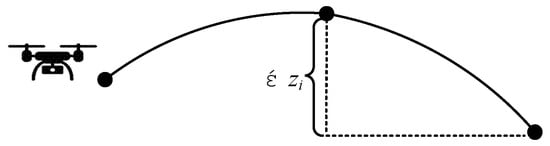
Figure 6.
The fluctuation of the flight (side view).
Therefore, the overall objective C of the model is , where and represent the weights of the two objectives, respectively, and they satisfy .
2.4.2. Constraints
- (a)
- Flight length
As defined in Assumption 3, the flight distance of a drone’s single delivery activity is twice the length of the planned route. Therefore, the planned route should satisfy the following constraint:
where represents the length of the planned route, and is the maximum single flight distance of the drone.
- (b)
- Goods weight
In order to ensure the safety of the delivery activities, the weight of the goods should be within the maximum carrying capacity range of the drone.
where denotes the weight of the delivery item, and is the maximum load capacity of the drone.
- (c)
- Yaw angle constraint
When the drone conducts a delivery, it is normal for it to change its navigation direction to avoid obstacles. As a result, its horizontal yaw angle should be within a reasonable range, as defined in Equation (13):
where is the maximum yaw angle.
- (d)
- Pitch angle constraint
In a mountainous environment, in order to achieve a shorter delivery route, the drone may fly following the contour of the mountain, which will result in changes in the pitch angle. For safety considerations, the pitch angle of the drone should also be specified within a reasonable range, as shown in Equation (16):
where is the maximum pitch angle.
- (e)
- Obstacle constraint
During UAV delivery activities, collision with the terrain environment or obstacles must be avoided. The model will select corresponding constraint expressions according to different environments.
In the next section, a multi-strategy improved artificial lemming algorithm (MsIALA) will be proposed to better solve the model proposed in this section.
3. Multi-Strategy Improved Artificial Lemming Algorithm
The artificial lemming algorithm [19], which has been proven to perform well in the test sets CEC2017 and CEC2022, is inspired by four different behaviors of lemmings in nature: long-distance migration, digging holes, foraging, and evading predators. However, when verifying the performance of ALA on the benchmark test set, it was found that ALA still has the defect of being prone to falling into local optimal solutions, which is not conducive to solving the model. Therefore, this paper proposes three strategies to improve ALA, and it names it MsIALA (multi-strategy improved artificial lemming algorithm).
3.1. Principle of Artificial Lemming Algorithm
- (a)
- Long-distance migration
When the population of lemmings is too large to obtain abundant food, lemmings will randomly carry out long-distance migrations to obtain better living conditions and food resources. Influenced by various factors, such as the ecological environment, the direction and distance of lemmings’ migrations are not fixed. Equation (18) simulates this behavior.
where represents the ith position of the search agent at the iteration; is the current optimal solution; , which is calculated by Equation (19), serves as a flag to change the search direction so as to explore a larger search space; denotes a random number vector that models Brownian motion, which employs dynamic and consistent step lengths to probe certain latent areas; is a vector of size generated by Equation (20); denotes the current position of the ith search individual; represents a randomly selected search individual from the population; and is an integer index within the range of 1 to .
- (b)
- Digging holes
The second behavior of lemmings is to dig holes in their habitats. The formed complex tunnels will provide them with safe shelters and places to store food, helping them to quickly escape from the threats of predators and search for food more effectively. This behavior is simulated in Equation (21).
where is random number related to the current number of iterations and is calculated according to Equation (22); represents a randomly selected search individual from the population; and is an integer index ranging from 1 to .
- (c)
- Foraging
Lemmings rely on their keen sense of smell and hearing to move extensively in the burrows of their habitats in search of food sources. Based on the abundance and availability of food, lemmings usually demarcate a relatively small foraging area within their habitats, and they will randomly wander within this foraging area. This stage can be simulated by a spiral winding mechanism, which is described as follows:
where represents the spiral shape of the random search during the foraging process, which is calculated by Equations (24) and (25).
where represents the radius of the foraging range, which is expressed by the Euclidean distance between the current position and the optimal position.
- (d)
- Evading predators
Finally, a model is established for the evasive and self-protective behaviors of lemmings in the face of danger. As soon as lemmings sense the presence of an enemy, they will make use of their distinct running capabilities to dash back to their burrows. Additionally, in an attempt to elude the predators’ chase, lemmings will execute misleading actions. The relevant mathematical formula is presented as Equation (26).
where is a parameter representing the lemmings’ escape ability, which decreases as the number of iterations increases, as shown in Equation (26); represents the maximum number of iterations; and is the Lévy flight function, which is used to simulate the deceptive movements of lemmings when they are fleeing.
In addition, lemmings maintain a balance between exploration and exploitation through an energy factor. When their energy levels are adequate, they will make a choice between migrating and digging holes; in cases of insufficient energy, they will engage in foraging activities and trying to elude predators. The calculation formula for the energy factor is as follows:
3.2. Improvement Strategies
3.2.1. Cubic Chaotic Map Initialization
The original ALA may have an uneven population distribution in the initial stage, resulting in a decrease in population diversity and making the algorithm prone to falling into local optimal solutions. To address this issue, Strategy 1 introduces the Cubic chaotic map to replace the random initialization of the original algorithm. The general form of the Cubic map is shown in Equation (29) [20]:
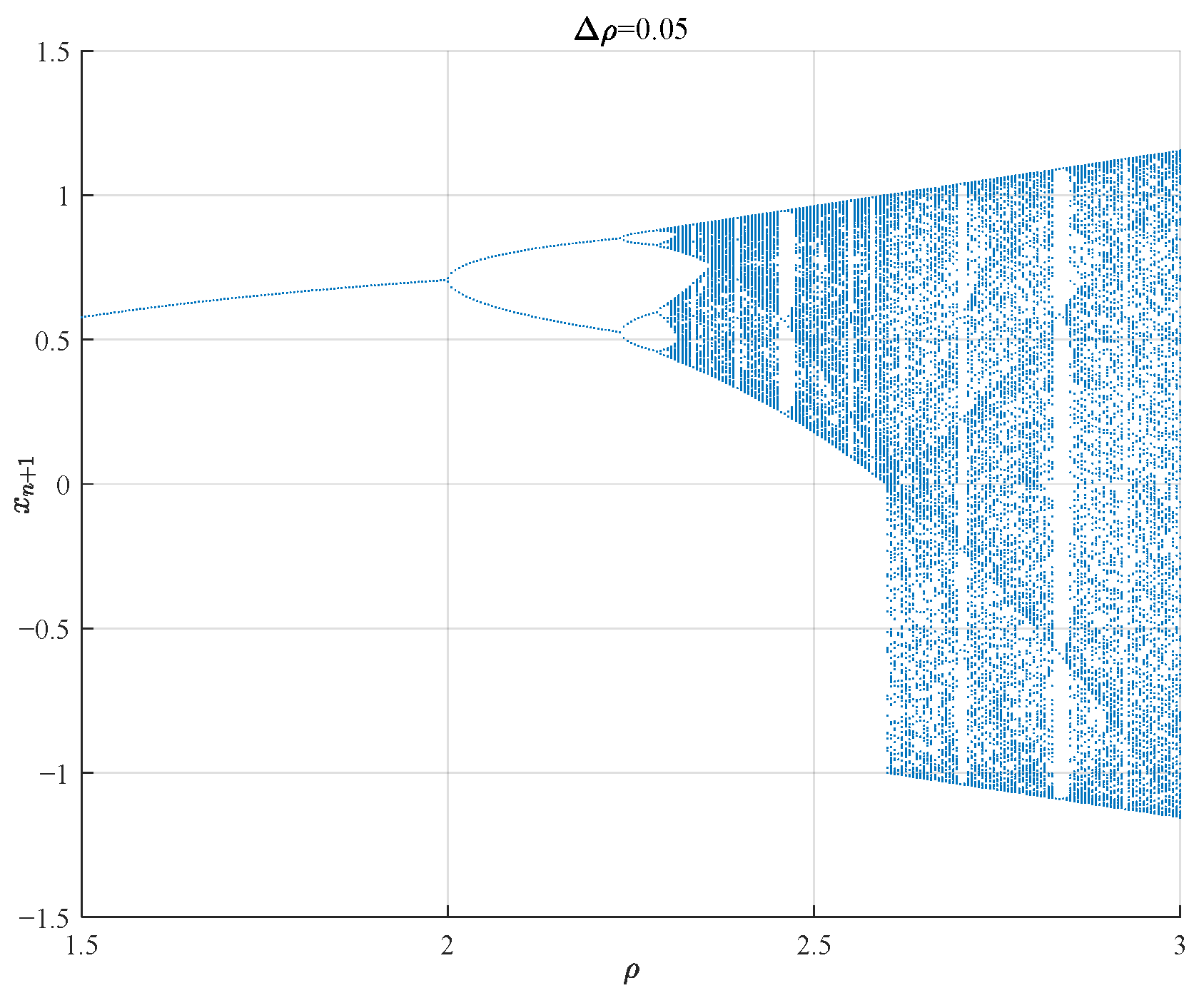
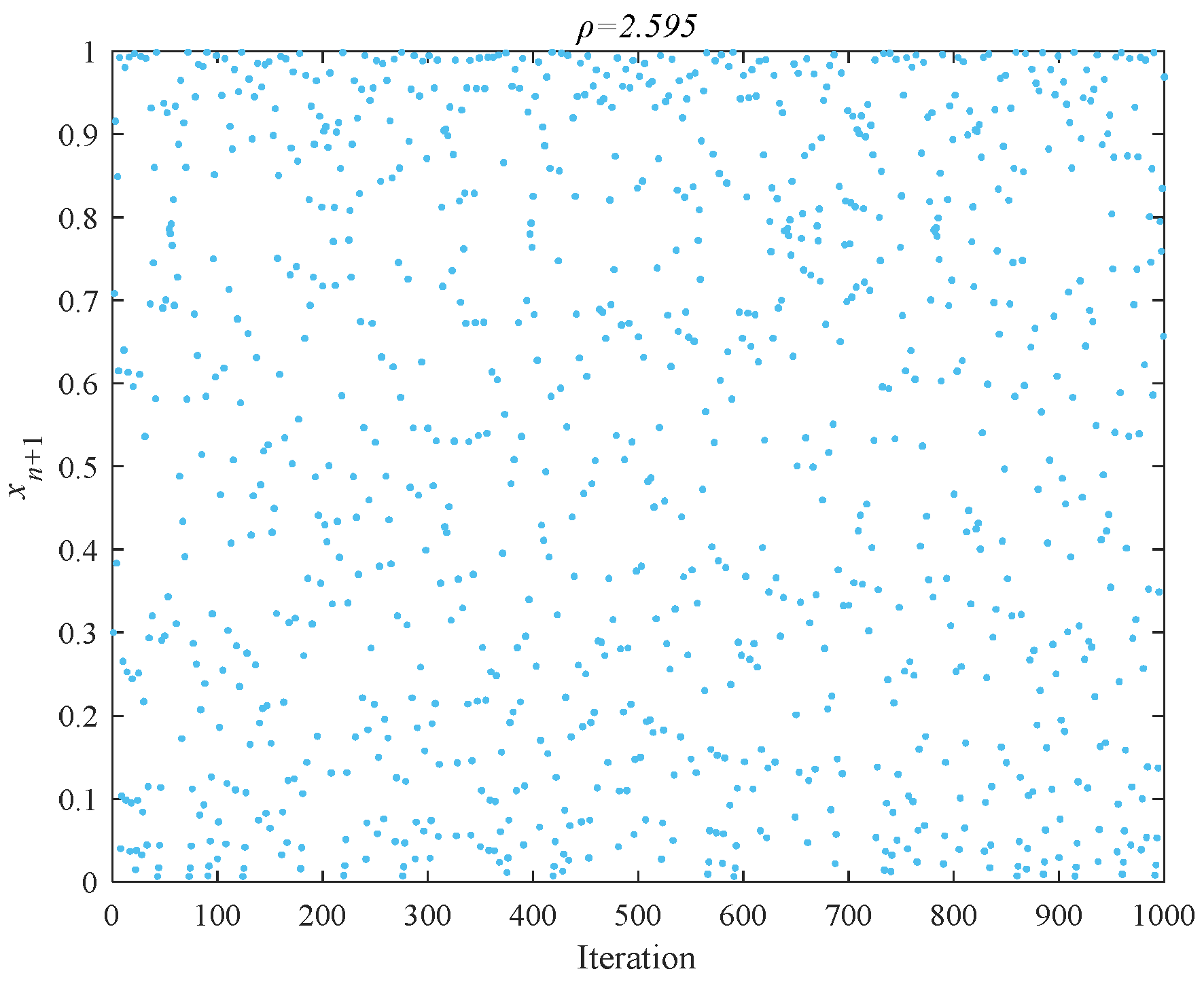
where is the mapping factor. Within a specific range of , the map exhibits chaotic characteristics. Figure 7 shows the bifurcation diagram of the Cubic map and when , where the iterative sequence demonstrates well chaotic ergodicity over the interval (0, 1), as shown in Figure 8.
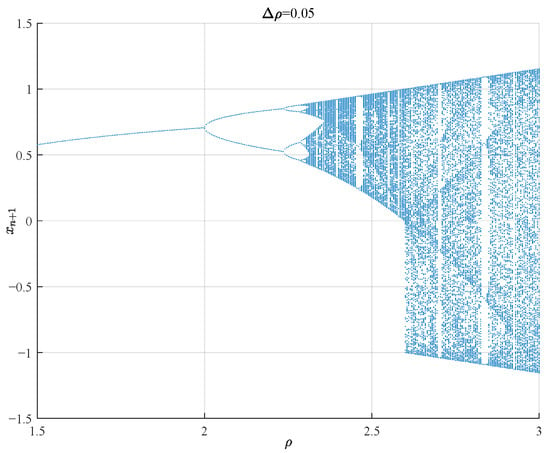
Figure 7.
Bifurcation diagram of the Cubic map.
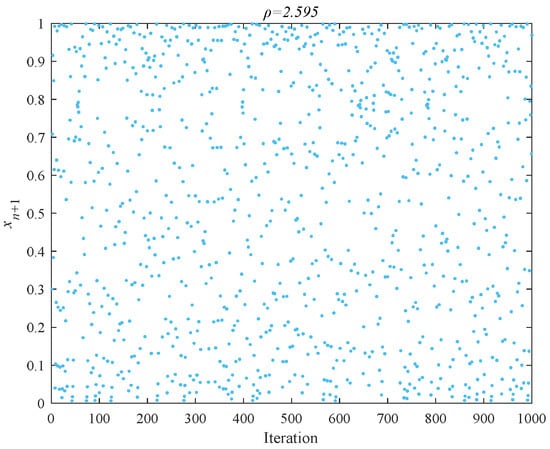
Figure 8.
Cubic chaotic map.
3.2.2. Double Adaptive T-Distribution Perturbation
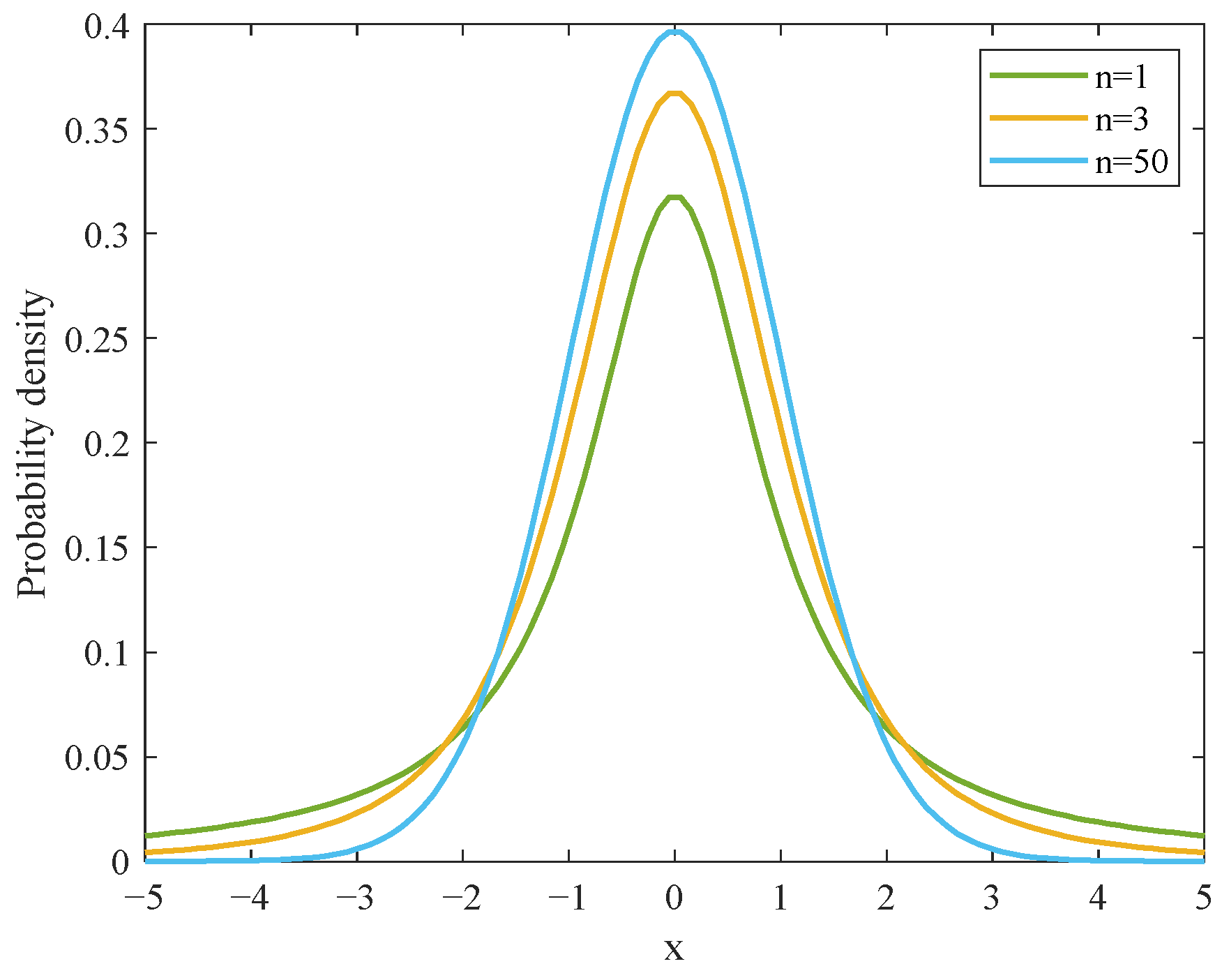
To alleviate the problem that the artificial lemming algorithm is prone to becoming trapped in local optima, this paper introduces a double adaptive t-distribution perturbation strategy, where the expectation is that lemmings can explore farther spaces to escape local optima. The t-distribution, also known as the Student’s distribution, has typical symmetry. It combines the advantages of the Cauchy distribution and the Gaussian distribution, and its probability density function is shown in Equation (30):
where is the degree of the freedom parameter, which affects the probability density of the t-distribution. When , the t-distribution turns into a Cauchy distribution; when approaches infinity, the t-distribution approaches a normal distribution. However, regardless of how the value of changes, the t-distribution maintains stable symmetry, as shown in Figure 9.
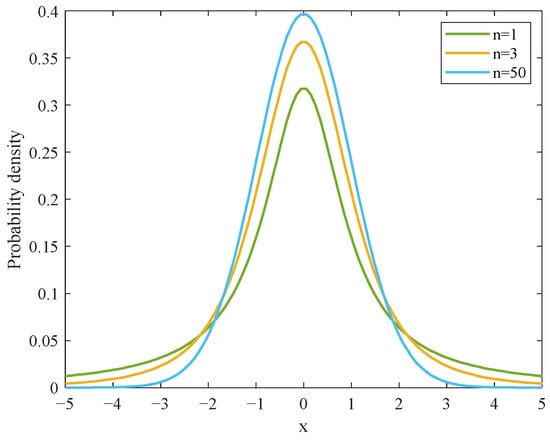
Figure 9.
Influence of different degrees of freedom on t-distribution.
The first aspect of adaptability lies in the adaptability of the degree of freedom. Equation (31) is used to automatically adjust the degree of freedom parameter of the t-distribution. In the early stage of iteration, when is small, the value of is also small. At this time, the tail of the t-distribution is heavier. As a result, individuals have a higher probability of making large-scale jumps when updating their positions, which is conducive to exploring a wider area within the solution space and reduces the possibility of becoming trapped in local optimal solutions in the initial stage. As the number of iterations increases, gradually becomes larger. The tail of the t-distribution becomes lighter and approaches a normal distribution. At this stage, the algorithm already has a good understanding of the solution space. By reducing the jump amplitude, it can more precisely search the area around the current optimal solution, thereby improving the accuracy of the solution. In addition, the symmetry of the t-distribution is helpful for exploring new spaces with equal probabilities in both directions when adjusting the direction. It prevents an excessive bias toward the currently known optimal solution and avoids overlooking potential superior solutions.
The second aspect of adaptability is reflected in the adaptive adjustment of the number of perturbed individuals as the iteration progresses. In the early stage of iteration, a relatively large proportion of individuals undergo t-distribution mutation. This is beneficial for the algorithm to explore the solution space from multiple directions and avoid being trapped in local optima. In the later stage of iteration, individuals are mainly updated using the original strategy, enabling the algorithm to focus more on local exploitation and improve the convergence speed. Therefore, the positions of lemming individuals are updated according to Equation (32):
3.2.3. Population Dynamic Optimization
During the iteration process, the individuals in the population with poor quality have low fitness values, and they may be located in less ideal positions within the search space. Retaining these individuals may cause the algorithm to continue exploring these suboptimal regions in subsequent iterations, thus slowing down the convergence speed toward the global optimal solution. We define the population with the lowest 20% of fitness values as the inferior population, and they will be dynamically adjusted through Equation (33) during the iteration process, thereby moving toward the optimal position within the population.
3.3. Algorithm Flow and Computational Complexity
The pseudocode of the multi-strategy improved ALA is shown in Algorithm 1.
| Algorithm 1. Multi-strategy improved artificial lemming algorithm. |
| Input: The maximum iterations ; the size of the population ; the dimension size . |
Output: The optimal position ; the optimal fitness value .
|
|
In this subsection, the computational complexity of the MsIALA is systematically evaluated. The algorithm is composed of three core components: population initialization, iterative position updates, and fitness evaluations. The complexity of each component is as follows.
Initialization: Generating the initial population using chaotic sequences involves individuals with dimensions, resulting in a complexity of .
Iterative position update: Each iteration (up to ) involves position updates for individuals across dimensions. Considering the multiple conditional checks, parameter adaptations, and adaptive perturbations, the complexity of this phase is .
Fitness evaluation: Evaluating the fitness of individuals in each iteration contributes a complexity of .
Thus, the overall computational complexity of MsIALA is .
3.4. Data Experiment
In this subsection, 10 benchmark test functions were selected to evaluate the performance of the improved algorithm, and the specific details of these functions are listed in Table 1. Meanwhile, four algorithms were selected for comparative analysis, including the most classic PSO algorithm [21]; some newly popular algorithms in the field of UAV route planning in recent years, namely the LO algorithm [22], the WOA [23], and the DBO algorithm [24]; and the original ALA. The parameters of each algorithm are set according to the relevant reference. To ensure a fair comparison, the fundamental parameters were uniformly set as follows: the population size was set to , and the maximum number of iterations was . Each algorithm was executed independently thirty times; subsequently, the optimal values, mean values, and standard deviations of the results were recorded. Table 2 presents the detailed experimental outcomes.

Table 1.
Introduction of the benchmark functions.

Table 2.
The experimental results for each algorithm.
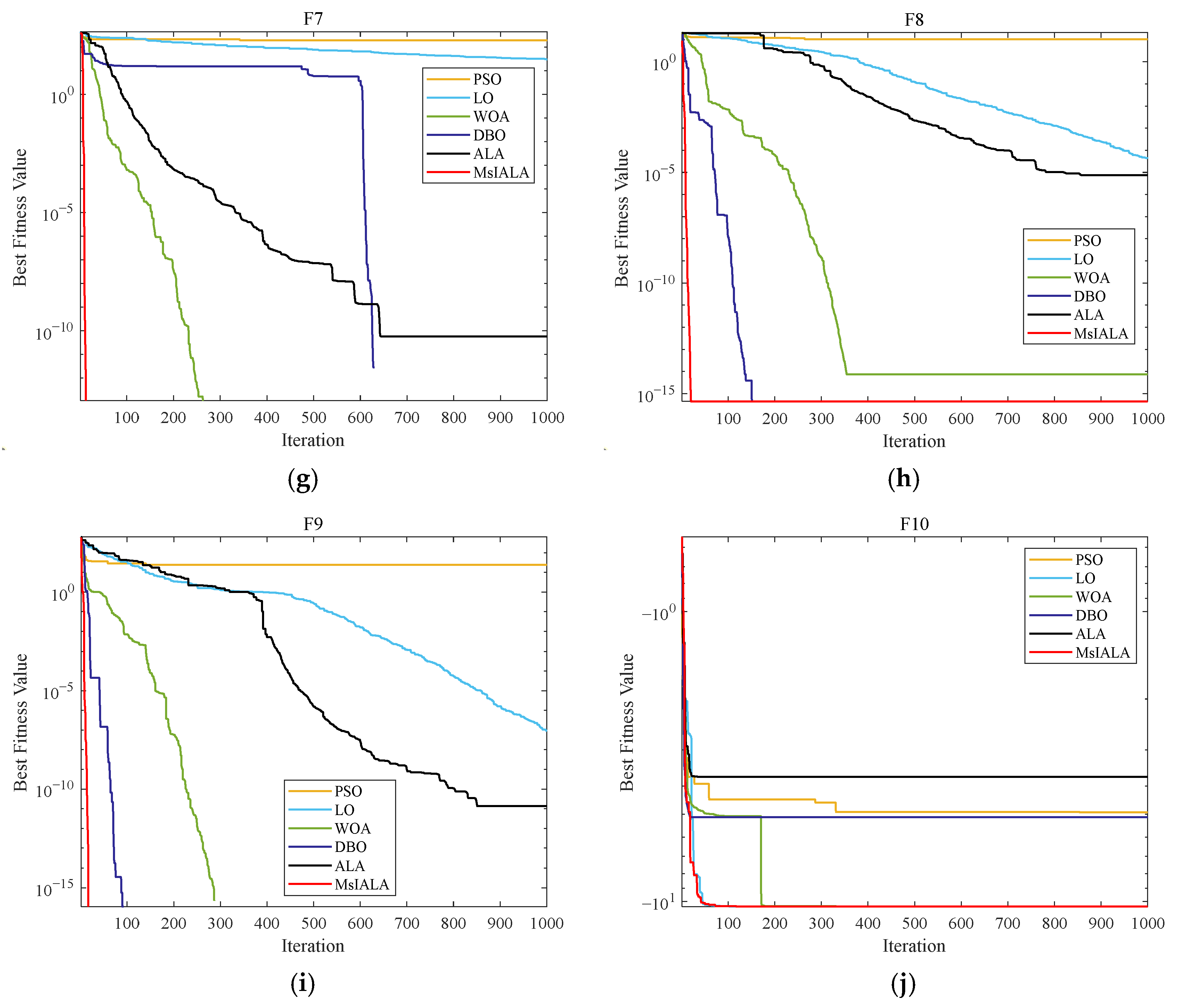
In Table 2, the optimal values of various indicators are presented in bold. It can be seen that that the MsIALA demonstrated excellent performance across all benchmark test functions, and the theoretical optimal values could be found in seven test functions. In the remaining three test functions, the average optimal values of MsIALA outperformed those of other algorithms in the group. Moreover, the standard deviation of MsIALA for each test function was generally small, which reflects that the degree of dispersion of the results obtained from multiple runs of the algorithm was low, indicating that the algorithm had strong stability.
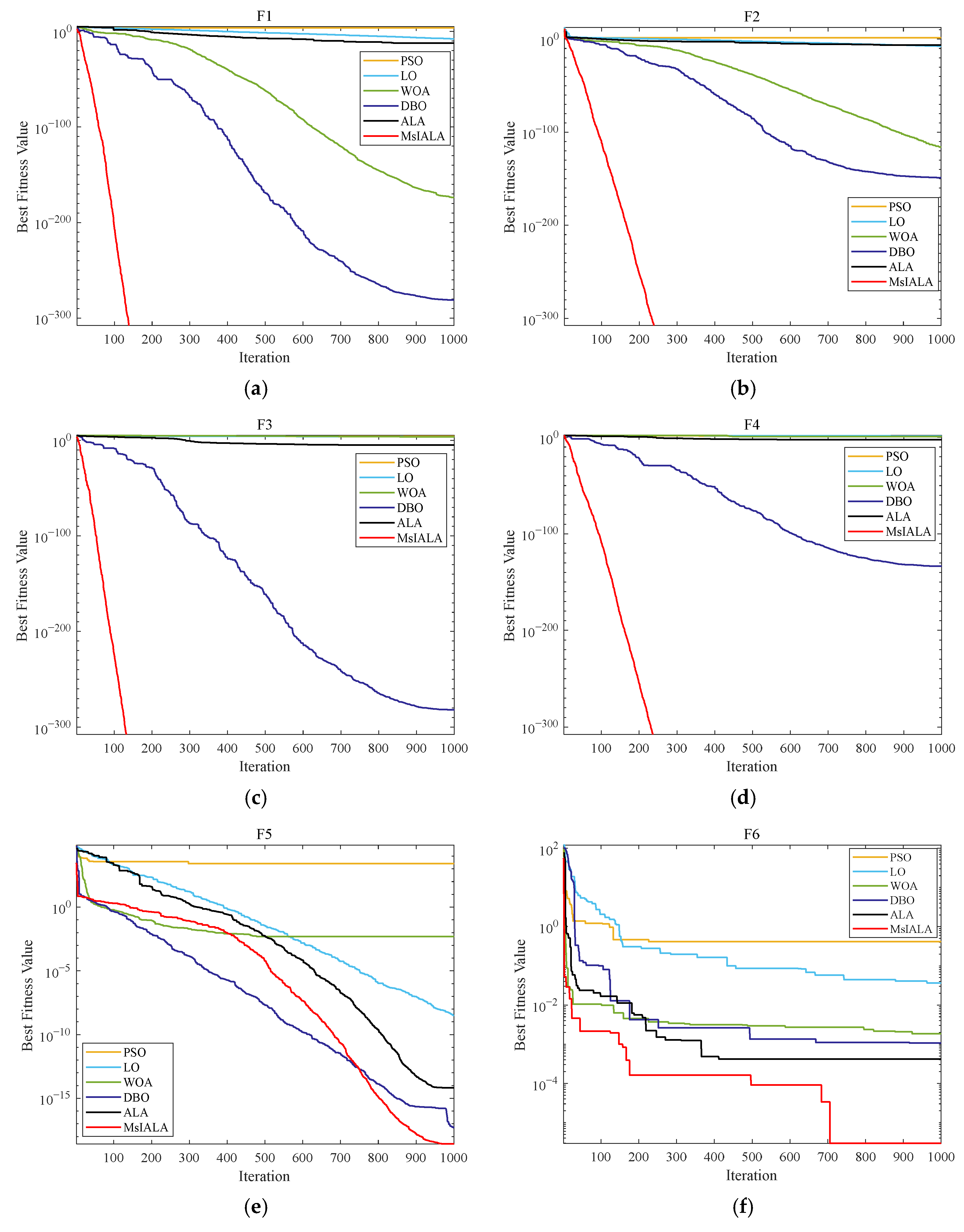
As can be seen from multiple sub-graphs in Figure 10a–d, in the initial stage of iteration, MsIALA decreased rapidly compared with other algorithms, indicating that the algorithm can quickly explore the solution space at the beginning. In the later stage of iteration, taking Figure 10e as an example, MsIALA can maintain a relatively stable decreasing trend in contrast to some other algorithms.
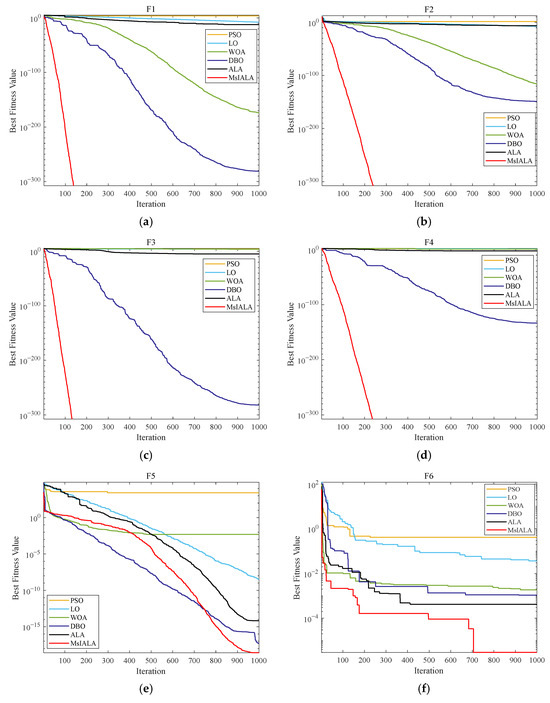
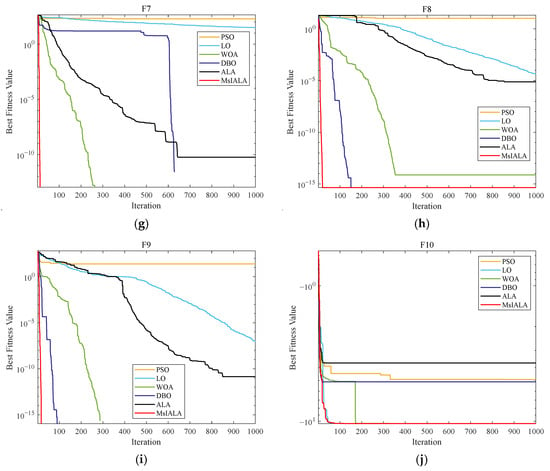
Figure 10.
Comparison of the convergence curves of each algorithm. (a) Convergence curve of F1. (b) Convergence curve of F2. (c) Convergence curve of F3. (d) Convergence curve of F4. (e) Convergence curve of F5. (f) Convergence curve of F6. (g) Convergence curve of F7. (h) Convergence curve of F8. (i) Convergence curve of F9. (j) Convergence curve of F10.
4. Simulation Experiment and Result Analysis
4.1. Experimental Environment and Parameter Settings
In order to verify the effectiveness of the improved algorithm in the 3D route planning model proposed in this paper, this paper constructed a variety of environments for simulation experiments. In two mountainous environments, the number of peaks was set to 10 and 20, respectively; in two urban environments, the number of obstacles was set to 30 and 60, respectively; and the radii of the no-fly zones were 25 and 30, respectively. In each environment, the UAV needed to complete a material delivery task from the starting point to the ending point. The main parameter settings are shown in Table 3.

Table 3.
Simulation experiment parameter settings.
4.2. Experimental Results
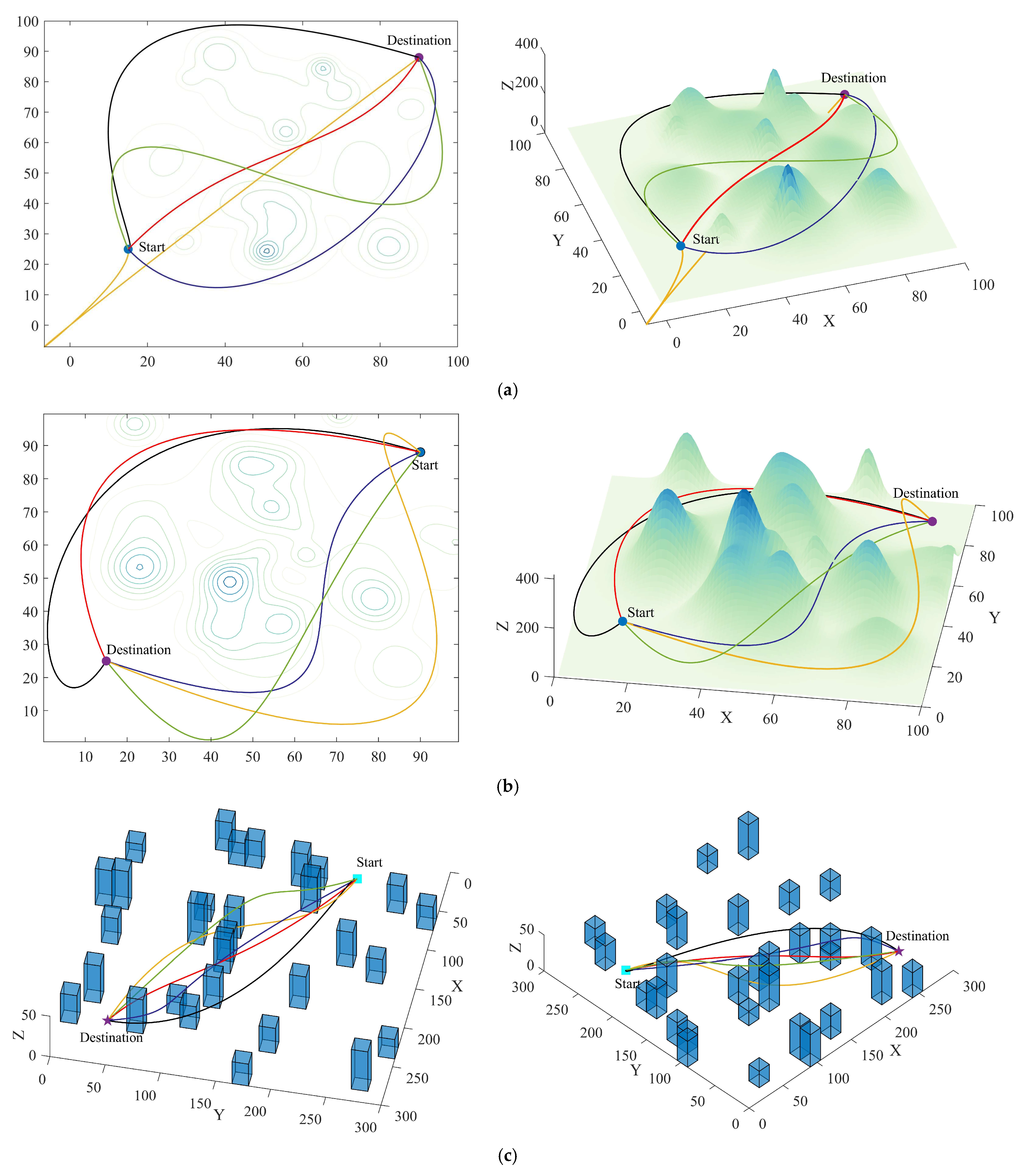
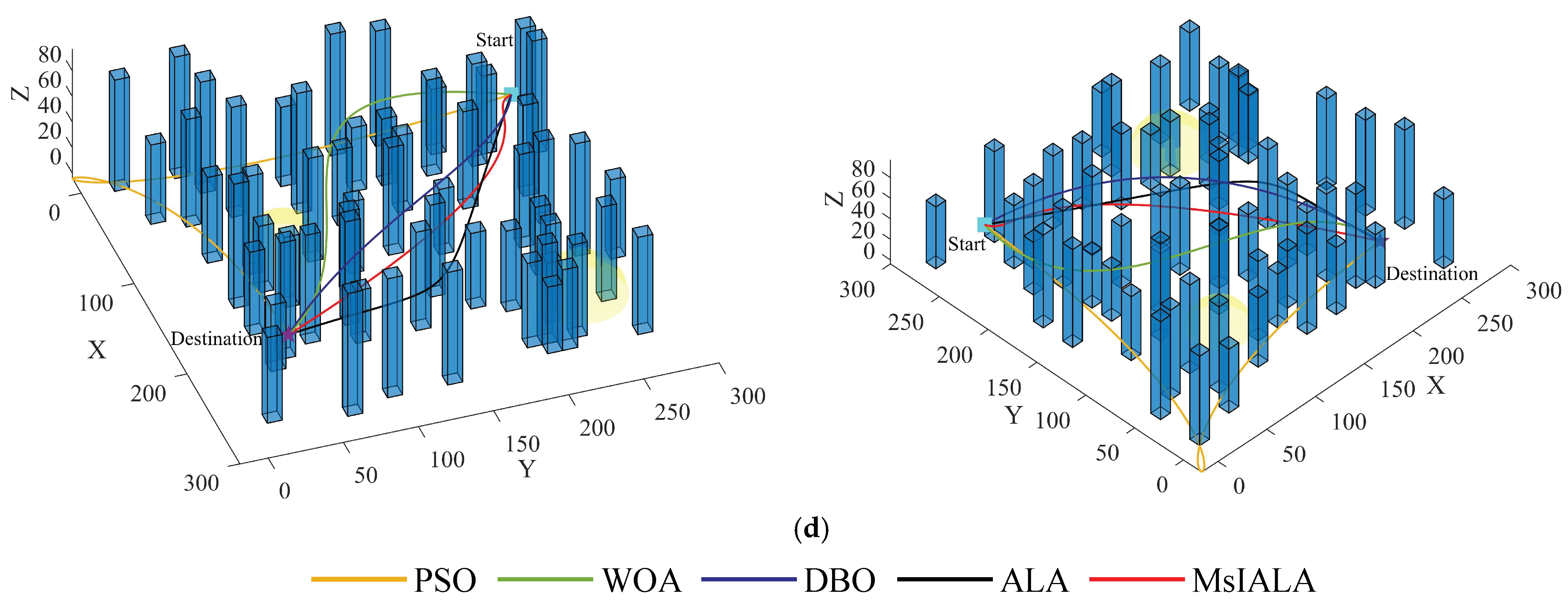
Since WOA and DBO performed well in the test set, the PSO, WOA, DBO, ALA, and MsIALA algorithms were simulated in the set environments based on the above parameters, and the results are shown in Figure 11. In the two mountainous area environments, as shown in Figure 11a, MsIALA chose to fly around following the mountain terrain. Although it sacrificed some flight undulation, the overall fitness value benefited from the shorter route length and outperformed the other four algorithms. As shown in Figure 11b, PSO, ALA, and MsIALA chose to fly around from the side. The smooth path and shorter route length enabled MsIALA to win. However, WOA and DBO, which flew around following the mountain terrain, had relatively large overall fitness values due to excessive flight undulation. In the two urban area environments, MsIALA was always able to find a relatively smooth delivery route and avoided obstacles by flying around the side of them.
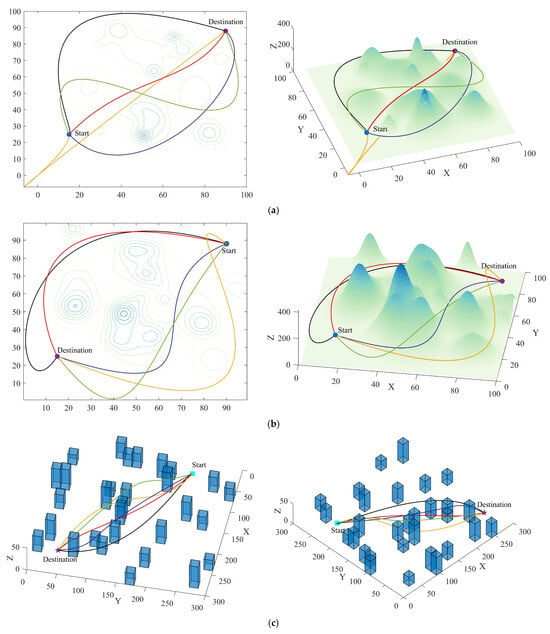
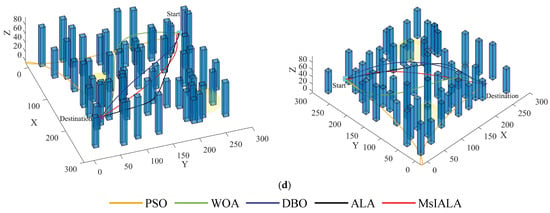
Figure 11.
Simulation experiment results. (a) Route planning in Mountainous Environment 1. (b) Route planning in Mountainous Environment 2. (c) Route planning in Urban Environment 1. (d) Route planning in Urban Environment 2.
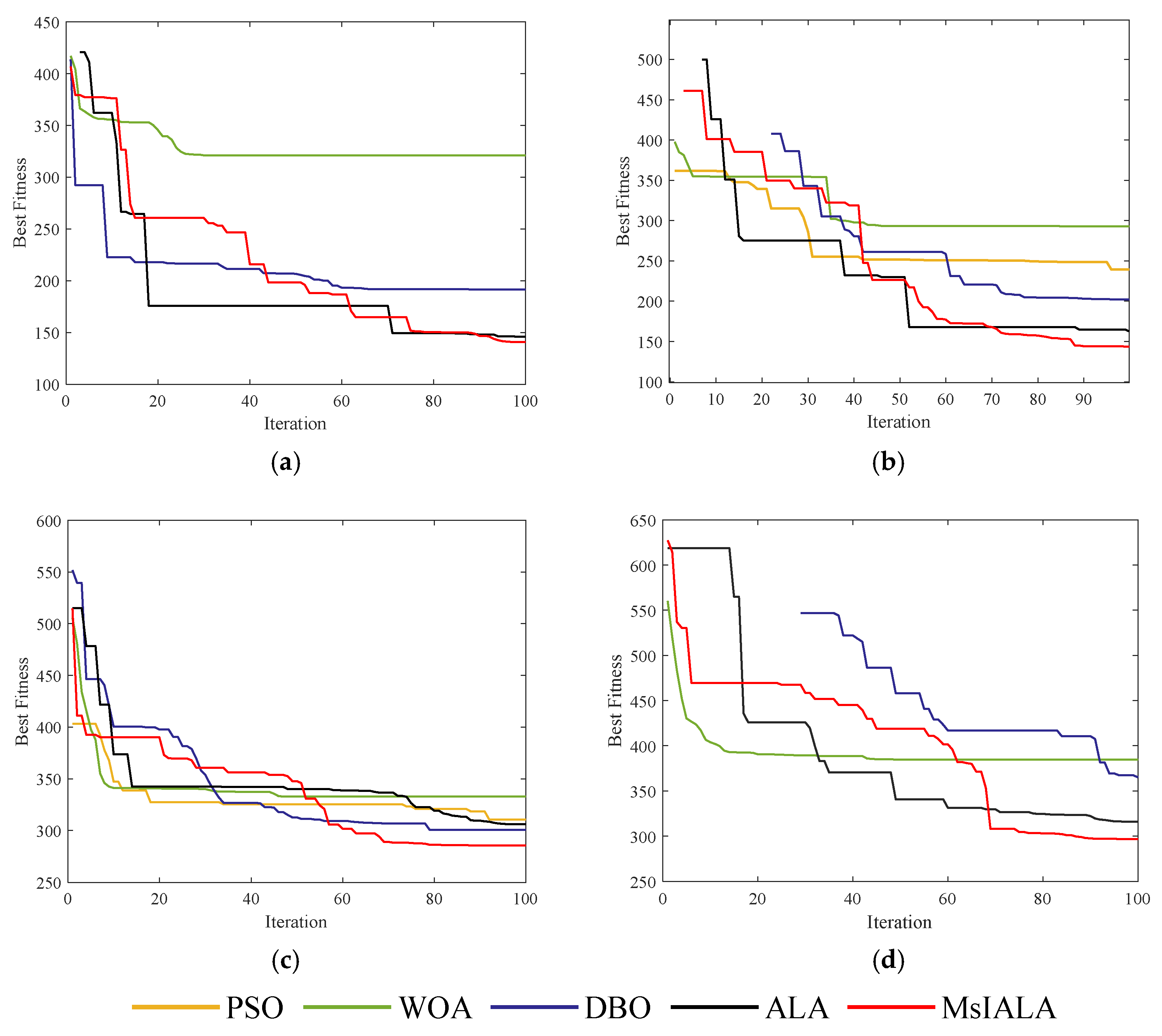
The simulation iteration curves for the four environments are shown in Figure 12. MsIALA performed outstandingly in all four environments. In the initial stage of iteration, it had a relatively fast decreasing speed, enabling it to fully explore the solution space. In the later stage of iteration, while some algorithms fell into local optima, MsIALA was still able to maintain a certain decreasing trend.
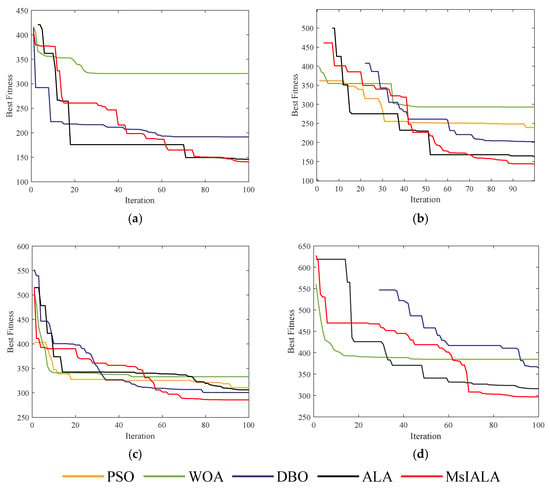
Figure 12.
Iteration curves of the simulation experiments. (a) Mountainous Environment 1. (b) Mountainous Environment 2. (c) Urban Environment 1. (d) Urban Environment 2.
4.3. Stability Analysis
To demonstrate the stable superiority of MsIALA, these algorithms were independently run 30 times in four scenarios. The optimal, average fitness values, standard deviations, and planning failure rate were all calculated and recorded. The experimental results are shown in Table 4.

Table 4.
Experimental results.
Although WOA performed well in the benchmark test functions, it showed the worst performance in specific route planning problems, while the original ALA had already demonstrated good performance in such problems. In the four environments, both PSO and WOA algorithms were inferior to the other three algorithms in optimization, with obvious gaps in the optimal values. Moreover, the two algorithms were prone to high failure rates in complex environments (e.g., Mountainous 2 and Urban 2). In Mountainous Environment 2, except for the MsIALA algorithm, all other algorithms had planning failures. The minimum fitness values found by DBO and MsALA were very close, but the former’s performance in average value and standard deviation was far worse than the latter. In Urban Environment 2, the PSO algorithm ranked second only to MsIALA in terms of fitness value and standard deviation, but it had no advantage in failure rate. Meanwhile, DBO, which also had a failure rate of 0, performed far worse than MsIALA in average value and standard deviation. Overall, MsIALA was able to stably output a path with superior quality and had the lowest planning failure rate, and it especially showed obvious advantages in complex environments.
5. Summary and Outlook
With the prosperous development of e-commerce, the use of drones for logistics and distribution activities has demonstrated its unique advantages. This paper established a 3D route planning model for drones applicable to various distribution environments. In order to plan a reasonable distribution route, an improved MsIALA algorithm is proposed. By introducing three different strategies, the convergence speed of the original ALA algorithm and its ability to escape from local optima are enhanced. Through data experiments and environment simulations, the proposed model and algorithm can provide certain references for the route planning of UAV deliveries.
In future research, task allocation could be further considered, and study on the 3D delivery route planning for UAVs from a single point to multiple points, with battery life constraints being a key focus, could be continued. Methods to optimize power consumption are worth exploring, such as efficient route planning incorporating energy-saving strategies, so as to extend UAV operation duration and enhance the overall efficiency of delivery tasks.
Additionally, dynamic obstacle avoidance can serve as another critical research direction. In practical scenarios, UAVs may face moving obstacles, such as birds, and they need to operate in highly dynamic and uncertain environments, like adverse weather conditions. Developing advanced algorithms to enable UAVs to rapidly and accurately detect obstacles and execute evasive maneuvers will become an important research content for ensuring the safe and smooth implementation of delivery tasks.
Author Contributions
Conceptualization, Y.X. and Z.S. (Zhe Sun); methodology, Z.S. (Zhe Sun); software, Y.X.; validation, Y.X. and Z.S. (Zhe Sun); formal analysis, Y.X.; investigation, K.Y.; resources, K.Y. and Z.S. (Zhixin Sun); data curation: K.Y.; writing—original draft preparation, Y.X., Z.S. (Zhe Sun); writing—review and editing, Y.X., Z.S. (Zhe Sun), K.Y. and Z.S. (Zhixin Sun); visualization, K.Y.; supervision, Z.S. (Zhixin Sun); funding acquisition, Z.S. (Zhe Sun) and Z.S. (Zhixin Sun). All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China under grant No. 62272239 and the Guizhou Provincial Key Technology R&D Program under grant [2023] 272.
Data Availability Statement
The data presented in this study are available upon request from the corresponding authors. The data are not publicly available due to privacy.
Conflicts of Interest
Author Kai Yuan is an employee of Anhui Yougu Express Intelligent Technology Co. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Fried, T.; Goodchild, A. E-commerce and logistics sprawl: A spatial exploration of last-mile logistics platforms. J. Transp. Geogr. 2023, 112, 103692. [Google Scholar] [CrossRef]
- Lee, H.-W. Research on multi-functional logistics intelligent Unmanned Aerial Vehicle. Eng. Appl. Artif. Intell. 2022, 116, 105341. [Google Scholar] [CrossRef]
- Mohamed, N.; Al-Jaroodi, J.; Jawhar, I.; Idries, A.; Mohammed, F. Unmanned aerial vehicles applications in future smart cities. Technol. Forecast. Soc. Change 2020, 153, 119293. [Google Scholar] [CrossRef]
- Mandloi, D.; Arya, R.; Verma, A.K. Unmanned aerial vehicle path planning based on A* algorithm and its variants in 3d environment. Int. J. Syst. Assur. Eng. Manag. 2021, 12, 990–1000. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, S. Research on 3D path planning algorithm based on fast RRT algorithm. J. Syst. Simul. 2022, 34, 503–511. [Google Scholar]
- Li, X.; Yu, S. Obstacle avoidance path planning for AUVs in a three-dimensional unknown environment based on the C-APF-TD3 algorithm. Ocean Eng. 2025, 315, 119886. [Google Scholar] [CrossRef]
- Saeed, R.A.; Omri, M.; Abdel-Khalek, S.; Ali, E.S.; Alotaibi, M.F. Optimal path planning for drones based on swarm intelligence algorithm. Neural Comput. Appl. 2022, 34, 10133–10155. [Google Scholar] [CrossRef]
- Phung, M.D.; Ha, Q.P. Safety-enhanced UAV path planning with spherical vector-based particle swarm optimization. Appl. Soft Comput. 2021, 107, 107376. [Google Scholar] [CrossRef]
- Jiang, W.; Lyu, Y.; Li, Y.; Guo, Y.; Zhang, W. UAV path planning and collision avoidance in 3D environments based on POMPD and improved grey wolf optimizer. Aerosp. Sci. Technol. 2022, 121, 107314. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, J.; Zeng, J.; Tang, J. Three-dimensional path planning for autonomous underwater vehicles based on a whale optimization algorithm. Ocean Eng. 2022, 250, 111070. [Google Scholar] [CrossRef]
- Fu, S.; Li, K.; Huang, H.; Ma, C.; Fan, Q.; Zhu, Y. Red-billed blue magpie optimizer: A novel metaheuristic algorithm for 2D/3D UAV path planning and engineering design problems. Artif. Intell. Rev. 2024, 57, 134. [Google Scholar] [CrossRef]
- Yu, Z.; Si, Z.; Li, X.; Wang, D.; Song, H. A novel hybrid particle swarm optimization algorithm for path planning of UAVs. IEEE Internet Things J. 2022, 9, 22547–22558. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, X.; Zhang, X.-Y.; Xiao, J.; Yu, X. RGG-PSO+: Random geometric graphs based particle swarm optimization method for UAV path planning. Int. J. Comput. Intell. Syst. 2024, 17, 127. [Google Scholar] [CrossRef]
- Liang, H.; Hu, W.; Gong, K.; Dai, J.; Wang, L. Solving UAV 3D Path Planning Based on the Improved Lemur Optimizer Algorithm. Biomimetics 2024, 9, 654. [Google Scholar] [CrossRef]
- Shen, Q.; Zhang, D.; Xie, M.; He, Q. Multi-Strategy enhanced dung beetle optimizer and its application in three-dimensional UAV path planning. Symmetry 2023, 15, 1432. [Google Scholar] [CrossRef]
- Wang, R.-B.; Wang, W.-F.; Geng, F.-D.; Pan, J.-S.; Chu, S.-C.; Xu, L. UAV path planning in mountain areas based on a hybrid parallel compact arithmetic optimization algorithm. Neural Comput. Appl. 2023, 1–16. [Google Scholar] [CrossRef]
- Mahony, R.; Kumar, V.; Corke, P. Multirotor Aerial Vehicles: Modeling, Estimation, and Control of Quadrotor. IEEE Robot. Autom. Mag. 2012, 19, 20–32. [Google Scholar] [CrossRef]
- McKinley, S.; Levine, M. Cubic spline interpolation. Coll. Redw. 1998, 45, 1049–1060. [Google Scholar]
- Xiao, Y.; Cui, H.; Abu Khurma, R.; Castillo, P.A. Artificial lemming algorithm: A novel bionic meta-heuristic technique for solving real-world engineering optimization problems. Artif. Intell. Rev. 2025, 58, 84. [Google Scholar] [CrossRef]
- Yuan, X.; Zhao, J.; Yang, Y.; Wang, Y. Hybrid parallel chaos optimization algorithm with harmony search algorithm. Appl. Soft Comput. 2014, 17, 12–22. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Abasi, A.K.; Makhadmeh, S.N.; Al-Betar, M.A.; Alomari, O.A.; Awadallah, M.A.; Alyasseri, Z.A.A.; Abu Doush, I.; Elnagar, A.; Alkhammash, E.H.; Hadjouni, M. Lemurs optimizer: A new metaheuristic algorithm for global optimization. Appl. Sci. 2022, 12, 10057. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).