A Novel Medical Image Encryption Algorithm Based on High-Dimensional Memristor Chaotic System with Extended Josephus-RNA Hybrid Mechanism

Abstract

Conventional image encryption schemes struggle to meet the high security demands of medical images due to their large data volume, strong pixel correlation, and structural redundancy. To address these challenges, we propose a grayscale medical image encryption algorithm based on a novel 5-D memristor chaotic system. The algorithm integrates a Symmetric L-type Josephus Spiral Scrambling (SLJSS) module and a Dynamic Codon-based Multi-RNA Diffusion (DCMRD) module to enhance spatial decorrelation and diffusion complexity. Simulation results demonstrate that the proposed method achieves near-ideal entropy (e.g., 7.9992), low correlation (e.g., 0.0043), and high robustness (e.g., NPCR: 99.62%, UACI: 33.45%) with time complexity of $\mathcal{O}\left(11MN\right)$, confirming its effectiveness and efficiency for medical image protection.

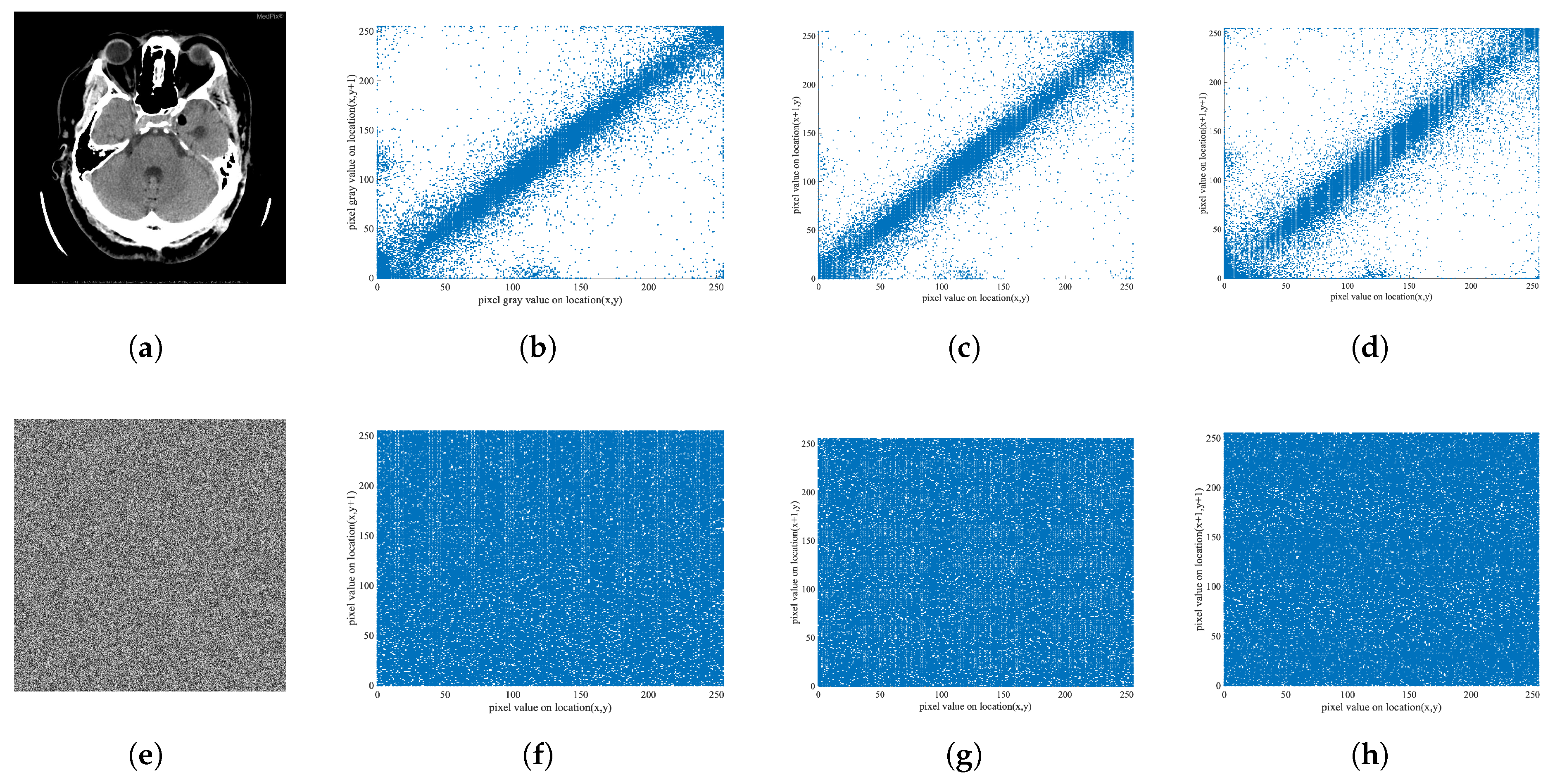
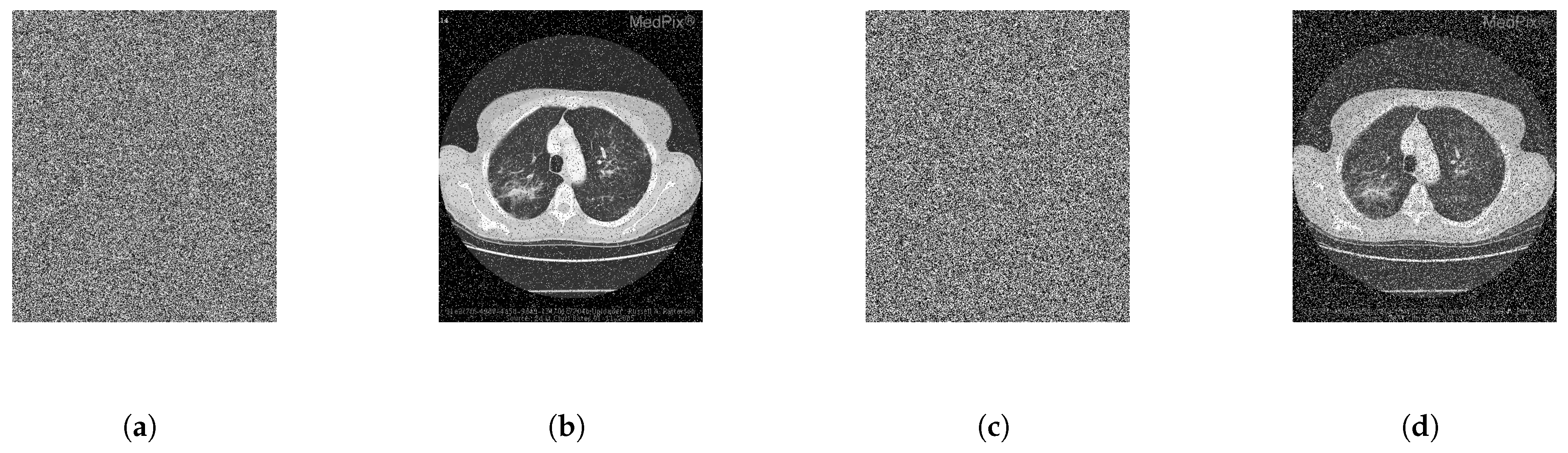
1. Introduction

Modern healthcare systems increasingly rely on Electronic Health Records (EHRs), which integrate and transmit medical images as part of patient data management. These images often contain sensitive personal information, exhibit high inter-pixel correlations, and involve large data volumes—especially in grayscale formats. Unauthorized access or misuse can result in serious privacy breaches, highlighting the critical need for secure image transmission to ensure confidentiality, integrity, and privacy [1,2].

Conventional data encryption algorithms such as AES (Advanced Encryption Standard), DES (Data Encryption Standard), and IDEA (International Data Encryption Algorithm) are primarily designed for textual data. These methods encrypt binary representations of digital data streams, but they are often inefficient for medical images due to their high redundancy and large size [3]. To address image-specific security challenges, various alternatives—such as steganography [4], watermarking [5], and image encryption [6]—have been proposed. Among them, image encryption is particularly effective in converting images into noise-like ciphertext, thereby concealing their content during transmission.

Numerous image encryption techniques have been explored, including DNA-based encryption [7,8,9], cellular automata [10], compressive sensing [11], fractional Fourier transforms [12], S-boxes [13], fractal theory [14], neural networks [15], and chaotic systems [6,16,17]. Among these techniques, chaotic systems have shown particular promise due to their inherent features, such as sensitivity to initial conditions, topological transitivity, and unpredictability, which align well with cryptographic principles.

The complexity of a chaotic system directly influences the security of the encryption algorithm. However, when implemented on finite-precision platforms, chaotic systems may suffer from degradation, wherein chaotic behavior deteriorates into periodic or predictable patterns, thereby compromising encryption strength. To overcome this limitation, researchers have explored methods to improve the dynamic complexity and robustness of chaotic systems.

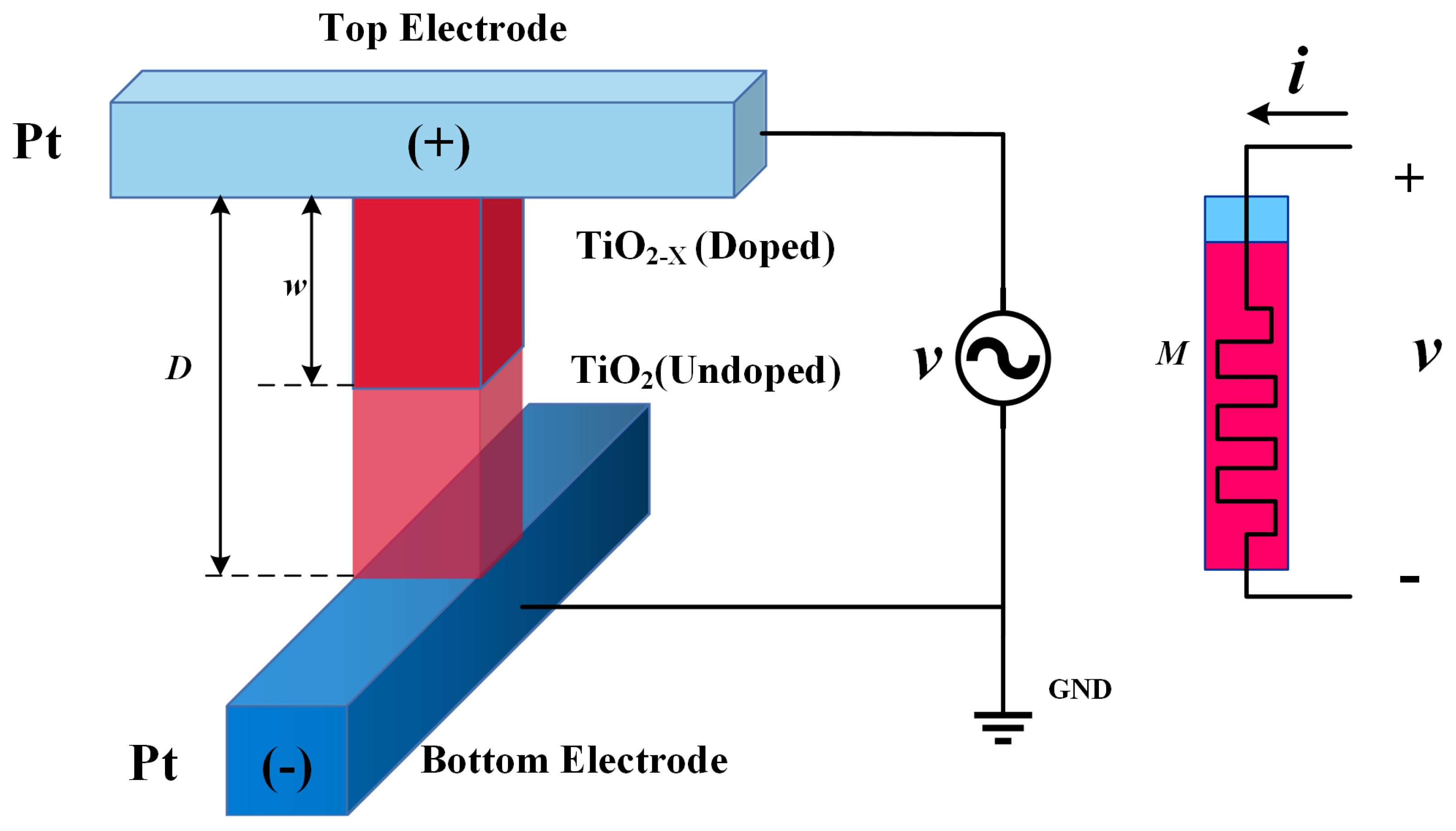
The concept of the memristor was first introduced by Professor Chua in 1971, who theoretically defined it as the fourth fundamental circuit element relating magnetic flux and electric charge [18]. In 2008, researchers at HP Labs fabricated the first physical memristor using titanium dioxide nanomaterials, reigniting global interest in this field [19]. Due to their non-volatility, nanoscale structure, and state-dependent behavior, memristors could be applied in various fields, including encryption algorithms [11,19], secure communications [20], neural networks [21], electrical engineering [22], and artificial intelligence [23].

Recent research has shown that integrating memristors into classical chaotic maps, such as sine maps, Hénon maps, and higher-order systems, can effectively improve the diversity of their dynamic behaviors [21]. By mitigating finite-precision degradation and enhancing system unpredictability, memristor-based chaotic systems provide a more secure foundation for cryptographic applications [19]. For instance, Yu et al. [24] proposed a 5-D memristor exponential hyperchaotic system based on a nonlinear flux-controlled model and demonstrated its feasibility for image encryption. Awais et al. [25] introduced a novel chaotic system constructed from two flux-controlled memristors, exhibiting symmetric bifurcation, multistability, and extreme sensitivity to initial conditions within a 4-D dynamical framework. These works validate the advantages of memristor-based systems in constructing robust chaotic models, though their application to medical image encryption remains underexplored [26].

Since Fridrich’s introduction of the scrambling–diffusion encryption framework using 2-D discrete chaotic maps, this structure has become foundational in image cryptography. In this model, scrambling alters pixel positions, while diffusion modifies pixel values. To enhance encryption performance, researchers have often combined such frameworks with novel chaotic systems [27].

Traditional image scrambling methods include row–column scrambling, Arnold transforms, curve transformations, scan-based traversal, and block scrambling. Despite their structural differences, these methods typically suffer from periodicity, limited randomness, and local effects, especially in some block-based algorithms that ignore inter-block correlation. Due to their non-periodic nature and ease of implementation, Josephus-based scrambling methods have gained attraction. Wang et al. [28] applied Josephus scrambling independently to image rows and columns in three iterative cycles, but the time complexity is relatively high. Guan et al. [29] enhanced the classical Josephus method by replacing removal operations with shift operations and introduced random step sizes from chaotic sequences, while there is still room for improvement in the robustness of the algorithm. Xie et al. [30] proposed block-wise Josephus scrambling based on traversal paths, improving global pixel scrambling, albeit at the cost of inter-block correlation. In addition, the above scrambling algorithms are mostly composed of a single Josephus algorithm, and there is still room for improving the complexity of pixel-point obfuscation.

On the diffusion side, DNA-inspired operations have shown promise due to their large storage capacity, low energy consumption, and fast computation [31,32]. Nevertheless, several limitations have emerged. Liu et al. [33] evaluated a DNA encryption algorithm from [34] and found it deficient in plaintext sensitivity and vulnerable to chosen-plaintext and known-plaintext attacks. Hermassi et al. [35] similarly identified irreversibility and poor resistance to statistical attacks in the DNA-based algorithm from [36]. In contrast to the double-helix structure of DNA, RNA operates as a single-stranded molecule, offering greater flexibility. RNA diffusion algorithms exploit base-pairing rules to form temporary helices and use codons—triplets of nucleotides that translate to amino acids—to enrich diffusion strategies [37]. For instance, Wang et al. [38] proposed a method involving modular RNA operations and random codon replacement. Zhou et al. [39] presented a 2-D hyperchaotic map-based RNA diffusion algorithm. However, current RNA-based methods still suffer from overly simplistic operations, redundant encoding rules, and limited variation in processing modes, reducing their resistance to plaintext attacks. Moreover, the potential of amino acid codon mappings remains underexplored in diffusion design.

Cryptography and cryptanalysis are two interrelated branches of cryptology. While encryption focuses on enhancing confusion, diffusion, and efficiency, cryptanalysis evaluates systems from an adversarial perspective, exposing structural vulnerabilities and key management flaws. Recent studies have identified several common weaknesses in chaos-based image encryption schemes, such as static key streams susceptible to chosen-plaintext attacks, over-reliance on external data, and redundant operations [40,41]. To address these issues, researchers suggest incorporating image-dependent features (e.g., hash values) into key generation, diversifying chaotic sequence usage, streamlining encryption steps, and applying more comprehensive security evaluations.

In summary, medical image encryption faces two fundamental challenges: (1) Due to the large data volume and high inter-pixel correlation inherent in medical images, conventional scrambling techniques often result in localized scrambling, which fails to sufficiently disrupt global structural dependencies—particularly along diagonal directions; and (2) DNA/RNA-based diffusion methods tend to be structurally simplistic, offering limited diffusion strength and involving redundant transformation rules with insufficient computational diversity. In light of these challenges, there is a growing imperative to develop encryption algorithms tailored to the protection of medical images—algorithms that are not only secure and efficient, but also lightweight, image-adaptive, and resource-conscious, with strong diffusion and high key sensitivity.

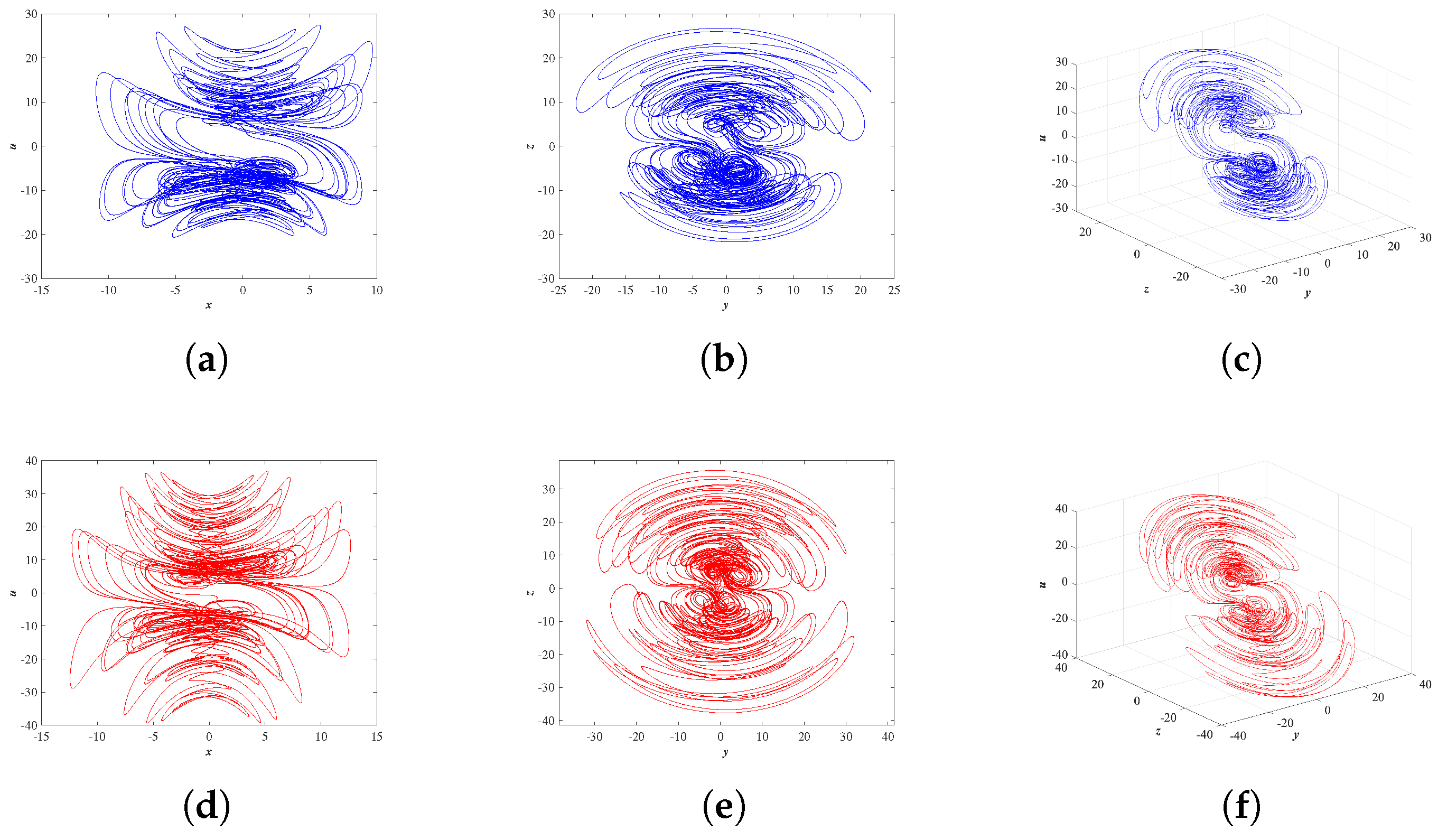
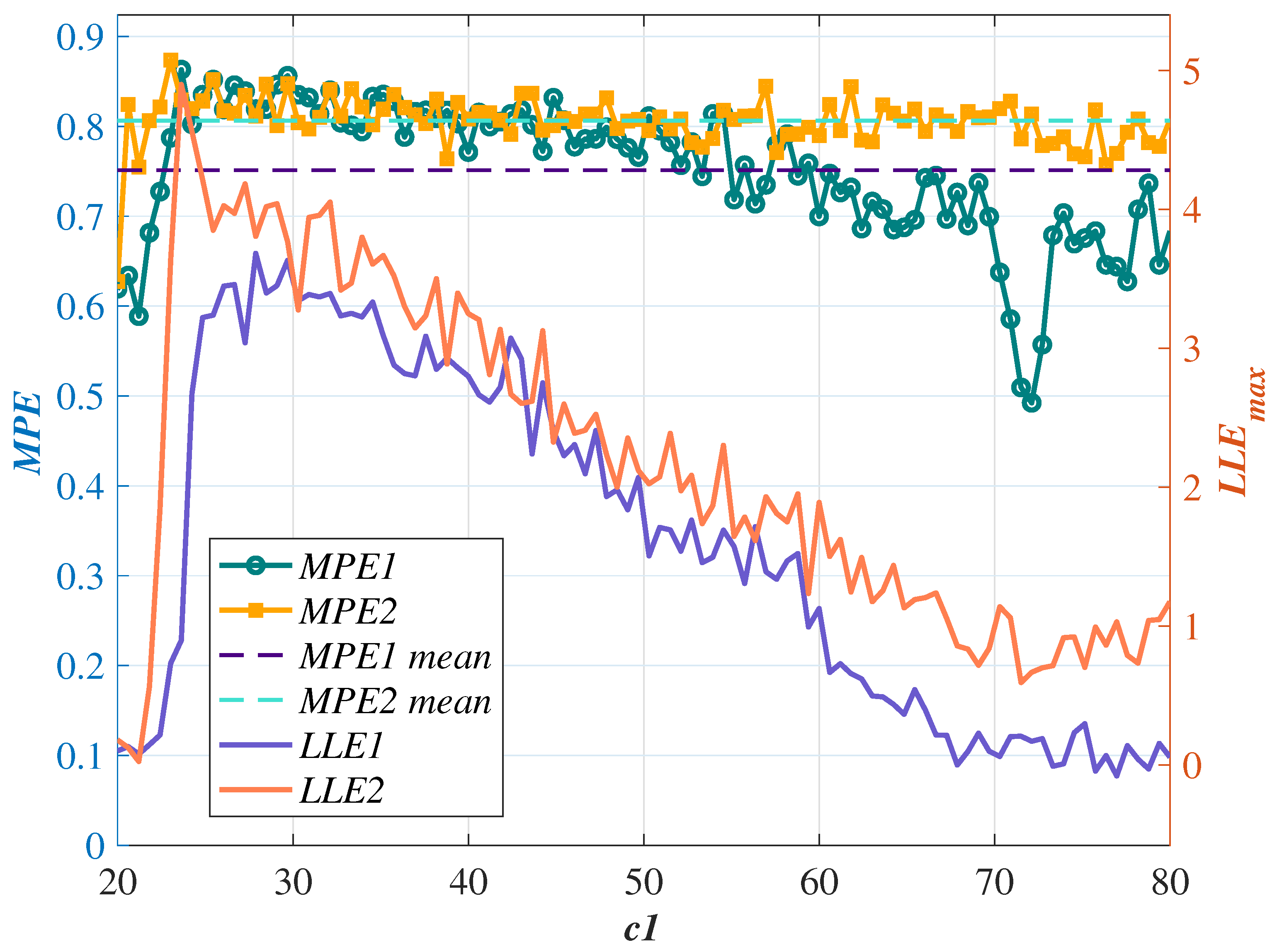
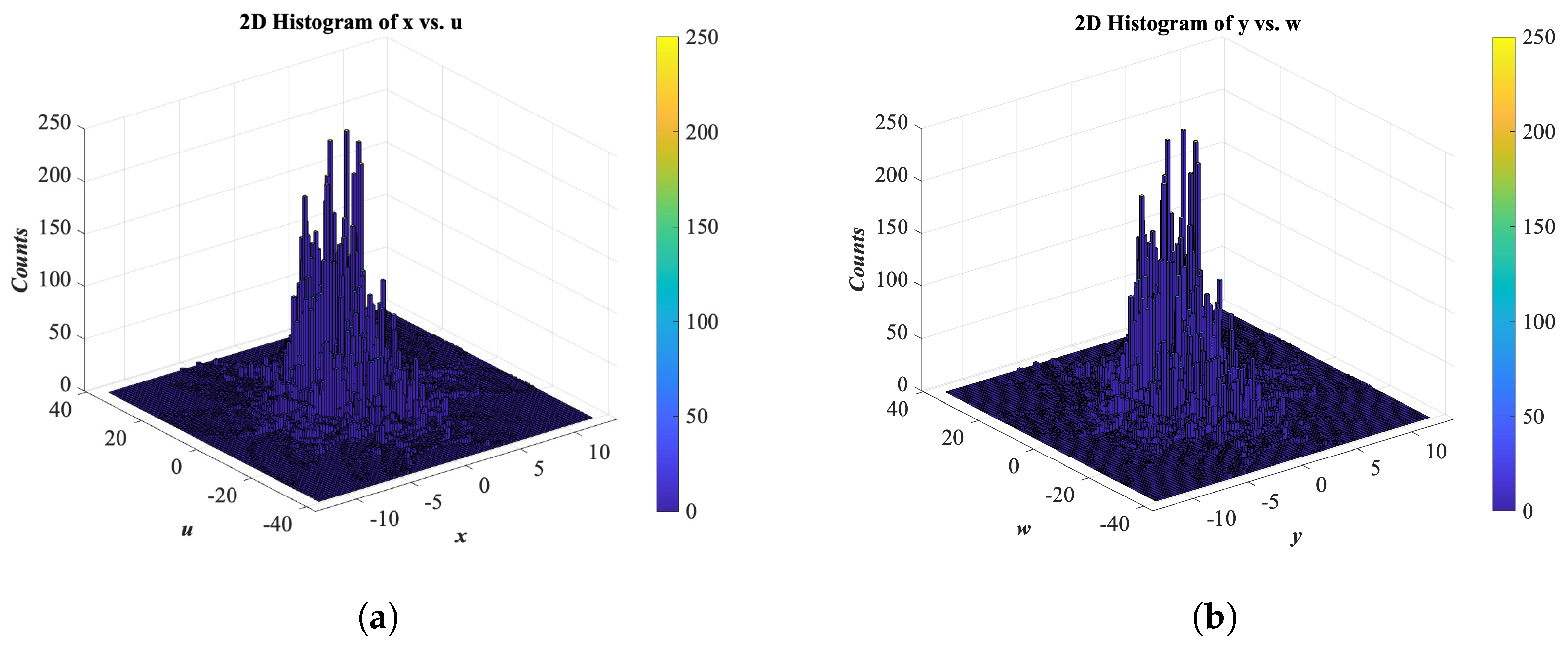
To address these gaps, this study proposes a novel grayscale medical image encryption algorithm. First, we construct a new high-dimensional memristor chaotic system based on the HP memristor model. Through bifurcation diagrams, Lyapunov exponent diagrams, complexity analysis, and histogram analysis, we demonstrate that the system exhibits broader chaotic ranges, superior ergodicity, and higher dynamic complexity. To enhance resistance against chosen-plaintext and equivalent-key attacks, the system’s initial conditions are derived from the plaintext image’s SHA-256 hash. The resulting chaotic sequences are further diversified and integrated into the following stages of encryption, avoiding static or repetitive use. The scrambling stage employs the SLJSS algorithm, which combines L-shaped decomposition, enhanced Josephus traversal, and spiral reconstruction to disrupt global pixel correlations efficiently with minimal redundancy. The diffusion process is implemented via the DCMRD algorithm, featuring dynamic RNA encoding, codon-level substitution, and multiple RNA operations before final reverse decoding. This structure aims to balance complexity and security while avoiding unnecessary computational overhead. Finally, we perform a comprehensive security evaluation beyond conventional statistical and randomness tests. The results collectively suggest that the proposed algorithm achieves strong key dependence, high diffusion strength, and structural robustness.

The main contributions of this work are as follows:

• A novel 5-D memristor chaotic system based on the HP model is proposed, offering high complexity and randomness suitable for secure encryption.
• In the scrambling phase, we introduce the SLJSS algorithm, which follows a symmetric design combining forward and reverse L-type decomposition, improved Josephus scrambling, and non-deterministic spiral reconstruction. This multi-layered strategy ensures low correlation across rows, columns, and diagonals. In the diffusion phase, the DCMRD algorithm is proposed to combine codon substitution and RNA base operations. In it, we optimize the operation rules to reduce the repetition and redundancy of the results and propose a multiple base operation model that contains addition, subtraction, XOR, multiplication, and custom base functions, which guarantees the diversity, randomness, and security of the whole encryption process.
• Simulation results demonstrate that the proposed algorithm achieves high encryption and decryption quality, exhibits strong statistical and differential resistance, and outperforms comparable methods in reducing pixel correlation.

The remainder of this paper is organized as follows. Section 2 details the construction of the proposed memristor chaotic system. Section 3 presents the design principles and process of the encryption algorithm. Section 4 provides simulation results and theoretical analysis regarding security and performance. Section 5 shows the conclusion of this paper.

2. Chaotic System

We have improved the 5-D chaotic system based on HP memristor and constructed a new 5-D memristor chaotic system. This section explains the idea and method of system improvement in detail, and analyzes the chaos, traversal, and randomness of the new system by phase diagram, bifurcation diagram, maximum Lyapunov exponential diagram, and MPE diagram.

2.1. HP Memristor Model

The physical model of the HP memristor is illustrated in Figure 1. It consists of two layers: a high-resistance $Ti{O}_2$ thin film and a positively charged, low-resistance $Ti{O}_{2-x}$ thin film, which lacks some oxygen atoms. When current flows counterclockwise through the device, the boundary between the two materials shifts, increasing the proportion of the $Ti{O}_{2-x}$ layer and reducing the overall resistance. Conversely, when current flows clockwise, the $Ti{O}_2$ layer dominates, increasing the resistance. Notably, when the current ceases, the resistance remains unchanged. This memory characteristic underpins its frequent use in enhancing the dynamic behavior of chaotic systems [20].

A general magnetic flux-controlled HP memristor model is expressed as follows [20]:

$$M\left(t\right)=\left\{\begin{array}{cc}{R}_{\mathrm{OFF}},\hfill & \phi \left(t\right)<c_1\hfill \\ \sqrt{2k\phi \left(t\right)+M^2\left(0\right)},\hfill & c_1\le \phi \left(t\right)<c_2\hfill \\ R_{\mathrm{ON}}.\hfill & \phi \left(t\right)\ge c_2\hfill \end{array}\right.$$

(1)

where

$$\left\{\begin{array}{cc}\hfill k& ={\displaystyle \frac{(R_{\mathrm{ON}}-R_{\mathrm{OFF}})·{\mu }_v·R_{\mathrm{ON}}}{D^2}},\hfill \\ \hfill c_1& ={\displaystyle \frac{R_{\mathrm{OFF}}^2-M^2}{2k}},\hfill \\ \hfill c_2& ={\displaystyle \frac{R_{\mathrm{ON}}^2-M^2}{2k}},\hfill \\ \hfill \phi \left(t\right)& ={\int }_0^{t}M\left(t\right)·i\left(t\right)dt\hfill \end{array}\right.$$

(2)

Here, $M\left(t\right)$ denotes the memristance. $w\left(t\right)$ is the time-varying thickness of the $Ti{O}_{2-x}$ film layer, and D is the total thickness of the $Pt-Ti{O}_{2-x}-Ti{O}_2-Pt$ semiconductor film of the memory resistor. The $R_{OFF}$ and $R_{ON}$ correspond to the resistance values when $w\left(t\right)=0$ and $w\left(t\right)=D$, respectively. ${\mu }_V$ represents the average mobility of oxygen vacancies, and $\phi \left(t\right)$ is the magnetic flux within the memristor.

2.2. 5-D Chaotic System Based on the HP Memristor

We adopt the 5-D chaotic system proposed by Eesa et al. [33] as the baseline model, defined as Equation (3). This system includes three cubic nonlinear product terms, eleven linear terms, and seven system parameters, offering flexibility in integrating the memristor model and a large key space suitable for secure encryption. The inherently complex dynamics of this system also provide a strong foundation for further optimization.

$$\left\{\begin{array}{c}\dot{x}=-c_{1}x+c_{1}y,\hfill \\ \dot{y}=c_{2}x+c_{2}y+w-xzu,\hfill \\ \dot{z}=-c_{3}y-c_{4}z-c_{5}u+xyu,\hfill \\ \dot{u}=-c_{6}u+xyz,\hfill \\ \dot{w}=-c_{7}x-c_{7}y.\hfill \end{array}\right.$$

(3)

Let $c_i(1\le i\le 7)$ be the control parameters, and $x\left(1\right), y\left(1\right), z\left(1\right), u\left(1\right), w\left(1\right)$ the initial conditions that define the phase space trajectories. When $c_i=[30, 10, 15.7, 5, 2.5, 4.45, 38.5]$, the system exhibits chaotic behavior.

In this work, we construct a new 5-D chaotic system by replacing the y-variable in the fifth differential equation of the original system with the memristor’s magnetic flux $\phi$, resulting in a memristor chaotic system. The state equations of the new system are shown in Equation (4):

$$\left\{\begin{array}{c}\dot{x}=-c_{1}x+c_{1}y,\hfill \\ \dot{y}=c_{2}x+c_{2}y+w-xzu,\hfill \\ \dot{z}=-c_{3}y-c_{4}z-c_{5}u+xyu,\hfill \\ \dot{u}=-c_{6}u+xyz,\hfill \\ \dot{w}=-c_{7}x-c_{7}f\left(\right|y\left|\right).\hfill \end{array}\right.$$

(4)

Here, $f(·)$ is the nonlinear term of the system which satisfies the relationship between magnetic flux and charge:

$$f\left(y\right)=\left\{\begin{array}{ccc}{\displaystyle \frac{y+{\displaystyle \frac{{(R_{\mathrm{OFF}}-M\left(0\right))}^2}{2k}}}{R_{\mathrm{OFF}}}},\hfill & \hfill & y<c_1\hfill \\ {\displaystyle \frac{\sqrt{2ky+M^2\left(0\right)}-M\left(0\right)}{k}},\hfill & \hfill & c_1\le y<c_2\hfill \\ {\displaystyle \frac{y+{\displaystyle \frac{{(R_{\mathrm{ON}}-M\left(0\right))}^2}{2k}}}{R_{\mathrm{ON}}}},\hfill & \hfill & y\ge c_2\hfill \end{array}\right.$$

(5)

where the y variable in the second deferential equation is the input magnetic flux $\phi$ of the memristor. Specifically, its relational equation is deduced from the above Equation (1), with $k,c_1,c_2,\phi$ parameters satisfying Equation (2).

2.3. Dynamical Analysis of the Chaotic System

To validate the enhanced randomness and complexity of the proposed 5-D memristor chaotic system (Equation (4)), we conduct a comprehensive analysis from five perspectives: attractor phase diagrams, Largest Lyapunov Exponents (LLEs), bifurcation diagrams, sequence complexity, and histogram-based statistical analysis. Notably, the histogram analysis focuses solely on the memristor-based system—used later for image encryption—to evaluate its pseudo-randomness and statistical suitability for secure applications, without comparison to the original system.

It is worth noting that the memristor model adopted in our work is the generic continuous magnetron titanium dioxide model proposed in [20], which has been rigorously demonstrated to exhibit the three fingerprint characteristics of memristors: (i) pinched hysteresis loops, (ii) passivity, and (iii) non-volatility. In particular, the hysteresis loop lobe areas of this model have been shown to monotonically decrease with increasing sinusoidal signal frequency, eventually collapsing into a single-valued function as the frequency tends to infinity. Given that these dynamic properties have been thoroughly validated in the original work, we do not repeat the hysteresis loop plots in this paper.

2.3.1. Attractor Phase Diagrams

$R_{OFF}=20 \mathrm{k}\Omega , R_{ON}=0.1 \mathrm{k}\Omega$ are the maximum and minimum values of the memristor resistance, respectively, $M\left(0\right)=1.6\times {10}^4\mathrm{k}\Omega$ denotes the initial state value of the memristor, ${\mu }_V={10}^{-10}{\mathrm{cm}}^2{\mathrm{s}}^{-1}{\mathrm{V}}^{-1}$ denotes the average mobility of the oxygen vacancies, and $D=10\mathrm{nm}$ denotes the thickness of the film of the memristor device; the system’s initial values are $x\left(1\right)=0.8,y\left(1\right)=4.9,z\left(1\right)=7.6,u\left(1\right)=3.7,w\left(1\right)=6.5$, and the control parameter values of the system are $c_i=[30,10,15.7,5,2.5,4.45,38.5]$. These parameters are used consistently in subsequent simulations.

The attractor phase diagrams of both systems, simulated using a fourth-order Runge–Kutta method, are presented in Figure 2. On the plane, both systems exhibit double-scroll attractor structures with similar spatial distributions—centered around the scroll cores and diffusing outward—indicating that our modified system retains the core attractor structure of the original system.

2.3.2. Bifurcation Diagrams

Bifurcation diagrams provide intuitive insights into how dynamical behavior changes with variations in control parameters [42,43]. As parameter $c_1$ varies over [20, 80], Figure 3a shows that the original system exhibits periodic behavior when $c_1<23$ or $c_1>63$, and chaotic behavior when $c_1\in [23,63]$. Figure 3b illustrates that the memristor system has a narrower periodic window and a significantly expanded chaotic range, suggesting improved complexity.

2.3.3. LLE and MPE

The Lyapunov exponent (LE) quantitatively characterizes how system trajectories diverge over time, with a positive maximum LE indicating chaos. Multi-scale Permutation Entropy (MPE), ranging between 0 and 1, assesses the complexity and nonlinearity of time series. Higher values of both LLE and MPE indicate greater system randomness and unpredictability [44].

As shown in Figure 4, when $c_1\approx 23$, the original system’s LLE1 is significantly lower than the memristor system’s LLE2. Furthermore, as $c_1\in [60,80]$, LLE1 approaches zero in the original system, while LLE2 in the memristor system remains near 1, indicating continued chaotic behavior—consistent with the bifurcation results.

Similarly, MPE exhibits trends aligned with LLE. For $c_1\in [20,80]$, the average MPE2 of the memristor system is 0.81, compared to 0.75 for MPE1 in the original system. Particularly in $c_1\in [20,23]\cup [60,80]$, MPE2 significantly exceeds MPE1. These results confirm that integrating the HP memristor enhances both the chaotic degree and the complexity of the original system.

2.3.4. Statistical Histogram Analysis

To further demonstrate the statistical complexity and pseudo-random behavior of the proposed 5-D memristor chaotic system, we performed both one-dimensional and two-dimensional histogram analyses based on the system’s state variable trajectories.

One-dimensional histograms: Figure 5 displays the PDFs (Probability Density Functions) of the five state variables $(x,y,z,u,w)$, computed from the last half of a simulated trajectory with a time step $h=0.0005$ and a total duration of N = 100,000 points. The histograms exhibit broad, irregular, and non-Gaussian distributions, which reflect the system’s strong nonlinearity, high complexity, and ergodicity. Notably, the variable u exhibits a bimodal shape, while w displays multimodal behavior, attributed to the nonlinear memory dynamics of the memristor model. These statistical features support the system’s suitability for secure cryptographic applications.

Two-dimensional histogram: To further assess joint statistical properties and inter-variable independence, we computed a 2-D histogram for the variables $(x,u)$, as shown in Figure 6. The vertical axis (z-axis) indicates the number of samples (i.e., Counts) that fall into each bin defined by the $(x,u)$ plane, representing the empirical joint probability density. The resulting distribution is dense, patternless, and well spread across the phase space, indicating strong statistical decorrelation between variables. This supports the system’s high-dimensional pseudo-randomness and good space-filling behavior—properties that are desirable for cryptographic key stream generation.

3. Proposed Encryption Algorithm

This section introduces a novel encryption algorithm for grayscale medical images of arbitrary size, based on the 5-D memristor chaotic system. The scrambling phase utilizes the SLJSS algorithm, while the diffusion phase employs the DCMRD algorithm. The algorithm achieves efficient encryption without requiring multiple iterative rounds and guarantees lossless recovery of the encrypted image.

Assume the plaintext image I has dimensions $m\times n$. The overall encryption process is summarized as follows and each step would be described in details in sub-sections:

Step 1:

Input the plaintext image I and key. As described in Section 3.1, compute the initial value using the SHA-256 hash of image-derived values. Perform a series of operations to obtain the initial conditions and parameters for the chaotic system.

Step 2:

As detailed in Section 3.2, a series of operations are performed on the chaotic system to obtain pseudo-random sequences referred to as the Key Sequence.

Step 3:

According to Section 3.3, perform symmetric L-type decomposition, Josephus scrambling, and spiral sequence reconstruction on I, yielding the scrambled matrix $P_2$.

Step 4:

As shown in Section 3.4, apply RNA dynamic encoding, codon substitution, multi-base operations, and RNA decoding to $P_2$, producing the final ciphertext Encrypted Image.

A flowchart summarizing the full encryption process is provided in Figure 7.

3.1. Generation of the Initial Values of Chaotic System

In chaos-based encryption systems, the security and sensitivity of the algorithm are closely tied to the choice of the chaotic system’s initial values and control parameters. While the control parameters are defined by the secret key ($c_i,1\le i\le 7$), the initial values must be dynamically linked to the plaintext image to resist chosen-plaintext and known-plaintext attacks.

To achieve this coupling, the cryptographic SHA-256 hash function is employed. Thanks to its irreversibility and strong avalanche effect, even a single-bit change in the input leads to a completely different hash output. Compared with lighter hash functions such as MD5, SHA-256 provides higher resistance to collision and preimage attacks, making it a more suitable choice for high-security scenarios like medical image encryption. This design ensures that any variation in the plaintext image will result in a different chaotic trajectory, thereby significantly enhancing the encryption algorithm’s plaintext sensitivity and security strength [45].

The construction process is as follows: the input image is first processed to extract statistical features in three directions—row, column, and diagonal—yielding three summation vectors: SumRow, SumCol, and SumDiag. These are individually hashed and then combined to generate a decimal key vector $KeyDec=k_1,k_2,\dots ,k_{32}$ as follows:

$$\left\{\begin{array}{ccc}\text{KeyDec}\hfill & =& \mathrm{SHA}256\left(\mathrm{SHA}256\left(\mathrm{SumRow}\right),\mathrm{SHA}256\left(\mathrm{SumCol}\right),\mathrm{SHA}256\left(\mathrm{SumDiag}\right)\right),\hfill \\ \mathrm{KeyFeature}\hfill & =& \left(\sum _{j=0}^7\underset{i=1}{\overset{4}{⨁}}{k}_{4j+i}\right)mod256.\hfill \end{array}\right.$$

(6)

To further enhance randomness, a key feature value $KeyFeature$ is computed using modular sums of XOR combinations. This value is then used to perturb each initial state, ensuring their dependence on the plaintext.

The initial values of the chaotic system’s five state variables $x\left(1\right),y\left(1\right),z\left(1\right),u\left(1\right),w\left(1\right)$ and the transient iteration count h are calculated as follows:

$$\left\{\begin{array}{cc}\hfill x\left(1\right)& ={\displaystyle \frac{k_1\oplus k_2\oplus k_3\oplus k_4\oplus k_5\oplus k_6\oplus \mathrm{KeyFeature}}{256}},\hfill \\ \hfill y\left(1\right)& ={\displaystyle \frac{k_7\oplus k_8\oplus k_9\oplus k_{10}\oplus k_{11}\oplus k_{12}\oplus \mathrm{KeyFeature}}{256}},\hfill \\ \hfill z\left(1\right)& ={\displaystyle \frac{k_{13}\oplus k_{14}\oplus k_{15}\oplus k_{16}\oplus k_{17}\oplus k_{18}\oplus \mathrm{KeyFeature}}{256}},\hfill \\ \hfill u\left(1\right)& ={\displaystyle \frac{k_{19}\oplus k_{20}\oplus k_{21}\oplus k_{22}\oplus k_{23}\oplus k_{24}\oplus \mathrm{KeyFeature}}{256}},\hfill \\ \hfill w\left(1\right)& ={\displaystyle \frac{k_{25}\oplus k_{26}\oplus k_{27}\oplus k_{28}\oplus k_{29}\oplus k_{30}\oplus \mathrm{KeyFeature}}{256}},\hfill \\ \hfill h& =k_{31}+k_{32}.\hfill \end{array}\right.$$

(7)

This approach ensures that the chaotic initial conditions are uniquely tied to the plaintext image, providing strong one-time randomness and enhancing the encryption system’s ability to withstand differential and statistical attacks. The complete process is illustrated in Algorithm 1.

Algorithm 1: Key Generation

Input: Plain Image I Output: $x\left(1\right),y\left(1\right),z\left(1\right),u\left(1\right),w\left(1\right),h$ 1  $x\leftarrow 0$ 2  $$\begin{gathered} KeyDec= \\ SHA256(SHA256\left(\mathrm{SumRow}\right),SHA256\left(\mathrm{SumCol}\right),SHA256\left(\mathrm{SumDiag}\right))= \\ \{k_1,k_2,\dots ,k_{32}\} \\ KeyFeature=mod\left(\right(k_1\oplus k_2\oplus k_3\oplus k_4)+\dots +(k_{29}\oplus k_{30}\oplus k_{31}\oplus k_{32}),256) \end{gathered}$$ 3  $x\left(1\right)=(k_1\oplus k_2\oplus k_3\oplus k_4\oplus k_5\oplus k_6\oplus KeyFeature)/256$ 4  $y\left(1\right)=(k_7\oplus k_8\oplus k_9\oplus k_{10}\oplus k_{11}\oplus k_{12}\oplus KeyFeature)/256$ 5  $z\left(1\right)=(k_{13}\oplus k_{14}\oplus k_{15}\oplus k_{16}\oplus k_{17}\oplus k_{18}\oplus KeyFeature)/256$ 6  $u\left(1\right)=(k_{19}\oplus k_{20}\oplus k_{21}\oplus k_{22}\oplus k_{23}\oplus k_{24}\oplus KeyFeature)/256$ 7  $w\left(1\right)=(k_{25}\oplus k_{26}\oplus k_{27}\oplus k_{28}\oplus k_{29}\oplus k_{30}\oplus KeyFeature)/256$ 8  $h=k_{31}+k_{32}$

3.2. Generation of Key Sequences

In a chaos-based image encryption framework, the core cryptographic operations—such as scrambling and diffusion—require secure and image-dependent pseudo-random sequences to drive nonlinear transformations. Therefore, in this stage, we construct a series of key sequences from the initial conditions and control parameters of the 5-D memristor chaotic system generated in Section 3.1. Since these chaotic states are directly influenced by the plaintext image, the resulting sequences inherit strong plaintext sensitivity, ensuring that even the slightest change in the input image produces a completely different encryption trajectory.

To further enhance unpredictability and mitigate finite-precision degradation during numerical integration, a periodic perturbation mechanism is introduced to the chaotic system. Meanwhile, the generated sequences are mapped to different rule vectors, which are required in downstream modules such as codon transformation, scrambling, and DNA-level diffusion. For ease of control and modular reuse, we apply expansion, rounding, and modulo operations to generate distinct sub-sequences (e.g., $CodeRule$, $CodonRule$, $KeyImage$, $opRule$, and $Operation$), each serving a dedicated functional role.

The complete generation process is outlined below:

Step 1:

The 5-D memristor chaotic system is initialized with $x\left(1\right)$, $y\left(1\right)$, $z\left(1\right)$, $u\left(1\right)$, and $w\left(1\right)$ and is numerically integrated using the fourth-order Runge–Kutta method. To eliminate transient behavior and enhance randomness, the first h iterations are discarded. Then, the system is iterated $4mn$ times to generate five chaotic sequences: X, Y, Z, U, and W. To suppress dynamical degradation caused by finite-precision computation, a perturbation is added every 2000 iterations using the following equation:

$$x0=x0+h\times sin\left(y0\right).$$

(8)

Step 2:

These chaotic sequences are processed to derive the operational rule vectors as follows:

$$\left\{\begin{array}{ccc}\mathrm{CodeRule}\hfill & =\hfill & mod(\mathrm{abs}\left(\mathrm{floor}(X·{10}^{12})\right),8)+1,\hfill \\ \mathrm{CodonRule}\hfill & =\hfill & Y,\hfill \\ \mathrm{KeyImage}\hfill & =\hfill & mod(\mathrm{abs}\left(\mathrm{floor}(Z·{10}^{12})\right),4),\hfill \\ \mathrm{opRule}\hfill & =\hfill & mod(\mathrm{abs}\left(\mathrm{floor}(U·{10}^{12})\right),4)+1,\hfill \\ \mathrm{Operation}\hfill & =\hfill & mod(\mathrm{abs}\left(\mathrm{floor}(W·{10}^{12})\right),5)+1.\hfill \end{array}\right.$$

(9)

Step 3:

The first $m+n$ elements of U and the first $2+8\lceil (m+n)/2\rceil$ elements of W are concatenated to form a sequence S.

Step 4:

The first half of S is used to compute scrambling control parameters $A_1$, $A_2$, $A_3$, $p_1$, and $sort1$:

$$\left\{\begin{array}{c}\mathrm{layer}=min(m,n),\hfill \\ A_1=\hspace{1em}mod\left.(\mathrm{floor}\left(S(n+m+1:n+m+\mathrm{layer})·{10}^{12}\right),\mathrm{layer}\right)+1,\hfill \\ A_2=\hspace{1em}mod\left.(\mathrm{floor}\left(S(n+m+\mathrm{layer}+1:n+m+2·\mathrm{layer})·{10}^{12}\right),10\right)+1,\hfill \\ A_3=\hspace{1em}mod\left.(\mathrm{abs}\left(\mathrm{floor}\left(S(n+m+2·\mathrm{layer}+1:n+m+3·\mathrm{layer})·{10}^{12}\right)\right),2\right),\hfill \\ p_1=\hspace{1em}mod\left.(\mathrm{abs}\left(\mathrm{floor}\left(S(n+m+3·\mathrm{layer}+1)·{10}^{12}\right)\right),4\right)+1,\hfill \\ [\sim ,\mathrm{sort}1]=\mathrm{sort}\left(S(n+m+3·\mathrm{layer}+2:n+m+4·\mathrm{layer}+1)\right).\hfill \end{array}\right.$$

(10)

Step 5:

The second half of S is processed similarly to obtain the parameters B₁, B₂, B₃, p₂, and sort2 for the second phase of scrambling.

These carefully constructed key sequences and control parameters serve as the backbone of subsequent encryption stages. Because they are generated from chaotic states that are image-dependent and perturbed periodically, they ensure high sensitivity, strong randomness, and resilience against cryptanalytic attacks. The full generation process is summarized in Algorithm 2.

3.3. Symmetric L-Type Josephus Spiral Scrambling

This section introduces the design rationale and implementation steps of the proposed symmetric L-type Josephus spiral scrambling (SLJSS) algorithm, which is responsible for the spatial permutation of pixel positions.

3.3.1. Design Background and Motivation

Traditional image scrambling methods often rely on row-wise, column-wise, or block-wise operations. While these methods disrupt local correlation, they frequently fail to sufficiently break long-range dependencies—especially diagonals and inter-block patterns—leading to potential cryptanalytic weaknesses. To address this limitation, we propose a multi-dimensional scrambling scheme that integrates the following:

• L-type stratification, to enable interconnection between row, column, and block regions and avoid local confinement;
• Extended Josephus permutation, to increase randomness through flexible control of direction, step size, and starting position;
• Spiral reconstruction, to enhance global reorganization and increase scrambling diversity;
• Symmetric bidirectional scrambling, to further reduce residual structural patterns.

Algorithm 2: Chaotic Sequence Generation
Input: x0: Initial values, N: sequence length, n: transient length Output: CodeRule, CodonRule, KeyImage, opRule, Operation, t1, t2, A1–A3, B1–B3, sort1, sort2, p1, p2
/* Step 1: Solve the chaotic system using RK45 integration	*/
1 $[X,Y,Z,U,W]\leftarrow \mathrm{RK}45\mathrm{Func}(x_0,N,t)$;
/* Step 2: Generate primary sequences	*/
2 $CodeRule\leftarrow mod(abs\left(floor(X·{10}^{12})\right),8)+1$;   3 $CodonRule\leftarrow Y$;   4 $KeyImage\leftarrow mod(abs\left(floor(Z·{10}^{12})\right),4)$;   5 $opRule\leftarrow mod(abs\left(floor(U·{10}^{12})\right),4)+1$;   6 $Operation\leftarrow mod(abs\left(floor(W·{10}^{12})\right),5))+1$;
/* Step 3: Construct S sequence	*/
7 $t_1\leftarrow m+n,t_2\leftarrow 2+8·ceil((m+n)/2x≔U(1:t1);h≔W(1:t2);S≔[x,h];$
/* Step 4: Derive scrambling parameters	*/
8 $\mathrm{layer}\leftarrow (m,n)$;   9 $A_1\leftarrow mod(floor(S(n+m+1:n+m+\mathrm{layer})·{10}^{12}),\mathrm{layer})+1$; 10  $A_2\leftarrow mod(floor(S(n+m+\mathrm{layer}+1:n+m+2·\mathrm{layer})·{10}^{12}),10)+1$; 11  $A_3\leftarrow mod(abs(floor(S(n+m+2·\mathrm{layer}+1:n+m+3·\mathrm{layer})·{10}^{12}),2)$; 12  $p_1\leftarrow mod(abs(floor(S(n+m+3·\mathrm{layer}+1)·{10}^{12}),4)+1$; 13  $[\sim ,\mathrm{sort}1]\leftarrow \mathrm{sort}\left(S\right(n+m+3·\mathrm{layer}+2:n+m+4·\mathrm{layer}+1\left)\right)$;
/* Step 5: Derive reverse parameters	*/
14  $B_1\leftarrow mod(floor(S(n+m+4·\mathrm{layer}+2:n+m+5·\mathrm{layer}+1)·{10}^{12}),\mathrm{layer})+1$; 15  $B_2\leftarrow mod(floor(S(n+m+5·\mathrm{layer}+2:n+m+6·\mathrm{layer}+1)·{10}^{12}),10)+1$; 16  $B_3\leftarrow mod(abs(floor(S(n+m+6·\mathrm{layer}+2:n+m+7·\mathrm{layer}+1)·{10}^{12}),2)$; 17  $p_2\leftarrow mod(abs(floor(S(n+m+7·\mathrm{layer}+2)·{10}^{12}),4)+1$; 18  $[\sim ,\mathrm{sort}2]\leftarrow \mathrm{sort}\left(S\right(n+m+7·\mathrm{layer}+3:n+m+8·\mathrm{layer}+2\left)\right)$;

Each of these components is carefully selected based on extensive experimental evaluation to maximize scrambling entropy and visual unrecognizability. The sequence and structure of each sub-step are determined through iterative testing and design reasoning, with the aim of avoiding insufficient or over-local scrambling.

3.3.2. Overview of the Josephus Scrambling Principle

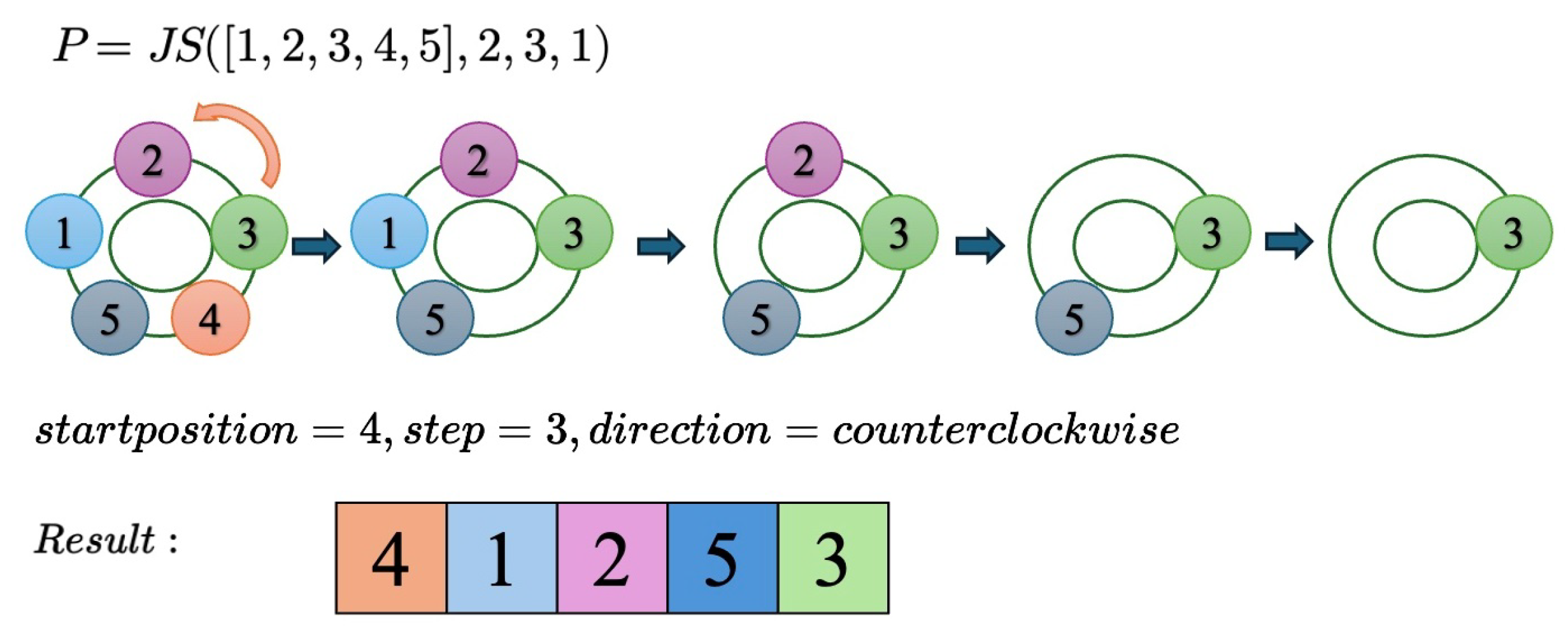
The core permutation logic is based on an extended form of the Josephus scrambling algorithm, which originates from the classical Josephus problem. In the classical variant, elements in a circular array are eliminated in a fixed step-size and direction. However, such static behavior results in limited permutation diversity. To overcome this, we define an extended Josephus function:

$$P=JS(I,w,v,d),$$

(11)

where I is the original sequence, $w+v-1$ denotes the starting index, v is the step size, and d indicates the traversal direction (odd d: counterclockwise; even d: clockwise). By dynamically deriving $(w,v,d)$ from chaotic sequences, each scrambling operation becomes data-dependent and unpredictable, thereby enhancing security.

As an illustrative example, consider $JS\left(\right[1,2,3,4,5],2,3,1)$. Starting from index $2+3-1=4$ in a clockwise circular array, we eliminate every 3rd element in counterclockwise order: 4 → 1 → 2 → 5 → 3, yielding the permutation $[4,1,2,5,3]$. A visual demonstration is shown in Figure 8.

3.3.3. Steps of Scrambling

The SLJSS algorithm integrates L-type decomposition, Josephus scrambling, and spiral reconstruction in a symmetric structure (forward and reverse). The following parameters derived from key sequences are used: $t_1,t_2,A_1,A_2,A_3,B_1,B_2$, $B_3,sort1,sort2,p_1,p_2$, as well as the plaintext image I. The design flow is as follows:

Step 1:

By means of Equation (12), the column scrambling of the plaintext image I is performed according to the $t_1$ sequence to achieve the initial randomization of the positions of the boundary and center pixel points to generate intermediate matrix $R1$.

$$R1(:,i)=I(:,t_1\left(i\right)),i=1,2,\dots n,$$

(12)

Step 2:

As illustrated in the upper right corner of Figure 9, the L-shaped stratification process starts from the top of the first column, traversing downward and then rightward to form the first L-shaped sequence (e.g., green region in $L_1$). The starting point then shifts one column to the right, and the process repeats to form the next L-shaped layer, until all elements are covered. This pattern resembles the shape of the letter “L”, hence the name L-shaped stratification.

The $L1$ array consisting of k-segment subsequences is first obtained by L-stratification of the $R1$ matrix. Then disarrangement is carried out for each subsequence $L1\left[i\right]$ in $L1$, where $A1\left[i\right]+A2\left[i\right]-1$ determines the position of the beginning of each disarrangement, $A2\left[i\right]$ determines the step size, and $A3\left[i\right]$ determines the direction of each disarrangement, and finally, the $R2$ array containing k-segment disarrangement sequences is obtained. The calculation is shown in Equation (13):

$$\left\{\begin{array}{ccc}\hfill k& =& \min (m,n),\hfill \\ \hfill L_1& =& \mathrm{Lsplit}(R_1,k),\hfill \\ \hfill R_2& =& \mathrm{JS}(L_1,A_1,A_2,A_3).\hfill \end{array}\right.$$

(13)

Step 3:

Concatenate the k scrambled sequences in $R_2$ using $sort1$, and reshape the resulting one-dimensional array into an $m\times n$ matrix $R_3$ using one of four spiral reconstruction paths determined by $p_1\in \{1,2,3,4\}$. The four paths are defined as follows:

• Pattern 1: Start from the top-left corner and traverse the matrix in a clockwise spiral.
• Pattern 2: Start from the top-right corner and traverse the matrix in a counterclockwise spiral.
• Pattern 3: Start from the bottom-left corner and traverse the matrix in a counterclockwise spiral.
• Pattern 4: Start from the bottom-right corner and traverse the matrix in a clockwise spiral.

These diversified splicing patterns enhance the diffusion and randomness of pixel positions in the final matrix.

Step 4:

Through Equation (14), the $R3$ matrix is row transformed according to the $t_2$ sequence, which further realizes the adjustment of the boundary and center pixel positions to obtain the $R4$ matrix.

$$R4(j,:)=R3(t_2\left(j\right),:),j=1,2,\dots ,m,$$

(14)

Step 5:

Like step 2, apply reverse L-type decomposition to $R4$, yielding sub-sequences $L2$. Each sub-sequence $L2\left[i\right]$ is scrambled using $B1\left[i\right],B2\left[i\right],B3\left[i\right]$, producing array $P5$.

Step 6:

Like step 3, assemble $R5$ using $sort2$, and apply spiral reconstruction (determined by $p2$) to form the final scrambled matrix $P2$.

The complete SLJSS scrambling pipeline is summarized in Algorithm 3. A visualization of each step is shown in Figure 9, using a $4\times 6$ grayscale image. The resulting scrambled image demonstrates significant structural obfuscation across rows, columns, and diagonals.

Figure 9. Explanation of the scrambling principle.

Figure 9. Explanation of the scrambling principle.

3.4. Dynamic Codon-Based Multi-RNA Diffusion

To further enhance the sensitivity and complexity of encryption, this section introduces a lightweight yet highly effective diffusion mechanism based on RNA encoding, codon, and arithmetic. Unlike traditional methods that rely solely on numerical diffusion, the proposed strategy leverages bio-inspired structures to achieve high diffusion in a reversible manner.

Algorithm 3: Scrambling Process

3.4.1. Design Background and Motivation

The core idea stems from the intrinsic diversity and combinatorial complexity of RNA sequences. RNA bases—A, C, G, and U—allow for compact quaternary encoding of pixel values, while codon structures (triplets of bases) offer a naturally classified replacement framework. Compared with conventional byte-level arithmetic, the RNA-based approach enables flexible base-level diffusion with biologically inspired substitution logic.

From a design standpoint, the codon substitution step draws on the diversity of amino acid categories, allowing for local transformation within the same semantic group, thus ensuring both randomness and reversibility. After extensive testing, the chosen amino acid classification scheme showed superior diffusion performance compared to alternative groupings. In the subsequent RNA arithmetic phase, five types of operations—addition, subtraction, XOR, multiplication, and customized random operations—are employed. These operations are designed not only for reversibility but also for output diversity. Through careful experimentation, the final operation set and their sequences were optimized to achieve maximum encryption strength while minimizing computational overhead.

3.4.2. Overview of the RNA Encryption Principle

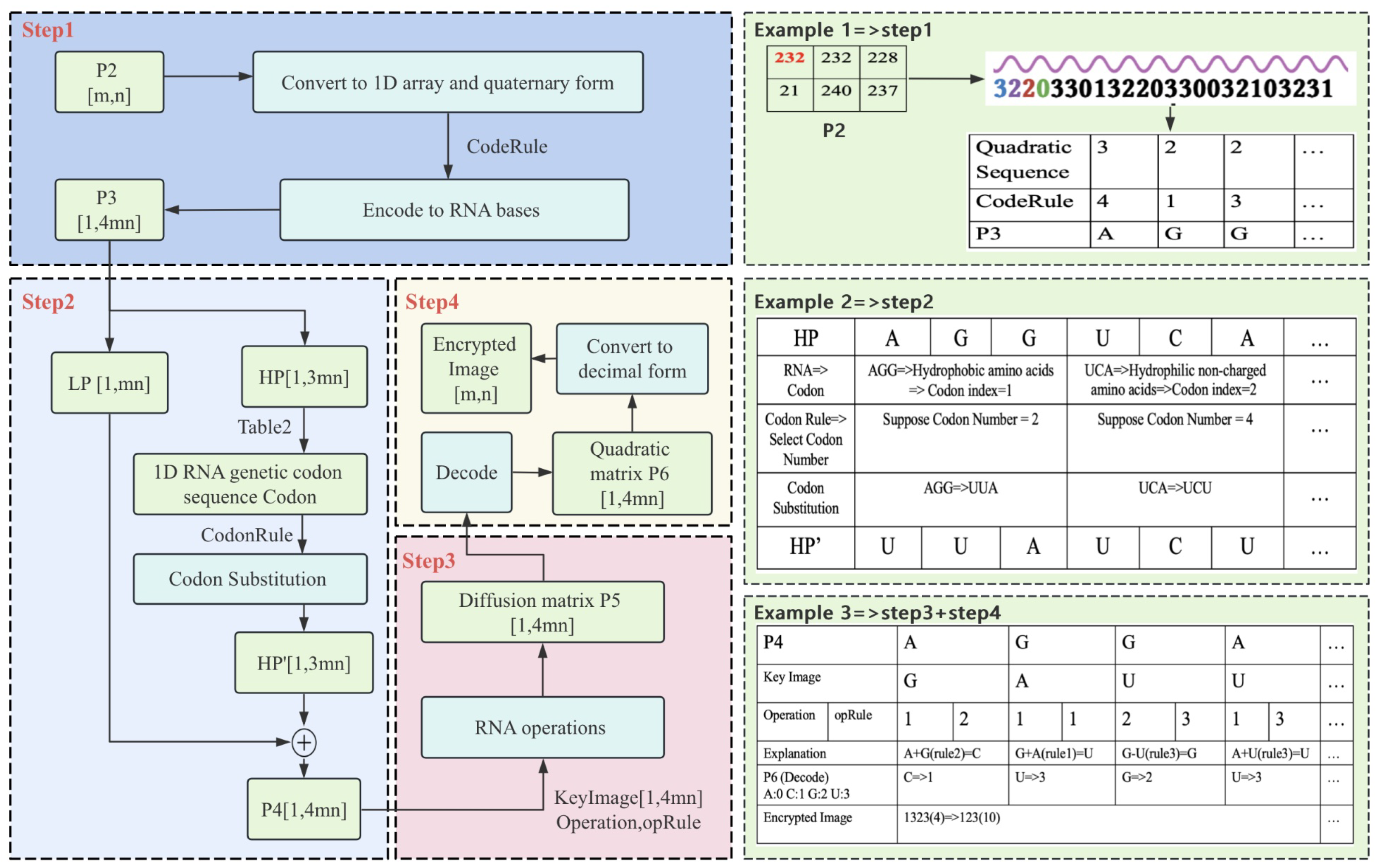
In our algorithm, grayscale pixel values are first converted from decimal to quaternary format and then encoded into RNA base sequences using one of eight encoding rules, as outlined in

Table 1. Encoding and decoding rules of RNA.

Binary	Quaternary	Rule 1	Rule 2	Rule 3	Rule 4	Rule 5	Rule 6	Rule 7	Rule 8
00	0-A	A	A	U	U	C	C	G	G
01	1-C	C	G	C	G	A	U	A	U
10	2-G	G	C	G	C	U	A	U	A
11	3-U	U	U	A	A	G	G	C	C

Note: The binary–quaternary conversion rules are indexed from Rule 1 to Rule 8, where each rule maps quaternary digits to RNA bases.

. For example, a pixel value of 220 in decimal corresponds to 3130 in quaternary. Assuming that the encryption rules are 0-A, 1-C, 2-G, and 3-U, the encryption result is UCUA.

Among the RNA types, mRNA (messenger RNA) is relevant here, as every three consecutive bases form a codon, which maps to specific amino acids during protein synthesis [37,38]. Theoretically, there are $4^3=64$ combinations of three neighboring bases, i.e., corresponding to 64 codons. Meanwhile, according to [45], these 64 kinds of codons can correspond six kinds of amino acids, as shown in

Table 2. Amino acid sequence generation in RNA.

Index	Amino Acid Category	RNA Codons	Number
1	Hydrophobic amino acids	UUU, UUA, UUC, UUG, CUA, CUC, CUG, CUU, CCA, CCC, CCG, CCU, GUA, GUC, GUG, GUU, GCA, GCC, GCG, GCU, GGA, GGC, GGG, GGU, AUA, AUC, AUU, UGG	28
2	Hydrophilic non-charged amino acids	UCA, UCC, UCG, UCU, CAA, CAC, CAG, CAU, ACA, ACC, ACG, ACU, UAU, UAC, AAU, AAC, AGU, AGC	18
3	Positively charged amino acids	CGA, CGC, CGG, CGU, AAA, AAG, AGA, AGG	8
4	Negatively charged amino acids	GAA, GAC, GAG, GAU	4
5	Cysteine	UGU, UGC	2
6	Start codon and Stop codons	UAA, UAG, UGA, AUG	4

. In our codon substitution strategy, each codon in the sequence is first identified by category and then randomly replaced with another codon from the same category to enhance local diffusion.

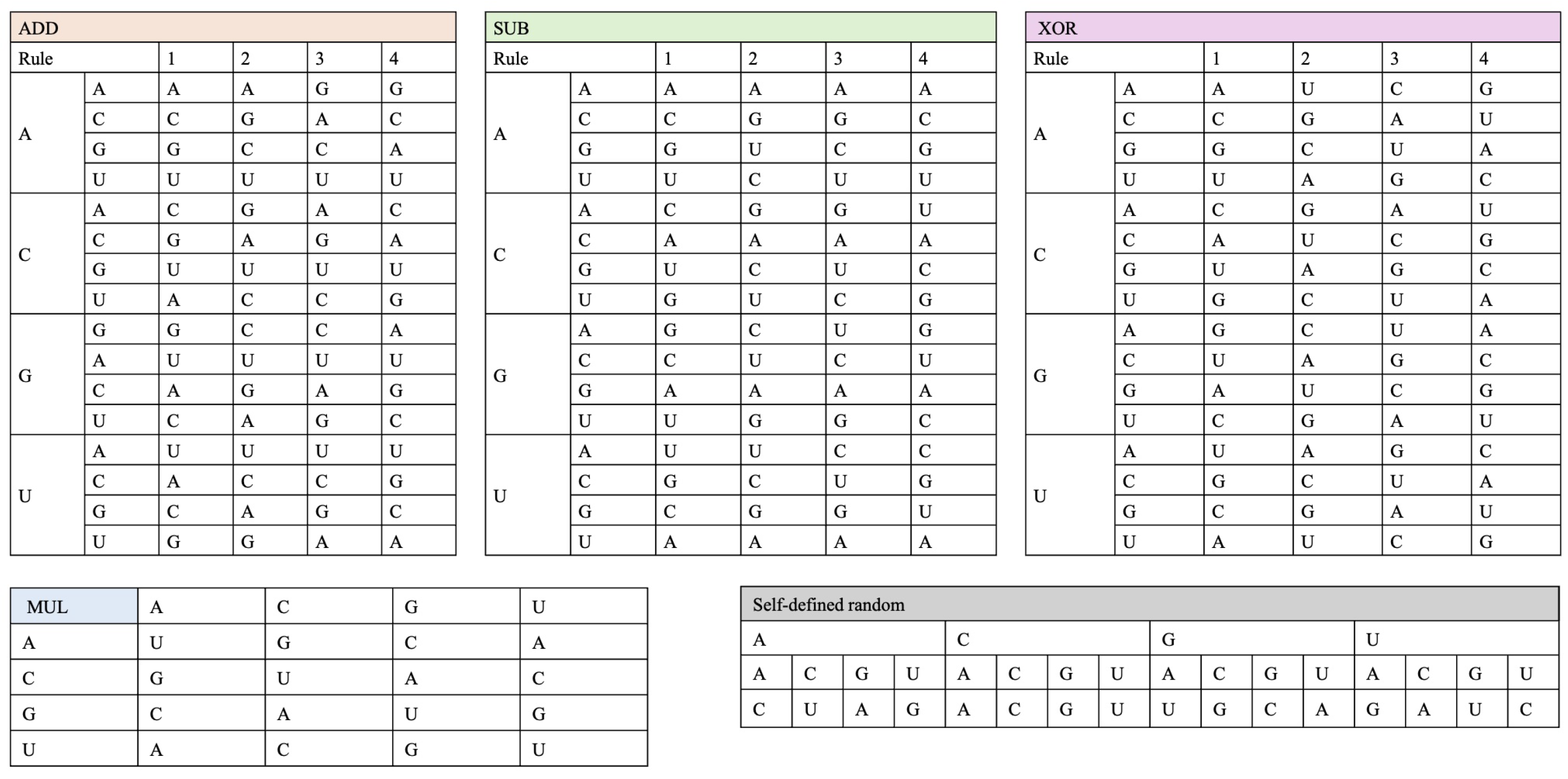
To reinforce pixel diffusion, the substituted RNA sequences undergo base-level arithmetic. Five operations are defined: addition, subtraction, XOR, multiplication, and a custom randomized operation. These operate under quaternary arithmetic rules and depend on the selected encoding. For instance, when base A (encoded as 00) and C (10) are added, the result varies depending on the encoding rule—demonstrating rule-sensitive behavior and enhancing key sensitivity.

Due to overlap across rule outputs, four distinct rule sets were finalized for addition, subtraction, XOR, and one for multiplication. The custom operation was manually defined to improve base diversity and eliminate bias toward any single nucleotide. All operations are designed to be reversible to ensure lossless decryption.

Figure 10 shows the encryption and decryption implementations of custom randomized computation, in which under the encryption rule, base1 represents the base from the encrypted image, base2 represents the base with which the RNA operation is performed, and Result is the result of the operation; under the decryption rule, base1 represents the base from the ciphertext image, and base2 is the same as that used in the ciphertext rule, and Result represents base1 in the ciphertext rule, e.g., A encrypts with A to get C, and C decrypts with A to get A. A complete list of the five computation rules is in Figure 11.

3.4.3. Steps of Diffusion

Scrambling completes the rearrangement of pixel positions in the image; after that, we will apply diffusion operation to the disordered image to change the pixel values of different pixels to realize the effect of diffusing the small changes in the plaintext to the whole ciphertext. In this section, we will use the $CodeRule,CodonRule,KeyImage,opRule,Operation$ computed from the key sequence.

Step 1:

Flatten the scrambled matrix $P2$ into a 1-D array, convert each pixel from decimal to quaternary, and encode it into a corresponding RNA base using $CodeRule$. This yields a 1-D RNA base sequence $P3$ of length $4mn$.

Step 2:

Divide $P3$ into two parts: $LP$ and $HP$, as shown in Equation (15). Codons are formed from every three bases in $HP$, which are then categorized using Table 2 and converted to the RNA genetic codon sequence consisting of codon category indexes. Based on $CodonRule$, a replacement codon is randomly selected within the same category using Equation (16). The updated sequence $H{P}^{\prime }$ is then concatenated with $LP$ to produce the full modified RNA base sequence $P4$. For example, one codon composed of three neighboring amino acids in $HP$ is GAA; then it corresponds to negatively charged amino acids, and the genetic codon sequence corresponds to its index of 4. There are four kinds of codons (GAA, GAC, GAG, and GAU) under this kind of amino acids, and the new codon will be obtained by the CodonRule using the Equation (16), assuming that the select codon number obtained is 2, then GAC will be used to replace GAA.

$$\left\{\begin{array}{cc}\hfill LP& =P_3(1:mn)\hfill \\ \hfill HP& =P_3(mn+1:4mn)\hfill \end{array}\right.$$

(15)

$$\mathrm{SelectCodonNumber}\left(i\right)=\left\{\begin{array}{c}\mathrm{mod}(\mathrm{abs}\left(\mathrm{floor}(\mathrm{CodonRule}\left(i\right)\times {10}^{12})\right),28)+1,\hfill \\ \mathrm{if}\mathrm{Codon}\left(i\right)=1\hfill \\ \mathrm{mod}(\mathrm{abs}\left(\mathrm{floor}(\mathrm{CodonRule}\left(i\right)\times {10}^{12})\right),18)+1,\hfill \\ \mathrm{if}\mathrm{Codon}\left(i\right)=2\hfill \\ \mathrm{mod}(\mathrm{abs}\left(\mathrm{floor}(\mathrm{CodonRule}\left(i\right)\times {10}^{12})\right),8)+1,\hfill \\ \mathrm{if}\mathrm{Codon}\left(i\right)=3\hfill \\ \mathrm{mod}(\mathrm{abs}\left(\mathrm{floor}(\mathrm{CodonRule}\left(i\right)\times {10}^{12})\right),4)+1,\hfill \\ \mathrm{if}\mathrm{Codon}\left(i\right)=4\mathrm{or}6\hfill \\ \mathrm{mod}(\mathrm{abs}\left(\mathrm{floor}(\mathrm{CodonRule}\left(i\right)\times {10}^{12})\right),2)+1,\hfill \\ \mathrm{if}\mathrm{Codon}\left(i\right)=5\hfill \end{array}\right.$$

(16)

Step 3:

The RNA bases of $P4$ will perform RNA operations by one-to-one correspondence with the RNA sequence $KeyImage$ generated by the chaotic system, and the $Operation$ determines the type of operation (addition, subtraction, XOR, multiplication, or customized random operation). Since there are different results when A, C, G, and U represent different values in each operation, the values of A, C, G, and U are determined by the opRule sequence. In short, each base in $P4$ is calculated with the corresponding base in the $KeyImage$ according to the set operation type and the value to get a new value, which results in the diffusion matrix P5, as shown in the following equation.

$$P_5\left(i\right)=\left\{\begin{array}{cc}\mathrm{ADD}(P_4\left(i\right)+1,\mathrm{KeyImage}\left(i\right)+1,\mathrm{opRule}\left(i\right)),\hfill & \hfill \mathrm{if}\mathrm{Operation}\left(i\right)=1\\ \mathrm{SUB}(P_4\left(i\right)+1,\mathrm{KeyImage}\left(i\right)+1,\mathrm{opRule}\left(i\right)),\hfill & \hfill \mathrm{if}\mathrm{Operation}\left(i\right)=2\\ \mathrm{XOR}(P_4\left(i\right)+1,\mathrm{KeyImage}\left(i\right)+1,\mathrm{opRule}\left(i\right)),\hfill & \hfill \mathrm{if}\mathrm{Operation}\left(i\right)=3\\ \mathrm{MUL}(P_4\left(i\right)+1,\mathrm{KeyImage}\left(i\right)+1),\hfill & \hfill \mathrm{if}\mathrm{Operation}\left(i\right)=4\\ \mathrm{RANDOM}(P_4\left(i\right)+1,\mathrm{KeyImage}\left(i\right)+1),\hfill & \hfill \mathrm{if}\mathrm{Operation}\left(i\right)=5\end{array}\right.$$

(17)

Step 4:

In order to simplify the arithmetic process, the diffusion matrix $P5$ is decoded into the quadratic matrix $P6$ according to A-0, C-1, G-2, and U-3, and finally the quadratic image $P6$ is converted into decimal form to obtain the final encrypted image $EncryptedImage$.

Algorithm 4 introduces the key steps in the diffusion. $RNAencode\left(\right),RNAdecode\left(\right)$ can realize the interconversion of quadrature numbers and RNA sequences, $Dec2Qua\left(\right)$, $Qua2Dec\left(\right)$ can realize the interconversion of decimal numbers and quadrature numbers, and the calculation results of $ADD\left(\right),SUB\left(\right),XOR\left(\right),MUL\left(\right),RANDOM\left(\right)$ are all in accordance with the arithmetic rules shown in Figure 11. Figure 12 visualizes the flow information of the diffusion module.

Algorithm 4: Diffusion Process Based on RNA Operations

3.5. Decryption

The proposed encryption algorithm is fully reversible, and the decryption process involves executing the inverse of each encryption step to recover the original plaintext image.

Step 1:

Input the encrypted image $EncryptedImage$ and key, and calculate the initial values for the chaotic system used in encryption.

Step 2:

Regenerate the chaotic sequences by performing the same iterations described in Section 3.2. This includes the generation of all key sequences used in scrambling and diffusion.

Step 3:

RNA encoding, inverse of multiple base operations, codon inverse substitution, and RNA dynamic decoding are performed sequentially on the $EncryptedImage$ to eliminate the effect of RNA-level diffusion and to obtain the image matrix $P2$ without diffusion effect.

Step 4:

The same spiral sequence deconstruction, inverse Josephs scrambling, and L-type decomposition are sequentially performed on $P2$ according to the symmetric structure, and the plaintext image I without scrambling effect can be obtained.

After completing the above steps, the original plaintext image is fully restored without any loss. This demonstrates the proposed algorithm’s reversibility and robustness.

4. Experimental Results and Security Analysis

4.1. Simulation Results

In this section, various types of medical images were used to test the security and effectiveness of the proposed encryption algorithm. The images were mainly sourced from two open-access and publicly available databases: MedPix and COVID-CT [42,46], encompassing CT, X-ray, ultrasound, and COVID-specific images with varying sizes and content. All experiments were conducted using MATLAB R2024a on a 64-bit MacBook Pro with an Apple M4 CPU, 16 GB RAM, 512 GB SSD, and macOS Sequoia 15.2.

As shown in Figure 13, the encrypted images reveal no perceptible visual information about the original plaintext images, while the decrypted images perfectly match the original inputs. This initial observation supports the visual effectiveness of the proposed algorithm.

We further evaluate the algorithm through key security, statistical analysis, information entropy, differential attack resistance, robustness, and time complexity.

4.2. Key Security Analysis

A robust encryption algorithm must offer a sufficiently large key space and exhibit high key sensitivity. When the key space exceeds $2^{100}$, the system can resist brute-force attacks [21]. In this work, the encrypted image could be decrypted with the secret key including $c_i(1\le i\le 7)$. Assuming a precision of ${10}^{15}$ for double-precision values, the total key space is approximately ${10}^{15\times 7}={10}^{105}\approx 2^{349}\gg 2^{100}$, satisfying the required threshold.

In addition, key sensitivity is another important indicator of key security, which means that a small change in the key will bring completely different encryption and decryption results. In order to visually verify the key sensitivity of the encryption algorithm, we apply the component-wise perturbation analysis to rigorously evaluate our algorithm [47]. In details, for each component, a minimal perturbation (${10}^{-12}$) causes a significant ciphertext difference and the ciphertext differences are calculated to be significant as well, which proves that our algorithm possesses excellent key sensitivity. The result is shown in Figure 14.

4.3. Statistical Analysis

4.3.1. Histogram Analysis

Image histograms visualize the distribution of pixel intensities. An ideal encrypted image should exhibit a uniform histogram that significantly differs from the original. This property helps resist statistical attacks. As shown in Figure 15, the histograms of the encrypted images are uniform and distinct from their plaintext counterparts [21].

To quantitatively assess histogram uniformity, we perform a chi-square (${\chi }^2$) test using multiple encrypted outputs. The test enables the comparison of the difference between the actual encrypted image and the expected uniformly distributed histogram, if the chi-square statistic is large, it means that the observed histogram is significantly different from the expected result, and vice versa, it means that the actual result is in accordance with the expected requirements.

The calculation method is as follows:

$${\chi }^2=\sum _{i=1}^{256}{\displaystyle \frac{{(O_i-EV)}^2}{EV}}.$$

(18)

where $O_i$ is the observed frequency for gray level i, and $EV=O/256$ is the expected frequency. With a significance level $\alpha =0.05$ and freedom of degree $d=255$, the critical value is ${\chi }_{(}{\alpha ,d)}^2=293.2478$.

Table 3. Results of ${\chi }^2$ test for different medical images.

Image	CT-2	X-Ray-2	Ultrasound	COVID-00001
${\chi }^2$ value	262.8449	276.6258	238.7735	261.7332

shows the chi-square values of the encrypted image, which are all less than 293, proving that the histogram of the encrypted image meets the requirements [26].

4.3.2. Correlation Analysis

Correlation reflects the relationship between adjacent pixels in an image. In medical images, adjacent pixels tend to be highly similar, so their correlation is usually close to 1 [27]. Effective encryption should significantly reduce this correlation, making them resistant to statistical analysis attacks. We randomly select 5000 pairs of adjacent pixels in horizontal, vertical, and diagonal directions and calculate their correlation using the following equation:

$$\left\{\begin{array}{ccc}{r}_{xy}\hfill & =& {\displaystyle \frac{cov(x,y)}{\sqrt{D\left(x\right)}·\sqrt{D\left(y\right)}}},\hfill \\ cov(x,y)\hfill & =& {\displaystyle \frac{1}{N}\sum _{i=1}^N(x_i-E\left(x\right))(y_i-E\left(y\right))},\hfill \\ D\left(x\right)\hfill & =& {\displaystyle \frac{1}{N}\sum _{i=1}^N{(x_i-E\left(x\right))}^2},\hfill \\ E\left(x\right)\hfill & =& {\displaystyle \frac{1}{N}\sum _{i=1}^N{x}_i},\hfill \end{array}\right.$$

(19)

where N represents the number of pixel pairs selected, x and y are two neighboring pixel values, $E\left(x\right)$ represents the mean, $D\left(x\right)$ represents the variance, and $cov(x,y)$ represents the covariance.

Figure 16 illustrates the correlation distribution between adjacent pixels before and after encryption. In subplots (b), (c), (d), (f), (g), and (h), the x-axis denotes the pixel gray value at location $(x,y)$, while the y-axis represents the gray value of neighboring pixels: (b) and (f) correspond to horizontal correlation with $(x,y+1)$, (c) and (g) to vertical correlation with $(x+1,y)$, and (d) and (h) to diagonal correlation with $(x+1,y+1)$. As shown, the plaintext image exhibits a strong linear clustering along the diagonal, reflecting high correlation between adjacent pixels. In contrast, the encrypted image shows a nearly uniform and dispersed distribution, indicating the effectiveness of the proposed algorithm in eliminating pixel correlation. Meanwhile,

Table 4. Correlation coefficients of original and encrypted images in horizontal, vertical, and diagonal directions.

Image	Original Image			Encrypted Image
	Horizontal	Vertical	Diagonal	Horizontal	Vertical	Diagonal
CT-1	0.9771	0.9672	0.9540	0.0007	0.0005	−0.0007
CT-2	0.9871	0.9921	0.9821	−0.0014	0.0001	$3.96\times {10}^{-5}$
Xray-1	0.9913	0.9924	0.9875	0.0006	−0.0018	$7.11\times {10}^{-6}$
Xray-2	0.9739	0.9943	0.9724	−0.0004	0.0001	0.0004
Ultrasound	0.9768	0.9771	0.9620	−0.0002	−0.0002	−0.0006
COVID-00001	0.9715	0.9730	0.9729	−0.0001	−0.0004	0.0001

quantitatively analyzes the correlation data of the test images. The correlation of all the test images before encryption is close to 1; however, after encryption the correlation decreases to near 0.

4.3.3. Shannon Entropy Analysis

Shannon Entropy quantifies the uncertainty in an image. The closer the entropy is to 8 for 8-bit grayscale images, the better the encryption [27,48]. It is calculated as follows:

$$H\left(m\right)=-\sum _{i=0}^{2^N-1}p\left(m_i\right){log}_2{\displaystyle \frac{1}{p\left(m_i\right)}},$$

(20)

where N denotes the gray level, and $p\left(m_i\right)$ represents the probability of a pixel having gray level $m_i$.

In addition to global entropy, inspired by the method in [48], we also adopt Local Shannon Entropy (LSE) to further evaluate the randomness and information dispersion within local blocks of the encrypted images.

Table 5. Shannon entropy and differential attack analysis of various medical images.

Image (Size)	Global Entropy (Plain)	Global Entropy (Cipher)	Local Entropy (Cipher)	NPCR (%)	UACI (%)
CT-1 (383 × 453)	6.0182	7.9989	7.9152	99.6073	33.4634
CT-2 (980 × 980)	3.9302	7.9998	7.9071	99.6103	33.4568
Xray-1 (659 × 1019)	6.5317	7.9997	7.9050	99.6102	33.4832
Xray-2 (640 × 932)	4.5116	7.9997	7.8967	99.6143	33.4785
Ultrasound (714 × 511)	6.2557	7.9995	7.9069	99.6059	33.4746
COVID-00001 (1151 × 972)	6.6640	7.9998	7.9182	99.6071	33.4785

provides both global and local entropy values for the test images. It can be observed that the Shannon entropy of the encrypted images is close to the theoretical maximum, which significantly mitigates the low uncertainty and information leakage issues in the original images.

4.4. Differential Attack Analysis

Differential attack is a common cryptanalysis method that exploits the sensitivity of ciphertext to slight changes in plaintext. A secure image encryption algorithm should ensure that even a 1-bit modification in the plaintext results in significant and unpredictable changes in the ciphertext. This resistance is typically evaluated using two widely accepted metrics: the Number of Pixels Change Rate (NPCR) and the Unified Average Changing Intensity (UACI), calculated as follows [47]:

$$\left\{\begin{array}{cc}\hfill \mathrm{NPCR}& ={\displaystyle \frac{1}{M\times N}}\sum _{i=1}^M\sum _{j=1}^{N}D(i,j)\times 100\%,\hfill \\ \hfill \mathrm{UACI}& ={\displaystyle \frac{1}{M\times N}}\left(\sum _{i=1}^M\sum _{j=1}^N{\displaystyle \frac{\left|c_1(i,j)-c_2(i,j)\right|}{255}}\right)\times 100\%,\hfill \\ \hfill D(i,j)& =\left\{\begin{array}{cc}0,\hfill & \mathrm{if}{c}_1(i,j)=c_2(i,j),\hfill \\ 1,\hfill & \mathrm{if}{c}_1(i,j)\ne c_2(i,j),\hfill \end{array}\right.\hfill \end{array}\right.$$

(21)

Here, $M\times N$ is the image size, and $c_1(i,j),c_2(i,j)$ represent pixel values at the same location in two ciphertext images whose corresponding plaintexts differ by one bit. Ideally, for 8-bit images, NPCR and UACI are expected to be around 99.6094% and 33.4635%, respectively.

To improve statistical reliability, we repeat each test 50 times and report the averaged results. Table 5 presents the NPCR and UACI values across multiple real-world medical image datasets.

To further enhance the rigor of evaluation, we compare our algorithm’s NPCR and UACI scores with the theoretical critical values proposed in [48], as shown in

Table 6. Comparison of NPCR and UACI values with theoretical critical thresholds at 0.05 level.

Image Size	NPCR (Ours)	NPCR Critical Value	UACI (Ours)	UACI Acceptable Range
256 × 256	99.6490%	${\mathcal{N}}_{0.05}^{\ast }=99.5693\%$	33.5112%	$[33.2824\%,33.6447\%]$
512 × 512	99.6162%	${\mathcal{N}}_{0.05}^{\ast }=99.5893\%$	33.4345%	$[33.3730\%,33.5541\%]$
1024 × 1024	99.6121%	${\mathcal{N}}_{0.05}^{\ast }=99.5994\%$	33.4717%	$[33.4183\%,33.5088\%]$

. For instance, at the 0.05 significance level, the critical value of NPCR for a 256 × 256 image is 99.5693%, and the acceptable UACI range is [33.2824%, 33.6447%]. Our algorithm’s performance consistently meets or exceeds these thresholds, demonstrating statistically significant resistance to differential attacks.

In summary, both empirical evaluations and statistical significance tests confirm that the proposed algorithm exhibits strong robustness against differential attacks, with stable performance across different image types and resolutions.

4.5. Robustness Analysis

In the security analysis of image encryption algorithms, robustness analysis is an important part. When the attacker cannot decipher the target image, he will hinder the transmission of information by interfering with the image content. Robustness, on the other hand, refers to the ability of an encryption algorithm to maintain the security integrity of critical information in the face of various image cuts, distortions, scrambling, tampering, and other common problems in network transmission [21]. Here, we will verify whether the algorithm has good robustness by simulating noise interference as well as partial information loss on encrypted images and analyzing whether it can recover the key parts of the original image. Figure 17a–d show the test results when 10% and 30% pretzel noise is applied to the encrypted image, which illustrates that even with the noise up to 30%, the key information in the original data can still be restored. Figure 18a–d shows the simulation results with different degrees of image loss, and it can be observed that when the encrypted image is sliced by 25% or even 50%, the key information of the original image can still be recognized after decryption. The above analysis shows that the algorithm has good robustness and high resistance to cropping attacks and noise attacks.

4.6. Time Complexity Analysis

In addition to the evaluation of security performance, the time complexity of an encryption algorithm is likewise a key metric for considering the feasibility of the algorithm. It is worth mentioning that many researchers also choose encryption time and decryption time as a quantitative index to measure the time effectiveness of the algorithm [11]. However, considering the diversity of hardware and software platforms, the way of code writing and the selection of encrypted image content, etc., all of which affect the specific running time of the algorithms, it is difficult to ensure that we can compare the differences in time consumed from the strict consistency conditions. However, this thesis still calculates the encryption and decryption times for graphics of different sizes as a reference, and

Table 7. Speed analysis of encryption and decryption (unit: second).

Image Size	Encryption Time (s)	Decryption Time (s)
180 × 180	0.0466	0.0313
256 × 256	0.0964	0.0644
512 × 512	0.4121	0.2913
980 × 980	1.7232	1.2596

shows the corresponding results.

Besides that, we will focus on analyzing the time efficiency by relying only on the time complexity of the algorithm itself. The main operations of this encryption algorithm include chaotic sequence generation, L-shaped hierarchical Josephus scrambling, and image diffusion based on RNA operations. First, we assume that the size of the test image is $m\times n$; in the chaotic sequence generation phase, the memristor chaotic system requires $4mn$ iterations; in the scrambling phase, the main computational consumption occurs in the hierarchical scrambling and ranks replacement, respectively, with a time complexity of $2mn+m+n$; and in the diffusion phase, the time complexity of the codon substitution and the RNA operation are $mn$ and $4mn$, respectively. In summary, the algorithm’s total time complexity is $4mn+2mn+m+n+mn+4mn\approx 11mn$.

Table 8. Computation complexity comparison of different image encryption algorithms.

Algorithm	Ref. [3]	Ref. [35]	Ref. [37]	Ours
Complexity	$\mathcal{O}\left(16MN\right)$	$\mathcal{O}\left(22MN\right)$	$\mathcal{O}\left(39MN\right)$	$\mathcal{O}\left(11MN\right)$

shows that our algorithm has low computational complexity by comparing with [3,46,49].

4.7. Comparative Performance Analysis

In this section, we will comprehensively compare the performance metrics of various advanced encryption algorithms. Considering the differences in the test images of different medical image encryption algorithms, we choose to use the most popular 512 × 512 Lena grayscale image as the test object for comparison and analysis.

Table 9. Comparative analysis of the proposed algorithm and existing methods.

Scheme	H	V	D	Entropy	NPCR (%)	UACI (%)	Key Space
Proposed	$-0.0001$	$-4.407\times {10}^{-5}$	$4.931\times {10}^{-5}$	7.9993	99.6091	33.4765	$2^{349}$
Ref. [3]	$-0.0026$	$-0.0033$	$0.0004$	7.9994	99.6167	33.4589	$2^{318}$
Ref. [50]	$-0.0001$	$0.0006$	$-0.0016$	7.9992	99.6102	33.4465	$2^{256}$
Ref. [51]	$0.0015$	$0.0003$	$-0.0038$	7.9994	99.6124	33.4474	$2^{212}$
Ref. [45]	$-0.0017$	$-0.0004$	$0.0028$	7.9976	99.6002	33.4592	${10}^{140}$

lists the relevant data of different algorithms’ encryption performance metrics, including the correlation, the information entropy, the NPCR, the UACI, and the size of the key space used for the analysis of differential attacks. It can be observed that, compared with other algorithms, the ciphertext image generated by our algorithm exhibits lower correlation, which demonstrates a notable improvement in security. Furthermore, the NPCR value is close to the theoretical value (99.6094%), and the UACI value is also close to its theoretical ideal (33.4635%). Although the information entropy and key space are weakly different compared to other algorithms, their data can still be considered as reasonable values close to the ideal results. In summary, the superiority and feasibility of our proposed encryption algorithm are further verified.

5. Conclusions

This paper presents a secure and efficient grayscale medical image encryption algorithm tailored to the characteristics of medical images, such as large data volume, high inter-pixel correlation, and strong structural redundancy.

The proposed framework integrates a high-dimensional 5-D memristor chaotic system with two specialized modules: Symmetric L-type Josephus Spiral Scrambling (SLJSS) and Dynamic Codon-based Multi-RNA Diffusion (DCMRD). The chaotic system, based on the HP memristor model, generates highly sensitive and ergodic sequences, as confirmed by bifurcation diagrams, Lyapunov exponents, and histogram analysis. SLJSS ensures global and diagonal pixel decorrelation through hierarchical L-shaped partitioning and symmetric spiral scrambling, while DCMRD enhances diffusion through codon substitution and multi-rule RNA operations.

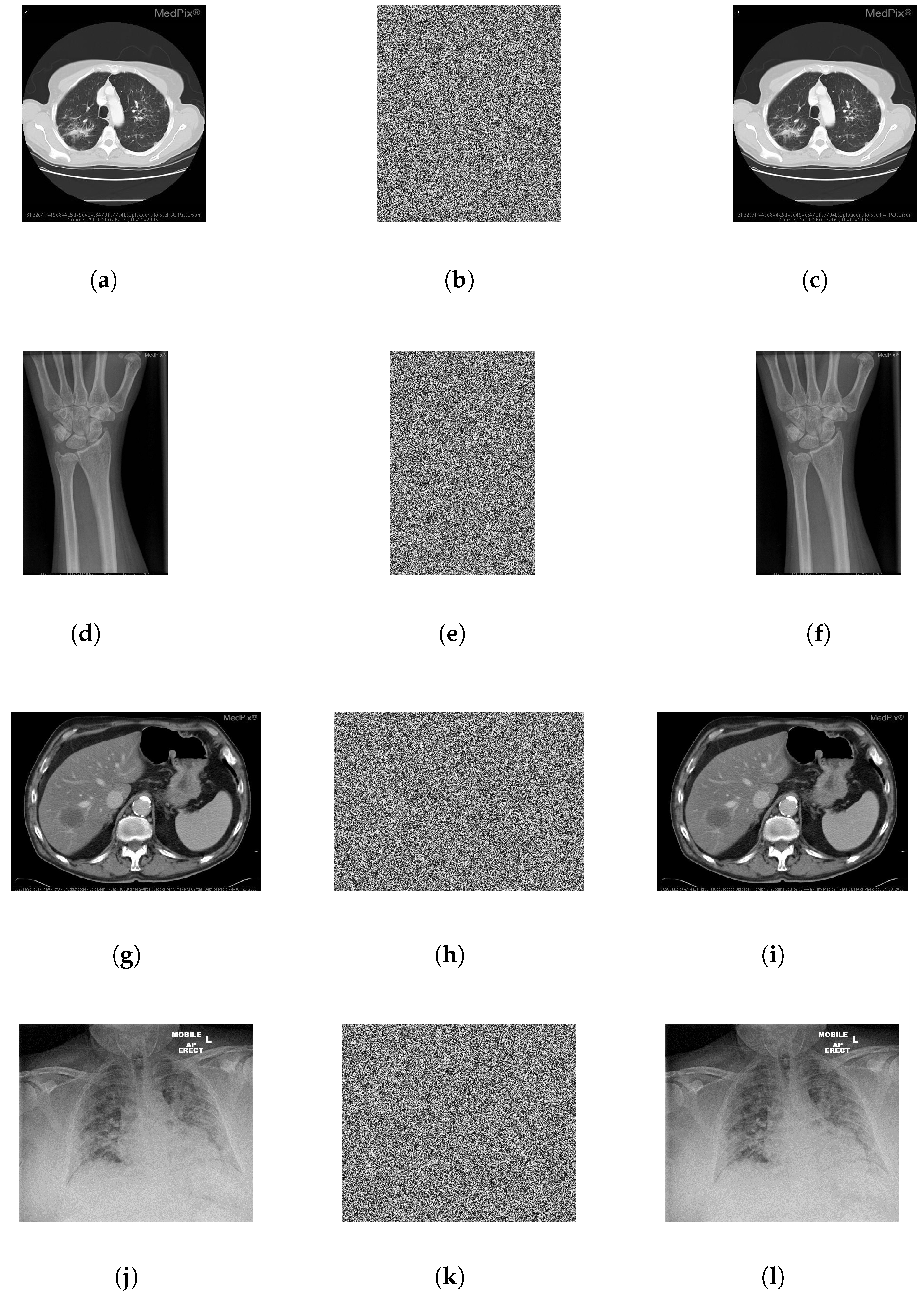
Simulation results demonstrate that the proposed method achieves near-ideal entropy (e.g., 7.9992), low pixel correlation (e.g., 0.0043), strong robustness (NPCR: 99.62%, UACI: 33.45%), and fast processing time (e.g., 0.0964 s encryption for 256 × 256 images). The algorithm exhibits strong resistance to statistical and differential attacks and shows stable performance across medical and natural image datasets, validating its general applicability.

In conclusion, the proposed method offers a lightweight, high-security solution for medical image protection, with potential applications in telemedicine, image archiving, and privacy-preserving diagnostics. Future work will explore hardware acceleration, adaptation to 3-D or multi-modal medical images, and integration with compression–encryption and federated learning frameworks.